A) Principle of operation

The architecture of the DPA [Reference Kim, Kim, Kim and Ha8] exploits the mechanism of active load modulation, which is provided by the peak device over the main device. Indeed, in the so called back-off state the main device output termination at fundamental frequency is 2·R _opt , where R _opt is the optimum load at peak power for the main device, at its intrinsic current generator. This termination is provided by transforming, with an impedance inverter, the termination R _opt /2 seen at the summing node toward the external load. In conventional designs, the impedance inverter is implemented by a QWTL, with characteristic impedance equal to R _opt . When driven in the saturated state, the peak device provides an additional current into the output termination, thus making the effective main device's termination decrease from 2·R _opt to R _opt . In this state, the main device is saturated and its output voltage remains constant through the entire region. In saturation, the main device can be modeled by a voltage source and its output impedance is thus transformed into an open circuit at the summing node, as shown in Fig. 1.

Fig. 1. Schematic representation of the RF power devices combination at the output of the DPA operating in the saturation state.

The conventional design approaches consider the peak device biased in class-C operation to maintain its off state in the entire back-off DPA state. Despite this bias difference, in principle, the two devices at peak power would drive the same fundamental component current; thus, at a first analysis, the same output termination would be required and the same power would be generated by the two devices. In practice, due to the reduced conduction angle of the peak device, a reduced current at fundamental is generated, so a lower load termination is required for the peak device [Reference Kang, Kim, Cho, Park, Kim and Kim17]. Thus, this justifies the peak device matching network shown in Fig. 1. In addition, the latter network ensures that the peak device provides its due current into the summing node and thus enables the correct load modulation.

The described DPA operation principle exhibits at least two limiting factors for its effective exploitation. The first limiting factor consists in the inherent behavior of the QWTL impedance inverter, which significantly limits the bandwidth at back-off (transformation from R _opt /2 to 2·R _opt ). The second consists in the interaction between the QWTL and the parasitic capacitors, which decreases the bandwidth for both back-off and peak power states; this becomes significant for DPA with large high-power devices. These limiting factors are quite well addressed in the literature [Reference Qureshi, Li, Neo, van Rijs, Blednov and de Vreede16], and the proposed solutions consider the compensation of the RF device's output capacitor and new topologies of the output networks [Reference Piazzon, Giofre, Colantonio and Giannini11, Reference Yu-Ting, Annes, Bokatius, Kravavac and Tucker18]. Yet in all these cases the expected fractional bandwidth for continuous wave (CW) signals at DPA back-off is hardly larger than 28%. In order to increase the bandwidth, new approaches to the design of the output combiner were introduced in the literature [Reference Qureshi, Sneijers, Keenan, de Vreede and van Rijs19]. These approaches are aimed at increasing the bandwidth of the impedance inverter and concentrating the efforts on the operation of the DPA at back-off. The completely different approach proposed in [Reference Gustafsson, Andersson and Fager20], instead considers to design the impedance inverter with a characteristic impedance equal to R _opt , thus making the DPA operation at back-off independent of frequency. The approach requires a proper amplitude and phase control of both the main and peak driving, which in [Reference Gustafsson, Andersson and Fager20] was implemented by an additional vector modulator.

B) DPA limitation to broadband modulated signals operation

We evaluate now the expected operative bandwidth of an ideal DPA, based on a conventional QWTL impedance inverter, as a function of exciting modulated signal peak-to-average power ratio (PAPR).

Let us assume the schematic representation of the DPA output network in Fig. 2, where the main and peak devices are represented by two current sources having fundamental output currents I _m and I _p that depend on the input voltage drive level 0 ≤ ξ ≤ 1,

(1) $${I_m} = \xi \displaystyle{{{I_{max}}} \over 2},$$

(2) $${I_p} = \left\{ {\matrix{ \hskip-42pt0 & {{\rm 0} \le \xi \le {\xi _{bo}}} \cr {\displaystyle{{{I_{max}}} \over 2}\displaystyle{{\xi - {\xi _{bo}}} \over {{\xi _{bo}}}}} & {{\xi _{bo}} \le \xi \le 1} \cr } } \right.,$$

where ξ _bo  = 0.5 is the drive level at the onset of the peak device and Imax is the maximum current of both the main and peak devices, assumed to be equal. The voltage at the summing node (node P in Fig. 2) can be evaluated by the 2-port analysis between the nodes “M” and “P” by considering the QWTL characterized by its Z-parameter matrix [Reference Qureshi, Li, Neo, van Rijs, Blednov and de Vreede16]. In order to calculate the DPA efficiency, we first calculate the output power, which after a simple manipulation and using (1) and (2) reads

(3) $${P_{out}} = \displaystyle{{V_{ds}^2} \over {{R_{opt}}}} \cdot \left\{ {\matrix{ {\displaystyle{{{{(\xi \cdot {\xi _{bo}})}^2}} \over {{{\cos} ^2}(\bar f) + {\xi _{bo}}{{\sin} ^2}(\bar f)}}{\rm, 0} \le \xi \le {\xi _{bo}}} \cr {\displaystyle{{{{\left \vert \matrix{\xi {\xi _{bo}} + (\xi - {\xi _{bo}}){\cos ^2}(\bar f) \hfill \cr \quad (\cos (\bar f) - j\sin (\bar f)) \hfill} \right \vert} ^2}} \over {{{\cos} ^2}(\bar f) + {\xi _{bo}}{{\sin} ^2}(\bar f)}}{\rm,} {\xi _{bo}} \lt \xi \le 1} \cr}} \right.,$$

where the normalized frequency $\bar f$ is defined as πf/2f ₀ with the design center frequency. The (3) is valid under the assumption of QWTL designed at f ₀ with characteristic impedance Z _c  = R _opt and back-off drive level ξ _bo  = 0.5. The DC power consumption under the simplifying assumption that the peak device operates in mild class-C reads

(4) $${P_{DC}} = \displaystyle{{{V_{ds}}( \vert {I_m} \vert + \vert {I_p} \vert )} \over \pi}. $$

Combining (3) and (4), we can finally derive the DPA DE, DE = P _out /P _DC, which is drawn in Fig. 3 as a function of the drive level ξ, and the fractional bandwidth |f − f ₀|/f ₀. From the figure, we observe that the curves spread more at back-off (i.e. ξ _bo  = 0.5), thus determining the worst case for the DE bandwidth; in this state, only at center frequency and for the CW signal at the back-off level, the DPA exhibits the peak DE. Instead, at peak power all the curves converge at the peak DE, thus determining a significant contribution for those signals having low PAPR.

Fig. 2. Schematic representation of the DPA output network; the main and peak devices are represented by two ideal controlled current sources.

Fig. 3. DE for an ideal DPA implemented with a QWTL impedance inverter designed at f ₀ with Z _c  = R _opt , as a function of the fractional bandwidth |f − f ₀|/f ₀, and drive level ξ.

Let us now assume a drive signal having a level probability distribution function characterized by the Rayleigh distribution

(5) $$pdf(\xi ) = \displaystyle{\xi \over {{\sigma ^2}}}{e^{ - ({\xi ^2}/2{\sigma ^2})}},$$

where the parameter σ is related to the linear PAPR by $\sigma = {\rm PAPR} \cdot \sqrt {2/\pi} $ . By integrating the curves in Fig. 3 weighted by (5), for the same signal peak power, we derive the average DE as a function of the fractional bandwidth,

(6) $$\left\langle {DE} \right\rangle = \int\limits_0^1 {DE(\xi, \overline f ) \cdot pdf(\xi, \!\sigma )} \cdot d\xi. $$

The results of the numerical integration of (6) are shown in Fig. 4. In the same figure we include for comparison the result of the calculated average DE for a CW signal at back-off (i.e. the input level of the onset for the peak device), as a function of the normalized frequency, f/f ₀. From the data we can calculate the bandwidth following the accepted criteria of 10% relative average DE drop at the band edge. The calculated bandwidth along with the maximum average DE is reported in Table 1. The bandwidth exhibits a significant reduction moving from PAPR = 3 dB to PAPR = 6 dB, while for higher PAPR it remains almost constant. Differently, the maximum of the average DE at the nominal design frequency, f ₀, shows an almost linearly decreasing trend as the PAPR increases. The data relative to the CW signal at back-off confirm that the DPA DE bandwidth equals the QWTL bandwidth.

Fig. 4. Average DE performance for an ideal DPA, versus normalized frequency f/f ₀, for modulated signals at different peak-to-average ratio (PAR) and same peak power. For comparison it is also reported the case of CW signal at back-off power.

Table 1. Bandwidth and average DE for ideal DPA.

It is worth highlighting that the results in Table 1 consider ideal devices, and we discuss hereinafter that the devices' output capacitance reduces significantly the bandwidth of the impedance inverter, also when a wideband absorbing technique is adopted [Reference Qureshi, Li, Neo, van Rijs, Blednov and de Vreede16]. The proper absorption of the main device parasitic is discussed in the next section.

A) Synthetic transmission lines properties

The synthesis of the proposed new wideband impedance inverter by transmission lines of proper lengths and shunt lumped elements is straightforward. With reference to Fig. 5, let us consider respectively Z ₀ and θ ₀ the characteristic impedance and the electrical length of a reference transmission line, and the corresponding transformed pi-network, composed of a transmission line having the characteristic impedance and the electrical length respectively Z ₁ and θ ₁, and being B _S the shunt susceptance connected at both its ends. The ABCD matrix of the reference transmission line is

(7) $$\left \vert {\matrix{ {\cos ({\theta _0})} & {j{Z_0}\sin ({\theta _0})} \cr {j{Y_0}\sin ({\theta _0})} & {\cos ({\theta _0})} \cr}} \right \vert, $$

while the corresponding one associated to the pi-network is

(8) $$\left \vert {\matrix{ {\cos {\theta _1} - {Z_1}{B_S}\sin {\theta _1}} & {j{Z_1}\sin {\theta _1}} \cr {j\sin {\theta _1}(1 - {{({Z_1}{B_S})}^2} + 2{Z_1}{B_S}\cot {\theta _1})} & {\cos {\theta _1} - {Z_1}{B_S}\sin {\theta _1}} \cr}} \right \vert, $$

assuming B _S  = ω C _p , with C _p the parasitic capacitor to be absorbed, between these parameters the following relations hold:

(9) $$\omega \cdot {C_P} = \displaystyle{{\cos ({\theta _0}) - \cos ({\theta _1})} \over {{Z_0}\cos ({\theta _1})}},$$

(10) $${Z_1} = {Z_0}\displaystyle{{\sin ({\theta _0})} \over {\sin ({\theta _1})}}.$$

Fig. 5. Transmission line equivalence with a pi-network.

From (9) we see that for large capacitance values we get very short line lengths with corresponding high characteristic impedance. This combination of parameters makes the transmission line synthesis impractical. Furthermore, the equivalence is exact only at a single frequency, making the bandwidth of the loaded line narrower than the original unloaded line. From the above considerations, it results that in practical applications the device technology determines the maximum RF bandwidth. In particular, the ratio between the output capacitance and peak power is a figure of merit of several device suppliers in GaN and LDMOS technologies. For GaN technology this figure is in the range of 0.05 pF/W, while for LDMOS-based 50 V technology this figure ranges about 0.14 pF/W [Reference Ahmed21]. Thus, as expected, GaN technology provides the conditions for the wider bandwidth [Reference Chuanhui, Wensheng, Shihai, Chaojin and Youxi12]. Nevertheless, the LDMOS technology is still the best suited for high power at the lower frequency band, mainly due to the high ruggedness, low thermal resistance and good efficiency performance. The latter consideration motivates the effort in the development of broadband DPAs for DVB-T in the UHF band [Reference Qureshi, Sneijers, Keenan, de Vreede and van Rijs19].

For the design of the impedance inverter, we introduce a new concept that does not require complex multi-objective optimization and allows the impedance inverter function across a bandwidth that is wider than in ideal QWTL. In the treatment that follows, the parasitics are considered to be constant across the entire signal dynamic range, although not necessarily identical for the two devices. We can rewrite (9) in the more general form

(11) $${b_S} = \displaystyle{{{B_S}} \over {{Y_0}}} = \displaystyle{{\cos ({\theta _0}) - \cos ({\theta _1})} \over {\cos ({\theta _1})}},$$

where b _S represents the shunt element at the ends of the transmission line. From (11) it results that if θ ₀ < θ ₁, i.e. when the line is shortened, the shunt element is positive, meaning a capacitive susceptance, while the case of elongation, θ ₀ > θ ₁, implies a negative, inductive susceptance.

The corresponding characteristic impedance is modified according to (10). In Fig. 6 we report a view of the line transformation expressed by (11), where the isoclines are associated with the shunt susceptance of the synthetic line. From the figure, it is evident that, starting from the reference electrical length, a transmission line can be either lengthened or shortened as long as the appropriate susceptance is shunted at the line ends, and the transformed impedance Z ₁ remains feasible. For instance, having selected a cascade of two transmission lines, namely TL _a and TL _b , with nominal electrical length $\theta \hskip 1pt_0^A $  = 40° and $\theta \hskip 1pt_0^B $  = 10°, we can consider their implementation by a shorter transmission line tl _a , of electrical length 20°, and a longer one, tl _b , of 20°. The electrical length frequency dependence of the two nominal lines in the 450–850 MHz bandwidth is also reported in Fig. 6, and from their intersections with the isoclines, we can evaluate the resulting |b _S |. Although the shunt susceptance values are not constant across the entire frequency range, the two trends are almost identical in absolute value. The advantage of this transformation is clear: since jBa and jBb follow almost the same path, they are intrinsically resonating over a broad band, thus giving a wide band equivalent line.

Fig. 6. Plot describing the normalized shunt susceptance needed to either shrink (red line) or lengthen (blue line) a transmission line with electrical length θ ₀.

It is remarkable that around the central area the isoclines exhibit similar slope, converging to exactly 45° for the particular condition θ ₀ = θ ₁, which implies no-transformation. About this line, the isocline curvature is mildly variable, meaning that for small length variation, the susceptance is almost invariant with respect to the ratio θ ₁/θ ₀. Opposite isoclines corresponding to ±b _S show the same distance from the bisect line, which is a hint of a natural balance between the two kinds of transformation. It has to be clarified that the analysis carried out is frequency-dependent. Thus, if the shunt susceptance for the synthetic line is implemented by either a capacitor or an inductor, the bandwidth of the transformed line is in principle narrow band.

B) Synthetic multi-line impedance inverter design

The frequency behavior dualism of both the transformations discussed in the previous section, and the inherent bandwidth limitation, due to the presence of the output devices parasitic capacitance that load the impedance inverter, suggest a different way to operate, which is discussed hereinafter.

Let us consider the conventional impedance inverter based on a QWTL, and assume it is divided into two parts, namely TL _a and TL _b , as depicted in Figs 7(a) and 7(b). With reference to this arrangement, the transmission line TL _a is made shorter, tl _a in the Fig. 7(b), with the electrical length moved from $\theta \hskip 1pt_0^A $ to $\theta \hskip 1pt_1^A $ with $\theta \hskip 1pt_0^A $  >  $\theta \hskip 1pt_1^A $ , while the transmission line TL _b is made longer, tl _b in the Fig. 7(b), with $\theta \hskip 1pt_0^A $  <  $\theta \hskip 1pt_1^A $ . According to Fig. 6, it is then possible to select the new lengths $\theta \hskip 1pt_1^A $ and $\theta \hskip 1pt_1^B $ Z such that the required two susceptances are opposite, jBa = −jBb, and thus compensate each other. It is easy to demonstrate that the opposite susceptances lead to the condition:

(12) $$\left \vert {{b_S}} \right \vert = \displaystyle{{\cos (\!\theta \hskip 1pt_1^A ) - \cos (\!\theta \hskip 1pt_0^A )} \over {\cos (\!\theta \hskip 1pt_0^A )}} = \displaystyle{{\cos (\!\theta \hskip 1pt_1^B ) - \cos (\!\theta \hskip 1pt_0^B )} \over {\cos (\!\theta \hskip 1pt_0^B )}},$$

which implies a further condition for the overall length:

(13) $${\theta _0} = \theta \,_0^A + \theta \,_0^B. $$

Fig. 7. Schematic description of the synthetic implementation of the impedance inverter (a) by two transmission lines (b) and compensating the transistors' parasitic capacitor, C _p (c).

While the characteristic impedances of the two splitting lines are the same: ${Z_0} = Z_0^A = Z_0^B $ , the characteristic impedances composing the synthetic lines $Z_1^A $ and $Z_1^B $ are dictated by (10). The splitting ratio in (13) results to be a degree of freedom leading to the proper |b _S |, thus yielding the proper capacitance for the left end of the synthetic tl _a line, being |b _S | = ω·C _p /Y ₀ with C _p the output device capacitance. In addition, the proper choice of the addends in (13) is driven by the constraint of feasibility of the characteristic impedance from (10). The synthetic impedance inverter design is completed by inserting a shunt inductor, L _p , at the right end of the tl _b |b _S | = 1/ω·L _p ·Y ₀. Because of (12), in practical implementation, two out of the four shunt lumped elements, namely the inner ones depicted in Fig. 7, cancel each other out and thus do not need to be implemented. The beneficial effect of this cancellation is the removal of the corresponding band limiting behavior. As both L _p and C _p are frequency-dependent, inserting them as a lumped element implies that their value would be estimated at the center band, which introduces the frequency limitation of the implementation. The splitting in (13) is regarded as a degree of freedom for the design of the synthetic impedance inverter.

C) Synthetic multi-line impedance inverter bandwidth properties

The plot of Fig. 6 includes the details for the specific implementation of a 600 MHz QWTL with characteristic impedance of 8 Ω. It is composed of the cascade two transmission lines, respectively, with electrical lengths of 65° and 25°, implemented by opposite strategies. The first is subject to shortening and results in a line having 17.79 Ω and an electrical length of 24.05° with a shunt susceptance of 67.66 mS at both the ends. The second line results from the lengthening of the nominal and exhibits a characteristic impedance of 4.59 Ω and an electrical length equal to 47.35°, with a shunt susceptance of 67.67 mS. Considering the center frequency of 600 MHz, the resulting structure is implemented by the topology shown in Fig. 8(a), where the shunt elements consist of a capacitor of 17.94 pF and an inductor of 3.92 nH, which is reduced to 2.91 nH to optimize the impedance inverter center frequency. In the actual implementation, the capacitor represents the device parasitic, or at least a part of it. The topology of the resulting impedance inverter is reported in Fig. 8 along with the topology of the compensated QWTL designed by the conventional capacitance absorbing method [Reference Qureshi, Li, Neo, van Rijs, Blednov and de Vreede16]. This latter can be considered as the benchmark of the proposed approach.

Fig. 8. Topology of the synthetic impedance inverter of this work (a), and compensated QWTL by shunt capacitors (b), both implementations considering the same center frequency of 600 MHz.

The Figs 9 and 10 show the comparison between the input impedance and reflection coefficient of the two networks in Fig. 8, along with that of the ideal QWTL (designed at 600 MHz with Z ₀ = 8 Ω), when the output is terminated to both 4 and 8 Ω, respectively. These values represent the terminations involved in the prototype implementation introduced hereinafter in Section IV. All the impedance inverters have a characteristic impedance of 8 Ω, and are analyzed in the 400–800 MHz bandwidth. In particular, Fig. 9 reports the normalized real part of the input impedance in the frequency range 400–800 MHz for the transformation involved in the DPA back-off operation, i.e., 4–16 Ω. From the comparison we can evaluate the capability of the proposed network to operate in a fractional bandwidth of 54%, which is twice the bandwidth of the ideal QWTL, and significantly larger than the more feasible compensated QWTL, which is limited to 21%. The proposed network in the same frequency band exhibits a maximum phase rotation of +17° to −25° at the opposite bandwidth extremes. When considering the transformation from 8 to 8 Ω reported in Fig. 10, the ideal QWTL exhibits no band limitation, while in this case the proposed impedance inverter technique exhibits an operative bandwidth, which is comparable with the one exhibited by the compensated QWTL. These results justify the expected wider bandwidth DPA operation with respect to conventional implementations.

Fig. 9. Comparison between normalized simulated input impedances for the ideal QWTL, the compensated QWTL by shunt capacitors, and the impedance inverter of this work; transformation R _L  = 4 to 16 Ω.

Fig. 10. Comparison between input reflection coefficients for the ideal QWTL (designed at 600 MHz with Z ₀ = 8 Ω), the compensated QWTL by shunt capacitors, and the impedance inverter of this work; transformation R _L  = 8 to 8 Ω, frequency range 400–800 MHz.

The synthetic impedance inverter capability to deal with modulated signal is numerically evaluated in the same conditions adopted in the Section IIB. An ideal DPA implementing the synthetic impedance inverter hereinabove discussed has been numerically analyzed, and the DE has been derived as a function of the drive level and carrier frequency; the results are reported in Fig. 11. According to the impedance inverter frequency behavior at the two fundamental states of the DPA, reported in Figs 9 and 10, we clearly observe different behavior with respect of the QWTL based impedance inverter. Namely, for the same fractional bandwidth values the DE results ranging between the maximum theoretical value of 78.5%, and a minimum of 54.6% at back-off, while a minimum of 31.4% is reached at peak power. It is worth to note that, in the case of QWTL at back-off the DE is 31.1% at the bandwidth limits. This is of dramatic importance for the performance of the DPA when driven by modulated signals with high PAPR.

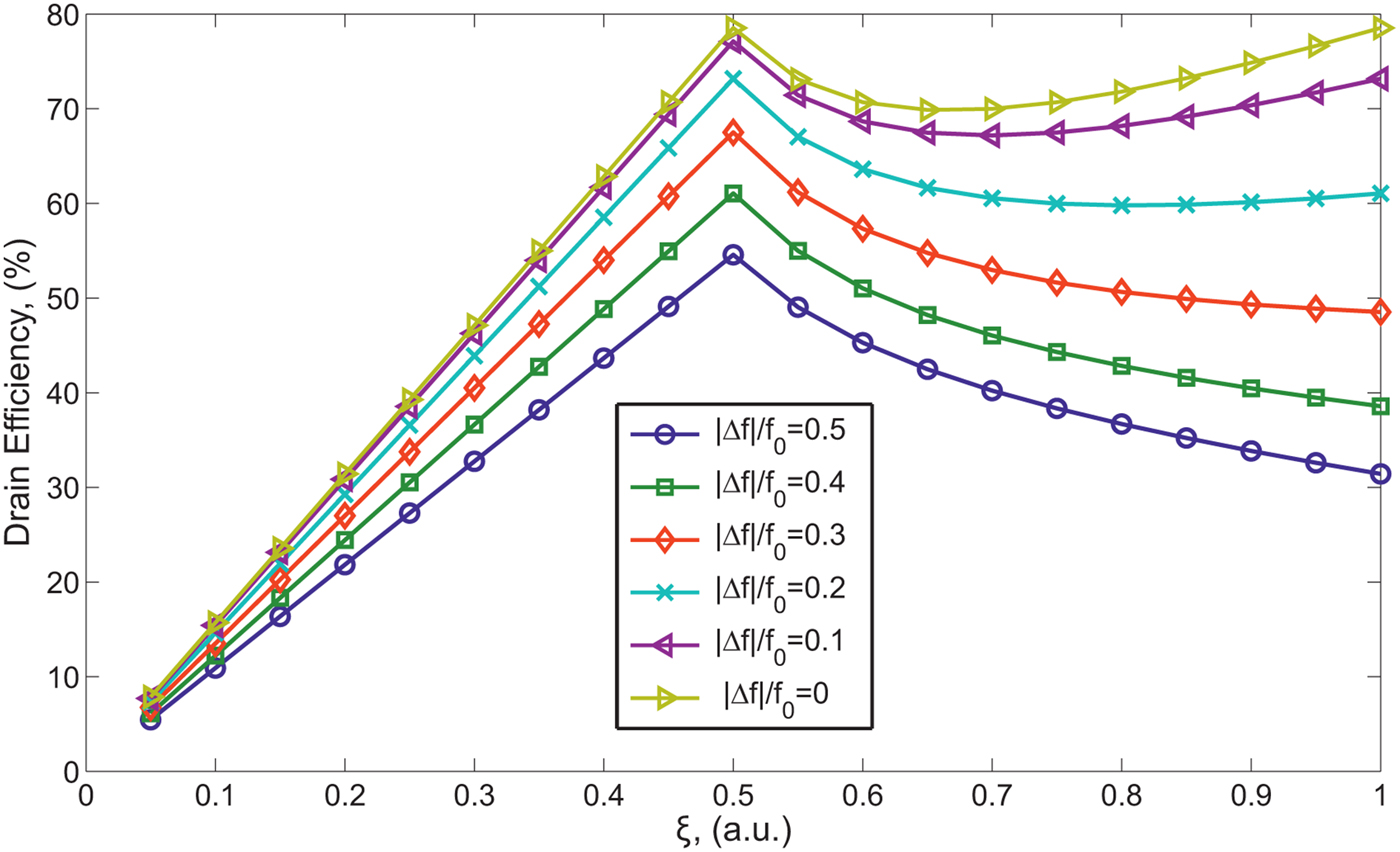
Fig. 11. DE for an ideal DPA implemented with the synthetic multi-line impedance inverter designed at f ₀ with Z _c  = R _opt , as a function of the fractional bandwidth |f − f ₀|/f ₀, and drive level ξ.

The DE reported in Fig. 11 has been integrated by the (6) maintaining the same peak power and the results are shown in Fig. 12, as a function of the normalized frequency, f/f ₀. As in the previous case, from the data we can calculate the bandwidth following the accepted criteria of 10% relative average DE drop at the band edge. The calculated bandwidth, along with the maximum average DE is reported in Table 2. When compared with the data in Table 1 we observe that the average DE at the design frequency remains unvaried; for the case of PAPR = 3 dB the proposed technique leads to a reduction of performance, while from PAPR = 6 dB and higher the improvement of fractional bandwidth is significant, for instance, for PAPR = 9 dB the improvement is about the 16%.

Fig. 12. Average DE performance for an ideal DPA implementing the synthetic impedance inverter, versus normalized frequency f/f ₀, for modulated signals at different peak-to-average ratio (PAR) and same peak power. For comparison it is also reported the case of CW signal at back-off power.

Table 2. Bandwidth and average DE for ideal DPA implementing the synthetic impedance inverter.

A) Large signal pulsed CW characterization

The pulsed CW characterization of the prototype is performed with an RF pulse width of 100 µs and 10% duty cycle; the resulting measured pulsed CW DE is reported in Fig. 17 as a function of the output power, across the 500–800 MHz bandwidth. The DE shows a peak of 62% at 53.9 dBm measured at 750 MHz, while the peak power of 54.9 dBm to which a DE of 54.5% corresponds is measured at 650 MHz. The DE reported in Fig. 17 at 6-dB output back-off spans form a minimum of 36.7% at 500 MHz to a maximum of 48.2% at 750 MHz. The Fig. 18 reports the power gain as a function of the output power, where a maximum is observed at all the measured frequencies. For the entire set of test frequencies, the gain expansion, due to a possible input mismatch of the main device, and the following compression are responsible of the observed reduction of the output power range, within which the DE remains about its maximum value.

Fig. 17. Measured DE versus output power in pulsed CW for several carrier frequencies.

Fig. 18. Measured power gain versus output power in pulsed CW for several carrier frequencies.

B) DVB-T modulated characterization

The test of the DPA prototype performance for DVB-T operation is carried out by the use of a DVB-T signal exciter. The set of input signals considers carriers spanning 475–850 MHz; the signal PAPR is 10.5 dB. All of the following data points are measured with a constant PAPR at the Doherty output of 7 dB, which corresponds to 3.5 dB of output level compression for each frequency point within the observed bandwidth. In Fig. 20 we report the corresponding average power as a function of the DVB-T carrier frequency. From the figure we observe that the maximum average power of 50.3 dBm is reached at 750 MHz, while across the bandwidth the average power remains within 49.3 dBm ± 1 dB. The values of the average power reported in the figure correspond to the maximum power at the prototype output, regardless of any other linearity concerns; in these cases the ACPR is slightly better than 20 dBc.

Fig. 19. Photograph of the broadband push-pull PA prototype designed by using the same device and adopted to benchmark the DPA prototype performance.

Fig. 20. Measured average output power as a function of the carrier frequency.

The corresponding values of the average DE are reported in Fig. 21. The maximum of 53% is obtained at 750 MHz, while the minimum of 40% is reached at 470 MHz. The 13% variation of the DE is considered an acceptable spread for practical applications; nevertheless, more effort in the optimization might lead to a flatter response. Recalling the theoretical analysis reported in Fig. 12 and summarized in Table 2 we observe that for PAPR = 10.5 dB an estimated average DE of 59.5% is expected, which should be considered as a performance benchmark , and represents an overestimation due to the non-idealities of the DPA not included in the analysis conducted in Section IIIC. The maximum shown in Fig. 21 results shifted at slightly higher frequency due to the effect of the DPA power gain, shown in Fig. 22, also shifted of the same amount due to imperfect matching of the input stage. The large signal power gain reported in Fig. 22 exhibits a maximum of 18 dB at 750 MHz and a behavior very similar to the trend seen for the DE, thus confirming that also the gain feature requires an optimization versus the frequency band.

Fig. 21. Comparison between measured average DE as a function of the carrier frequency for both the DPA and the push-pull prototypes developed with the same devices.

For a more comprehensive evaluation of the DPA performance, we provide the gain, DE and adjacent channel power ratio (ACPR) obtained by a push-pull PA designed using the same LDMOS device. The prototype photograph for the push-pull PA is provided in Fig. 19. The measured data for the DE, power gain and ACPR, under the same DVB-T excitation, are reported along with those of the DPA, respectively in Figs 21–23. The selection of a push-pull PA as a benchmark for the evaluation of the DPA design provided in this work is mainly motivated by the widely recognized characteristic of this design to provide a high-power level in a broad band due to the mechanism of doubling the output termination and thus reducing the output Q-factor of the output matching network. The comparisons show that the DE exhibited by the push-pull PA is constant across the bandwidth at about 28%, which is between 12 and 24% lower than the DPA prototype values. As expected, the inherent linearity of the DPA is worse than the raw linearity of the push-pull linearity. This is demonstrated by the ACPR raw data for the two prototypes shown in Fig. 23, which reports values for the push-pull that are on average 10 dB better than those of the DPA. These comparisons provide a qualitative, although meaningful, evaluation of the quality of the DPA design introduced in this paper.

Fig. 22. Comparison between measured gain as a function of the carrier frequency for both the DPA and the push-pull prototypes developed with the same devices.

Fig. 23. Comparison between measured ACPR as a function of the carrier frequency for both the DPA and the push-pull prototypes developed with the same devices.

C) Linearized DPA evaluation

The prototype is evaluated in a laboratory digital pre-distortion (DPD) platform supporting a bandwidth of 150 MHz. The platform consists of a vector signal generator for stimulus generation, a signal analyzer for capturing the feedback signal, and a host machine for system identification and stimulus pre-distortion using an indirect learning architecture implemented in MATLAB. The test signal adopted in the following set of experiments is the same as already presented in Section VB, though with different carrier amplitude levels in order to meet different energy efficiency versus linearity trade-offs. For all experiments, a generalized memory polynomial model [Reference Morgan, Ma, Kim, Zierdt and Pastalan23] of order 9 with memory 5 and envelope-lag 1 is used.

Two showcases are herein reported as representative of the prototype performance, and are of specific interest for the DVB-T applications. The first result, shown in Fig. 24, is a test with 60 W target power at a carrier frequency of 750 MHz. In this case, the output PAPR is equal to 7 dB and the DPD makes it possible to achieve better than −51 dBc of ACPR measured at 8 MHz offset. In this case, the total average output power is 47.8 dBm with a system average DE of 44.3%. It is worth to note that the power level is 2.5 dB lower than the average power reported in Fig. 20 for 3.5-dB of power compression. Before the application of the DPD the ACPR results −27.3 dBc, while for a better comprehension of the inherent DPA linearity, the AM/PM and AM/AM curve in the envelope domain are reported in the Fig. 25. The result of the second showcase, reported in Fig. 26, considers a high-linearity case with PAPR = 7.5 dB at the carrier frequency of 650 MHz. In this specific case, the output power is of 46.2 dBm with an ACPR of −58 dBc, while the resulting DE is 30.6%. For this test case, should be noticed that the power is 3.5 dB lower than the average power reported in Fig. 20. It results that, before the application of the DPD the ACPR results −33.73 dBc, while for a better comprehension of the inherent DPA linearity, the AM/PM and AM/AM curves in the envelope domain are reported in the Fig. 27. The discussed showcases demonstrate that the prototype is suitable for inclusion in a DPD platform with a significant expectation of linearity performance, while preserving output power and energy efficiency.

Fig. 24. Spectrum about the carrier of 750 MHz with memory digital pre-distortion; bandwidth = 7.61 MHz, output PAPR = 7 dB.

Fig. 25. AM/PM (a) and AM/AM (b) distortion for a DVB-T signal with carrier at 750 MHz before and after pre-distortion; with memory digital pre-distortion; bandwidth = 7.61 MHz, output PAPR = 7 dB and total channel power of 47.8 dBm.

Fig. 26. Spectrum about the carrier of 650 MHz with memory digital pre-distortion; bandwidth = 7.61 MHz, output PAPR = 7.5 dB.

Fig. 27. AM/PM (a) and AM/AM (b) distortion for a DVB-T signal with carrier at 650 MHz before and after pre-distortion; with memory digital pre-distortion; bandwidth = 7.61 MHz, output PAPR = 7.5 dB and total channel power of 46.2 dBm.