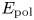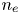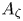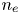1. Motivation for ‘frontiers’ and ‘fusion’ scientific collaboration

Fusion research is driven by the applied goal of energy production from fusion reactions. There is, however, a wealth of ‘frontier’ physics to be discovered and studied along the way. This paper discusses the topic of zonal flow, a phenomenon originally identified in the formation of the solar tachocline and stellar differential rotation, which is now considered a mechanism for the flow-shear-induced formation of transport barriers and associated transition of magnetic-confinement regimes in fusion (Melnikov Reference Melnikov2016). Promoting scientific collaboration with fusion science can advance plasma physics frontiers and vice versa. Research by ‘frontiers’ professors using fusion-oriented facilities has led to valuable insights and shared tools, has advanced the pursuit and understanding of fundamental plasma physics, has widened the scope of the plasma science and fusion research fields, and has generated ideas from cross-fertilizing between ‘frontiers’ and ‘fusion’. Here, the geodesic acoustic mode (GAM), a high-frequency branch of zonal flow, is intensively studied in T-10 tokamak (Melnikov et al. Reference Melnikov, Vershkov, Eliseev, Grashin, Gudozhnik, Krupnik, Lysenko, Mavrin, Perfilov and Sheluhkin2006, Reference Melnikov, Eliseev, Lysenko, Perfilov, Shurygin, Krupnik, Kozachek and Smolyakov2015a,Reference Melnikov, Eliseev, Perfilov, Lysenko, Shurygin, Zenin, Grashin, Krupnik, Kozachek and Solomatinb) because it is potentially important as a turbulence self-regulating mechanism (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005). Researchers using the T-10 tokamak, TJ-II stellarator, DIII-D tokamak, Texas Helimak and West Virginia University (WVU) Q Machine collaborated in this study.

Using bispectral analysis of HIBP data in the core plasmas, Melnikov et al. (Reference Melnikov, Krupnik, Eliseev, Barcala, Bravo, Chmyga, Deshko, Drabinskij, Hidalgo and Khabanov2017b) investigated the interaction between GAM and quasi-coherent turbulence, which demonstrated the existence of statistically significant auto- and cross-bicoherence at the GAM frequency that suggests wave–wave coupling. The results revealed details of the three-wave interaction between GAM and broadband electrostatic turbulence. Experiments were performed at the T-10 circular tokamak, located in the National Research Centre of Kurchatov Institute, Moscow, Russia. WVU was invited to collaborate to independently assess and confirm the correlation analysis and the bispectral analysis. Here, the interaction of GAM with ambient turbulence in T-10 (Eliseev et al. Reference Eliseev, Melnikov, Lysenko, Khabanov, Zenin, Drabinskij, Kharchev, Kozachek and Krupnik2018) is re-investigated using a functionally similar bicoherence analysis to quantify not only the coupling, but also the energy transfer, between local fluctuations in the magnetic potential $A_\zeta$, electron density $n_e$ and electrostatic potential $\phi$. The intention is to confirm or refine previous bicoherence interpretations (Melnikov et al. Reference Melnikov, Eliseev, Lysenko, Ufimtsev and Zenin2017a) and determine the wave–wave energy transfer direction. Findings confirm that the GAM frequency is significantly involved in three-wave interactions between the narrowband GAM at 17 kHz and the broadband turbulence at higher frequency. Findings also confirm that the degree of coupling between $\phi$ and either $n_e$ or $A_\zeta$ fluctuations is weaker than that between $n_e$ and $A_\zeta$. Findings refine the picture of energy transfer by establishing the transfer direction between the local fluctuations and identifying multi-signature consistency within subsets of biphase.

2. Broadband turbulence and GAM in the T-10 Tokamak

Gradients in density, temperature and pressure provide the main source of free energy for various linear instabilities. Broadband turbulence arises through nonlinear coupling between nonlinearly saturated instabilities. Increasing-frequency cascades and decreasing-frequency cascades can result in the viscous dissipation of energy at small scales and in the transfer of energy into larger scales, such as zonal flow and GAM. Energy can be removed from the broadband turbulence by dissipation through collisional and Landau damping.

Zonal flow is a flow-shear region structured into azimuthally symmetric bands having finite $k_r$, and having $n=m=0$ electric field fluctuations. Zonal flow co-exists with microinstabilities. Zonal flow regulates turbulence-induced transport by shearing, and thus quenching, the underlying microinstability.

The GAM is an oscillating zonal flow observed mainly in the edge region of a tokamak plasma. It oscillates in the range 10–20 kHz with a frequency that is proportional to the sound velocity $c_s$ divided by the tokamak major radius $R$ (Fujisawa et al. Reference Fujisawa, Ido, Shimizu, Okamura, Matsuoka, Iguchi, Hamada, Nakano, Ohshima and Itoh2007). By shearing the velocity profile, GAM can effect a reduction of turbulent transport and, thereby, become an important element of the turbulent system. The GAM is important to ‘fusion’ science because it factors into complex flow-shear regulation of interactions between plasma gradients, turbulence and flows, and the triggering of high-confinement equilibrium ‘H-mode’ (Conway et al. Reference Conway, Angioni, Ryter, Sauter and Vicente2011; Cziegler et al. Reference Cziegler, Tynan, Diamond, Hubbard, Hughes, Irby and Terry2015; Melnikov Reference Melnikov2019).

Broadband turbulence and GAM coexist in the T-10 tokamak. Figure 1 (consistent with figure 1 of Eliseev et al. Reference Eliseev, Melnikov, Lysenko, Khabanov, Zenin, Drabinskij, Kharchev, Kozachek and Krupnik2018) diagrams the geometry of the poloidal electric field $E_{\textrm {pol}}$ and velocity $V_{r}$ measurements. Same-flux-surface potentials $\phi _j$, $\phi _k$ are locally measured by slits $j$ and $k$ of the five-slit energy analyser, where $(j,k) = (1,2), (2,3), (3,4)$, and $(4,5)$ are commonly used. The inferred $E_{\textrm {pol}} = (\phi _{j}-\phi _{k})/dl_{jk}$, where $dl_{jk}$ is the neighbour-slit separation.

Figure 1. Outline of the electric field $E_{\textrm {pol}}$ and radial velocity $V_r$ measurement; $\phi _{j}$ and $\phi _{k}$ are potentials in sample volumes on the same flux surface, measured by slits $\#j$ and $\#k$, respectively, at a distance $dl_{jk}$.

Figure 6 of Eliseev et al. (Reference Eliseev, Melnikov, Lysenko, Khabanov, Zenin, Drabinskij, Kharchev, Kozachek and Krupnik2018), not shown here, graphs the 50–200 kHz frequency-integrated flux $\varGamma$ through the various pairs of HIBP slits. The mean flux suddenly increases upon the transition of the discharge from the ohmic (OH) stage ($2\times 10^{19}\ \textrm {m}^{-2}\,\textrm {s}^{-1}$) to the electron cyclotron resonant heating (ECRH) stage ($3\times 10^{19}\ \textrm {m}^{-2}\,\textrm {s}^{-1}$) as a result of a significant increase in amplitude of fluctuations of both $E_{\textrm {pol}}$ and density despite the decrease of coherence between those two quantities. In this report, as in Melnikov et al. (Reference Melnikov, Eliseev, Lysenko, Ufimtsev and Zenin2017a) and Gryaznevich et al. (Reference Gryaznevich, Stöckel, Van Oost, Del Bosco, Svoboda, Melnikov, Kamendje, Malaquias, Mank and Miklaszewski2020), bicoherence of the OH-stage fluctuations is presented. Specifically, we consider data collected from T-10 shot $\#62753$, with relevant plasma parameters $I_p = 180\text {--}250\ \textrm {kA}$ and $\bar {n}_e = (1.2\text {--}1.4)\times 10^{19}\ \textrm {m}^{-3}$.

3. Background

Local fluctuations of electrostatic potential, poloidal electric field, magnetic potential and electron density were simultaneously measured in the T-10 tokamak. The turbulent particle flux was measured in the plasma edge layer by multipin Langmuir probes, while inside the core plasmas, the flux was measured by multichannel HIBP (Dnestrovskij et al. Reference Dnestrovskij, Melnikov, Krupnik and Nedzelskij1994; Demers et al. Reference Demers, Schoch, Crowley, Connor and Ouroua2001; Melnikov et al. Reference Melnikov, Krupnik, Eliseev, Barcala, Bravo, Chmyga, Deshko, Drabinskij, Hidalgo and Khabanov2017b).

The HIBP is a unique diagnostic tool that can acquire simultaneous information about the local plasma potential $\phi$, plasma density $n_e$ and toroidal magnetic potential $A_\zeta$ in the core area of toroidal plasmas (Dnestrovskij et al. Reference Dnestrovskij, Melnikov, Krupnik and Nedzelskij1994; Melnikov et al. Reference Melnikov, Krupnik, Eliseev, Barcala, Bravo, Chmyga, Deshko, Drabinskij, Hidalgo and Khabanov2017b). The diagnostic functions by passing a primary probing beam of ions through a hot plasma, which exposes the energetic (up to 300 keV) ions to a toroidal magnetic field (Melnikov et al. Reference Melnikov, Eliseev, Perfilov, Andreev, Grashin, Dyabilin, Chudnovskiy, Isaev, Lysenko and Mavrin2013); to ensure the resulting Larmor radius exceeds the plasma area, heavy ions (in this case, Tl$^+$) are used (Melnikov et al. Reference Melnikov, Krupnik, Eliseev, Barcala, Bravo, Chmyga, Deshko, Drabinskij, Hidalgo and Khabanov2017b). In transit, collisions with plasma particles lead to secondary ionization of a proportion of the beam ions. With knowledge of the initial kinetic energy $\mathcal {E}_b$ of the beam, measurement of the kinetic energy $\mathcal {E}_d$ of the secondary ions provides the local plasma potential as $\phi = (\mathcal {E}_d-\mathcal {E}_b)/e$ (Jobes & Hickock Reference Jobes and Hickock1970). Additionally, the plasma density $n_e$ may be inferred from the secondary beam current $I_t$ (cf. (2)–(4) in Melnikov et al. Reference Melnikov, Eliseev, Jiménez-Gómez, Ascasibar, Hidalgo, Chmyga, Komarov, Kozachok, Krasilnikov and Khrebtov2010) and toroidal magnetic potential $A_\zeta$ is deduced from the toroidal beam shift $\zeta$ (cf. (7)–(10) in Melnikov et al. Reference Melnikov, Eliseev, Jiménez-Gómez, Ascasibar, Hidalgo, Chmyga, Komarov, Kozachok, Krasilnikov and Khrebtov2010).

We present analysis of the HIBP data to confirm the interpretations of Melnikov et al. (Reference Melnikov, Eliseev, Lysenko, Ufimtsev and Zenin2017a). In particular, there was found to be statistically significant nonlinear coupling between fluctuations in density and fluctuations in magnetic potential (cf. figure 7b in Melnikov et al. Reference Melnikov, Eliseev, Lysenko, Ufimtsev and Zenin2017a), and to a lesser extent, evidence of nonlinear coupling between magnetic and electrostatic potential fluctuations (cf. figure 7c in Melnikov et al. Reference Melnikov, Eliseev, Lysenko, Ufimtsev and Zenin2017a). The detection of these nonlinear interactions, in conjunction with the associated energy transfer, is facilitated by cross-bicoherence analysis (Kim & Powers Reference Kim and Powers1979; Kim, Beall & Powers Reference Kim, Beall and Powers1980; Xu et al. Reference Xu, Tynan, Holland, Yan, Muller and Yu2009).

4. Analysis of wave–wave cross-bicoherence

The bispectrum is a two-dimensional (2-D) Fourier transform of the triple correlation function (Kim et al. Reference Kim, Beall and Powers1980; Stauber Reference Stauber1995; Riggs Reference Riggs2020), which manifests as a triple product of Fourier components. Explicitly,

(4.1)\begin{equation} {\mathcal{B}}_{xyz}(f_1,f_2) = \left\langle \varPhi_x(f_1) \varPhi_y(f_2) {\varPhi_z^* ( f_1 + f_2 )} \right\rangle, \end{equation}

where angled brackets represent a time average over many realizations, and $\varPhi _i(f)$ is a Fourier coefficient at frequency $f$, for time series $i$. For an individual peak in the bispectrum at $(f_1,f_2)$, the sign of the real part $\mathrm {Re}({\mathcal {B}}_{xyz})$ encodes information about the phase relationship between modes $\varPhi _x(f_1)$, $\varPhi _y(f_2)$ and $\varPhi _z(f_1 + f_2)$ (Stauber Reference Stauber1995, p. 11; Xu et al. Reference Xu, Tynan, Holland, Yan, Muller and Yu2009). This may be understood by considering the biphase $\theta$ or associated phase angle. For a single realization,

(4.2)\begin{equation} \theta_{xyz}(f_1,f_2) = \varphi_{x}(f_1) +\varphi_{y}(f_2)-\varphi_{z}(f_1+f_2), \quad -{\rm \pi} <\theta<{\rm \pi}, \end{equation}

where $\varphi _{i}(f)$ is the phase angle of $\varPhi _i(f)$. If we consider quadratic coupling terms, parent modes and daughter modes have a triplet relationship recognized by parents at frequencies $f_a$ and $f_b$, with daughters at the sum and difference frequencies $f_a\pm f_b$ (Stauber Reference Stauber1995, p. 8; Riggs Reference Riggs2020, p. 27; Stauber & Koepke Reference Stauber and Koepke2021). In the special case $x=y=z$ (known as auto-bispectrum), parent–daughter interactions would produce bispectral peaks at $(f_a,f_b)$, $(f_b,f_a)$, $(f_a,f_b-f_a)$, $(f_b-f_a,f_a)$, $(-f_a,f_b)$, $(-f_b,f_a+f_b)$, $(f_a-f_b,f_b)$ and $(-f_a,f_a+f_b)$, where $f_b>f_a$. When associated with these peaks, $|\theta _{xxx}|<{\rm \pi} /2$ or $\mathrm {Re}({\mathcal {B}}_{xxx})>0$ corresponds to an in-phase daughter mode (with respect to the parents), while $|\theta _{xxx}|>{\rm \pi} /2$ or $\mathrm {Re}({\mathcal {B}}_{xxx})<0$ represents an out-of-phase daughter (Stauber Reference Stauber1995, p. 11; Stauber & Koepke Reference Stauber and Koepke2021). This information can implicate the direction of energy transfer even in the more general case $(x\neq y\neq z)$, as the rate of change of power in the mode $\varPhi _z(f_1+f_2)$ owing to the nonlinear interaction among $\varPhi _x(f_1)$, $\varPhi _y(f_2)$ and $\varPhi _z(f_1+f_2)$ is proportional to $\mathrm {Re}({\mathcal {B}}_{xyz}(f_1,f_2))$ (Kim & Powers Reference Kim and Powers1979; Stauber Reference Stauber1995, p. 10). Figure 2 illustrates how a triangular region in a map of $\mathrm {Re}({\mathcal {B}}_{xxx})$ spans the pertinent 2-D range of all possible interactions with one of the triplets $(f_1,f_2,f_1+f_2)$. Note how the triangular-pattern angles and orientations transform from region to region, and that prominent spectral features are repeated throughout the range of plotted frequencies. For example, features in region ‘B’ are mirrored in region ‘C’, with the addition of a vertical shift equal to the displacement of the point from the $y$-axis. This reference illustration is helpful when comparing and contrasting with quadrant representations in the literature, as cross-bispectra will, in general, break these symmetries. With this in mind, it is convenient to define the squared bicoherence spectrum,

(4.3)\begin{equation} b^2_{xyz}(f_1,f_2) = \frac{\left| \left\langle \varPhi_x(f_1) \varPhi_y(f_2) {\varPhi_z^* ( f_1 + f_2 )} \right\rangle \right|^2} { \left\langle \left|\varPhi_x(f_1) \varPhi_y(f_2)\right|^2 \right\rangle \left\langle \left|{\varPhi_z ( f_1 + f_2 )}\right|^2 \right\rangle }, \end{equation}

which normalizes bispectral values to the range $[0,1]$, and indicates the proportion of energy change arising from nonlinear coupling (Stauber Reference Stauber1995, pp. 14).

Figure 2. Visualization of symmetries implicit to the real part of the bispectrum (4.1) for real-valued time series, where $x=y=z$. Latin capitals and black lines are used to identify subregions of bi-frequency space, which will assist in assessment of upcoming figures. Axes have been normalized to Nyquist frequency; colour indicates how lines of constant sum frequency $f_3 = f_1+f_2$ in quadrant I transform to lines of constant $f_2$ in quadrant II, through $f_2 = f_3+(-f_1)$.

GAM, the only spectral feature at 17 kHz, plays a crucial role in the three-wave interaction that involves both upper- and lower-frequency halves of the higher-frequency broadband turbulence, as evidenced by the strong coupling apparent in multi-channel, HIBP measurements of turbulent particle flux and $\boldsymbol {E}\times \boldsymbol {B}$ rotation velocity in the gradient zone ($r/a$ = 0.8) of the plasma column (Eliseev et al. Reference Eliseev, Melnikov, Lysenko, Khabanov, Zenin, Drabinskij, Kharchev, Kozachek and Krupnik2018). Figure 3 shows cross-bicoherence $b_{nn\zeta }^2$ compared with the real part of the bispectrum $\mathrm {Re}({\mathcal {B}}_{nn\zeta })$, which compactly illustrates both the extent and direction of energy transfer between plasma density fluctuations and magnetic potential fluctuations. In this case, wave energy is gained in the range 40–80 kHz, whereas wave energy is lost in the range 90–130 kHz. The frequency range of 40–150 kHz belongs to the quasicoherent (QC) modes in T-10, the specific type of oscillations under intensive study with various diagnostics (Vershkov et al. Reference Vershkov, Shelukhin, Subbotin, Dnestrovskij, Danilov, Melnikov, Eliseev, Maltsev, Gorbunov and Sergeev2015, Reference Vershkov, Sarychev, Notkin, Shelukhin, Buldakov, Dnestrovskij, Grashin, Kirneva, Krupin and Klyuchnikov2017). In figure 4, we compare line-outs of the cross-bicoherences $b_{nn\zeta }^2$ and $b_{\phi \phi \zeta }^2$ at $f_1=f_{{\textrm {GAM}}}$, where statistically significant values are observed in $b_{nn\zeta }^2$ (but not $b_{\phi \phi \zeta }^2$). This demonstrates the quantitative differences between electrostatic potential and density fluctuations, with regard to their coupling and energy exchange with the magnetic potential. Specifically, significant three-wave coupling is suggested in $n,n,\zeta$ bispectra, whereas it is weak in $\phi ,\phi ,\zeta$ bispectra. This independently reinforces the interpretation that density fluctuations, not potential fluctuations, exhibit more pronounced nonlinear wave–wave coupling (cf. figure 7b,c in Melnikov et al. Reference Melnikov, Eliseev, Lysenko, Ufimtsev and Zenin2017a). Additionally, the cross-bicoherence $b_{n\zeta n}^2$ (figure 5a) and its line-out at $f_1=f_{{\textrm {GAM}}}$ (figure 6b) affirm the importance of magnetic potential fluctuations in the context of this nonlinear coupling. Notably, the cross-bicoherence $b_{\zeta n \phi }^2$ displayed in figure 5(b) reiterates the diminished role of electrostatic potential fluctuations.

Figure 3. Bispectral analysis of OH plasma: (a) cross-bicoherence $b_{nn\zeta }^2$, (b) real part of bispectrum $\mathrm {Re}({\mathcal {B}}_{nn\zeta })$. Notice lack of contribution from $f_\zeta = f_{\textrm {GAM}}$ (subregion defined as ‘D’ in figure 2).

Figure 4. Comparing the nonlinear mode–mode coupling found in line-out of (a) $b_{nn\zeta }^2$ and (b) $b_{\phi \phi \zeta }^2$ at GAM frequency (as indicted in figure 3a), the latter is significantly weaker than the former. This implies the coupling between $A_\zeta$ and $n_e$ is strongest and most informational (see figure 7).

Figure 5. Bispectral analysis of OH plasma: (a) cross-bicoherence $b_{n\zeta n}^2$, (b) cross-bicoherence $b_{\zeta n \phi }^2$. Note lack of significant nonlinear coupling when electrostatic potential is included; additionally, compare regions ‘A’ and ‘D’ in figure 3(a) (as dictated by figure 2) with their respective counterparts in (a).

Figure 6. Further analysis: (a) real part of bispectrum $\mathrm {Re}({\mathcal {B}}_{n\zeta n})$, (b) line-out of $b_{n\zeta n}^2$ at GAM frequency. These imply density and magnetic potential fluctuations are involved in complementary interactions with GAM.

Naturally, we check the cross-bispectrum ${\mathcal {B}}_{\zeta \zeta n}$ to assure our assessment of energy transfer is valid. The distributions of $\mathrm {Re}({\mathcal {B}}_{\zeta \zeta n})$ and $\mathrm {Re}({\mathcal {B}}_{n\zeta n})$ along the GAM frequency ($f_1\sim 17\ \textrm {kHz}$) displayed in figure 7(a) are clearly complementary. In conjunction, figure 7(b) documents the approximately $180^\circ$ phase difference between the cross-biphases $\theta _{nn\zeta }$ and $\theta _{\zeta \zeta n}$. When seen in the full context of $\mathrm {Re}({\mathcal {B}}_{nn\zeta })$ and $\mathrm {Re}({\mathcal {B}}_{n\zeta n})$ (figures 3b and 6a, respectively), this provides evidence for energy transfer arising from nonlinear wave–wave coupling between the magnetic potential and density fluctuations. Explicitly, magnetic potential fluctuations in the range 40–80 kHz exchange energy with density fluctuations the range 90–130 kHz. In all cases, this energy transfer is provided by the GAM frequency interacting with the broadband turbulent fluctuations.

Figure 7. Analysis of energy transfer in OH plasma: (a) comparison of line-outs of $\mathrm {Re}({\mathcal {B}}_{\zeta \zeta n})$ and $\mathrm {Re}({\mathcal {B}}_{n \zeta n})$, (b) comparison of cross-biphases $\theta _{nn\zeta }$ and $\theta _{\zeta \zeta n}$ along GAM frequency. Remarkably, these quantities are approximately $180^\circ$ out of phase across the entire frequency range of interest.