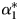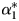1. Introduction
A recent Political Analysis symposium investigated applications of the popular general error correction method (GECM). Grant and Lebo (Reference Grant and Lebo2016) focus on common mistakes made with the GECM, particularly with interpreting the error correction parameter. A response by Keele et al. (Reference Keele, Linn and Webb2016) clarifies the meaning of often misunderstood parts of DeBoef and Keele (Reference DeBoef and Keele2008). The symposium sparked interest in both the usage of the method and the question of equation balance (e.g., Enns and Wlezien, Reference Enns and Wlezien2017; Lebo and Kraft, Reference Lebo and Kraft2017; Pickup and Kellstedt, Reference Pickup and Kellstedt2018). Here, we demonstrate interpretation problems when using multiple exogenous variables, even when all are unit roots. In particular, we outline the correct interpretation of the hypothesis test on the error correction coefficient, $\alpha _1^\ast$![]() . Rejecting the null does not indicate that all of the variables are cointegrated. Further, $\alpha _1^\ast$
. Rejecting the null does not indicate that all of the variables are cointegrated. Further, $\alpha _1^\ast$![]() cannot assess which x's are cointegrated with y, whether the equation is balanced, or what the correct critical values are for other coefficients. We highlight the implications for applied research with examples of Kelly and Enns's (Reference Kelly and Enns2010) and Volscho and Kelly's (Reference Volscho and Kelly2012) tests for cointegration.
cannot assess which x's are cointegrated with y, whether the equation is balanced, or what the correct critical values are for other coefficients. We highlight the implications for applied research with examples of Kelly and Enns's (Reference Kelly and Enns2010) and Volscho and Kelly's (Reference Volscho and Kelly2012) tests for cointegration.
2. Cointegration, the GECM, and Equation Balance
A simplified expression of an individual time series, y t, is:
in which the deterministic features—a constant or trend—are captured by D t and μ t is a white noise process. When ρ = 1, the series has a unit root (non-stationary, integrated, or I(1)) and meanders without tending toward a long-term mean. A series with ρ < 1 will have mean reversion and is classified as stationary, non-integrated, or I(0). A unit root series can be rendered stationary through the process of differencing—creating a new series from the changes between time-points, i.e. Δy t = y t − y t−1.
Cointegration exists when a linear combination of two or more unit-root series are jointly stationary. Cointegrated series are in a long-run equilibrium such that any movement away from each other is short-lived. Engle and Granger (Reference Engle and Granger1987) provide a two-step framework for understanding and testing for cointegration that begins with:
where y t and x t are both I(1) and the residuals are $\hat \varepsilon _t$![]() .Footnote 1 Testing $\hat \varepsilon _t$
.Footnote 1 Testing $\hat \varepsilon _t$![]() 's stationarity is a cointegration test. If $\hat \varepsilon _t$
's stationarity is a cointegration test. If $\hat \varepsilon _t$![]() is stationary, $\hat \varepsilon _{t-1}$
is stationary, $\hat \varepsilon _{t-1}$![]() can be used in a second regression to measure error correction—the rate at which equilibrium returns after a shock in ɛ separates y t and x t:
can be used in a second regression to measure error correction—the rate at which equilibrium returns after a shock in ɛ separates y t and x t:
The Engle–Granger method was once a popular approach in political science (e.g., Ostrom and Smith, Reference Ostrom and Smith1993; Clarke and Stewart, Reference Clarke and Stewart1995; Calderia and Zorn, Reference Calderia and Zorn1998). However, the simpler single-equation GECM became the go-to method following publication of DeBoef and Keele (Reference DeBoef and Keele2008). The Bårdsen (Reference Bårdsen1989) expression of a bivariate GECM is particularly popular:
where Δy t is the differenced version of the dependent variable, α0 is a constant, $\alpha _1^\ast$![]() is the error correction coefficient, $\beta _0^\ast$
is the error correction coefficient, $\beta _0^\ast$![]() is the short-term effect of Δx t, $\beta _1^\ast$
is the short-term effect of Δx t, $\beta _1^\ast$![]() is used to calculate the long-run effect (referred to as the long-run multiplier, LRM) of exogenous variable x t as ${\beta _1^\ast \over -\alpha _1^\ast }$
is used to calculate the long-run effect (referred to as the long-run multiplier, LRM) of exogenous variable x t as ${\beta _1^\ast \over -\alpha _1^\ast }$![]() , and η t is a well-behaved error term. With integrated data and a single x, $\alpha _1^\ast$
, and η t is a well-behaved error term. With integrated data and a single x, $\alpha _1^\ast$![]() tests a null of no cointegration against an alternative hypothesis that y t and x t are cointegrated. The test relies on non-standard “MacKinnon values” (Ericsson and MacKinnon, Reference Ericsson and MacKinnon2002).
tests a null of no cointegration against an alternative hypothesis that y t and x t are cointegrated. The test relies on non-standard “MacKinnon values” (Ericsson and MacKinnon, Reference Ericsson and MacKinnon2002).
Equation balance is a key factor when evaluating Equation 4. The order of integration of variables on the right-hand-side, either separately or in combination, must be the same as that of the dependent variable (Banerjee et al., Reference Banerjee, Dolado, Galbraith and Hendry1993; Lebo and Grant, Reference Lebo and Grant2016). A lack of balance “tells you that your model is either wrong or incomplete in a way that will prevent a meaningful interpretation of the model” (Pickup and Kellstedt, Reference Pickup and Kellstedt2018, p. 6). With cointegration, y t−1 and x t−1 are jointly stationary and—since Δy t and Δx t are each stationary—the equation is balanced. As such, each regressor can rely on a standard limiting distribution. However, if there is an integrated regressor that is not cointegrated with other variables in the equation, its coefficient cannot do so (Sims et al., Reference Sims, Stock and Watson1990).Footnote 2 Thus, a standard t-test is appropriate for a regressor's coefficient in a single equation autoregressive distributed lag model (ADL)Footnote 3 or GECM in the following (non-exhaustive) list of scenarios:
• A differenced x t, whether x t is integrated or not, though not if x t is I(2) or higher.
• An integrated x t in level form that is cointegrated with y t.
• An integrated x t alongside x t−1 (or other lags) making them jointly stationary.
• An integrated x 1t that is cointegrated with an integrated x 2t.
• An x t that is stationary with little autocorrelation.
Without cointegration, Equation 4 is unbalanced since it would regress a stationary Δy on an x t−1 that is non-stationary, on its own or in combination. Then, $\beta _1^\ast$![]() requires a non-standard distribution. In such cases, it is unclear what a long-term relationship between an I(0) y and I(1) x, or vice versa, would mean (Pickup and Kellstedt, Reference Pickup and Kellstedt2018). In sum, for a bivariate GECM with all I(1) data, $\alpha _1^\ast$
requires a non-standard distribution. In such cases, it is unclear what a long-term relationship between an I(0) y and I(1) x, or vice versa, would mean (Pickup and Kellstedt, Reference Pickup and Kellstedt2018). In sum, for a bivariate GECM with all I(1) data, $\alpha _1^\ast$![]() is a test of cointegration which must be present for balance and for the β's to all follow a t-distribution. Next, we show the alternative hypothesis for $\alpha _1^\ast$
is a test of cointegration which must be present for balance and for the β's to all follow a t-distribution. Next, we show the alternative hypothesis for $\alpha _1^\ast$![]() is not straightforward with multiple independent variables.
is not straightforward with multiple independent variables.
3. Testing $\alpha _1^\ast$ with multiple independent variables
with multiple independent variables
To review, in a bivariate GECM $\alpha _1^\ast$![]() is a cointegration test only if both y and x are I(1). Interpretation becomes difficult without I(1) data—estimates of $\alpha _1^\ast$
is a cointegration test only if both y and x are I(1). Interpretation becomes difficult without I(1) data—estimates of $\alpha _1^\ast$![]() can depend on many factors besides the effects of the independent variable. Any uncertainty in diagnosing the data creates uncertainty in what $\alpha _1^\ast$
can depend on many factors besides the effects of the independent variable. Any uncertainty in diagnosing the data creates uncertainty in what $\alpha _1^\ast$![]() is testing.
is testing.
However, even if all the data are undisputedly I(1) and even if one uses MacKinnon values, with more than a single independent variable, a significant ${\alpha _1^\ast }$![]() does not necessarily indicate that all the variables are cointegrated nor does it mean the equation is balanced. With multiple x's, the null hypothesis on $\alpha _1^\ast$
does not necessarily indicate that all the variables are cointegrated nor does it mean the equation is balanced. With multiple x's, the null hypothesis on $\alpha _1^\ast$![]() is still that there is no cointegration but the alternative hypothesis is that cointegration exists between at least one x and y (Harbo et al., Reference Harbo, Johansen, Neilsen and Rahbek1998). It is not that all of the x's are cointegrated with y.
is still that there is no cointegration but the alternative hypothesis is that cointegration exists between at least one x and y (Harbo et al., Reference Harbo, Johansen, Neilsen and Rahbek1998). It is not that all of the x's are cointegrated with y.
In the general case, we represent a potential cointegrating relationships between a set of variables in a vector error correction model (VECM, see Ericsson and MacKinnon Reference Ericsson and MacKinnon2002) as:
where $\vec z_t = ( y_t,\; x_{1t},\; ...,\; x_{k-1t}) '$![]() is a vector of k variables at time t, some of which may be cointegrated; $\vec D_t$
is a vector of k variables at time t, some of which may be cointegrated; $\vec D_t$![]() is a vector of d deterministic variables such as a constant term and a trend; and $\vec \varepsilon _t$
is a vector of d deterministic variables such as a constant term and a trend; and $\vec \varepsilon _t$![]() is a vector of k unobserved jointly normal and sequentially independent errors.Footnote 4 For parameters, $\mathbf {\pi }$
is a vector of k unobserved jointly normal and sequentially independent errors.Footnote 4 For parameters, $\mathbf {\pi }$![]() is a k × k matrix of coefficients on the lag of $\vec z_t$
is a k × k matrix of coefficients on the lag of $\vec z_t$![]() , $\mathbf {\Gamma }$
, $\mathbf {\Gamma }$![]() is a k × k matrix of coefficients on the difference of $\vec z_t$
is a k × k matrix of coefficients on the difference of $\vec z_t$![]() ,Footnote 5 and $\mathbf \Phi$
,Footnote 5 and $\mathbf \Phi$![]() is a k × d matrix of constant and trend coefficients.
is a k × d matrix of constant and trend coefficients.
The number of cointegrating vectors r is equal to the rank of $\mathbf \pi$![]() where 0 ≤ r ≤ k. Also, $\mathbf \pi$
where 0 ≤ r ≤ k. Also, $\mathbf \pi$![]() may be rewritten as $\mathbf {\alpha \beta }'$
may be rewritten as $\mathbf {\alpha \beta }'$![]() , where $\mathbf \beta$
, where $\mathbf \beta$![]() is a k × r matrix of cointegrating vectors that is of full rank, and $\mathbf \alpha$
is a k × r matrix of cointegrating vectors that is of full rank, and $\mathbf \alpha$![]() is a k × r matrix of adjustment coefficients. Within this framework, Johansen's (Reference Johansen1988, Reference Johansen1995) procedure determines the number of cointegrating vectors in Equation 5 based on the rank of $\mathbf \pi$
is a k × r matrix of adjustment coefficients. Within this framework, Johansen's (Reference Johansen1988, Reference Johansen1995) procedure determines the number of cointegrating vectors in Equation 5 based on the rank of $\mathbf \pi$![]() . The key insight is that while a cointegrating vector may contain all the variables in a system, this is not guaranteed. Instead, it may be composed only of a subset of the variables and may have elements equal to zero. In fact, the possibility of multiple cointegrating vectors in the system implies that not all of them contain every single variable.Footnote 6 As Banerjee et al. (Reference Banerjee, Dolado, Galbraith and Hendry1993, p. 145) notes: “If x t has n > 2 components, then there may be more than one co-integrating vector α; it is possible for several equilibrium relationships to govern the joint evolution of the variables.” Even if there is only a single cointegration vector (i.e., r = 1), Johansen (Reference Johansen1988, p. 236) says “it seems natural to test that certain variables do not enter into the cointegration vector.” Political scientists generally, but incorrectly, do not focus on the cointegrating vector(s). In their 1993 Econometrica article, Stock and Watson (Reference Stock and Watson1993) compare eight estimators of the cointegrating vector that allow researchers to test where cointegration is and where it is not. Assuming the independent variables are weakly exogenous and causally prior, the ECM and ADL approaches are appropriate for inference about cointegrating vector(s). Otherwise, researchers may rely on the Engle–Granger or Johnansen approaches. Enders (Reference Enders2015, pp. 395–396) offers a more accessible explanation in a section called Inference with Cointegrating Vectors.
. The key insight is that while a cointegrating vector may contain all the variables in a system, this is not guaranteed. Instead, it may be composed only of a subset of the variables and may have elements equal to zero. In fact, the possibility of multiple cointegrating vectors in the system implies that not all of them contain every single variable.Footnote 6 As Banerjee et al. (Reference Banerjee, Dolado, Galbraith and Hendry1993, p. 145) notes: “If x t has n > 2 components, then there may be more than one co-integrating vector α; it is possible for several equilibrium relationships to govern the joint evolution of the variables.” Even if there is only a single cointegration vector (i.e., r = 1), Johansen (Reference Johansen1988, p. 236) says “it seems natural to test that certain variables do not enter into the cointegration vector.” Political scientists generally, but incorrectly, do not focus on the cointegrating vector(s). In their 1993 Econometrica article, Stock and Watson (Reference Stock and Watson1993) compare eight estimators of the cointegrating vector that allow researchers to test where cointegration is and where it is not. Assuming the independent variables are weakly exogenous and causally prior, the ECM and ADL approaches are appropriate for inference about cointegrating vector(s). Otherwise, researchers may rely on the Engle–Granger or Johnansen approaches. Enders (Reference Enders2015, pp. 395–396) offers a more accessible explanation in a section called Inference with Cointegrating Vectors.
Applied research usually assumes weakly exogenous regressors and focuses on a single-equation GECM (i.e., only examining y t as a dependent variable rather than the entire system $\vec z_t$![]() ). With multiple regressors, this is:
). With multiple regressors, this is:

In Equation 6, the null for $\alpha _1^\ast = 0$![]() is no cointegrating vector between y and any of the x's. Having $\alpha _1^\ast < 0$
is no cointegrating vector between y and any of the x's. Having $\alpha _1^\ast < 0$![]() indicates there is cointegration involving y, but, crucially, the cointegrating vector may still contain elements equal to zero. Just as cointegrating relationships in a VAR may not include all the variables in the system, in a single equation model there may be cointegration between y and an incomplete subset of the remaining x's. A significant $\alpha _1^\ast$
indicates there is cointegration involving y, but, crucially, the cointegrating vector may still contain elements equal to zero. Just as cointegrating relationships in a VAR may not include all the variables in the system, in a single equation model there may be cointegration between y and an incomplete subset of the remaining x's. A significant $\alpha _1^\ast$![]() can occur in an unbalanced equation and is not evidence that all the variables are part of a cointegrating system. Some x's may be jointly stationary and some may not be. Thus, correct interpretation of the $\beta _1^\ast$
can occur in an unbalanced equation and is not evidence that all the variables are part of a cointegrating system. Some x's may be jointly stationary and some may not be. Thus, correct interpretation of the $\beta _1^\ast$![]() coefficients is not possible without further testing.
coefficients is not possible without further testing.
To illustrate, consider Equation 7 when data are all I(1), y is cointegrated with x 1, and x 2 is unrelated to both x 1 and y. The terms y t−1 and x 1t−1 would be jointly stationary and likely produce a significant ${\alpha _1^\ast }$![]() . However, with x 2t−1 included, the equation is unbalanced. Incorrect practice would use ${\alpha _1^\ast }$
. However, with x 2t−1 included, the equation is unbalanced. Incorrect practice would use ${\alpha _1^\ast }$![]() to infer that (a) y, x 1, and x 2 are all part of a cointegrating system, (b) the equation is balanced, and (c) an asymptotically normal test-statistic applies to $\beta ^\ast _{11}$
to infer that (a) y, x 1, and x 2 are all part of a cointegrating system, (b) the equation is balanced, and (c) an asymptotically normal test-statistic applies to $\beta ^\ast _{11}$![]() and $\beta ^\ast _{12}$
and $\beta ^\ast _{12}$![]() . Since x 2 is an integrated regressor, its coefficient cannot rely on the standard normal distribution. In fact, we cannot know which $\beta ^\ast _{1j}$
. Since x 2 is an integrated regressor, its coefficient cannot rely on the standard normal distribution. In fact, we cannot know which $\beta ^\ast _{1j}$![]() 's rely on a t-distribution and which do not unless we know which x is cointegrated. Without knowing the correct critical values, we do not know whether or not to reject the null.
's rely on a t-distribution and which do not unless we know which x is cointegrated. Without knowing the correct critical values, we do not know whether or not to reject the null.
4. Monte Carlo analysis
Among the many applications of error correction models in political science, some use a large number of independent variables and some use very few time points.Footnote 7 We simulate various scenarios containing between 1 and 9 independent variables and sample sizes of 50, 100, and 200. Each regressor is simulated according to the following unit-root process:
Then, we generate y t such that:
This DGP creates a cointegrating relationship between y and x 1, since both are I(1) and their difference is AR(1) with γ = 0.6.Footnote 8 The remaining independent variables $x_2,\; \dots ,\; x_9$![]() are each I(1) but unrelated to other variables. For each scenario, we generate 1000 simulated datasets and estimate GECMs of the form:
are each I(1) but unrelated to other variables. For each scenario, we generate 1000 simulated datasets and estimate GECMs of the form:

with k varying from 1 through 9. Starting with a balanced GECM where the only independent variable is x 1, we incrementally add unrelated I(1) regressors until we have included all of x 1 through x 9. Moving from left to right within each panel of Figure 1 shows the proportion of times ${\alpha _1^\ast }$![]() surpasses MacKinnon's critical values (p< 0.05) as unrelated regressors are added alongside the cointegrated x 1.
surpasses MacKinnon's critical values (p< 0.05) as unrelated regressors are added alongside the cointegrated x 1.

Fig. 1. The consequences of GECMs with unbalanced equations. Adding unrelated I(1) regressors does not sufficiently diminish the statistical significance of $\alpha _1^\ast$![]() .
.
In practice, it is clear that ${\alpha _1^\ast }$![]() tests whether cointegration is present, not whether all the variables are jointly cointegrated. For example, with eight unrelated I(1) regressors, $\alpha _1^\ast$
tests whether cointegration is present, not whether all the variables are jointly cointegrated. For example, with eight unrelated I(1) regressors, $\alpha _1^\ast$![]() identifies that cointegration is present in 100 and 82 percent of simulations for T = 200 and T = 100, respectively.Footnote 9 Additional unrelated I(1) regressors modestly reduce the frequency with which ${\alpha _1^\ast }$
identifies that cointegration is present in 100 and 82 percent of simulations for T = 200 and T = 100, respectively.Footnote 9 Additional unrelated I(1) regressors modestly reduce the frequency with which ${\alpha _1^\ast }$![]() reaches significance in shorter time series but, usually, ${\alpha _1^\ast }$
reaches significance in shorter time series but, usually, ${\alpha _1^\ast }$![]() does not alert the researcher that any particular x is not part of the equilibrium relationship with y. If a significant ${\alpha _1^\ast }$
does not alert the researcher that any particular x is not part of the equilibrium relationship with y. If a significant ${\alpha _1^\ast }$![]() indicated that all of the variables are a part of a cointegrating system, it would have to cease being significant once the model contained an unrelated I(1) regressor.
indicated that all of the variables are a part of a cointegrating system, it would have to cease being significant once the model contained an unrelated I(1) regressor.
Problems extend to long-run multipliers, calculated as ${\beta _{1j}^\ast \over -\alpha _1^\ast }$![]() . Conditional on ${\alpha _1^\ast }$
. Conditional on ${\alpha _1^\ast }$![]() surpassing MacKinnon critical values, Figure 2 displays the average proportion of times each LRM for the unrelated independent variables x 2 through x 9 are significantly different from zero. Rejecting the null conditional on $\alpha _1^\ast$
surpassing MacKinnon critical values, Figure 2 displays the average proportion of times each LRM for the unrelated independent variables x 2 through x 9 are significantly different from zero. Rejecting the null conditional on $\alpha _1^\ast$![]() , we observe inflated false-positive rates on all unrelated x's that are included in the model. Instead of an appropriate rejection rate of 5 percent (horizontal reference), unrelated regressors are statistically significant far too often. Additional x's also move $\alpha _1^\ast$
, we observe inflated false-positive rates on all unrelated x's that are included in the model. Instead of an appropriate rejection rate of 5 percent (horizontal reference), unrelated regressors are statistically significant far too often. Additional x's also move $\alpha _1^\ast$![]() further from 0 which might lead a researcher to erroneously describe a faster error correction rate.Footnote 10
further from 0 which might lead a researcher to erroneously describe a faster error correction rate.Footnote 10

Fig. 2. The consequences of GECMs with unbalanced equations. We observe inflated false positives on long run multipliers for unrelated regressors. The horizontal line indicates an acceptable significance rate of 0.05.
Using the incorrect alternative hypothesis for $\alpha _1^\ast$![]() with multiple I(1) x's and rejecting the null without further investigation means interpreting β's without knowing where one might be breaking the standard of zero-mean non-integrated regressors needed for trustworthy tests using a standard t-distribution. Before being able to consider the results of a GECM for substantive interpretation, applied researchers must make sure that the only I(1) x's included in the model are those that are indeed part of the cointegrating system. Again, Stock and Watson (Reference Stock and Watson1993) compare eight procedures to examine the cointegrating vector(s). Researchers need to be familiar with and apply some of these tests when attempting to make inferences with more than a single exogenous variable. The following section discusses examples where this practice has not been followed.
with multiple I(1) x's and rejecting the null without further investigation means interpreting β's without knowing where one might be breaking the standard of zero-mean non-integrated regressors needed for trustworthy tests using a standard t-distribution. Before being able to consider the results of a GECM for substantive interpretation, applied researchers must make sure that the only I(1) x's included in the model are those that are indeed part of the cointegrating system. Again, Stock and Watson (Reference Stock and Watson1993) compare eight procedures to examine the cointegrating vector(s). Researchers need to be familiar with and apply some of these tests when attempting to make inferences with more than a single exogenous variable. The following section discusses examples where this practice has not been followed.
5. Examples: Kelly and Enns (Reference Kelly and Enns2010) and Volscho and Kelly (Reference Volscho and Kelly2012)
Many GECM analyses in political science rely on $\alpha _1^\ast$![]() to judge cointegration and error correction between multiple variables simultaneously. For example, Enns et al. (Reference Enns, Kelly, Masaki and Wohlfarth2016, p. 4) apply MacKinnon values to data from Kelly and Enns (Reference Kelly and Enns2010) and claim to “find clear evidence of cointegration” between Liberal Policy Mood and various sets of independent variables in their GECMs.
to judge cointegration and error correction between multiple variables simultaneously. For example, Enns et al. (Reference Enns, Kelly, Masaki and Wohlfarth2016, p. 4) apply MacKinnon values to data from Kelly and Enns (Reference Kelly and Enns2010) and claim to “find clear evidence of cointegration” between Liberal Policy Mood and various sets of independent variables in their GECMs.
Even assuming the data are I(1), Enns et al. (Reference Enns, Kelly, Masaki and Wohlfarth2016) use a significant $\alpha _1^\ast$![]() to conclude that all of the series are cointegrated. Relying on only $\alpha _1^\ast$
to conclude that all of the series are cointegrated. Relying on only $\alpha _1^\ast$![]() , it is unknown if the equation is balanced. For example, Kelly and Enns's (Reference Kelly and Enns2010) Model 2 in Table 1 reports coefficients for policy liberalism and income inequality which may or may not be significant; the correct limiting distributions cannot be known without more testing.Footnote 11
, it is unknown if the equation is balanced. For example, Kelly and Enns's (Reference Kelly and Enns2010) Model 2 in Table 1 reports coefficients for policy liberalism and income inequality which may or may not be significant; the correct limiting distributions cannot be known without more testing.Footnote 11
Volscho and Kelly (Reference Volscho and Kelly2012) estimate the determinants of Income for the Top 1% using:Footnote 12

Without multiple lags of the x's, the integrated right-hand-side variables must all be mutually cointegrated for equation balance to hold and for the β 1's to rely on the t-distribution. How should we test cointegration here? Volscho and Kelly (Reference Volscho and Kelly2012) use a significant ${\alpha _1^\ast }$![]() as evidence that all I(1) regressors are cointegrated.
as evidence that all I(1) regressors are cointegrated.
Enns and Wlezien (Reference Enns and Wlezien2017) claim that Volscho and Kelly's equation is balanced so that $\beta _{1( UM) }^\ast$![]() , $\beta _{1( TMT) }^\ast$
, $\beta _{1( TMT) }^\ast$![]() , $\beta _{1( CGT) }^\ast$
, $\beta _{1( CGT) }^\ast$![]() , $\beta _{1( 3MTB) }^\ast$
, $\beta _{1( 3MTB) }^\ast$![]() , $\beta _{1( LogRGDP) }^\ast$
, $\beta _{1( LogRGDP) }^\ast$![]() , and $\beta _{1( RealS\&P) }^\ast$
, and $\beta _{1( RealS\&P) }^\ast$![]() can be evaluated using a standard normal distribution. The reasoning seems to be that, since a significant ${\alpha _1^\ast }$
can be evaluated using a standard normal distribution. The reasoning seems to be that, since a significant ${\alpha _1^\ast }$![]() indicates all the unit root x's are in a cointegrating system, and since stationary variables also rely on a t-test, everything on the right-hand-side of the equation must be stationary and can rely on a t-test. This rationale makes stationarity concerns inconsequential and is a step away from calls for more careful analyses.
indicates all the unit root x's are in a cointegrating system, and since stationary variables also rely on a t-test, everything on the right-hand-side of the equation must be stationary and can rely on a t-test. This rationale makes stationarity concerns inconsequential and is a step away from calls for more careful analyses.
What if, like our simulations, $Top 1\% Share$![]() is in fact cointegrated with some but not all of the I(1) x's? If so, some β's are trustworthy and others are not. How can we tell which is which? To experiment, we swapped out ΔCapitalGainsTaxRate t and 3MonthTBill t−1 in favor of ΔUnemployment t and Unemployment t−1. Volscho and Kelly (Reference Volscho and Kelly2012) acknowledge the latter two are not predictors of $Top 1 { percent} Share$
is in fact cointegrated with some but not all of the I(1) x's? If so, some β's are trustworthy and others are not. How can we tell which is which? To experiment, we swapped out ΔCapitalGainsTaxRate t and 3MonthTBill t−1 in favor of ΔUnemployment t and Unemployment t−1. Volscho and Kelly (Reference Volscho and Kelly2012) acknowledge the latter two are not predictors of $Top 1 { percent} Share$![]() and omit them from their preferred model. The new model's results do not alert us that the cointegrating system has an intruder. In fact, ${\alpha _1^\ast }$
and omit them from their preferred model. The new model's results do not alert us that the cointegrating system has an intruder. In fact, ${\alpha _1^\ast }$![]() moves farther from 0, from −0.648 to −0.759, remains significant, and surpasses the MacKinnon critical value.Footnote 13 A better approach within the GECM framework would do subsequent testing to piece together where cointegration is and where it is not. We conclude with a brief overview of best practices.
moves farther from 0, from −0.648 to −0.759, remains significant, and surpasses the MacKinnon critical value.Footnote 13 A better approach within the GECM framework would do subsequent testing to piece together where cointegration is and where it is not. We conclude with a brief overview of best practices.
6. Discussion
In a single equation model with I(1) data, a significant $\alpha _1^\ast$![]() indicates that at least one regressor is cointegrated with the dependent variable. It does not test whether multiple x's are all cointegrated with the dependent variable. Without understanding the alternative hypothesis, we can mistakenly think an equation is balanced and perhaps use the wrong limiting distribution and critical value to incorrectly reject a true null hypothesis. Many extant studies in political science run afoul of what we now know to be good practice. As Banerjee et al. (Reference Banerjee, Dolado, Galbraith and Hendry1993, p. 192) point out, “The moral of the econometricians’ story is the need to keep track of the orders of integration on both sides of the regression equation.” In light of our findings in this paper, we recommend prior studies be read cautiously and reexamined.
indicates that at least one regressor is cointegrated with the dependent variable. It does not test whether multiple x's are all cointegrated with the dependent variable. Without understanding the alternative hypothesis, we can mistakenly think an equation is balanced and perhaps use the wrong limiting distribution and critical value to incorrectly reject a true null hypothesis. Many extant studies in political science run afoul of what we now know to be good practice. As Banerjee et al. (Reference Banerjee, Dolado, Galbraith and Hendry1993, p. 192) point out, “The moral of the econometricians’ story is the need to keep track of the orders of integration on both sides of the regression equation.” In light of our findings in this paper, we recommend prior studies be read cautiously and reexamined.
How can practitioners make reliable inferences using the GECM? First, be less ambitious with short data sets. Keele et al. (Reference Keele, Linn and Webb2016) suggest one regressor for every ten observations as a rule of thumb. Second, demonstrate robustness by trying models with different assumptions regarding the underlying univariate processes. Third, if one assumes that y and multiple x's are I(1), take great care to properly identify the cointegrating system. One possibility is to apply the Engle and Granger (Reference Engle and Granger1987) two-step cointegration process iteratively by adding individual regressors in order to sort which variables are cointegrated and which are not. Alternatively, Reference JohansenJohansen's (Reference Johansen1988, Reference Johansen1995) procedure allows for direct inference on the cointegrating vector to identify variables included in the equilibrium relationship.Footnote 14 Also, Stock and Watson (Reference Stock and Watson1993) estimate the cointegrating vector using dynamic OLS and parse out which variables are cointegrated. Ultimately, researchers must include I(1) x's as regressors only when they are part of the cointegrating system or otherwise mutually stationary with another regressor.
Fourth, when using the GECM, rely on long-run multipliers instead of $\alpha _1^\ast$![]() (Banerjee et al., Reference Banerjee, Dolado, Galbraith and Hendry1993, Chapter 2; DeBoef and Keele, Reference DeBoef and Keele2008). Finally, consider new methods that forego the knife-edged classification decision between I(0) and I(1) (e.g., Lebo and Young, Reference Lebo and Young2009; Lebo and Norpoth, Reference Lebo and Norpoth2011) or that entirely avoid univariate identification such as the bounds procedure introduced by Webb et al. (Reference Webb, Linn and Lebo2019, Reference Webb, Linn and Lebo2020).
(Banerjee et al., Reference Banerjee, Dolado, Galbraith and Hendry1993, Chapter 2; DeBoef and Keele, Reference DeBoef and Keele2008). Finally, consider new methods that forego the knife-edged classification decision between I(0) and I(1) (e.g., Lebo and Young, Reference Lebo and Young2009; Lebo and Norpoth, Reference Lebo and Norpoth2011) or that entirely avoid univariate identification such as the bounds procedure introduced by Webb et al. (Reference Webb, Linn and Lebo2019, Reference Webb, Linn and Lebo2020).
Overall, researchers should be careful when positing about more than two variables as being part of a cointegrating “system” (e.g., Ramirez, Reference Ramirez2009; Ura and Wohlfarth, Reference Ura and Wohlfarth2010; Enns, Reference Enns2014; Ura, Reference Ura2014). Rather than quickly interpreting one parameter of a fully specified GECM as evidence for joint cointegration of all I(1) regressors, it is helpful to examine cointegrating vectors one independent variable at a time. Equation balance is a useful concept for understanding when hypothesis tests follow standard limiting distributions but exclusively relying on a single parameter in the GECM is insufficient to assess balance and make credible inferences.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/psrm.2021.41.