A) System model

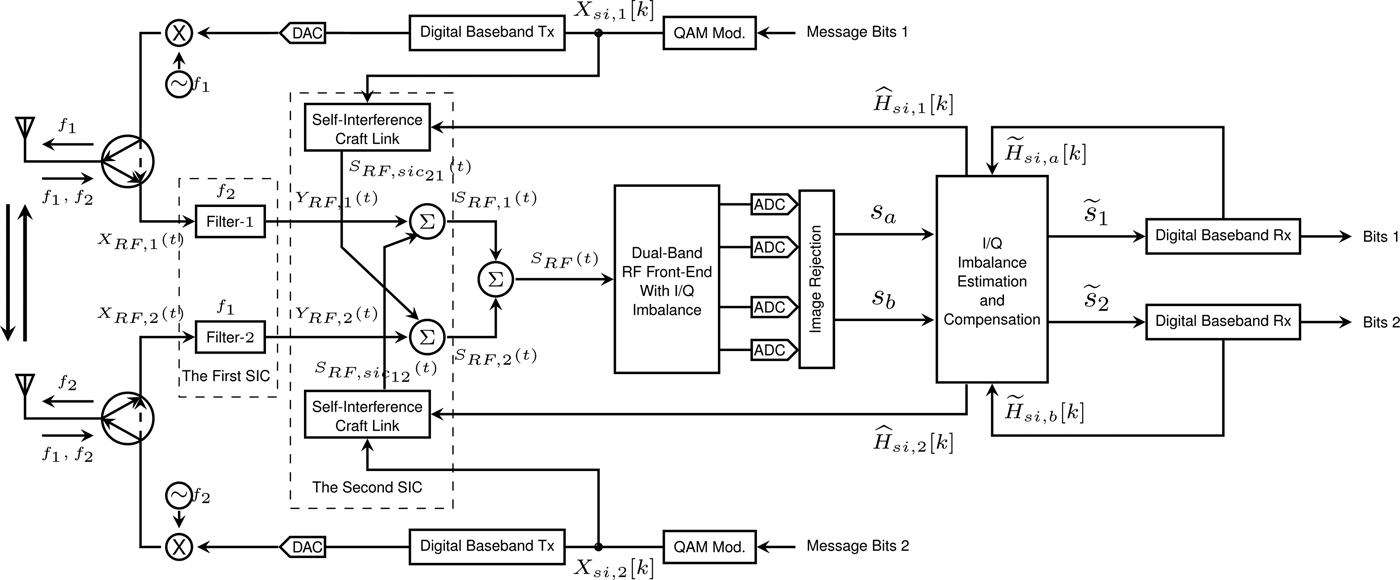
This section presents the general system model of the proposed flexible radio system as shown in Fig. 1 and the details of the FDDB OFDM radio node as shown in Fig. 2. Each of the proposed radio nodes employs two antennas, which are compatible with future multi-antenna systems. Each antenna is used for simultaneous transmission and reception via a circulator [Reference Bharadia, McMilin and Katti23, Reference Hong, McMilin and Katti24] separating the input and output signals. As this problem is symmetric, the radio node-B as shown in Fig. 1 is only studied. At the FDDB radio node-B, the first antenna transmits the RF signal with carrier frequency f ₁ and receives mixed RF signals including the RF signals from the distant radio node (FDDB radio node-A) with carrier frequency f ₁ and f ₂ and the RF signals from the local radio node (radio node-B) with carrier frequency f ₂. Therefore, the signals received by the ith antenna of the local radio node plus the self-interference signal leaked from the circulator can be expressed as:

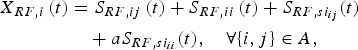(1)$$\eqalign{X_{RF,i}\, (t) & = S_{RF,ij}\, (t) + S_{RF,ii}\, (t) + S_{RF,si_{ij}}(t) \cr & \quad + aS_{RF,si_{ii}}(t),\quad \forall \{ i,j\} \in A,} $$

where S _RF,ij(t) and S _RF,ii(t) are the RF signals emitted from the jth antenna and the ith antenna of the distant radio node, respectively, and received by the ith antenna of the local radio node; ${S_{RF,si_{ij}}}$ denotes the internal RF self-interference signal transmitted from the jth antenna and received by the ith antenna of the local radio node; ${S_{RF,si_{ii}}}$ is the inner RF self-interference signal leaked from its own transmission, a being the inner-SI factor including multi-path reflection factor and inner leakage factor of the circulator and $A \triangleq \{ i \in [1,2],j \in [1,2],i + j = 3\} $. Due to the short distance between the antennas of the same radio node, the internal self-interference ${S_{RF,si_{ij}}}$ is much stronger than the signals from the distant radio node, e.g. 90~110 dB higher [Reference Bharadia, McMilin and Katti23, Reference Sabharwal, Schniter, Guo, Bliss, Rangarajan and Wichman25]. With respect to the inner self-interference, it is even stronger than the internal self-interference which relies on the fact that the circulator has only 15 dB of isolation [Reference Bharadia, McMilin and Katti23]. Therefore, the reception of the desired signal from the distant radio node is challenged by these two strong self-interference signals.

Fig. 1. Block diagram of the FDDB wireless radios.

Fig. 2. FDDB OFDM radio transceiver.

After each circulator, two self-interference cancellation stages are implemented to eliminate the inner self-interference signal leaked from its own transmission and reduce the internal self-interference signal from the other antenna of the local radio node.

B) Self-interference cancellation

If no measures are taken, the strong self-interference brought by the FDDB radio could saturate the receiver chain due to the fact that the ADC has a limited dynamic range. Therefore, it is necessary to suppress or reduce these self-interference signals to a tolerable level in order to obtain the expected system performance. In order to combat the inner and internal self-interference, two different self-interference cancellation methods are implemented.

1) THE FIRST SELF-INTERFERENCE CANCELLATION

The first self-interference cancellation is carried out by using BPF-i (BPF, perfect BPFs are assumed) with center frequency f _j to filter out the inner RF self-interference signal $aS_{RF,si_{ii}}$ induced by near-field reflection and the imperfect circulator isolation, as well as the RF signal S _RF,ii(t) with carrier frequency f _i from the ith antenna of the distant radio node. Then, the RF signals with carrier frequency f _j including the signal of interest S _RF,ij(t) and the over-the-air self-interference signal $S_{RF,si_{ij}}(t)$ can be represented by

(2)$${Y_{RF,i}}(t) = {S_{RF,ij}}(t) + {S_{RF,s{i_{ij}}}}(t),\quad \forall \{ i,j\} \in A.$$

2) THE SECOND SELF-INTERFERENCE CANCELLATION

In order to cancel the internal self-interference signal ${S_{RF,s{i_{ij}}}}(t)$ expressed in (2), [Reference Jain3, Reference Duarte, Dick and Sabharwal26] proposed ASIC and [Reference Everett, Sahai and Sabharwal11] studied the passive self-interference suppression. In this paper, we craft the RF cancellation signal as presented in [Reference Zhan, Villemaud and Gorce27] and carry out the cancellation at the RF stage as shown in Fig. 3.

Fig. 3. Architecture of self-interference cancellation for in-band full-duplex wireless with two antennas.

The system studied here is an OFDM based IEEE 802.11g WLAN with N = 64 subcarriers (N _nz = 52 non-zeros subcarriers). In each frame of IEEE 802.11g, the preamble consists of 10 identical short OFDM symbols (each of length 16) and two identical long training symbols (each of length 64). Each long training signal is generated via IFFT of 52 known BPSK symbols T _k, kε[1, N _nz], and 12 zeros.

Perfect frequency and timing synchronization are assumed in this paper. Therefore, at the receiver side, after the down-conversion of the RF signal received and removal of the cyclic prefix, the BB frequency domain signal can be obtained by the FFT of the time domain BB signal. The mth demodulated OFDM symbol can be expressed as

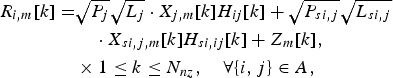(3)$$\eqalign{{R_{i,m}}[k] = & \sqrt {{P_j}} \sqrt {{L_j}} \cdot {X_{j,m}}[k]{H_{ij}}[k] + \sqrt {{P_{si,j}}} \sqrt {{L_{si,j}}} \cr & \quad \cdot {X_{si,j,m}}[k]{H_{si,ij}}[k] + {Z_m}[k], \cr & \times 1 \le k \le {N_{nz}},\quad \forall \{ i,j\} \in A,} $$

where P _j and P _si,j represent the transmit power of the signal of interest and self-interference signal, respectively, L _j and L _si,j are the propagation loss of the intended radio link and self-interference radio link, X _j,m[k] and X _si,j,m[k] denote the transmit symbol carried by the kth subcarrier from the distant radio node and local radio node, H _ij[k] and H _si,ij[k] represent the transfer function of the kth subcarrier channel of the distant radio link and self-interference radio link. Z _m[k] corresponds to the frequency domain expression of the thermal noise and follows the normal distribution ${\rm \cal N}(0,\delta _n^2 )$, N _nz denotes the number of nonzero subcarriers. X _j,m[k] can be treated as mutually independent random variables independent of H _ij[k]. X _si,j,m[k] has the same characteristics as X _j,m[k]. Without loss of generality, the transfer function H _ij[k] and H _si,ij[k] are normalized and with average channel gain E|H _ij[k]|² = E|H _si,ij[k]|² = 1.

From (3), the self-interference signal can be canceled if the Channel State Information of the self-interference channel is available because the transmit symbols X _si,j,m[k] are known. Therefore, the self-interference channel estimation is carried out in the following subsection before implementing the second self-interference cancellation.

Self-interference channel estimation.:

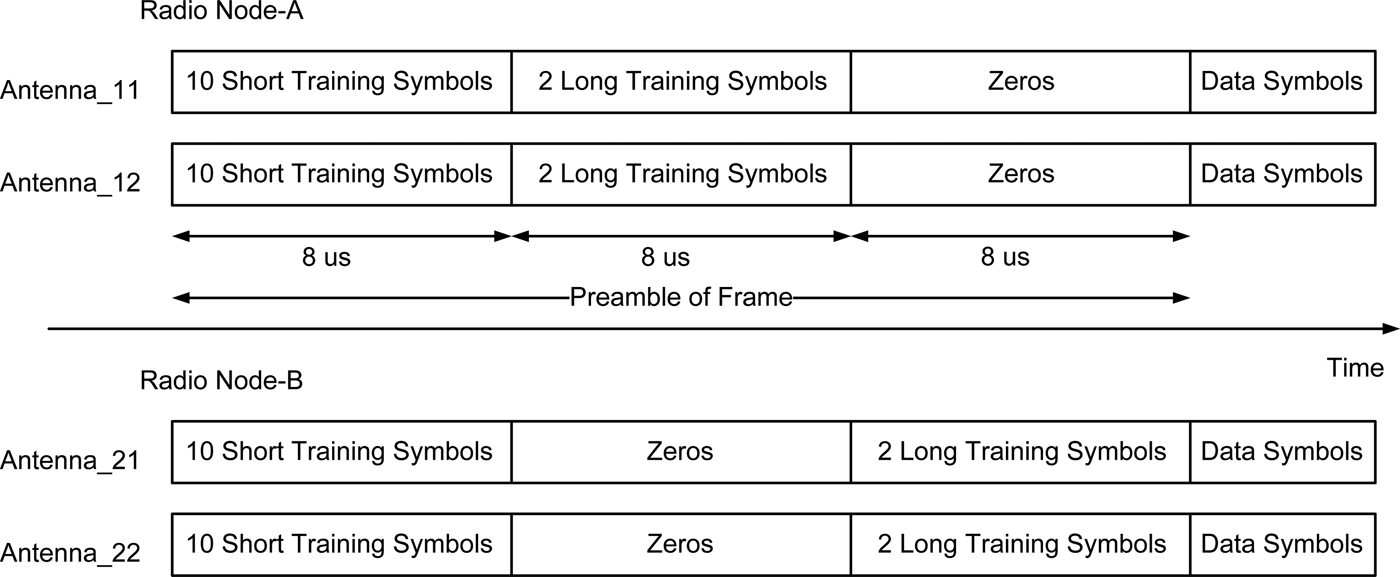
In IEEE 802.11g, the channel estimation is carried out by dividing the received demodulated long training symbols by the pilot pattern with the known BPSK symbol sequences T[k], kε[1, N _nz] with E{|T[k]|²} = 1. In order to avoid the self-interference channel estimation error caused by the signal of interest, the long training signals from different radio nodes are appointed to be transmitted at different time slots. Namely, the frame structure is modified as shown in Fig. 4. Therefore, the estimated channel transfer function after normalization is:

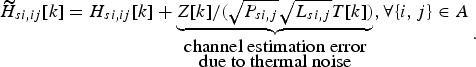(4)$$\eqalign{&{{\widetilde H}_{si,ij}}[k] = {H_{si,ij}}[k] + \underbrace {Z[k]/(\sqrt {{P_{si,j}}} \sqrt {{L_{si,j}}} T[k])}_{{\hbox{channel estimation error} \atop \hbox{due to thermal noise}}},\forall \{ i,j\} \in A}.$$

The second term of the right side of the equation (4) is denoted as the channel estimation error of the kth subcarrier channel due to the thermal noise.

Fig. 4. Frame structure for the FDDB IEEE 802.11g.

Self-interference cancellation.:

With the estimated coefficients of the self-interference channel available, the crafted RF cancellation signal as presented in [Reference Zhan, Villemaud and Gorce27] is represented by

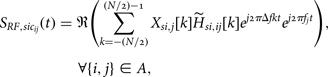(5)$$\eqalign{& {S_{RF,si{c_{ij}}}}(t) ={\frak R} \left( {\sum\limits_{k = - (N/2)}^{(N/2) - 1} {X_{si,j}}[k]{{\widetilde H}_{si,ij}}[k]{e^{j2\pi \Delta fkt}}{e^{j2\pi {f_j}t}}} \right), \cr & \qquad\qquad\quad\forall \{ i,j\} \in A,} $$

where ${\frak R}$ (·) denotes the real part of (·), X _{si, j}[k] is the complex symbol carried by the kth subcarrier and to be emitted from the jth antenna of the local radio node, ${\widetilde H}_{si,ij}[k]$ represents the estimated coefficient of kth subcarrier channel of the over-the-air self-interference channel from the jth antenna to the ith antenna of the local radio node, and Δf denotes the subcarrier space.

With the RF cancellation signal available, the second self-interference cancellation is carried out via subtracting the RF signal Y _RF,i(t) by the crafted RF cancellation signal ${S_{RF,si{c_{ij}}}}(t)$ at the RF adder stage. After that, the remaining signals to be input to the dual-band RF front-end is expressed as

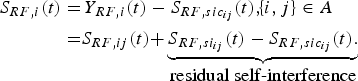(6)$$\eqalign{{S_{RF,i}}(t) = &\, {Y_{RF,i}}(t) - {S_{RF,si{c_{ij}}}}(t),\!\!\{ i,j\} \in A \cr = &{{S_{RF,ij}}(t) +} \underbrace {{S_{RF,s{i_{ij}}}}(t) - {S_{RF,si{c_{ij}}}}(t).}_{\hbox{residual self-interference}}} $$

Therefore, the RF signal S _{RF, i}(t) to be input into the dual-band RF front-end comprises the desired signal S _RF,ij(t) from the distant radio node and the residual self-interference. In order to quantify the impact of the residual self-interference on the proposed radio transceiver, the power of the residual self-interference will be calculated in the following subsection.

Residual self-interference

Although the self-interference cancellation is implemented at the RF component, the residual self-interference can be calculated and analyzed in the frequency domain. Therefore, we can equivalently understand that the self-interference cancellation is done by subtracting the cancellation signal $\sqrt {{P_{si,j}}} \sqrt {{{\widetilde L}_{si,j}}} {X_{si,j,m}}[k]{\widetilde H}_{si,ij,m}[k]$ from the self-interference signal received in the frequency domain. After the interference cancellation, the residual self-interference can be represented by

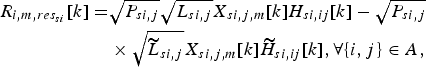(7)$$\eqalign{{R_{i,m,re{s_{si}}}}[k] = & \sqrt {{P_{si,j}}} \sqrt {{L_{si,j}}} {X_{si,j,m}}[k]{H_{si,ij}}[k] - \sqrt {{P_{si,j}}} \cr &\times\sqrt {{{\widetilde L}_{si,j}}} {X_{si,j,m}}[k] {\widetilde H}_{si,ij}[k],\forall \{ i,j\} \in A,} $$

L _si,j, denoting the large-scale fading of the self-interference link, can be obtained or calculated by previous measurements. Therefore, ${\widetilde L}_{si,j} = {L_{si,j}}$ can be guaranteed. Then, the residual self-interference can be simplified as

(8)$${R_{i,m,re{s_{si}}}}[k] = - \displaystyle{{{X_{si,j,m}}[k]} \over {T[k]}}{Z_{m^{\prime}}}[k].$$

Because of the independence between X _si,j,m[k] and T[k] in (8), the power of the residual self-interference is

(9)$$P_{i,si,residual} = E \left[ {\left\vert R_{i,m,res_{si}} [k] \right\vert ^2} \right] = \delta _n^2. $$

From (9), the power of residual self-interference after self-interference cancellation is equal to that of the receiver thermal noise [Reference Zhan, Villemaud and Gorce28]. Therefore, the residual self-interference can be regarded as another additive thermal noise superimposed on the desired signal.

C) Dual-band RF front-end

The two received RF signals ${S_{RF,1}^{\prime}}(t) \triangleq {S_{RF,2}}(t)$ with carrier frequency f ₁ and ${S_{RF,2}^{\prime}}(t) \triangleq {S_{RF,1}}(t)$ with carrier frequency f ₂, after self-interference cancellation, will be down-converted to BB signal by utilizing the double I/Q structure as shown in Fig. 5.

Fig. 5. Architecture of dual-band RF front-end.

1) DUAL-BAND RF FRONT-END WITHOUT I/Q IMBALANCE

In order to facilitate the theoretical study of the dual-band RF front-end, s ₁ = I ₁ + jQ ₁ and s ₂ = I ₂ + jQ ₂(j ² = −1) are used to denote the received equivalent BB complex symbols carried by the carrier frequencies f ₁ and f ₂. Then, the RF signals ${S_{RF,1}^{\prime}}(t)$ and ${S_{RF,2}^{\prime}}(t)$ at the input of the double I/Q structure are:

(10)$${S_{RF,1}^{\prime}}(t) = {I_1}(t)\,{\rm cos}(2\pi\, {f_1}t) - {Q_1}(t)\,{\rm sin}(2\pi\, {f_1}t),$$

(11)$${S_{RF,2}^{\prime}}(t) = {I_2}(t)\,{\rm cos}(2\pi\, {f_2}t) - {Q_2}(t)\,{\rm sin}(2\pi\, {f_2}t).$$

Note that the signal model in (10) and (11) is reasonably valid even for an interference and noisy environment because I _i(t) can represent the sum of the real part of the received symbol, including the desired data and the residual self-interference data symbol, and noise, Q _i(t) can represent the sum of the image part of the received symbol including desired data and residual self-interference data symbol and the receiver thermal noise.

As shown in Fig. 5, after the mixed signal ${S_{RF}}(t) = {S_{RF,1}^{\prime}}(t) + {S_{RF,2}^{\prime}}(t)$ going through the first frequency translation stage with carrier frequency f _LO = (f ₁ + f ₂)/2, the band pass signal is filtered out. Then, the I/Q branch of IF signal can be obtained as

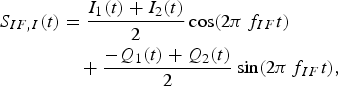(12)$$\eqalign{ {S_{IF,I}}(t) &= \displaystyle{{{I_1}(t) + {I_2}(t)} \over 2}\,{\rm cos}(2\pi\, {f_{IF}}t) \cr & \quad + \displaystyle{{ - {Q_1}(t) + {Q_2}(t)} \over 2}\,{\rm sin}(2\pi\, {f_{IF}}t),} $$

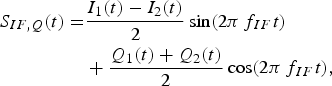(13)$$\eqalign{ {S_{IF,Q}}(t) =& \displaystyle{{{I_1}(t) - {I_2}(t)} \over 2}\,{\rm sin}(2\pi\, {f_{IF}}t) \cr & + \displaystyle{{{Q_1}(t) + {Q_2}(t)} \over 2}\,{\rm cos}(2\pi\, {f_{IF}}t),} $$

where f _IF = (f ₁ − f ₂)/2 = f ₁ − f _LO = f _LO − f ₂.

The BB signals s _II(t), s _IQ(t), s _QI(t), and s _QQ(t) obtained by down-converting the IF signals S _IF,I(t) and S _IF,Q(t) with carrier frequency f _IF can be expressed as

(14)$${s_{II}}(t) = \displaystyle{{{I_1}(t) + {I_2}(t)} \over 4},$$

(15)$${s_{IQ}}(t) = \displaystyle{{{Q_1}(t) - {Q_2}(t)} \over 4},$$

(16)$${s_{QI}}(t) = \displaystyle{{{Q_1}(t) + {Q_2}(t)} \over 4},$$

(17)$${s_{QQ}}(t) = \displaystyle{{ - {I_1}(t) + {I_2}(t)} \over 4}.$$

After the ADC, s _II = I ₁ + I ₂/4, s _IQ = Q ₁ − Q ₂/4, s _QI = (Q ₁ + Q ₂)/4, s _QQ = (−I ₁ + I ₂)/4 can be obtained. Then, using digital-image-rejection, the received BB complex symbols s _a and s _b corresponding to symbols s ₁ and s ₂ are given by

(18)$$\eqalign{{s_a} = {s_{II}} - {s_{QQ}} + j({s_{IQ}} + {s_{QI}}) = \displaystyle{{{I_1} + j{Q_1}} \over 2} = \displaystyle{{{s_1}} \over 2},} $$

(19)$$\eqalign{{s_b} = {s_{II}} + {s_{QQ}} + j( - {s_{IQ}} + {s_{QI}}) = \displaystyle{{{I_2} + j{Q_2}} \over 2} = \displaystyle{{{s_2}} \over 2}.} $$

From (18) and (19), the two different kinds of signals (even with different physical layer technologies) are perfectly separated by using double I/Q structure. That means that the dual-band radio receiver can simultaneously process two different kinds of signals with different carrier frequencies by using a relative simple RF front-end compared with conventional multiband radios. However, this noticeable flexibility can be obtained only when the RF front-end is theoretically ideal. In the practical implementation of wireless system, any part of the I/Q imbalance of the RF front-end may contribute to degrade the radio receiver performance and this is no exception for the FDDB OFDM radio. In the following Section II.C.2, the I/Q imbalance model and its impact on the FDDB OFDM radio receiver will be studied.

2) DUAL-BAND RF FRONT-END WITH I/Q IMBALANCE

The purpose of a radio front-end is to down-convert the RF signal to BB analog signal. However, all of the analog components (such as mixers, filters, and ADC) at the radio front-end lead to deviations from the desired 90° phase shift and the desired equal gain in the I and Q branches as shown in Fig. 6. Here, ΔA and Δϕ are used to denote the amplitude imbalance and the phase imbalance, respectively.Footnote ¹ In dual-band radio receivers, this I/Q imbalance causes undesirable mutual signal leakage. After double I/Q frequency translation with I/Q imbalance, the two BB analog signals can be expressed as [Reference Burciu, Villemaud, Verdier and Gautier4]

(20)$${s_a} = \alpha {s_1} + \beta s_2^{\ast}, $$

(21)$${s_b} = \alpha {s_2} + \beta s_1^{\ast}, $$

where s _a and s _b are the two output signals from the double I/Q structure with I/Q imbalance, (·)^* denotes complex conjugation, and the I/Q imbalance coefficients α and β [Reference Burciu, Villemaud, Verdier and Gautier4] are represented by

(22)$$\alpha = \displaystyle{{1 + (1 + \Delta A)\,{e^{ - j\Delta \phi}}} \over 2},$$

(23)$$\beta = \displaystyle{{1 - (1 + \Delta A)\,{e^{ + j\Delta \phi}}} \over 2}.$$

According to the definition (22) and (23), we get

(24)$$\alpha + {\beta ^{\ast}} = {\alpha ^{\ast}} + \beta = 1.$$

Especially, with an ideal I/Q, i.e. ΔA = 0 and Δϕ = 0, therefore α = 1 and β = 0, which means the received two different carrier frequency signals are separated completely by using double I/Q structure just as the study case in Section II.C.1.

Fig. 6. Dual-band RF front-end with I/Q imbalance.

From the equations (20) and (21), the I/Q imbalance makes the image of the other signal superimpose on the desired signal. This mutual leakage of signals will be regarded as interference to degrade the performance of the radio reception. However, if the I/Q imbalance parameters (α and β) are known, s ₁ and s ₂ can be calculated as

(25)$${s_1} = \displaystyle{{{\alpha ^{\ast}}{s_a} - \beta s_b^{\ast}} \over {\left\vert \alpha \right\vert{^{^2}} - \left\vert \beta \right\vert{^{^2}}}},$$

(26)$$s_{2} = {\displaystyle{\alpha ^{\ast} {s_b} - \beta s_a^{\ast}} \over {\left\vert \alpha \right\vert{^{^2}} - \left\vert \beta \right\vert{^{^2}}}}. $$

That means, even with I/Q imbalance, the two received signals can be separated completely just like the RF front-end without I/Q imbalance does if the values of α and β are known. Unfortunately, the exact values of α and β are difficult to obtain. However, α and β are quite stable due to the reason that the values of ΔA and Δϕ are dependent on the performance of analog devices in the RF front-end. Therefore, the values can be estimated by using a training sequence.

In order to mitigate the I/Q imbalance existing in the FDDB RF front-end, the algorithm of the I/Q imbalance estimation and compensation will be presented in Section III.

D) Complexity comparison

The proposed FDDB OFDM radio is based on a cooperative combination of full-duplex OFDM radio and dual-band RF front-end. Compared with the conventional half-duplex radio system, the full-duplex radio needs an auxiliary radio link to craft an RF cancellation signal, which requires some additional hardware components [Reference Zhan, Villemaud and Gorce27]. Dual-band RF front-end could significantly reduce the system complexity and power consumption compared with the current multimode radio system [Reference Burciu, Villemaud, Verdier and Gautier4]. Therefore, the flexible FDDB OFDM radio could realize a multimode radio with less complexity compared with the conventional multimode radio, but only at a cost of additional hardware components.

A) I/Q imbalance estimation

In our design, the I/Q imbalance estimation is carried out during the self-interference channel estimation. Therefore, the received symbols s ₁ and s ₂ in (20) and (21) just include the long training symbols from its own transmitter and the thermal noise during the I/Q imbalance estimation because different radio nodes take different time slots for transmitting the long training signals. Therefore, these two equations can be rewritten during the time of self-interference channel estimation as

(27)$${s_{lts,a}} = \alpha {s_{lt{s_{si}},12}} + \beta s_{lt{s_{si}},21}^{\ast}, $$

(28)$${s_{lts,b}} = \alpha {s_{lt{s_{si}},21}} + \beta s_{lt{s_{si}},12}^{\ast}, $$

where ${s_{lt{s_{si}},12}}$ is the long training symbols transmitted from the second antenna and received by the first antenna of the local radio node, and ${s_{lt{s_{si}},21}}$ is the long training symbols from the first antenna and received by the second antenna of the local radio node.

According to (27) and (28), and using the least square (LS) channel estimation algorithm in the frequency domain, the estimated coefficients of the self-interference channel-1 H _{si, a} and channel-2 H _{si, b} can be expressed as

(29)$$H_{si,a}[k] = \alpha {\widetilde H}_{si,12}[k] + \beta T^{\prime}[k] \cdot {\widetilde H}_{si,21}^{\ast} [N_{nz} - k + 1],$$

(30)$${H_{si,b}}[k] = \alpha {\widetilde {H}_{si,21}}[k] + \beta T^{\prime}[k] \cdot {\widetilde H}_{si,12}^{\ast} [{N_{nz}} - k + 1],$$

where denotes the coefficient of the kth subcarrier channel of the self-interference channel from the secnd antenna to the first antenna of the local radio node; ${\widetilde H}_{si,21}[k]$ denotes the coefficient of the kth subcarrier channel of the self-interference channel from the first antenna to the second antenna of the local radio node. ${\widetilde H}_{si,21}[{N_{nz}} - k + 1]$ and ${\widetilde H}_{si,12}[{N_{nz}} - k + 1]$ are the mirror images of the channel ${\widetilde H}_{si,21}[k]$ and ${\widetilde H}_{si,12}[k]$, $T^{\prime}[k] \triangleq T[k]T[{N_{nz}} - k + 1]$, and “·” denotes component-wise vector multiplication. (29) and (30) show that each channel estimation consists of two components: one is the self-interference channel which is scaled by a complex factor α ≈ 1 and the other one is the mirror image of the other self-interference channel scaled by factor βT′[k] ≈ 0. As a consequence, the I/Q imbalance in the double frequency structure makes the mirror image of the self-interference channel superimpose on the desired self-interference channel. This channel estimation error induced by I/Q imbalance will affect the equalization at the receiver.

In the FDDB wireless, the distance between the antennas of the same radio node is very short, so the power of the line-of-sight path dominates the self-interference channel. As a consequence, the self-interference channel is close to a frequency flat fading channel [Reference Everett, Sahai and Sabharwal11]. From (29) and (30), if α and β are known exactly, the self-interference channel ${\widetilde H}_{si,12}[k]$ and ${\widetilde H}_{si,21}[k]$ can be obtained as

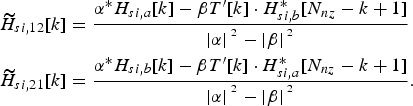(31)$$\eqalign{& {\widetilde H}_{si,12} [k] = {\displaystyle{{\alpha ^{\ast} H_{si,a}[k] - \beta T^{\prime}[k] \cdot H_{si,b}^{\ast} [N_{nz} - k + 1]} \over {\left\vert \alpha \right\vert{^{^2}} - \left\vert \beta \right\vert{^{^2}}}}} \cr & {\widetilde H}_{si,21}[k] = {\displaystyle{{\alpha ^{\ast} H_{si,b}[k] - \beta T^{\prime}[k] \cdot H_{si,a}^{\ast} [N_{nz} - k + 1]} \over {\left\vert \alpha \right\vert{^{^2}} - \left\vert \beta \right\vert{^{^2}}}}.}} $$

The self-interference channel ${\widetilde H}_{si,12}[k]$ and ${\widetilde H}_{si,21}[k]$ are frequency flat fading which can be shown as in Fig. 7, while the estimated self-interference channel H _si,a[k] and H _si,b[k] with I/Q imbalance are more likely a frequency selective fading channel. With the estimated ${\widetilde \alpha} $ and ${\widetilde \beta} $ under the I/Q imbalance condition, the virtual self-interference channel ${\widehat{H}_{si,12}}[k]$ and ${\widehat{H}_{si,21}}[k]$ can be obtained as

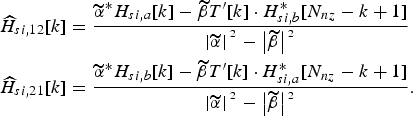(32)$$\eqalign{& {\widehat H}_{si,12}[k] = {\displaystyle{{\widetilde \alpha}^{\ast} H_{si,a}[k] - {\widetilde \beta}T^{\prime}[k] \cdot H_{si,b}^{\ast} [N_{nz} - k + 1]} \over {\left\vert {\widetilde \alpha} \right\vert{^{^2}} - \left\vert {\widetilde \beta} \right\vert{^{^2}}}} \cr & {\widehat H}_{si,21}[k] = {\displaystyle{{{\widetilde \alpha}^{\ast} H_{si,b}[k] - {\widetilde \beta}T^{\prime}[k] \cdot H_{si,a}^{\ast} [N_{nz} - k + 1]} \over {\left\vert{\widetilde \alpha} \right\vert{^{^2}} - \left\vert{\widetilde \beta} \right\vert{^{^2}}}}}.} $$

The more accurate the estimation of ${\widetilde \alpha} $ and ${\widetilde \beta} $, the more closely the virtual self-interference channels ${\widehat{H}_{si,12}}[k]$ and ${\widehat{H}_{si,21}}[k]$ are to the self-interference channel ${\widetilde H}_{si,12}[k]$ and ${\widetilde H}_{si,21}[k]$. Therefore, the I/Q imbalance parameters $({\widetilde \alpha}, {\widetilde \beta} )$ that make the virtual self-interference channel ${\widehat{H}_{si,1}}[k]$ and ${\widehat{H}_{si,2}}[k]$ as flat as possible like the self-interference channels do are what we want to obtain. The mean square error (MSE) of the consecutive subcarrier channels is defined as the criteria to measure how flat the virtual self-interference channel is as follows

(33)$${\rm MS}{{\rm E}_1} = \sum\limits_k \left\vert{\widehat{H}_{si,12}}[k + 1] - {\widehat{H}_{si,12}}[k] \right\vert{^2},$$

(34)$${\rm MS}{{\rm E}_2} = \sum\limits_k \left\vert{\widehat{H}_{si,21}}[k + 1] - {\widehat{H}_{si,21}}[k] \right\vert{^2}.$$

For the symmetric analysis, the case MSE ₁ is studied first. Then, according to (32), we obtain

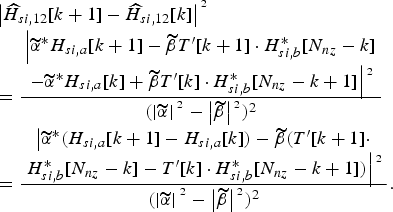(35)$$\eqalign{&\left\vert {\widehat H}_{si,12}[k + 1] - {\widehat H}_{si,12}[k] \right\vert{^{^2}}\cr &= \displaystyle{\matrix{\left\vert {\widetilde \alpha}^{\ast}H_{si,a}[k + 1] - {\widetilde \beta} T^{\prime}[k + 1] \cdot H_{si,b}^{\ast} [N_{nz} - k] \right. \cr \left. - {\widetilde \alpha}^{\ast}H_{si,a}[k] + {\widetilde \beta} T^{\prime}[k] \cdot H_{si,b}^{\ast} [N_{nz} - k + 1] \right\vert{^{^2}}} \over (\left\vert {\widetilde \alpha} \right\vert{^{^2}} - \left\vert {\widetilde \beta} \right\vert{^{^2}})^2} \cr &= \displaystyle{\matrix{\left\vert {\widetilde \alpha}^{\ast}(H_{si,a}[k + 1] - H_{si,a}[k]) - {\widetilde \beta} (T^{\prime}[k + 1]\cdot\right. \cr \left. H_{si,b}^{\ast} [N_{nz} - k] - T^{\prime}[k] \cdot H_{si,b}^{\ast} [N_{nz} - k + 1]) \right\vert{^{^2}}} \over (\left\vert {\widetilde \alpha} \right\vert{^{^2}} - \left\vert {\widetilde \beta} \right\vert{^{^2}})^2}.} $$

In order to simplify the expression (35), we define

(36)$$\Delta {H_{si,a}}[k] = {H_{si,a}}[k + 1] - {H_{si,a}}[k],$$

(37)$$\eqalign{ \Delta {H_{si,b}^{\prime}}[k] =& T^{\prime}[k + 1] \cdot H_{si,b}^{\ast} [{N_{nz}} - k] \cr & - T^{\prime}[k] \cdot H_{si,b}^{\ast} [{N_{nz}} - k + 1].} $$

After plugging (36) and (37) into (35), it can be rewritten as

(38)$$\eqalign{& \left\vert {\widehat{H}_{si,12}}[k + 1] - {\widehat{H}_{si,12}}[k] \right\vert{^2} \cr & \quad = \displaystyle{{\left\vert{{\widetilde \alpha} ^{\ast}} \cdot \Delta {H_{si,a}}[k] - {\widetilde \beta} \cdot \Delta {H^{\prime}_{si,b}}[k{]} \right\vert{^{^2}}} \over {{{(\left\vert{\widetilde \alpha} \right\vert{^{^2}} - \left\vert{\widetilde \beta} \right\vert{^{^2}})}^2}}}.}$$

Since the self-interference channel is a flat fading channel, the adjacent subcarrier channel should be very close to each other. However, the I/Q imbalance parameters (${\widetilde \alpha} $ and ${\widetilde \beta} $) increase the fluctuation of the flat fading self-interference channel ${\widehat{H}_{si,12}}[k]$ and ${\widehat{H}_{si,21}}[k]$. Then, the parameters (${\widetilde \alpha} $ and ${\widetilde \beta} $) which make the $\left\vert {\widehat{H}_{si,12}}[k + 1] - {\widehat{H}_{si,12}}[k] \right\vert$ as small as possible are the values we want to obtain. Therefore, the optimization problem can be expressed as

(39)$$\eqalign{\left({\widetilde \alpha}_{o,1},{\widetilde \beta}_{o,1} \right) & = \mathop{\arg \min} \limits_{{\widetilde \alpha} \in {\rm \cal C}, {\widetilde \beta} \in {\rm \cal C}} \left\{\sum\limits_k \left\Vert {\widehat H}_{si,12}[k + 1] - {\widehat H}_{si,12}[k] \right\Vert^2 \right\} \cr & = \mathop {\arg \min} \limits_{{\widetilde \alpha} \in {\rm \cal C}, {\widetilde \beta} \in {\rm \cal C}} \left\{ \displaystyle{\sum\limits_k \left\Vert {\widetilde \alpha}^{\ast} {\cdot} \Delta H_{si,a}[k] - {\widetilde \beta} {\cdot} \Delta H_{si,b}^{\prime}[k] \right\Vert^2 \over \left(\left\vert {\widetilde \alpha} \right\vert^2 - \left\vert {\widetilde \beta} \right\vert^2\right)^2} \right\},} $$

where ${\cal C}$ denotes the set of complex number.

Fig. 7. The estimated magnitude of each subcarrier channel of the over-the-air self-interference channel with or without I/Q Imbalance. When without I/Q imbalance, the estimated over-the-air self-interference channel is almost a frequency flat fading channel, while this self-interference channel will be a frequency selective fading channel when I/Q imbalance (ΔA = 0.2, Δϕ = 10°) exist in the FDDB radio front-end.

In order to get the optimal estimated values $({\widetilde \alpha} _{o,1},{\widetilde \beta} _{o,1})$, taking the partial derivative of the MSE₁ with respect to ${\widetilde \beta} $ as

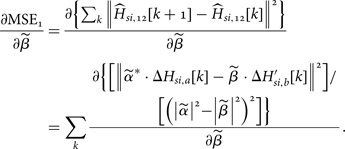(40)$$\eqalign{\displaystyle{\partial {\rm MS}{\rm E}_1 \over \partial {\widetilde \beta}} & = \displaystyle{\partial \left\{\sum\nolimits_k \left\Vert {\widehat{H}}_{si,12} [k + 1] - {\widehat{H}}_{si,12} [k] \right\Vert^2 \right\} \over \partial {\widetilde \beta}} \cr & = \sum\limits_k \displaystyle{\matrix{\partial \left\{ \left[\left\Vert {\widetilde \alpha}^{\ast} \cdot \Delta H_{si,a}[k] - {\widetilde \beta} \cdot \Delta H_{si,b}^{\prime}[k] \right\Vert^2 \right] / \right. \cr \left. \left[\left(\left\vert {\widetilde \alpha} \right\vert^2 - \left\vert {\widetilde \beta} \right\vert^2 \right)^2 \right] \right\}} \over \partial {\widetilde \beta}}.} $$

Since ${(\left\vert {\widetilde \alpha} \right\vert{^2} - \left\vert {\widetilde \beta} \right\vert{^2})^2} \approx 1$, remains valid for high gain imbalance (ΔA = 0.2) and phase imbalance (Δϕ = 10), then (40) can be simplified as

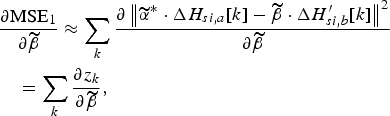(41)$$\eqalign{& \displaystyle{{\partial {\rm MSE}_1} \over {\partial {\widetilde \beta}}} \approx \sum\limits_k {\displaystyle{{\partial \left\Vert {\widetilde \alpha}^{\ast} \cdot \Delta{H_{si,a}}[k] - {\widetilde \beta} \cdot \Delta{H^{\prime}_{si,b}}[k] \right\Vert^2}} \over {\partial {\widetilde \beta}}} \cr & \quad = \sum\limits_k {\displaystyle{{\partial {z_k}} \over {\partial {\widetilde \beta}}}},} $$

where ${z_k} \triangleq {\left\Vert {{{\widetilde \alpha} ^{\ast}} \cdot \Delta {H_{si,a}}[k] - {\widetilde \beta} \cdot \Delta {H_{si,b}}^{\prime}[k]} \right\Vert ^2}$ which is function of ${\widetilde \beta} = {\frak R} ({\widetilde \beta} ) + j\Im ({\widetilde \beta} )$. (29) and (30) show that the complex value ${\widetilde \beta} $ is the key factor that makes the originally flat self-interference channel fluctuate more. Therefore, the problem of calculating the optimal ${\widetilde \beta} $ in (41) becomes solving the Cauchy-Riemann equations as following

(42)$$\sum\limits_k \displaystyle{{\partial {\frak R} ({z_k})} \over {\partial {\frak R} ({\widetilde \beta} )}} = \sum\limits_k \displaystyle{{\partial \Im ({z_k})} \over {\partial \Im ({\widetilde \beta} )}},$$

(43)$$\sum\limits_k - \displaystyle{{\partial {\frak R} ({z_k})} \over {\partial \Im ({\widetilde \beta} )}} = \sum\limits_k \displaystyle{{\partial \Im ({z_k})} \over {\partial {\frak R} ({\widetilde \beta} )}}.$$

As it can be seen, the definition z _k is function of ${\widetilde \beta} $, which can be expressed as

(44)$$\eqalign{{z_k} = & \left\vert {\widetilde \alpha} \right\vert^2 \left\vert \Delta {H_{si,a}}[k] \right\vert^2 + \left\vert{\widetilde \beta} \right\vert^2 \left\vert \Delta {{H}_{si,b}^{\prime}}[k]\right\vert^2 - {\widetilde \alpha} {\widetilde \beta} {\cdot} \Delta H_{si,a}^{\ast} [k] \cr & \quad {\cdot} \Delta {{H}_{si,b}^{\prime}}[k] - {\widetilde \alpha} ^{\ast}{\widetilde \beta} ^{\ast} \cdot \Delta {H_{si,a}}[k] \cdot \Delta {{H}^{\prime \ast}}_{si,b} [k].} $$

Then, the real and image part of z _k can be obtained as

(45)$$\eqalign{{\frak R} ({z_k}) & = \left\vert{\widetilde \alpha} \right\vert{^2}\left\vert \Delta H_{si,a}[k] \right\vert{^2} +\left({\frak R} \left({\widetilde \beta}\right)^2 + \Im \left({\widetilde \beta}\right)^2\right)\left\vert \Delta H_{si,b}^{\prime}[k] \right\vert{^2} \cr & \quad - 2{\frak R} \left({\widetilde \alpha} \cdot \Delta H_{si,a}^{\ast} [k] \cdot \Delta H_{si,b}^{\prime}[k]\right) {\frak R} \left({\widetilde \beta}\right) \cr & \quad + 2 \Im \left({\widetilde \alpha} \cdot \Delta H_{si,a}^{\ast} [k] \cdot \Delta H_{si,b}^{\prime}[k]\right) \Im \left({\widetilde \beta}\right),}$$

(46)$$\Im ({z_k}) = 0.$$

According to (45) and (46), (42) and (43) can be rewritten as

(47)$$\sum\limits_k \displaystyle{{\partial {\frak R} ({z_k})} \over {\partial {\frak R} ({\widetilde \beta} )}} = 0,$$

(48)$$\sum\limits_k - \displaystyle{{\partial {\frak R} ({z_k})} \over {\partial \Im ({\widetilde \beta} )}} = 0.$$

Based on (47) and (48), the real and image part of the optimal estimated ${\widetilde \beta} $ can be obtained as

(49)$${\frak R} ({\widetilde \beta}_{o,1}) = {\displaystyle{{\sum\nolimits_k {\frak R} ({\widetilde \alpha}_{o,1} \cdot \Delta H_{si,a}^{\ast} [k] \cdot \Delta {H^{\prime}}_{si,b}[k])} \over {\sum\nolimits_k \left\vert \Delta {H^{\prime}}_{si,b}[k] \right\vert^2}}}, $$

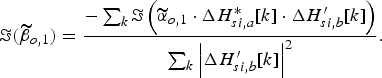(50)$$\Im ({\widetilde \beta} _{o,1}) = \displaystyle{{ - \sum\nolimits_k \Im \left({\widetilde \alpha} _{o,1} \cdot \Delta H_{si,a}^{\ast}[k] \cdot \Delta H_{si,b}^{\prime}[k]\right)} \over {\sum\nolimits_k {\left\vert \Delta H_{si,b}^{\prime}[k] \right\vert^2}}}. $$

Therefore, the optimal value ${\widetilde \beta} _{o,1}$ of the estimated ${\widetilde \beta} $ is expressed as

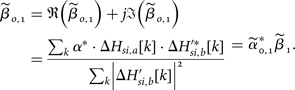(51)$$\eqalign{ {\widetilde \beta} _{o,1} &= {\frak R} \left({\widetilde \beta}_{o,1} \right) + j\Im \left({\widetilde \beta}_{o,1} \right) \cr & = {\displaystyle{{\sum\nolimits_{k} \alpha^{\ast} \cdot \Delta H_{si,a}[k] \cdot \Delta H_{si,b}^{\prime \ast}[k]} \over {\sum\nolimits_k \left\vert \Delta H_{si,b}^{\prime}[k] \right\vert^2}}} = {\widetilde \alpha}_{0,1}^{\ast} {\widetilde \beta}_1}. $$

Here, we define ${\widetilde \beta} _1$$

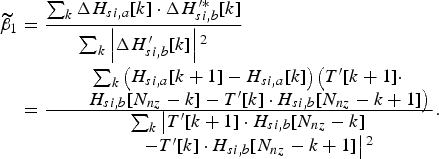(52)$$\eqalign{ {\widetilde \beta}_1 &= {\displaystyle{{\sum\nolimits_k \Delta H_{si,a}[k] \cdot \Delta H_{si,b}^{\prime \ast} [k] } \over {\sum\nolimits_k \left\vert \Delta H_{si,b}^{\prime}[k] \right\vert{^2}} }} \cr & = {\displaystyle{{\matrix{& \sum\nolimits_k \left(H_{si,a}[k + 1] - H_{si,a}[k] \right)\left(T^{\prime}[k + 1] \cdot \right. \cr & \quad \left. H_{si,b}[N_{nz} - k] - T^{\prime}[k] \cdot H_{si,b}[N_{nz} - k + 1]\right)}} \over {\matrix{& \sum\nolimits_k \left\vert T^{\prime}[k + 1] \cdot H_{si,b}[N_{nz} - k] \right. \cr & \quad \left. - T^{\prime}[k] \cdot H_{si,b}[N_{nz} - k + 1]\right\vert {^2}}}}}.} $$

That means ${\widetilde \beta} _1$ can be estimated by using the estimated self-interference channel coefficients H _{si, a}[k] and H _{si, b}[k] which are corrupted by the I/Q imbalance parameters (α and β). After getting the estimated ${\widetilde \beta} _1$, the optimal estimated value ${\widetilde \beta} _{o,1}$ can be obtained by

(53)$${\widetilde \beta} _{o,1} = {\widetilde \alpha} _{o,1}^{\ast} \cdot {\widetilde \beta} _1.$$

According to the characterization of ${\widetilde \alpha} _{o,1}$ and ${\widetilde \beta} _{o,1}$ as in (22) and (23), we can get

(54)$${\widetilde \alpha} _{o,1} + {\widetilde \beta} _{o,1}^{\ast} = 1.$$

Then, the optimal estimated I/Q imbalance parameters ${\widetilde \alpha} _o$ and ${\widetilde \beta} _o$ can be solved as

(55)$${\widetilde \alpha} _{o,1} = {\displaystyle{{1} \over {1 + {\widetilde \beta}}}}, $$

(56)$${\widetilde \beta} _{o,1} = 1 - {\widetilde \alpha} _{o,1}^{\ast}. $$

The same method can be used to obtain another pair of optimal I/Q imbalance parameters ${\widetilde \alpha} _{o,2}$ and ${\widetilde \beta} _{o,2}$ by solving the optimization problem

(57)$$\eqalign{& \left({\widetilde \alpha} _{o,2},{\widetilde \beta} _{o,2} \right) = \mathop {\rm argmin} \limits_{\widetilde \alpha} \in {\rm \cal C},{\widetilde \beta} \in {\rm \cal C} \cr & \quad \left\{ {\sum\limits_k \left\Vert {\widehat H}_{si,21}[k + 1] - {\widehat H}_{si,21}[k] \right\Vert^2} \right\}.}$$

Then, the optimal estimated value ${\widetilde \alpha} _o$ and ${\widetilde \beta} _o$ which are employed for compensating the receiver I/Q imbalance are

(58)$${\alpha _o} = \displaystyle{{{{\widetilde \alpha} _{o,1}} + {{\widetilde \alpha} _{o,2}}} \over 2},$$

(59)$${\beta _o} = \displaystyle{{{{\widetilde \beta} _{o,1}} + {{\widetilde \beta} _{o,2}}} \over 2}.$$

B) I/Q imbalance mitigation

With the estimated I/Q imbalance parameters α _o and β _o available, the I/Q imbalance existing in the FDDB RF front-end can be compensated and the two different symbol sequences carried by the two different carrier frequencies can be separated by solving (20) and (21) as

(60)$$\eqalign{{\widetilde s}_1 & = \displaystyle{\alpha _o^{\ast} s_a - \beta _os_b^{\ast} \over \left\vert \alpha _o \right \vert^2 - \left\vert \beta _o \right\vert^2} \cr {\widetilde s}_2 & = \displaystyle{\alpha _o^{\ast} s_b - \beta _os_a^{\ast} \over \left\vert \alpha _o \right\vert^2 - \left\vert \beta _o \right\vert^2}.}$$

The proposed I/Q imbalance estimator and compensation for the FDDB OFDM radio receiver is as shown in Fig. 8. The two BB symbol sequences ${\widetilde s}_1$ and ${\widetilde s}_2$ after I/Q imbalance compensation will be processed by the two BB WLAN receivers as previously shown in Fig. 2. After that, the two data sequences from the distant radio node can be recovered.

Fig. 8. The compensation block for I/Q imbalance.

C) Algorithm procedure

The procedure of the I/Q imbalance estimation and compensation is described in Algorithm 1. The received two BB long training signals (s _lts,a, s _lts,b) are used to obtain the channel estimates (H _si,a[k], H _si,b[k]) by LS algorithm. Then, the optimal estimates of the I/Q imbalance parameters (α _o, β_o) are calculated by utilizing cooperatively (H _si,a[k], H _si,b[k]). Finally, (α _o, β_o) are used to eliminate the image part in (s _a, s_b) and then the cleaned signal (${\tilde s_1},{\tilde s_2}$) can be obtained.

Algorithm 1 I/Q imbalance estimation and compensation algorithm

A) Numerical results

The bit error rate (BER) versus Eb/No for the proposed radio link are calculated by ADS-Matlab co-simulation and as shown in Figs 9–12. In all these figures, “FDDB WiFi-1” and “FDDB WiFi-2” refer to the FDDB IEEE 802.11g signals with carrier frequency f ₁ = 2.4 GHz and f ₂ = 2.2 GHz, respectively; “Ideal IQ” refers to the radio receiver without I/Q imbalance; “Conventional WiFi Link” refers to the standard IEEE 802.11g wireless link which is used as the reference; “with IQ Imb./No Comp.” refers to the proposed radio receiver with I/Q imbalance but without I/Q imbalance compensation; “with I/Q Imb./Comp.” refers to the proposed radio receiver with I/Q imbalance and with the I/Q imbalance compensation algorithm.

Fig. 9. The BER of FDDB 802.11g wireless system, with ideal I/Q.

2) FDDB OFDM RADIO TRANSCEIVER WITH I/Q IMBALANCE

The I/Q imbalance in the FDDB RF front-end causes undesired signal leakage as studied in Section III. The leaked image signal superimposed on the signal of interest degrades the performance of reception.

As it can be seen in Fig. 10, the high level I/Q imbalance (ΔA = 0.2, Δϕ = 10°) seriously degrades the proposed FDDB WiFi system. However, the proposed system performs very close to the ideal I/Q scenario after using the I/Q imbalance mitigation algorithm as presented in Section III. Specifically, there is about 1 dB residual leaked image signal caused by the I/Q imbalance estimation error when BER = 10⁻⁴.

Fig. 10. The BER of FDDB 802.11g wireless system, with I/Q imbalance (ΔA = 0.2, Δϕ = 10°).

As shown in Fig. 11, even with a medial level I/Q imbalance (ΔA = 0.1, Δϕ = 5°), there is around 5.5 dB gap induced by the leaked image signal when BER = 10⁻⁴. While after the I/Q imbalance compensation, the performance loss is negligible.

Fig. 11. The BER of FDDB 802.11g wireless system, with I/Q imbalance (ΔA = 0.1, Δϕ = 5°).

In order to show that the developed compensation method can also be applied to combat the low I/Q imbalance, we have simulated the scenario (ΔA = 0.05, Δϕ = 1°) as shown in Fig. 12. Note that the BER curve of FDDB WiFi system with low I/Q imbalance is very close to that of the ideal case. This is because the low I/Q imbalance causes low leaked image signal to the signal of interest. It can also be shown that the BER curve of the I/Q imbalance corrupted FDDB WiFi system with compensation scheme almost overlap with the ideal scenario.

Fig. 12. The BER of FDDB 802.11g wireless system, with I/Q imbalance (ΔA = 0.05, Δϕ = 1°).

Additionally, the Fig. 9 shows that the proposed FDDB OFDM radio transceiver can simultaneously receive two different RF signals with carrier frequency f ₁ and f ₂ correctly while transmit another two different RF signals. Besides, comparing the BER performance of the proposed FDDB OFDM radio transceiver without or with different level of I/Q mismatch shows that the I/Q imbalance in the FDDB RF front-end indeed affect the performance of the receiver. However, the developed I/Q imbalance combating method can compensate the impaired RF front-end and make it very close to the ideal scenario.