1. INTRODUCTION
In his treatise On the Causes of the Greatness of Cities (1588), the Italian thinker Giovanni Botero described the demographic dynamics of a city as resulting from the differential between the city’s capacity to generate new persons (i.e. the virtus generativa) and its capacity to produce means of subsistence (i.e. the virtus nutritiva). According to Botero, most causes of premature death at that time (famines, crimes, diseases) were related to an insufficient capacity to produce food. Botero was also interpreting human history – its wars and conflicts – as a history of struggle for land and, hence, for means of subsistence.
Many things have changed since Botero wrote his treatise four centuries ago: medical progress, technological progress, and democratic progress. At the demographic level also, advanced economies started, in the early 19th century, what is known as the demographic transition: survival conditions have substantially improved, and that change was followed, few generations later, by a significant fall in fertility. As explained in details by Lee (Reference Lee2003), those changes in mortality and fertility patterns caused a major growth in the population size, as well as a major shift in the age structure of populations. Nowadays, fertility is more or less stabilized in our economies, but life expectancy at birth – which has doubled since the early 19th century – is still growing, on average, by 3 months every year, so that the aging process is still at work.
The multiple causes of longevity improvements have been much debated among historians. Using data on the causes of death in England and Wales, McKeown (Reference McKeown1976) argued that medical progress cannot fully explain longevity gains, but that improved nutrition could be the key explanatory factor. The role of nutrition was studied by Fogel (Reference Fogel1994, Reference Fogel2004), who proposed a simple explanation for the joint occurrence of the economic and demographic take-off in the early 19th century. Improved quantity of food must have improved individual health and productivity, causing both the improvement of survival conditions and further rises in the output, giving rise to a virtuous cycle.
Besides the roles of medical progress and improved nutrition, some historians, such as Easterlin (Reference Easterlin1999), highlighted that the State played a key role in the improvement of survival conditions, since lots of market failures – externalities, free-riding problems, coordination failures – arise in the production of health. Easterlin argued that the large longevity gains associated to the three parts of the epidemic transition – (1) the sanitation revolution in the 1840s; (2) the discovery of vaccines in the 1890s; (3) the discovery of antimicrobials in the 1930s – could never have taken place if one had relied on market forces only. The State contributed to the sanitation revolution, by providing information to its citizens on habits that facilitate the transmission of diseases. The State also developed infrastructures aimed at limiting the propagation of diseases (sewage, water supply, etc.). Regarding the vaccines’ revolution, the State, by making vaccination mandatory, prevented the occurrence of free-riding problems, as well as problems of negligent parents.Footnote 1 Finally, the State also played a crucial role in organizing the distribution of drugs to uninformed patients.
While the State played a key role in the improvement of survival conditions in the past, it should be stressed that the lengthening of life has also raised new challenges to the Welfare State. The challenges are twofold. On the one hand, the aging of populations questions the sustainability of the Welfare State. As emphasized by Lee (Reference Lee2003), most social insurance devices – health insurance, pension systems, etc. – were built at a time where the average duration of life was much lower than nowadays. Thus, the increase in the life expectancy tends, by raising the size of older age groups in the population, to question the financial sustainability of those devices. On the other hand, the improvement of survival conditions is not equally shared by all individuals, in the sense that some of them still suffer from premature death. Given that longevity inequalities imply major inequalities in lifetime well-being, these invite also some redistribution. But the problem lies in the fact that social insurance systems, like pensions systems, which were built to reduce well-being inequalities between the surviving old, tend also to exacerbate well-being inequalities between the surviving old and the prematurely dead. The persistence of significant inequalities in realized longevity constitutes thus a key challenge for the State, since these tend to question the redistributive role of the Welfare State.
The goal of this paper is to examine some challenges raised by longevity variations for the Welfare State.Footnote 2 Varying longevity has forced public economists to turn back and question some of the fundamental tools used in their analyses, both at the positive level (i.e. describing what the economy is) and at the normative level (i.e. describing what the economy should be). At the positive level, variations in human longevity forced economists to reconsider how the attitude of individuals towards the risk of death was modeled, as well as how the expected life horizon influences individual decisions on various dimensions (savings, education, retirement). At the normative level, variations in human longevity encouraged economists to modify the way in which they look at inequalities, from a perspective based on expectations (i.e. the ex ante view) to a perspective based on realizations (i.e. the ex post view). The purpose of this paper is to review those recent advances, and to show how these allow us to cast a new light on the challenges that aging raises for the Welfare State.
This paper is organized as follows. Section 2 presents key empirical facts on the evolution of survival conditions. Section 3 develops a reduced-form life cycle model to examine how survival conditions affect decisions (savings, education, and retirement). Following Bommier’s works (Reference Bommier2006, Reference Bommier2007, Reference Bommier2010), a particular attention is paid to the role played by risk aversion with respect to the duration of life. Section 4 focuses on the challenges raised by unequal longevity for normative foundations. Then, Section 5 presents some challenges faced by the Welfare State regarding the design of optimal public policy in the context of risky and unequal lifetimes. Concluding remarks are drawn in Section 6.
2. DEMOGRAPHIC TRENDS
Let us begin our explorations with some stylized facts on the evolution of human longevity. For that purpose, a natural starting point consists of considering the evolution of life expectancy at birth during the last centuries. The period life expectancy at birth measures the average duration of life for a group of persons born at the same point in time, and who would face, during their life, the age-specific probabilities of death prevailing during a particular period (usually the year under study). As shown on Figure 1, period life expectancy at birth has strongly grown during the last three centuries. Whereas life expectancy was equal to about 35 years in 1750 in Sweden, it is nowadays higher than 80 years.

Figure 1. Life expectancy at birth (period) in several European countries, 1750–2013 (Sources: Human Mortality Database).
Figure 1 shows also that the extent of growth in life expectancy has not been constant over time: life expectancy growth has been particularly strong in the first part of the 20th century, but less afterwards. Another important thing that appears on Figure 1 is the convergence between countries: whereas significant inequalities existed in terms of life expectancy in the early 20th century, those inequalities are, one century later, much smaller.
When interpreting Figure 1, it is important to keep in mind that each point represents the expected duration of life conditionally on the survival conditions prevailing during that year. This explains why period life expectancy data vary strongly at the time of WWI and WWII. Another key feature of periodic data lies in the fact that those life expectancies only predict the effective average duration of life provided age-specific probabilities of death remain constant over time. In the light of this, it may well be the case that the large period life expectancy levels measured in the early 21st century underestimate the average duration of life for the people born in the early 21st century.
In order to give an idea of the potential bias, let us compare, for the 18th and the 19th centuries, the period life expectancy at birth with the cohort life expectancy at birth, that is, the average effective duration of life among a group of persons born at the same point in time. As shown on Figure 2 for Sweden, the gap between the period and the cohort life expectancies at birth has remained relatively small during the 18th century, but, after that, the cohort life expectancy has remained permanently above the period life expectancy.

Figure 2. Period life expectancy at birth and cohort life expectancy at birth, Sweden, 1751–1920. (Source: Human Mortality Database).
The gap between, on the one hand, the duration of life that could be expected on the basis of observed age-specific probabilities of death, and, on the other hand, the average realized duration of life, is growing over time. This suggests that the accuracy of period life expectancy figures as proxies for actual average durations of life – which is perfect in periods of stationary survival conditions – should not be overestimated. Actually, the observed trend in period life expectancy gives us a qualitative clue regarding the future patterns of the average duration of life, rather than an exact magnitude of the lengthening of life that will take place in the 21st century.
Besides the use of life expectancy statistics, another way to measure the fall of mortality consists of using survival curves. Period survival curves give us the proportion of a cohort that reaches each age of life, conditionally on the age-specific probabilities of death prevailing during that year. Such a focus on the probabilities to reach the different ages of life allows us to go beyond the mere analysis of the average duration of life.
As shown on Figure 3 with the example of Denmark, survival curves have substantially moved during the last two centuries. Two distinct movements have taken place. First, survival curves tended to shift upwards, implying that an increasingly large proportion of the population can reach high ages of life. This movement is known as the rectangularization of the survival curve. In the hypothetical case of a perfectly rectangular survival curve, there would be no risk about the duration of life, since all individuals would die at the same age. Accordingly, in that hypothetical case, there would be no inequality in terms of realized longevity. The second movement of the survival curve consists of a shift to the right, implying that the duration of life lived by the long-lived is increasing over time. This second movement can be regarded as a kind of increase in the limit-longevity. That second movement has also been at work in the last centuries. Note that this shift to the right is distinct from the shift upwards, since this does not necessarily imply a reduction in longevity risk. Although the two movements have been at work during the last two centuries, the rectangularization has been the dominant movement during the 19th century, and during the largest part of the 20th century, whereas the rise in the limit longevity has been dominant in the last 30 years.

Figure 3. Survival curves (period), total population, Denmark. (Source: Human Mortality Database).
An important thing that we learn from Figure 3 concern the size and extent of longevity inequalities. The survival curves for 1835 and 1900 show that child mortality was a widespread phenomena at those times, whose size has strongly decreased during the 20th century. But even if we concentrate on the survival curves for 1950 and 2011, we see that the proportion of Danish individuals reaching, let us say, the age of 60 years has strongly increased, from 82% in 1950 to 92% in 2011. That decreasing trend in inequality is unambiguously a good news. Note, however, that those figures can be interpreted in a less optimistic way. The 2011 survival curve tells us is that, on the basis of the survival conditions prevailing in 2011, there are still 8% of the Danish who will be dead before reaching the age of 60 years. That proportion is far from negligible, suggesting that longevity inequalities remain substantial nowadays.
Thus, although longevity inequalities have been falling over time, there remain, nonetheless, significant longevity differentials across individuals. Longevity differs across persons because of differences in lots of characteristics, such as, among other things, gender, ethnicity, or educational background. To illustrate this, let us first look at the evolution of life expectancy at birth for males and females in Sweden. As shown on Figure 4, women have exhibited, over the three centuries considered, a higher life expectancy than men. Although the gender gap has decreased during the last 30 years (it was equal to 6 years in 1980), it remains substantial nowadays, and is equal to 4 years in 2011.

Figure 4. Life expectancy at birth (period) for females and males, Sweden (1751–2012). (Source: Human Mortality Database).
Besides gender, another important characteristics that is correlated with longevity inequalities is ethnicity. This point was highlighted by Sen (Reference Sen1998), who argued that the life expectancy of black males in poor U.S. neighborhoods was in some cases lower than the one prevailing in developing countries. A recent study by Arias (Reference Arias2014) shows, for the US, that the white/black gap in life expectancy at birth is equal to 3.5 years for women and to 5.3 years for men. When considering life expectancy at age 65 years, longevity differentials remain, although their sizes are smaller. Black females’ life expectancy at age 65 years remains 1 year smaller than the one of white females, whereas for males the gap is about 2 years.
Another important source of longevity inequalities lies in the educational background. As shown on Figure 5 on the basis of US data, the life expectancy at age 25 years was, in 2006, 9.3 years smaller for men with low educational background than for men with a bachelor degree. For females, the education gap is a bit smaller, but still substantial: it is equal to 8.6 years. Education-based inequalities in longevity are growing over time. While life expectancy at age 25 years has increased by 2 years for highly educated men between 1996 and 2006, it has remained almost stable for low educated men. Regarding women, the picture is even worse: life expectancy at age 25 years has, for low educated women, decreased between 1996 and 2006, leading to an even larger educational gap.

Figure 5. Life expectancy at age 25 years by education level, males and females, US, 1996 and 2006. (Source: US Department of Health and Human Services, 2014).
In sum, those few figures suffice to illustrate that, despite a substantial improvement of survival conditions on average, there remain significant inequalities in longevity achievements. Those two demographic tendencies raise deep challenges to policy-makers: how can the Welfare State adapt to the increase in average longevity, while providing more redistribution towards the unlucky short-lived? Before considering that policy issue, the next section introduces some theoretical material.
3. SOME THEORETICAL ISSUES
In order to examine the challenges raised by longevity variations, it is first necessary to consider how the variation of survival conditions is taken into account in the standard economic model of the life cycle, which is used as a benchmark for studying decisions such as savings, retirement, education, and prevention.
For that purpose, we develop a 2-period life cycle model with risky lifetime, where all individuals live period 1 (i.e. the young age), but only a proportion 0 < π ⩽ 1 of the cohort enjoys period 2 (i.e. the old age), whose duration is equal to ℓ (0 < ℓ ⩽ 1).Footnote 3 This discrete time framework constitutes a reduced-form model, which makes the representation of life cycle decisions simpler by reducing life to two periods: the young age and the old age.Footnote 4
We discuss, within that model, how the representation of individual preferences reflects their attitude towards mortality risks. Then, we will focus on the existence of horizon effects in various economic decisions. Furthermore, we will consider the endogeneity of survival conditions.
3.1. Attitude Towards Mortality Risk
In the standard life cycle model, individual preferences over consumption profiles are represented by a weighted sum of temporal utility functions, where the weights represent individual time preferences. In a two-period case (young age, old age), this yields the following representation:
where c denotes first-period and d denotes second-period consumption, while β is a time preference parameter (0 ⩽ β ⩽ 1). The temporal utility function is usually supposed to be increasing and concave in consumption.
Let us now introduce some risk regarding the duration of life, and suppose that the probability of survival to the old age is equal to 0 < π ⩽ 1. Life expectancy at birth is equal to π(1 + ℓ) + (1 − π)1 = 1 + πℓ. Once the risk about the duration of life is introduced, preferences are now defined on lotteries of life, specifying a particular duration of life and its probability of occurrence. If one adopts the standard expected utility hypothesis, preferences on lotteries of life can be represented as follows:
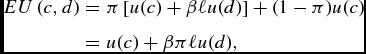 $$\begin{eqnarray}
EU\left( c,d\right) &=&\pi \left[ u(c)+\beta \ell u(d)\right] +(1-\pi )u(c) \nonumber \\
&=&u(c)+\beta \pi \ell u(d),
\end{eqnarray}$$
$$\begin{eqnarray}
EU\left( c,d\right) &=&\pi \left[ u(c)+\beta \ell u(d)\right] +(1-\pi )u(c) \nonumber \\
&=&u(c)+\beta \pi \ell u(d),
\end{eqnarray}$$
where the temporal utility associated to death is normalized to 0. Note that, in this representation, the survival probability π plays a similar role to the one of the pure discount factor β. This explains why π is often regarded as a natural or biological discount factor.
As stressed by Bommier (Reference Bommier2006, Reference Bommier2007, Reference Bommier2010), an interesting feature of this representation of individual preferences lies in the implicit postulate of net risk neutrality with respect to the duration of life. Net risk neutrality with respect to the duration of life is defined as follows. An individual exhibits net risk neutrality with respect to the duration of his life if, provided there is no pure time preference (β = 1) and provided consumption profiles are flat (c = d), he is strictly indifferent between lotteries of life that yield the same expected duration of life, independently on how risky those lotteries are.
In a two-period case, net risk neutrality about the duration of life implies, for instance, the strict indifference between the following two lotteries: lottery 1, where ![]() $c=d=\hat{c}$, π = 1 and ℓ = 1/2, and lottery 2, where
$c=d=\hat{c}$, π = 1 and ℓ = 1/2, and lottery 2, where ![]() $c=d=\hat{c}$, π = 1/2 and ℓ = 1. Those two lotteries exhibit the same life expectancy, but differ quite strongly: whereas lottery 1 is degenerate, and guarantees a life of duration 1.5 for sure, lottery 2 is far more risky, and involves two equally likely scenarios, where the duration of life equals 1 and 2, respectively.
$c=d=\hat{c}$, π = 1/2 and ℓ = 1. Those two lotteries exhibit the same life expectancy, but differ quite strongly: whereas lottery 1 is degenerate, and guarantees a life of duration 1.5 for sure, lottery 2 is far more risky, and involves two equally likely scenarios, where the duration of life equals 1 and 2, respectively.
The standard representation of individual preferences over lotteries of life shown above leads to the same kind of indifference. However, as Bommier pointed out, this kind of indifference is unlikely in real life. Hence, Bommier proposed to modify the standard model of the life cycle, by relaxing the assumption of additive lifetime welfare. When lifetime well-being becomes a strictly concave transform of the sum of temporal welfare:
with ϕ′( · ) > 0 and ϕ″(·) < 0, the expected lifetime well-being becomes
When preferences are represented by that function, individuals are no longer risk neutral with respect to the duration of their life. It is easy to see that they are risk-averse due to the concavity of ϕ( · ). To illustrate this, let us turn back to our example. The expected lifetime well-being of lottery 1 is equal to ![]() $\phi \left[ (1.5)u(\hat{c}) \right]$, whereas the one of lottery 2 is equal to
$\phi \left[ (1.5)u(\hat{c}) \right]$, whereas the one of lottery 2 is equal to ![]() $(1/2)\phi \left[ 2u( \hat{c})\right] +(1/2)\phi \left[ u(\hat{c})\right]$. Given the concavity of ϕ( · ), the expected lifetime well-being associated to lottery 1 now exceeds the one of lottery 2, implying that net risk neutrality with respect to the duration of life does not hold any longer.
$(1/2)\phi \left[ 2u( \hat{c})\right] +(1/2)\phi \left[ u(\hat{c})\right]$. Given the concavity of ϕ( · ), the expected lifetime well-being associated to lottery 1 now exceeds the one of lottery 2, implying that net risk neutrality with respect to the duration of life does not hold any longer.
Bommier’s critique of the life cycle model raises an important challenge. Indeed, economists consider since at least Bernoulli (Reference Bernoulli1730) that risk aversion with respect to money is an important feature of human behavior, which deserves to be taken into account in their analyses. However, before Bommier’s work, there was little emphasis on individual’s attitude towards a major risk in life: the risk of death. But at the same time, Bommier’s formulation raises the complexity of the study of the life cycle, which is a new challenge for economists.Footnote 5
3.2. Horizon Effects
Having discussed how the attitude towards risk with respect to the duration of life affects the representation of individual preferences on lotteries of life, let us now consider some implications of this for economic decisions.
A first decision to be considered is the savings decision, which has been studied in details by economists since Yaari (Reference Yaari1965).Footnote 6 It is intuitive to expect that, as survival conditions improve, individuals would rationally choose to save more. However, things may not be as simple as expected at first glance. In order to examine the impact of survival conditions on savings, let us assume that there exists a perfect annuity market with actuarially fair return, so that the interest factor for savings is equal to ![]() $\tilde{R}\equiv \frac{R}{\pi }$. Let us assume also that the individual works during the entire young age and receives a wage w, and that he retires at the beginning of the old age. The savings problem is
$\tilde{R}\equiv \frac{R}{\pi }$. Let us assume also that the individual works during the entire young age and receives a wage w, and that he retires at the beginning of the old age. The savings problem is
The first-order condition for optimal savings is
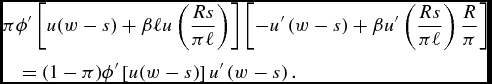 $$\begin{eqnarray}
&&\pi \phi ^{\prime }\left[ u(w-s)+\beta \ell u\left( \frac{Rs}{\pi \ell } \right) \right] \left[ -u^{\prime }\left( w-s\right) +\beta u^{\prime }\left( \frac{Rs}{\pi \ell }\right) \frac{R}{\pi }\right] \nonumber \\
&&\quad=(1-\pi )\phi ^{\prime }\left[ u(w-s)\right] u^{\prime }\left( w-s\right).
\end{eqnarray}$$
$$\begin{eqnarray}
&&\pi \phi ^{\prime }\left[ u(w-s)+\beta \ell u\left( \frac{Rs}{\pi \ell } \right) \right] \left[ -u^{\prime }\left( w-s\right) +\beta u^{\prime }\left( \frac{Rs}{\pi \ell }\right) \frac{R}{\pi }\right] \nonumber \\
&&\quad=(1-\pi )\phi ^{\prime }\left[ u(w-s)\right] u^{\prime }\left( w-s\right).
\end{eqnarray}$$
Obviously, if individuals are risk-neutral with respect to the duration of life, we have ϕ′( · ) equal to a constant κ. Hence, the condition becomes
We can see that a rise in π and a rise in ℓ have a symmetric effect on the optimal savings, and tend both to raise the optimal amount of savings ceteris paribus. Indeed, when either π or ℓ increases, this reduces the level of old age consumption for a given amount of savings, which raises the marginal utility of old-age consumption, inviting a rise in savings. Under risk-neutrality with respect to the duration of life, the source of the increase in life expectancy – i.e. π or ℓ – does not matter; only the fact that life expectancy grows matters.
However, those two sources of life expectancy gains are no longer equivalent once risk-aversion with respect to the length of life is introduced. To see this, note first that a rise in the duration of the old age ℓ does not affect the RHS of the FOC, but this reduces the first factor of the LHS (assuming ![]() $u\left( \frac{Rs}{\pi \ell }\right) -\frac{Rs}{\pi \ell } u^{\prime }( \frac{Rs}{\pi \ell }) >0$) and raises the second factor of the LHS. The impact of a rise in the duration of the old age on savings is thus ambiguous, unlike in the baseline model. Similarly, the effect of a rise in π is more complex. A rise in π raises the first factor of the LHS, but has an ambiguous effect on the second factor of the RHS, and reduces the LHS. Thus, the impact of a rise in π is also ambiguous.
$u\left( \frac{Rs}{\pi \ell }\right) -\frac{Rs}{\pi \ell } u^{\prime }( \frac{Rs}{\pi \ell }) >0$) and raises the second factor of the LHS. The impact of a rise in the duration of the old age on savings is thus ambiguous, unlike in the baseline model. Similarly, the effect of a rise in π is more complex. A rise in π raises the first factor of the LHS, but has an ambiguous effect on the second factor of the RHS, and reduces the LHS. Thus, the impact of a rise in π is also ambiguous.
To assess the implications of risk-aversion with respect to the duration of life on optimal savings, let us rewrite the FOC as
Obviously, when π = 1, we have ![]() $u^{\prime }\left( w-s\right) =\beta Ru^{\prime }\left( \frac{Rs}{\ell }\right)$, and the optimal savings is the same as under risk-neutrality. However, once π < 1, the LHS of this condition remains the same as in the benchmark case, but the first term of the RHS is now raised, pushing towards more savings in comparison to the baseline case, whereas the second term is negative, pushing towards less savings. If ϕ( · ) is strongly concave, we have
$u^{\prime }\left( w-s\right) =\beta Ru^{\prime }\left( \frac{Rs}{\ell }\right)$, and the optimal savings is the same as under risk-neutrality. However, once π < 1, the LHS of this condition remains the same as in the benchmark case, but the first term of the RHS is now raised, pushing towards more savings in comparison to the baseline case, whereas the second term is negative, pushing towards less savings. If ϕ( · ) is strongly concave, we have ![]() $\phi ^{\prime }\left[ u(w-s)\right] >>\phi ^{\prime }[ u(w-s)+\beta \ell u( \frac{Rs}{\pi \ell }) ]$, which would push towards less savings. Thus, the introduction of risk-aversion may lead, in theory, to either larger or smaller savings, the latter case being more plausible when individuals are strongly risk-averse.
$\phi ^{\prime }\left[ u(w-s)\right] >>\phi ^{\prime }[ u(w-s)+\beta \ell u( \frac{Rs}{\pi \ell }) ]$, which would push towards less savings. Thus, the introduction of risk-aversion may lead, in theory, to either larger or smaller savings, the latter case being more plausible when individuals are strongly risk-averse.
Regarding the impact of the lifetime horizon ℓ, note that a rise in ℓ raises the first term of the RHS, leading to more savings, as in the benchmark case, but, provided ![]() $u( \frac{Rs}{\pi \ell }) -\frac{Rs }{\pi \ell }u^{\prime }( \frac{Rs}{\pi \ell }) >0$, this tends also to raise the absolute value of the second term, which is negative, and which pushes towards less savings. Hence, in comparison to the risk-neutrality case, a rise in ℓ does no longer have the same – unambiguous – impact on savings. It may be the case that a rise in ℓ reduces the amount saved, unlike under risk neutrality.
$u( \frac{Rs}{\pi \ell }) -\frac{Rs }{\pi \ell }u^{\prime }( \frac{Rs}{\pi \ell }) >0$, this tends also to raise the absolute value of the second term, which is negative, and which pushes towards less savings. Hence, in comparison to the risk-neutrality case, a rise in ℓ does no longer have the same – unambiguous – impact on savings. It may be the case that a rise in ℓ reduces the amount saved, unlike under risk neutrality.
Let us further illustrate the impact of introducing risk-aversion with respect to the duration of life by considering education choices. In a seminal contribution, Ben-Porath (Reference Ben Porath1967) argued that the life horizon faced by individuals tends, by raising the welfare gains from educational investments, to push towards larger investments in education. This so-called “Ben Porath effect” has become, in the recent years, a major mechanism present in models of long-run economic dynamics (see de la Croix and Licandro 2013).
To show how risk aversion affects education choices, let us consider a framework where individuals, who can work in the two periods, decide to spend a fraction e of the young age for education (0 < e < 1), and receive, in the second period, a return on education under the form of a wage premium h(e) (with h′(e) > 0, h″(e) < 0). Assuming no savings, the individual’s problem is
The first-order condition for optimal education is
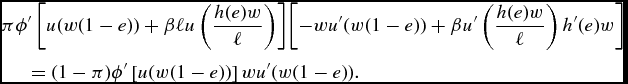 $$\begin{eqnarray}
&&\pi \phi ^{\prime }\left[ u(w(1-e))+\beta \ell u\left( \frac{h(e)w}{\ell } \right) \right] \left[ -wu^{\prime }(w(1-e))+\beta u^{\prime }\left( \frac{ h(e)w}{\ell }\right) h^{\prime }(e)w\right] \nonumber \\
&&\quad=(1-\pi )\phi ^{\prime }\left[ u(w(1-e))\right] wu^{\prime }(w(1-e)).
\end{eqnarray}$$
$$\begin{eqnarray}
&&\pi \phi ^{\prime }\left[ u(w(1-e))+\beta \ell u\left( \frac{h(e)w}{\ell } \right) \right] \left[ -wu^{\prime }(w(1-e))+\beta u^{\prime }\left( \frac{ h(e)w}{\ell }\right) h^{\prime }(e)w\right] \nonumber \\
&&\quad=(1-\pi )\phi ^{\prime }\left[ u(w(1-e))\right] wu^{\prime }(w(1-e)).
\end{eqnarray}$$
Under risk-neutrality with respect to longevity, this condition is
That condition equalizes, at the margin, the welfare loss due to education (LHS) and the welfare gain from education (RHS). Obviously, a rise in π raises the marginal welfare gain from education, leading to a rise in e. Similarly, a rise in ℓ raises the marginal welfare gain from education, pushing towards more education. Thus, under risk-neutrality with respect to the length of life, an improvement of survival conditions does necessarily imply more education.
Once risk-aversion with respect to the duration of life is introduced, the condition for optimal education can be written as
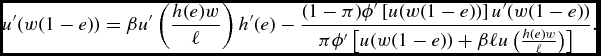 $$\begin{equation}
u^{\prime }(w(1-e))=\beta u^{\prime }\left( \frac{h(e)w}{\ell }\right) h^{\prime }(e)-\frac{(1-\pi )\phi ^{\prime }\left[ u(w(1-e))\right] u^{\prime }(w(1-e))}{\pi \phi ^{\prime }\left[ u(w(1-e))+\beta \ell u\left( \frac{h(e)w}{\ell }\right) \right] }.
\end{equation}$$
$$\begin{equation}
u^{\prime }(w(1-e))=\beta u^{\prime }\left( \frac{h(e)w}{\ell }\right) h^{\prime }(e)-\frac{(1-\pi )\phi ^{\prime }\left[ u(w(1-e))\right] u^{\prime }(w(1-e))}{\pi \phi ^{\prime }\left[ u(w(1-e))+\beta \ell u\left( \frac{h(e)w}{\ell }\right) \right] }.
\end{equation}$$
Obviously, under certain lifetime (i.e. π = 1), this condition would be the same as under risk-neutrality, leading to the same level of education. However, under π < 1, the LHS remains the same, but the first term of the RHS is now divided by π, which pushes towards more education, while the additional second term of the RHS is unambiguously negative, and pushing towards less education. Regarding the impact of the lifetime horizon ℓ, note that a rise in ℓ raises the first term of the RHS, leading to more education, as in the benchmark case, but, provided ![]() $u( \frac{h(e)w }{\ell }) -\frac{h(e)w}{\ell }u^{\prime }( \frac{h(e)w}{\ell } ) >0$, this tends also to raise the absolute value of the second term, which is negative, and which pushes towards less education. Hence, in comparison to the risk-neutrality case, a rise in ℓ does not have a clear impact on education. It may be the case that a rise in ℓ reduces education, unlike under risk neutrality.
$u( \frac{h(e)w }{\ell }) -\frac{h(e)w}{\ell }u^{\prime }( \frac{h(e)w}{\ell } ) >0$, this tends also to raise the absolute value of the second term, which is negative, and which pushes towards less education. Hence, in comparison to the risk-neutrality case, a rise in ℓ does not have a clear impact on education. It may be the case that a rise in ℓ reduces education, unlike under risk neutrality.
Finally, let us conclude our study of horizon effects by focusing on the retirement decision. For that purpose, let us suppose that individuals can decide the fraction z of the old age that they work (0 < z < ℓ). They face some disutility of old age labor v(z), which is increasing and convex. The choice of savings and retirement can be written as
The first-order condition for optimal savings is now
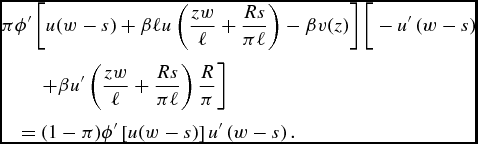 $$\begin{eqnarray}
&&\pi \phi ^{\prime }\left[ u(w-s)+\beta \ell u\left( \frac{zw}{\ell }+\frac{ Rs}{\pi \ell }\right) -\beta v(z)\right] \left[ \vphantom{\left( \frac{zw}{\ell }+\frac{Rs}{\pi \ell } \right)}-u^{\prime }\left( w-s\right)\right.\nonumber \\
&&\qquad\left. +\beta u^{\prime }\left( \frac{zw}{\ell }+\frac{Rs}{\pi \ell } \right) \frac{R}{\pi }\right] \nonumber \\
&&\quad=(1-\pi )\phi ^{\prime }\left[ u(w-s)\right] u^{\prime }\left( w-s\right).
\end{eqnarray}$$
$$\begin{eqnarray}
&&\pi \phi ^{\prime }\left[ u(w-s)+\beta \ell u\left( \frac{zw}{\ell }+\frac{ Rs}{\pi \ell }\right) -\beta v(z)\right] \left[ \vphantom{\left( \frac{zw}{\ell }+\frac{Rs}{\pi \ell } \right)}-u^{\prime }\left( w-s\right)\right.\nonumber \\
&&\qquad\left. +\beta u^{\prime }\left( \frac{zw}{\ell }+\frac{Rs}{\pi \ell } \right) \frac{R}{\pi }\right] \nonumber \\
&&\quad=(1-\pi )\phi ^{\prime }\left[ u(w-s)\right] u^{\prime }\left( w-s\right).
\end{eqnarray}$$
The first-order condition for optimal retirement is
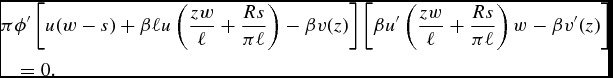 $$\begin{eqnarray}
&&\pi \phi ^{\prime }\left[ u(w-s)+\beta \ell u\left( \frac{zw}{\ell }+\frac{Rs }{\pi \ell }\right) -\beta v(z)\right] \left[ \beta u^{\prime }\left( \frac{ zw}{\ell }+\frac{Rs}{\pi \ell }\right) w-\beta v^{\prime }(z)\right]\nonumber\\
&&\quad =0.
\end{eqnarray}$$
$$\begin{eqnarray}
&&\pi \phi ^{\prime }\left[ u(w-s)+\beta \ell u\left( \frac{zw}{\ell }+\frac{Rs }{\pi \ell }\right) -\beta v(z)\right] \left[ \beta u^{\prime }\left( \frac{ zw}{\ell }+\frac{Rs}{\pi \ell }\right) w-\beta v^{\prime }(z)\right]\nonumber\\
&&\quad =0.
\end{eqnarray}$$
The condition for optimal retirement can hold only if
that is, provided the marginal utility of further work at the old age is equal to the marginal utility loss from further old-age work. This condition characterizes the optimal retirement age whatever the individual is risk-neutral or risk-averse with respect to the duration of his life. However, although the condition is formally similar in both cases, the level of the optimal retirement age differs depending on the degree of risk, since this affects, as we showed, the amount of savings, which influences the marginal welfare gain from old age labor. Clearly, if the individual is more risk averse with respect to longevity, he is likely, as we showed, to save less, which will push towards more labor at the old age, and, hence, towards the postponement of retirement.
3.3. Endogenous Mortality Risks
Up to now, we considered an economy where survival conditions are exogenous to individuals. This constitutes a significant simplification, since humans do, through their behavior, affect their survival chances. Actually, whereas exogenous factors, such as the genetic background, account for a significant part of longevity inequalities (about 30% according to Christensen et al. Reference Christensen, Johnson and Vaupel2006), human behaviors, such as eating behavior, drinking behavior, physical activity, smoking, and sleep patterns, are responsible for about 25% of longevity inequalities (see Contoyannis and Jones, Reference Contoyannis and Jones2004, Balia and Jones, Reference Balia and Jones2008). Among those behavioral factors, one can distinguish between inputs that contribute positively to health production (i.e. prevention, such as physical activity or diet) and inputs that contribute negatively (i.e. sin goods, such as tobacco, alcohol, and fat food).
In order to illustrate the impact of risk-aversion with respect to the duration of life on preventive behavior, let us consider the problem faced by an individual, who can invest an amount H at the young age, which reduces his consumption and well-being at that age, but increases the probability of reaching the old age, which is now a function π(H) that is increasing and concave.Footnote 7 In the following, we suppose that there exists a perfect annuity market, and that individuals take into account the impact of prevention on the returns from savings.Footnote 8
Assuming that all individuals retire at the end of the young age, the problem of the choice for optimal prevention can be written as
The first-order condition for optimal savings is
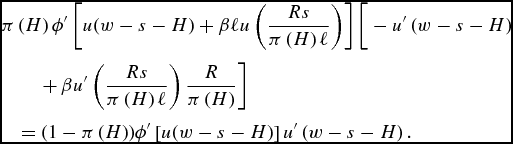 $$\begin{eqnarray}
&&\pi \left( H\right) \phi ^{\prime }\left[ u(w-s-H)+\beta \ell u\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \right] \left[ \vphantom{\left( \frac{Rs}{\pi \left( H\right) \ell }\right)} -u^{\prime }\left( w-s-H\right)\right.\nonumber\\
&&\left.\qquad +\,\beta u^{\prime }\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \frac{R}{\pi \left( H\right) }\right] \nonumber \\
&&\quad =(1-\pi \left( H\right) )\phi ^{\prime }\left[ u(w-s-H)\right] u^{\prime }\left( w-s-H\right).
\end{eqnarray}$$
$$\begin{eqnarray}
&&\pi \left( H\right) \phi ^{\prime }\left[ u(w-s-H)+\beta \ell u\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \right] \left[ \vphantom{\left( \frac{Rs}{\pi \left( H\right) \ell }\right)} -u^{\prime }\left( w-s-H\right)\right.\nonumber\\
&&\left.\qquad +\,\beta u^{\prime }\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \frac{R}{\pi \left( H\right) }\right] \nonumber \\
&&\quad =(1-\pi \left( H\right) )\phi ^{\prime }\left[ u(w-s-H)\right] u^{\prime }\left( w-s-H\right).
\end{eqnarray}$$
The first-order condition for optimal prevention is
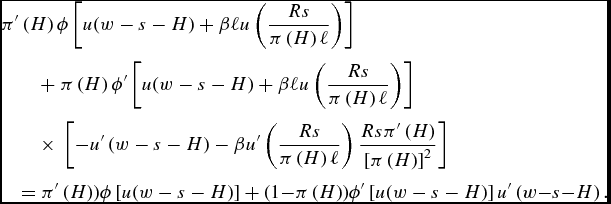 $$\begin{eqnarray}
&&\pi ^{\prime }\left( H\right) \phi \left[ u(w-s-H)+\beta \ell u\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \right] \nonumber \\
&&\qquad+\;\pi \left( H\right) \phi ^{\prime }\left[ u(w-s-H)+\beta \ell u\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \right]\nonumber\\
&&\qquad\times\; \left[ -u^{\prime }\left( w-s-H\right) -\beta u^{\prime }\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \frac{Rs\pi ^{\prime }\left( H\right) }{\left[ \pi \left( H\right) \right] ^{2}}\right] \nonumber \\
&&\quad=\pi ^{\prime }\left( H\right) )\phi \left[ u(w-s-H)\right] +(1{-}\pi \left( H\right) )\phi ^{\prime }\left[ u(w-s-H)\right] u^{\prime }\left( w{-}s{-}H\right).\nonumber\\
\end{eqnarray}$$
$$\begin{eqnarray}
&&\pi ^{\prime }\left( H\right) \phi \left[ u(w-s-H)+\beta \ell u\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \right] \nonumber \\
&&\qquad+\;\pi \left( H\right) \phi ^{\prime }\left[ u(w-s-H)+\beta \ell u\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \right]\nonumber\\
&&\qquad\times\; \left[ -u^{\prime }\left( w-s-H\right) -\beta u^{\prime }\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \frac{Rs\pi ^{\prime }\left( H\right) }{\left[ \pi \left( H\right) \right] ^{2}}\right] \nonumber \\
&&\quad=\pi ^{\prime }\left( H\right) )\phi \left[ u(w-s-H)\right] +(1{-}\pi \left( H\right) )\phi ^{\prime }\left[ u(w-s-H)\right] u^{\prime }\left( w{-}s{-}H\right).\nonumber\\
\end{eqnarray}$$
Under risk-neutrality, the FOC for optimal prevention can be reduced to
The first term in brackets captures the pure welfare gain from increasing the survival probability, for a given level of old-age consumption, whereas the second term in brackets captures the welfare loss due to old-age consumption reduction when survival conditions improve. In general, the first term dominates the second one. Given that, from the FOC for savings, we have ![]() $u^{\prime }\left( w-s-H\right) =\beta Ru^{\prime }( \frac{Rs}{ \pi \left( H\right) \ell })$, the condition for optimal H can be written as
$u^{\prime }\left( w-s-H\right) =\beta Ru^{\prime }( \frac{Rs}{ \pi \left( H\right) \ell })$, the condition for optimal H can be written as
A rise in ℓ raises, in general, the LHS of that condition. But it also raises the RHS, so that it is difficult to draw a general conclusion regarding the impact of ℓ on optimal prevention. The reason is that an increase in the duration of the old age tends, at the same time, to make survival to the old age more worthy, but, also, pushes some additional pressure on available resources, which pushes towards spending less on prevention. Whether prevention increases or not when ℓ increases depends on which effect dominates the other.
Note that things are even more complex when the individual exhibit risk aversion with respect to the duration of life. Substituting for the FOC for optimal savings in the FOC for prevention then yields
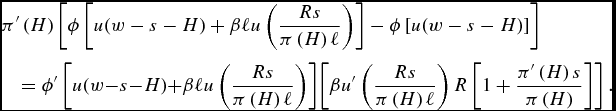 $$\begin{eqnarray}
&&\pi ^{\prime }\left( H\right) \left[ \phi \left[ u(w-s-H)+\beta \ell u\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \right] -\phi \left[ u(w-s-H)\right] \right] \nonumber \\
&&\quad=\phi ^{\prime }\left[ u(w{-}s{-}H){+}\beta \ell u\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \right] \left[ \beta u^{\prime }\left( \frac{Rs}{\pi \left( H\right) \ell }\right) R\left[ 1+\frac{\pi ^{\prime }\left( H\right) s }{\pi \left( H\right) }\right] \right]. \nonumber\\
\end{eqnarray}$$
$$\begin{eqnarray}
&&\pi ^{\prime }\left( H\right) \left[ \phi \left[ u(w-s-H)+\beta \ell u\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \right] -\phi \left[ u(w-s-H)\right] \right] \nonumber \\
&&\quad=\phi ^{\prime }\left[ u(w{-}s{-}H){+}\beta \ell u\left( \frac{Rs}{\pi \left( H\right) \ell }\right) \right] \left[ \beta u^{\prime }\left( \frac{Rs}{\pi \left( H\right) \ell }\right) R\left[ 1+\frac{\pi ^{\prime }\left( H\right) s }{\pi \left( H\right) }\right] \right]. \nonumber\\
\end{eqnarray}$$
The LHS of that expression reflects the pure marginal welfare gain from increasing the survival chance to the old age, ceteris paribus. Note that, the more concave ϕ( · ) is, the lower the LHS will be, since, in that case, the gains, in terms of lifetime well-being, from having an old age are more limited. Thus, a higher degree of risk aversion reduces the support for investing in prevention. The RHS captures the marginal welfare loss from increasing prevention. The RHS is close to the one under risk neutrality, except that ![]() $u^{\prime }( \frac{ Rs}{\pi \left( H\right) \ell }) R( 1+\frac{\pi ^{\prime }\left( H\right) s}{\pi \left( H\right) })$ is now multiplied by
$u^{\prime }( \frac{ Rs}{\pi \left( H\right) \ell }) R( 1+\frac{\pi ^{\prime }\left( H\right) s}{\pi \left( H\right) })$ is now multiplied by ![]() $\phi ^{\prime }[ u(w-s-H)+\beta \ell u( \frac{Rs}{\pi \left( H\right) \ell }) ] \beta$.
$\phi ^{\prime }[ u(w-s-H)+\beta \ell u( \frac{Rs}{\pi \left( H\right) \ell }) ] \beta$.
Regarding the impact of a rise in the life horizon ℓ, things are more complex than in the benchmark case. But it is likely that the impact of a variation in ℓ on the LHS will be smaller than under risk neutrality, whereas a rise in ℓ is likely to reduce also the first factor of the RHS. The effect is thus quite ambiguous. Obviously, more precise assumptions on the functions ϕ( · ), u( · ), and π( · ) are required in order to be able to draw more accurate conclusions regarding the existence of horizon effects for prevention decisions.
4. NORMATIVE FOUNDATIONS
Whereas we focused so far on positive issues – mainly the impact of changes in the life horizon on various economic decisions – it is also worth examining variations in survival conditions from a normative perspective. Since our goal is to examine challenges raised by varying survival conditions for policy-makers, it makes sense to consider the selection of a particular social welfare function that will serve as an objective for the derivation of optimal policies.
For that purpose, we are going to compare, in this section, two particular normative approaches: on the one hand, the utilitarian social objective; on the other hand, the ex post egalitarian social objective.
4.1. Utilitarianism and Unequal Longevity
A first, standard approach consists of taking as a social objective the sum of all individuals’ lifetime well-being levels. That classical utilitarian approach is in line with Bentham’s (Reference Bentham1789) Principle of Utility. In the present context, we focus on a population composed of individuals who are identical ex ante, but who differ only regarding the duration of their life realized ex post. If we consider a simple allocation problem where an amount W of resources is to be divided among the population, the problem of the social planner can be written asFootnote 9
The first-order conditions of that problem are
Note that, if individuals are risk-neutral with respect to the duration of life, those FOCs can be simplified to
Hence, when the population is composed of risk-neutral individuals with respect to the duration of their life, the utilitarian social planner recommends an equalization of consumption across individuals and across periods. This perfect smoothing of consumption along the life cycle would also be chosen by a single risk-neutral individual choosing his savings in such as way as to maximize his expected lifetime well-being while facing a risk 1 − π of dying prematurely.
However, when considering the general case individuals are risk-averse with respect to the duration of their life, such a perfect smoothing does not take place. Actually, combining the two FOCs yields
Under a linear ϕ( · ), the RHS would equal 1, and consumption would be smoothed along the life cycle. However, it is no longer true under risk aversion with respect to the duration of life. When ϕ( · ) is strongly concave, the factor ![]() $\frac{\phi ^{\prime } \left[ u(c)\right] }{\phi ^{\prime }\left[ u(c)+\ell u(d)\right] }$ is then larger than 1, leading to decreasing consumption along the life cycle: c > d. Thus, from a social perspective, the degree of individual risk aversion with respect to the duration of life is crucial, since this determines the slope of optimal consumption profiles from a utilitarian perspective.
$\frac{\phi ^{\prime } \left[ u(c)\right] }{\phi ^{\prime }\left[ u(c)+\ell u(d)\right] }$ is then larger than 1, leading to decreasing consumption along the life cycle: c > d. Thus, from a social perspective, the degree of individual risk aversion with respect to the duration of life is crucial, since this determines the slope of optimal consumption profiles from a utilitarian perspective.
An important thing to notice concerns the impact of the life horizon ℓ on the shape of the optimal consumption profile. Under risk neutrality with respect to the duration of life, the duration ℓ only affects the level of the consumption profile, but not its slope. In that case, the larger ℓ is, the lower the consumption profile is. However, under risk-averse individuals with respect to the length of life, the level of ℓ affects also the slope of the optimal consumption profile. The higher ℓ is, the larger is the second term in the above condition, yielding a lower level of consumption during the old age in comparison with the young age. Thus, a longer life horizon leads to a more decreasing optimal consumption profile.
Note that the utilitarian solution of that social planning problem can be questioned on some ethical grounds. Actually, although all individuals are equal ex ante (i.e. before the duration of life is revealed for each individual), those individuals differ strongly ex post (i.e. after the duration of life is revealed for each individual). In welfare terms, short-lived people are in general worse-off than long-lived persons. To see this, it suffices to compare the realized lifetime well-being of short-lived and long-lived persons:
Short-lived persons are worse-off than long-lived persons when u(d) > 0. That condition is most likely to be verified under risk neutrality. It is also likely to be verified – but to a lower extent – under risk aversion with respect to the duration of life, as shown in Leroux and Ponthiere (Reference Leroux and Ponthiere2013).
But the prevalence of well-being inequalities across individuals at the social optimum is not, in the present context, the worst corollary of the utilitarian social welfare function. Actually, it can be shown that, in many cases, utilitarianism tends to lead to well-being inequalities between short-lived and long-lived individuals that exceed the ones that would have prevailed at the laissez-faire. Put it differently, utilitarianism then leads to a kind of double penalty for the short-lived. These are penalized once by Nature (since well-being opportunities are reduced for the short-lived) and once by Bentham (since utilitarianism induces redistribution from the short-lived to the long-lived). Thus, under mild conditions, utilitarianism tends to reinforce rather than reduce inequalities in lifetime well-being between individuals.Footnote 10
To see this, let us illustrate the simplest case, without risk (i.e. π = 1 ).Footnote 11 Let us suppose that there are two individuals, one is short-lived and dies after the young age (i.e. ℓ = 0), whereas the other one is long-lived and enjoys the old age (i.e. ℓ = 1). At the laissez-faire, the first individual will consume his entire endowment w before dying (i.e. c 1 = w). On the contrary, the second individual will consume w/2 at each period of his life (i.e. c 2 = d 2 = w/2).
Let us now compare this allocation with the utilitarian optimum. The utilitarian social planner will solve the problem
which leads, as a solution
In the light of this, it appears clearly that the short-lived individual consumes, at the utilitarian optimum, less than what he consumed at the laissez-faire. On the contrary, long-lived individuals benefit, at the utilitarian optimum, of more resources in comparison with the laissez-faire.
This example shows that utilitarianism can, in some cases, exacerbate well-being inequalities between the short-lived and the long-lived, by redistributing resources from the former to the latter, against any ethical intuition. Put it differently, utilitarianism can make things even worse than at the laissez-faire for the unlucky short-lived. Obviously, introducing some risk-aversion with respect to longevity could affect this conclusion, by reducing the extent of redistribution from the short-lived to the long-lived. However, under mild degrees of risk aversion, this counterintuitive corollary of utilitarianism remains.Footnote 12
4.2. Ex Post Egalitarianism
This treatment of longevity inequalities under utilitarianism is hardly defendable, since individuals are here not responsible at all for inequalities in realized durations of life. Hence, if one follows Fleurbaey’s theory of fairness (Fleurbaey Reference Fleurbaey2008), those inequalities should be abolished by governments, since the victims of those inequalities can hardly be regarded as responsible for these. Therefore, it makes sense to consider an alternative social objective, which amounts to maximize the realized lifetime well-being of the short-lived persons.
Fleurbaey et al. (Reference Fleurbaey, Leroux and Ponthiere2014) show that, once that social objective is adopted, it is possible for the social planner to abolish inequalities in realized lifetime well-being across short-lived and long-lived individuals, provided the available aggregate resources are sufficiently large so as to insure u(c) > 0 at all periods for all individuals. Under that social objective, the problem is
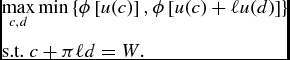 $$\begin{eqnarray*}
&&\max _{c,d}\min \left\lbrace \phi \left[ u(c)\right] ,\phi \left[ u(c)+\ell u(d) \right] \right\rbrace \\
&&\text{s.t. }c+\pi \ell d=W.
\end{eqnarray*}$$
$$\begin{eqnarray*}
&&\max _{c,d}\min \left\lbrace \phi \left[ u(c)\right] ,\phi \left[ u(c)+\ell u(d) \right] \right\rbrace \\
&&\text{s.t. }c+\pi \ell d=W.
\end{eqnarray*}$$
The objective function is not differentiable, but this problem can be rewritten as the maximization of the well-being of the short-lived subject to the constraint that the long-lived is not worse-off than the short-lived:
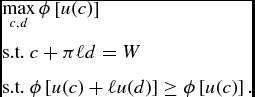 $$\begin{eqnarray*}
&&\max _{c,d}\phi \left[ u(c)\right] \\
&&\text{s.t. }c+\pi \ell d=W \\
&&\text{s.t. }\phi \left[ u(c)+\ell u(d)\right] \ge \phi \left[ u(c)\right].
\end{eqnarray*}$$
$$\begin{eqnarray*}
&&\max _{c,d}\phi \left[ u(c)\right] \\
&&\text{s.t. }c+\pi \ell d=W \\
&&\text{s.t. }\phi \left[ u(c)+\ell u(d)\right] \ge \phi \left[ u(c)\right].
\end{eqnarray*}$$
When the egalitarian constraint is binding, we have u(d) = 0, implying that old-age consumption is fixed to the neutral level for continuing existence, i.e. to the level ![]() $\bar{c}$ such that
$\bar{c}$ such that ![]() $u(\bar{c})=0$.Footnote 13 Then we have
$u(\bar{c})=0$.Footnote 13 Then we have
Under that allocation, consumption profiles are strongly decreasing. This solution may look counterintuitive, but this is the price to pay to minimize inequalities in realized lifetime well-being across short-lived and long-lived individuals. Concentrating the consumption of resources early in life (when all individuals are still alive) allows to provide higher well-being levels at the young age for all individuals. More importantly, this will maximize the realized lifetime well-being of the unlucky short-lived.
Regarding the impact of the life horizon ℓ, it follows from the above analysis that the larger ℓ is, the less decreasing the optimal consumption profile will be. Thus, in comparison with the utilitarian social optimum, the parameter ℓ has here an opposite effect on the slope of the socially optimal consumption profile.
If we turn back to the previous two-person example with risk-neutrality with respect to the duration of life, the problem of the social planner is here:Footnote 14
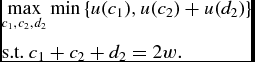 $$\begin{eqnarray*}
&&\max _{c_{1},c_{2},d_{2}}\min \left\lbrace u(c_{1}),u(c_{2})+u(d_{2})\right\rbrace \\
&&\text{s.t. }c_{1}+c_{2}+d_{2}=2w.
\end{eqnarray*}$$
$$\begin{eqnarray*}
&&\max _{c_{1},c_{2},d_{2}}\min \left\lbrace u(c_{1}),u(c_{2})+u(d_{2})\right\rbrace \\
&&\text{s.t. }c_{1}+c_{2}+d_{2}=2w.
\end{eqnarray*}$$
The solution to that problem is
Note that, at this allocation, there exists no inequality in lifetime well-being between the short-lived and the long-lived, since we have
since ![]() $u(\bar{c})=0$. Thus, contrary to what utilitarianism does, the ex post egalitarian optimum does not exacerbate well-being inequalities between short-lived and long-lived agents, but make these inequalities disappear.
$u(\bar{c})=0$. Thus, contrary to what utilitarianism does, the ex post egalitarian optimum does not exacerbate well-being inequalities between short-lived and long-lived agents, but make these inequalities disappear.
This section shows that adopting a standard utilitarian social welfare function or, alternatively, the ex post egalitarian social welfare function, has significant consequences regarding the form of the social optimum. Note, however, that our discussion has concentrated mainly on a highly abstract resource allocation problem. The next section will explore policy issues that are closer to the ones faced by contemporary policy-makers.
5. POLICY ISSUES
Having examined some conceptual issues, we can now focus on the policy challenges raised by varying longevity. Actually, shifting from an economy with fixed longevity to a more realistic economy with varying – and potentially unequal – longevity raises additional difficulties for the design of optimal public policy. As we will see, varying longevity tends to significantly complicate policy analysis in fields as diverse as labor market regulations, health policy, education policy, pensions, and the taxation of wealth and bequests.Footnote 15
5.1. Harsher Occupation and Shorter Life
Social security systems are under increased fiscal pressure due to the impact of population aging. With increasing life expectancies, it seems reasonable to require individuals to work longer. In recent years, several countries have increased the legal age of retirement and other countries are considering doing so. However, the chances of reaching and living retirement in good health differ significantly among individuals. It has been shown that the chances of living longer and in good health are closely correlated with occupation (see van Raalte et al. Reference van Raalte, Martikainen and Myrskylä2012). One can thus raise the question of allowing the pension policies, and in particular the retirement age, to differ by occupation.
Pestieau and Racionero (Reference Pestieau and Racinero2015) argue against favorable treatments in terms of retirement age and pension benefits for workers involved in hazardous jobs, such as underground mining. True, this type of work reduces, on average, life expectancy, thus shortening the time during which retirement benefits can be enjoyed. But such differentiated treatment cannot, in theory, be defended, since the correlation between longevity and occupation is imperfect. Even in safe jobs, some workers endanger their health and face-reduced longevity. Furthermore, because of asymmetric information, policy administrators are unable to observe individual health conditions without going through costly and imperfect tests.
In their paper, Pestieau and Racionero examine the design of special pension schemes in an asymmetric information framework, where individuals are better informed about their longevity prospects than the government. There is however some (imperfect) correlation between longevity and occupation, and occupation is observable. To make the presentation simple, Pestieau and Racionero adopt a two period model in which there are only two occupations and two longevity types. The occupational equilibrium implies that the wage is higher in the harsh occupation. Workers employed in a harsh occupation face a higher probability of a short life than those in a safe occupation. Longevity is private information and is learnt by the worker sometime in the first period. The life cycle utility of an agent with occupation i and longevity j takes the following form:
where the disutility of old age labor v(zij, ℓj) is assumed to be inversely related to longevity. In other words, a worker who expects to live longer has a lower disutility from delaying retirement than one with a shorter life expectancy.
Pestieau and Racionero employ an optimal nonlinear taxation approach: i.e. they identify the optimal bundle of consumption in both periods and of retirement age for each type of agent, and show how the optimal solution can be implemented with a social security scheme. They show that short-lived workers face marginal distortions on savings and prolonging activity. They are induced to consume relatively more when young than when old. This result is in the same vein as that of Fleurbaey et al. (Reference Fleurbaey, Leroux and Ponthiere2014) who argue that if one takes an ex post viewpoint some priority should be given to first-period consumption.
The definition of the socially optimal retirement age is also examined in Fleurbaey et al. (Reference Fleurbaey, Leroux, Pestieau and Ponthiere2016) in a framework where individuals differ in life expectancy and in realized longevity. Given that different occupations lead to unequal life expectancies, that framework is also relevant for the issue at stake here. Fleurbaey et al. (Reference Fleurbaey, Leroux, Pestieau and Ponthiere2016) insist on the fact that whether the retirement age should be differentiated or not according to the occupation depends on whether one adopts an ex ante or an ex post egalitarian view. From an ex ante perspective, it is justified to give priority to individuals having a lower life expectancy, and thus being in a harsher occupation. Hence, from that perspective, individuals with harsher occupations should be allowed to retire earlier. On the contrary, from the perspective of maximizing the ex post lifetime well-being of the worst-off – who is, in general, a victim of premature death – there is some argument for postponing retirement for all individuals, whatever their occupation is, in such a way as to transfer more resources towards the young (to compensate him for his shorter life). In that case, differences in life expectancies become irrelevant.
5.2. Preventive and Curative Health Care
As already alluded, rationality or farsightedness can contribute to a longer life and a better health. The possibility to invest in one’s future health raises some important challenges from a policy perspective. A well-known challenge consists of the choice of an optimal balance between preventive and curative health expenditures. Should the State spend more on prevention and less on curative expenditures, or the opposite? That question is complex, and the answer depends on the underlying assumption on individual rationality.
The preventive versus curative dilemma was studied by Cremer et al. (Reference Cremer, de Donder, Maldonado and Pestieau2012) in an economy where individuals live for two periods: the first one is of length one and the second has a length that depends on private investment in health and on some sinful consumption in the first period (i.e. alcohol, cigarettes, junk food, etc.). The lifetime welfare of individuals takes here the following form:
where x is the sin good, φ(x) is the utility from sin good consumption at the young age, whereas e is the curative health spending.
Some individuals may well perceive the impact of the consumption of sin good on their future health and longevity. But obviously not all agents are farsighted. It is likely that some people do not perceive well (out of myopia or ignorance) the impact of their lifestyle on their longevity. They do not anticipate correctly the effect an health lifestyle and preventive measure taken in the first period on the length of the second.
Cremer et al. (Reference Cremer, de Donder, Maldonado and Pestieau2012) study the design of the optimal public intervention when agents differ in terms of their farsightedness. They show that sin goods should be taxed, to an extent that depends on individual myopia/ignorance. They also find that prevention should be encouraged, but that curative expenditures should not necessarily be encouraged. In particular, when individuals are myopic, it is not necessarily the case that curative health spending should be subsidized. Two cases can occur. In the first case, individuals acknowledge and regret their past mistake once they are in the second period of their life. In the second case, there is no regret. Cremer et al. show that, in the first case, curative health care does not need to be subsidized. However, individual savings should be subsidized in that case. The underlying intuition is that individuals who realize their mistakes in the second period, will then dedicate their savings between either consumption or curative spending. On the contrary, if we focus now on the second case, where individuals formulate no regret, and keep ignoring the impact of their behavior on their longevity, the government needs to subsidize curative spending, so as to decentralize the first-best optimum, unlike what prevails in the first case. Once heterogeneity concerns both rationality and earnings, restoring the first-best optimum becomes even more difficult.
Note that, among the two cases considered in Cremer et al. (Reference Cremer, de Donder, Maldonado and Pestieau2012), the prevalence of regrets is the most widespread. Recent surveys showed that about 85% of smokers aged 65 years regret having started to smoke, in the sense that, if they could change the past, they would not have started to smoke (see Slovic Reference Slovic and Slovic2001, Jarvis et al. Reference Jarvis, McIntyre and Bates2002, Fong et al. Reference Fong, Hammond, Laux, Zanna, Cummings, Borland and Ross2004). Hence, when calibrating the optimal sin tax formula, it should be kept in mind that the proportion of individuals formulating regrets strongly dominates the proportion of individuals ignoring mistakes. This pushes towards a larger taxation of sin goods ceteris paribus.
5.3. Free-Riding and Longevity
Besides the prevention versus curation issue, the endogeneity of longevity raises also other challenges. The previous section considered individuals who may not be able to fully understand or internalize the impact of their behavior on their own future longevity, because of some myopia or ignorance. It should be stressed, however, that longevity-affecting choices affect not only individual well-being, but tend also, through various channels, to influence the well-being of the society as a whole. Those other influences may, here again, not be fully taken into account by individuals when making longevity-affecting choices, because either of ignorance or of conscious free-riding.
To illustrate this, it is relevant to make a parallel with fertility decisions. Fertility choices are made by parents, but those choices affect the society as a whole, through lots of externalities, which can be either positive – through intergenerational transfers (Samuelson Reference Samuelson1975) or scale effects (Kremer Reference Kremer1993) – or negative – through congestion or pollution. Adding some new living being involves lots of effects, which are usually not taken into account by parents. The same problem arises regarding longevity-affecting choices. Indeed, although investing in one’s health does not add a new person, it definitely adds some life-years to the population, yielding positive or negative externalities.
This fact was first highlighted by Davies and Kuhn (Reference Davies and Kuhn1992) and by Becker and Philipson (Reference Becker and Philipson1998). As shown by those authors, individuals do not necessarily take into account, when making longevity-affecting choices such as preventive spending, the negative impact of those decisions on the return on savings in an economy with annuities. Clearly, in an annuity market, the return on savings depends negatively on the proportion of survivors to the old age. Hence, the more individuals invest in their health, and the lower the return on annuities will be. This influence is obviously ignored by individuals, who may consider that each of them brings only a minor influence on the return. But as all individuals buying annuities are in the same situation, the negative impact on savings return may be non negligible.
To illustrate this, consider the following prevention choices under risk neutrality with respect to the duration of life. Individuals choose savings s and prevention H so as to maximize their expected lifetime well-being:
where c = w − s − H. Under a perfect annuity market, yielding an actuarially fair return, the gross return on savings is ![]() $\tilde{R}=\frac{R}{\pi \left( H\right) }$, which is decreasing in H. But in real life individuals ignore the impact of H on
$\tilde{R}=\frac{R}{\pi \left( H\right) }$, which is decreasing in H. But in real life individuals ignore the impact of H on ![]() $\tilde{R}$, and take
$\tilde{R}$, and take ![]() $\tilde{R}$ as given. Hence, the FOC for prevention is, at the laissez-faire:
$\tilde{R}$ as given. Hence, the FOC for prevention is, at the laissez-faire:
whereas at the social optimum, the FOC for optimal prevention would be
Taking into account the negative impact of prevention on the return on saving tends to reduce the marginal benefit from prevention, leading to a lower optimal prevention level in comparison with the laissez-faire.
Given that individuals neglect the impact of preventive spending on the return on savings, these tend to invest too much in their health in comparison with what would maximize their expected lifetime well-being. As a consequence, there is here an argument not for subsidizing, but for taxing prevention.Footnote 16 This argument would be also valid in an economy without private annuities, but with a PAYG pension scheme. Here again, individuals spending in their health do not take into account its impact on pension benefits, which invites for some taxation of prevention for the same reasons as the ones mentioned above.
This argument remains also valid once some degree of risk aversion with respect to the duration of life is introduced. Indeed, in that case, the FOCs for optimal prevention is, at the laissez-faire,
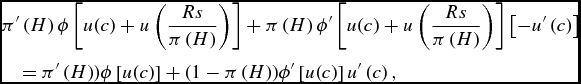 $$\begin{eqnarray}
&&\pi ^{\prime }\left( H\right) \phi \left[ u(c)+u\left( \frac{Rs}{\pi \left( H\right) }\right) \right] +\pi \left( H\right) \phi ^{\prime }\left[ u(c)+u\left( \frac{Rs}{\pi \left( H\right) }\right) \right] \left[ -u^{\prime }\left( c\right) \right] \nonumber \\
&&\quad =\pi ^{\prime }\left( H\right) )\phi \left[ u(c)\right] +(1-\pi \left( H\right) )\phi ^{\prime }\left[ u(c)\right] u^{\prime }\left( c\right),
\end{eqnarray}$$
$$\begin{eqnarray}
&&\pi ^{\prime }\left( H\right) \phi \left[ u(c)+u\left( \frac{Rs}{\pi \left( H\right) }\right) \right] +\pi \left( H\right) \phi ^{\prime }\left[ u(c)+u\left( \frac{Rs}{\pi \left( H\right) }\right) \right] \left[ -u^{\prime }\left( c\right) \right] \nonumber \\
&&\quad =\pi ^{\prime }\left( H\right) )\phi \left[ u(c)\right] +(1-\pi \left( H\right) )\phi ^{\prime }\left[ u(c)\right] u^{\prime }\left( c\right),
\end{eqnarray}$$
whereas the one for socially optimal prevention is
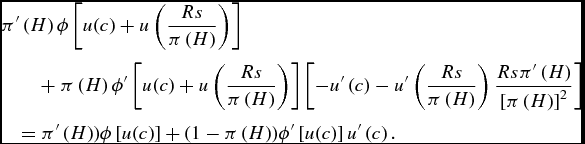 $$\begin{eqnarray}
&&\pi ^{\prime }\left( H\right) \phi \left[ u(c)+u\left( \frac{Rs}{\pi \left( H\right) }\right) \right] \nonumber \\
&&\qquad+\;\pi \left( H\right) \phi ^{\prime }\left[ u(c)+u\left( \frac{Rs}{\pi \left( H\right) }\right) \right] \left[ -u^{\prime }\left( c\right) -u^{\prime }\left( \frac{Rs}{\pi \left( H\right) }\right) \frac{Rs\pi ^{\prime }\left( H\right) }{\left[ \pi \left( H\right) \right] ^{2}}\right] \nonumber \\
&&\quad=\pi ^{\prime }\left( H\right) )\phi \left[ u(c)\right] +(1-\pi \left( H\right) )\phi ^{\prime }\left[ u(c)\right] u^{\prime }\left( c\right).
\end{eqnarray}$$
$$\begin{eqnarray}
&&\pi ^{\prime }\left( H\right) \phi \left[ u(c)+u\left( \frac{Rs}{\pi \left( H\right) }\right) \right] \nonumber \\
&&\qquad+\;\pi \left( H\right) \phi ^{\prime }\left[ u(c)+u\left( \frac{Rs}{\pi \left( H\right) }\right) \right] \left[ -u^{\prime }\left( c\right) -u^{\prime }\left( \frac{Rs}{\pi \left( H\right) }\right) \frac{Rs\pi ^{\prime }\left( H\right) }{\left[ \pi \left( H\right) \right] ^{2}}\right] \nonumber \\
&&\quad=\pi ^{\prime }\left( H\right) )\phi \left[ u(c)\right] +(1-\pi \left( H\right) )\phi ^{\prime }\left[ u(c)\right] u^{\prime }\left( c\right).
\end{eqnarray}$$
Thus, the tendency to overinvest in prevention also holds in this case. However, to the extent that risk aversion with respect to the duration of life pushes towards more consumption early in life and reduces the amount of prevention, this may potentially reduce the size of the extent of overinvestment in prevention.
5.4. Longevity, Education, and Growth
Whereas there exist various engines of growth, a large emphasis was laid in the recent decades on the crucial role played by education and human capital accumulation. Following the seminal contribution by Ben Porath (Reference Ben Porath1967), a strong attention was paid to the link between education, life expectancy, and growth. Using a 3-period OLG model with education and fertility choices, Ehrlich and Lui (Reference Ehrlich and Lui1991) showed that an improvement of survival conditions at the young age can, by reducing fertility, boost education and growth. Boucekkine et al. (Reference Boucekkine, Croix and Licandro2002) used a vintage human capital model to distinguish between three channels by which life expectancy affects human capital accumulation. First, a higher life expectancy raises the quantity of workers, by reducing the number of workers dying prematurely; second, a higher life expectancy induces more investment in education (i.e. the Ben-Porath effect). But besides those two positive effects, there is another, negative effect: the rise in life expectancy raises the average age of workers, which may reduce productivity and growth.
More recently, various OLG models studied the existence of a feedback effect: not only does longevity affect education and growth, but growth also allows for more investment in health, leading to an improvement of survival conditions. Hence, there exists some virtuous cycle, where better survival conditions lead to more education, and more education leads to better survival conditions. Models of that kind include, among others, Blackburn and Cipriani (Reference Blackburn and Cipriani2002) and Chakraborty (Reference Chakraborty2004), where the child decides how much education to attend, de la Croix and Licandro (Reference de la Croix and Licandro2013), where the education decision is taken by parents alone, and Leker and Ponthiere (Reference Leker and Ponthiere2015) where education is the outcome of an intrafamily bargaining process between the parent and the child.
But the interplay between longevity, education, and growth can also be studied from a policy perspective. Besides the widely studied Ben Porath conjecture, there are lots of studies both cross-sectional and intertemporal showing that education increases longevity. The latter effect can be explained by the fact that education implies better life-style, more emphasis on prevention, safer occupation. The crucial role played by education in this virtuous cycle suggests that inequalities in the capacity of children to convert educational effort into educational and professional achievements may be a key determinant of inequalities not only in income, but, also, in health and longevity.
Nishimura et al. (Reference Nishimura, Pestieau and Ponthiere2015) examine the design of the optimal public policy in an OLG economy where education affects life expectancy and where life expectancy affects education through the Ben Porath effect. They consider a model where young individuals borrow to fund their education, which will improve their future wage with some decay. They first re-examine the conditions under which an improvement in survival conditions raises education. Then, they consider the design of optimal public policy. Among the reasons for government intervention, there is the possibility that physical or human capital accumulation be suboptimal. Another reason is that if agents are myopic, they can choose too little education and this call for a Pigovian subsidy. There is also the objective of redistributing income across individuals having different learning capacities. With an utilitarian objective and asymmetric information, one ends up taxing the level of education of the individuals with the lower learning capacity. This implies, quite paradoxically, a widening of the longevity gap.
Finally, note that those studies, which take place in dynamic OLG models, usually assume, for the sake of simplicity, risk neutrality with respect to the duration of life. The reason is that relaxing that assumption would make it difficult to derive a closed-form solution for the education investment, making the resolution of the dynamic system difficult if not impossible. However, introducing some risk-aversion with respect to the duration of life could, as stated above, affect the form of the relation between education and longevity.
5.5. Longevity, Pensions, and Growth
Besides the link between education, longevity, and growth, a strong attention was also paid to the impact of longevity on capital accumulation and pensions. Demographic aging poses a major challenge to all industrialized economies and a large number of developing countries. Although an increase in the average age is a common trend around the world, the factors that lead to such changes vary across countries; they can be traced back to decreases in fertility rates and increases in longevity, albeit at different magnitudes in different economies. There exist a number of studies, which investigate how institutional factors and behavioral responses may affect the impact of aging on capital accumulation.
An interesting discussion on the effect of longevity increase on growth is provided by Bloom et al. (Reference Bloom, Canning and Moore2007). The authors point out that, in theory, improvements in healthy life expectancy should generate increases in the average age of retirement, with little effect on savings rates. In many countries, however, retirement incentives in social security programs prevent retirement ages from keeping pace with changes in life expectancy, leading to an increased need for life cycle savings. They empirically show that increased longevity raises aggregate savings rates in countries with universal pension coverage and retirement incentives. Similarly, Bloom et al. (Reference Bloom, Canning and Graham2003) show that aging leads to more capital accumulation even if retirement is endogenous. Echevarria (Reference Echevarria2004) reaches the same conclusion. Kalemli-Ozcan et al. (Reference Kalemli-Ozcan, Ryder and Weil2000) show that the positive effect of mortality decline on capital accumulation is made larger if education decisions are endogenous. De la Croix and Licandro (Reference de la Croix and Licandro1999) and Zhang et al. (Reference Zhang, Zhang and Lee2001, Reference Zhang, Zhang and Lee2003) argue that the effect of increasing longevity depends on its initial level. For low levels of life expectancy, the effect is positive but it can turn negative for high levels. Similarly, Miyazawa (Reference Miyazawa2006) also shows that the effect of an increase in longevity on economic growth has a hump-shaped pattern.
Increases in longevity can impact growth indirectly through the pay-as-you go social security system, whose return depends on both fertility and mortality. Among the studies that link the impact of aging with social security systems, Ito and Tabata (Reference Ito and Tabata2008) find that the unfunded social security system provides a sufficient mechanism to have such a hump shaped relationship between longevity and per capita output. Pestieau et al. (Reference Pestieau, Ponthiere and Sato2008) study the design of the optimal preventive health spending in a second-best context where the replacement rate of the PAYG system is taken as given, and show that the optimal health subsidy is decreasing with the prevailing replacement rate. Tabata (Reference Tabata2014) looks at the effect of a shift from a DB to a DC PAYG pension on growth. He shows that this shift is growth enhancing and alleviates the cost of aging. Heijdra and Mierau (Reference Heijdra and Mierau2011) also compare the relative effects of DB and DC PAYG pensions on economic growth with aging. They show that the DC formula fares better that the DB one in facilitating growth. They also show that raising the retirement age as a response to an increase in longevity dampens the growth gains. In the same vein, Dedry et al. (Reference Dedry, Onder and Pestieau2014) provides a comparison of several different institutional settings, i.e. different social security systems and retirement age policies, and types of aging in a unified framework. Their main conclusion is that from the long run welfare viewpoint, the ideal is a defined contribution scheme and a mandatory early retirement constraint.
5.6. Longevity, Wealth, and Bequests
Over the last decades, we have witnessed two striking trends, the steady increase of longevity and the growing role of inheritance in capital accumulation. It is difficult not to think that there are some relations between these two evolutions. Miyazawa (Reference Miyazawa2006) observes that the effect of an increase in longevity on capital accumulation is ambiguous. First, higher longevity increases the aggregate saving rate directly by increasing precautionary saving for the prolonged retirement and indirectly by increasing the accidental bequests (bequest-wage ratio is important because the higher income group has a higher propensity to save). Second, it reduces the frequency of accidental bequests, which implies that the population share of the higher income group decreases. This leads to a reduction in aggregate savings. The relative shares of these factors change over the aging horizon. This is also true for the income inequality (first positive, then negative). Kinugasa and Mason (Reference Kinugasa and Mason2006) provide empirical support to shows that an increase of wealth across countries is likely with mortality decline.
Theoretically, on the basis of some stylized facts, we have reasons to believe that longevity increase fosters bequests. Those facts are the following: (i) Mortality rates decrease but the uncertainty does not decrease. The process of rectangularization of the survival curves seems to have stopped, if not reversed, (ii) the shift from defined benefits into defined contribution in both public and pension schemes reduces the annuitization of retirement saving, (iii) increased longevity implies a higher demand for long-term care, which are rarely insured because of the thinness of the market and the lack of social insurance, (iv) the precautionary saving induced by these three facts seems to increase more than proportionally with income. Put together, those facts imply an increase in accidental bequests and in the inequality of inherited wealth.
Note that the size of the rise in inequality in inherited wealth is not invariant to the postulated preferences, and, in particular, to the attitude of individuals towards risk with respect to the duration of their life. To see this, remind the above discussions on life horizon effects in the choice of savings (Section 3.2). If an individual exhibits a high degree of risk aversion with respect to the duration of life, he will save less than a risk-neutral agent. As a consequence, the two individuals will, in case of premature death, leave accidental bequests of quite different sizes. Hence, it appears that another determinant of the extent of inequality in inherited wealth consists of the heterogeneity of parental tastes in terms of attitude towards risk of premature death. Highly risk-averse individuals save less and leave also lower accidental bequests, unlike risk-neutral individuals.
6. FINAL REMARKS
Our survey illustrates the deep challenges raised by varying longevity for policy-makers. The Welfare State, which was built at a time of worse survival conditions, cannot be left unchanged at a time of deep demographic changes. As Lee (Reference Lee2003) emphasized, aging can be a major opportunity for societies, provided these can adapt their institutions and policies. On the contrary, aging can become problematic in a society with fixed and inadequate institutions.
Our analyses suggest that “adapting” the Welfare State to the rise in longevity is not a simple task. As we emphasized, a major difficulty lies in the existence of significant and persistent inequalities between humans in terms of longevity. Given those inequalities, it is probably not fair to focus only on average statistics when thinking about “adapting” the Welfare State. But taking those inequalities into account is not simple, and an appropriate evolution of the Welfare State can only be done provided a strong attention is paid to the normative foundations for public intervention. From that perspective, the tensions between ex ante and ex post egalitarianism illustrate quite well the incompatible policy corollaries of conflicting normative principles.
Besides inequalities, another major source of difficulties lies in human heterogeneity in terms of preferences and rationality. In our survey, we paid a large attention to the attitude of individuals towards risk with respect to the duration of their life. But the heterogeneity of preferences concerns many other dimensions (e.g. taste for sin goods, (dis)utility of physical activity, etc.) and the design of optimal policies in the context of heterogeneous preferences in dimensions affecting longevity is particularly complex.Footnote 17
All in all, the adaptation of the Welfare State to the challenges raised by varying longevity is an ambitious task, which will remain at the policy agenda for some time. We have learnt from dynamic demo-economic models that the continuation of the observed demographic trends in the future may not be independent from the evolution of the Welfare State. Economic and demographic variables being jointly determined, thoughts about how to adjust the Welfare State must take into account how those adjustments will impact the demography, et vice versa. Undoubtedly, taking those bidirectional relations or “loops” into account makes the exercise more difficult, and also more necessary.



