1. INTRODUCTION
Everyone knows that business conditions can change for the worse, but
figuring out when conditions have radically declined and then actually
acting on this knowledge is exceedingly difficult. One of the managerial
difficulties of exit is that the change of state occurs randomly, without
apparent warning: Adverse change can occur “from the very height of
prosperity without any visible warning, without even a cloud the size of a
man's hand visible on the horizon, has the cloud gathered.”1
Henry Ward Beecher quoted in [3, p. 832].
One impetus for a radical
change of state from high to low is technological obsolescence, as can
occur with the introduction of a new competing product that obliterates a
substantial chunk of demand. The purpose of this article is to offer
managers assistance, via the stopping time τ*, in the unpleasant art
of exit. The optimal stopping time τ* is given in equation (8).
In our model, the investment project's cumulative return up to
time t is governed by a Brownian motion
{Bt : t ≥ 0} with drift μ and
volatility σ2. Because the drift μ is the average
profit rate, it is the key parameter of the model: The decision-maker
expects the project to make money if and only if μ > 0. We maintain
throughout that μ takes one of two values: μH
> 0 or μL < 0. If the drift is in the high
state (i.e., μ = μH), it remains in the high
state for an exponential amount of time with parameter η until
economic conditions change, at which time the value of the drift then
declines to μL. Upon entering the low state, the
value of the drift remains μL forever. For the
moment, assume that the drift is in the high state at time 0. (Later, we
consider the more general problem in which the process begins in the high
state with probability p0 and in the low state with
probability 1 − p0.)
The only control that the decision-maker can exercise over the project
is the decision to exit. If she exits at time t, the profit rate
from that time forward is zero. She seeks to maximize the total expected
profits obtainable from controlling the project over an infinite horizon.
Thus, the problem is to select an optimal stopping time
τ[starf ] that maximizes the total expected profits up to
τ[starf ], the time of exit.
In short, our model is one in which the investment project begins in
the good state and eventually falters and declines to the bad state.
Although the project's state at any given time t is never
known with certainty (unless t = 0), the project's profit
history enables the decision-maker to update her posterior probability
Pt that the project is in the high state.
Although rather difficult to establish, it comes as no surprise that it is
optimal to stop as soon as the posterior probability
Pt of being in the good state falls below a
threshold p[starf ]. A complete comparative statics
analysis is presented in Section 4, where we demonstrate that the value
V of the project at time 0 approaches μH
p0 /η, which is the value of the project if
the decision-maker were to be told precisely when μ changed value, as
|μL| goes to ∞. This
surprising result arises from the fact that an increase in
|μL| increases the ability to
discriminate between the high and low states.
2. WHY {Bt : t
≥ 0} PROVIDES THE EXIT SIGNAL
It is often argued that the appearance of a new (and eventually)
superior technology provides a clear signal of the necessity of exit. As
we will illustrate, history suggests otherwise. Regarding business
activity and decisions, Schumpeter [13,
pp.73,74] observed that nature responds with “ruthless
promptitude … both business success and business failure are
ideally precise,” so eventually obsolete methods will be
“eliminated, sometimes very promptly, sometimes with a lag.”
Schumpeter understood that some delay is likely because business
enterprise entails chance and the element of chance looms large on the
economic landscape. We concur and hasten to emphasize that the elimination
of obsolete and unprofitable methods may occur with a lag because the
signals supplied by nature may be neither prompt nor sharp. In alignment
with David Hume's advice to “harken to no arguments but those
which are derived from experience,” we contend that the need to exit
cannot readily be divined from the appearance of new competitors or other
such markers. It is difficult to know when sufficient information has
accumulated to make clear that the current project is unprofitable (or the
current technology obsolete). Instead, the entrepreneur must resolve his
problem by looking to his own profit stream as the key source of
information.
There are a great many well-known examples of industries in which
technological progress rendered the extant industry's product (or
process) obsolete: Exit was inevitable. Other changes, including new
regulations (e.g., the CAFE (Corporate Average Fuel Economy program),
gasoline mileage minimums, and the removal of lead and MTBE from gasoline
in California), also can lead to a rapid deterioration of sales and
profitability.
Sometimes, the new technology arrived in a flash and without warning,
necessitating timely exit. One such example is Freon refrigerants, for
which the time between invention and application was 1 year (see
[4, p.101]). But sometimes a new
technology takes a great many years to displace the incumbent.
Backed by considerable data, Mansfield [4, pp.115,116,117] concluded that “the
diffusion of a new technique is generally a slow process….
Sometimes it took decades for firms to install a new technique …
The number of years elapsing before half the firms had introduced an
innovation varied from 0.9 to 15.” Similarly, in light of “the
lag of an entire millennium between the invention of the water mill and
its widespread adoption” [11,
p.19], economic historian Nathan Rosenberg views technological
diffusion as a slow moving almost continuous process and notes that
“inventive activity is, itself, best described as a gradual process
of accretion …” [9,
p.7].
Naturally, when the diffusion is slow, the technologies will coexist
for an extended period of time. Although the diesel locomotive was
introduced in Europe in 1913, it was not until 1938 that diesel production
exceeded steam locomotive production in the United States, a full 25 years
after its introduction (see [4, pp.
113–114; 6]). Similarly, “while
steamships were introduced commercially as early as 1807, it was not until
the mid-1880s that steamships … assumed a clear ascendancy”
[14, p.127]. Clearly, the need to exit
because of this new technology was anything but urgent.
In summary, the ineluctable diffusion of superior technology is, more
often than not, shockingly slow. We must be careful not to ascribe
immediate success to a new technology and assume that the extant
technology will be replaced immediately.2
Furthermore, “the risks of early investment in
production are impressive—in some programs enormous quantities of
special tools and manufactured material became worthless due to unexpected
technical changes” [10, p. 529,
quoting Peck and Scherer]. For example, quadraphonic sound was
stillborn and totally failed to replace stereophonic sound, much to the
chagrin of its early investors (see [8]).
This suggests that firms, wishing
not to prejudge the speed of change, should pay particular attention to
their own profits as they are realized over time. It is the firm's
profit stream that reveals whether or not there has been a deterioration
in the underlying profit rate and thereby informs the firm's manager
whether or not exit is advisable.
3. MODEL
In this section, we study the optimal investment strategy for a
project that decreases in value over time. We assume that μ, the mean
profit rate, only takes two values: μH > 0 and
μL < 0. However, the value that μ takes is
not assumed to be constant in time. At time t = 0, μ =
μH with probability p0 and
μ = μL with probability 1 −
p0. If μ begins in the low state, it will stay in
the low state. On the other hand, if μ begins in the high state, it
will only remain in the high state for a random amount of time T.
After time T, μ drops down to μL and
remains there forever. The random time T is assumed to be
exponential with parameter η and is independent of the Brownian
motion B. The investor in this model knows the distribution of
μ at t = 0 and the distribution of T. At time
t, assuming that the investor has not yet decided to stop funding
the project, her total profit is
,
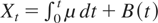
where the Brownian motion has drift 0.
Our investor observes this profit process, and only this process.
Using only the current history of X and the knowledge of
p0 and η as guides, the investor must decide
when, if ever, to stop funding the project as she seeks to maximize
expected profits. Ideally, the investor would stay in whenever μ >
0 and quit as soon as μ < 0. However, because of imperfect
information, she can only guess when the switch from the high to the low
state occurs. The crux of the problem the investor faces is to balance
Type I error (quitting when μ is still positive) and Type II error
(staying in after μ becomes negative).
This problem is quite similar to the problem analyzed in our previous
article [12]. In both cases, the
investor looks at the history of the profit stream X to determine
when the information about μ becomes so unfavorable that the only
rational choice is to quit. The initial information about μ at time
t = 0 is the same as in our previous article [i.e.,
P(μ = μH at t = 0) =
p0]. In our previous article, the value of μ
never changes. Thus, the difference is that the a priori information about
the value of μ at time t > 0 has changed. The notation in
this article is the same as in [12].
Given any stopping time
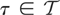
and any initial probability p0, the expected profit
from this project when using τ as the stopping strategy is
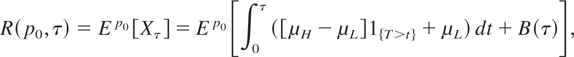
where we have redefined T to be the first time that μ =
μL, giving us
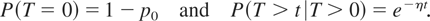
The goal is again to find the stopping time
that maximizes the functional
R(p0,τ)—that is, that satisfies
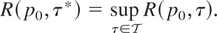
As earlier, we set
.
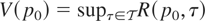
We begin our analysis of this problem by simplifying the expression
for R(p0,τ). Rewriting equation (1), we
have
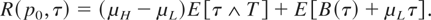
Noting that E [τ ∧ T] ≤
1/η for all τ and E [B(τ) +
μLτ] = −∞ whenever E
[τ] = ∞, we see that no stopping time with an infinite
expectation can be optimal. Thus, we can restrict the class of stopping
times over which we are optimizing to those in
with finite expectation. By Wald's equation, we know that E
[B(τ)] = 0, given E [τ] <
∞. Thus,
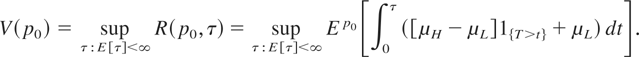
Before trying to find the optimal stopping time τ* for this
problem, we need to find the posterior probability distribution for μ,
given the history of X up to time t. As in [12], it is the special properties of the
posterior distribution that enable us to solve this optimization problem.
To this end, we state the following proposition.
Proposition 1: Let Pt =
Pp0(μ =
μH at time
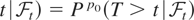
. Then, with κ = (μH
− μL)/σ and
μ = (μH +
μL)/2,
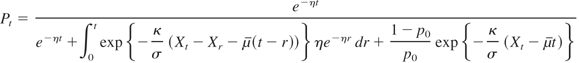
for s ∈ (0,t).
A rigorous proof of this proposition is given in Appendix A.
Equation (4) gives the functional form of the stochastic process
{Pt,t ≥ 0} in terms of the paths
of the process X. Equation (5) shows that the process P
depends on the past up to time s only through
Ps, its value at time s. This is, of
course, the description of a Markov process. In fact, much more can be
said about this posterior probability process.
Theorem 1: The process P =
{Pt,t ≥ 0} has the following
properties:
1. P is a continuous supermartingale with
respect to
.
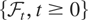
2. P is the unique solution to the stochastic
differential equation
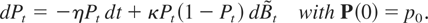
In this equation,
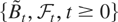
is a standard Brownian motion defined by
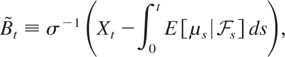
and μs =
(μH −
μL)1{T>s} +
μL, the value of μ at time
s.
3. P is a strong Markov process that is homogeneous
in time.
This theorem is analogous to Theorem 1 in [12]. The posterior probability processes in these
two models are identical except for the linear drift term in the second
model. The increment dPt, which updates the
posterior probability in this model, has two terms: the drift, which
accounts for our a priori knowledge that μ will inevitably become
μL, and the martingale term. This second term
responds to the movements of the process X. It uses the most
recent history of this process to update our guess as to the value of
μ. The proof of Theorem 1 proceeds exactly as the proof to Theorem 1
in [12] (see [12] for details).
As in our previous article [12],
the decision to stop funding the project at any time should depend only on
future profits. At any time t, the instantaneous expected profit
rate is μH Pt +
μL(1 − Pt).
Given that Pt is homogeneous in time, we can
use the theory of dynamic programming to find
V(p,t), the expected future profits at time
t when Pt = p. If an
optimal strategy is employed, V(p,t)
satisfies
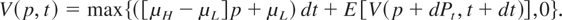
Noticing that equation (7) is homogeneous in time, we see that
V(p) = V(p,t). Due to the
monotonicity of V in p, there should exist some critical
probability p* for which V(p) > 0 when
p > p* and for which V(p) = 0 when
p ≤ p*. When p > p*, we should
continue funding the project. In this case,
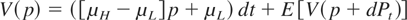
(i.e., expected profits after t = expected profits in
(t,t + dt] + expected profits after
t + dt). On the other hand, if p ≤
p*, then we are in the regime where it is optimal to stop, and
V(p) = 0.
Using equation (7) and Itô's lemma, we can derive an
ordinary differential equation (ODE) for V(p). For
p ∈ (p*,1], we obtain
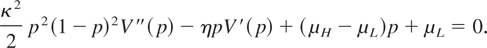
The first boundary condition V(p*) = 0 comes
directly from equation (7). Smooth pasting for the function V at
the point p* leads to the second boundary condition:
V′(p*) = 0. From the ODE, we also have the
condition that V′(1) = μH
/η. Solving this ODE system should then yield the optimal profit
V(p) and the cutoff probability p*.
Although the rigor of the above argument might be questionable, it
gives the basic intuition behind the solution to this optimization
problem. Solving this ODE does, in fact, yield the unique solution to our
problem. This solution is given in Theorem 2, and a rigorous proof is
given in Appendix B.
Theorem 2: For all p0 ∈ (0,1),
the optimal stopping problem given by equations (1) and (2) is solved by
the stopping time τ* = min{t ≥ 0 :
Pt ≤ p*}, where p*
satisfies
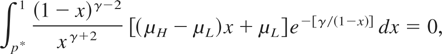
and γ =
2σ2η/(μH −
μL)2. Furthermore, when the
probability that μ = μH equals
p0 at time t = 0, the optimal expected
profit, associated with the stopping time τ*, is
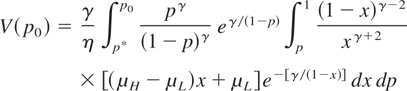
if p0 > p*, and
V(p0) = 0 if p0 ≤
p*.
This solution is not as elegant or explicit as that given in
[12]. Nevertheless, it enables us to
analyze various aspects of this investment model.
The general problem of discerning regime change is an immensely
difficult and complex task. This complexity amplifies the
decision-maker's difficulty in mustering the requisite willpower to
respond to a regime change. Our model is illustrative of a subset of these
real-world situations, the ones in which the regime change is
characterized by just one real variable and the decision to be made, based
on the value of this one variable, is binary. In our model, the real
variable is the profit rate μ, and the binary decision to be made by
the manager is whether or not to exit the project. Thus, there are two
factors that can impede action by a manager. First, she might not discern
the change in regime; second, she might not muster the nerve to act.
Exiting a business or an investment is an unpleasant task. Even when
the profit stream has turned south for an extended period of time, too
often the unpleasantness associated with a negative profit stream is
exacerbated by the failure to act and stop the losses. Of particular
relevance is the experimental study of Massey and Wu [5]. The experiment in their article, with 40 MBAs
as subjects, is precisely our model in discrete time. After observing the
profit in a given period, the subject indicates whether he believes a
regime change has occurred; then the subject is presented with the profit
for the next period and again indicates whether he believes a regime
change has occurred; and so on. Thus, their experiment addresses the
ability of managers to perceive a regime change, the first of the two
impediments to correct action. Their experiments uncover parameter values
in the model in which the subjects update their beliefs too slowly and
others in which the subjects extrapolate too readily from unusual outcomes
from the extant regime. However, the fundamental result of their intricate
econometric analysis was “the pervasiveness of under-reaction”
[5, p.17]. Although it is one thing to
recognize a problem, it is another to act on this recognition. Staw and
Ross [15] list a number of
psychological reasons why managers are reluctant to pull the plug and
exit. In short, empirical evidence reveals that both factors pull with
considerable force in the direction of not acting. Perhaps, managers,
armed with the results of our analysis and with the optimal stopping time
τ* in hand, can inure themselves for the unpleasant task of exiting a
failed investment project.
4. COMPARATIVE STATICS
As always, we wish to understand the value of information and how the
quality of information affects the optimal strategy and profit in this
investment situation. In [12], we were
able to effect a comprehensive, comparative-statics analysis. Due to the
partially implicit nature of the solution induced by the added complexity
of allowing the value of μ to change over time, such a complete
investigation into this model is not possible. However, much concerning
the effect of the parameters on the optimal profit and optimal decision
can still be established analytically. In addition, many results that
cannot be proven analytically can be demonstrated numerically.
In the following comparative-statics analysis, we ask what effect the
parameters γ, σ, μH, and
μL have on V(p0) and
on the cutoff probability p*. The parameter γ is a measure of
the speed with which the investment becomes unprofitable; σ measures
the strength of the noise that exists in the information about
profitability. Our first result pertains to the effect that changing the
parameters has on p*.
Proposition 2: The optimal cutoff probability p* =
p*(η,σ,μH,μL)
is
(i) strictly increasing in η and
σ
(ii) strictly decreasing in
μH
(iii) strictly decreasing as
μH − μL
increases, given μL
/μH = constant.
As one might expect, increasing the noise σ in the information
forces the investor to use a more conservative strategy. As σ
increases, less and less information can be gleaned from the profit stream
X. This means that Pt reacts more
slowly to changes in μ. Thus, if the investor does not behave more
conservatively, she will keep funding the project long after it has become
unprofitable. It seems clear that the value V of the investment
falls as η increases. However, it is not as obvious why the investor
should act more conservatively. The intuition behind this fact is that at
any posterior probability level p, the expected amount of time
μ spends in the high state falls as η increases. Therefore, as
η increases, the investment becomes unprofitable at higher and higher
probabilities.
When μH increases, the situation is reversed.
The investor can become more aggressive, thereby reducing the chance that
she will exit while the project is in the high state. There are two
reasons for this. First, with greater expected profits when in the high
state, the investor can take greater risks and still make a profit.
Second, because μH and μL
are farther part, the difference in the behavior of the profit stream
X when μ = μH and when μ =
μL will be more pronounced. Detecting the true
state of μ becomes easier when μH is larger.
With a larger value of μH, the investor can be
more aggressive because the posterior probability process reacts more
quickly when the project becomes unprofitable; this quick reaction reduces
potential losses. This same logic implies that as
μH − μL increases,
the optimal cutoff probability decreases. As μH
− μL goes up, detection goes up. If the
ratio μL /μH (which
measures the relative profitability in these states) does not change, the
investor can be more aggressive. In fact, combining points (ii) and (iii),
we see that p*↓ whenever μH −
μL↑, given that the ratio
|μL|/μH
does not increase.
The only parameter whose effect on p* we have not fully
investigated is μL. The implicit nature of the
definition of p* makes an analytic investigation of its effect
infeasible. Similar to the analytical work in [12], a numerical investigation reveals that
p* is a concave function of μL and, in
addition, that p* first increases and then decreases as
μL becomes more negative.
Proof: In what follows, we again set γ =
2σ2η/(μH −
μL)2. Let us first simplify the
functional definition of p* given in equation (8) by making the
change of variables r = x/(1 − x) in
the integral in this equation. With r* = p*/(1
− p*), equation (8) reduces to
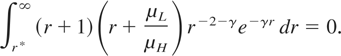
Provided μL /μH
remains constant, the parameters η, σ,
μH, and μL only affect
r* and, thus, p*, through their effect on γ. Setting
I(r;γ) ≡ (r + 1)(r +
(μL
/μH))r−2−γe−γr,
we note the following:
- I(r;γ) < 0 for 0 < r <
|μL|/μH,
and I(r;γ) > 0 for r >
|μL|/μH
- I(r;γ + ε) = (r + 1)(r +
(μH
/μL))r−2(rer)−(γ+ε)
=
I(r;γ)(rer)−ε.
Therefore, for any r that is less than R ≡
|μL|/μH,
Therefore, if γ1 < γ2,
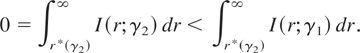
Because
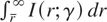
decreases as r↓ when r <
|μL|/μH,
the previous equation implies that r*(γ1) must be
less than r*(γ2). Thus, r*(γ)
increases with γ. Noting that p* increases with r*,
we see that p* increases with γ. This immediately proves
points (i), (ii), and (iii).
We now present a second proof of point (ii). To prove that increasing
μH decreases the optimal cutoff probability, we
break this problem into two parts. First, we increase
μH and η at the same time so that γ
remains fixed. Then we reduce η to its original value. If we increase
μH while keeping γ fixed, the integrand
I(r) increases for every r. Thus, as one
increases μH in this way, one must decrease
r* in order for the integral from r* to ∞ to
remain zero. Now, after we increase μH and η
(in order to keep γ fixed), we return η to its original value. We
have already proved that decreasing η decreases r*.
Therefore, increasing μH alone must decrease
r* and, thus, p*. █
Another question that naturally arises concerns what happens to the
value V(p0) of this investment as the model
parameters change. Analytic results for this function are difficult to
prove. We can, however, rigorously show the following.
Proposition 3: Let V(p0) =
V(p0,γ,μL) be
the value of the project when the optimal stopping time is used. Then the
following hold:
(i) V(p0) is decreasing
in η when p0 >
p*(η).
(ii) As μL →
−∞, V(p0) →
(μH /η)p0, the
value that this project would have if the investor had complete knowledge
of μ at all times.
Proof: To establish part (i), we take the derivative of
V with respect to η. Making the change of variables
r = p/(1 − p) and the change of
variables y = x/(1 − x) in equation
(9), we obtain
Taking the derivative of both sides of this equation yields
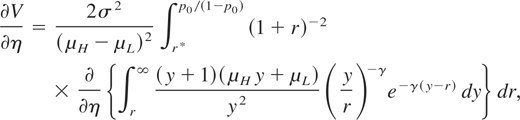
because V′(p*) = 0. With γ =
η[2σ2/(μH −
μL)2],
Now, let I′(y,r) = [(y
+ 1)(μH y +
μL)/y2](y/r)−γe−γ(y−r).
Then I′(y,r) is negative for all
y < R ≡
|μL|/μH
and positive for all y > R. Noting that the term
(y − r) + log(y/r) is
positive and increasing in y whenever y > r,
we have
where ∨ indicates maximum. By the definition of r*, we
know that for all r > r*,
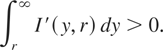
Putting this fact together with equations (10) and (11), we conclude
that ∂V(p0)/∂η < 0
whenever p0 > p*(η).
One approach to proving part (ii) is to just take the limit as
μL [nearr ] −∞ in equation (9).
However, the complexity of this expression for
V(p0,μL) prevents us
from directly calculating this limit. Instead, we find a suboptimal
strategy ρ(μL) for each value of
μL. The expected profit made when using
ρ(μL) establishes a lower bound on
V(p0,μL). Thus, it
suffices to prove that these lower bounds approach
μH p0 /η as
μL [nearr ] −∞. The idea is to choose a
sequence of stopping times that become closer to “optimal” as
μL [nearr ] −∞ . In other words, we
want a set of stopping times {ρ(μL) :
μL < 0} for which
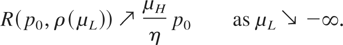
A simple stopping strategy is “quit the first time that the
process X takes a large drop in a short period of time.”
Set
These stopping times mimic a simple “real-life” strategy
that an investor might use in this situation. It turns out that we can,
with some work, estimate the expected profit when using such stopping
times. We leave Δt undetermined for now. Later, we define it
to suit our purposes. Suffice it to say, Δt decreases to zero
as μL decreases to −∞.
We want to prove that if we choose Δt carefully, then for
|μL| large, the probability of
stopping too early (ρ(μH) < T) is
small and the probability of stopping too late
(ρ(μH) > T + Δt) is
small. Once we have done this, we use these facts to prove that
R(p0,ρ(μL)) ≈
(μH /η)p0 +
O(|μL|−β)
for some β ∈ (0,1). To this end, we note that
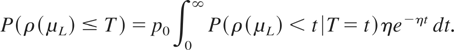
Also,
The last line uses the fact that the process
{BsΔt −
BsΔt−Δt :
s ∈ [n,(n + 1)]} is identical in
law to the process
{(Δt)1/2(Bs
− Bs−1) : s ∈
[1,2]}. If
we ignore the fact that the above probability concerns the minimum of a
process over an interval and pretend that we are only interested in the
probability that a single value, say B1 −
B0, is less than
−[(μH −
μL)/2](Δt)1/2,
finding an upper bound on this probability is trivial:
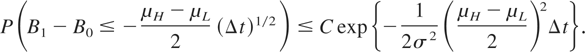
Because Bt is a continuous process, we
should expect that an upper bound similar to this holds for the original
set as well. This is in fact the case. To prove this, we use the theory of
large deviations for Brownian motion (see Deuschel and Stroock [2] for a comprehensive text on this subject).
Basic large deviation analysis yields the inequality
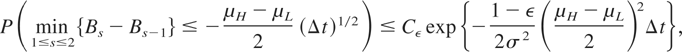
for any ε > 0. Putting this equation together with equations
(12) and (13), we obtain the inequality
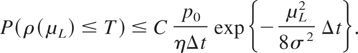
Next, we want to prove that if the investor has not stopped early, the
probability that she will stop as soon as possible after μ switches to
μL approaches 1 as μL
decreases to −∞. To prove this, we need to find a lower bound
on the probability that ρ(μL) = T +
Δt, given ρ(μL) > T.
This is a straightforward calculation:
Finally, we note that for any n = 1,2,…,
Putting all of these calculations together, we can now estimate
R(p0,ρ(μL)).
First, we need a upper bound on E
[ρ(μL)]. Suppressing
ρ(μL)'s dependence on
μL, we have
Because E [ρ] is finite, Wald's equation
implies E [Bρ] = 0. Thus,
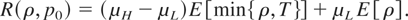
Having found an upper bound on E [ρ], we only
need a lower bound on E [min{ρ,T}]. We
first note that
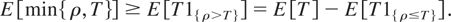
The Cauchy–Schwarz inequality then implies that E
[T1{ρ≤T}] ≤ (E
[T2]P(ρ ≤
T))1/2. Therefore,
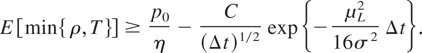
This leads to the inequality
If we set Δt =
|μL|−1−β
with β ∈ (0,1), then, as μL [nearr ]
−∞,
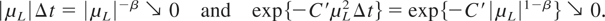
Thus, the expected profit
R(p0,ρ(μL))
→ μH p0 /η. This
completes the proof of part (ii). █
APPENDICES
Appendix A: Proof of Proposition 1
Because equation (5) is a simple consequence of equation (4), it
suffices to establish equation (4). We do this by means of approximation.
For a fixed t, we set σn =
σ{X(it/2n), i =
0,1,…,2n}, the sigma field of the random
variables
X(0),X(t/2n),X(2t/2n),…,X(t).
It is easy to see that
{σn}n=1∞ is
an increasing filtration and that the process
{Pn ≡ P(T >
t|σn)}n=1∞
is a martingale with respect to this filtration. Therefore, using basic
martingale convergence results and the fact that E
[Pn2] ≤ 1 for all
n, we see that
where σ∞ =
σ{X(it/2n), i =
0,1,…,2n, for n = 1,2,…}.
Because Xt is a continuous function in
t, σ∞ must equal
:
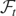
Knowing what happens to X on a dense set of
[0,t] is the same as knowing what happens to X
at every point in [0,t]. Thus,
limn→∞ Pn =
Pt a.s.
Now, we fix n and set
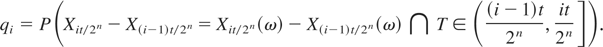
Thus, qi is the probability that (1) the
ith increment of X is equal to the value that we have
observed and (2) μ switches from high to low during this
(ith) interval of time. With this definition we have, via
Bayes' formula and A ≡ κ/σ,
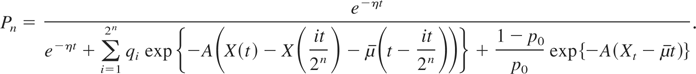
Now, taking the limit as n → ∞, we see that
Pn → the right-hand side of equation
(4), establishing that equation.
Appendix B: Proof of Theorem 2
We will again use diffusion theory to solve our optimal stopping
problem. To do this, we need to describe our problem in terms of a
diffusion process. As it stands, our problem is to find
such that
,
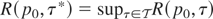
where
In order to rewrite R(p0,τ) in terms
of the diffusion process P, we claim that
,
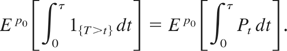
The proof of this claim is straightforward once one recalls that
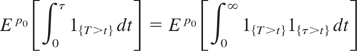
and that
for any stopping time τ. Applying Fubini's theorem on the
right-hand side of the above equation yields
Setting
,
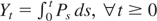
we see that
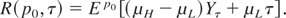
Solutions to optimal stopping problems with functionals such as
R, given above, are well known (see Oksendal [7, pp.212,213] for a complete discussion). This
body of work states that
,
is a smooth (C1) function on the interval
[0,1] and satisfies the ODE system
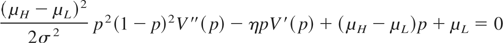
on the set D = {p ∈ [0,1] :
V(p) > 0} and for all p ∈
[0,1], and not in D, V(p) = 0.
In addition, there exists a unique optimal stopping strategy τ*.
This strategy states that the investor should discontinue funding as soon
as Pt leaves the continuation set D.
Thus, τ* = min{t ≥ 0 :
V(Pt) = 0}. Because the value of
Y at any point in time increases with p0 and
the value of R increases with the expected value of
Yτ, V(p0) must be
nondecreasing in p0. Therefore, if
V(p) > 0 and q > p, then
V(q) > 0. This implies that the continuation set
D must be of the form {p ∈ [0,1] :
p > p*} for some p* ∈ (0,1). Using this
fact and the fact that V is a smooth function, we can rewrite the
above ODE system as follows:
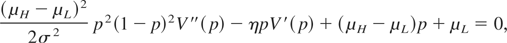
for all p ∈ (p*,1] with the boundary
conditions V(p*) = 0, V′(p*) =
0, and V′(1) = μH /η,
where the value of p* is determined in order to fulfill the
boundary conditions. The first boundary condition comes from the fact that
V(p) = 0 for p ≤ p*, and the second
boundary condition comes from this fact and the fact that V is a
smooth function. The third boundary condition is redundant, as it is
required by the ODE. We put it in this description of V only to
point out that we have not underdefined this function.
Via basic ODE methods, equation (A.1) can be reduced to
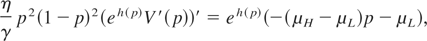
where h(p) = γ log((1 −
p)/p) − γ/(1 − p) and
γ = 2σ2η/(μH −
μL)2. Integrating this equation and
noting that
eh(p)V′(p)
must equal 0 when p = 1, we have
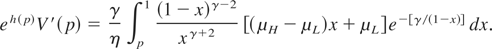
In order to satisfy the second boundary condition,
V′(p*) = 0, p* is defined to be the value
for the lower limit of the above integral for which the integral equals
zero. We have, therefore, proved that p* satisfies equation (8),
given in Theorem 2. Multiplying both sides of the above equation by
e−h(p) and integrating from
p* to p0 yields
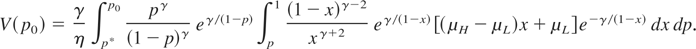
The function V satisfies our ODE system and, thus, must be
the expected profit when using the optimal strategy τ* =
min{t ≥ 0 : Pt ≤ p*}.
This completes our proof of Theorem 2.
