Classical physics and determinism

The desire to understand nature and the search for a causal explanation of all events have probably been among the driving forces in the evolution of humans for hundreds of thousands of years. Thus, it is no surprise that the philosophical debate on causality dates back to ancient times and many cultures, both East and West.

While scholars from different fields define causality often in different ways, modern natural science – starting in the 17th century with Galileo Galilei and Isaac Newton – established the clear framework of classical physics. There, the whole world follows not only causal but deterministic laws. The significance of this worldview is best illustrated by Pierre-Simon Laplace’s famous demon, a hypothetical entity, which knows precisely the position and the velocity of any single particle in the universe as well as all the acting forces. By using Newton’s laws it is then able to compute the past and the future evolution of the world with absolute certainty. In 1814, Laplace wrote:Reference Laplace¹

By the beginning of the 20th century, the deterministic framework of classical physics, which had started from mechanics, also incorporated the theory of light, electricity and magnetism (electrodynamics), the theory of heat (thermodynamics and statistical physics), as well as the special and general theories of relativity about space and time, which also encompass a modern post-Newtonian theory of gravitation.

However, a small number of open problems at the end of the 19th century, such as the radiation from black bodies studied by Max Planck, turned out to be of vast importance. Slowly but steadily, experiment by experiment, the foundational structure of classical physics came under attack. Albert Einstein had suggested a new heuristic aspect of the nature of light using particles in contradiction to waves. Niels Bohr had found phenomenological rules to describe the radiating electronic transitions in atoms, which were in plain contradiction with classical electrodynamics. Louis de Broglie postulated a theory of matter waves, stating that not only light but also material particles, like electrons, have a dualistic nature and can behave as a wave or as a particle. By the middle of the 1930s, the old classical worldview had been given up, as Werner Heisenberg, Erwin Schrödinger, Max Born, Pascual Jordan, Wolfgang Pauli, Paul Dirac and John von Neumann built a totally new theory – which accurately described all the new experimental findings – as one of the underlying foundational structures of physics: that is, quantum mechanics. Today, quantum mechanics or, broader, quantum physics (although both terms are often used in a synonymous way) is a central pillar of many aspects of modern high-tech industry, including the semiconductor industry, and therefore it is part of the inner workings of computers, and lasers, to just name two examples.

Quantum mechanics and information

Quantum mechanics in its Copenhagen interpretation was a paradigmatic shift in many ways. Most fundamentally, however, it abandoned the assumption of an all-embracing objective reality. In 1958, Heisenberg formulated this world view in the following way:Reference Heisenberg²

Contrary to the prerequisite in classical physics, it is not true that objects posses definite properties at all times. In general, we can only make probabilistic predictions. In fact, the quantum mechanical wave function, or state, which is associated with a physical system is precisely a catalog of information about it and, at the same time, the complete (albeit probabilistic) description of all possible outcomes in future experiments.

An immediate consequence of this is objective randomness. From the viewpoint that we can, in principle, only make a probabilistic prediction of, say, the position of a particle in a future measurement, its precise position does not exist as an element of reality. The outcome in the measurement must be irreducibly random and non-deterministic. Causality is hence preserved only in a weak sense. There is, of course, still a dependence of results in a measurement on the previous preparation of a system. In other words, in quantum mechanics there is apparently still a lot of structure and order in the time evolution of systems, and not complete chaos and randomness. However, in general, the evolution is such that the final individual measurement outcomes are not predetermined and that only their probabilities are determined by the theory. Causality in its deterministic reading – namely that the properties themselves are determined with certainty and that only one single outcome is possible at each measurement – is therefore given up.

Quantum randomness is connected with the superposition principle, i.e. the possibility that a system can be in a combination of a variety of different states. For example, the particle may be in a superposition of different places and therefore its position is not definite. In the famous double slit experiment, particles (e.g. photons or electrons) pass a wall with two slits, centered at x ₁ and x ₂ respectively. They do not have a classical trajectory through either one of the slits but they are in a superposition state of passing through the first slit centered at position x ₁and through the second slit centered at x ₂, formally written as ( (wave behavior). These possibilities later interfere on an observation screen, leading to an oscillating intensity pattern which, however, is built up from individual scintillations (particle behavior).

If two or more systems are in a superposition of different states, they are called entangled. For instance, one could prepare a pair of particles, A and B, in a superposition of the state ‘particle A is at position x ₁ and particle B is at position x ₃’ and the state ‘particle A is at position x ₂ and particle B is at position x ₄’, formally written as . In such an entangled state, the composite system is completely specified in the sense that the correlations between the individuals are well defined. Whenever particle A is found at position x ₁ (or x ₂), particle B is certainly found at x ₃ (or x ₄ respectively). However, there is no information at all about whether particle A is at x ₁ or x ₂ and whether B is at x ₃ or x ₄. In 1935, in his article ‘The present situation in quantum mechanics’ Schrödinger wrote:Reference Schrödinger³

Local realism and Bell’s theorem

In a letter from 1926 to Born, Einstein expressed his deep conviction that the randomness of individual quantum mechanical events can always be reduced to an unknown cause with the words:⁴

The answer attributed to Bohr was to suggest: ‘Einstein, don’t tell God what to do.’ While Einstein’s position can be seen as insisting that physics must answer ontological questions such as ‘What is?’, Bohr may be interpreted as limiting physics to answering epistemological questions such as ‘What can be said?’

In 1935, Einstein, Boris Podolsky and Nathan Rosen (EPR) published the seminal articleReference Einstein, Podolsky and Rosen⁵ ‘Can quantum-mechanical description of physical reality be considered complete?’ In it, they used certain entangled states – now called ‘EPR states’ – and exploited their ‘spooky’ correlations to argue that quantum mechanics is an incomplete description of physical reality. As an analog of this position, one could also say that the probabilities in 19th-century thermodynamics and statistical physics simply arise just out of ignorance of the underlying complex microscopic situations, which are considered to be fully deterministic. Why should it not be possible that something very similar is true for quantum mechanics?

In contrast to a closed world in which randomness is only subjective and due to ignorance of underlying causes, objective randomness manifests a genuinely open world. In 1954, Pauli expressed his viewpoint in a letter to Born:Reference Pauli⁶

The search for an underlying theory moved into the realm of experiments in the 1960s, when John Bell put forward his famous theorem. Bell made three assumptions about a possible physical worldview. (1) Realism: objects posses their properties prior to and independent of observation. (Determinism is a specific form of realism, in which all properties have predefined values at all times.) This means there are ‘hidden variables’ specifying the properties of systems. (2) Locality: this is the concept that if two systems no longer interact, no real change can take place in the second system in consequence of anything that may be done to the first system. (3) Freedom of choice: in Bell’s words,Reference Bell⁷ this hypothesis requires that the measurement settings chosen by the experimenters ‘can be considered as free or random’ such that ‘they are not influenced by the hidden variables’.

Bell mathematically proved that the combination of these three assumptions, denoted as ‘local realism’, is at variance with quantum mechanics. He derived an inequality, which is satisfied by all local realistic theories but which can be violated by entangled quantum states. Starting in the 1970s, a series of ground-breaking experiments disproved local realism and showed perfect agreement with the predictions from quantum theory. Up to the present, numerous experiments have been and are still being performed, achieving better and better accuracy and closing more and more of the loopholes of earlier experiments. In view of the importance of this question, a loophole-free Bell test should be performed experimentally, even though now it seems very unlikely that the concept of local realism – i.e. the concept of an objective external reality without any ‘spooky action at a distance’ – can be maintained.

A decisive feature in experiments violating Bell’s inequality is that entangled states of particle pairs are used. One particle of each pair is measured at one location by a party, usually called Alice. The other particle is detected at some distant location by another party, usually called Bob. Alice and Bob both independently and freely choose their measurement setting and note down the outcomes. Due to the entanglement of the initial state, the correlations between their outcomes are well defined. They are in a certain sense ‘stronger’ than what is possible in any (classical) local realistic theory and thus violate Bell’s inequality. However, according to the Copenhagen interpretation, Alice and Bob’s individual outcomes are objectively random and undefined in each run of the experiment until they manifest themselves in the measurement process. This is why there is no conflict with special relativity theory, although Alice and Bob might be far apart from each other and make their measurements at the same time. There is no need to transmit physical information from one side to the other. The resource for the quantum correlations is in the entangled state they share and not in any transmissions from one side to the other. It is the randomness (disliked by Einstein) that saves entanglement (disliked by Einstein) from violating special relativity (liked by Einstein).

It is worth noting that there have been suggestions where individual particles possess well-defined properties (like position and momentum) at all times. De Broglie’s pilot wave model from the 1920s implied a non-linear evolution in quantum mechanics. Based on this model, David Bohm developed, in the 1950s, his Bohmian interpretation of quantum mechanics, also often called the de Broglie–Bohm theory. In contrast to the Copenhagen interpretation, Bohmian mechanics saves the deterministic worldview by assuming that all particles have definite positions at all times (which are the hidden variables of the theory) and follow trajectories that are guided by a quantum potential given by the wave function. Randomness in this theory is indeed only subjective, stemming from ignorance of the hidden variables.

However, according to Bell’s theorem, the price to pay is that this guiding potential has to change non-locally (instantaneously), if one has an entangled state between two distant parties and one party makes a measurement. The measurement on one particle changes the quantum potential in the whole space, in particular at the place of the second particle. This leads to a strong tension with the special theory of relativity. While the testable predictions of Bohmian mechanics are isomorphic to standard Copenhagen quantum mechanics, its underlying hidden variables have to be, in principle, unobservable. If one could observe them, one would be able to take advantage of that and signal faster than light, which – according to the special theory of relativity – leads to physical temporal paradoxes.

Quantum information and technology

In the last few decades, it has turned out that foundational aspects of quantum physics are not only of philosophical interest but have opened up striking new possibilities of a new quantum information technology. Features such as superposition and entanglement can be exploited to solve certain tasks, which cannot be solved – or at least cannot be solved that efficiently – by purely classical machines. Among the most famous developments in this new field of quantum information, i.e. the union of quantum theory with information theory, are quantum computation and quantum cryptography.

In quantum computation, one exploits the entanglement of quantum systems as well as specific operations, such as transformations or measurements, to find the result of certain problems in fewer steps and thus faster than any classical computer can possibly do. In one particular realization of quantum cryptography, one sends pairs of entangled particles to two parties, Alice and Bob. Due to the quantum correlations, Alice and Bob can establish a secret key. Any eavesdropping can be revealed by checking Bell’s inequality. As long as it is violated, no eavesdropper could have possibly intercepted the particles and hence know the key. While quantum computation is still at the stage of fundamental research and limited to only a few quantum bits (‘qubits’) and simple calculations, quantum cryptography has already made the step to an industrial level.

Another task that relies on the laws of quantum theory is the teleportation of an unknown quantum state. Here, Alice and Bob share an entangled particle pair: particles 2 and 3 in Figure 1. Alice is provided with another particle, particle 1 in the figure, which is in an arbitrary input state. Alice then performs a joint measurement on particles 1 and 2 in the so-called Bell-basis, i.e. she projects her two particles on a maximally entangled state. She then sends her result to Bob, e.g. via telephone or internet. Depending on this information, Bob performs one out of four simple transformations on his particle 3. Finally, due to the initial entanglement, the state of Bob’s particle 3 is identical to the initial input state of Alice’s particle 1 which has lost its private properties.

Figure 1 The scheme of quantum teleportation. Alice and Bob share an entangled state which is produced by an EPR source. Alice performs a joint Bell state measurement (BSM) on her particle and on an input particle. She transmits her result to Bob who, depending on Alice’s message, performs an operation on his particle. The final state of Bob’s particle is then identical to Alice’s input state.Reference Bouwmeester, Pan, Mattle, Eibl, Weinfurter and Zeilinger⁸

Which of the four possible outcomes Alice gets is completely random. She has to transmit this information to Bob via a classical communication channel. Bob has to wait for this information to perform the correct operation to his particle. Therefore, due to the randomness of the Bell state measurement, there is no conflict with special relativity. After all, no information is transmitted faster than light. If Alice could somehow break the complete randomness, such that she would be able to change the statistics at Bob’s location, then she could communicate faster than the speed of light.

A foundational principle for quantum mechanics

It is worth asking whether there is a deeper message conveyed by the Copenhagen interpretation of quantum mechanics. Can one come up with a foundational principle for quantum mechanics that can explain some of its key features, such as randomness and entanglement?

In this regard, in 1999, one of us (AZ) proposed an idea that connects the concept of information with the notion of elementary systems. For the subsequent line of thought, we first have to make ourselves aware of the fact that our description of the physical world is represented by propositions, i.e. by logical statements about it. These propositions concern classical measurement results. Therefore, the measurement results must be irreducible primitives of any interpretation. And second, that we have knowledge or information about an object only through observations, i.e. by interrogating nature through yes-no questions. It does not make any sense to talk about reality without having information about it.

Any complex object that is represented by numerous propositions can be decomposed into constituent abstract systems that each need fewer propositions in order to be specified. The position of a particle, for instance, can be decomposed into a sequence of ‘left or right’ questions, subdividing space into smaller and smaller parts. The process of subdividing reaches its limit when the individual subsystems only represent a single proposition, and such a system is denoted as an elementary system. This notion is very closely related to Carl Friedrich von Weizsäcker’s binary alternative, called the ‘Ur’,Reference von Weizsäcker⁹ and to the qubit of modern quantum information theory. The truth value of a single proposition about an elementary system can be represented by one bit of information with ‘true’ being identified with the bit value ‘1’ and ‘false’ with ‘0’.

In ‘A foundational principle of quantum mechanics’Reference Zeilinger¹⁰ and a subsequent workReference Brukner and Zeilinger¹¹ it is then suggested to assume a principle of quantization of information:

Disregarding the mass, charge, position and momentum of an electron, its spin is such an elementary system. Now consider that we prepare many electrons, each in such a spin state that it is certainly deflected into the positive vertical, i.e. the +z, direction if it passes a Stern-Gerlach magnet that is also oriented along +z (see Figure 2).

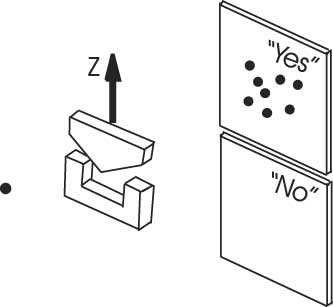
Figure 2 Each individual electron can be prepared in such a quantum spin state that it is deflected in the +z direction when it passes the inhomogeneous magnetic field of a Stern-Gerlach magnet oriented also along +z. The question ‘spin up along z?’ is hence answered with ‘yes’ by all the electrons.Reference Brukner and Zeilinger¹¹

The corresponding quantum state of each of these electrons is denoted by , and it specifies the truth value ‘true’ or ‘1’ of the 1-bit proposition:

Now we have used up our single bit per electron spin. Therefore, a measurement of an electron along any other direction, say along the direction θ must necessarily contain an element of randomness (see Figure 3). This randomness must be objective and irreducible. It cannot be reduced to unknown hidden properties as then the system would represent more than a single bit of information. Since there are more possible experimental questions than the system can answer definitely, it has to ‘guess’. Objective randomness is a consequence of the principle lack of information.

Figure 3 If electrons are again prepared with spin up along z, but are measured along a tilted direction θ, some of them are deflected in the θ-direction and some in the opposite direction. For each individual event, only the probability is determined by quantum theory. The question ‘spin up along θ?’ is answered with ‘yes’ by some of the electrons and with ‘no’ by the others.Reference Brukner and Zeilinger¹¹

In the extreme case, when the measurement direction is orthogonal to the preparation, say along y, the system does not carry any information whatsoever about the measurement result. Due to this full complementarity, the outcomes are completely random with probability each. After the measurement, however, the system is found to be in one of the states ‘up along y’ or ‘down along y’. This new one-bit information was spontaneously created in the measurement, while the old information is irrecoverably erased due to the limitation of one-bit ‘storage capacity’ in the electron spin.

Let us now proceed to multi-particle systems. First, the above information principle is generalized to

Let us start with the simple example of a product state of two spin particles, labeled 1 and 2: . The two bits of these two elementary systems represent the truth values of the two following propositions:

The two bits have thus been used up to define individual properties of the two electrons. But we can also choose to use the two bits to define joint properties of the two spins. For instance we may specify the truth of the following two propositions:

The corresponding quantum state is uniquely defined. It is the entangled (EPR-like) state

Given the principle of quantization of information, entanglement is therefore a consequence of the fact that the total information is used to define joint and not individual properties of a composite system. While, due it its quantum correlations, this entangled state is capable of violating local realism in a Bell test, it neither specifies whether the individual spins are up or down along z nor whether they are up or down along y. The individual properties remain completely undefined.

In realistic (deterministic) non-local theories, like Bohmian mechanics, every particle carries a huge amount of information, specifying the results of all possible measurement outcomes. However, being in accordance with the Copenhagen interpretation, the foundational principle of finiteness of information represented by elementary systems provides a new way of understanding objective randomness, complementarity and entanglement. Recently, the approach discussed here has also been connected with the notion of logical independence in pure mathematics.Reference Paterek, Kofler, Prevedel, Klimek, Aspelmeyer, Zeilinger and Brukner¹²