Introduction
The recent discovery that most stars likely have companion planets has renewed speculation over the possibility of extraterrestrial life (Sagan Reference Sagan1980; Cassan et al. Reference Cassan2012). While most of these worlds will not be life-sustaining – we know of only one out of eight in the Solar System – others, such as Kepler-452b, appear much more promising (Jenkins et al. Reference Jenkins2015). NASA estimates that 20 billion planetsFootnote 1 in the Milky Way Galaxy are in circumstellar habitable zones (Bonfils et al. Reference Bonfils2011).
The prevalence of habitable exoplanets and the probability of life emerging on one of those worlds are two key factors in the Drake equation (2015), the standard framework for estimating the number of technologically advanced civilizations in the Galaxy. The formula is a probabilistic argument composed of seven factors relevant to contact with alien life (see the Appendix). While billions of habitable planets significantly increase this possibility, many of the equation's other component probabilities, including the chances of life developing on a habitable planet, are either unknown or have large error intervals.
In this paper, we explore a different method of examining this question, one that replaces the various Drake factors with the single estimate for the probability of life existing on Earth. Some of the implications of this approach for finding life on exoplanets are discussed.
How likely is it that life formed on one and only one planet?
The likelihood of extraterrestrial life can be redefined in terms of the probability of a known event, the existence of life on at least one planet (i.e. Earth). This relationship can be described by the binomial distribution if the presence of life on a habitable planet is treated as a success in a Bernoulli trial. Named for 17th-century Swiss mathematician Jacob Bernoulli, a Bernoulli trial has only two possible outcomes, such as heads or tails in a coin flip, which can be equated to success or failure. The sum of the probabilities of these two outcomes (p and q) must equal 1. The binomial distribution is the discrete probability distribution of the number of successes (k) in a sequence of independent Bernoulli trials. The distribution has two parameters: the probability of a success (p); and the number of trials (n). For example, Fig. 1 shows the probabilities for 0, 1, 2, 3, 4 and 5 successes for 40 trials given a success probability of 0.02.
Fig. 1. Binomial distribution (with parameters p = 0.02, n = 40).
If the presence of life on a habitable planet in the Milky Way Galaxy is treated as a Bernoulli trial success, then the binomial distribution can be used to determine the probability of k successes. While estimates exist for the number of habitable planets in the Galaxy (n), the probability of a success (p) is unknownFootnote 2 . However, we can use the binominal distribution to replace this parameter with the probability that life exists on at least one planet (α)Footnote 3 . The question of exoplanet life can then be reformulated as follows – given the probability of one or more independent successes for a given number of trials, what is the probability of two or more successes?
The probability mass function for the binomial distribution is (Evans et al. Reference Evans, Hastings and Peacock2000):
$$f\,(k;n,p) = P_L (k) = \left( {\matrix{ n \cr k \cr}} \right) p^k q^{n - k} $$
for k = 0, 1, 2, 3, … , n (number of habitable planets in the Galaxy), where p is the probability of success (life forming on a given habitable planet); q = 1 – p, the probability of failure (life not forming on a given habitable planet); n, the number of trials (total number of habitable planets); P
L
(k), the probability of k successes (life on k planets), for a given p and n; and
$\left( {\matrix{ n \cr k \cr}} \right), \,{\hbox{the binomial coefficient}} = \displaystyle{{n!} \over {k!(n - k)!}}.$
For k = 0 (life exists on no planets), then
$\left( {\matrix{ n \cr k \cr}} \right) = 1$
, and
$$P_L (0) = q^n. $$
For k = 1 (life exists on only one planet), then
$\left( {\matrix{ n \cr k \cr}} \right) = n$
, and:
$$P_{\rm L} (1) = npq^{n - 1}. $$
For k ≥ 2 (life exists on more than one planet):
$$\eqalign{P_{\rm L} ( \ge \!2) & = 1 - P_{\rm L} (0) - P_{\rm L} (1) = 1 - q^n - npq^{n - 1} \cr & = 1 + (n - 1)q^n - nq^{n - 1}.}$$
The probability of life existing on at least one planet in the GalaxyFootnote 4 is therefore:
$$P_{\rm L} ( \ge\!\! 1) = 1 - q^n = {\rm \alpha} . $$
Thus,
$$q = (1 - {\rm \alpha} )^{1/n}, $$
$$P_{\rm L} (0) = 1 - {\rm \alpha,} $$
$$P_{\rm L} (1) = n\left[ {{\rm \alpha} + (1 - {\rm \alpha} )^{({n - 1)/n}} - 1} \right],$$
$$P_{\rm L} ( \ge\! 2) = {\rm \alpha} - n\left[ {{\rm \alpha} + (1 - {\rm \alpha} )^{({n - 1)/n}} - 1} \right].$$
As we know that life exists on Earth, it is necessary to calculate the conditional probability of life on more than one planet given that life exists on at least one planet. A conditional probability is defined as:
$$P(A \vert B) = \displaystyle{{P(A \cap B)} \over {P(B)}} . $$
We therefore need to adjust our estimate by dividing by 1 − qn (or α):
$$P_{\rm L} ( \ge\! 2 \vert k \ne 0) = 1 - n + \displaystyle{n \over {\rm \alpha}} \left[ {1 - (1 - {\rm \alpha} )^{(n - 1)/n}} \right] = {\rm \beta} . $$
The above equation allows us to compare the probability of life on more than one planet (β) to the probability of life on at least one planet (α). Figure 2 shows the relationship between these two probabilities for 10 000 habitable planetsFootnote 5 . The ratio β/α increases from 0.5 to 1 as α grows from very low values to certainty (i.e. as qn approaches 0). The relationship is nonlinear; for example, β/α = 0.50 for α = 0.01, 0.61 for α = 0.50, 0.72 for α = 0.75, and 0.83 for α = 0.90. While all we know for certain is that 0 < α < 1, a Bayesian argument can be made for α falling between 0.5 and 1 given the existence of life on Earth (Eddy Reference Eddy2004). At the midpoint of this range (α = 0.75), for a conservative estimate of 10 000 habitable planets β = 0.54, meaning that exoplanet life is more probable than not.
Fig. 2. Probability of exoplanet life by probability of life existing on at least one planet (for n = 10 000 habitable planets).
The value of β is a function of α and n, and α in turn is a function of p and n. With enough planets, even very low life probabilities translate into a likelihood of life on more than one planet. Figure 3 shows the relationship between α and p for 1000, 10 000 and 100 000 habitable planets. For 20 billion habitable planets, a p value as low as 7 × 10−11 still produces an α value of 0.75 (β > 0.5); for 1 billion habitable planets, the necessary p value is 1.4 × 10−9. As the number of planets increases, the value of p necessary to produce a given value of α decreases and vice versa (Fig. 4). Table 1 lists β values and the necessary p values and numbers of planets for various α probabilities.
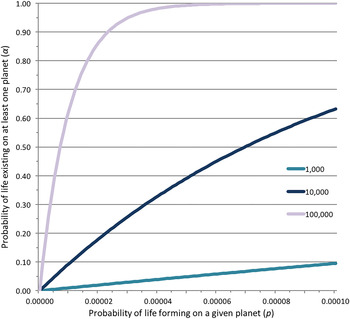
Fig. 3. Probability of life existing on at least one planet by probability of life forming on a given planet (for n = 1000, 10 000 and 100 000 habitable planets).
Fig. 4. Probability of life forming on a given planet by number of habitable planets (for α = 0.75).
Table 1. Probability of exoplanet life
Evolution
Life falls along a continuum of advancement: microorganisms, multicellular organisms, animals, intelligent beings, societies capable of interstellar communication. As higher life must evolve from lower life, the probability of any type of life emerging on a planet is higher than the probability for intelligent life (Sterelny & Griffiths Reference Sterelny and Griffiths1999). Therefore, the more advanced the life form, the smaller its p and α values.
Life first emerged on Earth 3.4 billion years ago, 1.1 billion years after its formation; humans, however, appeared only in the past 200 000 years. Given sufficient time, is it inevitable that basic life forms will evolve into intelligent life? Once simple molecules develop the ability to replicate, natural selection suggests those that adapt well will replace those that do not (Darwin Reference Darwin1859). However, the outcome of that process is not inevitable. Evolutionary factors such as initial conditions, environment, and random mutations all influence outcomes. Initial conditions and environment dictate what traits are favoured and thus shape natural selection. Mutations are also important, but as a rule more so in small than large populations.
Intelligent life may not be inevitable, and might not even be probable (Ward & Brownlee Reference Ward and Brownlee2000). Dennett (Reference Dennett1995) discusses ‘good tricks’ in design space – solutions that natural selection has repeatedly found. Vision, for example, has evolved independently in multiple lineages, suggesting this is a good enough trick to justify the expectation that natural selection will most often realize it, at least where light is present. While there are several traits that fall into this category, advanced intelligence may not be one of them; it apparently failed to evolve in dinosaurs, the dominant terrestrial vertebrates for over 100 million years. Although intelligence has emerged in a number of taxa, if we define higher intelligence as something at the human level, the only evidence available to us is that it evolved in one species on one planet. Furthermore, the most intelligent life forms might not be the most adaptive for survival (Gould Reference Gould1996). Consequently, complex life on other planets may not possess higher intelligence as we currently understand it.
Communication limits
The Fermi paradox is the supposed contradiction between the high probability some have proposed for the existence of intelligent alien life and our lack of evidence of such life (Crawford Reference Crawford2000). However, we can only learn of advanced civilizations on exoplanets through communication, which is limited by the speed of light. The Milky Way Galaxy is large, roughly 100 000 light years in diameter. Even after a millennium, a transmission from Earth would only reach a small fraction of its stars; a response would then take another 1000 years to return.
Extraterrestrial civilizations much older than ours might exist, and signals from even very distant planets could have reached Earth if sent far enough in the past. As a star ages; however, its size and temperature change and so its habitable zone moves. Consequently, habitable planets – and any advanced civilizations they may host – have a limited lifespan. In some cases, a planet may not exist long enough for higher life with interstellar communication abilities to evolve.
A signal from an advanced alien civilization has to intersect Earth's light cone to reach us. This means: (1) intelligent life must have formed on an exoplanet and evolved to the point of having a method of interstellar communication; (2) their planet must be close enough to Earth for their messages to have had time to reach us; and (3) their civilization must not have died out too long in the past given their distance from Earth (if they did, their signals would have arrived before we developed the technology to recognize them).
Figure 5 (a two-dimensional picture of a four-dimensional configuration) illustrates these requirements. It depicts three planets with advanced civilizations, one that intersects Earth's light cone (δ), and two that do not (ε and γ). Of the latter, one planet (ε) is so distant that we have not yet received its messages. The civilization of the other planet (γ) disappeared long ago, and its messages, which reached Earth in our far past, were ignored.
Fig. 5. Spatial-temporal communication range of extraterrestrial advanced civilizations.
The proportion of the Galaxy's history that has fallen within our planet's light cone since we developed a signal detection capability is extremely small. Moreover, the shorter the time a civilization engages in interstellar communication, the less likely its signals will be detected. How long such communication might last is unknown as the longevity of intelligent life, including our own, is uncertain. Unfortunately, the risks of self-destruction and environmental ruin appear to increase with growth and development (Diamond Reference Diamond2005; Doomsday Clock 2012).
Given these spatial and temporal limits, communication from an advanced civilization in our Galaxy may not be detected by us for a long time to come. Moreover, with a typical distance of 3 billion light years between galaxies, human life could well have disappeared before any signals from outside the Milky Way Galaxy ever have a chance to reach us.
Conclusion
The Bernoulli trial method reframes the likelihood of alien life in terms of the probability that life emerged on at least one planet (i.e. Earth). The value assigned to α can be considered a level of belief, a starting point for considering the question of whether other life forms exist in the Galaxy.
This approach assumes the binomial distribution is appropriate for modelling the probability of life emerging on a planet in our Galaxy and that Earth is not particularly unique (the mediocrity principle). The discussion further supposes limits imposed by the current laws of physics cannot be overcome, life requires a habitable (as currently defined) planet, and that extraterrestrial civilizations have not found traversable wormholes or engaged in interstellar migration. While these assumptions may not be all correct, they do reflect our current state of knowledge.
Even if the existence of intelligent life elsewhere in the Galaxy is likely, its detection in the near future is far from certain due to the distances involved. Of course, assuming it were possible to communicate with intelligent aliens, it may still not be wise to do so (Ambassador for Earth 2006). Our own world's history of what happens when an advanced civilization encounters a less developed one has not been particularly good.
Acknowledgements
I would like to thank Dr Steven Le Comber, School of Biological and Chemical Sciences, Queen Mary University of London, Dr Lucia Summers, School of Criminal Justice, Texas State University, and the anonymous reviewer for their helpful comments.
Appendix
The Drake equation is:
$$N = R^{^\ast} f_{\rm p} n_{\rm e} f_{\rm l} f_{\rm i} f_{\rm c} L,$$
where N, is the number of detectible extraterrestrial civilizations in the Milky Way Galaxy; R *, the mean rate of star formation per year in the Galaxy; f p, the fraction of the above that have planets; n e, the mean number of the above that can support life; f l, the fraction of the above that go on to develop life; f i, the fraction of the above that develop intelligent life; f c, the fraction of the above that send detectable signs of their existence into space; L, the length of time for which the above are sent into space.
The value of p for the probability of any type of life forming on a given habitable planet is equal to f l, while the value of p for the probability of intelligent life forming on a given habitable planet is equal to f l f i.
