Introduction
The timing of germination and seedling emergence are crucial in the life cycle of plants (Harper, Reference Harper1977). They influence posterior plant fitness components such as survival, growth and fecundity in different ways (Verdú and Traveset, Reference Verdú and Traveset2005), and in perennial species the benefits acquired by germinating and emerging early are perpetuated for many years after germination (e.g. De Luis et al., Reference De Luis, Verdú and Raventós2008). Germination is the first major developmental transition in the life of plants, affecting the evolution of post-germination traits, ecological niches and geographic ranges of plants (Donohue et al., Reference Donohue, de Casas, Burghardt, Kovach and Willis2010). In short, a plant bets its life in this all or nothing event (Welbaum et al., Reference Welbaum, Bradford, Yim, Booth and Oluoch1998).
Climate change may have very important consequences for the population and community dynamics of plant species through their effects on sexual plant reproduction (Hedhly et al., Reference Hedhly, Hormaza and Herrero2009; Walck et al., Reference Walck, Hidayati, Dixon, Thompson and Poschlod2011). The immediate effects of global warming have been shown to be mediated by early flowering (Menzel et al., Reference Menzel, Sparks, Estrella, Koch, Aasa, Ahas, Alm-Kübler, Bissolli, Braslavská, Briede, Chmielewski, Crepinsek, Curnel, Dahl, Defila, Donnelly, Filella, Jatcza, Måge, Mestre, Nordli, Peñuelas, Pirinen, Remisová, Scheifinger, Striz, Susnik, Van Vliet, Wielgolaski, Zach and Zust2006) and an increase in, or irregular, seed production (Porter, Reference Porter2005; Barnabás et al., Reference Barnabás, Jaeger and Feher2008). Climate change effects on seed germination have been examined by means of observational studies (Dainese, Reference Dainese2011) and common garden experiments (Willis and Hulme, Reference Willis and Hulme2002; De Frenne et al., Reference De Frenne, Graae, Kolb, Brunet, Chabrerie, Cousins, Decocq, Dhondt, Diekmann, Eriksson, Heinken, Hermy, Jogar, Saguez, Shevtsova, Stanton, Zindel, Zobel and Verheyen2010), and by modifying field temperatures (Zavaleta, Reference Zavaleta2006; Klady et al., Reference Klady, Henry and Lemay2011), CO2 concentration (Edwards et al., Reference Edwards, Clark and Newton2001; Zavaleta, Reference Zavaleta2006), and water availability (Cipriotti et al., Reference Cipriotti, Flombaum, Sala and Aguiar2008; Lampei and Tielbörger, Reference Lampei and Tielbörger2010), both in greenhouse (de Dios Miranda et al., Reference de Dios Miranda, Padilla and Pugnaire2009) and in laboratory experiments (Graae et al., Reference Graae, Alsos and Ejrnaes2008; McCarragher et al., Reference McCarragher, Goldblum and Rigg2011). However, most of these have not modelled germination under the whole range of conditions a species may experience in the future.
Temperature and water availability are important regulators of seed germination (Kebreab and Murdoch, Reference Kebreab and Murdoch1999; Bradford, Reference Bradford2002). Threshold models have been developed to understand how both factors affect the germination process. More specific, hydrothermal time (HTT) models (Gummerson, Reference Gummerson1986; Bradford, Reference Bradford1990; Alvarado and Bradford, Reference Alvarado and Bradford2002) indicate that the timing of germination is closely related to temperature and water potential thresholds for radicle emergence, which vary among individual seeds in a population (Welbaum et al., Reference Welbaum, Bradford, Yim, Booth and Oluoch1998). HTT models describe seed germination using parameters such as base, optimum and ceiling germination temperatures, hydrothermal time constant required for germination, and mean and standard deviation of the base water potential for the seed population (Dorado et al., Reference Dorado, Fernandez-Quintanilla and Grundy2009; Meyer and Allen, Reference Meyer and Allen2009). The latter is the threshold water potential for radicle emergence of a given seed or seed fraction (Bradford, Reference Bradford2002). Once these parameters are estimated, germination time courses can be predicted for any combination of temperature and water potential (Allen, Reference Allen2003). So far, HTT models have been developed mainly in an agronomical context to predict emergence of crop and weed species (e.g. Roman et al., Reference Roman, Thomas, Murphy and Swanton1999; Alvarado and Bradford, Reference Alvarado and Bradford2005). They were shown to be effective in disentangling the effect of pre-germination treatments (Cheng and Bradford, Reference Cheng and Bradford1999; Alvarado and Bradford, Reference Alvarado and Bradford2005), predicting dormancy loss and field germination (Meyer and Allen, Reference Meyer and Allen2009), and explaining differences in germination patterns associated with contrasting habitats (Allen et al., Reference Allen, Meyer and Khan2000), seed sizes (Wang et al., Reference Wang, Bai and Tanino2004) and genotypes (Ellis et al., Reference Ellis, Covell, Roberts and Summerfield1986; Dahal et al., Reference Dahal, Bradford and Jones1990). Because HTT models can predict how any specific fraction of a seed population will respond to alterations in environmental conditions (Bradford, Reference Bradford2002), these models can also be applied to study the response of rare and threatened plant species to climate change (Wei et al., Reference Wei, Bai and Henderson2009; Qiu et al., Reference Qiu, Bai, Fu and Wilmshurst2010). Although HTT models were mainly used in species with a short lifespan, they are also specifically relevant for species with long generation times, for which adaptation in response to a rapidly changing climate needs a century or over a millennium to occur (Davis et al., Reference Davis, Shaw and Etterson2005).
Species from mountain ecosystems, and particularly of mountain summits, are very susceptible to climate change, given their inability to keep up with the upward range shift and the accompanying habitat reduction (Fischlin et al., Reference Fischlin, Midgley, Price, Leemans, Gopal, Turley, Rounsevell, Dube, Tarazona and Velichko2007). One particular genus finding itself in this situation is Polylepis (Rosaceae). Species from this genus typically form monospecific stands in the Andean mountain range from Venezuela (9°N) to Argentina (32°S), where they provide valuable ecosystem services (Fjeldså and Kessler, Reference Fjeldså and Kessler1996; Fernández et al., Reference Fernández, Mercado, Arrázola and Martínez2001). An ecologically and economically important Polylepis species in Bolivia is P. besseri Hieron. It is distributed in the Peruvian Puna Province in Bolivia (Fjeldså and Kessler, Reference Fjeldså and Kessler1996; Navarro et al., Reference Navarro, Molina and De la Barra2005), and has a vulnerable conservation status (World Conservation Monitoring Center, 1998). Knowledge of germination requirements or possible dormancy mechanisms in Polylepis species is scarce. In general, little information is available on the germination ecology of tropical mountain plants. The seed germination of tropical high-mountain species is mainly determined by light, temperature and water availability (Teketay, Reference Teketay2005). It was found that the germination of five species of the sister genus Acaena (Rosaceae) from the subalpine zone in New Zealand (not in the tropics) had an optimum temperature of 20°C, except for A. glabra (17°C) (Conner, Reference Conner1987; Baskin and Baskin, Reference Baskin and Baskin1998). Germination of these species was promoted by light, increased at high water potentials and had a narrow temperature range for germination (14–21°C); cold storage or alternating temperatures did not affect germination, which was higher under light conditions compared to darkness (Conner, Reference Conner1987). As far as we know, there is no information on the germination ecology of P. besseri and, as for the other Polylepis species in Bolivia, its populations have an uncertain fate under current climate change (Gareca et al., Reference Gareca, Hermy, Fjeldså and Honnay2010).
Our general objectives were to apply HTT models to study the germination characteristics of P. besseri and its response to changes in water availability and temperature conditions. The specific objectives were to: (1) check for possible dormancy mechanisms; (2) construct a hydrothermal time model for the species and derive important germination thresholds and parameters; (3) examine whether fluctuating temperatures stimulate germination; and (4) based on the parameters obtained from the HTT model, discuss the effects of climate change, and specifically of increasing temperature, on the germination of P. besseri.
Materials and methods
Study species
Polylepis besseri Hieron. is a tree distributed at 3000–4100 m above sea level (asl) in Cochabamba and Chuquisaca – Bolivia, and grows to about 8 m tall (Fjeldså and Kessler, Reference Fjeldså and Kessler1996). In Sacha Loma (17°44′S, 65°34′W, Cochabamba) P. besseri flowers between July and December, with a peak in September and October, and produces fruits between September and April, with a peak in December (Martinez-Costas, Reference Martinez-Costas2003). Each fruit is typically a one-seeded achene and it is the dispersal unit (Simpson, Reference Simpson1979). Seeds germinate and seedlings emerge throughout the warm rainy season from January to April (unpublished data). The range of maximum, mean and minimum temperatures during this season are 12.7–18.4°C (during the day), 7.6–11.4°C and − 1.1 to 2.7°C (during the night), respectively [values retrieved from the Local Climate Estimator New Loc Clim v. 1.10 using Shepards' method with a vertical and horizontal correction (cf. Grieser et al., Reference Grieser, Gommes and Bernardi2006)].
Plant material
Fruits of P. besseri were collected between December 2009 and January 2010. Mature fruits were manually collected from at least 50 trees in each of four large fragments found near Sacha Loma at elevations between 3600 and 3810 m asl. The plant material was stored at room temperature (c. 20°C) for 1 week inside newspapers, allowing it to dry. Afterwards, fruits were cleaned (leaves and small branches removed) and healthy fruits (i.e. complete fruits without holes) were selected, mixed and sent to Belgium, where they arrived 2 weeks later and were immediately used for germination tests.
Fruit coat permeability and water imbibition
Permeability of the fruit coat for water was determined by means of scarification, whereby part of the fruit coat was chipped off with a scalpel. The experiment included two treatments, scarifying and non-scarifying fruits, with three replicates of 25 fruits each, making a total of 150 fruits. The fruits were incubated in germination chambers at 20°C during the day and 2°C during the night (12-h day and 12-h night) in Petri dishes with moist filter paper (MN 440). Light was provided by fluorescent tubes (Philips TLD 80) with a photon flux density of 52 μmol m− 2 s− 1, 400–700 nm. The weight of the 25 blotted fruits per Petri dish (replicate) was measured at the beginning of the experiment, every hour for 6 h, every 6 h for 18 h, every 24 h for 2 d, and every 72 h for 6 d, making a total of 216 h of the experiment. This evaluation timing was taken because of the known triphasic water uptake pattern of the seeds during the initial stage of germination (Finch-Savage and Leubner-Metzger, Reference Finch-Savage and Leubner-Metzger2006). The increase in weight of the 25 fruits was estimated at each evaluation event as the difference of the observed and initial weight divided by the initial weight of the fruits (Baskin and Baskin, Reference Baskin and Baskin1998).
Hydrothermal time model
The experiment included a full factorial design of treatments derived from two factors: water potential and temperature. The water potential levels were 0, − 0.3, − 0.6 and − 0.9 MPa and represent decreasing levels of water availability for seed germination; and the constant temperatures used were 5, 9, 15, 20, 25 and 30°C, making a total of 24 treatments. This range of temperatures covers the temperatures that seeds experience in nature during the germination period (5–15°C) and higher values to check for the effect global warming (20–30°C) on germination. The water potential levels were prepared with polyethylene glycol 8000 (PEG; Biochemica, Germany) according to Michel (Reference Michel1983), using different concentrations for different temperatures. Each treatment had three replicates; each replicate consisted of ten Petri dishes with 25 fruits each, making a total of 250 fruits per replicate. This number of fruits per replicate was used to account for the low and variable germination percentages reported for related species: Polylepis australis (Renison and Cingolani, Reference Renison and Cingolani1998; Enrico et al., Reference Enrico, Funes and Cabido2004; Marcora et al., Reference Marcora, Hensen, Renison, Seltmann and Wesche2008), P. incana (Driesch and Kessler, Reference Driesch and Kessler1996) and P. subtusalbida (Gareca et al., Reference Gareca, Martinez, Navarro and Cahill2007). Eight millilitres of the corresponding PEG solution was added to each Petri dish and it was sealed with Parafilm® to reduce evaporation. The solutions were renewed two times during the experiment, after the fifth and the tenth weeks of the experiment, to avoid fluctuations in water potential. Germination, which finishes with the visible emergence of embryonic tissues from the seed, or from the fruit in this case, was evaluated every week until no new germinations were detected for two consecutive weeks in most of the treatments (16 weeks). The number of white, firm seeds present in the fruits was evaluated at the end of the experiment by cutting fruits in half. The total number of seeds germinated was divided by the total number of available seeds, to obtain the percentage of germinated seeds. Germination percentages were averaged over the three replicates before continuing with the analysis.
To determine the optimum germination temperature (i.e. the temperature where germination rate is at its maximum) a plot of germination rate versus temperature was drawn (Fig. 1). Least squares regression lines were fitted to the 10th and 20th percentiles above and below the visually estimated optimum temperature (T o), which was between 20 and 25°C. Optimum temperature per percentile was estimated as the point where regression lines above and below the visually estimated T o crossed each other.

Figure 1 Germination rate of Polylepis besseri versus temperature for each percentile of germination.
The germination modelling was based on the HTT models (Gummerson, Reference Gummerson1986; Bradford, Reference Bradford1990; Alvarado and Bradford, Reference Alvarado and Bradford2002) which assume that the base temperature (T b) and the hydrothermal time required for germination (θHT) are constants, while the base water potential (ψb) varies according to a normal distribution and is characterized by its mean (ψb(50)) and standard deviation (σψb; Gummerson, Reference Gummerson1986). The models also assume that below the optimum temperature (T o), ψb is independent of temperature, and that the T b is independent of water potential (Kebreab and Murdoch, Reference Kebreab and Murdoch1999). Above T o, where it is assumed that the hydrothermal time accumulation is maximal, ψb increases with increasing temperature with a slope equal to k T (Alvarado and Bradford, Reference Alvarado and Bradford2002). The modelling was performed using repeated probit analyses (Ellis et al., Reference Ellis, Covell, Roberts and Summerfield1986) where the response variable, percentage of germination, was transformed to the probit scale using the PROBIT function in SAS (SAS, 2008). Values below 5% and above 95% of the final germination, considered data points that did not add any germination, as well as any observation where no increase in germination percentage occurred, were therefore excluded; as a consequence, 158 observations out of 1152 initial observations were used in the analysis. A simple linear regression of probits versus the respective predictor variable per model was performed using PROC REG in SAS for each model (Table 1; SAS, 2008). We changed different parameters repeatedly in the predictor variable until the highest R 2 was obtained for the simple linear regression, except for the hydrothermal time model below the optimum temperature, where besides maximizing the R 2 we aimed to retrieve similar parameters for the best hydrothermal time model above optimum temperatures. The equations and the predictor variables for obtaining the predicted germination, as well as the methods for obtaining the parameters, are summarized in Table 1. Goodness of fit of the models was checked by constructing plots of germination percentage versus the normalized thermal time (Alvarado and Bradford, Reference Alvarado and Bradford2002; Bradford, Reference Bradford2002).
Table 1 Equations, their sources, predictor variables and how the parameters were estimated for each germination model of Polylepis besseri

* T o = optimum temperature for germination; T = temperature in the experiment; T b = base temperature; t g = time to germination of the g fraction; θT(50) = mean thermal time; σθT = standard deviation of θT; θC = thermal time constant at supra-optimal temperatures; T c(50) = mean ceiling temperature; σTc = standard deviation of the ceiling temperatures; ψ = water potential of the experiment; θH = hydrotime constant; ψb(50) = mean base water potential; σψb = standard deviation of the base water potential; θHT = hydrothermal time constant; k T = slope of the relationship between ψb(g) and T in the supra-optimal range of T.
† a and b are the intercept and slope of the regression functions, respectively.
Fluctuating temperatures
Fruits were incubated in three treatments: a constant temperature of 20°C, and the daily fluctuating temperatures 20/2°C and 20/10°C (12-h day/12-h night), with three replicates. The 20/2°C treatment resembles the large daily temperature fluctuations in the study area and the 20/10°C treatment has been shown to stimulate germination of many species (Thompson et al., Reference Thompson, Grime and Mason1977; Thompson and Grime, Reference Thompson and Grime1983). Germination was evaluated as in the hydrothermal time experiment over 19 weeks. Finally, the mean germination rate was calculated as the inverse of the time to reach 50% of germination. The mean germination rate and the final percentage of germination (arcsin transformed) were compared between fluctuating temperature treatments using a one-way ANOVA with three levels of the factor temperature (20°C, 20/10°C and 20/2°C). The normality assumption was checked before the analysis. In case of a significant effect of temperature, one degree of freedom contrasts were estimated between the constant and fluctuating temperatures.
Predicting germination
Based on the germination models constructed, the germination percentages obtained in the constant and fluctuating temperature conditions were plotted on a normalized thermal time scale. Since the minimum temperature was higher than 0°C (i.e. 2°C), it was assumed that thermal time accumulation ceased below the base temperature and resumed when seeds were exposed to warmer temperatures (Ellis and Barret, Reference Ellis and Barret1994). If the time courses coincide, then the model accounts for the observed germination patterns (Bradford, Reference Bradford2002). The expected increase of temperature for the central Andes by 2080–2099 ranges between 1.7 and 4.6°C during the germination period (December to May) (Christensen et al., Reference Christensen, Hewitson, Busuioc, Chen, Gao, Held, Jones, Kolli, Kwon, Laprise, Magaña Rueda, Mearns, Menéndez, Räisänen, Rinke, Sarr and Whetton2007). In order to model the germination within these values we estimated germination percentages under constant temperatures after 14 weeks, in the range between 5°C below and 5°C above the average temperature during the germination period (9.5°C) in steps of 1°C.
Results
We found that >90% of viable P. besseri seeds germinated under appropriate laboratory conditions. In preliminary tests, warm (20°C) and cold (5°C) stratification, and wet (moist filter paper) and dry (silica gel chamber) regimes did not stimulate germination.
Fruit coat permeability and water imbibition
The increase in weight of scarified and non-scarified fruits was very similar at the end of the experiment (Fig. 2). About 156% and 134% of the gain in weight was attained during the first 24 h of the experiment in the scarified and non-scarified fruits, respectively. This difference disappeared completely towards the end of the experiment (9 d) as fruits in both treatments ended with a 210% and 212% increase in weight, respectively.
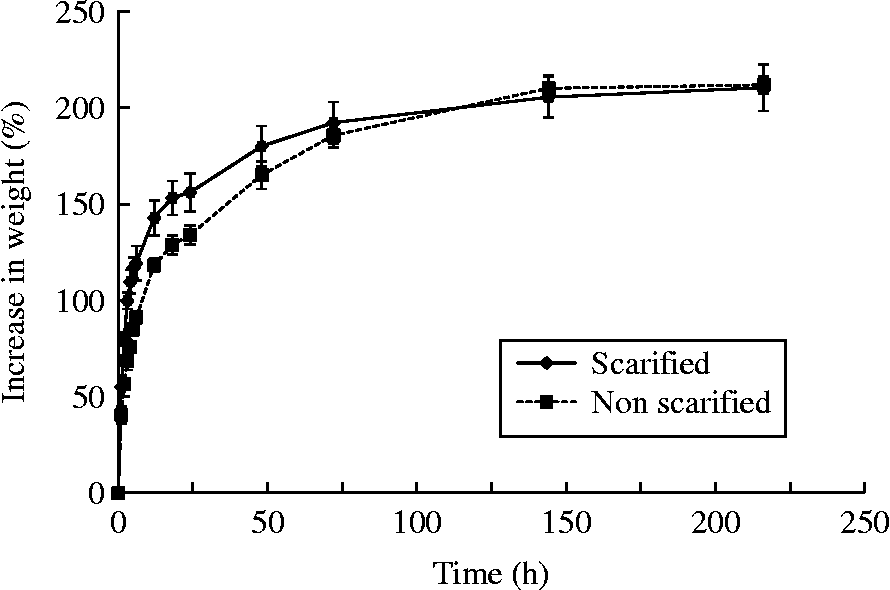
Figure 2 Increase in weight (%) as a function of time due to the water uptake of scarified and non-scarified fruits of Polylepis besseri. The bars represent standard errors.
Germination modelling
In total, 80.5% of the P. besseri fruits were empty, or contained grey or underdeveloped seeds. The results provided here are based only on the viable 19.5% of seeds. The estimated optimum temperature (T o) for P. besseri germination was 22.3°C for both the 10th and the 20th percentile. The thermal time model for the suboptimal temperatures at − 0.9 MPa explained only a small amount of the variation in germination (R 2 = 0.24; Table 2a). The models at higher water potentials performed much better as they explained more than 78% of the variation. The germination curves under normalized thermal time (i.e. a time scale with the number of °C above the base temperature for germination multiplied by the time to reach a given germination percentage) for the below and above optimum temperature showed that the models accounted for the observed germination patterns, as indicated by the overlap of the different data points (Figs 3 and 4).
Table 2 Parameters of the germination models for Polylepis besseri using the average of the three replicates per treatment for an optimum temperature between 20 and 25°C. (a) Thermal time for suboptimal temperatures at each water potential; (b) thermal time model for supra-optimal temperatures at each water potential; (c) hydrotime model for each temperature; (d) hydrothermal time model for suboptimal temperatures; and (e) hydrothermal time model for the supra-optimal temperatures. See Table 1 for a description of the parameters


Figure 3 Germination profiles of Polylepis besseri at (a) suboptimal temperatures (5, 9, 15 and 20°C) and (b) different water potentials (0.0, − 0.3, − 0.6 and − 0.9 MPa) on a normalized thermal time scale. The symbols are the actual data and the lines are the time courses predicted by the hydrothermal time model using the parameters in Table 2d.

Figure 4 Germination profiles of Polylepis besseri at suboptimal (5, 9, 15 and 20°C) and supra-optimal temperatures (25 and 30°C) in pure water (ψ = 0.0 MPa) and on a normalized thermal time scale. The symbols are the actual data and the lines are the time courses predicted by the hydrothermal time model using the parameters in Table 2e.
Regarding the parameters obtained from the thermal time model of germination below T o, the base temperature (T b) ranged from 0 to 3.7°C and the thermal time to reach 50% of the germination (θT(50)) increased exponentially as water potential decreased (Table 2a), with the shortest θT(50) equal to 33.5°C·weeks in pure water. Above T o, the thermal time model (Table 2b) predicted that the ceiling temperature for 50% of the seeds (T c(50)) was 27.9°C, with a very similar value for water availability equal to ψ = − 0.3 MPa (27.5°C). The values of the thermal time above optimum temperature (θC) increased with decreasing water potentials.
The amount of hydrotime required to germinate (θH) decreased with increasing temperature up to 25°C (Table 2c). Starting from 15°C, the mean base water potential (ψb(50)) increased with increasing temperatures. The standard deviation of the base water potential (σψb) in the hydrotime model decreased with increasing temperature until 20°C, above which it increased again (Table 2c). The increase in ψb(50) was more pronounced at high temperatures (25 and 30°C) than at low temperatures (5–20°C). The mean base water potential was different for each temperature below the optimum temperature, and no clear trend was observed.
The estimated base temperature in the HTT model below T o was 3.0°C and the water potential threshold preventing radicle emergence for 50% of the germinated seeds (ψb(50)) was − 0.74 MPa with a standard deviation (σψb) of 0.41 MPa (Table 2d). Finally, the HTT model above T o estimated a T o of 21.7°C, an increase of the ψb(50) with 0.1 MPa/°C of increase in temperature (k T), and a constant θHT of 23.7 MPa·°C·weeks.
Fluctuating temperatures
Fluctuating temperatures had a significant effect on the rate (F 2,6 = 216.0, P < 0.01) and final germination percentage (F 2,6 = 28.5, P < 0.01) of P. besseri fruits (Fig. 5). The final germination was similar between 20°C and the fluctuating temperature treatment 20/10°C (P =0.24) with a common mean of 93% of germination, but it was significantly different for the 20/2°C treatment (P =0.01) with a final germination of 71%. The time to reach 50% of germination was different in all treatments (P =0.01 for both comparisons between the constant and fluctuating temperatures), with 1.8 weeks for the fastest treatment (20°C), 2.7 weeks for 20/10°C and 5 weeks for the slowest treatment (20/2°C). Finally, fluctuating temperatures did not stimulate germination; on the contrary, they resulted in less germination in the 20/2°C treatment.

Figure 5 Observed percentages of germination for Polylepis besseri at constant (20°C) and fluctuating temperatures (20/10 and 20/2°C) on (a) a time and (b) a thermal time scale using the parameters in Table 2d. The bars represent standard errors.
Predicting germination
The hydrothermal time model developed for the germination of P. besseri at constant temperatures also performed well in predicting germination at the fluctuating 20/10°C treatment (Fig. 5). This can be seen by the overlapping curves at 20°C and 20/10°C (Fig. 5b), where a given germination percentage occurred after the accumulation of the same amount of thermal time, something that did not occur under a regular time scale (Fig. 5a). However, the model performed poorly in predicting germination in the fluctuating 20/2°C treatment, which included temperatures below the optimum. The HTT model below T o predicted that increasing temperatures from the field mean temperature (9.5°C) will increase germination under all water availability conditions (Fig. 6), and that decreasing temperatures will diminish germination with a more pronounced effect at water potentials close to 0 MPa. Additionally, the HTT models predicted that an increase in temperature near the base temperature for P. besseri will increase its germination because temperatures will be above T b for the species, allowing germination. Whereas when temperatures rise above T o they will reduce P. besseri germination because of the increase in base water potential given by k T (Table 2e).

Figure 6 Predicted germination percentages of Polylepis besseri under constant temperatures after 14 weeks, as a function of the deviations from the mean average temperature (9.5°C; cf. Grieser et al., Reference Grieser, Gommes and Bernardi2006) and the different water potentials. Different grey intensities represent different germination percentages. The predicted values were obtained using the parameters in Table 2d.
Discussion
Hydrothermal time models for P. besseri could be constructed straightforwardly due to the lack of seed dormancy. The models predicted germination of P. besseri under constant and alternating temperatures, except for those temperatures partially below the estimated base temperature (20/2°C). Alternating temperatures did not increase the germination percentage of Polylepis; on the contrary, they reduced the germination rate (at 20/10°C) and the final percentage of germination (at 20/2°C). HTT models predicted an initial increase in P. besseri germination under global warming and under constant temperatures for the analysed water potentials. This increase may, however, be countered if temperatures rise too much, reaching temperatures above the optimum (21.7°C).
We found that >90% of viable P. besseri seeds germinated under appropriate laboratory conditions. Because in preliminary tests warm and cold stratification, and wet and dry regimes did not stimulate germination, we concluded that P. besseri produces fruits with seeds ready to germinate. The absence of an effect of cold stratification on the germination was also reported for five species of Acaena in the subalpine zone in New Zealand (Conner, Reference Conner1987). If, as we propose, P. besseri seeds are non-dormant, then germination is the key component of its seedling emergence and increases the importance of modelling germination (Forcella et al., Reference Forcella, Arnold, Sanchez and Ghersa2000).
Modelling
Starting from the base temperature, germination rate increases when temperature rises until the optimum temperature for germination of a given species is attained, then it decreases until a ceiling temperature, above which germination stops (Alvarado and Bradford, Reference Alvarado and Bradford2002). Maximum temperatures in Sacha Loma during germination time (12.7–18.4°C) (cf. Grieser et al., Reference Grieser, Gommes and Bernardi2006) were at least 3.4°C below the optimum temperature for P. besseri (21.7°C; Table 2e), thus germination is not limited by maximum temperature at this site at the present time. The opposite result was found for the base temperature, since the estimates for the base temperature of P. besseri (between 2.9 and 3.7°C, except for ψ = − 0.9 MPa; Table 2a) were at least 0.2°C higher than the estimated minimum field temperatures ( − 1.1 to 2.7°C) (cf. Grieser et al., Reference Grieser, Gommes and Bernardi2006). Thus, accumulation of thermal time to germination can nowadays be limited by night temperatures in Sacha Loma. However, it is known that Polylepis woodlands create a less cold environment than the surrounding grasslands (Fjeldså and Kessler, Reference Fjeldså and Kessler1996), thus the effect of night temperatures on germination inside the woodlands may be buffered.
Despite the fact that the hydrotime model detected different mean base water potentials (ψb(50)) and standard deviations (σψb), the hydrothermal time models, which work with a single value for each of these two parameters and include temperature, explained a good proportion of variability below (R 2 = 0.78; Table 2d) and above (R 2 = 0.89; Table 2e) the optimum temperature for germination of P. besseri. The hydrothermal time model (Table 2d) predicted that under pure water (ψ = 0 MPa) and a constant temperature of 21.7°C (the estimated optimum temperature, Table 2e), 12%, 62%, 79% and 85% of germination are reached after 1, 2, 3 and 4 weeks of experiment, respectively. Maximum germination (94%) occurs after 11 weeks of experiment and 90% of germination occurs after 6 weeks. These percentages decrease with decreasing water potential. This information is useful for future germination tests with the species, as 4–6 weeks of experiment are recommended at this temperature and water potential, a value that is higher than the maximum of 3–4 weeks recommended for the majority of studies (Baskin and Baskin, Reference Baskin and Baskin1998). Under different conditions, a longer time is needed for the experiments.
A high ψb(50), which diminishes the germination rate and final percentage of germination (Bradford, Reference Bradford1995), and a high hydrothermal time constant, which diminishes germination rate (Bradford, Reference Bradford1995), both explain the long time needed for germination of P. besseri under optimal conditions and the high spread of germination over time under low water potentials or temperatures different from the optimum. For other plants, this spread in germination was not expected because early germination provides long-lasting benefits to seedlings, as early emergent seedlings are larger, may survive longer and reproduce more than late emergent seedlings (De Luis et al., Reference De Luis, Verdú and Raventós2008). However, heterogeneous germination rates can be the result of selection for competition among seedlings after years of high seed production, as reported for desert annuals (Tielbörger and Valleriani, Reference Tielbörger and Valleriani2005), because high seedling densities may cause an increase in seedling mortality which, in turn, may diminish fitness.
Predicting germination
The model developed for constant temperatures could predict the germination at alternating temperatures (20°C in light/10°C in darkness), but not at those including temperatures below the base temperature for P. besseri (3.0°C). The seeds at 20/2°C accumulated less thermal time than predicted by the model (Fig. 5) or, in other words, the model overestimated germination under this condition. Thus, caution must be taken when predicting germination. The model assumed that thermal time accumulation ceased below the base temperature and resumed at warmer temperatures, thus no delay in germination was possible when temperatures rose from below to above the base temperature. The overestimation in the model might be caused by a delay in the physiological processes to restart germination after the seeds have been exposed to temperatures below the base temperature. The decrease in the final percentage of germination in the fluctuating 20/2°C treatment in comparison to the 20/10°C or the constant 20°C treatment might be caused by the same delay in physiological processes, or it may be evidence of seed damage in P. besseri below the base temperature for germination. The latter is less likely because percentages of germination were estimated based on white, firm seeds only, thus potentially viable seeds; unless these seeds were damaged enough to avoid seed germination but not to be consumed by fungi, and therefore rot, during the experiment.
Before predicting germination based on the hydrothermal times, it is important to note that actual germination largely depends on prevailing field temperatures, which vary considerably in the high Andes, and much less on averages, which were used for obtaining the hydrothermal time model parameters. However, given: (1) that thermal history has no effect on germination rate (Ellis and Barret, Reference Ellis and Barret1994), which is true for P. besseri above the base temperature; (2) that germination rate responds instantaneously to current temperature (Ellis and Barret, Reference Ellis and Barret1994); and (3) analysing two cardinal temperatures obtained for the germination of P. besseri (base and optimum temperatures), we can make some predictions. An increase of 0.2°C in the current minimum field temperature may already release P. besseri germination from the limit imposed by its base temperature. At the other extreme, an increase of 3.4°C in the current maximum field temperature, likely to occur in the Central Andes by the end of the century (period 2080–2099) (Christensen et al., Reference Christensen, Hewitson, Busuioc, Chen, Gao, Held, Jones, Kolli, Kwon, Laprise, Magaña Rueda, Mearns, Menéndez, Räisänen, Rinke, Sarr and Whetton2007), may start limiting germination because the optimum temperature would be surpassed by the field temperature. In the intermediate condition, P. besseri germination will be increased by global warming. Regarding the water potential, it is expected that, if the precipitation regime remains constant through time, global warming will reduce water availability in the soils, and then it may limit germination (Fig. 6).
Thus, general germination pattern predictions through time can be made based on the HTT models: global warming will first increase P. besseri germination because minimum temperatures will no longer limit its germination. Then, germination will be the result of the balance between increased temperatures and reduced water potential. Finally, when maximum temperatures surpass the optimum temperature for P. besseri, germination will start to decrease. Since only the maximum estimates for field temperature increase predicted for the end of this century will negatively affect germination, global warming may not be an important limiting factor for P. besseri germination in the high Andes. However, the importance of global warming will also be a function of water availability, which depends in part on precipitation regimes, which have unreliable predictions in most global circulation models developed for mountainous regions (Christensen et al., Reference Christensen, Hewitson, Busuioc, Chen, Gao, Held, Jones, Kolli, Kwon, Laprise, Magaña Rueda, Mearns, Menéndez, Räisänen, Rinke, Sarr and Whetton2007). Threshold models were also used to predict that global warming, associated with an increase in winter and spring precipitation in the Canadian prairie, will likely increase germination of an endangered annual plant, Cryptantha minima Rydb. (Wei et al., Reference Wei, Bai and Henderson2009); while, a warmer and drier future climate may reduce regeneration success of the grass Festuca hallii (Vasey) Piper (Qiu et al., Reference Qiu, Bai, Fu and Wilmshurst2010). The information obtained may be also relevant for the study of long-term changes in P. besseri demography in response to climate change. In this case it will be important to disentangle which life stages are the demographic bottlenecks for the establishment of P. besseri.
Hydrothermal time models are an effective tool for studying germination ecology. The estimated parameters allowed us to discuss possible factors limiting germination in the field, to suggest the time required to perform germination studies for the species, and to make general predictions regarding the potential effects of global warming. HTT models can also give important information about population functioning if populations of different sizes, or located in environmental, latitudinal or altitudinal gradients, are studied. In this sense HTT models re-emerge as very useful tools for studying germination ecology.
Acknowledgements
The people of Sacha Loma and Cuturi allowed us access to their forests. L. Meneses, G. Uriona, N. Zambrana, Y. Martinez and M. Morales helped with the seed collection and selection in Bolivia. J. Cahill, L. Meneses, Y. Martinez and L.F. Aguirre helped in the paperwork and preparation for the transportation of the plant material to Belgium. K. Van Acker helped with the hydrothermal time experiments in Belgium. K.J. Bradford provided guidance during data analyses. H. Jacquemyn, K. Muylaert, E. Matthysen, B. Muys, the editor-in-chief H. Hilhorst and one anonymous reviewer provided useful comments to improve previous versions of the manuscript. E.E.G. has been supported by an SBA doctoral scholarship by KU Leuven in the framework of Selective Bilateral Agreements (SBA) with Universities in Latin America (UMSS).










