Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-06T15:55:11.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Modeling of laser–plasma interaction on hydrodynamic scales: Physics development and comparison with experiments

Published online by Cambridge University Press:  01 June 2004

S. WEBER ,
G. RIAZUELO ,
P. MICHEL ,
R. LOUBÈRE ,
F. WALRAET ,
V.T. TIKHONCHUK ,
V. MALKA ,
J. OVADIA  and
G. BONNAUD
S. WEBER
Affiliation:
Centre Lasers Intenses et Applications, Unité mixte de recherche 5107 Centre national de la recherche scientifique, Université Bordeaux 1, Commissariat à l'énergie atomique, Talence Cedex, France Département de Physique Théorique et Appliquée, Commissariat à l'énergie atomique/DIF, Bruyères-le-Châtel Cedex, France
G. RIAZUELO
Affiliation:
Département de Physique Théorique et Appliquée, Commissariat à l'énergie atomique/DIF, Bruyères-le-Châtel Cedex, France
P. MICHEL
Affiliation:
Département de Physique Théorique et Appliquée, Commissariat à l'énergie atomique/DIF, Bruyères-le-Châtel Cedex, France Laboratoire pour l'Utilisation des Lasers Intenses, Unité mixte de recherche 7605 Centre national de la recherche scientifique, École Polytechnique, Commissariat à l'énergie atomique, Université Paris VI, École Polytechnique, Palaiseau Cedex, France
R. LOUBÈRE
Affiliation:
Los Alamos National Laboratory, Group T-7, Los Alamos
F. WALRAET
Affiliation:
Département de Physique Théorique et Appliquée, Commissariat à l'énergie atomique/DIF, Bruyères-le-Châtel Cedex, France
V.T. TIKHONCHUK
Affiliation:
Centre Lasers Intenses et Applications, Unité mixte de recherche 5107 Centre national de la recherche scientifique, Université Bordeaux 1, Commissariat à l'énergie atomique, Talence Cedex, France
V. MALKA
Affiliation:
Laboratoire d'Optique Appliquée, Ecole Nationale Supérieure des Techniques Avancées, Centre national de la recherche scientifique, Unité mixte de recherche 7639, Palaiseau, France
J. OVADIA
Affiliation:
Commissariat à l'énergie atomique/DAM/CESTA/DEV/SIS, Le Barp, France
G. BONNAUD
Affiliation:
Commissariat à l'énergie atomique/DSE, Paris, France
Rights & Permissions [Opens in a new window]

Abstract

The forthcoming laser installations related to inertial confinement fusion, Laser Mégajoule (LMJ) (France) and National Ignition Facility (NIF) (USA), require multidimensional numerical simulation tools for interpreting current experimental data and to perform predictive modeling for future experiments. Simulations of macroscopic plasma volumes of the order of 1 mm3 and laser exposure times of the order of hundreds of picoseconds are necessary. We present recent developments in the PARAX code towards this goal. The laser field is treated in a standard paraxial approximation in three dimensions. The plasma response is described by single-fluid, two-temperature, fully nonlinear hydrodynamical equations in the plane transverse to the laser propagation axis. The code also accounts for the dominant nonlocal transport terms in spectral form originating from a linearized solution to the Fokker–Planck equation. The simulations of interest are hohlraum plasmas in the case of indirect drive or the plasma corona for direct drive. Recent experimental results on plasma-induced smoothing of RPP laser beams are used to validate the code.

Keywords

ICF plasmasLaser–plasma interactionNonlocal transportPlasma-induced smoothingTransport modeling of plasmas
Type
Research Article
Information
Laser and Particle Beams , Volume 22 , Issue 2 , June 2004 , pp. 189 - 195
Copyright
© 2004 Cambridge University Press

1. INTRODUCTION

A detailed understanding of the interaction of a laser beam with a preformed underdense plasma is of outstanding interest in the context of inertial confinement fusion (ICF). Due to the complexity of the interaction process, analytical models are only of limited use. Therefore numerical tools have to be conceived to be able to model laser–plasma interaction (LPI; Hüller et al., 1996; Elisseev et al., 1997; Berger et al., 1998; Myatt et al., 2002; Pesme et al., 2002). Much work has been done for conditions where the plasma response can be taken to be linear and where the specific transport properties of laser-produced plasmas play less of a role (Hüller et al., 1996; Elisseev et al., 1997). The forthcoming large-scale experiments for ICF in France (Laser Mégajoule (LMJ), Bordeaux) and the USA (National Ignition Facility (NIF), Livermore) require codes that are capable of simulating the interaction process with a sufficient reliability in order to have the possibility of doing predictive modeling of future experiments. This necessitates that the relevant physics is taken into account. Specifically, the following physical models must be included:

  1. The nonlinear aspect of plasma response cannot be neglected. A simple ion-acoustic wave (IAW) response for self-focusing and the three-wave model for stimulated scattering are of limited use for realistic laser parameters.
  2. Backscattering processes—the stimulated Raman and Brillouin scattering—have to be accounted for in a self-consistent picture of the interaction process. They are important for the energy balance in the target and for the effect of fast electrons on the pellet compression.
  3. Nonlocal aspect of the energy transport. For temperatures of several hundreds electron volts to a few kiloelectron volts and densities ∼ 0.1nc, the transport properties cannot be described by standard collisional equations. The transport is neither purely collisional (diffusive fluxes) nor collisionless (convective fluxes). The plasma is semicollisional, a state that establishes itself whenever the characteristic mean-free path (mfp) for electron–ion collisions is of the order of the gradient scale lengths of the thermodynamic variables (density, temperature, etc.). The consequence is a strongly modified pattern of temperature relaxation processes in the plasma. The issue of this so-called nonlocal transport (NLT) has been studied extensively in the literature (Luciani et al., 1983; Bychenkov et al., 1995, 1998; Brantov et al., 1996; Schurtz et al., 2000; Alouani-Bibi and Matte, 2002).

In addition, constraints on simulations due to large and disparate time and space scales exist:

  1. mixing of very disparate length scales. The plasma response takes place at scales of the order or less than the laser wavelength λ0 but the characteristic scale length of evolution of laser and plasma parameters amounts to several hundreds of laser wavelengths.
  2. long time of simulations. The characteristic time of the plasma response varies in a very wide range from a few laser periods (in the case of Raman scattering) to thousands of laser periods for slower processes that involve the ion response.
  3. large volume of simulations. The plasma volume to be treated in simulations is of the order of 1 mm3. This is necessary for adequate description of speckle statistics, the backscattering processes, and the nonlinear evolution of speckles.

Ideally one would like to model the interaction process with first-principle tools such as Fokker–Planck or particle-in-cell (PIC) methods coupled to the full set of Maxwell's equations. Unfortunately these kind of calculations can at present only be done for microscopic plasma volumes. Hence a certain coarse graining is necessary and the most promising approach at present would be to use some hydrodynamic model to describe the plasma.

As a whole, the contemporary LPI codes are complicated and difficult to validate. The most promising way is to have at hand simple and clean experiments that reduce the number of physical effects involved to a minimum and allow us to deduce certain global characteristics (e.g., coherence times) that can be compared to the calculations. Once these codes have been validated in a convincing way, they can then be used to perform predictive modeling of future experiments (design experiments). Nonlinear hydrodynamic calculations are particularly time consuming and a full parallelization of such codes is mandatory.

In the following, we present some physics packages that have been recently developed in the code PARAX (Riazuelo & Bonnaud, 2000; Walraet, 2003). The most important ingredients of this code and their implementation are briefly described as well as its first successful validation.

2. PRESENTATION OF THE MODEL

2.1. Electromagnetic module

The code is conceived to describe a propagation of a single laser beam in a weakly inhomogeneous, underdense plasma and the effects of ion density perturbations. For that, it is not necessary to solve the full set of Maxwell equations. The wave equation for the electric field can be simplified by assuming that the propagation takes place dominantly in one given direction (here denoted as the z-direction). One assumes that the light that is linearly polarized in the x-direction can be characterized by the frequency ω0 and the wave vector

and that the amplitude is a slowly varying function of space and time:

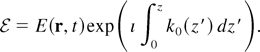
Then the laser amplitude E satisfies the paraxial equation (Feit & Fleck, 1988; Riazuelo & Bonnaud, 2000) that can be written in the following form:

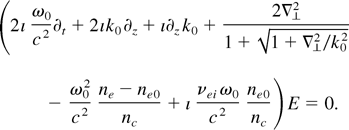
Here, ne is the local plasma density and ne0 the intial plasma density, nc = meε0ω02/e2 is the critical density. ∇⊥2 = ∂x2 + ∂y2 is the Laplacian in the plane transverse to the direction of propagation, it describes the diffraction of the propagating laser beam. The factor [1 + (1 + ∇⊥2/k02)1/2]−1 takes into account deviations from the exact paraxial equation and allows us to model light propagation within an opening angle of the order of 30° around the z-axis. Evidently it can be treated numerically only in a spectral approach (Feit & Fleck, 1988). The term containing the electron–ion collision frequency νei takes into account the laser energy losses due to inverse bremsstrahlung.

The paraxial approximation of the laser beam is based on several assumptions: ∂z << k0, ∂t << ω0, and ∂z2 << ∇⊥2. These conditions are supposed to be satisfied for the cases considered below.

2.2. Linearized plasma response

The simplest response of a plasma is due to the ponderomotive force that acts in the transverse direction. Quasineutrality is assumed and the response describes IAWs propagating in the plane transverse to the propagation direction of the laser beam:

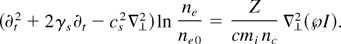
Here, γs is a damping term and the intensity is given as I = cε0|E|2/2. The characteristic speed of propagation of the density perturbations are determined by the acoustic velocity

.

There are two features in this equation that go beyond the standard IAW equation. First is the logarithmic term on the left-hand side instead of the linear density perturbation. This is an ad hoc attempt to extend the equation to the nonlinear case. It prevents unphysical negative values of ne and reproduces the Boltzmann density depletion. Second is the operator

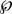
in front of the ponderomotive force on the right hand side. It is a spectral operator that takes account of nonlocal transport properties in the linear response regime (Brantov et al., 1998):

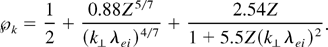
Here, Z is the charge state of the ion, λei is the mfp for electron–ion collisions and k⊥ the perpendicular wave number.

2.3. Nonlinear hydrodynamics

For intensities of the order of 1014 W/cm2 and density perturbations above 10%, the plasma response becomes nonlinear. In this case, the simple IAW equation (3) has to be replaced by the full Euler equations (Loubère, 2002). The model used are the single-fluid (due to quasineutrality, ne = Zni), two-temperature equations:

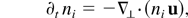
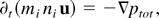
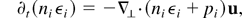
Here, ptot = pe + pi is the total plasma pressure, pe = (γe − 1)neεe is the electron pressure and pi = (γi − 1) (niεi − mi niu2/2) is the ion pressure, ε denotes the total energy, which is related to the pressure by an equation of state for a given adiabatic coefficient γ = cp /cv. The electron inertia has been neglected in the electron equation of state.

As before, the plasma response is in the transverse plane only. The hydrodynamics are solved in Lagrangian form on an unstructured triangular mesh using a discontinuous Galerkin-type approach that gives high-precision numerics with little numerical diffusion and oscillations. In the above equations the coupling to the electromagnetic field (the ponderomotive force) as well as the transport terms are still missing—they are presented in the following section.

Figure 1 gives a simple visual impression of how linear and nonlinear responses differ for high intensities. Amplitudes and frequency of self-focusing are clearly affected. This is especially important for density bumps that are severely overestimated in the linear model. Also the speed of propagation of density perturbations is no longer given by the ion-acoustic velocity, which is only correct in the initial stage, but will be larger. The dynamics of a laser–plasma interaction can be significantly modified.

Time evolution of a mono-speckle for I = 6·1014 W/cm2, ne = 0.1nc, and Te = 600 eV. The snapshots are taken at 17.5, 22.5, and 30 ps. The upper row presents the results of the linear plasma response, the lower one the full nonlinear calculation. The calculations include only the ponderomotive force as coupling term, not the nonlocal transport.

3. NONLOCAL TRANSPORT

3.1. The properties of nonlocal transport

Using an approach based on the linearized version of the Fokker–Planck equation, a set of transport coefficients in the context of semicollisional plasmas has been derived by Brantov et al. (1996) and Bychenkov et al. (1995). As mentioned in the introduction, the transport coefficients are in general strongly varying functions of the product kλei. Figure 2 shows the dependence of the electron heat conductivity on the parameter kλei.

The electron heat conductivity κe as a function of kλei. For kλei → 0 one recovers the standard collisional transport value; the limit kλei >> 1 corresponds to the collisionless regime. The conductivity coefficient is normalized by the Spitzer–Härm coefficient.

The mathematical procedure of implementation of the nonlocal transport coefficients in the code is similar for each term. As an example, let us consider the following simplified heat equation comprising just the time dependence of the temperature due to the heat flux:

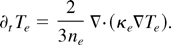
The electron heat conductivity κe is known in k-space only; hence the equation has to be evaluated in k-space itself. As one is above all interested in conditions where the semicollisionality dominates, the gradient scale length is of the order of the mfp and therefore the conductivity does not vary much over the gradient. One can therefore assume κe to be constant locally and approximate the source ∇·(κe∇Te) as κe ΔTe. Transforming to Fourier space then amounts to the following replacement:

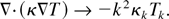
It has been assumed as well that the transport is isotropic in the transverse plane and that one can use the identification

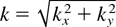
. The change in temperature is then given as:

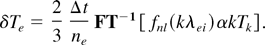
Note that the coefficient α = ne vTe is given in real space. The function fnl is a nonlinear function of kλei, which can be decomposed as:

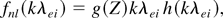
with g(Z) = (3.26 + 13.6Z)/(4.2 + Z) giving the charge dependence. If the function h would be equal to 1, one would simply recover the standard expression for the collisional Spitzer–Härm conductivity: κ = κSH = g(Z)ne vTe λei. In the general case the function is not equal to one and depends strongly on the collisionality of the plasma. It is possible to represent the function h as a harmonic mean between the strongly collisional and the collisionless state, which gives a good approximation over the whole range of collisionality parameters:

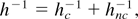
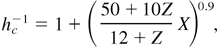
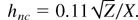
Here,

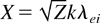
, hc is the collisional contribution, and hnc is the noncollisional one.

3.2. Temperature relaxation in a hot spot

The effect of nonlocal transport can be easily appreciated by looking at a simple hot-spot relaxation due to the heat flux into the ambient medium (Senecha et al., 1998). Assuming a uniform temperature background of 700 eV, a local temperature perturbation of the form T(r,t = 0) = T0 exp(−r2/R2) + 700 eV is imposed. The speckle radius R is taken to be 7μm and the perturbation amplitude is T0 = 70 eV. For a density of ne = 0.1nc and a charge state Z = 5, the resulting mfp is λei = 2.2 μm and hence of the order of the characteristic gradient scale length of the perturbation R. For this case the above heat equation can be solved analytically and the relaxation times of the hot spot for the collisional regime and the nonlocal transport regime can be calculated to give

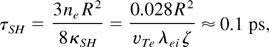
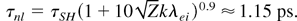
Here, ζ(Z) = (0.24 + Z)/(4.2 + Z) takes into account the dependence on the charge state.

Obviously for the given, realistic plasma conditions the relaxation times differ by a factor of 10, which implies a strong variation in the plasma response to be expected.

The procedure outlined here for the evaluation of the nonlocal heat flux applies in exactly the same way for all the possible transport coefficients and associated transport terms.

3.3. Nonlocal Navier–Stokes equations

The resulting transport terms modify the Euler equations such that one obtains nonlocal Navier–Stokes equations that can be written in the standard way as follows:

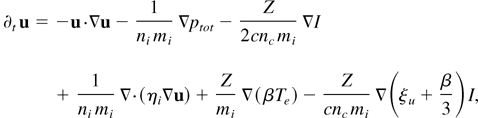
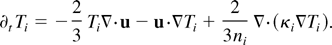
In the above equations are some transport terms that are purely local such as the absorption due to inverse bremsstrahlung and the ponderomotive force term. The remaining terms going beyond those coming from the Euler equations involve the nonlocal transport coefficients that are only known in k-space. From the numerical point of view this implies that a splitting scheme has to be employed in order to evaluate the transport. The transport is treated as a source for the Euler equations, which is evaluated in Fourier space. The coupling therefore requires the transfer of quantities between the k-space on a Eulerian grid and the real space on a Lagrangian grid. This leads to nontrivial numerical issues of coupling very different numerical schemes.

The nonlocal transport results from a linearization of the full Fokker–Planck equation and is nevertheless used in nonlinear hydrodynamics. This is, however, justified as comparisons with kinetic calculations have shown that this approach remains valid even in the weakly nonlinear regime (Brunner & Valeo, 2000, 2002). The present model is one of several available in the literature. Comparison with other models (Schurtz et al., 2000; Alouani-Bibi & Matte, 2002) is needed to better understand their robustness and the limits of validity.

4. COMPARISON WITH EXPERIMENTS

Comparison with other codes and with experiments is an important part of code development. The present code has already passed successfully a number of tests. Here we present a comparison of the code with the results of a recent experiment on plasma-induced laser beam smoothing.

4.1. Experiment on the plasma-induced incoherence

The experiment measured the time-resolved transmitted light of a RPP laser beam passing through a preformed plasma (Malka et al., 2003). An enhanced spatiotemporal smoothing of the laser beam was observed (Fig. 3). The plasma-induced smoothing of a laser beam has been observed before, albeit under very different conditions, where self-focusing of the beam played an important role. In these experiments, however, the average power in a speckle was of the order of 3% of the critical power for self-focusing. An important parameter is the measured coherence time, which in the experiment was of the order of 50 ps. The mechanism that was put forward to explain the loss of coherence induced by the plasma is multiple scattering. Even without self-focusing, the presence of the ponderomotive force creates small density perturbations. The incident light is then scattered off these density perturbations, which leads to an angular spreading of the light and to a loss of spatial and temporal coherence. The characteristic time constant should therefore be given by the transit time for an IAW across a speckle width. The random phase plate produced speckles with a characteristic radius of 2.8μm. For a plasma temperature of Te = 250 eV the acoustic velocity is cs = 0.06μm/ps. The resulting acoustic transit time is therefore tac = 50 ps, which agrees with the measured coherence time.

Time-resolved images of transmitted light using a RPP during 600 ps for 100 μm spatial extension. Left: with plasma, right: in vacuum.

4.2. Calculations of the plasma-induced incoherence

In the following some calculations are presented that allow us to validate the code for the simplest configuration: linear plasma response with nonlocal transport. This is justified as the experimental conditions were such that the level of backscattering was without significance and the laser intensity 〈I〉 ≈ 6 × 1013 W/cm2 and plasma density (ne = 0.01nc) such that the plasma response could be described by an IAW equation. The results are summarized in Figures 4, 5, and 6.

The increasing fluctuations of the laser intensity as a function of the plasma length. The curve is the mean value of 32 randomly chosen points in the transverse plane. The additional lower and upper curves give the mean square deviation of the values.

Temporal evolution of the central intensity. The intensity depicted is in units of 1.85 × 1014 W/cm2.

The transverse intensity distribution for the RPP case at an arbitrary point in the transverse plane. Left column: entrance of simulation box (z = 0); right column: end of simulation box (z = 2240μm). Upper row: at t = 0; lower row: at t = 100 ps.

Figure 4 shows increasing fluctuations of the laser intensity as a function of the plasma length, implying an increasing loss of coherence. The variation of the laser intensity ΔI/I was calculated as follows:

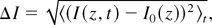
where I0(z) = 〈I(z,t)〉t and I = 〈〈I(z,t)〉t〉s. The temporal and spatial average are defined as 〈…〉t = T−1∫I(z,t) dt and 〈…〉s = L−1∫I(z,t) dz, respectively. Here, L is the plasma length and T the duration of the simulation.

The condition for multiple scattering to take place in the plasma can be shown to be (Malka et al., 2003)

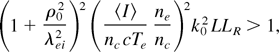
where LR = k0 ρ02 is the Rayleigh length. The term in the left parentheses takes into account the effect of the nonlocal transport as the speckle radius ρ0 = 2.8μm is of the order of the mfp λei = 4μm.

The important parameter is the plasma length L, which, in the experiment, was of the order of 2 mm. Even for very low intensities and densities, laser beam smoothing can be achieved if the light interacts with a sufficiently long plasma. The calculation clearly shows (see Fig. 5) that the intensity profile is stationary over the first millimeter of plasma before slow variations on the time scale of the ion-acoustic transit time set in. In a similar way Figure 6 shows an arbitrary transverse intensity profile at the beginning of the plasma and after the light propagated through 2 mm of plasma. At the beginning of the plasma, the profile does not change and remains strongly correlated for all times. In contrast, the initial correlation has been completely destroyed at the end of the simulation box.

The physical effect taking place is the following sequence: the stationary random phase structure of the incident laser beam leads to nonstationary density perturbations and subsequently multiple scattering of the light takes place.

5. CONCLUSION

We presented recent developments in the PARAX code, which was conceived to model the interaction of a paraxial laser beam with a preformed plasma in the context of inertial confinement fusion. The code structure requires the coupling of very different numerical modules, which are optimized each for specific physics applications. This module coupling plus the fact that one operates in parallel on the Eulerian and Langrangian grids is nontrivial. The code has been optimized with respect to this coupling and has been validated qualitatively and quantitatively in the linear regime using experimental data on plasma-induced smoothing. The next step is the validation of the nonlinear plasma response for smoothing under conditions of strong self-focusing.

One has to be aware of the fact that macroscopic calculations of LPI using a nonlinear plasma response are very demanding as far as CPU time is concerned. A linear plasma simulation that models roughly one eighth of one LMJ beam requires of the order of one day on 40 processors at 833 MHz. Performing the same calculation using the fully nonlinear plasma response and the most relevant nonlocal transport terms adds a factor of 10–20 to the CPU time. Hence, the nonlinear macroscopic calculations can only be done with high-speed, massively parallel machines.

The present code can be considered a first but large step towards macroscopic modeling of laser–plasma interactions. The various minimal ingredients for a realistic physics basis have been presented. However, this is still far from what one needs in the long run. Missing components are, for example: the backscattering processes (SRS and SBS), the expansion of the plasma in the parallel direction, and a nonlocal transport model that would be valid in the strongly nonlinear regime.

Once the code has been decently validated by interpreting and reproducing present experimental data it can be used for predictive modelling of the forthcoming plasmas in the large-scale facilities LMJ and NIF.

ACKNOWLEDGMENTS

The authors are thankful for helpful discussions with S. Hüller and L. Powers.

References

REFERENCES

Alouani-Bibi, F., Matte, J.-P. (2002). Influence of the electron distribution function shape on nonlocal electron heat transport in laser-heated plasmas. Phys. Rev. E 66, 066414-1–066414-5.Google Scholar
Berger, R.L., Still, C.H., Williams, E.A. & Langdon, A.B. (1998). On the dominant and subdominant behavior of stimulated Raman and Brillouin scattering driven by nonuniform laser beams. Phys. Plasmas 5, 4337–4356.Google Scholar
Brantov, A.V., Bychenkov, V.Yu., Tikhonchuk, V.T. & Rozmus, W. (1996). Nonlocal plasma electron hydrodynamics. JETP 83, 716–730.Google Scholar
Brantov, A.V., Bychenkov, V.Yu., Tikhonchuk, V.T. & Rozmus, W. (1998). Nonlocal electron transport in laser heated plasmas. Phys. Plasmas 5, 2742–2753.Google Scholar
Brunner, S. & Valeo, E. (2000). Linear delta-f simulations of nonlocal electron heat transport. Phys. Plasmas 7, 2810–2823.Google Scholar
Brunner, S. & Valeo, E. (2002). Simulations of electron transport in laser hot spots. Phys. Plasmas 9, 923–936.Google Scholar
Bychenkov, V.Yu., Rozmus, W.,, Tikhonchuk, V.T. & Brantov, A.V. (1995). Nonlocal electron transport in a plasma. Phys. Rev. Lett. 75, 4405–4408.Google Scholar
Bychenkov, V.Yu., Novikov, V.N. & Tikhonchuk, V.T. (1998). Theory of nonlocal transport for small perturbations in a plasma. JETP 87, 916–925.Google Scholar
Elisseev, V.V., Ourdev, I., Rozmus, W., Tikhonchuk, V.T., Capjack, C.E. & Young, P.E. (1997). Ion wave response to intense laser beams in underdense plasmas. Phys. Plasmas 4, 4333–4346.Google Scholar
Feit, M.D. & Fleck, J.A. (1988). Beam nonparaxiality, filament formation, and beam breakup in the self-focusing of optical beams. J. Opt. Soc. Am. B 5, 633–640.Google Scholar
Hüller, S., Mounaix, Ph. & Pesme, D. (1996). Numerical simulation of filamentation and its interplay with SBS in underdense plasmas. Physica Scripta T63, 151–157.Google Scholar
Loubère, R. (2002). Une méthode particulaire lagrangienne de type Galerkin discontinue. Applications à la mécanique des fluids et l'interaction laser/plasma. Ph.D. Thesis. Bordeaux, Bordeaux University.
Luciani, J.F., Mora, P. & Virmont, J. (1983). Nonlocal heat transport due to steep temperature gradients. Phys. Rev. Lett. 51, 1664–1667.Google Scholar
Malka, V., Faure, J., Hüller, S., Tikhonchuk, V.T., Weber, S. & Amiranoff, F. (2003). Enhanced spatiotemporal laser-beam smoothing in gas-jet plasmas. Phys. Rev. Lett. 90, 075002-1–075002-4.Google Scholar
Myatt, J., Maximov, A.V. & Short, R.W. (2002). Modelling laser-plasma interaction physics under direct-drive inertial confinement fusion conditions. pp. 93–101. LLE Review, Quarterly Report, Rochester, NY: University of Rochester.
Pesme, D., Hüller, S., Myatt, J., Riconda, C., Maximov, A., Tikhonchuk, V.T., Labaune, C., Fuchs, J., Depierreux, S. & Baldis, H.A. (2002). Laser-plasma interaction studies in the context of megajoule lasers for inertial fusion. Plasma Phys. Contr. Fusion 44, B53–B67.Google Scholar
Riazuelo, G. & Bonnaud, G. (2000). Coherence properties of a smoothed laser beam in a hot plasma. Phys. Plasmas 7, 3841–3844.Google Scholar
Schurtz, G.P., Nicolaï, P.D. & Busquet, M. (2000). A nonlocal electron conduction model for multidimensional radiation hydrodynamic codes. Phys. Plasmas 7, 4238–4249.Google Scholar
Senecha, V.K., Brantov, A.V., Bychenkov, V.Yu. & Tikhonchuk, V.T. (1998). Temperature relaxation in hot spots in a laser-produced plasma. Phys. Rev. E 57, 978–981.Google Scholar
Walraet, F. (2003). Propagation et rétrodiffusion d'un faisceau laser lissé dans un plasma de fusion inertielle. Ph.D. Thesis. Paris: Ecole Polytechnique.
Figure 0

Time evolution of a mono-speckle for I = 6·1014 W/cm2, ne = 0.1nc, and Te = 600 eV. The snapshots are taken at 17.5, 22.5, and 30 ps. The upper row presents the results of the linear plasma response, the lower one the full nonlinear calculation. The calculations include only the ponderomotive force as coupling term, not the nonlocal transport.

Figure 1

The electron heat conductivity κe as a function of kλei. For kλei → 0 one recovers the standard collisional transport value; the limit kλei >> 1 corresponds to the collisionless regime. The conductivity coefficient is normalized by the Spitzer–Härm coefficient.

Figure 2

Time-resolved images of transmitted light using a RPP during 600 ps for 100 μm spatial extension. Left: with plasma, right: in vacuum.

Figure 3

The increasing fluctuations of the laser intensity as a function of the plasma length. The curve is the mean value of 32 randomly chosen points in the transverse plane. The additional lower and upper curves give the mean square deviation of the values.

Figure 4

Temporal evolution of the central intensity. The intensity depicted is in units of 1.85 × 1014 W/cm2.

Figure 5

The transverse intensity distribution for the RPP case at an arbitrary point in the transverse plane. Left column: entrance of simulation box (z = 0); right column: end of simulation box (z = 2240μm). Upper row: at t = 0; lower row: at t = 100 ps.