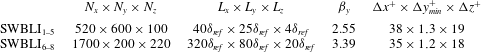1. Introduction
The reflection of shock waves at a fluid-domain boundary was first described by Ernst Mach in 1875, who experimentally observed two different wave configurations, namely the regular reflection (RR) and the irregular or Mach reflection (MR). This observation is generally regarded as the origin of classical gas-dynamics research (Krehl & van der Geest Reference Krehl and van der Geest1991). Since then, a considerable number of studies have tackled the question of when and how both types of reflection occur (see, for example, Hornung Reference Hornung1982, Reference Hornung1986, Ben-Dor Reference Ben-Dor2010, and references therein).
Figure 1. (a) Schematic of the regular reflection at a symmetry plane. (b) Schematic of the Mach reflection at a symmetry plane. (c) Shock polar representation of transition criteria and shock pattern for
$\mathit{Ma}_{0}=3$
.
In the classical inviscid gas-dynamics framework, a wall boundary is modelled as a symmetry plane and the reflection of a shock wave thus corresponds to the symmetric interaction of two incident shock waves. Characteristic wave patterns of shock reflections (see figure 1
a for RR and figure 1
b for MR) are restricted to certain parameter domains depending on the free-stream Mach number
$\mathit{Ma}_{0}$
and the deflection angle
${\it\vartheta}_{01}$
across the incident shock wave
$C_{1}$
. Criteria beyond which RR and MR are theoretically impossible are given by the detachment and the von Neumann condition, respectively. Both RR and MR wave configurations are possible within a narrow parameter space spanned between these two conditions, the so-called dual-solution domain. Figure 1(c) shows the pressure–deflection diagram (shock polars) for the different types of reflection and transition criteria for the symmetric intersection of two shock waves at a free-stream Mach number of
$\mathit{Ma}_{0}=3$
. The solid line is the pressure–deflection relation for the incident shock wave
$C_{1}$
and the four dashed lines represent the reflected shock wave
$C_{2}$
corresponding to four different deflections
${\it\vartheta}_{01}$
across
$C_{1}$
. The pressure downstream of a regular interaction follows from the intersection of the reflected-shock polar and the
$p$
-axis, for example at
$(2)^{RR}$
. At the von Neumann condition
${\it\vartheta}_{01}={\it\vartheta}^{N}$
the total pressure rise through incident and reflected shock equals the normal-shock solution. That is, both solutions would be in mechanical equilibrium. At the detachment condition
${\it\vartheta}_{01}={\it\vartheta}^{D}$
the reflected-shock polar is tangential to the
$p$
-axis at
$(2)^{D}$
. A regular pattern consisting of two shocks (RR, figure 1
a) exists only for
${\it\vartheta}_{01}\leqslant {\it\vartheta}^{D}$
, whereas the MR (figure 1
b) exists only for
${\it\vartheta}^{N}\leqslant {\it\vartheta}_{01}\leqslant {\it\vartheta}^{D_{inc.}}$
with
${\it\vartheta}^{N}$
and
${\it\vartheta}^{D_{inc.}}$
being the von Neumann and incident shock detachment criterion, respectively. In the case of an MR, a triple point
$tp$
exists, connecting the incident shock wave
$C_{1}$
, reflected shock wave
$C_{2}$
, the curved Mach stem
$m$
and slip line
$s$
.
Based on the dual-solution domain
${\it\vartheta}^{N}\leqslant {\it\vartheta}_{01}\leqslant {\it\vartheta}^{D}$
, which exists for
$\mathit{Ma}_{0}>2.202$
assuming a perfect gas with specific heat ratio
${\it\gamma}=1.4$
, Hornung, Oertel & Sandeman (Reference Hornung, Oertel and Sandeman1979) put forward the hypothesis that a hysteresis should exist in the transition process between RR and MR: if the deflection across the incident shock increases, transition from RR to MR can occur near the detachment criterion, while in the opposite case transition from MR to RR may occur at the von Neumann condition. This hypothesis was subsequently confirmed by numerical simulations (Ivanov, Gimelshein & Beylich Reference Ivanov, Gimelshein and Beylich1995; Vuillon, Zeitoun & Ben-Dor Reference Vuillon, Zeitoun and Ben-Dor1995) and experiments (Chpoun et al.
Reference Chpoun, Passerel, Li and Ben-Dor1995). On mathematical grounds a dual solution domain exists also for
$\mathit{Ma}_{0}<2.202$
; however, this situation requires the strong solution of the reflected shock wave
$C_{2}$
that usually does not occur unless special measures are taken (Hornung Reference Hornung1982; Ben-Dor Reference Ben-Dor2010). Note that, especially at lower Mach numbers, wave patterns can exist that are not covered by the classical three-shock theory (see Ben-Dor Reference Ben-Dor2010 for a comprehensive review).
In realistic supersonic flow configurations, such as intakes, nozzles and external flows, asymmetric intersections of shock waves occur more frequently than symmetric interactions (Li, Chpoun & Ben-Dor Reference Li, Chpoun and Ben-Dor1999). Since the boundary conditions for both RR and MR in asymmetric configurations are more numerous than in the symmetric case, the complexity of the reflection phenomenon increases. Li et al. (Reference Li, Chpoun and Ben-Dor1999) provided a detailed analysis of asymmetric shock-wave interactions in steady flows and proposed transition criteria corresponding to the detachment and von Neumann conditions. The hysteresis phenomenon has also been found to exist in the reflection of asymmetric shock waves. Furthermore, wave configurations that are impossible for quasi-stationary symmetric shock-wave intersections, for example the case where one of the Mach reflections is an inverse Mach reflection (that is, the velocity vector downstream of the triple point diverges from the centreline), have been recorded experimentally for the first time. Ivanov et al. (Reference Ivanov, Ben-Dor, Elperin, Kudryavtsev and Khotyanovsky2002) complemented these experimental and analytical findings by numerical simulations. More recently, Hu, Myong & Kim (Reference Hu, Myong and Kim2009) demonstrated that the RR can persist even at deflection angles greater than the detachment criterion, which requires more complex wave patterns, such as transonic curved shocks.
The Mach reflection effect and transition criteria have mostly been analysed in an inviscid framework. Inlet geometries that can be accurately modelled by inviscid gas dynamics may exist; however, in the majority of technical applications viscous boundary layers play an essential role (Smits & Dussauge Reference Smits and Dussauge2006). The interaction of shock waves with laminar or turbulent boundary layers (shock-wave/boundary-layer interaction – SWBLI) is thus one of the most prevalent phenomena in high-speed flight and has therefore received much attention in the past few decades (see, for example, the review papers of Dolling Reference Dolling2001 and Delery & Dussauge Reference Delery and Dussauge2009). Recently, Bermejo-Moreno et al. (Reference Bermejo-Moreno, Campo, Larsson, Bodart, Helmer and Eaton2014) and Campo & Eaton (Reference Campo and Eaton2015) investigated experimentally and numerically three-dimensional effects imposed by sidewalls on an oblique shock within a rectangular duct. Their results suggest that confinement effects are responsible for a strengthening of incident and separation shocks, leading to the formation of a Mach reflection that is not observed in the canonical configuration without sidewall boundary layers. This shows that SWBLI is inherently connected with a specific geometrical setup. Nevertheless, six basic configurations can be identified: the ramp flow, the forward facing step, the backward facing step, the incident–reflecting shock interaction, the transonic lambda shock interaction, and the adaptation shock at a nozzle exit. In the present study we consider the canonical case of a strong incident–reflecting shock interaction with a turbulent flat-plate boundary layer. In particular we are interested in the transition process between regular and irregular SWBLI (RSWBLI and ISWBLI, respectively), the latter being the viscous equivalent of a Mach reflection, and unsteady effects due to the turbulent boundary layer.
Figure 2 schematically depicts the strong RSWBLI, which is characterised by a noticeable separation of the boundary layer and a wall pressure distribution that clearly exhibits three inflection points (Delery & Marvin Reference Delery and Marvin1986). The boundary layer separates well upstream from the point
$x_{imp}$
, where the incident shock
$C_{1}$
would impinge in an inviscid flow. The adverse pressure gradient affects the upstream flow through the subsonic part of the boundary layer, causing the displacement of streamlines away from the wall. Compression waves are formed that propagate into the outer flow and coalesce into the separation shock
$C_{2}$
. Following Edney’s classification (Edney Reference Edney1968) the wave pattern formed by the shocks
$C_{1},C_{2},C_{3}$
and
$C_{4}$
is a type I shock/shock interference. We note that, depending on shock strength, Mach number and boundary layer characteristics, the interaction between shock and boundary layer can feature several other phenomena; for a comprehensive review of the various types of shock reflections in the presence of a boundary layer see Henderson (Reference Henderson1967) and Delery & Marvin (Reference Delery and Marvin1986).
Figure 2. Schematic illustration of the strong RSWBLI, cf. Delery & Dussauge (Reference Delery and Dussauge2009).
Though viscous effects play a crucial role in SWBLI phenomena, inviscid methods are capable of capturing and describing some of the main physics involved. Figure 3 shows the inviscid model of the strong RSWBLI, which we adapted from Delery & Marvin (Reference Delery and Marvin1986). The separated region is replaced by a wedge that leads to a sharp deflection of the flow by an angle
${\it\vartheta}_{02}$
away from the wall. When the deflection across
$C_{1}$
and
$C_{2}$
is known, the shock polar analysis shown in figure 4 allows a precise prediction of the states downstream of the reflected shocks
$C_{3}$
and
$C_{4}$
. Note that the deflection across
$C_{2}$
is generally different from that across
$C_{1}$
. In the case of an asymmetric intersection, velocity and entropy differ in regions
$(3)$
and
$(4)$
, whereas pressure and flow direction are the same. The existence of such a slip line has been experimentally proven by schlieren images, see Delery & Marvin (Reference Delery and Marvin1986). While the deflection across
$C_{1}$
is generally defined by a boundary condition (in the case of an incident–reflecting shock interaction), the deflection across the separation shock
$C_{2}$
is a priori unknown. The resulting question of a maximum deflection across the incident shock
$C_{1}$
, for which the intersection between incident and separation shock remains regular, is studied in the course of this work.
Figure 3. Inviscid flow model of the strong RSWBLI, after Delery & Marvin (Reference Delery and Marvin1986).
Figure 4. Shock polar representation of the inviscid flow model for the strong RSWBLI.
Figure 5. Schematic of the numerical setup.
In general, the incident–reflecting shock interaction, as considered in this work, has been studied in great depth in wind tunnel experiments (Bardsley & Mair Reference Bardsley and Mair1950; Liepmann, Roshko & Dhawan Reference Liepmann, Roshko and Dhawan1951; Gadd, Holder & Regan Reference Gadd, Holder and Regan1954; Green Reference Green1970; Humble, Scarano & van Oudheusden Reference Humble, Scarano and van Oudheusden2009; Souverein et al.
Reference Souverein, Dupont, Debiêve, Dussauge, van Oudheusden and Scarano2010) and numerical simulations (Pirozzoli & Grasso Reference Pirozzoli and Grasso2006; Piponniau et al.
Reference Piponniau, Dussauge, Debiêve and Dupont2009; Touber & Sandham Reference Touber and Sandham2009; Pasquariello et al.
Reference Pasquariello, Grilli, Hickel and Adams2014). As a result, the flow physics of the regular SWBLI are currently quite well understood. However, all these experimental and numerical studies were limited to deflection angles
${\it\vartheta}_{01}$
for which the intersection of incident shock
$C_{1}$
and separation shock
$C_{2}$
remains regular. In other words, SWBLI has mainly been studied at sufficiently small deflection angles, where transition processes to ISWBLI can be disregarded. Although the phenomenon of a Mach reflection in the context of incident–reflecting shock interaction is generally known, very little information is available regarding the transition between regular and irregular SWBLI. To our knowledge, this transition has been observed only in experiments, but not been analysed in turbulence resolving simulations yet.
In § 2 we develop a numerical model for studying the transition between regular and irregular SWBLI. This model is designed in such a way that it can be readily reproduced in wind tunnel experiments. Numerical results for a free-stream Mach number of
$\mathit{Ma}_{0}=2$
are analysed in § 3. We will demonstrate that turbulent fluctuations play a crucial role in triggering the transition between RSWBLI and ISWBLI and that classical gas-dynamics methods are suitable for the analysis of the transient data. In § 4 we apply the free interaction theory (Chapman, Kuehn & Larson Reference Chapman, Kuehn and Larson1958; Carrière, Sirieix & Solignac Reference Carrière, Sirieix and Solignac1969) for the approximation of the deflection across the separation shock (the reflected shock) and classical two- and three-shock theory for the determination of a critical deflection across the incident shock for which an ISWBLI can occur. Though the derived transition criteria should be seen as an engineering approach in the sense of a conservative worst-case estimate, the subsequent validation for the highly asymmetric SWBLI at
$\mathit{Ma}_{0}=3$
yields very promising results, see § 5. Conclusions and some additional remarks are given in § 6.
2. Setup and flow configuration
2.1. Test case definition
We consider the incident–reflecting shock interaction with a supersonic flat-plate turbulent boundary layer (TBL) at a free-stream Mach number of
$\mathit{Ma}_{0}=2$
. Figure 5 illustrates the investigated geometry and the computational domain. The incident oblique shock wave
$C_{1}$
is generated by a wedge with inclination
${\it\vartheta}_{01}$
that deflects the supersonic free stream. We performed large-eddy simulations (LES) for five deflection angles
${\it\vartheta}_{01}=\{11^{\circ },12^{\circ },12.5^{\circ },13^{\circ },14^{\circ }\}$
for
$\mathit{Ma}_{0}=2.0$
(hereafter referred to as
$\text{SWBLI}_{1,2,3,4,5}$
), see table 1. The Reynolds number based on the boundary-layer thickness
${\it\delta}_{imp}$
at the theoretical inviscid impingement point
$x_{imp}$
of the incident shock wave is
$\mathit{Re}_{{\it\delta}_{imp}}\approx 48.3\times 10^{3}$
for all cases
$\text{SWBLI}_{1{-}5}$
.
Table 1. Summary of relevant parameters:
$x_{exp}$
and
$x_{imp}$
are defined in figure 5;
$FTT_{t}$
is the total simulation time in flow through times (FFT);
$FTT_{s}$
is the FFTs used for the time-averaged flow field with an internal sample interval of
$0.05{\it\delta}_{ref}/u_{\infty }$
;
$N_{t}$
is the total number of instantaneous snapshots gathered with a sample interval of
$0.5{\it\delta}_{ref}/u_{\infty }$
;
$N_{s}$
is the total number of samples used for the time-averaged flow field;
$\langle {\it\beta}_{02}\rangle$
is the shock angle measured from the time-averaged flow field with respect to
$\langle {\it\vartheta}_{0}\rangle =0.2$
for
$\text{SWBLI}_{1{-}5}$
and with respect to
$\langle {\it\vartheta}_{0}\rangle =0.0$
for
$\text{SWBLI}_{6{-}8}$
;
$\langle {\it\vartheta}_{02}\rangle$
is the deflection across the separation shock calculated from
$\langle {\it\beta}_{02}\rangle$
with
$\langle \mathit{Ma}\rangle _{\infty }=1.995$
for
$\text{SWBLI}_{1{-}5}$
and
$\langle \mathit{Ma}\rangle _{\infty }=3.0$
for
$\text{SWBLI}_{6{-}8}$
.
Three features are relevant for the design of the shock-generator geometry. First, we ensure that a proper scaling can be applied to characteristic length scales of the SWBLI (e.g. separation length
$l_{sep}$
). By keeping the inviscid impingement location
$x_{imp}$
constant, TBL characteristics at
$x_{imp}$
, e.g. boundary-layer thickness
${\it\delta}_{imp}$
, offer a suitable characteristic length scale. Second, the wedge width
$w$
, which provides the length scale that essentially determines the Mach stem height (MSH) in the case of an ISWBLI, is to be kept constant in order to describe a realistic geometry that can be reproduced in experiments. To meet both requirements, the shock generator is simultaneously shifted horizontally and rotated around its trailing edge. As
${\it\vartheta}_{01}$
increases, the
$x$
-coordinate of the trailing edge
$x_{exp}$
moves downstream such that
$x_{imp}$
remains constant. Figure 5 shows the shock-generator configuration for two shock angles
${\it\beta}_{01}$
considered in this work. The third important feature concerns the ratio of channel height to wedge width
$g^{+}=g/w$
. This ratio affects the MSH and determines at which
$x$
-coordinate (with respect to
$x_{imp}$
) the first characteristic of the centred Prandtl–Meyer expansion (PME) emanating from the trailing edge of the wedge impinges on the flat plate. This is important because the PME has a major effect on the spatial extent of the separated region and can significantly reduce the adverse pressure gradient felt by the separated shear layer at reattachment. Note that the pressure rise towards separation and plateau pressure are not affected by the PME. Preliminary studies have shown that a too small value of
$g^{+}$
may lead to a massive separated region with
$l_{sep}$
easily exceeding the domain length
$L_{x}$
. A second reason concerns deflection angles for which an ISWBLI is obtained. In an inviscid framework and in the case of a symmetric shock intersection, the MSH normalised by the wedge width
$w$
can be expressed as
$m^{+}=f^{+}(\mathit{Ma}_{0},{\it\gamma},g^{+},{\it\vartheta}_{01})$
, where
$f^{+}$
is an unknown non-dimensional function, see Hornung (Reference Hornung1982). As a consequence, the normalised MSH is associated with the characteristic length scale
$g^{+}$
. In the present study the TBL itself provides an additional characteristic length scale. Up to the present date, it remains open to what extent the MSH is influenced by TBL characteristics (e.g.
${\it\delta}_{imp}$
) and the length scales resulting from the SWBLI itself (e.g.
$l_{sep}$
, see Souverein, Bakker & Dupont Reference Souverein, Bakker and Dupont2013). In an inviscid framework, it can be shown that
$m^{+}$
decreases as
$g^{+}$
increases, see e.g. Li & Ben-Dor (Reference Li and Ben-Dor1997), provided that all other variables are held constant. Since the flow topology must fit well within the computational domain,
$g^{+}$
was set to
$5/4$
, which results in a relatively small Mach stem. In summary, the test case geometry is fully determined by the deflection
${\it\vartheta}_{01}$
, the wedge width
$w$
, and the non-dimensional channel height
$g^{+}$
. All relevant geometric parameters are listed in table 1.
2.2. Numerical model for large eddy simulation
We solve the three-dimensional compressible Navier–Stokes equations in conservative form
$$\begin{eqnarray}\partial _{t}\boldsymbol{q}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{F}(\boldsymbol{q})-\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{D}(\boldsymbol{q})=0.\end{eqnarray}$$
The state vector
$\boldsymbol{q}=[{\it\rho},{\it\rho}u_{1},{\it\rho}u_{2},{\it\rho}u_{3},{\it\rho}E]^{\text{T}}$
consists of density
${\it\rho}$
, momentum
${\it\rho}u_{i}$
and total energy
${\it\rho}E={\it\rho}e+{\it\rho}u_{k}u_{k}/2$
, and
$\boldsymbol{u}=[u_{1},u_{2},u_{3}]^{\text{T}}$
is the velocity vector. The flux is split into an inviscid part
$\boldsymbol{F}=[\,\boldsymbol{f}_{1},\boldsymbol{f}_{2},\boldsymbol{f}_{3}]^{\text{T}}$
, where
$$\begin{eqnarray}\boldsymbol{f}_{i}=[u_{i}{\it\rho},u_{i}{\it\rho}u_{1}+{\it\delta}_{i1}p,u_{i}{\it\rho}u_{2}+{\it\delta}_{i2}p,u_{i}{\it\rho}u_{3}+{\it\delta}_{i3}p,u_{i}({\it\rho}E+p)]^{\text{T}},\end{eqnarray}$$
and a viscous contribution
$\boldsymbol{D}=[\boldsymbol{d}_{1},\boldsymbol{d}_{2},\boldsymbol{d}_{3}]^{\text{T}}$
, where
$$\begin{eqnarray}\boldsymbol{d}_{i}=[0,{\it\tau}_{i1},{\it\tau}_{i2},{\it\tau}_{i3},u_{k}{\it\tau}_{ik}-{\it\phi}_{i}]^{\text{T}}.\end{eqnarray}$$
According to the Stokes hypothesis for a Newtonian fluid, the viscous stress tensor is
$$\begin{eqnarray}{\bf\tau}={\it\mu}(\boldsymbol{{\rm\nabla}}\boldsymbol{u}+(\boldsymbol{{\rm\nabla}}\boldsymbol{u})^{\text{T}}-2/3\,\boldsymbol{I}~\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}),\end{eqnarray}$$
and Fourier’s law for the heat flux is
$$\begin{eqnarray}{\bf\phi}=-{\it\kappa}\boldsymbol{{\rm\nabla}}T.\end{eqnarray}$$
The above equations are solved in non-dimensional form (non-dimensionalised by the free-stream values of velocity, temperature and density, and the boundary-layer thickness) for a perfect gas with a constant specific heats’ ratio
${\it\gamma}=1.4$
and Prandtl number
$\mathit{Pr}=0.72$
. The governing non-dimensional flow parameters are the reference Reynolds number
$\mathit{Re}_{ref}={\it\rho}_{\infty }u_{\infty }{\it\delta}_{ref}/{\it\mu}_{\infty }$
and the reference Mach number
$\mathit{Ma}_{ref}=u_{\infty }/c_{\infty }$
, with
$c_{\infty }=\sqrt{{\it\gamma}\mathscr{R}T_{\infty }}$
being the free-stream speed of sound. Pressure
$p$
and temperature
$T$
are determined by the ideal-gas equation of state
$$\begin{eqnarray}p=({\it\gamma}-1){\it\rho}e=\mathscr{R}{\it\rho}T,\end{eqnarray}$$
where the non-dimensional gas constant is
$\mathscr{R}=1/({\it\gamma}\mathit{Ma}_{ref}^{2})$
. We use Sutherland’s law for modelling the temperature dependence of dynamic viscosity and thermal conductivity,
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}{\it\mu}={\displaystyle \frac{1}{\mathit{Re}_{ref}}}{\displaystyle \frac{1+C}{T+C}}T^{1.5},\\ {\it\kappa}={\displaystyle \frac{1}{({\it\gamma}-1)\mathit{Ma}_{ref}^{2}\mathit{Pr}}}~{\it\mu},\end{array}\right\}\end{eqnarray}$$
with
$C=0.40417$
.
The governing equations are discretised by a conservative finite-volume scheme on a Cartesian grid. Effects of unresolved subgrid scales (SGS) are modelled by the adaptive local deconvolution method (ALDM) of Hickel, Adams & Domaradzki (Reference Hickel, Adams and Domaradzki2006) and Hickel, Egerer & Larsson (Reference Hickel, Egerer and Larsson2014), which provides the discretisation of the inviscid flux. The compressible version of ALDM acknowledges that unresolved turbulence and shock waves are fundamentally different flow phenomena and thus require different SGS modelling. Employing a shock sensor to detect discontinuities, ALDM captures strong shock waves without spurious oscillations and accurately represents smooth waves and turbulence without excessive numerical dissipation. Though the physically consistent implicit turbulence model implies a second-order modification in the governing equations, ALDM provides a spectral resolution of linear waves (modified wavenumber) similar to sixth-order central difference schemes. See Hickel et al. (Reference Hickel, Egerer and Larsson2014) for a thorough validation based on canonical test cases and a modified wavenumber analysis. The viscous flux is discretised using a second-order central difference scheme, and the third-order explicit Runge–Kutta scheme of Gottlieb & Shu (Reference Gottlieb and Shu1998) is used for time integration. This numerical method has been proven particularly efficient for LES of shock–turbulence interaction; recent applications cover canonical shock–turbulence interaction (Hickel et al. Reference Hickel, Egerer and Larsson2014), flow control of SWBLI on a flat plate (Pasquariello et al. Reference Pasquariello, Grilli, Hickel and Adams2014), SWBLI at a compression–expansion ramp (Grilli, Hickel & Adams Reference Grilli, Hickel and Adams2013), and the shock train in a divergent nozzle (Quaatz et al. Reference Quaatz, Giglmaier, Hickel and Adams2014).
2.3. Grid and boundary conditions
All computations have been performed in a rectangular box with dimensions
$L_{x}=40{\it\delta}_{ref}$
in the streamwise,
$L_{y}=25{\it\delta}_{ref}$
in the wall-normal, and
$L_{z}=4{\it\delta}_{ref}$
in the spanwise directions, with
${\it\delta}_{ref}$
being the boundary-layer thickness at the domain inlet. This computational domain is discretised with
$N_{x}\times N_{y}\times N_{z}=520\times 600\times 100$
cells. For a well-resolved LES of the near-wall turbulence, a hyperbolic line bunching law
$$\begin{eqnarray}y_{j}=L_{y}\frac{\tanh \left({\displaystyle \frac{{\it\beta}_{y}(j-1)}{N_{y}-1}}\right)}{\tanh ({\it\beta}_{y})}\end{eqnarray}$$
with a stretching factor of
${\it\beta}_{y}=2.55$
is used in the wall-normal direction. Grid parameters and boundary-layer resolution,
${\rm\Delta}x^{+},{\rm\Delta}y_{min}^{+},{\rm\Delta}z^{+}$
, at the inviscid impingement point
$x_{imp}$
are summarised in table 2.
Table 2. Summary of grid parameters.
At the domain inlet, A in figure 5, a digital-filter-based boundary condition is used (Klein, Sadiki & Janicka Reference Klein, Sadiki and Janicka2003), for which first- and second-order statistical moments have been obtained through a precursor simulation. This inflow boundary condition ensures that no spurious low-frequency patterns are fed into the computational domain. The shock-generator geometry (in particular the wedge surface) is not part of the simulation domain. We, rather, introduce the leading-edge shock and trailing-edge expansion at the top of the domain, see B in figure 5, based on Riemann invariants corresponding to the aerodynamic and thermodynamic states upstream (0) and downstream (1) of
$C_{1}$
and downstream of the PME (2). The incident shock is imposed as a jump in the flow variables that satisfies the Rankine–Hugoniot relations
$\{(0)\rightarrow (1)\}$
for the considered shock angle
${\it\beta}_{01}$
. Downstream of the trailing edge
$(2)$
we impose a jump in the flow variables that satisfies the governing equations of a centred expansion fan
$\{(1)\rightarrow (2)\}$
with
${\it\vartheta}_{12}=-{\it\vartheta}_{01}$
. At the outlet (C) a linear extrapolation procedure of all flow variables is used. The size of domain has been chosen such that the inflow and outflow boundary conditions have no spurious effect on the region of interest. The wall (D) is isothermal at the nominal adiabatic temperature.
2.4. Baseline boundary-layer flow
In the following we briefly characterise the baseline
$\mathit{Ma}_{0}=2$
boundary-layer flow in the absence of the shock wave. The reliability of the numerical model is demonstrated through the comparison of LES results with direct numerical simulations (DNS), experimental data and empirical correlations. In order to compare the skin-friction evolution obtained by the LES with well-established correlations for incompressible flows and with reference data from DNS and experiments at different Mach numbers, it is necessary to transform the skin-friction coefficient
$\langle C_{f}\rangle$
into the incompressible regime (here and in the following, angle brackets denote averages over time and the homogeneous spanwise direction). Figure 6 shows the van Driest II (van Driest Reference van Driest1956) transformed incompressible skin-friction coefficient
$\langle C_{f,i}\rangle$
as a function of the Reynolds number
$\mathit{Re}_{{\it\theta}w}={\it\rho}_{w}u_{{\it\tau}}{\it\theta}/{\it\mu}_{w}$
based on the momentum thickness
${\it\theta}$
, the friction velocity
$u_{{\it\tau}}$
, and the density and viscosity at the wall,
${\it\rho}_{w}$
and
${\it\mu}_{w}$
. We observe an excellent agreement of the LES data with the incompressible relations of Smits, Matheson & Joubert (Reference Smits, Matheson and Joubert1983), Kármán–Schoenherr and Blasius (both documented in Hopkins & Inouye Reference Hopkins and Inouye1971), and available compressible and incompressible DNS and experimental data (for references see the caption of figure 6).
Figure 6. Incompressible skin friction as a function of the momentum-thickness Reynolds number
$\mathit{Re}_{{\it\theta}w}$
. ——, Present LES; –
$\bullet$
–, Kármán–Schoenherr and –▪–, Blasius (both from Hopkins & Inouye Reference Hopkins and Inouye1971); –▾–, Smits et al. (Reference Smits, Matheson and Joubert1983); ⬠, Pirozzoli, Grasso & Gatski (Reference Pirozzoli, Grasso and Gatski2004);
$\boxdot$
, Pirozzoli & Bernardini (Reference Pirozzoli and Bernardini2011);
$\odot$
, Komminaho & Skote (Reference Komminaho and Skote2002); ▵, Schlatter & Örlü (Reference Schlatter and Örlü2010); ▿, Simens et al. (Reference Simens, Jiménez, Hoyas and Mizuno2009); ♢, Coles (Reference Coles1953) (CAT5301, from Fernholz & Finley Reference Fernholz and Finley1977);
$+$
, Guarini et al. (Reference Guarini, Moser, Shariff and Wray2000);
$\times$
, Maeder, Adams & Kleiser (Reference Maeder, Adams and Kleiser2001).
Figure 7 shows the van Driest transformed mean velocity profile
$$\begin{eqnarray}\langle u_{VD}^{+}\rangle ={\displaystyle \frac{1}{u_{{\it\tau}}}}\int _{0}^{y}\sqrt{{\displaystyle \frac{\langle {\it\rho}\rangle }{{\it\rho}_{w}}}}{\displaystyle \frac{\text{d}\langle u\rangle }{\text{d}y^{\prime }}}\,\text{d}y^{\prime }\end{eqnarray}$$
and Reynolds stresses in Morkovin scaling at
$(x-x_{imp})/{\it\delta}_{ref}=-5.5$
, where the friction Reynolds number based on the local boundary-layer thickness
${\it\delta}_{0}$
and friction velocity
$u_{{\it\tau}}$
is
$\mathit{Re}_{{\it\tau}}={\it\rho}_{w}u_{{\it\tau}}{\it\delta}_{0}/{\it\mu}_{w}=671$
. The figure also includes reference DNS data of Schlatter & Örlü (Reference Schlatter and Örlü2010) for an incompressible TBL at the same
$\mathit{Re}_{{\it\tau}}$
and
$\mathit{Re}_{{\it\theta}w}\approx 2000$
. The turbulent mean velocity profile is in excellent agreement with the logarithmic law of the wall (constant of integration
$C=5.25$
) and the DNS data. For the Reynolds stresses very good agreement can be observed in the log layer and wake region. Near the wall (
$y^{+}<10$
) the compressible turbulence predicted by the LES is more anisotropic and shows larger fluctuations of the streamwise velocity than the incompressible reference DNS. This observation is consistent with the expected compressibility (or density stratification) effects in supersonic boundary layers, cf. DNS data of Foysi, Sarkar & Friedrich (Reference Foysi, Sarkar and Friedrich2004). Two-point correlations of all flow variables (not included here) show that all variables are fully de-correlated over a distance
$L_{z}/2$
, which confirms that the computational domain is sufficiently wide so as to not affect turbulence dynamics.
Figure 7. Mean profiles in inner scaling for the undisturbed incoming turbulent boundary layer at
$\mathit{Re}_{{\it\tau}}=671$
and
$(x-x_{imp})/{\it\delta}_{ref}=-5.5$
. (a) Van Driest transformed mean velocity profile. (b) Reynolds stresses with density correction
${\it\xi}=\sqrt{{\it\rho}/{\it\rho}_{w}}$
. ——, Present LES at
$\mathit{Ma}_{0}=2$
; – ⋅ – ⋅ –, incompressible DNS data of Schlatter & Örlü (Reference Schlatter and Örlü2010).
Figure 8. Results for (a) time-averaged skin-friction distribution and (b) time-averaged wall pressure for: ——,
$\text{SWBLI}_{1}$
; – – – –,
$\text{SWBLI}_{2}$
; - - - -,
$\text{SWBLI}_{3}$
;
$\cdots \cdots$
,
$\text{SWBLI}_{4}$
; – ⋅ – ⋅ –,
$\text{SWBLI}_{5}$
; and –
$\cdot \cdot$
–
$\cdot \cdot$
–, inviscid reflection for
${\it\vartheta}_{01}=11^{\circ }$
without PME downstream of the interaction. Symbols: ▾, point of separation; ▴, reattachment of the separated flow;
$\boxdot$
,
$x$
-coordinate at which the first characteristic of the PME impinges on the wall.
3. Numerical results for Mach 2
3.1. Mean flow
$\text{SWBLI}_{1}$
and
$\text{SWBLI}_{5}$
were simulated independently of each other to determine the boundaries in which the transition process takes place. It was found that transition occurs between a deflection of 11° and 14° across the incident shock
$C_{1}$
. Then, the simulations
$\text{SWBLI}_{2{-}4}$
were set up to more precisely determine the point of transition. To reduce the duration of the initial transient, simulation
$\text{SWBLI}_{i}$
was initialised with a quasi-steady flow field obtained from simulation
$\text{SWBLI}_{(i-1)}$
. Note that for Mach number
$\mathit{Ma}_{0}=2$
the converged steady-state solution is independent of the start-up history, because a dual solution domain exists only for
$\mathit{Ma}_{0}>2.202$
. A total time interval of more than 160 flow through times (FTT) of the full domain length has been simulated, of which more than 100 FTT represent steady-state flow, see table 1. Statistical properties have been obtained by averaging in time and spanwise direction with equally spaced samples at time intervals
$0.05{\it\delta}_{ref}/u_{\infty }$
after an initial transient. To additionally enable transient post-processing, three-dimensional snapshots of a narrow slice, which extend over
$L_{x}=40{\it\delta}_{ref}$
,
$L_{y}=25{\it\delta}_{ref}$
,
$L_{z}={\it\delta}_{ref}$
, have been obtained with a sample interval of
$0.5{\it\delta}_{ref}/u_{\infty }$
.
Figure 8 shows the mean skin-friction coefficient
$\langle C_{f}\rangle$
and wall pressure distributions
$\langle p\rangle /p_{\infty }$
. Symbols mark the points of separation (▾) and reattachment (▴), at which the mean skin friction coefficient vanishes. We observe that the separation length
$l_{sep}$
increases as the shock strength increases. The cases
$\text{SWBLI}_{3{-}5}$
exhibit a pressure plateau, which is typical for strong interactions. It is important to note that the maximum wall pressure is significantly smaller than across an inviscid reflection (see chain double-dotted line in figure 8
b) due to the subsonic flow near the wall and the pressure drop caused by the PME emanating from the trailing edge of the wedge. The theoretical inviscid impingement point of the leading characteristic of the PME is depicted by a square (
$\boxdot$
). The PME has a major effect on the obtained interaction length and thereby enables the simulation of SWBLI for such strong shocks. Furthermore, based on the findings for inviscid symmetric shock intersection (Hornung Reference Hornung1982; Li & Ben-Dor Reference Li and Ben-Dor1997) it must be assumed that the PME plays a crucial role regarding the obtained MSH and quasi-stationary stability of the obtained wave configuration.
Figure 9 gives an impression of the time- and spanwise-averaged flow field of the interaction for the cases
$\text{SWBLI}_{1,2,3,5}$
. The 13° case
$\text{SWBLI}_{4}$
will be discussed separately in the subsequent section. The plots show the density gradient magnitude as grey–cyan flooding and dashed iso-lines of constant local flow direction, which are labelled with respect to the undisturbed outer flow upstream of the incident shock
$C_{1}$
. Boundary-layer edge, subsonic region and region of reverse flow are indicated by the cyan blue, yellow and green line, respectively. In general, the boundary-layer edge is determined by a line along which
$\langle u\rangle$
is
$0.99u_{\infty }$
. This definition is inappropriate for the SWBLI since the free-stream velocity changes significantly across the interaction. We use a more practical definition based on the
$z$
-vorticity, which separates the rotational layer from the essentially irrotational outer flow. An iso-line with the
$z$
-vorticity value at the boundary-layer edge upstream of the interaction yields a reasonable qualitative representation of the boundary-layer edge across the interaction. Since the intersection point between
$C_{1}$
and
$C_{2}$
is located well above the boundary-layer edge, all interactions extend well into the outer flow. The cases
$\text{SWBLI}_{1,2,3}$
show a regular intersection of incident shock
$C_{1}$
and separation shock
$C_{2}$
(RSWBLI). For the
${\it\vartheta}_{01}=11^{\circ }$
case (
$\text{SWBLI}_{1}$
) the entire flow field downstream of the interaction in the outer flow is supersonic. With shock strength increasing, a subsonic region appears downstream of the shocks
$C_{3}$
and
$C_{4}$
for
${\it\vartheta}_{01}=12^{\circ }$
(
$\text{SWBLI}_{2}$
) and
${\it\vartheta}_{01}=12.5^{\circ }$
(
$\text{SWBLI}_{3}$
). Increasing the deflection across the incident shock
$C_{1}$
to
${\it\vartheta}_{01}=14^{\circ }$
(
$\text{SWBLI}_{5}$
) leads to the characteristic flow field of an ISWBLI. The observed wave pattern differs significantly from the one of a RSWBLI and resembles an Edney type II shock/shock interference (Edney Reference Edney1968). A Mach stem and two shear layers emanating from the two triple points can be observed. The subsonic flow downstream of the Mach stem and the reflected shocks
$C_{3}$
and
$C_{4}$
is accelerated again to supersonic conditions by both the PME centred at the trailing edge and the PME emanating from the top of the separated region. Thus, the cross-sectional area of the stream-tube downstream of the Mach stem decreases to a minimum at a sonic throat and then increases again in the region of accelerating supersonic flow.
Figure 9. Illustration of the interaction zone for the cases
$\text{SWBLI}_{1}$
(a),
$\text{SWBLI}_{2}$
(b),
$\text{SWBLI}_{3}$
(c),
$\text{SWBLI}_{5}$
(d). Grey–cyan scale flooding of the time- and spanwise-averaged density gradient magnitude and iso-lines of constant local flow direction. Boundary-layer edge, subsonic region and region of reverse flow are indicated by the cyan blue, yellow and green line, respectively.
Figure 10 schematically depicts all relevant features of the ISWBLI. It is important to note that depending on the free-stream Mach number
$\mathit{Ma}_{0}$
upstream of the interaction, the prescribed deflection
${\it\vartheta}_{01}$
across incident shock
$C_{1}$
and the resulting deflection
${\it\vartheta}_{02}$
across separation shock
$C_{2}$
, the flow downstream of the reflected shock
$C_{3}$
and
$C_{4}$
is either supersonic or subsonic. Nonetheless, the flow downstream of the Mach stem
$m$
is in either way subsonic. In figure 11 we show the corresponding inviscid model of the ISWBLI. It becomes apparent that the inviscid model and the classical double-wedge configuration, which has been widely used for the investigation of the Mach reflection phenomenon and transition criteria in particular, bear a certain resemblance. Therefore, the methods and transition criteria developed for the reflection of symmetric and asymmetric shock waves in steady flows can be applied to the ISWBLI flow field. Figure 12 shows the shock polar representation of this model. If the deflection across
$C_{1}$
and
$C_{2}$
is known (e.g. from LES results), the shock polar analysis as depicted in figure 12 allows a precise prediction of the states downstream of the Mach stem
$m$
and the reflected shocks
$C_{3}$
and
$C_{4}$
.
Figure 10. Schematic illustration of the ISWBLI, cf. Delery & Dussauge (Reference Delery and Dussauge2009).
Figure 11. Inviscid flow model of the ISWBLI with separation.
Figure 12. Shock polar representation of the inviscid flow model for the ISWBLI.
Recall figure 9 showing the time-averaged flow field for the cases
$\text{SWBLI}_{1,2,3,5}$
. There are two alternatives for the calculation of the deflection
$\langle {\it\vartheta}_{02}\rangle$
across the separation shock
$C_{2}$
: (a) based on the measured shock angle
$\langle {\it\beta}_{02}\rangle$
and (b) based on the isocontour levels of constant local flow direction. Method (a) has proven to be more reliable, whereas method (b) strongly depends on the visualisation method to extract the shock thickness. Table 1 summarises the obtained values for the separation shock angle
$\langle {\it\beta}_{02}\rangle$
, measured with respect to a mean deflection
$\langle {\it\vartheta}_{0}\rangle =0.2^{\circ }$
upstream of
$C_{2}$
(due to the displacement effect of the TBL upstream of the interaction). Based on
$\langle {\it\beta}_{02}\rangle$
and a pre-shock Mach number
$\langle \mathit{Ma}_{0}\rangle =1.995$
, we can calculate the deflection across
$C_{2}$
with the help of the oblique shock relations (see e.g. Anderson Reference Anderson2001). Note that the mean Mach number immediately upstream of the shock waves
$C_{1}$
and
$C_{2}$
is a bit lower than the nominal value of
$\mathit{Ma}_{0}=2$
due to compression waves emanating from the TBL. It is notable that, within the limits of accuracy of the measurements, the time-averaged shock angle
$\langle {\it\beta}_{02}\rangle$
and, hence, deflection across the separation shock
$\langle {\it\vartheta}_{02}\rangle$
remain constant for the cases
$\text{SWBLI}_{2{-}5}$
(
$\langle {\it\beta}_{02}\rangle \approx 41^{\circ }$
). A similar observation was made by Green (Reference Green1970), who stated that once separation has occurred, the shock strength of the separation shock
$C_{2}$
is independent of the incident shock that causes separation. This behaviour is characteristic for a free interaction (Chapman et al.
Reference Chapman, Kuehn and Larson1958), meaning that the pressure rise towards separation depends neither on the source of separation, in particular the shock intensity, nor on the downstream geometry (Delery & Dussauge Reference Delery and Dussauge2009).
3.2. Transient aspects
Figure 13 shows the inviscid RR
$\leftrightarrow$
MR transition criteria in the
$({\it\vartheta}_{01},{\it\vartheta}_{02})$
plane for
$\mathit{Ma}_{0}=2$
and
${\it\gamma}=1.4$
. The solid line denotes the detachment criterion hypothesised by Li et al. (Reference Li, Chpoun and Ben-Dor1999), while the dashed line correspond to the sonic-point criterion. The equations for the calculation of the corresponding transition criteria can be found in Li et al. (Reference Li, Chpoun and Ben-Dor1999) and Hu et al. (Reference Hu, Myong and Kim2009), for example. Axis labels
${\it\vartheta}_{01}$
and
${\it\vartheta}_{02}$
are related to the definition of incident (
$C_{1}$
) and separation shock (
$C_{2}$
) in figures 3 and 11. Recall that the mean deflection
$\langle {\it\vartheta}_{02}\rangle \approx 11.41^{\circ }$
across the separation shock
$C_{2}$
appears to remain constant for the cases
$\text{SWBLI}_{2{-}5}$
, see table 1. Based on this observation and the given transition criteria in figure 13, one can conclude that transition to ISWBLI in a time-averaged context would be expected at deflection angles greater than
$\langle {\it\vartheta}_{01}\rangle \approx 14^{\circ }$
across the incident shock wave
$C_{1}$
. In other words, for
$\langle {\it\vartheta}_{02}\rangle =11.41^{\circ }$
the corresponding detachment criterion for asymmetric shock wave intersections is given by
$\langle {\it\vartheta}_{D}\rangle =14.21^{\circ }$
. The present study however reveals that this is not the case. ISWBLI occurred unambiguously at a nominal deflection across
$C_{1}$
of
${\it\vartheta}_{01}=13^{\circ }$
(
$\text{SWBLI}_{4}$
). Even at
${\it\vartheta}_{01}=12.5^{\circ }$
(
$\text{SWBLI}_{3}$
), the flow partially exhibits characteristics of the ISWBLI.
Figure 13. RR
$\leftrightarrow$
MR transition criteria in the
$({\it\vartheta}_{01},{\it\vartheta}_{02})$
plane for
$\mathit{Ma}_{0}=2$
and
${\it\gamma}=1.4$
. The solid line (——) denotes the detachment criterion
${\it\vartheta}^{D}$
hypothesized by Li et al. (Reference Li, Chpoun and Ben-Dor1999), while the dashed line (- - - -) corresponds to the sonic-point criterion
${\it\vartheta}^{S}$
. The value
$\langle {\it\vartheta}_{02}\rangle =11.41^{\circ }$
is the recorded mean deflection across the separation shock
$C_{2}$
for the cases
$\text{SWBLI}_{2{-}4}$
.
Figure 14. Transient signal of the spanwise-averaged flow direction upstream of the interaction
${\it\vartheta}_{0}$
, the deflection
$|{\it\vartheta}_{01}|$
across the incident shock
$C_{1}$
and the deflection
${\it\vartheta}_{02}$
across the separation shock
$C_{2}$
(with respect to
$\langle {\it\vartheta}_{0}\rangle =0.2$
).
Figure 15. Instantaneous snapshots of the density gradient magnitude at (a)
$t_{1}=2257$
and (b)
$t_{2}=2341$
for
$\text{SWBLI}_{4}$
. Iso-lines of constant local flow direction are labeled with the corresponding angle with respect to the undisturbed outer flow upstream of the incident shock
$C_{1}$
. The instantaneous shock angle
${\it\beta}_{02}$
(a,
$40.2^{\circ }$
; b,
$40.9^{\circ }$
) is measured relative to
${\it\vartheta}_{0}=0.2^{\circ }$
.
Transient data reveal that fluctuations related to the incoming TBL, the shear layer formed at the edge of separation, and possibly, though to a lower extent, to the low-frequency motion of the separation shock trigger transition from RSWBLI to ISWBLI. Figure 14(a–c) shows the transient signal of the spanwise-averaged flow direction upstream of the intersection
${\it\vartheta}_{0}(t)$
, the absolute deflection
$|{\it\vartheta}_{01}(t)|$
across the incident shock
$C_{1}$
and the deflection
${\it\vartheta}_{02}(t)$
across the separation shock
$C_{2}$
(with respect to
$\langle {\it\vartheta}_{0}\rangle =0.2$
) for the cases
$\text{SWBLI}_{3}$
and
$\text{SWBLI}_{4}$
(
$12.5^{\circ }\rightarrow 13^{\circ }$
). The signal was recorded by placing probes relative to the intersection point of
$C_{1}$
and
$C_{2}$
. For this purpose a post-processing algorithm was developed that tracks the points of shock intersection in time and space. From the recorded signal
${\it\vartheta}_{02}(t)$
, the mean deflection across
$C_{2}$
for the cases
$\text{SWBLI}_{3}$
and
$\text{SWBLI}_{4}$
is found to be
$\langle {\it\vartheta}_{02}\rangle =11.96^{\circ }$
and
$\langle {\it\vartheta}_{02}\rangle =11.84^{\circ }$
, respectively. These values are in good agreement with the values obtained by relying on the time-averaged shock angle
$\langle {\it\beta}_{02}\rangle$
, which indicates that the deflection across
$C_{2}$
is accurately represented by the recorded signal. Furthermore, the fact that the time-averaged value of
${\it\vartheta}_{02}$
remains constant confirms the observation that the shock strength of the separation shock
$C_{2}$
is decoupled from the source of separation (namely the incident shock
$C_{1}$
). Figure 14 demonstrates that increasing the deflection across the incident shock
$C_{1}$
does not alter the recorded signal
${\it\vartheta}_{02}(t)$
. Note that changing the boundary condition from
$12.5^{\circ }$
to 13° across the incident shock
$C_{1}$
is accurately represented by signal
${\it\vartheta}_{01}(t)$
.
Classical inviscid theory applied to the mean flow data of
$\text{SWBLI}_{4}$
yields a regular intersection of
$C_{1}$
and
$C_{2}$
. However, transition to ISWBLI occurred unambiguously at a nominal deflection
${\it\vartheta}_{01}\leqslant 13^{\circ }$
. Figure 15(a) shows the instantaneous flow field at time instant
$t_{1}=2257$
. A Mach stem and two shear layers emanating from the triple points can be clearly identified, therefore, transition has occurred for
$t<t_{1}$
. Figure 15(b) shows the flow field at a later time
$t_{2}=2341$
. Since two shear layers are still visible this situation also constitutes an ISWBLI; however, the Mach stem is very small. This observation can be explained as follows: first, the deflection
${\it\vartheta}_{02}(t)$
across the separation shock
$C_{2}$
is highly transient, with significant deviations from its mean value, cf. figure 14. For
$\text{SWBLI}_{4}$
we measured
${\it\vartheta}_{02,max}=12.88$
and
${\it\vartheta}_{02,min}=10.08$
. A similar transient character is observed for the recorded signals upstream of the intersection (
${\it\vartheta}_{0}(t)$
) and downstream of the incident shock
$C_{1}(|{\it\vartheta}_{01}(t)|)$
, see figure 14(a–c). As a consequence, the regular intersection of
$C_{1}$
and
$C_{2}$
can become both possible and impossible within a transient inviscid framework, see figure 16. Second, it is well known that the low-frequency unsteadiness of the separated region shifts the separation shock
$C_{2}$
up- and downstream of its mean position (see e.g. Touber & Sandham Reference Touber and Sandham2011; Grilli et al.
Reference Grilli, Schmid, Hickel and Adams2012). For these reasons, and based on geometric considerations, the MSH cannot remain constant in the context of SWBLI. Such events, namely the growth and shrinking of the Mach stem for case
$\text{SWBLI}_{4}$
or the appearance of two slip lines with an infinitesimal small Mach stem for case
$\text{SWBLI}_{3}$
, can be observed at several points in time.
Figure 16. Shock polar representation of the intersection of incident shock
$C_{1}$
and separation shock
$C_{2}$
for case
$\text{SWBLI}_{4}$
. Numbering of the states according to figures 3 and 11. The solid lines (——) depict the polars in a time-averaged context, while the dashed lines (- - - -), which enclose the gray shaded region, correspond to the observed maximum and minimum deflections across
$C_{1}$
and
$C_{2}$
.
We now analyse the intersection of incident shock
$C_{1}$
and separation shock
$C_{2}$
for case
$\text{SWBLI}_{4}$
by means of shock polars, see figure 16. The free-stream polar is plotted for a mean Mach number
$\langle \mathit{Ma}_{0}\rangle =1.995$
upstream of the interaction. The numbering of the states
$(1){-}(6)$
is according to figures 3 and 11. In addition, we show two grey shaded regions enclosed by dashed lines, which denote the variation of deflection angles
${\it\vartheta}_{01}(t)$
and
${\it\vartheta}_{02}(t)$
that were observed across
$C_{1}$
and
$C_{2}$
. In the mean the interaction is regular as the mean polars
$C_{3}$
and
$C_{4}$
have an intersection point at
$(3)/(4)$
. However, only an ISWBLI is possible for the polar combination
${\it\vartheta}_{01,max}$
and
${\it\vartheta}_{02,max}$
, leading to the formation of a Mach stem
$m$
and the states
$(3)/(5)$
and
$(4)/(6)$
. Therefore, both the existence and the growth/shrinking of a Mach stem can be attributed to the inherent dynamics of the turbulent boundary layer. It should be pointed out that we are presently not able to unambiguously distinguish and quantify the contributions of incoming boundary layer and low-frequency separation-point movement.
Figure 17. Basic shock-wave/boundary-layer interactions after Delery & Marvin (Reference Delery and Marvin1986). (a) Ramp flow, (b) incident–reflecting shock interaction, (c) forward facing step, (d) schematic of the corresponding wall-pressure distribution.
4. Transition criteria
In the previous section we showed that for a Mach number of
$\mathit{Ma}_{0}=2$
and a Reynolds number
$\mathit{Re}_{{\it\delta}_{imp}}\approx 48.3\times 10^{3}$
transition from RSWBLI to ISWBLI occurred at a critical deflection across the incident shock
$C_{1}$
of
${\it\vartheta}_{01}\approx 13^{\circ }$
. This value is in close agreement with the inviscid detachment criterion for symmetric shock waves at
$\mathit{Ma}_{0}=2$
(
${\it\vartheta}_{sym}^{D}=12.899^{\circ }$
for
${\it\gamma}=1.4$
), which may lead to the fallacious conclusion that transition criteria valid for the symmetric intersection of shock waves are a good estimate also in case of an SWBLI. However, the LES results for
$\mathit{Ma}_{0}=2$
have also shown that the intersection between incident shock
$C_{1}$
and separation shock
$C_{2}$
becomes more and more asymmetric if the shock strength (that is, the incident shock deflection angle) is increased. Preliminary well-resolved LES for higher Mach number cases have confirmed this trend. Based on this observation, we develop an engineering approach for the estimation of the critical deflection
${\it\vartheta}_{01}^{crit}$
across the incident shock
$C_{1}$
at which the incident–reflecting shock interaction may become irregular.
Figure 18. Schematic of the free interaction, after Carrière et al. (Reference Carrière, Sirieix and Solignac1969) and Charwat (Reference Charwat1970).
Figure 17 shows three basic SWBLI configurations, namely the ramp flow, 17(a), the incident–reflecting shock interaction, 17(b), and the forward facing step 17(c). Even though these configurations correspond to rather distinct situations, it has been shown by many experiments that in particular the wall-pressure distributions for these cases, 17(d), bear a certain resemblance (see e.g. Gadd et al.
Reference Gadd, Holder and Regan1954; Bogdonoff Reference Bogdonoff1955; Chapman et al.
Reference Chapman, Kuehn and Larson1958; Zukoski Reference Zukoski1967; Settles, Bogdonoff & Vas Reference Settles, Bogdonoff and Vas1976; Shang, Hankey & Law Reference Shang, Hankey and Law1976; Delery & Marvin Reference Delery and Marvin1986). In the case of a strong interaction, wall-pressure distributions have three inflection points that are associated with the start of the interaction, the onset of reattachment and the reattachment compression. The observation that the major part of the interacting flow upstream of the separation depends neither on the source of separation nor on the downstream geometry led Chapman et al. (Reference Chapman, Kuehn and Larson1958) to formulate the free interaction concept. As described by Delery & Marvin (Reference Delery and Marvin1986): ‘Everything happens as if the flow were entirely determined by its properties at the onset of interaction’. The concept of the separation mechanism as a process in which the growth of the viscous layer is in local equilibrium with the external supersonic flow is the basis of several scaling and separation laws (Hankey Jr. & Holden Reference Hankey and HJrolden1975). In the following we give a brief introduction to the governing equations of the free interaction theory for the sake of completeness. We emphasise that more comprehensive reviews on the free interaction theory can be found, for example, in Erdos & Pallone (Reference Erdos and Pallone1963), Carrière et al. (Reference Carrière, Sirieix and Solignac1969), Charwat (Reference Charwat1970), Delery & Marvin (Reference Delery and Marvin1986), and Babinsky & Harvey (Reference Babinsky and Harvey2011). Consider figure 18, which schematically depicts the zone of free interaction. The adverse pressure gradient affects the upstream flow through the subsonic layer, causing a deflection
${\it\vartheta}(x)$
of the streamlines away from the wall. This deflection of the external inviscid flow is assumed to correspond precisely to the displacement effect of the boundary layer
$$\begin{eqnarray}\frac{\text{d}{\it\delta}^{\star }}{\text{d}x}={\it\vartheta}(x)-{\it\vartheta}_{0}.\end{eqnarray}$$
Normalising the streamwise extent with a reference length
$l$
and the displacement thickness
${\it\delta}^{\star }$
with a value
${\it\delta}_{0}^{\star }$
at the origin of the interaction yields
$$\begin{eqnarray}{\it\vartheta}(s)-{\it\vartheta}_{0}={\displaystyle \frac{{\it\delta}_{0}^{\star }}{l}}\left(\frac{\text{d}({\it\delta}^{\star }/{\it\delta}_{0}^{\star })}{\text{d}s}\right)=\frac{{\it\delta}_{0}^{\star }}{l}f_{1}(s)\end{eqnarray}$$
with
$s=(x-x_{0})/l$
and
$f_{1}(s)$
being, based on the similarity assumption, a universal function. Integration of the boundary-layer momentum equation at the wall
$$\begin{eqnarray}\frac{\text{d}p}{\text{d}x}=\left.\frac{\partial {\it\tau}}{\partial y}\right|_{w}\end{eqnarray}$$
from
$x=x_{0}$
to
$s$
and introducing appropriate reference quantities
$$\begin{eqnarray}{\it\tau}_{w,0}={\textstyle \frac{1}{2}}{\it\rho}_{0}u_{0}^{2}C_{f,0}\quad \text{and}\quad q_{0}={\textstyle \frac{1}{2}}{\it\rho}_{0}u_{0}^{2}={\textstyle \frac{1}{2}}p_{0}{\it\gamma}\mathit{Ma}_{0}^{2}\quad \text{at }x=x_{0}\end{eqnarray}$$
yields
$$\begin{eqnarray}\frac{p(s)-p_{0}}{q_{0}}=\frac{l}{{\it\delta}_{0}^{\star }}C_{f,0}\int _{0}^{s}\frac{\partial {\it\tau}_{w}/{\it\tau}_{w,0}}{\partial y/{\it\delta}_{0}^{\star }}\,\text{d}s.\end{eqnarray}$$
Based on the assumption that the pressure rise follows a law of similarity, the integral in (4.5) must depend only on
$s$
. That is,
$$\begin{eqnarray}\frac{p(s)-p_{0}}{q_{0}}=\frac{l}{{\it\delta}_{0}^{\star }}C_{f,0}f_{2}(s)\end{eqnarray}$$
with
$f_{2}(s)$
being a similarity function.
We can eliminate
$l/{\it\delta}_{0}^{\star }$
by multiplying (4.2) with (4.6) and obtain
$$\begin{eqnarray}\mathscr{F}(s)=\sqrt{f_{1}(s)\cdot f_{2}(s)}=\sqrt{\frac{p(s)-p_{0}}{q_{0}}\frac{{\it\vartheta}(s)-{\it\vartheta}_{0}}{C_{f,0}}}.\end{eqnarray}$$
In the analysis of Chapman et al. (Reference Chapman, Kuehn and Larson1958) the pressure variation induced in the outer inviscid flow is expressed via the linearised wave equation
$$\begin{eqnarray}{\it\vartheta}(s)-{\it\vartheta}_{0}\approx \frac{1}{2}\frac{p(s)-p_{0}}{q_{0}}\sqrt{\mathit{Ma }_{0}^{2}-1}.\end{eqnarray}$$
Combining (4.7) and (4.8) yields
$$\begin{eqnarray}\mathscr{F}(s)=\frac{p(s)-p_{0}}{q_{0}}(\mathit{Ma}_{0}^{2}-1)^{0.25}\,(2C_{f,0})^{-0.5},\end{eqnarray}$$
where
$\mathscr{F}(s)$
is assumed to be a universal correlation function that is independent of Mach and Reynolds numbers. For our purposes, equation (4.9) can be used to approximate the wall-pressure evolution for a given Mach number and friction coefficient, once
$\mathscr{F}(s)$
has been determined by experiments or numerical simulations.
Carrière et al. (Reference Carrière, Sirieix and Solignac1969) proposed a generalisation of Chapman’s theory to account for non-uniformities in the incoming outer flow, in particular, the adverse pressure gradient caused by wall curvature. They showed that the universal function has in the most general case the form
$$\begin{eqnarray}\widetilde{\mathscr{F}}(s)=\sqrt{\frac{p(s)-p_{0}}{q_{0}}\frac{\overline{{\it\nu}}(s)-\widetilde{{\it\nu}}(s)}{C_{f,0}}}\end{eqnarray}$$
where
$\widetilde{{\it\nu}}$
is the Prandtl–Meyer function for the actual pressure at
$s$
and
$\overline{{\it\nu}}(s)$
is the value that
${\it\nu}$
would take at the same
$s$
in the absence of separation (Delery & Marvin Reference Delery and Marvin1986). The Prandtl–Meyer function
${\it\nu}$
is given by
$$\begin{eqnarray}{\it\nu}(s)=\sqrt{\frac{{\it\gamma}+1}{{\it\gamma}-1}}\tan ^{-1}\sqrt{\frac{{\it\gamma}-1}{{\it\gamma}+1}(\mathit{Ma}^{2}(s)-1)}-\tan ^{-1}\sqrt{\mathit{Ma }^{2}(s)-1}.\end{eqnarray}$$
Figure 19. Similarity functions (a)
$\mathscr{F}(s)$
, equation (4.9), and (b)
$\widetilde{\mathscr{F}}(s)$
, equation (4.10), evaluated for the cases
$\text{SWBLI}_{1{-}5}$
;
$s=(x-x_{0})/(x_{ref}-x_{0})$
with
$x_{ref}$
being the coordinate at which
$\mathscr{F}(s)$
and
$\widetilde{\mathscr{F}}(s)$
take the value 4.22. Particular values of
$\mathscr{F}$
and
$\widetilde{\mathscr{F}}$
at the separation point (subscript
$s$
) and for the plateau pressure (subscript
$p$
) are highlighted.
Especially at low and moderate Reynolds numbers (
$\mathit{Re}_{{\it\delta}_{0}}<10^{5}$
), equations (4.9) and (4.10) have been used to establish scaling and separation laws. Erdos & Pallone (Reference Erdos and Pallone1963) proposed specific values
$\mathscr{F}_{s}=0.81$
at the separation point and
$\mathscr{F}_{p}=1.47$
for the plateau pressure in laminar flows, and
$\mathscr{F}_{s}=4.22$
and
$\mathscr{F}_{p}=6.00$
for turbulent flows. Zheltovodov & Yakovlev (Reference Zheltovodov and Yakovlev1986) and Zheltovodov (Reference Zheltovodov1996) reported a slightly different plateau value of
$\mathscr{F}_{p}=7.4$
. More recently,
$\widetilde{\mathscr{F}}(s)$
according to (4.10) has received new attention in the context of supersonic flow separation with applications to rocket engine nozzles, see e.g. Östlund (Reference Östlund2002), Reijasse & Birkemeyer (Reference Reijasse and Birkemeyer2002) and Reijasse (Reference Reijasse2005).
In figure 19 we compare
$\mathscr{F}(s)$
and
$\widetilde{\mathscr{F}}(s)$
evaluated for the cases
$\text{SWBLI}_{1{-}5}$
. To calculate
$\widetilde{\mathscr{F}}$
in case of a flat-plate (no curvature) incident–reflecting shock interaction, we evaluate
$\overline{{\it\nu}}(s)\equiv \overline{{\it\nu}}$
with
$$\begin{eqnarray}\overline{\mathit{Ma}}^{2}(s)\equiv \mathit{Ma}_{0}^{2}.\end{eqnarray}$$
Assuming an isentropic compression,
$\widetilde{{\it\nu}}(s)$
is calculated with
$$\begin{eqnarray}\widetilde{\mathit{Ma}}^{2}(s)=\frac{2}{{\it\gamma}-1}\left[\left(\frac{p_{0}}{p(s)}\right)^{({\it\gamma}-1)/{\it\gamma}}\left(1+\frac{{\it\gamma}-1}{2}\mathit{Ma}_{0}^{2}\right)-1\right].\end{eqnarray}$$
The reference length is defined as
$l=x_{ref}-x_{0}$
, where
$x_{ref}$
is the coordinate at which
$\mathscr{F}$
and
$\widetilde{\mathscr{F}}$
take the value 4.22 and
$x_{0}$
is the location where
$\text{d}p/\text{d}x|_{w}({\it\delta}_{0}(x)/p_{w}(x))=3.5\times 10^{-3}$
. The abscissa
$s$
thus is
$$\begin{eqnarray}s=\frac{x-x_{0}}{x_{ref}-x_{0}}.\end{eqnarray}$$
Figure 20. (a) Visualisation of the wave pattern for case
$\text{SWBLI}_{5}$
based on mean density gradient magnitude contour
$\sqrt{\sum (\partial \langle {\it\rho}\rangle /\partial x_{i})^{2}}=1$
, (b) corresponding wall-pressure distribution
$\langle p(x)\rangle$
.
The plateau values of
$\mathscr{F}_{p}$
and
$\widetilde{\mathscr{F}}_{p}$
are found to be 7.25 and 6.2, respectively. The value for
$\mathscr{F}_{p}$
differs significantly from the reported value of Erdos & Pallone (Reference Erdos and Pallone1963), while it is in very close agreement with the experimental data of Zheltovodov (Reference Zheltovodov1996). For the derivation of (4.9), the incoming outer flow is assumed to be uniform planar and two-dimensional (see e.g. Delery & Marvin Reference Delery and Marvin1986), whereas (4.10) takes non-uniformities in the incoming outer flow into account. In our case, the incoming outer free stream is uniform (in contrast to nozzle flows, e.g.) and thus (4.9) and (4.10) are supposed to yield the same result. As this is obviously not the case, the linearisation of (4.8) must be responsible for the observed discrepancies. We conclude that the linearisation may be inappropriate in case of a strong streamline curvature in the free interaction zone. It is well known that the pressure distribution for linearised supersonic flow becomes inaccurate beyond a deflection angle of approximately 4° (see e.g. Anderson Reference Anderson2001). Assuming an isentropic compression, the flow in the vicinity of the separation point is deflected up to approximately 17° with respect to the undisturbed incoming flow (for cases
$\text{SWBLI}_{1{-}5}$
). Therefore, the generalised form of the free interaction theory, given by (4.10), will be used in the subsequent discussion on RSWBLI
$\rightarrow$
ISWBLI transition criteria.
Figure 20 shows the numerically extracted wave structure for case
$\text{SWBLI}_{5}$
and the corresponding wall-pressure distribution
$\langle p\rangle /p_{\infty }$
. Plateau pressure
$\langle p_{p}\rangle$
and the pressure calculated with the oblique shock relations for the measured mean shock angle
$\langle {\it\beta}_{02}\rangle$
are indicated by symbols. The pressure rise as calculated from
$\langle {\it\beta}_{02}\rangle$
and
$\mathit{Ma}_{0}$
is less than the observed plateau pressure. Therefore we conclude that in a time-averaged context the plateau pressure
$\langle p_{p}\rangle$
is the maximum pressure that can be obtained across the separation shock
$C_{2}$
. Assuming the applicability of the free interaction theory and in particular that the plateau value
$\widetilde{\mathscr{F}}_{p}=6.2$
is universal, i.e. valid for different Reynolds and Mach numbers, we can calculate the deflection
${\it\vartheta}_{02}$
across the separation shock
$C_{2}$
: for a given Mach number
$\mathit{Ma}_{0}$
and skin-friction coefficient
$C_{f,0}$
together with
$\widetilde{\mathscr{F}}=\widetilde{\mathscr{F}}_{p}$
, equations (4.10)–(4.13) allow an iterative calculation of the plateau pressure ratio
${\it\xi}=p_{p}/p_{0}$
. This pressure ratio serves as input for a pressure deflection relation across an oblique shock wave (see e.g. Li et al.
Reference Li, Chpoun and Ben-Dor1999)
$$\begin{eqnarray}{\it\vartheta}_{02}=\arctan \left[\frac{({\it\xi}-1)^{2}[2{\it\gamma}(\mathit{Ma}_{0}-1)-({\it\gamma}-1)({\it\xi}-1)]}{[{\it\gamma}\mathit{Ma}_{0}^{2}-({\it\xi}-1)]^{2}[2{\it\gamma}+({\it\gamma}-1)({\it\xi}-1)]}\right]^{0.5}\end{eqnarray}$$
with
${\it\gamma}$
,
$\mathit{Ma}_{0}$
,
${\it\xi}=p_{p}/p_{0}$
and
${\it\vartheta}_{02}$
being the specific heat capacities ratio, the nominal free-stream Mach number upstream of the interaction, and the pressure ratio and deflection across the separation shock
$C_{2}$
, respectively. Based on the deflection
${\it\vartheta}_{02}$
across
$C_{2}$
, one can apply the available inviscid theory to the asymmetric intersection of shock waves (see e.g. Li et al.
Reference Li, Chpoun and Ben-Dor1999; Hu et al.
Reference Hu, Myong and Kim2009) and finally calculate the corresponding transition criteria at which the intersection between separation shock
$C_{2}$
and incident shock
$C_{1}$
may become irregular.
Figure 21(a, b) show the resulting analytical prediction (equations (4.10)–(4.13) with
$\widetilde{\mathscr{F}}=\widetilde{\mathscr{F}}_{p}=6.2$
) for the deflection
${\it\vartheta}_{02}$
across the separation shock
$C_{2}$
as function of
$\mathit{Ma}_{0}$
and
$C_{f,0}$
. The deflection angle
${\it\vartheta}_{02}$
across the separation shock increases with increasing upstream Mach number
$\mathit{Ma}_{0}$
(at fixed
$C_{f,0}$
), while
${\it\vartheta}_{02}$
decreases with decreasing
$C_{f,0}$
(or increasing Reynolds number). For the considered flow conditions (
$\mathit{Ma}_{0}=2$
and
$C_{f,0}\approx 2.410\times 10^{-3}$
), a deflection across the separation shock of
${\it\vartheta}_{02}\approx 13.8^{\circ }$
is predicted (cf. symbols in figure 21
b). Recall figure 13 showing the inviscid RR
$\leftrightarrow$
MR transition criteria in the
$({\it\vartheta}_{01},{\it\vartheta}_{02})$
plane for
$\mathit{Ma}_{0}=2$
. From this figure it is found that transition from RSWBLI to ISWBLI can be expected at a deflection across the incident shock
$C_{1}$
of
${\it\vartheta}_{01}=11.94^{\circ }$
. Apparently, this value is about 1° too small compared to the LES results for
$\mathit{Ma}_{0}=2$
. However, considering the assumptions made regarding the pressure rise across
$C_{2}$
, the theory provides a conservative worst-case estimate for the maximum possible deflection across
$C_{1}$
at which no ISWBLI is obtained.
Figure 21. (a) Iso-levels of the deflection
${\it\vartheta}_{02}$
across the separation shock
$C_{2}$
as a function of
$\mathit{Ma}_{0}$
and
$C_{f,0}$
, (b)
${\it\vartheta}_{02}$
as a function of
$C_{f,0}$
at
$\mathit{Ma}_{0}=2.0$
and
$\mathit{Ma}_{0}=3.0$
: ——, analytical prediction based on the free interaction theory (equations (4.10)–(4.13) with
$\widetilde{\mathscr{F}}=6.2$
); ▪, LES results for cases
$\text{SWBLI}_{1{-}8}$
, cf. figures 8(a) and 24(a).
Figure 22. Analytical results for the RR
$\leftrightarrow$
MR transition criteria in the
$({\it\vartheta}_{01},{\it\vartheta}_{02})$
plane for
$\mathit{Ma}_{0}=3$
and
${\it\gamma}=1.4$
. ——, Maximum deflection
$({\it\vartheta}^{MD})$
and - - - -, sonic
$({\it\vartheta}^{S})$
criteria as proposed by Hu et al. (Reference Hu, Myong and Kim2009). – – – –, Detachment
$({\it\vartheta}^{D})$
and (
$\cdots \cdots$
) von Neumann
$({\it\vartheta}^{N})$
criteria as proposed by Li et al. (Reference Li, Chpoun and Ben-Dor1999) for asymmetric shock intersections.
$\odot$
,
${\it\vartheta}^{N}$
and
${\it\vartheta}^{D}$
obtained through (4.10)–(4.13) with
$\mathit{Ma}_{0}=3$
,
$C_{f}=2.1\times 10^{-3}$
and
$\widetilde{\mathscr{F}}=6.2$
. ▪, LES results at
$\mathit{Ma}_{0}=3.0$
and
$\mathit{Re}_{{\it\delta}_{imp}}\approx 80\times 10^{3}$
(cf. figure 25).
It should be noted that the proposed model assumes that (i) the transition from RR to MR wave pattern occurs in massively separated flows for which (ii) the wall-pressure distribution shows a distinct plateau and (iii) the plateau value of the correlation function
$\widetilde{\mathscr{F}}$
is independent of Mach and Reynolds numbers. As the length of the separated region grows in direct proportion to the pressure rise, which for large shock angles
${\it\beta}_{01}$
is approximately proportional to the free-stream Mach number squared, we expect that the first two requirements are always fulfilled for sufficiently high Mach numbers (
$\mathit{Ma}_{0}\geqslant 2$
), see the textbook edited by Babinsky & Harvey (Reference Babinsky and Harvey2011). The generalised free interaction theory (requirement iii) is well confirmed for low and moderate Reynolds numbers (
$\mathit{Re}_{{\it\delta}_{0}}\leqslant 10^{5}$
), whereas for
$\mathit{Re}_{{\it\delta}_{0}}>10^{5}$
several studies report that the plateau pressure tends to become independent of the Reynolds number, see e.g. Zukoski (Reference Zukoski1967) and Delery & Marvin (Reference Delery and Marvin1986). Zukoski (Reference Zukoski1967) proposed a linear Mach number dependence for the plateau pressure,
$p_{p}/p_{0}=1+0.5\mathit{Ma}_{0}$
, which one could also use as input for the pressure deflection relation in (4.15). However, we believe that these experimental observations may equally well be due to roughness effects that lead to a levelling off of the friction coefficient once the viscous length scale approaches the wall-roughness height.
5. Application to SWBLI at Mach 3
5.1. Problem definition
In the case of strong interactions at higher Mach number, a very asymmetric intersection of incident and separation shock can be expected. For a Mach number of
$\mathit{Ma}_{0}=3$
, skin-friction coefficient
$C_{f,0}=2.1\times 10^{-3}$
upstream of the interaction and
$\widetilde{\mathscr{F}}_{p}=6.2$
, for example, the analytical model predicts a deflection across the separation shock of
${\it\vartheta}_{02}(\mathit{Ma}_{0},C_{f,0},\widetilde{\mathscr{F}}_{p})=15.48^{\circ }$
, cf. figure 21(a). Note that the value of
${\it\vartheta}_{02}$
theoretically is independent of the deflection
${\it\vartheta}_{01}$
across the incident shock wave, thus leading to an asymmetric intersection of
$C_{1}$
and
$C_{2}$
. The RR
$\leftrightarrow$
MR transition criteria for
$\mathit{Ma}_{0}=3$
can be read from figure 22. With
${\it\vartheta}_{02}=15.48^{\circ }$
we obtain
${\it\vartheta}^{D}=26.41^{\circ }$
for the detachment criterion and
${\it\vartheta}^{N}=23.74^{\circ }$
for the von Neumann criterion. Hence, transition from RSWBLI to ISWBLI is expected to occur at a wedge angle
${\it\vartheta}_{01}\gtrsim 23.74^{\circ }$
. If free-stream disturbances exceed a certain level, transition is most likely to take place at the von Neumann criterion, see for example Ivanov, Gimelshein & Markelov (Reference Ivanov, Gimelshein and Markelov1998), Ivanov et al. (Reference Ivanov, Vandromme, Fomin, Kudryavtsev, Hadjadj and Khotyanovsky2001), Kudryavtsev et al. (Reference Kudryavtsev, Khotyanovsky, Ivanov, Hadjadj and Vandromme2002), Ivanov et al. (Reference Ivanov, Kudryavtsev, Nikiforov, Pavlov and Shiplyuk2003) and Mouton & Hornung (Reference Mouton and Hornung2008). We assume that acoustic waves and fluctuations emitted by the incoming turbulent boundary layer may provide such high levels of disturbances.
To verify these analytical findings, we conducted LES at
$\mathit{Ma}_{0}=3$
and
$\mathit{Re}_{{\it\delta}_{imp}}\approx 8\times 10^{4}$
. The rectangular computational domain has the dimensions
$L_{x}\times L_{y}\times L_{z}=320{\it\delta}_{ref}\times 80{\it\delta}_{ref}\times 20{\it\delta}_{ref}$
and is discretised with
$N_{x}\times N_{y}\times N_{z}=1700\times 200\times 220$
cells, where
${\it\delta}_{ref}$
is the boundary-layer thickness at the domain inlet (
$\mathit{Re}_{ref}=22.8\times 10^{3}$
). As for the
$\mathit{Ma}_{0}=2$
case, the hyperbolic line bunching law (2.8) is used in the wall-normal direction, which yields a resolution of
${\rm\Delta}x^{+}\approx 35$
,
${\rm\Delta}y_{min}^{+}\approx 1.2$
and
${\rm\Delta}z^{+}\approx 18$
with a stretching factor of
${\it\beta}_{y}=3.39$
.
We consider two nominal wedge angles that correspond to conditions below the von Neumann criterion and within the dual-solution domain predicted by our analytical model for
$\mathit{Ma}_{0}=3.0$
,
$C_{f,0}=2.1\times 10^{-3}$
and
$\widetilde{\mathscr{F}}=6.2$
: the deflection across
$C_{1}$
is set to
${\it\vartheta}_{01}=22.5^{\circ }$
in
$\text{SWBLI}_{6}$
and to
${\it\vartheta}_{01}=24.5^{\circ }$
in
$\text{SWBLI}_{7}$
and
$\text{SWBLI}_{8}$
. The numerical experiments
$\text{SWBLI}_{7}$
and
$\text{SWBLI}_{8}$
differ in their initialisation procedure. While we jump-start
$\text{SWBLI}_{7}$
with an incident shock strength corresponding to
${\it\vartheta}_{01}=24.5^{\circ }$
,
$\text{SWBLI}_{8}$
is initialised with
${\it\vartheta}_{01}=0$
at
$t=t_{0}$
and then the deflection across the incident shock wave is continuously increased up to
${\it\vartheta}_{01}=24.5^{\circ }$
within 18.78 FTT. Total run times and the fraction used for the sampling of steady-state statistics are given in table 1. The geometry is defined in a same manner as for the cases
$\text{SWBLI}_{1{-}5}$
and fully determined by prescribing the deflection
${\it\vartheta}_{01}$
, the wedge width
$w$
and the channel height to wedge width ratio
$g^{+}$
. All relevant geometric parameters are listed in tables 1 and 2. As for the cases
$\text{SWBLI}_{1{-}5}$
, the PME does not interact with the incident shock wave
$C_{1}$
but limits the height of the Mach stem.
5.2. Results
To illustrate the overall wave configuration, figure 23 shows instantaneous snapshots of the interaction zone for the cases
$\text{SWBLI}_{6{-}8}$
.
$\text{SWBLI}_{6}$
, figure 23(a), shows a regular intersection between incident and separation shock. For the nominal deflection of
${\it\vartheta}_{01}=24.5^{\circ }$
across the incident shock we obtain both regular (
$\text{SWBLI}_{8}$
, figure 23
c) and irregular (
$\text{SWBLI}_{7}$
, figure 23
b) shock patterns. This confirms that the cases
$\text{SWBLI}_{7/8}$
lie within the dual-solution domain. The measured instantaneous shock angles
${\it\beta}_{01}$
and
${\it\beta}_{02}$
(values given in figure 23 are relative to the undisturbed outer flow) prove that the intersection is strongly asymmetric, as predicted by the analytical model.
Figure 23. Instantaneous density gradient magnitude for
$\text{SWBLI}_{6}$
(a),
$\text{SWBLI}_{7}$
(b),
$\text{SWBLI}_{8}$
(c) at
$\mathit{Ma}_{0}=3$
. Shock angles
${\it\beta}_{01}$
(a,
$40.5^{\circ }$
; b,
$42.8^{\circ }$
; c,
$42.8^{\circ }$
) and
${\it\beta}_{02}$
(a,
$32.5^{\circ }$
; b,
$31.7^{\circ }$
; c,
$34.3^{\circ }$
) are measured relative to the undisturbed outer flow (
${\it\vartheta}_{0}=0^{\circ }$
). (a) Regular SWBLI at
${\it\vartheta}_{01}=22.5^{\circ }$
, (b) irregular SWBLI at
${\it\vartheta}_{01}=24.5^{\circ }$
, (c) regular SWBLI at
${\it\vartheta}_{01}=24.5^{\circ }$
.
Figure 24(a) shows the time- and spanwise-averaged skin-friction distribution
$\langle C_{f}\rangle$
for cases
$\text{SWBLI}_{6{-}8}$
. At the beginning of the interaction
$x_{0}$
, we obtain a value of
$\langle C_{f}\rangle =2.095\times 10^{-3}$
for
$\text{SWBLI}_{6}$
and
$\langle C_{f}\rangle =2.179\times 10^{-3}$
for
$\text{SWBLI}_{7/8}$
. The Reynolds numbers based on the boundary-layer thickness
${\it\delta}_{0}$
at
$x_{0}$
are
$\mathit{Re}_{{\it\delta}_{0}}=62.4\times 10^{3}$
(
$\text{SWBLI}_{6}$
) and
$\mathit{Re}_{{\it\delta}_{0}}=56.1\times 10^{3}$
(
$\text{SWBLI}_{7/8}$
). Skin friction
$\langle C_{f}\rangle$
and pressure (not shown) evolution towards separation collapse for
$\text{SWBLI}_{7/8}$
. Downstream of the interaction we observe differences between the cases
$\text{SWBLI}_{7}$
and
$\text{SWBLI}_{8}$
as to be expected because the pressure jump associated with the reflected shock
$C_{4}$
and its streamwise position differ (compare figure 25). In figure 24(b) we plot the non-dimensional similarity functions
$\mathscr{F}$
, equation (4.9), and
$\widetilde{\mathscr{F}}$
, equation (4.10), for
$\text{SWBLI}_{4}$
(
$\mathit{Ma}_{0}=2$
) and
$\text{SWBLI}_{6}$
(
$\mathit{Ma}_{0}=3$
) in order to verify that the free interaction theory correlates the data at different Mach and Reynolds numbers. We observe that
$\widetilde{\mathscr{F}}$
, the generalised form of the free interaction theory (Carrière et al.
Reference Carrière, Sirieix and Solignac1969), correlates the data very well. It should be noted that the obtained plateau value
$\widetilde{\mathscr{F}}_{p}$
is slightly higher at
$\mathit{Ma}_{0}=3$
(
$\widetilde{\mathscr{F}}_{p}\approx 6.4$
) than at
$\mathit{Ma}_{0}=2$
(
$\widetilde{\mathscr{F}}_{p}\approx 6.2$
).
Figure 24. (a) Time-averaged skin-friction distribution
$\langle C_{f}\rangle$
for cases ——,
$\text{SWBLI}_{6}$
; - - - -,
$\text{SWBLI}_{7}$
;
$\cdots \cdots$
,
$\text{SWBLI}_{8}$
. (b) – ⋅ – ⋅ –,
$\mathscr{F}(s)$
according to (4.9) and ——,
$\widetilde{\mathscr{F}}(s)$
according to (4.10) for
$\text{SWBLI}_{4}$
(
$\mathit{Ma}_{0}=2.0$
,
$C_{f,0}=2.402\times 10^{-3}$
) and
$\text{SWBLI}_{6}$
(
$\mathit{Ma}_{0}=3.0$
,
$C_{f,0}=2.095\times 10^{-3}$
).
$s=(x-x_{0})/(x_{ref}-x_{0})$
with
$x_{ref}$
being the coordinate at which
$\mathscr{F}(s)$
and
$\widetilde{\mathscr{F}}(s)$
take the value 4.22.
The mean flow field (averaged in time and in the homogeneous spanwise direction) is visualised in figure 25. The mean density gradient magnitude is shown as grey–cyan flooding, and the sonic line is plotted in yellow. In contrast to the cases at lower Mach number, the flow downstream of the reflected shocks
$C_{3}$
and
$C_{4}$
is supersonic for
$\mathit{Ma}_{0}=3$
. For case
$\text{SWBLI}_{6}$
the measured shock angles for incident and separation shock are
$\langle {\it\beta}_{01}\rangle =40.5^{\circ }$
and
$\langle {\it\beta}_{02}\rangle =32.6^{\circ }$
. Note the identical separation shock angles for the cases
$\text{SWBLI}_{7/8}$
: for both cases we obtain
$\langle {\it\beta}_{01}\rangle =42.8^{\circ }$
and
$\langle {\it\beta}_{02}\rangle =33.4^{\circ }$
. As predicted by theory, the mean intersection is strongly asymmetric for all cases. The slightly higher separation shock angle (and therefore deflection angle) for
$\text{SWBLI}_{7/8}$
as compared to
$\text{SWBLI}_{6}$
follows the trend of an increasing shock strength with decreasing Reynolds number (or increasing
$C_{f,0}$
).
Within the available integration time of 76.82 FTT, no single event of an irregular shock reflection was observed for case
$\text{SWBLI}_{8}$
. We now analyse power spectral densities (PSD) of wall-pressure probes in order to quantify the captured number of low-frequency cycles (LFC) and to address unsteady aspects related to separation dynamics. Figure 26(a) shows the normalised wall-pressure signal
$p^{\prime }/\langle p\rangle$
at the reflected shock foot position. The pressure has been recorded at a mean sampling interval of
${\rm\Delta}t_{s}=7.1\times 10^{-3}{\it\delta}_{ref}/u_{\infty }$
. We discard the first 30.06 FTT of the simulation and perform a PSD analysis of the remaining timespan of 46.76 FTT, see figure 26(b). This leads to a maximum and minimum resolvable Strouhal number of
$St_{max}=70.42$
and
$St_{min}=3.34\times 10^{-5}$
based on
${\it\delta}_{ref}$
and
$u_{\infty }$
, see the upper abscissa of figure 26(b). The most energetic low-frequency signal has a Strouhal number of
$St_{l_{sep}}=0.098$
based on the separation length of
$l_{sep}=91.42{\it\delta}_{ref}$
; 16.08 of these low-frequency cycles are captured within the available integration time. The PSD spectrum also shows a second, less energetic low-frequency mode at
$St_{l_{sep}}=0.02$
. Both modes are associated with the separation-shock motion, for which typical values observed in experiments at lower deflection angles are in the range
$St_{l_{sep}}=0.02\dots 0.05$
, see Dussauge, Dupont & Debieve (Reference Dussauge, Dupont and Debieve2006).
Figure 25. Contours of the time- and spanwise-averaged density gradient magnitude at
$\mathit{Ma}_{0}=3$
for the cases
$\text{SWBLI}_{6}$
(
a
),
$\text{SWBLI}_{7}$
(b),
$\text{SWBLI}_{8}$
(c). Shock angles
${\it\beta}_{01}$
and
${\it\beta}_{02}$
are measured relative to the undisturbed outer flow (
${\it\vartheta}_{0}=0^{\circ }$
). (a) Regular SWBLI at
${\it\vartheta}_{01}=22.5^{\circ }$
, (b) irregular SWBLI at
${\it\vartheta}_{01}=24.5^{\circ }$
, (c) regular SWBLI at
${\it\vartheta}_{01}=24.5^{\circ }$
.
Figure 26. Fluctuating pressure signal evaluated at the reflected shock foot position and associated weighted PSD function for case
$\text{SWBLI}_{8}$
: (a) Wall-pressure signal, (b) weighted PSD. Note that, due to the boundary-layer growth, the Strouhal number based on the boundary-layer thickness at the inviscid impingement point is
$St_{{\it\delta}_{imp}}=3.5St$
.
Recalling figure 22, which shows the inviscid RR
$\leftrightarrow$
MR transition criteria at
$\mathit{Ma}_{0}=3$
, the LES results (symbols) agree very well with the analytically predicted values. The mean intersection of
$C_{1}$
and
$C_{2}$
for case
$\text{SWBLI}_{8}$
is clearly within the dual-solution domain. For the considered flow conditions and within the available integration time, fluctuations either caused by the TBL itself or by the low-frequency shock motion did not provide sufficiently strong disturbances to initiate transition from RSWBLI to ISWBLI. We therefore conclude that (i) within the dual-solution domain, transition is only triggered by those disturbances/events that lead to a shock intersection beyond the detachment criterion, and (ii) the startup procedure (of a supersonic inlet, e.g.) can provide such disturbances.
6. Summary and discussion
Well-resolved LES of the interaction of strong oblique shock waves with flat-plate turbulent boundary layers (SWBLI) were performed for five incident-shock deflection angles at
$\mathit{Ma}_{0}=2$
and Reynolds number
$\mathit{Re}_{{\it\delta}_{imp}}\approx 48\times 10^{3}$
and for two incident-shock deflection angles at
$\mathit{Ma}_{0}=3$
and
$\mathit{Re}_{{\it\delta}_{imp}}\approx 80\times 10^{3}$
. The computational setup was carefully designed with experimental feasibility in mind: properties of the considered turbulent boundary layers matched existing wind tunnel experiments; and the incident oblique shock waves were generated with a wedge. The chosen wedge width and distance from the flat plate ensured that the Prandtl–Meyer expansion emanating from the trailing edge of the wedge did not interfere with the incident shock wave for all deflection angles, but was sufficiently close to stabilise the interaction region by providing an integral length scale. The wedge angles were chosen such that both regular SWBLI and Mach reflection (irregular SWBLI) occurred.
For the SWBLI at a free-stream Mach number of
$\mathit{Ma}_{0}=2$
transition to a steady Mach reflection occurred at a nominal deflection of
${\it\vartheta}_{01}=13^{\circ }$
across the incident shock wave. However, we also observed transient bi-directional transition processes between regular and irregular SWBLI at a nominal deflection of
${\it\vartheta}_{01}=12.5^{\circ }$
. This indicates that perturbations related to the incoming turbulent boundary layer and the unsteady flow separation can trigger transition. We further corroborated this interpretation through a careful shock-polar analysis that takes into account the measured fluctuations. Note that this effect is different from the hysteresis process that Hornung et al. (Reference Hornung, Oertel and Sandeman1979) proposed for the dual-solution domain. For the considered perfect gas with
${\it\gamma}=1.4$
the critical Mach number above which a dual-solution domain exists is
$\mathit{Ma}_{0}=2.2$
.
On the basis of the observation that the mean shock strength of the separation shock appears to be decoupled from the incident shock wave, which is also experimentally well confirmed (e.g. Green Reference Green1970; Delery & Marvin Reference Delery and Marvin1986), we applied the free interaction theory to carefully analyse our numerical results. We found that only the generalised form of the free interaction theory (Carrière et al.
Reference Carrière, Sirieix and Solignac1969) correlates the wall-pressure rise towards separation for different Mach and Reynolds numbers. Our numerical data yield the value
$\widetilde{\mathscr{F}}_{p}=6.3\pm 0.1$
for the non-dimensional similarity function at the location that corresponds to the plateau pressure, which is in good agreement with the range found in the literature.
We then developed a simplified SWBLI model based on the generalised free interaction theory and classical gas-dynamics theories and derived SWBLI transition criteria: the plateau pressure ratio is iteratively computed from the free interaction theory (4.10)–(4.13), and the deflection across the reflected shock wave follows from the pressure deflection relation for an oblique shock wave (4.15). From the von Neumann and detachment criteria for asymmetric intersections applied to the incident shock and reflected shock, one finally obtains the critical incident shock deflection angles at which an irregular SWBLI pattern may (von Neumann condition) and must (detachment condition) occur.
The subsequent application to LES of an
$\mathit{Ma}_{0}=3$
turbulent boundary layer was very promising. As predicted by theory, the mean intersection of incident and separation shocks is strongly asymmetric. One of the chosen wedge angles (deflection
${\it\vartheta}_{01}=24.5^{\circ }$
across the incident shock) leads to a shock/shock interference within the dual-solution domain. For the considered flow conditions, neither free-stream perturbations emitted by the turbulent boundary layer nor the low-frequency dynamics of the shock-induced flow separation initiated transition from regular to irregular SWBLI. However, we found that the startup procedure can provide disturbances that cause transition to the irregular shock pattern during the initial transient. Once established, the irregular SWBLI remained stable for a wedge angle that is close to the calculated von Neumann condition and significantly below the detachment condition. This confirms that the dual-solution domain predicted by the inviscid theory actually exists in turbulent viscous flows.
We want to emphasise that the derived von Neumann condition represents a conservative estimate of the critical deflection across the incident shock at which an (undesirable) irregular SWBLI may occur. If one follows the arguments found in the literature, the generalised free interaction theory correlates experimental data very well at low and moderate Reynolds numbers, while at high Reynolds numbers the plateau pressure tends to become independent of the Reynolds number (see e.g. Zukoski Reference Zukoski1967; Delery & Marvin Reference Delery and Marvin1986). We believe that these observations may not mean a failure of free interaction theory but rather may be due to roughness effects that lead to a levelling off of the friction coefficient once the viscous length scale approaches the wall-roughness height. A larger uncertainty is the role of turbulent fluctuations and the low-frequency dynamics of the separation shock and separation bubble. Our LES results for
$\mathit{Ma}_{0}=2$
have shown that the transition process is highly transient and a representation by means of statistical averages is only half of the actual picture.
It is worth mentioning that the Mach reflection, and transition criteria in particular, were previously analysed mostly in an inviscid framework. SWBLI, on the other hand, was mainly studied at small deflection angles, where transition processes to an irregular interaction can be disregarded. For inviscid Mach reflections generated by double-wedge configurations, it is well known that the Mach stem can move upstream and ultimately out of the inlet (Li & Ben-Dor Reference Li and Ben-Dor1997). We observed the same process for irregular SWBLI if the wedge geometry does not support a stable Mach reflection through a trailing-edge PME (cf. Mouton & Hornung Reference Mouton and Hornung2007). If one considers typical Scramjet designs (X51-A, HyShot), for example, it becomes apparent that any assumption involving only the intersection of shocks within the outer flow is far from reality. We therefore believe that the derived transition criteria for the viscous SWBLI are useful for predicting the unstart of supersonic inlets and Scramjet engines.
Acknowledgements
We are especially grateful to V. Pasquariello for his hands-on support during the final stages of this project. We would like to thank M. Giglmaier, H. Hornung and S. Schmidt for inspiring discussions on gas dynamics and M. Vallikivi for valuable comments on a draft of this paper. S.H. acknowledges the German Research Foundation (Deutsche Forschungsgemeinschaft – DFG) for funding through the Collaborative Research Centre ‘Technological foundations for the design of thermally and mechanically highly loaded components of future space transportation systems’ (SFB TRR-40). Computational resources have been provided by the Leibniz Rechenzentrum München (LRZ).
