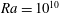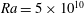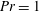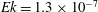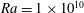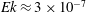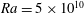1 Introduction
Natural convection is ubiquitous in Nature. It is found not only in the Earth’s interior and oceans, but also in planetary atmospheres and inside stars (Marshall & Schott Reference Marshall and Schott1999; Miesch Reference Miesch2000; Roberts & Glatzmaier Reference Roberts and Glatzmaier2000; Heimpel, Aurnou & Wicht Reference Heimpel, Aurnou and Wicht2005). In all of those flows, the background rotation induces a Coriolis force, which significantly affects the system, changing not only the flow phenomenology but in many cases also the heat transport and the amount of mixing of different species.
Rotating Rayleigh–Bénard (RB) convection, the flow between two rotating parallel plates heated from below and cooled from above, is commonly used as a model for studying rotating thermal convection. Rotating an RB system induces many changes. First, as found experimentally by Nakagawa & Frenzen (Reference Nakagawa and Frenzen1955) and demonstrated using linear stability analysis by Chandrasekhar (Reference Chandrasekhar1961), convective instability sets in at increasingly higher temperature differences when rotation is applied, or, in other words, the critical value of the Rayleigh number (the non-dimensionless temperature difference between the plates) rises as a function of the non-dimensional rotation rate, i.e. the inverse Ekman number. In experiments (Rossby Reference Rossby1969; Zhong, Ecke & Steinberg Reference Zhong, Ecke and Steinberg1993; Liu & Ecke Reference Liu and Ecke1997, Reference Liu and Ecke2009; King et al. Reference King, Stellmach, Noir, Hansen and Aurnou2009; Zhong et al. Reference Zhong, Stevens, Clercx, Verzicco, Lohse and Ahlers2009; Weiss et al. Reference Weiss, Stevens, Zhong, Clercx, Lohse and Ahlers2010; Zhong & Ahlers Reference Zhong and Ahlers2010; Kunnen et al. Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011; Weiss & Ahlers Reference Weiss and Ahlers2011a ,Reference Weiss and Ahlers b ; Ecke & Niemela Reference Ecke and Niemela2014; Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014; Cheng et al. Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015) and numerical simulations (Kunnen, Clercx & Geurts Reference Kunnen, Clercx and Geurts2006, Reference Kunnen, Clercx and Geurts2008a ; King et al. Reference King, Stellmach, Noir, Hansen and Aurnou2009; Zhong et al. Reference Zhong, Stevens, Clercx, Verzicco, Lohse and Ahlers2009; Schmitz & Tilgner Reference Schmitz and Tilgner2009, Reference Schmitz and Tilgner2010; Stevens, Clercx & Lohse Reference Stevens, Clercx and Lohse2010; Weiss et al. Reference Weiss, Stevens, Zhong, Clercx, Lohse and Ahlers2010; Horn & Shishkina Reference Horn and Shishkina2014; Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014; Cheng et al. Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015), when considering the dependence on rotation of the convective heat flux through the fluid layer, one can typically distinguish different regimes: (i) rotation is too weak to significantly alter the heat flux (‘rotation-unaffected’); (ii) rotation plays a role, and depending on the Prandtl number of the fluid, the heat flux may rise or fall with increasing rotation (‘rotation-affected’); and (iii) rotation is dominant, the principal force balance is the geostrophic balance (Greenspan Reference Greenspan1968), and the heat transfer is rapidly reduced as rotation increases (‘rotation-dominated’ or geostrophic regime). Based on estimates of the governing parameters for geophysical and astrophysical flow settings, these flows are expected to fall in the geostrophic regime of convection. By studying this regime, we aim to extend understanding of the aforementioned large-scale flows.
King et al. (Reference King, Stellmach, Noir, Hansen and Aurnou2009) performed the first comprehensive investigation into the transition between the rotation-affected and rotation-dominated (geostrophic) regimes. They argued, based on a large dataset of experimental and numerical results, that the transition happens when the kinetic boundary layer (of Ekman type; Greenspan Reference Greenspan1968) becomes smaller than the thermal boundary layer. Using numerical simulations with stress-free plates instead of the usual no-slip walls, they actually found a similar transition in the local scaling laws, however with different prefactors (King et al. Reference King, Stellmach, Noir, Hansen and Aurnou2009, supplement). This transition was later confirmed by the simulations of Schmitz & Tilgner (Reference Schmitz and Tilgner2009, Reference Schmitz and Tilgner2010).
Julien and coworkers took a different approach in order to be sure to study the geostrophic regime. In a series of articles (Sprague et al. Reference Sprague, Julien, Knobloch and Werne2006; Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012a ,Reference Julien, Rubio, Grooms and Knobloch b ; Rubio et al. Reference Rubio, Julien, Knobloch and Weiss2014), they derived a set of reduced equations representative of the limit of strong rotation (i.e. vanishing Rossby number) and described many properties of geostrophic convection. In particular, they identified different flow states. Just above onset, convection sets in with a cellular structure (also see e.g. Nakagawa & Frenzen Reference Nakagawa and Frenzen1955; Chandrasekhar Reference Chandrasekhar1961). Once the thermal forcing is increased, the flow becomes organised into columnar vortices covering the entire vertical extent of the domain, which are also referred to as convective Taylor columns (Sakai Reference Sakai1997; Sprague et al. Reference Sprague, Julien, Knobloch and Werne2006; Portegies et al. Reference Portegies, Kunnen, van Heijst and Molenaar2008; King et al. Reference King, Stellmach, Noir, Hansen and Aurnou2009; Grooms et al. Reference Grooms, Julien, Weiss and Knobloch2010; Kunnen, Clercx & Geurts Reference Kunnen, Clercx and Geurts2010a ; King & Aurnou Reference King and Aurnou2012). A remarkable characteristic feature of these structures is the sleeve of oppositely signed vorticity surrounding the vortical core. At even higher thermal forcing, the columns lose their vertical coherence. Instead, swirling plumes erupt vertically from the bottom and top boundary layers and do not cross the fluid layer entirely (Rossby Reference Rossby1969; Zhong et al. Reference Zhong, Ecke and Steinberg1993; Julien et al. Reference Julien, Legg, McWilliams and Werne1996; Kunnen et al. Reference Kunnen, Clercx and Geurts2006; King et al. Reference King, Stellmach, Noir, Hansen and Aurnou2009; Zhong et al. Reference Zhong, Stevens, Clercx, Verzicco, Lohse and Ahlers2009; Kunnen et al. Reference Kunnen, Clercx and Geurts2010a ). At the strongest thermal forcing, another state was observed, coined ‘geostrophic turbulence’, in which vertical coherence has vanished completely and a fluctuating field remains. Note that these four different flow states are all part of the rotation-dominated geostrophic regime. These flow structures have been reproduced in direct numerical simulations (DNS) of the full Navier–Stokes equations (Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014) and laboratory visualisations (Cheng et al. Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015). An intriguing feature of the geostrophic-turbulence state is the formation of an inverse energy cascade (Rubio et al. Reference Rubio, Julien, Knobloch and Weiss2014). In an inverse cascade, unlike the regular cascade of three-dimensional (3D) homogeneous isotropic turbulence, energy flows from the small length scales to larger ones. This leads to the formation of large-scale structures (the depth-independent barotropic mode (Rubio et al. Reference Rubio, Julien, Knobloch and Weiss2014)) that typically become comparable in size to the domain in which they reside. Such self-organisation and the inverse cascade have also been reported in recent DNS employing stress-free boundaries (Favier, Silvers & Proctor Reference Favier, Silvers and Proctor2014; Guervilly, Hughes & Jones Reference Guervilly, Hughes and Jones2014; Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014).
The difficulty of achieving the geostrophic regime is twofold. Both a high rotation rate and a significant level of thermal driving, to remain turbulent even with respect to the increased critical Rayleigh number, are needed to achieve the geostrophic regime. Most earlier experimental and numerical studies of rotating RB flow (Rossby Reference Rossby1969; Zhong et al.
Reference Zhong, Ecke and Steinberg1993; Julien et al.
Reference Julien, Legg, McWilliams and Werne1996; Liu & Ecke Reference Liu and Ecke1997; Vorobieff & Ecke Reference Vorobieff and Ecke2002; Kunnen et al.
Reference Kunnen, Clercx and Geurts2008a
; Kunnen, Clercx & Geurts Reference Kunnen, Clercx and Geurts2008b
; King et al.
Reference King, Stellmach, Noir, Hansen and Aurnou2009; Liu & Ecke Reference Liu and Ecke2009; Zhong et al.
Reference Zhong, Stevens, Clercx, Verzicco, Lohse and Ahlers2009; Schmitz & Tilgner Reference Schmitz and Tilgner2009, Reference Schmitz and Tilgner2010; Kunnen, Geurts & Clercx Reference Kunnen, Geurts and Clercx2010b
; Stevens et al.
Reference Stevens, Clercx and Lohse2010; Weiss et al.
Reference Weiss, Stevens, Zhong, Clercx, Lohse and Ahlers2010; Zhong & Ahlers Reference Zhong and Ahlers2010; Kunnen et al.
Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011; Liu & Ecke Reference Liu and Ecke2011; Weiss & Ahlers Reference Weiss and Ahlers2011a
,Reference Weiss and Ahlers
b
; Stevens, Clercx & Lohse Reference Stevens, Clercx and Lohse2012; Kunnen, Corre & Clercx Reference Kunnen, Corre and Clercx2013; Horn & Shishkina Reference Horn and Shishkina2014) – and see Stevens, Clercx & Lohse (Reference Stevens, Clercx and Lohse2013a
) for a recent review – have not conclusively ventured deep into the geostrophic regime, so that any scaling ranges in the geostrophic regime are rather narrow. Recent experiments (Ecke & Niemela Reference Ecke and Niemela2014; Cheng et al.
Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015) and DNS (Stellmach et al.
Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014), capable of simultaneously achieving very high Rayleigh numbers
![]() $Ra\gtrsim 10^{9}$
and very low Ekman numbers
$Ra\gtrsim 10^{9}$
and very low Ekman numbers
![]() $Ek\lesssim 10^{-6}$
, have found the transitions in the scaling laws for the heat transfer reported previously over a wider parameter range and could achieve wider scaling ranges in the geostrophic regime.
$Ek\lesssim 10^{-6}$
, have found the transitions in the scaling laws for the heat transfer reported previously over a wider parameter range and could achieve wider scaling ranges in the geostrophic regime.
The geostrophic regime is a natural extension of the weakly nonlinear theories developed for rotating convection near onset (Veronis Reference Veronis1968; Clune & Knobloch Reference Clune and Knobloch1993; Bassom & Zhang Reference Bassom and Zhang1994; Dawes Reference Dawes2001; Ecke Reference Ecke2015). A remarkable prediction of the theory is that, for strong enough rotation, the flow becomes independent of the boundary conditions (no-slip or stress-free; Niiler & Bisshopp Reference Niiler and Bisshopp1965; Heard & Veronis Reference Heard and Veronis1971; Clune & Knobloch Reference Clune and Knobloch1993; Dawes Reference Dawes2001). This result has been challenged recently (Stellmach et al.
Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014, and the current work). In terms of heat transfer, the weakly nonlinear theory (Bassom & Zhang Reference Bassom and Zhang1994; Dawes Reference Dawes2001) predicts a dependence
![]() $Nu=2{\it\epsilon}$
of the Nusselt number
$Nu=2{\it\epsilon}$
of the Nusselt number
![]() $Nu$
(dimensionless convective heat transfer) on the normalised distance from onset,
$Nu$
(dimensionless convective heat transfer) on the normalised distance from onset,
![]() ${\it\epsilon}=Ra/Ra_{c}-1$
, where
${\it\epsilon}=Ra/Ra_{c}-1$
, where
![]() $Ra_{c}$
is the critical Rayleigh number. This prediction matches nicely with the results near onset from the asymptotic equations (Julien et al.
Reference Julien, Knobloch, Rubio and Vasil2012a
) and, by extension, of the stress-free DNS (Stellmach et al.
Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014). Ecke (Reference Ecke2015) argues that also the no-slip DNS results of Stellmach et al. (Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014) are consistent with weakly nonlinear theory.
$Ra_{c}$
is the critical Rayleigh number. This prediction matches nicely with the results near onset from the asymptotic equations (Julien et al.
Reference Julien, Knobloch, Rubio and Vasil2012a
) and, by extension, of the stress-free DNS (Stellmach et al.
Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014). Ecke (Reference Ecke2015) argues that also the no-slip DNS results of Stellmach et al. (Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014) are consistent with weakly nonlinear theory.
However, a complete picture of what is happening during the transition to the geostrophic regime, and where it takes place in the parameter space, is still missing. In this paper we present numerical simulations covering the transition to geostrophic convective turbulence using the full Navier–Stokes equations for a single Prandtl number. We analyse in detail the effects of the choice of boundary conditions, i.e. including or omitting the Ekman layers. In § 2 we describe the numerical method and give the parameter values for the runs. The results for the convective heat transfer are presented in § 3. In § 4 we consider the effects of rotation on the boundary-layer scales and on the volumetric distribution of kinetic energy and thermal variance dissipation, an approach that has allowed for the Grossmann–Lohse theory of heat transfer in non-rotating RB flow (Grossmann & Lohse Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2001, Reference Grossmann and Lohse2004; Stevens et al. Reference Stevens, van der Poel, Grossmann and Lohse2013b ). The flow phenomenology and its relation with the spectral energy transfer is considered in § 5. We conclude with an interpretation and discussion of these findings in § 6.
2 Simulation details
We have conducted a set of DNS of 3D rotating RB in a horizontally periodic Cartesian computational box. By using a second-order energy-conserving, finite-difference code with fractional time stepping (Verzicco & Orlandi Reference Verzicco and Orlandi1996), we march in time the Navier–Stokes equations plus an advection–diffusion equation for temperature, with the usual Boussinesq approximations (Chandrasekhar Reference Chandrasekhar1961):
with the incompressibility constraint
Here
![]() $\boldsymbol{u}$
is the velocity vector;
$\boldsymbol{u}$
is the velocity vector;
![]() $t$
is time;
$t$
is time;
![]() $\boldsymbol{e}_{z}$
is the unit vector in the vertical direction;
$\boldsymbol{e}_{z}$
is the unit vector in the vertical direction;
![]() $Ra$
is the Rayleigh number, i.e. the non-dimensional temperature difference, defined as
$Ra$
is the Rayleigh number, i.e. the non-dimensional temperature difference, defined as
![]() $Ra=g{\it\beta}{\it\Delta}L^{3}/({\it\nu}{\it\kappa})$
, with
$Ra=g{\it\beta}{\it\Delta}L^{3}/({\it\nu}{\it\kappa})$
, with
![]() $L$
the height of the system,
$L$
the height of the system,
![]() ${\it\beta}$
the thermal expansion coefficient of the fluid,
${\it\beta}$
the thermal expansion coefficient of the fluid,
![]() $g$
the gravitational acceleration,
$g$
the gravitational acceleration,
![]() ${\it\Delta}$
the temperature difference between the bottom and top plates, and
${\it\Delta}$
the temperature difference between the bottom and top plates, and
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() ${\it\kappa}$
the kinematic viscosity and thermal diffusivity of the fluid, respectively;
${\it\kappa}$
the kinematic viscosity and thermal diffusivity of the fluid, respectively;
![]() $Ro$
is the Rossby number, i.e. the inverse rotation rate, defined as
$Ro$
is the Rossby number, i.e. the inverse rotation rate, defined as
![]() $Ro=\sqrt{({\it\beta}g{\it\Delta}/L)}/(2{\it\Omega})$
, with
$Ro=\sqrt{({\it\beta}g{\it\Delta}/L)}/(2{\it\Omega})$
, with
![]() ${\it\Omega}$
the angular rotation rate;
${\it\Omega}$
the angular rotation rate;
![]() $Pr$
is the Prandtl number of the fluid,
$Pr$
is the Prandtl number of the fluid,
![]() $Pr={\it\nu}/{\it\kappa}$
; and
$Pr={\it\nu}/{\it\kappa}$
; and
![]() ${\it\theta}$
is the non-dimensional temperature. Equations (2.1)–(2.3) are non-dimensionalised by using
${\it\theta}$
is the non-dimensional temperature. Equations (2.1)–(2.3) are non-dimensionalised by using
![]() $L$
,
$L$
,
![]() ${\it\Delta}$
and the so-called free-fall velocity scale
${\it\Delta}$
and the so-called free-fall velocity scale
![]() $U=\sqrt{{\it\beta}g{\it\Delta}L}$
. Note that centrifugal buoyancy is neglected here; this means that we are implicitly making the customary assumption that the Froude number
$U=\sqrt{{\it\beta}g{\it\Delta}L}$
. Note that centrifugal buoyancy is neglected here; this means that we are implicitly making the customary assumption that the Froude number
![]() $Fr={\it\Omega}^{2}R/g\ll 1$
(Stevens et al.
Reference Stevens, Clercx and Lohse2013a
), where
$Fr={\it\Omega}^{2}R/g\ll 1$
(Stevens et al.
Reference Stevens, Clercx and Lohse2013a
), where
![]() $R$
is the horizontal distance to the rotation axis, i.e. the radius of the cylinder in most experiments and simulations. We also define the Nusselt number, i.e. the non-dimensional heat transfer, as
$R$
is the horizontal distance to the rotation axis, i.e. the radius of the cylinder in most experiments and simulations. We also define the Nusselt number, i.e. the non-dimensional heat transfer, as
![]() $Nu=(\langle u_{z}{\it\theta}\rangle _{A,t}-{\it\kappa}\partial \langle {\it\theta}\rangle _{A,t})/({\it\kappa}{\it\Delta}L^{-1})$
, with
$Nu=(\langle u_{z}{\it\theta}\rangle _{A,t}-{\it\kappa}\partial \langle {\it\theta}\rangle _{A,t})/({\it\kappa}{\it\Delta}L^{-1})$
, with
![]() $\langle \cdots \rangle _{A,t}$
representing the averaging operator in time and also spatially over a horizontal plane.
$\langle \cdots \rangle _{A,t}$
representing the averaging operator in time and also spatially over a horizontal plane.
The explored parameter values are given in table 1. We vary the rotation rate
![]() $Ro$
at a constant thermal driving
$Ro$
at a constant thermal driving
![]() $Ra$
for two values of
$Ra$
for two values of
![]() $Ra$
, while fixing the Prandtl number to
$Ra$
, while fixing the Prandtl number to
![]() $Pr=1$
. The Ekman number, defined as
$Pr=1$
. The Ekman number, defined as
![]() $Ek={\it\nu}/(2{\it\Omega}L^{2})=Ro\sqrt{Pr/Ra}$
, is small enough to enter into the geostrophic regime, as can be seen from table 1. For completeness, we also define the Taylor number
$Ek={\it\nu}/(2{\it\Omega}L^{2})=Ro\sqrt{Pr/Ra}$
, is small enough to enter into the geostrophic regime, as can be seen from table 1. For completeness, we also define the Taylor number
![]() $Ta=Ek^{-2}$
. The aspect ratio,
$Ta=Ek^{-2}$
. The aspect ratio,
![]() ${\it\Gamma}=D/L$
, where
${\it\Gamma}=D/L$
, where
![]() $D$
is the simulation box periodicity length in the horizontal directions, is set to 10 times the most unstable wavelength for convective instability,
$D$
is the simulation box periodicity length in the horizontal directions, is set to 10 times the most unstable wavelength for convective instability,
![]() $L_{c}$
, i.e.
$L_{c}$
, i.e.
![]() ${\it\Gamma}=10L_{c}$
. Wavelength
${\it\Gamma}=10L_{c}$
. Wavelength
![]() $L_{c}$
scales asymptotically as
$L_{c}$
scales asymptotically as
![]() $L_{c}=4.82Ek^{1/3}$
, with minor corrections at finite
$L_{c}=4.82Ek^{1/3}$
, with minor corrections at finite
![]() $Ek$
(Chandrasekhar Reference Chandrasekhar1961; Niiler & Bisshopp Reference Niiler and Bisshopp1965; Heard & Veronis Reference Heard and Veronis1971). Here, we just take
$Ek$
(Chandrasekhar Reference Chandrasekhar1961; Niiler & Bisshopp Reference Niiler and Bisshopp1965; Heard & Veronis Reference Heard and Veronis1971). Here, we just take
![]() ${\it\Gamma}=48.2Ek^{1/3}$
. The boundary conditions for temperature are fixed as
${\it\Gamma}=48.2Ek^{1/3}$
. The boundary conditions for temperature are fixed as
![]() ${\it\theta}=1$
at the bottom plate and
${\it\theta}=1$
at the bottom plate and
![]() ${\it\theta}=0$
at the top plate. For velocity, we employ both no-slip (NS) boundary conditions, i.e.
${\it\theta}=0$
at the top plate. For velocity, we employ both no-slip (NS) boundary conditions, i.e.
![]() $\boldsymbol{u}=\mathbf{0}$
at both plates, and stress-free (SF) boundary conditions, i.e.
$\boldsymbol{u}=\mathbf{0}$
at both plates, and stress-free (SF) boundary conditions, i.e.
![]() $\partial _{z}u_{x}=\partial _{z}u_{y}=0$
and
$\partial _{z}u_{x}=\partial _{z}u_{y}=0$
and
![]() $u_{z}=0$
at the plates.
$u_{z}=0$
at the plates.
Table 1. Parameter values for the computations. For all runs,
![]() $Pr=1$
. Each parameter set has been run with both NS and SF boundary conditions. Included are: Rayleigh number
$Pr=1$
. Each parameter set has been run with both NS and SF boundary conditions. Included are: Rayleigh number
![]() $Ra$
, Ekman number
$Ra$
, Ekman number
![]() $Ek$
, Rossby number
$Ek$
, Rossby number
![]() $Ro$
,
$Ro$
,
![]() $\widetilde{Ra}=Ra\,Ek^{4/3}$
(Sprague et al.
Reference Sprague, Julien, Knobloch and Werne2006), domain aspect ratio
$\widetilde{Ra}=Ra\,Ek^{4/3}$
(Sprague et al.
Reference Sprague, Julien, Knobloch and Werne2006), domain aspect ratio
![]() ${\it\Gamma}=D/L$
(ratio of horizontal periodicity length
${\it\Gamma}=D/L$
(ratio of horizontal periodicity length
![]() $D$
to domain height
$D$
to domain height
![]() $L$
) and number of grid points
$L$
) and number of grid points
![]() $N_{x}\times N_{y}\times N_{z}$
in the periodic directions and the vertical direction, respectively. We also list the resulting Nusselt numbers
$N_{x}\times N_{y}\times N_{z}$
in the periodic directions and the vertical direction, respectively. We also list the resulting Nusselt numbers
![]() $Nu_{SF}$
and
$Nu_{SF}$
and
![]() $Nu_{NS}$
, as well as the number of grid points
$Nu_{NS}$
, as well as the number of grid points
![]() $N({\it\delta}_{{\it\nu}})$
within the kinetic boundary layer in the NS runs (see also § 4.1). Typical time step sizes are
$N({\it\delta}_{{\it\nu}})$
within the kinetic boundary layer in the NS runs (see also § 4.1). Typical time step sizes are
![]() $0.004$
and
$0.004$
and
![]() $0.002$
for
$0.002$
for
![]() $Ra=1\times 10^{10}$
and
$Ra=1\times 10^{10}$
and
![]() $5\times 10^{10}$
, respectively, expressed in convective time units
$5\times 10^{10}$
, respectively, expressed in convective time units
![]() $H/U$
.
$H/U$
.

The grid is uniformly discretised in the horizontal direction. In the vertical direction, a clipped Chebyshev distribution is used to cluster points near the boundary layers. While the resulting boundary-layer thicknesses will be presented in § 4.1, we comment here on the adequacy of the near-wall resolution. The number of grid points found within the kinetic boundary layer is reported in the last column of table 1. The most demanding simulation at
![]() $Ra=5\times 10^{10}$
and
$Ra=5\times 10^{10}$
and
![]() $Ek=1.34\times 10^{-7}$
has 12 grid points within the kinetic boundary layer; the same is true for the case
$Ek=1.34\times 10^{-7}$
has 12 grid points within the kinetic boundary layer; the same is true for the case
![]() $Ra=1\times 10^{10}$
and
$Ra=1\times 10^{10}$
and
![]() $Ek=4.00\times 10^{-7}$
. Higher Ekman numbers result in larger boundary-layer thicknesses and thus they are better resolved. The grid resolutions used here are in line with recent computations by Stellmach et al. (Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014), and thus we consider them to be adequate.
$Ek=4.00\times 10^{-7}$
. Higher Ekman numbers result in larger boundary-layer thicknesses and thus they are better resolved. The grid resolutions used here are in line with recent computations by Stellmach et al. (Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014), and thus we consider them to be adequate.
For statistical convergence, the simulations are run until the temperature gradient at both plates is equal to less than
![]() $1\,\%$
, and the temporal convergence error of the Nusselt number measured through a volume average is smaller than
$1\,\%$
, and the temporal convergence error of the Nusselt number measured through a volume average is smaller than
![]() $2\,\%$
. In practice, this means running the simulations between 100 and 200 convective time units, which are defined using the system height
$2\,\%$
. In practice, this means running the simulations between 100 and 200 convective time units, which are defined using the system height
![]() $L$
and the free-fall velocity
$L$
and the free-fall velocity
![]() $U$
. The total time varies: the lower
$U$
. The total time varies: the lower
![]() $Ek$
, the slower the convergence of statistics.
$Ek$
, the slower the convergence of statistics.
We tested the dependence on
![]() ${\it\Gamma}$
of the simulations by running two cases at
${\it\Gamma}$
of the simulations by running two cases at
![]() $Ra=1\times 10^{10}$
and
$Ra=1\times 10^{10}$
and
![]() $Ro=0.04$
with a twice larger
$Ro=0.04$
with a twice larger
![]() ${\it\Gamma}$
(thus increasing the computational box size by a factor four, and hence the computational load by at least that amount). The Nusselt number is the same for no-slip plates but shows some difference in the stress-free case. For no-slip plates, we do not expect a strong dependence on
${\it\Gamma}$
(thus increasing the computational box size by a factor four, and hence the computational load by at least that amount). The Nusselt number is the same for no-slip plates but shows some difference in the stress-free case. For no-slip plates, we do not expect a strong dependence on
![]() ${\it\Gamma}$
as long as it is large enough. However, for stress-free plates, differences may occur that are related to the flow structure. This will be addressed in more detail in § 5.
${\it\Gamma}$
as long as it is large enough. However, for stress-free plates, differences may occur that are related to the flow structure. This will be addressed in more detail in § 5.

Figure 1. Phase diagram of rotating convection (a) in the
![]() $(Ek,Ra/Ra_{c})$
parameter space, as suggested by Ecke & Niemela (Reference Ecke and Niemela2014), and (b) in the
$(Ek,Ra/Ra_{c})$
parameter space, as suggested by Ecke & Niemela (Reference Ecke and Niemela2014), and (b) in the
![]() $(Ta,Ra)$
parameter space (Vorobieff & Ecke Reference Vorobieff and Ecke2002). The blue circles indicate the parameter values for which we have performed simulations using both no-slip (NS) and stress-free (SF) boundary conditions. The circles are either open for
$(Ta,Ra)$
parameter space (Vorobieff & Ecke Reference Vorobieff and Ecke2002). The blue circles indicate the parameter values for which we have performed simulations using both no-slip (NS) and stress-free (SF) boundary conditions. The circles are either open for
![]() $Ra=1\times 10^{10}$
or filled for
$Ra=1\times 10^{10}$
or filled for
![]() $Ra=5\times 10^{10}$
. Three different regimes of convection can be discerned: non-rotating convection, rotation-affected convection and (rotation-dominated) geostrophic convection. The lines display various relations suggested in the literature that bound the regimes. Ecke & Niemela (Reference Ecke and Niemela2014) suggested
$Ra=5\times 10^{10}$
. Three different regimes of convection can be discerned: non-rotating convection, rotation-affected convection and (rotation-dominated) geostrophic convection. The lines display various relations suggested in the literature that bound the regimes. Ecke & Niemela (Reference Ecke and Niemela2014) suggested
![]() $Ra/Ra_{c}=3$
as a lower bound of the geostrophic regime (dotted black line),
$Ra/Ra_{c}=3$
as a lower bound of the geostrophic regime (dotted black line),
![]() $Ra=0.25Ek^{-1.8}$
for the transition between the geostrophic and rotation-affected regimes (solid black line), and
$Ra=0.25Ek^{-1.8}$
for the transition between the geostrophic and rotation-affected regimes (solid black line), and
![]() $Ro=0.35$
for the transition to the non-rotating regime (dashed black line). The dash-dotted black line is a transition valid for higher
$Ro=0.35$
for the transition to the non-rotating regime (dashed black line). The dash-dotted black line is a transition valid for higher
![]() $Pr\approx 6$
(Ecke & Niemela Reference Ecke and Niemela2014). Two alternative predictions for the transition to the geostrophic regime are also displayed: upper grey dashed line,
$Pr\approx 6$
(Ecke & Niemela Reference Ecke and Niemela2014). Two alternative predictions for the transition to the geostrophic regime are also displayed: upper grey dashed line,
![]() $Ra=1.4Ek^{-7/4}$
(King et al.
Reference King, Stellmach, Noir, Hansen and Aurnou2009); and lower grey dashed line,
$Ra=1.4Ek^{-7/4}$
(King et al.
Reference King, Stellmach, Noir, Hansen and Aurnou2009); and lower grey dashed line,
![]() $Ra\approx 10Ek^{-3/2}$
(King, Stellmach & Aurnou Reference King, Stellmach and Aurnou2012).
$Ra\approx 10Ek^{-3/2}$
(King, Stellmach & Aurnou Reference King, Stellmach and Aurnou2012).
To indicate how the current simulations fit in with the previous work on this topic, we display our current parameter values in the (
![]() $Ek,Ra/Ra_{c}$
) phase diagram of figure 1, where
$Ek,Ra/Ra_{c}$
) phase diagram of figure 1, where
![]() $Ra_{c}$
is the critical Rayleigh number for the onset of the convective instability with rotation, i.e.
$Ra_{c}$
is the critical Rayleigh number for the onset of the convective instability with rotation, i.e.
![]() $Ra_{c}=8.7Ek^{-4/3}$
(Chandrasekhar Reference Chandrasekhar1961), and in the (
$Ra_{c}=8.7Ek^{-4/3}$
(Chandrasekhar Reference Chandrasekhar1961), and in the (
![]() $Ta,Ra$
) phase diagram. Figure 1(a) is based on figure 4 of Ecke & Niemela (Reference Ecke and Niemela2014), and shows how the parameter values of the simulations in this paper are positioned relative to some of the proposed bounds on the geostrophic regime. Typically, a lower bound for the geostrophic regime is chosen such that the resulting flow is supercritical enough for a turbulent flow to develop. We follow Ecke & Niemela (Reference Ecke and Niemela2014) by choosing
$Ta,Ra$
) phase diagram. Figure 1(a) is based on figure 4 of Ecke & Niemela (Reference Ecke and Niemela2014), and shows how the parameter values of the simulations in this paper are positioned relative to some of the proposed bounds on the geostrophic regime. Typically, a lower bound for the geostrophic regime is chosen such that the resulting flow is supercritical enough for a turbulent flow to develop. We follow Ecke & Niemela (Reference Ecke and Niemela2014) by choosing
![]() $Ra/Ra_{c}=3$
(dotted black line in figure 1). Ecke & Niemela (Reference Ecke and Niemela2014) discern two additional transitions based on their heat-transfer measurements in cryogenic helium with
$Ra/Ra_{c}=3$
(dotted black line in figure 1). Ecke & Niemela (Reference Ecke and Niemela2014) discern two additional transitions based on their heat-transfer measurements in cryogenic helium with
![]() $Pr=0.7$
. When reducing the Rayleigh number at constant
$Pr=0.7$
. When reducing the Rayleigh number at constant
![]() $Ek$
, the first transition seen is when rotation starts to reduce the heat transfer. This is well described by
$Ek$
, the first transition seen is when rotation starts to reduce the heat transfer. This is well described by
![]() $Ro=0.35$
(dashed black line in figure 1). When
$Ro=0.35$
(dashed black line in figure 1). When
![]() $Ra$
is reduced even further, a transition to a steeper scaling law relating
$Ra$
is reduced even further, a transition to a steeper scaling law relating
![]() $Nu$
and
$Nu$
and
![]() $Ra$
was found. Ecke & Niemela (Reference Ecke and Niemela2014) interpreted this as the transition to the geostrophic regime. This transition was best described by the relation
$Ra$
was found. Ecke & Niemela (Reference Ecke and Niemela2014) interpreted this as the transition to the geostrophic regime. This transition was best described by the relation
![]() $Ra=0.25Ek^{-1.8}$
(solid black line in figure 1) according to their data. For completeness, two other suggested relations for the transfer to the geostrophic regime have also been included in figure 1:
$Ra=0.25Ek^{-1.8}$
(solid black line in figure 1) according to their data. For completeness, two other suggested relations for the transfer to the geostrophic regime have also been included in figure 1:
![]() $Ra=1.4Ek^{-7/4}$
as suggested by King et al. (Reference King, Stellmach, Noir, Hansen and Aurnou2009) (upper grey dashed line) and
$Ra=1.4Ek^{-7/4}$
as suggested by King et al. (Reference King, Stellmach, Noir, Hansen and Aurnou2009) (upper grey dashed line) and
![]() $Ra\approx 10Ek^{-3/2}$
from King et al. (Reference King, Stellmach and Aurnou2012) (lower grey dashed line). From the diagram, we expect our simulations to show a transition from the rotation-affected to the geostrophic regime for all criteria, except the one suggested by King et al. (Reference King, Stellmach, Noir, Hansen and Aurnou2009).
$Ra\approx 10Ek^{-3/2}$
from King et al. (Reference King, Stellmach and Aurnou2012) (lower grey dashed line). From the diagram, we expect our simulations to show a transition from the rotation-affected to the geostrophic regime for all criteria, except the one suggested by King et al. (Reference King, Stellmach, Noir, Hansen and Aurnou2009).
3 Heat transfer
In this section, we investigate the convective heat transfer through the fluid layer as a function of the applied control parameters. In the geostrophic regime, no consensus has been reached on the heat-transfer dependence
![]() $Nu(Ra,Pr,Ek)$
, in particular because it is challenging to achieve the extreme parameter values for
$Nu(Ra,Pr,Ek)$
, in particular because it is challenging to achieve the extreme parameter values for
![]() $Ra$
and
$Ra$
and
![]() $Ek$
in both experiments and simulations. We summarise the results from the literature reported earlier in table 2, and indicate the method (experimental, numerical or from theory) and range of parameters considered. It must be emphasised that most of these works are outside of the geostrophic regime; the exceptions are the theories by King et al. (Reference King, Stellmach and Aurnou2012) and Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a
), as well as the numerical simulations by the latter authors, which consider the asymptotically reduced equations for rapid rotation.
$Ek$
in both experiments and simulations. We summarise the results from the literature reported earlier in table 2, and indicate the method (experimental, numerical or from theory) and range of parameters considered. It must be emphasised that most of these works are outside of the geostrophic regime; the exceptions are the theories by King et al. (Reference King, Stellmach and Aurnou2012) and Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a
), as well as the numerical simulations by the latter authors, which consider the asymptotically reduced equations for rapid rotation.
Table 2. Proposed and observed scaling laws for the heat transfer in rotation-dominated convection found in the literature, expressed as
![]() $Nu(Ra,Ek)$
. The Prandtl number dependence has been omitted, as it is out of the scope for the present paper. We also mention the range of parameters for which the scalings are intended or observed, as well as the method by which the scalings have been obtained (‘exp.’ for experiments, ‘num.’ for numerical simulations and ‘theor.’ for scaling arguments). Finally, the boundary conditions for the numerical studies are mentioned. These are the topic of the current work. The simulations by Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a
) are based on the asymptotic equations and employ what amounts to stress-free boundary conditions. Note that Schmitz & Tilgner (Reference Schmitz and Tilgner2009, Reference Schmitz and Tilgner2010) have defined the Ekman number without the factor
$Nu(Ra,Ek)$
. The Prandtl number dependence has been omitted, as it is out of the scope for the present paper. We also mention the range of parameters for which the scalings are intended or observed, as well as the method by which the scalings have been obtained (‘exp.’ for experiments, ‘num.’ for numerical simulations and ‘theor.’ for scaling arguments). Finally, the boundary conditions for the numerical studies are mentioned. These are the topic of the current work. The simulations by Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a
) are based on the asymptotic equations and employ what amounts to stress-free boundary conditions. Note that Schmitz & Tilgner (Reference Schmitz and Tilgner2009, Reference Schmitz and Tilgner2010) have defined the Ekman number without the factor
![]() $2$
, hence the different parameter values in this table compared to their papers.
$2$
, hence the different parameter values in this table compared to their papers.

The two recent experimental investigations that enter into the geostrophic regime show quite different results. Ecke & Niemela (Reference Ecke and Niemela2014) achieved
![]() $4\times 10^{9}<Ra<4\times 10^{11}$
and
$4\times 10^{9}<Ra<4\times 10^{11}$
and
![]() $2\times 10^{-7}<Ek<3\times 10^{-5}$
at
$2\times 10^{-7}<Ek<3\times 10^{-5}$
at
![]() $Pr=0.7$
used cryogenic helium gas as the working fluid. Their data could be described as
$Pr=0.7$
used cryogenic helium gas as the working fluid. Their data could be described as
![]() $Nu\sim (Ra/Ra_{c})^{{\it\gamma}}$
, with
$Nu\sim (Ra/Ra_{c})^{{\it\gamma}}$
, with
![]() ${\it\gamma}\approx 1$
using direct measurement or
${\it\gamma}\approx 1$
using direct measurement or
![]() $1.2<{\it\gamma}<1.6$
after rescaling of the original data following existing theoretical arguments. The scaling ranges were not extensive enough to decisively discern between these scalings. On the other hand, Cheng et al. (Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015) employed water as the working fluid. In their tall, slender cell, they could achieve
$1.2<{\it\gamma}<1.6$
after rescaling of the original data following existing theoretical arguments. The scaling ranges were not extensive enough to decisively discern between these scalings. On the other hand, Cheng et al. (Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015) employed water as the working fluid. In their tall, slender cell, they could achieve
![]() $1\times 10^{10}<Ra<1\times 10^{13}$
and
$1\times 10^{10}<Ra<1\times 10^{13}$
and
![]() $2\times 10^{-8}<Ek<2\times 10^{-6}$
for
$2\times 10^{-8}<Ek<2\times 10^{-6}$
for
![]() $3.5<Pr<6.5$
. They also reported scaling as
$3.5<Pr<6.5$
. They also reported scaling as
![]() $Nu\sim (Ra/Ra_{c})^{{\it\gamma}}$
, with a monotonically increasing
$Nu\sim (Ra/Ra_{c})^{{\it\gamma}}$
, with a monotonically increasing
![]() ${\it\gamma}$
from
${\it\gamma}$
from
![]() $1.8$
at
$1.8$
at
![]() $Ek=10^{-3}$
to
$Ek=10^{-3}$
to
![]() $3.6$
at
$3.6$
at
![]() $Ek=10^{-7}$
, based on a combination of experimental and DNS results.
$Ek=10^{-7}$
, based on a combination of experimental and DNS results.
Figure 2 shows
![]() $Nu$
as a function of
$Nu$
as a function of
![]() $Ek$
obtained from the present simulations. By simple observation, it is clear that the boundary conditions (NS or SF) play a decisive role, even in the slope of the graph, i.e. the exponent
$Ek$
obtained from the present simulations. By simple observation, it is clear that the boundary conditions (NS or SF) play a decisive role, even in the slope of the graph, i.e. the exponent
![]() ${\it\alpha}$
of the local scaling law
${\it\alpha}$
of the local scaling law
![]() $Nu\sim Ek^{{\it\alpha}}$
. Both NS and SF boundary conditions display a transition in the scaling law (indicated with arrows in the graph) at
$Nu\sim Ek^{{\it\alpha}}$
. Both NS and SF boundary conditions display a transition in the scaling law (indicated with arrows in the graph) at
![]() $Ek\approx 9\times 10^{-7}$
for
$Ek\approx 9\times 10^{-7}$
for
![]() $Ra=1\times 10^{10}$
and at
$Ra=1\times 10^{10}$
and at
![]() $Ek\approx 3\times 10^{-7}$
for
$Ek\approx 3\times 10^{-7}$
for
![]() $Ra=5\times 10^{10}$
, as evidenced by the slope change. This transition is generally considered the boundary between rotation-affected and rotation-dominated convection (Ecke & Niemela Reference Ecke and Niemela2014). At Ekman numbers below the transition, we observe distinctly different scalings with
$Ra=5\times 10^{10}$
, as evidenced by the slope change. This transition is generally considered the boundary between rotation-affected and rotation-dominated convection (Ecke & Niemela Reference Ecke and Niemela2014). At Ekman numbers below the transition, we observe distinctly different scalings with
![]() $Ek$
. The SF exponents (
$Ek$
. The SF exponents (
![]() ${\it\alpha}=2.04$
for
${\it\alpha}=2.04$
for
![]() $Ra=1\times 10^{10}$
and
$Ra=1\times 10^{10}$
and
![]() ${\it\alpha}=2.21$
for
${\it\alpha}=2.21$
for
![]() $Ra=5\times 10^{10}$
) match fairly well (especially for the lower
$Ra=5\times 10^{10}$
) match fairly well (especially for the lower
![]() $Ra$
case) with the theoretically predicted exponent
$Ra$
case) with the theoretically predicted exponent
![]() ${\it\alpha}=2$
of Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a
), found to be valid for simulations of the reduced equations, with boundary conditions that can be described as stress-free.
${\it\alpha}=2$
of Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a
), found to be valid for simulations of the reduced equations, with boundary conditions that can be described as stress-free.
However, the NS runs reveal effective exponents
![]() ${\it\alpha}=1.07$
for
${\it\alpha}=1.07$
for
![]() $Ra=1\times 10^{10}$
and
$Ra=1\times 10^{10}$
and
![]() ${\it\alpha}=1.36$
for
${\it\alpha}=1.36$
for
![]() $Ra=5\times 10^{10}$
, considerably lower than the SF runs and pronouncedly lower than the correlations inferred by King et al. (Reference King, Stellmach and Aurnou2012), which predict
$Ra=5\times 10^{10}$
, considerably lower than the SF runs and pronouncedly lower than the correlations inferred by King et al. (Reference King, Stellmach and Aurnou2012), which predict
![]() ${\it\alpha}=4$
for NS plates. Schmitz & Tilgner (Reference Schmitz and Tilgner2009, Reference Schmitz and Tilgner2010) have reported simulations with both NS and SF boundaries; they reported good agreement with the exponent
${\it\alpha}=4$
for NS plates. Schmitz & Tilgner (Reference Schmitz and Tilgner2009, Reference Schmitz and Tilgner2010) have reported simulations with both NS and SF boundaries; they reported good agreement with the exponent
![]() $1.5$
, in fair agreement with the current NS runs (at least at
$1.5$
, in fair agreement with the current NS runs (at least at
![]() $Ra=5\times 10^{10}$
), but somewhat low for SF. The experiments by Ecke & Niemela (Reference Ecke and Niemela2014) have provided approximate scaling exponents between
$Ra=5\times 10^{10}$
), but somewhat low for SF. The experiments by Ecke & Niemela (Reference Ecke and Niemela2014) have provided approximate scaling exponents between
![]() $1.6$
and
$1.6$
and
![]() $2.1$
, depending on the exact plotting convention to attain data collapse.
$2.1$
, depending on the exact plotting convention to attain data collapse.
It is worth noting that there is quite a difference in the applied
![]() $Ra$
between the various works. Typically, values of
$Ra$
between the various works. Typically, values of
![]() $Ra$
up to
$Ra$
up to
![]() $5\times 10^{9}$
are applied in experiments and simulations (King et al.
Reference King, Stellmach, Noir, Hansen and Aurnou2009; Schmitz & Tilgner Reference Schmitz and Tilgner2009, Reference Schmitz and Tilgner2010; King et al.
Reference King, Stellmach and Aurnou2012; King, Stellmach & Buffett Reference King, Stellmach and Buffett2013), while only recently higher values have been attained – cf. simulations by Stellmach et al. (Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014), experiments by Ecke & Niemela (Reference Ecke and Niemela2014) and Cheng et al. (Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015), as well as the current simulations. It is plausible that what we observe is a new scaling regime opening up at such high
$5\times 10^{9}$
are applied in experiments and simulations (King et al.
Reference King, Stellmach, Noir, Hansen and Aurnou2009; Schmitz & Tilgner Reference Schmitz and Tilgner2009, Reference Schmitz and Tilgner2010; King et al.
Reference King, Stellmach and Aurnou2012; King, Stellmach & Buffett Reference King, Stellmach and Buffett2013), while only recently higher values have been attained – cf. simulations by Stellmach et al. (Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014), experiments by Ecke & Niemela (Reference Ecke and Niemela2014) and Cheng et al. (Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015), as well as the current simulations. It is plausible that what we observe is a new scaling regime opening up at such high
![]() $Ra$
, strongly affected by rapid rotation (very low
$Ra$
, strongly affected by rapid rotation (very low
![]() $Ek\sim O(10^{-7})$
) but still vigorously turbulent (highly supercritical, i.e.
$Ek\sim O(10^{-7})$
) but still vigorously turbulent (highly supercritical, i.e.
![]() $Ra/Ra_{c}\gg 1$
), i.e. the geostrophic regime.
$Ra/Ra_{c}\gg 1$
), i.e. the geostrophic regime.

Figure 2. Heat transfer (Nusselt number
![]() $Nu$
) as a function of the Ekman number
$Nu$
) as a function of the Ekman number
![]() $Ek$
: (a) SF plates; (b) NS plates. Open symbols are for
$Ek$
: (a) SF plates; (b) NS plates. Open symbols are for
![]() $Ra=1\times 10^{10}$
; filled symbols for
$Ra=1\times 10^{10}$
; filled symbols for
![]() $Ra=5\times 10^{10}$
. The dashed lines depict fitted power-law slopes. The arrows indicate the transition points as we inferred them from these graphs.
$Ra=5\times 10^{10}$
. The dashed lines depict fitted power-law slopes. The arrows indicate the transition points as we inferred them from these graphs.
To further quantify the scaling laws, we show in figure 3 the compensated Nusselt number with the two scaling laws proposed by both King et al. (Reference King, Stellmach and Aurnou2012) and Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a
). Again, we can see that the
![]() $Nu\sim Ek^{2}$
(Julien et al.
Reference Julien, Knobloch, Rubio and Vasil2012a
) captures well the Ekman-number dependence of the free-slip simulations below the transition, but the no-slip simulations present a very different dependence. The
$Nu\sim Ek^{2}$
(Julien et al.
Reference Julien, Knobloch, Rubio and Vasil2012a
) captures well the Ekman-number dependence of the free-slip simulations below the transition, but the no-slip simulations present a very different dependence. The
![]() $Nu\sim Ek^{4}$
scaling law (King et al.
Reference King, Stellmach and Aurnou2012) can be seen to be a clear overestimate of the scaling exponent relating
$Nu\sim Ek^{4}$
scaling law (King et al.
Reference King, Stellmach and Aurnou2012) can be seen to be a clear overestimate of the scaling exponent relating
![]() $Nu$
and
$Nu$
and
![]() $Ek$
.
$Ek$
.

Figure 3. Compensated heat transfer (Nusselt number
![]() $Nu$
) as a function of the Ekman number
$Nu$
) as a function of the Ekman number
![]() $Ek$
using the proposed scaling laws: (a)
$Ek$
using the proposed scaling laws: (a)
![]() $Nu\sim Ra^{3}Ek^{4}$
(King et al.
Reference King, Stellmach and Aurnou2012) and (b)
$Nu\sim Ra^{3}Ek^{4}$
(King et al.
Reference King, Stellmach and Aurnou2012) and (b)
![]() $Nu\sim Ra^{3/2}Ek^{2}$
(Julien et al.
Reference Julien, Knobloch, Rubio and Vasil2012a
). Open symbols are for
$Nu\sim Ra^{3/2}Ek^{2}$
(Julien et al.
Reference Julien, Knobloch, Rubio and Vasil2012a
). Open symbols are for
![]() $Ra=1\times 10^{10}$
; filled symbols for
$Ra=1\times 10^{10}$
; filled symbols for
![]() $Ra=5\times 10^{10}$
. The red squares represent no-slip boundary conditions, and blue circles free-slip boundary conditions.
$Ra=5\times 10^{10}$
. The red squares represent no-slip boundary conditions, and blue circles free-slip boundary conditions.
Another striking feature of this graph is that, at the same
![]() $Ra$
, there is a range for which
$Ra$
, there is a range for which
![]() $Nu$
is lower for SF than for NS boundaries (Stellmach et al.
Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014). Generally, NS boundaries are expected to reduce the turbulence intensity of the flow by introducing more friction than SF plates. However, the active nature of the Ekman boundaries, present for NS but absent for SF, can affect the dynamics of the entire fluid layer, enhancing the heat transfer instead of reducing it. We will revisit these results in later sections, where further differences between NS and SF runs are revealed and interpreted.
$Nu$
is lower for SF than for NS boundaries (Stellmach et al.
Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014). Generally, NS boundaries are expected to reduce the turbulence intensity of the flow by introducing more friction than SF plates. However, the active nature of the Ekman boundaries, present for NS but absent for SF, can affect the dynamics of the entire fluid layer, enhancing the heat transfer instead of reducing it. We will revisit these results in later sections, where further differences between NS and SF runs are revealed and interpreted.
4 Boundary-layer and bulk dissipation
For RB convection, one can derive from the Navier–Stokes equations with the Boussinesq approximation exact relations for the total dissipation of turbulent kinetic energy and thermal variance within the domain (Shraiman & Siggia Reference Shraiman and Siggia1990). The energy equations are obtained by taking the inner product of
![]() $\boldsymbol{u}$
with (2.1) and multiplying (2.2) with
$\boldsymbol{u}$
with (2.1) and multiplying (2.2) with
![]() ${\it\theta}$
, respectively. After applying the boundary conditions, the dissipation relations in dimensional form read
${\it\theta}$
, respectively. After applying the boundary conditions, the dissipation relations in dimensional form read
where
![]() ${\it\epsilon}_{u}$
is the (time- and volume-averaged) total dissipation of turbulent kinetic energy in the fluid layer and
${\it\epsilon}_{u}$
is the (time- and volume-averaged) total dissipation of turbulent kinetic energy in the fluid layer and
![]() ${\it\epsilon}_{{\it\theta}}$
is the total dissipation of thermal variance in the layer. These relations do not change when rotation is added: rotation only enters in the momentum equation (2.1), where we find for the Coriolis term in the energy equation that
${\it\epsilon}_{{\it\theta}}$
is the total dissipation of thermal variance in the layer. These relations do not change when rotation is added: rotation only enters in the momentum equation (2.1), where we find for the Coriolis term in the energy equation that
![]() $\boldsymbol{u}\boldsymbol{\cdot }(\boldsymbol{e}_{z}\times \boldsymbol{u})=0$
.
$\boldsymbol{u}\boldsymbol{\cdot }(\boldsymbol{e}_{z}\times \boldsymbol{u})=0$
.
The Grossmann–Lohse heat-transfer theory for non-rotating convection (see Ahlers, Grossmann & Lohse (Reference Ahlers, Grossmann and Lohse2009) for an overview) is based on a division of the total dissipations into bulk and boundary-layer (BL) contributions. Several scaling regimes can be found depending on the dominance of dissipation in either bulk or BL regions, for both
![]() ${\it\epsilon}_{u}$
and
${\it\epsilon}_{u}$
and
![]() ${\it\epsilon}_{{\it\theta}}$
. The theoretical arguments by Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a
) employ such a division for
${\it\epsilon}_{{\it\theta}}$
. The theoretical arguments by Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a
) employ such a division for
![]() ${\it\epsilon}_{{\it\theta}}$
(no division of
${\it\epsilon}_{{\it\theta}}$
(no division of
![]() ${\it\epsilon}_{u}$
given that in their SF case no kinetic BLs are formed) and show that the bulk limits the overall heat transfer in the geostrophic-turbulence state of the rotation-dominated geostrophic regime.
${\it\epsilon}_{u}$
given that in their SF case no kinetic BLs are formed) and show that the bulk limits the overall heat transfer in the geostrophic-turbulence state of the rotation-dominated geostrophic regime.
4.1 Boundary-layer scales
In this section we want to compare the distribution of dissipation for both NS and SF plates. To this end, we first need to discern between BL and bulk. Several BL scales have already been introduced in the RB literature. The thickness of the thermal BLs in the non-rotating case is well described by assuming that the bulk is isothermal, and that the temperature drop is fully accommodated by the BLs. This leads to the definition
![]() ${\it\delta}_{{\it\theta},Nu}/L=1/(2Nu)$
. This relation is not appropriate for rotating RB convection, given that a mean temperature drop across the bulk is sustained (Julien et al.
Reference Julien, Legg, McWilliams and Werne1996). We therefore rely on the common definition of BL thicknesses in turbulence that uses the position of the peak value of the root mean square of temperature fluctuations, denoted by
${\it\delta}_{{\it\theta},Nu}/L=1/(2Nu)$
. This relation is not appropriate for rotating RB convection, given that a mean temperature drop across the bulk is sustained (Julien et al.
Reference Julien, Legg, McWilliams and Werne1996). We therefore rely on the common definition of BL thicknesses in turbulence that uses the position of the peak value of the root mean square of temperature fluctuations, denoted by
![]() ${\it\delta}_{{\it\theta}}$
. Julien et al. (Reference Julien, Rubio, Grooms and Knobloch2012b
) found this definition to be the most appropriate one. For the kinetic (velocity) BLs we use the positions of the peak root mean square of horizontal velocities, marked
${\it\delta}_{{\it\theta}}$
. Julien et al. (Reference Julien, Rubio, Grooms and Knobloch2012b
) found this definition to be the most appropriate one. For the kinetic (velocity) BLs we use the positions of the peak root mean square of horizontal velocities, marked
![]() ${\it\delta}_{{\it\nu}}$
.
${\it\delta}_{{\it\nu}}$
.

Figure 4. Boundary-layer thicknesses and their dependence on
![]() $Ek$
: (a) SF plates, thermal BL thickness (
$Ek$
: (a) SF plates, thermal BL thickness (
![]() ${\it\delta}_{{\it\theta}}$
); (b) NS plates, thermal BL thickness (
${\it\delta}_{{\it\theta}}$
); (b) NS plates, thermal BL thickness (
![]() ${\it\delta}_{{\it\theta}}$
, red squares) and kinetic BL thickness (
${\it\delta}_{{\it\theta}}$
, red squares) and kinetic BL thickness (
![]() ${\it\delta}_{{\it\nu}}$
, black triangles). The arrows indicate the transition points as inferred from these graphs, when the steeply decreasing
${\it\delta}_{{\it\nu}}$
, black triangles). The arrows indicate the transition points as inferred from these graphs, when the steeply decreasing
![]() ${\it\delta}_{{\it\theta}}$
begins to flatten out. A power-law fit
${\it\delta}_{{\it\theta}}$
begins to flatten out. A power-law fit
![]() ${\it\delta}_{{\it\nu}}/L=4.0Ek^{0.51}$
is also included (black dashed line). In both panels, open symbols are for
${\it\delta}_{{\it\nu}}/L=4.0Ek^{0.51}$
is also included (black dashed line). In both panels, open symbols are for
![]() $Ra=1\times 10^{10}$
, and filled symbols for
$Ra=1\times 10^{10}$
, and filled symbols for
![]() $Ra=5\times 10^{10}$
.
$Ra=5\times 10^{10}$
.
A comparison of these BL scales is presented in figure 4. Starting from the kinetic BLs (black symbols), it is clear that they follow a single scaling, independent of
![]() $Ra$
, i.e. their thickness is exclusively determined by
$Ra$
, i.e. their thickness is exclusively determined by
![]() $Ek$
. A power law yields the relation
$Ek$
. A power law yields the relation
![]() ${\it\delta}_{{\it\nu}}/L=4.0Ek^{0.51}$
. Within error, the slope is consistent with the prediction
${\it\delta}_{{\it\nu}}/L=4.0Ek^{0.51}$
. Within error, the slope is consistent with the prediction
![]() ${\it\delta}_{{\it\nu}}\sim Ek^{1/2}$
for linear Ekman BLs (Greenspan Reference Greenspan1968). It is worth noting that this scaling also matches nicely with the BL scaling laws reported by Kunnen et al. (Reference Kunnen, Geurts and Clercx2010b
), even though the geometry (cylinder instead of periodic cube) and the Prandtl number (
${\it\delta}_{{\it\nu}}\sim Ek^{1/2}$
for linear Ekman BLs (Greenspan Reference Greenspan1968). It is worth noting that this scaling also matches nicely with the BL scaling laws reported by Kunnen et al. (Reference Kunnen, Geurts and Clercx2010b
), even though the geometry (cylinder instead of periodic cube) and the Prandtl number (
![]() $Pr=6.4$
instead of
$Pr=6.4$
instead of
![]() $Pr=1$
) are completely different.
$Pr=1$
) are completely different.
On the other hand, the thermal BL thicknesses do reveal some variation with
![]() $Ek$
. Before the transition, the thermal BL thickness steeply decreases when
$Ek$
. Before the transition, the thermal BL thickness steeply decreases when
![]() $Ek$
is increased, in contrast to the kinetic BLs. In that
$Ek$
is increased, in contrast to the kinetic BLs. In that
![]() $Ek$
range, the local scaling laws relating
$Ek$
range, the local scaling laws relating
![]() $Nu$
and
$Nu$
and
![]() $Ek$
are steeper for SF than for NS. King et al. (Reference King, Stellmach, Noir, Hansen and Aurnou2009) and King et al. (Reference King, Stellmach and Aurnou2012) proposed that the transition to the rotation-dominated heat-flux scaling is described by the crossing of the kinetic and thermal BL thicknesses, which happens around
$Ek$
are steeper for SF than for NS. King et al. (Reference King, Stellmach, Noir, Hansen and Aurnou2009) and King et al. (Reference King, Stellmach and Aurnou2012) proposed that the transition to the rotation-dominated heat-flux scaling is described by the crossing of the kinetic and thermal BL thicknesses, which happens around
![]() $Ek=7\times 10^{-7}$
for NS and
$Ek=7\times 10^{-7}$
for NS and
![]() $Ra=5\times 10^{10}$
in this case. However, the slope change in the scaling laws (figure 2) is found at lower values of
$Ra=5\times 10^{10}$
in this case. However, the slope change in the scaling laws (figure 2) is found at lower values of
![]() $Ek$
. For
$Ek$
. For
![]() $Ra=1\times 10^{10}$
a similar mismatch is observed.
$Ra=1\times 10^{10}$
a similar mismatch is observed.
A more natural definition of the transition, based on the BL scales as plotted in figure 4, would be the evident slope change of
![]() ${\it\delta}_{{\it\theta}}$
at
${\it\delta}_{{\it\theta}}$
at
![]() $Ek=8\times 10^{-7}$
for
$Ek=8\times 10^{-7}$
for
![]() $Ra=1\times 10^{10}$
and at
$Ra=1\times 10^{10}$
and at
![]() $Ek=3\times 10^{-7}$
for
$Ek=3\times 10^{-7}$
for
![]() $Ra=5\times 10^{10}$
, which remarkably occurs around the same
$Ra=5\times 10^{10}$
, which remarkably occurs around the same
![]() $Ek$
value for both NS and SF. This transition value matches better with the slope change in the heat-transfer statistics, even if they do not exactly coincide. The transition to the geostrophic regime thus appears to be gradual; different statistics display a change in behaviour at different values of
$Ek$
value for both NS and SF. This transition value matches better with the slope change in the heat-transfer statistics, even if they do not exactly coincide. The transition to the geostrophic regime thus appears to be gradual; different statistics display a change in behaviour at different values of
![]() $Ek$
.
$Ek$
.

Figure 5. Distribution of dissipations
![]() ${\it\epsilon}_{{\it\theta}}$
and
${\it\epsilon}_{{\it\theta}}$
and
![]() ${\it\epsilon}_{u}$
between bulk and BL: (a) SF plates,
${\it\epsilon}_{u}$
between bulk and BL: (a) SF plates,
![]() ${\it\epsilon}_{{\it\theta}}$
; (b) NS plates,
${\it\epsilon}_{{\it\theta}}$
; (b) NS plates,
![]() ${\it\epsilon}_{{\it\theta}}$
(red squares) and
${\it\epsilon}_{{\it\theta}}$
(red squares) and
![]() ${\it\epsilon}_{u}$
(black triangles). The fraction of total dissipation located in the BL region is displayed. Open symbols are for
${\it\epsilon}_{u}$
(black triangles). The fraction of total dissipation located in the BL region is displayed. Open symbols are for
![]() $Ra=1\times 10^{10}$
; filled symbols for
$Ra=1\times 10^{10}$
; filled symbols for
![]() $Ra=5\times 10^{10}$
. The arrows indicate the transition points as we inferred them from these graphs.
$Ra=5\times 10^{10}$
. The arrows indicate the transition points as we inferred them from these graphs.
4.2 Distribution of dissipation
Using the BL scales of § 4.1, we can now assess how the total dissipation is distributed between BL and bulk regions. This is shown in figure 5, which confirms the picture that, under rapid rotation, the dissipation is mostly concentrated in the bulk. This is the case even more for
![]() ${\it\epsilon}_{u}$
than for
${\it\epsilon}_{u}$
than for
![]() ${\it\epsilon}_{{\it\theta}}$
. However, we also note that the fraction of
${\it\epsilon}_{{\it\theta}}$
. However, we also note that the fraction of
![]() ${\it\epsilon}_{{\it\theta}}$
in the BLs appears to start growing when
${\it\epsilon}_{{\it\theta}}$
in the BLs appears to start growing when
![]() $Ek$
is reduced below
$Ek$
is reduced below
![]() ${\sim}\,5\times 10^{-7}$
(
${\sim}\,5\times 10^{-7}$
(
![]() ${\sim}\,2\times 10^{-7}$
) for
${\sim}\,2\times 10^{-7}$
) for
![]() $Ra=1\times 10^{10}$
(
$Ra=1\times 10^{10}$
(
![]() $5\times 10^{10}$
), with an earlier growth appearing for SF than for NS. Looking back to figure 4, it is obvious that the thermal BLs are expanding when
$5\times 10^{10}$
), with an earlier growth appearing for SF than for NS. Looking back to figure 4, it is obvious that the thermal BLs are expanding when
![]() $Ek$
is reduced. The larger part of the volume inside the thermal BLs along with a persistent input of thermal fluctuations from the Ekman BLs enhances the BL fraction of
$Ek$
is reduced. The larger part of the volume inside the thermal BLs along with a persistent input of thermal fluctuations from the Ekman BLs enhances the BL fraction of
![]() ${\it\epsilon}_{{\it\theta}}$
at the lowest considered
${\it\epsilon}_{{\it\theta}}$
at the lowest considered
![]() $Ek$
under NS conditions. For SF plates the thermal BLs are growing even more as
$Ek$
under NS conditions. For SF plates the thermal BLs are growing even more as
![]() $Ek$
is reduced; the increased volume of the BLs appears to be enough for a higher fraction of
$Ek$
is reduced; the increased volume of the BLs appears to be enough for a higher fraction of
![]() ${\it\epsilon}_{{\it\theta}}$
there.
${\it\epsilon}_{{\it\theta}}$
there.
Furthermore, the contribution of the kinetic BLs to the total
![]() ${\it\epsilon}_{u}$
is remarkable: for
${\it\epsilon}_{u}$
is remarkable: for
![]() $Ra=5\times 10^{10}$
, between
$Ra=5\times 10^{10}$
, between
![]() $Ek=1.3\times 10^{-7}$
and
$Ek=1.3\times 10^{-7}$
and
![]() $Ek=5\times 10^{-7}$
the BL thickness changes by a factor
$Ek=5\times 10^{-7}$
the BL thickness changes by a factor
![]() $2$
, yet the fraction of
$2$
, yet the fraction of
![]() ${\it\epsilon}_{u}$
in the BL remains roughly constant. This confirms that the Ekman BLs, first thought to become passive at low enough
${\it\epsilon}_{u}$
in the BL remains roughly constant. This confirms that the Ekman BLs, first thought to become passive at low enough
![]() $Ek$
(Niiler & Bisshopp Reference Niiler and Bisshopp1965; Heard & Veronis Reference Heard and Veronis1971; Julien & Knobloch Reference Julien and Knobloch1998), are still significantly affecting the flow dynamics (Stellmach et al.
Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014).
$Ek$
(Niiler & Bisshopp Reference Niiler and Bisshopp1965; Heard & Veronis Reference Heard and Veronis1971; Julien & Knobloch Reference Julien and Knobloch1998), are still significantly affecting the flow dynamics (Stellmach et al.
Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014).

Figure 6. Snapshot at mid-height (
![]() $z=0.5$
) of the vertical vorticity from runs at
$z=0.5$
) of the vertical vorticity from runs at
![]() $Ra=5\times 10^{10}$
and
$Ra=5\times 10^{10}$
and
![]() $Ek=1.34\times 10^{-7}$
: (a) SF plates; (b) NS plates. Red is positive (cyclonic) vorticity, while blue is negative (anticyclonic) vorticity. Both plots have the same colour scale.
$Ek=1.34\times 10^{-7}$
: (a) SF plates; (b) NS plates. Red is positive (cyclonic) vorticity, while blue is negative (anticyclonic) vorticity. Both plots have the same colour scale.
5 Flow phenomenology
A remarkable phenomenological change upon entering the geostrophic-turbulence state of the rotation-dominated geostrophic regime is the disappearance of convective Taylor columns and plumes as a result of a loss of vertical coherence (Sprague et al.
Reference Sprague, Julien, Knobloch and Werne2006; Julien et al.
Reference Julien, Rubio, Grooms and Knobloch2012b
; Stellmach et al.
Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014). These vortical structures have been frequently reported ever since the first observation in turbulent rotating RB flow by Rossby (Reference Rossby1969). In the geostrophic-turbulence state, however, such coherent structures seem to be absent. The boundary conditions largely determine the flow phenomenology. For SF plates, large barotropic vortices can be formed under the influence of an inverse energy cascade (Favier et al.
Reference Favier, Silvers and Proctor2014; Guervilly et al.
Reference Guervilly, Hughes and Jones2014; Rubio et al.
Reference Rubio, Julien, Knobloch and Weiss2014; Stellmach et al.
Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014), eventually growing to the scale of the domain. For NS plates, such a condensate is not formed. We compare the phenomenology in two snapshots shown in figure 6, which depict the spatial distribution of vertical vorticity
![]() ${\it\omega}_{z}=\partial _{x}u_{y}-\partial _{y}u_{x}$
in a horizontal cross-section at mid-height. Figure 6(a) clearly reveals the formation of a large cyclonic vortex in the top right, while the bottom-right part and its periodic continuation on opposite sides hint at the formation of an anticyclonic vortex. Note that this flow is still slowly evolving over time (Favier et al.
Reference Favier, Silvers and Proctor2014; Guervilly et al.
Reference Guervilly, Hughes and Jones2014; Rubio et al.
Reference Rubio, Julien, Knobloch and Weiss2014). Figure 6(b) shows no condensate vortices. Instead, a fluctuating state is found without large-scale long-lived coherent structure. Ekman pumping, present only in the case of NS boundary conditions, can thus be a source of small-scale fluctuations that prevent condensation into large-scale vortices.
${\it\omega}_{z}=\partial _{x}u_{y}-\partial _{y}u_{x}$
in a horizontal cross-section at mid-height. Figure 6(a) clearly reveals the formation of a large cyclonic vortex in the top right, while the bottom-right part and its periodic continuation on opposite sides hint at the formation of an anticyclonic vortex. Note that this flow is still slowly evolving over time (Favier et al.
Reference Favier, Silvers and Proctor2014; Guervilly et al.
Reference Guervilly, Hughes and Jones2014; Rubio et al.
Reference Rubio, Julien, Knobloch and Weiss2014). Figure 6(b) shows no condensate vortices. Instead, a fluctuating state is found without large-scale long-lived coherent structure. Ekman pumping, present only in the case of NS boundary conditions, can thus be a source of small-scale fluctuations that prevent condensation into large-scale vortices.
5.1 Relation with spectral energy transfer
In previous works (Favier et al. Reference Favier, Silvers and Proctor2014; Rubio et al. Reference Rubio, Julien, Knobloch and Weiss2014), the energy transfer as a function of wavenumber has been considered to indicate the presence of an inverse energy cascade. Given that figure 6 reveals such a significant difference in flow phenomenology between SF and NS, we anticipate that the spectral energy transfer must also be considerably different. Following Favier et al. (Reference Favier, Silvers and Proctor2014), we define the spectral energy equation as
which gives the temporal evolution of the energy
![]() $E(K)$
as a function of horizontal wavenumber
$E(K)$
as a function of horizontal wavenumber
![]() $K$
in terms of the energy transfer
$K$
in terms of the energy transfer
![]() $T(Q,K)$
from wavenumber shell
$T(Q,K)$
from wavenumber shell
![]() $Q$
to shell
$Q$
to shell
![]() $K$
, the dissipation
$K$
, the dissipation
![]() $D(K)$
and the buoyant forcing
$D(K)$
and the buoyant forcing
![]() $F(K)$
. We are particularly interested in the transfer term
$F(K)$
. We are particularly interested in the transfer term
![]() $T(Q,K)$
, which we evaluate and average vertically over the entire computational domain minus the BLs. We note that this quantity is antisymmetric by definition, i.e.
$T(Q,K)$
, which we evaluate and average vertically over the entire computational domain minus the BLs. We note that this quantity is antisymmetric by definition, i.e.
![]() $T(K_{1},K_{2})=-T(K_{2},K_{1})$
and
$T(K_{1},K_{2})=-T(K_{2},K_{1})$
and
![]() $T(K_{1},K_{1})=0$
for any two wavenumbers
$T(K_{1},K_{1})=0$
for any two wavenumbers
![]() $K_{1}$
and
$K_{1}$
and
![]() $K_{2}$
.
$K_{2}$
.

Figure 7. Spectral energy transfer
![]() $T(Q,K)$
between wavenumber shells
$T(Q,K)$
between wavenumber shells
![]() $Q$
and
$Q$
and
![]() $K$
: (a) for SF and (b) for NS. Positive values indicate that energy is taken from shell
$K$
: (a) for SF and (b) for NS. Positive values indicate that energy is taken from shell
![]() $Q$
and transferred to shell
$Q$
and transferred to shell
![]() $K$
; negative values imply that
$K$
; negative values imply that
![]() $Q$
receives energy from
$Q$
receives energy from
![]() $K$
. Both plots have the same colour scale.
$K$
. Both plots have the same colour scale.
The spectral transfer at
![]() $Ra=5\times 10^{10}$
and
$Ra=5\times 10^{10}$
and
![]() $Ek=1.34\times 10^{-7}$
is depicted in figure 7, for both SF and NS conditions. We note that we are only showing the first 30 modes, of a total of 256 in the simulation, so the dispersive errors of finite-difference schemes are negligible in this range. The SF picture compares favourably to the earlier studies by Favier et al. (Reference Favier, Silvers and Proctor2014) and Rubio et al. (Reference Rubio, Julien, Knobloch and Weiss2014): a strong localised exchange of energy between neighbouring wavenumbers across the diagonal, i.e. a certain mode
$Ek=1.34\times 10^{-7}$
is depicted in figure 7, for both SF and NS conditions. We note that we are only showing the first 30 modes, of a total of 256 in the simulation, so the dispersive errors of finite-difference schemes are negligible in this range. The SF picture compares favourably to the earlier studies by Favier et al. (Reference Favier, Silvers and Proctor2014) and Rubio et al. (Reference Rubio, Julien, Knobloch and Weiss2014): a strong localised exchange of energy between neighbouring wavenumbers across the diagonal, i.e. a certain mode
![]() $P$
interacts predominantly with its neighbouring modes
$P$
interacts predominantly with its neighbouring modes
![]() $P-1$
and
$P-1$
and
![]() $P+1$
. The sign of the transfer reveals that this part of the cascade is direct: energy is transferred to larger wavenumbers. At low
$P+1$
. The sign of the transfer reveals that this part of the cascade is direct: energy is transferred to larger wavenumbers. At low
![]() $K\lesssim 7$
and higher
$K\lesssim 7$
and higher
![]() $Q\gtrsim 7$
, a range of inverse transfer is found where small-
$Q\gtrsim 7$
, a range of inverse transfer is found where small-
![]() $K$
modes receive energy from modes
$K$
modes receive energy from modes
![]() $Q>K$
. The input of energy into the large-scale vortex of figure 6(a) can be recognised as an interaction of the smallest wavenumbers receiving energy from a broad range of higher-order wavenumbers. Such a non-local inverse cascade has been observed before in rotating convection by Favier et al. (Reference Favier, Silvers and Proctor2014), who could display a clearer effect due to a considerably larger domain. It is also similar to the inverse energy cascade in rotating turbulence (Mininni, Alexakis & Pouquet Reference Mininni, Alexakis and Pouquet2009). The non-locality indicates that the largest flow scale directly receives energy from the smaller scales without passing through intermediate scales. In contrast, in the direct cascade, energy is transferred from large to small while passing through all intermediate scales.
$Q>K$
. The input of energy into the large-scale vortex of figure 6(a) can be recognised as an interaction of the smallest wavenumbers receiving energy from a broad range of higher-order wavenumbers. Such a non-local inverse cascade has been observed before in rotating convection by Favier et al. (Reference Favier, Silvers and Proctor2014), who could display a clearer effect due to a considerably larger domain. It is also similar to the inverse energy cascade in rotating turbulence (Mininni, Alexakis & Pouquet Reference Mininni, Alexakis and Pouquet2009). The non-locality indicates that the largest flow scale directly receives energy from the smaller scales without passing through intermediate scales. In contrast, in the direct cascade, energy is transferred from large to small while passing through all intermediate scales.
For the NS case (figure 7
b), the picture changes. In particular, the ‘staircase’ of energy transfer along the diagonal, which is prominent for SF, is not as strongly present for the larger wavenumbers. Instead, the interactions between modes are less localised, meaning that the interactions are spread more and mode combinations farther from the diagonal are transferring energy. A direct cascade is formed along the diagonal for
![]() $K,Q\gtrsim 5$
. Curiously, some signs of an inverse cascade remain: (i) for
$K,Q\gtrsim 5$
. Curiously, some signs of an inverse cascade remain: (i) for
![]() $K\leqslant 5$
, and (ii) transfers from modes around
$K\leqslant 5$
, and (ii) transfers from modes around
![]() $Q\approx 5$
to
$Q\approx 5$
to
![]() $K\approx 10$
, which are non-localised. The absence of a large-scale structure can be explained by the fact that the lowest wavenumber is receiving considerably less energy and from a narrower range of scales than in SF.
$K\approx 10$
, which are non-localised. The absence of a large-scale structure can be explained by the fact that the lowest wavenumber is receiving considerably less energy and from a narrower range of scales than in SF.
5.2 Relation with mean temperature gradient
The characteristic flow phenomenology of rotating RB convection has been related to the occurrence (and strength) of the persistent mean temperature gradient across the bulk (Julien et al.
Reference Julien, Legg, McWilliams and Werne1996), unlike the statistically isothermal bulk of non-rotating RB. The origin of this temperature gradient has been proposed to be increased by lateral mixing, induced by interactions of like-signed vortical plumes. As in the geostrophic-turbulence state the flow phenomenology is altered (cf. figure 6), we can expect that this also affects the strength of the mean temperature gradient. Figure 8 shows the mean temperature gradient as a function of
![]() $Ek$
. In the rotation-affected RB, lateral mixing being stronger than vertical mixing leads to mean temperature gradients as large as
$Ek$
. In the rotation-affected RB, lateral mixing being stronger than vertical mixing leads to mean temperature gradients as large as
![]() $-0.5$
for NS and
$-0.5$
for NS and
![]() $-0.4$
for SF. However, upon entering the geostrophic-turbulence state by further reducing
$-0.4$
for SF. However, upon entering the geostrophic-turbulence state by further reducing
![]() $Ek$
, the magnitude of the gradient is gradually diminished. We thus expect that in the geostrophic-turbulence state the mixing can become slightly more 3D again.
$Ek$
, the magnitude of the gradient is gradually diminished. We thus expect that in the geostrophic-turbulence state the mixing can become slightly more 3D again.
This behaviour is consistent with previous simulations of the asymptotic equations (Julien et al. Reference Julien, Rubio, Grooms and Knobloch2012b ), which predict that the geostrophic-turbulence state indeed still has a mean temperature gradient, but less steep than when coherent vortical plumes are present. Finally, even though the behaviour of the mean temperature gradient is qualitatively similar for SF and NS plates, the location of the minimum temperature gradient, which could be taken as an additional indicator for the transition, certainly does not coincide between the two cases.

Figure 8. Mean temperature gradient at midplane: (a) for SF and (b) for NS. Open symbols are for
![]() $Ra=1\times 10^{10}$
; filled symbols for
$Ra=1\times 10^{10}$
; filled symbols for
![]() $Ra=5\times 10^{10}$
. The arrows indicate the transition points as inferred from these graphs.
$Ra=5\times 10^{10}$
. The arrows indicate the transition points as inferred from these graphs.
6 Discussion
In the previous sections we have compared the transition to the geostrophic regime of turbulent rotating RB convection between SF and NS boundary conditions on the horizontal plates. From the current results, it seems clear that the nature of the bulk turbulence is extremely dependent on the boundary conditions. Nevertheless, both types of boundary conditions display a transition in a similar range of Ekman numbers around
![]() $Ek=9\times 10^{-7}$
(
$Ek=9\times 10^{-7}$
(
![]() $3\times 10^{-7}$
) for
$3\times 10^{-7}$
) for
![]() $Ra=1\times 10^{10}$
(
$Ra=1\times 10^{10}$
(
![]() $5\times 10^{10}$
). This transition is found to be gradual, unlike other transitions in rotating RB flow, such as those reported in confined geometries at higher
$5\times 10^{10}$
). This transition is found to be gradual, unlike other transitions in rotating RB flow, such as those reported in confined geometries at higher
![]() $Ek$
(Stevens et al.
Reference Stevens, Zhong, Clercx, Ahlers and Lohse2009). Many diagnostic signs of flow transition can be found near the onset of the geostrophic regime: the scaling with
$Ek$
(Stevens et al.
Reference Stevens, Zhong, Clercx, Ahlers and Lohse2009). Many diagnostic signs of flow transition can be found near the onset of the geostrophic regime: the scaling with
![]() $Ek$
of many quantities including Nusselt number, thermal BL thickness, bulk–BL distribution of dissipation rates as well as the midplane mean temperature gradient show a changing behaviour. We do not expect this list to be exhaustive. All quantities show a transition centred at a specific
$Ek$
of many quantities including Nusselt number, thermal BL thickness, bulk–BL distribution of dissipation rates as well as the midplane mean temperature gradient show a changing behaviour. We do not expect this list to be exhaustive. All quantities show a transition centred at a specific
![]() $Ek$
, so that the full range of changes covers at least half a decade in
$Ek$
, so that the full range of changes covers at least half a decade in
![]() $Ek$
. In particular, at
$Ek$
. In particular, at
![]() $Ra=1\times 10^{10}$
we inferred transitions in various statistics in the range
$Ra=1\times 10^{10}$
we inferred transitions in various statistics in the range
![]() $6\times 10^{-7}\lesssim Ek\lesssim 1.3\times 10^{-6}$
; at
$6\times 10^{-7}\lesssim Ek\lesssim 1.3\times 10^{-6}$
; at
![]() $Ra=5\times 10^{10}$
in the range
$Ra=5\times 10^{10}$
in the range
![]() $2.4\times 10^{-7}\lesssim Ek\lesssim 4.5\times 10^{10}$
. These ranges are the same for SF and NS plates; however, individual statistics display transitions at different
$2.4\times 10^{-7}\lesssim Ek\lesssim 4.5\times 10^{10}$
. These ranges are the same for SF and NS plates; however, individual statistics display transitions at different
![]() $Ek$
when comparing the two boundary conditions. So it appears to be all but impossible to define a single criterion to distinguish the rotation-dominated geostrophic regime from the rotation-affected regime, as indeed the flow may be transitioning, but the different diagnostic quantities may be sensitive slightly before or slightly after the transition.
$Ek$
when comparing the two boundary conditions. So it appears to be all but impossible to define a single criterion to distinguish the rotation-dominated geostrophic regime from the rotation-affected regime, as indeed the flow may be transitioning, but the different diagnostic quantities may be sensitive slightly before or slightly after the transition.
Regarding the actual nature of the transition, it is quite remarkable that the SF and NS transition ranges coincide in
![]() $Ek$
for similar
$Ek$
for similar
![]() $Ra$
. This would suggest a common origin. One of two candidates (or a combination of both) suggested in the literature may be the cause: either marginal (in)stability of the thermal BL, as suggested by King et al. (Reference King, Stellmach and Aurnou2012), which leads to a theoretical scaling
$Ra$
. This would suggest a common origin. One of two candidates (or a combination of both) suggested in the literature may be the cause: either marginal (in)stability of the thermal BL, as suggested by King et al. (Reference King, Stellmach and Aurnou2012), which leads to a theoretical scaling
![]() $Nu\sim Ra^{3}Ek^{4}$
; or a change in the bulk dynamics where plumes cannot enter the stiff geostrophic bulk that throttles the heat transport, suggested by Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a
), which gives a scaling
$Nu\sim Ra^{3}Ek^{4}$
; or a change in the bulk dynamics where plumes cannot enter the stiff geostrophic bulk that throttles the heat transport, suggested by Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a
), which gives a scaling
![]() $Nu\sim Ra^{3/2}Ek^{2}$
. Both arguments could in principle be independent of the velocity boundary conditions, given that either the thermal BLs or the bulk flow away from the BLs is involved. We find mostly evidence supporting the Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a
) mechanism, but it is certainly not conclusive:
$Nu\sim Ra^{3/2}Ek^{2}$
. Both arguments could in principle be independent of the velocity boundary conditions, given that either the thermal BLs or the bulk flow away from the BLs is involved. We find mostly evidence supporting the Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a
) mechanism, but it is certainly not conclusive:
-
(i) The geostrophic Nusselt-number scaling of figure 2 matches fairly with the Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a ) scaling for SF plates, but not for NS. The scaling proposed by King et al. (Reference King, Stellmach and Aurnou2012) does not match with the current results for either boundary condition. In line with the recent experimental results of Cheng et al. (Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015), it is becoming clear that the heat-transfer scaling exponent
 ${\it\beta}$
for
${\it\beta}$
for
 $Nu\sim Ra^{{\it\beta}}$
measured at constant
$Nu\sim Ra^{{\it\beta}}$
measured at constant
 $Ek$
is not the same for all
$Ek$
is not the same for all
 $Ek$
; equivalently, the exponent
$Ek$
; equivalently, the exponent
 ${\it\gamma}$
for
${\it\gamma}$
for
 $Nu\sim Ek^{{\it\gamma}}$
at constant
$Nu\sim Ek^{{\it\gamma}}$
at constant
 $Ra$
will take different values for different
$Ra$
will take different values for different
 $Ra$
.
$Ra$
. -
(ii) For the BL thickness (figure 4) we find a change in scaling at
 $Ek=8\times 10^{-7}$
(
$Ek=8\times 10^{-7}$
(
 $3\times 10^{-7}$
) at
$3\times 10^{-7}$
) at
 $Ra=1\times 10^{10}$
(
$Ra=1\times 10^{10}$
(
 $5\times 10^{10}$
) for both SF and NS, with steeper scaling with
$5\times 10^{10}$
) for both SF and NS, with steeper scaling with
 $Ek$
below the transition. The transition does not coincide with the crossing of the kinetic and thermal BL thicknesses, which is the criterion proposed by King et al. (Reference King, Stellmach, Noir, Hansen and Aurnou2009, Reference King, Stellmach and Aurnou2012) to describe its origin. The sharp change of scaling indicates changes in the structure of the thermal BL, which could be due to the crossing of the marginal stability criterion for the BL. However, the corresponding limit of validity
$Ek$
below the transition. The transition does not coincide with the crossing of the kinetic and thermal BL thicknesses, which is the criterion proposed by King et al. (Reference King, Stellmach, Noir, Hansen and Aurnou2009, Reference King, Stellmach and Aurnou2012) to describe its origin. The sharp change of scaling indicates changes in the structure of the thermal BL, which could be due to the crossing of the marginal stability criterion for the BL. However, the corresponding limit of validity
 $Ra\lesssim Ek^{-3/2}$
for the argument (King et al.
Reference King, Stellmach and Aurnou2012) would at the current
$Ra\lesssim Ek^{-3/2}$
for the argument (King et al.
Reference King, Stellmach and Aurnou2012) would at the current
 $Ra=5\times 10^{10}$
predict a transition at
$Ra=5\times 10^{10}$
predict a transition at
 $Ek\approx 7\times 10^{-8}$
, at significantly smaller
$Ek\approx 7\times 10^{-8}$
, at significantly smaller
 $Ek$
than we observe.
$Ek$
than we observe. -
(iii) Finally, the spatial distribution of dissipation of both turbulent kinetic energy (
 ${\it\epsilon}_{{\it\theta}}$
) and thermal variance (
${\it\epsilon}_{{\it\theta}}$
) and thermal variance (
 ${\it\epsilon}_{u}$
) between bulk and BL (figure 5) reveals that most of the dissipation is found to occur in the bulk, even more so for
${\it\epsilon}_{u}$
) between bulk and BL (figure 5) reveals that most of the dissipation is found to occur in the bulk, even more so for
 ${\it\epsilon}_{u}$
than for
${\it\epsilon}_{u}$
than for
 ${\it\epsilon}_{{\it\theta}}$
. The fractional distribution between bulk and BL reveals a slope change at
${\it\epsilon}_{{\it\theta}}$
. The fractional distribution between bulk and BL reveals a slope change at
 $Ek\approx 6\times 10^{-7}$
(
$Ek\approx 6\times 10^{-7}$
(
 $2\times 10^{-7}$
) at
$2\times 10^{-7}$
) at
 $Ra=1\times 10^{10}$
(
$Ra=1\times 10^{10}$
(
 $5\times 10^{10}$
) for both SF and NS.
$5\times 10^{10}$
) for both SF and NS.
For SF plates, the Julien et al. (Reference Julien, Knobloch, Rubio and Vasil2012a ) arguments fit best with our findings. However, the case of NS plates requires a different description given the presence of Ekman layers that are significantly affecting the flow dynamics in the entire fluid layer. We presently cannot give a theoretical description, but we expect that these results, together with the recent findings by Stellmach et al. (Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014) and Cheng et al. (Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015), can form a starting point for theories of no-slip geophysical convection. In that respect we want to mention here the recent work by Julien et al. (Reference Julien, Aurnou, Calkins, Knobloch, Marti, Stellmach and Vasil2016) where Ekman pumping is incorporated into the asymptotically reduced equations.
In conclusion, it has become apparent in the last few years that the Ekman layers remain a decisive and active part of geostrophic convection with no-slip plates, in spite of their diminishing thickness. We have compared the transition to the geostrophic regime between no-slip and stress-free boundaries. Both undergo a transition, at roughly the same Ekman number, but the scaling laws for heat transfer on both sides of the transition are strongly dependent on the boundary conditions. The physical picture of geostrophic convection is not fully complete, especially for no-slip plates.
Acknowledgements
We would like to thank S. Grossmann, C. Sun and Y. Yang for various stimulating discussions. We also thank the reviewers for their detailed and constructive comments, which have helped tremendously to improve the introductory paragraphs in particular. We acknowledge FOM, an ERC Advanced Grant, the PRACE resource Hermit based in Stuttgart at HLRS, and NWO for the use of Cartesius under grant no. SH-202.