2 Governing equations

Following the work of many classic texts (see for example Hamilton et al. (Reference Hamilton and Blackstock1998) chap. 3) we begin with the inviscid mass and momentum conservation equations

(2.1a ) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D70C}\boldsymbol{u})=0, & \displaystyle\end{eqnarray}$$

(2.1b ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}\left(\frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}\right)=-\unicode[STIX]{x1D735}p, & \displaystyle\end{eqnarray}$$

$\unicode[STIX]{x1D70C}$

$p$

$\boldsymbol{u}$

(2.2a-c ) $$\begin{eqnarray}p=\unicode[STIX]{x1D70C}_{0}c_{0}^{2}\hat{p},\quad \unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{0}\hat{\unicode[STIX]{x1D70C}},\quad \boldsymbol{u}=c_{0}\hat{\boldsymbol{u}},\end{eqnarray}$$

where $\unicode[STIX]{x1D70C}_{0}$ and $c_{0}$ are the reference density and speed of sound for the stationary fluid respectively. Perturbations about a state of rest are then considered

(2.3a-c ) $$\begin{eqnarray}\hat{p}=\hat{p}_{0}+\hat{p}^{\prime },\quad \hat{\unicode[STIX]{x1D70C}}=\hat{\unicode[STIX]{x1D70C}}_{0}+\hat{\unicode[STIX]{x1D70C}}^{\prime },\quad \hat{\boldsymbol{u}}=\hat{\boldsymbol{u}}^{\prime },\end{eqnarray}$$

with $\hat{p}^{\prime }\sim \hat{\unicode[STIX]{x1D70C}}^{\prime }\sim \hat{\boldsymbol{u}}^{\prime }\sim M$ where $M<1$ is the perturbation Mach number, which is assumed to be small but finite. This approximation holds true in many situations. The conversion from Mach number to root mean square (r.m.s.) sound pressure level (SPL) in decibels for a sinusoidal pressure source in air at $20\,^{\circ }$ C is approximately

(2.4) $$\begin{eqnarray}\text{SPL}\sim (194+20\log _{10}M)~\text{dB}.\end{eqnarray}$$

For pressure sources such as that of the mouthpiece of the trombone when played fortissimo, SPLs can typically be around 170 dB corresponding to a Mach number of up to around 0.1. As such, the small but finite Mach number approximation is a very realistic one.

Discarding terms of $\mathit{O}(M^{3})$ and higher in (2.1a ) and (2.1b ) gives

(2.5a ) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{c_{0}}\frac{\unicode[STIX]{x2202}\hat{\unicode[STIX]{x1D70C}}^{\prime }}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{\prime }=-\hat{\boldsymbol{u}}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\hat{\unicode[STIX]{x1D70C}}^{\prime }-\hat{\unicode[STIX]{x1D70C}}^{\prime }\unicode[STIX]{x1D735}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{\prime }, & \displaystyle\end{eqnarray}$$

(2.5b ) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{c_{0}}\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{\prime }}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\hat{p}^{\prime }=-\hat{\boldsymbol{u}}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}^{\prime }+\hat{\unicode[STIX]{x1D70C}}^{\prime }\unicode[STIX]{x1D735}\hat{p}^{\prime }, & \displaystyle\end{eqnarray}$$

$\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{\prime }/\unicode[STIX]{x2202}t=-c_{0}\unicode[STIX]{x1D735}\hat{p}^{\prime }$

$\mathit{O}(M)$

$\mathit{O}(M^{2})$

$\mathit{O}(M^{3})$

We now consider the entropy equation

(2.6) $$\begin{eqnarray}\frac{\text{D}S}{\text{D}t}=0,\end{eqnarray}$$

which holds everywhere, since our weakly nonlinear assumptions means any shocks are weak shocks. We shall take our fluid to have initially uniform entropy $S_{0}$ . By (2.6) our fluid will retain this value at all times. As a result, we may Taylor expand the equation of state $p=p(S,\unicode[STIX]{x1D70C})$ at fixed entropy about $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{0}$ , $S=S_{0}$ , to get

(2.7) $$\begin{eqnarray}p^{\prime }=A\left(\frac{\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x1D70C}_{0}}\right)+\frac{B}{2!}\left(\frac{\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x1D70C}_{0}}\right)^{2}+\cdots =c_{0}^{2}\unicode[STIX]{x1D70C}^{\prime }+\frac{B}{2A}\frac{c_{0}^{2}}{\unicode[STIX]{x1D70C}_{0}}\unicode[STIX]{x1D70C}^{\prime 2}+\cdots \,,\end{eqnarray}$$

where

(2.8a,b ) $$\begin{eqnarray}A=\unicode[STIX]{x1D70C}_{0}\left(\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}}\right)_{S,0}=\unicode[STIX]{x1D70C}_{0}c_{0}^{2},\quad \text{and}\quad B=\unicode[STIX]{x1D70C}_{0}^{2}\left(\frac{\unicode[STIX]{x2202}^{2}p}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{2}}\right)_{S,0}.\end{eqnarray}$$

For a perfect gas $B/A=\unicode[STIX]{x1D6FE}-1$ where $\unicode[STIX]{x1D6FE}$ is the ratio of specific heats. In non-dimensional variables

(2.9) $$\begin{eqnarray}\hat{p}^{\prime }=\hat{\unicode[STIX]{x1D70C}}^{\prime }+\frac{B}{2A}\hat{\unicode[STIX]{x1D70C}}^{\prime 2}.\end{eqnarray}$$

Inverting this equation (correct to second order) gives

(2.10) $$\begin{eqnarray}\hat{\unicode[STIX]{x1D70C}}^{\prime }=\hat{p}^{\prime }-\frac{B}{2A}\hat{p}^{\prime 2},\end{eqnarray}$$

which can be used to eliminate density from the mass and momentum equations. This gives

(2.11a ) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{c_{0}}\frac{\unicode[STIX]{x2202}\hat{p}^{\prime }}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{\prime }=-\hat{p}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\hat{\boldsymbol{u}}^{\prime }-\hat{\boldsymbol{u}}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\hat{p}+\frac{1}{c_{0}}\frac{B}{2A}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(\hat{p}^{\prime 2}), & \displaystyle\end{eqnarray}$$

(2.11b ) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{c_{0}}\frac{\unicode[STIX]{x2202}\hat{\boldsymbol{u}}^{\prime }}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\hat{p}^{\prime }=-\hat{\boldsymbol{u}}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\hat{\boldsymbol{u}}^{\prime }+\hat{p}^{\prime }\unicode[STIX]{x1D735}\hat{p}^{\prime }. & \displaystyle\end{eqnarray}$$

$\unicode[STIX]{x1D714}$

(2.12a,b ) $$\begin{eqnarray}\hat{p}=\mathop{\sum }_{a=-\infty }^{\infty }P^{a}(\boldsymbol{x})\text{e}^{-\text{i}a\unicode[STIX]{x1D714}t},\quad \hat{\boldsymbol{u}}=\mathop{\sum }_{a=-\infty }^{\infty }\boldsymbol{U}^{a}(\boldsymbol{x})\text{e}^{-\text{i}a\unicode[STIX]{x1D714}t},\end{eqnarray}$$

where $P^{-a}={P^{a}}^{\ast }$ and $\boldsymbol{U}^{-a}={\boldsymbol{U}^{a}}^{\ast }$ (with $\ast$ denoting the complex conjugate) so that both $\hat{p}$ and $\hat{\boldsymbol{u}}$ are real (and can be substituted into quadratic terms without worry). Both $P^{0}$ and $U^{0}$ are taken to be identically zero (see appendix A).

Equations (2.11a ) and (2.11b ) then become

(2.13a ) $$\begin{eqnarray}\displaystyle \mathop{\sum }_{a=-\infty }^{\infty }(-\text{i}akP^{a}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{U}^{a})\text{e}^{-\text{i}a\unicode[STIX]{x1D714}t} & = & \displaystyle \mathop{\sum }_{b,c=-\infty }^{\infty }\left(\vphantom{\frac{B}{2A}}-P^{b}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{U}^{c}-\boldsymbol{U}^{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}P^{c}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{B}{2A}\text{i}(b+c)kP^{b}P^{c}\right)\text{e}^{-\text{i}(b+c)\unicode[STIX]{x1D714}t},\end{eqnarray}$$

(2.13b ) $$\begin{eqnarray}\displaystyle \mathop{\sum }_{a=-\infty }^{\infty }(-\text{i}ak\boldsymbol{U}^{a}+\unicode[STIX]{x1D735}P^{a})\text{e}^{-\text{i}a\unicode[STIX]{x1D714}t} & = & \displaystyle \mathop{\sum }_{b,c=-\infty }^{\infty }(-\boldsymbol{U}^{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{U}^{c}+P^{b}\unicode[STIX]{x1D735}P^{c})\text{e}^{-\text{i}(b+c)\unicode[STIX]{x1D714}t},\qquad\end{eqnarray}$$

$k=\unicode[STIX]{x1D714}/c_{0}$

(2.14a ) $$\begin{eqnarray}\displaystyle -\text{i}akP^{a}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{U}^{a} & = & \displaystyle \mathop{\sum }_{b=-\infty }^{\infty }\left(-P^{a-b}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{U}^{b}-\boldsymbol{U}^{a-b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}P^{b}-\frac{B}{2A}\text{i}akP^{b}P^{a-b}\right),\qquad\end{eqnarray}$$

(2.14b ) $$\begin{eqnarray}\displaystyle -\text{i}ak\boldsymbol{U}^{a}+\unicode[STIX]{x1D735}P^{a} & = & \displaystyle \mathop{\sum }_{b=-\infty }^{\infty }(-\boldsymbol{U}^{a-b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{U}^{b}+P^{a-b}\unicode[STIX]{x1D735}P^{b}).\end{eqnarray}$$

2.1 Duct geometry

Figure 1. Illustration of the geometry of the duct.

Figure 1 illustrates the geometry of our duct. We define our duct by its centreline $\boldsymbol{q}(s)$ in terms of the longitudinal arc length $s$ from the pressure source inlet. The general position vector in the duct is given by

(2.15) $$\begin{eqnarray}\boldsymbol{x}(s,r)=\boldsymbol{q}(s)+r\hat{\boldsymbol{n}},\end{eqnarray}$$

where $h_{-}(s)\leqslant r\leqslant h_{+}(s)$ (with $h_{-}(s)<0$ ) defines the transverse position inside the duct of width $h=(h_{+}-h_{-})$ and $\hat{\boldsymbol{n}}=\hat{\boldsymbol{n}}(s)$ is the unit normal to the duct defined by the Frenet–Serret formulas,

(2.16a-c ) $$\begin{eqnarray}\frac{\text{d}\boldsymbol{q}}{\text{d}s}=\hat{\boldsymbol{t}},\quad \frac{\text{d}\hat{\boldsymbol{t}}}{\text{d}s}=\unicode[STIX]{x1D705}(s)\hat{\boldsymbol{n}},\quad \frac{\text{d}\hat{\boldsymbol{n}}}{\text{d}s}=-\unicode[STIX]{x1D705}(s)\hat{\boldsymbol{t}},\end{eqnarray}$$

with $\unicode[STIX]{x1D705}(s)$ being the local curvature of the centreline and $\hat{\boldsymbol{t}}=\hat{\boldsymbol{t}}(s)$ the unit tangent vector to the centreline. The basis vectors and their corresponding Lamé coefficients are

(2.17a-d ) $$\begin{eqnarray}\boldsymbol{e}_{s}=\hat{\boldsymbol{t}},\quad h_{s}=1-\unicode[STIX]{x1D705}r,\quad \boldsymbol{e}_{r}=\hat{\boldsymbol{n}},\quad h_{r}=1.\end{eqnarray}$$

Using these, equations (2.14a ) and (2.14b ) can now be expanded in their coordinate specific forms resulting in three coupled equations for the Fourier modes of pressure $P^{a}$ , longitudinal velocity $U^{a}$ and transverse velocity $V^{a}$

(2.18a ) $$\begin{eqnarray}\displaystyle & & \displaystyle -\text{i}akP^{a}+\frac{1}{1-\unicode[STIX]{x1D705}r}\frac{\unicode[STIX]{x2202}U^{a}}{\unicode[STIX]{x2202}s}+\frac{\unicode[STIX]{x2202}V^{a}}{\unicode[STIX]{x2202}r}-\frac{\unicode[STIX]{x1D705}V^{a}}{1-\unicode[STIX]{x1D705}r}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{b=-\infty }^{\infty }\left(-\text{i}bkP^{a-b}P^{b}-\text{i}bkU^{a-b}U^{b}-\text{i}bkV^{a-b}V^{b}-\frac{B}{2A}\text{i}akP^{b}P^{a-b}\right),\end{eqnarray}$$

(2.18b ) $$\begin{eqnarray}\displaystyle & & \displaystyle -\text{i}akU^{a}+\frac{1}{1-\unicode[STIX]{x1D705}r}\frac{\unicode[STIX]{x2202}P^{a}}{\unicode[STIX]{x2202}s}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{b=-\infty }^{\infty }\left(-\frac{U^{a-b}}{1-\unicode[STIX]{x1D705}r}\frac{\unicode[STIX]{x2202}U^{b}}{\unicode[STIX]{x2202}s}-V^{a-b}\frac{\unicode[STIX]{x2202}U^{b}}{\unicode[STIX]{x2202}r}+\frac{\unicode[STIX]{x1D705}}{1-\unicode[STIX]{x1D705}r}U^{a-b}V^{b}+\text{i}bkP^{a-b}U^{b}\right),\end{eqnarray}$$

(2.18c ) $$\begin{eqnarray}\displaystyle & & \displaystyle -\text{i}akV^{a}+\frac{\unicode[STIX]{x2202}P^{a}}{\unicode[STIX]{x2202}r}=\mathop{\sum }_{b=-\infty }^{\infty }\left(\frac{-U^{a-b}}{1-\unicode[STIX]{x1D705}r}\frac{\unicode[STIX]{x2202}V^{b}}{\unicode[STIX]{x2202}s}-V^{a-b}\frac{\unicode[STIX]{x2202}V^{b}}{\unicode[STIX]{x2202}r}-\frac{\unicode[STIX]{x1D705}}{1-\unicode[STIX]{x1D705}r}U^{a-b}U^{b}+\text{i}bkP^{a-b}V^{b}\right).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

From here, the temporal Fourier modes are expanded about a basis of spatial straight duct modes

(2.19a-c ) $$\begin{eqnarray}P^{a}=\mathop{\sum }_{p=0}^{\infty }P_{p}^{a}(s)\unicode[STIX]{x1D713}_{p}(s,r),\quad U^{a}=\mathop{\sum }_{p=0}^{\infty }U_{p}^{a}(s)\unicode[STIX]{x1D713}_{p}(s,r),\quad V^{a}=\mathop{\sum }_{p=0}^{\infty }V_{p}^{a}(s)\unicode[STIX]{x1D713}_{p}(s,r),\end{eqnarray}$$

where the $\unicode[STIX]{x1D713}_{p}$ satisfy

(2.20a-c ) $$\begin{eqnarray}\frac{\text{d}^{2}\unicode[STIX]{x1D713}_{p}}{\text{d}r^{2}}+\unicode[STIX]{x1D702}_{p}^{2}\unicode[STIX]{x1D713}_{p}=0,\quad \int _{h_{-}}^{h_{+}}\unicode[STIX]{x1D713}_{p}\unicode[STIX]{x1D713}_{q}\,\text{d}r=\unicode[STIX]{x1D6FF}_{pq},\quad \left.\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{p}}{\unicode[STIX]{x2202}r}\right|_{r=h_{\pm }}=0,\end{eqnarray}$$

and are therefore given by

(2.21a-c ) $$\begin{eqnarray}\unicode[STIX]{x1D713}_{p}=C_{p}\cos \left(p\unicode[STIX]{x03C0}\frac{(r-h_{-})}{(h_{+}-h_{-})}\right),\quad C_{p}=\sqrt{\frac{2-\unicode[STIX]{x1D6FF}_{p0}}{h_{+}-h_{-}}},\quad \unicode[STIX]{x1D702}_{p}=\frac{p\unicode[STIX]{x03C0}}{h_{+}-h_{-}}.\end{eqnarray}$$

Here, we have expanded both the longitudinal and the transverse velocity components in terms of the duct basis, contrary to Félix & Pagneux (Reference Félix and Pagneux2001) who eliminated $V^{a}$ from the analogous linear equations at this point. It turns out that the higher radial derivatives that would arise from eliminating $V^{a}$ from the above equations make it more complicated to apply the correct boundary conditions at the duct wall in the quadratic terms on the right-hand side, as described below. Projecting the equations onto the modal basis first, then eliminating the modal amplitudes of the transverse velocity $V_{p}^{a}$ , turns out to be much simpler than eliminating the $V^{a}$ from the above equations and then projecting onto the modal basis. At linear order, the two methods produce identical results (see appendix F).

As an aside, one may question the validity of expanding the temporal modes as a series of spatial duct modes, each with zero derivative on the boundary. This issue is dealt with in more detail in Pagneux et al. (Reference Pagneux, Amir and Kergomard1996), however we will briefly mention that this causes no difficulty, since an infinite series of terms with zero derivative at the boundary do not necessarily have a zero derivative. (For example, the function $y(x)=x$ has the Fourier cosine series expansion $y(x)={\textstyle \frac{1}{2}}-(4/\unicode[STIX]{x03C0}^{2})\sum _{n=0}^{\infty }(1/(2n+1)^{2})\cos \big((2n+1)\unicode[STIX]{x03C0}x\big)$ , convergent for $x\in [0,1]$ . At both boundaries $y(x)$ has derivative $1$ , despite each term in the sum having zero derivative at both boundaries.) Rather, care must be taken to apply the correct boundary conditions before expanding in terms of the $\unicode[STIX]{x1D713}_{p}$ basis.

We now wish to project the above equations onto the basis of modes. We first multiply the equations by a factor $(1-\unicode[STIX]{x1D705}r)$ , then by a general duct mode $\unicode[STIX]{x1D713}_{p}$ and integrate across the duct width, ensuring to apply the no penetration boundary condition at the duct wall. This is given by

(2.22a,b ) $$\begin{eqnarray}\boldsymbol{U}^{a}|_{r=h_{\pm }}\boldsymbol{\cdot }\boldsymbol{n}^{\pm }=0,\quad \boldsymbol{n}^{\pm }(s)=h_{\pm }^{\prime }\boldsymbol{e}_{s}-(1-\unicode[STIX]{x1D705}h_{\pm })\boldsymbol{e}_{r},\end{eqnarray}$$

where $\boldsymbol{n}^{\pm }$ are the normals to the duct wall. This corresponds to

(2.23) $$\begin{eqnarray}h_{\pm }^{\prime }U^{a}=(1-\unicode[STIX]{x1D705}h_{\pm })V^{a}\quad \text{at }r=h_{\pm }.\end{eqnarray}$$

(Note that this simple relation between $U^{a}$ and $V^{a}$ at the duct wall would have been significantly complicated by nonlinear terms had we used (2.18c ) to eliminate $V^{a}$ above.) Equation (2.23) can be used to eliminate $V^{a}$ at the boundaries. For example (summation convention assumed),

(2.24) $$\begin{eqnarray}\int _{h_{-}}^{h_{+}}\frac{\unicode[STIX]{x2202}V^{a}}{\unicode[STIX]{x2202}r}\unicode[STIX]{x1D713}_{p}\,\text{d}r=\left[\frac{h^{\prime }}{1-\unicode[STIX]{x1D705}h}\unicode[STIX]{x1D713}_{p}\unicode[STIX]{x1D713}_{q}\right]_{h_{-}}^{h_{+}}U_{q}^{a}-\int _{h_{-}}^{h_{+}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{p}}{\unicode[STIX]{x2202}r}\unicode[STIX]{x1D713}_{q}\,\text{d}rV_{q}^{a}.\end{eqnarray}$$

Similarly,

(2.25) $$\begin{eqnarray}\int _{h_{-}}^{h_{+}}\frac{\unicode[STIX]{x2202}U^{a}}{\unicode[STIX]{x2202}s}\unicode[STIX]{x1D713}_{p}\,\text{d}r=\frac{\unicode[STIX]{x2202}U_{p}^{a}}{\unicode[STIX]{x2202}s}-[h^{\prime }\unicode[STIX]{x1D713}_{p}\unicode[STIX]{x1D713}_{q}]_{h_{-}}^{h_{+}}U_{q}^{a}-\int _{h_{-}}^{h_{+}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{p}}{\unicode[STIX]{x2202}s}\unicode[STIX]{x1D713}_{q}\,\text{d}rU_{q}^{a}.\end{eqnarray}$$

Other terms of note include

(2.26) $$\begin{eqnarray}\displaystyle \int _{h_{-}}^{h_{+}}U^{a-b}\frac{\unicode[STIX]{x2202}U^{b}}{\unicode[STIX]{x2202}s}\unicode[STIX]{x1D713}_{p}\,\text{d}r & = & \displaystyle \frac{1}{2}\frac{\text{d}}{\text{d}s}\left(\int _{h_{-}}^{h_{+}}\unicode[STIX]{x1D713}_{p}\unicode[STIX]{x1D713}_{q}\unicode[STIX]{x1D713}_{r}\,\text{d}r\right)U_{q}^{a-b}U_{r}^{b}-\frac{1}{2}\left[h^{\prime }\unicode[STIX]{x1D713}_{p}\unicode[STIX]{x1D713}_{q}\unicode[STIX]{x1D713}_{r}\right]_{h_{-}}^{h_{+}}U_{q}^{a-b}U_{r}^{b}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}\int _{h_{-}}^{h_{+}}\unicode[STIX]{x1D713}_{p}\unicode[STIX]{x1D713}_{q}\unicode[STIX]{x1D713}_{r}\,\text{d}r\left(U_{r}^{b}\frac{\text{d}}{\text{d}s}U_{q}^{a-b}+U_{q}^{a-b}\frac{\text{d}}{\text{d}s}U_{r}^{b}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\int _{h_{-}}^{h_{+}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{p}}{\unicode[STIX]{x2202}s}\unicode[STIX]{x1D713}_{q}\unicode[STIX]{x1D713}_{r}\,\text{d}rU_{q}^{a-b}U_{r}^{b},\end{eqnarray}$$

where the sum over $b$ has been reordered, and

(2.27) $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{h_{-}}^{h_{+}}(1-\unicode[STIX]{x1D705}r)V^{a-b}\frac{\unicode[STIX]{x2202}U^{b}}{\unicode[STIX]{x2202}r}\unicode[STIX]{x1D713}_{p}\,\text{d}r\nonumber\\ \displaystyle & & \displaystyle \quad =[h^{\prime }U^{a-b}U^{b}\unicode[STIX]{x1D713}_{p}]_{h_{-}}^{h_{+}}-\int _{h_{-}}^{h_{+}}(1-\unicode[STIX]{x1D705}r)V^{a-b}U^{b}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{p}}{\unicode[STIX]{x2202}r}\,\text{d}r\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D705}\int _{h_{-}}^{h_{+}}V^{a-b}U^{b}\unicode[STIX]{x1D713}_{p}\,\text{d}r-\int _{h_{-}}^{h_{+}}(1-\unicode[STIX]{x1D705}r)\frac{\unicode[STIX]{x2202}V^{a-b}}{\unicode[STIX]{x2202}r}U^{b}\unicode[STIX]{x1D713}_{p}\,\text{d}r\nonumber\\ \displaystyle & & \displaystyle \quad =[h^{\prime }U^{a-b}U^{b}\unicode[STIX]{x1D713}_{p}]_{h_{-}}^{h_{+}}-\int _{h_{-}}^{h_{+}}(1-\unicode[STIX]{x1D705}r)V^{a-b}U^{b}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{p}}{\unicode[STIX]{x2202}r}\,\text{d}r\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\int _{h_{-}}^{h_{+}}\text{i}(a-b)k(1-\unicode[STIX]{x1D705}r)P^{a-b}U^{b}\unicode[STIX]{x1D713}_{p}\,\text{d}r+\int _{h_{-}}^{h_{+}}\frac{\unicode[STIX]{x2202}U^{a-b}}{\unicode[STIX]{x2202}s}U^{b}\unicode[STIX]{x1D713}_{p}\,\text{d}r,\end{eqnarray}$$

where the linear part of (2.18a ) has been used to substitute for $\unicode[STIX]{x2202}V^{a-b}/\unicode[STIX]{x2202}r$ . Using these, equations (2.18a ) and (2.18b ) become

(2.28a ) $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}}{\text{d}s}U_{p}^{a}-\text{i}ak\unicode[STIX]{x1D733}_{pq}[1-\unicode[STIX]{x1D705}r]P_{q}^{a}-\unicode[STIX]{x1D733}_{\{p\}q}U_{q}^{a}-\unicode[STIX]{x1D733}_{[\,p]q}[1-\unicode[STIX]{x1D705}r]V_{q}^{a}\nonumber\\ \displaystyle & & \displaystyle \quad =-\left(\text{i}bk+\text{i}ak\frac{B}{2A}\right)\unicode[STIX]{x1D733}_{pqr}[1-\unicode[STIX]{x1D705}r]P_{q}^{a-b}P_{r}^{b}-\text{i}bk\unicode[STIX]{x1D733}_{pqr}[1-\unicode[STIX]{x1D705}r]U_{q}^{a-b}U_{r}^{b}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\text{i}bk\unicode[STIX]{x1D733}_{pqr}[1-\unicode[STIX]{x1D705}r]V_{q}^{a-b}V_{r}^{b},\end{eqnarray}$$

(2.28b ) $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}}{\text{d}s}P_{p}^{a}-\text{i}ak\unicode[STIX]{x1D733}_{pq}[1-\unicode[STIX]{x1D705}r]U_{q}^{a}-([h^{\prime }\unicode[STIX]{x1D713}_{p}\unicode[STIX]{x1D713}_{q}]_{h_{-}}^{h_{+}}+\unicode[STIX]{x1D733}_{\{p\}q})P_{q}^{a}\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\unicode[STIX]{x1D733}_{\{p\}qr}-\frac{\text{d}}{\text{d}s}(\unicode[STIX]{x1D733}_{pqr})\right)U_{q}^{a-b}U_{r}^{b}+\text{i}ak\unicode[STIX]{x1D733}_{pqr}[1-\unicode[STIX]{x1D705}r]P_{q}^{a-b}U_{r}^{b}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(\unicode[STIX]{x1D705}\unicode[STIX]{x1D733}_{pqr}+\unicode[STIX]{x1D733}_{[\,p]qr}[1-\unicode[STIX]{x1D705}r])U_{q}^{a-b}V_{r}^{b}-\unicode[STIX]{x1D733}_{pqr}\left(U_{r}^{b}\frac{\text{d}}{\text{d}s}U_{q}^{a-b}+U_{q}^{a-b}\frac{\text{d}}{\text{d}s}U_{r}^{b}\right)\!.\qquad\end{eqnarray}$$

Here, we have used $\unicode[STIX]{x1D733}$ as a shorthand to denote integrals over the modes. Square brackets around an index represent radial derivatives on that mode, and curly brackets represent longitudinal derivatives. The square brackets after the $\unicode[STIX]{x1D733}$ are the integral kernel (assumed to be 1 if no brackets are present). So for example

(2.29) $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D733}_{[\,p]q}=\displaystyle \int _{h_{-}}^{h_{+}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{p}}{\unicode[STIX]{x2202}r}}\unicode[STIX]{x1D713}_{q}\,\text{d}r=(\unicode[STIX]{x1D733}_{p[q]})^{\text{T}}\\ \unicode[STIX]{x1D733}_{\{p\}qr}[1-\unicode[STIX]{x1D705}r]=\displaystyle \int _{h_{-}}^{h_{+}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{p}}{\unicode[STIX]{x2202}s}}\unicode[STIX]{x1D713}_{q}\unicode[STIX]{x1D713}_{r}(1-\unicode[STIX]{x1D705}r)\,\text{d}r.\end{array}\right\}\end{eqnarray}$$

We now turn our attention to (2.18c ). Using the linear relationship between $V$ and $P$ from the left-hand side of (2.18c ) and the symmetry of mixed partials, we can find the linear expression for $\unicode[STIX]{x2202}V/\unicode[STIX]{x2202}s$ ,

(2.30) $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}V^{a}}{\unicode[STIX]{x2202}s}=\frac{1}{\text{i}ak}\frac{\unicode[STIX]{x2202}^{2}P^{a}}{\unicode[STIX]{x2202}s\unicode[STIX]{x2202}r}=(1-\unicode[STIX]{x1D705}r)\frac{\unicode[STIX]{x2202}U^{a}}{\unicode[STIX]{x2202}r}-\unicode[STIX]{x1D705}U^{a}.\end{eqnarray}$$

We also require the linear expression for $V_{p}^{a}$ in terms of $P_{p}^{a}$ , also from the left-hand side of (2.18c ),

(2.31) $$\begin{eqnarray}V_{p}^{a}=\frac{1}{\text{i}ak}[\unicode[STIX]{x1D713}_{p}\unicode[STIX]{x1D713}_{q}]_{h_{-}}^{h_{+}}P_{q}^{a}-\frac{1}{\text{i}ak}\unicode[STIX]{x1D733}_{[\,p]q}P_{q}^{a}=\frac{1}{\text{i}ak}\unicode[STIX]{x1D733}_{p[q]}P_{q}^{a}.\end{eqnarray}$$

Using these, we can eliminate $V^{a}$ from the right-hand side of the projection of (2.18c ),

(2.32) $$\begin{eqnarray}\displaystyle & & \displaystyle -\text{i}ak\unicode[STIX]{x1D733}_{pq}[1-\unicode[STIX]{x1D705}r]V_{q}^{a}+([\unicode[STIX]{x1D713}_{p}\unicode[STIX]{x1D713}_{q}(1-\unicode[STIX]{x1D705}r)]_{h_{-}}^{h_{+}}-\unicode[STIX]{x1D733}_{[\,p]q}[1-\unicode[STIX]{x1D705}r]+\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FF}_{pq})P_{q}^{a}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}\left(\vphantom{\frac{h^{\prime 2}}{1-\unicode[STIX]{x1D705}h}}-[\unicode[STIX]{x1D713}_{p}\unicode[STIX]{x1D713}_{q}\unicode[STIX]{x1D713}_{r}(1-\unicode[STIX]{x1D705}r)]_{h_{-}}^{h_{+}}+\unicode[STIX]{x1D733}_{[\,p]qr}[1-\unicode[STIX]{x1D705}r]\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\left.\unicode[STIX]{x1D705}\unicode[STIX]{x1D733}_{pqr}-\left[\frac{h^{\prime 2}}{1-\unicode[STIX]{x1D705}h}\unicode[STIX]{x1D713}_{p}\unicode[STIX]{x1D713}_{q}\unicode[STIX]{x1D713}_{r}\right]_{h_{-}}^{h_{+}}\right)U_{q}^{a-b}U_{r}^{b}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{1}{2k^{2}(a-b)b}(\unicode[STIX]{x1D733}_{[\,p]qr}[1-\unicode[STIX]{x1D705}r]-\unicode[STIX]{x1D705}\unicode[STIX]{x1D733}_{pqr})([\unicode[STIX]{x1D713}_{q}\unicode[STIX]{x1D713}_{s}]_{h_{-}}^{h_{+}}-\unicode[STIX]{x1D733}_{[q]s})([\unicode[STIX]{x1D713}_{r}\unicode[STIX]{x1D713}_{t}]_{h_{-}}^{h_{+}}-\unicode[STIX]{x1D733}_{[r]t})P_{s}^{a-b}P_{t}^{b}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D733}_{pqr}[1-\unicode[STIX]{x1D705}r]([\unicode[STIX]{x1D713}_{r}\unicode[STIX]{x1D713}_{t}]_{h_{-}}^{h_{+}}-\unicode[STIX]{x1D733}_{[r]t})P_{q}^{a-b}P_{t}^{b}.\end{eqnarray}$$

Using (2.31) and (2.32) we can eliminate $V$ from (2.28a ) and (2.28b ) to get

(2.33a ) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}^{\prime }+\unicode[STIX]{x1D648}\boldsymbol{p}+\unicode[STIX]{x1D642}\boldsymbol{u}={\mathcal{A}}[\boldsymbol{u},\boldsymbol{u}]+{\mathcal{B}}[\,\boldsymbol{p},\boldsymbol{p}], & \displaystyle\end{eqnarray}$$

(2.33b ) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{p}^{\prime }-\unicode[STIX]{x1D649}\boldsymbol{u}-\unicode[STIX]{x1D643}\boldsymbol{p}={\mathcal{C}}[\boldsymbol{u},\boldsymbol{p}]+{\mathcal{D}}[\boldsymbol{u},\boldsymbol{u}], & \displaystyle\end{eqnarray}$$

where we have switched to vector notation for ease of algebraic manipulations and a prime denotes $\text{d}/\text{d}s$ . Matrix multiplication is defined over spatial modes in the following manner

(2.34) $$\begin{eqnarray}(\unicode[STIX]{x1D648}\boldsymbol{p})_{p}^{a}=\mathop{\sum }_{q=0}^{\infty }\unicode[STIX]{x1D648}_{pq}^{a}P_{q}^{a}.\end{eqnarray}$$

Calligraphic letters denote rank-5 tensors, with square brackets denoting the following action

(2.35) $$\begin{eqnarray}({\mathcal{A}}[\boldsymbol{x},\boldsymbol{y}])_{p}^{a}=\mathop{\sum }_{b=-\infty }^{\infty }\mathop{\sum }_{q,r=0}^{\infty }{\mathcal{A}}_{pqr}^{ab}X_{q}^{a-b}Y_{r}^{b}.\end{eqnarray}$$

The matrices and tensors are given by

(2.36a ) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D648}_{pq}^{a} & = & \displaystyle -\text{i}ak\unicode[STIX]{x1D733}_{pq}[1-\unicode[STIX]{x1D705}r]-\frac{1}{\text{i}ak}\unicode[STIX]{x1D733}_{[\,p]s}[1-\unicode[STIX]{x1D705}r]\unicode[STIX]{x1D733}_{s[q]},\end{eqnarray}$$

(2.36b ) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D649}_{pq}^{a} & = & \displaystyle \text{i}ak\unicode[STIX]{x1D733}_{pq}[1-\unicode[STIX]{x1D705}r],\end{eqnarray}$$

(2.36c ) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D642}_{pq}^{a} & = & \displaystyle -\unicode[STIX]{x1D733}_{\{p\}q},\end{eqnarray}$$

(2.36d ) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D643}_{pq}^{a} & = & \displaystyle -\unicode[STIX]{x1D733}_{p\{q\}},\end{eqnarray}$$

(2.36e ) $$\begin{eqnarray}\displaystyle {\mathcal{A}}_{pqr}^{ab} & = & \displaystyle -\text{i}bk\unicode[STIX]{x1D733}_{pqr}[1-\unicode[STIX]{x1D705}r]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2}\unicode[STIX]{x1D733}_{[\,p]s}[1-\unicode[STIX]{x1D705}r](\unicode[STIX]{x1D649}^{-1})_{st}^{a}\left(\vphantom{\left[\frac{h}{1}\right]_{h}^{h}}-[\unicode[STIX]{x1D713}_{t}\unicode[STIX]{x1D713}_{q}\unicode[STIX]{x1D713}_{r}(1-\unicode[STIX]{x1D705}r)]_{h_{-}}^{h_{+}}+\unicode[STIX]{x1D733}_{[t]qr}[1-\unicode[STIX]{x1D705}r]\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\unicode[STIX]{x1D705}\unicode[STIX]{x1D733}_{tqr}-\left[\frac{h^{\prime 2}}{1-\unicode[STIX]{x1D705}h}\unicode[STIX]{x1D713}_{t}\unicode[STIX]{x1D713}_{q}\unicode[STIX]{x1D713}_{r}\right]_{h_{-}}^{h_{+}}\right),\end{eqnarray}$$

(2.36f ) $$\begin{eqnarray}\displaystyle {\mathcal{B}}_{pqr}^{ab} & = & \displaystyle -\left(\text{i}bk+\text{i}ak\frac{B}{2A}\right)\unicode[STIX]{x1D733}_{pqr}[1-\unicode[STIX]{x1D705}r]-\frac{1}{\text{i}(a-b)k}\underbrace{\unicode[STIX]{x1D733}_{pst}[1-\unicode[STIX]{x1D705}r]\unicode[STIX]{x1D733}_{s[q]}\unicode[STIX]{x1D733}_{t[r]}}_{\unicode[STIX]{x1D733}_{p[q][r]}[1-\unicode[STIX]{x1D705}r]}\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D733}_{[\,p]s}[1-\unicode[STIX]{x1D705}r](\unicode[STIX]{x1D649}^{-1})_{st}^{a}\left(\frac{-1}{2k^{2}(a-b)b}(\unicode[STIX]{x1D733}_{[t]uv}[1-\unicode[STIX]{x1D705}r]-\unicode[STIX]{x1D705}\unicode[STIX]{x1D733}_{tuv})\unicode[STIX]{x1D733}_{u[q]}\unicode[STIX]{x1D733}_{v[r]}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D733}_{tqu}[1-\unicode[STIX]{x1D705}r]\unicode[STIX]{x1D733}_{u[r]}\vphantom{\frac{1}{k}}\right),\end{eqnarray}$$

(2.36g ) $$\begin{eqnarray}\displaystyle {\mathcal{C}}_{pqr}^{ab} & = & \displaystyle \text{i}ak\unicode[STIX]{x1D733}_{pqr}[1-\unicode[STIX]{x1D705}r]+\frac{1}{\text{i}bk}\underbrace{(\unicode[STIX]{x1D705}\unicode[STIX]{x1D733}_{pqs}+\unicode[STIX]{x1D733}_{[\,p]qs}[1-\unicode[STIX]{x1D705}r])\unicode[STIX]{x1D733}_{s[r]}}_{\unicode[STIX]{x1D705}\unicode[STIX]{x1D733}_{pq[r]}+\unicode[STIX]{x1D733}_{[\,p]q[r]}[1-\unicode[STIX]{x1D705}r]}+\,2\unicode[STIX]{x1D733}_{pqs}\unicode[STIX]{x1D648}_{sr}^{b},\end{eqnarray}$$

(2.36h ) $$\begin{eqnarray}\displaystyle {\mathcal{D}}_{pqr}^{ab} & = & \displaystyle \unicode[STIX]{x1D733}_{\{p\}qr}-\frac{\text{d}}{\text{d}s}(\unicode[STIX]{x1D733}_{pqr})+2\unicode[STIX]{x1D733}_{pqs}\unicode[STIX]{x1D642}_{sr}^{b}.\end{eqnarray}$$

The $\unicode[STIX]{x1D733}$ can also be calculated analytically (see appendix B). Here, $\unicode[STIX]{x1D648}$ , $\unicode[STIX]{x1D649}$ , ${\mathcal{A}}$ , ${\mathcal{B}}$ and ${\mathcal{C}}$ encode the curvature of the duct, while $\unicode[STIX]{x1D642},\unicode[STIX]{x1D643}$ and ${\mathcal{D}}$ arise from variation in the duct width, vanishing when it is uniform.

Due to the presence of evanescent modes these equations are numerically unstable and cannot be integrated directly (Pagneux et al. Reference Pagneux, Amir and Kergomard1996). Following the work of Félix & Pagneux (Reference Félix and Pagneux2001), we define a relation between the pressure and velocity in terms of the admittance. When solving for pressure it is easier to work with the admittance rather than the impedance to avoid inverting large matrices in the work that will follow.

The following relationship is defined

(2.37) $$\begin{eqnarray}\boldsymbol{u}=\unicode[STIX]{x1D654}\boldsymbol{p}+{\mathcal{Y}}[\,\boldsymbol{p},\boldsymbol{p}],\end{eqnarray}$$

where $\unicode[STIX]{x1D654}=\unicode[STIX]{x1D654}(s)$ is the linear part of the admittance ( $\unicode[STIX]{x1D654}=\unicode[STIX]{x1D655}^{-1}$ where $\unicode[STIX]{x1D655}$ is the impedance matrix of Félix & Pagneux (Reference Félix and Pagneux2001)) and ${\mathcal{Y}}={\mathcal{Y}}(s)$ is the second-order nonlinear correction to the impedance, henceforth referred to as the ‘nonlinear admittance’ term. We differentiate (2.37) with respect to $s$ ,

(2.38) $$\begin{eqnarray}\boldsymbol{u}^{\prime }=\unicode[STIX]{x1D654}^{\prime }\boldsymbol{p}+\unicode[STIX]{x1D654}\boldsymbol{p}^{\prime }+{\mathcal{Y}}^{\prime }[\,\boldsymbol{p},\boldsymbol{p}]+{\mathcal{Y}}[\,\boldsymbol{p}^{\prime },\boldsymbol{p}]+{\mathcal{Y}}[\,\boldsymbol{p},\boldsymbol{p}^{\prime }],\end{eqnarray}$$

substitute in (2.33a ) and (2.33b ),

(2.39) $$\begin{eqnarray}\displaystyle & & \displaystyle -\unicode[STIX]{x1D648}\boldsymbol{p}-\unicode[STIX]{x1D642}\boldsymbol{u}+{\mathcal{A}}[\boldsymbol{u},\boldsymbol{u}]+{\mathcal{B}}[\,\boldsymbol{p},\boldsymbol{p}]=\unicode[STIX]{x1D654}^{\prime }\boldsymbol{p}+\unicode[STIX]{x1D654}(\unicode[STIX]{x1D649}\boldsymbol{u}+\unicode[STIX]{x1D643}\boldsymbol{p}+{\mathcal{C}}[\boldsymbol{u},\boldsymbol{p}]+{\mathcal{D}}[\boldsymbol{u},\boldsymbol{u}])\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\mathcal{Y}}^{\prime }[\,\boldsymbol{p},\boldsymbol{p}]+{\mathcal{Y}}[\unicode[STIX]{x1D649}\boldsymbol{u}+\unicode[STIX]{x1D643}\boldsymbol{p},\boldsymbol{p}]+{\mathcal{Y}}[\,\boldsymbol{p},\unicode[STIX]{x1D649}\boldsymbol{u}+\unicode[STIX]{x1D643}\boldsymbol{p}]\end{eqnarray}$$

and use (2.37) to express $\boldsymbol{u}$ in terms of $\boldsymbol{p}$

(2.40) $$\begin{eqnarray}\displaystyle & & \displaystyle -\unicode[STIX]{x1D648}\boldsymbol{p}-\unicode[STIX]{x1D642}\unicode[STIX]{x1D654}\boldsymbol{p}-\unicode[STIX]{x1D642}{\mathcal{Y}}[\,\boldsymbol{p},\boldsymbol{p}]+{\mathcal{A}}[\unicode[STIX]{x1D654}\boldsymbol{p},\unicode[STIX]{x1D654}\boldsymbol{p}]+{\mathcal{B}}[\,\boldsymbol{p},\boldsymbol{p}]=\unicode[STIX]{x1D654}^{\prime }\boldsymbol{p}+\unicode[STIX]{x1D654}(\!\unicode[STIX]{x1D649}\unicode[STIX]{x1D654}\boldsymbol{p}+\unicode[STIX]{x1D649}{\mathcal{Y}}[\,\boldsymbol{p},\boldsymbol{p}]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D643}\boldsymbol{p}+{\mathcal{C}}[\unicode[STIX]{x1D654}\boldsymbol{p},\boldsymbol{p}]+{\mathcal{D}}[\unicode[STIX]{x1D654}\boldsymbol{p},\unicode[STIX]{x1D654}\boldsymbol{p}]\!)+{\mathcal{Y}}^{\prime }[\,\boldsymbol{p},\boldsymbol{p}]+{\mathcal{Y}}[\unicode[STIX]{x1D649}\unicode[STIX]{x1D654}\boldsymbol{p}+\unicode[STIX]{x1D643}\boldsymbol{p},\boldsymbol{p}]+{\mathcal{Y}}[\,\boldsymbol{p},\unicode[STIX]{x1D649}\unicode[STIX]{x1D654}\boldsymbol{p}+\unicode[STIX]{x1D643}\boldsymbol{p}].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

This equation has two distinct orders of magnitude: terms linear in $\boldsymbol{p}$ , and terms quadratic in $\boldsymbol{p}$ . We can equate linear terms and the quadratic terms separately to get two distinct equations

(2.41a ) $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D654}^{\prime }\boldsymbol{p}+\unicode[STIX]{x1D654}\unicode[STIX]{x1D649}\unicode[STIX]{x1D654}\boldsymbol{p}+\unicode[STIX]{x1D648}\boldsymbol{p}+\unicode[STIX]{x1D654}\unicode[STIX]{x1D643}\boldsymbol{p}+\unicode[STIX]{x1D642}\unicode[STIX]{x1D654}\boldsymbol{p}=0, & \displaystyle\end{eqnarray}$$

(2.41b ) $$\begin{eqnarray}\displaystyle & {\mathcal{Y}}^{\prime }[\,\boldsymbol{p},\boldsymbol{p}]+{\mathcal{Y}}[\unicode[STIX]{x1D649}\unicode[STIX]{x1D654}\boldsymbol{p},\boldsymbol{p}]+{\mathcal{Y}}[\,\boldsymbol{p},\unicode[STIX]{x1D649}\unicode[STIX]{x1D654}\boldsymbol{p}]+\unicode[STIX]{x1D654}\unicode[STIX]{x1D649}{\mathcal{Y}}[\,\boldsymbol{p},\boldsymbol{p}]+\unicode[STIX]{x1D654}{\mathcal{C}}[\unicode[STIX]{x1D654}\boldsymbol{p},\boldsymbol{p}]-{\mathcal{A}}[\unicode[STIX]{x1D654}\boldsymbol{p},\unicode[STIX]{x1D654}\boldsymbol{p}] & \displaystyle \nonumber\\ \displaystyle & -\,{\mathcal{B}}[\,\boldsymbol{p},\boldsymbol{p}]+{\mathcal{Y}}[\unicode[STIX]{x1D643}\boldsymbol{p},\boldsymbol{p}]+{\mathcal{Y}}[\,\boldsymbol{p},\unicode[STIX]{x1D643}\boldsymbol{p}]+\unicode[STIX]{x1D642}{\mathcal{Y}}[\,\boldsymbol{p},\boldsymbol{p}]+\unicode[STIX]{x1D654}{\mathcal{D}}[\unicode[STIX]{x1D654}\boldsymbol{p},\unicode[STIX]{x1D654}\boldsymbol{p}]=0. & \displaystyle\end{eqnarray}$$

Equation (2.40) will therefore solved, for any $\boldsymbol{p}$ , provided the linear part of the admittance and the nonlinear part of the admittance satisfy

(2.42a ) $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D654}^{\prime }+\unicode[STIX]{x1D654}\unicode[STIX]{x1D649}\unicode[STIX]{x1D654}+\unicode[STIX]{x1D648}+\unicode[STIX]{x1D654}\unicode[STIX]{x1D643}+\unicode[STIX]{x1D642}\unicode[STIX]{x1D654}=0 & \displaystyle\end{eqnarray}$$

(2.42b ) $$\begin{eqnarray}\displaystyle & {\mathcal{Y}}^{\prime }[\unicode[STIX]{x1D644},\unicode[STIX]{x1D644}]+{\mathcal{Y}}[\unicode[STIX]{x1D649}\unicode[STIX]{x1D654},\unicode[STIX]{x1D644}]+{\mathcal{Y}}[\unicode[STIX]{x1D644},\unicode[STIX]{x1D649}\unicode[STIX]{x1D654}]+\unicode[STIX]{x1D654}\unicode[STIX]{x1D649}{\mathcal{Y}}[\unicode[STIX]{x1D644},\unicode[STIX]{x1D644}]+\unicode[STIX]{x1D654}{\mathcal{C}}[\unicode[STIX]{x1D654},\unicode[STIX]{x1D644}]-{\mathcal{A}}[\unicode[STIX]{x1D654},\unicode[STIX]{x1D654}] & \displaystyle \nonumber\\ \displaystyle & -\,{\mathcal{B}}[\unicode[STIX]{x1D644},\unicode[STIX]{x1D644}]+{\mathcal{Y}}[\unicode[STIX]{x1D643},\unicode[STIX]{x1D644}]+{\mathcal{Y}}[\unicode[STIX]{x1D644},\unicode[STIX]{x1D643}]+\unicode[STIX]{x1D642}{\mathcal{Y}}[\unicode[STIX]{x1D644},\unicode[STIX]{x1D644}]+\unicode[STIX]{x1D654}{\mathcal{D}}[\unicode[STIX]{x1D654},\unicode[STIX]{x1D654}]=0, & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D644}_{pq}^{a}=\unicode[STIX]{x1D6FF}_{pq}\forall a$ is the identity tensor. Here, the square bracket notation acting on matrices denotes

(2.43) $$\begin{eqnarray}(\unicode[STIX]{x1D655}{\mathcal{A}}[\unicode[STIX]{x1D653},\unicode[STIX]{x1D654}])_{pqr}^{ab}=\mathop{\sum }_{s,t,u=0}^{\infty }\unicode[STIX]{x1D655}_{pu}^{a}{\mathcal{A}}_{ust}^{ab}\unicode[STIX]{x1D653}_{sq}^{a-b}\unicode[STIX]{x1D654}_{tr}^{b}.\end{eqnarray}$$

These equations are solved from the outlet of the duct – where an appropriate radiation condition boundary condition is imposed – to the inlet. Once both parts of the admittance are found throughout the duct, they can be used to express the velocity modes in terms of pressure modes in (2.33b ). The result is a numerically stable first order equation for the pressure which can be solved from the inlet to the outlet using suitable initial conditions at the inlet to describe the waveform (both temporally and spatially) there,

(2.44) $$\begin{eqnarray}\boldsymbol{p}^{\prime }=\unicode[STIX]{x1D649}\unicode[STIX]{x1D654}\boldsymbol{p}+\unicode[STIX]{x1D649}{\mathcal{Y}}[\,\boldsymbol{p},\boldsymbol{p}]+{\mathcal{C}}[\unicode[STIX]{x1D654}\boldsymbol{p},\boldsymbol{p}]+\unicode[STIX]{x1D643}\boldsymbol{p}+{\mathcal{D}}[\unicode[STIX]{x1D654}\boldsymbol{p},\unicode[STIX]{x1D654}\boldsymbol{p}].\end{eqnarray}$$

Due to the varying admittance this equation takes into account a superposition of forwards and backwards travelling modes, as determined by the radiation condition at the outlet and any reflections due to the varying duct geometry, as well as the nonlinear interactions between modes. As such, this method is suitable for ducts where reflected waves are important, such as those that are curved or have an open/closed exit. For details of how to decompose this wave into its forward and backward propagating modes using a linear and nonlinear reflection coefficient, see § 7.

To summarise the proposed method, for a given duct and a given frequency, equations (2.42a ) and (2.42b ) need to be solved from the duct outlet, where an appropriate radiation condition is imposed, to the duct inlet. These equations are independent of the actual forcing at the inlet, and characterise the linear and weakly nonlinear response of the duct at the given frequency. One result of this is the linear and nonlinear admittance at the duct inlet, given by (2.37), which describes the input admittance of the duct and generalises the usual linear admittance to include Mach number dependent effects. Given the pressure forcing at the inlet, equation (2.44) may be solved from the inlet to the outlet to give the pressure oscillation at all points in the duct. In general, solving (2.42a ) and (2.42b ) is performed numerically, although analytic progress may be made in certain simplifying cases. One such case is a 1-D straight duct, given in appendix C. Another such case is a uniform constant-curvature duct, the solution to which may be used as the downstream impedance boundary condition for more complicated ducts, which we consider next.

3 An infinite uniform duct

Consider an infinitely long uniform duct of constant curvature for which we have only outgoing propagating waves and decaying evanescent waves. In such a duct no point can be distinguished from another longitudinally, therefore we must have the admittance being a fixed point of the admittance equations. To find the fixed points, we begin by combining (2.33a ) and (2.33b ) (ignoring the quadratic terms for the moment), to form a second-order ordinary differential equation for the pressure modes

(3.1) $$\begin{eqnarray}\boldsymbol{p}^{\prime \prime }+\unicode[STIX]{x1D649}\unicode[STIX]{x1D648}\boldsymbol{p}=0.\end{eqnarray}$$

Here we are considering a uniform duct of constant curvature, so $\unicode[STIX]{x1D642},\unicode[STIX]{x1D643}$ and the derivatives of $\unicode[STIX]{x1D648}$ and $\unicode[STIX]{x1D649}$ vanish. As previously noted, this equation is numerically unstable. We can however make progress analytically. The solution in terms of forward and backwards modes is given by

(3.2) $$\begin{eqnarray}\boldsymbol{p}=\boldsymbol{p}^{+}+\boldsymbol{p}^{-}=\mathop{\sum }_{i=1}^{\infty }(c_{i}^{+}\boldsymbol{v}_{i}\text{e}^{\text{i}\unicode[STIX]{x1D706}_{i}s}+c_{i}^{-}\boldsymbol{v}_{i}\text{e}^{-i\unicode[STIX]{x1D706}_{i}s}),\end{eqnarray}$$

where the $\boldsymbol{v}_{i}$ are the eigenvectors of $\unicode[STIX]{x1D649}\unicode[STIX]{x1D648}$ with eigenvalues $\unicode[STIX]{x1D706}_{i}^{2}$ , with arbitrary $c_{i}^{+}$ and $c_{i}^{-}$ . Here, we have split the solution into forward and backward waves. The roots of the $\unicode[STIX]{x1D706}_{i}$ are chosen as follows

(3.3) $$\begin{eqnarray}\unicode[STIX]{x1D706}_{i}=\left\{\begin{array}{@{}ll@{}}(\unicode[STIX]{x1D706}_{i}^{2})^{1/2},\quad & \unicode[STIX]{x1D706}_{i}^{2}>0,\\ \text{i}(-\unicode[STIX]{x1D706}_{i}^{2})^{1/2},\quad & \unicode[STIX]{x1D706}_{i}^{2}<0,\end{array}\right.\end{eqnarray}$$

to ensure either propagating or decaying evanescent modes in the positive direction. Based on extensive numerical evaluations, we observe that all of the eigenvectors of $\unicode[STIX]{x1D649}\unicode[STIX]{x1D648}$ are real (even though $\unicode[STIX]{x1D649}\unicode[STIX]{x1D648}$ it is not necessarily symmetric for $\unicode[STIX]{x1D705}\neq 0$ ). We now introduce the characteristic forward and backwards admittance, linearly relating the forwards and backwards modes

(3.4) $$\begin{eqnarray}\boldsymbol{u}^{\pm }=\unicode[STIX]{x1D654}^{\pm }\boldsymbol{p}^{\pm }.\end{eqnarray}$$

Using this, together with the linear equation relating pressure and velocity $(\boldsymbol{p}^{\pm })^{\prime }=\unicode[STIX]{x1D649}\boldsymbol{u}^{\pm }$ , we obtain and expression for $\unicode[STIX]{x1D654}^{\pm }$

(3.5) $$\begin{eqnarray}\unicode[STIX]{x1D654}^{\pm }=\pm \unicode[STIX]{x1D649}^{-1}\unicode[STIX]{x1D651}\unicode[STIX]{x1D726}\unicode[STIX]{x1D651}^{-1}=\pm \text{i}\unicode[STIX]{x1D649}^{-1}\sqrt{\unicode[STIX]{x1D649}\unicode[STIX]{x1D648}},\end{eqnarray}$$

where $\unicode[STIX]{x1D651}=(\boldsymbol{v}_{1},\boldsymbol{v}_{2},\ldots )$ and $\unicode[STIX]{x1D726}=\text{diag}(\text{i}\unicode[STIX]{x1D706}_{1},~\text{i}\unicode[STIX]{x1D706}_{2},\ldots )$ . These can be shown to be fixed points of the linear admittance equation by direct substitution into (2.42a ) (again, ignoring $\unicode[STIX]{x1D642}$ and $\unicode[STIX]{x1D643}$ as the duct is assumed uniform)

(3.6) $$\begin{eqnarray}{\unicode[STIX]{x1D654}^{\pm }}^{\prime }=\unicode[STIX]{x1D649}^{-1}\sqrt{\unicode[STIX]{x1D649}\unicode[STIX]{x1D648}}\unicode[STIX]{x1D7EC}^{-1}\sqrt{\unicode[STIX]{x1D649}\unicode[STIX]{x1D648}}-\unicode[STIX]{x1D648}=0.\end{eqnarray}$$

Therefore, $\unicode[STIX]{x1D654}=\unicode[STIX]{x1D654}^{+}$ is the admittance of a uniform, constant-curvature duct supporting only outgoing propagating waves and decaying evanescent waves.

Using these characteristic linear admittances, we now wish to find the fixed points of the nonlinear admittance in (2.42b ). In order to do so we first introduce a matrix $\unicode[STIX]{x1D652}$ with columns given by the eigenvectors of $\unicode[STIX]{x1D654}^{\pm }\unicode[STIX]{x1D649}$ with corresponding eigenvalue matrix $\pm \unicode[STIX]{x1D726}$ . Fixed points of the nonlinear admittance equation satisfy

(3.7) $$\begin{eqnarray}{\mathcal{Y}}^{\pm }[\unicode[STIX]{x1D649}\unicode[STIX]{x1D654}^{\pm },\unicode[STIX]{x1D644}]+{\mathcal{Y}}^{\pm }[\unicode[STIX]{x1D644},\unicode[STIX]{x1D649}\unicode[STIX]{x1D654}^{\pm }]+\unicode[STIX]{x1D654}^{\pm }\unicode[STIX]{x1D649}{\mathcal{Y}}^{\pm }[\unicode[STIX]{x1D644},\unicode[STIX]{x1D644}]+\unicode[STIX]{x1D654}^{\pm }{\mathcal{C}}[\unicode[STIX]{x1D654}^{\pm },\unicode[STIX]{x1D644}]-{\mathcal{A}}[\unicode[STIX]{x1D654}^{\pm },\unicode[STIX]{x1D654}^{\pm }]-{\mathcal{B}}[\unicode[STIX]{x1D644},\unicode[STIX]{x1D644}]=0.\end{eqnarray}$$

We apply $\unicode[STIX]{x1D652}^{-1}$ on the left of this equation and $\unicode[STIX]{x1D651}$ to the right on both terms in the square brackets

(3.8) $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D652}^{-1}{\mathcal{Y}}^{\pm }[\pm \unicode[STIX]{x1D651}\unicode[STIX]{x1D726},\unicode[STIX]{x1D651}]+\unicode[STIX]{x1D652}^{-1}{\mathcal{Y}}^{\pm }[\unicode[STIX]{x1D651},\pm \unicode[STIX]{x1D651}\unicode[STIX]{x1D726}]+\unicode[STIX]{x1D652}^{-1}\unicode[STIX]{x1D654}^{\pm }\unicode[STIX]{x1D649}{\mathcal{Y}}^{\pm }[\unicode[STIX]{x1D651},\unicode[STIX]{x1D651}]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D652}^{-1}\unicode[STIX]{x1D654}^{\pm }{\mathcal{C}}[\unicode[STIX]{x1D654}^{\pm }\unicode[STIX]{x1D651},\unicode[STIX]{x1D651}]-\unicode[STIX]{x1D652}^{-1}{\mathcal{A}}[\unicode[STIX]{x1D654}^{\pm }\unicode[STIX]{x1D651},\unicode[STIX]{x1D654}^{\pm }\unicode[STIX]{x1D651}]-\unicode[STIX]{x1D652}^{-1}{\mathcal{B}}[\unicode[STIX]{x1D651},\unicode[STIX]{x1D651}]=0,\end{eqnarray}$$

where we recall that $\unicode[STIX]{x1D651}$ , $\unicode[STIX]{x1D652}$ and $\unicode[STIX]{x1D726}$ each have an upper index and the matrix square bracket algebra is defined by (2.43). Next, we transform ${\mathcal{Y}}^{\pm }$ in the following manner

(3.9) $$\begin{eqnarray}{\mathcal{Y}}^{\pm }[\boldsymbol{x},\boldsymbol{y}]=\unicode[STIX]{x1D652}\tilde{{\mathcal{Y}}}^{\pm }[\unicode[STIX]{x1D651}^{-1}\boldsymbol{x},\unicode[STIX]{x1D651}^{-1}\boldsymbol{y}]\end{eqnarray}$$

to obtain

(3.10) $$\begin{eqnarray}\displaystyle & & \displaystyle \tilde{{\mathcal{Y}}}^{\pm }[\pm \unicode[STIX]{x1D726},\unicode[STIX]{x1D644}]+\tilde{{\mathcal{Y}}}^{\pm }[\unicode[STIX]{x1D644},\pm \unicode[STIX]{x1D726}]\pm \unicode[STIX]{x1D726}\tilde{{\mathcal{Y}}}^{\pm }[\unicode[STIX]{x1D644},\unicode[STIX]{x1D644}]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D652}^{-1}\unicode[STIX]{x1D654}^{\pm }{\mathcal{C}}[\unicode[STIX]{x1D654}^{\pm }\unicode[STIX]{x1D651},\unicode[STIX]{x1D651}]-\unicode[STIX]{x1D652}^{-1}{\mathcal{A}}[\unicode[STIX]{x1D654}^{\pm }\unicode[STIX]{x1D651},\unicode[STIX]{x1D654}^{\pm }\unicode[STIX]{x1D651}]-\unicode[STIX]{x1D652}^{-1}{\mathcal{B}}[\unicode[STIX]{x1D651},\unicode[STIX]{x1D651}]=0.\end{eqnarray}$$

As we are acting $\tilde{{\mathcal{Y}}}$ on purely diagonal matrices, its components can easily be read off

(3.11) $$\begin{eqnarray}(\tilde{{\mathcal{Y}}}^{\pm })_{pqr}^{ab}=\frac{(\unicode[STIX]{x1D652}^{-1}{\mathcal{A}}[\unicode[STIX]{x1D654}^{\pm }\unicode[STIX]{x1D651},\unicode[STIX]{x1D654}^{\pm }\unicode[STIX]{x1D651}]+\unicode[STIX]{x1D652}^{-1}{\mathcal{B}}[\unicode[STIX]{x1D651},\unicode[STIX]{x1D651}]-\unicode[STIX]{x1D652}^{-1}\unicode[STIX]{x1D654}^{\pm }{\mathcal{C}}[\unicode[STIX]{x1D654}^{\pm }\unicode[STIX]{x1D651},\unicode[STIX]{x1D651}])_{pqr}^{ab}}{\pm i\unicode[STIX]{x1D706}_{p}^{a}\pm i\unicode[STIX]{x1D706}_{q}^{a-b}\pm i\unicode[STIX]{x1D706}_{r}^{b}}.\end{eqnarray}$$

The reverse transformation is then applied to obtain the characteristic nonlinear part of the admittance. It can easily be seen that ${\mathcal{Y}}^{+}=-{\mathcal{Y}}^{-}$ . As the equation governing ${\mathcal{Y}}$ is linear, the ${\mathcal{Y}}^{+}$ is unique (up to the equivalence class under summation – see appendix D) for a given choice of $\unicode[STIX]{x1D654}^{+}$ .

The linear and nonlinear impedances $\unicode[STIX]{x1D654}=\unicode[STIX]{x1D654}^{+}$ and ${\mathcal{Y}}={\mathcal{Y}}^{+}$ for a uniform constant-curvature duct may be used as a downstream boundary condition to (2.42a ) and (2.42b ) for arbitrary ducts. The solutions $\unicode[STIX]{x1D654}=\unicode[STIX]{x1D654}^{+}$ and ${\mathcal{Y}}={\mathcal{Y}}^{+}$ correspond to the radiation condition

(3.12) $$\begin{eqnarray}\boldsymbol{u}=\unicode[STIX]{x1D654}^{+}\boldsymbol{p}+{\mathcal{Y}}^{+}[\,\boldsymbol{p},\boldsymbol{p}],\end{eqnarray}$$

relating pressure and velocity modes at the exit, implying only outgoing waves and decaying evanescent waves in the uniform duct outlet of constant curvature.

3.1 Stability of fixed points of the admittance

One may question the stability of these fixed points by considering a small perturbation. For the linear part of the admittance take a small matrix perturbation $\unicode[STIX]{x1D73A}$

(3.13) $$\begin{eqnarray}\unicode[STIX]{x1D654}^{\pm }=\pm \unicode[STIX]{x1D649}^{-1}\unicode[STIX]{x1D651}\unicode[STIX]{x1D726}\unicode[STIX]{x1D651}^{-1}+\unicode[STIX]{x1D649}^{-1}\unicode[STIX]{x1D651}\unicode[STIX]{x1D73A}\unicode[STIX]{x1D651}^{-1}.\end{eqnarray}$$

In (2.42a ) this becomes

(3.14) $$\begin{eqnarray}\unicode[STIX]{x1D73A}^{\prime }=\mp \unicode[STIX]{x1D73A}\unicode[STIX]{x1D726}\mp \unicode[STIX]{x1D726}\unicode[STIX]{x1D73A}+\mathit{O}(\unicode[STIX]{x1D700}^{2}).\end{eqnarray}$$

Hence, $\unicode[STIX]{x1D654}^{+}$ is (at least Lyapunov) stable to small perturbations provided all the components of $\unicode[STIX]{x1D726}$ have $\text{Re}\unicode[STIX]{x1D726}\leqslant 0$ (remembering that we are solving in the negative $s$ direction, so a positive exponential solution corresponds to a decaying perturbation) which is the case given our choice of decaying evanescent solutions. In a physical situation, we would in fact expect all of the components of $\unicode[STIX]{x1D6EC}$ to have at least a small negative real part (due to losses in the system), in which case this would be an asymptotically stable fixed point. On the other hand, due to the opposite signs our $\unicode[STIX]{x1D654}^{-}$ can be seen to be unstable (it is possible to form a stable $\unicode[STIX]{x1D654}^{-}$ corresponding to backwards propagating waves with forward decaying evanescent modes, however these would be unphysical). This justifies the use of $\mathsf{Y}^{+}$ as a boundary condition for our linear admittance.

Similarly for the nonlinear part of the admittance consider a corresponding tensor perturbation $\unicode[STIX]{x1D700}$

(3.15) $$\begin{eqnarray}{\mathcal{Y}}={\mathcal{Y}}^{+}+\unicode[STIX]{x1D652}\unicode[STIX]{x1D700}[\unicode[STIX]{x1D651}^{-1},\unicode[STIX]{x1D651}^{-1}].\end{eqnarray}$$

In (2.42b ), we get

(3.16) $$\begin{eqnarray}\unicode[STIX]{x1D700}^{\prime }[\unicode[STIX]{x1D644},\unicode[STIX]{x1D644}]=-\unicode[STIX]{x1D700}[\unicode[STIX]{x1D726},\unicode[STIX]{x1D644}]-\unicode[STIX]{x1D700}[\unicode[STIX]{x1D644},\unicode[STIX]{x1D726}]-\unicode[STIX]{x1D726}\unicode[STIX]{x1D700}[\unicode[STIX]{x1D644},\unicode[STIX]{x1D644}].\end{eqnarray}$$

So similarly, we have (at least Lyapunov) stability provided all the components of $\unicode[STIX]{x1D726}$ have $\text{Re}\unicode[STIX]{x1D726}\leqslant 0$ , again justifying the use of ${\mathcal{Y}}^{+}$ as a boundary condition for the nonlinear admittance.

4 Numerical method

To implement our method we truncate the summations at $a_{max}$ temporal harmonics and $p_{max}$ spatial modes. We shall not go into great detail on the convergence of this method with respect to the number of modes taken, but one can expect a Fourier series type convergence temporally. Spatially, the number of modes required varies greatly on the shape of the duct – uniform ducts typically require fewer modes than variable width ones to the correctly apply the boundary conditions. For an example of convergence, we consider the uniform curved duct described later in § 5.4 with sinusoidal planar source and $M=0.10$ . We define the error to be

(4.1) $$\begin{eqnarray}\text{error}={\displaystyle \frac{\displaystyle \int _{0}^{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}}\int _{0}^{s_{max}}\int _{h_{-}}^{h_{+}}|p-p_{ref}|\,\text{d}r\,\text{d}s\,\text{d}t}{\displaystyle \int _{0}^{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}}\int _{0}^{s_{max}}\int _{h_{-}}^{h_{+}}|p_{ref}|\,\text{d}r\,\text{d}s\,\text{d}t}}.\end{eqnarray}$$

We take our reference pressure $p_{ref}$ to be the solution produced by 10 spatial and 10 temporal modes. Figure 2 shows the error resulting from varying the number of spatial modes with fixed number of temporal and vice versa. Varying the number of spatial modes we obtain convergence ${\sim}1/N^{3.21}$ . This is almost identical to the value obtained by Félix & Pagneux (Reference Félix and Pagneux2001). Varying the number of temporal modes we obtain convergence ${\sim}1/N^{1.28}$ . This number is dependant on the Mach number with smaller Mach numbers resulting in a greater convergence. For high Mach numbers the solution is described by a sawtooth wave throughout most of the duct (see appendix C) for which the convergence of the Fourier series is ${\sim}1/N$ . This gives the lower bound on the convergence.

Figure 2. Convergence of the method for (a) fixed number of temporal modes and (b) fixed number of spatial modes.

Convergence of the pressure solution can take quite a few modes (and consequently a large amount of computational time), depending on the frequency, Mach number and duct geometry, and in any given case a convergence study such as given in figure 2 would be needed to confirm convergence. However, good approximations can be made with very few modes – indeed many of the duct properties calculated later (such as power output and reflectance) can be calculated with good accuracy with as few as 5 spatial and 5 temporal modes for the parameters considered.

For the remainder of the paper we shall be dealing with ducts with an infinite uniform outlet. As such, we set $\unicode[STIX]{x1D654}=\unicode[STIX]{x1D654}^{+}$ for the initial condition of (2.42a ) and solve backwards through the duct to calculate $\unicode[STIX]{x1D654}=\unicode[STIX]{x1D654}(s)$ at every point in the duct. Next, we solve (2.42b ) with initial condition ${\mathcal{Y}}={\mathcal{Y}}^{+}$ . Again, we solve backwards through the duct using the previously found values of $\unicode[STIX]{x1D654}$ in our evaluations of (2.42b ). Finally we solve (2.44) forwards through the duct using both the previously found $\unicode[STIX]{x1D654}$ and ${\mathcal{Y}}$ in the evaluations of the equation. For the initial condition of the pressure we will generally be using a sinusoidal plane piston source so that

(4.2) $$\begin{eqnarray}P_{p}^{a}(0)={\textstyle \frac{1}{2}}\sqrt{h_{+}(0)-h_{-}(0)}M\unicode[STIX]{x1D6FF}_{p0}\unicode[STIX]{x1D6FF}^{|a|1}.\end{eqnarray}$$

Many other pressure sources can be modelled, with initial conditions chosen by decomposing the desired initial waveform into the modal/Fourier basis. Once both $\unicode[STIX]{x1D654}$ and ${\mathcal{Y}}$ are found throughout the duct for a particular wavenumber $k$ , different pressure waveforms and amplitudes can be solved for without re-evaluation of (2.42a ) and (2.42b ).

To solve (2.42a ) and (2.42b ) we use a fixed step 4th order Runge–Kutta algorithm. For most cases this is adequate. Due to the temporally decoupled nature of these equations a high degree of parallelisation is possible. Indeed, when taking $a_{max}$ temporal modes there are $3a_{max}(a_{max}-1)/2$ independent equations for ${\mathcal{Y}}$ (for each $a\in [1,a_{max}]$ we have $b\in [a-a_{max},a_{max}]$ minus the cases when $b=0$ or $a=b$ ) which can be solved in parallel. An issue, however, with this method is the large size of ${\mathcal{Y}}$ which scales like $\mathit{O}(a_{max}^{2}\,p_{max}^{3})$ with number of spatial modes $p_{max}$ . As a result, computational memory can be an issue. To overcome this, we opt to use a first-order exponential integrator method for the pressure as this requires the calculation and evaluation of ${\mathcal{Y}}$ at fewer points.

If we consider the equation for the pressure as the sum of a linear operator $\unicode[STIX]{x1D647}$ acting on $\boldsymbol{p}$ and a nonlinear part ${\mathcal{N}}$

(4.3) $$\begin{eqnarray}\boldsymbol{p}^{\prime }=\unicode[STIX]{x1D647}\,\boldsymbol{p}+{\mathcal{N}}\end{eqnarray}$$

the exact solution is given by

(4.4) $$\begin{eqnarray}\boldsymbol{p}(s)=\exp \left(\int _{0}^{s}\unicode[STIX]{x1D647}(t)\,\text{d}t\right)\boldsymbol{p}(0)+\int _{0}^{s}\exp \left(\int _{t}^{s}\unicode[STIX]{x1D647}(u)\,\text{d}u\right){\mathcal{N}}(t)\,\text{d}t.\end{eqnarray}$$

We now consider a small step $\unicode[STIX]{x1D6FF}s$ and make the approximation that both $\unicode[STIX]{x1D647}$ and ${\mathcal{N}}$ are constant over this interval (in many cases this is valid – for infinite uniform ducts of constant curvature $\unicode[STIX]{x1D647}$ is a fixed point and so this method provides the correct solution to the linear problem), we obtain our stepping algorithm

(4.5) $$\begin{eqnarray}\boldsymbol{p}(s+\unicode[STIX]{x1D6FF}s)=\exp (\unicode[STIX]{x1D6FF}s\unicode[STIX]{x1D647}(s))\boldsymbol{p}(s)-\unicode[STIX]{x1D647}^{-1}(\unicode[STIX]{x1D644}-\exp (\unicode[STIX]{x1D6FF}s\unicode[STIX]{x1D647}(s))){\mathcal{N}}(s).\end{eqnarray}$$

Matrix exponentiation was performed using a Fortran 90 routine written by John Burkardt based on the scaling and squaring algorithm used in MATLAB (see Moler & Van Loan Reference Moler and Van Loan2003). Other matrix operations were performed using LAPACK routines (Anderson et al. Reference Anderson, Bai, Bischof, Blackford, Demmel, Dongarra, Du Croz, Greenbaum, Hammarling and McKenney1999). Running the code on an 8 core 3.40 GHz i7 processor with 15 GB of RAM can take of the order of tens of minutes when running with 5 spatial and 5 temporal modes, up to of the order of several hours when running with 10 $+$ spatial and 10 $+$ temporal modes.

4.1 Numerical viscosity

To overcome the errors (and numerical instabilities that can arise thereof) associated with truncation of the infinite series we add a numerical viscosity. If one considers (see (C 9) in appendix C, where we demonstrated the sawtooth wave as a solution to our equations), we can calculate the exact error associated with a finite truncation

(4.6) $$\begin{eqnarray}\text{error}=\frac{\text{i}\unicode[STIX]{x1D6FD}kM^{2}\sqrt{h_{+}-h_{-}}}{(1+\unicode[STIX]{x1D70E})^{2}}\text{e}^{\text{i}aks}\left(\mathop{\sum }_{b=a-a_{max}}^{a_{max}}\frac{a}{2(a-b)b(1+\unicode[STIX]{x1D70E})^{2}}-\mathop{\sum }_{b=-\infty }^{\infty }\frac{a}{2(a-b)b(1+\unicode[STIX]{x1D70E})^{2}}\right),\end{eqnarray}$$

where $\unicode[STIX]{x1D6FD}=1+B/2A$ and $\unicode[STIX]{x1D70E}=s/(\unicode[STIX]{x1D6FD}Mk)$ is the distance normalised by the shock formation distance. After some algebra, this can be found to give

(4.7) $$\begin{eqnarray}\text{error}=\frac{\text{i}\unicode[STIX]{x1D6FD}kM^{2}\sqrt{h_{+}-h_{-}}}{(1+\unicode[STIX]{x1D70E})^{2}}\text{e}^{\text{i}aks}\mathop{\sum }_{b=0}^{a}\frac{1}{a_{max}-b}.\end{eqnarray}$$

The summation can be approximated to $-\log (1-(a/a_{max}))$ using Euler’s asymptotic expansion of the harmonic numbers. The factor multiplying this is proportional to the pressure. This gives us a numerical viscosity term which can be deducted from the right-hand side of our pressure equation

(4.8) $$\begin{eqnarray}-\frac{\unicode[STIX]{x1D6FD}Mka}{1+\unicode[STIX]{x1D70E}}\log \left(1-\frac{a}{a_{max}}\right)P^{a}.\end{eqnarray}$$

For $a\ll a_{max}$ the logarithm can be Taylor expanded. For small distances we obtain the mode number squared numerical viscosity used by other authors (e.g. Fernando et al. Reference Fernando, Druon, Coulouvrat and Marchiano2011)

(4.9) $$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FD}Mka^{2}}{a_{max}}P^{a},\end{eqnarray}$$

however, the logarithmic error is more accurate and provides better numerical results, and shall be used for the remainder of the paper. We incorporate the viscosity by modification of  $\unicode[STIX]{x1D647}$ :

(4.10) $$\begin{eqnarray}\unicode[STIX]{x1D647}^{\unicode[STIX]{x1D656}}\mapsto \unicode[STIX]{x1D647}^{\unicode[STIX]{x1D656}}+\frac{\unicode[STIX]{x1D6FD}Mka}{1+\unicode[STIX]{x1D70E}}\log \left(1-\frac{a}{a_{max}}\right)\unicode[STIX]{x1D644}^{\unicode[STIX]{x1D656}}.\end{eqnarray}$$

As the sawtooth shape is the limiting form of all weakly nonlinear wave propagation (and the most harmonically rich) this provides a very good least upper bound for viscosity, preventing a ‘pooling’ of energy at truncation and ensuring that the simulations remain stable without compromising the solution unduly.

4.2 Ducts of increasing width

As observed by Pagneux et al. (Reference Pagneux, Amir and Kergomard1996), ducts increasing in width – particularly those with a large degree of flare – exhibit a strong degree of coupling between spatial modes. This coupling can prove problematic numerically, especially when a large number of spatial modes are retained. To ensure good accuracy in $\unicode[STIX]{x1D654}$ and especially in ${\mathcal{Y}}$ , one must take smaller step sizes in the integration scheme as one increases $p_{max}$ . This further compounds the issue of computational complexity with increasing $p_{max}$ already noted.

A workaround to this issue is to truncate the number of spatial modes in proportion to the change in duct width. We retain the number of modes $p_{ret}$ given by

(4.11) $$\begin{eqnarray}p_{ret}=\left\lceil p_{max}\frac{h_{+}(s)-h_{-}(s)}{h_{max}}\right\rceil .\end{eqnarray}$$

So, in an increasing width duct, as we solve backwards for $\unicode[STIX]{x1D654}$ and ${\mathcal{Y}}$ we truncate more modes as we approach the inlet. Then, solving forwards for the pressure, we start with a reduced number of modes and include more as we approach the exit. In practice, where solutions remain stable, with a sufficient maximum number of modes, this truncation makes little difference to the output – the transverse resolution is still preserved. This issue does not arise in ducts of decreasing width as modes undergo cutoff rather than cuton, however an unrelated mathematical difficulty does appear and is discussed in § 5.5.

6 Comparisons between ducts

In the previous section we showed the effects of the introduction of nonlinearity into various different, previously studied ducts. We now consider the effect of the duct itself on the nonlinear sound propagation. To do so, we consider four different ducts all of the same length $L=1.5\unicode[STIX]{x03C0}h$ , with a sinusoidal planar pressure source at the entrance of frequency $kh=3$ and Mach number given by $M=2/(L\unicode[STIX]{x1D6FD}k)$ such that the shock formation distance (for a straight duct at least) is halfway through the duct. Each of the ducts is terminated by an infinite straight outlet. The four ducts are:

1. (i) a uniform straight duct;

2. (ii) a $180^{\circ }$ circular bend;

3. (iii) an exponential horn with exit width $2h$ ;

4. (iv) a $180^{\circ }$ circular horn with exit width $2h$ .

Thus we can separately compare the effects of curvature, varying width, and the combination.

Figure 9. Comparing the modal amplitudes throughout the curved uniform duct along different paths to the straight uniform duct. $M=2/(L\unicode[STIX]{x1D6FD}k)$ . (a) The outside of the bend, (b) the centre of the bend, (c) the inside of the bend.

Figure 10. Comparing the modal amplitudes of the straight horn and straight uniform duct, for $M=2/(L\unicode[STIX]{x1D6FD}k)$ . Note that the amplitudes are normalised by $1/\sqrt{h}$ to remove the effect of the varying duct area.

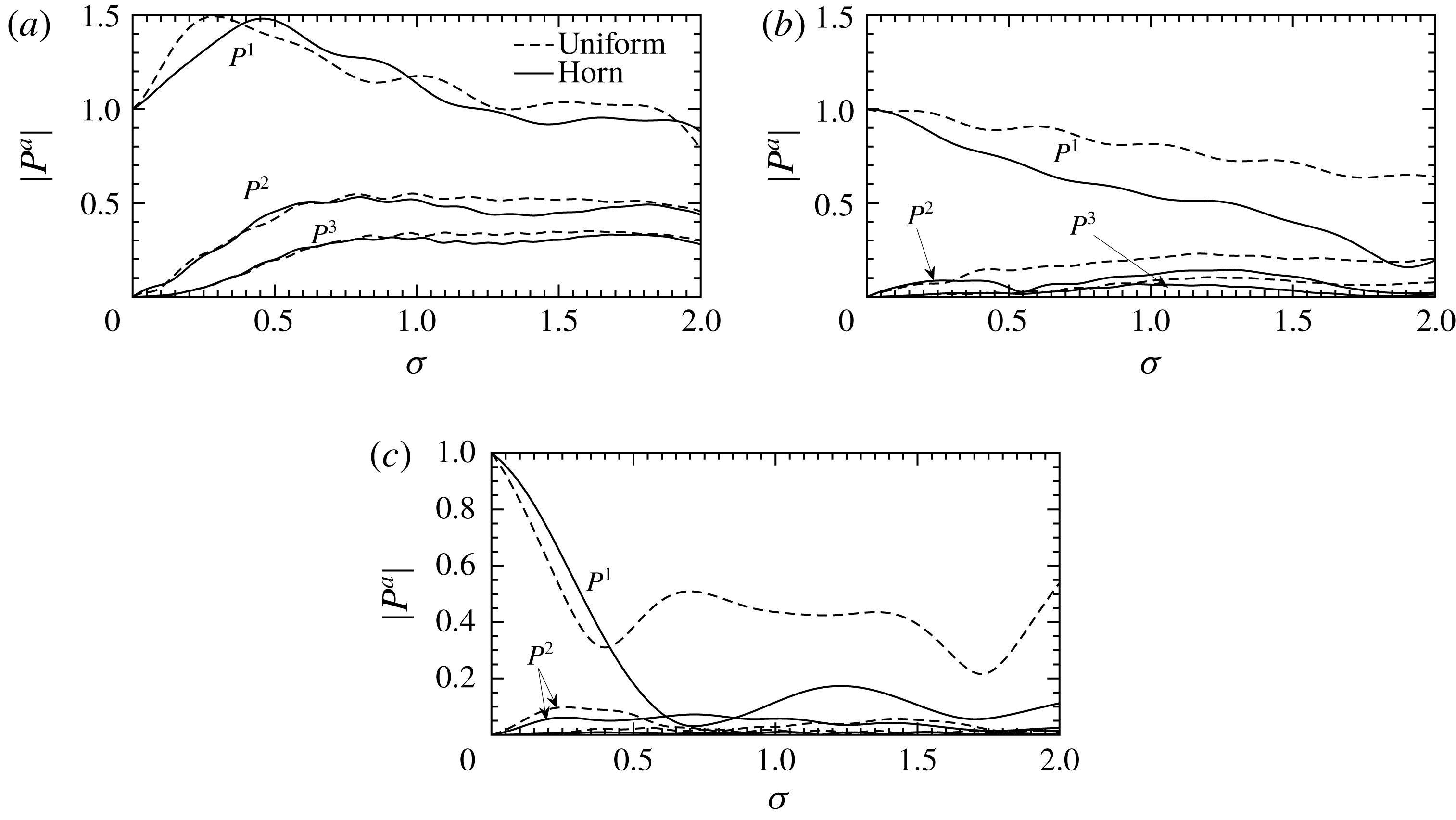
Figure 11. Comparing the modal amplitudes throughout the curved uniform duct to the curved horn along different paths. $M=2/(L\unicode[STIX]{x1D6FD}k)$ . (a) The outside of the bend, (b) the centre of the bend, (c) the inside of the bend.

Figures 9–11 compare the modal amplitudes throughout the ducts. As previously observed, the curved duct shows a strong harmonic enrichment on the outside of the duct bend at the cost of enrichment towards the centre and inside. Therefore it would seem that the ‘observability’ of the bend in a duct system – i.e. whether one could detect if there is a bend upstream – is dependant on whether the ensuing duct can support propagation of higher spatial modes. For low frequencies or narrow ducts it would seem likely that this extra harmonic enrichment would be lost due to reflection, but for high frequencies one could expect highly enriched localised sound to propagate downstream of a bend.

For the horn we compare the pressure normalised to the square root of the duct width to account for the spreading of the waveform. The harmonic enrichment is indeed less than a straight duct, with more energy remaining in the fundamental. However, as noted before, there is the potential for more energy to escape through these nonlinear effects.

These two effects can be seen to combine when comparing the curved uniform duct and the curved horn. While the horn effect reduces enrichment for most points across the duct, the curvature focuses the sound at the outer edge such that it is of comparable amplitude to the uniform curve. As the exit width is larger for the horn, some of these more localised modes can propagate out.

To better examine the downstream effects of the varying duct shape we consider the power spectrum associated with each of the duct modes. We vary the input power of our plane wave source and find the output power of the duct for each of the spatial modes and temporal harmonics (see figure 12). For the planar modes the straight duct provides the most enrichment with the curved ducts providing significantly less. When one looks at the higher spatial modes however, one finds a similar degree of enrichment, particularly with the curved horn (which has fewer cut off modes). As an aside it is also interesting to note that modes which would traditionally be cutoff and transmit no power in a linear regime can now do so at sufficiently high Mach numbers (see $P_{1}^{1}$ for the uniform curved duct).

Figure 12. Comparing the power outputs of the different ducts. (a) The planar modes, (b) mode 1, (c) mode 2.

7 Nonlinear reflection

As we have previously noted at several points, nonlinearity can transfer energy to higher modes and allow them to propagate in to regions where a linear wave would not. We have also observed modes which would not traditionally carry energy under a linear regime now doing so. This suggests it is important to reformulate our notions of reflection coefficients and matrices to also take into account the amplitude of the sound waves we are dealing with. We begin with the characteristic admittance relation for forward and backward propagating modes

(7.1) $$\begin{eqnarray}\boldsymbol{u}^{\pm }=\unicode[STIX]{x1D654}^{\pm }\boldsymbol{p}^{\pm }+{\mathcal{Y}}^{\pm }[\,\boldsymbol{p}^{\pm },\boldsymbol{p}^{\pm }].\end{eqnarray}$$

We now define a nonlinear reflection relation, relating forwards and backwards propagating pressure modes

(7.2) $$\begin{eqnarray}\boldsymbol{p}^{-}=\unicode[STIX]{x1D64D}\boldsymbol{p}^{+}+{\mathcal{R}}[\,\boldsymbol{p}^{+},\boldsymbol{p}^{+}],\end{eqnarray}$$

where $\unicode[STIX]{x1D64D}$ is the common reflection matrix encountered in the linear literature and ${\mathcal{R}}$ is the new nonlinear reflectance, both of which vary throughout the duct. From the standard impedance relation we have

(7.3) $$\begin{eqnarray}\boldsymbol{u}=\boldsymbol{u}^{+}+\boldsymbol{u}^{-}=\unicode[STIX]{x1D654}\boldsymbol{p}+{\mathcal{Y}}[\,\boldsymbol{p},\boldsymbol{p}]=\unicode[STIX]{x1D654}(\boldsymbol{p}^{+}+\boldsymbol{p}^{-})+{\mathcal{Y}}[\,\boldsymbol{p}^{+}+\boldsymbol{p}^{-},\boldsymbol{p}^{+}+\boldsymbol{p}^{-}].\end{eqnarray}$$

The $\boldsymbol{u}^{\pm }$ can be expressed in terms of $\boldsymbol{p}^{\pm }$ using (7.1) and, subsequently, the $\boldsymbol{p}^{-}$ can be expressed in terms of $\boldsymbol{p}^{+}$ using the reflection relation (7.2) to get

(7.4) $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D654}^{+}\boldsymbol{p}^{+}+{\mathcal{Y}}^{+}[\,\boldsymbol{p}^{+},\boldsymbol{p}^{+}]+\unicode[STIX]{x1D654}^{-}(\unicode[STIX]{x1D64D}\boldsymbol{p}^{+}+{\mathcal{R}}[\,\boldsymbol{p}^{+},\boldsymbol{p}^{+}])+{\mathcal{Y}}^{-}[\unicode[STIX]{x1D64D}\boldsymbol{p}^{+},\unicode[STIX]{x1D64D}\boldsymbol{p}^{+}]\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D654}(\boldsymbol{p}^{+}+\unicode[STIX]{x1D64D}\boldsymbol{p}^{+}+{\mathcal{R}}[\,\boldsymbol{p}^{+},\boldsymbol{p}^{+}])+{\mathcal{Y}}[\,\boldsymbol{p}^{+}+\unicode[STIX]{x1D64D}\boldsymbol{p}^{+},\boldsymbol{p}^{+}+\unicode[STIX]{x1D64D}\boldsymbol{p}^{+}].\end{eqnarray}$$

As with formulating our impedance relations, orders of magnitude can then be taken to form two distinct equations, and the $\boldsymbol{p}^{+}$ can be cancelled off. From this we obtain the usual definition of the reflection matrix

(7.5) $$\begin{eqnarray}\unicode[STIX]{x1D64D}=(\unicode[STIX]{x1D654}-\unicode[STIX]{x1D654}^{-})^{-1}(\unicode[STIX]{x1D654}^{+}-\unicode[STIX]{x1D654})\end{eqnarray}$$

and the new nonlinear reflectance

(7.6) $$\begin{eqnarray}{\mathcal{R}}=(\unicode[STIX]{x1D654}-\unicode[STIX]{x1D654}^{-})^{-1}({\mathcal{Y}}^{+}+{\mathcal{Y}}^{-}[\unicode[STIX]{x1D64D},\unicode[STIX]{x1D64D}]-{\mathcal{Y}}[\unicode[STIX]{x1D644}+\unicode[STIX]{x1D64D},\unicode[STIX]{x1D644}+\unicode[STIX]{x1D64D}]).\end{eqnarray}$$

We can use these to obtain the reflective properties of a duct. If we have an incident wave $\boldsymbol{p}^{+}$ , we can calculate the power associated with such a wave

(7.7) $$\begin{eqnarray}W^{+}=\text{Re}(\boldsymbol{p}^{+}\boldsymbol{\cdot }\overline{\boldsymbol{u}^{+}})=\text{Re}(\boldsymbol{p}^{+}\overline{\unicode[STIX]{x1D654}^{+}\boldsymbol{p}^{+}}+\boldsymbol{p}^{+}\overline{{\mathcal{Y}}^{+}}[\overline{\boldsymbol{p}^{+}},\overline{\boldsymbol{p}^{+}}]).\end{eqnarray}$$

The total pressure is given by

(7.8) $$\begin{eqnarray}\boldsymbol{p}=(\unicode[STIX]{x1D644}+\unicode[STIX]{x1D64D})\boldsymbol{p}^{+}+{\mathcal{R}}[\,\boldsymbol{p}^{+},\boldsymbol{p}^{+}].\end{eqnarray}$$

Therefore the total power is

(7.9) $$\begin{eqnarray}W=\text{Re}(\boldsymbol{p}\overline{\unicode[STIX]{x1D654}}\overline{\boldsymbol{p}}+\boldsymbol{p}\overline{{\mathcal{Y}}}[\overline{\boldsymbol{p}},\overline{\boldsymbol{p}}]).\end{eqnarray}$$

Unlike in the linear case the total energy flux is not a sum of $W^{+}$ and the analogous $W^{-}$ as there are nonlinear interactions. Instead we take our amplitude reflection modulus to be

(7.10) $$\begin{eqnarray}R=\sqrt{\frac{W-W^{+}}{W^{+}}}.\end{eqnarray}$$

Figure 13 shows how the amount of energy reflected in the depends both on frequency of the signal and the amplitude for the uniform curved duct studied in § 5.4. Low frequencies have a much lower dependence on amplitude than higher frequencies and larger amplitudes have a much more sensitive dependence on frequency, with interesting new resonances arising. Also plotted are the experimental results of Cabelli (Reference Cabelli1980). Nonlinearity may account for the discrepancy between the experimental results and the linear multimodal method, though as no amplitude was stated one cannot be certain.

Figure 14 is a similar plot for the elephant’s trunk described in § 5.5. In this case the effects of nonlinearity have little effect on the reflection coefficient – presumably due to the decreasing width not only reflecting many of the fundamental duct modes, but also many of the modes of the temporal harmonics as well. Thus, even though the sound is enriched, it is not enriched enough to propagate down the narrow exit.

Figure 15 illustrates the opposite effect for the horn described in § 5.3. Due to the increasing width, many of the modes of the harmonics produced by spectral enrichment can propagate, whereas the fundamental modes cannot. Therefore, as noted earlier, more energy can escape the horn as the enrichment increases. This is confirmed by this graph with higher Mach numbers reducing the reflection coefficient.

Figure 13. Modulus of the reflection coefficient at various amplitudes for the uniform curved duct described in § 5.4. The ‘ $\circ$ ’ are the experimental results of Cabelli (Reference Cabelli1980).

Figure 14. Modulus of the reflection coefficient at various amplitudes for the elephant’s trunk described in § 5.5.

Figure 15. Modulus of the reflection coefficient at various amplitudes for the elephant’s trunk described in § 5.3.