When an ultraintense (I₀ > 10¹⁷ W/cm²) and ultrashort (<1 ps) high-contrast laser beam interacts with a solid target, the density as well as the temperature gradients in the plasma are very steep because the energy deposition occurs almost instantaneously and within the skin depth (Brunel, 1987). At the highest intensities, the dominant processes of energy absorption are collisionless, and the energy is given to a minority population of high energy electrons. These collisionless mechanisms are particularly important at oblique incidence and with P-polarization. The contrast is crucial: Even a modest-intensity nanosecond prepulse can create a plasma with which the main pulse would interact, and the deposition would then occur at critical instead of at solid density (Kruer, 1988; Zhidkov et al., 2000). Here, we assume that energy is deposited at solid density.

The present study has been motivated by the Institut National de la Recherche Scientifique (INRS) experiments (Kieffer et al., 1996; Dorichies et al., 2001) to create a short duration, pointlike hard X-ray source, generated by the interaction of hot and thermal electrons with bound electrons in the solid material for medical purposes as well as for investigating molecular dynamics. Another reason for the great interest in hot electron transport in dense matter has arisen during the last few years because of the fast ignitor scheme (Tabak et al., 1994) for inertial confinement fusion (ICF). Our goal then is to quantify theoretically the transport of hot electrons or suprathermals into solid density plasmas, and their effect on the heating and ionization of the bulk plasma by numerically solving the electron kinetic equation. The generation of these electrons is not the subject of the present work; instead, we assume a source velocity distribution of hot electrons, partly based on K_α measurements (Kieffer et al., 1996; Dorichies et al., 2001) and we simulate their transport and their interaction with the bulk material.

The physical situation considered here can be summarized as follows: Due to the anomalous absorption mechanism during the laser beam interaction with the solid target, a minority population of high energy electrons is created in a region of about one skin depth (Brunel, 1987), which leave the target under the effect of the laser field component that oscillates in the direction normal to the target surface. Afterward, these electrons are pulled back to the target by the effect of electric field due to the less mobile target ions. For a large focal spot, this effect is immediate, so that the hot electron flux into the target has the same diameter and duration as the incident laser beam. But, for small spot sizes (<10 μm), as in the INRS experiments, the electrons can do more lengthy excursions in the vacuum before being pulled back, as evidenced by the fact that the X-ray emission size is larger than the laser spot and lasts longer than the incident laser pulse (Kieffer et al., 1996; Dorichies et al., 2001).

Because of the relevance of such studies for ICF, there have been several investigations in this subject by fully kinetic codes, especially particle-in-cell (PIC) ones (Gibbon & Bell, 1992; Sheng et al., 2000). However, the numerical constraints inherent to such codes did not allow investigating beyond 10 or 20 n_c, where n_c is the critical density for a given laser beam, whereas solid density is far higher. Also, the initial temperature had to be fairly high (one to several kiloelectron volts), so that the initial ionization physics could not be investigated. There is also another approach to investigating the hot electron transport in solid density plasmas, called “Hybrid,” in which hot electrons are simulated by the PIC approach while the cold or thermals are considered as a fluid (Davies et al., 1999). The reason for this is the fact that one needs to have a more accurate description of the transport of hot electrons in plasma, as they are mainly responsible for different anomalies and heating, and also, because of their relatively low density compared to the cold electrons, a kinetic treatment by the PIC method, which has a statistical limitation is then possible and valid. The thermal electrons are only responsible for return currents and the slowing down of the hot electron so they can be seen as a fluid component. Another alternative to the hybrid codes that is adopted in the present work is the Fokker–Planck approach, which consists of solving the Boltzmann equation with a Fokker–Planck collision operator. This equation gives the time dependence of the electron distribution function in phase space (x,v_x,v_⊥). The electron transport characteristics are then deduced from the different moments of this distribution function. This has the advantage that the “hot” as well as “cold” electrons are both treated kinetically. The Fokker–Planck equation is numerically solved with our code “FPI” (Matte & Virmont, 1982; Matte et al., 1988). This code is one dimensional in space (along the plasma inhomogeneity), and two dimensional in velocity space (v, μ = cos θ = v_x /v); the μ dependence is expanded in Legendre polynomials to order 3:

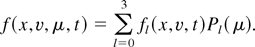
The Vlasov part includes advection (transport term: v_x∂f/∂x), as well as the electric field for quasi-neutrality and the resulting acceleration (−eE/m∂f/∂v_x). For Coulomb collisions there are the Fokker–Planck terms for e-i and e-e collisions. For the atomic physics we use the average ion model with the following processes: ionization, three-body recombination, excitation, collisional and radiative deexcitation, and pressure ionization. The implementation of this model in FPI is described by Ethier and Matte (2001). The code is nonrelativistic, which can be considered as a limitation that can be avoided by assuming a truncation of the electron distribution function below the speed of light, but this precludes very high hot electron temperatures. The ions are considered as a cold and immobile neutralizing background. The collisional heating mechanism is not taken into account for such short and high intensity pulses, as it was shown not to be important in such a situation (Yang et al., 1995). The boundary conditions were: reflecting on the left or hot side; fixed temperature on the right or cold side, that is, incoming particles are absorbed and an equivalent flux half-Maxwellian at the cold temperature (10 eV initially) is emitted.

At the beginning of the calculations, we consider a uniform and homogeneous aluminum plasma at solid density (N_i = 6 × 10²² cm⁻³). The initial electron distribution function is assumed to be an isotropic Maxwellian at a temperature of 10 eV, and the degree of ionization is 〈Z〉 = 3.15, which corresponds to local thermal equilibrium (LTE) for this density and temperature. As the process of hot electron generation is not treated here, we account for them as a source term in the following manner: At each time step, in the first four spatial cells, we reduce the electron distribution function by a factor F₂(t) that will be explained below and replace the removed particles by a hot Maxwellian. The amount of generated hot electrons is deduced from the assumption that the energy deposition, which is equal to the difference between the thermal energy of hot electrons and the energy of the electrons of the bulk in the first four cells (length L_H) per unit time is a fixed proportion of the absorbed laser energy, that is,

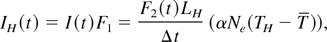
where F₁ is the fraction of the laser intensity I(t) absorbed by the plasma, which is chosen according to the experimental data (Kieffer et al., 1996), T_H is the temperature of hot electrons, which is a free parameter assumed to be between 20 and 40 keV, N_e is the electron density, F₂ is the portion of electrons that is replaced by hot electrons as the pulse interacts with the target. T is the average temperature of electrons in the depth L_H, which corresponds in our case to 4Δx:

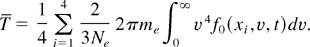
For the hot electron source in the L_H region, we considered two types of energy distributions, “1D” or “3D.” These notations are related to velocity dimensions; their meaning is simply

where

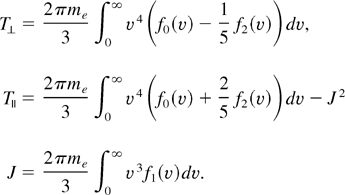
T_⊥, T_∥, and J are the perpendicular and parallel temperatures and the plasma current, respectively. Due to quasi-neutrality, we have J ≈ 0.

Two alternative hot electron source angular distributions were used: (1) isotropic, which means that the only nonzero component is the angle averaged distribution f_0Hot; (2) beamlike, where the hot electrons have only two possible orientations, backward and forward through the cold target; in such a case the hot electron source is represented not only by f_0Hot, but also with the set of even angular harmonics S_H2(v) = (2n + 1)S_H0(v), where n is a positive integer. The hot electrons emitted in the backward direction are reflected as soon as they reach the (reflecting) boundary on the left or laser side, so that in practice, this is equivalent to a beam injection, but it helped to stabilize the code. These variations on the energy and angle distribution of hot electrons concern only the source term. The evolution in space and time of the hot electrons (and of the thermals) is calculated self-consistently by the code.

To make the calculation relevant for intense femtolaser science as well as fast ignitor studies, we considered the following sets of parameters: solid density plasma of aluminum N_i = 6 × 10²² cm⁻³. Initially we have T_e = 10 eV and 〈Z〉 = 3.15. The laser beam characteristics are: single pulse with intensity into hot electrons I_0H = F₁ I₀ from 10¹⁶ to 10¹⁸ W/cm²; full width at half maximum (FWHM) of 600 fs to 1.2 ps. Below we present results concerning principally three cases:

This is a variation of case 1, to assess the effect of the angular distribution of the source. This is the case that we believe is more relevant to the INRS experiments (Kieffer et al., 1996; Dorichies et al., 2001).

Such a distribution corresponds to a very narrow cone in velocity space. In all cases, the time dependence of the laser intensity is assumed to be Gaussian, and the source temperature is assumed to vary with intensity as T_H(t)/T_0H = (I(t)/I₀)^1/3.

In Figures 1, 2, and 3, we have plotted the electron density, temperature, and heat flux at or near the peak of the pulse for each of these cases. These diagnostics include all electrons, and thus the temperature is two-thirds of the average electron energy, including both hots and thermals. As the ions are held fixed in this simulation, the density increase above N_e = 1.89 × 10²³ cm⁻³ (3.15 × 6 × 10²² cm⁻³) is entirely due to ionization. The plots (Figs. 1–3) show a stronger penetration of the heat and ionization fronts with a beamlike hot electron source (Fig. 2) compared to the isotropic assumption (Fig. 1). This can be intuitivley understood as the hot electrons stream directly inward for the beamlike case, whereas for an isotropic source, there is more energy deposition closer to the surface by those hot electrons whose initial velocity was more oblique. However, for the third case, the penetration is not deeper, although the hot electrons have a longer mean free path (T_H of 40 keV instead of 20 keV), and the reduction by half of the pulse length is clearly not enough to explain it. Rather, it is due to the greatly increased flux of hot electrons (J_H = 3I_H /2T_H), which in turn imposes a greatly increased E-field to ensure quasi-neutrality. This electric field reduces the penetration of the hot electrons, but also implies an enhanced joule heating of the bulk electrons.

Density, temperature and energy flux. I0Hot = 5 × 1016 W/cm2, T0Hot = 20 keV, isotropic, temporal FWHM = 1.2 ps, t = pulse maximum + 100 fs.

Density, temperature and energy flux. I0Hot = 5 × 1016 W/cm2, T0Hot = 20 keV, Beamlike, temporal FWHM = 1.2 ps, t = pulse maximum + 100 fs.

Density, temperature and energy flux. I0Hot = 1018 W/cm2, T0Hot = 40 keV, Beamlike, temporal FWHM = 0.6 ps, t = pulse maximum.

By making a two Maxwellian fit of the electron distribution functions obtained at different time steps, we can analyze the behavior of the cold and the hot components of plasma and their interaction with each other. The fit is obtained so that the moments of the approximation coincide with four moments of the real distribution function, that is,

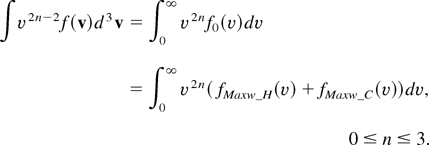
For n = 1 and n = 2 this means that the fit must match the particle number and total energy. f_{Maxw_H} is the Maxwellian distribution function that fits the hot or superthermal component of the plasma while f_{Maxw_C} represents the bulk or cold part. The fitting of the hot or cold Maxwellians is equivalent to obtaining “hot” and “cold” temperatures and densities, which we note, respectively, T_H, T_C, N_H, and N_C. An example of these quantities is illustrated in Figure 4, obtained by fitting the Fokker–Planck-derived electron distribution function for (case 2) 100 ps after the peak of the pulse. The large value of T_C near the left edge seen in Figure 4 is due to the strong resistive heating caused by the need to balance the intense flux of hot electrons.

Two Maxwellian fits: cold and hot densities and temperatures. I0Hot = 5 × 1016 W/cm2, T0Hot = 20 keV, Beamlike, temporal FWHM = 1.2 ps, t = pulse maximum + 100 fs.

Other important aspects of the hot electron transport were investigated as a part of the data processing of the results obtained in this work, among them the ion-acoustic and Weibel instabilities (Weibel, 1959; Bychenkov et al., 1988). To analyze the first kind of instability, that is, ion-acoustic, we have simply compared the drift velocity of electrons in the cold target to the sound speed, defined here as C_s* = (k_BT_e*/m_i)^1/2 and k_BT_e* = m_e /〈v⁻²〉, which is actually equivalent to the phase velocity for high k sound waves, and is due principally to slow electrons. The traditional sound speed, which is expressed as C_s = (k_BT_e /m_i)^1/2 and k_BT_e = (2/3)m_e〈v²〉, is not a good indicator as it takes into account both slow and high energy electrons. We have found that, for higher intensities (case 3), the drift velocity is higher than the sound speed C_s*, which indicates a likely growth of this instability, whereas the opposite was true for the low intensity cases 1 and 2. The Weibel instability was investigated by using the semicollisional dispersion relations described by Bendib and Luciani (1987), and previously used by Matte et al. (1987), in a more classical ICF context. This phenomenon is known to be the result of strong anisotropy in the electron distribution function, that is, 〈v_⊥²〉/〈v_∥²〉 ≠ 2 or a high ratio | f₂|/f₀, where f₀ and f₂ are, respectively, the isotropic and the second anisotropic components of the electron distribution function, which is indeed the case when a very strong laser field interacts with a cold solid target, and the instability can cause self-generated magnetic fields. In this context, if we consider the transport direction as the x-direction and the transverse one as the y-direction, then we have for f₂ < 0 an excited K_x mode, and for f₂ > 0 the K_y mode is excited. The results obtained show that only the K_y mode is excited for the beamlike hot electron distribution (strongly for the high intensity case 3, but weakly for the lower intensity case 2), whereas for an isotropic hot electron distribution (case 1), the K_x mode is weakly excited near the hot electron source, because fast electrons with large |v_x| spend less time near surface than electrons with the same v but with a larger v_⊥.

It is important to note that both instabilities could have an impact on the characteristics of the hot electron transport into the target, which includes, in particular, the hot and cold temperatures T_H, T_C: As the coupling of the hot and cold components of plasma is affected, the heat flux and degree of ionization could also be changed by the turbulence due to these instabilities.

The results presented in this work are helpful steps toward a full understanding of the kinetic character of hot electrons' dynamics in solid target under high intensity laser radiation, and the interaction with the bulk plasma. Nevertheless, there are many other important characteristics of hot electrons transport such as the electrical resistivity or electrical conductivity, multidimensional effects, relativistic effects, and others that are still to be investigated, so that one could have a clearer picture of the physics of hot electrons and their transport into solid targets. Some of these will be further studied in a future, more detailed article.