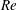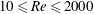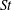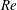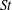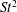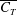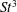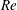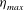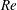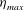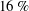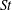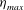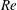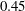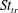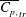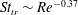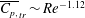1 Introduction
Unsteady flapping foil based thrusters have emerged as ideal candidates for enabling propulsion in bio-inspired and bio-mimetic devices such as autonomous underwater vehicles (Triantafyllou, Triantafyllou & Yue Reference Triantafyllou, Triantafyllou and Yue2000). To a large extent, this emergence has been driven by the extensive utilization of undulatory body motions in a wide spectrum of small to medium-sized swimming aquatic organisms. The prevalence of unsteady flapping-like undulatory thrust generating motions is indicative of their efficacy over a vast range of Reynolds numbers (
![]() $Re$
). Nevertheless, despite their versatility, unsteady flapping based thrust generation techniques remain vastly distinct from propulsive methods utilized by micro-sized organisms to overcome viscous drag at low
$Re$
). Nevertheless, despite their versatility, unsteady flapping based thrust generation techniques remain vastly distinct from propulsive methods utilized by micro-sized organisms to overcome viscous drag at low
![]() $Re$
(Lighthill Reference Lighthill1975). This disparity between propulsive techniques used by tiny (
$Re$
(Lighthill Reference Lighthill1975). This disparity between propulsive techniques used by tiny (
![]() $Re\ll 1$
) and large (
$Re\ll 1$
) and large (
![]() $Re\gg 1$
) living organisms, suggests that a deterioration in propulsive efficiency is expected below a certain threshold
$Re\gg 1$
) living organisms, suggests that a deterioration in propulsive efficiency is expected below a certain threshold
![]() $Re$
for flapping foils that employ time-reversible kinematics to generate thrust. This argument is supported by the findings of Birch, Dickson & Dickinson (Reference Birch, Dickson and Dickinson2004) who show that a reduction in
$Re$
for flapping foils that employ time-reversible kinematics to generate thrust. This argument is supported by the findings of Birch, Dickson & Dickinson (Reference Birch, Dickson and Dickinson2004) who show that a reduction in
![]() $Re$
from 1400 to 120 alters the flow topology significantly (also see Harbig, Sheridan & Thompson Reference Harbig, Sheridan and Thompson2013), leading to an appreciable reduction in the hydrodynamic forces in a flapping wing configuration. Given the recent thrust towards miniaturization of autonomous underwater and micro-air vehicles, a quantification of the propulsive performance at low
$Re$
from 1400 to 120 alters the flow topology significantly (also see Harbig, Sheridan & Thompson Reference Harbig, Sheridan and Thompson2013), leading to an appreciable reduction in the hydrodynamic forces in a flapping wing configuration. Given the recent thrust towards miniaturization of autonomous underwater and micro-air vehicles, a quantification of the propulsive performance at low
![]() $Re$
, and an inquiry into the existence of a threshold
$Re$
, and an inquiry into the existence of a threshold
![]() $Re$
for performance deterioration in flapping foil based thrust generating systems is of utmost importance and is a prerequisite for their successful utilization in small scale self-propelling devices.
$Re$
for performance deterioration in flapping foil based thrust generating systems is of utmost importance and is a prerequisite for their successful utilization in small scale self-propelling devices.
In this work, we investigate the existence of such a threshold of propulsive performance for a representative unsteady thrust generating configuration that consists of a single rigid pitching foil. In particular, we focus on establishing the dependency of the mean thrust, power consumption and propulsive efficiency on the prescribed kinematics (pitching frequency) at low and moderate Reynolds numbers (
![]() $10\leqslant Re\leqslant 2000$
). To begin with, we consider a fixed small angular amplitude of
$10\leqslant Re\leqslant 2000$
). To begin with, we consider a fixed small angular amplitude of
![]() $5^{\circ }$
that prevents flow separation at the leading edge, and a sinusoidal pitching profile for which the kinematics can be described simply through one single parameter, namely, the pitching frequency. Working in the aforementioned range of
$5^{\circ }$
that prevents flow separation at the leading edge, and a sinusoidal pitching profile for which the kinematics can be described simply through one single parameter, namely, the pitching frequency. Working in the aforementioned range of
![]() $Re$
, we span a wide range of Strouhal numbers
$Re$
, we span a wide range of Strouhal numbers
![]() $St$
(non-dimensional pitching frequency), for a clear identification of the efficiency peaks at each
$St$
(non-dimensional pitching frequency), for a clear identification of the efficiency peaks at each
![]() $Re$
(§ 3). The peak efficiency trends allows us to conclusively establish the range of
$Re$
(§ 3). The peak efficiency trends allows us to conclusively establish the range of
![]() $Re$
(
$Re$
(
![]() $Re\gtrapprox 1000$
) over which pitching foils produce thrust at low energetic cost. We observe a pronounced steep decline in peak efficiency from the global maximum asymptotic limit only below a threshold
$Re\gtrapprox 1000$
) over which pitching foils produce thrust at low energetic cost. We observe a pronounced steep decline in peak efficiency from the global maximum asymptotic limit only below a threshold
![]() $Re$
of
$Re$
of
![]() $1000$
. In the process, we also uncover a link between the relatively steep intermittent rise in the propulsive efficiency and the transitions in the wake patterns. Subsequently, we examine the generality of our principal conclusions concerning efficiency of thrust generation by investigating the effect of pitching angle on the propulsive performance for four additional angular amplitudes of
$1000$
. In the process, we also uncover a link between the relatively steep intermittent rise in the propulsive efficiency and the transitions in the wake patterns. Subsequently, we examine the generality of our principal conclusions concerning efficiency of thrust generation by investigating the effect of pitching angle on the propulsive performance for four additional angular amplitudes of
![]() ${\it\theta}_{0}=2^{\circ },8^{\circ },12^{\circ }$
and
${\it\theta}_{0}=2^{\circ },8^{\circ },12^{\circ }$
and
![]() $16^{\circ }$
(§ 5).
$16^{\circ }$
(§ 5).
Owing to their simplicity, pitching foils have been the subject of several experimental and simulation based investigations. Experimental and numerical investigations aimed at establishing the effect of pitching frequency on the wake and mean thrust characteristics of a NACA 0012 foil pitching about quarter chord with angular amplitudes of
![]() $2^{\circ }$
and
$2^{\circ }$
and
![]() $4^{\circ }$
at
$4^{\circ }$
at
![]() $Re$
of 12 000 were undertaken in Koochesfahani (Reference Koochesfahani1989) and Ramamurti & Sandberg (Reference Ramamurti and Sandberg2001), respectively. Improved estimates of the thrust produced by pitching foils at
$Re$
of 12 000 were undertaken in Koochesfahani (Reference Koochesfahani1989) and Ramamurti & Sandberg (Reference Ramamurti and Sandberg2001), respectively. Improved estimates of the thrust produced by pitching foils at
![]() $Re$
of 12 600 were obtained in Bohl & Koochesfahani (Reference Bohl and Koochesfahani2009) from a momentum deficit analysis that takes into account the streamwise velocity fluctuations. In a recent experimental investigation Mackowski & Williamson (Reference Mackowski and Williamson2015) report a peak propulsive efficiency of
$Re$
of 12 600 were obtained in Bohl & Koochesfahani (Reference Bohl and Koochesfahani2009) from a momentum deficit analysis that takes into account the streamwise velocity fluctuations. In a recent experimental investigation Mackowski & Williamson (Reference Mackowski and Williamson2015) report a peak propulsive efficiency of
![]() $12\,\%$
from load cell based direct measurements of the forces and moment acting on a NACA 0012 foil undergoing pure pitching motion at
$12\,\%$
from load cell based direct measurements of the forces and moment acting on a NACA 0012 foil undergoing pure pitching motion at
![]() $Re=16\,600$
.
$Re=16\,600$
.
Our interest, in contrast to these prior works, is in establishing an upper threshold of
![]() $Re$
below which the propulsive efficiency deteriorates appreciably. Note that such a deterioration must necessarily occur since the isotropic action of viscous forces precludes the possibility of thrust generation from symmetric pitching motions in the viscosity dominated Stokes regime at
$Re$
below which the propulsive efficiency deteriorates appreciably. Note that such a deterioration must necessarily occur since the isotropic action of viscous forces precludes the possibility of thrust generation from symmetric pitching motions in the viscosity dominated Stokes regime at
![]() $Re\ll 1$
(Scallop theorem). To our knowledge, an investigation aimed at establishing this practically relevant threshold of performance through a quantification of the energetic cost of thrust production from low
$Re\ll 1$
(Scallop theorem). To our knowledge, an investigation aimed at establishing this practically relevant threshold of performance through a quantification of the energetic cost of thrust production from low
![]() $Re$
pitching foils has not been undertaken until now. It is worth noting that the focus of prior low-
$Re$
pitching foils has not been undertaken until now. It is worth noting that the focus of prior low-
![]() $Re$
pitching foil investigations by Godoy-Diana, Aider & Wesfreid (Reference Godoy-Diana, Aider and Wesfreid2008) and Schnipper, Andersen & Bohr (Reference Schnipper, Andersen and Bohr2009) (also see Godoy-Diana et al.
Reference Godoy-Diana, Marais, Aider and Wesfreid2009) was purely on wake transitions at fixed
$Re$
pitching foil investigations by Godoy-Diana, Aider & Wesfreid (Reference Godoy-Diana, Aider and Wesfreid2008) and Schnipper, Andersen & Bohr (Reference Schnipper, Andersen and Bohr2009) (also see Godoy-Diana et al.
Reference Godoy-Diana, Marais, Aider and Wesfreid2009) was purely on wake transitions at fixed
![]() $Re$
of approximately
$Re$
of approximately
![]() $10^{3}$
. As shown in § 4 of this paper, the specific case investigated in Godoy-Diana et al. (Reference Godoy-Diana, Aider and Wesfreid2008) appears as a trend line on a general two-dimensional regime map that we have presented in figure 8 to illustrate the significant impact of a variation in
$10^{3}$
. As shown in § 4 of this paper, the specific case investigated in Godoy-Diana et al. (Reference Godoy-Diana, Aider and Wesfreid2008) appears as a trend line on a general two-dimensional regime map that we have presented in figure 8 to illustrate the significant impact of a variation in
![]() $Re$
and
$Re$
and
![]() $St$
on the wake behind a sinusoidally pitching foil.
$St$
on the wake behind a sinusoidally pitching foil.
Pitching foils belong to the more general class of flapping foil based propulsive configurations that rely on combined pitch and heave motions to generate mean thrust. Thrust generating rigid and flexible foils undergoing pure heave and combined pitch and heave motions have received enormous attention (Katz & Weihs Reference Katz and Weihs1978; Anderson et al.
Reference Anderson, Streitlien, Barrett and Triantafyllou1998; Wang Reference Wang2000; Lewin & Haj-Hariri Reference Lewin and Haj-Hariri2003; Heathcote & Gursul Reference Heathcote and Gursul2007; Eldredge, Toomey & Medina Reference Eldredge, Toomey and Medina2010; Dewey et al.
Reference Dewey, Boschitsch, Moored, Stone and Smits2013; Zhu, He & Zhang Reference Zhu, He and Zhang2014a
,Reference Zhu, He and Zhang
b
; Quinn, Lauder & Smits Reference Quinn, Lauder and Smits2015) due primarily to a strong connection with bio-locomotion (also see reviews of Triantafyllou et al.
Reference Triantafyllou, Triantafyllou and Yue2000; Shyy et al.
Reference Shyy, Aono, Chimakurthi, Trizila, Kang, Cesnik and Liu2010). In the present work, we study one of the more simple of these configurations, the pitching rigid foil, focussing our attention on the effect of
![]() $Re$
at relatively small angular amplitudes (
$Re$
at relatively small angular amplitudes (
![]() ${\it\theta}_{0}\leqslant 16^{\circ }$
). For this choice of
${\it\theta}_{0}\leqslant 16^{\circ }$
). For this choice of
![]() ${\it\theta}_{0}$
, the leading edge of a purely pitching foil experiences only small displacements, limiting both the maximum effective angle of attack and flow separation at the leading edge. Consequently, complex interactions between the vortices shed from the leading and trailing edges are minimal so that the wake patterns and the intensities of the shed vortices are determined predominantly by the trailing edge excursions. The effective isolation of the leading and trailing edge effects in a small-amplitude pitching foil enables a more focused exploration of the connection between the energetic cost of thrust generation and the wake patterns. Nevertheless, we do expect that some of the broad results from the present work, especially the ones concerning the effect of
${\it\theta}_{0}$
, the leading edge of a purely pitching foil experiences only small displacements, limiting both the maximum effective angle of attack and flow separation at the leading edge. Consequently, complex interactions between the vortices shed from the leading and trailing edges are minimal so that the wake patterns and the intensities of the shed vortices are determined predominantly by the trailing edge excursions. The effective isolation of the leading and trailing edge effects in a small-amplitude pitching foil enables a more focused exploration of the connection between the energetic cost of thrust generation and the wake patterns. Nevertheless, we do expect that some of the broad results from the present work, especially the ones concerning the effect of
![]() $Re$
on maximum propulsive efficiency, would extend to the other related configurations.
$Re$
on maximum propulsive efficiency, would extend to the other related configurations.
2 Problem definition and simulation methodology
The set-up we consider is similar to the one investigated by Koochesfahani (Reference Koochesfahani1989). We simulate the uniform incompressible flow of a Newtonian fluid with constant viscosity past a two-dimensional NACA 0012 foil undergoing sinusoidal pitching motion about its quarter chord. The set-up is described completely by the non-dimensional parameters
![]() $Re=U_{\infty }c/{\it\nu}$
and
$Re=U_{\infty }c/{\it\nu}$
and
![]() $St=fA/U_{\infty }$
, where
$St=fA/U_{\infty }$
, where
![]() $U_{\infty }$
,
$U_{\infty }$
,
![]() $c$
,
$c$
,
![]() ${\it\nu}$
,
${\it\nu}$
,
![]() $f$
and
$f$
and
![]() $A$
denote free stream velocity, foil chord, kinematic viscosity of the fluid, pitching frequency and the peak-to-peak trailing edge displacement, which serves as a good indicator of the wake width (Triantafyllou et al.
Reference Triantafyllou, Triantafyllou and Yue2000). The instantaneous pitching angle
$A$
denote free stream velocity, foil chord, kinematic viscosity of the fluid, pitching frequency and the peak-to-peak trailing edge displacement, which serves as a good indicator of the wake width (Triantafyllou et al.
Reference Triantafyllou, Triantafyllou and Yue2000). The instantaneous pitching angle
![]() ${\it\theta}={\it\theta}_{0}\cos (2{\rm\pi}ft)$
with
${\it\theta}={\it\theta}_{0}\cos (2{\rm\pi}ft)$
with
![]() ${\it\theta}_{0}=5^{\circ }$
. The influence of the amplitude of pitching angle
${\it\theta}_{0}=5^{\circ }$
. The influence of the amplitude of pitching angle
![]() ${\it\theta}_{0}$
on thrust generation and flow characteristics is considered later in § 5.
${\it\theta}_{0}$
on thrust generation and flow characteristics is considered later in § 5.
Next, we introduce performance metrics to quantify the energetic cost of thrust production from the pitching foil. The non-dimensional thrust coefficient
![]() $C_{T}=2T/({\it\rho}U_{\infty }^{2}c)$
, where
$C_{T}=2T/({\it\rho}U_{\infty }^{2}c)$
, where
![]() $T$
and
$T$
and
![]() ${\it\rho}$
represent the thrust force experienced by the foil and the density of fluid, respectively. Net power consumed in producing the thrust
${\it\rho}$
represent the thrust force experienced by the foil and the density of fluid, respectively. Net power consumed in producing the thrust
![]() $T$
is given by the non-dimensional power coefficient
$T$
is given by the non-dimensional power coefficient
![]() $C_{P}=-2M_{z}\dot{{\it\theta}}/({\it\rho}U_{\infty }^{3}c)$
, where
$C_{P}=-2M_{z}\dot{{\it\theta}}/({\it\rho}U_{\infty }^{3}c)$
, where
![]() $M_{z}$
is the instantaneous moment that acts on the foil about the pitching point at quarter chord and
$M_{z}$
is the instantaneous moment that acts on the foil about the pitching point at quarter chord and
![]() $\dot{{\it\theta}}=\text{d}{\it\theta}/\text{d}t$
denotes the angular velocity of the foil. The propulsive efficiency
$\dot{{\it\theta}}=\text{d}{\it\theta}/\text{d}t$
denotes the angular velocity of the foil. The propulsive efficiency
![]() ${\it\eta}=\overline{C_{T}}/\overline{C_{P}}$
gives a quantitative measure of the energetic cost of thrust production, where an overbar has been used to indicate mean quantities obtained through averaging over sufficiently long time intervals.
${\it\eta}=\overline{C_{T}}/\overline{C_{P}}$
gives a quantitative measure of the energetic cost of thrust production, where an overbar has been used to indicate mean quantities obtained through averaging over sufficiently long time intervals.
To establish the dependence of
![]() $\overline{C_{T}}$
,
$\overline{C_{T}}$
,
![]() $\overline{C_{P}}$
and
$\overline{C_{P}}$
and
![]() ${\it\eta}$
on
${\it\eta}$
on
![]() $Re$
and
$Re$
and
![]() $St$
, we simulate the set-up described above with prescribed foil kinematics on an unbounded two-dimensional domain using a high-resolution viscous vortex particle method. Given the good agreement between experimental findings and predictions from two-dimensional numerical simulations at a substantially high
$St$
, we simulate the set-up described above with prescribed foil kinematics on an unbounded two-dimensional domain using a high-resolution viscous vortex particle method. Given the good agreement between experimental findings and predictions from two-dimensional numerical simulations at a substantially high
![]() $Re$
of
$Re$
of
![]() $12\,000$
(Ramamurti & Sandberg Reference Ramamurti and Sandberg2001; Mackowski & Williamson Reference Mackowski and Williamson2015), it is reasonable to expect that three-dimensional effects would remain insignificant over the
$12\,000$
(Ramamurti & Sandberg Reference Ramamurti and Sandberg2001; Mackowski & Williamson Reference Mackowski and Williamson2015), it is reasonable to expect that three-dimensional effects would remain insignificant over the
![]() $Re$
and
$Re$
and
![]() $St$
range investigated here. We therefore expect our two-dimensional simulations to provide a fairly accurate description of the flow field associated with a pitching foil of infinite span.
$St$
range investigated here. We therefore expect our two-dimensional simulations to provide a fairly accurate description of the flow field associated with a pitching foil of infinite span.
The viscous vortex particle method (VVPM) (Cottet & Koumoutsakos Reference Cottet and Koumoutsakos2000; Koumoutsakos Reference Koumoutsakos2005) employed in our simulations is very similar to that of Eldredge (Reference Eldredge2007). It approximates the time-dependent incompressible Navier–Stokes equations in their Lagrangian form employing a representation of the vorticity field with a distribution of discrete overlapping vortex particles that possess a finite core. The method allows for the creation and evolution of these particles in such a way that the vorticity generation at the foil surface and its diffusion and advection throughout the fluid domain are modelled accurately. The distinguishing features of the VVPM include its natural adaptivity, which is a direct consequence of the Lagrangian treatment, and the transparency in application over unbounded domains which eliminates the complications that could arise from the prescription of outflow boundary conditions. Except for some key advances in the implementation related aspects (such as integration with the GPU (graphics processing unit) accelerated fast adaptive multipole method of Goude & Engblom (Reference Goude and Engblom2013)), which enables GPU-accelerated simulations employing multi-million particles to be run at an order of magnitude lower computational expense (compared to conventional CPU implementation), the methodology adopted in our work is the same as Eldredge (Reference Eldredge2007). Details of our GPU implementation along with results from comparative tests aimed at assessing the efficacy of the GPU implementation are provided in the accompanying supplementary material available at http://dx.doi.org/10.1017/jfm.2016.399.
3 Propulsive efficiency of thrust generation

Figure 1. Time-averaged (a) thrust and (b) power coefficients as a function of
![]() $St$
for varying
$St$
for varying
![]() $Re$
at a fixed
$Re$
at a fixed
![]() ${\it\theta}_{0}=5^{\circ }$
. Solid line in (b) is a cubic fit through the discrete data points.
${\it\theta}_{0}=5^{\circ }$
. Solid line in (b) is a cubic fit through the discrete data points.
We conduct simulations spanning the parametric space defined by
![]() $10\leqslant Re\leqslant 2000$
and a wide range of
$10\leqslant Re\leqslant 2000$
and a wide range of
![]() $St$
. Figure 1 depicts the mean thrust (
$St$
. Figure 1 depicts the mean thrust (
![]() $\overline{C_{T}}$
) and power coefficients (
$\overline{C_{T}}$
) and power coefficients (
![]() $\overline{C_{P}}$
) as a function of
$\overline{C_{P}}$
) as a function of
![]() $St$
obtained from these simulations over a range of
$St$
obtained from these simulations over a range of
![]() $Re$
. At zero
$Re$
. At zero
![]() $St$
, the foil remains stationary and experiences a net drag force represented by a corresponding drag coefficient (
$St$
, the foil remains stationary and experiences a net drag force represented by a corresponding drag coefficient (
![]() $C_{D0}$
), which decreases with
$C_{D0}$
), which decreases with
![]() $Re$
as seen in figure 1(a). We find the variation of
$Re$
as seen in figure 1(a). We find the variation of
![]() $C_{D0}$
with
$C_{D0}$
with
![]() $Re$
to be of the form
$Re$
to be of the form
![]() $C_{D0}=5.91Re^{-0.56}$
, where the exponent
$C_{D0}=5.91Re^{-0.56}$
, where the exponent
![]() $-0.56$
is found to be close to the
$-0.56$
is found to be close to the
![]() $1/\sqrt{Re}$
form, indicative of the dominance of viscous forces from the unseparated boundary layer over the stationary streamlined foil surface. An increase in
$1/\sqrt{Re}$
form, indicative of the dominance of viscous forces from the unseparated boundary layer over the stationary streamlined foil surface. An increase in
![]() $St$
results in a gradual decrease in the total drag. For a given
$St$
results in a gradual decrease in the total drag. For a given
![]() $Re$
, beyond a threshold
$Re$
, beyond a threshold
![]() $St$
, a crossover from drag to thrust (
$St$
, a crossover from drag to thrust (
![]() $\overline{C_{T}}>0$
) is observed. We denote the critical
$\overline{C_{T}}>0$
) is observed. We denote the critical
![]() $St$
for drag-to-thrust transition by
$St$
for drag-to-thrust transition by
![]() $St_{tr}=St(C_{T}=0)$
. At a given
$St_{tr}=St(C_{T}=0)$
. At a given
![]() $St$
, the mean thrust produced from the pitching motion rises substantially with an increase in
$St$
, the mean thrust produced from the pitching motion rises substantially with an increase in
![]() $Re$
over the range
$Re$
over the range
![]() $Re\leqslant 350$
. Subsequently, at
$Re\leqslant 350$
. Subsequently, at
![]() $Re>350$
, the rise in
$Re>350$
, the rise in
![]() $\overline{C_{T}}$
with further increments in
$\overline{C_{T}}$
with further increments in
![]() $Re$
becomes increasingly insignificant, which suggests a transition from viscous-to-inertial scaling for
$Re$
becomes increasingly insignificant, which suggests a transition from viscous-to-inertial scaling for
![]() $\overline{C_{T}}$
at sufficiently high
$\overline{C_{T}}$
at sufficiently high
![]() $St$
and
$St$
and
![]() $Re$
. In contrast, the power consumed in sustaining the pitching motions (
$Re$
. In contrast, the power consumed in sustaining the pitching motions (
![]() $\overline{C_{P}}$
) exhibits a strong inertial scaling of
$\overline{C_{P}}$
) exhibits a strong inertial scaling of
![]() $St^{3}$
(also see the explanation below) that is almost insensitive to a change in
$St^{3}$
(also see the explanation below) that is almost insensitive to a change in
![]() $Re$
(figure 1
b).
$Re$
(figure 1
b).

Figure 2. (a) Propulsive efficiency
![]() ${\it\eta}$
as a function of
${\it\eta}$
as a function of
![]() $St$
for varying
$St$
for varying
![]() $Re$
at a fixed
$Re$
at a fixed
![]() ${\it\theta}_{0}=5^{\circ }$
. The symbols and lines that are used to distinguish between different
${\it\theta}_{0}=5^{\circ }$
. The symbols and lines that are used to distinguish between different
![]() $Re$
are the same as in figure 1. For each
$Re$
are the same as in figure 1. For each
![]() $Re$
, the points corresponding to drag-to-thrust transition and maximum
$Re$
, the points corresponding to drag-to-thrust transition and maximum
![]() ${\it\eta}$
are marked with (●) and (▪), respectively. The dotted black line represents a large
${\it\eta}$
are marked with (●) and (▪), respectively. The dotted black line represents a large
![]() $St$
upper envelope of all the
$St$
upper envelope of all the
![]() ${\it\eta}$
versus
${\it\eta}$
versus
![]() $St$
curves associated with constant
$St$
curves associated with constant
![]() $Re$
. The dash dots (– ⋅ – ⋅ –) indicate a fit through the points (▪) associated with maximum
$Re$
. The dash dots (– ⋅ – ⋅ –) indicate a fit through the points (▪) associated with maximum
![]() ${\it\eta}$
. (b) Drag-to-thrust transition Strouhal number
${\it\eta}$
. (b) Drag-to-thrust transition Strouhal number
![]() $St_{tr}$
(●) and corresponding mean power coefficient
$St_{tr}$
(●) and corresponding mean power coefficient
![]() $\overline{C_{P}}_{,tr}$
(○) as a function of
$\overline{C_{P}}_{,tr}$
(○) as a function of
![]() $Re$
.
$Re$
.
Figure 2(a) illustrates the propulsive efficiency
![]() ${\it\eta}$
computed from the ratio of
${\it\eta}$
computed from the ratio of
![]() $\overline{C_{T}}$
and
$\overline{C_{T}}$
and
![]() $\overline{C_{P}}$
depicted in figure 1. At low
$\overline{C_{P}}$
depicted in figure 1. At low
![]() $St$
, the propulsive efficiency remains negative as the foil experiences a net drag. For
$St$
, the propulsive efficiency remains negative as the foil experiences a net drag. For
![]() $St>St_{tr}$
,
$St>St_{tr}$
,
![]() ${\it\eta}$
becomes positive and continues to rise further with
${\it\eta}$
becomes positive and continues to rise further with
![]() $St$
. At each
$St$
. At each
![]() $Re$
, a distinct sharp increment in efficiency is clearly evidenced from figure 2(a). The specific
$Re$
, a distinct sharp increment in efficiency is clearly evidenced from figure 2(a). The specific
![]() $St$
at which this sharp increase in
$St$
at which this sharp increase in
![]() ${\it\eta}$
occurs decreases with
${\it\eta}$
occurs decreases with
![]() $Re$
and is intricately linked to the extent of wake deflection (see § 4). For more rigorous pitching at moderate
$Re$
and is intricately linked to the extent of wake deflection (see § 4). For more rigorous pitching at moderate
![]() $St$
, the rate of increase of
$St$
, the rate of increase of
![]() $\overline{C_{P}}$
overwhelms that of
$\overline{C_{P}}$
overwhelms that of
![]() $\overline{C_{T}}$
so that the efficiency decreases after attaining a maximum. We denote this maximum
$\overline{C_{T}}$
so that the efficiency decreases after attaining a maximum. We denote this maximum
![]() ${\it\eta}$
and the corresponding Strouhal number by
${\it\eta}$
and the corresponding Strouhal number by
![]() ${\it\eta}_{max}$
and
${\it\eta}_{max}$
and
![]() $St_{max}$
, respectively. For sufficiently large
$St_{max}$
, respectively. For sufficiently large
![]() $St$
, the high intensity of pitching yields inertial scalings of the form
$St$
, the high intensity of pitching yields inertial scalings of the form
![]() $\overline{C_{T}}\sim St^{2}$
and
$\overline{C_{T}}\sim St^{2}$
and
![]() $\overline{C_{P}}\sim St^{3}$
, which are reflected in the asymptotic behaviour of
$\overline{C_{P}}\sim St^{3}$
, which are reflected in the asymptotic behaviour of
![]() ${\it\eta}$
at large
${\it\eta}$
at large
![]() $St$
(
$St$
(
![]() ${\it\eta}\sim St^{-1}$
for
${\it\eta}\sim St^{-1}$
for
![]() $Re\geqslant 1000$
and
$Re\geqslant 1000$
and
![]() $St>0.6$
as shown in figure 2
a). The aforementioned scaling laws for
$St>0.6$
as shown in figure 2
a). The aforementioned scaling laws for
![]() $\overline{C_{T}}$
,
$\overline{C_{T}}$
,
![]() $\overline{C_{P}}$
and
$\overline{C_{P}}$
and
![]() ${\it\eta}$
at high
${\it\eta}$
at high
![]() $St$
can be derived from physical arguments as shown later in this section. It may be noted here that this trend persists even at lower
$St$
can be derived from physical arguments as shown later in this section. It may be noted here that this trend persists even at lower
![]() $Re=10$
,
$Re=10$
,
![]() $50$
and
$50$
and
![]() $100$
, but occurs at higher
$100$
, but occurs at higher
![]() $St$
that extends beyond the range (
$St$
that extends beyond the range (
![]() $St\leqslant 1$
) illustrated in figure 2(a). The general form of dependency of
$St\leqslant 1$
) illustrated in figure 2(a). The general form of dependency of
![]() ${\it\eta}$
on
${\it\eta}$
on
![]() $St$
observed in our work is consistent with earlier experimental investigations on pitching foils (Dewey et al.
Reference Dewey, Boschitsch, Moored, Stone and Smits2013; Mackowski & Williamson Reference Mackowski and Williamson2015), and other flapping foil motions (Anderson et al.
Reference Anderson, Streitlien, Barrett and Triantafyllou1998; Lewin & Haj-Hariri Reference Lewin and Haj-Hariri2003; Heathcote & Gursul Reference Heathcote and Gursul2007).
$St$
observed in our work is consistent with earlier experimental investigations on pitching foils (Dewey et al.
Reference Dewey, Boschitsch, Moored, Stone and Smits2013; Mackowski & Williamson Reference Mackowski and Williamson2015), and other flapping foil motions (Anderson et al.
Reference Anderson, Streitlien, Barrett and Triantafyllou1998; Lewin & Haj-Hariri Reference Lewin and Haj-Hariri2003; Heathcote & Gursul Reference Heathcote and Gursul2007).
The crossover from negative to positive propulsive efficiencies allows for a clear identification of
![]() $St_{tr}$
for drag-to-thrust transition from figure 2(a). It is possible to derive a relationship that expresses the dependency of drag-to-thrust transition Strouhal number
$St_{tr}$
for drag-to-thrust transition from figure 2(a). It is possible to derive a relationship that expresses the dependency of drag-to-thrust transition Strouhal number
![]() $St_{tr}$
on
$St_{tr}$
on
![]() $Re$
by considering a balance between the time-averaged drag force arising out of skin friction that acts along the foil surface, and the thrust generated from the time-periodic sinusoidal pitching motion. To arrive at such a relationship we first derive expressions that relate time-averaged drag force and the thrust generated to the kinematic parameters and fluid properties as shown below.
$Re$
by considering a balance between the time-averaged drag force arising out of skin friction that acts along the foil surface, and the thrust generated from the time-periodic sinusoidal pitching motion. To arrive at such a relationship we first derive expressions that relate time-averaged drag force and the thrust generated to the kinematic parameters and fluid properties as shown below.
An estimate for the viscous resistance to the foil motion must account for a potential increase in the skin friction due to a reduction in the boundary layer thickness on the surface towards which the rigid airfoil moves. Application of the Bone–Lighthill boundary layer thinning hypothesis (Lighthill Reference Lighthill1971; Ehrenstein & Eloy Reference Ehrenstein and Eloy2013; Ehrenstein, Marquillie & Eloy Reference Ehrenstein, Marquillie and Eloy2014) then leads to the following estimate
for the cycle-averaged axial (longitudinal) drag force per unit length
![]() $\overline{D_{A}}$
experienced by the foil, where
$\overline{D_{A}}$
experienced by the foil, where
![]() $\overline{|U_{N}|}$
represents the mean absolute value of the normal foil velocity (Ehrenstein et al.
Reference Ehrenstein, Marquillie and Eloy2014) and the exponent of
$\overline{|U_{N}|}$
represents the mean absolute value of the normal foil velocity (Ehrenstein et al.
Reference Ehrenstein, Marquillie and Eloy2014) and the exponent of
![]() $Re$
is in accord with the previously obtained scaling exponent for
$Re$
is in accord with the previously obtained scaling exponent for
![]() $C_{D0}$
. Furthermore, since
$C_{D0}$
. Furthermore, since
![]() $\overline{|U_{N}|}\sim Af$
we obtain the mean axial drag coefficient
$\overline{|U_{N}|}\sim Af$
we obtain the mean axial drag coefficient
To obtain an expression for the thrust generated by the foil motion we follow the arguments outlined in Gazzola, Argentina & Mahadevan (Reference Gazzola, Argentina and Mahadevan2014). The pitching motion of the airfoil induces a local fluid acceleration that scales as
![]() $Af^{2}$
. The resulting reaction force exerted on the airfoil by the surrounding fluid therefore scales as
$Af^{2}$
. The resulting reaction force exerted on the airfoil by the surrounding fluid therefore scales as
![]() ${\it\rho}c^{2}Af^{2}$
. Furthermore, since the angle between the foil axis and the free stream
${\it\rho}c^{2}Af^{2}$
. Furthermore, since the angle between the foil axis and the free stream
![]() ${\sim}A/c$
, the thrust generated from the pitching action of the airfoil is given by
${\sim}A/c$
, the thrust generated from the pitching action of the airfoil is given by
![]() $\overline{T_{N}}\sim {\it\rho}cA^{2}f^{2}$
. The mean normal thrust coefficient therefore assumes the following form:
$\overline{T_{N}}\sim {\it\rho}cA^{2}f^{2}$
. The mean normal thrust coefficient therefore assumes the following form:
At drag-to-thrust transition, a balance between the mean normal thrust coefficient and the cycle-averaged axial drag coefficient (
![]() $\overline{C_{T}^{(N)}}=\overline{C_{D}^{(A)}}$
) yields
$\overline{C_{T}^{(N)}}=\overline{C_{D}^{(A)}}$
) yields
![]() $St_{tr}\sim Re^{-0.37}$
. We find that the discrete data points for
$St_{tr}\sim Re^{-0.37}$
. We find that the discrete data points for
![]() $St_{tr}$
at various
$St_{tr}$
at various
![]() $Re$
obtained from our simulation runs are in remarkable consistency with the scaling law derived above (see figure 2
b). Moreover, for this self-propelling state, we find that the mean power coefficient
$Re$
obtained from our simulation runs are in remarkable consistency with the scaling law derived above (see figure 2
b). Moreover, for this self-propelling state, we find that the mean power coefficient
![]() $\overline{C_{P}}_{,tr}=\overline{C_{P}}(\overline{C_{T}}=0)$
too can be expressed through a simple relationship:
$\overline{C_{P}}_{,tr}=\overline{C_{P}}(\overline{C_{T}}=0)$
too can be expressed through a simple relationship:
![]() $\overline{C_{P}}_{,tr}\sim Re^{-1.12}$
, the
$\overline{C_{P}}_{,tr}\sim Re^{-1.12}$
, the
![]() $Re$
exponent in this case being 3 times the
$Re$
exponent in this case being 3 times the
![]() $Re$
exponent for
$Re$
exponent for
![]() $St_{tr}$
. This again is in accordance with our earlier observation and the analysis presented below in that
$St_{tr}$
. This again is in accordance with our earlier observation and the analysis presented below in that
![]() $\overline{C_{P}}\sim St^{3}$
.
$\overline{C_{P}}\sim St^{3}$
.

Figure 3. The mean (a) normal and (b) axial thrust coefficients (
![]() $\overline{C_{T}^{(N)}}$
and
$\overline{C_{T}^{(N)}}$
and
![]() $\overline{C_{T}^{(A)}}$
, respectively) as a function of
$\overline{C_{T}^{(A)}}$
, respectively) as a function of
![]() $St$
for varying
$St$
for varying
![]() $Re$
at a fixed
$Re$
at a fixed
![]() ${\it\theta}_{0}=5^{\circ }$
.
${\it\theta}_{0}=5^{\circ }$
.
To further assess the validity of the scaling laws derived above, we illustrate the dependence of the mean axial (
![]() $\overline{C_{T}^{(A)}}$
) and normal (
$\overline{C_{T}^{(A)}}$
) and normal (
![]() $\overline{C_{T}^{(N)}}$
) contributions to the net thrust, on
$\overline{C_{T}^{(N)}}$
) contributions to the net thrust, on
![]() $St$
, for varying
$St$
, for varying
![]() $Re$
in figure 3. The fact that the normal contribution
$Re$
in figure 3. The fact that the normal contribution
![]() $\overline{C_{T}^{(N)}}$
is thrust producing and, more importantly, scales as
$\overline{C_{T}^{(N)}}$
is thrust producing and, more importantly, scales as
![]() $St^{2}$
independently of
$St^{2}$
independently of
![]() $Re$
, lends support to the expression (3.3) derived from physical arguments. Furthermore, we find that the axial contribution
$Re$
, lends support to the expression (3.3) derived from physical arguments. Furthermore, we find that the axial contribution
![]() $\overline{C_{T}^{(A)}}$
to be negative and drag producing in accordance with the prior findings and the Bone–Lighthill boundary layer thinning hypothesis (Lighthill Reference Lighthill1971; Ehrenstein & Eloy Reference Ehrenstein and Eloy2013; Ehrenstein et al.
Reference Ehrenstein, Marquillie and Eloy2014). Moreover, the drag-producing axial contribution
$\overline{C_{T}^{(A)}}$
to be negative and drag producing in accordance with the prior findings and the Bone–Lighthill boundary layer thinning hypothesis (Lighthill Reference Lighthill1971; Ehrenstein & Eloy Reference Ehrenstein and Eloy2013; Ehrenstein et al.
Reference Ehrenstein, Marquillie and Eloy2014). Moreover, the drag-producing axial contribution
![]() $-\overline{C_{T}^{(A)}}$
exhibits a strong
$-\overline{C_{T}^{(A)}}$
exhibits a strong
![]() $Re$
dependence and monotonic increase with
$Re$
dependence and monotonic increase with
![]() $St$
before, up to and slightly beyond the drag-to-thrust transition point just before the onset of significant asymmetry in the wake. This is again consistent with the expected
$St$
before, up to and slightly beyond the drag-to-thrust transition point just before the onset of significant asymmetry in the wake. This is again consistent with the expected
![]() $Re$
-dependent increase in the viscous resistance to the airfoil motion owing to a reduction in the boundary layer thickness on the surface towards which the rigid airfoil moves during the half-cycle (Lighthill Reference Lighthill1971; Ehrenstein & Eloy Reference Ehrenstein and Eloy2013; Ehrenstein et al.
Reference Ehrenstein, Marquillie and Eloy2014). It is worth noting that the estimate for
$Re$
-dependent increase in the viscous resistance to the airfoil motion owing to a reduction in the boundary layer thickness on the surface towards which the rigid airfoil moves during the half-cycle (Lighthill Reference Lighthill1971; Ehrenstein & Eloy Reference Ehrenstein and Eloy2013; Ehrenstein et al.
Reference Ehrenstein, Marquillie and Eloy2014). It is worth noting that the estimate for
![]() $\overline{C_{D}^{(A)}}$
(or equivalently
$\overline{C_{D}^{(A)}}$
(or equivalently
![]() $\overline{C_{T}^{(A)}}=-\overline{C_{D}^{(A)}}$
) given by (3.2) has a limited range of applicability. In particular, the estimate is certainly not applicable in the limit
$\overline{C_{T}^{(A)}}=-\overline{C_{D}^{(A)}}$
) given by (3.2) has a limited range of applicability. In particular, the estimate is certainly not applicable in the limit
![]() $St\rightarrow 0$
, in which case the boundary layer thickness is determined by the free stream velocity and not the vanishingly small normal foil velocity. Moreover, beyond a certain
$St\rightarrow 0$
, in which case the boundary layer thickness is determined by the free stream velocity and not the vanishingly small normal foil velocity. Moreover, beyond a certain
![]() $St$
, the wake deflection becomes significant so that the pressure contribution to the axial thrust becomes increasingly important. The expression (3.2) which considers contributions from skin friction drag only is certainly not applicable in such scenarios.
$St$
, the wake deflection becomes significant so that the pressure contribution to the axial thrust becomes increasingly important. The expression (3.2) which considers contributions from skin friction drag only is certainly not applicable in such scenarios.
Interestingly, the scaling law of
![]() $St_{tr}\sim Re^{-0.37}$
derived for drag-to-thrust transition in the present rigid pitching airfoil configuration differs markedly from the scaling law of
$St_{tr}\sim Re^{-0.37}$
derived for drag-to-thrust transition in the present rigid pitching airfoil configuration differs markedly from the scaling law of
![]() $St\sim Re^{-0.25}$
for undulatory propulsion that is obtained from a balance of normal thrust and viscous resistance without accounting for the normal motion-induced reduction in the boundary layer thickness (Gazzola et al.
Reference Gazzola, Argentina and Mahadevan2014). The difference between these two scaling laws is indicative of the disparity between the present set-up that relies on pure rigid pitching motions and aquatic locomotion where a reduction in boundary layer thickness is most likely prevented through travelling-wave-like undulatory motion of flexible tails. Nonetheless, our simulation results and the analysis above clearly indicate that a
$St\sim Re^{-0.25}$
for undulatory propulsion that is obtained from a balance of normal thrust and viscous resistance without accounting for the normal motion-induced reduction in the boundary layer thickness (Gazzola et al.
Reference Gazzola, Argentina and Mahadevan2014). The difference between these two scaling laws is indicative of the disparity between the present set-up that relies on pure rigid pitching motions and aquatic locomotion where a reduction in boundary layer thickness is most likely prevented through travelling-wave-like undulatory motion of flexible tails. Nonetheless, our simulation results and the analysis above clearly indicate that a
![]() $St$
-dependent normal surface-motion-induced reduction in the boundary layer thickness and a corresponding increase in the viscous resistance are both expected to prevail in configurations wherein rigid surfaces undergo motion perpendicular to the free stream direction.
$St$
-dependent normal surface-motion-induced reduction in the boundary layer thickness and a corresponding increase in the viscous resistance are both expected to prevail in configurations wherein rigid surfaces undergo motion perpendicular to the free stream direction.
At relatively high
![]() $St$
, the mean normal contribution to the thrust is expected to completely overwhelm the drag-producing axial contribution. In such cases, since
$St$
, the mean normal contribution to the thrust is expected to completely overwhelm the drag-producing axial contribution. In such cases, since
![]() $\overline{C_{T}}\approx \overline{C_{T}^{(N)}}$
, as evident from figure 3(a), one would expect the mean thrust generated from the pitching motion to follow the scaling law
$\overline{C_{T}}\approx \overline{C_{T}^{(N)}}$
, as evident from figure 3(a), one would expect the mean thrust generated from the pitching motion to follow the scaling law
![]() $\overline{C_{T}}\sim St^{2}$
. Moreover, since the moment
$\overline{C_{T}}\sim St^{2}$
. Moreover, since the moment
![]() $M_{z}\sim St^{2}$
, one obtains
$M_{z}\sim St^{2}$
, one obtains
![]() $\overline{C_{P}}\sim St^{3}$
in good accord with the trends depicted in figure 1(b). Thus, for sufficiently high
$\overline{C_{P}}\sim St^{3}$
in good accord with the trends depicted in figure 1(b). Thus, for sufficiently high
![]() $St$
, the scaling laws for
$St$
, the scaling laws for
![]() $\overline{C_{T}}$
and
$\overline{C_{T}}$
and
![]() $\overline{C_{P}}$
yield
$\overline{C_{P}}$
yield
![]() ${\it\eta}\sim St^{-1}$
in good agreement with the propulsive efficiency trends depicted in figure 2(a).
${\it\eta}\sim St^{-1}$
in good agreement with the propulsive efficiency trends depicted in figure 2(a).

Figure 4. Variation with
![]() $Re$
of (a) the maximum efficiency (
$Re$
of (a) the maximum efficiency (
![]() ${\it\eta}_{max}$
) and (b) the corresponding Strouhal number (
${\it\eta}_{max}$
) and (b) the corresponding Strouhal number (
![]() $St_{max}$
) at
$St_{max}$
) at
![]() ${\it\theta}_{0}=5^{\circ }$
for the present work and prior investigations on pitching foils at higher
${\it\theta}_{0}=5^{\circ }$
for the present work and prior investigations on pitching foils at higher
![]() $Re$
. Lu, Xie & Zhang (Reference Lu, Xie and Zhang2013) and Mackowski & Williamson (Reference Mackowski and Williamson2015) investigate a NACA 0012 foil pitching about its quarter chord with
$Re$
. Lu, Xie & Zhang (Reference Lu, Xie and Zhang2013) and Mackowski & Williamson (Reference Mackowski and Williamson2015) investigate a NACA 0012 foil pitching about its quarter chord with
![]() ${\it\theta}_{0}=5^{\circ }$
and
${\it\theta}_{0}=5^{\circ }$
and
![]() $8^{\circ }$
, respectively. Dewey et al. (Reference Dewey, Boschitsch, Moored, Stone and Smits2013) examine a truncated foil with a flat plate pitching about its leading edge, attached to its rear.
$8^{\circ }$
, respectively. Dewey et al. (Reference Dewey, Boschitsch, Moored, Stone and Smits2013) examine a truncated foil with a flat plate pitching about its leading edge, attached to its rear.
The efficiency trends depicted in figure 2(a) also allow for an explicit identification of the maximum achievable efficiency
![]() ${\it\eta}_{max}$
and the corresponding Strouhal number
${\it\eta}_{max}$
and the corresponding Strouhal number
![]() $St_{max}$
for each
$St_{max}$
for each
![]() $Re$
, as shown in figure 4. In the viscosity dominated regime (
$Re$
, as shown in figure 4. In the viscosity dominated regime (
![]() $Re\ll 1$
), the symmetric action of the pitching foil produces no thrust so that the corresponding
$Re\ll 1$
), the symmetric action of the pitching foil produces no thrust so that the corresponding
![]() ${\it\eta}_{max}$
is expected to remain negligibly small. With increase in
${\it\eta}_{max}$
is expected to remain negligibly small. With increase in
![]() $Re$
,
$Re$
,
![]() ${\it\eta}_{max}$
rises gradually from about 0.65 % at
${\it\eta}_{max}$
rises gradually from about 0.65 % at
![]() $Re=10$
to almost
$Re=10$
to almost
![]() $1.71\,\%$
at
$1.71\,\%$
at
![]() $Re=50$
. For intermediate
$Re=50$
. For intermediate
![]() $Re\sim O(10^{2})$
,
$Re\sim O(10^{2})$
,
![]() ${\it\eta}_{max}$
rises sharply reaching 15.1 % at
${\it\eta}_{max}$
rises sharply reaching 15.1 % at
![]() $Re=10^{3}$
. In particular, a rapid rise in
$Re=10^{3}$
. In particular, a rapid rise in
![]() ${\it\eta}_{max}$
is observed between
${\it\eta}_{max}$
is observed between
![]() $Re=100$
and
$Re=100$
and
![]() $350$
, with the enhancement in
$350$
, with the enhancement in
![]() ${\it\eta}_{max}$
diminishing substantially for
${\it\eta}_{max}$
diminishing substantially for
![]() $Re>350$
. Beyond
$Re>350$
. Beyond
![]() $Re=1000$
,
$Re=1000$
,
![]() ${\it\eta}_{max}$
remains largely unchanged and saturates to an upper threshold of approximately
${\it\eta}_{max}$
remains largely unchanged and saturates to an upper threshold of approximately
![]() $16\,\%$
as shown in figure 4(a). The corresponding Strouhal number for peak propulsive efficiency also exhibits a similar trend, with
$16\,\%$
as shown in figure 4(a). The corresponding Strouhal number for peak propulsive efficiency also exhibits a similar trend, with
![]() $St_{max}$
decreasing monotonically with
$St_{max}$
decreasing monotonically with
![]() $Re$
, and reaching an asymptotic value of about
$Re$
, and reaching an asymptotic value of about
![]() $0.45$
(see figure 4
b).
$0.45$
(see figure 4
b).
The global maximum peak efficiency estimate of
![]() $16\,\%$
from our simulations is in fairly good agreement with the peak efficiencies of
$16\,\%$
from our simulations is in fairly good agreement with the peak efficiencies of
![]() $16\,\%$
for a flat plate pitching about its leading edge at
$16\,\%$
for a flat plate pitching about its leading edge at
![]() $Re=7200$
(Dewey et al.
Reference Dewey, Boschitsch, Moored, Stone and Smits2013, experiments) and
$Re=7200$
(Dewey et al.
Reference Dewey, Boschitsch, Moored, Stone and Smits2013, experiments) and
![]() $18\,\%$
for a NACA 0012 foil pitching about its quarter chord at
$18\,\%$
for a NACA 0012 foil pitching about its quarter chord at
![]() $Re=13\,500$
(Lu et al.
Reference Lu, Xie and Zhang2013, two-dimensional simulations). Our global maximum of 16 % is higher than the maximum efficiency of 12 % reported in the experiments of Mackowski & Williamson (Reference Mackowski and Williamson2015) for a set-up similar to ours, but for an amplitude of
$Re=13\,500$
(Lu et al.
Reference Lu, Xie and Zhang2013, two-dimensional simulations). Our global maximum of 16 % is higher than the maximum efficiency of 12 % reported in the experiments of Mackowski & Williamson (Reference Mackowski and Williamson2015) for a set-up similar to ours, but for an amplitude of
![]() $8^{\circ }$
at higher
$8^{\circ }$
at higher
![]() $Re=16\,600$
. This discrepancy may be due to the smaller range of Strouhal numbers investigated in their experiments (
$Re=16\,600$
. This discrepancy may be due to the smaller range of Strouhal numbers investigated in their experiments (
![]() $St<0.33$
), with our simulations predicting a
$St<0.33$
), with our simulations predicting a
![]() $St_{max}$
value of approximately 0.45 at high
$St_{max}$
value of approximately 0.45 at high
![]() $Re$
.
$Re$
.
The asymptotic
![]() $St_{max}$
of
$St_{max}$
of
![]() $0.45$
obtained from our present investigation is on the higher side and lies outside the
$0.45$
obtained from our present investigation is on the higher side and lies outside the
![]() $St$
range of 0.2–0.4 that generally holds for high propulsive efficiency undulatory bio-locomotion (Taylor, Nudds & Thomas Reference Taylor, Nudds and Thomas2003). The fact that the asymptotic limit of
$St$
range of 0.2–0.4 that generally holds for high propulsive efficiency undulatory bio-locomotion (Taylor, Nudds & Thomas Reference Taylor, Nudds and Thomas2003). The fact that the asymptotic limit of
![]() $St_{max}=0.45$
determined in our work is higher than the upper limit of
$St_{max}=0.45$
determined in our work is higher than the upper limit of
![]() $0.4$
for undulatory propulsion is consistent with the expectation that the optimal
$0.4$
for undulatory propulsion is consistent with the expectation that the optimal
![]() $St$
for high-efficiency thrust generation would in general exceed the optimal
$St$
for high-efficiency thrust generation would in general exceed the optimal
![]() $St$
for energetically efficient self-propulsion. Moreover, over the moderate Reynolds numbers range of
$St$
for energetically efficient self-propulsion. Moreover, over the moderate Reynolds numbers range of
![]() $500\leqslant Re\leqslant 2000$
, we observe that the drag-to-thrust transition Strouhal number
$500\leqslant Re\leqslant 2000$
, we observe that the drag-to-thrust transition Strouhal number
![]() $St_{tr}$
corresponding to a self-propelling pitching foil decreases monotonically from
$St_{tr}$
corresponding to a self-propelling pitching foil decreases monotonically from
![]() $0.39$
(at
$0.39$
(at
![]() $Re=500$
) to
$Re=500$
) to
![]() $0.23$
(at
$0.23$
(at
![]() $Re=2000$
, see figure 2
b). Thus, for
$Re=2000$
, see figure 2
b). Thus, for
![]() $500\leqslant Re\leqslant 2000$
,
$500\leqslant Re\leqslant 2000$
,
![]() $St_{tr}$
lies well within the Strouhal number range of 0.2–0.4 for high-efficiency self-propulsion, in accordance with the observation of Taylor et al. (Reference Taylor, Nudds and Thomas2003).
$St_{tr}$
lies well within the Strouhal number range of 0.2–0.4 for high-efficiency self-propulsion, in accordance with the observation of Taylor et al. (Reference Taylor, Nudds and Thomas2003).
4 Wake characterization

Figure 5. Effect of (a)
![]() $Re$
at
$Re$
at
![]() $St=0.4$
and (b)
$St=0.4$
and (b)
![]() $St$
at
$St$
at
![]() $Re=750$
on the vorticity field for a fixed
$Re=750$
on the vorticity field for a fixed
![]() ${\it\theta}_{0}=5^{\circ }$
. Dashed vertical lines (orange) indicate the location at which an appreciable asymmetry can be detected in the arrangement of the wake vortices. The six wake patterns in (b) at
${\it\theta}_{0}=5^{\circ }$
. Dashed vertical lines (orange) indicate the location at which an appreciable asymmetry can be detected in the arrangement of the wake vortices. The six wake patterns in (b) at
![]() $Re=750$
correspond to the points (1) to (6) marked in figure 2(a).
$Re=750$
correspond to the points (1) to (6) marked in figure 2(a).
Variations in
![]() $Re$
and
$Re$
and
![]() $St$
induce systematic changes in the wake that are reflected in the sizes and arrangement of shed vortices. These changes in the wake signature are quite informative and provide useful insights into both thrust production and propulsive efficiency characteristics of the pitching foil. Figure 5(a) illustrates the sensitivity of the wake to variations in
$St$
induce systematic changes in the wake that are reflected in the sizes and arrangement of shed vortices. These changes in the wake signature are quite informative and provide useful insights into both thrust production and propulsive efficiency characteristics of the pitching foil. Figure 5(a) illustrates the sensitivity of the wake to variations in
![]() $Re$
through the instantaneous vorticity contours at a fixed
$Re$
through the instantaneous vorticity contours at a fixed
![]() $St=0.4$
. At low
$St=0.4$
. At low
![]() $Re\leqslant 200$
, the dominance of viscosity is clearly evidenced in the thick boundary layers that are formed at the foil surface and the localized trailing edge vortices which dissipate rapidly within a few chord lengths in the near wake. The harmonic motion of the trailing edge leads to formation of the classical von Kármán vortex street at
$Re\leqslant 200$
, the dominance of viscosity is clearly evidenced in the thick boundary layers that are formed at the foil surface and the localized trailing edge vortices which dissipate rapidly within a few chord lengths in the near wake. The harmonic motion of the trailing edge leads to formation of the classical von Kármán vortex street at
![]() $Re=50,100$
and 200 that is aligned with the free stream. With increase in
$Re=50,100$
and 200 that is aligned with the free stream. With increase in
![]() $Re$
, the wake undergoes a transition from von Kármán to reverse von Kármán vortex street as evidenced from a switch in the relative positions of the clockwise and counter-clockwise vortices with respect to the centreline at
$Re$
, the wake undergoes a transition from von Kármán to reverse von Kármán vortex street as evidenced from a switch in the relative positions of the clockwise and counter-clockwise vortices with respect to the centreline at
![]() $Re=350$
(see figure 5
a). Our classification of wake vortices into the two distinct categories of classical and reverse von Kármán vortex street is based on not just the arrangement of vortices but also on the direction of the jet flow that is produced in the wake of the pitching foil, in a reference frame attached to the free stream. Throughout this work, we have labelled the wake vortices to be classical or reverse von Kármán depending on whether this jet is directed against (forward jet) or along (rear jet) the flow direction. With further increase in
$Re=350$
(see figure 5
a). Our classification of wake vortices into the two distinct categories of classical and reverse von Kármán vortex street is based on not just the arrangement of vortices but also on the direction of the jet flow that is produced in the wake of the pitching foil, in a reference frame attached to the free stream. Throughout this work, we have labelled the wake vortices to be classical or reverse von Kármán depending on whether this jet is directed against (forward jet) or along (rear jet) the flow direction. With further increase in
![]() $Re$
, the vortex street develops asymmetry and deflects upwards at an angle with respect to the free stream. The wake deflection is intensified and the strength of shed vortices progressively enhanced between
$Re$
, the vortex street develops asymmetry and deflects upwards at an angle with respect to the free stream. The wake deflection is intensified and the strength of shed vortices progressively enhanced between
![]() $Re=350$
and
$Re=350$
and
![]() $2000$
.
$2000$
.
The complex interplay between viscous and inertial effects that gives rise to the wake transitions is more clearly revealed in figure 5(b) through an illustration of the effect of
![]() $St$
on wake dynamics at a fixed
$St$
on wake dynamics at a fixed
![]() $Re=750$
. The propulsive efficiency (
$Re=750$
. The propulsive efficiency (
![]() ${\it\eta}$
) corresponding to the 6 cases shown here may be seen from the corresponding points marked (1) to (6) in figure 2(a). At a low pitching frequency, corresponding to
${\it\eta}$
) corresponding to the 6 cases shown here may be seen from the corresponding points marked (1) to (6) in figure 2(a). At a low pitching frequency, corresponding to
![]() $St=0.275$
, the wake is already in the form of a reverse von Kármán street, but with a net drag (point
$St=0.275$
, the wake is already in the form of a reverse von Kármán street, but with a net drag (point
![]() $(1)$
in figure 2
a). With an increase in
$(1)$
in figure 2
a). With an increase in
![]() $St$
, the thrust production rises monotonically, and we find the wake patterns to be discernibly more asymmetric downstream of the foil. Even at
$St$
, the thrust production rises monotonically, and we find the wake patterns to be discernibly more asymmetric downstream of the foil. Even at
![]() $St=0.275$
, one can see asymmetry developing approximately 4 chord lengths downstream of the foil (marked using the dashed vertical line (orange)). However, with increase in
$St=0.275$
, one can see asymmetry developing approximately 4 chord lengths downstream of the foil (marked using the dashed vertical line (orange)). However, with increase in
![]() $St$
, the location at which the asymmetry becomes appreciable (marked using the vertical dashed lines (orange)) shifts continuously towards the trailing edge. A careful inspection of the efficiency trends depicted in figure 2(a), and the wake patterns depicted in figure 5(b), indicates that pronounced increments that are observed in the efficiency around
$St$
, the location at which the asymmetry becomes appreciable (marked using the vertical dashed lines (orange)) shifts continuously towards the trailing edge. A careful inspection of the efficiency trends depicted in figure 2(a), and the wake patterns depicted in figure 5(b), indicates that pronounced increments that are observed in the efficiency around
![]() $St\approx 0.4$
correspond directly to the increased interaction between the pitching foil and the deflected wake owing to the shift in the location of asymmetry. For
$St\approx 0.4$
correspond directly to the increased interaction between the pitching foil and the deflected wake owing to the shift in the location of asymmetry. For
![]() $St=0.450$
, the asymmetry sets in almost at the trailing edge of the pitching foil and further increments in
$St=0.450$
, the asymmetry sets in almost at the trailing edge of the pitching foil and further increments in
![]() $St$
lead to only marginal gains in the efficiency of thrust production (see figure 2
a).
$St$
lead to only marginal gains in the efficiency of thrust production (see figure 2
a).
In general, the net time-averaged force exerted on the airfoil can be resolved into components along and perpendicular to the direction of the free stream. In the deflected wake regime, the component perpendicular to the direction of the free stream does not vanish and results in a mean lift. Since only a fraction of the net force exerted on the airfoil is converted into a net thrust, one would expect
![]() $\overline{C_{T}}$
to actually decrease after the onset of wake deflection. In this sense, the steep increase in
$\overline{C_{T}}$
to actually decrease after the onset of wake deflection. In this sense, the steep increase in
![]() $\overline{C_{T}}$
and
$\overline{C_{T}}$
and
![]() ${\it\eta}$
with wake deflection and the occurrence of peak efficiency in the deflected wake regime are both counter-intuitive.
${\it\eta}$
with wake deflection and the occurrence of peak efficiency in the deflected wake regime are both counter-intuitive.
To shed light on the link between the observed enhancement in the mean thrust coefficient and the increased interaction between the airfoil and the deflected wake, we analyse the change in pressure and viscous contributions to the total thrust with rising
![]() $St$
at a fixed
$St$
at a fixed
![]() $Re$
of 750. As shown in figure 6(a), the viscous contribution to the net thrust (
$Re$
of 750. As shown in figure 6(a), the viscous contribution to the net thrust (
![]() $\overline{C_{T}^{(v)}}$
) is negative for a stationary airfoil (
$\overline{C_{T}^{(v)}}$
) is negative for a stationary airfoil (
![]() $St=0$
) and decreases further with an increase in
$St=0$
) and decreases further with an increase in
![]() $St$
. Thus, the viscous stresses lead to a net drag that rises gradually with increasing
$St$
. Thus, the viscous stresses lead to a net drag that rises gradually with increasing
![]() $St$
. The monotonic increase in
$St$
. The monotonic increase in
![]() $-\overline{C_{T}^{(v)}}$
with
$-\overline{C_{T}^{(v)}}$
with
![]() $St$
is indicative of an overall decrease in the boundary layer thickness on the surface towards which the rigid airfoil moves during the half-cycle and is consistent with prior findings and the Bone–Lighthill boundary layer thinning hypothesis (Lighthill Reference Lighthill1971; Ehrenstein & Eloy Reference Ehrenstein and Eloy2013; Ehrenstein et al.
Reference Ehrenstein, Marquillie and Eloy2014).
$St$
is indicative of an overall decrease in the boundary layer thickness on the surface towards which the rigid airfoil moves during the half-cycle and is consistent with prior findings and the Bone–Lighthill boundary layer thinning hypothesis (Lighthill Reference Lighthill1971; Ehrenstein & Eloy Reference Ehrenstein and Eloy2013; Ehrenstein et al.
Reference Ehrenstein, Marquillie and Eloy2014).

Figure 6. (a) Time-averaged thrust coefficient (
![]() $\overline{C_{T}}$
) and the pressure and viscous contributions (
$\overline{C_{T}}$
) and the pressure and viscous contributions (
![]() $\overline{C_{T}^{(p)}}$
and
$\overline{C_{T}^{(p)}}$
and
![]() $\overline{C_{T}^{(v)}}$
, respectively) as a function of
$\overline{C_{T}^{(v)}}$
, respectively) as a function of
![]() $St$
at
$St$
at
![]() $Re=750$
and
$Re=750$
and
![]() ${\it\theta}_{0}=5^{\circ }$
. (b) Thrust coefficient (
${\it\theta}_{0}=5^{\circ }$
. (b) Thrust coefficient (
![]() $C_{T}$
) and the pressure and viscous contributions to the thrust coefficient (
$C_{T}$
) and the pressure and viscous contributions to the thrust coefficient (
![]() $C_{T}^{(p)}$
and
$C_{T}^{(p)}$
and
![]() $C_{T}^{(v)}$
, respectively) as a function of time at
$C_{T}^{(v)}$
, respectively) as a function of time at
![]() $Re=750$
and
$Re=750$
and
![]() ${\it\theta}_{0}=5^{\circ }$
for
${\it\theta}_{0}=5^{\circ }$
for
![]() $St=0.375$
,
$St=0.375$
,
![]() $0.400$
and
$0.400$
and
![]() $0.425$
. Here,
$0.425$
. Here,
![]() $T$
denotes the time period of pitching motion and
$T$
denotes the time period of pitching motion and
![]() $t_{0}\gg T$
.
$t_{0}\gg T$
.
In contrast, the pressure contribution to the net thrust (
![]() $\overline{C_{T}^{(p)}}$
) is positive for almost all
$\overline{C_{T}^{(p)}}$
) is positive for almost all
![]() $St$
(except for very small
$St$
(except for very small
![]() $St$
for which the drag-producing pressure and viscous contributions combine to yield a negative thrust). The rate of increase of
$St$
for which the drag-producing pressure and viscous contributions combine to yield a negative thrust). The rate of increase of
![]() $\overline{C_{T}^{(p)}}$
with
$\overline{C_{T}^{(p)}}$
with
![]() $St$
overwhelms the rate at which
$St$
overwhelms the rate at which
![]() $\overline{C_{T}^{(v)}}$
decreases and rises sharply beyond
$\overline{C_{T}^{(v)}}$
decreases and rises sharply beyond
![]() $St\approx 0.4$
(see figure 6
a). Moreover, beyond
$St\approx 0.4$
(see figure 6
a). Moreover, beyond
![]() $St\approx 0.4$
, the location at which an appreciable asymmetry in the arrangement of shed vortices can be detected moves to within a cord length from the airfoil trailing edge. Thus, the increased interaction between the pitching airfoil and the deflected wake leads to a sharp rise in
$St\approx 0.4$
, the location at which an appreciable asymmetry in the arrangement of shed vortices can be detected moves to within a cord length from the airfoil trailing edge. Thus, the increased interaction between the pitching airfoil and the deflected wake leads to a sharp rise in
![]() $\overline{C_{T}^{(p)}}$
and therefore
$\overline{C_{T}^{(p)}}$
and therefore
![]() $\overline{C_{T}}$
. The reduction in proximity between the location of the wake deflection and the airfoil’s trailing edge, however, has no noticeable influence on the drag-producing viscous contribution
$\overline{C_{T}}$
. The reduction in proximity between the location of the wake deflection and the airfoil’s trailing edge, however, has no noticeable influence on the drag-producing viscous contribution
![]() $\overline{C_{T}^{(v)}}$
.
$\overline{C_{T}^{(v)}}$
.
The temporal variations of the instantaneous pressure and viscous contributions to
![]() $\overline{C_{T}}$
at
$\overline{C_{T}}$
at
![]() $St=0.375$
,
$St=0.375$
,
![]() $0.4$
and
$0.4$
and
![]() $0.425$
, as shown in figure 6(b), clearly indicate that the sharp increase in the mean
$0.425$
, as shown in figure 6(b), clearly indicate that the sharp increase in the mean
![]() $\overline{C_{T}^{(p)}}$
(and therefore
$\overline{C_{T}^{(p)}}$
(and therefore
![]() $\overline{C_{T}}$
) results from a prominent rise in the peak
$\overline{C_{T}}$
) results from a prominent rise in the peak
![]() $C_{T}^{(p)}$
. In particular, an increase in
$C_{T}^{(p)}$
. In particular, an increase in
![]() $St$
from
$St$
from
![]() $0.375$
to
$0.375$
to
![]() $0.400$
leads to only a marginal rise in the peak
$0.400$
leads to only a marginal rise in the peak
![]() $C_{T}^{(p)}$
and
$C_{T}^{(p)}$
and
![]() $C_{T}$
. However, a further increase in
$C_{T}$
. However, a further increase in
![]() $St$
by the same amount from
$St$
by the same amount from
![]() $0.400$
to
$0.400$
to
![]() $0.425$
results in a much more prominent increase in the peak
$0.425$
results in a much more prominent increase in the peak
![]() $C_{T}^{(p)}$
, the rise being maximum at time instants that correspond to phases of
$C_{T}^{(p)}$
, the rise being maximum at time instants that correspond to phases of
![]() $180^{\circ }$
and
$180^{\circ }$
and
![]() $0^{\circ }$
for which the foil attains its extreme angular positions. On the contrary, the minimum
$0^{\circ }$
for which the foil attains its extreme angular positions. On the contrary, the minimum
![]() $C_{T}^{(p)}$
exhibits no appreciable change with
$C_{T}^{(p)}$
exhibits no appreciable change with
![]() $St$
. The viscous contribution to the net thrust
$St$
. The viscous contribution to the net thrust
![]() $C_{T}^{(v)}$
too remains relatively insensitive to the changes in
$C_{T}^{(v)}$
too remains relatively insensitive to the changes in
![]() $St$
from
$St$
from
![]() $0.375$
to
$0.375$
to
![]() $0.4$
and
$0.4$
and
![]() $0.425$
. In essence, the steep increase in the time-averaged thrust coefficient
$0.425$
. In essence, the steep increase in the time-averaged thrust coefficient
![]() $\overline{C_{T}}$
for
$\overline{C_{T}}$
for
![]() $St\gtrapprox 0.4$
is directly linked to a sharp rise in both the mean and the peak
$St\gtrapprox 0.4$
is directly linked to a sharp rise in both the mean and the peak
![]() $C_{T}^{(p)}$
.
$C_{T}^{(p)}$
.
The sharp rise in the
![]() $C_{T}^{(p)}$
between
$C_{T}^{(p)}$
between
![]() $St=0.4$
and
$St=0.4$
and
![]() $0.425$
is observed at time instants that correspond to the maximum airfoil acceleration. A close inspection of the flow field in the vicinity of the leading edge at the lowermost position of the airfoil’s leading edge (
$0.425$
is observed at time instants that correspond to the maximum airfoil acceleration. A close inspection of the flow field in the vicinity of the leading edge at the lowermost position of the airfoil’s leading edge (
![]() $0^{\circ }$
phase) reveals a substantial change in the vorticity distribution between
$0^{\circ }$
phase) reveals a substantial change in the vorticity distribution between
![]() $St=0.4$
and
$St=0.4$
and
![]() $0.425$
cases (see figure 7
a). Furthermore, the reduced proximity between the location corresponding to the onset of wake deflection and the airfoil’s trailing edge leads to a stronger interaction between the boundary layer on the airfoil surface and the asymmetrically shed vortices. These deflected wake-induced changes in the vorticity distribution in the vicinity of the leading edge have a significant impact on the pressure contribution to the thrust coefficient.
$0.425$
cases (see figure 7
a). Furthermore, the reduced proximity between the location corresponding to the onset of wake deflection and the airfoil’s trailing edge leads to a stronger interaction between the boundary layer on the airfoil surface and the asymmetrically shed vortices. These deflected wake-induced changes in the vorticity distribution in the vicinity of the leading edge have a significant impact on the pressure contribution to the thrust coefficient.

Figure 7. (a) Vorticity field in the vicinity of the leading edge of the airfoil for
![]() $St=0.4$
and
$St=0.4$
and
![]() $0.425$
at
$0.425$
at
![]() $Re=750$
,
$Re=750$
,
![]() ${\it\theta}_{0}=5^{\circ }$
and a phase of
${\it\theta}_{0}=5^{\circ }$
and a phase of
![]() $0^{\circ }$
(corresponding to the lowermost position of the airfoil’s leading edge). (b) Contributions to
$0^{\circ }$
(corresponding to the lowermost position of the airfoil’s leading edge). (b) Contributions to
![]() $\overline{C_{T}^{(p)}}$
from the airfoil’s leading edge (
$\overline{C_{T}^{(p)}}$
from the airfoil’s leading edge (
![]() $\overline{C_{T,LE}^{(p)}}$
) and the remaining section behind the pivot point (
$\overline{C_{T,LE}^{(p)}}$
) and the remaining section behind the pivot point (
![]() $\overline{C_{T}^{(p)}}$
–
$\overline{C_{T}^{(p)}}$
–
![]() $\overline{C_{T,LE}^{(p)}}$
) as a function of
$\overline{C_{T,LE}^{(p)}}$
) as a function of
![]() $St$
at
$St$
at
![]() $Re=750$
and
$Re=750$
and
![]() ${\it\theta}_{0}=5^{\circ }$
.
${\it\theta}_{0}=5^{\circ }$
.
To quantify the effect of variations in the vorticity distribution at the leading edge on cycle-averaged
![]() $C_{T}^{(p)}$
, we define
$C_{T}^{(p)}$
, we define
![]() $C_{T,LE}^{(p)}$
as the leading edge contribution to
$C_{T,LE}^{(p)}$
as the leading edge contribution to
![]() $C_{T}^{(p)}$
obtained by integrating the pressure distribution (vorticity flux in vortex methods, see Wu, Ma & Zhou (Reference Wu, Ma and Zhou2007)) over the portion of the airfoil surface that lies ahead of the pivot point (between the pivot point and the leading edge). Figure 7(b) depicts
$C_{T}^{(p)}$
obtained by integrating the pressure distribution (vorticity flux in vortex methods, see Wu, Ma & Zhou (Reference Wu, Ma and Zhou2007)) over the portion of the airfoil surface that lies ahead of the pivot point (between the pivot point and the leading edge). Figure 7(b) depicts
![]() $\overline{C_{T,LE}^{(p)}}$
and the time-averaged contribution to
$\overline{C_{T,LE}^{(p)}}$
and the time-averaged contribution to
![]() $\overline{C_{T}^{(p)}}$
from the airfoil section behind the pivot point (
$\overline{C_{T}^{(p)}}$
from the airfoil section behind the pivot point (
![]() $\overline{C_{T}^{(p)}}-\overline{C_{T,LE}^{(p)}}$
) as a function of
$\overline{C_{T}^{(p)}}-\overline{C_{T,LE}^{(p)}}$
) as a function of
![]() $St$
at a fixed Reynolds number of 750. We find that for
$St$
at a fixed Reynolds number of 750. We find that for
![]() $St\in (0.1,0.4)$
, the leading edge contribution
$St\in (0.1,0.4)$
, the leading edge contribution
![]() $\overline{C_{T,LE}^{(p)}}$
amounts to a net drag that remains insensitive to the changes in the wake pattern (von-Kármán to reverse von Kármán). Beyond
$\overline{C_{T,LE}^{(p)}}$
amounts to a net drag that remains insensitive to the changes in the wake pattern (von-Kármán to reverse von Kármán). Beyond
![]() $St\gtrapprox 0.4$
, however, the interaction of the pitching foil with the asymmetric wake leads to a sharp rise in
$St\gtrapprox 0.4$
, however, the interaction of the pitching foil with the asymmetric wake leads to a sharp rise in
![]() $\overline{C_{T,LE}^{(p)}}$
and an eventual crossover from drag production to thrust generation (
$\overline{C_{T,LE}^{(p)}}$
and an eventual crossover from drag production to thrust generation (
![]() $\overline{C_{T,LE}^{(p)}}$
undergoes sign inversion). In contrast, the section behind the pivot point contributes to a net thrust that rises gradually with
$\overline{C_{T,LE}^{(p)}}$
undergoes sign inversion). In contrast, the section behind the pivot point contributes to a net thrust that rises gradually with
![]() $St$
for all
$St$
for all
![]() $St>0.1$
.
$St>0.1$
.
The trends described above allow us to conclusively establish that the sharp increase in the pressure contribution to the thrust generated at the leading edge, owing to a strong interaction between the pitching foil and the deflected wake, is the principal reason behind the steep rise in cycle-averaged thrust coefficient. Clearly the steep rise in the pressure contribution more than compensates for not just the increase in viscous drag with
![]() $St$
but also the inevitable loss in thrust that results from a fraction of excess wake momentum being converted to mean lift in the deflected wake regime. Moreover, as evidenced from figure 1(b),
$St$
but also the inevitable loss in thrust that results from a fraction of excess wake momentum being converted to mean lift in the deflected wake regime. Moreover, as evidenced from figure 1(b),
![]() $\overline{C_{P}}$
increases only gradually with
$\overline{C_{P}}$
increases only gradually with
![]() $St$
over the entire range
$St$
over the entire range
![]() $0\leqslant St\leqslant 1$
, for all
$0\leqslant St\leqslant 1$
, for all
![]() $Re$
, and, unlike
$Re$
, and, unlike
![]() $\overline{C_{T}}$
, exhibits no sharp variation with
$\overline{C_{T}}$
, exhibits no sharp variation with
![]() $St$
. Hence, the relatively sharp increase in
$St$
. Hence, the relatively sharp increase in
![]() $\overline{C_{T}}$
with decreasing proximity between the mean position of the trailing edge and the location associated with the onset of significant wake deflection translates directly to a steep rise in the propulsive efficiency
$\overline{C_{T}}$
with decreasing proximity between the mean position of the trailing edge and the location associated with the onset of significant wake deflection translates directly to a steep rise in the propulsive efficiency
![]() ${\it\eta}$
(as observed from figure 2
a).
${\it\eta}$
(as observed from figure 2
a).

Figure 8. Wake map illustrating the three different wake patterns associated with a pitching foil as a function of
![]() $St$
and
$St$
and
![]() $Re$
for a fixed
$Re$
for a fixed
![]() ${\it\theta}_{0}=5^{\circ }$
. Also shown are the drag-to-thrust transition
${\it\theta}_{0}=5^{\circ }$
. Also shown are the drag-to-thrust transition
![]() $St_{tr}$
line (blue) and the line on which the efficiency is maximum for a given
$St_{tr}$
line (blue) and the line on which the efficiency is maximum for a given
![]() $Re$
(orange). Closed and open symbols indicate the results from the present work and those from Godoy-Diana et al. (Reference Godoy-Diana, Aider and Wesfreid2008), respectively. ▹ indicates aligned vortices in Godoy-Diana et al. (Reference Godoy-Diana, Aider and Wesfreid2008).
$Re$
(orange). Closed and open symbols indicate the results from the present work and those from Godoy-Diana et al. (Reference Godoy-Diana, Aider and Wesfreid2008), respectively. ▹ indicates aligned vortices in Godoy-Diana et al. (Reference Godoy-Diana, Aider and Wesfreid2008).
Figure 8 presents a comprehensive summary of the various wake patterns over the entire parametric space of
![]() $St$
and
$St$
and
![]() $Re$
in the form of a regime map. Depending on the parameters
$Re$
in the form of a regime map. Depending on the parameters
![]() $Re$
and
$Re$
and
![]() $St$
, the wake exhibits qualitatively different patterns that can be distinguished by the arrangement of the shed vortices and their inclination with respect to the free stream. For a given
$St$
, the wake exhibits qualitatively different patterns that can be distinguished by the arrangement of the shed vortices and their inclination with respect to the free stream. For a given
![]() $Re$
below a critical
$Re$
below a critical
![]() $St$
(
$St$
(
![]() $St<0.22$
at
$St<0.22$
at
![]() $Re=750$
, for instance), the classical von Kármán vortex street is formed in the wake of the pitching foil. Above this critical
$Re=750$
, for instance), the classical von Kármán vortex street is formed in the wake of the pitching foil. Above this critical
![]() $St$
, a transition from the regular von Kármán to a reverse von Kármán wake characterized by excess momentum is observed. As seen in figure 5(b), the reverse von Kármán wake exhibits asymmetry about the centreline at higher
$St$
, a transition from the regular von Kármán to a reverse von Kármán wake characterized by excess momentum is observed. As seen in figure 5(b), the reverse von Kármán wake exhibits asymmetry about the centreline at higher
![]() $St$
. We classify wakes as asymmetric when an appreciable deflection in the arrangement of wake vortices can be detected at approximately 2.5 chord lengths. With this definition, we find that at
$St$
. We classify wakes as asymmetric when an appreciable deflection in the arrangement of wake vortices can be detected at approximately 2.5 chord lengths. With this definition, we find that at
![]() $Re=750$
, wakes for
$Re=750$
, wakes for
![]() $St\gtrapprox 0.37$
are asymmetric wakes. At very low
$St\gtrapprox 0.37$
are asymmetric wakes. At very low
![]() $Re$
such as
$Re$
such as
![]() $Re=10$
, a von Kármán vortex street forms for all
$Re=10$
, a von Kármán vortex street forms for all
![]() $St<1$
; a transition to the reverse von Kármán vortex street does occur but only at significantly higher
$St<1$
; a transition to the reverse von Kármán vortex street does occur but only at significantly higher
![]() $St=1.5$
. As the
$St=1.5$
. As the
![]() $Re$
is increased, the
$Re$
is increased, the
![]() $St$
at which a transition from a von Kármán to a reverse von Kármán and from a reverse von Kármán to a deflected wake takes place decreases sharply for
$St$
at which a transition from a von Kármán to a reverse von Kármán and from a reverse von Kármán to a deflected wake takes place decreases sharply for
![]() $Re\lessapprox 10^{3}$
. For
$Re\lessapprox 10^{3}$
. For
![]() $Re>1000$
, these transitions seem to occur at
$Re>1000$
, these transitions seem to occur at
![]() $St$
of 0.17 and 0.35 that remains largely unchanged with further increments in
$St$
of 0.17 and 0.35 that remains largely unchanged with further increments in
![]() $Re$
. The invariance of wake transitions with respect to
$Re$
. The invariance of wake transitions with respect to
![]() $Re$
beyond
$Re$
beyond
![]() $Re\gtrapprox 10^{3}$
is indicative of the ever growing dominance of inertial effects. This is also supported by the experimental observations of Ohmi et al. (Reference Ohmi, Coutanceau, Daube and Loc1991) on a related pitching foil set-up but with high mean angles of attack, which show that the
$Re\gtrapprox 10^{3}$
is indicative of the ever growing dominance of inertial effects. This is also supported by the experimental observations of Ohmi et al. (Reference Ohmi, Coutanceau, Daube and Loc1991) on a related pitching foil set-up but with high mean angles of attack, which show that the
![]() $St$
for wake transitions is insensitive to
$St$
for wake transitions is insensitive to
![]() $Re$
in the range of 1500–
$Re$
in the range of 1500–
![]() $10\,000$
.
$10\,000$
.
Figure 8 also illustrates the trends for drag-to-thrust transition (
![]() $St_{tr}=St_{tr}(Re)$
) and peak efficiency (
$St_{tr}=St_{tr}(Re)$
) and peak efficiency (
![]() $St_{max}=St_{max}(Re)$
). As seen in the figure, the transition from a von Kármán to a reverse von Kármán wake does not occur along the drag-to-thrust transition curve as also pointed out by Godoy-Diana et al. (Reference Godoy-Diana, Aider and Wesfreid2008). Further, the peak propulsive efficiency is attained in the asymmetric wake region corresponding to a deflected vortex street. The wake transition predictions from the present investigation are broadly in agreement with the experimental study of Godoy-Diana et al. (Reference Godoy-Diana, Aider and Wesfreid2008) at
$St_{max}=St_{max}(Re)$
). As seen in the figure, the transition from a von Kármán to a reverse von Kármán wake does not occur along the drag-to-thrust transition curve as also pointed out by Godoy-Diana et al. (Reference Godoy-Diana, Aider and Wesfreid2008). Further, the peak propulsive efficiency is attained in the asymmetric wake region corresponding to a deflected vortex street. The wake transition predictions from the present investigation are broadly in agreement with the experimental study of Godoy-Diana et al. (Reference Godoy-Diana, Aider and Wesfreid2008) at
![]() $Re=1150$
also shown in the figure, the minor differences being likely related to the differences in foil shape and pitching amplitude between the two studies.
$Re=1150$
also shown in the figure, the minor differences being likely related to the differences in foil shape and pitching amplitude between the two studies.
5 Effect of pitching amplitude
The results so far presented in this study have all been at a fixed angular oscillation amplitude (
![]() ${\it\theta}_{0}$
) of
${\it\theta}_{0}$
) of
![]() $5^{\circ }$
. A natural question that arises then is the effect of the angular oscillation amplitude (
$5^{\circ }$
. A natural question that arises then is the effect of the angular oscillation amplitude (
![]() ${\it\theta}_{0}$
) on the results presented so far. At higher
${\it\theta}_{0}$
) on the results presented so far. At higher
![]() ${\it\theta}_{0}$
values, one of the important changes expected from the flow side is the formation of a leading edge vortex, as has been discussed for example in McCroskey (Reference Mccroskey1982) and Ohmi et al. (Reference Ohmi, Coutanceau, Daube and Loc1991) for airfoils rapidly pitching at higher angles of attack. With the broad objective of examining the generality of our principal results concerning thrust generation, deduced from simulation runs at a fixed
${\it\theta}_{0}$
values, one of the important changes expected from the flow side is the formation of a leading edge vortex, as has been discussed for example in McCroskey (Reference Mccroskey1982) and Ohmi et al. (Reference Ohmi, Coutanceau, Daube and Loc1991) for airfoils rapidly pitching at higher angles of attack. With the broad objective of examining the generality of our principal results concerning thrust generation, deduced from simulation runs at a fixed
![]() ${\it\theta}_{0}=5^{\circ }$
, we now investigate the effect of pitching angle on the propulsive performance for four additional angular amplitudes of
${\it\theta}_{0}=5^{\circ }$
, we now investigate the effect of pitching angle on the propulsive performance for four additional angular amplitudes of
![]() ${\it\theta}_{0}=2^{\circ },8^{\circ },12^{\circ }$
and
${\it\theta}_{0}=2^{\circ },8^{\circ },12^{\circ }$
and
![]() $16^{\circ }$
.
$16^{\circ }$
.
The formation of a leading edge vortex at higher
![]() ${\it\theta}_{0}$
values may be seen from the close up of the vorticity field around the airfoil depicted in figure 9(a). All the plots shown in this figure are at the same
${\it\theta}_{0}$
values may be seen from the close up of the vorticity field around the airfoil depicted in figure 9(a). All the plots shown in this figure are at the same
![]() $St=0.4$
and
$St=0.4$
and
![]() $Re=750$
and correspond to the same phase of the airfoil motion, with the only difference being the variation of
$Re=750$
and correspond to the same phase of the airfoil motion, with the only difference being the variation of
![]() ${\it\theta}_{0}$
. For an unambiguous identification of the leading edge vortex formation, we have superposed on the vorticity fields in figure 9 the local peak in the
${\it\theta}_{0}$
. For an unambiguous identification of the leading edge vortex formation, we have superposed on the vorticity fields in figure 9 the local peak in the
![]() $Q$
-criterion (indicated using filled circles (
$Q$
-criterion (indicated using filled circles (
![]() $\bullet$
)). In the past, the
$\bullet$
)). In the past, the
![]() $Q$
-criterion (Hunt, Wray & Moin Reference Hunt, Wray and Moin1988) has been extensively employed for identification of vortical structures in a variety of complex flow fields. At relatively large angular amplitudes of
$Q$
-criterion (Hunt, Wray & Moin Reference Hunt, Wray and Moin1988) has been extensively employed for identification of vortical structures in a variety of complex flow fields. At relatively large angular amplitudes of
![]() $8^{\circ }$
,
$8^{\circ }$
,
![]() $12^{\circ }$
and
$12^{\circ }$
and
![]() $16^{\circ }$
, the
$16^{\circ }$
, the
![]() $Q$
-criterion clearly identifies the centre of the leading edge vortex formed on the upper half of the airfoil, besides the one formed on the lower half. After formation near the leading edge, this vortex travels along the airfoil surface, unlike in the heaving case, where the leading edge vortex separates from the airfoil surface (Wang Reference Wang2000; Lewin & Haj-Hariri Reference Lewin and Haj-Hariri2003; Heathcote & Gursul Reference Heathcote and Gursul2007). In the present pitching case, this leading edge vortex first interacts with the boundary layer as it traverses along the airfoil surface and then eventually becomes a part of the vortex shed from the trailing edge, influencing the wake formation downstream, as noted by Ohmi et al. (Reference Ohmi, Coutanceau, Daube and Loc1991) for a pitching foil at high angles of attack. The corresponding distribution of shed vortices in the wake region further downstream in each of the cases is illustrated in figure 9(b). As
$Q$
-criterion clearly identifies the centre of the leading edge vortex formed on the upper half of the airfoil, besides the one formed on the lower half. After formation near the leading edge, this vortex travels along the airfoil surface, unlike in the heaving case, where the leading edge vortex separates from the airfoil surface (Wang Reference Wang2000; Lewin & Haj-Hariri Reference Lewin and Haj-Hariri2003; Heathcote & Gursul Reference Heathcote and Gursul2007). In the present pitching case, this leading edge vortex first interacts with the boundary layer as it traverses along the airfoil surface and then eventually becomes a part of the vortex shed from the trailing edge, influencing the wake formation downstream, as noted by Ohmi et al. (Reference Ohmi, Coutanceau, Daube and Loc1991) for a pitching foil at high angles of attack. The corresponding distribution of shed vortices in the wake region further downstream in each of the cases is illustrated in figure 9(b). As
![]() ${\it\theta}_{0}$
is increased from
${\it\theta}_{0}$
is increased from
![]() $2^{\circ }$
, the wake is seen to progressively become more symmetric, with the location at which the asymmetry is evident moving further downstream.
$2^{\circ }$
, the wake is seen to progressively become more symmetric, with the location at which the asymmetry is evident moving further downstream.

Figure 9. Effect of
![]() ${\it\theta}_{0}$
on the vorticity field at
${\it\theta}_{0}$
on the vorticity field at
![]() $St=0.4$
and
$St=0.4$
and
![]() $Re=750$
for time instants at which the location of the pitching airfoil coincides with its mean position and when the trailing edge moves downwards. (a) A zoomed-in view around the airfoil. Filled circles (
$Re=750$
for time instants at which the location of the pitching airfoil coincides with its mean position and when the trailing edge moves downwards. (a) A zoomed-in view around the airfoil. Filled circles (
![]() $\bullet$
) in (a) indicate the local maximum of the
$\bullet$
) in (a) indicate the local maximum of the
![]() $Q$
-criterion for leading edge vortex identification.
$Q$
-criterion for leading edge vortex identification.

Figure 10. (a) Propulsive efficiency
![]() ${\it\eta}$
as a function of
${\it\eta}$
as a function of
![]() $St$
at
$St$
at
![]() $Re=750$
for
$Re=750$
for
![]() ${\it\theta}_{0}=2^{\circ }$
,
${\it\theta}_{0}=2^{\circ }$
,
![]() $5^{\circ }$
,
$5^{\circ }$
,
![]() $8^{\circ }$
,
$8^{\circ }$
,
![]() $12^{\circ }$
and
$12^{\circ }$
and
![]() $16^{\circ }$
. (b) Maximum propulsive efficiency
$16^{\circ }$
. (b) Maximum propulsive efficiency
![]() ${\it\eta}_{max}$
as a function of
${\it\eta}_{max}$
as a function of
![]() ${\it\theta}_{0}$
(in degrees) for
${\it\theta}_{0}$
(in degrees) for
![]() $Re=350$
,
$Re=350$
,
![]() $750$
and
$750$
and
![]() $1500$
.
$1500$
.
The dependence of propulsive efficiency
![]() ${\it\eta}$
on
${\it\eta}$
on
![]() $St$
for the different
$St$
for the different
![]() ${\it\theta}_{0}$
cases at
${\it\theta}_{0}$
cases at
![]() $Re=750$
is illustrated in figure 10(a). The qualitative trends for all the
$Re=750$
is illustrated in figure 10(a). The qualitative trends for all the
![]() ${\it\theta}_{0}$
cases investigated are similar to the one seen earlier for
${\it\theta}_{0}$
cases investigated are similar to the one seen earlier for
![]() ${\it\theta}_{0}=5^{\circ }$
, despite formation of a relatively strong leading edge vortex at higher
${\it\theta}_{0}=5^{\circ }$
, despite formation of a relatively strong leading edge vortex at higher
![]() ${\it\theta}_{0}$
. There are, however, some quantitative differences. In particular, a noticeable shift to higher
${\it\theta}_{0}$
. There are, however, some quantitative differences. In particular, a noticeable shift to higher
![]() $St_{max}$
with increasing
$St_{max}$
with increasing
![]() ${\it\theta}_{0}$
is observed (at
${\it\theta}_{0}$
is observed (at
![]() $Re=750$
,
$Re=750$
,
![]() $St_{max}$
increases from
$St_{max}$
increases from
![]() $0.48$
to
$0.48$
to
![]() $0.66$
as
$0.66$
as
![]() ${\it\theta}_{0}$
is varied from
${\it\theta}_{0}$
is varied from
![]() $2^{\circ }$
to
$2^{\circ }$
to
![]() $16^{\circ }$
). Thus, for
$16^{\circ }$
). Thus, for
![]() $Re=750$
,
$Re=750$
,
![]() $St_{max}$
does not saturate with
$St_{max}$
does not saturate with
![]() ${\it\theta}_{0}$
. Our simulations indicate that this observation continues to hold even at a higher pitching amplitude of
${\it\theta}_{0}$
. Our simulations indicate that this observation continues to hold even at a higher pitching amplitude of
![]() ${\it\theta}_{0}=24^{\circ }$
, in which case we find
${\it\theta}_{0}=24^{\circ }$
, in which case we find
![]() $St_{max}=0.8$
with the corresponding maximum propulsive efficiency
$St_{max}=0.8$
with the corresponding maximum propulsive efficiency
![]() ${\it\eta}_{max}=14\,\%$
. Hence, at
${\it\eta}_{max}=14\,\%$
. Hence, at
![]() $Re=750$
,
$Re=750$
,
![]() $St_{max}$
exhibits significant dependence on
$St_{max}$
exhibits significant dependence on
![]() ${\it\theta}_{0}$
. On the contrary, the peak efficiency
${\it\theta}_{0}$
. On the contrary, the peak efficiency
![]() ${\it\eta}_{max}$
is found to be weakly dependent on
${\it\eta}_{max}$
is found to be weakly dependent on
![]() ${\it\theta}_{0}$
, with relatively small changes in the maximum propulsive efficiency (
${\it\theta}_{0}$
, with relatively small changes in the maximum propulsive efficiency (
![]() ${\it\eta}_{max}$
) between
${\it\eta}_{max}$
) between
![]() ${\it\theta}_{0}$
of
${\it\theta}_{0}$
of
![]() $5^{\circ }$
and
$5^{\circ }$
and
![]() $16^{\circ }$
. The dependency of
$16^{\circ }$
. The dependency of
![]() ${\it\eta}_{max}$
on
${\it\eta}_{max}$
on
![]() $Re$
and
$Re$
and
![]() ${\it\theta}_{0}$
, as depicted in figure 10(b), shows that even the above mentioned small changes in
${\it\theta}_{0}$
, as depicted in figure 10(b), shows that even the above mentioned small changes in
![]() ${\it\eta}_{max}$
at a fixed
${\it\eta}_{max}$
at a fixed
![]() $Re$
of 750 (from figure 10
a) are quite insignificant. At a fixed
$Re$
of 750 (from figure 10
a) are quite insignificant. At a fixed
![]() $Re$
,
$Re$
,
![]() ${\it\eta}_{max}$
is found to increase with
${\it\eta}_{max}$
is found to increase with
![]() ${\it\theta}_{0}$
, and reach a nearly constant value beyond a certain
${\it\theta}_{0}$
, and reach a nearly constant value beyond a certain
![]() ${\it\theta}_{0}$
, this value being approximately
${\it\theta}_{0}$
, this value being approximately
![]() $8^{\circ }$
at
$8^{\circ }$
at
![]() $Re=750$
and
$Re=750$
and
![]() $5^{\circ }$
at
$5^{\circ }$
at
![]() $Re=1500$
. These results suggest that at large
$Re=1500$
. These results suggest that at large
![]() $Re$
, the maximum propulsive efficiency
$Re$
, the maximum propulsive efficiency
![]() ${\it\eta}_{max}$
is reasonably independent of
${\it\eta}_{max}$
is reasonably independent of
![]() ${\it\theta}_{0}$
, and close to approximately 16 %, for all the cases considered in this work. This weak dependence of
${\it\theta}_{0}$
, and close to approximately 16 %, for all the cases considered in this work. This weak dependence of
![]() ${\it\eta}_{max}$
on
${\it\eta}_{max}$
on
![]() ${\it\theta}_{0}$
is also consistent with the measurements of Mackowski & Williamson (Reference Mackowski and Williamson2015) at moderate values of
${\it\theta}_{0}$
is also consistent with the measurements of Mackowski & Williamson (Reference Mackowski and Williamson2015) at moderate values of
![]() ${\it\theta}_{0}$
considered here. This is however in contrast to the heaving foil case, where the results of Lewin & Haj-Hariri (Reference Lewin and Haj-Hariri2003) indicate that the propulsive efficiency is significantly affected by the nature of the interaction between the leading and trailing edge vortices.
${\it\theta}_{0}$
considered here. This is however in contrast to the heaving foil case, where the results of Lewin & Haj-Hariri (Reference Lewin and Haj-Hariri2003) indicate that the propulsive efficiency is significantly affected by the nature of the interaction between the leading and trailing edge vortices.
6 Conclusions
In conclusion, a systematic evaluation of the energetic cost of thrust production from a NACA 0012 foil pitching about its quarter chord with an angular amplitude of
![]() $5^{\circ }$
was performed numerically over a wide range of Reynolds (
$5^{\circ }$
was performed numerically over a wide range of Reynolds (
![]() $10\leqslant Re\leqslant 2000$
) and Strouhal numbers with a high-resolution viscous vortex particle method. The numerical data for the time-averaged power coefficient exhibited a near-perfect collapse on a power-law scaling
$10\leqslant Re\leqslant 2000$
) and Strouhal numbers with a high-resolution viscous vortex particle method. The numerical data for the time-averaged power coefficient exhibited a near-perfect collapse on a power-law scaling
![]() $\overline{C_{P}}\sim St^{3}$
almost independent of
$\overline{C_{P}}\sim St^{3}$
almost independent of
![]() $Re$
, as would be expected from a strong inertial dependency. In contrast, the time-averaged thrust coefficient
$Re$
, as would be expected from a strong inertial dependency. In contrast, the time-averaged thrust coefficient
![]() $\overline{C_{T}}$
was found to significantly rise with
$\overline{C_{T}}$
was found to significantly rise with
![]() $Re$
in addition to the monotonic increase with
$Re$
in addition to the monotonic increase with
![]() $St$
. The variation of
$St$
. The variation of
![]() $\overline{C_{T}}$
with
$\overline{C_{T}}$
with
![]() $St$
, and consequently the propulsive efficiency,
$St$
, and consequently the propulsive efficiency,
![]() ${\it\eta}=\overline{C_{T}}/\overline{C_{P}}$
, showed a distinct steep increase that was linked to the observed shift in streamwise location at which the wake vortices undergo a deflection from the wake centreline. An increase in
${\it\eta}=\overline{C_{T}}/\overline{C_{P}}$
, showed a distinct steep increase that was linked to the observed shift in streamwise location at which the wake vortices undergo a deflection from the wake centreline. An increase in
![]() $St$
beyond the value at which the asymmetry in the wake begins at the trailing edge of the foil led to only a marginal rise in
$St$
beyond the value at which the asymmetry in the wake begins at the trailing edge of the foil led to only a marginal rise in
![]() ${\it\eta}$
. Further increase in
${\it\eta}$
. Further increase in
![]() $St$
lead to a peak followed by an eventual asymptotic decline (
$St$
lead to a peak followed by an eventual asymptotic decline (
![]() ${\it\eta}\sim St^{-1}$
) that was consistent with the inertial scalings for the mean power and thrust coefficients at high
${\it\eta}\sim St^{-1}$
) that was consistent with the inertial scalings for the mean power and thrust coefficients at high
![]() $St$
and
$St$
and
![]() $Re$
. Most importantly, the peak propulsive efficiency (
$Re$
. Most importantly, the peak propulsive efficiency (
![]() ${\it\eta}_{max}$
), at a given
${\it\eta}_{max}$
), at a given
![]() $Re$
, increased sharply with
$Re$
, increased sharply with
![]() $Re$
till
$Re$
till
![]() $Re=1000$
, beyond which it showed a gradual saturation to an asymptotic value of approximately 16 %. This global peak propulsive efficiency of
$Re=1000$
, beyond which it showed a gradual saturation to an asymptotic value of approximately 16 %. This global peak propulsive efficiency of
![]() $16\,\%$
predicted from our simulations agrees reasonably well with previous higher
$16\,\%$
predicted from our simulations agrees reasonably well with previous higher
![]() $Re$
experimental and numerical results on pitching foils. Additional simulation runs at angular pitching amplitudes of
$Re$
experimental and numerical results on pitching foils. Additional simulation runs at angular pitching amplitudes of
![]() $2^{\circ }$
,
$2^{\circ }$
,
![]() $8^{\circ }$
,
$8^{\circ }$
,
![]() $12^{\circ }$
and
$12^{\circ }$
and
![]() $16^{\circ }$
confirmed this peak to be relatively insensitive to variations in
$16^{\circ }$
confirmed this peak to be relatively insensitive to variations in
![]() ${\it\theta}_{0}$
over the range
${\it\theta}_{0}$
over the range
![]() ${\it\theta}_{0}\leqslant 16^{\circ }$
.
${\it\theta}_{0}\leqslant 16^{\circ }$
.
A comprehensive characterization of the wake was performed over the range of Reynolds (
![]() $10\leqslant Re\leqslant 2000$
) and Strouhal numbers (
$10\leqslant Re\leqslant 2000$
) and Strouhal numbers (
![]() $St\leqslant 1$
). The resulting regime map clearly shows the strong effect of
$St\leqslant 1$
). The resulting regime map clearly shows the strong effect of
![]() $Re$
in addition to
$Re$
in addition to
![]() $St$
for
$St$
for
![]() $Re<1000$
, with the effect of
$Re<1000$
, with the effect of
![]() $Re$
becoming gradually insignificant for
$Re$
becoming gradually insignificant for
![]() $Re>1000$
. The map shows that the von Kármán to reverse von Kármán wake transition precedes the drag-to-thrust transition at all
$Re>1000$
. The map shows that the von Kármán to reverse von Kármán wake transition precedes the drag-to-thrust transition at all
![]() $Re$
. Further, the Strouhal number at which the transition occurred showed a remarkable agreement with a power scaling,
$Re$
. Further, the Strouhal number at which the transition occurred showed a remarkable agreement with a power scaling,
![]() $St_{tr}\sim Re^{-0.37}$
, derived from a balance of the thrust generated from pitching motion and drag force arising out of skin friction. The corresponding power coefficient too exhibited remarkable consistency with a power law,
$St_{tr}\sim Re^{-0.37}$
, derived from a balance of the thrust generated from pitching motion and drag force arising out of skin friction. The corresponding power coefficient too exhibited remarkable consistency with a power law,
![]() $\overline{C_{P,}}_{tr}\sim Re^{-1.12}$
that was shown to naturally follow from our scaling analysis. The map also showed that
$\overline{C_{P,}}_{tr}\sim Re^{-1.12}$
that was shown to naturally follow from our scaling analysis. The map also showed that
![]() $St_{max}$
exceeded the
$St_{max}$
exceeded the
![]() $St$
for the onset of asymmetry, so that the peak propulsive efficiency was always achieved in the deflected wake regime. An analysis of the mean pressure and viscous contributions to the thrust coefficient established that the steep increase in the propulsive efficiency and the resulting maximum in the deflected wake regime are caused principally by a sharp rise in the time-averaged pressure contribution to the thrust from the leading edge of the airfoil.
$St$
for the onset of asymmetry, so that the peak propulsive efficiency was always achieved in the deflected wake regime. An analysis of the mean pressure and viscous contributions to the thrust coefficient established that the steep increase in the propulsive efficiency and the resulting maximum in the deflected wake regime are caused principally by a sharp rise in the time-averaged pressure contribution to the thrust from the leading edge of the airfoil.
Pitching foils are one of the many flapping foil based propulsion configurations which include, among others, heaving and combined pitching and heaving. In the case of heaving foils, lower
![]() $Re$
results (
$Re$
results (
![]() $Re=500$
) of Lewin & Haj-Hariri (Reference Lewin and Haj-Hariri2003) and Martín-Alcántara, Fernandez-Feria & Sanmiguel-Rojas (Reference Martín-Alcántara, Fernandez-Feria and Sanmiguel-Rojas2015) show that the peak propulsive efficiency is approximately 10 %. On the other hand, Heathcote & Gursul (Reference Heathcote and Gursul2007) have shown that for a heaving foil, the propulsive efficiency and other global flow features at
$Re=500$
) of Lewin & Haj-Hariri (Reference Lewin and Haj-Hariri2003) and Martín-Alcántara, Fernandez-Feria & Sanmiguel-Rojas (Reference Martín-Alcántara, Fernandez-Feria and Sanmiguel-Rojas2015) show that the peak propulsive efficiency is approximately 10 %. On the other hand, Heathcote & Gursul (Reference Heathcote and Gursul2007) have shown that for a heaving foil, the propulsive efficiency and other global flow features at
![]() $Re$
of 10 000, 20 000 and 30 000 are significantly higher (approximately 28 %) and nearly the same. This suggests that, as in the pitching case, there exists a threshold
$Re$
of 10 000, 20 000 and 30 000 are significantly higher (approximately 28 %) and nearly the same. This suggests that, as in the pitching case, there exists a threshold
![]() $Re$
below which the performance drops considerably. Given these similarities, we expect the findings from our work to generalize to other flapping foil based propulsive systems with each configuration having a threshold
$Re$
below which the performance drops considerably. Given these similarities, we expect the findings from our work to generalize to other flapping foil based propulsive systems with each configuration having a threshold
![]() $Re$
below which the performance degrades considerably. This could be an important input for the design of small vehicles based on flapping propulsion. Our ongoing work is focused on exploration of such universal trends across general thrust generating flapping foil configurations.
$Re$
below which the performance degrades considerably. This could be an important input for the design of small vehicles based on flapping propulsion. Our ongoing work is focused on exploration of such universal trends across general thrust generating flapping foil configurations.
Acknowledgements
The authors acknowledge support received from the NVIDIA Corporation (hardware donation program) and Supercomputing Education and Research Center-Indian Institute of Science (runtime on Cray XC40). The second author acknowledges support from the Department of Science and Technology (DSTO 1329).
Supplementary material
Supplementary material is available at http://dx.doi.org/10.1017/jfm.2016.399.