I. INTRODUCTION
Because of rising energy demands, the production of CO2 emissions is increasing at alarming rates (Jenkinson et al., Reference Jenkinson, Adams and Wild1991; Holtz-Eakin and Selden, Reference Holtz-Eakin and Selden1995; MacKellar et al., Reference MacKellar, Lutz, Prinz and Goujon1995; Lakshmanan and Han, Reference Lakshmanan and Han1997; Raupach et al., Reference Raupach, Marland, Ciais, Le Quéré, Canadell, Klepper and Field2007; Botzen et al., Reference Botzen, Gowdy and van den Bergh2008). To counteract the exponential increase of flue gas (combustion exhaust containing nitrogen and CO2), current methods employ aqueous solutions of alkanolamine-based solvents (Rochelle, Reference Rochelle2009). The amine scrubbers absorb CO2, and then water vapor is boiled off, leaving the captured CO2. This method is effective but expensive (Rao and Rubin, Reference Rao and Rubin2002; D'Alessandro et al., Reference D'Alessandro, Smit and Long2010). Hence adsorbent materials, such as metal-organic frameworks (MOFs) (Caskey et al., Reference Caskey, Wong-Foy and Matzger2008) and octahedral molecular sieves (OMS) (Espinal et al., Reference Espinal, Wong-Ng, Kaduk, Allen, Snyder, Chiu and Espinal2012), are also being explored. MOFs are a more recent discovery with high CO2 selectivity, but the diffusion mechanism of gases in the MOFs is still not well studied (D'Alessandro et al., Reference D'Alessandro, Smit and Long2010). Therefore, the OMS series poses as another potential solution to efficiently capture CO2.
OMS is comprised of the columns of edge-sharing of MnO6 octahedra. MnO2 can form an infinite number of OMS structures with alternating 1 × 1 tunnels and m × n tunnels. Suib and co-workers first synthesized thermally stable OMS-1, comprised of a 3 × 3 (i.e. m = 3, n = 3) manganese oxide structure with a pore size of 6.9 Å (Shen et al., Reference Shen, Zerger, DeGuzman, Suib, McCurdy, Potter and O'young1993). Their work then focused on determining how the morphology of OMS-1 could be controlled. Shortly after, new morphology OMS-2 was synthesized. OMS-2 is known as α-MnO2 and is comprised of edge-sharing MnO6 octahedra forming a 2 × 2 tunnel structure (i.e. m = 2, n = 2) and reducing the pore size to 4.6 Å (DeGuzman et al., Reference DeGuzman, Shen, Neth, Suib, O'Young, Levine and Newsam1994). As synthesis techniques improved, the tunnel arrangements began to vary. A 2 × 4 tunnel structure (i.e. m = 2, n = 4) with pore sizes of 4.6 Å × 9.2 Å, i.e. OMS-5, was discovered (Shen et al., Reference Shen, Ding, Liu, Cai, Laubernds, Zerger and Suib2005; Zhang et al., Reference Zhang, Sun, Zhang, Li and Ma2014). In addition, doping MnOx with metal cations has been shown to improve electronic and catalytic performance (Suib and Iton, Reference Suib and Iton1994; Suib, Reference Suib1998; Hou et al., Reference Hou, Liu, Li, Mao, Lv and Zhao2013), and can also serve as templates for OMS synthesis (Liu et al., Reference Liu, Makwana, Cai, Suib and Aindow2003; Shen et al., Reference Shen, Ding, Liu, Cai, Laubernds, Zerger and Suib2005).
Accomodating cations, such as Na+, K+, Ba2+, Ca2+, facilitates the stability of the equilibrium of the porous OMS materials. The tunnel structures of the OMS materials are potentially used as adsorbents for gas separation and storage. The guest/host separation efficiency depends on pore features, such as pore shape and size, and interaction between gas molecules and pore surface. For carbon capture and storage aplications, the selectivity of CO2 from a mixture of gases can be tuned by controlling the pore features of the OMS materials. The type and charge of cations doped in the OMS materials are found to affect both pore features and CO2 selectivity.
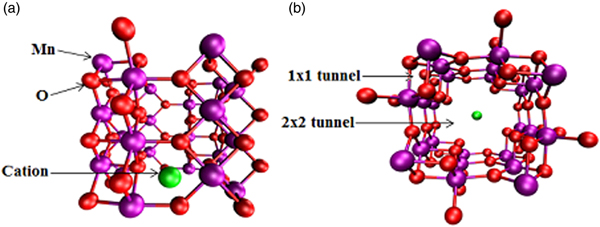
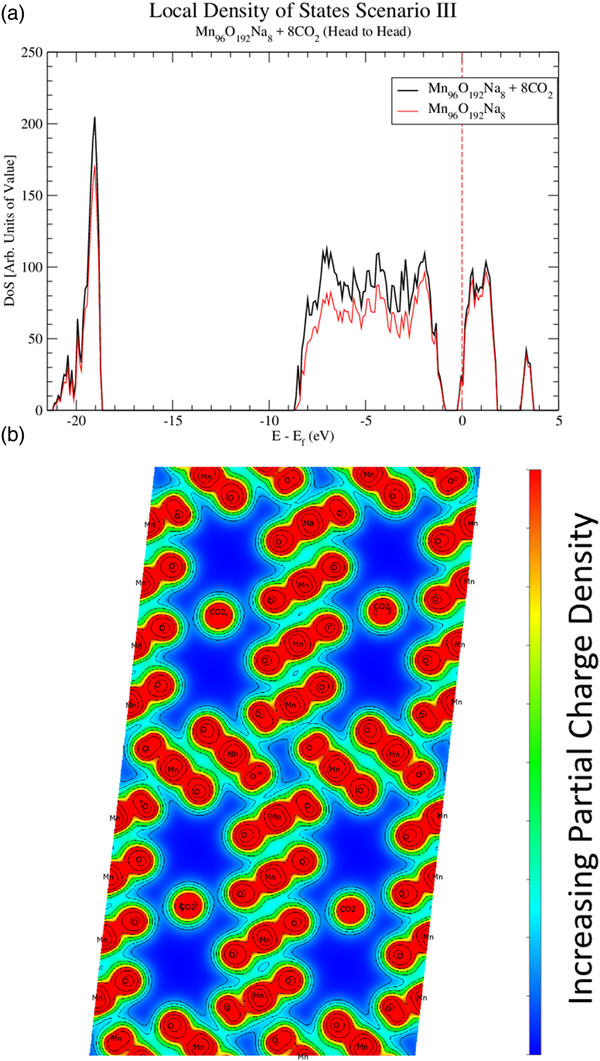
Because of its pore size of 4.6 Å being comparable to the kinetic diameter of 3.3 Å for CO2, OMS-2 has been considered for use in carbon capture and storage. Our previous studies applied first-principles density functional theory (DFT)-based calculations to comprehensively explore its atomic, electronic, and magnetic properties; cation, water, and other hydrate effects; CO2 adsorption; and diffusion mechanisms. As seen in Figure 1, the lowest-energy structure of cation-doped Mn24O48 consisted of alternating 1 × 1 and 2 × 2 tunnels, where the cation was energetically positioned in the 2 × 2 tunnel because of the larger space (Cockayne and Li, Reference Cockayne and Li2012). Because of Mn4+ ions, the Mn–Mn coupling between corner-sharing MnO6 was antiferromagnetic while the interactions between edge-sharing octahedra in neighboring columns were weakly ferromagnetic. The antiferromagnetic interactions were stronger, so the quasi-one-dimensional units were formed by the four columns of MnO6 octahedra that surrounded a 1 × 1 tunnel. The presence of cations could affect the charge of Mn. Local density of state (LDoS) calculations exhibited the electron donation from cations to MnO2. The donated electrons were shared by neighboring Mn atoms, resulting in the reduction of an appropriate amount of Mn4+ to Mn3+ in order to maintain charge balance. According to experimental observations, the synthesis of OMS-2 incorporated water or other hydrates in the sample. DFT calculations clarified that those species formed a weak bond to a cation because of dipole–ion interactions. It should be easy to completely dehydrate the sample without impacting the cation in order to increase the adsorption uptake of CO2 in the OMS-2.
Figure 1. (Color online) OMS-2 with alternating 1 × 1 and 2 × 2 tunnels, accommodating with a cation in the 2 × 2 tunnel, with Mn in purple, O in red, and cation in green. (a) Side view of a single cell, and (b) a single cell down tunnel axes.
Through DFT-based energetic calculations, we further predicted CO2 adsorption and diffusion mechanisms in the OMS-2 and compared the effects of different cations, such as K+, Na+, and Ba2+. The doped cations present in OMS-2 not only stabilized its porous structure but also tailored CO2–pore interaction. We firstly focused on the K+ cation. Our previous experiments exhibited CO2 sorption hysteresis, where the adsorption isotherm curve of CO2 uptake differed from that of the desorption curve (Espinal et al., Reference Espinal, Wong-Ng, Kaduk, Allen, Snyder, Chiu and Espinal2012). At a temperature of 303 K, a significant hysteresis existed between the adsorption and desorption isotherm paths. The width of the hysteresis loop also increased with equilibrium time. However, the hysteresis only occurred when the pressure exceeded 7 bar. Experiments suggested that the OMS-2 material was able to capture CO2, but had a difficulty releasing CO2 above 7 bars. These results raised crucial questions related to CO2 adsorption and diffusion mechanisms and the driving force for the hysteresis. DFT-based energetic calculations indicated that the hysteresis could be explained by the presence of K+ cations acting as “gate keepers” hindering the diffusion of CO2 in the 2 × 2 tunnels of OMS-2. A large activation energy was required for CO2 in a low concentration to bypass K+, so CO2 would diffuse until it encountered K+ and then remained at an optimum distance from K+. Upon desorption, CO2 could easily exit the tunnel with no hysteresis, in agreement with experimental observations below 7 bar. Increasing CO2 concentration with pressure could dramatically decrease the activation energy required for CO2 diffusion deep in the OMS-2 tunnel, in agreement with experimental observations above 7 bar. However, upon desorption CO2 had to overcome the high-energy barrier to pass through K+ in reverse, resulting in hysteretic behavior. In addition, the high concentration of CO2 possibly caused the formation of stable carbonate-like complexes because of the limited space of the OMS-2 tunnel and dipole interactions between CO2 molecules (Li et al., Reference Li, Cockayne, Williamson, Espinal and Wong-Ng2013).
In comparison between K+ and other types of cations, we found the charge, type, and mobility of the cation could affect not only the OMS-2 structural features but also CO2 sorption performance, implying that modifying these features could optimize the carbon capture properties of OMS-2. We extended our DFT-based energetic and electronic structure calculations to Na+ and Ba2+ cations for comparison with K+ (Williamson et al., Reference Williamson, Nelson and Li2015). Because of the higher charge and more electrons donated to the MnO2, Ba2+ had a more than twice stronger interaction with the OMS-2 porous surface than both K+ and Na+ did. However, the Ba-doped OMS-2 would have the lower CO2 uptake because of the stronger Ba–MnO2 interaction and the higher activation energy for CO2 to bypass Ba2+ for further diffusion. We then predicted that Na+ would have the best CO2 uptake performance for two key reasons. One was the relatively weaker Na–MnO2 interaction, while the second was a high mobility of Na+ in the OMS-2 tunnel. When CO2 encountered Na+, it would continue diffusing by pushing Na+ aside. This scenario could not only enhance the CO2 uptake amount but also improve its adsorption–desorption hysteresis. Finally, we summarized three possible diffusion mechanisms for CO2 in the OMS-2 tunnel, depending on the activation energy barrier for further CO2 diffusion and cation mobility. Scenario I involved CO2 kinetically trapped in an equilibrium position with no further diffusion. Scenario II was to bypass the cation to further diffuse along the OMS-2 tunnel. Scenario III was to continue diffusing by pushing the cation aside. We suggested that Scenarios I and II would occur in the K-doped OMS-2 sample because of the relatively low activation energy barrier for CO2 at high concentration to bypass K+. With the high mobility of Na+, Scenarios I and III would be favorable in the Na-doped OMS-2 sample. The strong Ba–MnO2 interaction suggested that only Scenario I occurs in the Ba-doped OMS-2. We also predicted that Na-doped OMS-2 should have the highest CO2 uptake, followed by the K-doped OMS-2, and finally Ba-doped OMS-2.
Our previous studies suggested that we could control CO2 sorption hysteresis and uptake by optimizing the chemistry, size, and concentration of cations accommodated in the OMS-2 tunnel, and Na+ had the best CO2 sorption performance. As a follow-up, this paper emphasizes our computational efforts to study OMS-5 with the larger size of tunnels (i.e. m = 2 and n = 4) and determine how cations affect CO2 sorption in the tunnels. OMS-5 is expected to intake a larger amount of CO2 because of its larger pore size, but it could lead to different CO2 sorption mechanisms. Besides DFT-based energetic and electronic structural calculations, we further performed partial charge density analyses to advance our understanding on the nature of bonding among OMS-5, Na+ cations, and CO2 molecules.
II. METHODS
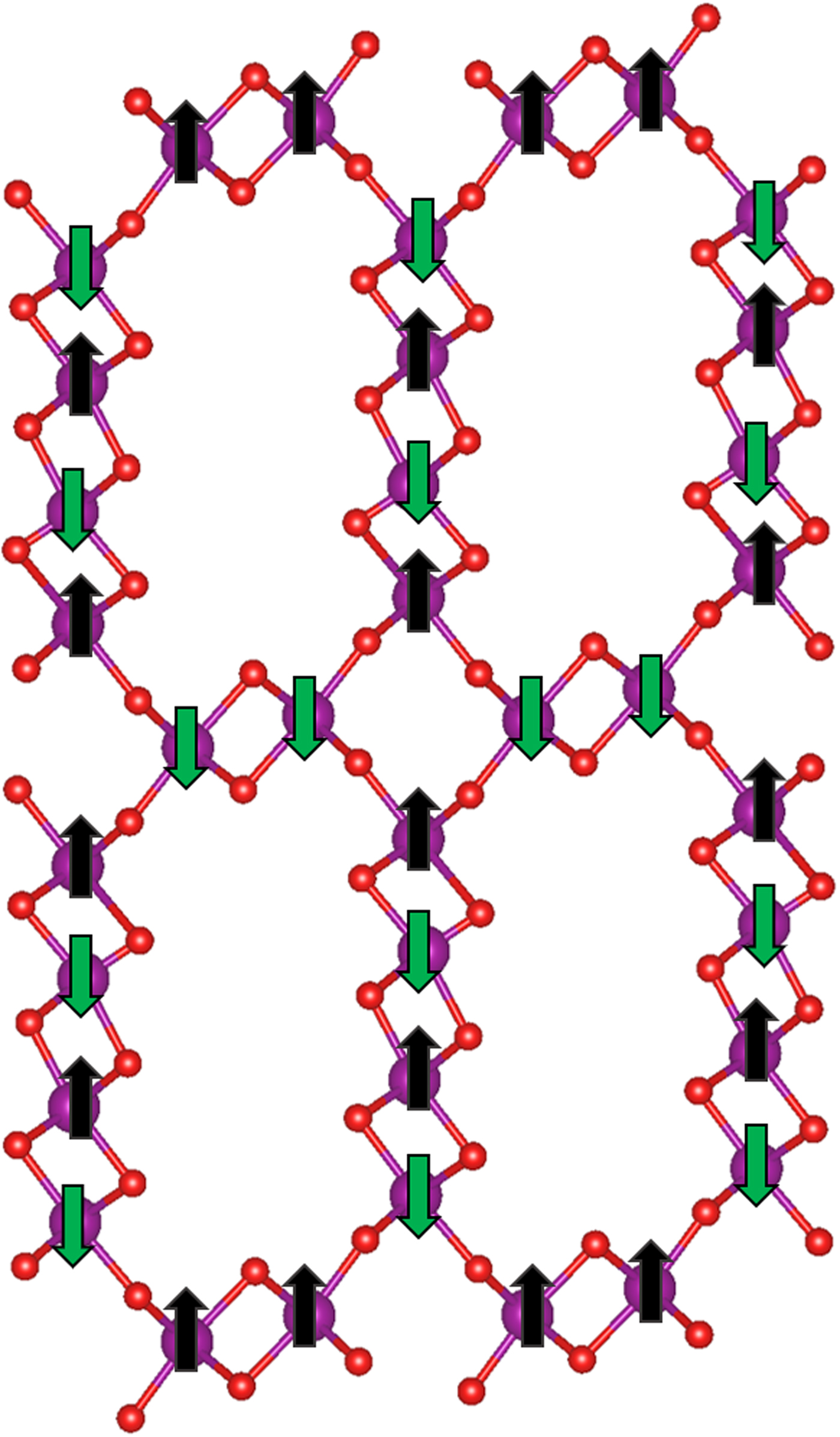
We continued conducting DFT-based studies of OMS-5 with the bigger pore size, Na+ cation dopants, and CO2 adsorption. Because of Mn4+, we first found the lowest-energy magnetic state of OMS-5, as shown in Figure 2. Mn atoms have an antiferromagnetic interaction with the magnetic moments of ±4 µB. To account for the dipole–dipole interactions, van der Waals forces were also considered by applying the D2 method of Grimme (Grimme, Reference Grimme2006). A plane-wave cutoff energy of 300 eV was implemented with the spin-polarized generalized gradient approximation (GGA) and Perdew–Burke Ernzerhof (Perdew et al. Reference Perdew, Burke and Ernzerhof1996) exchange-correlation functional. For strongly correlated element Mn, we used the GGA + U approach by Liechtenstein et al. (Reference Liechtenstein, Anisimov and Zaanen1995), with the effective on-site Coulomb value (U) of 2.8 eV and the effective on-site exchange (J) value of 1.2 eV for Mn (Li et al., Reference Li, Cockayne, Williamson, Espinal and Wong-Ng2013). Cell and atomic positions were fully relaxed until the residual forces reached 0.01 eV Å−1. The ground-state unit cell consists of lattice parameters a = 12.353 Å, b = 2.708 Å, and c = 23.050 Å. We then extended the unit cell along the b axis (i.e. the tunnel axis) by four times to form a Mn96O192 compound in order to accommodate CO2 molecules in the 2 × 4 tunnels.
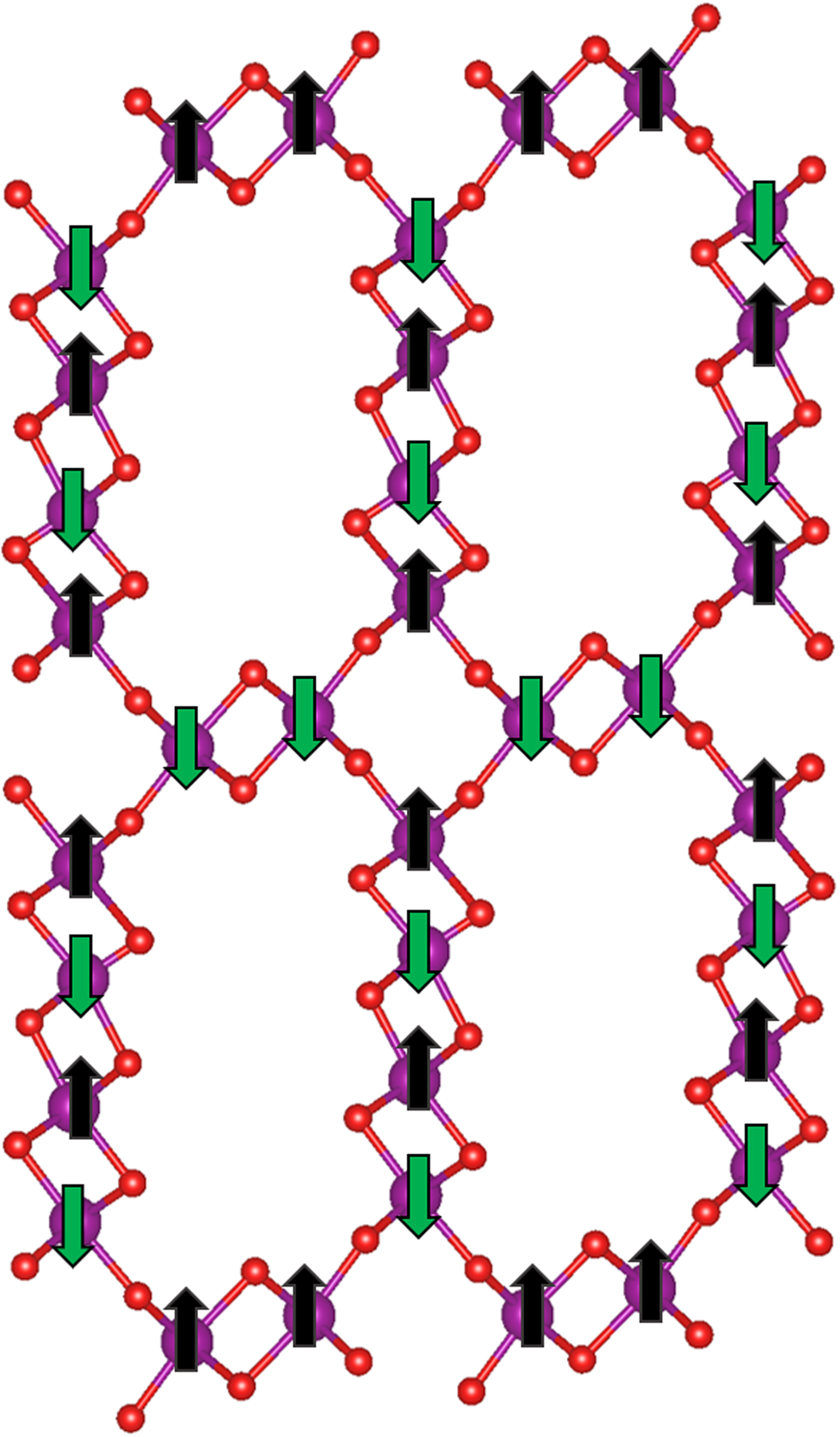
Figure 2. (Color online) Unit cell of OMS-5 with alternating 1 × 1 and 2 × 4 tunnels. Spin states “up” in black and “down” in dark green are applied to Mn atoms in purple. O atoms are represented in red.
Our previous work with OMS-2 showed that cations could stabilize not only the tunnel size and shape of the porous structure, but also play a role as a “gate keeper” to induce an energy barrier for CO2 to diffuse along the tunnel (Williamson et al., Reference Williamson, Nelson and Li2015). The larger tunnel size of the OMS-5 structure would undoubtedly affect its adsorption mechanism of CO2, so we focus on three following scenarios:
• Scenario I: OMS-5 without cations
• Scenario II: OMS-5 with a low concentration of Na+ cations
• Scenario III: OMS-5 with a high concentration of Na+ cations
For comparison, a low concentration refers to one Na+ cation for each 2 × 4 tunnel, i.e. Mn96O192Na4 while a high concentration is two Na+ cations per 2 × 4 tunnel, i.e. Mn96O192Na8. In this study, we are primarily interested in how stability of the OMS-5 structure changes as the concentration of Na+ changes in each pore. There are two possible orientations of CO2 molecules in the tunnels, including the “head-to-head” orientation, where the CO2 molecules align linearly along the tunnel, and the “stacked” orientation, where the CO2 molecules stack on top of each other in the tunnel. We evaluated the stability of Na+ or CO2 in the OMS-5 tunnel by calculating its formation energy E f, as follows:
![]() $E_{{\rm OMS}-5\; {\rm with\; Na\; or\; C}{\rm O}_{\rm 2}}$ and
$E_{{\rm OMS}-5\; {\rm with\; Na\; or\; C}{\rm O}_{\rm 2}}$ and ![]() $E_{{\rm OMS}-5\; {\rm without\; Na\; or\; C}{\rm O}_{\rm 2}}$ represent the total energies for OMS-5 with and without Na+ or CO2 added, respectively.
$E_{{\rm OMS}-5\; {\rm without\; Na\; or\; C}{\rm O}_{\rm 2}}$ represent the total energies for OMS-5 with and without Na+ or CO2 added, respectively. ![]() $N_{{\rm Na\; or\; C}{\rm O}_{\rm 2}}$ is the total number of Na+ or CO2 added.
$N_{{\rm Na\; or\; C}{\rm O}_{\rm 2}}$ is the total number of Na+ or CO2 added.![]() $\; E_{{\rm Na\; or\; C}{\rm O}_2}$ is an energy of individual Na+ or CO2. If E f is a negative value, it refers to a binding energy, indicating that the configuration is energetically stable. If E f is a positive value, it refers to an energy penalty to form the configuration, which is relatively unstable.
$\; E_{{\rm Na\; or\; C}{\rm O}_2}$ is an energy of individual Na+ or CO2. If E f is a negative value, it refers to a binding energy, indicating that the configuration is energetically stable. If E f is a positive value, it refers to an energy penalty to form the configuration, which is relatively unstable.
Density of states (DoS) was also calculated to provide insight into electronic interactions and Na+ cation effects. The electronic contributions of the OMS-5 framework, CO2 molecules, and Na+ cations were then projected on the LDoS. Finally, the partial charge densities were calculated for the electronic energy range between −5 eV and the Fermi energy to study the bonding characteristics of the CO2 molecules and OMS-5 framework on the electronic scale. This energy range was chosen to analyze the distribution of valence electrons on the atomic sites.
III. RESULTS AND DISCUSSION
A. OMS-5 structure
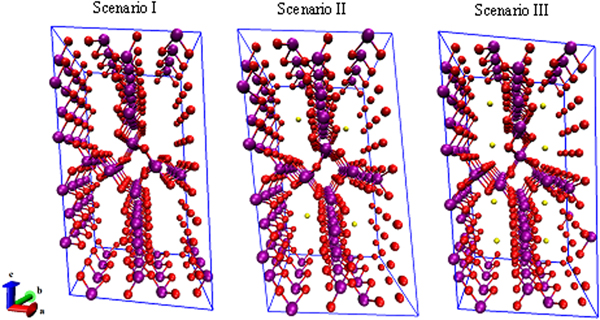
Figure 3 shows three scenarios for studying the CO2 adsorption/desorption mechanism, including OMS-5 without cations (i.e. Scenario I Mn96O192), with a low concentration of Na+ cations (i.e. Scenario II Mn96O192Na4), and with a high concentration of Na+ cations (i.e. Scenario III Mn96O192Na8) to determine cation effects on the structural stability of OMS-5. In Scenario I, Mn–O bond lengths are approximately 1.9 Å. In Scenario II, adding four Na+ cations would allow for a single cation in each 2 × 4 tunnel. Na+ does not always stay in the middle of the tunnel. Its position depends on the size and shape of the pore. Interestingly, the Mn–O bonds close to Na+ can retain bond lengths of 1.9 Å, while the Mn–O bonds far from Na+ have a significant change in their bond lengths, ranging from 1.82 to 1.92 Å. In Scenario III, the large pore size of OMS-5 could accommodate two Na+ cations in each 2 × 4 tunnel. Na–Na distances are approximately 4.8 Å. Similar to Scenario II, the change of the Mn–O bond lengths depends on the position of Na+. Table I shows that the lattice parameters of OMS-5 for all three scenarios do not change significantly. In comparison between Scenarios I and II, adding Na+ slightly increases the a and c lattice parameters by 0.1 and 0.5%, respectively, while the b lattice parameter decreases 0.7%. Similarly, in comparison between Scenarios I and III, adding more Na+ increases the a and c lattice parameters by 0.07 and 0.5%, respectively, and decreases the b lattice parameter by 0.8%. Obviously, the change of <1% in each lattice parameter could be negligible. With β = ~ 970 and α = γ = ~90°, the OMS-5 cell remains monoclinic in the presence of Na+ cations. However, the cell volume shrinks by 0.3% with a low concentration of Na+ cations and 0.8% with a high concentration of Na+ cations, which also happens in the OMS-2 materials (Williamson et al., Reference Williamson, Nelson and Li2015). The volume decrease is the concequence of the shorter tunnel length along the b axis. The tunnel size, i.e. a × c or pore size, remains the same. Our computational results suggest that the presence of Na+ slightly shrinks the cell volume, but it maintains the pore size and shape.
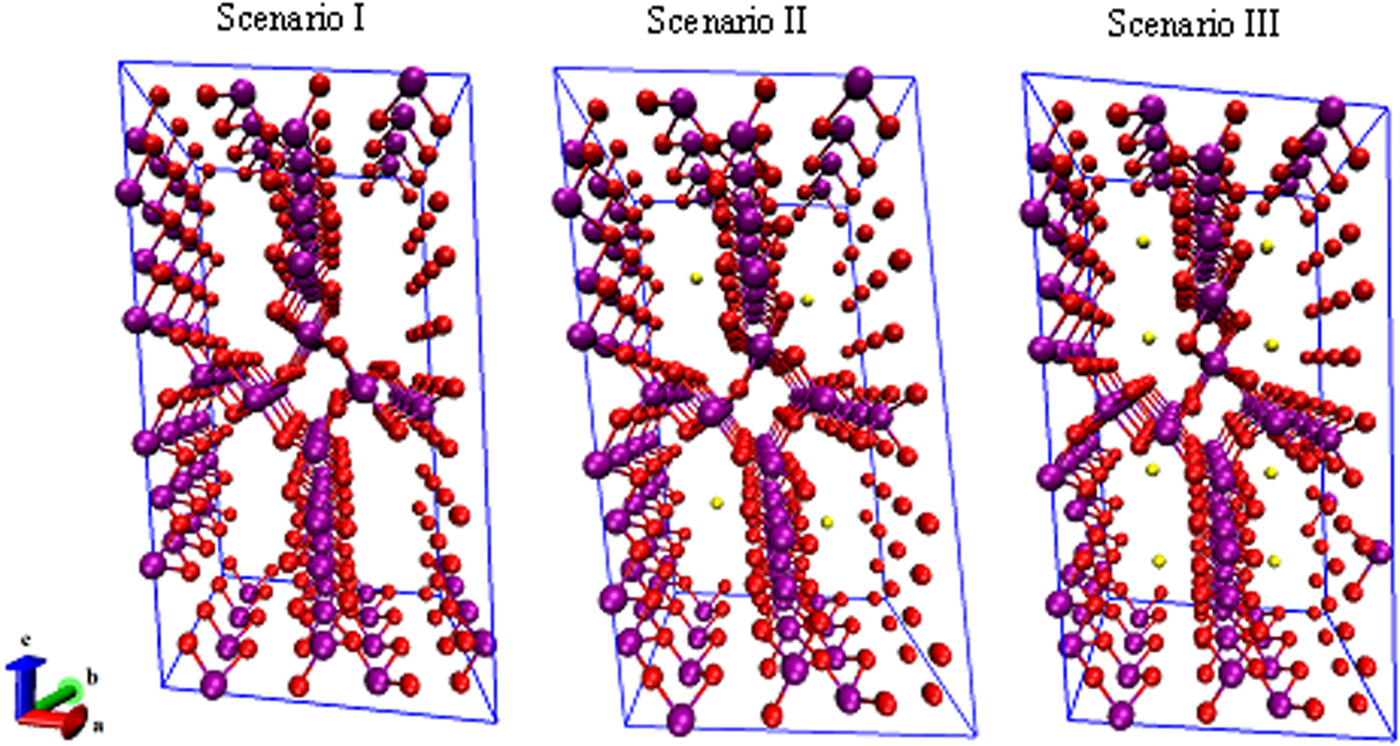
Figure 3. (Color online) Three OMS-5 scenarios our studies focus on, including OMS-5 without cations (Mn96O192), with a low concentration of Na+ cations (Mn96O192Na4), and with a high concentration of Na+ cations (Mn96O192Na8). Mn in purple, O in red, and Na in gold.
Table I. Lattice parameters and tunnel dimensions for OMS-5 without any Na+ (i.e. Scenario I Mn96O192 as a reference), with a low concentration of Na+ cations (i.e. Scenario II Mn96O192Na8), and a high concentration of Na+ cations (i.e. Scenario III Mn96O192Na8).

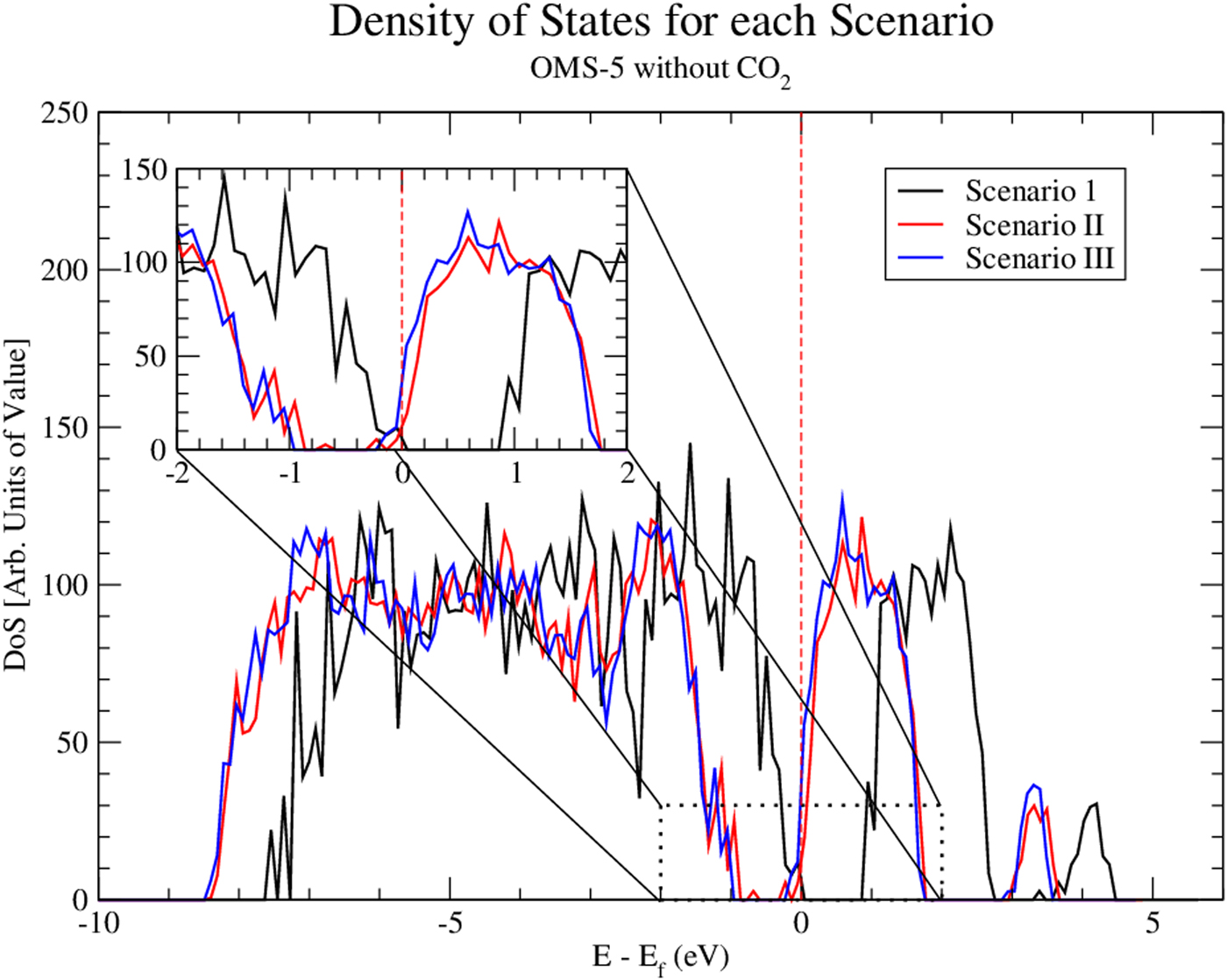
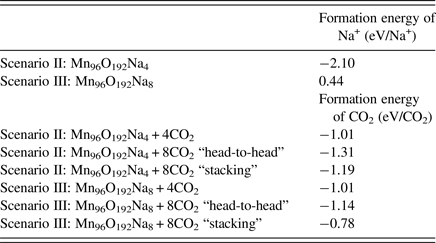
Using Eq. (1), we could determine the stability of Na+ cations accommodated in the OMS-5 tunnels. The corresponding formation energy per Na+ cation is listed in Table II. In the low concentration Mn96O192Na4, the formation energy of a Na+ cation is −2.10 eV/Na+. This negative value indicates that the presence of Na+ is stable, and Na+ forms a strong bond with the OMS-5 framework. As its concentration increases, the formation energy of a Na+ cation gradually increases and becomes less negative. For Mn96O192Na8, its formation energy is 0.44 eV/Na+. The positive value represents an energy penalty for incorporating an additional Na+ cation in each 2 × 4 tunnel. As a result, the presence of a single Na+ in each pore stabilizes the porous structure of OMS-5, but it costs energy to incorporate an additional Na+ in each pore. Thus, a low concentration of Na+ is more energetically favorable. To further study the interaction between Na+ and OMS-5, we projected electronic DoS on the OMS-5 before and after adding Na+ cations. Figure 4 shows that the DoS of OMS-5 before adding Na+ (black solid) has a band gap at the Fermi energy (red dash at E–E f = 0), representing its semiconducting feature. With a low concentration of Na+ cations (red solid), the conduction band for the DoS of OMS-5 slightly shifts below the Fermi energy, indicating that electrons are accumulated at the Fermi energy, and OMS-5 becomes n-type semiconducting. The accumulated electrons are donated from Na+ cations to OMS-5, resulting in ionic bonds between Na+ and OMS-5. As the concentration of Na+ cations increases (blue solid), more electrons donated by Na+ are accumulated at the Fermi energy.
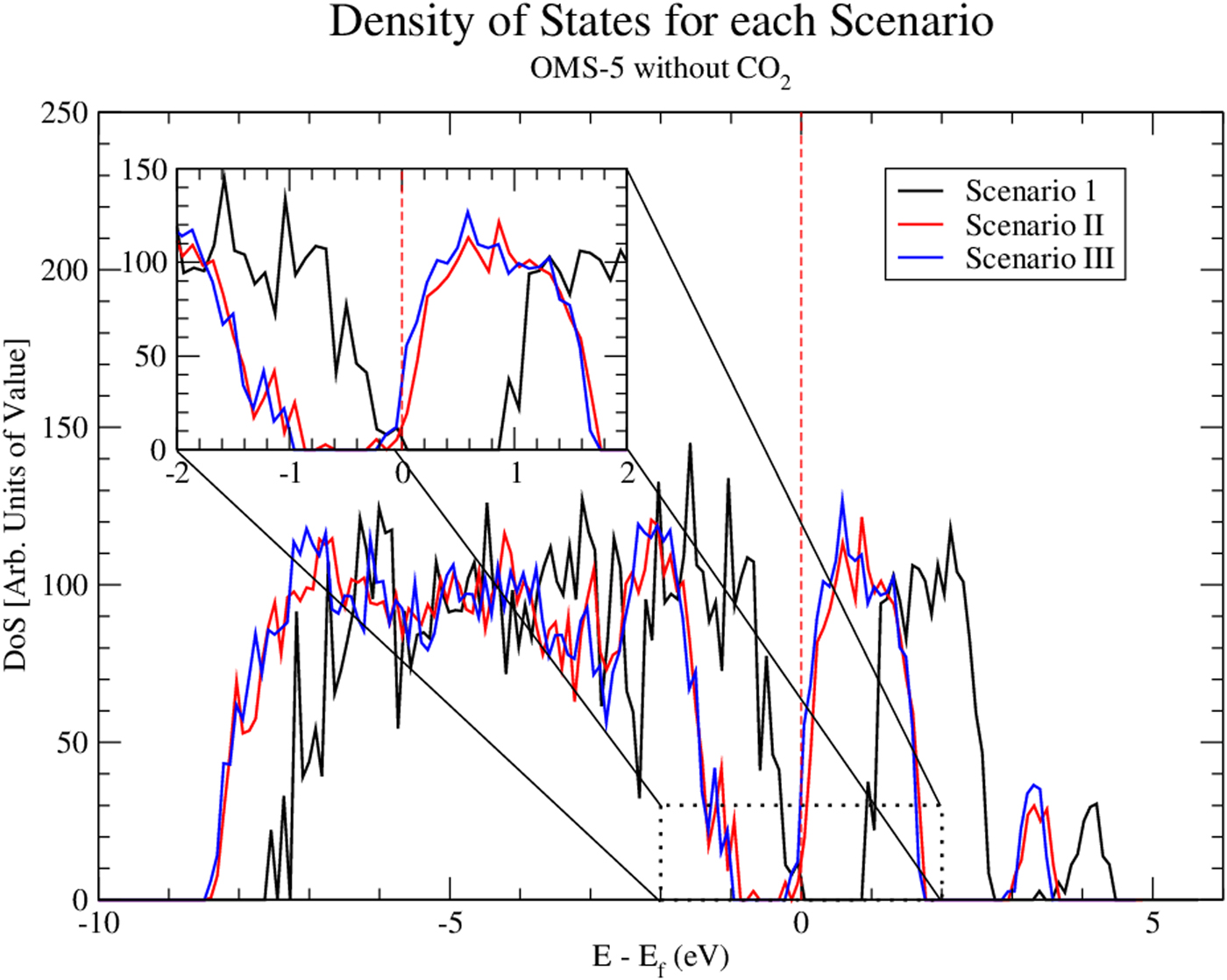
Figure 4. (Color online) Density of states (DoS) for three scenarios. Both Mn96O192Na4 (i.e. Scenario II) and Mn96O192Na8 (i.e. Scenario III) shift the Dos to the lower energy values, compared with Mn96O192 (i.e. Scenario I as a reference). The Fermi energy is shown at the dashed red line.
Table II. The calculated formations energies of Na+ and CO2 in OMS-5.
B. CO2 adsorption in OMS-5
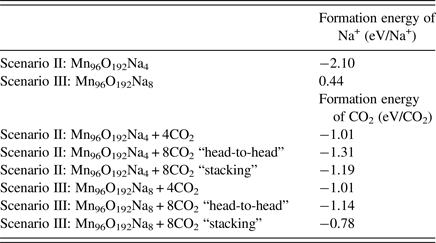
We then added CO2 molecules in the OMS-5 with different concentrations of Na+ cations. We calculated the formation energy of CO2, DoS, and partial charge density to study the position and orientation of CO2 adsorbed in the OMS-5, and its interaction with Na+. Like Na+ cations, the unit of Mn96O192 could accommodate one or two CO2 molecules in each 2 × 4 tunnel. Table II lists the formation energy of a CO2 molecule for different scenarios. Generally speaking, its value remains negative, indicating that the adsorption of CO2 in the OMS-5 is energetically favorable without any energy penalty. As the concentration of CO2 increases, its formation energy becomes slightly smaller, i.e. more negative and stable. This decrease suggests that CO2 uptake is energetically favorable before OMS-5 is fully saturated with CO2. Our future work will examine the “saturation limit” of CO2. In comparison between one and two Na+ cations per 2 × 4 tunnel, it is easier to adsorb CO2 in Mn96O192Na4 than Mn96O192Na8 because of the smaller formation energy and more space available for CO2. When each 2 × 4 tunnel contains two CO2 molecules, the formation energy of CO2 strongly depends on its orientation in the tunnel. Figure 5 illustrates two possible orientations for CO2 molecules, including head-to-head and stacking orientations. The head-to-head orientation refers to two CO2 molecules aligning head-to-head along the 2 × 4 tunnel [Figure 5(a)]. The distance between two CO2 molecules is 3.09 Å. The distances between CO2 and two neighboring Na+ cations are 2.76 and 2.63 Å. The stacking is an alternative orientation where two CO2 molecules stack on top of each other and both align along the 2 × 4 tunnel [Figure 5(b)]. The distance between two CO2 molecules is 4.06 Å. The distances between the terminal O of CO2 and two neighboring Na+ cations are both 2.66 Å. The formation energy for the head-to-head orientation is smaller than that for the stacking orientation in either a low or high concentration of Na+ cations, suggesting that CO2 molecules prefer to align head-to-head in the tunnel.
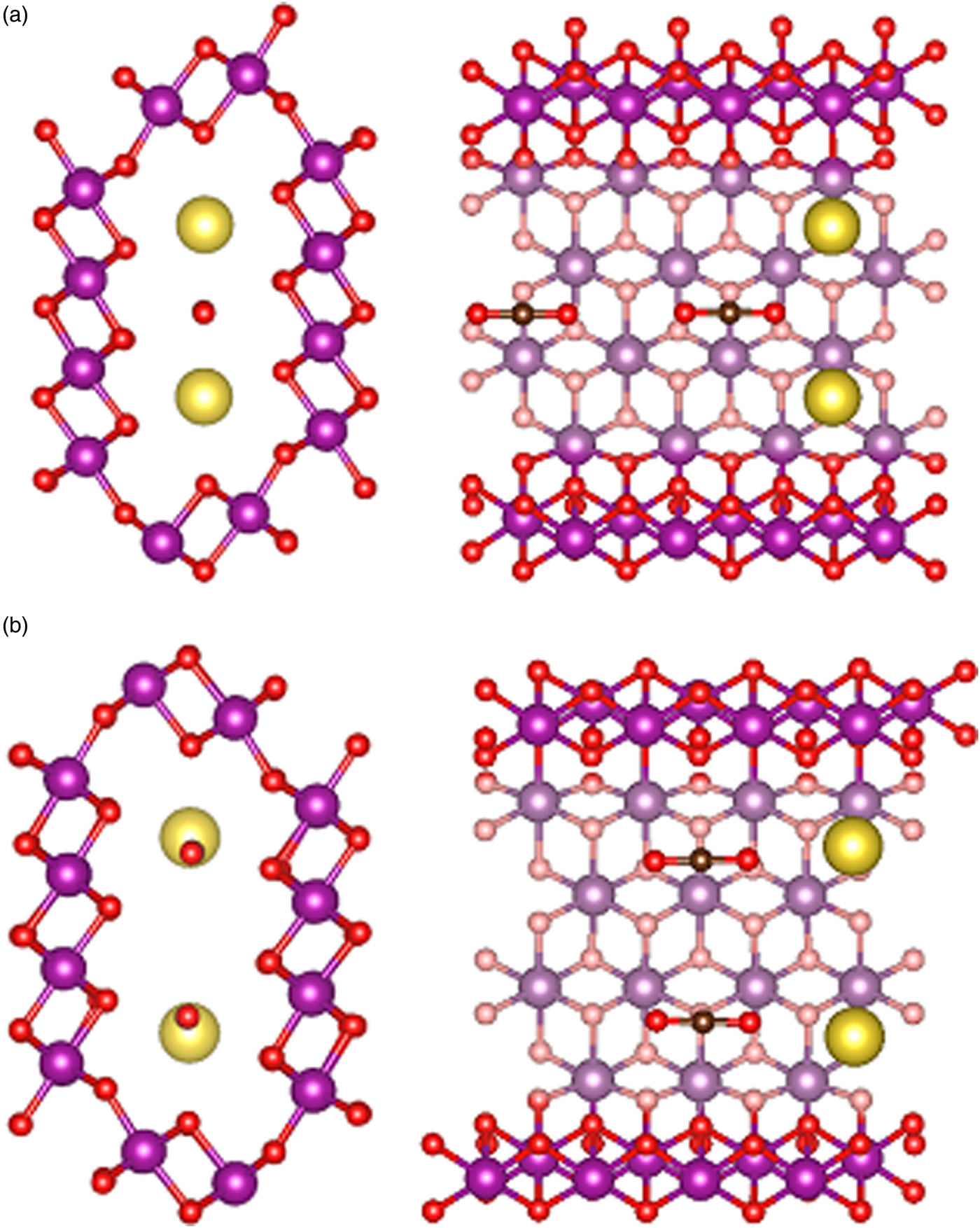
Figure 5. (Color online) Atomic strutures of a single OMS-5 tunnel with Na+ and CO2, illustrating (a) “head-to-head” orientation and (b) “stacked” orientation for two CO2 molecules in the OMS-5 tunnel. Mn in purple, O in red, C in black, and Na in gold.
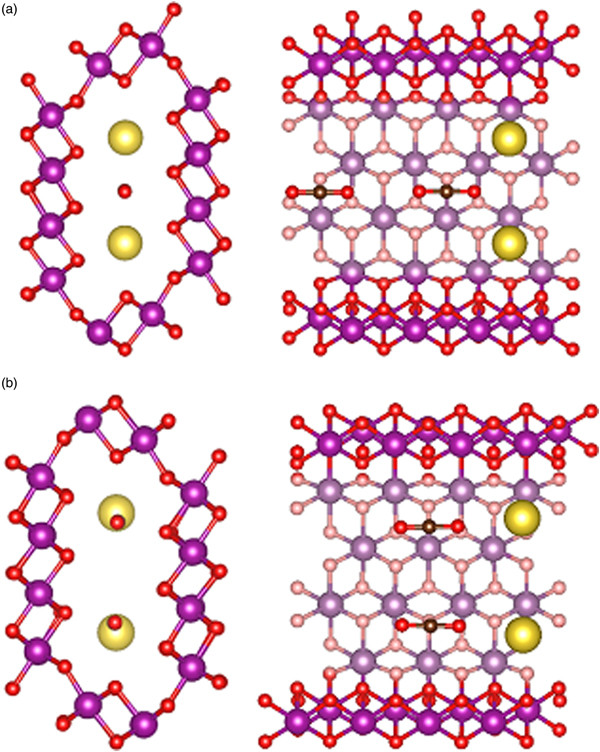
In order to reveal bonding characteristics among CO2, OMS-5, and Na+, Figure 4 shows the DoS of OMS-5 for all three scenarios without CO2. These data confirm that OMS-5 demonstrates semiconducting behavior. Like OMS-2, the DoS of OMS-5 shifts to the lower energy values in the presence of Na+ cations (Williamson et al., Reference Williamson, Nelson and Li2015). This shift stems from the Na+ donating electrons to the OMS-5. To examine a CO2 effect on the electronic structure of OMS-5, electronic DoS and partial charge densities are both shown in Figure 6 for Mn96O192Na4 + 8CO2 and in Figure 7 for Mn96O192Na8 + 8CO2 with different concentrations of Na+ cations but with the same amount of CO2 molecules. For both configurations, CO2 molecules align head-to-head along the 2 × 4 tunnels, as seen in Figure 5a, because the head-to-head orientation is more stable. The DoS figures are projected for Mn96O192Na4 [Figure 6(a)] and Mn96O192Na8 [Figure 7(a)] before and after CO2 adsorption. Unlike Na+ cations, the presence of CO2 molecules does not cause a significant difference in the DoS figures (black and red solid for comparison), suggesting that CO2 is physically adsorbed in the OMS-5, resulting in a weak bond.
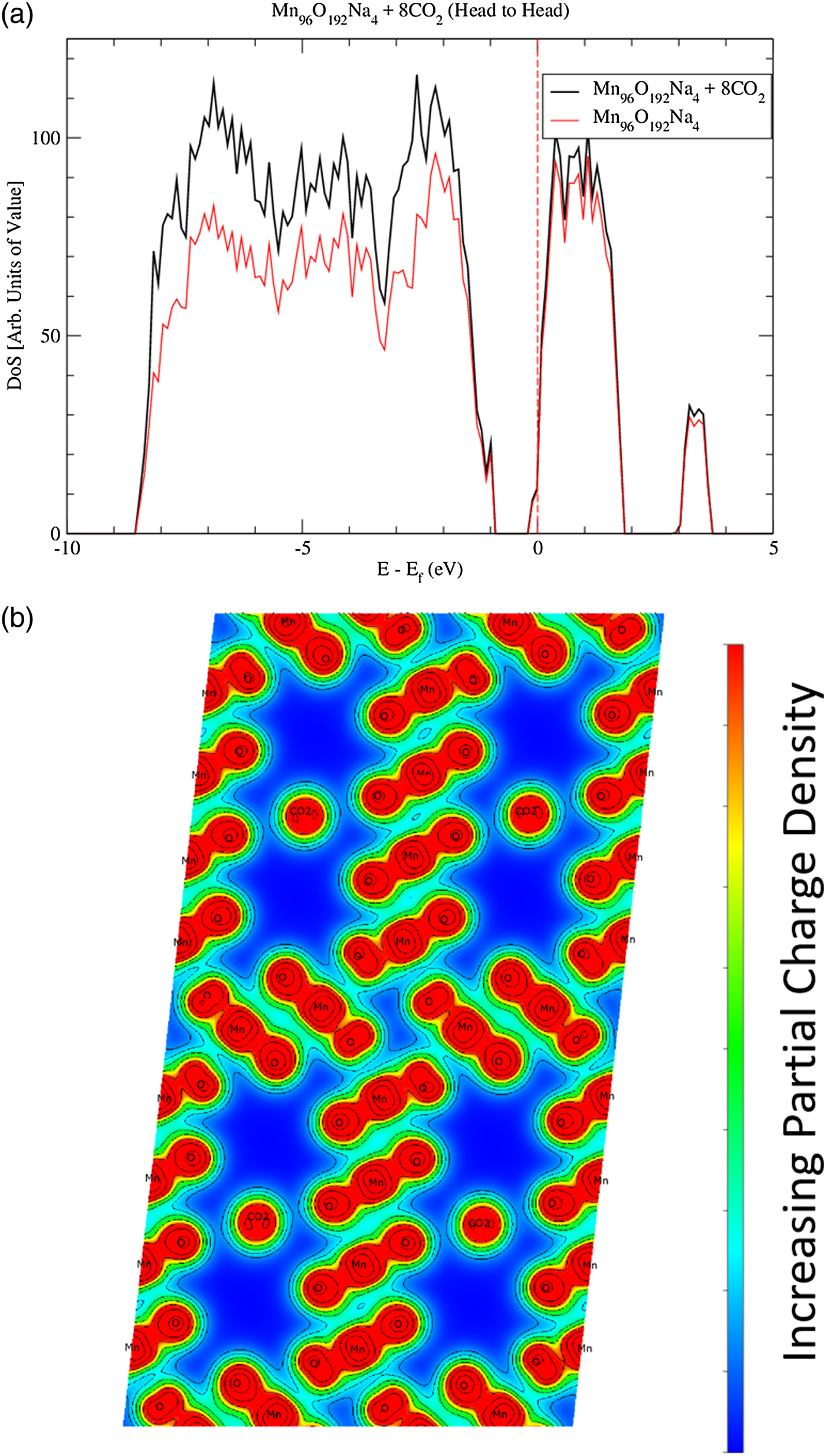
Figure 6. (Color online) Local density of states (a) projecting the contributions of Mn96O192Na4 + 8CO2 and Mn96O192Na4. The Fermi energy is shown with the dashed line. The partial charge densities (b) for Mn96O192Na4 + 8CO2 is projected along the OMS-5 tunnels in the b axis.
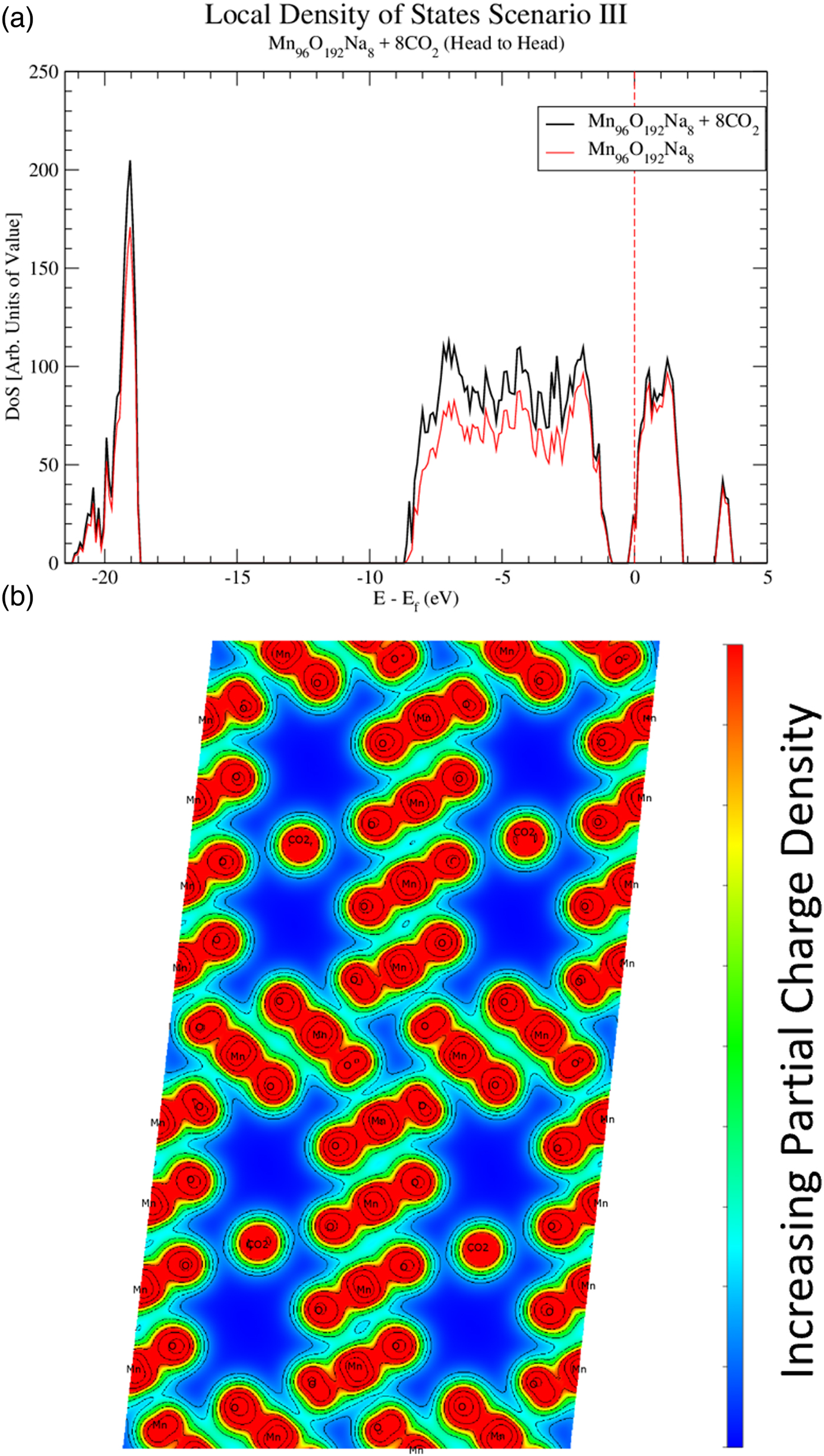
Figure 7. (Color online) Local density of states (a) projecting the contributions of Mn96O192Na8 + 8CO2 and Mn96O192Na8. The Fermi energy is shown with the dashed line. The partial charge densities (b) for Mn96O192Na8 + 8CO2 is projected along the OMS-5 tunnel in the b axis.
Calculating the partial charge density near the Fermi energy could further explore the bonding characteristics between the CO2 molecules and OMS-5 framework. Figures 6(b) and 7(b) are the partial charge densities projected along the OMS-5 tunnels in the b axis for the valence electrons with the energies of −5 eV to the Fermi energy (i.e. E–E f = 0). Contour lines are drawn to show the regions of equal charge densities. The dark red regions of the OMS-5 framework represent the Mn–O bonds, and are strongly bonded to each other through overlapping contour lines. The partial charge densities of CO2 molecules are highly localized, so no shared or donated electrons between CO2 and OMS-5 or between CO2 and Na+ are found. This evidence indicates that CO2 molecules do not covalently or ionically bond to OMS-5 or Na+. A weak van der Waals interaction might exist for CO2 adsorbed in the OMS-5. This type of secondary bonding is much weaker than covalent and ionic bonds. Desorption of CO2 from the OMS-5 should be easy. Adsorption–desorption hysteresis should also be small. The computational predictions will be validated with our future experiments.
IV. CONCLUSIONS
We utilized DFT-based calculations to understand the structural and electronic properties of OMS-5. The presence of Na+ cations does not significantly distort the structure of OMS-5. Na+ ions change the lattice parameters and pore volumes of OMS-5 by <1%. CO2 adsorption is favorable. According to the analysis of the electronic structure of OMS-5 with Na+ and CO2, the Na+ cations donate electrons to the OMS-5 framework while the CO2 molecules do not significantly affect the electronic structure of OMS-5. The partial charge densities reveal that the CO2 molecules are likely captured in the OMS-5 framework through weak van der Waals forces, allowing an easy desorption of CO2 from the OMS-5. Our studies provide insight into the initial stage and driving force for the adsorption of CO2 in the OMS-5 series, guiding the OMS materials design for effective carbon capture and storage. For further studies, we will predict CO2 diffusion mechanisms and estimate CO2 uptake limits in the OMS-5.
ACKNOWLEDGEMENTS
This research made use of the resources of the High Performance Computing Center at Idaho National Laboratory, which is supported by the Office of Nuclear Energy of the US Department of Energy and the Nuclear Science User Facilities under Contract No. DE-AC07-05ID14517. Further computational resources were provided by the R2 cluster (DOI: 10.18122/B2S41H) administrated by Boise State University's Research Computing Department. SLS acknowledges the US Department of Energy, Office of Basic Energy Sciences, Division of Chemical, Biological and Geological Sciences under grant DE-FG02-86ER13622.A000.