2. BEAM TARGET CONFIGURATION

A sketch of the considered beam-target configuration is shown in Figure 1. The target is a hollow cylinder of solid high-density material, for example, lead (ρ_Pb = 11.3 g/cm³) or gold (ρ_Au = 19.3 g/cm³). The sample material that has to be compressed is located inside the cylindrical cavity. We consider a cylindrical sample of cryogenic hydrogen at temperature T_H = 10 K and density ρ_H = 0.0886 g/cm³. The radius of this cylinder is R_H = 400 μm.

Sketch of the beam–target configuration showing the rotating beam with a Gaussian power profile in space. The inner hydrogen cylinder is surrounded by a high-density absorber. The target length is shorter than the ion range.

As shown in Figure 1, the target length is smaller than the ion range (subrange target). The Bragg peak will therefore lie outside the target, which will lead to a fairly uniform energy deposition along the particle trajectory. We consider that the target is driven by a heavy ion beam whose center is assumed to rotate with a frequency ν, forming a circular ring of radius r_c. The rotation frequency ν should be high enough to give a sufficiently uniform ion energy deposition to avoid a nonuniform cylindrical compression.

The heavy ion beam considered in the present study is formed by a bunch of uranium ions and is characterized by a parabolic intensity profile in time and a Gaussian shape in space. The total number of U ions in the bunch is assumed to be N_U = 2 × 10¹¹ and the ions are supposed to be accelerated up to a kinetic energy of 2.7 GeV/u.

The parabolic time dependence of the ion beam is given by

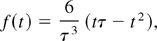
where τ is the pulse duration. Presently, the SIS18 facility allows for a high compression of the ion bunch providing bunches of 300 ns duration. The future SIS100 facility at GSI is expected to be able to provide bunches with a temporal spread of a few tens of nanoseconds. In the present study, we consider a pulse length of τ = 100 ns. The spatial ion beam profile has been considered to be Gaussian and is characterized by its full width at half maximum (Δ = FWHM).

The specific power deposition as a function of the radial coordinate r can be well approximated by the following equation:

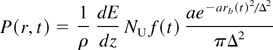
where N_U is the number of uranium ions in the bunch and dE/dz is the ion stopping power, r_b is the instantaneous distance between the considered position r and the rotating beam center r_c(t). The distance r_b is a function of time given by r_b² = r² + r_C² − 2r_C r cos(2πνt). Constant a = −4 ln(1/2) is obtained by normalization to the total beam energy.

Due to the beam rotation, the energy deposition at a given angular position results in a series of N = ντ pulses that are modulated in time by the parabolic shape. In Figure 2, the profiles of the specific power deposition P(r, t) as a function of time are shown. The lines correspond to the selected radii, r = 0.0, r_c /3, 2r_c/3, and r_c, respectively. In this example, we consider a lead absorber and the beam parameters are ν = 100 MHz, τ = 100 ns, dE/dz = 10¹⁰ [eV cm²/g], and N_U = 2 × 10¹¹. These beam–target parameters allow for depositing of a total energy of 3.5 kJ/cm length in the target.

Specific power deposition as a function of time evaluated at different radii; r = 0.0, 2rc /3, rc/3, and rc, where rc is the radius of the trajectory of the center of the focal spot.

The specific energy deposition as a function of the radius r is evaluated by the time integral of Eq. (2). The numerical integration of P(r, t) over the pulse duration τ provides the specific energy deposition, ε, shown in Figure 3. In this figure, the Gaussian shape of the ion beam pulse intensity is also shown (dotted line, arbitrary units). It is seen that due to the beam rotation, the maximum of the specific energy deposition is shifted inward, and due to the long tail of the Gaussian distribution, the specific energy deposition is nonsymmetric and is higher at a lower radius. The total energy deposited per centimeter in the target as a function of the radius is also shown.

Total time-integrated specific energy deposition, ε, and the integral of the total deposited energy, E, versus target radius. The intensity of the Gaussian beam profile is shown in arbitrary units (dotted line).

The stopping power of the uranium ions in a solid cold target has been calculated by using the code SRIM (Ziegler et al., 1996). In Figure 4, the stopping power of a uranium ion in solid lead (dotted line) and in solid gold (solid line) has been plotted as a function of the range. In the same picture, the residual kinetic energy of the uranium ions have also been shown.

Stopping power of U ions in Au (full line) and Pb (dotted line) solid targets versus the range. The residual ion kinetic energy is also shown.

The calculations of these two stopping powers have been carried out considering that the initial kinetic energy of the U ions was 3 GeV/u. As is seen in Figure 4, the stopping power of the U ions with energy greater than 1 GeV/u is practically constant and is nearly equal to dE/dz = 10¹⁰ eV cm²/g in lead as well as in gold. By considering U ions accelerated to 2 GeV/u, the ion energy deposition results to be roughly constant over a distance bigger than L_Au = 1.3 cm in gold and L_Pb = 2.2 cm in lead. This allows one to use subrange targets with a relatively long length for which the specific energy deposition is practically uniform along the ion path. The SRIM code has also been used to evaluate the stopping power of the U ions passing through the cryogenic hydrogen. Of course, due to the very low density of the hydrogen, ρ_H = 0.0886 g/cm³, the range result is as large as 2.5 m. The value of the stopping power outside the Bragg peak zone is nearly constant at about (dE/dz)_H = 3.4 × 10¹⁰ eV cm²/g.

3. 1D TARGET COMPRESSION

A set of 1D simulations of the target dynamics has been performed using the MULTI-1D code. The beam parameters were considered to be those available at the future SIS100 facility at the GSI Darmstadt.

A set of simulations has been performed by considering a total number of 2 × 10¹¹ ions per bunch and a Gaussian pulse shape with Δ = 1 mm and pulse length τ = 100 ns. For these cases, the absorber is considered to be made of lead. For each simulation, we looked for the maximum density and temperature of the central hydrogen sample. The radial position of the rotating beam center, r_c, is increased starting with the case of coaxial focal spot, r_c = 0 up to 3.5 mm. The results are shown in Figure 5, where the full line corresponds to the average maximum hydrogen density (g/cm³) and the dotted line corresponds to the maximum hydrogen temperatures in electron volts.

Average hydrogen density (full line) and temperature (dotted line) achieved at stagnation, as a function of the radius rc. The data refer to the target with a Pb absorber and a Gaussian beam with Δ = 1 mm.

These results clearly show that there are two regions: one corresponding to relatively smaller radii r_c providing lower hydrogen compression and the second, for large radii r_c, that allows for higher target compression. If the rotating beam center is situated at around 1.8 mm, the temperature is lower than 0.1 eV and the hydrogen density becomes higher than 0.8 g/cm³. This stepped behavior can be qualitatively understood by considering that only a relatively large value of the beam center, r_c, allows for the generation of a shaped energy deposition. This shaping creates a zone within the absorber just outside the hydrogen sample that is characterized by a lower specific energy deposition. This zone acts as an inertial pusher that leads to more efficient dynamics of the compression. At the same time a larger r_c reduces the energy deposited in the inner hydrogen sample, allowing for a higher compression.

Analogous simulations have been performed considering a gold absorber instead of lead. A set of simulation has also been done varying the FWHM of the Gaussian distribution. Namely, we consider Δ = 0.5, 1, and 2 mm. In these simulations we still use the same beam intensity N_U = 2 × 10¹¹. The results concerning the maximum average hydrogen temperature and maximum density are shown in Figures 6a and 6b, respectively.

Average maximum hydrogen temperatures (a) and density (b) as a function of radius rc for beams with different values of the FWHM: Δ = 0.5 (void circle), 1 (full circle), and 2 mm (box). The data refer to a target made of an Au absorber.

As seen clearly in Figure 6b, corresponding to the Gaussian pulse with a Δ = 1 mm, the density increases in comparison with the previous case when a lead absorber has been used. With the gold absorber, the maximum average hydrogen density increases up to 1.4 g/cm³. It is also to be noted that using a Gaussian shape with a smaller spread (see the cases with Δ = 0.5 mm), the maximum density increases up to 1.8 g/cm³ for a radius r_c = 1.2 mm. In contrast, by considering a wider Gaussian profile with a Δ = 2 mm, the density is reduced and is nearly constant, close to ρ = 0.7 g/cm³. This is because the beam heats a larger absorber mass, thus reducing the specific deposited energy. Moreover, the long Gaussian tail avoids the generation of an efficient pusher, contributing also to the preheating of the central hydrogen sample. Both effects play a negative role, thereby avoiding an efficient hydrogen compression.

Figure 7 shows the time evolution of the interface between the absorber and the hydrogen and the average density of the hydrogen. The results correspond to the case of a gold absorber using a Gaussian beam profile with Δ = 1 mm and r_c = 1.8 mm. The parabolic time dependence of the beam is plotted in the same figure. It is seen that during the first 100 ns, when the beam is still switched on, there is practically no motion of the absorber–hydrogen interface. A few hundred nanoseconds after the end of the pulse, the shock reaches the hydrogen sample and its compression is initiated. Stagnation is reached at around 500 ns, and a maximum density larger than 1.4 g/cm³ is achieved providing a compression factor of around 16.

Temporal evolution of the hydrogen–gold interface and of the average hydrogen density. The parabolic beam power profile is shown in arbitrary units (dotted line).

It is interesting to note that, considering a wider Gaussian distribution, the final hydrogen density result is practically constant, as shown in Figure 6. The final hydrogen compression is quite large even in the case when the beam is just centered and aligned with the cylindrical sample (r_c = 0) and it is not rotating. In this case, the temperature is higher than in the previous case, about 0.4 eV. However, a study of the EOS of hydrogen in this region is also of great scientific interest.

A series of simulations for different values of Δ using the same conditions as before has also been done. The maximum hydrogen compression and sample temperature are shown in Figure 8 as a function of the FWHM beam spread. The hydrogen density and temperature slowly decrease as the FWHM increases. Although the temperature decreases rapidly, for a large Gaussian spread (see, e.g., the data at Δ = 3 mm), it is reduced to 0.24 eV.

Hydrogen density and temperature at the stagnation versus Δ. Full circles correspond to the case where the ion beam is axially aligned with the target (rc = 0.0). See the main text for the meaning of the data labeled with mask (void circles).

The relatively high temperature of the sample arises from the fact that it is directly heated by the uranium ions. An ideal solution to provide high density at a lower temperature is to consider a high-density cylindrical plug between the incoming ions and the hydrogen sample. This mask must have the same radius as the central sample, thus avoiding the direct heating of the inner hydrogen. In the same figure we have also reported the densities and temperatures (dotted lines) reached neglecting the energy deposition of the ions entering into the hydrogen.

As expected, in this case, the hydrogen is compressed more efficiently (e.g., Δ = 2 mm allows for ρ > 1 g/cm³) and at the same time the temperature is reduced below the level of 1000 K.

4. ANALYSIS OF THE NONUNIFORMITY

The study of the nonuniformity generated by a rotating beam (peak-to-valley of the target surface) has been recently presented. It has been pointed out that the asymmetry depends on the time profile of the pulse and on the number of beam revolutions N (Piriz et al., 2003a). For a parabolic time profile, we have found that the relative asymmetry Δp/p (Piriz et al., 2003b) in the driving pressure is proportional to 1/N² (p is the mean pressure in the absorber layer at the end of the pulse).

In the present case, we have performed a series of simulations with a version of a 2D hydro-code BIG2 that include the energy deposition due to the rotating beam. In such simulations, we have used a Gaussian energy distribution for the beam focal spot with a parabolic temporal power profile. Besides, we have considered the optimal case corresponding to r_c = 1.8 mm. In Figure 9, we present the simulation results showing that the pressure asymmetry Δp/p is still proportional to 1/N².

Relative pressure asymmetry Δp/p versus the beam revolutions number, N, where p is the mean pressure in the absorber layer at the end of the pulse.

An asymmetry of the level of 1% can be achieved by considering a rotating beam system able to generate a minimum number of beam revolutions, N_1%, during the beam pulse. As is shown in Figure 9, such a threshold lies around N_1% = 10 for the Gaussian profile, similar to the results obtained previously for a parabolic energy distribution (Piriz et al., 2003b).