Introduction
Calendar calculating (CC) is the ability to swiftly name the weekday given any date. The ability is viewed as a savant syndrome phenomenon, but is also observed in typically developed mathematicians. The savant syndrome is a condition of mental or sensory disability paired with an outstanding capacity in a circumscribed domain of intellectual or artistic function (Bölte & Poustka, Reference Bölte and Poustka2004). Despite the classical definition of all savants being mentally retarded (Down, Reference Down1887), intelligence quotient (IQ) can vary between profound mental retardation and normal cognitive function with a peak in the area of borderline normal IQ. While the population prevalence of the savant syndrome is around 0.6% in mental retardation (Hill, Reference Hill1977), Rimland (Reference Rimland and Serban1978) reports a rate of 9.8% in autism.
There is a rich history of anecdotal reports on savant CC (Down, Reference Down1887; Binet, Reference Binet1894; Tredgold, Reference Tredgold1914; Horwitz et al. Reference Horwitz, Kestenbaum and Person1965; Hill, Reference Hill1975). They show a considerable interindividual variation of performance and CC span from years (Rubin & Monaghan, Reference Rubin and Monaghan1965) to millenniums (Horwitz et al. Reference Horwitz, Deming and Winter1969; Sacks, Reference Sacks1985). Although occasional cases of CC onset under the age of 8 years have been reported (O'Connor & Hermelin, Reference O'Connor and Hermelin1992), most CC skills seem to appear between the ages of 8 and 15 years. CC is frequently accompanied by other savant talents, among them outstanding musical performance (Judd, Reference Judd, Obler and Fein1988).
The mechanisms underlying CC skills are still poorly understood. Self-reports by savants have not yielded testable hypotheses (Horwitz et al. Reference Horwitz, Deming and Winter1969; Rosen, Reference Rosen1981). Aside from the hypothesis of eidetic imagery (e.g. Jones, Reference Jones1926) being ruled out by a blind CC (Rubin & Monaghan, Reference Rubin and Monaghan1965), approaches may be classified in usage of ‘unique memory’ (Spitz & LaFontaine, Reference Spitz and LaFontaine1973; Hill, Reference Hill1975) and ‘rule-based arithmetic skills’ (O'Connor & Hermelin, Reference O'Connor and Hermelin1984; Hermelin & O'Connor, Reference Hermelin and O'Connor1986). Hill (Reference Hill1975) postulated ‘rote memory’ to account for savant CC. Rote memory is a technique which avoids grasping the inner complexities and inferences of the subject that is being learnt and instead focuses on memorizing the material mechanically, so that it can be recalled by the learner exactly the way it was read or heard. O'Connor & Hermelin (Reference O'Connor and Hermelin1984) found that error rates and response times increased linearly for past dates and temporal remoteness to present dates, suggesting a better recall of experienced or recently used day-to-date assignments. However, they also observed a similar pattern for future dates. Thus, retrieval of information stored in a mechanical memory system may not be able to fully explain CC (O'Connor & Hermelin, Reference O'Connor and Hermelin1984; Young & Nettelbeck, Reference Young and Nettelbeck1994). The application of rules which govern the structure of the Gregorian calendar might be an additional factor in CC (Hermelin & O'Connor, Reference Hermelin and O'Connor1986; Ho et al. Reference Ho, Tsang and Ho1991; Young & Nettelbeck, Reference Young and Nettelbeck1994). Spitz (Reference Spitz1994) demonstrated that the use of rule-based algorithms led to correct day-to-date solutions. Nevertheless, mathematical algorithms may not explain an increased difficulty for leap years or the ability to answer reverse questions (‘In which year does November the 6th fall on a Wednesday?’), for which an algorithm cannot be applied without a complex modification of the formula (Young & Nettelbeck, Reference Young and Nettelbeck1994). Because savant CC almost exclusively fail on even simple arithmetic tasks and exhibit extremely short response latencies, the use of an algorithm appears implausible (Horwitz et al. Reference Horwitz, Kestenbaum and Person1965, Reference Horwitz, Deming and Winter1969).
In conclusion, many questions regarding the roots of savant CC remain unanswered. The objective of the present study was to compare savant and ‘normal’ CC in order to determine similarities and differences between respective performances and thereby extract savant-specific mechanisms. We hypothesized the following: first, rote memory functions discriminate between CC in savants and healthy calendar calculators (HCC). If this is true, then autistic calendar calculators (ACC) should exhibit superior performance to HCC when calculating past and present dates, but not future dates. Second, based on the results of Miller (Reference Miller, Colangelo, Assoulinem and Ambroson1987) and O'Connor & Hermelin (Reference O'Connor and Hermelin1992) we postulated that intense practice cannot account for the performances of ACC. So we predict, that even after intensive practice, the performance of HCC will not be comparable with that of ACC. Third, in line with findings by Hill (Reference Hill1975) and Rosen (Reference Rosen1981), we expected patterns of results indicating a dependency of the behavioural performance on calendar variables (e.g. month-ten-day section, month, year), and therefore the usage of anchor dates (memory of specific dates from which can be calculated back and forth) in ACC. Fourth, owing to the work by O'Connor & Hermelin (Reference O'Connor and Hermelin1984) we predicted error rates and response times to increase linearly with the remoteness to dates of the present in ACC.
Method
Participants
CC was examined in four groups: three ACC, six non-savant individuals with autism (A), three HCC and 18 healthy CC laymen (H). The sample sizes were determined by the availability of ACC and HCC. ACC and HCC sample characteristics are summarized in Table 1. The groups of ACC and A were recruited in cooperation with the Department of Child and Adolescent Psychiatry and Psychotherapy of J. W. Goethe University (Frankfurt, Germany). They fulfilled the International Classification of Diseases (ICD)-10 research criteria for the disorder (F84.0) as well as the autism algorithm cut-offs using the German versions of the Autism Diagnostic Interview – Revised (Bölte et al. Reference Bölte, Rühl, Schmötzer and Poustka2006) and the Autism Diagnostic Observation Schedule (Rühl et al. Reference Rühl, Bölte, Feineis-Matthews and Poustka2004). The three ACC were all male; IQ data were available for two of these participants. The A group consisted of five males and one female. Their age varied between 9 and 35 years with a mean of 19.7 years (s.d.=9.7 years), their IQ between 100 and 130 with a mean of 119.2 years (s.d.=10.4 years). Individuals with autism received a non-monetary gift for their participation.
Table 1. Sample characteristics of ACC and HCC
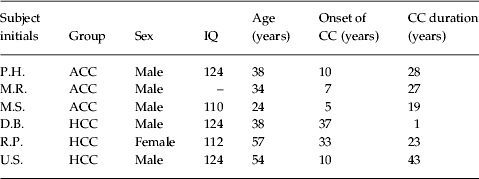
ACC, Savant calendar calculators with autism; HCC, healthy calendar calculators; IQ, intelligence quotient; CC, calendar calculating.
HCC were recruited through a summons of the Swiss television channel SF1 in the context of a scientific telecast. There were one female and two male participants in this sample (see Table 1). Members of the H group were recruited by personal contact. Sixteen were male and two female, with a mean age of 28.3 years (s.d.=12.3 years), and a mean IQ of 119.67 (s.d.=6.7). Participants in this group were compensated for their participation in the study (€8 per h, total duration 5 h).
Handedness was accessed using the Edinburgh Handedness Inventory (Oldfield, Reference Oldfield1971), non-verbal intelligence using the Standard Progressive Matrices (Raven et al. Reference Raven, Court and Raven1979). Several subscales from the Wechsler Memory Scale – Revised (WMS-R; Wechsler, Reference Wechsler1987), Wechsler Intelligence Scales for Adults – Revised (Tewes, Reference Tewes1994) and Learning and Memory Test-3 (Bäumler, Reference Bäumler1974) were administered to check for differences on psychometric memory tests.
The study was approved by the Ethical Committee of the University of Tübingen Medical School. Informed consent was collected from all participants, parents or caregivers.
Tasks and procedure
All participants were examined at the magnetoencephalography (MEG) laboratory of Eberhard Karls University (Tübingen, Germany). Two types of tasks were generated for this study: CC tasks and pseudodate tasks. In the CC tasks participants had to decide whether date-to-day assignments were correct or not (e.g. 6 November 1974=Thursday?). A total of 126 CC tasks were presented: 42 tasks for current dates (October 2003), 42 for past dates (1950–1999) and 42 for future dates (2003–2050). In all of the three time periods each weekday occurred six times. Tasks for current CC comprised all 31 days of October 2003 plus 11 date repetitions. To control for dependencies of the behavioural performance on different calendar variables, for past and future CC tasks, dates were also counterbalanced regarding the week and the decade of the month they belonged to (month-seven-day sections/month-ten-day sections), the month (January to December) and the decade of years they belonged to (10-year intervals). The ACC and HCC group were presented CC tasks for all time periods, whereas the A and the H group only processed tasks for current dates. An anchor date was given to the A and the H group from which they could calculate backwards and forwards.
In the pseudodate task subjects had to decide whether the letters written in the middle of a pseudodate were the same as quoted in the proffered answer (e.g. 13th YYYY 1986=YYYY?→yes versus 13th YYYY 1986=ZZZZ→no). This task was introduced to control for the visual load as well as general demands on working memory in terms of the two-choice paradigm and problems of ACC to solve simple tasks. Forty-two pseudodate control tasks were used in the study.
All tasks were presented on a white screen at a distance of 92 cm at a vertical visual angle of 1.245° and a horizontal visual angle of maximum 6.203°. CC tasks and pseudodate tasks were displayed in random order with no more than four of each type of task in a row. Each task was indicated by the presentation of a fixation cross that lasted 1 s. Participants had to answer the tasks by pressing a button as fast and as correct as possible using their right and left index finger, respectively, whereas the assignment was counterbalanced across subjects. Tasks were shown for a maximum of 15 s. The interval between the each task varied between 2.2 and 2.5 s. The maximum duration of the session was about 10 min for the A and H groups and 35 min for the ACC and HCC groups.
A structured questionnaire was generated to explore underlying strategies, knowledge concerning calendar regularities and sciences, CC span, onset of CC and CC duration in ACC and HCC. Moreover, information was gathered on mathematical school attainment and savant abilities other than CC. Questionnaire data was collected directly after CC task performance.
Statistics
Reaction time and percentage correct responses (PCR) were recorded as dependent variables of CC task performance. Groups' results concerning current dates were compared with a two-way simultaneous ANOVA, with type of task (CC versus pseudodate task) as the within-subject factor and group (ACC, A, HCC, H) as the between-subject factor. For the comparisons between the ACC and HCC groups, an additional two way ANOVA including time (current dates, past dates, future dates) as the within-subject factor and group (ACC, HCC) as the between-subject factor was carried out. Hence, current dates were included in both variance analytic plans in order to compare the results for current dates and the pseudodate task on the one hand and the results for different times on the other hand. In the case of significant ANOVAs, t tests were used for post-hoc group comparisons.
Against the background of linear curve fittings linear regressions with time as the explanatory variable were used to search for linear dependencies between the calendar variables month-seven-day sections, month-ten-day sections, months, 10-year intervals and the behavioural performance (reaction time/PCR), respectively. To examine, whether a U-shaped relationship exists between reaction time/PCR and the distance between current and past or future dates, moreover, for the 10-year intervals, separate polynomial curve fittings were calculated via non-linear regression equations (second-order polynomial). An α-level of p=0.05 was adopted throughout.
Results
All participants were right-handers and comparable regarding non-verbal intelligence [F(3, 24)=0.084, p=0.989]. Groups differed for age [F(3, 25)=4.134, p=0.016]: HCC were significantly older than A (p=0.011). Therefore, age had to be considered as a confounding variable. However, age neither correlated with reaction time nor PCR and no additional effects or interactions could be observed. Hence, age differences were not considered as a confounder in the main analysis. The only significant between-group difference on a memory test was on visual digit span backwards in the WMS-R [t(3,865)=3.0, p=0.042], where HCC showed better performance than ACC.
Present dates (ACC, HCC, A, H)
Reaction times for the CC tasks were longer than for the pseudodate control tasks [F(1, 26)=87.7, p<0.001, partial η2=0.771]. ANOVA showed that the factor group explained a significant amount of reaction time variance [F(3, 26)=4.2, p=0.015, partial η2=0.325]. Post-hoc tests revealed significantly shorter reaction times in ACC than in HCC (p=0.046) and than in A (p=0.045). However, this effect was mainly due to differences in the CC task, resulting in the interaction of group×task [F(3, 26)=4.2, p=0.015, partial η2=0.325]. Post-hoc tests revealed shorter reaction times in the CC task for ACC than HCC (p=0.035) and A (p=0.044), and additionally for H than A (p=0.039). HCC showed no superior performance in CC than any other group. Whereas HCC, A and H showed longer reaction times for the CC than for the pseudodate task (p=0.033, p=0.004 and p<0.001, respectively), no significant difference was found for ACC.
Analysis of task accuracy also revealed an interaction effect of group×task [F(3, 26)=10.2, p<0.001, partial η2=0.541]: in the CC task, PCR were higher in the ACC than in all other groups (HCC: p=0.039; A: p=0.019; H: p<0.001). Contrary to HCC, A and H, the ACC group performed poorly on the control task, as two out of three ACC showed high error rates. However, due to the large variance within the control task in ACC, this difference failed to reach significance. Descriptive data concerning reaction time and PCR are summarized in Tables 2 and 3.
Table 2. Reaction times (s) in calendar calculating and pseudodate control tasks

s.d., Standard deviation; s.e., standard error; CI, confidence interval; H, healthy calendar calculator laymen; A, non-savant subjects with autism; HCC, healthy calendar calculators; ACC, savant calendar calculators with autism.
* p<0.05.
Table 3. Percentage correct responses in calendar calculating and pseudodate control tasks

s.d., Standard deviation; s.e., standard error; CI, confidence interval; H, healthy calendar calculator laymen; A, non-savant subjects with autism; HCC, healthy calendar calculators; ACC, savant calendar calculators with autism.
* p<0.05, ** p<0.001.
Past, current and future dates (ACC, HCC)
Complete descriptive results for reaction time and PCR are summarized in Tables 4 and 5. Analysis of reaction times showed a main effect of group [F(1, 4)=8.2, p=0.046, partial η2=0.671], with shorter responses for ACC than for HCC across all dates. No interaction effect of group×time was found. However, on the basis of the hypothesis, which predicted superior performance in ACC than HCC only when calculating past and present dates, post-hoc t tests were carried out. These indicated shorter responses for ACC than for HCC for past (p=0.046) and current (p=0.035), but not for future dates. ACC showed significantly longer reaction times for future than for current dates (p=0.040), while HCC showed longer reaction times for past than for current dates (p=0.013).
Table 4. Reaction times (s) for all time periods
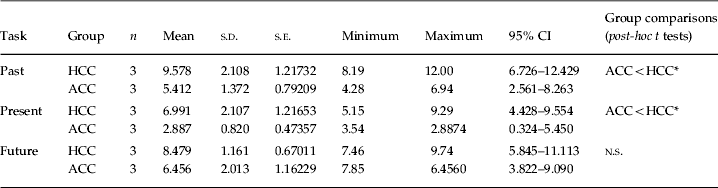
s.d., Standard deviation; s.e., standard error; CI, confidence interval; HCC, healthy calendar calculators; ACC, savant calendar calculators with autism; n.s., not significant.
* p<0.05.
Table 5. Percentage correct responses for all time periods
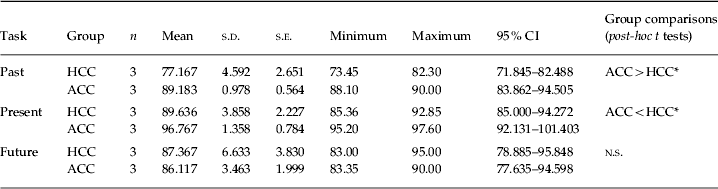
s.d., Standard deviation; s.e., standard error; CI, confidence interval; HCC, healthy calendar calculators; ACC, savant calendar calculators with autism; n.s., not significant.
* p<0.05.
A significant group×time interaction was detected for accuracy of performance [F(2, 8)=6.9, p=0.018, partial η2=0.634]. Post-hoc t tests showed that PCR were higher in ACC than in HCC for past (p=0.011) and present (p=0.039), but not future dates. ACC gave more correct responses for current than for past (p=0.26) and future (p=0.20) dates. HCC were more accurate regarding future than past dates (p=0.16) and equally accurate regarding future and current dates.
Linear dependencies on calendar variables
In ACC, across all time periods, linear relationships were found between reaction times and the month-ten-day section [r=0.98, R 2=0.99, F(1, 2)=185.47, p=0.047] and the month [r=−0.58, R 2=0.34, F(1, 11)=5.16, p=0.046]. That is, the later the date within a month and the later the month within a year, the longer was the reaction time. For 10-year intervals, a linear dependency was only found between reaction time and past dates [r=−0.89, R 2=0.78, F(1, 5)=13.82, p=0.02], but not between reaction time and future dates. For past dates reaction time increased for more remote years in ACC. In the HCC group, no reaction time or PCR linear dependencies were detected, except for PCR and the variable 10-year intervals [r=0.88, R 2=0.77, F(1, 5)=13.84, p=0.02] for past dates. Here PCR decreased with remoteness from the present.
When constructing a scatterplot, we noticed that a parabola might be a better fit for the relationship between reaction time and PCR and the distance to the present. Quadratic regression equation modelling confirmed this presumption. Findings for the calendar variable 10-year intervals showed for both ACC and HCC that a U-shaped relationship is likely for reaction time [R 2=0.53, F(2, 10)=4.566, p=0.047; R 2=0.59, F(2, 10)=5.69, p=0.028]: reaction time increases for future and past dates with remoteness to the present. For PCR, an inverted U-shaped relationship was found for HCC [R 2=0.76, F(2, 10)=13.04, p=0.003]: the further the date from the present, the lower was the PCR.
Questionnaire information
HCC reported to use algorithms to calculate date-to-day assignments and exhibited a profound explicit knowledge of the regularities of the Gregorian calendar. In contrast, ACC showed introspection difficulties when trying to explain the strategies underlying their CC abilities. Moreover, they stated never to have dealt with a perpetual calendar or calendar sciences and reported markedly poorer performance than HCC regarding school achievement in mathematics. On the other hand, all ACC demonstrated extraordinary memory skills in a circumscribed area (e.g. birthdates, history, timetables).
ACC as well as HCC were able to CC over a minimum span of 100 years, including future as well as past dates. They did neither differ with regard to the onset of CC nor the CC duration (see Table 1 for details). Apparently, onset of CC was earlier in ACC than in HCC, but due to the huge variance this difference failed to reach significance.
Discussion
Numerous behavioural approaches have attempted to explain the factors underlying CC in savants. The objective of the present study was to elaborate existing theories by comparing CC in savants with autism, individuals with autism without savant skills, HCC and healthy CC laymen. To the authors' knowledge, this study is the first of its kind in research on the savant syndrome. It should be mentioned first that like almost all studies on savant skills this study, too, suffers from small sample size and therefore limited generalizability. Thus, also the usage of parametric statistics is somewhat arbitrary. However, in light of the low frequency of savant skills and HCC and a lack of adequate procedures for small samples these problems are hard to avoid. In addition, post-hoc power analysis showed that given the partly huge effect sizes the power to detect differences (1−β) was not overly small. For instance, partial η2 was 0.671 for the comparison of reaction time between ACC and HCC, resulting in power of 74% given an α of 0.05 in a sample of n=6 and two groups in an ANOVA.
We found that ACC gave more correct responses for current dates than all other groups and showed shorter reaction times than A and HCC. They were also superior to HCC with regard to PCR and reaction time when processing past dates, but not future dates. These patterns of results indicate different CC strategies in ACC and HCC, the latter having acquired this ability as healthy individuals.
In line with previous studies (Horwitz et al. Reference Horwitz, Deming and Winter1969; Rosen, Reference Rosen1981) and despite good language abilities, ACC in our study exhibited difficulties in explaining their strategies when performing CC. The CC abilities of ACC could hardly be explained in terms of rule-based arithmetic skills. First, and most importantly, like other studies (Horwitz et al. Reference Horwitz, Deming and Winter1969; Young & Nettelbeck, Reference Young and Nettelbeck1994), ACC showed poor mathematical skills at school, while it is known that the use of algorithms demand substantial abilities in mathematics. Moreover, aside from their special CC ability and consistent with the definition of the savant syndrome (e.g. Bölte & Poustka, Reference Bölte and Poustka2004), two out of three ACC showed problems to understand the quite simple pseudodate control task. Moreover, and in accord with Horwitz et al. (Reference Horwitz, Deming and Winter1969) and Young & Nettelbeck (Reference Young and Nettelbeck1994), the response times of ACC were so short that the use of algorithms is unlikely. They gave their answers for the CC task as fast as in the simple pseudodate control task, while all other groups needed longer for the CC tasks. Compared with HCC, ACC had shorter response latencies across the whole calculating period (1950–2050). Overall, their performance might be best explained in terms of rote processes and direct memory retrieval. This conclusion might also be strengthened by the fact that ACC reported knowledge on timetables and birthdates that are associated with rote memory mechanisms. The CC savants in the studies by Horwitz et al. (Reference Horwitz, Deming and Winter1969), Rosen (Reference Rosen1981) and Young & Nettelbeck (Reference Young and Nettelbeck1994) were also described to have extraordinary memory for sports data, birthdates or the weather of any given date. Rote memory is defined as the veridical encoding of information (Heaton & Wallace, Reference Heaton and Wallace2004; p. 901) not interfered by top-down cognition. Its significance as the underlying factor in savant CC (Horwitz et al. Reference Horwitz, Deming and Winter1969; Hill, Reference Hill1975; Norris, Reference Norris1990; Young & Nettelbeck, Reference Young and Nettelbeck1994) and as a core savant skill in general (Mottron & Belleville, Reference Mottron and Belleville1993; Mottron et al. Reference Mottron, Belleville, Stip and Morasse1998; Bölte & Poustka, Reference Bölte and Poustka2004) has often been pointed out in the literature. However, calculation of future dates demanded longer response latencies. As reported earlier (e.g. Rosen, Reference Rosen1981), a general memory superiority of savants seems unlikely, owing to the fact that we did not detect any increased performance on any conventional psychometric memory scale. Thus, for future dates additional mental operations may be needed. Hermelin & O'Connor (Reference Hermelin and O'Connor1986) interpreted their finding of shorter reaction times for past than future dates in savants in terms of future dates requiring algorithmic calculations, while for past dates rote memory processes are sufficient. Our data might be interpreted in the same way.
Consistent with O'Connor & Hermelin (Reference O'Connor and Hermelin1984), we found that response times increased with remoteness to current dates. Nevertheless, unlike O'Connor & Hermelin (Reference O'Connor and Hermelin1984), a linear increase was only identified for past dates in ACC. This might indicate fast recall of day-to-date assignments from rote memory for past dates and rather easy access to current dates owing to actuality. For both ACC and HCC a U-shaped relationship between the remoteness from current and future dates and reaction time was found. Furthermore, for HCC an inverted U-shaped relationship for PCR was found between the remoteness from current and future dates via quadratic regression. This may underline the assumption that memory alone may be insufficient to account for CC performance in savants with autism. The U-shaped distribution could rather indicate the involvement of a further system, namely anchor dates (Hill, Reference Hill1975; Rosen, Reference Rosen1981) – dates, from which they could calculate back and forth. While it seems that this system could be equally important for ACC and HCC, savants with autism may be particularly operating with anchor dates in December. In accord with findings by Hill (Reference Hill1975) and Rosen (Reference Rosen1981), ACC showed linear dependencies of the behavioural performance on the calendar variables ‘month-ten-day section’ and ‘month’. That is, the earlier the decade within a month and the later a month within a year, the shorter was the reaction time.
Recent findings by Mottron et al. (Reference Mottron, Lemmens, Gagnon and Seron2006) favour a non-algorithmic retrieval model of CC. In line with this framework and contrary to other previous studies (e.g. Hill, Reference Hill1975), ACC in our study reported never to have dealt with a perpetual calendar or calendar sciences. On the other hand, HCC had profound knowledge of the regularities of the Gregorian calendar. However, the way ACC calculated future dates may point to the usage of at least some calendar regularities, although to a much less extent than HCC.
Another pivotal finding of this study concerns the role of rehearsal. It has been claimed that intense practice may be a key player for CC (Kelly et al. Reference Kelly, Macaruso and Sokol1997). Indeed, ACC and HCC performed best when calculating current dates, which might be interpreted as evidence for this hypothesis, as current dates are probably processed the most in everyday life. Nevertheless, even after substantial training, we could not observe that HCC reached the level of performance shown by ACC for current and past dates. This result in the face of the two groups not differing with regard to duration of the skill possession, the early onset of CC in ACC (also noted by Miller, Reference Miller, Colangelo, Assoulinem and Ambroson1987) and its stability (O'Connor & Hermelin, Reference O'Connor and Hermelin1992) indicates that rehearsal alone is insufficient to explain prodigious CC skills in savants with autism. Therefore, practice probably forms a necessary rather than a sufficient circumstance in the acquisition of CC in ACC.
In conclusion, our findings suggest that CC in savants with autism involves rote memory processing when calculating current and past dates, which may not be a part of CC in HCC. Treffert (Reference Treffert2006, p. 200) has hypothesized that all savants share some sort of extraordinary memory capacities. However, memory mechanisms alone cannot account for ACC performance in our study. It is likely that the use of anchor dates and some strategies based on the regularities of the Gregorian calendar also contribute to outstanding CC performance. We assume a model of past and current dates being learned easily by ACC using simple day-to-date associations that are stored by mechanical repetition and retrieved quickly. These rote memory processes are facilitated by interweaved anchor dates and the usage of simple regularities. This strategy may not apply to future dates. Here, the CC mechanisms might be comparable with those used by HCC, who use regularities and anchor dates for all types of dates, resulting in their relatively long reaction times even when calculating present dates. As rote memory processes of ACC seem to be hard to validate by conventional psychometric memory testing, the aforementioned cohesion could only be examined by direct comparison of ACC and HCC.
Acknowledgements
This study was supported by the Graduate Research Training Program on Cognitive Neurobiology of the Deutsche Forschungsgemeinschaft (DFG) at the University of Tübingen. We are indebted to all patients who participated in the study.
Declaration of Interest
None.







