We show that the spectrum of a sentence ϕ in Counting Monadic Second Order Logic (CMSOL) using one binary relation symbol and finitely many unary relation symbols, is ultimately periodic, provided all the models of ϕ are of clique width at most k, for some fixed k. We prove a similar statement for arbitrary finite relational vocabularies τ and a variant of clique width for τ-structures. This includes the cases where the models of ϕ are of tree width at most k. For the case of bounded tree-width, the ultimate periodicity is even proved for Guarded Second Order Logic GSOL. We also generalize this result to many-sorted spectra, which can be viewed as an analogue of Parikh's Theorem on context-free languages, and its analogues for context-free graph grammars due to Habel and Courcelle.

Our work was inspired by Gurevich and Shelah (2003), who showed ultimate periodicity of the spectrum for sentences of Monadic Second Order Logic where only finitely many unary predicates and one unary function are allowed. This restriction implies that the models are all of tree width at most 2, and hence it follows from our result.

We prove that for every simple theory T (or even simple thick compact abstract theory) there is a (unique) compact abstract theory whose saturated models are the lovely pairs of T. Independence-theoretic results that were proved in [5] when is a first order theory are proved for the general case: in particular is simple and we characterise independence.

We show that the quasi-order of continuous embeddability between finitely branching dendrites (a natural class of fairly simple compacta) is -complete. We also show that embeddability between countable linear orders with infinitely many colors is -complete.

Assume that all algebras are atomless. (1) Spind(A × B) = Spind(A) ∪ Spind(B). (2) Spind(Ai). Now suppose that κ and λ are infinite cardinals, with κ uncountable and regular and with κ < λ. (3) There is an atomless Boolean algebra A such that u(A) = κ and i(A) = λ. (4) If λ is also regular, then there is an atomless Boolean algebra A such that t(A) = s(A) = κ and α (A) = λ. All results are in ZFC, and answer some problems posed in Monk [01] and Monk [∞].

In reverse mathematics, one formalizes theorems of ordinary mathematics in second order arithmetic and attempts to discover which set theoretic axioms are required to prove these theorems. Often, this project involves making choices between classically equivalent definitions for the relevant mathematical concepts. In this paper, we consider a number of equivalent definitions for the notions of well quasi-order and better quasi-order and examine how difficult it is to prove the equivalences of these definitions.

As usual in reverse mathematics, we work in the context of subsystems of second order arithmetic and take RCA0 as our base system. RCA0 is the subsystem formed by restricting the comprehension scheme in second order arithmetic to formulas and adding a formula induction scheme for formulas. For the purposes of this paper, we will be concerned with fairly weak extensions of RCA0 (indeed strictly weaker than the subsystem ACA0 which is formed by extending the comprehension scheme in RCA0 to cover all arithmetic formulas) obtained by adjoining certain combinatorial principles to RCA0. Among these, the most widely used in reverse mathematics is Weak König's Lemma; the resulting theory WKL0 is extensively documented in [11] and elsewhere.

We give three other combinatorial principles which we use in this paper. In these principles, we use k to denote not only a natural number but also the finite set {0, …, k − 1}.

A set A is m-reducible (or Karp-reducible) to B if and only if there is a polynomial-time computable function f such that, for all x, x ∈ A if and only if f(x) ∈ B. Two sets are:

• 1-equivalent if and only if each is m-reducible to the other by one-one reductions;

• p-invertible equivalent if and only if each is m-reducible to the other by one-one, polynomial-time invertible reductions; and

• p-isumorphic if and only if there is an m-reduction from one set to the other that is one-one, onto, and polynomial-time invertible.

In this paper we show the following characterization.

Theorem. The following are equivalent:

(a) P = PSPACE.

(b) Every two 1-equivalent sets are p-isomorphic.

(c) Every two p-invertible equivalent sets are p-isomorphic.

We study the preservation under projective ccc forcing extensions of the property of L(ℝ) being a Solovay model. We prove that this property is preserved by every strongly- absolutely-ccc forcing extension, and that this is essentially the optimal preservation result, i.e., it does not hold for absolutely-ccc forcing notions. We extend these results to the higher projective classes of ccc posets, and to the class of all projective ccc posets, using definably-Mahlo cardinals. As a consequence we obtain an exact equiconsistency result for generic absoluteness under projective absolutely-ccc forcing notions.

We begin with a prepositional language Lp containing conjunction (Λ), a class of sentence names {Sα}αϵA, and a falsity predicate F. We (only) allow unrestricted infinite conjunctions, i.e., given any non-empty class of sentence names {Sβ}βϵB,

is a well-formed formula (we will use WFF to denote the set of well-formed formulae).

The language, as it stands, is unproblematic. Whether various paradoxes are produced depends on which names are assigned to which sentences. What is needed is a denotation function:

For example, the LP sentence “F(S1)” (i.e., Λ{F(S1)}), combined with a denotation function δ such that δ(S1)“F(S1)”, provides the (or, in this context, a) Liar Paradox.

To give a more interesting example, Yablo's Paradox [4] can be reconstructed within this framework. Yablo's Paradox consists of an ω-sequence of sentences {Sk}kϵω where, for each n ϵ ω:

Within LP an equivalent construction can be obtained using infinite conjunction in place of universal quantification - the sentence names are {Si}iϵω and the denotation function is given by:

We can express this in more familiar terms as:

etc.

A model is said to be Leibnizian if it has no pair of indiscernibles. Mycielski has shown that there is a first order axiom LM (the Leibniz-Mycielski axiom) such that for any completion T of Zermelo-Fraenkel set theory ZF. T has a Leibnizian model if and only if T proves LM. Here we prove:

Theorem A. Every complete theory T extending ZF + LM has nonisomorphic countable Leibnizian models.

Theorem B. If κ is a prescribed definable infinite cardinal ofa complete theory T extending ZF + V = OD, then there are nonisomorphic Leibnizian models of T of power ℵ1such thatis ℵ1-like.

Theorem C. Every complete theory T extendingZF + V = ODhas nonisomorphic ℵ1-like Leibnizian models.

We prove here that the intuitionistic theory T0↾ + UMIDN. or even EETJ↾ + UMIDN, of Explicit Mathematics has the strength of –CA0. In Section 1 we give a double-negation translation for the classical second-order μ-calculus, which was shown in [Mö02] to have the strength of –CA0. In Section 2 we interpret the intuitionistic μ-calculus in the theory EETJ↾ + UMIDN. The question about the strength of monotone inductive definitions in T0 was asked by S. Feferman in 1982, and — assuming classical logic — was addressed by M. Rathjen.

We examine the question of how many Boolean algebras, distinct up to isomorphism, that are quotients of the powerset of the naturals by Borel ideals, can be proved to exist in ZFC alone. The maximum possible value is easily seen to be the cardinality of the continuum ; earlier work by Ilijas Farah had shown that this was the value in models of Martin's Maximum or some similar forcing axiom, but it was open whether there could be fewer in models of the Continuum Hypothesis.

We develop and apply a new technique for constructing many ideals whose quotients must be nonisomorphic in any model of ZFC. The technique depends on isolating a kind of ideal, called shallow, that can be distinguished from the ideal of all finite sets even after any isomorphic embedding, and then piecing together various copies of the ideal of all finite sets using distinct shallow ideals. In this way we are able to demonstrate that there are continuum-many distinct quotients by Borel ideals, indeed by analytic P-ideals, and in fact that there is in an appropriate sense a Borel embedding of the Vitali equivalence relation into the equivalence relation of isomorphism of quotients by analytic P-ideals. We also show that there is an uncountable definable wellordered collection of Borel ideals with distinct quotients.

We interpret the algebra of finite rank operators as imaginaries inside a Hilbert space. We prove that the Hilbert space enlarged with these imaginaries has built-in canonical bases.

In this paper, we prove the wellfoundedrtess of recursive notation systems for reflecting ordinals up to Π3-reflection by relevant inductive definitions.

Let be an o-minimal expansion of the ordered field of real numbers , and let S be an -definable subset (parameters allowed unless otherwise stated) of ℝn. In this note I investigate questions concerning the distribution of points on S with integer coordinates. My main theorem gives an estimate which, though probably far from best possible, at least shows that the o-minimal assumption does have diophantine consequences. This is, perhaps, surprising in view of the flexibility that we now seem to have in constructing o-minimal expansions of (see, e. g. [7], [8], [9]).

We present a comparatively simple way to construct Martin-Löf random and rec-random sets with certain additional properties, which works by diagonalizing against appropriate martingales. Reviewing the result of Gács and Kučera, for any given set X we construct a Martin-Löf random set from which X can be decoded effectively.

By a variant of the basic construction we obtain a rec-random set that is weak truth-table autoreducible and we observe that there are Martin-Löf random sets that are computably enumerable self-reducible. The two latter results complement the known facts that no rec-random set is truth-table autoreducible and that no Martin-Löf random set is Turing-autoreducible [8, 24].

We characterize (both from a syntactic and an algebraic point of view) the normal K4-logics for which unification is filtering. We also give a sufficient semantic criterion for existence of most general unifiers, covering natural extensions of K4.2+ (i.e., of the modal system obtained from K4 by adding to it, as a further axiom schemata, the modal translation of the weak excluded middle principle).

We study reals with infinitely many incompressible prefixes. Call A ∈ 2ωKolmogorov random if . where C denotes plain Kolmogorov complexity. This property was suggested by Loveland and studied by Martin-Löf. Schnorr and Solovay. We prove that 2-random reals are Kolmogorov random. Together with the converse—proved by Nies. Stephan and Terwijn [11]—this provides a natural characterization of 2-randomness in terms of plain complexity. We finish with a related characterization of 2-randomness.

A Turing degree a is said to be almost everywhere dominating if, for almost all X ∈ 2ω with respect to the “fair coin” probability measure on 2ω, and for all g: ω → ω Turing reducible to X, there exists f: ω → ω of Turing degree a which dominates g. We study the problem of characterizing the almost everywhere dominating Turing degrees and other, similarly defined classes of Turing degrees. We relate this problem to some questions in the reverse mathematics of measure theory.

Let us say that a geometric theory T is of presheaf type if its classifying topos is (equivalent to) a presheaf topos. (We adhere to the convention that geometric logic allows arbitrary disjunctions, while coherent logic means geometric and finitary.) Write Mod(T) for the category of Set-models and homomorphisms of T. The next proposition is well known; see, for example, MacLane–Moerdijk [13], pp. 381-386, and the textbook of Adámek–Rosický [1] for additional information:

Proposition 0.1. For a category 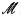, the following properties are equivalent:

(i) 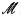is a finitely accessible category in the sense of Makkai–Paré [14], i.e., it has filtered colimits and a small dense subcategory 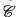of finitely presentable objects

ii) 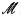is equivalent to Pts, the category of points of some presheaf topos

(iii) 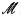is equivalent to the free filtered cocompletion (also known as Ind-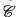) of a small category .

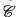(iv) 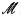is equivalent to Mod(T) for some geometric theory of presheaf type.

Moreover, if these are satisfied for a given 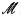, then the 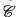—in any of (i), (ii) and (iii)—can be taken to be the full subcategory of 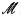consisting of finitely presentable objects. (There may be inequivalent choices of 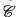, as it is in general only determined up to idempotent completion; this will not concern us.)

This seems to completely solve the problem of identifying when T is of presheaf type: check whether Mod(T) is finitely accessible and if so, recover the presheaf topos as Set-functors on the full subcategory of finitely presentable models. There is a subtlety here, however, as pointed out (probably for the first time) by Johnstone [10].