1. Introduction
Much of the world's population, especially the poor in rural areas of developing countries, rely on biomass (crop residues, animal dung, and fuelwood) for basic household energy requirements. In rural Sub-Saharan Africa (SSA), for example, 80 per cent of the population depends on biomass for daily cooking fuel, with most of the biomass coming from fuelwood (International Energy Agency, 2014). This dependency on fuelwood carries many implications for the environment and for households' livelihoods, gender roles, and health.
The environmental impacts of fuelwood use include greenhouse gas (GHG) emissions and deforestation. In the year 2000, net residential GHG emissions in SSA totaled 79 million metric tons of carbon (MtC), 61 per cent of which were due to fuelwood use (Bailis et al., Reference Bailis, Ezzati and Kammen2005). These emissions are projected to increase. Under a ‘business as usual’ scenario, cumulative residential GHG emissions in SSA are estimated to reach 6.7 billion tons of carbon by 2050, or 134 MtC per year – the equivalent of more than four large coal-fired power plants operating at full capacity over the period (World Wide Fund for Nature, 2007). Fuelwood off-farm collection, along with charcoal production, also contributes to widespread deforestation (Hosonuma et al., Reference Hosonuma, Herold, De Sy, De Fries, Brockhaus, Verchot, Angelsen and Romijn2012). From all sources, the last decade witnessed 13 million hectares of trees lost every year globally (Food and Agriculture Organization, 2010), including 290,000 hectares in Africa (Joint Research Center: The European Commission, 2013). Other environmental concerns include the loss of animal habitat and decreases in soil nutrients and moisture, leading to desertification (World Meteorological Organization, 2010).
In addition to environmental concerns, the use of fuelwood as an energy source places a particular burden on women in the household, given that women in SSA are often responsible for both fuelwood collection and food preparation. Increasing scarcity of fuelwood means increasing collection times. This adds to the labor burden of women, as traditional roles such as raising children, cooking, and other household tasks create a ‘double workday’ and mean that women often work much longer hours than their male spouses (Kes and Swaminathan, Reference Kes, Swaminathan, Blackden and Wodon2006). Moreover, smoke from all biomass sources (including fuelwood) is associated with millions of deaths per year in SSA due to respiratory diseases (Lim et al., Reference Lim, Vos, Flaxman, Danaei, Shibuya and Adair-Rohani2012). As incomes increase, households are unlikely to quickly switch in large numbers to more modern fuels such as kerosene or liquefied petroleum gas (LPG) (Cooke et al., Reference Cooke, Köhlin and Hyde2008). Instead, households often engage in ‘fuel stacking,’ gradually adding new sources of energy while continuing to consume traditional biomass such as fuelwood (Masera et al., Reference Masera, Saatkamp and Kammen2000; Van Der Kroon et al., Reference Van Der Kroon, Brouwer and Van Beukering2013).
Renewable forestry management has frequently been viewed as a potential remedy for these related problems. On-farm fuelwood production and agroforestry, for example, can reduce the environmental impacts of fuelwood and charcoal use (Mbow et al., Reference Mbow, Smith, Skole, Duguma and Bustamante2014) and mitigate household search costs associated with deforestation. Since the 1970s, many research and non-governmental organizations have focused on promoting agroforestry in SSA,Footnote 1 with many projects paying particular attention to transferring agroforestry skills to women (Bradley and Huby, Reference Bradley and Huby1993; Maathai, Reference Maathai1993; Kiptot and Franzel, Reference Kiptot and Franzel2012). These projects have been influential in shifting on-farm tree management from non-fuelwood uses to fuelwood usage and in increasing the absolute number of trees on-farm.
The main goals of this paper are to investigate: 1) whether household fuelwood sources (fuelwood collected off-farm, that produced on-farm, or purchased) are close substitutes or differentiated products, and 2) whether gender roles persist in fuelwood on-farm production and off-farm collection. Few studies have analyzed whether multiple fuelwood sources themselves are close substitutes to one another using shadow prices. The answer to this question, however, can have important implications for policies centered on reducing forest degradation or promoting agroforestry to produce a renewable fuelwood source. Most of the empirical literature examining household energy needs thus far has focused on understanding the substitution between aggregate fuelwood consumption (or consumption from a single source) and other biomass options such as agricultural residues, and has relied on data from South Asia, with only a few studies of fuelwood demand in SSA (table 1).
Table 1. Estimates of fuelwood elasticities from the existing literature
Notes: †These papers provide elasticity estimates for two distinct populations and do not provide a combined estimate.
*** p < 0.01, * p < 0.1, – not statistically significant.
We examine fuelwood substitution and gender roles in the context of western Kenya. In the area of our study, fuelwood markets are imperfect and household production and consumption decisions are non-separable.Footnote 2 Following Heltberg et al. (Reference Heltberg, Arndt and Sekhar2000) and Palmer and MacGregor (Reference Palmer and MacGregor2009), we modify the agricultural household model to focus on the substitution among different fuelwood sources and on the role of a household's labor endowment. Empirically, we first estimate shadow prices for different fuelwood sources using household-specific male and female wages. Controlling for potential selection bias and endogeneity, we then estimate demand equations for different sources of fuelwood: fuelwood collected off-farm, fuelwood produced on-farm, and that bought at the market. The data used in the empirical estimation come from a recent detailed production and consumption survey of over 300 households in the western Kenyan highlands (Berazneva et al., Reference Berazneva, Lee, Place and Jakubson2017). Since the majority of existing fuelwood demand studies focus on South Asia, our analysis offers new evidence of fuelwood consumption patterns in East Africa.
We show that cross-price elasticities between fuelwood sources are very low (ranging from 0.02 to 0.24), suggesting that Kenyan households do not readily substitute between fuelwood sources. As expected, we also find that own-price demand elasticities for non-purchased fuelwood are negative and inelastic (−0.55 to −0.61). As the implicit cost increases for a particular source of fuelwood, there is only limited substitution with other fuelwood sources. This limited substitution is, we suggest, partially explained by gender roles. The data show that women are primary collectors of fuelwood off-farm and men are primary producers of fuelwood on-farm. This gender division is also reflected in the econometric results, with female and male shadow wages tied to off-farm fuelwood collection and on-farm fuelwood production, respectively. It appears that the lack of labor substitutability contributes to limited opportunities to substitute between fuelwood sources.
This paper is related to a rich body of research in economics that examines household energy decisions. As fuelwood scarcity increases, households react to the rising implicit cost of obtaining fuelwood in various ways: they substitute other fuels, purchase fuelwood from the market, plant trees on their own farm, adopt higher efficiency stoves, or increase off-farm collection times (see Cooke et al. (Reference Cooke, Köhlin and Hyde2008) for a review of the literature). The empirical evidence in support of these hypotheses, however, has been mixed. Several studies that look at the use of fuelwood, crop residues, and animal dung find no evidence of substitution (Pattanayak et al., Reference Pattanayak, Sills and Kramer2004; Palmer and MacGregor, Reference Palmer and MacGregor2009; Damte et al., Reference Damte, Koch and Mekonnen2012), while others find evidence of complementarity between fuelwood and cut grass and leaf fodder (Cooke, Reference Cooke1998a) and animal dung (Mekonnen, Reference Mekonnen1999). Other studies analyze fuelwood sourcing from forest reserves. Cooke (Reference Cooke, Robinson and Bluffstone2014), for example, shows that the level of restrictions on fuelwood collection in the community managed forests in South Asia determines the quantity that is collected from other sources, while in Uganda, Miteva et al. (Reference Miteva, Kramer, Brown and Smith2017) find that proximity to forest resources increases the likelihood of fuelwood collection (and the likelihood of purchasing fuelwood increases as the distance to market decreases). Amacher et al. (Reference Amacher, Hyde and Joshee1993), Amacher et al. (Reference Amacher, Hyde and Kanel1996, Reference Amacher, Hyde and Kanel1999), and Pattanayak et al. (Reference Pattanayak, Sills and Kramer2004) find that owning more efficient stoves leads to a significant decrease in fuelwood consumption, although Heltberg et al. (Reference Heltberg, Arndt and Sekhar2000) find no such effect. Finally, the response of labor supply to increases in the scarcity of fuelwood (and in the implicit cost of fuelwood) is always positive, but the evidence is mixed as to whether the magnitude is greater than or less than that of the own-price elasticity (Amacher et al., Reference Amacher, Hyde and Kanel1996; Cooke, Reference Cooke1998a; Heltberg et al., Reference Heltberg, Arndt and Sekhar2000; Palmer and MacGregor, Reference Palmer and MacGregor2009).
To our knowledge, no existing study has specifically focused on the substitution among rural households' three major sources of fuelwood – fuelwood collected off-farm, produced on-farm, and purchased. In perfectly functioning fuelwood and labor markets, the costs of the fuelwood coming from different sources would be equal (given the same quality of fuelwood demanded). Market imperfections, however, can create divergences between the household-specific implicit or shadow prices of different fuelwood sources and the market price, and can lead to source-specific own-price and cross-price elasticities. Several studies that estimate the demand for off-farm collection and on-farm fuelwood production do not, however, estimate cross-price elasticities to measure their substitution (Amacher et al., Reference Amacher, Hyde and Joshee1993; Heltberg et al., Reference Heltberg, Arndt and Sekhar2000). They also use collection time as a proxy variable for the shadow price and, in the case of Heltberg et al. (Reference Heltberg, Arndt and Sekhar2000), combine fuelwood produced on-farm with crop residues and animal dung. In contrast, we estimate own-price elasticities for three separate fuelwood sources using shadow prices and market prices, and then analyze the substitution patterns among the sources given by cross-price elasticities. An understanding of household substitution among fuelwood sources can help reveal whether households treat fuelwood as a homogeneous product, as is often implicitly assumed in the literature, or whether it is a differentiated product based on its source. If indeed households do differentiate among fuelwood based on its source and if strong preferences exist for certain fuelwood sources, policies that promote agroforestry will likely be ineffective unless the factors influencing these preferences are first addressed.
The rest of this paper is organized as follows. In section 2 we describe the background to the research area and data collected in western Kenya in 2011–2012. Section 3 presents a non-separable agricultural household model that takes into account the various fuelwood sources and household labor endowments. In section 4 we describe our empirical strategy, which includes maximum likelihood estimation of the Heckman estimators to control for selection bias in the imputed wages and fuelwood source groups, and two-stage least squares estimation to control for endogeneity in the shadow prices. We present our results in section 5 and highlight their management and policy implications in section 6.
2. Background
Forests cover less than 7 per cent of Kenya's land area, yet they make a significant contribution to the national economy and provide many direct and indirect goods and services to its people (Republic of Kenya: Ministry of Environment, 2014). Historically, Kenyan forests have been cleared both to create land for agriculture and for the sale and subsistence use of forest products. In recent years, deforestation has been largely driven by the latter, as the private consumption of forest products doubled between 2000 and 2010 (Crafford et al., Reference Crafford, Strohmaier, Muñoz, De Oliveira, Lambrechts, Wilkinson, Burger and Bosch2012). The rate of deforestation has averaged about 5000 hectares per year in the Kenyan montane forests (Crafford et al., Reference Crafford, Strohmaier, Muñoz, De Oliveira, Lambrechts, Wilkinson, Burger and Bosch2012) and has had substantial effects on many aspects of the Kenyan environment and economy. Evidence suggests, for example, that deforestation has raised ambient surface temperatures and increased the incidence of malaria (Yasuoka and Levins, Reference Yasuoka and Levins2007), augmented river sedimentation and harmed fish habitats (Simonit and Perrings, Reference Simonit and Perrings2011), and reduced water flow used for irrigation and energy production by hydropower plants (Crafford et al., Reference Crafford, Strohmaier, Muñoz, De Oliveira, Lambrechts, Wilkinson, Burger and Bosch2012), among other impacts. The impacts of deforestation have been estimated to have cost the Kenyan economy 5.8 billion Kenyan shillings (USD69 million) in 2010 (Crafford et al., Reference Crafford, Strohmaier, Muñoz, De Oliveira, Lambrechts, Wilkinson, Burger and Bosch2012).
Roughly 80 per cent of Kenyan households and businesses still depend on fuelwood as a primary energy source (Republic of Kenya: Ministry of Environment, 2014). The Kenyan government and many non-governmental organizations have promoted private tree cultivation on household lots in an effort to curb further deforestation (see, for example, Kenya Forest Service, 2009; Mathu, Reference Mathu2011). As a result of these longstanding policies and programs, fuelwood in rural Kenya is often collected both from off-farm sources and from private farm woodlots. In many villages, fuelwood is also purchased either from neighbors or in local markets. The labor division in fuelwood sourcing is strict. Similar to women in other SSA countries, women in Kenya are engaged both in ‘productive’ activities, such as fuelwood and water collection, and ‘reproductive’ activities, such as cooking, cleaning, and childcare (Kes and Swaminathan, Reference Kes, Swaminathan, Blackden and Wodon2006). Men, on the other hand, are generally engaged only in ‘productive’ activities, both on-farm (growing crops and trees, rearing livestock) and off-farm wage labor. The ‘double workday’ for women often means that women work longer hours than men, which limits their opportunity for participation in the off-farm labor market (Kes and Swaminathan, Reference Kes, Swaminathan, Blackden and Wodon2006).
Qualitative studies from the early 1990s show strong cultural taboos against women participating in on-farm tree management (Chavangi and Adoyo, Reference Chavangi, Adoyo, Bradley and Huby1993; Kiptot and Franzel, Reference Kiptot and Franzel2012; Mugure and Oino, Reference Mugure and Oino2013). In Kakamega County in western Kenya, for example, the belief exists that ‘if a woman plants a tree, she will become barren’ (Chavangi and Adoyo, Reference Chavangi, Adoyo, Bradley and Huby1993: 66). This differs from practices in South Asia: while Amacher et al. (Reference Amacher, Hyde and Joshee1993) and Heltberg et al. (Reference Heltberg, Arndt and Sekhar2000) find that women and children are the primary collectors of fuelwood off-farm and men are the primary collectors on-farm, Kohlin and Amacher (Reference Kohlin and Amacher2005) and St.Clair (Reference Clair2016) show significant contributions of men to off-farm fuelwood collection in India and Nepal, respectively. In data collected for this study, 94 per cent of primary fuelwood collectors off-farm are women and 67 per cent of on-farm woodlots are managed by men. We reflect these gender differences in fuelwood collection in our theoretical model below and subsequently empirically test whether male or female shadow wages are correlated with a particular method of fuelwood acquisition.
The household data used in our analysis were collected in 2011–2012 in 15 villages in Kakamega, Kericho, Kisumu, Siaya, Uasin Gishu, and Vihiga counties of Kenya (Berazneva et al., Reference Berazneva, Lee, Place and Jakubson2017).Footnote 3 The full survey included 21 randomly sampled households in each village and covered a wide range of Living Standards Measurement Study (LSMS) components. Importantly, the survey included a detailed module on household energy consumption and production from all available sources. Households were asked about their energy use from fuelwood, agricultural residues, charcoal, kerosene, LPG, and electricity during each month of the 2011 calendar year, as well the sourcing of energy from on-farm, off-farm, and market.
The vast majority of households in the sample (98 per cent) use fuelwood as a primary source of cooking energy and most acquire their fuelwood from more than one location. In the research area, land is privately owned. While the majority of households reports collecting fuelwood from neighboring farms or unfarmed area in their communities, paying access fees is not common. A small number of households reports collecting fuelwood from government forest reserves. These forest reserves do have restrictions on fuelwood collection activities, but anecdotal evidence suggests that they are not often enforced. Only a small portion of households (about 15 per cent) grows trees on dedicated woodlots that are generally close to the homestead; most households grow trees on their farms – along the farm boundaries, plot edges, and scattered throughout plots. The majority of trees are planted by households (very few are native species left from land clearing). Main species are Eucalyptus saligna, Cupressus lusitanica, Markhamia lutea, Grevillea robusta, Persea Americana, Psidium guajava, Mangifera indica, and Sesbania sesban, among others, and many are planted with several goals in mind: fuelwood production, erosion control, property boundaries, shade around the homestead, etc.
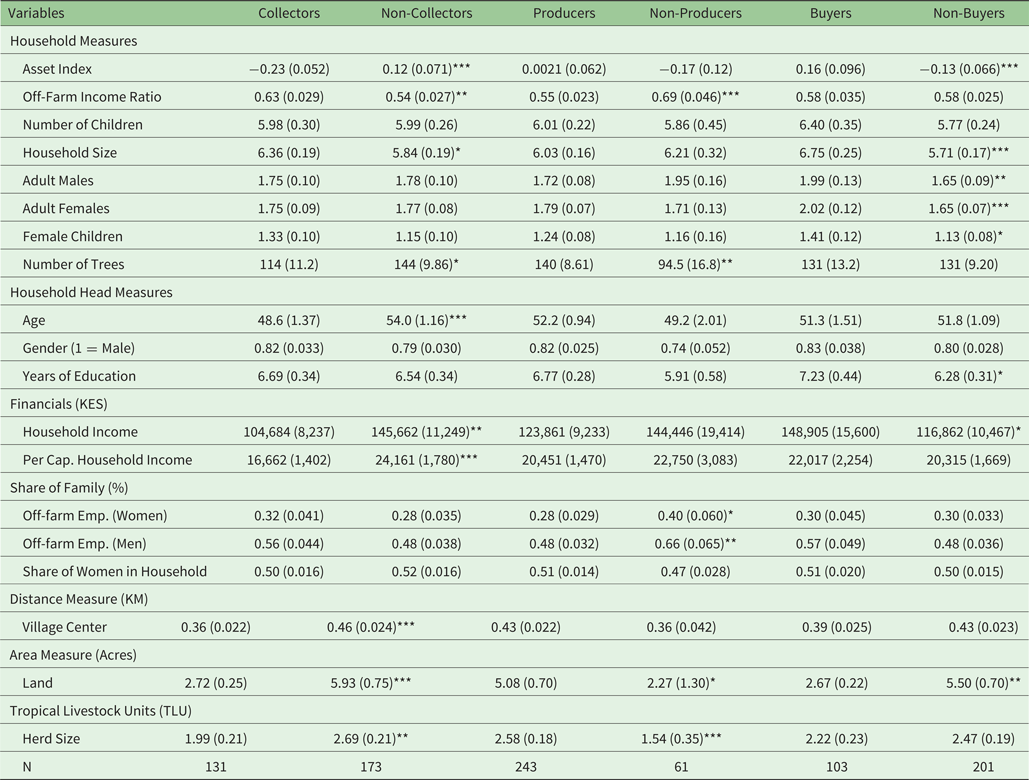
In our analysis, following the methodology of Acharya and Barbier (Reference Acharya and Barbier2002) and Palmer and MacGregor (Reference Palmer and MacGregor2009), if a household uses fuelwood from different sources, we consider the household to be present in each of the three source groups. For example, a household that obtains fuelwood both from off-farm and on-farm sources is considered to be both in the off-farm fuelwood collection group and the on-farm production fuelwood group. As a consequence, as in table 2, the total number of observations in the three fuelwood groups added together is greater than the total number of households in the sample.
Table 2. Summary statistics
Notes: Standard deviations located next to respective means. Total sample is 304 observations. The three category sets are not mutually exclusive. *** p < 0.01, **p < 0.05, *p < 0.1.
Several differences among source groups are immediately apparent (table 2). Fuelwood buyers, for example, on average have larger households, higher annual incomes (though not per capita incomes), more education, and less land area than the other two groups. All of these differences are to be expected. Households with greater incomes can more readily afford to buy fuelwood, and smaller land areas mean less room for on-farm woodlots. Off-farm collectors, on the other hand, have the lowest mean income of the three groups, have younger household heads, a lower number of trees on-farm, smaller land parcels, and have a lower asset index.Footnote 4 In addition, lower incomes among fuelwood off-farm collectors limit fuelwood purchases and fewer on-farm trees imply lower fuelwood production from private woodlots. Finally, on-farm fuelwood producers have larger landholdings, a greater absolute number of trees, a larger herd size, lower wages for men and women, and a smaller share of income earned off the farm. Larger landholdings suggest lower opportunity costs for on-farm woodlots, all else being equal, as more land is available for tree cultivation. A larger herd size and smaller share of income earned off-farm suggest that on-farm fuelwood producers expend more labor hours working on-farm. This may lead to lower opportunity costs of on-farm production as farmers may be able to practice tree management concurrent with other on-farm activities.
3. Theoretical household model
In rural Kenya, as elsewhere in SSA, a typical household consumes much of its own production. As a result, and given likely imperfections in markets for both labor and goods, market wages may not reflect household opportunity costs when it comes to off-farm collection and on-farm fuelwood production (Skoufias, Reference Skoufias1994; Amacher et al., Reference Amacher, Hyde and Kanel1996). While hired labor is used in this part of Kenya for agricultural activities, no households in our sample hired labor for fuelwood acquisition. In a constrained labor market, labor allocated to private energy collection is thus subject to an unobserved shadow wage that forms the basis for households' production decisions (Strauss, Reference Strauss, Singh, Squire and Strauss1986). In our dataset, 63 per cent of households consuming fuelwood purchased none from the market.
The opportunity cost, as measured by the shadow price or shadow cost, of fuelwood for these households can therefore be substantially different from the market price. Strauss (Reference Strauss, Singh, Squire and Strauss1986), Jacoby (Reference Jacoby1993), and Skoufias (Reference Skoufias1994) were among the first to develop the concept of shadow wages and shadow prices in a general agricultural context, and Amacher et al. (Reference Amacher, Hyde and Kanel1996) were first to apply it specifically to fuelwood. Heltberg et al. (Reference Heltberg, Arndt and Sekhar2000) and Palmer and MacGregor (Reference Palmer and MacGregor2009) extended the non-separable agricultural household model to focus on traditional energy substitutes and, in the case of Palmer and MacGregor (Reference Palmer and MacGregor2009), the substitution between fuelwood collected and purchased. We build on their model and include three different fuelwood sources (fuelwood collected off-farm, fuelwood produced on-farm, and that purchased), as well as accounting for the substitution of fuelwood with traditional fuels (e.g., agricultural residues) and other alternatives (e.g., kerosene).
More formally, let a representative agricultural household maximize a monotonic, continuous, quasi-concave utility function U:
$$\mathop {{\rm Max}U}\limits_{C_E,C_X,C_L^M ,C_L^F } = U(C_E,C_X,C_L^M ,C_L^F ;{\bi z}^h),$$ where C E stands for consumed goods requiring energy inputs, C X represents all other consumed goods, 
$C_{L}^{M}$ is leisure consumed by men in the household, 
$C_{L}^{F}$ is leisure consumed by women in the household, and zh is a vector of household characteristics that affect consumption.
Household goods C E are produced according to function θ using a mixture of energy types and technology:
$$C_E=\theta(C_{FW},C_B,C_A;S).$$Here, C FW represents fuelwood consumed, which can be from fuelwood collected off-farm, produced on-farm, or purchased. C B stands for other traditional biomass fuels such as crop or animal residues usually produced on farm, C A represents the consumption of more advanced fuels such as kerosene, and S represents stove technology.
Based on our data from Kenya, in our model we assume women are the primary collectors of fuelwood off-farm and men are the primary producers of fuelwood on-farm. We also assume that male and female labor is not perfectly substitutable. Therefore, the consumption of leisure in the model is divided between women and men, 
$C_{L}^{F\comma M}$, and is given by:
$$C_L^{F,M}=L^{F,M}-l_{AG}^{F,M}-l_{off}^{F,M}-l_{FW}^{F,M},$$where L is the total endowment of labor, l AG is labor devoted to agricultural activities, l off is off-farm labor, and l FW is labor allocated to fuelwood on-farm production or off-farm collection. Fuelwood production on-farm (P) and fuelwood collection off-farm (C) are given by continuous, quasi-concave functions of household labor:
$$\eqalign{q_{FW}^P&=f_{FW}^P(l_{FW}^M;{\bi z}_{FW}^P),}$$
$$\eqalign{q_{FW}^C&=f_{FW}^C(l_{FW}^F;{\bi z}_{FW}^C),}$$where q FW is the quantity of fuelwood produced on-farm or collected off-farm and z FW includes other household characteristics.
For simplicityFootnote 5 we assume that all fuelwood collected off-farm, produced on-farm, or purchased by the household is consumed such that
$$q_{FW}^{B}=C_{FW}-q_{FW}^{P}-q_{FW}^{C}\geq 0,$$ where 
$q_{FW}^{B}$ is the quantity of fuelwood bought by a household. Net consumption is positive for buyers and equal to zero for non-buyers. The agricultural production, q AG, is a function of male and female labor (l AG), agricultural residues used for soil fertility management and animal feed (q B), agricultural inputs such as land (a AG), and other household endowments (zAG), as follows:
$$\eqalign{q_{AG}&=f_{AG}(l_{AG}^M,l_{AG}^F,q_B, a_{AG} ;{\bi z}^{AG}),}$$
$$\eqalign{q_B&=\alpha q_{AG}-a_{AG},}$$where α is the proportion of the agricultural production that results in residues, so that q B is the amount of residues left after use for agricultural production.
The household budget constraint is given by equation (9):
$$P_X C_X+P_{FW}(C_{FW}-q_{FW}^P-q_{FW}^C)+P_AC_A=P_{AG}q_{AG}+w_Ml_{off}^M+w_Fl_{off}^F+V,$$where P X, P FW, P A, P AG are the prices of the respective goods, w M, F are wage rates for men and women, and V represents other household income such as remittances.
Assuming an interior solution and substituting equations (2) and (3) into equation (1), we thus have the following Lagrangian:
$$\eqalign{{\rm {\cal L}} = & U[\theta (C_{FW},C_B,C_A;S),C_X,L^M - l_{AG}^M - l_{off}^M - l_{FW}^M ,L^F - l_{AG}^F - l_{off}^F - l_{FW}^F ;{\bi z}^h] \cr & - \lambda [P_XC_X + P_{FW}(C_{FW} - q_{FW}^P - q_{FW}^C ) + P_AC_A - P_{AG}q_{AG} \cr & - w^Ml_{off}^M - w^Fl_{off}^F - V] \cr & - \mu _{AG}[q_{AG} - f_{AG}(l_{AG}^M ,l_{AG}^F ,\alpha q_{AG} - q_B;{\bi z}_{AG})] - \mu _{FW}^P [q_{FW}^P - f_{FW}^P (l_{FW}^M ;{\bi z}_{FW}^P )] \cr & - \mu _{FW}^C [q_{FW}^C - f_{FW}^C (l_{FW}^F ;{\bi z}_{FW}^C )] + \eta [C_{FW} - q_{FW}^P - q_{FW}^C )],} $$ where λ, μ, and η are the multipliers on the budget, production, and consumption constraints. We also assume that the shadow prices of fuelwood and agricultural production (e.g., yields) are positive (
$\mu _{AG}\comma \; \, \mu _{FW}>0$).
Selected first-order conditions for utility maximization are given as:
$$\displaystyle{{\partial {\rm {\cal L}}} \over {\partial C_{FW}}} = \displaystyle{{\partial U} \over {\partial \theta }}\displaystyle{{\partial \theta } \over {\partial C_{FW}}} - \lambda P_{FW} + \eta = 0,$$
$$\displaystyle{{\partial {\rm {\cal L}}} \over {\partial C_X}} = \displaystyle{{\partial U} \over {\partial C_X}} - \lambda P_X = 0,$$
$$\displaystyle{{\partial {\rm {\cal L}}} \over {\partial q_{AG}}} = \lambda P_{AG} + \mu _{AG}\left[ {\alpha \displaystyle{{\partial f_{AG}} \over {\partial q_{AG}}} - 1} \right] = 0,$$
$$\displaystyle{{\partial {\rm {\cal L}}} \over {\partial q_{FW}^P }} = \lambda P_{FW} - \mu _{FW}^P - \eta = 0,$$
$$\displaystyle{{\partial {\rm {\cal L}}} \over {\partial q_{FW}^C }} = \lambda P_{FW} - \mu _{FW}^C - \eta = 0,$$
$$\displaystyle{{\partial {\rm {\cal L}}} \over {\partial l_{AG}^{F,M} }} = \mu _{AG}\displaystyle{{\partial f_{AG}} \over {\partial l_{AG}^{F,M} }} - \displaystyle{{\partial U} \over {\partial C_L^{F,M} }} = 0,$$
$$\displaystyle{{\partial {\rm {\cal L}}} \over {\partial l_{off}^{F,M} }} = \lambda w^{F,M} - \displaystyle{{\partial U} \over {\partial C_L^{F,M} }} = 0,$$
$$\displaystyle{{\partial {\rm {\cal L}}} \over {\partial l_{FW}^F }} = \mu _{FW}^C \displaystyle{{\partial f_{FW}^C } \over {\partial l_{FW}^F }} - \displaystyle{{\partial U} \over {\partial C_L^F }} = 0,$$
$$\displaystyle{{\partial {\rm {\cal L}}} \over {\partial l_{FW}^M }} = \mu _{FW}^P \displaystyle{{\partial f_{FW}^P } \over {\partial l_{FW}^M }} - \displaystyle{{\partial U} \over {\partial C_L^M }} = 0,$$
$$C_{FW}-q_{FW}^P-q_{FW}^C\geq 0.$$Rearranging the first-order conditions produces a number of important relationships. Equations (11), (14), and (15), for example, suggest that the marginal utility of fuelwood consumption is equal to the shadow price of fuelwood:
$$\displaystyle{{\partial U} \over {\partial \theta }}\displaystyle{{\partial \theta } \over {\partial C_{FW}}} = \lambda \left( {P_{FW} - \displaystyle{\eta \over \lambda }} \right) = \mu _{FW}^P = \mu _{FW}^C ,$$ where 
$\mu _{FW}^{P}$ and 
$\mu _{FW}^{C}$ are, respectively, the shadow prices of on-farm fuelwood production and off-farm fuelwood collection, which in equilibrium are equal. In practice, however, these shadow prices can differ due to household preferences, lack of substitutability of labor between male and female household members, and environmental factors, among other reasons.
Rearranging equations (16)–(19), we have:
$$\matrix{ {\displaystyle{{\partial U} \over {\partial C_L^F }}} \hfill & { = \mu _{FW}^C \displaystyle{{\partial f_{FW}^C } \over {\partial l_{FW}^F }} = \mu _{AG}\displaystyle{{\partial f_{AG}} \over {\partial l_{AG}^F }} = \lambda w^F,} \hfill \cr } $$
$$\matrix{ {\displaystyle{{\partial U} \over {\partial C_L^M }}} \hfill & { = \mu _{FW}^P \displaystyle{{\partial f_{FW}^P } \over {\partial l_{FW}^M }} = \mu _{AG}\displaystyle{{\partial f_{AG}} \over {\partial l_{AG}^M }} = \lambda w^M.} \hfill \cr } $$ Equations (22) and (23) demonstrate that the marginal utility of leisure is equal to the marginal value product of labor in fuelwood production on-farm/off-farm collection and the marginal value product of labor in agriculture, which also depends on the household specific wage rate for men and women. The non-separability of households' on-farm and off-farm fuelwood consumption decisions thus implies that household labor activities are subject to household-specific unobserved opportunity costs or shadow prices. In particular, the household consumption of fuelwood depends on the household-specific shadow price of fuelwood (for non-buyers), which is further divided into the shadow prices of on-farm production, 
$\mu _{FW}^{P}$, and off-farm collection, 
$\mu _{FW}^{C}$.
From the first-order conditions we also obtain the following reduced-form equations for the quantity of fuelwood produced on-farm, 
$ q_{FW}^{P}$, collected off-farm, 
$q_{FW}^{C}$, and purchased, 
$q_{FW}^{B}$:
$$\left. {\matrix{ {q_{FW}^P } \cr {q_{FW}^C } \cr {q_{FW}^B } \cr } } \right\} = f(P_{FW},P_X,P_{AG},P_A,w^{F,M},{\rm }{\bi z}^h,{\bi z}_{FW}^{P,C} ,L,S,V).$$It is not clear whether the price of fuelwood, P FW, must be the market price in the case of fuelwood collected off-farm or produced on-farm in a labor constrained market. More likely, the price is endogenous and a function of shadow prices. The wage rate, w F, M, is also not exogenous but a function of implicit household wage rates.
4. Estimation strategy
In order to estimate the demand equations (equation (24)), we first need to estimate shadow prices of fuelwood from different sources that take into account the opportunity costs of production on-farm and collection off-farm. The shadow price of off-farm fuelwood collection, for example, captures the time spent collecting fuelwood off-farm as well as the opportunity cost of labor, so that the increased time it takes to collect each kilogram of fuelwood, or the higher the opportunity cost of the labor, the more expensive each unit of fuelwood becomes (Mekonnen, Reference Mekonnen1999). The variable used to represent the shadow price of collecting fuelwood has varied in the literature. Cooke (Reference Cooke1998a,Reference Cookeb), Mekonnen (Reference Mekonnen1999), and Baland et al. (Reference Baland, Bardhan, Das, Mookherjee and Sarkar2010), for example, use the opportunity cost of labor (shadow wage) multiplied by the time spent collecting each unit of fuelwood. The data on amounts of fuelwood collected, however, are often difficult to obtain, so Amacher et al. (Reference Amacher, Hyde and Joshee1993), Heltberg et al. (Reference Heltberg, Arndt and Sekhar2000), and Palmer and MacGregor (Reference Palmer and MacGregor2009), for example, use the time spent collecting fuelwood as a proxy. This variable, however, does not capture the value of time and often leads to underestimates of the elasticity of demand for fuelwood (see table 1).
Following Cooke (Reference Cooke1998a,Reference Cookeb), Mekonnen (Reference Mekonnen1999), and Baland et al. (Reference Baland, Bardhan, Das, Mookherjee and Sarkar2010), we define the average shadow price of fuelwood collected from off-farm for household i in the collecting group C as:
$$\mu _{i}^{C}=\left( \displaystyle{{H_{i}^{C}}\over{q_{i}^{C}}}\right) \omega _{i}^{F},$$where H is the monthly number of hours spent collecting fuelwood, q is the monthly amount of fuelwood collected, and ω is the household-specific opportunity cost of female labor, i.e., female shadow wage.Footnote 6 Since the shadow wage is given in Kenyan Shillings per hour, the unit value of the shadow price is Kenyan Shillings per kilogram (KES/kg).
Similarly, we define the shadow price of fuelwood produced on-farm. In western Kenya, as elsewhere in SSA, on-farm fuelwood production is often a by-product or co-product of growing trees for timber and other purposes (Buck et al., Reference Buck, Lassoie and Fernandes1999). Since producing fuelwood on-farm does not necessarily require felling trees, data on the time spent producing fuelwood on-farm only are not available. We approximate the number of hours spent producing fuelwood on-farm by the number of on-farm trees, and the time necessary to cultivate and manage an individual tree:
$$\mu _{i}^{P}=\left( \displaystyle{{\gamma^{P}T_{i}^{P}}\over{q_{i}^{P}}}\right) \omega _{i}^{M},$$where γ is the average number of hours needed to grow one tree, T is the number of on-farm trees, q is the amount of fuelwood per month produced by household i in the on-farm producing group P, and ω is the household-specific opportunity cost of male labor {—} the male shadow wage. The value for γ comes from the Kenya Forestry Research Institute (KEFRI) estimates for growing Eucalyptus trees (Oballa et al., Reference Oballa, Konuche, Muchiri and Kigomo2010). Eucalyptus is very common in the research area and is a primary choice for agroforestry in Kenya — being among the most popular tree species planted on household farms in this area (Scherr, Reference Scherr1995; Henry et al., Reference Henry, Tittonell, Manlay, Bernoux, Albrecht and Vanlauwe2009).Footnote 7 In the survey, households that purchased fuelwood were asked their individual price paid for a particular quantity. Because this market price may be correlated with unobserved household characteristics, we follow a two-stage least squares (2SLS) strategy as outlined below.
Estimating both equations (25) and (26) also requires shadow wages for men and women. Since not all households in the sample engage in off-farm wage labor, we estimate the household-specific shadow wages for men and women following the methodology to account for self-selection proposed by Heckman (Reference Heckman1979) and Olsen (Reference Olsen1980) and used by Cooke (Reference Cooke1998a,Reference Cookeb), in a similar setting.Footnote 8 We estimate these shadow wages using maximum likelihood for greater efficiency, especially important due to the sample size restrictions in the data.Footnote 9 Results for these estimations are in table A2 in the online appendix.
There are several additional aspects to our estimation of demand elasticities. First, in order to estimate cross-price elasticities, it is necessary to proxy shadow prices and market prices for households that do not participate in all groups. For example, households that only collect fuelwood off-farm do not have estimates for shadow prices for fuelwood produced on-farm or prices for fuelwood bought at the market. To create these full sample variables, we follow the strategy suggested by Mekonnen (Reference Mekonnen1999) and use the village-specific maximum values for hours spent collecting, the number of on-farm trees, and market prices, when household-specific values are absent. The household's decision to participate (or not) in each of the fuelwood groups (producing on-farm, collecting off-farm, and purchasing) must reflect the household-specific cost of participation. So, if the household is not observed in a particular group, it is likely the case that its cost of participation is greater than the cost of any other participating household in the village.
Second, we are concerned that households may self-select into their respective fuelwood source group(s), which may bias our results. To account for this selection bias, we add a variable to the second stage estimation of the demand elasticities following Olsen (Reference Olsen1980) and Wooldridge (Reference Wooldridge2002).Footnote 10 Third, we take precautions against endogeneity due to the likelihood of simultaneity and omitted variable bias arising from the shadow price variable and report results from the 2SLS estimation. We borrow an instrumental variable estimation strategy from the demand literature. To instrument for the market price, we use the average of all (except own) market prices in the sample. As in Hausman et al. (Reference Hausman, Leonard and Zona1994), the key assumption is that random household-level factors influencing the market price are independent of other households.
As for the likely endogenous shadow prices for on-farm producers and off-farm collectors, we match each household with five other households in the sample outside their own block (households in the same village and two neighboring villages) based on the most similar shadow price. For off-farm collectors, we use the average of the hours spent collecting of the matched households as an instrument on the shadow price of fuelwood collecting of the first household, while for on-farm producers, we use the average number of trees owned as the instrument on the shadow price of on-farm production of the first household.Footnote 11 By excluding households in the own-block in the matching, we prevent possible validity issues arising from geographic proximity of some villages.Footnote 12 First-stage IV results are provided in table A4 in the online appendix.
In order to allow for inter-household comparisons, continuous variables (e.g., shadow prices, shadow wages, land area) are scaled by adult equivalent units, which accounts for differing numbers and ages of participants in each household (Cavendish, Reference Cavendish, Campbell and Luckert2002).Footnote 13 Our results can then be interpreted as per-capita monthlyFootnote 14 values. We estimate the household-specific demand equations for fuelwood collected off-farm, 
$q_{i}^{C}$, produced on-farm, 
$q_{i}^{P}$, and bought in the market, 
$q_{i}^{B}$:
$$q_i^j = \beta _0 + \beta _1\mu _i^j + \beta _2\nu _i^k + \beta _3\varphi _i + \beta _4\omega _i^M + \beta _5\omega _i^F + \beta _6{\bi X}_i + \zeta + \varepsilon _i^j ,$$
$$q_i^B = \beta _0 + \beta _1P_i^B + \beta _2\nu _i^C + \beta _3\psi _i^P + \beta _4\omega _i^M + \beta _5\omega _i^F + \beta _6{\bi X}_i + \zeta + \varepsilon _i^B .$$In equation (27), superscripts j, k represent either collecting off-farm or producing on-farm (j ≠ k), μi is the shadow price of either collecting off-farm or producing on-farm, ν and φ are the shadow prices and market prices with full observations, ωM and ωF are the average shadow wages for men and women, Xi are household variables that influence fuelwood use, ζ are geographic fixed effects (at the block level), and ε is the error term. In equation (28), P i is the market price paid by a household that purchases fuelwood and νC and ψP are shadow prices for fuelwood collected off-farm and produced on-farm with full observations, respectively. Given possible automated regressor bias, we bootstrap all standard errors.
5. Results
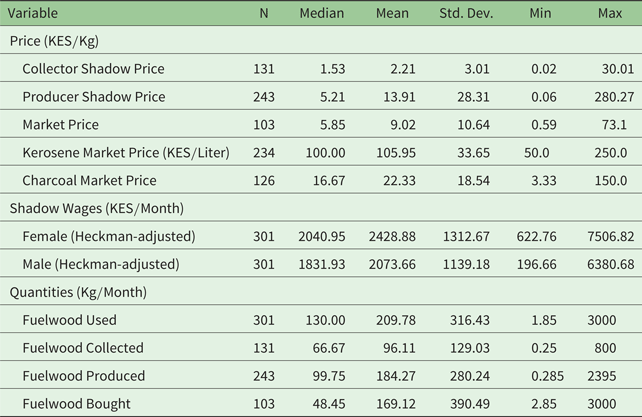
We first estimate household-specific shadow prices of collecting fuelwood off-farm and producing fuelwood on-farm, following equations (25) and (26), and using household-specific wages for men and women. Our results, reported in table 3, suggest imperfections in fuelwood and labor markets in western Kenya. The median off-farm collection shadow price (1.53 KES/kg) is below the median on-farm production shadow price (5.21 KES/kg), which is in turn below the median market price (5.85 KES/kg). This ordering is consistent with the traditional agricultural household model. When shadow prices for a particular fuelwood source approach and exceed the market price, the household switches to purchasing from the market (given that one is available) (Key et al., Reference Key, Sadoulet and Janvry2000). On-farm production shadow prices above those of off-farm collection shadow prices can have several explanations, including higher time requirements for managing woodlots on-farm compared to collecting from off-farm, as well as the opportunity cost of planting woodlots instead of food crops.
Table 3. Fuelwood cost and quantity statistics
Note: Statistics are for households who participate in the particular fuelwood source group/energy source group.
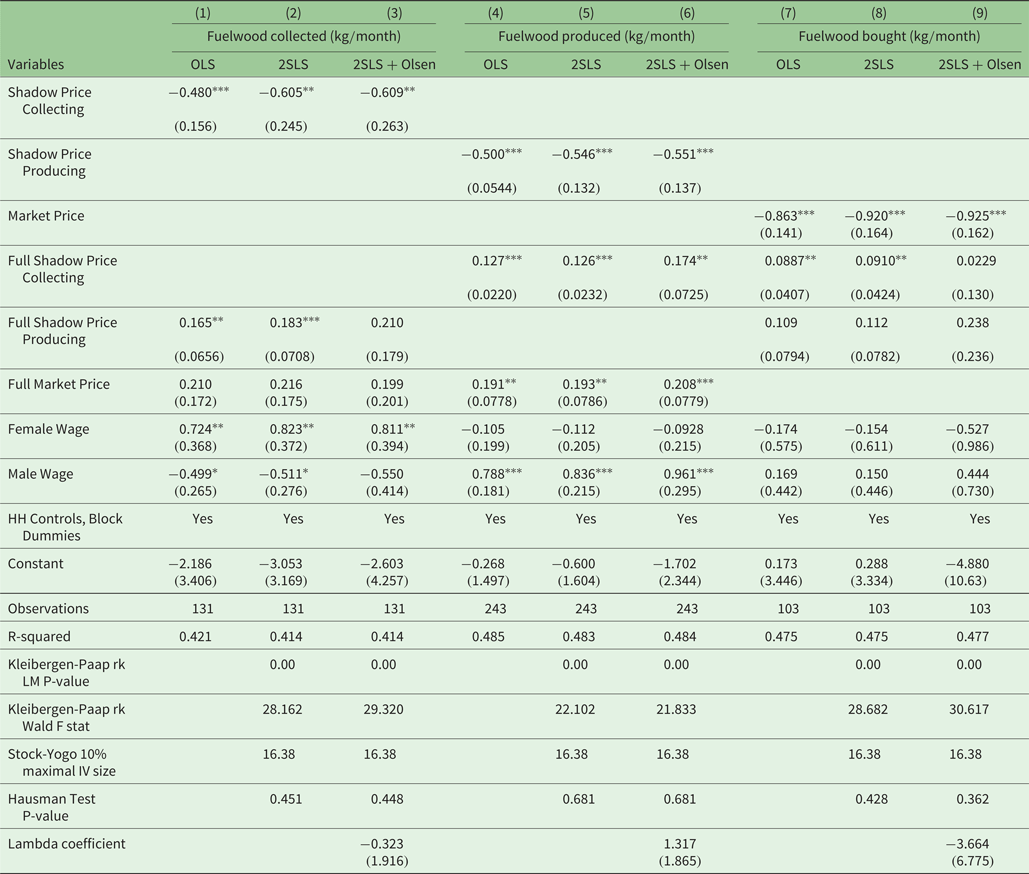
We then estimate demand equations (equations (27) and (28)) for different fuelwood sources, including the respective shadow prices, fuelwood market price, and wages as right-hand side variables. Table 4 shows the regression results from ordinary least squares (OLS) estimation, as well as the results from 2SLS estimations that control for the endogeneity of shadow prices and potential selection bias. The results across the three estimations (OLS, 2SLS, and 2SLS+Olsen Estimator) are quite similar. Although the tests of endogeneity and selection bias suggest exogeneity in both off-farm collection and on-farm fuelwood production regressions, for the sake of caution, we use coefficient values from the 2SLS-Olsen regressions when interpreting our results (third column for each fuelwood source group). The coefficients on shadow prices in table 4 can be interpreted as elasticities as all variables are used in log form. As expected, own-price elasticities are negative, inelastic, and statistically significant at a p-value of 5 per cent or less across all groups and specifications. Moreover, they are very similar across non-purchased fuelwood sources: own-price elasticities range from −0.48 to −0.61 for off-farm fuelwood collectors and −0.50 to −0.55 for on-farm fuelwood producers for all specifications. The inelastic own-price elasticity means that increases in fuelwood costs lead to less than equi-proportionate decreases in the amount of fuelwood obtained from that source, suggesting that fuelwood is a necessity good for the households in our sample. Our own-price elasticity values are somewhat higher in magnitude than elasticities found in other studies (table 1). Geography can play a large role in the elasticity differences in fuelwood demand. Amacher et al. (Reference Amacher, Hyde and Kanel1996) and Amacher et al. (Reference Amacher, Hyde and Kanel1999), for example, find large differences in own-price elasticities between hill and plain-dwelling populations in Nepal. Most of the existing studies on this subject are primarily from South Asia, and none are from household samples in East Africa or Kenya specifically.
Table 4. Fuelwood demand elasticities
Notes: HH Controls and additional variables are included in appendix Table A6. All continuous variables are in log form and in adjusted per capita units after Cavendish (Reference Cavendish, Campbell and Luckert2002). ‘Full’ variables include imputed values for households not participating in the respective fuelwood source groups. Instruments for the shadow prices of fuelwood collection and production are the shadow prices of a matched household located outside the ‘own-block (additional explanation provided in text). Instrument for market price is the village average of except-own market price. Bootstrapped standard errors (1000 replications) in parentheses. ***p < 0.01, **p < 0.05.
Cross-price elasticities are also inelastic, but positive. The very low cross-price elasticities suggest that substitution between fuelwood sources is low. Although fuelwood is often considered to be a homogeneous product, households in western Kenya do not readily substitute between fuelwood sources. For example, an increase of 10 per cent in the shadow price of on-farm production of fuelwood (corresponding to an increase of 1.40 KES/kg), leads to a decrease in fuelwood produced on-farm of 10.13 kg per month, evaluated at the mean. Moreover, substitution to a different source is low: an increase of 10 per cent in the shadow price of on-farm production leads to the increase of fuelwood both bought and collected off-farm by only 5.19 kg per month, evaluated at the mean. This shadow price increase, therefore, leads to a net decrease of 4.19 kg per month in fuelwood consumed, holding other fuelwood costs constant. This low quantity is surprising, given the mean consumption of about 210 kg per month, and illustrates the lack of substitutability between fuelwood groups.
This lack of substitution between fuelwood sources demonstrated by our results can be explained in part by the gender division in household labor. We find that female shadow wages in the demand equations are statistically significant with respect to fuelwood collected and male shadow wages are likewise statistically significant with respect to fuelwood produced on-farm (table 4). The coefficients in both cases are positive, similar to findings in other studies (Amacher et al., Reference Amacher, Hyde and Kanel1996, Reference Amacher, Hyde and Kanel1999; Cooke, Reference Cooke1998a). Higher female wages increase the amount of fuelwood collected off-farm, demonstrating the impact of female labor opportunity on fuelwood collection. Meanwhile, male wages have no significant effect on fuelwood quantity collected off-farm, consistent with our data showing men are not actively engaged in off-farm fuelwood collection in this area. The opposite relationship is found with respect to fuelwood produced on-farm, as men's work opportunity is correlated with fuelwood produced on-farm through their shadow wage, and the time women work has no significant effect on fuelwood produced on-farm. This again is consistent with our data and qualitative evidence from the area that women are less engaged in on-farm fuelwood production than men.
Our results also show that changes in the shadow price of off-farm collecting lead to significant increases in the amount of female labor spent gathering fuelwood off-farm. Using the same 2SLS regression as above (equation (27)) but with the number of hours spent collecting off-farm per month as the dependent variable, we find that a 10 per cent increase in the shadow price of off-farm collecting increases the hours spent collecting off-farm by 3.6 per cent (table A5 in the online appendix. See table 1 for comparisons with other papers). The magnitude of the elasticity of labor for fuelwood collection is greater than the magnitudes of the cross-price elasticities of off-farm collecting with respect to either on-farm producing or buying fuelwood. This illustrates that households prefer to increase labor devoted to the off-farm collecting of fuelwood rather than substitute toward on-farm producing or purchasing fuelwood in the wake of shadow price increases.
Coefficients for additional estimation regressors, including household characteristics and charcoal and kerosene prices, are shown in online appendix table A6. We find few variables to be statistically significant. The coefficient on age of household head is one exception, which is positive and statistically significant with respect to fuelwood produced on-farm, and negative and significant for fuelwood collected off-farm. In addition, while substitution with alternative energy sources is not a focus of this study (due to data constraints), we include the price of charcoal and kerosene in the regressions. The price of charcoal lacks statistical significance for any fuelwood source group, while the price of kerosene is negatively correlated and marginally statistically significant with fuelwood produced on-farm, suggesting a complementary relationship. Due to the relatively small number of individuals using charcoal and kerosene in the sample, we are cautious to give weight to these findings.
6. Conclusion and policy implications
This paper examines households' energy use in the western Kenya highlands, focusing specifically on the substitution among different fuelwood sources – fuelwood produced on-farm, collected off-farm, and purchased – and the role of households' labor endowments in energy sourcing. We find that the median household shadow price of fuelwood collected off-farm (1.5 KES/kg) is well below the median shadow price of fuelwood produced on-farm (5.2 KES/kg) and the median market price of purchased fuelwood (5.8 KES/kg). The most plausible explanations for this result, suggested by the patterns in our data and estimation, are the potential lack of off-farm employment opportunities for women (that depress the shadow price of fuelwood collected off-farm) and possible competition of agroforestry with on-farm crops, among other factors (that increase the shadow price of fuelwood produced on-farm). In our sample of households, women earn less than men: 3000 KES (USD36) per month compared to 4000 KES (USD47), 95 per cent of fuelwood collectors are women, and most woodlots are managed by men (male household heads or male children or grandchildren in households headed by women). In line with the data, coefficients on the female shadow wages in the demand equations are statistically significant with respect to fuelwood collected off-farm and coefficients on the male shadow wages are likewise statistically significant with respect to fuelwood produced on-farm. These results echo earlier findings from qualitative studies in western Kenya that show strong social and cultural norms behind the household division of labor (Chavangi and Adoyo, Reference Chavangi, Adoyo, Bradley and Huby1993).
Looking specifically at fuelwood collected off-farm, we also find that the own-price elasticity for non-purchased fuelwood is greater in absolute value terms than the labor supply elasticity. Households prefer to increase the labor dedicated to exploiting a fuelwood source with an increasing shadow price rather than substitute away from it. Given higher shadow prices for fuelwood collected off-farm, rural Kenyan households respond by increasing female labor, rather than substituting toward other fuelwood sources. This finding has important implications for efforts against forest degradation. It shows, for example, that as fuelwood scarcity increases, households will expend more time and effort to collect fuelwood off-farm rather than switch to fuelwood production on-farm or fuelwood purchases, which may come from more renewable sources.
Our findings also imply that fuelwood is not a homogeneous resource. The very limited substitution shown by our results suggests that increases in the shadow price of fuelwood from any particular source can potentially have significant effects on household labor. Increasing opportunities for female work off-farm increases the relative cost of fuelwood collected off-farm, which could lead to greater relative dependence on on-farm fuelwood production and lower overall use as fewer people are at home during the day (Burke and Dundas, Reference Burke and Dundas2015). Planting woodlots and producing fuelwood on-farm are arguably more sustainable practices than collecting off-farm, as the trees planted on-farm in agroforestry systems partially offset GHG emissions from biomass use and have other environmental and agricultural benefits; these include decreases in air and soil temperatures from greater tree coverage in the landscape, decreased soil erosion, and improved water retention, among others (Unruh et al., Reference Unruh, Houghton and Lefebvre1993; Mbow et al., Reference Mbow, Smith, Skole, Duguma and Bustamante2014). In the short run, however, any increases in the shadow price of fuelwood collected off-farm are likely to increase the work burden for women. As Bluffstone (Reference Bluffstone1995) finds, off-farm labor opportunities will stabilize tree coverage by increasing the opportunity cost of labor. However, these labor opportunities must exist for both genders, which implies increasing the labor substitutability between men and women in the labor force.
A very different technology, improved cookstoves, also has the potential to decrease fuelwood use in SSA. Improved combustion or pyrolysis stoves are more efficient, can use substitutes for fuelwood (e.g., crop residues, grasses), require fewer units of biomass for cooking than traditional stoves, and can produce valuable soil amendments such as biochar (Torres et al., Reference Torres, Lehmann, Hobbs, Joseph and Neufeldt2011). However, more efficient stoves can lead to a ‘rebound effect’, wherein households continue to use similar quantities of biomass but increase cooking activities (Nepal et al., Reference Nepal, Nepal and Grimsrud2011). Moreover, projects in Kenya seeking to increase the use of improved cookstoves have found adoption rates to be low, given many households' attachments to traditional cooking techniques (Tigabu, Reference Tigabu2017). Further research is needed to identify strategies to increase the use of improved cookstoves in Kenya and to mitigate rebound effects.
Our results suggest that reforestation efforts in western Kenya that include promotion of on-farm agroforestry may be ineffective in inducing households to collect less fuelwood off-farm unless there are changes to traditional norms regarding female participation in on-farm tree management and in the off-farm labor market. These norms indeed appear to be gradually changing. The new Kenyan constitution, approved by a significant majority of Kenyan citizens in 2010, codifies new rights for women (Kramon and Posner, Reference Kramon and Posner2011). Over the upcoming years, changing norms may lead to increasing substitution between male and female labor in rural labor markets, with consequent increases in agroforestry practices, tree coverage and the associated environmental benefits, as this paper suggests.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/S1355770X1800027X.
Acknowledgements
We are grateful to participants at seminars at Cornell University and the Annual Meeting of the Agricultural and Applied Economics Association for valuable input and comments on earlier drafts, and the comments and suggestions of two anonymous reviewers. The data for this paper were gathered as part of the second author's dissertation fieldwork at Cornell University and supported by the World Agroforestry Center (ICRAF) and the David R. Atkinson Center for a Sustainable Future, Cornell University. We gratefully acknowledge financial support from the Fondation des Fondateurs, an AAEA Tweeten Scholarship, the Mario Einaudi Center for International Studies, and various grants at Cornell University.
