II. EXPERIMENTAL

Polycrystalline samples of Co_0.7Al₂Se_3.7 and NiAl₂Se_3.7 were prepared via conventional solid-state method using Co powder, Ni powder, Al wire, and Se shot (Alfa, 99.999, 99.999, 99.9, and 99.999%, respectively) as starting materials. Al₂Se₃ precursors were prepared via the reaction of Al wire and Se shot at 1150 K for 24 h in sealed quartz tubes. CoSe and NiSe precursors were prepared via the reaction of Co/Ni powder and Se powder at 1150 K for 24 h in sealed quartz tubes. The obtained Al₂Se₃ precursors together with stoichiometric amount of CoSe/NiSe precursors were pulverized, pressed into a pellet, sealed in a quartz tube with Ar gas, and then heated and kept at 1073 K for 72 h. The obtained polycrystalline samples were black and air-sensitive. Because of the sensitivity to air and moisture of raw materials, all operations were performed in an argon-filled glove box.

Room temperature powder X-ray diffraction (PXRD) data were collected using a PANalytical X'Pert PRO diffractometer (CuKα radiation) with a graphite monochromator in a reflection mode from 2θ = 10° to 130° and step = 0.017° (Chen et al., Reference Chen, Liang and Wang1995b). Rietveld refinements were performed with the FULLPROF package (Rodriguez-Carvajal, Reference Rodriguez-Carvajal2001). The magnetic susceptibilities were measured using a vibrating sample magnetometer (VSM, Quantum Design). AC magnetizations were measured on a Magnetic Properties Measurement System (MPMS, Quantum Design). The XPS measurements were performed with an ESCALAB Mk II (Vacuum Generators) spectrometer using AlKα X-rays (240 W). The binding energies were calibrated against the C 1s signal (284.8 eV) of adventitious carbon.

III. RESULTS AND DISCUSSION

Figure 1(a) and (b) show the PXRD patterns of polycrystalline Co_0.7Al₂Se_3.7 and NiAl₂Se_3.7 sample collected at room temperature, respectively. The reflection peaks could be indexed with a trigonal symmetry with lattice parameters a = 3.8089(1) Å, c = 12.676(1) Å for Co_0.7Al₂Se_3.7 and a = 3.7880(1) Å, c = 12.650(1) Å for NiAl₂Se_3.7, respectively. According to the extinction conditions, the possible space group is P-3m1(No. 164), which is isostructural with the previously reported compound FeAl₂Se₄. Adopting the possible space group P-3m1, the indexed values of 2θ _obs, 2θ _cal, Δ2θ, d _obs, d _cal, I _obs, and (hkl) are listed in Supplementary materials with the figures of merit F(30) = 68.7(0.007, 72) for Co_0.7Al₂Se_3.7 and F(30) = 91.2(0.0041, 83) for NiAl₂Se_3.7, respectively. Compared with the reported lattice parameters a = 3.8335(1) Å, c = 12.737(1) Å in FeAl₂Se₄, the lattice parameter a of Co_0.7Al₂Se_3.7 and NiAl₂Se_3.7 shrinks by 0.64 and 1.19%, while c shrinks by 0.48 and 0.68%, respectively. The evolution of lattice parameters is reasonable, considering the gradual decrease of ionic radius for Fe²⁺, Co²⁺, and Ni²⁺. Rietveld refinements against the PXRD data were performed by adopting the FeAl₂Se₄ structure as an initial model. Considering the volatility of Se and the reported isostructural compound Ni_0.7Al₂S_3.7, we set occupancy of Al atom to be 1 (Higo et al., Reference Higo, Ishii, Menard, Chan, Yamaguchi, Hagiwara and Nakatsuji2011). The refinements smoothly converged to R _p = 4.22%, R _wp = 6.19%, R _exp = 2.41% for Co_0.7Al₂Se_3.7 and R _p = 2.99%, R _wp = 4.36%, R _exp = 2.67% for NiAl₂Se_3.7, respectively. The sample compositions determined from the refinement are Co_0.66Al₂Se_3.53 and Ni_0.61Al₂Se_3.55, respectively, which are used in the text hereafter. We calculate the theoretical density of both samples, which are 3.86 and 3.91 g cm⁻³ for Co_0.66Al₂Se_3.53 and Ni_0.61Al₂Se_3.55, respectively. The composition of Co_0.7Al₂Se_3.7 was checked by inductively coupled plasma atomic emission spectrometer, giving an atomic ratio of Co_0.69Al₂Se_3.61, consistent with our Rietveld refinements. The reason for the large quantity of vacancies in the proposed structure is not quite clear. But based on previous reports, NiGa₂S₄ is full occupancy while Ni_0.7Al₂S_3.7 possesses a large quantity of vacancies. Since atom radius is crucial for holding a structure, we can infer that the small atom radius of Al compared with Ga might be responsible for this phenomenon. Detailed structural parameters are listed in Table I. As shown in Figure 1(c), the compound is built by stacking of layers consisting of edge-sharing CoSe₆/NiSe₆ octahedra connected by a top and a bottom sheet of AlSe₄ tetrahedra. The layer spacing is separated with each other by a van der Waals gap. Figure 1(d) and (e) shows the central CoSe₆/NiSe₆ octahedra layer viewed along the [001] and [100] direction. The Co/Ni ions form a triangular lattice plane, which is isostructural to the CoO₂ layer of the known superconductor Na_xCoO₂·yH₂O. The CoSe₆/NiSe₆ octahedra probably gives Co²⁺ and Ni²⁺ a $t_{{\rm 2g}}^{\rm 4} e_{\rm g}^{\rm 2} $ configuration with a high spin S = 3/2 and 1, respectively (Nakatsuji et al., Reference Nakatsuji, Tonomura, Onuma, Nambu, Sakai, Maeno, Macaluso and Chan2007).

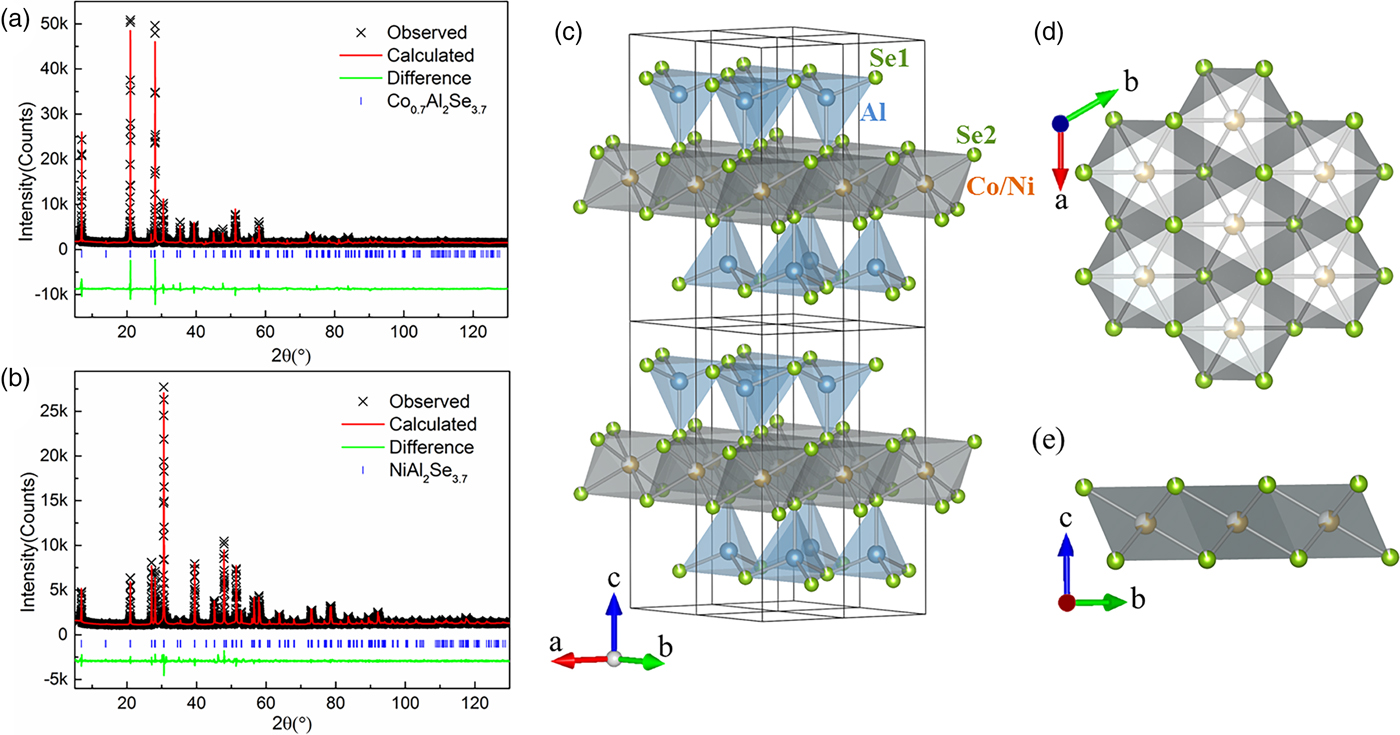
Figure 1. (Color online) (a)–(b) Powder X-ray diffractions and Rietveld refinements of Co_0.7Al₂Se_3.7 and NiAl₂Se_3.7 at room temperature, respectively. (c) The schematic crystal structure of Co_0.7Al₂Se_3.7/NiAl₂Se_3.7. (d) The crystal structure of CoSe₆/NiSe₆ octahedral layer viewed along [001] direction. (e) The crystal structure of CoSe₆/NiSe₆ octahedral layer viewed along [100] direction.

Table I. Room temperature structure details of Co_0.66Al₂Se_3.53 and Ni_0.61Al₂Se_3.55.

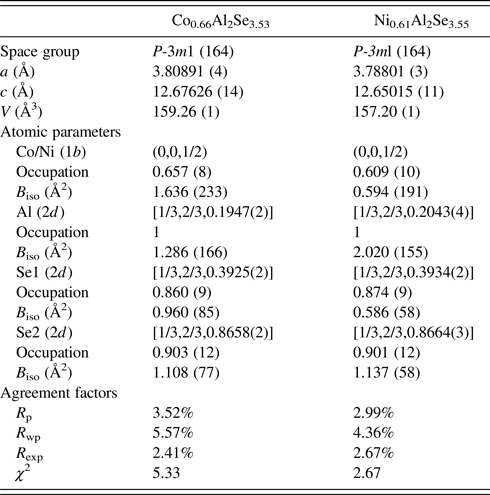
Figure 2(a) shows the temperature-dependent DC magnetic susceptibility χ and its inverse χ ⁻¹ under applied fields of 0.01, 1, and 8 T for Co_0.66Al₂Se_3.53. A bifurcation (denoted as T _f) at 4.5 K can be seen under 0.01 T for Co_0.66Al₂Se_3.53, which is suppressed when the applied field reaches 1 T. This transition is probably associated with a spin-freezing transition (Mydosh and Ebrary, Reference Mydosh and Ebrary1993). The temperature-dependent susceptibility from 100 to 300 K obeys the Curie–Weiss law χ = C/(T − θ _cw), where C is the Curie constant and θ _cw the Weiss temperature as illustrated in the inset of Figure 2(a). An effective moment of 4.92 µ _B was obtained from the fitted Curie constant. The Weiss temperature θ _cw = −216 K indicates strong antiferromagnetic interactions. The frustration index, defined by f = −θ _cw/T _f, is estimated as 48, which is a relatively large value compared with FeAl₂Se₄ (Li et al., Reference Li, Jin, Guo, Xu, Su, Feng, Liu, Zhou, Ying, Li, Wang and Chenunpublished). Thus, we conclude that Co_0.66Al₂Se_3.53 is a highly magnetically frustrated system. Figure 2(b) shows the temperature-dependent DC magnetic susceptibility χ and its inverse χ ⁻¹ for Ni_0.61Al₂Se_3.55. Unlike FeAl₂Se₄ and Co_0.66Al₂Se_3.53, no bifurcation down to 2 K can be seen under a field of 0.01 T. However, fitting the temperature-dependent susceptibility from 100 to 300 K with the Curie–Weiss law gives an effective moment of 2.38 µ _B and Weiss temperature θ _cw of −62 K, indicating a strong magnetically frustrated system.

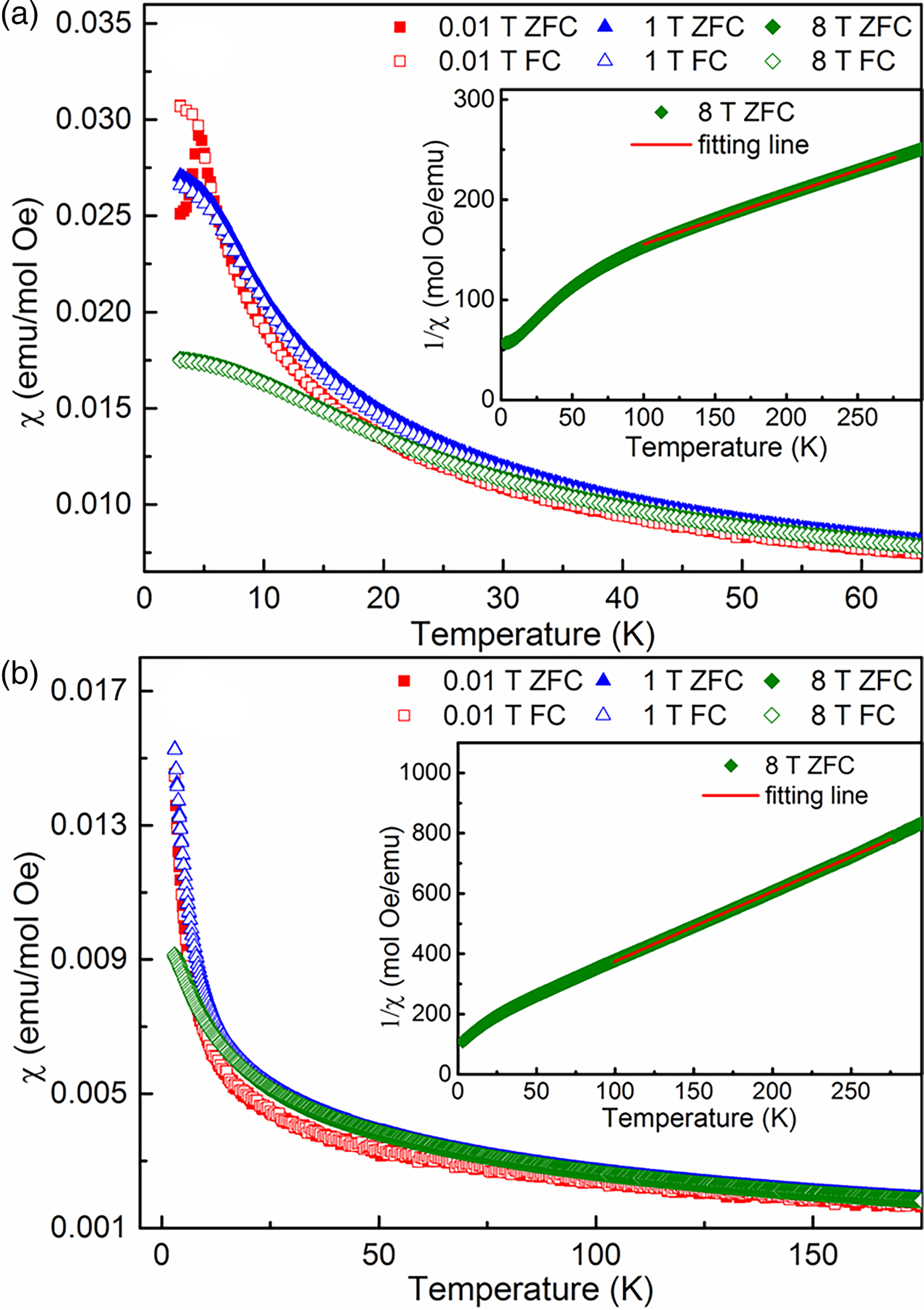
Figure 2. (Color online) (a)–(b) Zero-field-cold (ZFC) and field-cold (FC) χ(T) data taken under different applied fields from 2 to 300 K for Co_0.66Al₂Se_3.53 and Ni_0.61Al₂Se_3.55, respectively. Inset: the inversed χ ⁻¹(T) data with an applied field of 8 T. The solid red lines are linear fits with a Curie–Weiss law χ = C/(T − θ _cw).

To characterize the magnetism of Co_0.66Al₂Se_3.53 at temperatures near the bifurcation, we measured its temperature-dependent AC susceptibility from 2 to 10 K at different frequencies. As shown in Figure 3, a peak at about 4.5 K is observed in the real part, which is the signature of the susceptibility bifurcation. A small but clear peak shift towards high temperatures can be seen as increasing frequency, which suggests a spin relaxation behavior. The shift of the peak temperature as a function of frequency described by the expression, (ΔT _f)/(T _fΔlogω), can be used to distinguish spin glass and spin glass-like materials (Mydosh and Ebrary, Reference Mydosh and Ebrary1993; Krizan and Cava, Reference Krizan and Cava2014). The value obtained for Co_0.66Al₂Se_3.53 is 0.038, which is slightly larger than expected for a canonical spin glass but is in the range of spin glass-like materials. The Volger–Fulcher law is then applied to characterize the relaxation feature with a function correlating the bifurcation temperature (T _f) and frequency (f): T _f = T₀ − (E _a)/(k _B)1/ln(τ ₀f), where τ ₀ is the intrinsic relaxation time, E _a the activation energy of the process, and T ₀ the ideal glass temperature (Mydosh and Ebrary, Reference Mydosh and Ebrary1993). Fixing the ideal glass temperature T ₀ = 4.5 K, the obtained relaxation time τ ₀ is 5.4 × 10⁻¹⁰ s, and the activation energy E _a is 0.14 meV. It should be noted that the small peak at approximately 7 K originates from the instrument error.

Figure 3. (Color online) Temperature dependence of the real part of the AC magnetic susceptibilities as a function of frequency for Co_0.66Al₂Se_3.53 sample. Inset shows the parameterization of the spin freezing (as determined by the AC susceptibility) and fitting line to the Volgel–Fulcher law.

Spin glass transition usually originates from atom disorder in the compounds; thus, XPS measurements were carried out to check the intersite mixing between Co²⁺ and Al³⁺. Figure 4(a) shows Co 2p spectra of the Co_0.66Al₂Se_3.53 samples. Because of the spin–orbit coupling, the Co 2p spectra were split into two different parts: Co 2p _3/2 and Co 2p _1/2, the fitted binding energy values are 793.6 and 778.6 eV. The full width at half maxim (FWHM) of the peak of Co 2p _1/2 is 1.21. Figure 4(b) shows Al 2s spectra of the Co_0.66Al₂Se_3.53 samples. The fitted binding energy value is 119.8 eV with FWHM of 1.71, corresponding to that of the previously reported Co²⁺ and Al³⁺ oxidation states (McGuire et al., Reference McGuire, Schweitzer and Carlson1973; Mandale et al., Reference Mandale, Badrinarayanan, Date and Sinha1984). No sign of widening and unsymmetrical can be observed from the peak shape, indicating there is no sign of intersite mixing between Co²⁺ and Al³⁺ (Zha et al., Reference Zha, Zhou, Zhao and Feng2016). Thus, the observed spin glass transition should not originate from the intersite mixing disorder between Co²⁺ and Al³⁺ ions.

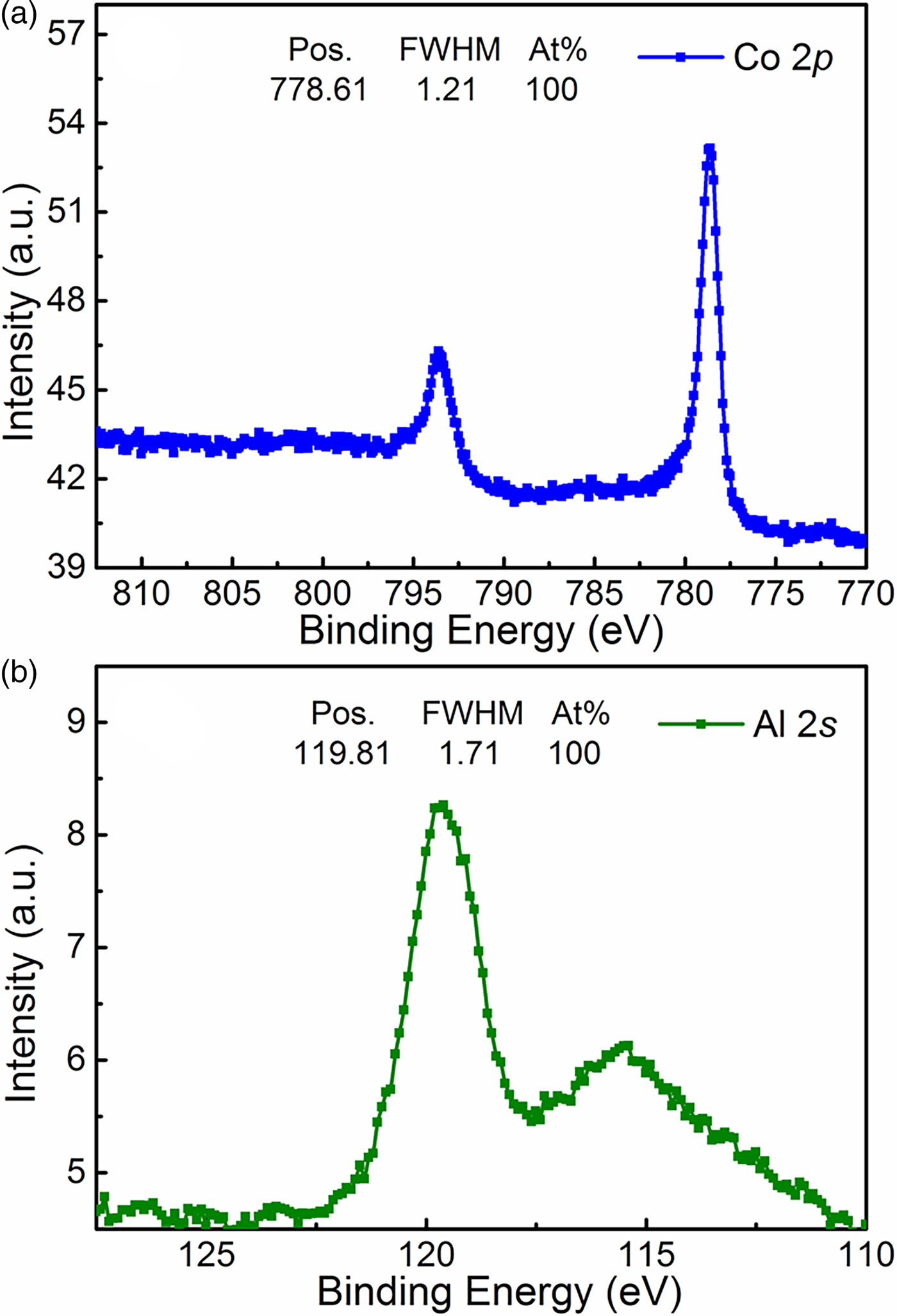
Figure 4. (Color online) XPS spectra of Co_0.66Al₂Se_3.53 sample for Co 2p (a) and Al 2s (b).

The reported isostructural FeAl₂Se₄ compound possesses a spin-freezing transition at T _f = 14 K with a frustration index of 14. For Co_0.66Al₂Se_3.53 samples, although there is no intersite mixing between Co²⁺ and Al³⁺, susceptibility measurements yield a spin-freezing transition at T _f = 4.5 K with a frustration index of 48, nearly three times larger than that in FeAl₂Se₄ compound. In the case of Ni_0.61Al₂Se_3.55 samples, no sign of spin-freezing transition can be observed down to 2 K with a Weiss temperature θ _cw of −62 K. As Collins and Petrenko showed, magnetic frustration would occur in a 2D triangular lattice, if no disturbance occurs from other sources such as interlayer coupling or magnetic impurities (Collins and Petrenko, Reference Collins and Petrenko1997). In our case, the stoichiometric FeAl₂Se₄ shows spin-freezing transition, while Ni_0.61Al₂Se_3.55 shows no sign of spin-freezing transition with vacancies. Thus, we can speculate that vacancies might not be crucial for magnetic properties and its impact on these three materials needs further investigation. Moreover, the fluctuations of the spins in a spin liquid can be classical or quantum. For systems with large S, classical spin fluctuations dominate and are driven by thermal activation energy. Spins can be thought of as reorienting randomly with time, cycling through different microstates. When the energy k _BT becomes too small, classical fluctuations cease and the spins either freeze or order (Balents, Reference Balents2010). With S being comparable to 1/2, energy change because of the spin flips is relatively small. Entangled spin pairs will remain to have a considerable lifetime. The fluctuations because of the spin flips will result in a large number of states with the same energy, i.e. the quantum spin liquid, which can persist down to T = 0 K. Thus, a transition from spin liquid to spin glass is possible when the spin changes from S = 1/2 in Lu₂Mo₂O₅N₂ to S = 1 Lu₂Mo₂O₇ (Clark et al., Reference Clark, Nilsen, Kermarrec, Ehlers, Knight, Harrison, Attfield and Gaulin2014). Therefore, it can be understood that the magnetic frustration becomes stronger from the case of FeAl₂Se₄ to Co_0.66Al₂Se_3.53 and Ni_0.61Al₂Se_3.55.