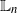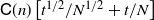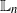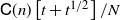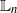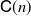1. Introduction
The filtering problem concerns the recursive estimation of a partially observed Markov process conditioned on a path of observations. It is found in a wide class of real applications, including finance, applied mathematics, and engineering; see e.g. [Reference Bain and Crisan2, Reference Del Moral8, Reference Stuart, Law and Zygalakis20]. This article focuses upon the computation of the normalizing constant for certain classes of filtering problems, to be introduced below. These normalizing constants can be of interest in statistics and engineering for model selection and/or parameter estimation.
In this article we study linear and Gaussian models in continuous time. It is well known that, for such models, under some minimal assumptions, the filter is Gaussian, with mean satisfying the Kalman–Bucy (KB) equations and the covariance matrix obeying a Riccati equation. In many cases of practical interest, these latter equations may not be computable, for instance if one does not have access to an entire trajectory of data. Instead one can use some suitable approximations obtained via time-discretization methods. However, even then, if the dimension
![]() $r_1$
of the state vector is very large, the numerical approximation of the KB and Riccati equations can become computationally prohibitive, often requiring a computational effort of at least
$r_1$
of the state vector is very large, the numerical approximation of the KB and Riccati equations can become computationally prohibitive, often requiring a computational effort of at least
![]() $\mathcal{O}(r_1^2)$
per update. The case where
$\mathcal{O}(r_1^2)$
per update. The case where
![]() $r_1$
is large occurs in many applications, including ocean and atmosphere science (e.g. [Reference Allen, Eknes and Evensen1]) and oil reservoir simulations (e.g. [Reference Skjervheim18]). A rather elegant and successful solution to this problem, in discrete time, was developed in [Reference Evensen11] in the form of the ensemble Kalman filter (EnKF), which can reduce the cost to
$r_1$
is large occurs in many applications, including ocean and atmosphere science (e.g. [Reference Allen, Eknes and Evensen1]) and oil reservoir simulations (e.g. [Reference Skjervheim18]). A rather elegant and successful solution to this problem, in discrete time, was developed in [Reference Evensen11] in the form of the ensemble Kalman filter (EnKF), which can reduce the cost to
![]() $\mathcal{O}(r_1)$
.
$\mathcal{O}(r_1)$
.
To develop an analogue of the EnKF in continuous time, the starting point is often a class of conditional McKean–Vlasov diffusions (the KB diffusion). These latter diffusions share the same law as the filter associated to the linear and Gaussian model in continuous time. Hence a possible alternative to recursively solving the KB and Riccati equations is to generate
![]() $N\in\mathbb{N}$
independent copies from the KB diffusion and use a simple Monte Carlo estimate for expectations with respect to the filter. However, the diffusion process cannot be simulated exactly, but can be approximated in a principled way by allowing the N samples to interact; precise details are given in Section 2. The resulting method, called the ensemble Kalman–Bucy filter (EnKBF), is by now rather well understood, with several contributions on its convergence (as
$N\in\mathbb{N}$
independent copies from the KB diffusion and use a simple Monte Carlo estimate for expectations with respect to the filter. However, the diffusion process cannot be simulated exactly, but can be approximated in a principled way by allowing the N samples to interact; precise details are given in Section 2. The resulting method, called the ensemble Kalman–Bucy filter (EnKBF), is by now rather well understood, with several contributions on its convergence (as
![]() $N\rightarrow\infty$
) analysis; see for instance [Reference Bishop and Del Moral5, Reference Bishop and Del Moral3, Reference Del Moral and Tugaut9, Reference Le Gland, Monbet and Tran14, Reference Tong, Majda and Kelly21].
$N\rightarrow\infty$
) analysis; see for instance [Reference Bishop and Del Moral5, Reference Bishop and Del Moral3, Reference Del Moral and Tugaut9, Reference Le Gland, Monbet and Tran14, Reference Tong, Majda and Kelly21].
In this work we focus upon using several versions of EnKBF for online estimation of the normalization constant. In particular the contributions of this work are as follows:
-
1. New results on the conditional bias of the mean using the EnKBF.
-
2. A derivation of an estimate of the normalization constant using the EnKBF.
-
3. A proof that the
 $\mathbb{L}_n$
-error of the estimate on the log-scale is bounded above by
$\mathbb{L}_n$
-error of the estimate on the log-scale is bounded above by
 $\mathsf{C}(n)\big[t^{1/2}/N^{1/2} + t/N\big]$
or
$\mathsf{C}(n)\big[t^{1/2}/N^{1/2} + t/N\big]$
or
 $\mathsf{C}(n)/N^{1/2}$
, depending on the nonlinear KB diffusion, with t the time parameter and
$\mathsf{C}(n)/N^{1/2}$
, depending on the nonlinear KB diffusion, with t the time parameter and
 $\mathsf{C}(n)$
a constant that depends only on n, not on N or t.
$\mathsf{C}(n)$
a constant that depends only on n, not on N or t. -
4. A proof that the
 $\mathbb{L}_n$
-conditional bias of the estimate on the log-scale is bounded above by
$\mathbb{L}_n$
-conditional bias of the estimate on the log-scale is bounded above by
 $\mathsf{C}(n)\big[t+t^{1/2}\big]/N$
or
$\mathsf{C}(n)\big[t+t^{1/2}\big]/N$
or
 $\mathsf{C}(n)/N$
, depending on the nonlinear KB diffusion.
$\mathsf{C}(n)/N$
, depending on the nonlinear KB diffusion. -
5. A development of a method that uses the normalization constant estimate to perform online static parameter estimation.
The result in item 1 is of independent interest, but is used directly in item 4. To the best of our knowledge the estimate in item 2 is new and can be computed with a little extra computational cost over applying an EnKBF (under time discretization). Whilst several authors have used the EnKF for normalization constant estimation, e.g. [Reference Drovandi, Everitt, Golightly and Prangle10], we have not seen the EnKBF version investigated in the literature.
In addition to the contributions 3 and 4, the results establish the decay of the mean squared error (MSE), for instance, of the log-normalizing constant estimate as the time parameter increases. This rate is expected to occur in practice, as we will see in simulations, and parallels other results found in the literature for particle estimates of the normalization constant (e.g. [Reference Cérou, Del Moral and Guyader7]). In relation to item 5, if one assumes that the model of interest has several unknown and time-homogeneous parameters,
![]() $\theta$
say, then one is interested in estimating such parameters, for instance using likelihood-based methods. We show how our estimate can be leveraged for this latter task. In this paper we use the simultaneous perturbation stochastic approximation (SPSA) method [Reference Spall19], which is popular in engineering applications. SPSA is based upon a finite difference estimator of the gradient, with respect to
$\theta$
say, then one is interested in estimating such parameters, for instance using likelihood-based methods. We show how our estimate can be leveraged for this latter task. In this paper we use the simultaneous perturbation stochastic approximation (SPSA) method [Reference Spall19], which is popular in engineering applications. SPSA is based upon a finite difference estimator of the gradient, with respect to
![]() $\theta$
, of the log-normalizing constant. It constructs a stochastic approximation scheme for the estimation of static parameters. We are not aware of this method being used for the EnKBF. As it is a zero-order optimization method, we expect it to be computationally less expensive than resorting to using other estimates of the gradient (of the log-normalizing constant). It should be noted that our work focuses upon the standard or ‘vanilla’ EnKBF, the deterministic EnKBF [Reference Sakov and Oke17] and deterministic-transport-type EnKBFs [Reference Reich and Cotter16]; other extensions are possible, for instance, to the feedback particle filter [Reference Yang, Mehta and Meyn22].
$\theta$
, of the log-normalizing constant. It constructs a stochastic approximation scheme for the estimation of static parameters. We are not aware of this method being used for the EnKBF. As it is a zero-order optimization method, we expect it to be computationally less expensive than resorting to using other estimates of the gradient (of the log-normalizing constant). It should be noted that our work focuses upon the standard or ‘vanilla’ EnKBF, the deterministic EnKBF [Reference Sakov and Oke17] and deterministic-transport-type EnKBFs [Reference Reich and Cotter16]; other extensions are possible, for instance, to the feedback particle filter [Reference Yang, Mehta and Meyn22].
This article is structured as follows. In Section 2 we provide details on the class of filtering problems that we address, as well as a review on the enKBF. The conditional bias of the mean associated to various EnKBFs is also presented there. In Section 3 we discuss how to compute the normalizing constant estimate, as well as its
![]() $\mathbb{L}_n$
-error and conditional bias. The latter is supported by numerical results checking that the order of the convergence rate indeed holds even under Euler discretization. In Section 4 we show how the normalizing constant estimate can be used in online static parameter estimation problems.
$\mathbb{L}_n$
-error and conditional bias. The latter is supported by numerical results checking that the order of the convergence rate indeed holds even under Euler discretization. In Section 4 we show how the normalizing constant estimate can be used in online static parameter estimation problems.
2. Description of the model and algorithms
2.1. The Kalman–Bucy filter
Let
![]() $(\Omega ,\mathcal{F},\mathbb{P})$
be a probability space together with a filtration
$(\Omega ,\mathcal{F},\mathbb{P})$
be a probability space together with a filtration
![]() $( \mathcal{G}_t) _{t\ge 0}$
which satisfies the usual conditions. On
$( \mathcal{G}_t) _{t\ge 0}$
which satisfies the usual conditions. On
![]() $(\Omega ,\mathcal{F},\mathbb{P})$
we consider two
$(\Omega ,\mathcal{F},\mathbb{P})$
we consider two
![]() $\mathcal{G}_t$
-adapted processes
$\mathcal{G}_t$
-adapted processes
![]() $X=\{X_t,\ t\ge 0\}$
and
$X=\{X_t,\ t\ge 0\}$
and
![]() $Y=\{Y_t,\ t\ge 0\}$
that form a time-homogeneous linear-Gaussian filtering model of the following form:
$Y=\{Y_t,\ t\ge 0\}$
that form a time-homogeneous linear-Gaussian filtering model of the following form:
 \begin{equation}\left\{\begin{array}{l}dX_t = A\,X_t\,dt\,+\,R^{1/2}_{1}\,dW_t,\\[6pt]dY_t = C\,X_t\,dt\,+\,R^{1/2}_{2}\,dV_{t},\end{array}\right.\end{equation}
\begin{equation}\left\{\begin{array}{l}dX_t = A\,X_t\,dt\,+\,R^{1/2}_{1}\,dW_t,\\[6pt]dY_t = C\,X_t\,dt\,+\,R^{1/2}_{2}\,dV_{t},\end{array}\right.\end{equation}
![]() $Y_0=0$
. In the above display, we have the following:
$Y_0=0$
. In the above display, we have the following:
 $(W_t,V_t)$
is a
$(W_t,V_t)$
is a
 $\mathcal{G}_t$
-adapted
$\mathcal{G}_t$
-adapted
 $(r_1+r_2)$
-dimensional Brownian motion.
$(r_1+r_2)$
-dimensional Brownian motion.Independent of
 $(W_t,V_t)$
,
$(W_t,V_t)$
,
 $X_0$
is a
$X_0$
is a
 $\mathcal{G}_0$
-measurable
$\mathcal{G}_0$
-measurable
 $r_1$
-valued Gaussian random vector with mean and covariance matrix
$r_1$
-valued Gaussian random vector with mean and covariance matrix
 $(\mathbb{E}(X_0),P_0)$
.
$(\mathbb{E}(X_0),P_0)$
.The symmetric matrices
 $R^{1/2}_{1}$
and
$R^{1/2}_{1}$
and
 $R^{1/2}_{2}$
are invertible.
$R^{1/2}_{2}$
are invertible.A is a square
 $r_1\times r_1$
matrix; C is an
$r_1\times r_1$
matrix; C is an
 $r_2\times r_1$
matrix.
$r_2\times r_1$
matrix.
We let
![]() ${\mathcal{F}}_t=\sigma\!\left(Y_s, s\leq t\right)$
be the filtration generated by the observation process. It is well known that the conditional distribution
${\mathcal{F}}_t=\sigma\!\left(Y_s, s\leq t\right)$
be the filtration generated by the observation process. It is well known that the conditional distribution
![]() $\eta_t$
of the signal state
$\eta_t$
of the signal state
![]() $X_t$
given
$X_t$
given
![]() ${\mathcal{F}}_t$
is an
${\mathcal{F}}_t$
is an
![]() $r_1$
-dimensional Gaussian distribution with mean and covariance matrix
$r_1$
-dimensional Gaussian distribution with mean and covariance matrix
given by the KB and Riccati equations
The Riccati drift function in (3), from
![]() $\mathbb{S}^+_{r_1}$
into
$\mathbb{S}^+_{r_1}$
into
![]() $\mathbb{S}_{r_1}$
, is given by
$\mathbb{S}_{r_1}$
, is given by
where
![]() $\mathbb{S}^+_{r_1}$
(resp.
$\mathbb{S}^+_{r_1}$
(resp.
![]() $\mathbb{S}_{r_1}$
) is the collection of symmetric and positive definite (resp. semi-definite)
$\mathbb{S}_{r_1}$
) is the collection of symmetric and positive definite (resp. semi-definite)
![]() $r_1\times r_1$
matrices defined for any
$r_1\times r_1$
matrices defined for any
![]() $Q\in \mathbb{S}^+_{r_1}$
.
$Q\in \mathbb{S}^+_{r_1}$
.
2.2. Nonlinear Kalman–Bucy diffusions
We now consider three conditional nonlinear McKean–Vlasov-type diffusion processes
where
![]() $\big(\overline{W}_t,\overline{V}_t,\overline{X}_0\big)$
are independent copies of
$\big(\overline{W}_t,\overline{V}_t,\overline{X}_0\big)$
are independent copies of
![]() $(W_t,V_t,X_0)$
(thus independent of the signal and the observation path). In the above formulas,
$(W_t,V_t,X_0)$
(thus independent of the signal and the observation path). In the above formulas,
![]() ${\mathcal{P}}_{\eta_t}$
stands for the covariance matrix
${\mathcal{P}}_{\eta_t}$
stands for the covariance matrix
and we use the generic notation
![]() $\eta_t(f)=\int_{\mathbb{R}^{r_1}}f(x)\eta_t(dx)$
for any
$\eta_t(f)=\int_{\mathbb{R}^{r_1}}f(x)\eta_t(dx)$
for any
![]() $f\,:\,\mathbb{R}^{r_1}\rightarrow\mathbb{R}^{r}$
that is
$f\,:\,\mathbb{R}^{r_1}\rightarrow\mathbb{R}^{r}$
that is
![]() $\eta_t$
-integrable (in particular,
$\eta_t$
-integrable (in particular,
![]() $r=r_1$
in (6) and (7) and
$r=r_1$
in (6) and (7) and
![]() $r=r_1^2$
in (8)). Any of these probabilistic models will be commonly referred to as KB (nonlinear) diffusion processes. In the following we will denote by
$r=r_1^2$
in (8)). Any of these probabilistic models will be commonly referred to as KB (nonlinear) diffusion processes. In the following we will denote by
![]() ${\mathcal G}_t$
the augmented filtration generated by
${\mathcal G}_t$
the augmented filtration generated by
![]() $\overline{X}_0$
and the triplet
$\overline{X}_0$
and the triplet
![]() $(Y_t,\overline{W}_t,\overline{V}_t)$
. The process (5) corresponds to the vanilla-type EnKBF that is typically used in the literature. The process (6) is associated with the so-called deterministic EnKBF [Reference Sakov and Oke17], and (7) is a deterministic-transport-inspired equation [Reference Reich and Cotter16].
$(Y_t,\overline{W}_t,\overline{V}_t)$
. The process (5) corresponds to the vanilla-type EnKBF that is typically used in the literature. The process (6) is associated with the so-called deterministic EnKBF [Reference Sakov and Oke17], and (7) is a deterministic-transport-inspired equation [Reference Reich and Cotter16].
We have the following result, which is considered, for instance, in [Reference Del Moral and Tugaut9].
Lemma 2.1. Let
![]() $\overline{X}_{t}$
be a process such that
$\overline{X}_{t}$
be a process such that
![]() $\mathbb{E}\big[\left\vert \overline{X}_{0}\right\vert^{2}\big]<\infty$
, and that satisfies any one of (5)–(7). Then the conditional mean and the conditional covariance matrix (given
$\mathbb{E}\big[\left\vert \overline{X}_{0}\right\vert^{2}\big]<\infty$
, and that satisfies any one of (5)–(7). Then the conditional mean and the conditional covariance matrix (given
![]() ${\mathcal{F}}_{t}$
) of any of the nonlinear KB diffusions (5)–(7) satisfy Equations (2) and (3), respectively.
${\mathcal{F}}_{t}$
) of any of the nonlinear KB diffusions (5)–(7) satisfy Equations (2) and (3), respectively.
Lemma 2.1 enables us to approximate the mean and covariance associated to the linear filtering problem in (1) by simulating N independent and identically distributed (i.i.d.) samples from one of the processes (5)–(7) exactly and then use the sample mean and sample covariance to approximate the mean and covariance of the filter. Since this exact simulation is seldom possible, we consider how one can generate N-particle systems whose sample mean and sample covariance can be used to replace the exact simulation.
Remark 2.1. Let us observe that Equations (5)–(7) indeed have a unique solution in the class of processes
![]() $Z_{t}$
such that
$Z_{t}$
such that
![]() $\mathbb{E}\big[\!\sup_{t\in [0,T]}\left\vert Z_{t}\right\vert^{2}\big]<\infty $
. To show existence, one considers the (linear version of the) equations (5)–(7) with the conditional expectations
$\mathbb{E}\big[\!\sup_{t\in [0,T]}\left\vert Z_{t}\right\vert^{2}\big]<\infty $
. To show existence, one considers the (linear version of the) equations (5)–(7) with the conditional expectations
![]() $\eta _{t}(e)$
and
$\eta _{t}(e)$
and
![]() $\eta _{t}\!\left[ (e-\eta _{t}(e))(e-\eta_{t}(e))^{\prime }\right] $
replaced by the solution of the equations (2) and (3), respectively, that is,
$\eta _{t}\!\left[ (e-\eta _{t}(e))(e-\eta_{t}(e))^{\prime }\right] $
replaced by the solution of the equations (2) and (3), respectively, that is,
Equations (9)–(11) have a unique solution (as they are linear) that indeed satisfies the corresponding (nonlinear) equations (5)–(7). To show the uniqueness of the solutions of Equations (5)–(7), one observes first that any solution
![]() $\eta_t$
of the (nonlinear) equations (5)–(7) has its conditional expectations
$\eta_t$
of the (nonlinear) equations (5)–(7) has its conditional expectations
![]() $\eta _{t}(e)$
and
$\eta _{t}(e)$
and
![]() $\eta _{t}\!\left[ (e-\eta _{t}(e))(e-\eta_{t}(e))^{\prime }\right] $
uniquely characterized by the equations (2) and (3). Therefore they satisfy the corresponding linear versions of the equations (5)–(7), with the conditional expectations
$\eta _{t}\!\left[ (e-\eta _{t}(e))(e-\eta_{t}(e))^{\prime }\right] $
uniquely characterized by the equations (2) and (3). Therefore they satisfy the corresponding linear versions of the equations (5)–(7), with the conditional expectations
![]() $\eta _{t}(e)$
and
$\eta _{t}(e)$
and
![]() $\eta _{t}\!\left[ (e-\eta _{t}(e))(e-\eta_{t}(e))^{\prime }\right] $
replaced by the solution of the equations (2) and (3). In other words, they satisfy Equations (9)–(11) and therefore they are unique as the corresponding linear equations (9)–(11) have a unique solution.
$\eta _{t}\!\left[ (e-\eta _{t}(e))(e-\eta_{t}(e))^{\prime }\right] $
replaced by the solution of the equations (2) and (3). In other words, they satisfy Equations (9)–(11) and therefore they are unique as the corresponding linear equations (9)–(11) have a unique solution.
Remark 2.2. If one modifies (1) to
 \begin{equation*}\left\{\begin{array}{l}dX_t = f(X_t)\,dt\,+\,R^{1/2}_{1}\,dW_t,\\[5pt]dY_t = C\,X_t\,dt\,+\,R^{1/2}_{2}\,dV_{t},\end{array}\right.\end{equation*}
\begin{equation*}\left\{\begin{array}{l}dX_t = f(X_t)\,dt\,+\,R^{1/2}_{1}\,dW_t,\\[5pt]dY_t = C\,X_t\,dt\,+\,R^{1/2}_{2}\,dV_{t},\end{array}\right.\end{equation*}
for some nonlinear function
![]() $f\,:\,\mathbb{R}^{r_1}\rightarrow\mathbb{R}^{r_1}$
, one can consider a modification of any of (5)–(7). For instance in the case (5)
$f\,:\,\mathbb{R}^{r_1}\rightarrow\mathbb{R}^{r_1}$
, one can consider a modification of any of (5)–(7). For instance in the case (5)
We note, however, that any approximation of this process, as alluded to above, does not typically provide an approximation of the nonlinear filter. Nonetheless it is considered in many works in the field.
2.3. Ensemble Kalman–Bucy filters
We now consider three ensemble Kalman–Bucy filters that correspond to the mean-field particle interpretation of the nonlinear diffusion processes (5)–(7). To be more precise we let
![]() $\big(\overline{W}_{t}^{i},\overline{V}_{t}^{i},\xi _{0}^{i}\big)_{1\leq i\leq N}$
be
$\big(\overline{W}_{t}^{i},\overline{V}_{t}^{i},\xi _{0}^{i}\big)_{1\leq i\leq N}$
be
![]() $N$
independent copies of
$N$
independent copies of
![]() $\big(\overline{W}_{t},\overline{V}_{t},\overline{X}_{0}\big)$
. In this notation, we have the three McKean–Vlasov-type interacting diffusion processes for
$\big(\overline{W}_{t},\overline{V}_{t},\overline{X}_{0}\big)$
. In this notation, we have the three McKean–Vlasov-type interacting diffusion processes for
![]() $i\in\{1,\dots,N\}$
,
$i\in\{1,\dots,N\}$
,
with the rescaled particle covariance matrices
 \begin{equation}p_{t}\,:\!=\,\left( 1-\frac{1}{N}\right) ^{-1}\, \mathcal{P}_{\eta _{t}^{N}}=\frac{1}{N-1}\sum_{1\leq i\leq N}\left( \xi _{t}^{i}-m_{t}\right) \left( \xi_{t}^{i}-m_{t}\right) ^{\prime } \end{equation}
\begin{equation}p_{t}\,:\!=\,\left( 1-\frac{1}{N}\right) ^{-1}\, \mathcal{P}_{\eta _{t}^{N}}=\frac{1}{N-1}\sum_{1\leq i\leq N}\left( \xi _{t}^{i}-m_{t}\right) \left( \xi_{t}^{i}-m_{t}\right) ^{\prime } \end{equation}
and the empirical measures
Note that for (14) one needs
![]() $N\geq r_1$
for the almost sure invertibility of
$N\geq r_1$
for the almost sure invertibility of
![]() $p_{t}$
, but it is also sufficient to use the pseudo-inverse instead of the inverse.
$p_{t}$
, but it is also sufficient to use the pseudo-inverse instead of the inverse.
These processes have been thoroughly studied in the literature, and a review can be found in [Reference Bishop and Del Moral5]. We have, as shown in [Reference Del Moral and Tugaut9, Theorem 3.1], the evolution equations for (12) and (13),
 \begin{align*}dm_t & = \displaystyle A\, m_tdt+p_t\,C^{\prime}R_2^{-1}\,\big(dY_t-Cm_t\, dt\big)+\frac{1}{\sqrt{N+1}}\, d\overline{M}_t,\\dp_t & = \displaystyle\mbox{ Ricc}(p_t)\, dt+\frac{1}{\sqrt{N}}\, dM_t,\end{align*}
\begin{align*}dm_t & = \displaystyle A\, m_tdt+p_t\,C^{\prime}R_2^{-1}\,\big(dY_t-Cm_t\, dt\big)+\frac{1}{\sqrt{N+1}}\, d\overline{M}_t,\\dp_t & = \displaystyle\mbox{ Ricc}(p_t)\, dt+\frac{1}{\sqrt{N}}\, dM_t,\end{align*}
with pairwise orthogonal martingales
![]() $M_t$
and
$M_t$
and
![]() $\overline{M}_t$
described in [Reference Del Moral and Tugaut9, Theorem 3.1]. Note that for any
$\overline{M}_t$
described in [Reference Del Moral and Tugaut9, Theorem 3.1]. Note that for any
![]() $t\geq 0$
, the absolute moments of
$t\geq 0$
, the absolute moments of
![]() $\overline{M}_t$
and
$\overline{M}_t$
and
![]() $M_t$
are uniformly, with respect to N, bounded above. We remark that the mathematical theory for (14) in the linear-Gaussian setting reverts to that of the standard KB filter as detailed in [Reference Bishop and Del Moral3].
$M_t$
are uniformly, with respect to N, bounded above. We remark that the mathematical theory for (14) in the linear-Gaussian setting reverts to that of the standard KB filter as detailed in [Reference Bishop and Del Moral3].
Remark 2.3. Returning to the context of Remark 2.2, one could, for instance, run the following version of (12) for
![]() $i\in\{1,\dots,N\}$
:
$i\in\{1,\dots,N\}$
:
Again, one should note that this will typically not produce a consistent approximation of the nonlinear filter, as would be the case for (12) with the model (1). A substantial discussion of the application and theory of the EnKBF in the nonlinear setting can be found in [Reference Bishop and Del Moral5, Section 9].
Below we use
![]() $\|\cdot\|$
to denote the
$\|\cdot\|$
to denote the
![]() $L_2$
-norm for vectors. For a square matrix B, say,
$L_2$
-norm for vectors. For a square matrix B, say,
![]() $B_{\textrm{sym}}=\tfrac{1}{2}(B+B^{\prime})$
and
$B_{\textrm{sym}}=\tfrac{1}{2}(B+B^{\prime})$
and
![]() $\mu(B)$
is the largest eigenvalue of
$\mu(B)$
is the largest eigenvalue of
![]() $B_{\textrm{sym}}$
. In the cases of (12) and (13), the authors of [Reference Del Moral and Tugaut9] consider the following assumption (recall (4)): we have
$B_{\textrm{sym}}$
. In the cases of (12) and (13), the authors of [Reference Del Moral and Tugaut9] consider the following assumption (recall (4)): we have
![]() $\mu(S)>0$
with
$\mu(S)>0$
with
where Id is the
![]() $r_1\times r_1$
identity matrix (in general we use Id to denote the identity matrix of ‘appropriate dimension’, appropriate depending on the context). The paper [Reference Del Moral and Tugaut9] proves the following time-uniform convergence theorem for the mean.
$r_1\times r_1$
identity matrix (in general we use Id to denote the identity matrix of ‘appropriate dimension’, appropriate depending on the context). The paper [Reference Del Moral and Tugaut9] proves the following time-uniform convergence theorem for the mean.
Theorem 2.1. Consider the cases of (12) and (13). Assume that (16) holds and that
![]() $\mu(A)<0$
. Then for any
$\mu(A)<0$
. Then for any
![]() $n\geq 1$
and N sufficiently large, we have that
$n\geq 1$
and N sufficiently large, we have that
where
![]() $\mathsf{C}(n)<\infty$
is a constant that does not depend upon N.
$\mathsf{C}(n)<\infty$
is a constant that does not depend upon N.
Below we assume that
![]() $\Big(A,R_1^{1/2}\Big)$
and (A, C) are controllable and observable pairs; see for instance [Reference Bishop and Del Moral5, Equation (2.7)]. Under this assumption,
$\Big(A,R_1^{1/2}\Big)$
and (A, C) are controllable and observable pairs; see for instance [Reference Bishop and Del Moral5, Equation (2.7)]. Under this assumption,
![]() $P_{\infty}$
, the solution to
$P_{\infty}$
, the solution to
![]() $\mbox{ Ricc}(P_{\infty})=0$
, exists and is unique. Set
$\mbox{ Ricc}(P_{\infty})=0$
, exists and is unique. Set
![]() $\mu(A-P_{\infty}S)$
as the largest eigenvalue of
$\mu(A-P_{\infty}S)$
as the largest eigenvalue of
![]() $\tfrac{1}{2}(A-P_{\infty}S+(A-P_{\infty}S)^{\prime})$
. For the case of (13), the following result, presented in [Reference Bishop and Del Moral5], can be shown.
$\tfrac{1}{2}(A-P_{\infty}S+(A-P_{\infty}S)^{\prime})$
. For the case of (13), the following result, presented in [Reference Bishop and Del Moral5], can be shown.
Theorem 2.2. Consider the case of (13). Assume that
![]() $\Big(A,R_1^{1/2}\Big)$
and (A, C) are controllable and observable pairs and that
$\Big(A,R_1^{1/2}\Big)$
and (A, C) are controllable and observable pairs and that
![]() $\mu(A-P_{\infty}S)<0$
and
$\mu(A-P_{\infty}S)<0$
and
![]() $S\in\mathbb{S}_{r_1}^+$
. Then for any
$S\in\mathbb{S}_{r_1}^+$
. Then for any
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $N\geq 2$
there exists a
$N\geq 2$
there exists a
![]() $t(n, N)>0$
with
$t(n, N)>0$
with
![]() $t(n, N)\rightarrow\infty$
as
$t(n, N)\rightarrow\infty$
as
![]() $N\rightarrow\infty$
, such that for any
$N\rightarrow\infty$
, such that for any
![]() $t\in[0,t(n, N)]$
$t\in[0,t(n, N)]$
where
![]() $\mathsf{C}(n)<\infty$
is a constant that does not depend upon N. The quantity t(n, N) is characterized in [Reference Bishop and Del Moral4].
$\mathsf{C}(n)<\infty$
is a constant that does not depend upon N. The quantity t(n, N) is characterized in [Reference Bishop and Del Moral4].
We note that t(n, N) is
![]() $\mathcal{O}(\!\log\!(N))$
; see [Reference Bishop and Del Moral4, Theorem 2.1] with
$\mathcal{O}(\!\log\!(N))$
; see [Reference Bishop and Del Moral4, Theorem 2.1] with
![]() $\epsilon=1/\sqrt{N}$
(
$\epsilon=1/\sqrt{N}$
(
![]() $\epsilon$
is as in [Reference Bishop and Del Moral4, Theorem 2.1]).
$\epsilon$
is as in [Reference Bishop and Del Moral4, Theorem 2.1]).
For the case of (14) we have the following result. Also note that we use the inverse of
![]() $p_{t}$
in (14), but one could use the pseudo-inverse instead, and then the constraint on N in the below statement would not be required.
$p_{t}$
in (14), but one could use the pseudo-inverse instead, and then the constraint on N in the below statement would not be required.
Theorem 2.3. Consider the case of (14). Assume that
![]() $\Big(A,R_1^{1/2}\Big)$
and (A, C) are controllable and observable pairs. Then for any
$\Big(A,R_1^{1/2}\Big)$
and (A, C) are controllable and observable pairs. Then for any
![]() $n\geq 1$
there exist
$n\geq 1$
there exist
![]() $\mathsf{C}(n)<\infty$
,
$\mathsf{C}(n)<\infty$
,
![]() $\kappa\in(0,1)$
such that for any
$\kappa\in(0,1)$
such that for any
![]() $N\geq r_1$
and
$N\geq r_1$
and
![]() $t\geq 0$
we have that
$t\geq 0$
we have that
where
![]() $\mathsf{C}(n)<\infty$
is a constant that does not depend upon N.
$\mathsf{C}(n)<\infty$
is a constant that does not depend upon N.
2.4. Conditional bias result
We set
We consider bounds on
These bounds do not currently exist in the literature and will allow us to investigate our new estimator for the normalization constant, later on in the article. In the case (14) we have (see e.g. [Reference Bishop and Del Moral3])
so we focus only on (12) and (13).
Using the second-order Taylor-type expansions presented in [Reference Bishop and Del Moral6] when the pair
![]() $\Big(A,R_1^{1/2}\Big)$
is stabilizable and
$\Big(A,R_1^{1/2}\Big)$
is stabilizable and
![]() $\big(A,S^{1/2}\big)$
is detectable, we have the uniform almost-sure bias and the
$\big(A,S^{1/2}\big)$
is detectable, we have the uniform almost-sure bias and the
![]() $\mathbb{L}_n$
-mean error estimates (
$\mathbb{L}_n$
-mean error estimates (
![]() $n\geq 1$
)
$n\geq 1$
)
as soon as N is chosen sufficiently large, for some deterministic constants
![]() $\mathsf{C}_1,\mathsf{C}_2(n)$
that do not depend on the time horizon or N (but
$\mathsf{C}_1,\mathsf{C}_2(n)$
that do not depend on the time horizon or N (but
![]() $\mathsf{C}_2(n)$
does depend upon n). Whenever
$\mathsf{C}_2(n)$
does depend upon n). Whenever
![]() $\mu(A)<0$
, Theorem 2.1 yields the rather crude estimate
$\mu(A)<0$
, Theorem 2.1 yields the rather crude estimate
Our objective is to improve the estimate (19). We observe that
 \begin{align}d\big(m_t-\widehat{X}_t\big)&=\displaystyle A\big(m_t-\widehat{X}_t\big)dt +(p_t-P_t)\, C^{\prime}R_2^{-1}\, \big(dY_t-Cm_t\, dt\big)\nonumber\\&+P_t\, C^{\prime}\Sigma^{-1} \,\big(dY_t-Cm_t\, dt\big)-P_t\, C^{\prime}R_2^{-1}\, \big(dY_t-C\widehat{X}_t\, dt\big)+\frac{1}{\sqrt{N+1}}\, d\overline{M}_t,\end{align}
\begin{align}d\big(m_t-\widehat{X}_t\big)&=\displaystyle A\big(m_t-\widehat{X}_t\big)dt +(p_t-P_t)\, C^{\prime}R_2^{-1}\, \big(dY_t-Cm_t\, dt\big)\nonumber\\&+P_t\, C^{\prime}\Sigma^{-1} \,\big(dY_t-Cm_t\, dt\big)-P_t\, C^{\prime}R_2^{-1}\, \big(dY_t-C\widehat{X}_t\, dt\big)+\frac{1}{\sqrt{N+1}}\, d\overline{M}_t,\end{align}
which yields
Equation (21) is deduced by conditioning both terms in (20) with respect to
![]() ${\mathcal{F}}_t$
, exchanging the (stochastic) integration with the conditional expectation for all the terms on the right-hand side of (20). To justify this Fubini-like exchange one can use, for example, Lemma 3.21 in [Reference Bain and Crisan2]. One also needs to use the fact that, for arbitrary
${\mathcal{F}}_t$
, exchanging the (stochastic) integration with the conditional expectation for all the terms on the right-hand side of (20). To justify this Fubini-like exchange one can use, for example, Lemma 3.21 in [Reference Bain and Crisan2]. One also needs to use the fact that, for arbitrary
![]() $0\le s \le t$
,
$0\le s \le t$
,
![]() $\widehat{m}_s=\mathbb{E}(m_s\,|\,{\mathcal{F}}_s)=\mathbb{E}(m_s\,|\,{\mathcal{F}}_t)$
and
$\widehat{m}_s=\mathbb{E}(m_s\,|\,{\mathcal{F}}_s)=\mathbb{E}(m_s\,|\,{\mathcal{F}}_t)$
and
![]() $ \widehat{p}_s\,:\!=\,\mathbb{E}(p_s\,|\,{\mathcal{F}}_s)=\mathbb{E}(p_s\,|\,{\mathcal{F}}_t)$
. To justify this, one can use, for example, Proposition 3.15 in [Reference Bain and Crisan2]. We note that both Proposition 3.15 and Lemma 3.21 hold true when the conditioning is done with respect the equivalent probability measure
$ \widehat{p}_s\,:\!=\,\mathbb{E}(p_s\,|\,{\mathcal{F}}_s)=\mathbb{E}(p_s\,|\,{\mathcal{F}}_t)$
. To justify this, one can use, for example, Proposition 3.15 in [Reference Bain and Crisan2]. We note that both Proposition 3.15 and Lemma 3.21 hold true when the conditioning is done with respect the equivalent probability measure
![]() $\tilde{\mathbb{P}}$
under which Y is a Brownian motion. However, since
$\tilde{\mathbb{P}}$
under which Y is a Brownian motion. However, since
![]() $\big(\overline{W}_{t},\overline{V}_{t},\overline{X}_{0}\big)$
are independent of Y under
$\big(\overline{W}_{t},\overline{V}_{t},\overline{X}_{0}\big)$
are independent of Y under
![]() $\mathbb{P}$
, they remain independent of Y under
$\mathbb{P}$
, they remain independent of Y under
![]() $\tilde{\mathbb{P}}$
, and therefore conditioning the processes
$\tilde{\mathbb{P}}$
, and therefore conditioning the processes
![]() $\xi^i$
under
$\xi^i$
under
![]() $\tilde{\mathbb{P}}$
is the same as conditioning them under
$\tilde{\mathbb{P}}$
is the same as conditioning them under
![]() $\mathbb{P}$
. Note that this argument does not apply to the original signal X.
$\mathbb{P}$
. Note that this argument does not apply to the original signal X.
Let
![]() ${\mathcal{E}}_{s,t}$
be the exponential semigroup (or the state transition matrix) associated with the smooth flow of matrices
${\mathcal{E}}_{s,t}$
be the exponential semigroup (or the state transition matrix) associated with the smooth flow of matrices
![]() $t\mapsto \big(A-P_tS\big)$
defined for any
$t\mapsto \big(A-P_tS\big)$
defined for any
![]() $s\leq t$
by the forward and backward differential equations
$s\leq t$
by the forward and backward differential equations
with
![]() ${\mathcal{E}}_{s,s}=Id$
. Equivalently, in terms of the matrices
${\mathcal{E}}_{s,s}=Id$
. Equivalently, in terms of the matrices
![]() ${\mathcal{E}}_t\,:\!=\,{\mathcal{E}}_{0,t}$
, we have
${\mathcal{E}}_t\,:\!=\,{\mathcal{E}}_{0,t}$
, we have
![]() ${\mathcal{E}}_{s,t}={\mathcal{E}}_t{\mathcal{E}}_s^{-1}$
. Under some observability and controllability conditions, we have that the drift matrices
${\mathcal{E}}_{s,t}={\mathcal{E}}_t{\mathcal{E}}_s^{-1}$
. Under some observability and controllability conditions, we have that the drift matrices
![]() $\big(A-P_tS\big)$
deliver a uniformly stable time-varying linear system in the sense that
$\big(A-P_tS\big)$
deliver a uniformly stable time-varying linear system in the sense that
See for instance Equation (2.13) in the review article [Reference Bishop and Del Moral5]. In this notation, recalling that
![]() $\widehat{m}_0=\widehat{X}_0$
, we have the bias formulae
$\widehat{m}_0=\widehat{X}_0$
, we have the bias formulae
 \begin{align*}\widehat{m}_t-\widehat{X}_t &=\int_0^t{\mathcal{E}}_{s,t}\, \underbrace{\big(\widehat{p}_s-P_s\big)}_{\in [{-}c_1/N,0]\, a.e.}\, C^{\prime}R_2^{-1}\, \big(dY_s-C\widehat{X}_s\, dt\big)\\\qquad &\qquad\qquad\qquad\qquad\qquad+\int_0^t{\mathcal{E}}_{s,t}\, \mathbb{E}\!\left((P_s-p_s)\, S\big(m_s-\widehat{X}_s\big)\,|\,{\mathcal{F}}_s\right)\, ds.\end{align*}
\begin{align*}\widehat{m}_t-\widehat{X}_t &=\int_0^t{\mathcal{E}}_{s,t}\, \underbrace{\big(\widehat{p}_s-P_s\big)}_{\in [{-}c_1/N,0]\, a.e.}\, C^{\prime}R_2^{-1}\, \big(dY_s-C\widehat{X}_s\, dt\big)\\\qquad &\qquad\qquad\qquad\qquad\qquad+\int_0^t{\mathcal{E}}_{s,t}\, \mathbb{E}\!\left((P_s-p_s)\, S\big(m_s-\widehat{X}_s\big)\,|\,{\mathcal{F}}_s\right)\, ds.\end{align*}
Note that the claim that
![]() $\big(\widehat{p}_s-P_s\big)\in [{-}c_1/N,0]$
almost everywhere can be justified via (18). Combining the Burkholder–Davis–Gundy inequality with the almost sure and uniform bias estimate (18) and the exponential decay (22), we obtain the uniform estimate
$\big(\widehat{p}_s-P_s\big)\in [{-}c_1/N,0]$
almost everywhere can be justified via (18). Combining the Burkholder–Davis–Gundy inequality with the almost sure and uniform bias estimate (18) and the exponential decay (22), we obtain the uniform estimate
for some deterministic constant
![]() $\mathsf{C}(n)$
that does not depend upon t or N. Conversely, combining Hölder’s inequality with the uniform variance estimate (18), we have the inequality
$\mathsf{C}(n)$
that does not depend upon t or N. Conversely, combining Hölder’s inequality with the uniform variance estimate (18), we have the inequality
for some deterministic constant
![]() $\mathsf{C}(n)$
that does not depend upon t or N. Applying the generalized Minkowski inequality, we have thus proved the following theorem, which is the
$\mathsf{C}(n)$
that does not depend upon t or N. Applying the generalized Minkowski inequality, we have thus proved the following theorem, which is the
![]() $\mathbb{L}_n$
-conditional bias (we shall also say, interchangeably, the conditional bias) of the mean.
$\mathbb{L}_n$
-conditional bias (we shall also say, interchangeably, the conditional bias) of the mean.
Theorem 2.4. Consider the cases of (12) and (13). Assume that (16) holds and that
![]() $\mu(A)<0$
. Then for any
$\mu(A)<0$
. Then for any
![]() $n\geq 1$
and N sufficiently large, we have
$n\geq 1$
and N sufficiently large, we have
where
![]() $\mathsf{C}(n)<\infty$
is a constant that does not depend upon N.
$\mathsf{C}(n)<\infty$
is a constant that does not depend upon N.
3. Computing the normalizing constant
3.1. Estimation
Consider the time interval [0, t], where
![]() $t>0$
is arbitrary; then the law of (X, W) is absolutely continuous with respect to the law of the process (X, Y), and its Radon–Nikodym derivative is
$t>0$
is arbitrary; then the law of (X, W) is absolutely continuous with respect to the law of the process (X, Y), and its Radon–Nikodym derivative is
![]() $Z_t^{-1}$
. That is,
$Z_t^{-1}$
. That is,
One can show (see [Reference Bain and Crisan2, Exercise 3.14, p. 56]) that
Following a standard approach (see, e.g., [Reference Bain and Crisan2, Chapter 3]), we introduce a probability measure
![]() $\tilde{\mathbb{P}}$
by specifying its Radon–Nikodym derivative with respect to
$\tilde{\mathbb{P}}$
by specifying its Radon–Nikodym derivative with respect to
![]() $\mathbb{P}$
to be given by
$\mathbb{P}$
to be given by
![]() $Z_t(X,Y)^{-1}$
, i.e.
$Z_t(X,Y)^{-1}$
, i.e.
Under
![]() $\tilde{\mathbb{P}}$
, the observation process Y is a scaled Brownian motion independent of X; additionally, the law of the signal process X under
$\tilde{\mathbb{P}}$
, the observation process Y is a scaled Brownian motion independent of X; additionally, the law of the signal process X under
![]() $\tilde{\mathbb{P}}$
is the same as its law under
$\tilde{\mathbb{P}}$
is the same as its law under
![]() $\mathbb{P}$
. The proof of this statement is an immediate application of Girsanov’s theorem and follows in a similar manner to the proof of Proposition 3.13 in [Reference Bain and Crisan2].
$\mathbb{P}$
. The proof of this statement is an immediate application of Girsanov’s theorem and follows in a similar manner to the proof of Proposition 3.13 in [Reference Bain and Crisan2].
Moreover, for every f defined on the signal path space, we have the Bayes formula
where
![]() $\tilde{\mathbb{E}}({\cdot})$
means expectation with respect to
$\tilde{\mathbb{E}}({\cdot})$
means expectation with respect to
![]() $\tilde{\mathbb{P}}$
. The formula (231) is commonly known as the Kallianpur–Striebel formula. For a proof, see, e.g., Proposition 3.16 in [Reference Bain and Crisan2]. Since, under
$\tilde{\mathbb{P}}$
. The formula (231) is commonly known as the Kallianpur–Striebel formula. For a proof, see, e.g., Proposition 3.16 in [Reference Bain and Crisan2]. Since, under
![]() $\tilde{\mathbb{P}}$
, X and Y are independent, we can interpret
$\tilde{\mathbb{P}}$
, X and Y are independent, we can interpret
![]() $\tilde{\mathbb{E}}\!\left(f\big((X_s)_{s\in [0,t]}\big)\, Z_t(X,Y) \,\vert\, {\mathcal{F}}_t\right)$
and
$\tilde{\mathbb{E}}\!\left(f\big((X_s)_{s\in [0,t]}\big)\, Z_t(X,Y) \,\vert\, {\mathcal{F}}_t\right)$
and
![]() $\tilde{\mathbb{E}}\!\left(Z_t(X,Y) \,\vert\, {\mathcal{F}}_t\right)$
as integrals with respect to the law of the signal, where the integrand has the observation process path fixed as Y. This interpretation can be made rigorous; see e.g. the robust representation formulation of the filtering problem described in Chapter 5 in [Reference Bain and Crisan2]. We can therefore let
$\tilde{\mathbb{E}}\!\left(Z_t(X,Y) \,\vert\, {\mathcal{F}}_t\right)$
as integrals with respect to the law of the signal, where the integrand has the observation process path fixed as Y. This interpretation can be made rigorous; see e.g. the robust representation formulation of the filtering problem described in Chapter 5 in [Reference Bain and Crisan2]. We can therefore let
![]() $\overline{Z}_t(Y)$
be the likelihood function defined by
$\overline{Z}_t(Y)$
be the likelihood function defined by
where
![]() $\mathbb{E}_Y({\cdot})$
stands for the expectation with respect to the signal process when the observation is fixed and independent of the signal. In this notation, the Bayes formula (23) takes the form
$\mathbb{E}_Y({\cdot})$
stands for the expectation with respect to the signal process when the observation is fixed and independent of the signal. In this notation, the Bayes formula (23) takes the form
We have
 \begin{align*}dZ_t(X,Y) & = \left[\big\langle CX_t, R_2^{-1} dY_t\big\rangle-\frac{1}{2}\langle X_t,SX_t\rangle\, dt\right]Z_t+\frac{1}{2} \,\langle X_t,SX_t\rangle\, Z_t\, dt\\ & = Z_t(X,Y)\, \big\langle CX_t,R_2^{-1} dY_t\big\rangle.\end{align*}
\begin{align*}dZ_t(X,Y) & = \left[\big\langle CX_t, R_2^{-1} dY_t\big\rangle-\frac{1}{2}\langle X_t,SX_t\rangle\, dt\right]Z_t+\frac{1}{2} \,\langle X_t,SX_t\rangle\, Z_t\, dt\\ & = Z_t(X,Y)\, \big\langle CX_t,R_2^{-1} dY_t\big\rangle.\end{align*}
This implies that
 \begin{align*}\overline{Z}_t(Y) &=1+\int_0^t\, \overline{Z}_s(Y)\, \overline{Z}_s(Y)^{-1}\mathbb{E}_Y\!\left(Z_s(X,Y)\, \big\langle CX_s, R_2^{-1} dY_s\big\rangle\right)\\&=1+\int_0^t\, \overline{Z}_s(Y)\, \big\langle C\widehat{X}_s,R_2^{-1} dY_s\big\rangle,\end{align*}
\begin{align*}\overline{Z}_t(Y) &=1+\int_0^t\, \overline{Z}_s(Y)\, \overline{Z}_s(Y)^{-1}\mathbb{E}_Y\!\left(Z_s(X,Y)\, \big\langle CX_s, R_2^{-1} dY_s\big\rangle\right)\\&=1+\int_0^t\, \overline{Z}_s(Y)\, \big\langle C\widehat{X}_s,R_2^{-1} dY_s\big\rangle,\end{align*}
from which we conclude that
or equivalently
This suggests the estimator
which satisfies the equation
We remark that any of the three processes (12)–(14) can be used to compute
![]() $\overline{Z}_t^N(Y)$
.
$\overline{Z}_t^N(Y)$
.
3.2. Justification of the estimator
We now seek to justify the estimator
![]() $\overline{Z}_t^N(Y)$
. We have
$\overline{Z}_t^N(Y)$
. We have
 \begin{align*}&\overline{Z}_t(X,Y)\\&\,:\!=\,\overline{Z}_t(Y)^{-1}Z_t(X,Y)\\&=\exp\Bigg[\int_0^t \Bigg( \big\langle C\big(X_s-\widehat{X}_s\big), R_2^{-1} \big(dY_s-C\widehat{X}_sds\big)\big\rangle \\&\qquad \qquad\qquad-\Bigg[\frac{1}{2}\big\langle X_s,SX_s\big\rangle-\frac{1}{2}\big\langle \widehat{X}_s,S\widehat{X}_s\big\rangle-\big\langle X_s-\widehat{X}_s,S\widehat{X}_s\big\rangle \Bigg]\Bigg)ds\Bigg]\\&=\exp{\left[\int_0^t \Bigg(\big\langle C\big(X_s-\widehat{X}_s\big), R_2^{-1} \big(dY_s-C\widehat{X}_sds\big)\big\rangle -\frac{1}{2}\big\langle \big(X_s-\widehat{X}_s\big),S\big(X_s-\widehat{X}_s\big)\big\rangle\, ds\Bigg)\right]},\end{align*}
\begin{align*}&\overline{Z}_t(X,Y)\\&\,:\!=\,\overline{Z}_t(Y)^{-1}Z_t(X,Y)\\&=\exp\Bigg[\int_0^t \Bigg( \big\langle C\big(X_s-\widehat{X}_s\big), R_2^{-1} \big(dY_s-C\widehat{X}_sds\big)\big\rangle \\&\qquad \qquad\qquad-\Bigg[\frac{1}{2}\big\langle X_s,SX_s\big\rangle-\frac{1}{2}\big\langle \widehat{X}_s,S\widehat{X}_s\big\rangle-\big\langle X_s-\widehat{X}_s,S\widehat{X}_s\big\rangle \Bigg]\Bigg)ds\Bigg]\\&=\exp{\left[\int_0^t \Bigg(\big\langle C\big(X_s-\widehat{X}_s\big), R_2^{-1} \big(dY_s-C\widehat{X}_sds\big)\big\rangle -\frac{1}{2}\big\langle \big(X_s-\widehat{X}_s\big),S\big(X_s-\widehat{X}_s\big)\big\rangle\, ds\Bigg)\right]},\end{align*}
from which we conclude that
Now, we have
 \begin{align*}&\overline{Z}_t^N(Y)\overline{Z}_t^{-1}(Y)\\&=\exp{\left[\int_0^t\left[ \big\langle C\big(m_s-\widehat{X}_s\big), R_2^{-1} dY_s\big\rangle -\frac{1}{2}\left[\big\langle m_s,Sm_s\big\rangle-\big\langle \widehat{X}_s,S\widehat{X}_s\big\rangle\right]\, ds\right]\right]}\\&=\exp{\left[\int_0^t\left[ \big\langle C\big(m_s-\widehat{X}_s\big), R_2^{-1} dY_s\big\rangle -\frac{1}{2}\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle\, ds\right] \right]} \\&\qquad \times\exp{\left[\int_0^t\left[ \frac{1}{2}\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle-\frac{1}{2}\left[\big\langle m_s,Sm_s\big\rangle-\big\langle \widehat{X}_s,S\widehat{X}_s\big\rangle\, ds \right]\right]\right]}\\&=\exp{\left[\int_0^t\!\left[ \big\langle C\big(m_s-\widehat{X}_s\big), R_2^{-1} dY_s\big\rangle -\frac{1}{2}\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle\, ds \right] \right]}\\&\qquad \times\exp{\left[\int_0^t\big\langle \widehat{X}_s-m_s,S\widehat{X}_s\big\rangle\, ds\right]}\\&=\exp{\left[\int_0^t\left[ \big\langle C\big(m_s-\widehat{X}_s\big), R_2^{-1} dY_s\big\rangle -\frac{1}{2}\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle\, ds\right] \right]}\\&\qquad \times\exp{\left[{-}\int_0^t\big\langle C\big(m_s-\widehat{X}_s\big),R^{-1}C\widehat{X}_s\big\rangle\, ds\right]}\\&=\exp{\left[\int_0^t\left[ \big\langle C\big(m_s-\widehat{X}_s\big), R_2^{-1} \big(dY_s-C\widehat{X}_sds\big)\big\rangle -\frac{1}{2}\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle\, ds \right] \right]}.\end{align*}
\begin{align*}&\overline{Z}_t^N(Y)\overline{Z}_t^{-1}(Y)\\&=\exp{\left[\int_0^t\left[ \big\langle C\big(m_s-\widehat{X}_s\big), R_2^{-1} dY_s\big\rangle -\frac{1}{2}\left[\big\langle m_s,Sm_s\big\rangle-\big\langle \widehat{X}_s,S\widehat{X}_s\big\rangle\right]\, ds\right]\right]}\\&=\exp{\left[\int_0^t\left[ \big\langle C\big(m_s-\widehat{X}_s\big), R_2^{-1} dY_s\big\rangle -\frac{1}{2}\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle\, ds\right] \right]} \\&\qquad \times\exp{\left[\int_0^t\left[ \frac{1}{2}\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle-\frac{1}{2}\left[\big\langle m_s,Sm_s\big\rangle-\big\langle \widehat{X}_s,S\widehat{X}_s\big\rangle\, ds \right]\right]\right]}\\&=\exp{\left[\int_0^t\!\left[ \big\langle C\big(m_s-\widehat{X}_s\big), R_2^{-1} dY_s\big\rangle -\frac{1}{2}\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle\, ds \right] \right]}\\&\qquad \times\exp{\left[\int_0^t\big\langle \widehat{X}_s-m_s,S\widehat{X}_s\big\rangle\, ds\right]}\\&=\exp{\left[\int_0^t\left[ \big\langle C\big(m_s-\widehat{X}_s\big), R_2^{-1} dY_s\big\rangle -\frac{1}{2}\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle\, ds\right] \right]}\\&\qquad \times\exp{\left[{-}\int_0^t\big\langle C\big(m_s-\widehat{X}_s\big),R^{-1}C\widehat{X}_s\big\rangle\, ds\right]}\\&=\exp{\left[\int_0^t\left[ \big\langle C\big(m_s-\widehat{X}_s\big), R_2^{-1} \big(dY_s-C\widehat{X}_sds\big)\big\rangle -\frac{1}{2}\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle\, ds \right] \right]}.\end{align*}
Observe that
![]() $dY_s-C\widehat{X}_sds$
is an
$dY_s-C\widehat{X}_sds$
is an
![]() ${\mathcal{F}}_s$
-martingale increment. We also have
${\mathcal{F}}_s$
-martingale increment. We also have
Now to conclude, it follows that
![]() $\overline{Z}_t^N(Y)\overline{Z}_t^{-1}(Y)$
is a positive local martingale and therefore a supermartingale; hence
$\overline{Z}_t^N(Y)\overline{Z}_t^{-1}(Y)$
is a positive local martingale and therefore a supermartingale; hence
for all
![]() $t\ge 0$
. To justify the martingale property of
$t\ge 0$
. To justify the martingale property of
![]() $\overline{Z}_t^N(Y)\overline{Z}_t^{-1}(Y)$
one can use, for example, an argument based on [Reference Karatzas and Shreve12, Chapter 3, Corollary 5.14]. As a result we can deduce that
$\overline{Z}_t^N(Y)\overline{Z}_t^{-1}(Y)$
one can use, for example, an argument based on [Reference Karatzas and Shreve12, Chapter 3, Corollary 5.14]. As a result we can deduce that
![]() $\overline{Z}_t^N(Y)$
is in some sense well-defined (i.e.
$\overline{Z}_t^N(Y)$
is in some sense well-defined (i.e.
![]() $\overline{Z}_t^N(Y)\overline{Z}_t^{-1}(Y)$
is almost surely finite), but a biased estimator of the normalization constant. Therefore, we will focus on the logarithm of the normalization constant, as it is this latter quantity that is used in practical algorithms. We begin by investigating the conditional bias.
$\overline{Z}_t^N(Y)\overline{Z}_t^{-1}(Y)$
is almost surely finite), but a biased estimator of the normalization constant. Therefore, we will focus on the logarithm of the normalization constant, as it is this latter quantity that is used in practical algorithms. We begin by investigating the conditional bias.
3.3. Conditional bias
We now consider the estimate of the logarithm of the normalizing constant
with the notation
![]() $U_t(Y)=\log\!\big(\overline{Z}_t(Y)\big)$
.
$U_t(Y)=\log\!\big(\overline{Z}_t(Y)\big)$
.
Set
![]() $\widehat{U}_t^N(Y)\,:\!=\,\mathbb{E}\big(U_t^N(Y)\,|\,{\mathcal{F}}_t\big)$
. Then, using (26), we have
$\widehat{U}_t^N(Y)\,:\!=\,\mathbb{E}\big(U_t^N(Y)\,|\,{\mathcal{F}}_t\big)$
. Then, using (26), we have
 \begin{align*}U_t^N(Y)&-U_t(Y) \\&= \log\!\big(\overline{Z}_t^N(Y)/\overline{Z}_t(Y)\big)\\&=\int_0^t\!\left[ \big\langle C\big(m_s-\widehat{X}_s\big), R_2^{-1} \big(dY_s-C\widehat{X}_sds\big)\big\rangle -\frac{1}{2}\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle\, ds\right].\end{align*}
\begin{align*}U_t^N(Y)&-U_t(Y) \\&= \log\!\big(\overline{Z}_t^N(Y)/\overline{Z}_t(Y)\big)\\&=\int_0^t\!\left[ \big\langle C\big(m_s-\widehat{X}_s\big), R_2^{-1} \big(dY_s-C\widehat{X}_sds\big)\big\rangle -\frac{1}{2}\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle\, ds\right].\end{align*}
This yields the bias formula
 \begin{align}\widehat{U}_t^N(Y)-U_t(Y)&=\int_0^t\Bigg[ \big\langle C(\widehat{m}_s-\widehat{X}_s), R_2^{-1} \big(dY_s-C\widehat{X}_sds\big)\big\rangle \nonumber \\& -\frac{1}{2}\, \mathbb{E}\!\left(\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle \,\big|\,{\mathcal{F}}_s\right)\, ds \Bigg].\end{align}
\begin{align}\widehat{U}_t^N(Y)-U_t(Y)&=\int_0^t\Bigg[ \big\langle C(\widehat{m}_s-\widehat{X}_s), R_2^{-1} \big(dY_s-C\widehat{X}_sds\big)\big\rangle \nonumber \\& -\frac{1}{2}\, \mathbb{E}\!\left(\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle \,\big|\,{\mathcal{F}}_s\right)\, ds \Bigg].\end{align}
Taking the expectation in the above display, when (16) holds and
![]() $\mu(A)<0$
, and applying Theorem 2.1, we readily check that
$\mu(A)<0$
, and applying Theorem 2.1, we readily check that
which is the bias, but is not of particular interest. So we will focus on the conditional bias
In the case (14), recall (17). In this context, using the generalized Minkowski inequality and under the assumptions of Theorem 2.3, we find that
where
![]() $\mathsf{C}(n)<\infty$
is a constant that does not depend upon N.
$\mathsf{C}(n)<\infty$
is a constant that does not depend upon N.
For the cases of (12) and (13), we start with the fact that the conditional bias in (27) is decomposed into two terms,
and
Using the uniform estimates presented in Section 2.3 we have
for some deterministic constants
![]() $\mathsf{C}(n)$
that do not depend on the time horizon. On the other hand, combining the Burkholder–Davis–Gundy inequality with the uniform bias estimate (19), we have the rather crude estimate
$\mathsf{C}(n)$
that do not depend on the time horizon. On the other hand, combining the Burkholder–Davis–Gundy inequality with the uniform bias estimate (19), we have the rather crude estimate
for some deterministic constants
![]() $\mathsf{C}(n)$
that do not depend on the time horizon. Arguing as for the proof of Theorem 2.4, we check that
$\mathsf{C}(n)$
that do not depend on the time horizon. Arguing as for the proof of Theorem 2.4, we check that
Observe that the above improves the crude estimate stated in (28). This yields the following corollary.
Corollary 3.1. Consider the cases of (12) and (13). Assume that (16) holds and that
![]() $\mu(A)<0$
. Then for any
$\mu(A)<0$
. Then for any
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $t\geq 0$
and N sufficiently large, we have that
$t\geq 0$
and N sufficiently large, we have that
where
![]() $\mathsf{C}(n)<\infty$
is a constant that does not depend upon t or N.
$\mathsf{C}(n)<\infty$
is a constant that does not depend upon t or N.
3.4.
 $\boldsymbol{\mathbb{L}}_{\boldsymbol{n}}$
-error
$\boldsymbol{\mathbb{L}}_{\boldsymbol{n}}$
-error
We now consider the
![]() $\mathbb{L}_n$
-error of the estimate of the log of the normalizing constant,
$\mathbb{L}_n$
-error of the estimate of the log of the normalizing constant,
![]() $U_t^N(Y) = \log\!\big(\overline{Z}_t^N(Y)\big).$
$U_t^N(Y) = \log\!\big(\overline{Z}_t^N(Y)\big).$
In the cases of (12) and (13) we have the following.
Proposition 3.1. Consider the cases of (12) and (13). Assume that (16) holds and that
![]() $\mu(A)<0$
. Then for any
$\mu(A)<0$
. Then for any
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $t\geq 0$
and N sufficiently large, we have that
$t\geq 0$
and N sufficiently large, we have that
 \begin{equation*}\mathbb{E}\!\left(\left|U_t^N(Y)-U_t(Y)\right|^n\right)^{1/n} \leq \mathsf{C}(n)\left(\sqrt{\frac{t}{N}} + \frac{t}{N}\right),\end{equation*}
\begin{equation*}\mathbb{E}\!\left(\left|U_t^N(Y)-U_t(Y)\right|^n\right)^{1/n} \leq \mathsf{C}(n)\left(\sqrt{\frac{t}{N}} + \frac{t}{N}\right),\end{equation*}
where
![]() $\mathsf{C}(n)<\infty$
is a constant that does not depend upon t or N.
$\mathsf{C}(n)<\infty$
is a constant that does not depend upon t or N.
Proof. We have that
So one can apply the Minkowski inequality to yield that
 \begin{align}\mathbb{E}\!\left(\left|U_t^N(Y)-U_t(Y)\right|^n\right)^{1/n} & \leq \mathbb{E}\!\left(\Big|\int_0^t \big\langle C\big(m_s - \widehat{X}_s\big), R_2^{-1} \big(dY_s-C\widehat{X}_sds\big)\big\rangle ds\Big|^n\right)^{1/n}\nonumber\\& +\frac{1}{2}\, \mathbb{E}\!\left(\Big|\int_0^t\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle ds\Big|^n\right)^{1/n}.\end{align}
\begin{align}\mathbb{E}\!\left(\left|U_t^N(Y)-U_t(Y)\right|^n\right)^{1/n} & \leq \mathbb{E}\!\left(\Big|\int_0^t \big\langle C\big(m_s - \widehat{X}_s\big), R_2^{-1} \big(dY_s-C\widehat{X}_sds\big)\big\rangle ds\Big|^n\right)^{1/n}\nonumber\\& +\frac{1}{2}\, \mathbb{E}\!\left(\Big|\int_0^t\big\langle \big(m_s-\widehat{X}_s\big),S\big(m_s-\widehat{X}_s\big)\big\rangle ds\Big|^n\right)^{1/n}.\end{align}
For the left term on the right-hand side of (29) one can use the Burkholder–Davis–Gundy inequality along with Theorem 2.3 to yield that
for some
![]() $\mathsf{C}(n)<\infty$
which is a constant that does not depend upon t or N. For the right term on the right-hand side of (29) one can use the generalized Minkowski inequality and Theorem 2.1 to give
$\mathsf{C}(n)<\infty$
which is a constant that does not depend upon t or N. For the right term on the right-hand side of (29) one can use the generalized Minkowski inequality and Theorem 2.1 to give
for some
![]() $\mathsf{C}(n)<\infty$
which is a constant that does not depend upon t or N. The proof is now easily concluded.
$\mathsf{C}(n)<\infty$
which is a constant that does not depend upon t or N. The proof is now easily concluded.
In the case of (13) we can refine further.
Proposition 3.2. Consider the case of (13). Assume that
![]() $\Big(A,R_1^{1/2}\Big)$
and (A, C) are controllable and observable pairs and that
$\Big(A,R_1^{1/2}\Big)$
and (A, C) are controllable and observable pairs and that
![]() $\mu(A-P_{\infty}S)<0$
and
$\mu(A-P_{\infty}S)<0$
and
![]() $S\in\mathbb{S}_{r_1}^+$
. Then for any
$S\in\mathbb{S}_{r_1}^+$
. Then for any
![]() $N\geq 2$
there exists a
$N\geq 2$
there exists a
![]() $t(N)>0$
, with
$t(N)>0$
, with
![]() $t(N)\rightarrow\infty$
as
$t(N)\rightarrow\infty$
as
![]() $N\rightarrow\infty$
, such that for any
$N\rightarrow\infty$
, such that for any
![]() $t\in[0,t(N)]$
,
$t\in[0,t(N)]$
,
 \begin{equation*}\mathbb{E}\!\left(\left|U_t^N(Y)-U_t(Y)\right|^n\right)^{1/n} \leq \mathsf{C}(n)\left(\sqrt{\frac{t}{N}} + \frac{t}{N}\right),\end{equation*}
\begin{equation*}\mathbb{E}\!\left(\left|U_t^N(Y)-U_t(Y)\right|^n\right)^{1/n} \leq \mathsf{C}(n)\left(\sqrt{\frac{t}{N}} + \frac{t}{N}\right),\end{equation*}
where
![]() $\mathsf{C}(n)<\infty$
is a constant that does not depend upon t or N.
$\mathsf{C}(n)<\infty$
is a constant that does not depend upon t or N.
Proof. The proof is essentially like that of Proposition 3.1, except one should use Theorem 2.2 instead of Theorem 2.1.
In the case of (14) we have the following, whose proof is again similar to those of the above results.
Proposition 3.3. Consider the case of (14). Assume that
![]() $\Big(A,R_1^{1/2}\Big)$
and (A, C) are controllable and observable pairs. Then for any
$\Big(A,R_1^{1/2}\Big)$
and (A, C) are controllable and observable pairs. Then for any
![]() $t\geq 0$
and
$t\geq 0$
and
![]() $N\geq r_1$
, we have that
$N\geq r_1$
, we have that
where
![]() $\mathsf{C}(n)<\infty$
is a constant that does not depend upon t or N.
$\mathsf{C}(n)<\infty$
is a constant that does not depend upon t or N.
Both Proposition 3.1 and Proposition 3.2 establish that one can estimate the log of the normalization constant using the ensemble KB-type filters, with an MSE (for instance) that grows at most linearly in time. Proposition 3.3 provides an error that is uniform in time, mostly following from the deterministic nature of the algorithm and the dependence on standard KB theory.
One can say more, as we now state, when considering the average estimation error over a window of time w. We restrict ourselves to the MSE below. In the cases of both (12) and (13) we have the time-uniform upper bound.
Corollary 3.2. Consider the case of (12) and (13). Assume that (16) holds and that
![]() $\mu(A)<0$
. Then for any
$\mu(A)<0$
. Then for any
![]() $t>0$
,
$t>0$
,
![]() $0<w<t$
and N sufficiently large, we have that
$0<w<t$
and N sufficiently large, we have that
 \begin{equation*}\mathbb{E}\Bigg[\Bigg(\frac{1}{w}\Bigg\{\log\!\Bigg(\frac{\overline{Z}_t^N(Y)}{\overline{Z}_{t-w}^N(Y)}\Bigg)-\log\!\Bigg(\frac{\overline{Z}_t(Y)}{\overline{Z}_{t-w}(Y)}\Bigg)\Bigg\}\Bigg)^2\Bigg] \leq \frac{\mathsf{C}}{N},\end{equation*}
\begin{equation*}\mathbb{E}\Bigg[\Bigg(\frac{1}{w}\Bigg\{\log\!\Bigg(\frac{\overline{Z}_t^N(Y)}{\overline{Z}_{t-w}^N(Y)}\Bigg)-\log\!\Bigg(\frac{\overline{Z}_t(Y)}{\overline{Z}_{t-w}(Y)}\Bigg)\Bigg\}\Bigg)^2\Bigg] \leq \frac{\mathsf{C}}{N},\end{equation*}
where
![]() $\mathsf{C}<\infty$
is a constant that does not depend upon t, w or N.
$\mathsf{C}<\infty$
is a constant that does not depend upon t, w or N.
In the case of (13) we refine further and have the following time-uniform upper bound.
Corollary 3.3. Consider the case of (13). Assume that
![]() $\Big(A,R_1^{1/2}\Big)$
and (A, C) are controllable and observable pairs and that
$\Big(A,R_1^{1/2}\Big)$
and (A, C) are controllable and observable pairs and that
![]() $\mu(A-P_{\infty}S)<0$
and
$\mu(A-P_{\infty}S)<0$
and
![]() $S\in\mathbb{S}_{r_1}^+$
. Then for any
$S\in\mathbb{S}_{r_1}^+$
. Then for any
![]() $N\geq 2$
there exists a
$N\geq 2$
there exists a
![]() $t(N)>0$
, with
$t(N)>0$
, with
![]() $t(N)\rightarrow\infty$
as
$t(N)\rightarrow\infty$
as
![]() $N\rightarrow\infty$
, such that for any
$N\rightarrow\infty$
, such that for any
![]() $t\in(0,t(N)]$
,
$t\in(0,t(N)]$
,
![]() $0<w<t$
, we have
$0<w<t$
, we have
 \begin{equation*}\mathbb{E}\Bigg[\Bigg(\frac{1}{w}\Bigg\{\log\!\Bigg(\frac{\overline{Z}_t^N(Y)}{\overline{Z}_{t-w}^N(Y)}\Bigg)-\log\!\Bigg(\frac{\overline{Z}_t(Y)}{\overline{Z}_{t-w}(Y)}\Bigg)\Bigg\}\Bigg)^2\Bigg] \leq \frac{\mathsf{C}}{N},\end{equation*}
\begin{equation*}\mathbb{E}\Bigg[\Bigg(\frac{1}{w}\Bigg\{\log\!\Bigg(\frac{\overline{Z}_t^N(Y)}{\overline{Z}_{t-w}^N(Y)}\Bigg)-\log\!\Bigg(\frac{\overline{Z}_t(Y)}{\overline{Z}_{t-w}(Y)}\Bigg)\Bigg\}\Bigg)^2\Bigg] \leq \frac{\mathsf{C}}{N},\end{equation*}
where
![]() $\mathsf{C}<\infty$
is a constant that does not depend upon t, w or N.
$\mathsf{C}<\infty$
is a constant that does not depend upon t, w or N.
Note that, as we require
![]() $t\in(0,t(N)]$
and
$t\in(0,t(N)]$
and
![]() $t(N)=\mathcal{O}(\!\log\!(N))$
in Corollary 3.4, this may not be as useful as Corollary 3.2, but the assumption of a stable system in Corollary 3.3 is much stronger than the hypotheses in Corollary 3.3; see [Reference Bishop and Del Moral5] for a discussion.
$t(N)=\mathcal{O}(\!\log\!(N))$
in Corollary 3.4, this may not be as useful as Corollary 3.2, but the assumption of a stable system in Corollary 3.3 is much stronger than the hypotheses in Corollary 3.3; see [Reference Bishop and Del Moral5] for a discussion.
3.5. Simulation results
For
![]() $(i,k,L)\in \{1,\cdots,N\} \times \mathbb{N}_0\times \mathbb{N}_0$
, let
$(i,k,L)\in \{1,\cdots,N\} \times \mathbb{N}_0\times \mathbb{N}_0$
, let
![]() $\Delta_L=2^{-L}$
and consider the Euler discretization of (12)–(14),
$\Delta_L=2^{-L}$
and consider the Euler discretization of (12)–(14),
 \begin{equation}\begin{array}{l@{\quad}ccl}(\textbf{F1}) & \xi_{(k+1)\Delta_L}^i &\, =\, & \ \xi_{k\Delta_L}^i + A \xi_{k\Delta_L}^i \Delta_L + R_1^{1/2} \Big\{\overline{W}_{(k+1)\Delta_L}^i-\overline{W}_{k\Delta_L}^i \Big\} + \\[5pt]& & & \ p_{k\Delta_L} C^{\prime} R_2^{-1} \Big( \big\{Y_{(k+1)\Delta_L} - Y_{k\Delta_L} \big\} - \Big[ C \xi_{k\Delta_L}^i \Delta_L + R_2^{1/2} \Big \{\overline{V}_{(k+1)\Delta_L}^i - \overline{V}_{k\Delta_L}^i \Big\} \Big] \Big),\\[5pt](\textbf{F2}) & \xi_{(k+1)\Delta_L}^i &\, =\, & \ \xi_{k\Delta_L}^i + A \xi_{k\Delta_L}^i \Delta_L + R_1^{1/2} \Big\{\overline{W}_{(k+1)\Delta_L}^i-\overline{W}_{k\Delta_L}^i \Big\} + \\[5pt]& & & \ p_{k\Delta_L} C^{\prime} R_2^{-1} \left( \big\{Y_{(k+1)\Delta_L} - Y_{k\Delta_L} \big\} - C \left(\dfrac{ \xi_{k\Delta_L}^i + m_{k\Delta_L}}{2} \right)\Delta_L \right),\\[5pt](\textbf{F3}) & \xi_{(k+1)\Delta_L}^i &\, =\, & \ \xi_{k\Delta_L}^i + A \xi_{k\Delta_L}^i \Delta_L + R_1\! \left(p_{k\Delta_L}\right)^{-1} \left(\xi_{k\Delta_L}^i - m_{k\Delta_L} \right) \Delta_L +\\[5pt]& & & \ p_{k\Delta_L} C^{\prime} R_2^{-1} \left( \big\{Y_{(k+1)\Delta_L} - Y_{k\Delta_L} \big\} - C\! \left(\dfrac{ \xi_{k\Delta_L}^i + m_{k\Delta_L}}{2} \right)\Delta_L \right),\end{array}\end{equation}
\begin{equation}\begin{array}{l@{\quad}ccl}(\textbf{F1}) & \xi_{(k+1)\Delta_L}^i &\, =\, & \ \xi_{k\Delta_L}^i + A \xi_{k\Delta_L}^i \Delta_L + R_1^{1/2} \Big\{\overline{W}_{(k+1)\Delta_L}^i-\overline{W}_{k\Delta_L}^i \Big\} + \\[5pt]& & & \ p_{k\Delta_L} C^{\prime} R_2^{-1} \Big( \big\{Y_{(k+1)\Delta_L} - Y_{k\Delta_L} \big\} - \Big[ C \xi_{k\Delta_L}^i \Delta_L + R_2^{1/2} \Big \{\overline{V}_{(k+1)\Delta_L}^i - \overline{V}_{k\Delta_L}^i \Big\} \Big] \Big),\\[5pt](\textbf{F2}) & \xi_{(k+1)\Delta_L}^i &\, =\, & \ \xi_{k\Delta_L}^i + A \xi_{k\Delta_L}^i \Delta_L + R_1^{1/2} \Big\{\overline{W}_{(k+1)\Delta_L}^i-\overline{W}_{k\Delta_L}^i \Big\} + \\[5pt]& & & \ p_{k\Delta_L} C^{\prime} R_2^{-1} \left( \big\{Y_{(k+1)\Delta_L} - Y_{k\Delta_L} \big\} - C \left(\dfrac{ \xi_{k\Delta_L}^i + m_{k\Delta_L}}{2} \right)\Delta_L \right),\\[5pt](\textbf{F3}) & \xi_{(k+1)\Delta_L}^i &\, =\, & \ \xi_{k\Delta_L}^i + A \xi_{k\Delta_L}^i \Delta_L + R_1\! \left(p_{k\Delta_L}\right)^{-1} \left(\xi_{k\Delta_L}^i - m_{k\Delta_L} \right) \Delta_L +\\[5pt]& & & \ p_{k\Delta_L} C^{\prime} R_2^{-1} \left( \big\{Y_{(k+1)\Delta_L} - Y_{k\Delta_L} \big\} - C\! \left(\dfrac{ \xi_{k\Delta_L}^i + m_{k\Delta_L}}{2} \right)\Delta_L \right),\end{array}\end{equation}
and the discretization of
![]() $\overline{Z}_T^N(Y)$
, for
$\overline{Z}_T^N(Y)$
, for
![]() $T\in\mathbb{N}$
,
$T\in\mathbb{N}$
,
 \begin{align}\overline{Z}_T^{N,L}(Y) = \exp\left\{ \sum_{k=0}^{T/\Delta_L-1} \left\langle m_{k\Delta_L}, C^{\prime} R_2^{-1} \big[ Y_{(k+1)\Delta_L} - Y_{k\Delta_L} \big]\right\rangle - \frac{1}{2} \left\langle m_{k\Delta_L}, S\, m_{k\Delta_L} \right\rangle \Delta_L \right\},\end{align}
\begin{align}\overline{Z}_T^{N,L}(Y) = \exp\left\{ \sum_{k=0}^{T/\Delta_L-1} \left\langle m_{k\Delta_L}, C^{\prime} R_2^{-1} \big[ Y_{(k+1)\Delta_L} - Y_{k\Delta_L} \big]\right\rangle - \frac{1}{2} \left\langle m_{k\Delta_L}, S\, m_{k\Delta_L} \right\rangle \Delta_L \right\},\end{align}
such that
 \begin{align*}P_{k\Delta_l}^N & = \frac{1}{N -1}\sum_{i=1}^N\! \Big(\xi_{k\Delta_l}^i-m^N_{k\Delta_l}\Big)\Big(\xi_{k\Delta_l}^i-m_{k\Delta_l}^N\Big)^{\top}, \\m_{k\Delta_l}^N & = \frac{1}{N }\sum_{i=1}^N \xi_{k\Delta_l}^i.\end{align*}
\begin{align*}P_{k\Delta_l}^N & = \frac{1}{N -1}\sum_{i=1}^N\! \Big(\xi_{k\Delta_l}^i-m^N_{k\Delta_l}\Big)\Big(\xi_{k\Delta_l}^i-m_{k\Delta_l}^N\Big)^{\top}, \\m_{k\Delta_l}^N & = \frac{1}{N }\sum_{i=1}^N \xi_{k\Delta_l}^i.\end{align*}
We take
![]() $T\in\mathbb{N}$
, as this is all that will be used in our numerical simulations.
$T\in\mathbb{N}$
, as this is all that will be used in our numerical simulations.
Table 1. The MSE and MSE
![]() $/(t/N)$
for
$/(t/N)$
for
![]() $N\in\{250, 500, 1000\}$
in the (F1) case.
$N\in\{250, 500, 1000\}$
in the (F1) case.

Table 2. The MSE and MSE
![]() $/(t/N)$
for
$/(t/N)$
for
![]() $N\in\{250, 500, 1000\}$
in the (F2) case.
$N\in\{250, 500, 1000\}$
in the (F2) case.


Figure 1. The MSE associated to the EnKBF in the (F1) (left) and (F2) (right) cases. This plots the MSE against the time parameter for
![]() $N\in\{250, 500, 1000\}$
. For each
$N\in\{250, 500, 1000\}$
. For each
![]() $N=250, 500, 1000$
, the MSE in (F1) is
$N=250, 500, 1000$
, the MSE in (F1) is
![]() $\approx$
5.9E-03
$\approx$
5.9E-03
![]() $\left(\frac{t}{N}\right)$
, 6.1E-03
$\left(\frac{t}{N}\right)$
, 6.1E-03
![]() $\left(\frac{t}{N}\right)$
, 5.6E-03
$\left(\frac{t}{N}\right)$
, 5.6E-03
![]() $\left(\frac{t}{N}\right)$
, and in (F2) is
$\left(\frac{t}{N}\right)$
, and in (F2) is
![]() $\approx$
6.4E-03
$\approx$
6.4E-03
![]() $\left(\frac{t}{N}\right)$
, 5.5E-03
$\left(\frac{t}{N}\right)$
, 5.5E-03
![]() $\left(\frac{t}{N}\right)$
, 6.4E-03
$\left(\frac{t}{N}\right)$
, 6.4E-03
![]() $\left(\frac{t}{N}\right)$
, respectively.
$\left(\frac{t}{N}\right)$
, respectively.
Our objective is to show that the MSE of the estimate of the log of the normalization constant in the cases (F1) and (F2) is
![]() $\mathcal{O}\big(\frac{t}{N}\big)$
and in the case (F3) is
$\mathcal{O}\big(\frac{t}{N}\big)$
and in the case (F3) is
![]() $\mathcal{O}\big(\frac{1}{N}\big)$
. We take
$\mathcal{O}\big(\frac{1}{N}\big)$
. We take
![]() $r_1=r_2=1$
,
$r_1=r_2=1$
,
![]() $A=-2$
,
$A=-2$
,
![]() $R_1^{1/2}=1$
,
$R_1^{1/2}=1$
,
![]() $R_2^{1/2}=2$
, C a uniform random number in (0, 1], and
$R_2^{1/2}=2$
, C a uniform random number in (0, 1], and
![]() $\xi_0^i \overset{i.i.d.}{\sim} \mathcal{N}(0.5,0.2)$
(normal distribution with mean 0.5 and variance 0.2). In Tables 1–2 and Figure 1, we show that the rate of the MSE of the estimate in (31) for the cases (F1) and (F2) is
$\xi_0^i \overset{i.i.d.}{\sim} \mathcal{N}(0.5,0.2)$
(normal distribution with mean 0.5 and variance 0.2). In Tables 1–2 and Figure 1, we show that the rate of the MSE of the estimate in (31) for the cases (F1) and (F2) is
![]() $\mathcal{O}\big(\frac{t}{N}\big)$
, even though we have used a naive time discretization for our results. In Table 3 and Figure 2 we show that the rate in the (F3) case is
$\mathcal{O}\big(\frac{t}{N}\big)$
, even though we have used a naive time discretization for our results. In Table 3 and Figure 2 we show that the rate in the (F3) case is
![]() $\mathcal{O}(1/N)$
.
$\mathcal{O}(1/N)$
.
Table 3. The MSE and MSE
![]() $\times N$
for
$\times N$
for
![]() $t=100$
in the (F3) case.
$t=100$
in the (F3) case.


Figure 2. The MSE associated to the EnKBF in the (F3) case. This plots the MSE against the ensemble size N for fixed time
![]() $t=100$
. MSE
$t=100$
. MSE
![]() $\approx $
5.4E-04
$\approx $
5.4E-04
![]() $/N$
.
$/N$
.
We also compare the error-to-cost rates of the EnKBF estimation of the log-normalizing constant using (F1), (F2), and (F3). We take
![]() $r_1=r_2=2$
,
$r_1=r_2=2$
,
![]() $A=2\,Id$
,
$A=2\,Id$
,
 \begin{equation*}R_1^{1/2}=\begin{bmatrix}2/3 & \quad 1/3\\[4pt]1/3 & \quad 2/3\end{bmatrix},\end{equation*}
\begin{equation*}R_1^{1/2}=\begin{bmatrix}2/3 & \quad 1/3\\[4pt]1/3 & \quad 2/3\end{bmatrix},\end{equation*}
![]() $R_2^{1/2}=Id$
, C a uniform random matrix, and
$R_2^{1/2}=Id$
, C a uniform random matrix, and
![]() $\xi_0^i \overset{i.i.d.}{\sim} \mathcal{N}(0.1\,\textbf{1}_{r_1},0.05\,Id)$
. The estimate of the log-normalizing constant is the mean of 104 simulations computed at discretization levels
$\xi_0^i \overset{i.i.d.}{\sim} \mathcal{N}(0.1\,\textbf{1}_{r_1},0.05\,Id)$
. The estimate of the log-normalizing constant is the mean of 104 simulations computed at discretization levels
![]() $L\in\{8,9,10,11\}$
. The number of ensembles
$L\in\{8,9,10,11\}$
. The number of ensembles
![]() $N_L$
is different for each EnKBF variant and is chosen so that all three cases return approximately the same MSE. The reference value is the mean of 208 simulations at level 13 with ensemble size of 500. As we see in Figure 3, to attain a certain MSE, the cost of (F1) is larger than that of (F2) and the cost of (F2) is larger than that of (F1). This is expected as (F1) has two sources of noise, while (F2) has only one and (F3) is fully deterministic.
$N_L$
is different for each EnKBF variant and is chosen so that all three cases return approximately the same MSE. The reference value is the mean of 208 simulations at level 13 with ensemble size of 500. As we see in Figure 3, to attain a certain MSE, the cost of (F1) is larger than that of (F2) and the cost of (F2) is larger than that of (F1). This is expected as (F1) has two sources of noise, while (F2) has only one and (F3) is fully deterministic.

Figure 3. The cost versus the MSE associated to estimating the log-normalizing constant using the EnKBF variants (F1)–(F3). The left plot is the cost per simulation, calculated through the formula
![]() $N_L \Delta_L^{-1}$
for
$N_L \Delta_L^{-1}$
for
![]() $L\in\{8,9,10,11\}$
. The right plot is the computational time per simulation, measured in seconds.
$L\in\{8,9,10,11\}$
. The right plot is the computational time per simulation, measured in seconds.
4. Application to static parameter estimation
4.1. Approach
We now assume that there are a collection of unknown parameters,
![]() $\theta\in\Theta\subseteq\mathbb{R}^{d_{\theta}}$
, associated to the model (1). For instance
$\theta\in\Theta\subseteq\mathbb{R}^{d_{\theta}}$
, associated to the model (1). For instance
![]() $\theta$
could consist of some or all of the elements of
$\theta$
could consist of some or all of the elements of
![]() $A, C, R_1, R_2$
. We will then include an additional subscript
$A, C, R_1, R_2$
. We will then include an additional subscript
![]() $\theta$
in each of the mathematical objects that have been introduced in the previous two sections. As an example, we would write
$\theta$
in each of the mathematical objects that have been introduced in the previous two sections. As an example, we would write
For
![]() $0<s<t$
we introduce the notation
$0<s<t$
we introduce the notation
with the obvious extension to
![]() $\overline{Z}_{s,t,\theta}^N(Y)\,:\!=\,\overline{Z}_{t,\theta}^N(Y)/\overline{Z}_{s,\theta}^N(Y)$
.
$\overline{Z}_{s,t,\theta}^N(Y)\,:\!=\,\overline{Z}_{t,\theta}^N(Y)/\overline{Z}_{s,\theta}^N(Y)$
.
The basic idea of our approach is to consider the recursive estimation of
![]() $\theta$
on the basis of the arriving observations. In particular, for notational convenience, we shall consider a method which will update our current estimate of
$\theta$
on the basis of the arriving observations. In particular, for notational convenience, we shall consider a method which will update our current estimate of
![]() $\theta$
at unit times. Our objective is to follow a recursive maximum likelihood (RML) method (e.g. [Reference Le Gland and Mevel13]) which is based upon the following update at any time
$\theta$
at unit times. Our objective is to follow a recursive maximum likelihood (RML) method (e.g. [Reference Le Gland and Mevel13]) which is based upon the following update at any time
![]() $t\in\mathbb{N}$
:
$t\in\mathbb{N}$
:
where
![]() $\{\zeta_t\}_{t\in\mathbb{N}}$
is a sequence of real numbers with
$\{\zeta_t\}_{t\in\mathbb{N}}$
is a sequence of real numbers with
![]() $\zeta_t>0$
,
$\zeta_t>0$
,
![]() $\sum_{t\in\mathbb{N}}\zeta_t=\infty$
,
$\sum_{t\in\mathbb{N}}\zeta_t=\infty$
,
![]() $\sum_{t\in\mathbb{N}}\zeta_t^2<\infty$
. Computing the gradient of
$\sum_{t\in\mathbb{N}}\zeta_t^2<\infty$
. Computing the gradient of
![]() $\overline{Z}_{t-1,t,\theta}(Y)$
can be computationally expensive, so our approach is to use a type of finite difference estimator via SPSA. We note that a classical finite difference estimator would require
$\overline{Z}_{t-1,t,\theta}(Y)$
can be computationally expensive, so our approach is to use a type of finite difference estimator via SPSA. We note that a classical finite difference estimator would require
![]() $2d_{\theta}$
evaluations of
$2d_{\theta}$
evaluations of
![]() $\overline{Z}_{t-1,t,\theta}(Y)$
, whereas the SPSA method keeps this evaluation down to 2; as computational cost is a concern, we prefer the aforementioned method.
$\overline{Z}_{t-1,t,\theta}(Y)$
, whereas the SPSA method keeps this evaluation down to 2; as computational cost is a concern, we prefer the aforementioned method.
Algorithm 1 Algorithm for Online Parameter Estimation

Our approach is given in Algorithm 1, noting that we will use the argument (k) to denote the kth element of a vector. We note that in practice, one must run a time-discretization of the EnKBF, rather than the EnKBF itself. We remark also that the use of SPSA for parameter estimation associated to hidden Markov models has been considered previously, for instance in [Reference Poyiadjis, Singh and Doucet15].
4.2. Simulation results
We use Algorithm 1 along with the Euler discretization in (30) to estimate the parameters in three different models. In particular, we show that the algorithm works in both linear and nonlinear models. In all of our examples, the data are generated from the model with the true parameters. We also remark that in the nonlinear examples below we replace the term
![]() $A\xi_{k\Delta_L}^i$
in the cases (F1)–(F3) in (30) with
$A\xi_{k\Delta_L}^i$
in the cases (F1)–(F3) in (30) with
![]() $f\big(\xi_{k\Delta_L}^i\big)$
for some nonlinear function f. Then the mean is approximated through the formula
$f\big(\xi_{k\Delta_L}^i\big)$
for some nonlinear function f. Then the mean is approximated through the formula
 \begin{align*}m_{k\Delta_l}^N & = \frac{1}{N }\sum_{i=1}^N \xi_{k\Delta_l}^i\end{align*}
\begin{align*}m_{k\Delta_l}^N & = \frac{1}{N }\sum_{i=1}^N \xi_{k\Delta_l}^i\end{align*}
and afterwards plugged into
![]() $\overline{Z}_{t-1,t,\theta_{t-1}^\pm}^N(Y)$
.
$\overline{Z}_{t-1,t,\theta_{t-1}^\pm}^N(Y)$
.
4.2.1. Linear Gaussian model
In the first example, we take
![]() $A=\theta_1 Id$
;
$A=\theta_1 Id$
;
![]() $R_1^{1/2}=\theta_2 R$
, where
$R_1^{1/2}=\theta_2 R$
, where
 \begin{align*}R = \begin{bmatrix} 1 & \quad 0.5 \\[4pt]0.5& \quad 1 & \quad 0.5 \\[4pt] & \quad 0.5 & \quad \ddots & \quad \ddots \\[4pt] & \quad & \quad \ddots & \quad \ddots & \quad 0.5 \\[4pt] & \quad & \quad & \quad 0.5 & \quad 1 \end{bmatrix};\end{align*}
\begin{align*}R = \begin{bmatrix} 1 & \quad 0.5 \\[4pt]0.5& \quad 1 & \quad 0.5 \\[4pt] & \quad 0.5 & \quad \ddots & \quad \ddots \\[4pt] & \quad & \quad \ddots & \quad \ddots & \quad 0.5 \\[4pt] & \quad & \quad & \quad 0.5 & \quad 1 \end{bmatrix};\end{align*}
![]() $C = \alpha_1(r_1,r_2) C^*$
, where
$C = \alpha_1(r_1,r_2) C^*$
, where
![]() $C^*$
is a uniform random matrix and
$C^*$
is a uniform random matrix and
![]() $\alpha_1(r_1,r_2)$
is a constant; and
$\alpha_1(r_1,r_2)$
is a constant; and
![]() $R_2^{1/2}=\alpha_2(r_2) Id$
, where
$R_2^{1/2}=\alpha_2(r_2) Id$
, where
![]() $\alpha_2(r_2)$
is a constant. In Figures 4–9 we show the results for the parameter estimation of
$\alpha_2(r_2)$
is a constant. In Figures 4–9 we show the results for the parameter estimation of
![]() $\theta_1$
and
$\theta_1$
and
![]() $\theta_2$
in the cases
$\theta_2$
in the cases
![]() $r_1=r_2=2$
and
$r_1=r_2=2$
and
![]() $r_1=r_2=100$
. In all cases we take
$r_1=r_2=100$
. In all cases we take
![]() $N=100$
, except in the case when
$N=100$
, except in the case when
![]() $r_1=r_2=100$
in (F3), where we take
$r_1=r_2=100$
in (F3), where we take
![]() $N=200$
to ensure the invertibility of
$N=200$
to ensure the invertibility of
![]() $p_t^N$
; otherwise, the condition number of
$p_t^N$
; otherwise, the condition number of
![]() $p_t^N$
will be huge. The discretization level is
$p_t^N$
will be huge. The discretization level is
![]() $L=8$
in all cases. The initial state is
$L=8$
in all cases. The initial state is
![]() $X_0\sim \mathcal{N}(4\textbf{1}_{r_1},Id)$
, where
$X_0\sim \mathcal{N}(4\textbf{1}_{r_1},Id)$
, where
![]() $\textbf{1}_{r_1}$
is a vector of 1s in
$\textbf{1}_{r_1}$
is a vector of 1s in
![]() $\mathbb{R}^{r_1}$
.
$\mathbb{R}^{r_1}$
.

Figure 4. The curves along with their average (gray dashed lines) are trajectories from the execution of Algorithm 1 for the estimation of
![]() $(\theta_1,\theta_2)$
in the case (F1) with
$(\theta_1,\theta_2)$
in the case (F1) with
![]() $r_1=r_2=2$
. The initial values of the parameters are
$r_1=r_2=2$
. The initial values of the parameters are
![]() $({-}1,2)$
. The horizontal lines represent the true parameter values
$({-}1,2)$
. The horizontal lines represent the true parameter values
![]() $\big(\theta_1^*,\theta_2^*\big)=({-}2,1)$
. We take
$\big(\theta_1^*,\theta_2^*\big)=({-}2,1)$
. We take
![]() $\nu_t=t^{-0.1}$
and
$\nu_t=t^{-0.1}$
and
![]() $\zeta_t = 0.09$
when
$\zeta_t = 0.09$
when
![]() $t\leq 400$
and
$t\leq 400$
and
![]() $\zeta_t=3 \times t^{-0.601}$
otherwise.
$\zeta_t=3 \times t^{-0.601}$
otherwise.

Figure 5. The curves along with their average (gray dashed lines) are trajectories from the execution of Algorithm 1 for the estimation of
![]() $(\theta_1,\theta_2)$
in the case (F1) with
$(\theta_1,\theta_2)$
in the case (F1) with
![]() $r_1=r_2=100$
. The initial values of the parameters are
$r_1=r_2=100$
. The initial values of the parameters are
![]() $({-}1,2)$
. The green horizontal lines represent the true parameter values
$({-}1,2)$
. The green horizontal lines represent the true parameter values
![]() $\big(\theta_1^*,\theta_2^*\big)=({-}2,1)$
. We take
$\big(\theta_1^*,\theta_2^*\big)=({-}2,1)$
. We take
![]() $\nu_t=t^{-0.1}$
and
$\nu_t=t^{-0.1}$
and
![]() $\zeta_t = 0.1$
when
$\zeta_t = 0.1$
when
![]() $t\leq 400$
and
$t\leq 400$
and
![]() $\zeta_t=3 \times t^{-0.601}$
otherwise.
$\zeta_t=3 \times t^{-0.601}$
otherwise.

Figure 6. The curves along with their average (gray dashed lines) are trajectories from the execution of Algorithm 1 for the estimation of
![]() $(\theta_1,\theta_2)$
in the case (F2) with
$(\theta_1,\theta_2)$
in the case (F2) with
![]() $r_1=r_2=2$
. The initial values of the parameters are
$r_1=r_2=2$
. The initial values of the parameters are
![]() $({-}1,2)$
. The green horizontal lines represent the true parameter values
$({-}1,2)$
. The green horizontal lines represent the true parameter values
![]() $\big(\theta_1^*,\theta_2^*\big)=({-}2,1)$
. We take
$\big(\theta_1^*,\theta_2^*\big)=({-}2,1)$
. We take
![]() $\nu_t=t^{-0.1}$
and
$\nu_t=t^{-0.1}$
and
![]() $\zeta_t = 0.09$
when
$\zeta_t = 0.09$
when
![]() $t\leq 300$
and
$t\leq 300$
and
![]() $\zeta_t=t^{-0.7}$
otherwise.
$\zeta_t=t^{-0.7}$
otherwise.

Figure 7. The curves along with their average (gray dashed lines) are trajectories from the execution of Algorithm 1 for the estimation of
![]() $(\theta_1,\theta_2)$
in the case (F2) with
$(\theta_1,\theta_2)$
in the case (F2) with
![]() $r_1=r_2=100$
. The initial values of the parameters are
$r_1=r_2=100$
. The initial values of the parameters are
![]() $({-}1,2)$
. The green horizontal lines represent the true parameter values
$({-}1,2)$
. The green horizontal lines represent the true parameter values
![]() $\big(\theta_1^*,\theta_2^*\big)=({-}2,1)$
. We take
$\big(\theta_1^*,\theta_2^*\big)=({-}2,1)$
. We take
![]() $\nu_t=t^{-0.1}$
and
$\nu_t=t^{-0.1}$
and
![]() $\zeta_t = 0.08$
when
$\zeta_t = 0.08$
when
![]() $t\leq 400$
and
$t\leq 400$
and
![]() $\zeta_t=3 \times t^{-0.64}$
otherwise.
$\zeta_t=3 \times t^{-0.64}$
otherwise.

Figure 8. The curves along with their average (gray dashed lines) are trajectories from the execution of Algorithm 1 for the estimation of
![]() $(\theta_1,\theta_2)$
in the case (F3) with
$(\theta_1,\theta_2)$
in the case (F3) with
![]() $r_1=r_2=2$
. The initial values of the parameters are
$r_1=r_2=2$
. The initial values of the parameters are
![]() $({-}1,2.2)$
. The green horizontal lines represent the true parameter values
$({-}1,2.2)$
. The green horizontal lines represent the true parameter values
![]() $\big(\theta_1^*,\theta_2^*\big)=({-}2,1)$
. We take
$\big(\theta_1^*,\theta_2^*\big)=({-}2,1)$
. We take
![]() $\nu_t=t^{-0.1}$
and
$\nu_t=t^{-0.1}$
and
![]() $\zeta_t = 0.09$
when
$\zeta_t = 0.09$
when
![]() $t\leq 100$
and
$t\leq 100$
and
![]() $\zeta_t= t^{-0.8}$
otherwise.
$\zeta_t= t^{-0.8}$
otherwise.

Figure 9. The curves along with their average (gray dashed lines) are trajectories from the execution of Algorithm 1 for the estimation of
![]() $(\theta_1,\theta_2)$
in the case (F3) with
$(\theta_1,\theta_2)$
in the case (F3) with
![]() $r_1=r_2=100$
. The initial values of the parameters are
$r_1=r_2=100$
. The initial values of the parameters are
![]() $({-}1,2)$
. The green horizontal lines represent the true parameter values
$({-}1,2)$
. The green horizontal lines represent the true parameter values
![]() $\big(\theta_1^*,\theta_2^*\big)=({-}2,1)$
. We take
$\big(\theta_1^*,\theta_2^*\big)=({-}2,1)$
. We take
![]() $\nu_t=t^{-0.1}$
and
$\nu_t=t^{-0.1}$
and
![]() $\zeta_t = 0.09$
when
$\zeta_t = 0.09$
when
![]() $t\leq 200$
and
$t\leq 200$
and
![]() $\zeta_t=2 \times t^{-0.601}$
otherwise.
$\zeta_t=2 \times t^{-0.601}$
otherwise.
The results show that in a reasonable case, one can estimate low-dimensional parameters using RML via SPSA. We now consider a few nonlinear models.
4.2.2. Lorenz 63 model
We now consider the following nonlinear model with
![]() $r_1=r_2=3$
, which is a simplified mathematical model for atmospheric convection:
$r_1=r_2=3$
, which is a simplified mathematical model for atmospheric convection:
 \begin{align*}dX_t & = f(X_t)\, dt + R^{1/2}_{1}\, dW_t,\\[3pt]dY_t & = C\, X_t\, dt + R^{1/2}_{2}\, dV_{t},\end{align*}
\begin{align*}dX_t & = f(X_t)\, dt + R^{1/2}_{1}\, dW_t,\\[3pt]dY_t & = C\, X_t\, dt + R^{1/2}_{2}\, dV_{t},\end{align*}
where
 \begin{align*}f_1(X_t) &= \theta_1 (X_t(2) - X_t(1)),\\f_2(X_t) &= \theta_2 X_t(1) - X_t(2) - X_t(1) X_t(3),\\f_3(X_t) &= X_t(1) X_t(2) - \theta_3 X_t(3),\end{align*}
\begin{align*}f_1(X_t) &= \theta_1 (X_t(2) - X_t(1)),\\f_2(X_t) &= \theta_2 X_t(1) - X_t(2) - X_t(1) X_t(3),\\f_3(X_t) &= X_t(1) X_t(2) - \theta_3 X_t(3),\end{align*}
where
![]() $X_t(i)$
is the ith component of
$X_t(i)$
is the ith component of
![]() $X_t$
. We also have
$X_t$
. We also have
![]() $R_1^{1/2}=Id$
,
$R_1^{1/2}=Id$
,
 \begin{align*}C_{ij} = \left\{\begin{array}{c@{\quad}l}\frac{1}{2} & \text{if } i=j,\\[4pt]\frac{1}{2} & \text{if } i=j-1,\\[4pt]0 & \text{otherwise, }\end{array}\right. \qquad i, j \in \{1,2,3\},\end{align*}
\begin{align*}C_{ij} = \left\{\begin{array}{c@{\quad}l}\frac{1}{2} & \text{if } i=j,\\[4pt]\frac{1}{2} & \text{if } i=j-1,\\[4pt]0 & \text{otherwise, }\end{array}\right. \qquad i, j \in \{1,2,3\},\end{align*}
and
![]() $\big(R_2^{1/2}\big)_{ij}=2\, q\left(\frac{2}{5}\min\{|i-j|,r_2-|i-j|\}\right)$
,
$\big(R_2^{1/2}\big)_{ij}=2\, q\left(\frac{2}{5}\min\{|i-j|,r_2-|i-j|\}\right)$
,
![]() $ i, j \in \{1,2,3\}$
, where
$ i, j \in \{1,2,3\}$
, where
 \begin{align*}q(x) = \left\{\begin{array}{c@{\quad}l}1-\frac{3}{2}x +\frac{1}{2}x^3 & \text{if } 0\leq x\leq 1,\\[5pt]0 & \text{otherwise.}\end{array}\right.\end{align*}
\begin{align*}q(x) = \left\{\begin{array}{c@{\quad}l}1-\frac{3}{2}x +\frac{1}{2}x^3 & \text{if } 0\leq x\leq 1,\\[5pt]0 & \text{otherwise.}\end{array}\right.\end{align*}
In Figures 10–12 we show the results for the parameter estimation of
![]() $\theta=(\theta_1,\theta_2,\theta_3)$
in the
$\theta=(\theta_1,\theta_2,\theta_3)$
in the
![]() $\textbf{F1}$
,
$\textbf{F1}$
,
![]() $\textbf{F2}$
, and
$\textbf{F2}$
, and
![]() $\textbf{F3}$
cases. The ensemble size is
$\textbf{F3}$
cases. The ensemble size is
![]() $N=100$
and the discretization level is
$N=100$
and the discretization level is
![]() $L=8$
in all cases. The initial state is
$L=8$
in all cases. The initial state is
![]() $X_0\sim \mathcal{N}\big(\textbf{1}_{r_1},\frac{1}{2}Id\big)$
, where
$X_0\sim \mathcal{N}\big(\textbf{1}_{r_1},\frac{1}{2}Id\big)$
, where
![]() $\textbf{1}_{r_1}$
is a vector of 1s in
$\textbf{1}_{r_1}$
is a vector of 1s in
![]() $\mathbb{R}^{r_1}$
.
$\mathbb{R}^{r_1}$
.

Figure 10. The curves along with their average (gray dashed lines) are trajectories from the execution of Algorithm 1 for the estimation of
![]() $(\theta_1,\theta_2, \theta_3)$
in the case (F1). The initial values of the parameters are
$(\theta_1,\theta_2, \theta_3)$
in the case (F1). The initial values of the parameters are
![]() $(7.5,26.7,6.5)$
. The green horizontal lines represent the true parameter values
$(7.5,26.7,6.5)$
. The green horizontal lines represent the true parameter values
![]() $\big(\theta_1^*,\theta_2^*,\theta_3^*\big)=\big(10,28,\frac{8}{3}\big)$
. We take
$\big(\theta_1^*,\theta_2^*,\theta_3^*\big)=\big(10,28,\frac{8}{3}\big)$
. We take
![]() $\nu_t=t^{-0.2}$
and
$\nu_t=t^{-0.2}$
and
![]() $\zeta_t = 0.0314$
when
$\zeta_t = 0.0314$
when
![]() $t\leq 100$
and
$t\leq 100$
and
![]() $\zeta_t= t^{-0.71}$
otherwise.
$\zeta_t= t^{-0.71}$
otherwise.

Figure 11. The curves along with their average (gray dashed lines) are trajectories from the execution of Algorithm 1 for the estimation of
![]() $(\theta_1,\theta_2, \theta_3)$
in the case (F2). The initial values of the parameters are
$(\theta_1,\theta_2, \theta_3)$
in the case (F2). The initial values of the parameters are
![]() $(7.5,26.7,6.5)$
. The green horizontal lines represent the true parameter values
$(7.5,26.7,6.5)$
. The green horizontal lines represent the true parameter values
![]() $\big(\theta_1^*,\theta_2^*,\theta_3^*\big)=\big(10,28,\frac{8}{3}\big)$
. We take
$\big(\theta_1^*,\theta_2^*,\theta_3^*\big)=\big(10,28,\frac{8}{3}\big)$
. We take
![]() $\nu_t=t^{-0.2}$
and
$\nu_t=t^{-0.2}$
and
![]() $\zeta_t = 0.0139$
when
$\zeta_t = 0.0139$
when
![]() $t\leq 300$
and
$t\leq 300$
and
![]() $\zeta_t= t^{-0.75}$
otherwise.
$\zeta_t= t^{-0.75}$
otherwise.

Figure 12. The curves along with their average (gray dashed lines) are trajectories from the execution of Algorithm 1 for the estimation of
![]() $(\theta_1,\theta_2, \theta_3)$
in the case (F3). The initial values of the parameters are
$(\theta_1,\theta_2, \theta_3)$
in the case (F3). The initial values of the parameters are
![]() $(7.5,26.7,6.5)$
. The green horizontal lines represent the true parameter values
$(7.5,26.7,6.5)$
. The green horizontal lines represent the true parameter values
![]() $\big(\theta_1^*,\theta_2^*,\theta_3^*\big)=\big(10,28,\frac{8}{3}\big)$
. We take
$\big(\theta_1^*,\theta_2^*,\theta_3^*\big)=\big(10,28,\frac{8}{3}\big)$
. We take
![]() $\nu_t=t^{-0.2}$
and
$\nu_t=t^{-0.2}$
and
![]() $\zeta_t = 0.0314$
when
$\zeta_t = 0.0314$
when
![]() $t\leq 100$
and
$t\leq 100$
and
![]() $\zeta_t= t^{-0.71}$
otherwise.
$\zeta_t= t^{-0.71}$
otherwise.
4.2.3. Lorenz 96 model
Finally, we consider the nonlinear Lorenz 96 model, with
![]() $r_1=r_2=40$
. The solution of this model has a chaotic behavior and it describes the evolution of a scalar quantity on a circle of latitude. The model is as follows:
$r_1=r_2=40$
. The solution of this model has a chaotic behavior and it describes the evolution of a scalar quantity on a circle of latitude. The model is as follows:
 \begin{align*}dX_t &= f(X_t)\, dt + R^{1/2}_{1}\, dW_t,\\dY_t &= X_t\, dt + R^{1/2}_{2}\, dV_{t},\end{align*}
\begin{align*}dX_t &= f(X_t)\, dt + R^{1/2}_{1}\, dW_t,\\dY_t &= X_t\, dt + R^{1/2}_{2}\, dV_{t},\end{align*}
where
where
![]() $X_t(i)$
is the ith component of
$X_t(i)$
is the ith component of
![]() $X_t$
, and it is assumed that
$X_t$
, and it is assumed that
![]() $X_t({-}1)=X_t(r_1-1)$
,
$X_t({-}1)=X_t(r_1-1)$
,
![]() $X_t(0)=X_t(r_1)$
, and
$X_t(0)=X_t(r_1)$
, and
![]() $X_t(r_1+1)=X_t(1)$
. We also have
$X_t(r_1+1)=X_t(1)$
. We also have
![]() $R_1^{1/2}=\sqrt{2} Id$
and
$R_1^{1/2}=\sqrt{2} Id$
and
![]() $R_2^{1/2}=\frac{1}{2} Id$
. Here
$R_2^{1/2}=\frac{1}{2} Id$
. Here
![]() $\theta$
represents the external force in the system, while
$\theta$
represents the external force in the system, while
![]() $(X_t(i+1) - X_t(i-2)) X_t(i-1)$
is the advection-like term and
$(X_t(i+1) - X_t(i-2)) X_t(i-1)$
is the advection-like term and
![]() $-X_t(i)$
is the damping term. In Figure 13, we show the results for the parameter estimation of
$-X_t(i)$
is the damping term. In Figure 13, we show the results for the parameter estimation of
![]() $\theta$
in the (F1), (F2), and (F3) cases. The ensemble size is
$\theta$
in the (F1), (F2), and (F3) cases. The ensemble size is
![]() $N=100$
and the discretization level is
$N=100$
and the discretization level is
![]() $L=8$
in all cases. In the (F1) and (F2) cases,
$L=8$
in all cases. In the (F1) and (F2) cases,
![]() $X_t$
is initialized as follows:
$X_t$
is initialized as follows:
![]() $X_0(1) = 8.01$
and
$X_0(1) = 8.01$
and
![]() $X_0(k)=8$
for
$X_0(k)=8$
for
![]() $1<k \leq 40$
. In (F3), to avoid having the matrix
$1<k \leq 40$
. In (F3), to avoid having the matrix
![]() $p_0^N$
equal to zero, we take
$p_0^N$
equal to zero, we take
![]() $X_0 \sim \mathcal{N}(8\textbf{1}_{r_1},0.05 Id)$
.
$X_0 \sim \mathcal{N}(8\textbf{1}_{r_1},0.05 Id)$
.

Figure 13. The curves along with their average (gray dashed lines) are trajectories from the execution of Algorithm 1 for the estimation of
![]() $\theta$
in the case (F1) (left), (F2) (middle), and (F3) (right). The initial value of
$\theta$
in the case (F1) (left), (F2) (middle), and (F3) (right). The initial value of
![]() $\theta$
is 10. The green horizontal lines represent the true parameter value
$\theta$
is 10. The green horizontal lines represent the true parameter value
![]() $\theta^*=8$
. We take
$\theta^*=8$
. We take
![]() $\nu_t=t^{-0.1}$
and
$\nu_t=t^{-0.1}$
and
![]() $\zeta_t = 0.0314$
when
$\zeta_t = 0.0314$
when
![]() $t\leq 50$
and
$t\leq 50$
and
![]() $\zeta_t= t^{-0.75}$
otherwise.
$\zeta_t= t^{-0.75}$
otherwise.
Acknowledgements
We thank an editor and two referees for very useful comments which have greatly improved the paper.
Funding information
A. J. and H. R. were supported by KAUST baseline funding. D. C. was partially supported by EU project STUOD—DLV-856408.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process for this article.