Gas discharge in a gas peaking switch

XINXIN WANG; YUAN HU; XINHAI SONG

doi:10.1017/S0263034605050743

Gas discharge in a gas peaking switch

Published online by Cambridge University Press: 05 December 2005

XINXIN WANG ,

YUAN HU and

XINHAI SONG

Show author details

XINXIN WANG: Affiliation:
Department of Electrical Engineering, Tsinghua University, Beijing, China
YUAN HU: Affiliation:
Department of Electrical Engineering, Tsinghua University, Beijing, China
XINHAI SONG: Affiliation:
Department of Electrical Engineering, Tsinghua University, Beijing, China

Article contents

Abstract
1. INTRODUCTION
2. MODELS
3. RESULTS AND DISCUSSION
4. CONCLUSION
References

Rights & Permissions

Abstract

The gas discharge in a gas peaking switch was experimentally studied and numerically simulated. For simulation, the discharge was divided into two phases, gas breakdown and voltage collapse. The criterion for an electron avalanche to transit to streamer was considered as the criterion of gas breakdown. The spark channel theory developed by Rompe-Weizel was used to calculate the spark resistance. It was found that the prepulse considerably lowers the voltage pulse applied to the gap. Even for a given input pulse, the voltage pulse applied to a peaking gap is different for different gap distance due to existence of a different prepulse. In this case, the breakdown voltage of a gas peaking gap depends on gas pressure and gap distance, individually. For nitrogen pressure varying from 3 MPa to 10 MPa and gap distance from 0.6 mm to 1.2 mm, the peak electric field higher than 2 MV/cm was achieved when breakdown. The output 10% to 90% rise time, tr, varies from 145 ps to 192 ps. As gas pressure increases, tr decreases, which can be explained by the fact that the breakdown field increases with the increase of gas pressure. It was found in experiment that the jitter in tr could be attributed to the jitter in breakdown field. Instead of getting longer, the averaged experimental tr gets shorter as gap distance increases from 0.6 mm to 1.2 mm, which differs from the results of calculation and indicates there may exist something, other than electric field, that is also related to tr. The reason for this difference may lies in the inverse coefficient of spark resistance varying with gap distance. On the whole, the results from the calculations agree with the experimental ones.

Keywords

Electron avalanche Gas breakdown Peaking switch Spark resistance Streamer

Type: Research Article
Information: Laser and Particle Beams , Volume 23 , Issue 4 , October 2005 , pp. 553 - 558

DOI: https://doi.org/10.1017/S0263034605050743 [Opens in a new window]
Copyright: © 2005 Cambridge University Press

1. INTRODUCTION

Pulsed power provides the technological basis for the production and application of intense particle and laser beams (Mesyats, 2003; Korovin et al., 2003; Mesyats et al., 2003). Ultrafast switch (Frost et al., 1993) is a key component for constructing an ultra-wideband source (Agee et al., 1998; Prather et al., 2000; Andreev et al., 2003) that is of interest for a variety of potential applications ranging from transient radar system to underground objects detection. In order to deliver a fast-rising pulse to a load, an ultrafast closing switch, called peaking switch, is usually used. For a gas peaking switch it is critical to make as high as possible the electric field between two closely spaced electrodes. If subnanosecond rise time is desired, it is usually to operate the peaking gap at gas pressure of about 100 atm and to pulsed charge the gap as quickly as possible.

The closing process of a spark gap could be divided into two phases, gas breakdown and voltage collapse. The first phase begins from an electron avalanche and ends at a streamer bridging electrodes. It determines switch delay and breakdown voltage. In the second phase a well conducting current channel was produced due to Joule heating, leading to a rapid falling of the gap voltage. Thus, it determines the rise time of output pulse.

Although much research work was done on spark gap switches (Schaefer et al., 1990), few reports were found on gas discharge in the gas peaking switch operating under high stress, short pulse conditions. In this paper, two models were established for the discharge in a gas peaking switch, one for gas breakdown phase and another for voltage collapse phase. Based on these models the gas discharge of a gas peaking switch was numerically simulated. The calculation results were compared with the experimental ones.

2. MODELS

2.1. Model for gas breakdown phase

For a gas peaking gap being pulsedly charged and self-breaking down, switch delay t_d is an important parameter since the breakdown voltage U_b can be determined by U_b = U(t)|_{t=t_d}, where U(t) the pulsed voltage is applied to the gap. As we know (Kuffel & Zaengl, 1984), t_d can be expressed as formula (1):

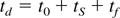
where U₀ is the static breakdown voltage of the gap. t_s and t_f are statistical delay and formative delay, respectively.

Among the three components of t_d, t₀ is the easiest one to be determined. For the commonly used gases, such as hydrogen and nitrogen, in gas peaking switches, U₀ can be found in the paper by Avilov & Belkin (1975). With the known U₀, t₀ can be easily determined from formula (2). In general, t_s is the most difficult one to be determined. However, it is reasonable to consider that any initial electron will become breakdown initiating electron and, for simplicity, to assume t_s = 0 in the case of a gas peaking switch using non-attaching gas such as nitrogen at high pressure and under extremely high electric field. As for t_f, it is the transit time of gas breakdown phase and consists of two portions. The first one is the time it takes an electron avalanche to transit to streamer, the second one is the time it takes the streamer to connect electrodes. The advent of streamer serves to greatly enhance the propagation speed of the discharge in gas breakdown phase. Thus, the major portion of t_f is the time of electron avalanche development. Based on this point, a model of the discharge in gas breakdown phase was established, in which the criterion, proposed by Raether (1964), for an electron avalanche to transit to streamer is considered as the criterion of gap breakdown. With this assumption, the calculation of discharge in gas breakdown phase was simplified to the calculation of an electron avalanche.

Electron ionization coefficient α, electron drift velocity v_de, and electron diffusion coefficient D are the important parameters for calculating space charge resulting from an electron avalanche. While it is easy to find the experimental data of these parameters, it is difficult to find the data obtained from experiments with gas pressure and electric field as high as that in a gas peaking gap. Fortunately, the theory of motions of electrons in gases, confirmed by innumerable measurements, shows that the fundamental experimental parameter is not gas pressure p or electric field E individually, but their ratio E/p (Bates, 1962).

2.2. Model for voltage collapse phase

Figure 1 shows the experiment on a gas peaking gap as well as the equivalent circuit. In the circuit z₀ is the impedance of the transmission cable that is used to charge the switch. R is the match resistor. C is the capacitance of peaking gap that could be calculated from the gap geometry. K is an ideal switch that is closed when the gas gap breaks down, that is, K is closed when the voltage collapse phase begins. L_channel and R_channel are the inductance and resistance of the spark channel of the switch, respectively. Just the same as gap inductance C, L_channel could also be calculated from the gap geometry. R_channel is a time-dependent resistance that will be discussed below (Figs. 1a and 1b).

The experiment on a gas peaking gap and the equivalent circuit used to model the experiment.

The time-dependent spark channel resistance was the subject of research by many investigators since the early 1900s (Engel et al., 1989) and many models were established to describe the resistive phase, the decrease of spark channel resistance. In general, the energy balance in the spark channel was considered. The energy losses by thermal conduction and radiation were usually necessary to be taken into account.

Since the resistive phase of a peaking switch takes a very short time, less than 1 ns, there is no marked expansion of the discharge channel in the gap, and the loss of energy by thermal conduction and radiation is negligibly small. The stored energy is expanded principally in transferring kinetic energy to the electrons and in ionizing and exciting atoms and molecules of the gas. By taking these effects into consideration, we believe that the theory of spark channel resistance by Rompe & Weizel (1944) is most suitable to a gas peaking switch. The spark channel resistance could be determined by the following formula:

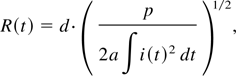
where d is the gap length, p is gas pressure, i(t) is the current flowing through the channel, a is a coefficient characterizing the nature of the gas.

3. RESULTS AND DISCUSSION

In order for calculation results to be compared with experimental ones, the calculation was performed with the same conditions as that in experiment. The experimental apparatus is shown schematically in Figure 1. The pulse generator is similar as that described by Frost. Figure 2 is the waveform measured with the input monitor installed at a position about 1 meter from the peaking gap. The first peak, about 135 kV in amplitude and 1 ns in rise time, is the input voltage pulse to the peaking gap, the second one, about 10 ns from the first one, is voltage pulse reflected from the peaking gap. The reflected pulse is lower than the input pulse due to the gap breaking down. The data of the input voltage pulse sampled with a digital oscilloscope were fed into discharge simulating code. The peaking gap is in between two plate electrodes of 14 mm in diameter and the gap spacing varies from 0.6 mm to 1.2 mm. Nitrogen at a pressure varying from 3 MPa to 10 MPa was chosen as working gas.

Input voltage pulse to the gap and the reflected pulse from the gap.

3.1. Gas breakdown

As was well known, the small interelectrode distance does yield high capacitance, even for relatively small diameter electrodes. Moreover, this high spark gap capacitance, 1.7 pF to 3.4 pF in our case, and the fast charging time leads to a strong displacement current which manifest itself as an undesirable prepulse, as shown in Figure 3.

The output voltage pulse measured with monitor 2 and the calculation one.

It was found that the prepulse has an influence on the discharge in gas breakdown phase. In the past it was usually considered that the voltage pulse applied to a peaking gap equals to the input voltage pulse doubling due to reflection, that is, U_gap(t) = 2U_input(t). Actually, the prepulse considerably lowers U_gap(t) by U_gap(t) = 2[U_input(t) − U_prepulse(t)]. Since the gap capacitance is inversely proportional to the gap distance d, as d decreases, the prepulse increases for a given input voltage pulse, which leads to decrease of the voltage applied to the gap.

It was usually believed that the breakdown voltage of a gas gap depends on the product of gas pressure and gap distance, that is, U_b = f (pd). However, our calculation, confirmed by our experiment, shows that U_b = f (p,d), as is shown in Figure 4. The reason for this difference lies in the existence of a considerable prepulse. Even for a given input voltage pulse, the voltage pulse applied to a peaking gap is different for different gap distance. In this case, people should not expect U_b = f (pd).

The breakdown voltage of the peaking gap depends on gas pressure and gap distance individually.

The averaged breakdown field was obtained by E_b = U_b /d. It was found that the highest breakdown field for each gap exceeds 2 MV/cm. As we expected, the shorter the gap, the higher is the breakdown field. This tendency is similar to a gas gap when it breaks down by a static voltage.

The breakdown voltage from calculation was compared with that from experiment, as shown in Figure 5. Every data point on the experimental curve is a value averaged over five shots. On the whole, the calculation results agree with the experimental results. As the pressure goes up, the rise rate of the experimental breakdown voltage slows down, which leads to bigger discrepancy between the calculation results and the experimental ones at higher pressures. The reason for this bigger discrepancy may be that the electron emission from cathode due to strong electric field at higher pressures was not taken into account in the calculation. From Figure 5, it could be seen that the whole experimental curve should lie above the calculation curve if the increase of the experimental breakdown voltage was not slowed down at higher pressure. This may be explained by the fact that the statistical delay was assumed to be zero in calculation, it made the switch delay shorter and breakdown voltage from calculation lower.

The comparison of the calculated breakdown voltages with the experimental ones.

3.2. Voltage collapse

The rise time of a pulse, t_r, is usually defined as the time it takes the pulse to rise from 10% amplitude to 90% amplitude. When a gas peaking gap breaks down, the output voltage pulse rises not from zero due to the existence of a considerable prepulse before breakdown, as shown in Figure 2. Thus, it is difficult to locate the 10% point on the curve of the output pulse after breakdown. In this paper, the rise time was defined as the time it takes the leading edge of the output pulse after prepulse to rise from 10% leading edge to 90% leading edge.

The t_r from calculation decreases as pressure increases. This is easy to understand since the breakdown field increases with the increase of pressure. The fact that t_r is sensitive to the breakdown field was further confirmed by experimental results. It was found in an experiment that t_r changes from shot to shot even with same gas pressure and gap distance. This jitter in t_r could be attributed to the jitter in breakdown field, which was shown in Figure 6. In Figure 6, four curves were plotted using four arbitrarily chosen sets of the experimental data, each set comes from five shots with the same gas pressure and gap distance. It is clear that under same experimental conditions, i.e., gas pressure and gap distance, the higher is the breakdown field, the shorter is the rise time.

The dependence of rise time on the breakdown field.

When the calculated t_r was compared with the experimental one, a noticeable disagreement was found. While the calculated t_r, as expected, decreases with the decrease of gap distance, the experimental t_r increases with the decrease of gap distance. This extraordinary change tendency of the experimental t_r with gap distance is difficult to explain. If the experimental results are correct, the reason for the disagreement between the calculated t_r and the experimental t_r may lies in that the coefficient a in formula (3) used to calculate spark resistance was incorrectly assumed to be a constant in our calculations. From a book by Shao (1982) translated from a Russian book by Mesyats & Korshunov (1968), the coefficient a for air and nitrogen was said to be in a range from 0.8 to 1.0. For simplicity, it was assumed to be a constant equal to 1 in our calculations. However, we just find a paper by the same author in which it was shown that a for air at pressure lower than 0.9 MPa varies with the gap distance (Mesyats & Korshunov, 1968), as shown in Figure 7. Although the results of Figure 7 were obtained from an experiment on air gap of pressure lower than 0.9 MPa, much lower than the gas pressures we considered, the change of a with gap distance may be similar. Considering our gap distance varying from 0.6 mm to 1.2 mm and a going up with the increase of d, spark resistance as well as t_r should be possible to reduce with the increase of d.

Dependence of a on gap distance for air at pressure lower than 0.9 Mpa.

Figure 8 shows the comparison of the calculated t_r with the experimental t_r that was averaged over five shots. On the whole, they agree with each other. If the change of a with gap distance is taken into account in calculation, we believe, the calculated t_r will agree better with the experimental t_r. This will be done in our next research.

The comparison of the calculated tr with the experimental tr.

4. CONCLUSION

The discharge of a gas peaking switch was divided into two phases, gas breakdown and voltage collapse. The criterion for an electron avalanche to transit to streamer was considered as the criterion of gas breakdown. The spark channel theory developed by Rompe-Weizel was used to calculate the spark resistance. The discharge in a peaking switch with pressurized nitrogen under very fast charging voltage was numerically simulated. The breakdown voltage and the rise time of output voltage pulse from the switch were determined. It was found that the prepulse has an influence on the discharge in gas breakdown phase. The prepulse considerably lowers the voltage pulse applied to the gap by U_gap(t) = 2[U_input(t) − U_prepulse(t)]. Since the gap capacitance is inversely proportional to the gap distance d, as d decreases, the prepulse increases. Even for a given input pulse, the voltage pulse applied to a peaking gap is different for different gap distance. In this case, the breakdown voltage of a gas peaking gap depends on gas pressure and gap distance, individually, and people should not expect U_b = f (pd) as usually considered. For nitrogen pressure varying from 3 MPa to 10 MPa and gap distance from 0.6 mm to 1.2 mm, the peak electric field higher than 2 MV/cm was achieved when breakdown. The output 10% to 90% rise time varies from 145 ps to 192 ps. As pressure increases, t_r decreases which can be easily explained by the fact that the breakdown field increases with the increase of pressure. The jitter in t_r could be attributed to the jitter in breakdown field. Instead of getting longer, the averaged experimental t_r gets shorter as gap distance increases from 0.6 mm to 1.2 mm, which differs from the results of calculation and indicates there exists something, other than electric field, that is also related to t_r. The reason for this difference may lies in the inverse coefficient of spark resistance varying with gap distance. On the whole, the results from the calculations agree with the experimental ones.

References

REFERENCES

Agee, F.J., Baum, C.E., Prather, W.D., Lehr, J.M., O'loughlin, J.P., Burger, J.W., Schoenberg, S.H., Scholfield D.W., Torres, R.J., Hull, J.P., &Gaudet, J.A. (1998). Ultra-wideband transmitter research. IEEE Trans. Plasma Sci. 26, 860–873.Google Scholar

Andreev, Y.A., Gubanov, V.P., Efremov, A.M., Koshelev, V.I., Korovin, S.D., Kovalchuk, B.M., Kremnev, V.V., Plisko, V.V., Stepchenko, A.S. & Sukhushin, K.N. (2003). High-power ultra wideband radiation source. Laser Part. Beams 21, 211–217.Google Scholar

Avilov, E.A. & Belkin, N.V. (1975). Electrical strength of nitrogen and hydrogen at high pressures. Sov. Phys. Tech. Phys. 19, 1631–1632.Google Scholar

Bates, D.R. (1962). Atomic and Molecular Processes. New York: Academic Press.

Engel, T.G., Donaldson, A.L. & Kristiansen, M. (1989). The pulsed discharge arc resistance and its functional behavior. IEEE Trans. Plasma Sci. 17, 323–329.Google Scholar

Frost, C.A., Martin, T.H., Patterson, P.E., Rinehart, L.F., Rohwein, G.J., Roose, L.D. & Aurand, J.E. (1993). Ultrafast gas switching experiments. Proc. 9^th IEEE Intern. Pulsed Power Conf. 491–494

Korovin, S.D., Kurkan, I.K., Loginov, S.V., Pegel, I.V., Polevin, S.D., Volkov, S.N. & Zherlitsyn, A.A. (2003). Decimeter-band frequency-tunable sources of high-power microwave pulses. Laser Part. Beams 21, 175–185.Google Scholar

Kuffel, E. & Zaengl, W. (1984). High-Voltage Engineering: Fundamentals, p. 383. Oxford: Pergamon Press.

Mesyats, G.A. & Korshunov, G.S. (1968). Formation of nanosecond sparks in static breakdown of a gap. Sov. Phys. Techn. Phys. 13, 483–487.Google Scholar

Mesyats, G.A. (2003). 25th anniversary of the Institute of High Current Electronics of the Russian Academy of Aciences, guest editors forward to the special issue. Laser Part. Beams 21, 121.Google Scholar

Mesyats, G.A., Korovin, S.D., Gunin, A.V., Gubanov, V.P., Stepchenko, A.S., Grishin, D.M., Landl, V.F. & Alekseenko, P.I. (2003). Repetitively pulsed high-current accelerators with transformer charging of forming lines. Laser Part. Beams 21, 197–209.Google Scholar

Prather, W.D., Baum, C.E., Lehr, J.M., O'Loughlin, J.P., Tyo, S., Schoenberg, Torres, R.J., Tran, T.C., Scholfield, D.W., Gaudet, J., &Burger, J.W. (2000). Ultra-wideband Source and Antenna Research. IEEE Trans. Plasma Sci. 28, 1624–1630.Google Scholar

Raether, H. (1964). Electron Avalanches And Breakdown In Gases. London: Butterworths.