Theory

To numerically calculate the SBS threshold, we study the following coupled-wave equations describing the process of SBS generation (Boyd et al., Reference Boyd, Rzazewski and Narum1990):

(1)$$\displaystyle{{\partial E_{\rm P}} \over {\partial z}} + \displaystyle{n \over c}\displaystyle{{\partial E_{\rm P}} \over {\partial t}} = ig{\rm {\rm \rho}} E_{\rm S}-\displaystyle{1 \over 2}{{\rm \sigma}} E_{\rm P}$$

(2)$$\displaystyle{{\partial E_{\rm S}} \over {\partial z}}-\displaystyle{n \over c}\displaystyle{{\partial E_{\rm S}} \over {\partial t}} = -ig{{\rm \rho}} ^{^\ast}E_{\rm P} + \displaystyle{1 \over 2}{{\rm \sigma}} E_{\rm S}$$

(3)$$\displaystyle{{\partial {{\rm \rho}}} \over {\partial t}} + \displaystyle{1 \over 2}{\rm \Gamma} {{\rm \rho}} = \displaystyle{{{\rm i}{{\rm \gamma}} q^2} \over {16{{\rm \pi}} {\rm \Omega} _{\rm B}}}E_{\rm P}E_{\rm S}^{^\ast} + f$$

where E _P, E _S, and ρ respectively represent amplitude of the pump, Stokes light, and acoustic wave; n is the refractive index of Brillouin medium; c is the velocity of light in vacuum; ω is the angular frequency of the pump; γ is the electrostrictive constant; q is the wave vector of acoustic wave; g is the gain factor; σ is the absorption coefficient of the medium; Ω_B and Γ respectively represent the Brillouin frequency shift and Brillouin linewidth; f represents the Langevin noise source that describes the random thermal noise in the medium, and it follows the relation 〈f(z, t)〉 = 0 and 〈f(z, t)f*(z ^′, t ^′)〉 = Qδ(z − z ^′)δ(t − t ^′), in which Q = 2kTρ ₀Γ/V ²A, k is the Boltzmann constant, T is the temperature of medium, and A is the cross-sectional area of the beam (Boyd et al., Reference Boyd, Rzazewski and Narum1990; Wang et al., Reference Wang, Zhu, Lu and Zhang2016).

By numerically solving the three-wave-coupled equations of (1)–(3), the SBS process can be simulated when the pump is injected into the Brillouin medium. In the algorithm, we use an implicit finite differencing in time and a backward differencing scheme in space similar as the model proposed by Chu et al. (Reference Chu, Kanefsky and Falk1992). The analytical expression for the super-Gaussian-shaped pump pulse added with a sinusoidal intensity modulation caused by the FM-to-AM effect is described as follows:

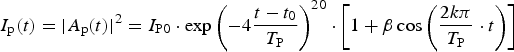(4)$$I_{\rm p}(t) = \vert A_{\rm p}(t) \vert ^2 = I_{{\rm P}0}\cdot \exp \left( {-4\displaystyle{{t-t_0} \over {T_{\rm P}}}} \right)^{20}\cdot \left[ {1 + {{\rm \beta}} \cos \left( {\displaystyle{{2k{{\rm \pi}}} \over {T_{\rm P}}}\cdot t} \right)} \right]$$

where I _P0 is the peak intensity of the 20th order super-Gaussian-shaped pump, t ₀ represents the central time, T _P is the pulse width, β is the temporal modulation index of the FM-to-AM effect, and k denotes the number of the modulation peaks in the top of the pump pulse. The initial condition can be described as follows: the pump pulse is injected from one end of the Brillouin medium, and the other local pump intensity along the longitudinal axis of the medium; none of the Stokes light excited at the beginning and its amplitude is set to be zero; the acoustic wave ρ is a complex Gaussian random distribution function with zero mean.

The main parameters of Brillouin medium and laser source used in our calculation are shown in Table 1. Heavy fluorocarbon liquid materials FC-40 is selected as the nonlinear material for the numerically simulation. Among the parameters, refractive index, phonon lifetime, Brillouin frequency shift, and gain coefficient are taken from Wang et al. (Reference Wang, Zhu, Lu and Zhang2015).

Table 1. Main parameters of Brillouin medium and laser source

Numerical results and discussion

With the proposed numerical model and the main parameters mentioned above, SBS threshold with sinusoidally modulated pump pulses was studied. To describe the temporal modulation of the pump pulse, the distortion criterion, and the modulation frequency are taken into consideration.

The distortion criterion α is defined by the following expression (Hocquet et al., Reference Hocquet, Penninckx, Bordenave, Gouédard and Jaouën2008):

(5)$${{\rm \alpha}} = 2\displaystyle{{I_{\max} -I_{\min}} \over {I_{\max} + I_{\min}}} \times 100\% $$

where I _max and I _min represent the peak and valley intensity of the pump in the fluctuation duration. The α factor ranges from 0 to 200%, and α = 0 denotes that there is no intensity modulation of the pump pulse. When different pump pulses with the changing α factors are used, the SBS effect is simulated with the abovementioned modal. Five different distortion criteria of 0, 40, 80, 120, and 160% are used for numerically calculation, and the results are shown in Figure 1.

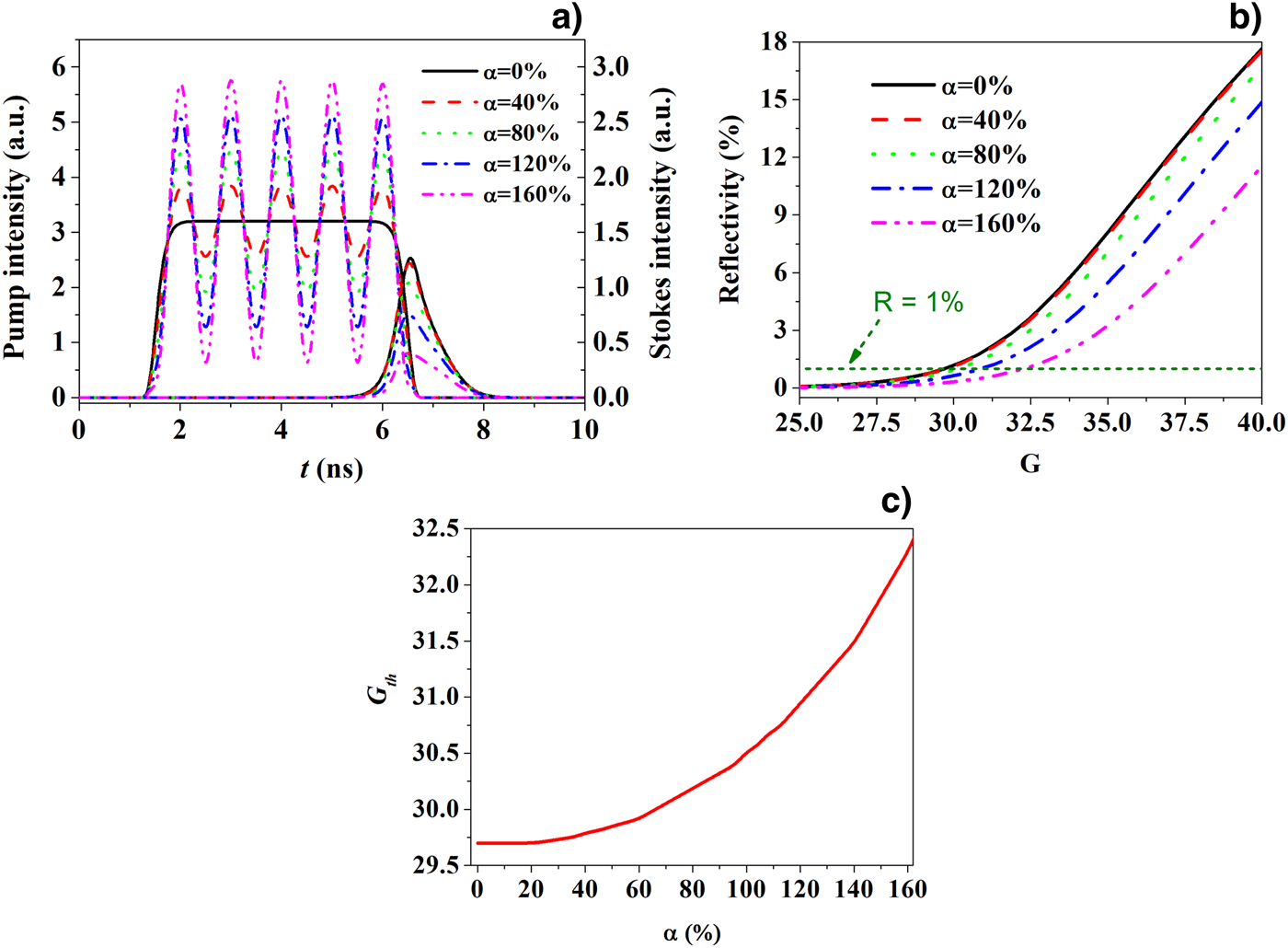
Fig. 1. The influence of distortion criterion α on the SBS generation. (a) Waveforms of pump and corresponding Stokes light, (b) reflectivity versus Brillouin gain, and (c) calculated SBS threshold with different α factors.

Figure 1a shows the waveforms of the pump and the correspond Stokes light with different distortion criteria and fixed average pump intensity (320 MW/cm²). It can be clearly seen from this figure that the intensity of Stokes pulse changes with the variation of α factor. The higher the value of α, the lower the intensity of the reflected Stokes light. It indicates that the temporal intensity modulation of the pump suppresses the generation of SBS to some extent. The SBS reflectivity versus the Brillouin gain with different α factors are drawn in Figure 1b. The horizontal green dash line denotes the level of SBS reflectivity of 1%, which is a well-known criteria for SBS threshold research. The intersections of this line and the reflectivity curves indicate the related SBS threshold with different value of α. We can see from this figure that the higher the level of the α factor, the higher SBS threshold happens.

To study the relationship between threshold gain and the distortion criterion, the SBS threshold G _th with α changes from 0 to 160% are calculated, and the results are shown in Figure 1c. When the intensity modulation factor is below about 30%, the SBS threshold remains almost stable with negligible increase. The threshold value increases exponentially with the α factor when it is higher than 30%. Then, we can draw a conclusion that when the temporal intensity modulation factor is below 30%, the generation of SBS effect will be not influenced. The reason why SBS threshold increase with α can be detailed as follows. The pump pulses shown in Figure 1a can be seen as a stack of five individual short pulses and a long base with a pulse duration of 5 ns. Pulse width of each sub-pulse is about 1 ns, whose related SBS threshold is higher than that of the 5 ns base. The percentage of sub-pulses increases linearly with α. Thus, the total energy reflectivity decreases and the SBS threshold increases with the increasing of α.

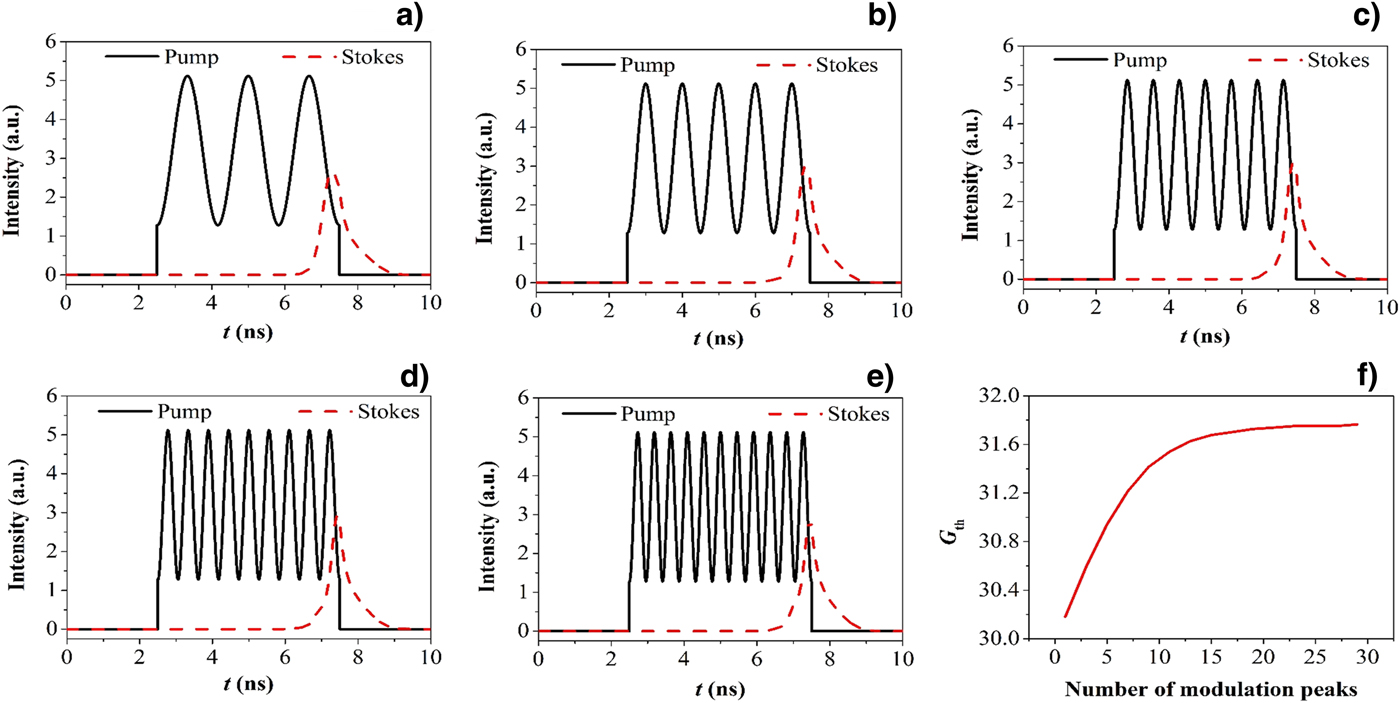
The modulation frequency of the sinusoidal modulated pump pulse can be described by the number of modulation peaks with a fixed pulse duration of 5 ns. For fixed pump average intensity (320 MW/cm²) and pulse width, the waveforms of pump and Stokes light was calculated and shown in Figure 2a–2e with 3, 5, 7, 9, and 11 modulation peaks. It can be seen from the figures that the duration of Stokes pulse shorten with the increase of modulation peaks, and the peak intensity of the Stokes pulse remains nearly the same. That is to say, the reflected energy decreases with the increase of modulation frequency of pump pulse with the same energy. Thus, the higher the modulation frequency, the higher the SBS threshold. The dependence of SBS threshold and the number of modulation peaks are shown in Figure 2f. This figure indicates that SBS threshold increases with the increase of modulation peaks when the number is below nearly 15, and remains stable with larger number of modulation peaks.

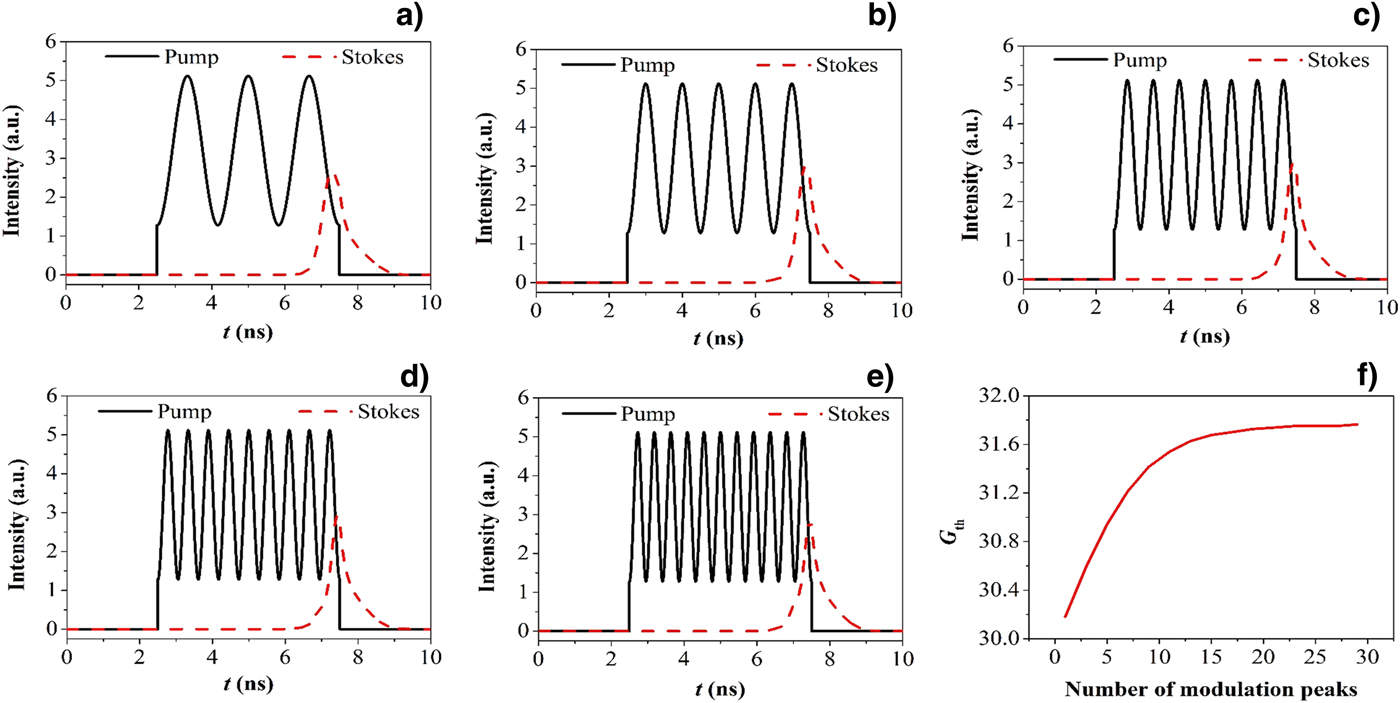
Fig. 2. The influence of modulation frequency (number of modulation peaks during a 5 ns square pump pulse) on the SBS generation.

The sinusoidal modulated pump pulse can be considered as a stack of several sub-pulses (see Fig. 2). Each of the sub-pulses excites SBS independently, and the threshold is determined by the total reflectivity. With the increase of the number of the modulation peaks, pulse duration of each peak drops and the transient effect becomes prominent. When the pump pulse width shortens toward the phonon lifetime of the Brillouin medium, the SBS threshold increases dependently (Su et al., Reference Su, Zhou, Lü, Wang, Luo and Xu2014). When the number of modulation peaks is larger than 15, the sub-pulse duration below three times the phonon lifetime and its variation range narrows, which leads to a smooth changing of the SBS threshold (see Fig. 2f).

The FM-to-AM effect caused sinusoidal modulated laser pulse is popular in high power laser systems (Hocquet et al., Reference Hocquet, Penninckx, Bordenave, Gouédard and Jaouën2008). When this kind of laser pulses is used as the pump source, the dependence of SBS threshold on the temporal modulation is necessary to be detailed. The above numerically calculated results illustrate clearly the relationship between SBS threshold and the modulation characteristic of pump pulses, which plays an important role in high power laser applications.