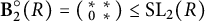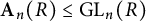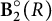1 Introduction
The finiteness length
![]() $\phi (G)$
of a group G is the supremum of the
$\phi (G)$
of a group G is the supremum of the
![]() $n \in \mathbb {Z}_{\geq 0}$
for which G admits an Eilenberg–MacLane space
$n \in \mathbb {Z}_{\geq 0}$
for which G admits an Eilenberg–MacLane space
![]() $K(G,1)$
with compact n skeleton. The finiteness length is a quasi-isometry invariant [Reference Alonso6] which can be interpreted as a tool measuring “how finite” G is, from the topological point of view. For instance, if G is either finite or of homotopical type
$K(G,1)$
with compact n skeleton. The finiteness length is a quasi-isometry invariant [Reference Alonso6] which can be interpreted as a tool measuring “how finite” G is, from the topological point of view. For instance, if G is either finite or of homotopical type
![]() $\text {F}$
—the latter meaning that G admits a compact
$\text {F}$
—the latter meaning that G admits a compact
![]() $K(G,1)$
—then
$K(G,1)$
—then
![]() $\phi (G) = \infty $
. Also, G is finitely presented if and only if
$\phi (G) = \infty $
. Also, G is finitely presented if and only if
![]() $\phi (G) \geq 2$
; see e.g., [Reference Ratcliffe46].
$\phi (G) \geq 2$
; see e.g., [Reference Ratcliffe46].
Throughout, R always denotes a commutative ring with unity. By a classical group, we mean an affine
![]() $\mathbb {Z}$
-group scheme
$\mathbb {Z}$
-group scheme
![]() $\mathcal {G}$
which is either
$\mathcal {G}$
which is either
![]() $ \operatorname {\textrm {GL}}_n$
for some
$ \operatorname {\textrm {GL}}_n$
for some
![]() $n \geq 2$
or a universal Chevalley–Demazure group scheme
$n \geq 2$
or a universal Chevalley–Demazure group scheme
![]() $\mathcal {G}_{\Phi }^{\text {sc}}$
, such as
$\mathcal {G}_{\Phi }^{\text {sc}}$
, such as
![]() $\mathcal {G}_{\text {A}_{n-1}}^{\text {sc}} = \operatorname {\textrm {SL}}_n$
or
$\mathcal {G}_{\text {A}_{n-1}}^{\text {sc}} = \operatorname {\textrm {SL}}_n$
or
![]() $\mathcal {G}_{\text {C}_{n}}^{\text {sc}} = \text {Sp}_{2n}$
; refer e.g., to [Reference Vavilov and Plotkin58] for an extensive survey on Chevalley–Demazure groups over arbitrary rings. In this work, we are interested in the groups of R-points of certain soluble subgroups of
$\mathcal {G}_{\text {C}_{n}}^{\text {sc}} = \text {Sp}_{2n}$
; refer e.g., to [Reference Vavilov and Plotkin58] for an extensive survey on Chevalley–Demazure groups over arbitrary rings. In this work, we are interested in the groups of R-points of certain soluble subgroups of
![]() $\mathcal {G}$
. An important role will be played by the Borel subgroup of rank one,
$\mathcal {G}$
. An important role will be played by the Borel subgroup of rank one,
We shall also consider the affine groups
![]() $\mathbb {A}\text {ff} \cong \left ( \begin {smallmatrix} * & * \\ 0 & 1 \end {smallmatrix} \right ) \leq \operatorname {\textrm {GL}}_2$
and
$\mathbb {A}\text {ff} \cong \left ( \begin {smallmatrix} * & * \\ 0 & 1 \end {smallmatrix} \right ) \leq \operatorname {\textrm {GL}}_2$
and
![]() $\mathbb {A}\text {ff}_- \cong \left ( \begin {smallmatrix} 1 & * \\ 0 & * \end {smallmatrix} \right ) \leq \operatorname {\textrm {GL}}_2$
.
$\mathbb {A}\text {ff}_- \cong \left ( \begin {smallmatrix} 1 & * \\ 0 & * \end {smallmatrix} \right ) \leq \operatorname {\textrm {GL}}_2$
.
The purpose of this paper is twofold. First, using algebraic methods, we give an upper bound on the finiteness length of groups with certain soluble R-representations, including many parabolic subgroups of classical groups. Second, we record the current state of knowledge on the finiteness lengths of Abels’ soluble matrix groups
![]() $\left \{ \textbf {A}_n(R) \right \}_{n \geq 2}$
. This includes a different, topological proof of an unpublished result of Strebel, who classified which
$\left \{ \textbf {A}_n(R) \right \}_{n \geq 2}$
. This includes a different, topological proof of an unpublished result of Strebel, who classified which
![]() $\textbf {A}_n(R)$
are finitely presented. Our main results are the following.
$\textbf {A}_n(R)$
are finitely presented. Our main results are the following.
Theorem 1.1 Let
![]() $\mathcal {G}$
be either classical or one of the affine groups
$\mathcal {G}$
be either classical or one of the affine groups
![]() $\mathbb {A}\text {ff}$
,
$\mathbb {A}\text {ff}$
,
![]() $\mathbb {A}\text {ff}_-$
. Let also
$\mathbb {A}\text {ff}_-$
. Let also
![]() $\mathfrak {X}$
and
$\mathfrak {X}$
and
![]() $\mathcal {H}$
denote, respectively, a unipotent root subgroup and a maximal torus of
$\mathcal {H}$
denote, respectively, a unipotent root subgroup and a maximal torus of
![]() $\mathcal {G}$
. (In the affine cases,
$\mathcal {G}$
. (In the affine cases,
![]() $\mathfrak {X} \rtimes \mathcal {H}$
is just the whole group scheme.) Suppose a group G admits a representation
$\mathfrak {X} \rtimes \mathcal {H}$
is just the whole group scheme.) Suppose a group G admits a representation
![]() $\rho : G \to \mathcal {G}(R)$
whose image is
$\rho : G \to \mathcal {G}(R)$
whose image is
![]() $\text {Im}(\rho ) = \mathfrak {X}(R) \rtimes \mathcal {H}(R)$
and such that the sequence
$\text {Im}(\rho ) = \mathfrak {X}(R) \rtimes \mathcal {H}(R)$
and such that the sequence
![]() $\ker (\rho ) \hookrightarrow G \twoheadrightarrow \text {Im}(\rho )$
splits. Then
$\ker (\rho ) \hookrightarrow G \twoheadrightarrow \text {Im}(\rho )$
splits. Then
![]() $\phi (G) \leq \phi (\textbf {B}_2^{\circ }(R))$
.
$\phi (G) \leq \phi (\textbf {B}_2^{\circ }(R))$
.
Theorem 1.2 If R is not finitely generated as a ring, then
![]() $\phi (\textbf {A}_n(R)) = 0$
for all
$\phi (\textbf {A}_n(R)) = 0$
for all
![]() $n \geq 2$
. Otherwise, the following hold.
$n \geq 2$
. Otherwise, the following hold.
-
(1)
 $\phi (\textbf {A}_2(R))> 0$
if and only if R is finitely generated as a
$\phi (\textbf {A}_2(R))> 0$
if and only if R is finitely generated as a
 $\mathbb {Z}$
-module, in which case
$\mathbb {Z}$
-module, in which case
 $\phi (\textbf {A}_n(R)) = \phi (\textbf {B}_2^{\circ }(R)) = \infty $
for all
$\phi (\textbf {A}_n(R)) = \phi (\textbf {B}_2^{\circ }(R)) = \infty $
for all
 $n \geq 2$
.
$n \geq 2$
. -
(2) If R is infinitely generated as a
 $\mathbb {Z}$
-module, then
$\mathbb {Z}$
-module, then
 $\phi (\textbf {A}_3(R)) =~\min \{ 1, \phi (\textbf {B}_2^{\circ }(R)) \}$
.
$\phi (\textbf {A}_3(R)) =~\min \{ 1, \phi (\textbf {B}_2^{\circ }(R)) \}$
. -
(3) If
 $n \geq 4$
and R is infinitely generated as a
$n \geq 4$
and R is infinitely generated as a
 $\mathbb {Z}$
-module, then
$\mathbb {Z}$
-module, then
 $\phi (\textbf {A}_n(R))\leq \phi (\textbf {B}_2^{\circ }(R))$
and, given
$\phi (\textbf {A}_n(R))\leq \phi (\textbf {B}_2^{\circ }(R))$
and, given
 $\ell \in \{ 1,2\}$
, one has
$\ell \in \{ 1,2\}$
, one has
 $\phi (\textbf {A}_n(R)) \geq \ell $
whenever
$\phi (\textbf {A}_n(R)) \geq \ell $
whenever
 $\phi (\textbf {B}_2^{\circ }(R)) \geq \ell $
.
$\phi (\textbf {B}_2^{\circ }(R)) \geq \ell $
.
This article is organized as follows. In Sections 1.1 and 1.2, we motivate the main Theorems 1.1 and 1.2, respectively. Section 1.1 includes a new proof of Bux’s main result in [Reference Bux22], and in Section 1.2, we state a conjecture about the finiteness lengths of Abels’ groups. We recall in Section 2 some standard facts to be used throughout. Theorems 1.1 and 1.2 are proved in Sections 3 and 4, respectively.
1.1 Theorem 1.1—motivation and examples
The problem of determining the finiteness length of an S-arithmetic group is an ongoing challenge; see, for instance, the introductions of [Reference Bux22, Reference Bux, Köhl and Witzel25, Reference Bux and Wortman27] for an overview.
Suppose
![]() $\mathcal {B}$
is a Borel subgroup of a Chevalley–Demazure group and let
$\mathcal {B}$
is a Borel subgroup of a Chevalley–Demazure group and let
![]() $\mathcal {O}_S$
be a Dedekind ring of arithmetic type and positive characteristic, such as
$\mathcal {O}_S$
be a Dedekind ring of arithmetic type and positive characteristic, such as
![]() $\mathbb {F}_q[t]$
or
$\mathbb {F}_q[t]$
or
![]() $\mathbb {F}_q[t,t^{-1},(t-1)^{-1}]$
. In [Reference Bux22], Bux showed that the S-arithmetic group
$\mathbb {F}_q[t,t^{-1},(t-1)^{-1}]$
. In [Reference Bux22], Bux showed that the S-arithmetic group
![]() $\mathcal {B}(\mathcal {O}_S)$
satisfies the equality
$\mathcal {B}(\mathcal {O}_S)$
satisfies the equality
![]() $\phi (\mathcal {B}(\mathcal {O}_S)) = \vert S\vert - 1$
. The first step of his geometric proof [Reference Bux22, Theorem 5.1] yields the upper bound
$\phi (\mathcal {B}(\mathcal {O}_S)) = \vert S\vert - 1$
. The first step of his geometric proof [Reference Bux22, Theorem 5.1] yields the upper bound
![]() $\phi (\mathcal {B}(\mathcal {O}_S)) \leq \vert S\vert - 1$
. The number
$\phi (\mathcal {B}(\mathcal {O}_S)) \leq \vert S\vert - 1$
. The number
![]() $\vert S\vert - 1$
, in turn, had already been observed to equal
$\vert S\vert - 1$
, in turn, had already been observed to equal
![]() $\phi (\textbf {B}_2^{\circ }(\mathcal {O}_S))$
[Reference Bux22, Corollary 3.5]. Our inspiration for Theorem 1.1 was to give a simple algebraic explanation for the inequality
$\phi (\textbf {B}_2^{\circ }(\mathcal {O}_S))$
[Reference Bux22, Corollary 3.5]. Our inspiration for Theorem 1.1 was to give a simple algebraic explanation for the inequality
![]() $\phi (\mathcal {B}(\mathcal {O}_S)) \leq \phi (\textbf {B}_2^{\circ }(\mathcal {O}_S))$
since this would likely extend to larger classes of rings. And this is in fact the case; see Section 3 for the proof of Theorem 1.1. We also expect Theorem 1.1 to have an appropriate analog in the context of Kac–Moody groups.
$\phi (\mathcal {B}(\mathcal {O}_S)) \leq \phi (\textbf {B}_2^{\circ }(\mathcal {O}_S))$
since this would likely extend to larger classes of rings. And this is in fact the case; see Section 3 for the proof of Theorem 1.1. We also expect Theorem 1.1 to have an appropriate analog in the context of Kac–Moody groups.
In the arithmetic set-up, we combine Theorem 1.1 with results due to Bestvina et al. [Reference Bestvina, Eskin and Wortman11] and Gandini [Reference Gandini36] to obtain the following generalization of Bux’s equality.
Theorem 1.3 Let
![]() $\textbf {P}$
be a proper parabolic subgroup of a noncommutative, connected, reductive, split linear algebraic group
$\textbf {P}$
be a proper parabolic subgroup of a noncommutative, connected, reductive, split linear algebraic group
![]() $\textbf {G}$
defined over a global field
$\textbf {G}$
defined over a global field
![]() $\mathbb {K}$
. Denote by
$\mathbb {K}$
. Denote by
![]() $\textbf {U}_{\textbf {P}}$
the unipotent radical of
$\textbf {U}_{\textbf {P}}$
the unipotent radical of
![]() $\textbf {P}$
and by
$\textbf {P}$
and by
![]() $\textbf {T}_{\textbf {P}}$
a maximal torus of
$\textbf {T}_{\textbf {P}}$
a maximal torus of
![]() $\textbf {G}$
contained in
$\textbf {G}$
contained in
![]() $\textbf {P}$
. For any S-arithmetic subgroup
$\textbf {P}$
. For any S-arithmetic subgroup
![]() $\Gamma \leq \textbf {U}_{\textbf {P}} \rtimes \textbf {T}_{\textbf {P}}$
, the following inequalities hold.
$\Gamma \leq \textbf {U}_{\textbf {P}} \rtimes \textbf {T}_{\textbf {P}}$
, the following inequalities hold.
Moreover, if
![]() $\mathbb {K}$
has positive characteristic, then
$\mathbb {K}$
has positive characteristic, then
![]() $\phi (\Gamma ) = \phi(\textbf{B}_2^{\circ}(\mathcal{O}_S)) = \vert S\vert - 1$
.
$\phi (\Gamma ) = \phi(\textbf{B}_2^{\circ}(\mathcal{O}_S)) = \vert S\vert - 1$
.
Proof Standard arguments allow us to assume, without loss of generality, that
![]() $\textbf {G}$
is classical; see e.g., the steps in [Reference Behr9, Section 2.6(c)] and pass over to parabolic subgroups—notice that Satz 1 cited by Behr holds regardless of characteristic. Since S-arithmetic subgroups of a given linear algebraic group are commensurable, we may further restrict ourselves to the (now well-defined) group of
$\textbf {G}$
is classical; see e.g., the steps in [Reference Behr9, Section 2.6(c)] and pass over to parabolic subgroups—notice that Satz 1 cited by Behr holds regardless of characteristic. Since S-arithmetic subgroups of a given linear algebraic group are commensurable, we may further restrict ourselves to the (now well-defined) group of
![]() $\mathcal {O}_S$
-points
$\mathcal {O}_S$
-points
![]() $\textbf {U}_{\textbf {P}}(\mathcal {O}_S) \rtimes \textbf {T}_{\textbf {P}}(\mathcal {O}_S) \leq \textbf {G}(\mathcal {O}_S)$
. In the set-up above, the first inequality follows from [Reference Bestvina, Eskin and Wortman11, Theorem 6] and Lemma 2.1 since
$\textbf {U}_{\textbf {P}}(\mathcal {O}_S) \rtimes \textbf {T}_{\textbf {P}}(\mathcal {O}_S) \leq \textbf {G}(\mathcal {O}_S)$
. In the set-up above, the first inequality follows from [Reference Bestvina, Eskin and Wortman11, Theorem 6] and Lemma 2.1 since
![]() $\Gamma $
is an extension of
$\Gamma $
is an extension of
![]() $\textbf {U}_{\textbf {P}}(\mathcal {O}_S) \rtimes \textbf {A}_{\textbf {P}}(\mathcal {O}_S)$
by a finitely generated abelian group (due to Dirichlet’s unit theorem), where
$\textbf {U}_{\textbf {P}}(\mathcal {O}_S) \rtimes \textbf {A}_{\textbf {P}}(\mathcal {O}_S)$
by a finitely generated abelian group (due to Dirichlet’s unit theorem), where
![]() $\textbf {A}_{\textbf {P}}$
is the maximal torus in the center of the Levi factor of
$\textbf {A}_{\textbf {P}}$
is the maximal torus in the center of the Levi factor of
![]() $\textbf {P}$
. The second inequality is a direct consequence of our Theorem 1.1.
$\textbf {P}$
. The second inequality is a direct consequence of our Theorem 1.1.
For the last claim, suppose
![]() $ \operatorname {\textrm {char}}(\mathbb {K})> 0$
. Since
$ \operatorname {\textrm {char}}(\mathbb {K})> 0$
. Since
![]() $\textbf {B}_2^{\circ }(\mathcal {O}_S) \supseteq \left ( \begin {smallmatrix} 1 & * \\ 0 & 1 \end {smallmatrix} \right ) \cong (\mathcal {O}_S,+)$
, one has that
$\textbf {B}_2^{\circ }(\mathcal {O}_S) \supseteq \left ( \begin {smallmatrix} 1 & * \\ 0 & 1 \end {smallmatrix} \right ) \cong (\mathcal {O}_S,+)$
, one has that
![]() $\textbf {B}_2^{\circ }(\mathcal {O}_S)$
has no bounds on the orders of its finite subgroups because
$\textbf {B}_2^{\circ }(\mathcal {O}_S)$
has no bounds on the orders of its finite subgroups because
![]() $\mathcal {O}_S$
contains infinite dimensional vector spaces over the prime field of
$\mathcal {O}_S$
contains infinite dimensional vector spaces over the prime field of
![]() $\mathbb {K}$
[Reference O'Meara45, Section 23]. But
$\mathbb {K}$
[Reference O'Meara45, Section 23]. But
![]() $\textbf {B}_2^{\circ }(\mathcal {O}_S)$
acts by cell-permuting homeomorphisms on the product of
$\textbf {B}_2^{\circ }(\mathcal {O}_S)$
acts by cell-permuting homeomorphisms on the product of
![]() $\vert S \vert $
Bruhat–Tits trees, each such tree being associated to the locally compact group
$\vert S \vert $
Bruhat–Tits trees, each such tree being associated to the locally compact group
![]() $ \operatorname {\textrm {SL}}_2( \operatorname {\textrm {Frac}}(\mathcal {O}_S)_v)$
attached to the place
$ \operatorname {\textrm {SL}}_2( \operatorname {\textrm {Frac}}(\mathcal {O}_S)_v)$
attached to the place
![]() $v \in S$
; cf. [Reference Serre51]. Since the stabilizers of this action are finite [Reference Bruhat and Tits21, Section 3.3], it follows that
$v \in S$
; cf. [Reference Serre51]. Since the stabilizers of this action are finite [Reference Bruhat and Tits21, Section 3.3], it follows that
![]() $\textbf {B}_2^{\circ }(\mathcal {O}_S)$
belongs to Kropholler’s
$\textbf {B}_2^{\circ }(\mathcal {O}_S)$
belongs to Kropholler’s
![]() $\textbf {H}\mathfrak {F}$
class and thus Gandini’s theorem [Reference Gandini36] applies, yielding
$\textbf {H}\mathfrak {F}$
class and thus Gandini’s theorem [Reference Gandini36] applies, yielding
![]() $\phi (\textbf {B}_2^{\circ }(\mathcal {O}_S)) \leq \vert S \vert - 1$
.▪
$\phi (\textbf {B}_2^{\circ }(\mathcal {O}_S)) \leq \vert S \vert - 1$
.▪
An alternative proof of the inequality
![]() $\phi (\Gamma ) \leq \vert S\vert -1$
(positive characteristic) was announced by Wortman [Reference Bestvina, Eskin and Wortman11, p. 2169]. While giving a stronger version of Bux’s result, Theorem 1.3 furnishes further examples of nonmetabelian soluble linear groups with prescribed finiteness properties. To the best of our knowledge, the only known cases were Abels–Witzel’s groups (see Section 4.3 and [Reference Witzel59]) and Bux’s own examples [Reference Bux22].
$\phi (\Gamma ) \leq \vert S\vert -1$
(positive characteristic) was announced by Wortman [Reference Bestvina, Eskin and Wortman11, p. 2169]. While giving a stronger version of Bux’s result, Theorem 1.3 furnishes further examples of nonmetabelian soluble linear groups with prescribed finiteness properties. To the best of our knowledge, the only known cases were Abels–Witzel’s groups (see Section 4.3 and [Reference Witzel59]) and Bux’s own examples [Reference Bux22].
It is natural to wonder which properties of S-arithmetic subgroups, or of associated symmetric spaces and buildings, are intrinsic to the underlying algebraic group and thus independent of the field of definition. (Compare e.g., cohomological finiteness properties [Reference Borel and Serre15, Reference Bux, Köhl and Witzel25] and distortion dimension [Reference Bestvina, Eskin and Wortman11, Reference Bux and Wortman27] in the semisimple case.) For our groups, although the work of Tiemeyer [Reference Tiemeyer55, Theorem 4.3 and (the proof of) Theorem 4.4] implies the stronger result
![]() $\phi (\Gamma ) = \infty $
when
$\phi (\Gamma ) = \infty $
when
![]() $\mathbb {K}$
has characteristic zero, Theorem 1.3 is advantageous in the sense that its inequalities are uniform, i.e., independent of characteristic.
$\mathbb {K}$
has characteristic zero, Theorem 1.3 is advantageous in the sense that its inequalities are uniform, i.e., independent of characteristic.
Examples of nonsoluble groups that fit into the framework of Theorems 1.1 and 1.3 arise, for instance, from parabolic subgroups of classical groups.
Example 1.4 Recall that the (standard) parabolic subgroups of
![]() $ \operatorname {\textrm {SL}}_n$
over a field
$ \operatorname {\textrm {SL}}_n$
over a field
![]() $\mathbb {K}$
are the subgroups of block (upper or lower) triangular matrices. Pictorially, a parabolic
$\mathbb {K}$
are the subgroups of block (upper or lower) triangular matrices. Pictorially, a parabolic
![]() $\mathcal {P} \leq \operatorname {\textrm {SL}}_n$
is e.g., of the form
$\mathcal {P} \leq \operatorname {\textrm {SL}}_n$
is e.g., of the form

where
![]() $k \leq n$
is the number of blocks. In particular,
$k \leq n$
is the number of blocks. In particular,
![]() $\mathcal {P}$
contains the diagonal subgroup—the standard maximal torus—of
$\mathcal {P}$
contains the diagonal subgroup—the standard maximal torus—of
![]() $ \operatorname {\textrm {SL}}_n$
, and each
$ \operatorname {\textrm {SL}}_n$
, and each
![]() $ {\textbf n_i \times \textbf n_i}$
block on the diagonal with
$ {\textbf n_i \times \textbf n_i}$
block on the diagonal with
![]() $n_i> 1$
is isomorphic to
$n_i> 1$
is isomorphic to
![]() $ \operatorname {\textrm {SL}}_{n_i}$
. Now suppose
$ \operatorname {\textrm {SL}}_{n_i}$
. Now suppose
![]() $\mathbb {K}$
is a global function field, i.e., a finite extension of
$\mathbb {K}$
is a global function field, i.e., a finite extension of
![]() $\mathbb {F}_p(t)$
for some prime p. If there exists an index
$\mathbb {F}_p(t)$
for some prime p. If there exists an index
![]() $j < k$
for which
$j < k$
for which
![]() $n_j = 1 = n_{j+1}$
, then Theorem 1.3 yields
$n_j = 1 = n_{j+1}$
, then Theorem 1.3 yields
![]() $\phi (\Gamma ) < \vert S\vert $
for any S-arithmetic subgroup
$\phi (\Gamma ) < \vert S\vert $
for any S-arithmetic subgroup
![]() $\Gamma \leq \mathcal {P}$
.
$\Gamma \leq \mathcal {P}$
.
Computing the finiteness lengths of S-arithmetic parabolics in positive characteristic is an open problem. Example 1.4 provides a new result in this direction.
Going back to arbitrary base rings, we stress that results on the finiteness length of non-S-arithmetic discrete linear groups are scarce. The most prominent examples were obtained by Bux–Mohammadi–Wortman [Reference Bux, Mohammadi and Wortman26] and Gandini [Reference Gandini36, Corollary 4.1] using Bruhat–Tits buildings, and by Kropholler–Mullaney [Reference Kropholler and Mullaney41] building upon works of Åberg and Groves–Kochloukova.
As shown, the class of groups to which Theorem 1.1 applies is quite large. One can notably summarize many such examples via the so-called groups of type (R). These were studied by Demazure and Grothendieck in the 1960s and generalize parabolic subgroups of reductive affine group schemes; see [Reference Demazure and Grothendieck33, Exposé XXII, Chapitre 5].
Corollary 1.5 Let
![]() $\textbf {G}$
be an affine group scheme defined over
$\textbf {G}$
be an affine group scheme defined over
![]() $\mathbb {Z}$
and let
$\mathbb {Z}$
and let
![]() $\textbf {H} \leq \mathcal {G}$
be a
$\textbf {H} \leq \mathcal {G}$
be a
![]() $\mathbb {Z}$
-subgroup, of type (R) with soluble geometric fibers, of a classical group
$\mathbb {Z}$
-subgroup, of type (R) with soluble geometric fibers, of a classical group
![]() $\mathcal {G}$
. If there exists a
$\mathcal {G}$
. If there exists a
![]() $\mathbb {Z}$
-retract
$\mathbb {Z}$
-retract
![]() $r : \textbf {G} \to \textbf {H}$
, then
$r : \textbf {G} \to \textbf {H}$
, then
![]() $\phi (\textbf {G}(R)) \leq \phi (\textbf {B}_2^{\circ }(R))$
for every commutative ring R with unity.
$\phi (\textbf {G}(R)) \leq \phi (\textbf {B}_2^{\circ }(R))$
for every commutative ring R with unity.
Proof This follows immediately from Theorem 1.1 and [Reference Demazure and Grothendieck33, Exposé XXII, Proposition 5.6.1 and Corollaire 5.6.5].▪
The following gives a concrete series of finitely generated, nonamenable, nonarithmetic groups with prescribed upper bounds on the finiteness length. Other such examples include (Stallings–Bieri–)Bestvina–Brady’s groups and certain members of the family of generalized Thompson groups; cf. [Reference Skipper, Witzel and Zaremsky52] and references therein for an overview.
Example 1.6 Similarly to Example 1.4, let
![]() $\mathcal {P}$
be a parabolic
$\mathcal {P}$
be a parabolic
![]() $\mathbb {Z}$
-subscheme of
$\mathbb {Z}$
-subscheme of
![]() $ \operatorname {\textrm {SL}}_n$
with k diagonal blocks of sizes
$ \operatorname {\textrm {SL}}_n$
with k diagonal blocks of sizes
![]() $n_j$
, with at least one block of size at least two and with at least one index
$n_j$
, with at least one block of size at least two and with at least one index
![]() $j < k$
for which
$j < k$
for which
![]() $n_j = 1 = n_{j+1}$
. For instance, we can take
$n_j = 1 = n_{j+1}$
. For instance, we can take
![]() $\mathcal {P}$
to be
$\mathcal {P}$
to be
 $$ \begin{align*} \left( \begin{smallmatrix} * & * & * & * \\ * & * & * & * \\ 0 & 0 & * & * \\ 0 & 0 & 0 & * \end{smallmatrix} \right) \leq \operatorname{\textrm{SL}}_4 \, \text{ or } \, \left( \begin{smallmatrix} * & * & * & * & * & * & * \\ * & * & * & * & * & * & * \\ * & * & * & * & * & * & * \\ 0 & 0 & 0 & * & * & * & * \\ 0 & 0 & 0 & 0 & * & * & * \\ 0 & 0 & 0 & 0 & 0 & * & * \\ 0 & 0 & 0 & 0 & 0 & * & * \end{smallmatrix} \right) \leq \operatorname{\textrm{SL}}_7. \end{align*} $$
$$ \begin{align*} \left( \begin{smallmatrix} * & * & * & * \\ * & * & * & * \\ 0 & 0 & * & * \\ 0 & 0 & 0 & * \end{smallmatrix} \right) \leq \operatorname{\textrm{SL}}_4 \, \text{ or } \, \left( \begin{smallmatrix} * & * & * & * & * & * & * \\ * & * & * & * & * & * & * \\ * & * & * & * & * & * & * \\ 0 & 0 & 0 & * & * & * & * \\ 0 & 0 & 0 & 0 & * & * & * \\ 0 & 0 & 0 & 0 & 0 & * & * \\ 0 & 0 & 0 & 0 & 0 & * & * \end{smallmatrix} \right) \leq \operatorname{\textrm{SL}}_7. \end{align*} $$
Following Kropholler–Mullaney [Reference Kropholler and Mullaney41], fix
![]() $\ell \in \mathbb {N}$
and let
$\ell \in \mathbb {N}$
and let
![]() $R_{\ell }$
be the integral domain
$R_{\ell }$
be the integral domain
The groups
![]() $\mathcal {P}(R_{\ell })$
are nonamenable because they contain
$\mathcal {P}(R_{\ell })$
are nonamenable because they contain
![]() $ \operatorname {\textrm {SL}}_2(\mathbb {Z})$
, and it is an exercise (e.g., using the relations from Section 2) to check that they are finitely generated. Corollary 1.5 gives
$ \operatorname {\textrm {SL}}_2(\mathbb {Z})$
, and it is an exercise (e.g., using the relations from Section 2) to check that they are finitely generated. Corollary 1.5 gives
![]() $\phi (\mathcal {P}(R_{\ell })) < \ell + 2$
since
$\phi (\mathcal {P}(R_{\ell })) < \ell + 2$
since
![]() $\phi (\textbf {B}_2^{\circ }(R_{\ell })) = \ell + 1$
by [Reference Kochloukova40, Reference Kropholler and Mullaney41].
$\phi (\textbf {B}_2^{\circ }(R_{\ell })) = \ell + 1$
by [Reference Kochloukova40, Reference Kropholler and Mullaney41].
We remark that Theorem 1.1 admits a slight geometric modification by weakening the hypothesis on the map
![]() $G \to \mathfrak {X}(R) \rtimes \mathcal {H}(R)$
at the cost of an extra assumption on the base ring R; see Section 3.1 for details.
$G \to \mathfrak {X}(R) \rtimes \mathcal {H}(R)$
at the cost of an extra assumption on the base ring R; see Section 3.1 for details.
1.2 Theorem 1.2—the group schemes of Herbert Abels
For every natural number
![]() $n \geq 2$
, consider the following
$n \geq 2$
, consider the following
![]() $\mathbb {Z}$
-group scheme.
$\mathbb {Z}$
-group scheme.
 $$ \begin{align*} \textbf{A}_n := \left( \begin{smallmatrix} 1 & * & \cdots & \cdots & * \\ 0 & * & \ddots & & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots & 0 & * & * \\ 0 & \cdots & \cdots & 0 & 1 \end{smallmatrix} \right) \leq \operatorname{\textrm{GL}}_n. \end{align*} $$
$$ \begin{align*} \textbf{A}_n := \left( \begin{smallmatrix} 1 & * & \cdots & \cdots & * \\ 0 & * & \ddots & & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots & 0 & * & * \\ 0 & \cdots & \cdots & 0 & 1 \end{smallmatrix} \right) \leq \operatorname{\textrm{GL}}_n. \end{align*} $$
Interest in the infinite family
![]() $\left \{ \textbf {A}_n \right \}_{n \geq 2}$
, nowadays known as Abels’ groups, was sparked in the late 1970s when Abels [Reference Abels1] published a proof of finite presentability of the group
$\left \{ \textbf {A}_n \right \}_{n \geq 2}$
, nowadays known as Abels’ groups, was sparked in the late 1970s when Abels [Reference Abels1] published a proof of finite presentability of the group
![]() $\textbf {A}_4(\mathbb {Z}[1/p])$
, where p is any prime number; see also [Reference Abels2, Sections 0.2.7 and 0.2.14]. Abels’ groups emerged as counterexamples to long-standing problems in group theory—see, for instance, [Reference Benli, Grigorchuk and de la Harpe10, Proposition A5]—and later became a source to construct groups with peculiar properties; cf. [Reference Becker, Lubotzky and Thom8, Reference Bieri and Strebel14, Reference Carrión, Dadarlat and Eckhardt28, Reference de Cornulier, Guyot and Pitsch31] for recent examples.
$\textbf {A}_4(\mathbb {Z}[1/p])$
, where p is any prime number; see also [Reference Abels2, Sections 0.2.7 and 0.2.14]. Abels’ groups emerged as counterexamples to long-standing problems in group theory—see, for instance, [Reference Benli, Grigorchuk and de la Harpe10, Proposition A5]—and later became a source to construct groups with peculiar properties; cf. [Reference Becker, Lubotzky and Thom8, Reference Bieri and Strebel14, Reference Carrión, Dadarlat and Eckhardt28, Reference de Cornulier, Guyot and Pitsch31] for recent examples.
Regarding their finiteness lengths, not long after Abels announced that
![]() $\phi (\textbf {A}_4(\mathbb {Z} [1/p])) \geq 2$
, Strebel went on to generalize this in the handwritten notes [Reference Strebel54], which never got to be published and only came to our attention after Theorem 1.2 was established. He actually gives necessary and sufficient conditions for Abels–Strebel’s groups, defined by
$\phi (\textbf {A}_4(\mathbb {Z} [1/p])) \geq 2$
, Strebel went on to generalize this in the handwritten notes [Reference Strebel54], which never got to be published and only came to our attention after Theorem 1.2 was established. He actually gives necessary and sufficient conditions for Abels–Strebel’s groups, defined by
to have
![]() $\phi (A_n(R,Q)) \geq 2$
. (Note that
$\phi (A_n(R,Q)) \geq 2$
. (Note that
![]() $A_n(R,R^{\times }) = \textbf {A}_n(R)$
.) It had been announced by Remeslennikov [Reference Abels1, p. 210] that
$A_n(R,R^{\times }) = \textbf {A}_n(R)$
.) It had been announced by Remeslennikov [Reference Abels1, p. 210] that
![]() $\textbf {A}_4(\mathbb {Z}[x,x^{-1},(x+1)^{-1}])$
admits a finite presentation—a similar example is treated in detail in Strebel’s manuscript. Shortly thereafter, Bieri [Reference Bieri12] observed that
$\textbf {A}_4(\mathbb {Z}[x,x^{-1},(x+1)^{-1}])$
admits a finite presentation—a similar example is treated in detail in Strebel’s manuscript. Shortly thereafter, Bieri [Reference Bieri12] observed that
![]() $\phi (\textbf {A}_n(\mathbb {Z}[1/p])) \leq n-2$
.
$\phi (\textbf {A}_n(\mathbb {Z}[1/p])) \leq n-2$
.
In the mid 1980s, Holz and Lyul’ko proved independently that
![]() $\textbf {A}_n(\mathbb {Z}[1/p])$
and
$\textbf {A}_n(\mathbb {Z}[1/p])$
and
![]() $\textbf {A}_n(\mathbb {Z}[1/m])$
, respectively, are finitely presented as well—for all
$\textbf {A}_n(\mathbb {Z}[1/m])$
, respectively, are finitely presented as well—for all
![]() $n, m, p \in \mathbb {N}$
with
$n, m, p \in \mathbb {N}$
with
![]() $n \geq 4$
and p prime [Reference Holz39, Anhang], [Reference Lyul'ko42]. Their techniques differ from Strebel’s in that they consider large subgroups of
$n \geq 4$
and p prime [Reference Holz39, Anhang], [Reference Lyul'ko42]. Their techniques differ from Strebel’s in that they consider large subgroups of
![]() $\textbf {A}_n$
and relations among them to check for finite presentability of the overgroup. Holz [Reference Holz39] pushed the theory further by giving the first example of a soluble, nonmetabelian group of finiteness length exactly three, namely
$\textbf {A}_n$
and relations among them to check for finite presentability of the overgroup. Holz [Reference Holz39] pushed the theory further by giving the first example of a soluble, nonmetabelian group of finiteness length exactly three, namely
![]() $\textbf {A}_5(\mathbb {Z}[1/p])$
. Abels–Brown [Reference Abels and Brown3] later showed that
$\textbf {A}_5(\mathbb {Z}[1/p])$
. Abels–Brown [Reference Abels and Brown3] later showed that
![]() $\phi (\textbf {A}_n(\mathbb {Z}[1/p])) \geq n-2$
. (This actually holds in greater generality; see Section 4.3.) In [Reference Witzel59], Witzel generalizes the family
$\phi (\textbf {A}_n(\mathbb {Z}[1/p])) \geq n-2$
. (This actually holds in greater generality; see Section 4.3.) In [Reference Witzel59], Witzel generalizes the family
![]() $\left \{ \textbf {A}_n \right \}_{n\geq 2}$
and proves that such groups over
$\left \{ \textbf {A}_n \right \}_{n\geq 2}$
and proves that such groups over
![]() $\mathbb {Z}[1/p]$
for p an odd prime have, in addition, varying Bredon finiteness properties.
$\mathbb {Z}[1/p]$
for p an odd prime have, in addition, varying Bredon finiteness properties.
Besides the above examples in characteristic zero and Strebel’s manuscript, the only published case of a finitely presented Abels’ group over a torsion ring is also S-arithmetic. In [Reference de Cornulier and Tessera32], Cornulier and Tessera prove, among other things, that
![]() $\phi (\textbf {A}_4(\mathbb {F}_p[t,t^{-1},(t-1)^{-1}])) \geq 2$
. They remark that
$\phi (\textbf {A}_4(\mathbb {F}_p[t,t^{-1},(t-1)^{-1}])) \geq 2$
. They remark that
![]() $\phi (\textbf {A}_4(\mathbb {F}_p[t])) = 0$
and
$\phi (\textbf {A}_4(\mathbb {F}_p[t])) = 0$
and
![]() $\phi (\textbf {A}_4(\mathbb {F}_p[t,t^{-1}])) = 1$
, and point out that similar results, including the one on finite presentability over
$\phi (\textbf {A}_4(\mathbb {F}_p[t,t^{-1}])) = 1$
, and point out that similar results, including the one on finite presentability over
![]() $\mathbb {F}_p[t,t^{-1},(t-1)^{-1}]$
, should hold for
$\mathbb {F}_p[t,t^{-1},(t-1)^{-1}]$
, should hold for
![]() $n \geq 4$
with mechanical changes [Reference de Cornulier and Tessera32, Remark 5.5].
$n \geq 4$
with mechanical changes [Reference de Cornulier and Tessera32, Remark 5.5].
As far as generators and relations are concerned, Theorem 1.2 generalizes to arbitrary rings the above mentioned results on presentations of Abels’ groups. The previous discussion also indicates the following natural problem.
Conjecture 1.7 Let R be a finitely generated commutative unital ring. If R is infinitely generated as a
![]() $\mathbb {Z}$
-module, then
$\mathbb {Z}$
-module, then
![]() $\phi (\textbf {A}_n(R)) = \min \{ n-2, \phi (\textbf {B}_2^{\circ }(R))\}$
for all
$\phi (\textbf {A}_n(R)) = \min \{ n-2, \phi (\textbf {B}_2^{\circ }(R))\}$
for all
![]() $n \geq 2$
.
$n \geq 2$
.
For completeness, we provide in Section 4.3 a proof of Conjecture 1.7 in the known S-arithmetic cases.
Let us briefly record a series of non-S-arithmetic examples of Abels’ groups, again borrowing from the works of Kochloukova [Reference Kochloukova40] and Kropholler–Mullaney [Reference Kropholler and Mullaney41].
Example 1.8 Recall from Example 1.6 the rings
![]() $R_{\ell } = \mathbb {Z}[x,x^{-1},(1+x)^{-1},\ldots ,(\ell +x)^{-1},\frac {1}{\ell !}]$
for
$R_{\ell } = \mathbb {Z}[x,x^{-1},(1+x)^{-1},\ldots ,(\ell +x)^{-1},\frac {1}{\ell !}]$
for
![]() $\ell \in \mathbb {N}$
. Since
$\ell \in \mathbb {N}$
. Since
![]() $\phi (\textbf {B}_2^{\circ }(R_{\ell })) = \ell + 1$
, we have that Abels’ groups
$\phi (\textbf {B}_2^{\circ }(R_{\ell })) = \ell + 1$
, we have that Abels’ groups
![]() $\textbf {A}_n(R_{\ell })$
with
$\textbf {A}_n(R_{\ell })$
with
![]() $n \geq 3$
are finitely generated, and they become finitely presented if
$n \geq 3$
are finitely generated, and they become finitely presented if
![]() $n \geq 4$
. In low dimensions one has more precisely
$n \geq 4$
. In low dimensions one has more precisely
and the equality
![]() $\phi (\textbf {A}_4(R_1)) = 2$
in the case
$\phi (\textbf {A}_4(R_1)) = 2$
in the case
![]() $\ell = 1$
.
$\ell = 1$
.
As for the proof of Theorem 1.2, our approach differs from Strebel’s and both have their own advantages. His proof in [Reference Strebel54] is purely algebraic and, under the needed hypotheses, he explicitly constructs a convenient finite presentation for
![]() $A_n(R,Q) \cong \textbf {U}_n(R) \rtimes Q^{n-2}$
. In contrast, the proof of Theorem 1.2 given here has a topological flavor. Indeed, we make use of horospherical subgroups and nerve complexes à la Abels–Holz [Reference Abels1, Reference Abels2, Reference Abels and Holz4, Reference Holz39], the early
$A_n(R,Q) \cong \textbf {U}_n(R) \rtimes Q^{n-2}$
. In contrast, the proof of Theorem 1.2 given here has a topological flavor. Indeed, we make use of horospherical subgroups and nerve complexes à la Abels–Holz [Reference Abels1, Reference Abels2, Reference Abels and Holz4, Reference Holz39], the early
![]() $\Sigma $
-invariant for metabelian groups introduced by Bieri and Strebel himself [Reference Bieri, de Cornulier, Guyot and Strebel13], and Brown’s criterion for finite presentability [Reference Brown17] via actions on simply-connected complexes; see Section 4 for details.
$\Sigma $
-invariant for metabelian groups introduced by Bieri and Strebel himself [Reference Bieri, de Cornulier, Guyot and Strebel13], and Brown’s criterion for finite presentability [Reference Brown17] via actions on simply-connected complexes; see Section 4 for details.
Although Strebel’s original theorem [Reference Strebel54] is slightly more general than Theorem 1.2 as stated, our proof carries over to his case as well after appropriate changes. Namely, one needs only replace the necessary conditions “
![]() $\phi (\textbf {B}_2^{\circ }(R)) \geq 1$
(resp.
$\phi (\textbf {B}_2^{\circ }(R)) \geq 1$
(resp.
![]() $\geq 2$
)” by “the group
$\geq 2$
)” by “the group
is finitely generated (resp. finitely presented).”
Further remarks about our methods and those of Strebel point to interesting phenomena concerning the structure of Abels’ groups; see Section 4.2.
2 Preliminaries and notation
The facts collected here are standard. The reader is referred e.g., to the classics [Reference Demazure and Grothendieck33, Reference Hahn and O'Meara38, Reference Steinberg53] and to [Reference Geoghegan37, Chapter 7] for the results on classical groups and finiteness length, respectively, that will be used throughout. Though we derived corollaries for S-arithmetic groups (refer to [Reference Margulis43] for more on them), familiarity with such groups is not required for the proofs of our main results. A group commutator shall be written
![]() $[x,y] = xyx^{-1}y^{-1}$
.
$[x,y] = xyx^{-1}y^{-1}$
.
Given
![]() $i,j \in \left \{ 1,\ldots ,n \right \}$
with
$i,j \in \left \{ 1,\ldots ,n \right \}$
with
![]() $i \neq j$
and
$i \neq j$
and
![]() $r \in R$
, we denote by
$r \in R$
, we denote by
![]() $e_{ij}(r) \in \operatorname {\textrm {GL}}_n(R)$
the corresponding elementary matrix (also called elementary transvection), i.e.,
$e_{ij}(r) \in \operatorname {\textrm {GL}}_n(R)$
the corresponding elementary matrix (also called elementary transvection), i.e.,
![]() $e_{ij}(r)$
is the matrix whose diagonal entries all equal
$e_{ij}(r)$
is the matrix whose diagonal entries all equal
![]() $1$
and whose only off-diagonal nonzero entry is r in the position
$1$
and whose only off-diagonal nonzero entry is r in the position
![]() $(i,j)$
.
$(i,j)$
.
Elementary matrices and commutators between them have the following properties, which are easily checked.
 $$ \begin{align} [e_{ij}(r),e_{kl}(s)] = \begin{cases} e_{il}(rs) & \text{if } j=k,\\ 1 & \text{if } i \neq l, k \neq j. \end{cases} \end{align} $$
$$ \begin{align} [e_{ij}(r),e_{kl}(s)] = \begin{cases} e_{il}(rs) & \text{if } j=k,\\ 1 & \text{if } i \neq l, k \neq j. \end{cases} \end{align} $$
In particular, each subgroup
is isomorphic to the underlying additive group
![]() ${\mathbb {G}_a}(R) =~(R,+) \cong ~\left \{ \left ( \begin {smallmatrix} 1 & r \\ 0 & 1 \end {smallmatrix}\right ) \mid r \in R \right \}$
.
${\mathbb {G}_a}(R) =~(R,+) \cong ~\left \{ \left ( \begin {smallmatrix} 1 & r \\ 0 & 1 \end {smallmatrix}\right ) \mid r \in R \right \}$
.
Direct matrix computations also show that
where
![]() $ \operatorname {\textrm {Diag}}(u_1,\ldots ,u_n)$
denotes the
$ \operatorname {\textrm {Diag}}(u_1,\ldots ,u_n)$
denotes the
![]() $n \times n$
diagonal matrix whose diagonal entries are
$n \times n$
diagonal matrix whose diagonal entries are
![]() $u_1,\ldots ,u_n \in R^{\times }$
. The identity matrix
$u_1,\ldots ,u_n \in R^{\times }$
. The identity matrix
![]() $\mathrm{Diag}(1,\ldots,1) \in \mathrm{GL}_n(R)$
will be denoted by
$\mathrm{Diag}(1,\ldots,1) \in \mathrm{GL}_n(R)$
will be denoted by
![]() $\boldsymbol{1}_n$
. Given
$\boldsymbol{1}_n$
. Given
![]() $i \in \{ 1,\ldots ,n\}$
, we let
$i \in \{ 1,\ldots ,n\}$
, we let
![]() $D_i(R)$
denote the subgroup
$D_i(R)$
denote the subgroup
![]() $\{ \operatorname {\textrm {Diag}}(u_1,\ldots ,u_n) \mid u_j = 1 \text { if } j \neq i\} \leq \operatorname {\textrm {GL}}_n(R)$
. Write
$\{ \operatorname {\textrm {Diag}}(u_1,\ldots ,u_n) \mid u_j = 1 \text { if } j \neq i\} \leq \operatorname {\textrm {GL}}_n(R)$
. Write
![]() $\textbf {D}_n(R)$
for the subgroup of
$\textbf {D}_n(R)$
for the subgroup of
![]() $ \operatorname {\textrm {GL}}_n(R)$
generated by all
$ \operatorname {\textrm {GL}}_n(R)$
generated by all
![]() $ \operatorname {\textrm {Diag}}(u_1, \ldots , u_n)$
. One then has
$ \operatorname {\textrm {Diag}}(u_1, \ldots , u_n)$
. One then has
 $$ \begin{align*} \textbf{D}_n(R) = \prod\limits_{i=1}^n D_i(R) \cong \mathbb{G}_m(R)^n, \end{align*} $$
$$ \begin{align*} \textbf{D}_n(R) = \prod\limits_{i=1}^n D_i(R) \cong \mathbb{G}_m(R)^n, \end{align*} $$
where
![]() ${\mathbb {G}_m}(R) = (R^{\times }, \cdot ) \cong \operatorname {\textrm {GL}}_1(R)$
is the group of units of the base ring R. The matrix group scheme
${\mathbb {G}_m}(R) = (R^{\times }, \cdot ) \cong \operatorname {\textrm {GL}}_1(R)$
is the group of units of the base ring R. The matrix group scheme
![]() $\textbf {D}_n \cong \mathbb {G}_m^n$
, which is defined over
$\textbf {D}_n \cong \mathbb {G}_m^n$
, which is defined over
![]() $\mathbb {Z}$
, is also known as the standard (maximal) torus of
$\mathbb {Z}$
, is also known as the standard (maximal) torus of
![]() $ \operatorname {\textrm {GL}}_n$
. The following relations between diagonal and elementary matrices are easily verified.
$ \operatorname {\textrm {GL}}_n$
. The following relations between diagonal and elementary matrices are easily verified.
Relations similar to the above hold for all classical groups. Recall that a universal Chevalley–Demazure group scheme of type
![]() $\Phi $
is the split, semisimple, simply-connected, affine
$\Phi $
is the split, semisimple, simply-connected, affine
![]() $\mathbb {Z}$
-group scheme
$\mathbb {Z}$
-group scheme
![]() $\mathcal {G}_{\Phi }^{\text {sc}}$
associated to the (reduced, irreducible) root system
$\mathcal {G}_{\Phi }^{\text {sc}}$
associated to the (reduced, irreducible) root system
![]() $\Phi $
. It is a result of Chevalley’s that such group schemes exist, and they are unique by Demazure’s theorem; refer to [Reference Demazure and Grothendieck33] for existence, uniqueness, and structure theory of Chevalley–Demazure groups. Our notation below for root subgroups of
$\Phi $
. It is a result of Chevalley’s that such group schemes exist, and they are unique by Demazure’s theorem; refer to [Reference Demazure and Grothendieck33] for existence, uniqueness, and structure theory of Chevalley–Demazure groups. Our notation below for root subgroups of
![]() $\mathcal {G}_{\Phi }^{\text {sc}}$
closely follows that of Steinberg [Reference Steinberg53].
$\mathcal {G}_{\Phi }^{\text {sc}}$
closely follows that of Steinberg [Reference Steinberg53].
For every root
![]() $\alpha \in \Phi $
and ring element
$\alpha \in \Phi $
and ring element
![]() $r \in R$
, the group
$r \in R$
, the group
![]() $\mathcal {G}_{\Phi }^{\text {sc}}(R)$
contains a corresponding unipotent root element
$\mathcal {G}_{\Phi }^{\text {sc}}(R)$
contains a corresponding unipotent root element
![]() $x_{\alpha }(r) \in \mathcal {G}_{\Phi }^{\text {sc}}(R)$
—these play in
$x_{\alpha }(r) \in \mathcal {G}_{\Phi }^{\text {sc}}(R)$
—these play in
![]() $\mathcal {G}_{\Phi }^{\text {sc}}(R)$
the same role as the elementary matrices
$\mathcal {G}_{\Phi }^{\text {sc}}(R)$
the same role as the elementary matrices
![]() $e_{ij}(r)$
in
$e_{ij}(r)$
in
![]() $ \operatorname {\textrm {GL}}_n(R)$
. Accordingly, one has the unipotent root subgroup
$ \operatorname {\textrm {GL}}_n(R)$
. Accordingly, one has the unipotent root subgroup
For each
![]() $\alpha \in \Phi $
and
$\alpha \in \Phi $
and
![]() $u \in R^{\times }$
, one also has a semisimple root element
$u \in R^{\times }$
, one also has a semisimple root element
![]() $h_{\alpha }(u) \in \mathcal {G}_{\Phi }^{\text {sc}}(R)$
, and we define
$h_{\alpha }(u) \in \mathcal {G}_{\Phi }^{\text {sc}}(R)$
, and we define
![]() $\mathcal {H}_{\alpha }(R) = \langle {\{ h_{\alpha }(u) \mid u \in R^{\times } \}} \rangle \cong \mathbb {G}_m(R)$
, the semisimple root subgroup associated to
$\mathcal {H}_{\alpha }(R) = \langle {\{ h_{\alpha }(u) \mid u \in R^{\times } \}} \rangle \cong \mathbb {G}_m(R)$
, the semisimple root subgroup associated to
![]() $\alpha $
. The subgroups
$\alpha $
. The subgroups
![]() $\mathcal {H}_{\alpha }(R)$
and
$\mathcal {H}_{\alpha }(R)$
and
![]() $\mathcal {H}_{\beta }(R)$
commute for all roots
$\mathcal {H}_{\beta }(R)$
commute for all roots
![]() $\alpha , \beta \in \Phi $
. The (standard) torus of
$\alpha , \beta \in \Phi $
. The (standard) torus of
![]() $\mathcal {G}_{\Phi }^{\text {sc}}(R)$
is the abelian subgroup
$\mathcal {G}_{\Phi }^{\text {sc}}(R)$
is the abelian subgroup
The unipotent root subgroups in Chevalley–Demazure groups are related via Chevalley’s famous commutator formulae, which generalize the commutator relations (2.1) between elementary matrices; see e.g., [Reference Carter29, Reference Steinberg53, Reference Vavilov and Plotkin58]. As for relations between unipotent and semisimple root elements, Steinberg derives from Chevalley’s formulae a series of equations now known as Steinberg relations; cf. [Reference Steinberg53, p. 23]. In particular, given
![]() $h_{\beta }(u) \in \mathcal {H}_{\beta }(R)$
and
$h_{\beta }(u) \in \mathcal {H}_{\beta }(R)$
and
![]() $x_{\alpha }(r) \in \mathfrak {X}_{\alpha }(R)$
, Steinberg shows
$x_{\alpha }(r) \in \mathfrak {X}_{\alpha }(R)$
, Steinberg shows
where
![]() $(\alpha ,\beta ) := 2\frac {\langle {\alpha ,\beta } \rangle }{\langle {\beta ,\beta } \rangle } \in \left \{ 0, \pm 1, \pm 2, \pm 3 \right \}$
is the corresponding Cartan integer.
$(\alpha ,\beta ) := 2\frac {\langle {\alpha ,\beta } \rangle }{\langle {\beta ,\beta } \rangle } \in \left \{ 0, \pm 1, \pm 2, \pm 3 \right \}$
is the corresponding Cartan integer.
Let W be the Weyl group associated to
![]() $\Phi $
. The Steinberg relations (2.3) behave well with respect to the W-action on the roots
$\Phi $
. The Steinberg relations (2.3) behave well with respect to the W-action on the roots
![]() $\Phi $
. More precisely, let
$\Phi $
. More precisely, let
![]() $\alpha \in \Phi \subseteq \mathbb {R}^{ \operatorname {\textrm {rk}}(\Phi )}$
and let
$\alpha \in \Phi \subseteq \mathbb {R}^{ \operatorname {\textrm {rk}}(\Phi )}$
and let
![]() $r_{\alpha } \in W$
be the associated reflection. The group W has a canonical copy (up to ordering of roots) in
$r_{\alpha } \in W$
be the associated reflection. The group W has a canonical copy (up to ordering of roots) in
![]() $\mathcal {G}_{\Phi }^{\text {sc}}$
obtained via the assignment
$\mathcal {G}_{\Phi }^{\text {sc}}$
obtained via the assignment
With the above notation, given arbitrary roots
![]() $\beta , \gamma \in \Phi $
, one has
$\beta , \gamma \in \Phi $
, one has
 $$ \begin{align} \begin{split} h_{r_{\alpha}(\gamma)}(v) x_{r_{\alpha}(\beta)}(s) h_{r_{\alpha}(\gamma)}(v)^{-1} & = w_{\alpha} (h_{\gamma}(v) x_{\beta}(s)^{\pm 1} h_{\gamma}(v)^{-1}) w_{\alpha}^{-1} \\ & = x_{r_{\alpha}(\beta)}(v^{(\beta, \gamma)}s)^{\pm 1}, \end{split} \end{align} $$
$$ \begin{align} \begin{split} h_{r_{\alpha}(\gamma)}(v) x_{r_{\alpha}(\beta)}(s) h_{r_{\alpha}(\gamma)}(v)^{-1} & = w_{\alpha} (h_{\gamma}(v) x_{\beta}(s)^{\pm 1} h_{\gamma}(v)^{-1}) w_{\alpha}^{-1} \\ & = x_{r_{\alpha}(\beta)}(v^{(\beta, \gamma)}s)^{\pm 1}, \end{split} \end{align} $$
where the sign
![]() $\pm 1$
above does not depend on
$\pm 1$
above does not depend on
![]() $v \in R^{\times }$
nor on
$v \in R^{\times }$
nor on
![]() $s \in R$
.
$s \in R$
.
Throughout this paper, we shall make repeated use of the following well-known bounds on the finiteness length.
Lemma 2.1 Given a short exact sequence
![]() $N \hookrightarrow G \twoheadrightarrow Q$
, the following hold.
$N \hookrightarrow G \twoheadrightarrow Q$
, the following hold.
-
(1) If
 $\phi (N)$
and
$\phi (N)$
and
 $\phi (Q)$
are at least n, then so is
$\phi (Q)$
are at least n, then so is
 $\phi (G)$
.
$\phi (G)$
. -
(2) If
 $\phi (Q) = \infty $
, then
$\phi (Q) = \infty $
, then
 $\phi (N) \leq \phi (G)$
.
$\phi (N) \leq \phi (G)$
. -
(3) If
 $\phi (N) = \infty $
, then
$\phi (N) = \infty $
, then
 $\phi (Q) = \phi (G)$
.
$\phi (Q) = \phi (G)$
. -
(4) If the sequence splits (equivalently,
 $G = N \rtimes Q$
), then
$G = N \rtimes Q$
), then
 $\phi (G) \leq \phi (Q)$
.
$\phi (G) \leq \phi (Q)$
. -
(5) If the sequence splits trivially, i.e.,
 $G = N \times Q$
, then
$G = N \times Q$
, then
 $\phi (G) =~\min \left \{ \phi (N), \phi (Q) \right \}$
.
$\phi (G) =~\min \left \{ \phi (N), \phi (Q) \right \}$
.
Proof Part (1) is just [Reference Ratcliffe46, Theorem 4(ii)] restated in the language of finiteness length, and (2) follows immediately from (1). Parts (3) and (4) follow from [Reference Ratcliffe46, Theorems 4(i) and 6]. Part (5) is an immediate consequence of (4) and (1).▪
We point out that the finiteness length is often seen in the literature in the language of homotopical finiteness properties. The concept goes back to the work of Wall in the 1950s. By definition, a group G is of homotopical type
![]() $\text {F}_{n}$
if
$\text {F}_{n}$
if
![]() $\phi (G) \geq n$
, and of type
$\phi (G) \geq n$
, and of type
![]() $\text {F}_{\infty }$
in case
$\text {F}_{\infty }$
in case
![]() $\phi (G) = \infty $
; see e.g., [Reference Geoghegan37, Chapter 7] for more on this. A well-known fact that will be often used throughout this work is that a finitely generated abelian group Q has
$\phi (G) = \infty $
; see e.g., [Reference Geoghegan37, Chapter 7] for more on this. A well-known fact that will be often used throughout this work is that a finitely generated abelian group Q has
![]() $\phi (Q) = \infty $
, i.e., it is of type
$\phi (Q) = \infty $
, i.e., it is of type
![]() $\text {F}_{\infty }$
(equivalently, of type
$\text {F}_{\infty }$
(equivalently, of type
![]() $\text {F}_{n}$
for all
$\text {F}_{n}$
for all
![]() $n \in \mathbb {Z}_{\geq 0}$
). This is readily seen because the torsion-free part of Q, say
$n \in \mathbb {Z}_{\geq 0}$
). This is readily seen because the torsion-free part of Q, say
![]() $\mathbb {Z}^m$
with
$\mathbb {Z}^m$
with
![]() $m \geq 0$
, admits the m-Torus as an Eilenberg–Maclane space
$m \geq 0$
, admits the m-Torus as an Eilenberg–Maclane space
![]() $K(\mathbb {Z}^m,1)$
.
$K(\mathbb {Z}^m,1)$
.
3 Proof of Theorem 1.1
The hypotheses of Theorem 1.1 already yield an obvious bound on the finiteness length of the given group. Indeed, in the notation of Theorem 1.1, we have that
![]() $\phi (G) \leq \phi (\mathfrak {X}(R) \rtimes \mathcal {H}(R))$
by Lemma 2.1(4) because retracts preserve homotopical finiteness properties. (A group Q is called a retract of G if G is a semidirect product
$\phi (G) \leq \phi (\mathfrak {X}(R) \rtimes \mathcal {H}(R))$
by Lemma 2.1(4) because retracts preserve homotopical finiteness properties. (A group Q is called a retract of G if G is a semidirect product
![]() $G \cong N \rtimes Q$
for some
$G \cong N \rtimes Q$
for some
![]() $N \triangleleft G$
. Equivalently, the sequence
$N \triangleleft G$
. Equivalently, the sequence
![]() $N \hookrightarrow G \twoheadrightarrow Q$
splits.) The actual work thus consists in proving that
$N \hookrightarrow G \twoheadrightarrow Q$
splits.) The actual work thus consists in proving that
![]() $\phi (\mathfrak {X}(R) \rtimes \mathcal {H}(R))$
is no greater than the desired value,
$\phi (\mathfrak {X}(R) \rtimes \mathcal {H}(R))$
is no greater than the desired value,
![]() $\phi (\textbf {B}_2^{\circ }(R))$
.
$\phi (\textbf {B}_2^{\circ }(R))$
.
We begin with the following simple observation.
Remark 3.1 If the group of units
![]() $\mathbb {G}_m(R) = (R^{\times }, \cdot )$
is not finitely generated, then Theorem 1.1 holds. Indeed, in this case one has
$\mathbb {G}_m(R) = (R^{\times }, \cdot )$
is not finitely generated, then Theorem 1.1 holds. Indeed, in this case one has
because both the torus
![]() $\mathcal {H}(R)$
and
$\mathcal {H}(R)$
and
![]() $\textbf {B}_2^{\circ }(R)$
retract onto
$\textbf {B}_2^{\circ }(R)$
retract onto
![]() $\mathbb {G}_m(R)$
; cf. Section 2.
$\mathbb {G}_m(R)$
; cf. Section 2.
In view of the above, we adopt the following.
Convention throughout this section:
Unless stated otherwise, we assume that the group of units
![]() $\mathbb {G}_m(R) = (R^{\times },\cdot )$
of the base ring R is finitely generated.
$\mathbb {G}_m(R) = (R^{\times },\cdot )$
of the base ring R is finitely generated.
In what follows, we denote by
![]() $\textbf {B}_n(R)$
the subgroup of upper triangular matrices of
$\textbf {B}_n(R)$
the subgroup of upper triangular matrices of
![]() $ \operatorname {\textrm {GL}}_n(R)$
. Similarly, we define
$ \operatorname {\textrm {GL}}_n(R)$
. Similarly, we define
![]() $\textbf {B}_n^{\circ }(R) = \textbf {B}_n(R) \cap \operatorname {\textrm {SL}}_n(R)$
. The schemes
$\textbf {B}_n^{\circ }(R) = \textbf {B}_n(R) \cap \operatorname {\textrm {SL}}_n(R)$
. The schemes
![]() $\textbf {B}_n$
and
$\textbf {B}_n$
and
![]() $\textbf {B}_n^{\circ }$
are examples of Borel subgroups of classical groups.
$\textbf {B}_n^{\circ }$
are examples of Borel subgroups of classical groups.
We start by clearing the case where our representation
![]() $\rho : G \to \mathcal {G}(R)$
has one of the affine groups as target. Recall that the group of affine transformations of the base ring R, denoted here by
$\rho : G \to \mathcal {G}(R)$
has one of the affine groups as target. Recall that the group of affine transformations of the base ring R, denoted here by
![]() $\mathbb {A}\text {ff}(R)$
and sometimes by
$\mathbb {A}\text {ff}(R)$
and sometimes by
![]() $\text {AGL}_1(R)$
in the literature, is the set of affine permutations
$\text {AGL}_1(R)$
in the literature, is the set of affine permutations
![]() $R \to R : x \mapsto ux+r$
, with
$R \to R : x \mapsto ux+r$
, with
![]() $u \in R^{\times }$
and
$u \in R^{\times }$
and
![]() $r \in R$
. It is a standard exercise to check that
$r \in R$
. It is a standard exercise to check that
![]() $\mathbb {A}\text {ff}(R)$
is isomorphic to the semidirect product
$\mathbb {A}\text {ff}(R)$
is isomorphic to the semidirect product
![]() $\mathbb {G}_a(R) \rtimes \mathbb {G}_m(R)$
, with
$\mathbb {G}_a(R) \rtimes \mathbb {G}_m(R)$
, with
![]() $\mathbb {G}_m(R)$
acting on
$\mathbb {G}_m(R)$
acting on
![]() $\mathbb {G}_a(R)$
by multiplication.
$\mathbb {G}_a(R)$
by multiplication.
Identifying
![]() $x \in R$
with
$x \in R$
with
![]() $\left ( \begin {smallmatrix} x \\ 1 \end {smallmatrix} \right )$
, we readily obtain the well-known matrix representation of
$\left ( \begin {smallmatrix} x \\ 1 \end {smallmatrix} \right )$
, we readily obtain the well-known matrix representation of
![]() $\mathbb {A}\text {ff}(R)$
as a subgroup of
$\mathbb {A}\text {ff}(R)$
as a subgroup of
![]() $ \operatorname {\textrm {GL}}_2(R)$
, namely
$ \operatorname {\textrm {GL}}_2(R)$
, namely
now acting on
![]() $R \cong \{ \left ( \begin {smallmatrix} * \\ 1 \end {smallmatrix} \right ) \}$
via matrix multiplication. Using the relations from Section 2 and because the diagonal and unipotent parts of
$R \cong \{ \left ( \begin {smallmatrix} * \\ 1 \end {smallmatrix} \right ) \}$
via matrix multiplication. Using the relations from Section 2 and because the diagonal and unipotent parts of
![]() $\left ( \begin {smallmatrix} * & * \\ 0 & 1 \end {smallmatrix} \right )$
intersect at the identity matrix, the above representation of
$\left ( \begin {smallmatrix} * & * \\ 0 & 1 \end {smallmatrix} \right )$
intersect at the identity matrix, the above representation of
![]() $\mathbb {A}\text {ff}(R)$
also yields its semidirect product decomposition
$\mathbb {A}\text {ff}(R)$
also yields its semidirect product decomposition
In certain situations, it is also convenient to consider a version of
![]() $\mathbb {A}\text {ff}(R)$
, denoted here by
$\mathbb {A}\text {ff}(R)$
, denoted here by
![]() $\mathbb {A}\text {ff}_-(R)$
, whose multiplicative part
$\mathbb {A}\text {ff}_-(R)$
, whose multiplicative part
![]() $\mathbb {G}_m(R)$
acts on
$\mathbb {G}_m(R)$
acts on
![]() $\mathbb {G}_a(R)$
by reverse multiplication. That is, we consider
$\mathbb {G}_a(R)$
by reverse multiplication. That is, we consider
![]() $\mathbb {A}\text {ff}_-(R) \cong \mathbb {G}_a(R) \rtimes _{-1} \mathbb {G}_m(R)$
with action
$\mathbb {A}\text {ff}_-(R) \cong \mathbb {G}_a(R) \rtimes _{-1} \mathbb {G}_m(R)$
with action
The group
![]() $\mathbb {A}\text {ff}_-(R)$
also has an obvious matrix representation, namely
$\mathbb {A}\text {ff}_-(R)$
also has an obvious matrix representation, namely
Lemma 3.2 The groups
![]() $\mathbb {A}\text {ff}(R)$
,
$\mathbb {A}\text {ff}(R)$
,
![]() $\textbf {B}_2^{\circ }(R)$
and
$\textbf {B}_2^{\circ }(R)$
and
![]() $\mathbb {A}\text {ff}_-(R)$
are commensurable. In particular,
$\mathbb {A}\text {ff}_-(R)$
are commensurable. In particular,
![]() $\phi (\mathbb {A}\text {ff}(R)) = \phi (\textbf {B}_2^{\circ }(R)) = \phi (\mathbb {A}\text {ff}_-(R))$
. Thus, Theorem 1.1 holds for
$\phi (\mathbb {A}\text {ff}(R)) = \phi (\textbf {B}_2^{\circ }(R)) = \phi (\mathbb {A}\text {ff}_-(R))$
. Thus, Theorem 1.1 holds for
![]() $\mathcal {G} = \mathbb {A}\text {ff}$
or
$\mathcal {G} = \mathbb {A}\text {ff}$
or
![]() $\mathbb {A}\text {ff}_-$
.
$\mathbb {A}\text {ff}_-$
.
Proof Here, we are under the assumption that
![]() $\mathbb {G}_m(R)$
is finitely generated. If
$\mathbb {G}_m(R)$
is finitely generated. If
![]() $\mathbb {G}_m(R)$
is itself finite the lemma follows immediately, for in this case the unipotent subgroup
$\mathbb {G}_m(R)$
is itself finite the lemma follows immediately, for in this case the unipotent subgroup
![]() $\left ( \begin {smallmatrix} 1 & * \\ 0 & 1 \end {smallmatrix} \right )$
has finite index in the three groups considered. Otherwise
$\left ( \begin {smallmatrix} 1 & * \\ 0 & 1 \end {smallmatrix} \right )$
has finite index in the three groups considered. Otherwise
![]() $\textbf {B}_2^{\circ }(R)$
is seen to contain a subgroup of finite index which is isomorphic to a group of the form
$\textbf {B}_2^{\circ }(R)$
is seen to contain a subgroup of finite index which is isomorphic to a group of the form
for some torsion-free subgroup of units
![]() $S \leq R^{\times }$
—recall that the action of an element
$S \leq R^{\times }$
—recall that the action of an element
![]() $\left ( \begin {smallmatrix} u & 0 \\ 0 & u^{-1} \end {smallmatrix} \right ) \in \textbf {B}_2^{\circ }(R)$
on
$\left ( \begin {smallmatrix} u & 0 \\ 0 & u^{-1} \end {smallmatrix} \right ) \in \textbf {B}_2^{\circ }(R)$
on
![]() $\left ( \begin {smallmatrix} 1 & r \\ 0 & 1 \end {smallmatrix} \right )$
yields
$\left ( \begin {smallmatrix} 1 & r \\ 0 & 1 \end {smallmatrix} \right )$
yields
![]() $\left ( \begin {smallmatrix} 1 & u^2r \\ 0 & 1 \end {smallmatrix} \right )$
by the Steinberg relations (2.3). Since the group above is a subgroup of finite index of
$\left ( \begin {smallmatrix} 1 & u^2r \\ 0 & 1 \end {smallmatrix} \right )$
by the Steinberg relations (2.3). Since the group above is a subgroup of finite index of
![]() $\mathbb {A}\text {ff}(R)$
, the first claim follows. Now
$\mathbb {A}\text {ff}(R)$
, the first claim follows. Now
![]() $\mathbb {A}\text {ff}(R)$
is isomorphic to
$\mathbb {A}\text {ff}(R)$
is isomorphic to
![]() $\mathbb {A}\text {ff}_-(R)$
by inverting the action of the diagonal. More precisely, the map
$\mathbb {A}\text {ff}_-(R)$
by inverting the action of the diagonal. More precisely, the map
is an isomorphism. The equalities on the finiteness length follow from the fact that
![]() $\phi $
is a quasi-isometry invariant [Reference Alonso6, Corollary 9].▪
$\phi $
is a quasi-isometry invariant [Reference Alonso6, Corollary 9].▪
The following relates the finiteness lengths of Borel subgroups of
![]() $ \operatorname {\textrm {SL}}_n$
and
$ \operatorname {\textrm {SL}}_n$
and
![]() $ \operatorname {\textrm {GL}}_n$
.
$ \operatorname {\textrm {GL}}_n$
.
Lemma 3.3 For any R (with
![]() $\mathbb {G}_m(R)$
not necessarily finitely generated), the Borel subgroups
$\mathbb {G}_m(R)$
not necessarily finitely generated), the Borel subgroups
![]() $\textbf {B}_n(R) \leq \operatorname {\textrm {GL}}_n(R)$
and
$\textbf {B}_n(R) \leq \operatorname {\textrm {GL}}_n(R)$
and
![]() $\textbf {B}_n^{\circ }(R) \leq ~ \operatorname {\textrm {SL}}_n(R)$
have the same finiteness length, which in turn is no greater than
$\textbf {B}_n^{\circ }(R) \leq ~ \operatorname {\textrm {SL}}_n(R)$
have the same finiteness length, which in turn is no greater than
![]() $\phi (\textbf {B}_2^{\circ }(R))$
.
$\phi (\textbf {B}_2^{\circ }(R))$
.
Proof Though stated for arbitrary (commutative, unital) rings, the proof of the lemma is essentially Bux’s proof in the S-arithmetic case in positive characteristic [Reference Bux22, Remark 3.6]. If
![]() $\mathbb {G}_m(R)$
is not finitely generated, then
$\mathbb {G}_m(R)$
is not finitely generated, then
![]() $\phi (\textbf {B}_n(R)) = \phi (\textbf {B}_n^{\circ }(R)) = \phi (\textbf {B}_2^{\circ }(R)) = 0$
, so that we go back to our standing assumption that
$\phi (\textbf {B}_n(R)) = \phi (\textbf {B}_n^{\circ }(R)) = \phi (\textbf {B}_2^{\circ }(R)) = 0$
, so that we go back to our standing assumption that
![]() $\mathbb {G}_m(R)$
is finitely generated.
$\mathbb {G}_m(R)$
is finitely generated.
Consider the central subgroup
![]() $\textbf {Z}_n(R) \leq \textbf {B}_n(R)$
given by
$\textbf {Z}_n(R) \leq \textbf {B}_n(R)$
given by
Its intersection with
![]() $\textbf {B}_2^{\circ }(R) \leq \operatorname {\textrm {SL}}_n(R)$
is the group
$\textbf {B}_2^{\circ }(R) \leq \operatorname {\textrm {SL}}_n(R)$
is the group
![]() $\mu _n(R)$
of nth roots of unity of R, i.e.,
$\mu _n(R)$
of nth roots of unity of R, i.e.,
Given an arbitrary abelian group A and
![]() $m \in \mathbb {N}$
, let us denote by
$m \in \mathbb {N}$
, let us denote by
![]() $(A)^m \leq A$
the subgroup of mth powers, that is
$(A)^m \leq A$
the subgroup of mth powers, that is
![]() $(A)^m = \{ a^m \mid a \in A \}$
. We observe that the determinant map, when restricted to
$(A)^m = \{ a^m \mid a \in A \}$
. We observe that the determinant map, when restricted to
![]() $\textbf {Z}_n(R) \leq \textbf {B}_n(R)$
, induces the nth power map
$\textbf {Z}_n(R) \leq \textbf {B}_n(R)$
, induces the nth power map
![]() $u \mapsto u^n$
on
$u \mapsto u^n$
on
![]() $\textbf {Z}_n(R) \cong \mathbb {G}_m(R)$
, the kernel of this map being precisely
$\textbf {Z}_n(R) \cong \mathbb {G}_m(R)$
, the kernel of this map being precisely
![]() $\mu _n(R)$
.
$\mu _n(R)$
.
Thus, using the determinant and passing over to the projective groups
![]() $\mathbb {P}\textbf {B}_n^{\circ }(R) := \textbf {B}_n^{\circ }(R)/\mu _n(R)$
and
$\mathbb {P}\textbf {B}_n^{\circ }(R) := \textbf {B}_n^{\circ }(R)/\mu _n(R)$
and
![]() $\mathbb {P}\textbf {B}_n(R) := \textbf {B}_n(R) / \textbf {Z}_n(R)$
, we obtain the following commutative diagram of short exact sequences.
$\mathbb {P}\textbf {B}_n(R) := \textbf {B}_n(R) / \textbf {Z}_n(R)$
, we obtain the following commutative diagram of short exact sequences.

Since
![]() $\mathbb {G}_m(R)$
is finitely generated abelian, the groups
$\mathbb {G}_m(R)$
is finitely generated abelian, the groups
![]() $\mu _n(R)$
and
$\mu _n(R)$
and
![]() ${\mathbb {G}_m(R)}/{(\mathbb {G}_m(R))^n}$
are finite, from which
${\mathbb {G}_m(R)}/{(\mathbb {G}_m(R))^n}$
are finite, from which
![]() $\phi (\textbf {B}_n^{\circ }(R)) = \phi (\mathbb {P}\textbf {B}_n^{\circ }(R))$
and
$\phi (\textbf {B}_n^{\circ }(R)) = \phi (\mathbb {P}\textbf {B}_n^{\circ }(R))$
and
![]() $\phi (\mathbb {P}\textbf {B}_n^{\circ }(R)) = \phi (\mathbb {P}\textbf {B}_n(R))$
follow by Lemma 2.1(3) and quasi-isometry invariance of
$\phi (\mathbb {P}\textbf {B}_n^{\circ }(R)) = \phi (\mathbb {P}\textbf {B}_n(R))$
follow by Lemma 2.1(3) and quasi-isometry invariance of
![]() $\phi $
[Reference Alonso6, Corollary 9]. But again Lemma 2.1(3) yields
$\phi $
[Reference Alonso6, Corollary 9]. But again Lemma 2.1(3) yields
![]() $\phi (\textbf {B}_n(R)) = \phi (\mathbb {P}\textbf {B}_n(R))$
, whence the first claim of the lemma.
$\phi (\textbf {B}_n(R)) = \phi (\mathbb {P}\textbf {B}_n(R))$
, whence the first claim of the lemma.
Finally, any
![]() $\textbf {B}_n(R)$
retracts onto
$\textbf {B}_n(R)$
retracts onto
![]() $\textbf {B}_2(R)$
via the map
$\textbf {B}_2(R)$
via the map

which yields the second claim.▪
To prove the desired inequality
![]() $\phi (\mathfrak {X}(R) \rtimes \mathcal {H}(R)) \leq \phi (\textbf {B}_2^{\circ }(R))$
, we shall use well-known matrix representations of classical groups. We warm-up by settling the simpler case where the given classical group
$\phi (\mathfrak {X}(R) \rtimes \mathcal {H}(R)) \leq \phi (\textbf {B}_2^{\circ }(R))$
, we shall use well-known matrix representations of classical groups. We warm-up by settling the simpler case where the given classical group
![]() $\mathcal {G}$
containing
$\mathcal {G}$
containing
![]() $\mathfrak {X} \rtimes \mathcal {H}$
is the general linear group itself, which will set the tune for the remaining cases. (Recall that
$\mathfrak {X} \rtimes \mathcal {H}$
is the general linear group itself, which will set the tune for the remaining cases. (Recall that
![]() $\mathcal {H}$
is a maximal torus of
$\mathcal {H}$
is a maximal torus of
![]() $\mathcal {G}$
.)
$\mathcal {G}$
.)
Proposition 3.4 Theorem 1.1 holds if
![]() $\mathcal {G} = \operatorname {\textrm {GL}}_n$
.
$\mathcal {G} = \operatorname {\textrm {GL}}_n$
.
Proof Here, we take a matrix representation of
![]() $\mathcal {G} = \operatorname {\textrm {GL}}_n$
such that the given soluble subgroup
$\mathcal {G} = \operatorname {\textrm {GL}}_n$
such that the given soluble subgroup
![]() $\mathfrak {X} \rtimes \mathcal {H}$
is upper triangular. In this case, the maximal torus
$\mathfrak {X} \rtimes \mathcal {H}$
is upper triangular. In this case, the maximal torus
![]() $\mathcal {H}$
is the subgroup of diagonal matrices of
$\mathcal {H}$
is the subgroup of diagonal matrices of
![]() $ \operatorname {\textrm {GL}}_n$
, i.e.,
$ \operatorname {\textrm {GL}}_n$
, i.e.,
 $$ \begin{align*} \mathcal{H}(R) \cong \textbf{D}_n(R) = \prod\limits_{i=1}^n D_i(R) \leq \operatorname{\textrm{GL}}_n(R), \end{align*} $$
$$ \begin{align*} \mathcal{H}(R) \cong \textbf{D}_n(R) = \prod\limits_{i=1}^n D_i(R) \leq \operatorname{\textrm{GL}}_n(R), \end{align*} $$
and
![]() $\mathfrak {X}$
is identified with a subgroup of elementary matrices in a single fixed position, say
$\mathfrak {X}$
is identified with a subgroup of elementary matrices in a single fixed position, say
![]() $(i,j)$
with
$(i,j)$
with
![]() $i < j$
. That is,
$i < j$
. That is,
Recall that the action of the torus
![]() $\mathcal {H}(R) \cong \textbf {D}_n(R)$
on the unipotent root subgroup
$\mathcal {H}(R) \cong \textbf {D}_n(R)$
on the unipotent root subgroup
![]() $\mathfrak {X}(R) \cong \textbf {E}_{ij}(R)$
is given by the diagonal relations (2.2). But such relations also imply the decomposition
$\mathfrak {X}(R) \cong \textbf {E}_{ij}(R)$
is given by the diagonal relations (2.2). But such relations also imply the decomposition
because all diagonal subgroups
![]() $D_k(R)$
with
$D_k(R)$
with
![]() $k \neq i,j$
act trivially on the elementary matrices
$k \neq i,j$
act trivially on the elementary matrices
![]() $e_{ij}(r)$
. Since we are assuming
$e_{ij}(r)$
. Since we are assuming
![]() $\mathbb {G}_m(R)$
to be finitely generated, it follows from Lemmata 2.1(5) and 3.3 that
$\mathbb {G}_m(R)$
to be finitely generated, it follows from Lemmata 2.1(5) and 3.3 that
▪
It remains to investigate the situation where the classical group
![]() $\mathcal {G}$
in the statement of Theorem 1.1 is a universal Chevalley–Demazure group scheme. Write
$\mathcal {G}$
in the statement of Theorem 1.1 is a universal Chevalley–Demazure group scheme. Write
![]() $\mathcal {G} = \mathcal {G}_{\Phi }^{\text {sc}}$
, with underlying root system
$\mathcal {G} = \mathcal {G}_{\Phi }^{\text {sc}}$
, with underlying root system
![]() $\Phi $
associated to the given maximal torus
$\Phi $
associated to the given maximal torus
![]() $\mathcal {H} \leq \mathcal {G}_{\Phi }^{\text {sc}}$
and with a fixed set of simple roots
$\mathcal {H} \leq \mathcal {G}_{\Phi }^{\text {sc}}$
and with a fixed set of simple roots
![]() ${\Delta } \subset \Phi $
. One has
${\Delta } \subset \Phi $
. One has
and
![]() $\mathfrak {X}$
is the unipotent root subgroup associated to some (positive) root
$\mathfrak {X}$
is the unipotent root subgroup associated to some (positive) root
![]() $\eta \in \Phi ^+$
, that is,
$\eta \in \Phi ^+$
, that is,
The proof proceeds by a case-by-case analysis on
![]() $\Phi $
and
$\Phi $
and
![]() $\eta $
. Instead of diving straight into all possible cases, some obvious reductions can be done.
$\eta $
. Instead of diving straight into all possible cases, some obvious reductions can be done.
Lemma 3.5 If Theorem 1.1 holds when
![]() $\mathcal {G}$
is a universal Chevalley–Demazure group scheme
$\mathcal {G}$
is a universal Chevalley–Demazure group scheme
![]() $\mathcal {G}_{\Phi }^{\text {sc}}$
of rank at most four and
$\mathcal {G}_{\Phi }^{\text {sc}}$
of rank at most four and
![]() $\mathfrak {X} = \mathfrak {X}_{\eta }$
with
$\mathfrak {X} = \mathfrak {X}_{\eta }$
with
![]() $\eta \in \Phi ^+$
simple, then it holds for any universal Chevalley–Demazure group scheme.
$\eta \in \Phi ^+$
simple, then it holds for any universal Chevalley–Demazure group scheme.
Proof Write
![]() $\mathfrak {X}(R) = \mathfrak {X}_{\eta }(R)$
and
$\mathfrak {X}(R) = \mathfrak {X}_{\eta }(R)$
and
![]() $\mathcal {H}(R) = \prod _{\alpha \in \Delta } \mathcal {H}_{\alpha }(R)$
as above. By (2.4), we can find an element w in the Weyl group W of
$\mathcal {H}(R) = \prod _{\alpha \in \Delta } \mathcal {H}_{\alpha }(R)$
as above. By (2.4), we can find an element w in the Weyl group W of
![]() $\Phi $
and a corresponding element
$\Phi $
and a corresponding element
![]() $\omega \in \mathcal {G}_{\Phi }^{\text { sc}}(R)$
such that
$\omega \in \mathcal {G}_{\Phi }^{\text { sc}}(R)$
such that
![]() $w(\eta ) \in \Phi ^+$
is a simple root and
$w(\eta ) \in \Phi ^+$
is a simple root and
(The conjugation above takes place in the overgroup
![]() $\mathcal {G}_{\Phi }^{\text {sc}}(R)$
.) We may thus assume
$\mathcal {G}_{\Phi }^{\text {sc}}(R)$
.) We may thus assume
![]() $\eta \in \Phi ^+$
to be simple. From the Steinberg relations (2.3), we have that
$\eta \in \Phi ^+$
to be simple. From the Steinberg relations (2.3), we have that
 $$ \begin{align*} \mathfrak{X}(R) \rtimes \mathcal{H}(R) = \left( \mathfrak{X}_{\eta}(R) \rtimes \left( \underset{\langle {\eta, \alpha} \rangle \neq 0}{\prod\limits_{\alpha \in \Delta}} \mathcal{H}_{\alpha}(R) \right) \right) \times \underset{\langle {\eta, \beta} \rangle = 0}{\prod\limits_{\beta \in \Delta}} \mathcal{H}_{\beta}(R), \end{align*} $$
$$ \begin{align*} \mathfrak{X}(R) \rtimes \mathcal{H}(R) = \left( \mathfrak{X}_{\eta}(R) \rtimes \left( \underset{\langle {\eta, \alpha} \rangle \neq 0}{\prod\limits_{\alpha \in \Delta}} \mathcal{H}_{\alpha}(R) \right) \right) \times \underset{\langle {\eta, \beta} \rangle = 0}{\prod\limits_{\beta \in \Delta}} \mathcal{H}_{\beta}(R), \end{align*} $$
yielding
![]() $\phi (\mathfrak {X}(R) \rtimes \mathcal {H}(R)) = \phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}^{\circ }(R))$
by Lemma 2.1(5), where
$\phi (\mathfrak {X}(R) \rtimes \mathcal {H}(R)) = \phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}^{\circ }(R))$
by Lemma 2.1(5), where
 $$ \begin{align*} \mathcal{H}^{\circ}(R) = \underset{\langle {\eta, \alpha} \rangle \neq 0}{\prod\limits_{\alpha \in \Delta}} \mathcal{H}_{\alpha}(R). \end{align*} $$
$$ \begin{align*} \mathcal{H}^{\circ}(R) = \underset{\langle {\eta, \alpha} \rangle \neq 0}{\prod\limits_{\alpha \in \Delta}} \mathcal{H}_{\alpha}(R). \end{align*} $$
Inspecting all possible Dynkin diagrams, it follows that the number of simple roots
![]() $\alpha \in \Delta $
for which
$\alpha \in \Delta $
for which
![]() $\langle {\eta , \alpha } \rangle \neq 0$
is at most four. The lemma follows.▪
$\langle {\eta , \alpha } \rangle \neq 0$
is at most four. The lemma follows.▪
Thus, in view of Proposition 3.4 and Lemma 3.5, the proof of Theorem 1.1 will be complete once we establish the following.
Proposition 3.6 Theorem 1.1 holds whenever
![]() $\mathcal {G}$
is a universal Chevalley–Demazure group scheme
$\mathcal {G}$
is a universal Chevalley–Demazure group scheme
![]() $\mathcal {G}_{\Phi }^{\text {sc}}$
with
$\mathcal {G}_{\Phi }^{\text {sc}}$
with
and
![]() $\mathfrak {X} \rtimes \mathcal {H}$
of the form
$\mathfrak {X} \rtimes \mathcal {H}$
of the form
 $$ \begin{align*} \mathfrak{X} \rtimes \mathcal{H} = \mathfrak{X}_{\eta} \rtimes \left( \underset{\langle {\eta, \alpha} \rangle \neq 0}{\prod\limits_{\alpha \in \Delta}} \mathcal{H}_{\alpha} \right) \text{ with } \eta \in \Phi^+ \text{ simple.} \end{align*} $$
$$ \begin{align*} \mathfrak{X} \rtimes \mathcal{H} = \mathfrak{X}_{\eta} \rtimes \left( \underset{\langle {\eta, \alpha} \rangle \neq 0}{\prod\limits_{\alpha \in \Delta}} \mathcal{H}_{\alpha} \right) \text{ with } \eta \in \Phi^+ \text{ simple.} \end{align*} $$
Proof The idea of the proof is quite simple. In each case, we find a matrix group
![]() $G(\Phi ,\eta ,R)$
satisfying
$G(\Phi ,\eta ,R)$
satisfying
![]() $\phi (G(\Phi ,\eta ,R)) = \phi (\textbf {B}_2^{\circ }(R))$
and which fits into a short exact sequence
$\phi (G(\Phi ,\eta ,R)) = \phi (\textbf {B}_2^{\circ }(R))$
and which fits into a short exact sequence
where
![]() $Q(\Phi ,\eta ,R)$
is finitely generated abelian. In fact,
$Q(\Phi ,\eta ,R)$
is finitely generated abelian. In fact,
![]() $G(\Phi ,\eta ,R)$
can often be taken to be
$G(\Phi ,\eta ,R)$
can often be taken to be
![]() $\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
itself so that
$\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
itself so that
![]() $Q(\Phi ,\eta ,R)$
is trivial in many cases. The proposition then follows from Lemma 2.1(2).
$Q(\Phi ,\eta ,R)$
is trivial in many cases. The proposition then follows from Lemma 2.1(2).
To construct the matrix groups
![]() $G(\Phi ,\eta ,R)$
above, we use mostly Ree’s matrix representations of classical groups [Reference Ree47] as worked out by Carter in [Reference Carter29]. (Recall that the case of Type
$G(\Phi ,\eta ,R)$
above, we use mostly Ree’s matrix representations of classical groups [Reference Ree47] as worked out by Carter in [Reference Carter29]. (Recall that the case of Type
![]() $\text {B}_n$
was cleared by Dieudonné [Reference Dieudonné35] after left open in Ree’s paper.) In the exceptional case
$\text {B}_n$
was cleared by Dieudonné [Reference Dieudonné35] after left open in Ree’s paper.) In the exceptional case
![]() $\text {G}_2$
, we follow Seligman’s identification from [Reference Seligman50]. We remark that Seligman’s numbering of indices agrees with that of Carter’s for
$\text {G}_2$
, we follow Seligman’s identification from [Reference Seligman50]. We remark that Seligman’s numbering of indices agrees with that of Carter’s for
![]() $\text {G}_2$
as a subalgebra of
$\text {G}_2$
as a subalgebra of
![]() $\text {B}_3$
.
$\text {B}_3$
.
Type A: Identify
![]() $\mathcal {G}^{\text {sc}}_{A_n}$
with
$\mathcal {G}^{\text {sc}}_{A_n}$
with
![]() $ \operatorname {\textrm {SL}}_{n+1}$
so that the soluble subgroup
$ \operatorname {\textrm {SL}}_{n+1}$
so that the soluble subgroup
![]() $\mathfrak {X}_{\eta } \rtimes \mathcal {H} \leq \operatorname {\textrm {SL}}_{n+1}$
is upper triangular and the given maximal torus
$\mathfrak {X}_{\eta } \rtimes \mathcal {H} \leq \operatorname {\textrm {SL}}_{n+1}$
is upper triangular and the given maximal torus
![]() $\mathcal {H}$
of
$\mathcal {H}$
of
![]() $ \operatorname {\textrm {SL}}_{n+1}$
is the subgroup of diagonal matrices. Now, if
$ \operatorname {\textrm {SL}}_{n+1}$
is the subgroup of diagonal matrices. Now, if
![]() $ \operatorname {\textrm {rk}}(\Phi )=1$
, then there is nothing to check, for in this case
$ \operatorname {\textrm {rk}}(\Phi )=1$
, then there is nothing to check, for in this case
![]() $\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
is itself isomorphic to
$\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
is itself isomorphic to
![]() $\textbf {B}_2^{\circ }(R)$
. If
$\textbf {B}_2^{\circ }(R)$
. If
![]() $\Phi = \text {A}_2$
, identify
$\Phi = \text {A}_2$
, identify
![]() $\mathfrak {X}_{\eta }(R)$
with the root subgroup
$\mathfrak {X}_{\eta }(R)$
with the root subgroup
![]() $\textbf {E}_{12}(R) \leq \operatorname {\textrm {SL}}_3(R)$
so that
$\textbf {E}_{12}(R) \leq \operatorname {\textrm {SL}}_3(R)$
so that
In this case,
![]() $G(\text {A}_2,\eta ,R) := \mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
is isomorphic to
$G(\text {A}_2,\eta ,R) := \mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
is isomorphic to
![]() $\textbf {B}_2(R)$
via
$\textbf {B}_2(R)$
via

The case
![]() $\text {A}_2$
thus follows from Lemma 3.3. If now
$\text {A}_2$
thus follows from Lemma 3.3. If now
![]() $\Phi = \text {A}_3$
, we identify
$\Phi = \text {A}_3$
, we identify
![]() $\mathfrak {X}_{\eta }(R)$
with the root subgroup
$\mathfrak {X}_{\eta }(R)$
with the root subgroup
![]() $\textbf {E}_{23}(R) \leq \operatorname {\textrm {SL}}_4(R)$
, which gives
$\textbf {E}_{23}(R) \leq \operatorname {\textrm {SL}}_4(R)$
, which gives
 $$ \begin{align*} \mathfrak{X}_{\eta}(R) \rtimes \mathcal{H}(R) \cong \left\{ \left(\begin{smallmatrix} a & 0 & 0 & 0 \\ 0 & b & r & 0 \\ 0 & 0 & c & 0 \\ 0 & 0 & 0 & (abc)^{-1} \end{smallmatrix} \right) \in \operatorname{\textrm{SL}}_3(R) \, \middle| \, a, b, c \in R^{\times}, r \in R \right\}. \end{align*} $$
$$ \begin{align*} \mathfrak{X}_{\eta}(R) \rtimes \mathcal{H}(R) \cong \left\{ \left(\begin{smallmatrix} a & 0 & 0 & 0 \\ 0 & b & r & 0 \\ 0 & 0 & c & 0 \\ 0 & 0 & 0 & (abc)^{-1} \end{smallmatrix} \right) \in \operatorname{\textrm{SL}}_3(R) \, \middle| \, a, b, c \in R^{\times}, r \in R \right\}. \end{align*} $$
Here,
![]() $G(\text {A}_3,\eta ,R) := \mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
is isomorphic to the group
$G(\text {A}_3,\eta ,R) := \mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
is isomorphic to the group
![]() $\textbf {B}_2(R) \times ~\mathbb {G}_m(R)$
via the map
$\textbf {B}_2(R) \times ~\mathbb {G}_m(R)$
via the map

Thus,
![]() $\phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)) = \phi (\textbf {B}_2^{\circ }(R))$
by Lemmata 2.1(5) and 3.3.
$\phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)) = \phi (\textbf {B}_2^{\circ }(R))$
by Lemmata 2.1(5) and 3.3.
Type C: Suppose
![]() $\Phi = \text {C}_n$
. Following Ree and Carter, we identify
$\Phi = \text {C}_n$
. Following Ree and Carter, we identify
![]() $\mathcal {G}^{\text {sc}}_{\text {C}_n}$
with the symplectic group
$\mathcal {G}^{\text {sc}}_{\text {C}_n}$
with the symplectic group
![]() $\text {Sp}_{2n} \leq \operatorname {\textrm {SL}}_{2n}$
. If
$\text {Sp}_{2n} \leq \operatorname {\textrm {SL}}_{2n}$
. If
![]() $\Phi = \text {C}_2$
, denote by
$\Phi = \text {C}_2$
, denote by
![]() $\Delta = \left \{ \alpha , \beta \right \}$
the set of simple roots, where
$\Delta = \left \{ \alpha , \beta \right \}$
the set of simple roots, where
![]() $\alpha $
is short and
$\alpha $
is short and
![]() $\beta $
is long. The unipotent root subgroups are given by
$\beta $
is long. The unipotent root subgroups are given by
whereas the maximal torus
![]() $\mathcal {H}(R)$
is the diagonal subgroup
$\mathcal {H}(R)$
is the diagonal subgroup
 $$ \begin{align*} \mathcal{H}(R) = \langle {\mathcal{H}_{\alpha}(R), \mathcal{H}_{\beta}(R)} \rangle \cong \langle \{ & \operatorname{\textrm{Diag}}(a,a^{-1},a^{-1},a), \\ & \operatorname{\textrm{Diag}}(1,b,1,b^{-1}) \in \operatorname{\textrm{SL}}_4(R) \mid a,b \in R^{\times} \} \rangle. \end{align*} $$
$$ \begin{align*} \mathcal{H}(R) = \langle {\mathcal{H}_{\alpha}(R), \mathcal{H}_{\beta}(R)} \rangle \cong \langle \{ & \operatorname{\textrm{Diag}}(a,a^{-1},a^{-1},a), \\ & \operatorname{\textrm{Diag}}(1,b,1,b^{-1}) \in \operatorname{\textrm{SL}}_4(R) \mid a,b \in R^{\times} \} \rangle. \end{align*} $$
Now, if
![]() $\eta = \alpha $
(that is, if
$\eta = \alpha $
(that is, if
![]() $\eta $
is short), then
$\eta $
is short), then
![]() $\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
is the group
$\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
is the group
 $$ \begin{align*} \mathfrak{X}_{\eta}(R) \rtimes \mathcal{H}(R) \cong \left\{ \left( \begin{smallmatrix} u & r & 0 & 0 \\ 0 & v & 0 & 0 \\ 0 & 0 & u^{-1} & 0 \\ 0 & 0 & -r & v^{-1} \end{smallmatrix} \right) \in \operatorname{\textrm{Sp}}_4(R) \, \middle| \, u, v \in R^{\times}, r \in R \right\}. \end{align*} $$
$$ \begin{align*} \mathfrak{X}_{\eta}(R) \rtimes \mathcal{H}(R) \cong \left\{ \left( \begin{smallmatrix} u & r & 0 & 0 \\ 0 & v & 0 & 0 \\ 0 & 0 & u^{-1} & 0 \\ 0 & 0 & -r & v^{-1} \end{smallmatrix} \right) \in \operatorname{\textrm{Sp}}_4(R) \, \middle| \, u, v \in R^{\times}, r \in R \right\}. \end{align*} $$
Hence,
![]() $G(\text {C}_2,\eta ,R) := \mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
is isomorphic to
$G(\text {C}_2,\eta ,R) := \mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
is isomorphic to
![]() $\textbf {B}_2(R)$
via
$\textbf {B}_2(R)$
via

which yields
![]() $\phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)) = \phi (\textbf {B}_2^{\circ }(R))$
by Lemma 3.3. On the other hand, if
$\phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)) = \phi (\textbf {B}_2^{\circ }(R))$
by Lemma 3.3. On the other hand, if
![]() $\eta = \beta $
(i.e.,
$\eta = \beta $
(i.e.,
![]() $\eta $
is long), then
$\eta $
is long), then
![]() $\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
is given by
$\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
is given by
 $$ \begin{align*} \mathfrak{X}_{\eta}(R) \rtimes \mathcal{H}(R) \cong \left\{ \left( \begin{smallmatrix} u & 0 & 0 & 0 \\ 0 & v & 0 & r \\ 0 & 0 & u^{-1} & 0 \\ 0 & 0 & 0 & v^{-1} \end{smallmatrix} \right) \in \operatorname{\textrm{Sp}}_4(R) \, \middle| \, u, v \in R^{\times}, r \in R \right\}, \end{align*} $$
$$ \begin{align*} \mathfrak{X}_{\eta}(R) \rtimes \mathcal{H}(R) \cong \left\{ \left( \begin{smallmatrix} u & 0 & 0 & 0 \\ 0 & v & 0 & r \\ 0 & 0 & u^{-1} & 0 \\ 0 & 0 & 0 & v^{-1} \end{smallmatrix} \right) \in \operatorname{\textrm{Sp}}_4(R) \, \middle| \, u, v \in R^{\times}, r \in R \right\}, \end{align*} $$
which is isomorphic to
![]() $\textbf {B}_2^{\circ }(R) \times \mathbb {G}_m(R)$
via
$\textbf {B}_2^{\circ }(R) \times \mathbb {G}_m(R)$
via

Thus,
![]() $\phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)) = \phi (\textbf {B}_2^{\circ }(R))$
by Lemma 2.1(5).
$\phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)) = \phi (\textbf {B}_2^{\circ }(R))$
by Lemma 2.1(5).
Lastly, assume
![]() $\Phi = \text {C}_3$
and denote its set of simple roots by
$\Phi = \text {C}_3$
and denote its set of simple roots by
![]() $\Delta =\left \{ \alpha _1, \alpha _2, \beta \right \}$
, where
$\Delta =\left \{ \alpha _1, \alpha _2, \beta \right \}$
, where
![]() $\beta $
is the long root. We have
$\beta $
is the long root. We have
![]() $\mathcal {G}^{\text {sc}}_{\text {C}_3} = \operatorname {\textrm {Sp}}_6$
with the root subgroups given by the following matrix subgroups.
$\mathcal {G}^{\text {sc}}_{\text {C}_3} = \operatorname {\textrm {Sp}}_6$
with the root subgroups given by the following matrix subgroups.
and
 $$ \begin{align*} & \mathcal{H}(R) = \langle {\mathcal{H}_{\alpha_1}(R), \mathcal{H}_{\alpha_2}(R), \mathcal{H}_{\beta}(R)} \rangle \cong \langle \, \{ \operatorname{\textrm{Diag}}(a_1, a_1^{-1}, 1, a_1^{-1}, a_1, 1), \\ & \operatorname{\textrm{Diag}}(1,a_2,a_2^{-1},1,a_2^{-1},a_2), \operatorname{\textrm{Diag}}(1, 1, b, 1, 1, b^{-1}) \mid a_1, a_2, b \in R^{\times} \}\, \rangle. \end{align*} $$
$$ \begin{align*} & \mathcal{H}(R) = \langle {\mathcal{H}_{\alpha_1}(R), \mathcal{H}_{\alpha_2}(R), \mathcal{H}_{\beta}(R)} \rangle \cong \langle \, \{ \operatorname{\textrm{Diag}}(a_1, a_1^{-1}, 1, a_1^{-1}, a_1, 1), \\ & \operatorname{\textrm{Diag}}(1,a_2,a_2^{-1},1,a_2^{-1},a_2), \operatorname{\textrm{Diag}}(1, 1, b, 1, 1, b^{-1}) \mid a_1, a_2, b \in R^{\times} \}\, \rangle. \end{align*} $$
Here, we are only interested in the case where
![]() $\eta $
is the central root
$\eta $
is the central root
![]() $\alpha _2$
, for otherwise
$\alpha _2$
, for otherwise
![]() $\eta $
would be orthogonal to one of the other simple roots. Thus,
$\eta $
would be orthogonal to one of the other simple roots. Thus,
 $$ \begin{align*} \mathfrak{X}_{\eta}(R) \rtimes \mathcal{H}(R) \cong \left\{ \left( \begin{smallmatrix} u & 0 & 0 & 0 & 0 & 0 \\ 0 & v & r & 0 & 0 & 0 \\ 0 & 0 & w & 0 & 0 & 0 \\ 0 & 0 & 0 & u^{-1} & 0 & 0 \\ 0 & 0 & 0 & 0 & v^{-1} & 0 \\ 0 & 0 & 0 & 0 & -r & w^{-1} \end{smallmatrix} \right) \in \operatorname{\textrm{Sp}}_6(R) \, \middle| \, u, v, w \in R^{\times}, r \in R \right\}. \end{align*} $$
$$ \begin{align*} \mathfrak{X}_{\eta}(R) \rtimes \mathcal{H}(R) \cong \left\{ \left( \begin{smallmatrix} u & 0 & 0 & 0 & 0 & 0 \\ 0 & v & r & 0 & 0 & 0 \\ 0 & 0 & w & 0 & 0 & 0 \\ 0 & 0 & 0 & u^{-1} & 0 & 0 \\ 0 & 0 & 0 & 0 & v^{-1} & 0 \\ 0 & 0 & 0 & 0 & -r & w^{-1} \end{smallmatrix} \right) \in \operatorname{\textrm{Sp}}_6(R) \, \middle| \, u, v, w \in R^{\times}, r \in R \right\}. \end{align*} $$
The isomorphism

between
![]() $G(\text {C}_3,\eta ,R) := \mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
and
$G(\text {C}_3,\eta ,R) := \mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)$
and
![]() $\textbf {B}_2(R) \times \mathbb {G}_m(R)$
then yields
$\textbf {B}_2(R) \times \mathbb {G}_m(R)$
then yields
![]() $\phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)) = \phi (\textbf {B}_2^{\circ }(R))$
by Lemmata 2.1(5) and 3.3.
$\phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)) = \phi (\textbf {B}_2^{\circ }(R))$
by Lemmata 2.1(5) and 3.3.
Type D: The case of maximal rank concerns the root system
![]() $\Phi = \text {D}_4$
, with set of simple roots
$\Phi = \text {D}_4$
, with set of simple roots
![]() $\left \{ \alpha _1, \alpha _2, \alpha _3, \alpha _4 \right \}$
and the given simple root
$\left \{ \alpha _1, \alpha _2, \alpha _3, \alpha _4 \right \}$
and the given simple root
![]() $\eta $
being equal to the central root
$\eta $
being equal to the central root
![]() $\alpha _2$
which is not orthogonal to any other simple root. Here,
$\alpha _2$
which is not orthogonal to any other simple root. Here,
![]() $\mathcal {G}^{\text {sc}}_{\text {D}_4} = \text {Spin}_8$
. Following Ree and Carter, the root subgroups and the maximal torus are given as follows.
$\mathcal {G}^{\text {sc}}_{\text {D}_4} = \text {Spin}_8$
. Following Ree and Carter, the root subgroups and the maximal torus are given as follows.
and
 $$ \begin{align*} \mathcal{H}(R) = & \langle {\mathcal{H}_{\alpha_1}(R), \, \mathcal{H}_{\alpha_2}(R), \, \mathcal{H}_{\alpha_3}(R), \, \mathcal{H}_{\alpha_4}(R)} \rangle \\ \cong & \langle \, \{ \operatorname{\textrm{Diag}}(a_1, a_1^{-1}, 1, 1, a_1^{-1}, a_1, 1, 1), \, \, \operatorname{\textrm{Diag}}(1, a_2, a_2^{-1}, 1, 1, a_2^{-1}, a_2, 1), \\ & \operatorname{\textrm{Diag}}(1, 1, a_3, a_3^{-1}, 1, 1, a_3^{-1}, a_3), \quad \operatorname{\textrm{Diag}}(1, 1, a_4, a_4, 1, 1, a_4^{-1}, a_4^{-1}) \\ & \in \operatorname{\textrm{SL}}_8(R) \mid a_1, a_2, a_3, a_4 \in R^{\times} \} \, \rangle. \end{align*} $$
$$ \begin{align*} \mathcal{H}(R) = & \langle {\mathcal{H}_{\alpha_1}(R), \, \mathcal{H}_{\alpha_2}(R), \, \mathcal{H}_{\alpha_3}(R), \, \mathcal{H}_{\alpha_4}(R)} \rangle \\ \cong & \langle \, \{ \operatorname{\textrm{Diag}}(a_1, a_1^{-1}, 1, 1, a_1^{-1}, a_1, 1, 1), \, \, \operatorname{\textrm{Diag}}(1, a_2, a_2^{-1}, 1, 1, a_2^{-1}, a_2, 1), \\ & \operatorname{\textrm{Diag}}(1, 1, a_3, a_3^{-1}, 1, 1, a_3^{-1}, a_3), \quad \operatorname{\textrm{Diag}}(1, 1, a_4, a_4, 1, 1, a_4^{-1}, a_4^{-1}) \\ & \in \operatorname{\textrm{SL}}_8(R) \mid a_1, a_2, a_3, a_4 \in R^{\times} \} \, \rangle. \end{align*} $$
The torus
![]() $\mathcal {H}(R)$
is a subgroup of the following diagonal group.
$\mathcal {H}(R)$
is a subgroup of the following diagonal group.
Recall that
![]() $\eta = \alpha _2$
, the central root. Set
$\eta = \alpha _2$
, the central root. Set
![]() $G(\text {D}_4,\alpha _2,R) := \mathfrak {X}_{\eta }(R) \rtimes T(R)$
. We have a short exact sequence
$G(\text {D}_4,\alpha _2,R) := \mathfrak {X}_{\eta }(R) \rtimes T(R)$
. We have a short exact sequence
 $$ \begin{align*} \mathfrak{X}_{\eta}(R) \rtimes \mathcal{H}(R) \hookrightarrow G(\text{D}_4,\alpha_2,R) \twoheadrightarrow \frac{T(R)}{\mathcal{H}(R)} \end{align*} $$
$$ \begin{align*} \mathfrak{X}_{\eta}(R) \rtimes \mathcal{H}(R) \hookrightarrow G(\text{D}_4,\alpha_2,R) \twoheadrightarrow \frac{T(R)}{\mathcal{H}(R)} \end{align*} $$
with quotient
![]() $T(R)/\mathcal {H}(R)$
finitely generated abelian. But
$T(R)/\mathcal {H}(R)$
finitely generated abelian. But
![]() $G(\text {D}_4,\alpha _2,R)$
is isomorphic to
$G(\text {D}_4,\alpha _2,R)$
is isomorphic to
![]() $\textbf {B}_2(R) \times \mathbb {G}_m(R)^2$
via
$\textbf {B}_2(R) \times \mathbb {G}_m(R)^2$
via

whence
![]() $\phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)) \leq \phi (\textbf {B}_2^{\circ }(R))$
by Lemmata 2.1(5) and 3.3.
$\phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)) \leq \phi (\textbf {B}_2^{\circ }(R))$
by Lemmata 2.1(5) and 3.3.
Types B and G: We approach the remaining cases using the embedding of the group of type
![]() $\text {G}_2$
into the spin group of type
$\text {G}_2$
into the spin group of type
![]() $\text {B}_3$
. Assume for the remainder of the proof that the base ring R has
$\text {B}_3$
. Assume for the remainder of the proof that the base ring R has
![]() $ \operatorname {\textrm {char}}(R) \neq 2$
in order to simplify the choice of a symmetric matrix preserved by the elements of
$ \operatorname {\textrm {char}}(R) \neq 2$
in order to simplify the choice of a symmetric matrix preserved by the elements of
![]() $\mathcal {G}^{\text {sc}}_{\text {B}_3}(R) = \text {Spin}_7(R)$
. This assumption is harmless, for the proof in the case
$\mathcal {G}^{\text {sc}}_{\text {B}_3}(R) = \text {Spin}_7(R)$
. This assumption is harmless, for the proof in the case
![]() $ \operatorname {\textrm {char}}(R) = 2$
follows analogously (after a change of basis) using Dieudounné’s matrix representation [Reference Dieudonné35].
$ \operatorname {\textrm {char}}(R) = 2$
follows analogously (after a change of basis) using Dieudounné’s matrix representation [Reference Dieudonné35].
Denote by
![]() $\Delta = \left \{ \alpha _1, \alpha _2, \beta \right \}$
the set of simple roots of
$\Delta = \left \{ \alpha _1, \alpha _2, \beta \right \}$
the set of simple roots of
![]() $\text {B}_3$
, where
$\text {B}_3$
, where
![]() $\beta $
is the short root. The root subgroups are given below. (Here,
$\beta $
is the short root. The root subgroups are given below. (Here,
![]() $E_{ij} $
denotes the square matrix whose only nonzero entry is 1 on the position (i,j).)
$E_{ij} $
denotes the square matrix whose only nonzero entry is 1 on the position (i,j).)
and
Now let
![]() $\Lambda = \left \{ \alpha , \gamma \right \}$
denote the set of simple roots of
$\Lambda = \left \{ \alpha , \gamma \right \}$
denote the set of simple roots of
![]() $\text {G}_2$
, where
$\text {G}_2$
, where
![]() $\gamma $
is the short root. In the identification above, the embedding of
$\gamma $
is the short root. In the identification above, the embedding of
![]() $\text {G}_2$
into
$\text {G}_2$
into
![]() $\text {B}_3$
maps the long root
$\text {B}_3$
maps the long root
![]() $\alpha \in \text {G}_2$
to the (long) root
$\alpha \in \text {G}_2$
to the (long) root
![]() $\alpha _1 \in \text {B}_3$
, and the root subgroups of
$\alpha _1 \in \text {B}_3$
, and the root subgroups of
![]() $\mathcal {G}^{\text {sc}}_{\text {G}_2} \leq \mathcal {G}^{\text {sc}}_{\text {B}_3}$
are listed below.
$\mathcal {G}^{\text {sc}}_{\text {G}_2} \leq \mathcal {G}^{\text {sc}}_{\text {B}_3}$
are listed below.
and
We now return to the soluble subgroup
![]() $\mathfrak {X}_{\eta } \rtimes \mathcal {H} \leq \mathcal {G}_{\Phi }^{\text {sc}}$
. In the case
$\mathfrak {X}_{\eta } \rtimes \mathcal {H} \leq \mathcal {G}_{\Phi }^{\text {sc}}$
. In the case
![]() $\Phi = \text {B}_3$
, the maximal torus
$\Phi = \text {B}_3$
, the maximal torus
![]() $\mathcal {H}(R)$
is the diagonal subgroup
$\mathcal {H}(R)$
is the diagonal subgroup
![]() $\mathcal {H}(R) = \langle {\mathcal {H}_{\alpha _1}(R), \, \mathcal {H}_{\alpha _2}(R), \, \mathcal {H}_{\beta }(R)} \rangle $
and
$\mathcal {H}(R) = \langle {\mathcal {H}_{\alpha _1}(R), \, \mathcal {H}_{\alpha _2}(R), \, \mathcal {H}_{\beta }(R)} \rangle $
and
![]() $\eta $
is the middle simple root
$\eta $
is the middle simple root
![]() $\alpha _2$
which is not orthogonal to the other simple roots, so that
$\alpha _2$
which is not orthogonal to the other simple roots, so that
![]() $\mathfrak {X}_{\eta }(R) = \mathfrak {X}_{\alpha _2}(R)$
. Let
$\mathfrak {X}_{\eta }(R) = \mathfrak {X}_{\alpha _2}(R)$
. Let
![]() $T(R)$
be the diagonal group
$T(R)$
be the diagonal group
Setting
![]() $G(\text {B}_3,\alpha _2,R) := \mathfrak {X}_{\eta }(R) \rtimes T(R)$
, we obtain a short exact sequence
$G(\text {B}_3,\alpha _2,R) := \mathfrak {X}_{\eta }(R) \rtimes T(R)$
, we obtain a short exact sequence
 $$ \begin{align*} \mathfrak{X}_{\eta}(R) \rtimes \mathcal{H}(R) \hookrightarrow G(\text{B}_3,\alpha_2,R) \twoheadrightarrow \frac{T(R)}{\mathcal{H}(R)}, \end{align*} $$
$$ \begin{align*} \mathfrak{X}_{\eta}(R) \rtimes \mathcal{H}(R) \hookrightarrow G(\text{B}_3,\alpha_2,R) \twoheadrightarrow \frac{T(R)}{\mathcal{H}(R)}, \end{align*} $$
which gives
![]() $\phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)) \leq \phi (G(\text {B}_3,\alpha _2,R))$
by Lemma 2.1(2). But the isomorphism
$\phi (\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R)) \leq \phi (G(\text {B}_3,\alpha _2,R))$
by Lemma 2.1(2). But the isomorphism
![]() $G(\text {B}_3,\alpha _2,R) \cong \textbf {B}_2(R) \times \mathbb {G}_m(R)$
given by
$G(\text {B}_3,\alpha _2,R) \cong \textbf {B}_2(R) \times \mathbb {G}_m(R)$
given by

yields
![]() $\phi (G(\text {B}_3,\alpha _2,R)) = \phi (\textbf {B}_2^{\circ }(R))$
by Lemmata 2.1(5) and 3.3.
$\phi (G(\text {B}_3,\alpha _2,R)) = \phi (\textbf {B}_2^{\circ }(R))$
by Lemmata 2.1(5) and 3.3.
Suppose now that
![]() $\Phi = \text {G}_2$
. The maximal torus
$\Phi = \text {G}_2$
. The maximal torus
![]() $\mathcal {H}(R)$
is the diagonal subgroup
$\mathcal {H}(R)$
is the diagonal subgroup
![]() $\mathcal {H}(R) = \langle {\mathcal {H}_{\alpha }(R), \, \mathcal {H}_{\gamma }(R)} \rangle $
. This time, we consider the diagonal subgroup
$\mathcal {H}(R) = \langle {\mathcal {H}_{\alpha }(R), \, \mathcal {H}_{\gamma }(R)} \rangle $
. This time, we consider the diagonal subgroup
and let
![]() $G(\text {G}_2,\eta ,R) := \mathfrak {X}_{\eta }(R) \rtimes T(R)$
, again obtaining a short exact sequence
$G(\text {G}_2,\eta ,R) := \mathfrak {X}_{\eta }(R) \rtimes T(R)$
, again obtaining a short exact sequence
![]() $\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R) \hookrightarrow G(\text {G}_2,\eta ,R) \twoheadrightarrow T(R)/\mathcal {H}(R)$
which yields
$\mathfrak {X}_{\eta }(R) \rtimes \mathcal {H}(R) \hookrightarrow G(\text {G}_2,\eta ,R) \twoheadrightarrow T(R)/\mathcal {H}(R)$
which yields
![]() $\phi (\mathfrak {X}_{\eta }(R) \rtimes ~\mathcal {H}(R)) \leq \phi (G(\text {G}_2,\eta ,R))$
. If
$\phi (\mathfrak {X}_{\eta }(R) \rtimes ~\mathcal {H}(R)) \leq \phi (G(\text {G}_2,\eta ,R))$
. If
![]() $\eta $
is the long root
$\eta $
is the long root
![]() $\alpha = \alpha _1$
, then the map
$\alpha = \alpha _1$
, then the map

yields an isomorphism
![]() $G(\text {G}_2,\eta ,R) \cong \textbf {B}_2(R)$
, whence
$G(\text {G}_2,\eta ,R) \cong \textbf {B}_2(R)$
, whence
![]() $\phi (G(\text {G}_2,\eta ,R)) = \phi (\textbf {B}_2^{\circ }(R))$
by Lemma 3.3. If
$\phi (G(\text {G}_2,\eta ,R)) = \phi (\textbf {B}_2^{\circ }(R))$
by Lemma 3.3. If
![]() $\eta $
is the short root
$\eta $
is the short root
![]() $\gamma $
, we observe that
$\gamma $
, we observe that
because the following holds for any
![]() $x_{\gamma }(r) = \exp (r \cdot (2 \cdot \text {E}_{12} + \text {E}_{37} - \text {E}_{46} - \text {E}_{51})) \in \mathfrak {X}_{\gamma }(R)$
and
$x_{\gamma }(r) = \exp (r \cdot (2 \cdot \text {E}_{12} + \text {E}_{37} - \text {E}_{46} - \text {E}_{51})) \in \mathfrak {X}_{\gamma }(R)$
and
![]() $d~=~ \operatorname {\textrm {Diag}}(1,u,v,u^{-1}v^{-1},u^{-1},v^{-1},uv) \in T(R)$
.
$d~=~ \operatorname {\textrm {Diag}}(1,u,v,u^{-1}v^{-1},u^{-1},v^{-1},uv) \in T(R)$
.
 $$ \begin{align*} d x_{\gamma}(r) d^{-1} = d \left( \begin{smallmatrix} 1 & 2r & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & r \\ 0 & 0 & 0 & 1 & 0 & -r & 0 \\ -r & -r^2 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{smallmatrix} \right) d^{-1} = \left( \begin{smallmatrix} 1 & u^{-1}2r & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & u^{-1}r \\ 0 & 0 & 0 & 1 & 0 & -u^{-1}r & 0 \\ -u^{-1}r & -u^{-2}r^2 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{smallmatrix} \right). \end{align*} $$
$$ \begin{align*} d x_{\gamma}(r) d^{-1} = d \left( \begin{smallmatrix} 1 & 2r & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & r \\ 0 & 0 & 0 & 1 & 0 & -r & 0 \\ -r & -r^2 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{smallmatrix} \right) d^{-1} = \left( \begin{smallmatrix} 1 & u^{-1}2r & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & u^{-1}r \\ 0 & 0 & 0 & 1 & 0 & -u^{-1}r & 0 \\ -u^{-1}r & -u^{-2}r^2 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{smallmatrix} \right). \end{align*} $$
Hence,
![]() $\phi (G(\text {G}_2,\eta ,R)) = \phi (\mathfrak {X}_{\gamma }(R) \rtimes \mathcal {H}_{\alpha }(R))$
.
$\phi (G(\text {G}_2,\eta ,R)) = \phi (\mathfrak {X}_{\gamma }(R) \rtimes \mathcal {H}_{\alpha }(R))$
.
The group
![]() $\mathfrak {X}_{\gamma }(R) \rtimes \mathcal {H}_{\alpha }(R)$
above is in turn isomorphic to the affine group
$\mathfrak {X}_{\gamma }(R) \rtimes \mathcal {H}_{\alpha }(R)$
above is in turn isomorphic to the affine group
![]() $\mathbb {A}\text {ff}_-(R)$
, which is commensurable with
$\mathbb {A}\text {ff}_-(R)$
, which is commensurable with
![]() $\textbf {B}_2^{\circ }(R)$
by Lemma 3.2. Thus,
$\textbf {B}_2^{\circ }(R)$
by Lemma 3.2. Thus,
by Lemmata 2.1(5) and 3.2. This finishes the proof of the proposition and thus of Theorem 1.1.▪
3.1 A geometric version of Theorem 1.1
We remark that Theorem 1.1 can be slightly modified as to avoid a representation
![]() $\rho ~:~G \twoheadrightarrow \mathfrak {X}(R) \rtimes \mathcal {H}(R)$
with sequence
$\rho ~:~G \twoheadrightarrow \mathfrak {X}(R) \rtimes \mathcal {H}(R)$
with sequence
![]() $\ker (\rho ) \hookrightarrow G \twoheadrightarrow \mathfrak {X}(R) \rtimes \mathcal {H}(R)$
split. We shall relax the hypothesis on
$\ker (\rho ) \hookrightarrow G \twoheadrightarrow \mathfrak {X}(R) \rtimes \mathcal {H}(R)$
split. We shall relax the hypothesis on
![]() $\rho $
at the cost of an assumption on the base ring R.
$\rho $
at the cost of an assumption on the base ring R.
Recall that a metric space Y is a quasi-retract of a metric space X if there exists a pair
![]() $r : X \to Y$
and
$r : X \to Y$
and
![]() $\iota : Y \to X$
of
$\iota : Y \to X$
of
![]() $(C,D)$
-Lipschitz functions such that
$(C,D)$
-Lipschitz functions such that
![]() $d_Y(r \circ \iota (y), y) \leq D$
for all
$d_Y(r \circ \iota (y), y) \leq D$
for all
![]() $y \in Y$
; see [Reference Alonso6]. The point now is that quasi-retracts also inherit homotopical finiteness properties. In particular, if G and H are finitely generated groups such that
$y \in Y$
; see [Reference Alonso6]. The point now is that quasi-retracts also inherit homotopical finiteness properties. In particular, if G and H are finitely generated groups such that
![]() $r : G \to H$
is a quasi-retract, Alonso proved that
$r : G \to H$
is a quasi-retract, Alonso proved that
![]() $\phi (G) \leq \phi (H)$
; see [Reference Alonso6, Theorem 8]. Of course, group retracts are particular examples of quasi-retracts.
$\phi (G) \leq \phi (H)$
; see [Reference Alonso6, Theorem 8]. Of course, group retracts are particular examples of quasi-retracts.
The advantage here is that a quasi-retract
![]() $r : G \to H$
needs not be a group homomorphism. In a recent remarkable paper, Skipper et al. [Reference Skipper, Witzel and Zaremsky52] used the finiteness length and quasi-retracts to construct infinitely many quasi-isometry classes of finitely presented simple groups.
$r : G \to H$
needs not be a group homomorphism. In a recent remarkable paper, Skipper et al. [Reference Skipper, Witzel and Zaremsky52] used the finiteness length and quasi-retracts to construct infinitely many quasi-isometry classes of finitely presented simple groups.
Using the geometric language above, we have the following.
Theorem 3.7 Let G be a group and let R be a commutative ring with unity for which
![]() $\mathbb {A}\text {ff}(R)$
is finitely generated. If there exists a quasi-retract
$\mathbb {A}\text {ff}(R)$
is finitely generated. If there exists a quasi-retract
![]() $\rho : G \to \mathfrak {X}(R) \rtimes \mathcal {H}(R)$
, where
$\rho : G \to \mathfrak {X}(R) \rtimes \mathcal {H}(R)$
, where
![]() $\mathfrak {X}$
and
$\mathfrak {X}$
and
![]() $\mathcal {H}$
denote, respectively, a unipotent root subgroup and a maximal torus of any of the affine groups
$\mathcal {H}$
denote, respectively, a unipotent root subgroup and a maximal torus of any of the affine groups
![]() $\mathbb {A}\text {ff}$
,
$\mathbb {A}\text {ff}$
,
![]() $\mathbb {A}\text {ff}_-$
or of a classical group, then
$\mathbb {A}\text {ff}_-$
or of a classical group, then
![]() $\phi (G)\leq \phi (\textbf {B}_2^{\circ }(R))$
.
$\phi (G)\leq \phi (\textbf {B}_2^{\circ }(R))$
.
Proof The assumption on R implies that
![]() $\mathfrak {X}(R) \rtimes \mathcal {H}(R)$
is finitely generated. Now, if G is not finitely generated, then
$\mathfrak {X}(R) \rtimes \mathcal {H}(R)$
is finitely generated. Now, if G is not finitely generated, then
![]() $\phi (G) \leq \phi (\textbf {B}_2^{\circ }(R))$
holds trivially. Otherwise one has
$\phi (G) \leq \phi (\textbf {B}_2^{\circ }(R))$
holds trivially. Otherwise one has
![]() $\phi (G) \leq \phi (\mathfrak {X}(R) \rtimes \mathcal {H}(R))$
by Alonso’s theorem [Reference Alonso6, Theorem 8]. The fact that
$\phi (G) \leq \phi (\mathfrak {X}(R) \rtimes \mathcal {H}(R))$
by Alonso’s theorem [Reference Alonso6, Theorem 8]. The fact that
![]() $\phi (\mathfrak {X}(R)~\rtimes ~\mathcal {H}(R)) \leq \phi (\textbf {B}_2^{\circ }(R))$
was proved in Section 3, whence the theorem.▪
$\phi (\mathfrak {X}(R)~\rtimes ~\mathcal {H}(R)) \leq \phi (\textbf {B}_2^{\circ }(R))$
was proved in Section 3, whence the theorem.▪
4 The finiteness lengths of Abels’ groups
In what follows we give a full proof of Theorem 1.2 and discuss open problems regarding finiteness properties of Abels’ groups.
We first observe that
![]() $\textbf {A}_n(R)$
decomposes as a semidirect product
$\textbf {A}_n(R)$
decomposes as a semidirect product
![]() $\textbf {A}_n(R) = \textbf {U}_n(R) \rtimes \textbf {T}_n(R)$
, where
$\textbf {A}_n(R) = \textbf {U}_n(R) \rtimes \textbf {T}_n(R)$
, where
 $$ \begin{align*} \textbf{U}_n(R) = \left( \begin{smallmatrix} 1 & * & \cdots & \cdots & * \\ 0 & 1 & \ddots & & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots & 0 & 1 & * \\ 0 & \cdots & \cdots & 0 & 1 \end{smallmatrix} \right), \textbf{T}_n(R) = \left( \begin{smallmatrix} 1 & 0 & \cdots & \cdots & 0 \\ 0 & * & \ddots & & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots & 0 & * & 0 \\ 0 & \cdots & \cdots & 0 & 1 \end{smallmatrix} \right) = \textbf{A}_n(R) \cap \textbf{D}_n(R). \end{align*} $$
$$ \begin{align*} \textbf{U}_n(R) = \left( \begin{smallmatrix} 1 & * & \cdots & \cdots & * \\ 0 & 1 & \ddots & & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots & 0 & 1 & * \\ 0 & \cdots & \cdots & 0 & 1 \end{smallmatrix} \right), \textbf{T}_n(R) = \left( \begin{smallmatrix} 1 & 0 & \cdots & \cdots & 0 \\ 0 & * & \ddots & & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots & 0 & * & 0 \\ 0 & \cdots & \cdots & 0 & 1 \end{smallmatrix} \right) = \textbf{A}_n(R) \cap \textbf{D}_n(R). \end{align*} $$
Just as with Abels’ original group
![]() $\textbf {A}_4(\mathbb {Z}[1/p])$
from [Reference Abels1], we see using relations (2.1) and (2.2) that the center of
$\textbf {A}_4(\mathbb {Z}[1/p])$
from [Reference Abels1], we see using relations (2.1) and (2.2) that the center of
![]() $\textbf {A}_n(R)$
is the additive group
$\textbf {A}_n(R)$
is the additive group
![]() $Z(\textbf {A}_n(R)) = \textbf {E}_{1n}(R) \cong \mathbb {G}_a(R)$
generated by all elementary matrices in the upper right corner.
$Z(\textbf {A}_n(R)) = \textbf {E}_{1n}(R) \cong \mathbb {G}_a(R)$
generated by all elementary matrices in the upper right corner.
The first claims of Theorem 1.2 are well-known and follow from standard methods. For the sake of completeness, we shall also prove them in detail below in Section 4.2. The tricky part of Theorem 1.2 is the claim (3). The outline of its proof is as follows. The first inequality follows from Theorem 1.1, and it is also not hard to see that
![]() $\textbf {A}_n(R)$
is finitely generated whenever
$\textbf {A}_n(R)$
is finitely generated whenever
![]() $\textbf {B}_2^{\circ }(R)$
is so. Now, for a pair
$\textbf {B}_2^{\circ }(R)$
is so. Now, for a pair
![]() $(n,R)$
with
$(n,R)$
with
![]() $n \in \mathbb {Z}_{\geq 4}$
, we construct a finite-dimensional connected simplicial complex
$n \in \mathbb {Z}_{\geq 4}$
, we construct a finite-dimensional connected simplicial complex
![]() $CC(\mathscr{H}\;(n,R))$
on which
$CC(\mathscr{H}\;(n,R))$
on which
![]() $\textbf {A}_n(R)$
acts cocompactly by cell-permuting homeomorphisms. Generalizing a result due to Holz, we show that the space
$\textbf {A}_n(R)$
acts cocompactly by cell-permuting homeomorphisms. Generalizing a result due to Holz, we show that the space
![]() $CC(\mathscr{H}\;(n,R))$
is simply-connected regardless of R. Using
$CC(\mathscr{H}\;(n,R))$
is simply-connected regardless of R. Using
![]() $\Sigma $
-theory for metabelian groups [Reference Bieri, de Cornulier, Guyot and Strebel13], we prove that all cell stabilizers of the given action
$\Sigma $
-theory for metabelian groups [Reference Bieri, de Cornulier, Guyot and Strebel13], we prove that all cell stabilizers of the given action
![]() $\textbf {A}_n(R) \curvearrowright CC(\mathscr{H}\;(n,R))$
are finitely presented whenever
$\textbf {A}_n(R) \curvearrowright CC(\mathscr{H}\;(n,R))$
are finitely presented whenever
![]() $\textbf {B}_2^{\circ }(R)$
is so. We finish off the proof by invoking the following well-known criterion whose final form below is due to Brown.
$\textbf {B}_2^{\circ }(R)$
is so. We finish off the proof by invoking the following well-known criterion whose final form below is due to Brown.
Theorem 4.1 [Reference Brown17]
Let G be a group acting by cell-permuting homeomorphisms on a connected, simply-connected CW-complex X such that (a) all vertex-stabilizers are finitely presented, (b) all edge-stabilizers are finitely generated, and (c) the G-action on the two-skeleton
![]() $X^{(2)}$
is cocompact. Then G is finitely presented, that is,
$X^{(2)}$
is cocompact. Then G is finitely presented, that is,
![]() $\phi (G) \geq 2$
.
$\phi (G) \geq 2$
.
4.1 A space for
 $\textbf {A}_n(R)$
$\textbf {A}_n(R)$
Recall that a covering of a set X is a collection of subsets
![]() $\left \{ X_{\lambda } \right \}_{\lambda \in \Lambda }$
of X whose union is the whole of X, i.e.,
$\left \{ X_{\lambda } \right \}_{\lambda \in \Lambda }$
of X whose union is the whole of X, i.e.,
![]() $X = \cup _{\lambda \in \Lambda } X_{\lambda }$
. The nerve of the covering
$X = \cup _{\lambda \in \Lambda } X_{\lambda }$
. The nerve of the covering
![]() $\left \{ X_{\lambda } \right \}_{\lambda \in \Lambda }$
is the simplicial complex
$\left \{ X_{\lambda } \right \}_{\lambda \in \Lambda }$
is the simplicial complex
![]() ${N(\left \{ X_{\lambda } \right \}_{\lambda \in \Lambda })}$
defined as follows. Its vertices are the sets
${N(\left \{ X_{\lambda } \right \}_{\lambda \in \Lambda })}$
defined as follows. Its vertices are the sets
![]() $X_{\lambda }$
for
$X_{\lambda }$
for
![]() $\lambda \in \Lambda $
, and
$\lambda \in \Lambda $
, and
![]() $k+1$
vertices
$k+1$
vertices
![]() $X_{\lambda _0}, X_{\lambda _1}, \ldots , X_{\lambda _k}$
span a k-simplex whenever the intersection of all such
$X_{\lambda _0}, X_{\lambda _1}, \ldots , X_{\lambda _k}$
span a k-simplex whenever the intersection of all such
![]() $X_{\lambda _i}$
is nonempty, i.e.,
$X_{\lambda _i}$
is nonempty, i.e.,
![]() $\cap _{i=0}^k X_{\lambda _i} \neq \varnothing $
.
$\cap _{i=0}^k X_{\lambda _i} \neq \varnothing $
.
In [Reference Abels and Holz4, Reference Holz39], Holz and Abels investigate nerve complexes attached to groups as follows. Fixing a family of subgroups, they take the nerve of the covering of the group by all cosets of subgroups of the given family. (Such spaces are also called coset posets or coset complexes in the literature.) More precisely, given a group G and a family
![]() $\mathscr{H} = \left \{ H_{\lambda } \right \}_{\lambda \in \Lambda }$
of subgroups of G, let
$\mathscr{H} = \left \{ H_{\lambda } \right \}_{\lambda \in \Lambda }$
of subgroups of G, let
![]() $\mathfrak {H}$
denote the covering
$\mathfrak {H}$
denote the covering
![]() $\mathfrak {H} = \left \{ gH \mid g \in G, \, H \in \mathscr{H}\;\right \}$
of G by all left cosets of all members of
$\mathfrak {H} = \left \{ gH \mid g \in G, \, H \in \mathscr{H}\;\right \}$
of G by all left cosets of all members of
![]() $\mathscr{H}$
. The coset complex
$\mathscr{H}$
. The coset complex
![]() ${CC(\mathscr{H})}$
is defined as the nerve of the covering
${CC(\mathscr{H})}$
is defined as the nerve of the covering
![]() $N(\mathfrak {H}\;)$
. In particular, if the family
$N(\mathfrak {H}\;)$
. In particular, if the family
![]() $\mathscr{H}$
is finite, then
$\mathscr{H}$
is finite, then
![]() $CC(\mathscr{H})$
is
$CC(\mathscr{H})$
is
![]() $(\vert \mathscr{H}\;\vert -1)$
-dimensional.
$(\vert \mathscr{H}\;\vert -1)$
-dimensional.
Inspiration for the above came primarily from the theory of buildings: if G is a group with a BN-pair
![]() $(G,B,N,S)$
, then the coset poset
$(G,B,N,S)$
, then the coset poset
![]() $CC(\mathscr{H}\;)$
associated to the family
$CC(\mathscr{H}\;)$
associated to the family
![]() $\mathscr{H}$
of all maximal standard parabolic subgroups of G is by definition the building
$\mathscr{H}$
of all maximal standard parabolic subgroups of G is by definition the building
![]() $\Delta (G,B)$
associated to the system
$\Delta (G,B)$
associated to the system
![]() $(G,B,N,S)$
; see [Reference Abramenko and Brown5, Section 6.2] and [Reference Brück19]. As it turns out, coset complexes show up in many other contexts, such as Deligne complexes [Reference Charney and Davis30], Bass–Serre theory [Reference Serre51],
$(G,B,N,S)$
; see [Reference Abramenko and Brown5, Section 6.2] and [Reference Brück19]. As it turns out, coset complexes show up in many other contexts, such as Deligne complexes [Reference Charney and Davis30], Bass–Serre theory [Reference Serre51],
![]() $\Sigma $
-invariants of right-angled Artin groups [Reference Meier, Meinert and VanWyk44], and higher generating families of braid groups [Reference Bux, Baake, Götze and Hoffmann23, Reference Bux, Fluch, Marschler, Witzel and Zaremsky24] and automorphism groups of free groups [Reference Brück20, Reference Brück19].
$\Sigma $
-invariants of right-angled Artin groups [Reference Meier, Meinert and VanWyk44], and higher generating families of braid groups [Reference Bux, Baake, Götze and Hoffmann23, Reference Bux, Fluch, Marschler, Witzel and Zaremsky24] and automorphism groups of free groups [Reference Brück20, Reference Brück19].
Since vertices of
![]() $CC(\mathscr{H}\;)$
are cosets in the group G, it follows that G acts naturally on
$CC(\mathscr{H}\;)$
are cosets in the group G, it follows that G acts naturally on
![]() $CC(\mathscr{H}\;)$
by cell-permuting homeomorphisms, namely the action induced by left multiplication on the cosets
$CC(\mathscr{H}\;)$
by cell-permuting homeomorphisms, namely the action induced by left multiplication on the cosets
![]() $gH$
for
$gH$
for
![]() $g \in G$
and
$g \in G$
and
![]() $H \in \mathscr{H}$
.
$H \in \mathscr{H}$
.
Going back to Abels’ groups, consider the following
![]() $\mathbb {Z}$
-subschemes of
$\mathbb {Z}$
-subschemes of
![]() $\textbf {A}_n$
.
$\textbf {A}_n$
.
 $$ \begin{align*} H_1 = \left( \begin{smallmatrix} 1 & * & \cdots & * & 0 \\ 0 & * & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & * & \vdots \\ 0 & & 0 & * & 0 \\ 0 & 0 & \cdots & 0 & 1 \end{smallmatrix} \right), \, H_2 = \left( \begin{smallmatrix} 1 & 0 & \cdots & \cdots & 0 \\ 0 & * & * & \cdots & * \\ \vdots & \ddots & \ddots & * & \vdots \\ 0 & & 0 & * & * \\ 0 & 0 & \cdots & 0 & 1 \end{smallmatrix} \right), \, H_3 = \left( \begin{smallmatrix} 1 & * & 0 & \cdots & 0 \\ 0 & * & 0 & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 & 0 \\ 0 & & 0 & * & * \\ 0 & 0 & \cdots & 0 & 1 \end{smallmatrix} \right). \end{align*} $$
$$ \begin{align*} H_1 = \left( \begin{smallmatrix} 1 & * & \cdots & * & 0 \\ 0 & * & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & * & \vdots \\ 0 & & 0 & * & 0 \\ 0 & 0 & \cdots & 0 & 1 \end{smallmatrix} \right), \, H_2 = \left( \begin{smallmatrix} 1 & 0 & \cdots & \cdots & 0 \\ 0 & * & * & \cdots & * \\ \vdots & \ddots & \ddots & * & \vdots \\ 0 & & 0 & * & * \\ 0 & 0 & \cdots & 0 & 1 \end{smallmatrix} \right), \, H_3 = \left( \begin{smallmatrix} 1 & * & 0 & \cdots & 0 \\ 0 & * & 0 & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 & 0 \\ 0 & & 0 & * & * \\ 0 & 0 & \cdots & 0 & 1 \end{smallmatrix} \right). \end{align*} $$
For
![]() $n = 4$
, we consider, in addition, the following subscheme.
$n = 4$
, we consider, in addition, the following subscheme.
 $$ \begin{align*} H_4 = \begin{pmatrix} 1 & 0 & * & 0 \\ 0 & * & * & * \\ 0 & 0 & * & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \leq \textbf{A}_4. \end{align*} $$
$$ \begin{align*} H_4 = \begin{pmatrix} 1 & 0 & * & 0 \\ 0 & * & * & * \\ 0 & 0 & * & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \leq \textbf{A}_4. \end{align*} $$
The unipotent radicals of the matrix groups above—i.e., the intersections of each
![]() $H_i$
with the group
$H_i$
with the group
![]() $\textbf {U}_n$
of upper unitriangular matrices—are examples of group schemes arising from (maximal) contracting subgroups. Indeed, consider the locally compact group
$\textbf {U}_n$
of upper unitriangular matrices—are examples of group schemes arising from (maximal) contracting subgroups. Indeed, consider the locally compact group
![]() $\textbf {A}_n(\mathbb {K})$
for
$\textbf {A}_n(\mathbb {K})$
for
![]() $\mathbb {K}$
a nonarchimedean local field. In this case, each unipotent radical
$\mathbb {K}$
a nonarchimedean local field. In this case, each unipotent radical
![]() $\mathcal {U}_i(\mathbb {K}) = H_i(\mathbb {K}) \cap \textbf {U}_n(\mathbb {K})$
is the contracting subgroup associated to the automorphism given by conjugation by some element t contained in the torus
$\mathcal {U}_i(\mathbb {K}) = H_i(\mathbb {K}) \cap \textbf {U}_n(\mathbb {K})$
is the contracting subgroup associated to the automorphism given by conjugation by some element t contained in the torus
![]() $\textbf {T}_n(\mathbb {K})$
; see [Reference Abels2, Reference Baumgartner and Willis7, Reference Holz39]. Holz shows [Reference Holz39, Sections 2.7.3 and 2.7.4] that this defines a unipotent group scheme over
$\textbf {T}_n(\mathbb {K})$
; see [Reference Abels2, Reference Baumgartner and Willis7, Reference Holz39]. Holz shows [Reference Holz39, Sections 2.7.3 and 2.7.4] that this defines a unipotent group scheme over
![]() $\mathbb {Z}$
depending on
$\mathbb {Z}$
depending on
![]() $t \in \textbf {T}_n(\mathbb {K})$
. Following Abels, we call the schemes
$t \in \textbf {T}_n(\mathbb {K})$
. Following Abels, we call the schemes
![]() $H_i$
above horospherical and their unipotent radicals
$H_i$
above horospherical and their unipotent radicals
![]() $\mathcal {U}_i = H_i \cap \textbf {U}_n$
contracting subgroups of
$\mathcal {U}_i = H_i \cap \textbf {U}_n$
contracting subgroups of
![]() $\textbf {A}_n$
.
$\textbf {A}_n$
.
For R a commutative ring with unity and
![]() $n \geq 4$
, let
$n \geq 4$
, let
![]() $\mathscr{H}\;(n, R)$
denote the family of groups of R-points of horospherical subgroups of
$\mathscr{H}\;(n, R)$
denote the family of groups of R-points of horospherical subgroups of
![]() $\textbf {A}_n(R)$
, i.e.,
$\textbf {A}_n(R)$
, i.e.,
 $$ \begin{align*} {\mathscr{H}\;(n,R)} = \begin{cases} \left\{ H_1(R), \, H_2(R), \, H_3(R), \, H_4(R) \right\}, & \text{if } n = 4;\\ \left\{ H_1(R), \, H_2(R), \, H_3(R) \right\} & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} {\mathscr{H}\;(n,R)} = \begin{cases} \left\{ H_1(R), \, H_2(R), \, H_3(R), \, H_4(R) \right\}, & \text{if } n = 4;\\ \left\{ H_1(R), \, H_2(R), \, H_3(R) \right\} & \text{otherwise}. \end{cases} \end{align*} $$
We also let
In the notation above, the space we shall consider is the nerve complex
associated to the covering of
![]() $\textbf {A}_n(R)$
by the left cosets
$\textbf {A}_n(R)$
by the left cosets
![]() $\mathfrak {H}(n,R)$
of the horospherical subgroups listed above. As mentioned previously, the group
$\mathfrak {H}(n,R)$
of the horospherical subgroups listed above. As mentioned previously, the group
![]() $\textbf {A}_n(R)$
acts on the simplicial complex
$\textbf {A}_n(R)$
acts on the simplicial complex
![]() $CC(\mathscr{H}\;(n,R))$
by cell-permuting homeomorphisms via left multiplication.
$CC(\mathscr{H}\;(n,R))$
by cell-permuting homeomorphisms via left multiplication.
The space
![]() $CC(\mathscr{H}\;(n,R))$
has many useful features. Some of the facts we are about to list here actually hold more generally for arbitrary coset complexes. In the case of the following lemma, the properties that are particular to our groups come from the facts that the chosen family
$CC(\mathscr{H}\;(n,R))$
has many useful features. Some of the facts we are about to list here actually hold more generally for arbitrary coset complexes. In the case of the following lemma, the properties that are particular to our groups come from the facts that the chosen family
![]() $\mathscr{H}\;(n,R)$
is finite and that the group
$\mathscr{H}\;(n,R)$
is finite and that the group
![]() $\textbf {A}_n(R)$
is a split extension
$\textbf {A}_n(R)$
is a split extension
![]() $\textbf {A}_n(R) = \textbf {U}_n(R) \rtimes \textbf {T}_n(R)$
such that the contracting subgroups
$\textbf {A}_n(R) = \textbf {U}_n(R) \rtimes \textbf {T}_n(R)$
such that the contracting subgroups
![]() $\mathcal {U}_i(R) = H_i(R) \cap \textbf {U}_n(R)$
(as well as intersections of contracting subgroups) are all
$\mathcal {U}_i(R) = H_i(R) \cap \textbf {U}_n(R)$
(as well as intersections of contracting subgroups) are all
![]() $\textbf {T}_n(R)$
-invariant.
$\textbf {T}_n(R)$
-invariant.
Lemma 4.2 The complex
![]() $CC(\mathscr{H}\;(n,R))$
is colorable and homogeneous, and the given
$CC(\mathscr{H}\;(n,R))$
is colorable and homogeneous, and the given
![]() $\textbf {A}_n(R)$
-action is type-preserving and cocompact. Any cell-stabilizer is isomorphic to a finite intersection of members of
$\textbf {A}_n(R)$
-action is type-preserving and cocompact. Any cell-stabilizer is isomorphic to a finite intersection of members of
![]() $\mathscr{H}\;(n,R)$
.
$\mathscr{H}\;(n,R)$
.
Proof Since the intersection of cosets in a group is a coset of the intersection of the underlying subgroups, it follows that
![]() $CC(\mathscr{H}\;(n,R))$
is homogeneous . That is to say, every simplex is contained in a simplex of dimension
$CC(\mathscr{H}\;(n,R))$
is homogeneous . That is to say, every simplex is contained in a simplex of dimension
![]() $k = \vert \mathscr{H}\;(n,R) \vert -1$
and every maximal simplex has dimension exactly k. (Note that
$k = \vert \mathscr{H}\;(n,R) \vert -1$
and every maximal simplex has dimension exactly k. (Note that
![]() $CC(\mathscr{H}\;(n,R))$
is even a chamber complex if
$CC(\mathscr{H}\;(n,R))$
is even a chamber complex if
![]() $n \geq 5$
.) We observe that
$n \geq 5$
.) We observe that
![]() $CC(\mathscr{H}\;(n,R))$
is colored, with types (or colors) given precisely by the family of subgroups
$CC(\mathscr{H}\;(n,R))$
is colored, with types (or colors) given precisely by the family of subgroups
![]() $\mathscr{H}\;(n,R)$
. Also, the given action of
$\mathscr{H}\;(n,R)$
. Also, the given action of
![]() $\textbf {A}_n(R)$
on
$\textbf {A}_n(R)$
on
![]() $CC(\mathscr{H}\;(n,R))$
is type-preserving and transitive on the set of maximal simplices. Thus, the maximal simplex given by the intersection
$CC(\mathscr{H}\;(n,R))$
is type-preserving and transitive on the set of maximal simplices. Thus, the maximal simplex given by the intersection
is a fundamental domain for the
![]() $\textbf {A}_n(R)$
-action. In particular, since
$\textbf {A}_n(R)$
-action. In particular, since
![]() $\vert \mathscr{H}\;(n,R)\vert $
is finite, it follows that the action of
$\vert \mathscr{H}\;(n,R)\vert $
is finite, it follows that the action of
![]() $\textbf {A}_n(R)$
is cocompact.
$\textbf {A}_n(R)$
is cocompact.
The stabilizers of the
![]() $\textbf {A}_n(R)$
-action are also not difficult to determine. For instance, given a maximal simplex
$\textbf {A}_n(R)$
-action are also not difficult to determine. For instance, given a maximal simplex
![]() $\sigma = \left \{ g_1 H_1(R), \, g_2 H_2(R), \, g_3 H_3(R) \right \}$
in
$\sigma = \left \{ g_1 H_1(R), \, g_2 H_2(R), \, g_3 H_3(R) \right \}$
in
![]() $CC(\mathscr{H}\;(n,R))$
with
$CC(\mathscr{H}\;(n,R))$
with
![]() $n \geq 5$
, there exists
$n \geq 5$
, there exists
![]() $g \in \textbf {A}_n(R)$
such that
$g \in \textbf {A}_n(R)$
such that
![]() $\sigma = g \cdot \left \{ H_1(R), \, H_2(R), \, H_3(R) \right \}$
. A group element
$\sigma = g \cdot \left \{ H_1(R), \, H_2(R), \, H_3(R) \right \}$
. A group element
![]() $h \in \textbf {A}_n(R)$
fixes
$h \in \textbf {A}_n(R)$
fixes
![]() $\sigma $
if and only if
$\sigma $
if and only if
![]() $h \in g \cdot (H_1(R) \cap H_2(R) \cap H_3(R)) \cdot g^{-1}$
. A similar argument shows that a cell-stabilizer of
$h \in g \cdot (H_1(R) \cap H_2(R) \cap H_3(R)) \cdot g^{-1}$
. A similar argument shows that a cell-stabilizer of
![]() $CC(\mathscr{H}\;(n,R))$
for any
$CC(\mathscr{H}\;(n,R))$
for any
![]() $n \geq 4$
is a conjugate of some intersection of subgroups that belong to the family
$n \geq 4$
is a conjugate of some intersection of subgroups that belong to the family
![]() $\mathscr{H}\;(n,R)$
.▪
$\mathscr{H}\;(n,R)$
.▪
The existence of a single simplex as fundamental domain, and the fact that cell-stabilizers are conjugates of finite intersections of members of a fixed family of subgroups, are properties that characterize coset complexes; see e.g., [Reference Bux, Fluch, Marschler, Witzel and Zaremsky24, Observation A.4 and Proposition A.5].
Having determined the cell-stabilizers, we now prove that they are finitely presented whenever we need them to be.
Proposition 4.3 Suppose
![]() $\textbf {B}_2^{\circ }(R)$
is finitely presented and
$\textbf {B}_2^{\circ }(R)$
is finitely presented and
![]() $n \geq 4$
. Then any finite intersection of members of
$n \geq 4$
. Then any finite intersection of members of
![]() $\mathscr{H}\;(n,R)$
is finitely presented.
$\mathscr{H}\;(n,R)$
is finitely presented.
Proof We shall prove that, under the given assumption, the vertex-stabilizers are finitely presented. It will be clear from the arguments below that the same holds for stabilizers of higher dimensional cells. We remind the reader that the multiplicative group
![]() $\mathbb {G}_m(R)$
, which is a retract of
$\mathbb {G}_m(R)$
, which is a retract of
![]() $\textbf {B}_2^{\circ }(R)$
, is finitely presented because
$\textbf {B}_2^{\circ }(R)$
, is finitely presented because
![]() $\textbf {B}_2^{\circ }(R)$
itself is so; cf. Section 2. In particular,
$\textbf {B}_2^{\circ }(R)$
itself is so; cf. Section 2. In particular,
![]() $\textbf {T}_n(R)$
is also finitely presented.
$\textbf {T}_n(R)$
is also finitely presented.
By Lemma 4.2, we need only show that the members of
![]() $\mathscr{H}\;(n,R)$
are finitely presented. By the commutator (2.1) and diagonal relations (2.2), we see that the “last-column subgroup”
$\mathscr{H}\;(n,R)$
are finitely presented. By the commutator (2.1) and diagonal relations (2.2), we see that the “last-column subgroup”
![]() $\mathcal {C}_{n-1}$
of
$\mathcal {C}_{n-1}$
of
![]() $H_1$
, given by
$H_1$
, given by
 $$ \begin{align*} \mathcal{C}_{n-1} = \left( \begin{smallmatrix} 1 & 0 & \cdots & 0 & * & 0 \\ 0 & 1 & \ddots & \vdots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & \vdots & \vdots \\ \vdots & & \ddots & 1 & * & \vdots \\ & & & 0 & * & 0 \\ 0 & \cdots & & \cdots & 0 & 1 \end{smallmatrix} \right), \end{align*} $$
$$ \begin{align*} \mathcal{C}_{n-1} = \left( \begin{smallmatrix} 1 & 0 & \cdots & 0 & * & 0 \\ 0 & 1 & \ddots & \vdots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & \vdots & \vdots \\ \vdots & & \ddots & 1 & * & \vdots \\ & & & 0 & * & 0 \\ 0 & \cdots & & \cdots & 0 & 1 \end{smallmatrix} \right), \end{align*} $$
is normal in
![]() $H_1$
. The quotient
$H_1$
. The quotient
![]() $H_1 / \mathcal {C}_{n-1}$
is isomorphic to the subgroup
$H_1 / \mathcal {C}_{n-1}$
is isomorphic to the subgroup
 $$ \begin{align*} Q_{n-1} = \left( \begin{smallmatrix} 1 & * & \cdots & * & 0 & 0 \\ 0 & * & \ddots & \vdots & \vdots & \vdots \\ \vdots & \ddots & \ddots & * & \vdots & \vdots \\ \vdots & & \ddots & * & 0 & \vdots \\ & & & 0 & 1 & 0 \\ 0 & \cdots & & \cdots & 0 & 1 \end{smallmatrix} \right) \leq H_1. \end{align*} $$
$$ \begin{align*} Q_{n-1} = \left( \begin{smallmatrix} 1 & * & \cdots & * & 0 & 0 \\ 0 & * & \ddots & \vdots & \vdots & \vdots \\ \vdots & \ddots & \ddots & * & \vdots & \vdots \\ \vdots & & \ddots & * & 0 & \vdots \\ & & & 0 & 1 & 0 \\ 0 & \cdots & & \cdots & 0 & 1 \end{smallmatrix} \right) \leq H_1. \end{align*} $$
We claim that the column subgroup
![]() $\mathcal {C}_{n-1}$
is itself finitely presented. To check this, let us briefly recall some concepts from the
$\mathcal {C}_{n-1}$
is itself finitely presented. To check this, let us briefly recall some concepts from the
![]() $\Sigma $
-theory of Bieri–Strebel [Reference Bieri, de Cornulier, Guyot and Strebel13]. Given an abelian group Q and a homomorphism
$\Sigma $
-theory of Bieri–Strebel [Reference Bieri, de Cornulier, Guyot and Strebel13]. Given an abelian group Q and a homomorphism
![]() $v : Q \to (\mathbb {R},+)$
, denote by
$v : Q \to (\mathbb {R},+)$
, denote by
![]() $Q_v$
the monoid
$Q_v$
the monoid
![]() $Q_v = \left \{ q \in Q \mid v(q) \geq 0 \right \}$
. We say that a
$Q_v = \left \{ q \in Q \mid v(q) \geq 0 \right \}$
. We say that a
![]() $\mathbb {Z}[Q]$
-module A is tame when A is finitely generated over
$\mathbb {Z}[Q]$
-module A is tame when A is finitely generated over
![]() $\mathbb {Z}[Q_v]$
or over
$\mathbb {Z}[Q_v]$
or over
![]() $\mathbb {Z}[Q_{-v}]$
(possibly both) for every homomorphism
$\mathbb {Z}[Q_{-v}]$
(possibly both) for every homomorphism
![]() $v : Q \to (\mathbb {R},+)$
. One of the main results of [Reference Bieri, de Cornulier, Guyot and Strebel13] states that a finitely generated group
$v : Q \to (\mathbb {R},+)$
. One of the main results of [Reference Bieri, de Cornulier, Guyot and Strebel13] states that a finitely generated group
![]() $A \rtimes Q$
(with A and Q abelian) is finitely presented if and only if A is a tame
$A \rtimes Q$
(with A and Q abelian) is finitely presented if and only if A is a tame
![]() $\mathbb {Z}[Q]$
-module.
$\mathbb {Z}[Q]$
-module.
Going back to our proof, since
![]() $\textbf {B}_2^{\circ }(R)$
is assumed to be finitely presented, then so is the group
$\textbf {B}_2^{\circ }(R)$
is assumed to be finitely presented, then so is the group
by Lemma 3.2. In particular, the
![]() $\mathbb {Z}[\mathbb {G}_m(R)]$
-module
$\mathbb {Z}[\mathbb {G}_m(R)]$
-module
![]() $\mathbb {G}_a(R)$
with the given action
$\mathbb {G}_a(R)$
with the given action
is tame by [Reference Bieri, de Cornulier, Guyot and Strebel13, Theorem 5.1]. But
![]() $\mathcal {C}_{n-1}$
is seen to be isomorphic to
$\mathcal {C}_{n-1}$
is seen to be isomorphic to
![]() $\mathbb {G}_a(R)^{n-2} \rtimes \mathbb {G}_m(R)$
, where the action of
$\mathbb {G}_a(R)^{n-2} \rtimes \mathbb {G}_m(R)$
, where the action of
![]() $\mathbb {G}_m(R)$
on each copy of
$\mathbb {G}_m(R)$
on each copy of
![]() $\mathbb {G}_a(R)$
is the reverse multiplication as above, and the action
$\mathbb {G}_a(R)$
is the reverse multiplication as above, and the action
![]() $\mathbb {G}_m(R) \curvearrowright \mathbb {G}_a(R)^{n-2}$
is just the diagonal action. Thus, by [Reference Bieri, de Cornulier, Guyot and Strebel13, Proposition 2.5(i)] it follows that
$\mathbb {G}_m(R) \curvearrowright \mathbb {G}_a(R)^{n-2}$
is just the diagonal action. Thus, by [Reference Bieri, de Cornulier, Guyot and Strebel13, Proposition 2.5(i)] it follows that
![]() $\mathbb {G}_a(R)^{n-2}$
is also a tame
$\mathbb {G}_a(R)^{n-2}$
is also a tame
![]() $\mathbb {Z}[\mathbb {G}_m(R)]$
-module, whence one has—again by [Reference Bieri, de Cornulier, Guyot and Strebel13, Theorem 5.1]—that
$\mathbb {Z}[\mathbb {G}_m(R)]$
-module, whence one has—again by [Reference Bieri, de Cornulier, Guyot and Strebel13, Theorem 5.1]—that
![]() $\mathcal {C}_{n-1} \cong \mathbb {G}_a(R)^{n-2} \rtimes \mathbb {G}_m(R)$
is finitely presented.
$\mathcal {C}_{n-1} \cong \mathbb {G}_a(R)^{n-2} \rtimes \mathbb {G}_m(R)$
is finitely presented.
We have shown that
![]() $H_1$
fits into a (split) short exact sequence
$H_1$
fits into a (split) short exact sequence
where
![]() $\mathcal {C}_{n-1}$
is finitely presented. Decomposing
$\mathcal {C}_{n-1}$
is finitely presented. Decomposing
![]() $Q_{n-1}$
similarly via the last column, as we did with
$Q_{n-1}$
similarly via the last column, as we did with
![]() $H_1$
, a simple induction on n shows that
$H_1$
, a simple induction on n shows that
![]() $Q_{n-1}$
is also finitely presented. Lemma 2.1(1) thus shows that
$Q_{n-1}$
is also finitely presented. Lemma 2.1(1) thus shows that
![]() $H_1$
is finitely presented.
$H_1$
is finitely presented.
By considering the “first-row subgroup”
 $$ \begin{align*} \mathcal{R}_{n-1} = \left( \begin{smallmatrix} 1 & 0 & & \cdots & & 0 \\ 0 & * & * & \cdots & * & * \\ \vdots & 0 & 1 & 0 & 0 & 0 \\ \vdots & & \ddots & \ddots & \ddots & \vdots \\ & & & 0 & 1 & 0 \\ 0 & \cdots & & \cdots & 0 & 1 \end{smallmatrix} \right) \end{align*} $$
$$ \begin{align*} \mathcal{R}_{n-1} = \left( \begin{smallmatrix} 1 & 0 & & \cdots & & 0 \\ 0 & * & * & \cdots & * & * \\ \vdots & 0 & 1 & 0 & 0 & 0 \\ \vdots & & \ddots & \ddots & \ddots & \vdots \\ & & & 0 & 1 & 0 \\ 0 & \cdots & & \cdots & 0 & 1 \end{smallmatrix} \right) \end{align*} $$
of
![]() $H_2$
, which is also normal by (2.1) and (2.2), an argument analogous to the previous one, now using
$H_2$
, which is also normal by (2.1) and (2.2), an argument analogous to the previous one, now using
![]() $\mathbb {A}\text {ff}(R) \cong \mathbb {G}_a(R) \rtimes \mathbb {G}_m(R) \cong \left ( \begin {smallmatrix} * & * \\ 0 & 1 \end {smallmatrix} \right ) \leq \operatorname {\textrm {GL}}_2(R)$
, shows that
$\mathbb {A}\text {ff}(R) \cong \mathbb {G}_a(R) \rtimes \mathbb {G}_m(R) \cong \left ( \begin {smallmatrix} * & * \\ 0 & 1 \end {smallmatrix} \right ) \leq \operatorname {\textrm {GL}}_2(R)$
, shows that
![]() $H_2$
is also finitely presented.
$H_2$
is also finitely presented.
The case of
![]() $H_3$
is more straightforward since it equals the direct product
$H_3$
is more straightforward since it equals the direct product
 $$ \begin{align*} \left( \begin{smallmatrix} 1 & * & 0 & \cdots & 0 & 0 \\ 0 & * & 0 & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & \vdots & \vdots \\ \vdots & & \ddots & * & 0 & \vdots \\ & & & 0 & 1 & 0 \\ 0 & \cdots & & \cdots & 0 & 1 \end{smallmatrix} \right) \times \left( \begin{smallmatrix} 1 & 0 & \cdots & 0 & 0 & 0 \\ 0 & 1 & \ddots & \vdots & \vdots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots & \vdots \\ \vdots & & \ddots & 1 & 0 & \vdots \\ & & & 0 & * & * \\ 0 & \cdots & & \cdots & 0 & 1 \end{smallmatrix} \right) \cong \mathbb{A}\text{ff}_-(R) \times \mathbb{G}_m(R)^{n-4} \times \mathbb{A}\text{ff}(R) \end{align*} $$
$$ \begin{align*} \left( \begin{smallmatrix} 1 & * & 0 & \cdots & 0 & 0 \\ 0 & * & 0 & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & \vdots & \vdots \\ \vdots & & \ddots & * & 0 & \vdots \\ & & & 0 & 1 & 0 \\ 0 & \cdots & & \cdots & 0 & 1 \end{smallmatrix} \right) \times \left( \begin{smallmatrix} 1 & 0 & \cdots & 0 & 0 & 0 \\ 0 & 1 & \ddots & \vdots & \vdots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots & \vdots \\ \vdots & & \ddots & 1 & 0 & \vdots \\ & & & 0 & * & * \\ 0 & \cdots & & \cdots & 0 & 1 \end{smallmatrix} \right) \cong \mathbb{A}\text{ff}_-(R) \times \mathbb{G}_m(R)^{n-4} \times \mathbb{A}\text{ff}(R) \end{align*} $$
and all factors on the right-hand side are finitely presented; see Lemma 3.2 and Section 2.
Establishing finite presentability of
![]() $H_4 \leq \textbf {A}_4(R)$
is slightly different. Consider the subgroups
$H_4 \leq \textbf {A}_4(R)$
is slightly different. Consider the subgroups
and let
![]() $p_1 : \Gamma _1 \twoheadrightarrow Q$
and
$p_1 : \Gamma _1 \twoheadrightarrow Q$
and
![]() $p_2 : \Gamma _2 \twoheadrightarrow Q$
denote the natural projections onto the diagonal subgroup
$p_2 : \Gamma _2 \twoheadrightarrow Q$
denote the natural projections onto the diagonal subgroup
With this notation, we have that
![]() $H_4$
is isomorphic to the fiber product
$H_4$
is isomorphic to the fiber product
We observe now that
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
are finitely presented—i.e., of homotopical type
$\Gamma _2$
are finitely presented—i.e., of homotopical type
![]() $\text {F}_{2}$
—since
$\text {F}_{2}$
—since
are so. (In particular,
![]() $\ker (p_1)$
is of type
$\ker (p_1)$
is of type
![]() $\text {F}_{1}$
.) Again, the finite presentability of
$\text {F}_{1}$
.) Again, the finite presentability of
![]() $\textbf {B}_2^{\circ }(R)$
implies that the abelian group
$\textbf {B}_2^{\circ }(R)$
implies that the abelian group
![]() $Q \cong \mathbb {G}_m(R)$
is finitely generated, whence it is of type
$Q \cong \mathbb {G}_m(R)$
is finitely generated, whence it is of type
![]() $\text {F}_{3}$
; cf. Section 2. Therefore, the fiber product
$\text {F}_{3}$
; cf. Section 2. Therefore, the fiber product
![]() $P \cong H_4$
is finitely presented by the (asymmetric) 1-2-3-Theorem [Reference Bridson, Howie, Miller and Short16, Theorem B].
$P \cong H_4$
is finitely presented by the (asymmetric) 1-2-3-Theorem [Reference Bridson, Howie, Miller and Short16, Theorem B].
Entirely analogous arguments for the nontrivial intersections of members of
![]() $\mathscr{H}\;(n,R)$
show that all such groups are also finitely presented, which yields the proposition.▪
$\mathscr{H}\;(n,R)$
show that all such groups are also finitely presented, which yields the proposition.▪
We now investigate connectivity properties of the complex
![]() $CC(\mathscr{H}\;(n,R))$
. The following observation, whose proof we omit, is originally due to Holz [Reference Holz39]. To verify it directly, consider the homotopy equivalences given in [Reference Abels and Holz4, Theorem 1.4]. Alternatively, a generalization has been recently obtained by Brück; see [Reference Brück20, Theorem 3.17 and Corollary 3.18] for a proof.
$CC(\mathscr{H}\;(n,R))$
. The following observation, whose proof we omit, is originally due to Holz [Reference Holz39]. To verify it directly, consider the homotopy equivalences given in [Reference Abels and Holz4, Theorem 1.4]. Alternatively, a generalization has been recently obtained by Brück; see [Reference Brück20, Theorem 3.17 and Corollary 3.18] for a proof.
Lemma 4.4 ([Reference Holz39, Korollar 5.18])
Let
![]() $G = N \rtimes Q$
and suppose
$G = N \rtimes Q$
and suppose
![]() $\mathscr{H}$
is a family of Q-invariant subgroups of N. Then there exists a homotopy equivalence between the coset complex
$\mathscr{H}$
is a family of Q-invariant subgroups of N. Then there exists a homotopy equivalence between the coset complex
![]() $CC(\mathscr{H})$
of
$CC(\mathscr{H})$
of
![]() $\mathscr{H}$
with respect to N and the coset complex
$\mathscr{H}$
with respect to N and the coset complex
![]() $CC(\left \{ H \rtimes Q \mid H \in \mathscr{H} \right \})$
with respect to overgroup G.
$CC(\left \{ H \rtimes Q \mid H \in \mathscr{H} \right \})$
with respect to overgroup G.
For our groups, Lemma 4.4 yields the following.
Corollary 4.5 Let
![]() $\mathscr{H}_u(n,R)$
denote the family of unipotent radicals
$\mathscr{H}_u(n,R)$
denote the family of unipotent radicals
![]() $\mathcal {U}_i(R) = H_i(R) \cap \textbf {U}_n(R)$
of members of
$\mathcal {U}_i(R) = H_i(R) \cap \textbf {U}_n(R)$
of members of
![]() $\mathscr{H}\;(n,R)$
and consider the following covering of
$\mathscr{H}\;(n,R)$
and consider the following covering of
![]() $\textbf {U}_n(R)$
.
$\textbf {U}_n(R)$
.
Then the spaces
![]() $CC(\mathscr{H}_u(n,R)) = N(\mathfrak {H}_u(n,R))$
(with respect to
$CC(\mathscr{H}_u(n,R)) = N(\mathfrak {H}_u(n,R))$
(with respect to
![]() $\textbf {U}_n(R)$
) and
$\textbf {U}_n(R)$
) and
![]() $CC(\mathscr{H}\;(n,R))$
(with respect to
$CC(\mathscr{H}\;(n,R))$
(with respect to
![]() $\textbf {A}_n(R)$
) are homotopy equivalent.
$\textbf {A}_n(R)$
) are homotopy equivalent.
Proof This follows at once from Lemma 4.4 since the
![]() $\textbf {T}_n(R)$
-action by conjugation preserves each
$\textbf {T}_n(R)$
-action by conjugation preserves each
![]() $\mathcal {U}_i(R)$
by the diagonal relations (2.2).▪
$\mathcal {U}_i(R)$
by the diagonal relations (2.2).▪
Thus, to show that
![]() $CC(\mathscr{H}\;(n,R))$
is connected and simply-connected, it suffices to prove that the coset complex
$CC(\mathscr{H}\;(n,R))$
is connected and simply-connected, it suffices to prove that the coset complex
![]() $CC(\mathscr{H}_u(n,R))$
of contracting subgroups, with cosets taken in the unipotent radical
$CC(\mathscr{H}_u(n,R))$
of contracting subgroups, with cosets taken in the unipotent radical
![]() $\textbf {U}_n(R)$
, is connected and simply-connected. To do so, we take advantage of the algebraic meaning of connectivity properties of coset complexes discovered by Tits [Reference Tits57].
$\textbf {U}_n(R)$
, is connected and simply-connected. To do so, we take advantage of the algebraic meaning of connectivity properties of coset complexes discovered by Tits [Reference Tits57].
Recall that the colimit
![]() $\text {colim}\, F$
of a diagram
$\text {colim}\, F$
of a diagram
![]() $F : I \to \text {Grp}$
from a small category I to the category of groups is a group K together with a family of maps
$F : I \to \text {Grp}$
from a small category I to the category of groups is a group K together with a family of maps
![]() $\Psi = \left \{ \psi _O : F(O) \to K \right \}_{O \in \text {Obj}(I)}$
satisfying the following properties.
$\Psi = \left \{ \psi _O : F(O) \to K \right \}_{O \in \text {Obj}(I)}$
satisfying the following properties.
-
•
 $\psi _P \circ F(f) = \psi _O$
for all
$\psi _P \circ F(f) = \psi _O$
for all
 $f \in \operatorname {\textrm {Hom}}(O, P)$
.
$f \in \operatorname {\textrm {Hom}}(O, P)$
. -
• If
 $(K', \Psi ')$
is another pair also satisfying the conditions above, then there exists a unique group homomorphism
$(K', \Psi ')$
is another pair also satisfying the conditions above, then there exists a unique group homomorphism
 $\varphi : K \to K'$
such that
$\varphi : K \to K'$
such that
 $\varphi \circ \psi _O = \psi _O'$
for all
$\varphi \circ \psi _O = \psi _O'$
for all
 $O \in \text {Obj}(I)$
.
$O \in \text {Obj}(I)$
.
In this case, we write
![]() $K = \text {colim}\, F$
, omitting the maps
$K = \text {colim}\, F$
, omitting the maps
![]() $\Psi $
. Now suppose
$\Psi $
. Now suppose
![]() $\mathscr{H}$
is a family of subgroups of a given group. This induces a diagram
$\mathscr{H}$
is a family of subgroups of a given group. This induces a diagram
![]() $F_\mathscr{H} : I_\mathscr{H} \to \text {Grp}$
by defining the category
$F_\mathscr{H} : I_\mathscr{H} \to \text {Grp}$
by defining the category
![]() $I_\mathscr{H}$
to be the poset given by members of
$I_\mathscr{H}$
to be the poset given by members of
![]() $\mathscr{H}$
and their pairwise intersections, ordered by inclusion. For example, if
$\mathscr{H}$
and their pairwise intersections, ordered by inclusion. For example, if
![]() $\mathscr{H} = \left \{ A,B \right \}$
with
$\mathscr{H} = \left \{ A,B \right \}$
with
![]() $A, B \leq G$
and
$A, B \leq G$
and
![]() $C = A \cap B$
, then
$C = A \cap B$
, then
![]() $F_\mathscr{H}$
is just the usual diagram
$F_\mathscr{H}$
is just the usual diagram
![]() $A \hookleftarrow C \hookrightarrow B$
and thus the colimit
$A \hookleftarrow C \hookrightarrow B$
and thus the colimit
![]() $\text {colim}\, F_\mathscr{H}$
is simply the push-out (or amalgamated product)
$\text {colim}\, F_\mathscr{H}$
is simply the push-out (or amalgamated product)
![]() $\text {colim}\, F_\mathscr{H} = A \ast _C B$
.
$\text {colim}\, F_\mathscr{H} = A \ast _C B$
.
Theorem 4.6 ([Reference Tits57]; see also [Reference Abels and Holz4, Theorem 2.4])
Let
![]() $\mathscr{H}$
be a family of subgroups of a group G and let
$\mathscr{H}$
be a family of subgroups of a group G and let
![]() $\pi : \text {colim}\, F_\mathscr{H} \to G$
denote the natural map from the colimit of
$\pi : \text {colim}\, F_\mathscr{H} \to G$
denote the natural map from the colimit of
![]() $F_\mathscr{H}$
to G. Then the coset complex
$F_\mathscr{H}$
to G. Then the coset complex
![]() $CC(\mathscr{H})$
is connected if and only if
$CC(\mathscr{H})$
is connected if and only if
![]() $\pi $
is surjective, and
$\pi $
is surjective, and
![]() $CC(\mathscr{H})$
is additionally simply-connected if and only if
$CC(\mathscr{H})$
is additionally simply-connected if and only if
![]() $\pi $
is an isomorphism.
$\pi $
is an isomorphism.
To apply Theorem 4.6 in our context, we will need a bit of commutator calculus. The following identities are well-known; see e.g., [Reference Abels2, Section 2.2].
Lemma 4.7 Let G be a group and let
![]() $a,b,c \in G$
. Then
$a,b,c \in G$
. Then
and
We also need a convenient, well-known presentation for
![]() $\textbf {U}_n(R)$
. To describe this standard presentation, we need some notation. Fix
$\textbf {U}_n(R)$
. To describe this standard presentation, we need some notation. Fix
![]() $T \subseteq R$
a generating set, containing the unit
$T \subseteq R$
a generating set, containing the unit
![]() $1$
, for the underlying additive group
$1$
, for the underlying additive group
![]() $\mathbb {G}_a(R)$
of the base ring R. That is, we view R as a quotient of the free abelian group
$\mathbb {G}_a(R)$
of the base ring R. That is, we view R as a quotient of the free abelian group
![]() $\bigoplus \limits _{t \in T} \mathbb {Z} t$
.
$\bigoplus \limits _{t \in T} \mathbb {Z} t$
.
We fix furthermore
![]() $\mathcal {R} \subseteq \bigoplus _{t \in T} \mathbb {Z} t$
a set of additive defining relations of R. In other words,
$\mathcal {R} \subseteq \bigoplus _{t \in T} \mathbb {Z} t$
a set of additive defining relations of R. In other words,
![]() $\mathcal {R}$
is a set of expressions
$\mathcal {R}$
is a set of expressions
 $\left \{ \sum \limits _{\ell } a_{\ell } t_{\ell } \mid a_{\ell } \in \mathbb {Z}, t_{\ell } \in T \right \} \subseteq \bigoplus \limits _{t \in T} \mathbb {Z} t$
(where all but finitely many coefficients
$\left \{ \sum \limits _{\ell } a_{\ell } t_{\ell } \mid a_{\ell } \in \mathbb {Z}, t_{\ell } \in T \right \} \subseteq \bigoplus \limits _{t \in T} \mathbb {Z} t$
(where all but finitely many coefficients
![]() $a_{\ell }$
are zero) such that
$a_{\ell }$
are zero) such that
![]() $\mathbb {G}_a(R) \cong \left (\bigoplus \limits _{t \in T} \mathbb {Z} t\right ) / \langle {\mathcal {R}} \rangle _{\mathbb {Z}}$
.
$\mathbb {G}_a(R) \cong \left (\bigoplus \limits _{t \in T} \mathbb {Z} t\right ) / \langle {\mathcal {R}} \rangle _{\mathbb {Z}}$
.
For every pair
![]() $t,s\in T$
of additive generators, we choose an expression
$t,s\in T$
of additive generators, we choose an expression
![]() $m(t,s) = m(s,t) \in \bigoplus _{t \in T} \mathbb {Z} t$
such that the image of
$m(t,s) = m(s,t) \in \bigoplus _{t \in T} \mathbb {Z} t$
such that the image of
![]() $m(s,t)$
in R under the given projection
$m(s,t)$
in R under the given projection
![]() $\bigoplus _{t \in T} \mathbb {Z} t \twoheadrightarrow R$
equals the products
$\bigoplus _{t \in T} \mathbb {Z} t \twoheadrightarrow R$
equals the products
![]() $ts$
and
$ts$
and
![]() $st$
. In case
$st$
. In case
![]() $t = 1$
, we take
$t = 1$
, we take
![]() $m(1,s)$
to be s itself, i.e.,
$m(1,s)$
to be s itself, i.e.,
![]() $m(1,s) = s = m(s,1)$
.
$m(1,s) = s = m(s,1)$
.
Lemma 4.8 With the notation above, the group
![]() $\textbf {U}_n(R) \leq \textbf {A}_n(R)$
admits a presentation
$\textbf {U}_n(R) \leq \textbf {A}_n(R)$
admits a presentation
![]() $\textbf {U}_n(R) \cong \langle {\mathcal {Y} \mid \mathcal {S}} \rangle $
with generating set
$\textbf {U}_n(R) \cong \langle {\mathcal {Y} \mid \mathcal {S}} \rangle $
with generating set
and a set of defining relations
![]() $\mathcal {S}$
given as follows. For all
$\mathcal {S}$
given as follows. For all
![]() $(i,j)$
with
$(i,j)$
with
![]() $1 \leq i < j \leq n$
and all pairs
$1 \leq i < j \leq n$
and all pairs
![]() $t, s \in T$
,
$t, s \in T$
,
 $$ \begin{align} [e_{ij}(t),e_{kl}(s)] = \begin{cases} \prod\limits_u e_{il}(u)^{a_u}, & \text{ if } j=k;\\ 1, & \text{ if } i \neq l, k \neq j, \end{cases} \end{align} $$
$$ \begin{align} [e_{ij}(t),e_{kl}(s)] = \begin{cases} \prod\limits_u e_{il}(u)^{a_u}, & \text{ if } j=k;\\ 1, & \text{ if } i \neq l, k \neq j, \end{cases} \end{align} $$
where
![]() $m(t,s) = \sum \limits _{u} a_u u \in \bigoplus \limits _{t \in T} \mathbb {Z} t$
is the fixed expression
$m(t,s) = \sum \limits _{u} a_u u \in \bigoplus \limits _{t \in T} \mathbb {Z} t$
is the fixed expression
![]() $m(t,s)$
as above for the product
$m(t,s)$
as above for the product
![]() $ts = st \in R$
.
$ts = st \in R$
.
For all
![]() $(i,j)$
with
$(i,j)$
with
![]() $1 \leq i < j \leq n$
,
$1 \leq i < j \leq n$
,
The set
![]() $\mathcal {S}$
is defined as the set of all relations (4.2) and (4.3) given above.
$\mathcal {S}$
is defined as the set of all relations (4.2) and (4.3) given above.
Lemma 4.8 is far from new, so we omit its proof. The presentation above has been considered many times in the literature, most notably in the case where R is a field and in connection to buildings and amalgams; see e.g., [Reference Steinberg53, Chapter 3], [Reference Tits57], [Reference Tits56, Appendix 2], [Reference Devillers and Mühlherr34], and [Reference Abramenko and Brown5, Chapters 7 and 8]. In general, such presentation is extracted from the commutator relations (2.1) between elementary matrices—recall that, in the Chevalley–Demazure set-up,
![]() $\textbf {U}_n$
is a maximal unipotent subscheme (over
$\textbf {U}_n$
is a maximal unipotent subscheme (over
![]() $\mathbb {Z}$
) in type
$\mathbb {Z}$
) in type
![]() $\text {A}_{n-1}$
. The only difference between the presentation we spelled out and other versions typically occurring elsewhere is that we made the ring structure of R more explicit in the relations occurring in
$\text {A}_{n-1}$
. The only difference between the presentation we spelled out and other versions typically occurring elsewhere is that we made the ring structure of R more explicit in the relations occurring in
![]() $\textbf {U}_n(R)$
. The interested reader is referred e.g., to [Reference Santos Rego48, Section 1.1.2] for a detailed proof of Lemma 4.8.
$\textbf {U}_n(R)$
. The interested reader is referred e.g., to [Reference Santos Rego48, Section 1.1.2] for a detailed proof of Lemma 4.8.
Using the above results, we shall have the last ingredient for the proof of Theorem 1.2(3) once we establish the following generalization of a result due to Holz [Reference Holz39, Proposition A.3].
Proposition 4.9 For every
![]() $n \geq 4$
one has that
$n \geq 4$
one has that
![]() $\textbf {U}_n(R)\cong \text {colim}~F_{\mathscr{H}_u(n,R)}$
.
$\textbf {U}_n(R)\cong \text {colim}~F_{\mathscr{H}_u(n,R)}$
.
Proof The idea is to write down a convenient presentation for
![]() $\textbf {U}_n(R)$
which shows that it is the desired colimit. To do so, we first spell out canonical presentations for the members of
$\textbf {U}_n(R)$
which shows that it is the desired colimit. To do so, we first spell out canonical presentations for the members of
![]() $\mathscr{H}_u(n,R)$
. For the course of this proof we fix (and follow strictly) the notation of Lemma 4.8. In particular,
$\mathscr{H}_u(n,R)$
. For the course of this proof we fix (and follow strictly) the notation of Lemma 4.8. In particular,
![]() $T \subseteq R$
will denote an arbitrary, but fixed, additive generating set for
$T \subseteq R$
will denote an arbitrary, but fixed, additive generating set for
![]() $(R,+) = \mathbb {G}_a(R)$
containing
$(R,+) = \mathbb {G}_a(R)$
containing
![]() $1$
. As in Lemma 4.8, we fix
$1$
. As in Lemma 4.8, we fix
![]() $\mathcal {R}$
a set of additive defining relations of
$\mathcal {R}$
a set of additive defining relations of
![]() $\mathbb {G}_a(R)$
.
$\mathbb {G}_a(R)$
.
We observe that
![]() $\mathcal {U}_3(R)$
and
$\mathcal {U}_3(R)$
and
![]() $\mathcal {U}_4(R)$
are abelian, by the commutator relations (2.1). It is also not hard to see that
$\mathcal {U}_4(R)$
are abelian, by the commutator relations (2.1). It is also not hard to see that
![]() $\mathcal {U}_1(R) \cong \textbf {U}_{n-1}(R) \cong \mathcal {U}_2(R)$
by translating the indices of elementary matrices accordingly. Thus, we have the following presentations.
$\mathcal {U}_1(R) \cong \textbf {U}_{n-1}(R) \cong \mathcal {U}_2(R)$
by translating the indices of elementary matrices accordingly. Thus, we have the following presentations.
 $$ \begin{align*} \mathcal{U}_1(R) \cong & \langle \left\{ e_{ij}(t) \mid t \in T, \, 1 \leq i < j \leq n-1 \right\} \mid \text{ Relations (4.2) and (4.3)} \\ & \text{for all } i,j \text{ with } 1 \leq i < j \leq n-1, \text{ and all } t,s \in T \rangle. \end{align*} $$
$$ \begin{align*} \mathcal{U}_1(R) \cong & \langle \left\{ e_{ij}(t) \mid t \in T, \, 1 \leq i < j \leq n-1 \right\} \mid \text{ Relations (4.2) and (4.3)} \\ & \text{for all } i,j \text{ with } 1 \leq i < j \leq n-1, \text{ and all } t,s \in T \rangle. \end{align*} $$
 $$ \begin{align*} \mathcal{U}_2(R) \cong & \langle \left\{ e_{ij}(t) \mid t \in T, 2 \leq i < j \leq n \right\} \mid \text{ Relations (4.2) and (4.3)} \\ & \text{for all } i,j \text{ with } 2 \leq i < j \leq n, \text{ and all } t,s \in T \rangle. \end{align*} $$
$$ \begin{align*} \mathcal{U}_2(R) \cong & \langle \left\{ e_{ij}(t) \mid t \in T, 2 \leq i < j \leq n \right\} \mid \text{ Relations (4.2) and (4.3)} \\ & \text{for all } i,j \text{ with } 2 \leq i < j \leq n, \text{ and all } t,s \in T \rangle. \end{align*} $$
 $$ \begin{align*} \mathcal{U}_3(R) \cong & \langle \left\{ e_{12}(t), e_{n-1,n}(s) \mid t,s \in T \right\} \mid [e_{12}(t), e_{n-1,n}(s)] = 1 \text{ for all } t,s \in T, \\ & \text{and relations (4.3) for all } t,s \in T \text{ and } (i,j) \in \left\{ (1,2), (n-1,n) \right\} \rangle. \end{align*} $$
$$ \begin{align*} \mathcal{U}_3(R) \cong & \langle \left\{ e_{12}(t), e_{n-1,n}(s) \mid t,s \in T \right\} \mid [e_{12}(t), e_{n-1,n}(s)] = 1 \text{ for all } t,s \in T, \\ & \text{and relations (4.3) for all } t,s \in T \text{ and } (i,j) \in \left\{ (1,2), (n-1,n) \right\} \rangle. \end{align*} $$
 $$ \begin{align*} \mathcal{U}_4(R) \cong & \langle \left\{ e_{13}(p), \, e_{23}(t), \, e_{24}(s) \mid p,t,s \in T \right\} \, \mid \, [e_{ij}(t), e_{kl}(s)] = 1 \text{ for all } \\ & t, s \in T \mbox { and } (i,j), (k,l) \in \left\{ (1,3),(2,3),(2,4) \right\}, \text{ and} \\ & \text{relations (4.3) for all } t,s \in T \text{ and } (i,j) \in \left\{ (1,3),(2,3),(2,4) \right\} \rangle. \end{align*} $$
$$ \begin{align*} \mathcal{U}_4(R) \cong & \langle \left\{ e_{13}(p), \, e_{23}(t), \, e_{24}(s) \mid p,t,s \in T \right\} \, \mid \, [e_{ij}(t), e_{kl}(s)] = 1 \text{ for all } \\ & t, s \in T \mbox { and } (i,j), (k,l) \in \left\{ (1,3),(2,3),(2,4) \right\}, \text{ and} \\ & \text{relations (4.3) for all } t,s \in T \text{ and } (i,j) \in \left\{ (1,3),(2,3),(2,4) \right\} \rangle. \end{align*} $$
The pairwise intersections
![]() $\mathcal {U}_i(R) \cap \mathcal {U}_j(R)$
also admit similar presentations by restricting the generators (and corresponding relations) to the indices occurring in both
$\mathcal {U}_i(R) \cap \mathcal {U}_j(R)$
also admit similar presentations by restricting the generators (and corresponding relations) to the indices occurring in both
![]() $\mathcal {U}_i(R)$
and
$\mathcal {U}_i(R)$
and
![]() $\mathcal {U}_j(R)$
. For instance,
$\mathcal {U}_j(R)$
. For instance,
 $$ \begin{align*} \mathcal{U}_1(R) \cap \mathcal{U}_2(R) = \left( \begin{smallmatrix} 1 & 0 & \cdots & \cdots & 0 & 0 \\ 0 & 1 & * & \cdots & * & 0 \\ \vdots & \ddots & \ddots & \ddots & \vdots & \vdots \\ & & 0 & 1 & * & 0 \\ & & & 0 & 1 & 0 \\ 0 & \cdots & & \cdots & 0 & 1 \end{smallmatrix} \right) \cong \textbf{U}_{n-2}(R) \end{align*} $$
$$ \begin{align*} \mathcal{U}_1(R) \cap \mathcal{U}_2(R) = \left( \begin{smallmatrix} 1 & 0 & \cdots & \cdots & 0 & 0 \\ 0 & 1 & * & \cdots & * & 0 \\ \vdots & \ddots & \ddots & \ddots & \vdots & \vdots \\ & & 0 & 1 & * & 0 \\ & & & 0 & 1 & 0 \\ 0 & \cdots & & \cdots & 0 & 1 \end{smallmatrix} \right) \cong \textbf{U}_{n-2}(R) \end{align*} $$
with presentation
 $$ \begin{align*} \mathcal{U}_1(R) \cap \mathcal{U}_2(R) \cong & \langle \left\{ e_{ij}(t) \mid t \in T, \, 2 \leq i < j \leq n-1 \right\} \mid \text{ Relations (4.2) and} \\ & \text{(4.3) for all } i,j \text{ with } 2 \leq i < j \leq n-1, \text{ and all } t,s \in T \rangle. \end{align*} $$
$$ \begin{align*} \mathcal{U}_1(R) \cap \mathcal{U}_2(R) \cong & \langle \left\{ e_{ij}(t) \mid t \in T, \, 2 \leq i < j \leq n-1 \right\} \mid \text{ Relations (4.2) and} \\ & \text{(4.3) for all } i,j \text{ with } 2 \leq i < j \leq n-1, \text{ and all } t,s \in T \rangle. \end{align*} $$
Now consider the group
![]() $U_n$
defined as follows. As generating set we take
$U_n$
defined as follows. As generating set we take
The set of defining relations
![]() $\mathcal {S}_n$
is formed as follows. For all
$\mathcal {S}_n$
is formed as follows. For all
![]() $t,s \in T$
and indices
$t,s \in T$
and indices
![]() $i,j,k,l$
which are either all in
$i,j,k,l$
which are either all in
![]() $\left \{ 1,\ldots ,n-1 \right \}$
or all in
$\left \{ 1,\ldots ,n-1 \right \}$
or all in
![]() $\left \{ 2,\ldots ,n \right \}$
, consider the relations
$\left \{ 2,\ldots ,n \right \}$
, consider the relations
 $$ \begin{align} [e_{ij}(t),e_{kl}(s)] = \begin{cases} \prod\limits_u e_{il}(u)^{a_u}, & \text{ if } j=k;\\ 1, & \text{ if } i \neq l, k \neq j, \end{cases} \end{align} $$
$$ \begin{align} [e_{ij}(t),e_{kl}(s)] = \begin{cases} \prod\limits_u e_{il}(u)^{a_u}, & \text{ if } j=k;\\ 1, & \text{ if } i \neq l, k \neq j, \end{cases} \end{align} $$
and
where
![]() $m(t,s) = \sum \limits _{u} a_u u \in \bigoplus \limits _{t \in T} \mathbb {Z} t$
is as in Lemma 4.8. For all
$m(t,s) = \sum \limits _{u} a_u u \in \bigoplus \limits _{t \in T} \mathbb {Z} t$
is as in Lemma 4.8. For all
![]() $t,s \in T$
and pairs
$t,s \in T$
and pairs
![]() $i,j$
which are either all in
$i,j$
which are either all in
![]() $\left \{ 1,\ldots ,n-1 \right \}$
or all in
$\left \{ 1,\ldots ,n-1 \right \}$
or all in
![]() $\left \{ 2,\ldots ,n \right \}$
, consider additionally the relations
$\left \{ 2,\ldots ,n \right \}$
, consider additionally the relations
 $$ \begin{align} \prod_{\ell=1}^m e_{ij}(t_{\ell})^{a_{\ell}} = 1 \text{ for each } \sum_{\ell=1}^m a_{\ell} t_{\ell} \in \mathcal{R}, \end{align} $$
$$ \begin{align} \prod_{\ell=1}^m e_{ij}(t_{\ell})^{a_{\ell}} = 1 \text{ for each } \sum_{\ell=1}^m a_{\ell} t_{\ell} \in \mathcal{R}, \end{align} $$
where
![]() $\mathcal {R}$
is the fixed set of additive defining relations of
$\mathcal {R}$
is the fixed set of additive defining relations of
![]() $\mathbb {G}_a(R)$
as in Lemma 4.8. If
$\mathbb {G}_a(R)$
as in Lemma 4.8. If
![]() $n = 4$
we need also consider the relations
$n = 4$
we need also consider the relations
for all pairs
![]() $t,s \in T$
. We take
$t,s \in T$
. We take
![]() $\mathcal {S}_n$
to be the set of all relations (4.4)–(4.6) (in case
$\mathcal {S}_n$
to be the set of all relations (4.4)–(4.6) (in case
![]() $n \geq 5$
), and
$n \geq 5$
), and
![]() $\mathcal {S}_4$
is the set of all relations (4.4) through (4.7) above. We then define
$\mathcal {S}_4$
is the set of all relations (4.4) through (4.7) above. We then define
![]() $U_n$
by means of the presentation
$U_n$
by means of the presentation
Reading off the presentations for the
![]() $\mathcal {U}_i(R)$
and for their pairwise intersections, it follows from von Dyck’s theorem that
$\mathcal {U}_i(R)$
and for their pairwise intersections, it follows from von Dyck’s theorem that
![]() $\text {colim}\, F_{\mathscr{H}_u(n,R)}$
is isomorphic to the group
$\text {colim}\, F_{\mathscr{H}_u(n,R)}$
is isomorphic to the group
![]() $U_n$
above.
$U_n$
above.
Thus, to prove the proposition it suffices to show that
![]() $\textbf {U}_n(R)$
is isomorphic to
$\textbf {U}_n(R)$
is isomorphic to
![]() $U_n$
. To avoid introducing even more symbols, we proceed as follows. Recall that
$U_n$
. To avoid introducing even more symbols, we proceed as follows. Recall that
![]() $\textbf {U}_n(R)$
admits the presentation
$\textbf {U}_n(R)$
admits the presentation
![]() $\textbf {U}_n(R) \cong \langle {\mathcal {Y} \mid \mathcal {S}} \rangle $
given in Lemma 4.8. Abusing notation and comparing the presentations
$\textbf {U}_n(R) \cong \langle {\mathcal {Y} \mid \mathcal {S}} \rangle $
given in Lemma 4.8. Abusing notation and comparing the presentations
![]() $U_n = \langle {\mathcal {X}_n \mid \mathcal {S}_n} \rangle $
and
$U_n = \langle {\mathcal {X}_n \mid \mathcal {S}_n} \rangle $
and
![]() $\textbf {U}_n(R) \cong \langle {\mathcal {Y} \mid \mathcal {S}} \rangle $
, it suffices to define in
$\textbf {U}_n(R) \cong \langle {\mathcal {Y} \mid \mathcal {S}} \rangle $
, it suffices to define in
![]() $U_n$
the missing generators
$U_n$
the missing generators
![]() $e_{1n}(t)$
(for
$e_{1n}(t)$
(for
![]() $t \in T$
) and also show that all the relations from
$t \in T$
) and also show that all the relations from
![]() $\mathcal {S}$
missing from
$\mathcal {S}$
missing from
![]() $\mathcal {S}_n$
do hold in
$\mathcal {S}_n$
do hold in
![]() $U_n$
. (Inspecting the indices, the missing relations are those involving the commutators
$U_n$
. (Inspecting the indices, the missing relations are those involving the commutators
![]() $[e_{1j}(t),e_{kn}(s)]$
for
$[e_{1j}(t),e_{kn}(s)]$
for
![]() $j = 2, \ldots , n$
and
$j = 2, \ldots , n$
and
![]() $k = 1, \ldots , n-1$
, and
$k = 1, \ldots , n-1$
, and
![]() $(j,k) \neq (2,n-1)$
and those involving only the new generators
$(j,k) \neq (2,n-1)$
and those involving only the new generators
![]() $e_{1n}(t)$
.)
$e_{1n}(t)$
.)
For every
![]() $t \in T$
, define in
$t \in T$
, define in
![]() $U_n$
the element
$U_n$
the element
![]() $e_{1n}(t) = [e_{12}(t), e_{2n}(1)]$
. With this new commutator at hand, the proof will be concluded once we show that the following equalities hold in
$e_{1n}(t) = [e_{12}(t), e_{2n}(1)]$
. With this new commutator at hand, the proof will be concluded once we show that the following equalities hold in
![]() $U_n$
.
$U_n$
.
For all
![]() $s,t \in T$
and
$s,t \in T$
and
![]() $j,k \in \left \{ 2,\ldots ,n-1 \right \}$
with
$j,k \in \left \{ 2,\ldots ,n-1 \right \}$
with
![]() $j \neq k$
and
$j \neq k$
and
![]() $(j,k) \neq (2,n-1)$
,
$(j,k) \neq (2,n-1)$
,
For all
![]() $t \in T$
and
$t \in T$
and
![]() $j \in \left \{ 2,\ldots ,n-1 \right \}$
,
$j \in \left \{ 2,\ldots ,n-1 \right \}$
,
For all
![]() $t, s \in T$
and
$t, s \in T$
and
![]() $i,j$
with
$i,j$
with
![]() $1 \leq i < j \leq n$
,
$1 \leq i < j \leq n$
,
For all
![]() $\sum _{\ell =1}^m a_{\ell } t_{\ell } \in \mathcal {R}$
,
$\sum _{\ell =1}^m a_{\ell } t_{\ell } \in \mathcal {R}$
,
 $$ \begin{align} \prod_{\ell=1}^m e_{1n}(t_{\ell})^{a_{\ell}} = 1. \end{align} $$
$$ \begin{align} \prod_{\ell=1}^m e_{1n}(t_{\ell})^{a_{\ell}} = 1. \end{align} $$
Relation (4.8) holds: If
![]() $n = 4$
, there is nothing to show, since in this case, the only equation to verify is
$n = 4$
, there is nothing to show, since in this case, the only equation to verify is
![]() $[e_{13}(t),e_{24}(s)] = 1$
, which holds by (4.7). Assume
$[e_{13}(t),e_{24}(s)] = 1$
, which holds by (4.7). Assume
![]() $n \geq 5$
. We first observe that
$n \geq 5$
. We first observe that
for all
![]() $t,s \in T$
and
$t,s \in T$
and
![]() $j \in \left \{ 3,\ldots ,n-2 \right \}$
since
$j \in \left \{ 3,\ldots ,n-2 \right \}$
since
 $$ \begin{align*} e_{1j}(t) e_{n-1,n}(s) & \overset{\text{(4.4)}}{=} e_{12}(t) e_{2j}(1) e_{12}(t)^{-1} e_{2j}(1)^{-1} e_{n-1,n}(s) \\ & \overset{\text{(4.4)}}{=} e_{12}(t) e_{2j}(1) e_{12}(t)^{-1} e_{n-1,n}(s) e_{2j}(1)^{-1} \\ & \overset{\text{(4.5)}}{=} e_{12}(t) e_{2j}(1) e_{n-1,n}(s) e_{12}(t)^{-1} e_{2j}(1)^{-1} \\ & \overset{\text{(4.4)}}{=} e_{12}(t) e_{n-1,n}(s) e_{2j}(1) e_{12}(t)^{-1} e_{2j}(1)^{-1} \\ & \overset{\text{(4.5)}}{=} e_{n-1,n}(s) e_{12}(t) e_{2j}(1) e_{12}(t)^{-1} e_{2j}(1)^{-1} \\ & \overset{\text{(4.4)}}{=} e_{n-1,n}(s) e_{1j}(t). \end{align*} $$
$$ \begin{align*} e_{1j}(t) e_{n-1,n}(s) & \overset{\text{(4.4)}}{=} e_{12}(t) e_{2j}(1) e_{12}(t)^{-1} e_{2j}(1)^{-1} e_{n-1,n}(s) \\ & \overset{\text{(4.4)}}{=} e_{12}(t) e_{2j}(1) e_{12}(t)^{-1} e_{n-1,n}(s) e_{2j}(1)^{-1} \\ & \overset{\text{(4.5)}}{=} e_{12}(t) e_{2j}(1) e_{n-1,n}(s) e_{12}(t)^{-1} e_{2j}(1)^{-1} \\ & \overset{\text{(4.4)}}{=} e_{12}(t) e_{n-1,n}(s) e_{2j}(1) e_{12}(t)^{-1} e_{2j}(1)^{-1} \\ & \overset{\text{(4.5)}}{=} e_{n-1,n}(s) e_{12}(t) e_{2j}(1) e_{12}(t)^{-1} e_{2j}(1)^{-1} \\ & \overset{\text{(4.4)}}{=} e_{n-1,n}(s) e_{1j}(t). \end{align*} $$
Proceeding similarly, we conclude that
for all
![]() $t, s \in T$
and
$t, s \in T$
and
![]() $k \in \left \{ 3,\ldots ,n-2 \right \}$
. Now suppose
$k \in \left \{ 3,\ldots ,n-2 \right \}$
. Now suppose
![]() $j < k$
. Then
$j < k$
. Then
because
![]() $e_{1j}(t)$
commutes with
$e_{1j}(t)$
commutes with
![]() $e_{n-1,n}(1)$
, by (4.12), and with
$e_{n-1,n}(1)$
, by (4.12), and with
![]() $e_{k,n-1}(s)$
, by (4.4). Analogously, if
$e_{k,n-1}(s)$
, by (4.4). Analogously, if
![]() $j> k$
, then
$j> k$
, then
by (4.4) and (4.13). Thus, the relations (4.8) hold in
![]() $U_n$
.
$U_n$
.
Relation (4.9) holds: To check (4.9) we need Lemma 4.7. First,
Setting
![]() $a = e_{12}(t)$
,
$a = e_{12}(t)$
,
![]() $b = e_{23}(1)$
, and
$b = e_{23}(1)$
, and
![]() $c = e_{3n}(1)$
, Hall's identity yields
$c = e_{3n}(1)$
, Hall's identity yields
 $$ \begin{align*} 1 & = [cac^{-1},[b,c]] \cdot [bcb^{-1},[a,b]] \cdot [aba^{-1},[c,a]] \\ & \overset{\text{(4.4)}}{=} [e_{12}(t),e_{2n}(1)] \cdot [e_{23}(1) e_{3n}(1) e_{23}(1)^{-1}, e_{13}(t)] \\ & \overset{\text{(4.4)}}{=} [e_{12}(t),e_{2n}(1)] \cdot [e_{2n}(1) e_{3n}(1), e_{13}(t)] \\ & \overset{\text{(4.1)}}{=} [e_{12}(t),e_{2n}(1)] \cdot e_{2n}(1) \cdot [e_{3n}(1),e_{13}(t)] \cdot e_{2n}(1)^{-1} \cdot [e_{2n}(1),e_{13}(t)] \\ & \overset{\text{(4.4)&(4.8)}}{=} [e_{12}(t),e_{2n}(1)] \cdot [e_{3n}(1),e_{13}(t)], \end{align*} $$
$$ \begin{align*} 1 & = [cac^{-1},[b,c]] \cdot [bcb^{-1},[a,b]] \cdot [aba^{-1},[c,a]] \\ & \overset{\text{(4.4)}}{=} [e_{12}(t),e_{2n}(1)] \cdot [e_{23}(1) e_{3n}(1) e_{23}(1)^{-1}, e_{13}(t)] \\ & \overset{\text{(4.4)}}{=} [e_{12}(t),e_{2n}(1)] \cdot [e_{2n}(1) e_{3n}(1), e_{13}(t)] \\ & \overset{\text{(4.1)}}{=} [e_{12}(t),e_{2n}(1)] \cdot e_{2n}(1) \cdot [e_{3n}(1),e_{13}(t)] \cdot e_{2n}(1)^{-1} \cdot [e_{2n}(1),e_{13}(t)] \\ & \overset{\text{(4.4)&(4.8)}}{=} [e_{12}(t),e_{2n}(1)] \cdot [e_{3n}(1),e_{13}(t)], \end{align*} $$
that is,
![]() $e_{1n}(t) = [e_{13}(t),e_{3n}(1)]$
. On the other hand,
$e_{1n}(t) = [e_{13}(t),e_{3n}(1)]$
. On the other hand,
Setting
![]() $a = e_{12}(1)$
,
$a = e_{12}(1)$
,
![]() $b = e_{23}(t)$
, and
$b = e_{23}(t)$
, and
![]() $c = e_{3n}(1)$
, Hall's identity and (4.4) yield
$c = e_{3n}(1)$
, Hall's identity and (4.4) yield
 $$ \begin{align*} 1 & {=} [e_{12}(1),e_{2n}(t)] \cdot [e_{23}(t) e_{3n}(1) e_{23}(1)^{-1}, e_{13}(t)] \\ & \overset{\text{(4.4)}}{=} [e_{12}(1),e_{2n}(t)] \cdot [e_{2n}(t) e_{3n}(1), e_{13}(t)] \\ & \overset{\text{(4.1)}}{=} [e_{12}(1),e_{2n}(t)] \cdot e_{2n}(t) \cdot [e_{3n}(1),e_{13}(t)] \cdot e_{2n}(t)^{-1} \cdot [e_{2n}(t),e_{13}(t)] \\ & \overset{\text{(4.4)&(4.8)}}{=} [e_{12}(1),e_{2n}(t)] \cdot [e_{3n}(1),e_{13}(t)]. \end{align*} $$
$$ \begin{align*} 1 & {=} [e_{12}(1),e_{2n}(t)] \cdot [e_{23}(t) e_{3n}(1) e_{23}(1)^{-1}, e_{13}(t)] \\ & \overset{\text{(4.4)}}{=} [e_{12}(1),e_{2n}(t)] \cdot [e_{2n}(t) e_{3n}(1), e_{13}(t)] \\ & \overset{\text{(4.1)}}{=} [e_{12}(1),e_{2n}(t)] \cdot e_{2n}(t) \cdot [e_{3n}(1),e_{13}(t)] \cdot e_{2n}(t)^{-1} \cdot [e_{2n}(t),e_{13}(t)] \\ & \overset{\text{(4.4)&(4.8)}}{=} [e_{12}(1),e_{2n}(t)] \cdot [e_{3n}(1),e_{13}(t)]. \end{align*} $$
The last product above equals
![]() $[e_{12}(1),e_{2n}(t)] e_{1n}(t)^{-1}$
by the previous computations. We have thus proved that
$[e_{12}(1),e_{2n}(t)] e_{1n}(t)^{-1}$
by the previous computations. We have thus proved that
Since
![]() $[e_{12}(1),e_{2n}(t)]$
also equals
$[e_{12}(1),e_{2n}(t)]$
also equals
![]() $[e_{12}(1),[e_{23}(1),e_{3n}(t)]]$
, again by (4.4), computations similar to the above also yield
$[e_{12}(1),[e_{23}(1),e_{3n}(t)]]$
, again by (4.4), computations similar to the above also yield
![]() $[e_{13}(t),e_{3n}(1)] = [e_{13}(1),e_{3n}(t)]$
. Entirely analogous arguments show that
$[e_{13}(t),e_{3n}(1)] = [e_{13}(1),e_{3n}(t)]$
. Entirely analogous arguments show that
for all
![]() $j \in \left \{ 2, \ldots , n-1 \right \}$
.
$j \in \left \{ 2, \ldots , n-1 \right \}$
.
Relations (4.10) hold: We now prove that the subgroup
![]() $Z :=~\langle {\,\left \{ e_{1n}(t) \mid t \in T \right \}\,} \rangle \leq U_n$
is central. Let
$Z :=~\langle {\,\left \{ e_{1n}(t) \mid t \in T \right \}\,} \rangle \leq U_n$
is central. Let
![]() $t, s \in T$
and let
$t, s \in T$
and let
![]() $i,j$
be such that
$i,j$
be such that
![]() $1 \leq i < j \leq n$
. We want to show that
$1 \leq i < j \leq n$
. We want to show that
![]() $e_{1n}(t)$
and
$e_{1n}(t)$
and
![]() $e_{ij}(s)$
commute in
$e_{ij}(s)$
commute in
![]() $U_n$
. To begin with,
$U_n$
. To begin with,
i.e., Z is abelian. If
![]() $i = 1$
and
$i = 1$
and
![]() $j \neq n$
, then
$j \neq n$
, then
![]() $j \geq 2$
and we can pick
$j \geq 2$
and we can pick
![]() $k \in ~\left \{ 2, \ldots , n-1 \right \}$
such that
$k \in ~\left \{ 2, \ldots , n-1 \right \}$
such that
![]() $k \neq j$
because
$k \neq j$
because
![]() $n \geq 4$
, yielding
$n \geq 4$
, yielding
 $$ \begin{align*} e_{1n}(t) e_{1j}(s) \overset{\text{(4.9)}}{=} [e_{1k}(t), e_{kn}(1) ] e_{1j}(s) & \overset{\text{(4.8)&(4.4)}}{=} e_{1j}(s) [e_{1k}(t), e_{kn}(1)] \\ & \overset{{\phantom{111}(4.9)\phantom{x11}}}{=} e_{1j}(s) e_{1n}(t). \end{align*} $$
$$ \begin{align*} e_{1n}(t) e_{1j}(s) \overset{\text{(4.9)}}{=} [e_{1k}(t), e_{kn}(1) ] e_{1j}(s) & \overset{\text{(4.8)&(4.4)}}{=} e_{1j}(s) [e_{1k}(t), e_{kn}(1)] \\ & \overset{{\phantom{111}(4.9)\phantom{x11}}}{=} e_{1j}(s) e_{1n}(t). \end{align*} $$
Similarly, if
![]() $j = n$
and
$j = n$
and
![]() $i \neq 1$
, choose
$i \neq 1$
, choose
![]() $k \in \left \{ 2, \ldots , n-1 \right \}$
such that
$k \in \left \{ 2, \ldots , n-1 \right \}$
such that
![]() $k \neq i$
. We obtain
$k \neq i$
. We obtain
It remains to prove
![]() $[e_{1n}(t), e_{ij}(s)] = 1$
for
$[e_{1n}(t), e_{ij}(s)] = 1$
for
![]() $1 < i < j < n$
. In this case,
$1 < i < j < n$
. In this case,
 $$ \begin{align*} e_{1n}(t) e_{ij}(s) & \overset{{\phantom{x11}(4.9)\phantom{x11}}}{=} e_{1i}(1) e_{in}(t) e_{1i}(1)^{-1} e_{in}(t)^{-1} e_{ij}(s) \\ & \overset{{\phantom{x11}(4.4)\phantom{x11}}}{=} e_{1i}(1) e_{in}(t) e_{1i}(1)^{-1} e_{ij}(s) e_{in}(t)^{-1} \\ & \overset{\text{(4.6)&(4.4)}}{=} e_{1i}(1) e_{in}(t) e_{1j}(s)^{-1} e_{ij}(s) e_{1i}(1)^{-1} e_{in}(t)^{-1} \\ & \overset{\text{(4.8)&(4.4)}}{=} e_{1j}(s)^{-1} e_{1i}(1) e_{in}(t) e_{ij}(s) e_{1i}(1)^{-1} e_{in}(t)^{-1} \\ & \overset{{\phantom{x11}(4.4)\phantom{x11}}}{=} e_{1j}(s)^{-1} e_{1i}(1) e_{ij}(s) e_{in}(t) e_{1i}(1)^{-1} e_{in}(t)^{-1} \\ & \overset{\text{(4.6)&(4.4)}}{=} e_{1j}(s)^{-1} e_{1j}(s) e_{ij}(s) e_{1i}(1) e_{in}(t) e_{1i}(1)^{-1} e_{in}(t)^{-1} \\ & \overset{{\phantom{x11}(4.9)\phantom{x11}}}{=} e_{ij}(s) e_{1n}(t). \end{align*} $$
$$ \begin{align*} e_{1n}(t) e_{ij}(s) & \overset{{\phantom{x11}(4.9)\phantom{x11}}}{=} e_{1i}(1) e_{in}(t) e_{1i}(1)^{-1} e_{in}(t)^{-1} e_{ij}(s) \\ & \overset{{\phantom{x11}(4.4)\phantom{x11}}}{=} e_{1i}(1) e_{in}(t) e_{1i}(1)^{-1} e_{ij}(s) e_{in}(t)^{-1} \\ & \overset{\text{(4.6)&(4.4)}}{=} e_{1i}(1) e_{in}(t) e_{1j}(s)^{-1} e_{ij}(s) e_{1i}(1)^{-1} e_{in}(t)^{-1} \\ & \overset{\text{(4.8)&(4.4)}}{=} e_{1j}(s)^{-1} e_{1i}(1) e_{in}(t) e_{ij}(s) e_{1i}(1)^{-1} e_{in}(t)^{-1} \\ & \overset{{\phantom{x11}(4.4)\phantom{x11}}}{=} e_{1j}(s)^{-1} e_{1i}(1) e_{ij}(s) e_{in}(t) e_{1i}(1)^{-1} e_{in}(t)^{-1} \\ & \overset{\text{(4.6)&(4.4)}}{=} e_{1j}(s)^{-1} e_{1j}(s) e_{ij}(s) e_{1i}(1) e_{in}(t) e_{1i}(1)^{-1} e_{in}(t)^{-1} \\ & \overset{{\phantom{x11}(4.9)\phantom{x11}}}{=} e_{ij}(s) e_{1n}(t). \end{align*} $$
Thus, relations (4.10) hold for all
![]() $t, s \in T$
and
$t, s \in T$
and
![]() $i,j$
with
$i,j$
with
![]() $1 \leq i < j \leq n$
.
$1 \leq i < j \leq n$
.
Relations (4.11) hold: Given any pair
![]() $t,s \in T$
,
$t,s \in T$
,
 $$ \begin{align} \nonumber [e_{12}(t) e_{12}(s), e_{2n}(1)] & \overset{{\phantom{x11}(4.1)\phantom{x11}}}{=} e_{12}(t)[e_{12}(s), e_{2n}(1)] e_{12}(t)^{-1} [e_{12}(t), e_{2n}(1)] \\ \nonumber & \overset{\text{(4.9)&(4.10)}}{=} [e_{12}(s), e_{2n}(1)] [e_{12}(t), e_{2n}(1)] \\ & \overset{\text{(4.9)&(4.10)}}{=} [e_{12}(t), e_{2n}(1)] [e_{12}(s), e_{2n}(1)]. \end{align} $$
$$ \begin{align} \nonumber [e_{12}(t) e_{12}(s), e_{2n}(1)] & \overset{{\phantom{x11}(4.1)\phantom{x11}}}{=} e_{12}(t)[e_{12}(s), e_{2n}(1)] e_{12}(t)^{-1} [e_{12}(t), e_{2n}(1)] \\ \nonumber & \overset{\text{(4.9)&(4.10)}}{=} [e_{12}(s), e_{2n}(1)] [e_{12}(t), e_{2n}(1)] \\ & \overset{\text{(4.9)&(4.10)}}{=} [e_{12}(t), e_{2n}(1)] [e_{12}(s), e_{2n}(1)]. \end{align} $$
Now let
![]() $\sum \limits _{\ell = 1}^m a_{\ell } t_{\ell } \in \mathcal {R}$
be an additive defining relation in R. (Recall that
$\sum \limits _{\ell = 1}^m a_{\ell } t_{\ell } \in \mathcal {R}$
be an additive defining relation in R. (Recall that
![]() $t_{\ell } \in T$
and
$t_{\ell } \in T$
and
![]() $a_{\ell } \in \mathbb {Z}$
as in Lemma 4.8.) Induction on
$a_{\ell } \in \mathbb {Z}$
as in Lemma 4.8.) Induction on
![]() $\sum \limits _{\ell = 1}^{m} |a_{\ell }|$
and (4.14) yield
$\sum \limits _{\ell = 1}^{m} |a_{\ell }|$
and (4.14) yield
 $$ \begin{align*} \prod\limits_{\ell = 1}^{m} e_{1n}(t_{\ell})^{a_{\ell}} \overset{\text{Def.}}{=} \prod\limits_{\ell = 1}^{m} \left([e_{12}(t_{\ell}), e_{2n}(1)]\right)^{a_{\ell}} \overset{\text{(4.14)}}{=} \left[ \prod\limits_{\ell = 1}^{m} e_{12}(t_{\ell})^{a_{\ell}}, e_{2n}(1) \right] \overset{\text{(4.4)}}{=} 1. \end{align*} $$
$$ \begin{align*} \prod\limits_{\ell = 1}^{m} e_{1n}(t_{\ell})^{a_{\ell}} \overset{\text{Def.}}{=} \prod\limits_{\ell = 1}^{m} \left([e_{12}(t_{\ell}), e_{2n}(1)]\right)^{a_{\ell}} \overset{\text{(4.14)}}{=} \left[ \prod\limits_{\ell = 1}^{m} e_{12}(t_{\ell})^{a_{\ell}}, e_{2n}(1) \right] \overset{\text{(4.4)}}{=} 1. \end{align*} $$
Since the relations (4.8)–(4.11) missing from the presentation for
![]() $\textbf {U}_n(R)$
from Lemma 4.8 also hold in
$\textbf {U}_n(R)$
from Lemma 4.8 also hold in
![]() $U_n$
, it follows that
$U_n$
, it follows that
![]() $U_n \cong \textbf {U}_n(R)$
, as claimed.▪
$U_n \cong \textbf {U}_n(R)$
, as claimed.▪
4.2 Proof of Theorem 1.2
If
![]() $\phi (\textbf {A}_n(R))> 0$
for some
$\phi (\textbf {A}_n(R))> 0$
for some
![]() $n \geq 3$
, then
$n \geq 3$
, then
![]() $\textbf {A}_n(R)$
and its retract
$\textbf {A}_n(R)$
and its retract
![]() $\mathbb {A}\text {ff}(R) \cong { \left ( \begin {smallmatrix} * & * \\ 0 & 1 \end {smallmatrix} \right ) } \leq \operatorname {\textrm {GL}}_2(R)$
are finitely generated. Thus, the abelian group
$\mathbb {A}\text {ff}(R) \cong { \left ( \begin {smallmatrix} * & * \\ 0 & 1 \end {smallmatrix} \right ) } \leq \operatorname {\textrm {GL}}_2(R)$
are finitely generated. Thus, the abelian group
![]() $\mathbb {G}_m(R)$
is finitely generated and
$\mathbb {G}_m(R)$
is finitely generated and
![]() $\mathbb {G}_a(R)$
is finitely generated as a
$\mathbb {G}_a(R)$
is finitely generated as a
![]() $\mathbb {Z}[\mathbb {G}_m(R)]$
-module, which shows that R is finitely generated as a ring. This deals with the very first claim of Theorem 1.2 (except possibly when
$\mathbb {Z}[\mathbb {G}_m(R)]$
-module, which shows that R is finitely generated as a ring. This deals with the very first claim of Theorem 1.2 (except possibly when
![]() $n = 2$
).
$n = 2$
).
Now, if
![]() $\phi (\textbf {A}_2(R))> 0$
, then
$\phi (\textbf {A}_2(R))> 0$
, then
![]() $\textbf {A}_2(R) \cong \mathbb {G}_a(R)$
is finitely generated as a
$\textbf {A}_2(R) \cong \mathbb {G}_a(R)$
is finitely generated as a
![]() $\mathbb {Z}$
-module. This implies, for every
$\mathbb {Z}$
-module. This implies, for every
![]() $n \geq 2$
, that the unipotent radical
$n \geq 2$
, that the unipotent radical
![]() $\textbf {U}_n(R)$
of
$\textbf {U}_n(R)$
of
![]() $\textbf {A}_n(R)$
is a finitely generated nilpotent group and thus has
$\textbf {A}_n(R)$
is a finitely generated nilpotent group and thus has
![]() $\phi (\textbf {U}_n(R)) = \infty $
. (The equality follows e.g., from Lemma 2.1 by induction on the nilpotency class because all terms of the lower central series of a finitely generated nilpotent group are themselves finitely generated.) Moreover,
$\phi (\textbf {U}_n(R)) = \infty $
. (The equality follows e.g., from Lemma 2.1 by induction on the nilpotency class because all terms of the lower central series of a finitely generated nilpotent group are themselves finitely generated.) Moreover,
![]() $\textbf {A}_2(R) \cong \mathbb {G}_a(R)$
being finitely generated also implies that the group of units
$\textbf {A}_2(R) \cong \mathbb {G}_a(R)$
being finitely generated also implies that the group of units
![]() $\mathbb {G}_m(R)$
is finitely generated by Samuel’s generalization of Dirichlet’s unit theorem [Reference Samuel49, Section 4.7]. Thus,
$\mathbb {G}_m(R)$
is finitely generated by Samuel’s generalization of Dirichlet’s unit theorem [Reference Samuel49, Section 4.7]. Thus,
![]() $\textbf {D}_n(R)\leq \operatorname {\textrm {GL}}_n(R)$
and
$\textbf {D}_n(R)\leq \operatorname {\textrm {GL}}_n(R)$
and
![]() $\textbf {T}_n(R) \leq \textbf {A}_n(R)$
also have
$\textbf {T}_n(R) \leq \textbf {A}_n(R)$
also have
![]() $\phi (\textbf {T}_n(R)) = \phi (\textbf {D}_n(R)) = \infty $
. Since
$\phi (\textbf {T}_n(R)) = \phi (\textbf {D}_n(R)) = \infty $
. Since
![]() $\textbf {A}_n(R) = \textbf {U}_n(R) \rtimes \textbf {T}_n(R)$
and
$\textbf {A}_n(R) = \textbf {U}_n(R) \rtimes \textbf {T}_n(R)$
and
![]() $\textbf {B}_2(R) = \textbf {U}_2(R) \rtimes \textbf {D}_2(R)$
, it follows from Lemmata 2.1 and 3.3 that
$\textbf {B}_2(R) = \textbf {U}_2(R) \rtimes \textbf {D}_2(R)$
, it follows from Lemmata 2.1 and 3.3 that
![]() $\phi (\textbf {A}_n(R)) = \phi (\textbf {B}_2^{\circ }(R)) = \infty $
.
$\phi (\textbf {A}_n(R)) = \phi (\textbf {B}_2^{\circ }(R)) = \infty $
.
Assume from now on that R is not finitely generated as a
![]() $\mathbb {Z}$
-module. For
$\mathbb {Z}$
-module. For
![]() $n \geq 3$
, we first observe that
$n \geq 3$
, we first observe that
![]() $\phi (\textbf {A}_n(R)) \geq 1$
whenever
$\phi (\textbf {A}_n(R)) \geq 1$
whenever
![]() $\phi (\textbf {B}_2^{\circ }(R)) \geq 1$
. Indeed, assume the latter, i.e.,
$\phi (\textbf {B}_2^{\circ }(R)) \geq 1$
. Indeed, assume the latter, i.e.,
![]() $\textbf {B}_2^{\circ }(R)$
is finitely generated. Then, for every
$\textbf {B}_2^{\circ }(R)$
is finitely generated. Then, for every
![]() $i \in \left \{ 2, \ldots , n-2 \right \}$
, the subgroups
$i \in \left \{ 2, \ldots , n-2 \right \}$
, the subgroups
are also finitely generated by Lemma 3.2. By relations (2.1) and (2.2), the subgroups above generate all of
![]() $\textbf {A}_n(R)$
, whence
$\textbf {A}_n(R)$
, whence
![]() $\phi (\textbf {A}_n(R)) \geq 1$
. Secondly, it is straightforward that
$\phi (\textbf {A}_n(R)) \geq 1$
. Secondly, it is straightforward that
![]() $\textbf {A}_n(R)$
—still for
$\textbf {A}_n(R)$
—still for
![]() $n \geq 3$
—retracts e.g., onto
$n \geq 3$
—retracts e.g., onto
![]() $\mathbb {A}\text {ff}(R)$
, which implies
$\mathbb {A}\text {ff}(R)$
, which implies
![]() $\phi (\textbf {A}_n(R)) \leq \phi (\textbf {B}_2^{\circ }(R))$
by Theorem 1.1.
$\phi (\textbf {A}_n(R)) \leq \phi (\textbf {B}_2^{\circ }(R))$
by Theorem 1.1.
From the observations above, the proof of part (2) will be concluded once we show that
![]() $\textbf {A}_3(R)$
can never be finitely presented, i.e.,
$\textbf {A}_3(R)$
can never be finitely presented, i.e.,
![]() $\phi (\textbf {A}_3(R)) \leq 1$
. To see this, in case
$\phi (\textbf {A}_3(R)) \leq 1$
. To see this, in case
![]() $\mathbb {G}_m(R)$
is itself finite or is infinitely generated, then
$\mathbb {G}_m(R)$
is itself finite or is infinitely generated, then
![]() $\phi (\textbf {A}_3(R)) = \phi (\textbf {U}_3(R)) = 0$
. In case
$\phi (\textbf {A}_3(R)) = \phi (\textbf {U}_3(R)) = 0$
. In case
![]() $\mathbb {G}_m(R)$
has torsion-free rank at least one and if
$\mathbb {G}_m(R)$
has torsion-free rank at least one and if
![]() $\textbf {A}_3(R)$
were finitely presented, then its metabelian quotient
$\textbf {A}_3(R)$
were finitely presented, then its metabelian quotient
![]() $\textbf {A}_3(R)/Z(\textbf {A}_3(R)) = \textbf {A}_3(R) / \textbf {E}_{13}(R)$
would also be finitely presented by [Reference Bieri, de Cornulier, Guyot and Strebel13, Corollary 5.6]. But the complement of the
$\textbf {A}_3(R)/Z(\textbf {A}_3(R)) = \textbf {A}_3(R) / \textbf {E}_{13}(R)$
would also be finitely presented by [Reference Bieri, de Cornulier, Guyot and Strebel13, Corollary 5.6]. But the complement of the
![]() $\Sigma $
-invariant [Reference Bieri, de Cornulier, Guyot and Strebel13] of the
$\Sigma $
-invariant [Reference Bieri, de Cornulier, Guyot and Strebel13] of the
![]() $\mathbb {Z}[\textbf {T}_1(R)]$
-module
$\mathbb {Z}[\textbf {T}_1(R)]$
-module
![]() $\textbf {U}_3(R) / \textbf {E}_{13}(R) \cong \textbf {E}_{12}(R) \oplus \textbf {E}_{23}(R)$
is readily seen to contain antipodal points, which for us means that
$\textbf {U}_3(R) / \textbf {E}_{13}(R) \cong \textbf {E}_{12}(R) \oplus \textbf {E}_{23}(R)$
is readily seen to contain antipodal points, which for us means that
![]() $\textbf {U}_3(R) / \textbf {E}_{13}(R)$
is not tame as a
$\textbf {U}_3(R) / \textbf {E}_{13}(R)$
is not tame as a
![]() $\mathbb {Z}[\textbf {T}_1(R)]$
-module. This would contradict [Reference Bieri, de Cornulier, Guyot and Strebel13, Theorem 5.1] and we are done with part (2).
$\mathbb {Z}[\textbf {T}_1(R)]$
-module. This would contradict [Reference Bieri, de Cornulier, Guyot and Strebel13, Theorem 5.1] and we are done with part (2).
Turning to part (3) after the previous remarks, it remains to check for
![]() $n\geq 4$
that
$n\geq 4$
that
![]() $\phi (\textbf {A}_n(R)) \geq 2$
when
$\phi (\textbf {A}_n(R)) \geq 2$
when
![]() $\phi (\textbf {B}_2^{\circ }(R)) \geq 2$
. Suppose the latter holds, i.e.,
$\phi (\textbf {B}_2^{\circ }(R)) \geq 2$
. Suppose the latter holds, i.e.,
![]() $\textbf {B}_2^{\circ }(R)$
is finitely presented. By Lemma 4.2, the group
$\textbf {B}_2^{\circ }(R)$
is finitely presented. By Lemma 4.2, the group
![]() $\textbf {A}_n(R)$
for
$\textbf {A}_n(R)$
for
![]() $n \geq 4$
acts cocompactly and by cell-permuting homeomorphisms on the simplicial complex
$n \geq 4$
acts cocompactly and by cell-permuting homeomorphisms on the simplicial complex
![]() $CC(\mathscr{H}\;(n,R))$
. Since
$CC(\mathscr{H}\;(n,R))$
. Since
![]() $\phi (\textbf {B}_2^{\circ }(R)) \geq 2$
, we know from Lemma 4.2 and Proposition 4.3 that the stabilizer in
$\phi (\textbf {B}_2^{\circ }(R)) \geq 2$
, we know from Lemma 4.2 and Proposition 4.3 that the stabilizer in
![]() $\textbf {A}_n(R)$
of any cell of
$\textbf {A}_n(R)$
of any cell of
![]() $CC(\mathscr{H}\;(n,R))$
is finitely presented. Since
$CC(\mathscr{H}\;(n,R))$
is finitely presented. Since
![]() $CC(\mathscr{H}\;(n,R))$
(for
$CC(\mathscr{H}\;(n,R))$
(for
![]() $n \geq 4$
) is connected and simply-connected by Proposition 4.9 and Theorem 4.6, it follows from Theorem 4.1 that
$n \geq 4$
) is connected and simply-connected by Proposition 4.9 and Theorem 4.6, it follows from Theorem 4.1 that
![]() $\textbf {A}_n(R)$
is finitely presented. That is,
$\textbf {A}_n(R)$
is finitely presented. That is,
![]() $\phi (\textbf {A}_n(R)) \geq 2$
, as required.▪
$\phi (\textbf {A}_n(R)) \geq 2$
, as required.▪
Remarks on the proof of Theorem 1.2
The author was unable to prove purely geometrically that
![]() $CC(\mathscr{H}\;(n,R))$
is simply-connected. The argument given here, whose main technical ingredient is Proposition 4.9, is the only step in the proof of Theorem 1.2 whose methods are similar to those of Strebel’s in [Reference Strebel54]. Altogether, there are two key differences between our techniques.
$CC(\mathscr{H}\;(n,R))$
is simply-connected. The argument given here, whose main technical ingredient is Proposition 4.9, is the only step in the proof of Theorem 1.2 whose methods are similar to those of Strebel’s in [Reference Strebel54]. Altogether, there are two key differences between our techniques.
Assuming
![]() $\left \{ \left (\begin {smallmatrix} \diamond & * \\ 0 & 1 \end {smallmatrix}\right ) \mid * \in R, \diamond \in Q \right \} \leq \operatorname {\textrm {GL}}_2(R)$
to be finitely presented (and fixing such a presentation), Strebel gives concrete generators and relations for his groups
$\left \{ \left (\begin {smallmatrix} \diamond & * \\ 0 & 1 \end {smallmatrix}\right ) \mid * \in R, \diamond \in Q \right \} \leq \operatorname {\textrm {GL}}_2(R)$
to be finitely presented (and fixing such a presentation), Strebel gives concrete generators and relations for his groups
![]() $A_n(R,Q)$
for
$A_n(R,Q)$
for
![]() $n \geq 4$
. (Recall that
$n \geq 4$
. (Recall that
![]() $A_n(R,R^{\times }) = \textbf {A}_n(R)$
.) Presentations of
$A_n(R,R^{\times }) = \textbf {A}_n(R)$
.) Presentations of
![]() $\textbf {A}_n(R)$
using our methods can be extracted using [Reference Brown17, Theorem 1]. Alternatively, one can combine the presentation for
$\textbf {A}_n(R)$
using our methods can be extracted using [Reference Brown17, Theorem 1]. Alternatively, one can combine the presentation for
![]() $\textbf {U}_n(R)$
from Proposition 4.9 with a presentation of the torus
$\textbf {U}_n(R)$
from Proposition 4.9 with a presentation of the torus
![]() $\textbf {T}_n(R)$
to construct a presentation for
$\textbf {T}_n(R)$
to construct a presentation for
![]() $\textbf {A}_n(R) = \textbf {U}_n(R) \rtimes \textbf {T}_n(R)$
. Such presentations, however, are somewhat cumbersome. Thus on the one hand, Strebel’s proof has an advantage in that his sets of generators and relations are cleaner.
$\textbf {A}_n(R) = \textbf {U}_n(R) \rtimes \textbf {T}_n(R)$
. Such presentations, however, are somewhat cumbersome. Thus on the one hand, Strebel’s proof has an advantage in that his sets of generators and relations are cleaner.
On the other hand, our proof of Proposition 4.9 drawing from Holz’s ideas [Reference Holz39, Anhang] is advantageous in that it suggests a K-theoretical phenomenon behind finiteness properties of Abels’ groups. It is well-known that classical nonexceptional groups are finitely generated (resp. finitely presented) whenever their ranks are large enough or the base ring has good
![]() $K_1$
- and
$K_1$
- and
![]() $K_2$
-groups; cf. [Reference Hahn and O'Meara38]. For instance, a large rank n gives one enough space in
$K_2$
-groups; cf. [Reference Hahn and O'Meara38]. For instance, a large rank n gives one enough space in
![]() $ \operatorname {\textrm {GL}}_n(R)$
to work with elementary matrices via commutator calculus and thus deduce many relations from the standard ones. The same happens with
$ \operatorname {\textrm {GL}}_n(R)$
to work with elementary matrices via commutator calculus and thus deduce many relations from the standard ones. The same happens with
![]() $\textbf {A}_n(R)$
—the hypothesis
$\textbf {A}_n(R)$
—the hypothesis
![]() $n \geq 4$
is necessary for positive results, but Holz observes further that one can spare some generators (and some relations) for
$n \geq 4$
is necessary for positive results, but Holz observes further that one can spare some generators (and some relations) for
![]() $\textbf {A}_n(\mathbb {Z}[1/p])$
in the case
$\textbf {A}_n(\mathbb {Z}[1/p])$
in the case
![]() $n \geq 5$
in comparison to
$n \geq 5$
in comparison to
![]() $\textbf {A}_4(\mathbb {Z}[1/p])$
. This observation is incorporated in our generalization and is the reason why
$\textbf {A}_4(\mathbb {Z}[1/p])$
. This observation is incorporated in our generalization and is the reason why
![]() $CC(\mathscr{H}\;(n,R))$
is three-dimensional for
$CC(\mathscr{H}\;(n,R))$
is three-dimensional for
![]() $n = 4$
but merely two-dimensional for
$n = 4$
but merely two-dimensional for
![]() $n \geq 5$
.
$n \geq 5$
.
4.3 Conjecture 1.7 in the arithmetic set-up
We close the paper by spelling out a proof of the following special case of Conjecture 1.7. Though it has not appeared in this general form in the literature before, we claim no originality—it is a simple combination of famous results mentioned in the introduction.
Proposition 4.10 Let
![]() $\mathcal {O}_S$
be a Dedekind domain of arithmetic type. If either
$\mathcal {O}_S$
be a Dedekind domain of arithmetic type. If either
![]() $ \operatorname {\textrm {char}}(\mathcal {O}_S) = 0$
or if
$ \operatorname {\textrm {char}}(\mathcal {O}_S) = 0$
or if
![]() $ \operatorname {\textrm {char}}(\mathcal {O}_S)> 0$
and S has at most three elements, then the S-arithmetic Abels’ groups
$ \operatorname {\textrm {char}}(\mathcal {O}_S)> 0$
and S has at most three elements, then the S-arithmetic Abels’ groups
![]() $\textbf {A}_n(\mathcal {O}_S)$
satisfy Conjecture 1.7. That is,
$\textbf {A}_n(\mathcal {O}_S)$
satisfy Conjecture 1.7. That is,
Proof If
![]() $ \operatorname {\textrm {char}}(\mathcal {O}_S) = 0$
, the Kneser–Tiemeyer local-global principle [Reference Tiemeyer55, Theorem. 3.1] allows us to assume that S contains a single nonarchimedean place. Also, the equality
$ \operatorname {\textrm {char}}(\mathcal {O}_S) = 0$
, the Kneser–Tiemeyer local-global principle [Reference Tiemeyer55, Theorem. 3.1] allows us to assume that S contains a single nonarchimedean place. Also, the equality
![]() $\phi (\textbf {B}_2^{\circ }(\mathcal {O}_S)) = \infty $
holds by [Reference Tiemeyer55, Corollary 4.5]. By restriction of scalars (see e.g., [Reference Margulis43, Lemma 3.1.4]), it suffices to consider the case where
$\phi (\textbf {B}_2^{\circ }(\mathcal {O}_S)) = \infty $
holds by [Reference Tiemeyer55, Corollary 4.5]. By restriction of scalars (see e.g., [Reference Margulis43, Lemma 3.1.4]), it suffices to consider the case where
![]() $ \operatorname {\textrm {Frac}}(\mathcal {O}_S) = \mathbb {Q}$
. In this set-up,
$ \operatorname {\textrm {Frac}}(\mathcal {O}_S) = \mathbb {Q}$
. In this set-up,
![]() $\mathcal {O}_S$
is of the form
$\mathcal {O}_S$
is of the form
![]() $\mathcal {O}_S = \mathbb {Z}[1/p]$
for some prime number
$\mathcal {O}_S = \mathbb {Z}[1/p]$
for some prime number
![]() $p \in \mathbb {N}$
. Here,
$p \in \mathbb {N}$
. Here,
![]() $\textbf {A}_n(\mathbb {Z}[1/p])$
has
$\textbf {A}_n(\mathbb {Z}[1/p])$
has
![]() $\phi (\textbf {A}_n(\mathbb {Z}[1/p])) < n-1$
, for otherwise it would be of homological type
$\phi (\textbf {A}_n(\mathbb {Z}[1/p])) < n-1$
, for otherwise it would be of homological type
![]() $\text {FP}_{n-1}$
and thus of type
$\text {FP}_{n-1}$
and thus of type
![]() $\text {FP}_{\infty }$
by [Reference Bieri12, Proposition]. In particular, its center
$\text {FP}_{\infty }$
by [Reference Bieri12, Proposition]. In particular, its center
![]() $Z(\textbf {A}_n(\mathbb {Z}[1/p]))$
would be finitely generated by [Reference Bieri12, Corollary 2]. However,
$Z(\textbf {A}_n(\mathbb {Z}[1/p]))$
would be finitely generated by [Reference Bieri12, Corollary 2]. However,
![]() $Z(\textbf {A}_n(\mathbb {Z}[1/p]))$
is the elementary subgroup
$Z(\textbf {A}_n(\mathbb {Z}[1/p]))$
is the elementary subgroup
![]() $\textbf {E}_{1n}(\mathbb {Z}[1/p]) \cong \mathbb {G}_a(\mathbb {Z}[1/p])$
, which is not finitely generated, yielding a contradiction. Since
$\textbf {E}_{1n}(\mathbb {Z}[1/p]) \cong \mathbb {G}_a(\mathbb {Z}[1/p])$
, which is not finitely generated, yielding a contradiction. Since
![]() $\phi (\textbf {A}_n(\mathbb {Z}[1/p])) \geq n-2$
by [Reference Abels and Brown3, Theorem B] and Brown’s criteria (Theorem 4.1 and [Reference Brown18, Proposition 1.1]), we obtain
$\phi (\textbf {A}_n(\mathbb {Z}[1/p])) \geq n-2$
by [Reference Abels and Brown3, Theorem B] and Brown’s criteria (Theorem 4.1 and [Reference Brown18, Proposition 1.1]), we obtain
In case
![]() $ \operatorname {\textrm {char}}(\mathcal {O}_S)> 0$
, we have
$ \operatorname {\textrm {char}}(\mathcal {O}_S)> 0$
, we have
![]() $\phi (\textbf {B}_2^{\circ }(\mathcal {O}_S)) = |S|-1$
by Theorem 1.3. Thus, if S has at most three elements, it follows from Theorem 1.2 that
$\phi (\textbf {B}_2^{\circ }(\mathcal {O}_S)) = |S|-1$
by Theorem 1.3. Thus, if S has at most three elements, it follows from Theorem 1.2 that
▪
Acknowledgment
Part of this work grew out of interesting discussions with Herbert Abels, Stephan Holz, Benjamin Brück, and Alastair Litterick, whom I thank most sincerely. I am indebted to Ralph Strebel for the mathematical correspondences and for sharing with me his manuscripts, and to my Ph.D. advisor, Kai-Uwe Bux, for his guidance. The author also thanks the anonymous referees for valuable suggestions.