Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-11T12:10:44.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Laser-driven generation of high-current ion beams using skin-layer ponderomotive acceleration

Published online by Cambridge University Press:  05 December 2005

J. BADZIAK ,
S. GŁOWACZ ,
S. JABŁOŃSKI ,
P. PARYS ,
J. WOŁOWSKI  and
H. HORA
J. BADZIAK
Affiliation:
Institute of Plasma Physics and Laser Microfusion, EURATOM Association, Warsaw, Poland
S. GŁOWACZ
Affiliation:
Institute of Plasma Physics and Laser Microfusion, EURATOM Association, Warsaw, Poland
S. JABŁOŃSKI
Affiliation:
Institute of Plasma Physics and Laser Microfusion, EURATOM Association, Warsaw, Poland
P. PARYS
Affiliation:
Institute of Plasma Physics and Laser Microfusion, EURATOM Association, Warsaw, Poland
J. WOŁOWSKI
Affiliation:
Institute of Plasma Physics and Laser Microfusion, EURATOM Association, Warsaw, Poland
H. HORA
Affiliation:
Department of Theoretical Physics, University of New South Wales, Sydney, Australia
Rights & Permissions [Opens in a new window]

Abstract

Basic properties of generation of high-current ion beams using the skin-layer ponderomotive acceleration (S-LPA) mechanism, induced by a short laser pulse interacting with a solid target are studied. Simplified scaling laws for the ion energies, the ion current densities, the ion beam intensities, and the efficiency of ions' production are derived for the cases of subrelativistic and relativistic laser-plasma interactions. The results of the time-of-flight measurements performed for both backward-accelerated ion beams from a massive target and forward-accelerated beams from a thin foil target irradiated by 1-ps laser pulse of intensity up to ∼ 1017 W/cm2 are presented. The ion current densities and the ion beam intensities at the source obtained from these measurements are compared to the ones achieved in recent short-pulse experiments using the target normal sheath acceleration (TNSA) mechanism at relativistic (>1019 W/cm2) laser intensities. The possibility of application of high-current ion beams produced by S-LPA at relativistic intensities for fast ignition of fusion target is considered. Using the derived scaling laws for the ion beam parameters, the achievement conditions for ignition of compressed DT fuel with ion beams driven by ps laser pulses of total energy ≤ 100 kJ is shown.

Keywords

High-current ion beamsLaser plasma interactionPlasma block accelerationSkin-layer ponderomotive acceleration
Type
Workshop on Fast High Density Plasma Blocks Driven By Picosecond Terawatt Lasers
Information
Laser and Particle Beams , Volume 23 , Issue 4 , October 2005 , pp. 401 - 409
Copyright
© 2005 Cambridge University Press

1. INTRODUCTION

High-current collimated ion beams produced by the interaction of intense short (≤ 1ps) laser pulses with solid targets have potential to be used in various fields of research, including high energy density physics, and inertial confinement fusion (ICF), as well as in some medical applications such as hadron therapy. An excellent recognized method of laser-induced production of high quality ion beams is target normal sheat acceleration (TNSA) (Wilks et al., 2001). Using relativistic laser intensities (IL ≥ Irel ≈ 4.1 × 1018/λL2 [W/cm2, μm], λL − laser wavelength), this method enables generation of low-emittance high-current ion beams with mean ion energies of several MeV (Snavely et al., 2000; Borghesi et al., 2002; Hegelich et al., 2002; Zepf et al., 2003; Cowan et al., 2004; Pegoraro et al., 2004; Roth et al., 2005), and maximum ion energies approaching 50 MeV for protons (Snavely et al., 2000) and 100 MeV for heavier ions (Hegelich et al., 2002). Since the ions are (forward) accelerated predominantly along the normal of the target rear surface, a curving of this surface makes it possible to focus the ion beam ballistically, and as a result, to increase the ion current density and the ion beam intensity significantly. This idea was confirmed by the particle-in-cell (PIC) simulation of Wilks et al. (2001) and by measurements of Patel et al. (2003), where an increase in the proton current density, j, and the proton beam intensity, Ii, by an order of magnitude (to estimated values of j ∼109 A/cm2 and of Ii ∼2 × 1015 W/cm2) was observed when the planar thin foil target was replaced by a hemispherical one. The using of focused proton beams driven by the TNSA mechanism for fast ignition of ICF target (Roth et al., 2001) and isochoric heating of dense matter (Patel et al., 2003) was proposed.

The other laser-based method of producing collimated ion beams of very high current densities and beam intensities—just recently proposed and demonstrated (Badziak et al., 2004a, 2004b, 2005; Hora et al., 2004)—is skin-layer ponderomotive acceleration (S-LPA). This method employs strong ponderomotive forces induced at the skin-layer interaction of a short laser pulse with a thin preplasma layer (of Lpre << df ) produced by the laser prepulse in front of a solid target (Lpre—the preplasma layer thickness, df —the laser focal spot diameter). The main short laser pulse interacts most intensely with the plasma in the skin layer near the surface of the critical electron density nec and the geometry of the interaction is almost planar (since Lpre << df ). The high plasma density gradient in the interaction region induces two opposite ponderomotive forces which break the plasma and drive two thin (∼ λL) plasma blocks toward the vacuum and the plasma interior, respectively. As the density of the plasma blocks is high (the ion density ni ≈ nec /z, where z is the ion charge state) even at moderate ion velocities vi ∼ 108 cm/s, the ion current densities and beam intensities can be very high. The time duration τis of the ion flux flowing out of the interaction region (being the ion source) is approximately equal to the laser pulse duration τL and the block area Ss is close to the area of the laser focal spot Sf . Due to almost planar acceleration geometry, the angular divergence of the ion beam is small.

In this paper, basic properties of generation of fast plasma (ion) block by S-LPA at subrelativistic laser intensities are studied using simplified theory, numerical hydrodynamic simulations, and the time-of-flight measurements. Both backward-accelerated ion beams from a massive target and forward-accelerated beams from a thin foil target irradiated by 1-ps laser pulse of intensity up to ∼ 1017 W/cm2 were investigated. The results of the measurements, and particularly ion current densities and ion beam intensities at the source (close to the target), are compared to the ones achieved in recent short-pulse experiments using TNSA at relativistic intensities. Necessary conditions for an efficient generation of fast plasma blocks by S-LPA at relativistic intensities are briefly discussed and simplified scaling laws for parameters of the plasma block are derived. The possibility of application of fast plasma blocks for fast ignition of ICF target is considered.

2. SIMPLIFIED THEORY OF S-LPA FOR SUBRELATIVISTIC LASER INTENSITIES AND RESULTS OF NUMERICAL SIMULATIONS

Because the process of plasma block acceleration by ponderomotive force occurs in a close vicinity of the critical plasma surface, for a rough estimate of ion flux parameters at the source we can assume that ni ≈ nec /z. Taking into account general formulae for the ion current density:

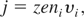
and for the ion beam intensity:

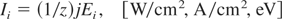
and also the fact that for subrelativistic laser intensities (IL << Irel ≈ 4.1 × 1018/λL2, [W/cm2, μm]) the ion energy can be expressed by the formula (Badziak et al., 2004a, 2004b):

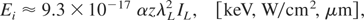
we obtain the following scaling laws for the ion current density at the source, js, and the ion beam intensity at the source, Iis, in the subrelativistic intensity region:

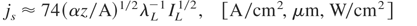
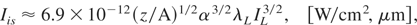
where IL is laser intensity in vacuum, A is the atomic mass number, α = S for the forward-accelerated ions or α = S − 1 for the backward-accelerated ions and S is the dielectric swelling factor (Hora, 1991). Assuming τis ≈ τL and Ss ≈ Sf (Badziak et al., 2004a, 2004b), from (5) we arrive at the following scaling law for the energetic efficiency ηi of ion beam production:

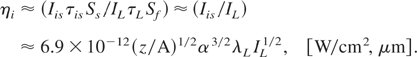
We can note an increase in the efficiency with laser intensity and fairly strong dependences of the efficiency on the dielectric swelling factor. Taking as an example: z/A = 1 (protons), α = 1, λL = 1 μm, IL = 1017 W/cm2, we obtain: Ei ≈ 9.3 keV, js ≈ 2.3 × 1010 A/cm2, Iis ≈ 2.2 × 1014 W/cm2, ηi ≈ 0.22%. We can see that even at quite moderate laser intensity, the ion current density and the ion beam intensity of the plasma block generated by the ponderomotive force can be very high.

Equations (3) to (6) give simple, approximate scaling laws for the ion beam parameters and the efficiency ηi as a function of the laser intensity and the laser wavelength. However, there exists a dielectric swelling factor in the equations, which depends on the plasma density gradient scale length Ln. As the plasma density profile is modified by the ponderomotive pressure of a laser pulse during its interaction with plasma, in general, the effective (averaged over the interaction time) swelling factor S introduced in Eqs. (3)–(6) is a function (usually slowly varying) of the laser pulse parameters (IL, τL, λL). As a result, the scaling laws (3)–(6) can be modified by the S (IL, τL, λL) dependence and the degree of the modification will depend on the interaction conditions.

The effect of the plasma density gradient scale length on Iis and Ei of forward-accelerated ions—computed for 1-ps Nd:glass laser pulses with the use of two-fluid plasma hydrodynamic model (Głowacz et al., 2004; Badziak et al., 2004b)—is shown in Figure 1. The density gradient influenced significantly the ion beam parameters and the optimum values of Ln /λL occurred. For the forward-accelerated ion beams high plasma density gradients (Ln < λL) are preferred as opposed to the backward-accelerated ones for which moderate density gradients (Ln > λL) result in the highest beam parameters. We also see that both ion energies and ion beam intensities are higher for laser pulses of longer wavelength (1 ω), as predicted by Eqs. (3) and (5). A more detailed numerical analysis, fully confirming the physical picture of S-LPA outlined here, is presented in Głowacz et al. (2004) and Badziak et al. (2004b).

The effect of initial plasma density gradient scale length, Ln, on parameters of a forward-accelerated proton beam. 1 ω is the first harmonic and 2 ω is the second harmonic of Nd:glass laser.

To calculate the ion current density and the ion beam intensity from experimental data (e.g., from the time-of-flight measurements), we can use the following expressions (Badziak et al., 2004a, 2004b):

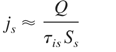
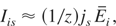
where Q is the total charge of fast ions measured in the far expansion zone, Ss is the fast ion source area and Ei is the mean energy of fast ions. Knowing parameters of the ion beam at the source (subscript s) and assuming that the energy dispersion in the ion beam is the main reason for an elongation of the ion pulse during its propagations, the ion pulse duration, τi(x), the ion current density, j (x), and the ion beam intensity, Ii(x), at the distance x from the source can be estimated from the following equations:

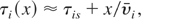
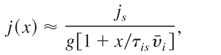
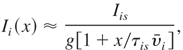
where: υi is the mean ion velocity, g = S(x)/Ss ≈ [1 + (x/rs)tg(θ/2)]2 is the geometrical factor, S (x) is the area of the ion beam cross section at the distance x, rs is the ion source radius, and θ is the angular divergence of the beam (full angle cone).

3. EXPERIMENT AT SUBRELATIVISTIC LASER INTENSITIES

The experiment was performed with the use of 1-ps, 1.05-μm sub joule laser pulse generated by a terawatt CPA Nd:glass laser (Badziak et al., 1997). A specific feature of the ps pulse was its temporal shape comprising the long-lasting (>0.3 ns) low-intensity background and the short-lasting prepulse (a sequence of a few ps pulses covering the time period ∼10−10 s) of the intensity ∼104 times lower than the intensity of the main ps pulse (Badziak et al., 2001). As the intensity of the long-lasting background was at least 108 times lower than that of the main pulse (Badziak et al., 1997, 2001), no preplasma was produced by it on the target surface. The short-lasting prepulse produced the preplasma of the thickness Lpre ≤ 5 μm (Badziak et al., 2001, 2003). This preplasma thickness was at least several times smaller than the laser focal spot diameter df , so the condition for the quasi-planar skin-layer interaction of the laser beam with the preplasma was fairly well fulfilled (Section 1). Fulfilling this condition is an essential feature of our experiment as opposed to most other short-pulse experiments, particularly those performed at relativistic intensities (Snavely et al., 2000; Zepf et al., 2003; Borghesi et al., 2004). In those experiments—due to a substantial laser prepulse—a preplasma of Lpre > df was produced permitting relativistic self-focusing (filamentation) of the laser beam in the plasma and causing the interaction geometry to deviate from the planar case.

Using the time-of-flight method we measured fast ion beams emitted backward (against the laser beam) from massive targets as well as the ion beams emitted forward from thin foil targets. For the measurements of the backward-emitted ion beams, the linearly polarised laser beam of the CPA laser was focused by an on-axis f/2.5 parabolic mirror, with a hole in the centre, onto a massive Au target at an angle of 0° with respect to the target normal (Fig. 2). The maximum intensity of the focused laser beam (df ≈ 20 μm) was about 1017 W/cm2. The measurements of the ion beam parameters were performed with the use of ion collectors (ICs) and an electrostatic ion-energy analyzer (IEA) (Badziak et al., 2001). The IEA and the ring ion collector (IC1) measured the backward-emitted ions passing through the hole in the parabolic mirror along the target normal and the laser beam axis. For a rough estimation of the angular distribution of ion emission two additional collectors, viewing the target at angles Θ of 26° and 34° with respect to the target normal, were applied.

Simplified scheme of the experimental arrangement. IEA—electrostatic ion-energy analyzer; IC1, IC2, IC3—ion collectors.

To measure the forward-emitted ion beams the parabolic mirror in the experimental set-up presented in Figure 2 was replaced by f/1 aspheric lens focusing the laser beam on a thin foil target normally to its surface. The maximum laser intensity approached 2 × 1017 W/cm2 at 30–40% of laser energy concentrated in the focal spot of df ≈ 10 μm. The forward-emitted ions were recorded with the ICs and the IEA situated behind the thin foil target in the same geometry as in the case of the parabolic mirror. The polystyrene targets 0.5 μm, 1 μm, and 2 μm thick (marked as PS0.5, PS1, and PS2, respectively) were used in this part of the experiment. The thickness of the targets was selected to be comparable to or smaller than the characteristic path length of the heat wave in the target generated by the leading edge of the laser pulse (including the prepulse), calculated from the classical heat transport formulas. Thus, it could be expected that the rear target surface was overheated while the ps pulse interacted with the target, and as a result, the TNSA mechanism of the ion acceleration was substantially suppressed (Wilks et al., 2001; Mackinnon et al., 2001; Kaluza et al., 2004).

As an example of the measurements of backward-emitted ion beams, Figure 3 presents the dependencies of the ion current density, js, and the ion beam intensity, Iis, at the source on the laser intensity in the intensity range ∼ 1016–1017 W/cm2. The values js and Iis were obtained with the use of Eqs. (7) and (8) assuming Q = QIC1 and τis = τL, Ss = Sf (Badziak et al., 2004b), where QIC1 is the fast ion charge passing through the IC1 collector seen within the angle of 3° from the source, τL is the laser pulse duration and Sf is the laser focal spot area. Moreover, we assumed z = 1 in Eq. (8), as the fast ion group emitted from Au target was dominated by protons (Badziak et al., 2003, 2004a). It can be seen that within the measurement error the dependencies js(IL) and Iis(IL) follow the scaling laws determined by Eqs. (4) and (5), respectively. Also, the absolute values of js and Iis obtained from the measurements agree fairly well with those predicted from Eqs. (4) and (5), and for instance, at IL ≈ 1017 W/cm2 they reach the values of ≈1010 A/cm2 and ≈2 × 1014 W/cm2, respectively. It should be noted however, that real values of the ion current density and the ion beam intensity at the source can be higher than those in Figure 3, since the ion beam angular divergence is expected to be greater than 3°, and as a result, only a part of total amount of produced ions could be recorded by the IC1 collector.

The fast ion current density (a) and beam intensity (b) at the source for the ions emitted backward within the angle of 3° as a function of 1-ps laser pulse intensity.

A typical ion collector signal from PS0.5 target, recorded by the IC1 collector in the forward direction normally to the target, is presented in Figure 4a. It can be seen that only a single fast proton group (identified by the IEA), well separated in time from other ion groups, is produced. The energy distribution of fast protons is shown in Figure 4b. The mean proton energy for PS0.5 target (averaged over many shots) was calculated to be ≈17 keV and the maximum recorded energy was slightly above 100 keV. The number of protons of energy in the range of 5–100 keV, emitted within 3° angle cone, was estimated to be ≈1010. This value is smaller than the number of protons Ni ∼ nec Sf λL ≈ 8 × 1010 expected to be generated by the S-LPA mechanism near the critical surface. There are two possible reasons of this discrepancy. The first reason is the angular divergence of proton beam. Though the measurements indicate that the proton beam is highly collimated (as no fast protons were recorded by the ion collectors placed outside the target normal —Fig. 2), it is very probable that the angular divergence of the beam, θi, is greater than the angle 3° seen by the IC1 collector. Since the number of protons recorded in a far expansion zone is roughly proportional to the square of the angle within which they are recorded, a significant part of generated protons could not be recorded by the IC1 (e.g., at θi = 6° only one-fourth of the total number of protons can be recorded by the IC1). The second reason is the damping of fast protons produced near the critical surface while they propagate through the target. The effect of protons' damping inside the target is demonstrated in Figure 5, where a quick decrease in the current density and the beam intensity of forward-emitted protons with an increase in the target thickness can be observed. This figure also suggests that for subrelativistic laser intensities used in our experiment, the highest output parameters of the proton beam could be achieved using the target of the thickness << 1 μm.

The ion collector signals recorded along the target normal (a) and the energy distribution (b) of protons emitted forward from PS0.5 target. IL = 1.6 × 1017 W/cm2.

The current density and the beam intensity at the source (at the back target surface) of protons emitted forward within the angle of 3° as a function of the target thickness. IL ≈ (1.2 ± 0.3) × 1017 W/cm2.

Our results for forward-emitted proton beams from PS0.5 target, obtained at subrelativistic laser intensities, we compared with the results achieved with the TNSA method at relativistic intensities. For this comparison we used Eqs. (7) and (8), and the data related to the mean energy and the total charge of fast protons, the area of the proton source and the laser pulse duration (we assumed τis = τL) achievable from recent short-pulse experiments (Snavely et al., 2000; Zepf et al., 2003; Borghesi et al., 2004; Cowan et al., 2004). As the angle cones within which the protons were recorded were essentially different in different experiments, the values of the proton current density and the proton beam intensity at the source were recalculated to the same angle cone fixed as 3° (according to our experiment). From the results of the comparison presented in Table 1, the following conclusions can be reached: (a) the proton beam intensities at the source generated within a fixed angle cone by subrelativistic S-LPA are comparable to those produced (within the same angle cone) by TNSA at relativistic laser intensities and much higher laser energies, (b) the proton current densities at the source generated within a fixed angle cone are significantly higher for S-LPA than those for TNSA, (c) the proton densities at the source produced by S-LPA are about a thousand times higher than those generated by TNSA within the same angle cone (this conclusion was drawn from the fact that ni ∝ js /Ei1/2). High proton densities at the source concluded from the above comparison are the main reason for the observed very high proton current densities, and beam intensities produced by S-LPA in spite of fairly moderate energies of generated protons. The other reason is quasi-planar geometry of the plasma block acceleration enabling generation of proton beams of low angular divergence.

Parameters of proton beams produced in various experiments. [a] Cowan et al. (2004); [b] Borghesi et al. (2004); [c] Zepf et al. (2003); [d] Snavely et al. (2000)

4. S-LPA AT RELATIVISTIC LASER INTENSITIES

One drawback of S-LPA induced by a laser pulse of subrelativistic intensity is relatively low energy of generated ions, limited to ∼ 1 MeV/nucleon. This drawback could be overcome if the advantages of subrelativistic S-LPA—who's most important symptom is a quasi-planar acceleration of the high-density plasma block—could be preserved in the relativistic intensity region. It seems to be feasible if the laser pulse and the target thickness is carefully optimised, and particularly: (1) the laser prepulse (background) intensity is very low (no preplasma is produced); (2) the laser pulse leading edge is very short: τle << 1 ps (the leading edge produces only a thin high-density plasma layer); (3) the laser focal spot is relatively large: df ≥ 10 λL (to secure the quasi-planar acceleration geometry); (4) the target thickness is small: LT ≤ λL (to ensure, regarding the effect of relativistic transparency that significant part of the target interacts directly with the light wave). However, the above criteria are only qualitative and intuitive, and they need to be confirmed by detailed numerical or experimental studies. A special case of the relativistic regime of S-LPA was demonstrated just recently with the use of three-dimensional PIC simulations (Esirkepov et al., 2004) (the authors called this regime the “laser piston”). The interaction of a 25-fs laser pulse of intensity 1023 W/cm2 with a 1-μm solid-density plasma slab resulted in a quasi-planar generation of relativistic (Ei ≈ 3 GeV) high-density (ni ≈ 3nec) proton block with the estimated proton current density ≈ 1013A/cm2, the beam intensity ≈3 × 1022 W/cm2 and proton production efficiency ∼30–40%. Although such extreme ion blocks parameters is still a matter of the future, the production of high-density ion blocks with multi-MeV ion energies using relativistic S-LPA seems to be realistic with the current laser technology.

In order to obtain approximate scaling laws for parameters of ion beams driven by the S-LPA mechanism at relativistic intensities, it should be taken into account that due to relativistic change of electron mass me = me0γ (me0 is the electron rest mass, γ is the relativistic Lorenz factor) both the quiver energy of electron oscillating in the laser field, Ee, and the critical electron density are nonlinear function of laser intensity (Hora, 1991, 2003, Wilks et al., 1992; Umstadter, 2001):

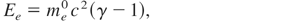
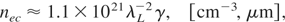
where γ = (1 + 3SIL /Irel)1/2, S is the dielectric swelling factor and IL is the laser intensity in vacuum. Assuming that the time of acceleration of a plasma block by a laser pulse, τac, is longer than some minimum acceleration time τm ∼ (Mi /zme0γ)1/2Tosc (Sentoku et al., 2003), where Mi is the ion mass and Tosc is the laser oscillation period, the energies of forward-accelerated ions can be estimated from (Hora, 1991, 2003):

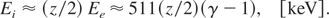
Then from (1), (2), (13), and (14), we obtain the following formulae for the ion current density and the ion beam intensity at the source:

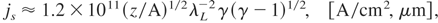
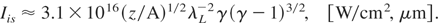
Equations (14), (15), and (16) can be expressed in a more simple form for very high laser intensities, IL >> Irel. In such a case, we arrive at the following scaling laws:

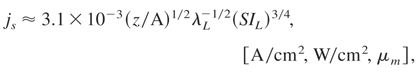
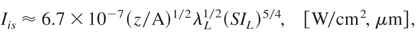
In order to derive the equation for the ion beam production efficiency, ηi, it was assumed additionally, as for the subrelativistic case, that τis ≈ τL and Ss ≈ Sf . Comparing (17–20) with (3–6) we can see that with the exclusion of js, all remaining ion beam parameters increase more slowly with the increase of laser intensity in the relativistic case than those in the subrelativistic case.

Equations 17–20 make it possible to assess basic ion beam parameters in a very simple way and to become convinced that for relativistic laser intensities these parameters, and especially the ion current densities and beam intensities can be really extremely high. For instance, at IL = 1020 W/cm2, λL = 1 μm, S = 1, z/A = 1 (protons) we obtain: Ei ≈ 2.2 MeV, js ≈ 3.1 × 1012 A/cm2, Iis ≈ 6.7 × 1018 W/cm2, ηi ≈ 6.7%. It is worth noting that the values of js and Iis obtained in the above example are ∼30 times (js) and ∼2 times (Iis) higher than the corresponding values achieved from PIC simulation (Wilks et al., 2001) in the proton beam driven by TNSA at IL = 4 × 1020 W/cm2 and focused ballistically on the spot <1 μm. However, it should be underlined that Eqs. (14–16) and (17–20) allow only very rough estimations, as at relativistic intensities also other than ponderomotive mechanisms of acceleration can potentially drive ions. Among these the Coulomb explosion seems to be one of the most important. On the one hand, this mechanism should cause an increase in ion energies (Sentoku et al., 2003) but on the other hand, it can disturb quasi-planar geometry of the ion acceleration causing an increase in angular divergence and lowering density of the ion beam.

5. THE POSSIBILITY OF USING PLASMA BLOCKS DRIVEN BY S-LPA FOR FAST IGNITION OF FUSION TARGETS

Multi-MeV ion energies and very high ion current densities and beam intensities derived from the simplified theory of relativistic S-LPA in the previous section, as well as the results of the three-dimensional PIC simulation by Esirkepov et al. (2004) imply that plasma blocks driven by the S-LPA mechanism at relativistic laser intensities could be used for fast ignition of a compressed fusion target.

One possible scheme of fast ignition by plasma blocks (FIPB) is presented in Figure 6. FIPB employs here N ps laser beams directed toward the dense DT fuel core. Each laser beam interacts with a thin planar target producing fast high-density plasma block moving along the laser beam axis and the target normal. Both the laser beams and the plasma blocks propagate inside a guiding cone protecting them against the influence of DT plasma while it is compressed (Kodama et al., 2001; Atzeni et al., 2002).

The idea of fast ignition by plasma blocks (FIPB). See the text.

For the above scheme of FIPB, the parameters of ion flux heating the fuel, namely the total flux intensity, Iht, power, Wht, energy, Eht, and the ion pulse duration, τh, can be calculated using the following simple formulae:

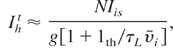
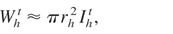
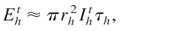
where: N, the number of laser beams; Iis, the ion beam intensity at the source; υi, the mean ion velocity; τL, the laser pulse duration; lth, the distance from the target to the fuel surface; rh, the required radius of heated fuel; g = f (lth/rs, θi, βn), geometrical factor; θI, the ion beam angular divergence; βn, the angle between the n-th laser beam axis and the guiding cone axis. Equations (21–24) take into account the energy dispersion of ion beams (as they are basically non-monoenergetic) and geometry of the system. The ion beam intensity at the source, Iis, and the mean ion velocity, υi, included in these equations can be calculated from Eqs. (19) and (17).

To appreciate the potential of FIPB, let us try to compare the parameters of ion flux calculated from Eqs. (21–24) and some exemplary input parameters with the requirements for DT fuel ignition obtained from detailed numerical simulations by Atzeni (1999; Atzeni et al., 2002). According to these simulations, for nearly optimal dimension of the heating fuel, the duration of the igniting particle beam should be comparable to or shorter than ∼20 ps, and the ignition threshold values for the particle beam intensity, Iig, power, Wig, and energy, Eig, can be calculated from the expressions:

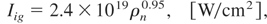
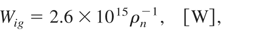
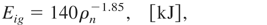
where ρn = ρ/(100 g/cm2) is the normalized fuel density. For the reference values ρ = 300 g/cm3, rh = 20 μm (ρrh = 0.6 g/cm3), and 0.15 g/cm2 ≤ R ≤ 1.2 g/cm2 (R is the particle penetration depth) we arrived at:

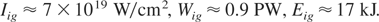
As an example, let us assume that plasma blocks in the scheme of Figure 6 are driven by 10 2-ps, 10-kJ laser pulses (ELt = 100 kJ). Moreover, let us assume: λL = 1 μm, df = 25 μm, S = 1.5, z/A = 1 (protons), θi = 5°, lth = 0.2 mm, and as previously, rh = 20 μm (ρrh = 0.6 g/cm2). The parameters of the ion flux heating the fuel, calculated from (21–24) and (17), (19), are as follows:

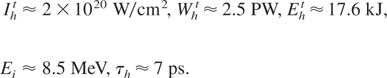
Comparing (29) and (28) we can see that all parameters of the ion flux are above the ignition threshold at laser energy of 100 kJ, in spite of the fact that the input parameters of the system are not optimized. It should be noticed that attaining such proton beam parameters using the TNSA mechanism can be a more difficult task, first of all, due to significantly lower proton density at the source (∼102–103 times, Section 3). The result is that achieving the proton beam intensity above the ignition threshold requires strong focusing of the beam. Because only part of produced ions can be focused on a required spot, the total efficiency of igniting beam production can be lower than in the case of quasi-planar plasma block generation considered here (compare ηi ∼ 1% from PIC simulation of the focused proton beam by Wilks et al. (2001) with ηi ∼ 17% in the example presented above and ηi ∼ 30–40% for proton block simulated by Esirkepov et al. (2004).

Though the estimates for FIPB presented above seem to be very promising, we are aware that they have to be proved by detailed numerical and/or experimental studies. Such studies we have just initiated.

6. CONCLUSIONS

The main results of this work can be summarised as follows: (a) S-LPA makes it possible to produce highly collimated high-density ion beams (plasma blocks) of extremely high intensities and current densities comparable to those produced by TNSA at significantly higher energy and power of a laser pulse; (b) due to relatively small energy of a driving laser pulse, subrelativistic S-LPA enables the generation of high-current ion beams with a high repetition rate; it opens a prospect for tabletop experiments related to high energy-density physics as well as for technological and medical application; (c) quasi-planar generation of high-density plasma block in the relativistic intensity region seems to be feasible provided that the laser pulse duration and shape (the laser prepulse) as well as the target thickness are carefully optimised; and (d) fast ignition by plasma blocks using relativistic S-LPA seems to be a promising way for fusion that is well worth detailed studying.

ACKNOWLEDGMENTS

This work was supported in part by the State Committee for Scientific Research (KBN), Poland under Grant No 1 PO3B 043 26 and by the International Atomic Energy Agency in Vienna under Contract No 11535/RO and as well as by the European Communities under the Contract of Association between EURATOM and IPPLM. The views and opinions expressed herein do not necessarily reflect those of European Commission.

References

REFERENCES

Atzeni, S. (1999). Inertial fusion fast ignitor: Igniting pulse parameter window vs the penetration depth of the heating particles and the density of the precompressed fuel. Phys. Plasmas 6, 3316–3326.Google Scholar
Atzeni, S., Temporal, M. & Honrubia, J.J. (2002). A first analysis of fast ignition of precompressed ICF fuel by laser-accelerated protons. Nucl. Fusion 42, L1–L4.Google Scholar
Badziak, J., Chizhov, S.A., Kozlov, A.A., Makowski, J., Paduch, M., Tomaszewski, K., Vankov, A.B. & Yashin, V.E. (1997). Picosecond, terawatt, all-Nd:glass CPA laser system. Opt. Commun. 134, 495–502.Google Scholar
Badziak, J., Makowski, J., Parys, P., Ryć, L., Wołowski, J., Woryna, E. & Vankov, A.B. (2001). Intensity-dependent characteristics of a picosecond laser-produced Cu plasma. J. Phys. D: Appl. Phys. 34, 1885–1891.Google Scholar
Badziak, J., Hora, H., Woryna, E., Jabłoński, S., Laśka, L., Parys, P., Rohlena, K. & Wołowski, J. (2003). Experimental evidence of differences in properties of fast ion fluxes from short-pulse and long-pulse laser-plasma interactions. Phys. Lett. A 315, 452–457.Google Scholar
Badziak, J., Głowacz, S., Jabłoński, S., Parys, P., Wołowski, J. & Hora, H. (2004a). Production of ultrahigh-current-density ion beams by short-pulses skin-layer laser-plasma interaction. Appl. Phys. Lett. 85, 3041–3043.Google Scholar
Badziak, J., Głowacz, S., Jabłoński, S., Parys, P., Wołowski, J. & Hora, H. (2004b). Production of ultrahigh ion current densities at skin-layer subrelativistic laser-plasma interaction. Plasma Phys. Contr. Fusion 46, B541–B555.Google Scholar
Badziak, J., Głowacz, S., Jabłoński, S., Parys, P., Wołowski, J. & Hora, H. (2005). Generation of picosecond high-density ion fluxes by skin-layer laser-plasma interaction. Laser Part. Beams 23, 143–147.Google Scholar
Borghesi, M., Campbell, D.H., Schiavi, A., Willi, O., Galimberti, M., Gizzi, L.A., Mackinnon, A.J., Snavely, R.D., Patel, P., Hatchett, S., Key, M. & Nazarov, W. (2002). Propagation issues and energetic particle production in laser-plasma interactions at intensities exceeding 1019 W/cm2. Laser Part. Beams 20, 31–38.Google Scholar
Borghesi, M., Mackinnon, A.J., Campbell, D.H., Hicks, D.G., Kar, S., Patel, P.K., Price, D., Romagnani, L., Schiavi, A. & Willi, O. (2004). Multi-MeV protons source investigations in ultraintense laser-foil interactions. Phys. Rev. Lett. 92, 055003-1–055003-4.Google Scholar
Cowan, T.E., Fuchs, J., Ruhl, H., Kemp, A., Audebert, P., Roth, M., Stephens, R., Barton, I., Blazevic, A., Brambrink, E., Cobble, J., Fernández, J., Gauthier, J.-C., Geissel, M., Hegelich, M., Kaae, J., Karsch, S., Le Sage, G.P., Letzring, S., Manclossi, M., Meyroneinc, S., Newkirk, A., Pépin, H. & Renard-leGalloudec, N. (2004). Ultralow emittance, multi-MeV proton beams from a laser virtual-cathode plasma accelerator. Phys. Rev. Lett. 92, 204801-1–204801-4.Google Scholar
Esirkepov, T., Borghesi, M., Bulanov, S.V., Mourou, G. & Tajima, T. (2004). Highly efficient relativistic-ion generation in the laser-piston regime. Phys. Rev. Lett. 92, 175003-1–175003-4.Google Scholar
Głowacz, S., Badziak, J. Jabłoński, S., &Hora, H. (2004). Numerical modelling of production of ultrahigh-current-density ion beams by short-pulse laser-plasma interaction. Czech. J. Phys. 54, C460–C467.Google Scholar
Hegelich, M., Karsch, S., Pretzler, G., Habs, D., Witte, K., Guenther, W., Allen, M., Blazevic, A., Fuchs, J., Gauthier, J.C., Geissel, M., Audebert, P., Cowan, T. & Roth, M. (2002). MeV ion jets from short-pulse laser interaction with thin foils. Phys. Rev. Lett. 89, 085002-1–085002-4.Google Scholar
Hora, H. (1991). Plasmas at High Temperature and Density. Heildelberg: Springer.
Hora, H. (2003). Skin-depth theory explaining anomalous picosecond-terawatt laser plasma interaction II. Czech. J. Phys. 53, 199–217.Google Scholar
Hora, H., Osman, F., Cang, Y., Badziak, J., Jabłoński, S., Głowacz, S., Miley, G.H., Hammerling, P., Wołowski, J., Jungwirth, K., Rohlena, K., He, X., Peng, H. & Zhang, J. (2004). TW-ps laser driven blocks for light ion beam fusion in solid density DT. Proc. SPIE 5627, 51–63.Google Scholar
Kaluza, M., Schreiber, J., Santala, M.I.K., Tsakiris, G.D., Eidmann, K., Meyer-ter-Vehn, J. & Witte, K.J. (2004). Influence of the laser prepulse on proton acceleration in thin-foil experiments. Phys. Rev. Lett. 93, 045003-1–045003-4.Google Scholar
Kodama, R., Norreys, P.A., Mima, K., Dangor, A.E., Evans, R.G., Fujita, H., Kitagawa, Y., Miyakoshi, T., Miyanag, N., Norimatsu, T., Rose, S.J., Shozaki, T., Shigemori, K., Sunahara, A., Tampo, M., Tanaka, K.A., Toyama, Y., Yamanaka, T., & Zepf, M. (2001). Fast heating of ultrahigh-density plasma as a step towards laser fusion ignition. Nature 412, 798–802.Google Scholar
Mackinnon, A.J., Borghesi, M., Hatchett, S., Key, M.H., Patel, P.K., Campbell, H., Schiavi, A., Snavely, R., Wilks, S.C. & Willi, O. (2001). Effect of plasma scale length on multi-MeV proton production by intense laser pulses. Phys. Rev. Lett. 86, 1769–1772.Google Scholar
Patel, P.K., Mackinnon, A.J., Key, M.H., Cowan, T.E., Foord, M.E., Allen, M., Price, D.F., Ruhl, H., Springer, P.T. & Stephens, R. (2003). Isochoric heating of solid-density matter with and ultrafast proton beam. Phys. Rev. Lett. 91, 125004-1–125004-4.Google Scholar
Pegoraro, F., Atzeni, S., Borghesi, M., Bulanov, S., Esirkepov, T., Honrubia, J., Kato, Y., Khoroshkov, V., Nishihara, K., Tajima, T., Temporal, M. & Willi, O. (2004). Production of ion beams in high-power laser-plasma interactions and their applications. Laser Part. Beams 22, 19–24.Google Scholar
Roth, M., Cowan, T.E., Key, M.H., Hatchett, S.P., Brown,C., Fountain, W., Johnson, J., Pennington, D.M., Snavely, R.A., Wilks, S.C., Yasuike, K., Ruhl, H., Pegoraro, F., Bulanov, S.V., Campbell, E.M., Perry, M.D., &Powell, H. (2001). Fast ignition by intense laser-accelerated proton beams. Phys. Rev. Lett. 89, 436–439.Google Scholar
Roth, M., Brambrink, E., Audebert, P., Blazevic, A., Clarke, R., Cobble, J., Cowan, T.E., Fernandez, J., Fuchs, J., Geissel, M., Habs, D., Hegelich, M., Karsch, S., Ledingham, K., Neely, D., Ruhl, H., Schlegel, T. & Schreiber, J. (2005). Laser accelerated ions and electron transport in ultra-intense laser matter interaction. Laser Part. Beams 23, 95–100.Google Scholar
Sentoku, Y., Cowan, A., Kemp, A. & Ruhl, H. (2003). High energy proton acceleration in interaction of short laser pulse with dense plasma target. Phys. Plasmas 10, 2009–2015.Google Scholar
Snavely, R.A., Key, M.H., Hatchett, S.P., Cowan, T.E., Roth, M., Phillips, T.W., Stoyer, M.A., Henry, E.A., Sangster, T.C., Singh, M.S., Wilks, S.C., MacKinnon, A., Offenberger, A., Pennington, D.M., Yasuike, K., Langdon, A.B., Lasinski, B.F., Johnson, J., Perry, M.D. & Campbell, E.M. (2000). Intense high-energy proton beams from petawatt-laser irradiation of solids. Phys. Rev. Lett. 86, 1769–1772.Google Scholar
Wilks, S.C., Kruer, W.L., Tabak, M. & Langdon, A.B. (1992). Absorption of ultra-intense laser pulses. Phys. Rev. Rev. Lett. 69, 1383–1386.Google Scholar
Wilks, S.C., Langdon, A.B., Cowan, T.E., Roth, M., Singh, M., Hatchett, S., Key, M.H., Pennington, D., MacKinnon, A. & Snavely, R.A. (2001). Energetic proton generation in ultra-intense laser-solid interactions. Phys. Plasmas 8, 542–549.Google Scholar
Umstadter, D. (2001). Review of physics and applications of relativistic plasmas driven by ultra-intense lasers. Phys. Plasmas 8, 1774–1785.Google Scholar
Zepf, M., Clark, E.L., Beg, F.N., Clarke, R.J., Dangor, A.E., Gopal, A., Krushelnick, K., Norreys, P.A., Tatarakis, M., Wagner, U. & Wei, M.S. (2003). Proton accelerations from high-intensity laser interactions with thin foil targets. Phys. Rev. Lett. 90, 064801-1–064801-4.Google Scholar
Figure 0

The effect of initial plasma density gradient scale length, Ln, on parameters of a forward-accelerated proton beam. 1 ω is the first harmonic and 2 ω is the second harmonic of Nd:glass laser.

Figure 1

Simplified scheme of the experimental arrangement. IEA—electrostatic ion-energy analyzer; IC1, IC2, IC3—ion collectors.

Figure 2

The fast ion current density (a) and beam intensity (b) at the source for the ions emitted backward within the angle of 3° as a function of 1-ps laser pulse intensity.

Figure 3

The ion collector signals recorded along the target normal (a) and the energy distribution (b) of protons emitted forward from PS0.5 target. IL = 1.6 × 1017 W/cm2.

Figure 4

The current density and the beam intensity at the source (at the back target surface) of protons emitted forward within the angle of 3° as a function of the target thickness. IL ≈ (1.2 ± 0.3) × 1017 W/cm2.

Figure 5

Parameters of proton beams produced in various experiments. [a] Cowan et al. (2004); [b] Borghesi et al. (2004); [c] Zepf et al. (2003); [d] Snavely et al. (2000)

Figure 6

The idea of fast ignition by plasma blocks (FIPB). See the text.