1. Introduction
Income inequality has been a major issue in economics for centuries. Ricardo (Reference Ricardo1817: 72) noted the tendency of land rents to grow, crowding out income going to others, and concluded that eventually ‘. . .almost the whole produce of the country, after paying the laborers [a subsistence wage] will be the property of the owners of land and the receivers of tithes and taxes.’ More recently, Piketty (Reference Piketty2014) has argued that because the return on capital is greater than the growth of the overall economy, capital owners find their incomes growing faster than those who earn labor income, and because capital ownership is concentrated, income inequality tends to grow over time in capitalist economies as a natural outcome of market forces. This paper examines the extent to which market institutions are associated with higher income shares for the economic elite.
Piketty is not alone in his concern about inequality, but his argument that growing inequality is a result of market forces in a capitalist economy differs from the argument of many others. A more common argument in the twenty-first century is that inequality is largely the product of government policies designed to favor the elites over the masses. Stiglitz (Reference Stiglitz2012) makes the argument that inequality is a product of government policies designed to favor the elite, as does Stockman (Reference Stockman2013), Gilens (Reference Gilens2012), Hacker and Pierson (Reference Hacker and Pierson2010), Bartels (Reference Bartels2008), and Huber and Stephens (Reference Huber and Stevens2015). The argument that income inequality is a product of government policy is not new. Marx and Engels (Reference Marx and Engels1948: 10–11) conclude, ‘Each step in the development of the bourgeoisie was accompanied by a corresponding political advance of that class. . . . the bourgeoisie has at last, since the establishment of modern industry and of the world market, conquered for itself, in the modern representative state, exclusive political sway. The executive of the modern state is but a committee for managing the common affairs of the whole bourgeoisie.’ Piketty, along with Ricardo, see inequality as the product of market forces, whereas, taking a viewpoint that goes back at least to Marx and Engels, much of the contemporary discussion focuses on government policy. This paper sets aside the political issues to evaluate the degree to which income inequality is a product of market forces.
2. Quantifying market institutions and capitalism
Capitalism is an economic system in which the means of production are privately owned and the owners of the means of production receive the income it generates. Market institutions provide a framework within which buyers and sellers can voluntarily engage in exchanges of goods, services, and resources they own. Market institutions and capitalism are not exactly the same things. Markets have existed for thousands of years, whereas capitalism as an economic system dates back to the beginning of the Industrial Revolution. However, they will be treated as empirically synonymous here, partly because the measure we use to quantify the degree to which economies are characterized by market institutions also embodies what are commonly considered the characteristics of capitalist economies. Using the (perhaps obsolete) taxonomy from the twentieth-century study of comparative economic systems, economies were characterized as allocating resources through markets or through central economic planning. Capitalist economies were those that allocated resources through markets and socialist economies were those that allocated resources through central planning, although all economies are some combination of both.
The degree to which an economy allocates resources through market institutions is measured by the Fraser Institute's Economic Freedom of the World (EFW) index. Higher scores on the EFW index indicate an economy that relies more on markets to allocate resources; lower scores indicate economies in which there is more government intervention to override the market mechanism for allocating resources. Thus, the EFW index does a good job of quantifying the similar concepts of market institutions and capitalism. Because the empirical work that follows uses the EFW index as a measure of institutions, what it shows is the relationship between income inequality, measured by the income share of the top 10%, and economic freedom, as measured by the EFW index. We feel at least as comfortable with this measure of market institutions, or capitalism, as we do with measuring income inequality as the income share of the top income earners, as do Piketty (Reference Piketty2014) and others, for reasons explained in the next several paragraphs.
The construction of the EFW index is described in detail in Gwartney et al. (Reference Gwartney, Lawson and Hall2014). The index is aggregated from 43 individual components which are grouped into five areas: size of government, protection of property rights and rule of law, freedom to trade internationally, the soundness of the money supply, and the degree of regulation in the economy. The index was specifically designed to quantify the degree to which market institutions are used to allocate resources. The areas measured by the index also quantify the characteristics that are commonly associated with capitalism: protection of property rights, rule of law, low taxes, low levels of regulation, and freedom of trade. The index is available only since 1980, and until 2000 only in five-year intervals, so the dataset used in this paper includes only those years for which the EFW index data is available.
As its name suggests, the EFW index is designed to measure economic freedom, which we equate with market institutions: the degree to which resources are privately owned and are allocated through market exchange rather than by government, either directly or indirectly through regulation. Because markets pre-date capitalism by many centuries, it is reasonable to ask whether the EFW index is also a good measure of the degree to which countries have capitalist institutions. While markets existed well before capitalism, the market institutions measured in the EFW index, for the most part, did not. The factors quantified in the EFW index appear to correspond with both contemporary market institutions and capitalism.
Heilbroner (Reference Heilbroner1962) identifies a market economy as one in which there are markets for factors of production: land, labor, and capital, and notes that these markets emerged only shortly prior to the Industrial Revolution, and laid the foundation for the development of capitalism. People can trade in markets without the market institutions that characterize market economies. The centrally-planned socialist economies of the mid-twentieth century, for example, had underground markets and even above-ground markets. Workers on collective farms had individual plots on which they could grow crops and sell them, and other small-scale market activities were also allowed. But while there were markets in these centrally-planned economies, these markets did not exist in what the EFW would characterize as a market economy. There is a difference between the existence of markets and the existence of market institutions as defined by the EFW index.
Heilbroner refers to economies prior to the Industrial Revolution as pre-market economies. Heilbroner (Reference Heilbroner1962: 69) says
A market society could not coexist with a form of legal organization which, for example, did not recognize the freedom of the individual to contract for employment as he wished. Nor could it exist under a code of law which barely recognized ‘private property’ as we know it. Neither could it flourish under a political system in which privilege accrued to birth rather than to achievement, or in which the landed nobility by law and usage possessed the main power to regulate society's affairs.
Feudalism, and economic systems prior to feudalism, were pre-market economies, in Heilbroner's taxonomy. Following Heilbroner's reasoning, the market institutions that are quantified in the EFW index also describe the institutions that also characterize capitalism. Market institutions, following Heilbroner, are more than just markets and trade.
The parallel between market institutions and capitalism with reference to the EFW index is not based on Heilbroner's terminology that identifies market and pre-market economies, but on the substance behind that terminology. The markets that existed prior to capitalism did not have the features of economic freedom that are quantified in the EFW index, so those markets did not exist within the institutional framework that the EFW identifies as a market economy. The empirical analysis below looks at the relationship between economic freedom, as measured by the EFW index, and the top 10% income share, using two different measures. Heilbroner's (Reference Heilbroner1962) analysis of economic systems differentiates market institutions, which he argues are recent, from the existence of markets and trade, which dates back thousands of years. The logic behind this taxonomy of economic systems supports the idea that the EFW index is a good measure of the degree to which economies can be characterized as market economies, and as capitalist economies.
3. Measuring inequality
In keeping with Piketty's (Reference Piketty2014) reasoning, this analysis measures income inequality by looking at the income shares of those with the highest incomes, rather than looking at Gini coefficients, poverty rates, or other summary measures. This measure fits well with the current literature, largely because of Piketty's influence, even though other measures may give a different picture of the degree of inequality. This way of looking at income inequality shows the share of output going to the economic elite compared with everyone else. While one can debate the value of various summary measures of inequality, using the income share going to the economic elite keeps the analysis within the framework Piketty used in his widely-recognized book.
Piketty (Reference Piketty2014) uses data from the WTID dataset he constructed to undertake his analysis. The WTID dataset has income share data for 28 countries that, in some cases, goes back to the early twentieth century. Because the key institutional variable we use, the EFW index, is available at five-year intervals and goes back to 1980, we use the WTID income share data for 1980 and later in five-year intervals so observations match the EFW data. This yields 109 observations for income share going to the top 10% of individuals by income from the WTID dataset.
The World Bank (WB) also provides data on the income share held by the highest 10% for over 100 countries. Though collected annually, WB data are collected sporadically so there are many missing years. To address this issue, data are collected from 1980–2010 in five year intervals when available. However, if data are missing for the year beginning the five year interval, the average of the income share of the top 10% for the previous two years and next two years is recorded in its place. For example, if the top 10% income share data is unavailable for a country in 1990, then the average of 1988, 1989, 1991, and 1992 is recorded in its place. This yields 460 observations from WB data for the income share of the top 10%.
Because of differences in time periods and countries, only 23 observations from those two datasets overlap. The correlation coefficient between the two datasets for those 23 observations is 0.12. For most countries, the WTID dataset shows a higher income share for the top 10% than the WB dataset, but for a few lower-income countries (Malaysia is an example), the opposite is true, leading to the very low correlation.
Table 1 shows the correlation between the log income share of the top 10% and the log of per capita income for the two different datasets. The first regression shows that there is a slight negative and statistically significant correlation between the income share of the top 10% and per capita income using the WB data. The second regression shows a positive and statistically significant correlation between the income share of the top 10% and per capita income using the WTID data. Figure 1 graphically illustrates this general relationship between the top 10% income share and per capita income in the two datasets. The top panel shows the WB data and the negative relationship between the variables, and the bottom panel shows the WTID data plotted against per capita income showing the positive relationship in that dataset.
Table 1. Income shares and per capita income, unadjusted, and adjusted data
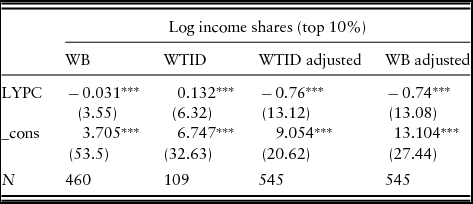
Note - |t| statistics in parentheses. Country and Year Fixed Effects included in all specifications. *p < 0.10, **p < 0.05, ***p < 0.01. Each specification refers to the Polity2 score from the PolityIV index. WTID adjusted refers to adjustments to WB. WB adjusted refers to adjustments to WTID.

Figure 1. Relationship between top 10% income share and income.
The two datasets can be adjusted to eliminate this relationship between per capita income and top 10% income share in the WTID data, or to introduce that relationship in the WB data, by using the coefficients in the first two regressions in Table 1. To adjust the WTID data to eliminate the positive relationship between top 10% income share and per capita income, representing the WTID data adjusted to WB as TOP10%(WTID->WB),
 \begin{eqnarray}
&&{\rm TOP}10\% ({\rm WTID} - > {\rm WB}) = \alpha ({\rm WB}) - \alpha ({\rm WTID}) + (\beta ({\rm WB})\nonumber\\
&&\quad -\, (\beta ({\rm WTID})){\rm LPCI} + \varepsilon
\end{eqnarray}
\begin{eqnarray}
&&{\rm TOP}10\% ({\rm WTID} - > {\rm WB}) = \alpha ({\rm WB}) - \alpha ({\rm WTID}) + (\beta ({\rm WB})\nonumber\\
&&\quad -\, (\beta ({\rm WTID})){\rm LPCI} + \varepsilon
\end{eqnarray}
where α(WB) is the constant in the WB regression – the first one – and α(WTID) is the constant in the second regression. Similarly, β(WB) and β(WTID) are the coefficients on LYPC in both of those regressions. This removes the positive relationship between per capita income and the income share of the top 10% from the WTID data, making it consistent in that regard with the WB data. Substituting the numbers from Table 1 into equation (1) gives
as the equation that adjusts the WTID data on top 10% income share so it has the same relationship to per capita income as the WB data.
Similarly, the WB data can be adjusted to have the same relationship with per capita income as the WTID data by using
as the adjustment equation.
Using these adjustment equations produces two different data sets for the top 10% income share; one using the WB data along with the WTID data after it has been adjusted to have the same relationship to per capita income as the WB data, and the other using the WTID data with the WB data adjusted to have the same relationship to per capita income as the WTID data. This allows the analysis that follows to evaluate the relationship between the income share of the top 10% and market institutions using the same observations, and increasing the sample size to 545 by combining the datasets. Two advantages of combining the datasets this way are that it provides more observations, but more important, both datasets use observations for the same countries and the same years.
The second two regressions in Table 1 use the adjusted observations the two datasets have in common to look at the relationship between top 10% income share and per capita income. The third regression uses the WTID data adjusted to WB and the fourth uses WB data adjusted to WTID. The third regression shows that when the WTID data are adjusted to conform with WB, the sign on β remains negative and significant, although the coefficient is larger. However, the coefficient is also negative in the fourth regression, where the WB data are adjusted to conform with the WTID relationship between top 10% income share and per capita income. The reason the signs are different in regressions 2 and 4 is that in addition to adjusting the observations for the relationships between the two variables, the WB data adds observations from more countries, and even when those observations are adjusted, the relationship between top 10% income share and per capita income remains negative.
This can be seen more clearly in Table 2, which looks only at the 23 observations that the two datasets have in common. The value for β in the WB dataset, shown in the first regression, is negative, but not statistically significant. Using only the overlapping observations, the negative and significant relationship shown in Table 1 is no longer statistically significant in Table 2. The value for β in the second regression using the WTID dataset is positive and statistically significant, and similar in magnitude to the coefficient in the second regression in Table 1. This shows that using only the overlapping observations, the relationships shown in Table 1 are very similar for the WTID data, but not so similar using the WB data. Part of the difference in the two datasets is that they depict different relationships between the top 10% share and per capita income, but part of the difference is that they contain different observations.
Table 2. Income shares and per capita income, unadjusted, and adjusted data
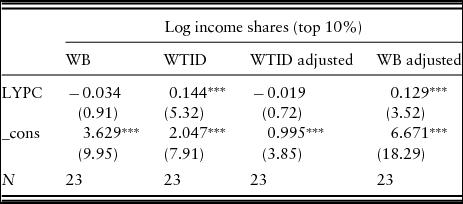
Note - |t| statistics in parentheses. *p < 0.10, **p < 0.05, ***p < 0.01. WTID adjusted refers to adjustments to WB. WB adjusted refers to adjustments to WTID.
The third regression in Table 2 uses the WTID data adjusted as in equation (2) to conform to the relationship between top 10% and per capita income in the WB dataset, and as in the first regression, the relationship is negative but not statistically significant. The fourth regression uses the WB data adjusted to conform to the WTID relationship, and the WB data now yields a positive and statistically significant coefficient, like the WTID data in the second regression. Table 2 shows that using only the overlapping observations, the adjustment procedure given in equation (1) produces the same relationships between top 10% income share and per capita income in the two datasets. When the WB data are adjusted to WTID, the relationship looks like the WTID dataset, and when the WTID data are adjusted to WB, the relationship looks like the WB dataset.
Tables 1 and 2 show that the differences in the two datasets are due not only to the different relationships they show with per capita income but also in the observations that are in the datasets. The WTID dataset has observations for fewer countries than the WB dataset, and Table 1 shows that when all observations in both datasets are accounted for, there is not much of a difference between them in the relationships the observations have with per capita income.
The reason for making these adjustments to produce two data sets for top 10% income share is that there may be some question about the construction of the datasets in light of their very different relationships with per capita income and market institutions (more on that below). One reason for the difference might be that the WTID is based on tax data whereas the WB uses survey data. Rather than choose one dataset or the other as the ‘correct’ dataset, this enables both to be used so the results using them can be compared. We use the two different measures of top 10% income share without passing judgment on which is more accurate.Footnote 1
4. The relationship between market institutions and income inequality
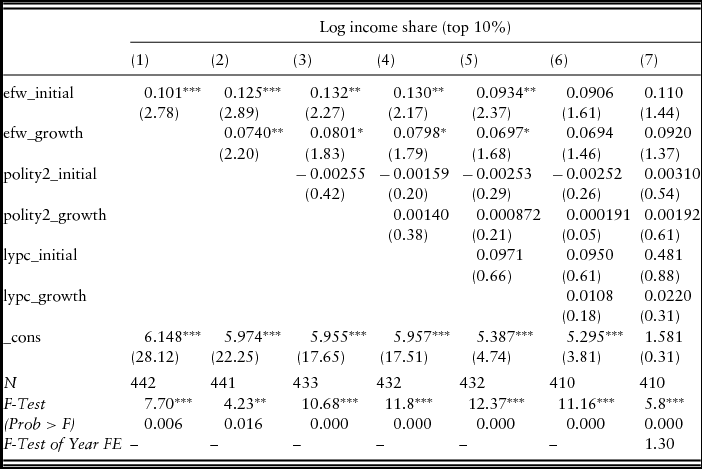
Table 3 examines the relationship between the income share of the top 10% of the population and market institutions, as measured by the EFW index, using the WTID data on top 10% income share along with the WB data adjusted to conform to WTID. Observations are in five-year intervals, and because of the hypothesis that capitalist institutions create greater inequality, the initial value of EFW is lagged five years, with the idea that income inequality at one point in time is the result of economic institutions prior to that time. So, for example, if the dependent variable – the measure of inequality – is from 1995, the initial EFW variable is from 1990. The first regression in Table 3 shows that there is a positive relationship, statistically significant at the 5% level, between market institutions and income inequality. The second regression adds the change in EFW over the previous five years, and the relationship remains positive and statistically significant, this time at the 1% level. The second regression shows that the amount of income inequality in a given year is positively related to both the degree to which the country was characterized as having market institutions five years previously, and the degree to which that country's institutions became more market-oriented in the previous five years.
Table 3. Income shares and institutions (WB adjusted to WTID)

Note - |t| statistics in parentheses. WB data adjusted to WTID. Country Fixed Effects included in all specifications. Year Fixed Effects included in column (7). *p < 0.10, **p < 0.05, ***p < 0.01.
Political institutions might also have an effect on income inequality, so to take them into account, the third regression adds the country's Polity2 score from the PolityIV data (Marshall and Jaggers Reference Marshall and Jaggers2005), which measures on a scale of from –10 to 10 the degree to which a country has democratic political institutions, with –10 being the most autocratic and 10 being the most democratic. Political institutions, measured this way, are not statistically significant, and do not alter the positive relationship between market institutions and the income share of the top 10%. The fourth regression includes the change in the Polity2 index over the past five years, and again is not statistically significant and does not alter the positive relationship between inequality and market institutions.
Income inequality might also be related to per capita income, so the fifth regression adds per capita income and finds that it is not statistically significant, and that the positive relationship between the income share of the top 10% and EFW remains. When the growth in per capita income is added in the sixth regression, EFW is no longer statistically significant. The seventh regression adds year fixed effects, and EFW is again insignificant.
The literature shows a strong correlation between EFW scores and per capita income (e.g. Berggren Reference Berggren2003; De Haan et al. Reference De Haan, Lundstrom and Sturm2006), so it is not surprising that when per capita income is added to the regressions, the statistical significance of EFW falls. Looking at the results in Table 3, the first five regressions show a positive and statistically significant relationship between the degree to which countries have market institutions (as measured by EFW) and the income share of the top 10%.
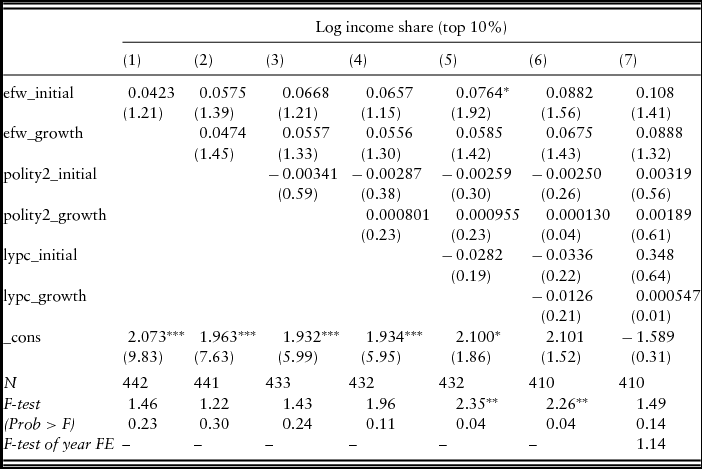
Table 4 shows the results of undertaking the same exercise, but substituting the WB data and WTID data adjusted to conform with WB. Using this data, the same regressions show no statistically significant relationship between the degree to which countries have market institutions and the income share of the top 10%. Whether there is evidence that market institutions are associated with a greater income share going to the top 10% depends on which data series for top 10% is used. The data series with the positive relationship between per capita income and top 10% share that is in the WTID data shows a positive correlation, whereas the data series with the WB relationship shows no correlation.Footnote 2
Table 4. Income shares and institutions (WTID adjusted to WB)

Note -|t| statistics in parentheses. WTID adjusted to WB data. Country Fixed Effects included in all specifications. Year Fixed Effects included in column (7).*p < 0.10, **p < 0.05, ***p < 0.01.
Figure 2 provides another look at this relationship, showing the simple correlation between the income shares of the top 10% and EFW as a measure of market institutions. The relationship is the same as estimated in the first regressions in Tables 3 and 4, but does not include the adjusted data. The top panel only uses data from the WTID data set and the bottom panel only uses data from the WB data set. The top panel in Figure 2 clearly shows the positive relationship between income inequality (as measured by share of the top 10%) and market institutions in the WTID data, and just as clearly shows that there is no relationship between income inequality and market institutions in the WB data set.

Figure 2. Relationship between top 10% income share and EFW.
5. Conclusion
Income inequality has been an important issue in economics for centuries, but much of the discussion in the twenty-first century has pointed toward government policies as the source of inequality. Piketty (Reference Piketty2014) argues, as Ricardo did two centuries ago, that growing income inequality is an inherent product of capitalist institutions, and provided some data to support the claim. This paper takes another look at the relationship between market institutions and income inequality using the WTID data Piketty has compiled and another dataset compiled by the WB. Piketty argues that the best way to measure income inequality is to look at the share of total income going to the economic elite, and this paper follows Piketty's lead, measuring income inequality by looking at the income shares of the top 10% of the income distribution.
An empirical study can only be as accurate as the data that is used, and a comparison of the WTID data with WB data on the income share of the top 10% shows that the two datasets are not comparable. The WTID data shows a strong positive correlation between the top 10% income share and per capita income, whereas the WB data does not. This is true for the entire datasets and when looking only at the overlapping observations. Rather than choose one dataset or the other, we chose to combine them, and to adjust the data from one to match the relationship between top 10% and per capita income of the other. That provided two data series for top 10% income share: one with the WTID data and WB data adjusted to the WTID per capita income relationship, and the other with the WB data and WTID adjusted data. The Fraser Institute's EFW index was used as a measure of capitalist institutions, because it was designed to quantify the degree to which a country's institutions direct economic activity through markets.
The results show that when the WTID dataset is used, it appears that the greater the degree to which a country relies on market institutions, the greater the income share of the top 10%, so market institutions are associated with inequality by that measure. However, when the same empirical models are run using the WB dataset, there is no correlation between the two variables, so using the different dataset produces a different result. Are market institutions associated with greater inequality? Using one measure of inequality the answer is yes; using another intended to measure the exact same thing, the answer is no.
The results using the two datasets are different for two reasons, as the regressions in Tables 1 and 2 showed. First, the observations in the WTID dataset exhibit a strong positive correlation between the income shares of the top 10% and per capita income, whereas the WB data show no relationship between the top 10% income share and per capita income. Second, the WB dataset has observations for many more countries than the WTID dataset. The WTID dataset includes 28 countries, whereas more than 100 countries are represented in the WB dataset.
Regarding the paper's research question about whether market institutions lead to greater income inequality, the conclusion is ambiguous. Using similar measures of inequality from two different sources, one measure indicates there is a relationship and the other indicates there is not. This finding may be of interest because of the interest in the WTID dataset after Piketty's (Reference Piketty2014) book was published. Empirical results are often published extending to many significant digits (we reported at least three), but there is a false precision there because of possible inaccuracies in data measurement. We found that two data series purporting to measure the same thing yield very different results. This suggests that some caution is warranted when using any data to try to measure income inequality.