NOMENCLATURE
- an
-
constants in drag equation (n = 1, 2, . . ., 5)—see Equation (6)
- B
-
beam of craft
- B SH
-
beam (width) of individual sidehull
- C
-
hemline length of seal or skirt
- C Do
-
aerodynamic profile drag coefficient
- C Di
-
aerodynamic induced drag coefficient
- Cf
-
hydrodynamic skin friction coefficient
- D/W
-
drag-weight ratio of craft
- di
-
sidehull inside immersion depth (relative to mean wave slope)
- F
-
Froude number (=
$\ \frac{V}{{\sqrt {gL} }}$
) - FH
-
Froude number at hump speed
- F ( L / D )max
-
Froude number at speed for maximum L/D
- g
-
acceleration due to gravity
- h
-
leakage air gap beneath skirt or seal
- Ki , Ko
-
shape parameters of sidehull
- Kn
-
constants in drag equation (n = 1, 2, . . . , 9)— see Table 1
- L
-
characteristic length of craft
- L/D
-
lift-drag ratio of craft
- (L/D)EFF
-
effective lift-drag ratio—see Equation (18)
- LCAC
-
landing craft air cushion
- LC
-
mean length of air cushion
- L SH
-
length of sidehull of craft
- P
-
total power installed in craft (propulsion plus lift)
- pC
-
air cushion pressure supporting craft
- Q
-
air cushion flow
- SF
-
frontal area of craft
- S
-
cushion area of craft
- S SH
-
wetted area of sidehulls
- SES
-
surface effect ship
- WV/P
-
transport efficiency of craft—see Equation (19)
- V
-
speed of craft
- W
-
weight of craft
- β
-
deadrise angle of sidehull
- ηL
-
lift system efficiency
- ηP
-
propulsion system efficiency
- λ
-
slenderness ratio of sidehull (= L SH/B SH)
- ρ
-
air density (= 0.00238 slug/ft3, standard atmosphere at sea level)
- ρw
-
water density (= 1.99 slug/ft3 for salt water)
1.0 INTRODUCTION
The drag of air cushion craft shares similar characteristics to both conventional aircraft and conventional ships as well as features unique to its own class of vehicles. The paper takes the detailed drag breakdown related to the hydrodynamics of moving the air cushion through water, the skin friction of sidehulls (in the non-amphibious type), the aerodynamic drag and other drag forces, then develops equations that describe the characteristic drag curves and provides a method for design optimisation of the craft to achieve performance with high values of lift-drag ratio for economic advantage. Specific formulae are developed for the design points in the drag curve such as hump drag and its speed; the condition for minimum drag and maximum lift-drag ratio and associated speed; and other key features of air cushion craft drag. The method developed provides a mechanism for a design optimisation technique of the craft geometric features for the designer to design the craft specifically to achieve the maximum value of the lift-drag ratio.
This paper is an expanded version of work that originally appeared in High Speed Marine Craft: One Hundred Knots at Sea (Cambridge University Press, 2015).
2.0 TYPES OF AIR CUSHION CRAFT CONSIDERED
There are essentially two main types of aerostatic air cushion craft. These are (a) the amphibious type capable of operating over land and sea, and (b) the non-amphibious type that operates over water only. There have been many types and craft built and operated since the inception of the hovercraft (named by its inventor, Sir Christopher Cockerell) in 1953. The two types considered in this paper are illustrated in Figs 1 and 2.
Figure 1. Characteristic amphibious air cushion craft.
Figure 2. Characteristic non-amphibious air cushion craft.
Figure 1 shows the US Navy Landing Craft Air Cushion (LCAC 38) that currently is part of the US Navy Assault Elements of the Marine Air-Ground Task Force. For that mission, 91 such craft have been delivered to the US Navy. It is approximately 175+ tons displacement including ability to carry a 60-ton Abrams tank. It has a speed capability of 40+ Kn and can cross the shoreline to deliver its troops and materiel inland.
Figure 2 shows an example of the non-amphibious type. It is the SES-100B Test Craft that was part of the US Navy's efforts in the late 1970s to develop a frigate-size ship capable of operating at sea at 80 Kn or more. The SES-100B had a displacement of 105 tons and achieved a speed under US Navy Trials of 91.90 Kn in 1976. The US Navy program into frigate-size ships was later cancelled in 1980. The technology legacy from that program provides an extensive data base for all aerostatic forms of air cushion craft.
3.0 CHARACTERISTIC DRAG CURVE OF AIR CUSHION CRAFT
Except for some ‘Havelock humps’ caused by hull-wave cancellation phenomena, the conventional displacement ship has a drag curve that has a generally monotonic increase in drag with speed with no distinct hydrodynamic optimum speed in terms of ‘minimum drag’ or ‘maximum lift-drag ratio’ across all operating conditions. The air cushion craft, on the other hand, has a drag curve that has similar characteristics to that of conventional aircraft with definitive optimum speeds for minimum drag. It has two major drag components (among others to be discussed)—one that decreases (after the hump speed) at a rate that is inversely proportional to the speed squared, and one that increases at a rate roughly directly proportional to the speed squared which produces a definitive speed for economic operation. While the reasons for these drag components are different between aircraft and air cushion craft, the behaviour of the drag components are similar and allow for selection of craft design speeds for optimum operation for fuel economy, range and endurance.
Figure 3 shows the general form of the drag curve that can be characterised by three design speeds, viz: (Reference Lamb1) hump speed (Reference Havelock2) speed for minimum drag and maximum lift drag ratio, and (Reference Crewe and Eggington3) maximum speed set by the propulsion and thrust available. Given these three speeds and the contributing drag components, it becomes possible to design the craft to meet specified performance requirements.
Figure 3. Air cushion craft generic drag curve.
4.0 HUMP DRAG AND HUMP SPEED
A major drag component for the air cushion craft (when operating over water) is that caused by pushing the pressurised supporting air cushion beneath the craft through the water. As the craft moves forward under its propulsion mechanism, it drags the supporting air cushion through the water building up an (induced) wave ahead of the craft until the wave falls away due to hydrodynamic interaction between craft and water. A similar mechanism is at work for conventional planing craft. This causes a ‘hump’ in the drag curve as shown in Fig. 3. The phenomenon of the induced wave drag has received extensive analysis and testing over the last 100 years and is well documented. Lamb(Reference Lamb1) published the first two-dimensional theory for a moving depression in the water generated by a cushion pressure (pC) and cushion length (L) in 1879. Havelock(Reference Havelock2) provided the solution in 1922 for a moving point source in the water with an emphasis on the shallow-water effects that bring in the effects of the interaction of the wave reflections off the sea bottom. Crewe and Eggington(Reference Crewe and Eggington3) in 1959 applied Lamb's theory to the air cushion craft and found good agreement with the first air cushion craft (hovercraft). More complete treatments for the induced wave drag of air cushion craft followed by Newman and Poole(Reference Newman and Poole4) in 1962, Barratt(Reference Barratt5) in 1965 (complete with extensive experimental data) and Doctors(Reference Doctors6) in 1970. These later treatments included such factors as the effect of the cushion planform, water depth and shape (edge) effects. Everest and Hogben(Reference Everest and Hogben7) in 1967 conducted extensive model tests in both shallow and deep water and compared those test results with the theoretical treatments by Newman and Poole and by Doctors.
Working with that extensive background on the characteristics of the induced wave drag, Mantle(Reference Mantle8) developed a set of formulae sufficient to define the drag curve around the hump speed based on recognisable craft parameters. The above-mentioned researchers expressed the induced wave drag (D wave) of a moving pressurised air cushion in a non-dimensional form as:
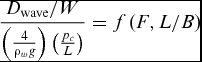$$\begin{equation}
\frac{{{D_{{\rm{wave}}}}/W}}{{\left( {\frac{4}{{{\rho _w}g}}} \right)\left( {\frac{{{p_c}}}{L}} \right)}} = f\left( {F,L/B} \right)
\end{equation}$$
In this expression, the speed is in the non-dimensional form of Froude number,
$F = \frac{V}{{\sqrt {gL} }}$
, and the craft geometric parameters are the cushion length to beam ratio (L/B) and the cushion pressure expressed as (pC
/L) called ‘cushion density’. Comparing the various theories, it was found that a reasonable agreement was found for the value of the hump drag as shown in Fig. 4.
Figure 4. Hump drag of moving air cushion.
Mantle(9) showed that the hump drag could be represented by the simple relationship:
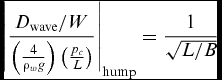$$\begin{equation}
\ {\left| {\frac{{{D_{{\rm{wave}}}}/W}}{{\left( {\frac{4}{{{\rho _w}g}}} \right)\left( {\frac{{{p_c}}}{L}} \right)}}} \right|_{{\rm{hump}}}} = \frac{1}{{\sqrt {L/B} }}
\end{equation}$$
This formulation most closely followed Barratt's results and the full-scale test results of Crewe and Eggington(Reference Crewe and Eggington3) and Everest and Hogben(Reference Everest and Hogben7), but as Fig. 4 shows, the theoretical results of Newman and Poole(4) and Doctors(Reference Doctors6) follow similar trends albeit at a lower magnitude by about 10–20%. The many possible variations in specific craft designs suggest that more precision is unwarranted in preliminary design pending more detailed experimentation under controlled conditions for specific geometries.
The hump speed at which this value of hump drag occurs showed a closer agreement between the various researchers as shown in Fig. 5 and the following relationship was developed(10) in terms of the non-dimensional speed Froude number:
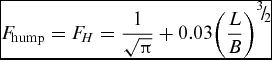$$\begin{equation}
{F_{{\rm{hump}}}} = {F_H} = \frac{1}{{\sqrt \pi }} + 0.03{\left( {\frac{L}{B}} \right)^{{\raise0.7ex\hbox{$\hbox{\fontsize{7}{7}\selectfont{3}}$} \!
/ \!\lower0.7ex\hbox{$\hbox{\fontsize{7}{7}\selectfont{2}}$}}}}
\end{equation}$$
Figure 5. Hump speed of moving air cushion.
In this expression, it is noticed that as the cushion L/B ratio is lowered the hump speed approaches the two-dimensional value of
$( {1/\sqrt \pi } )\ \ $
as predicted by Lamb.
The third characteristic of the induced wave drag is the variation with speed of D wave at above hump speed. The various theories discussed above were not provided in closed-form solutions and again it was necessary to ‘curve fit’ the theoretical results. It was found that a good representation of the wave drag dependence on speed above hump (superhump speeds, F >1.0) and for low values of the cushion length to beam ratio (L/B < 3) could be expressed as:
$$\begin{equation}
{\left| {\frac{{{D_{wave}}/W}}{{\left( {\frac{4}{{{\rho _w}g}}} \right)\left( {\frac{{{p_c}}}{L}} \right)}}} \right|_{{\rm{superhump}}}} = \ \ \frac{{\ \ \ 0.35{{\left( {L/B} \right)}^{{\raise0.7ex\hbox{$\hbox{\fontsize{7}{7}\selectfont{1}}$} \!
/ \!\lower0.7ex\hbox{$\hbox{\fontsize{7}{7}\selectfont{2}}$}}}}}}{{{F^2}}}
\end{equation}$$
Figure 6 shows this expression compared to the theoretical results by Doctors. With the above expressions, it is now possible to scope out the first part of the total drag curve shown in Fig. 3.
Figure 6. Induced wave drag at superhump speeds.
5.0 TOTAL DRAG COMPONENTS
The next key part of the drag curve is that around the minimum drag point in Fig. 3 and this requires a more extensive treatment, as will be discussed. The development of all the drag components has been treated exhaustively by many researchers since the introduction of the concept in 1953 in England and it is not necessary to repeat that development in this paper. It is well-documented, and a detailed treatment and summary may be found in Reference MantleRef. 8.
If the total drag is expressed as the ratio of drag to weight (D/W), it is possible to express the total drag as:
$$\begin{equation}
\frac{{{D_{{\rm{total}}}}}}{W} = \ \sum \left( {\frac{{{D_{{\rm{wave}}}}}}{W},\ \frac{{{D_{{\rm{aero}}}}}}{W},\frac{{{D_{{\rm{mom}}}}}}{W},\ \frac{{{D_{{\rm{skirt}}}}}}{W},\ \frac{{{D_{SH}}}}{W}} \right)
\end{equation}$$
The actual form of the drag terms in Equation (5) will vary for amphibious and non-amphibious craft but the five major components are:
-
$\frac{{{D_{{\rm{wave}}}}}}{W}$
Induced Wave Drag discussed above
-
$\frac{{{D_{{\rm{aero}}}}}}{W}$
Aerodynamic Profile Drag
-
$\frac{{{D_{{\rm{mom}}}}}}{W}$
Momentum drag incurred by air cushion flow (Q)
-
$\frac{{{D_{{\rm{skirt}}}}}}{W}$
Drag of the skirt or seal around the craft (wetting and wave-making)
-
$\frac{{{D_{SH}}}}{W}$
Hydrodynamic drag of sidehulls (buoyancy, dynamic and skin friction)
Table 1 shows the equations for the case of calm-water operation. For the particular class of air cushion craft using aerodynamic lift (not considered in this paper), there is an additional component called aerodynamic induced drag (see Mantle(Reference Mantle11) for detailed treatment for this particular case).
Table 1 Calm water drag components dependence on speed (Froude number)
IMPORTANT NOTE: The above listed five major drag components have received extensive treatments, including both theoretical and empirical treatments, and have been used successfully in many designs and operational craft. While there are minor variations in different researchers work (due mainly to complex geometries in craft components), all treatments agree on the effect of speed. This agreement greatly aids the treatment of optimisation as developed in this paper.
The shape of the drag curve above hump speed requires an understanding of the form of the drag equation. While the detailed form of the drag equations is summarised in Table 1 showing all the detailed dependency on craft parameters, it is seen that they may be grouped into a simple closed-form equation when expressed as a function of speed (Froude number) in Equation (6).
$$\begin{equation}
\frac{{{D_{{\rm{total}}}}}}{W} = \frac{{{a_1}}}{{{F^2}}} + {a_2}F + a{}_3{F^2} + {a_4} + \frac{{{a_5}}}{{{F^4}}}
\end{equation}$$
The constants a 1, a 2, a 3, a 4, a 5 are easily determined from the geometry and other craft values given in Table 1 and are:
$$\begin{equation}
{a_1} &=& {K_1}\left( {1 + {K_5} + {K_1}{K_6}} \right)
\end{equation}$$
$$\begin{equation}
{a_2} &=& {K_3}
\end{equation}$$
$$\begin{equation}
{a_3} &=& {K_2} + {K_4} + {K_8}
\end{equation}$$
$$\begin{equation}
{a_4} &=& {K_1}{K_9}
\end{equation}$$
$$\begin{equation}
{a_5} &=& {K_7} K_{1}^{2}
\end{equation}$$
Such a formulation greatly simplifies the ability to analyse the conditions for such design speeds as speed for minimum drag and speed for maximum lift-drag ratio.
6.0 SPEED FOR MAXIMUM LIFT-DRAG RATIO
The speed for minimum drag and for maximum lift-drag ratio can be found by differentiating the drag equation with respect to speed (Froude number) and equating to zero. This gives the result:
$$\begin{equation}
\frac{{\partial \left( {{D_{total}}/W} \right)}}{{\partial F}} = - \frac{{2{a_1}}}{{{F^3}}} + \ {a_2} + 2{a_3}F - 4\frac{{{a_5}}}{{{F^5}}} = \ 0
\end{equation}$$
This sextic equation does not have a general or closed form solution except in special circumstances. Upon examination of the relative terms in the equation, it is seen that the last term only occurs for the non-amphibious form of air cushion craft and further is the term associated with the buoyancy of the sidehulls, which is very small compared to the other drag terms. If the reasonable assumption is made that this will have minimal effect on the results, it becomes possible to express the total drag as a solvable quartic equation which can be written:
$$\begin{equation}
2{a_3}{F^4} + \ {a_2}{F^3} - 2{a_1} = 0
\end{equation}$$
In any particular craft design, this quartic equation can be solved easily by the usual methods available in the literature, e.g., Ferrari's method, Descartes's method and others. Each of these classic methods are essential to solving quartic equations in either the general form or in the depressed form as appears in Equation 13. However, such general solutions are complex and cumbersome in form and not directly amenable to setting up ‘user-friendly’ design rules.
It is possible to obtain useful equations for the use in design by noting that certain terms in the drag equation dominate the final form for most craft. This can be seen in the case of the sidehull craft SES-100B design (see Fig. 2). The drag curve using the above equations is shown in Fig. 7 compared to the US Navy Trials data, showing good agreement between the developed theory shown here and the US Navy trials data and giving confidence in the method.
Figure 7. Drag theory and test for SES-100B.
It is known that there are two main contributors to the total drag (D total/W) that allow for a more tractable solution to the quartic equation. These are (a) the induced wave drag term inversely proportional to speed squared and (b) the sum of the terms that exhibit drag that is directly proportional to speed squared. If those two major drag components, characterised by the drag term constants a 1 and a 3 , are plotted on the total drag curve plot, this appears as Fig. 8. This allows for a ‘quick solution’ or base case for determining the speed for maximum lift-drag ratio |F|(L/D)max and for the value of (L/D)maxfor the air cushion craft, as will be shown.
Figure 8. Two main drag components of total drag.
7.0 QUICK SOLUTION FOR LIFT-DRAG RATIO
Using the quartic equation Equation (13) and retaining only the two dominant drag components, it can be seen from Equation (13) that the speed for maximum lift-drag ratio becomes:
$$\begin{equation}
{\left| F \right|_{\left( {L/D} \right){\rm{max}}}} = \ \sqrt[4]{{\frac{{{a_1}}}{{{a_3}}}}}
\end{equation}$$
If this value is now inserted into the drag equation, this yields the slightly optimistic maximum value of the lift-drag ratio to be:
$$\begin{equation}
{\left( {\frac{L}{D}} \right)_{{\rm{max}}}} = \ \frac{1}{{2\sqrt {{a_1}{a_3}} }}
\end{equation}$$
8.0 MORE COMPLETE SOLUTION OF THE QUARTIC EQUATION
A quick glance at Fig. 8 suggests that the speed for minimum drag and maximum lift-drag ratio would be a slow functional variation with speed. In which case, if that speed in Equation (14) is inserted into Equation (6), it produces a value for the maximum lift-drag ratio that now includes all five drag components, as shown in Equation (16):
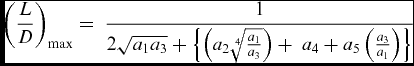$$\begin{equation}
{\left( {\frac{L}{D}} \right)_{{\rm{max}}}} = \ \frac{1}{{2\sqrt {{a_1}{a_3}} + \left\{ {\left( {{a_2}\sqrt[4]{{\frac{{{a_1}}}{{{a_3}}}}}} \right) + \ {a_4} + {a_5}\left( {\frac{{{a_3}}}{{{a_1}}}} \right)} \right\}}}
\end{equation}$$
In this approximation, it is assumed that the speed for (L/D)max is as before:
$$\begin{equation}
{\left| F \right|_{{{\left( {L/D} \right)}_{{\rm{max}}}}}} = \ \sqrt[4]{{\frac{{{a_1}}}{{{a_3}}}}}
\end{equation}$$
Over a test set of examples it was found that the terms in the brackets {. . .} in Equation (16) contribute about an additional 5–10% of the total drag, which allows reasonable early assessments to be made in the design values for (L/D)max, thus providing a useful tool for design optimisation. Figure 9 shows how these results apply to the example case of SES-100B. In Fig. 9, the horizontal line shown as ‘Case 1’ applies to the quick-solution (two drag components) value Equation (15) that slightly overestimates the value for (L/D)max. The line shown as ‘Case 2’ includes all five drag components in Equation (16) for a slightly lower value of (L/D)max more in line with the US Navy Trials Data.
Figure 9. Display of (L/D)max prediction.
Once given these general findings, it now becomes possible to dissect the ‘constants’ (a 1, . . . , a 5) into the craft geometric parameters (K 1, . . . , K 9) to explore design variations that open up possibilities to refine the design for greater values of lift-drag ratio and more efficient design.
9.0 LIFT-DRAG RATIO AND TRANSPORT EFFICIENCY
The lift-drag ratio (L/D) has an important role in the design of all craft and the above method allows for optimisation of the craft parameters to achieve the highest ‘aerodynamic’ or ‘hydrodynamic’ efficiency in the design. While not expanded upon here, it is known that for those craft using power mechanisms for propulsion (propellers, waterjets, etc.), the maximisation of the range of the craft is directly proportional to (L/D)max. For those craft propelled by direct thrust (jet engine) means, the range of the craft is directly proportional to the product V(L/D). In both types of craft it is seen that the maximum value of L/D is a key parameter in the design.
In the case of the air cushion craft, there are two sources of power in their operation, one devoted to propulsion and one devoted to providing the lift mechanism of the pressurised air cushion. In this case, the L/D value is modified to give an effective L/D such that:
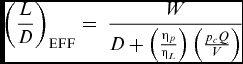$$\begin{equation}
{\left( {\frac{L}{D}} \right)_{{\rm{EFF}}}} = \ \frac{W}{{D + \left( {\frac{{{\eta _p}}}{{{\eta _L}}}} \right)\left( {\frac{{{p_c}Q}}{V}} \right)}}\
\end{equation}$$
In this expression, the L/D is modified by the lift system with the term
$( {\frac{{{\eta _p}}}{{{\eta _L}}}} )( {\frac{{{p_c}Q}}{V}} )$
which has the dimensions of drag. The lift power (pcQ) appears in this expression related to craft speed (V) and the efficiencies of the propulsion (ηP
) and lift (ηL
) systems. Typically, the inclusion of the lift system reduces the L/D ratio by a factor of approximately 2:1, depending on the propulsion and lift system efficiencies, to yield (L/D)EFF and is a major consideration in the design of the craft.
In terms of the ability of the craft to transport a given weight (W) at a given speed (V) for a given expenditure of power (P), which is a measure of work efficiency, this can be measured by the Transport Efficiency (WV/P) which is directly related to the effective lift-drag ratio:
$$\begin{equation}
\frac{{WV}}{P} = \ {\eta _P}{\left( {\frac{L}{D}} \right)_{{\rm{EFF}}}}\
\end{equation}$$
10.0 POTENTIAL FOR CRAFT DESIGN OPTIMISATION
Given the above derivation of the equations for maximum lift-drag ratio it now becomes possible to examine techniques for design optimisation. The equations for the maximum lift-drag ratio (L/D)max, effective lift-drag ratio (L/D)EFF and transport efficiency (WV/P) in Equations (16), (18) and (19) appear, at first glance, to be complex combinations of craft parameters, propulsion and lift system efficiencies, and installed power. Fortunately, they are characterised by just a few easily recognised craft design parameters, as follows:
$$\begin{equation}
{a_1}&=& f\left( {{p_c}/L,L/B,\ \left\{ {{S_{SH}}/S,\ \;\lambda ,\;\ \beta } \right\}} \right)
\end{equation}$$
$$\begin{equation}
{a_2} &=& f\left( {{p_c}/L,L/B\ ,\ Q,\ L\ }\!\!\right)
\end{equation}$$
$$\begin{equation}
{a_3} &=& f\left( {{C_{Do}},{p_c}/L,\ h/C\ ,\left\{ {{L_{SH}}/{L_c}\ \!,\ {d_i}/{L_{SH}}\ } \right\}} \right)
\end{equation}$$
$$\begin{equation}
{a_4} &=& f\left( {{p_c}/L,\ L/B,\left\{ {{L_{SH}}/{L_c}} \right\}\ }\!\! \right)
\end{equation}$$
$$\begin{equation}
{a_5} &=& f\left( {{p_c}/L,\ L/B,\ \left\{ {{S_{SH}}/S,\ \beta } \right\}} \right)
\end{equation}$$
The terms in the curly brackets {. . .} are those shape parameters for the hydrodynamic sidehulls that apply to the non-amphibious form of craft only.
10.1 For amphibious craft
The key parameters for maximum lift-drag ratio (L/D) of such craft shown in the above set are seen to be a much-reduced set of controllable craft parameters, viz:
-
Overall sizing: Cushion Density (pc /L) and Craft Length to Beam Ratio (L/B )
-
Lift system: Cushion Pressure (pc ) and Air Flow (Q)
The effective lift-drag ratio (L/D)EFF brings in the additional effect of the propulsion and lift system efficiencies (ηp,ηL) and ship speed (V). Finally, the key economic parameter, the transport efficiency (WV/P) brings in the effect of total on-board power (lift and propulsion) for the craft.
10.2 For non-amphibious craft
The key parameters for this class of craft are the same as for the amphibious class with the addition of the sidehull hydrodynamic parameters, viz: sidehull wetted area (S SH/S), hull slenderness ratio (λ), hull depth (di /L SH) and hull deadrise angle (β).
With these entities, it now becomes an easy optimisation process to trade these known characteristics of the craft to determine the conditions for the maximum value of lift-drag ratio (and its design speed) and its related economic factors in the design process. Of course, the designer will have to include in the design optimisation process the impact on other features such as stability, structural weight and other characteristics in addition to performance that are influenced by many of the same parameters. Because of these many interacting variations, it is not possible to provide universal rules for the design optimisation process, but the treatment derived here provides the basic starting point in any design procedure.
It should be pointed out that the emphasis in this paper has been on the aerostatic form of air cushion craft where the aerodynamic drag is that treated by the profile drag coefficient (C Do). The additional feature for aerodynamic forms of air cushion craft is that of the aerodynamic induced drag coefficient (C Di), which has been treated separately elsewhere (Reference MantleRef. 11).
11.0 TRANSPORT EFFICIENCY AND MAXIMUM SPEED
The last key part of the drag curve (Fig. 3) is that anchored by the maximum speed of the craft. The maximum speed now invokes the form of the propulsion (thrust) in addition to the drag of the craft. Because of the influence of the propulsion system in its many forms, there is no general or closed-form solution for maximum speed. It is possible, however, to categorise the general areas of ‘work efficiency’ discussed above for the different classes of vehicles. In the context of this paper, the three classes of displacement ships, air cushion craft and conventional aircraft demonstrate how the maximum speeds of such craft compare with each other on the transportation spectrum where transport efficiency (WV/P) in Equation (19) varies with the maximum speed of the vehicles. Figure 10 shows these three categories. Each region of the three types of craft is heavily influenced by the dominant forces acting on the system. For ships, the dominant forces are hydrostatic and hydrokinetic forces; for air cushion craft, the dominant forces are aerostatic and hydrodynamic; and for aircraft, the dominate forces are aerodynamic. A detailed treatment of the actual craft data points shown and explanation of the envelopes (or boundaries) for each of the three classes of vehicles displayed in Fig. 10 may be found in Reference MantleRef. 8.
Figure 10. Transport efficiencies of ships, air cushion craft and aircraft.
The propulsion schemes of water-or-air propellers and water-or-air jets interact with those same forces to provide the intersection of the thrust curve and the drag curve to yield the maximum speed shown in Fig. 10. Note that the maximum speed is determined by the maximum power installed that sizes each vehicle type. The maximum transport efficiency (and maximum lift-drag ratio) will be generally equal to or some lower value than that predicted by Equation (15) or Equation (16), as discussed above in the drag optimisation section. The value of transport efficiency at maximum speed will always be lower than that at the speed for (L/D)max because of the higher power requirements.
In Fig. 10, it is seen that the air cushion craft fills a unique niche in the transportation spectrum between displacement ships and aircraft, and that stringent design decisions must be made to keep the transport efficiencies (and the underlying (L/D) values explored here) at an efficient and high value to be competitive. As stated above, it can be seen from Fig. 10 that there are three distinct regimes for (a) ships that are supported by water, (b) aircraft supported by air and (c) the unique grouping of air cushion craft that use air for support over water. Each of these groupings invoke different laws of aerodynamics and hydrodynamics that set boundaries for their operation. The groupings of ships are seen to be grouped close to the boundaries as designers over many decades have sought optimum designs. While not shown, a similar grouping of aircraft designs nestle against the boundaries, again because of extensive development to produce efficient designs.
The air cushion craft, on the other hand, has not enjoyed efficient treatments over time, as indicated by the wide spread of the key measure of transport efficiency data points of the many craft developed. The tools developed in this paper for maximising the L/D values will facilitate such design optimisation and provide an opportunity to refine the design process for air cushion craft.
12.0 SUMMARY
A method has been developed to provide estimates to be made of the key design points in the drag curves of air cushion craft with a concentration on determination of the value of the maximum lift-drag ratio, which is a key ingredient in the analysis of the efficiency of the design. The method developed provides a useful tool to guide selection of craft design features and to quickly determine their impact on the final design performance of the craft before proceeding into more complex and expensive development. The method developed allows for an optimisation technique of analysing the craft geometric parameters directly as they affect the maximum lift-drag ratio, its associated design speed, and other related key economic efficiency design parameters.
