I. INTRODUCTION
The aim of this paper is to analyze and compare two attempts at introducing search unemployment in macroeconomic theory. The first, due to Peter Diamond and entitled “Aggregate-Demand Management in Search Equilibrium” (Diamond Reference Diamond1982a), took place in the early 1980s; the second is due to David Andolfatto and Monika Merz, writing independently, in the mid-1990s (Andolfatto Reference Andolfatto1996; Merz Reference Merz1995). Andolfatto’s paper was entitled “Business Cycles and Labor-Market Search”; Merz’s was entitled “Search in the Labor Market and the Real Business Cycle.” Although praised as a gem of a model, Diamond’s paper had little direct offspring. By contrast, Andolfatto’s and Merz’s contributions, though less ambitious, were considered an established result.
The spontaneous interpretation of this sequence of attempts is to regard it as a poster child of the trial-and-error process through which scientific progress is often seen as occurring. Diamond, the story would be, blazed the trail, and Andolfatto and Merz finished the job. We contend that things were not as simple. True, the three economists pursued the same objective of constructing a macroeconomic model having search unemployment as one of its distinctive features. However, differences in broader purpose, background, and historical circumstances impede regarding their contributions as standing in a relationship of continuity. By bringing out these differences, our paper provides a richer understanding of this episode in the history of macroeconomics.
The paper is organized as follows. We start with sketching out the methodological standpoint underpinning the paper, and the vision, motivation, and historical context in which the three economists we study were working (sections II and III). In section IV we summarize the state of labor market search theory before the view arose that integration of search and macroeconomics was a worthwhile enterprise. Footnote 1 These preliminaries settled, in the subsequent sections we enter into the heart of the matter by studying the contents of the papers. In section V, we study Diamond’s (Reference Diamond1982a) paper. We also examine how Diamond’s work relates to Robert Lucas’s. Section VI is devoted to the Andolfatto/Merz research line. Finally, in section VII, we confront the two attempts.
II. METHODOLOGICAL STANDPOINT
Our paper evolves at the crossing of two notions: the ‘scientific revolution’ idea and Axel Leijonhufvud’s vision of the development of economic theory. The latter asserts that this development can be regarded as a decision tree.
Major economists force their contemporaries to face choices—the choice of what to ask, what to assume, what to regard as evidence and what methods and models to employ—and persuade the profession or some fraction of it to follow the choice they make. The path that any particular school has followed traces a sequence of such decisions. Many of the choices faced in such a sequence were not anticipated by the founder to which we trace the development in question but were created by subsequent contributors; some of the decisions made we may judge to have been wrong in hindsight. (Leijonhufvud Reference Leijonhufvud, Hagemann and Hamouda1994, p. 148)
There are two components to Leijonhufvud’s standpoint. The first is the backtracking idea. Any major new bifurcation on the tree—i.e., a new research line—starts as an original contribution, which in the beginning is like a thin new branch burgeoning on a bigger one. Its success hinges on the attention it receives. The original work must be considered sufficiently interesting to be elaborated upon. The ensuing chain of contributions superseding each other makes the branch sturdier, possibly becoming an autonomous research program. Symmetrically, once mature, a research track may gradually lose its momentum: puzzles arise, objections are leveled, and doubt about its validity set in. This may lead to what Leijonhufvud called “backtracking”: traveling back down the decision tree to an earlier bifurcation that at the time was neglected, but now seems a viable and appealing alternative.
The second component of Leijonhufvud’s standpoint is that the notion of progress ought to be relativized. Progress makes sense when describing what is happening on a specific branch or bifurcation of the decision tree. Once backtracking enters the picture, however, and especially when it goes a long way back on the decision tree, the notion of progress becomes ambiguous. To those who support the backtracking process, the abandonment of a line deemed to be barren is declared progress, yet those of the opposite opinion will consider it a regress. Footnote 2
The backtracking process, when sufficiently extended, evokes the idea of a scientific revolution. This concept has been overused in economics, but we find it as apposite for both the transformation of macroeconomics triggered by Lucas that led to DSGE macroeconomics as well as for the change that took place in labor economics as the result of the invention of the search perspective. The backtracking undertaken by Lucas led him to return to two basic methodological nodes of macroeconomics. The first was the Marshall–Walras bifurcation. Lucas decided to switch from the first to the second. The second node pertained to the object of analysis of macroeconomics. Keynes decided to zero in on the explanation of “involuntary unemployment,” and Keynesian economists followed suit. For his part, Lucas assigned macroeconomics the task of explaining business fluctuations. The scientific revolution notion also fits what happened in labor economics in the 1970s with the emergence of search models of unemployment. Traditional labor economists followed an empirical, institutional research line, and were skeptical with regards to neoclassical principles. By contrast, search theorists decided to base their analysis of the labor market on neoclassical principles, studying unemployment through the equilibrium lens while, at least in the beginning, giving less emphasis to empirical work.
III. DRAMATIS PERSONAE
Our story comprises three main protagonists: Diamond, Andolfatto, and Merz. The aim of this section is to briefly describe their motivations and the context in which they were working. Footnote 3
Diamond
In our interview, Diamond Footnote 4 stated at once that he “was a Keynesian from the beginning,” echoing what he said to Giuseppe Moscarini and Randall Wright in an earlier interview: his having picked up the “Yale macro vibe” during an internship at the Cowles Foundation in the interval between his undergraduate years at Yale and his graduate time at MIT, befriending Yale’s Keynesian macroeconomists James Tobin, Arthur Okun, and William Brainard (Moscarini and Wright Reference Moscarini and Wright2007, p. 547). From John Maynard Keynes’s General Theory, Diamond retained two main ideas: first, the possibility that economies can be stuck in a suboptimal equilibrium due to insufficient aggregate demand; and, second, the role of ‘animal spirits’ in explaining business cycles. However, he was hardly enthusiastic about Keynesian macroeconomic theory, regretting its lack of microfoundations, its undue emphasis on wage rigidity, and its poor dynamics: “My dissatisfaction did not relate to basic Keynesian concepts, but to the nature of modeling. I wanted to see a microfoundation that would enhance the ability to do normative analysis and to develop policy insights” (Diamond Reference Diamond2011, p. 1056).
In short, Diamond was a Keynesian in terms of his vision of the market system—defending the latter, yet admitting that it could fall prey to malfunctions—but less so in terms of conceptual apparatus and method. With respect to these, he definitely leaned towards the neo-Walrasian approach, the result of his mathematical education and of Gérard Debreu’s influence. But here too, Diamond had reservations. In particular, he was dissatisfied with the mechanism this approach adopted for allowing equilibrium to be reached: the auctioneer hypothesis. More basically, he was against its strategy of first defining equilibrium, postponing the study of convergence to a subsequent step. In his eyes, the right way to proceed was to do the opposite: that is, addressing the question, “If I have a plausible mechanism, to which equilibrium does it converge?” Footnote 5
Diamond soon realized that the search trade technology was a good starting point for his quest, an insight that he quickly implemented. His search externality paper (Diamond Reference Diamond1982a) on which we will focus can be regarded as the culminating point of his work in this line.
Andolfatto
Andolfatto was a graduate student at the University of Western Ontario from 1987 to 1991. His doctorate committee was composed of Peter Howitt, Glenn McDonald, and Stephen Williamson; his dissertation was entitled “Essays on the Theory of Growth and Unemployment.” Andolfatto’s graduate macroeconomics education was definitely fresh water, consisting of a sequence called “Dynamic general equilibrium I and II,” taught by Jeremy Greenwood and Gregory Huffman.
The event that played a decisive role in Andolfatto’s career was his enrollment in a macro topic course centered on search theory and taught by Howitt. The course covered the whole range of the contemporary search literature, as well as other macro models at the frontier of knowledge. The macro classes taken by Andolfatto had familiarized him with the ‘labor market productivity puzzle’ in Real Business Cycle (RBC) theory, as well as other labor supply issues facing this theory. He also knew about the criticisms addressed to the models studied in these classes, such as the compelling Pareto-optimal character of equilibrium and the lack of consideration given to notions like involuntary unemployment. So, when he was required to write a final paper for Howitt’s class, the idea dawned on him that a nice thing to do was to “smash” search and RBC (Danthine and De Vroey Reference Danthine and De Vroey2016, p. 11). Luckily enough, as Andolfatto noticed later, at the time he was unaware that top researchers like Randall Wright had broken teeth working on the issue.
To succeed in this endeavor, different hurdles had to be addressed. For example, distribution effects had to be overcome, which, on Howitt’s suggestion, Andolfatto did by assuming homothetic preferences. After much groping, he ended up ironing out heterogeneity by assuming a perfect insurance scheme, thereby allowing agents to enjoy the same utility, whatever their employment status. At the time, making this assumption irked him. As he said in his interview with us, “ I can’t say I was entirely satisfied with the assumption” (Danthine and De Vroey, p. 11). Once the way opened, however, his remorse evaporated; to him, it was just a mechanism to afford some degree of analytical and computational simplicity. It took Andolfatto several years to transform his 1988 course paper into an article published in the American Economic Review (1996). During these years, his project met with ebbs and flows, among which was his discovery that both Dale Mortensen and Merz were on the verge of publishing similar papers. Footnote 6
The irony in this course of events is that the person who, according to Andolfatto, was the most helpful in putting his insights on track was Howitt. Howitt was an eminent member of the Keynesian tribe, close to Robert Clower and Axel Leijonhufvud, and an ardent endorser of Diamond’s search externality model. In a 1986 lecture at the Canadian Economic Association meeting, entitled “The Keynesian Recovery,” Howitt argued that macroeconomics faced a crucial bifurcation between two competing research paths: transaction externalities à la Diamond and RBC modeling. In his eyes, the race was open—“Which of these two paths will be the main attractor of graduate students in the years to come is impossible to predict” (Howitt [1986] 1990, p. 79)—yet both the title and the contents of the lecture make it clear that he was optimistic about the chances of the Keynesian side to win the race. Two years later, we see him encouraging one of his students to take the rival route.
Merz
Merz’s Reference Merz1995 article, “Search in the Labor Market and the Real Business Cycle,” was part of her doctorate dissertation presented at Northwestern University. Her thesis committee was composed of Larry Christiano, Dale Mortensen, and Mark Watson. Her starting point was definitely macroeconomics rather than labor economics. As she recounts in her interview, during her studies she took no labor economics course. Christiano, who was visiting from the Federal Reserve Bank of Minneapolis (before subsequently getting a position at Northwestern), was the person who drew her to study the integration of search in RBC. At the time, an important concern of macroeconomists was the discrepancy between labor elasticity in the aggregate, which the standard RBC model requires to be very high, and the micro data about this elasticity, which econometric testing showed to be very small. While this was the issue that triggered her work, Merz’s contribution to it was lateral. Her take was to broaden the scope of households’ choice set. The standard RBC model considered only the intensive margin, the choice between labor and leisure. Her conjecture was that introducing the extensive margin—participation in the labor market and hence a split between the employed and the unemployed—into the picture would allow improving on the deficiencies of the standard RBC model by explaining why the existence of trade frictions causes the real wage to deviate from labor productivity. This is where Mortensen came into play. He himself had, of course, worked the problematic of labor search, and he could support Merz’s attempt at using this framework to introduce the extensive margin in the RBC model.
As with Andolfatto, one of the key points to overcome was the heterogeneity that arose once unemployment was in the picture. Neither mathematical techniques nor computing power allowed to solve and simulate outright heterogeneous models at the time. Per Krusell, Anthony Smith, and Victor Rios Rull had barely started working on the issue. Here, Merz remembers Larry Christiano telling her that she had two options, “either to wait yet another ten years for them to invent the tools or to develop an alternative doable route in order to get your paper done” (Danthine and De Vroey Reference Danthine and De Vroey2016, p. 16). For her, the straightforward way was to assume agents to be part of large households, with perfect (familial) insurance ironing out the heterogeneity across agents. This, it would turn out, was akin to the trick Andolfatto used, which was assuming perfect insurance.
Although Merz and Andolfatto worked independently, they pursued the same project of introducing unemployment and job vacancies in a RBC framework. This similarity is less a surprise than what appears at first sight.
IV. THE RANDOM SEARCH AND BARGAINING (RSB) MODEL
The Rise of the Search Approach
Up to the 1970s, labor economics was a field marked by empiricism, institutionalism, and a strong distrust of neoclassical theory. This state of affairs changed with the emergence of a new research line—the search approach—that by contrast was firmly anchored in neoclassical theory, since one of its premises was that unemployment could be conceived of as an equilibrium occurrence.
The search literature Footnote 7 grew out of the realization by a number of economists—George Stigler (Reference Stigler1961, Reference Stigler1962) most notably—that many observable situations could not be explained using the neoclassical, frictionless view of the market. Rationing—i.e., heterogeneity of treatment of similar individuals—was a glaring example. Another looming problem was the question of adjustment to equilibrium. How do markets converge to equilibrium? Are adjustments instantaneous, or is there a transition process that eventually yields the equilibrium outcome?
The first search models were due to John McCall (Reference McCall1970), Mortensen (Reference Mortensen and Phelps1970), and Reuben Gronau (1970). In these papers, the emphasis is put on one side of the market, typically the employer side. An exogenous wage distribution is assumed. Workers randomly face wage offers and must decide whether to accept these offers, or reject them in the hope of subsequently getting a better offer. Diamond was another pioneering contributor to this approach. In his 1971 Journal of Economic Theory article, “A Model of Price Adjustment,” he brought out what became known as the “Diamond Paradox”: introducing small search costs in a standard model has the effect of raising equilibrium prices from competitive to monopoly levels. As a result, the issue of inefficiency came to the forefront. However, it was soon realized that regarding search as one-sided was wanting. There is no reason to believe that only one side of markets would exert search effort.
To describe the implementation of this broader program, it is useful to resort to Leijonhufvud’s decision tree. Figure 1 summarizes the whole process.
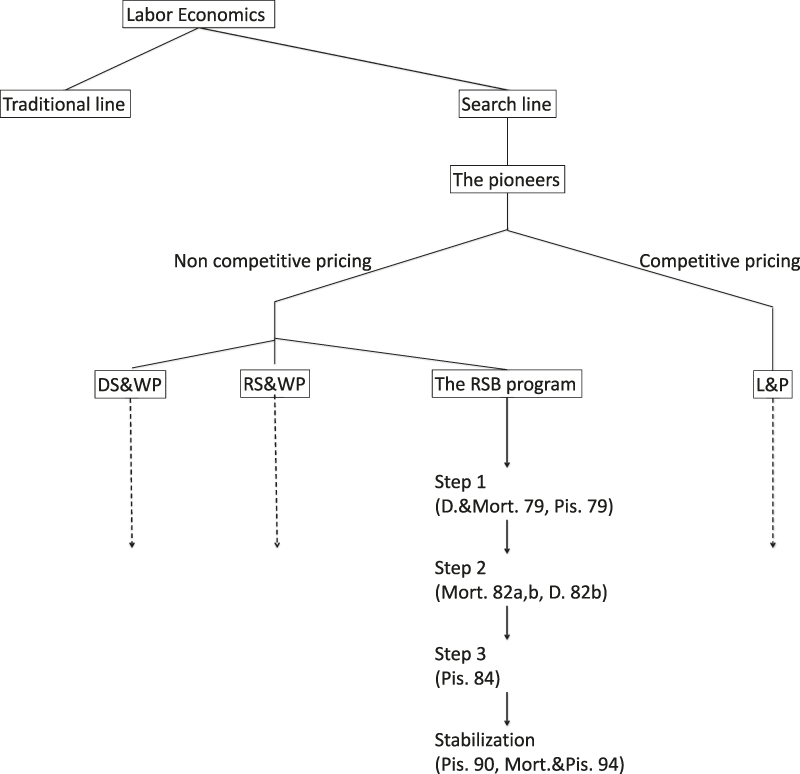
Figure 1. The Rise of RSB Modeling. Footnote 8
A first bifurcation to be faced was between adopting a perfect competition, assuming price-taking agents, or an imperfect competition framework, with at least one side of the market setting prices. In their 1974 paper, “Equilibrium Search and Unemployment,” Lucas and Edward Prescott took the first of these two routes, basing themselves on Edmund Phelps’s island parable. In this setting, the economy is subdivided into submarkets: that is, spatially separated islands, each experimenting with specific market conditions. Both firms and workers are price takers. Island employment and wages are such that the supply of and demand for labor match. That is, firms employ labor up to the point at which wages equal the marginal product of labor. For their part, workers are mobile; they can move from one island to the other according to their expectations of economy-wide market conditions. As long as the wage on the island they inhabit makes employment at least as valuable as opting out, workers will remain on the island, supplying a unit of labor. Otherwise, they will leave it. As it is furthermore assumed that they are ineligible for employment on another island at once, at any time a fraction of the workforce turns out to be unemployed.
For all its ingenuity, the Lucas–Prescott model triggered little following (at least at the time). Most economists interested in the search approach opted for departing from the perfect competition framework. At this juncture, they encountered a double bifurcation. The first was to choose between assuming meetings as random or not; the second was about either giving the power to set prices to one side of the market or having it resulting from bargaining. Four modeling strategies ensued, only three of which became active. The first active one is directed search with wage posting (Butters Reference Butters1977; Burdett and Judd Reference Burdett and Judd1983; Mortensen 1990; Burdett and Mortensen Reference Burdett and Mortensen1998)—DS+WP in Figure 1. In this modeling strategy, ex ante homogeneous workers search for a job by sampling wages decided by firms. Firms compete to attract workers. Setting a higher wage offer results in workers’ directing their search to the most attractive alternatives. For wage dispersion to arise, on-the-job search and search frictions are required. The second is random search with wage posting (MacMinn Reference MacMinn1980; Albrecht and Axell Reference Albrecht and Axell1984)—RS+WP in Figure 1. Here, the query bears on understanding “pure wage dispersion”: i.e., why workers with identical productivity can be paid different wages. It is assumed that workers are heterogeneous with respect to some element unrelated to productivity. Firms with monopsony power may then be indifferent, in equilibrium, between setting high or low wages. It can be shown that, in general, the distribution of wages will coincide with some subset of worker reservation wages. Firms’ heterogeneity may be required for robustness. The third one is random search with bargaining—RSB in Figure 1. Although the first two modeling strategies have been and are still very active fields of research, only the third one must retain our attention, because the attempts at an integration of a search perspective in macroeconomics we study have been based on it—partly, as far as Diamond is concerned; fully, as far as Andolfatto and Merz are.
The Ascent and Stabilization of the RSB Model
As Figure 1 illustrates, the construction of the RSB model occurred in a stepwise fashion, each step devoted to a specific building block. The first step consisted of making the concept of random meeting operational. The second related to ways of judging whether the sharing of the surplus yielded as the result of matching is efficient. The third bore on the explanation of job creation. The final step was the stabilization stage.
Random Matching
Given searchers on both sides of the market, and the number of agents on each side, the issue is how to define the conditions of an encounter. This founding stone was laid out at the same time by Christopher Pissarides (Reference Pissarides1979) and Diamond and Eric Maskin (1979) in quite different contexts.
While attracted to earlier search models because of their realistic definition of unemployment, Pissarides was dissatisfied with one of their features: that the long-term unemployed were deemed to be in their situation because of a persistent failure to locate high enough wage offers. His hunch was that characterizing job offers as mere wage offers was misleading. Much more was involved: the problem of matching jobs with workers, each having different attributes. To this end, he imagined a meeting mechanism, which he dubbed the “matching function.” Wage distribution was absent from it, but unemployed and vacancies co-existed. In Pissarides’s 1979 paper, the matching function was meant to represent a specific labor market institution, the British Employment Agency. Unemployed workers, the story went, can apply to the agency, and firms with vacancies can post their vacancies in the agency repository. But workers and firms can also sidestep the agency, with firms privately posting advertising for jobs, and workers randomly encountering advertised jobs. This was Pissarides’s initial way of positing the issue; it would subsequently evolve.
For their part, in their 1979 article, “An Equilibrium Analysis of Search and Breach of Contract, I. Steady States,” Diamond and Maskin reasoned in a different context. Unlike Pissarides’s, their paper did not study the labor market specifically. It was part of a law and economics project dealing with contracts in general—by which they meant agreements to carry out a single project: e.g., the renting of a summer house—including their breaching and the ensuing damage problems. Diamond and Maskin’s aim was to study how agents come in contact: that is, as stated in their paper’s abstract, to analyze “steady state equilibria in models where individuals meet pairwise in a costly stochastic search process and negotiate contracts to produce output” (Diamond and Maskin Reference Diamond and Maskin1979, p. 282). In such a framework, matches can be good or bad, and agents may want to breach contracts. Investigating the impact of different damage rules on equilibrium search and breach behavior, Diamond and Maskin decided to separate two types of meeting technology. The first one, which they dubbed the “quadratic technology,” features increasing returns; as a result, the aggregate number of matches increases linearly with the number of searchers. More specifically, they assumed that the number of meetings increases with the square of the number of searchers (hence their terminology). Assuming a low density of potential partners, the greater the number of searchers, the higher the meeting probability. Thus, a searcher creates a positive externality for other searchers. The second meeting technology, which they called the “linear technology,” exhibits constant returns to scale. Here, the meeting probability is independent of the number of searchers, but the chance of meeting a free partner is affected by the meeting probability—hence the existence of a negative externality. The general conclusion of the paper is that, given these externalities, search and decisions to breach are in general inefficient. Multiple equilibria may also exist. Despite the contextual difference from Pissarides’s paper, Diamond and Maskin’s two technologies can be called a “matching function” in that they describe how agents meet through a random search. After having worked on this paper, which, as will be seen, is also addressed in the second step, “Efficiency,” Maskin and Diamond parted ways. The former centered his attention on his main field of interest, game theory, and the latter pursued their program in two articles. The first is his search externality 1982 model (Diamond Reference Diamond1982a), in which he integrated search in macroeconomics and which will be our subject of study in section V. The second is a paper specifically geared to the study of the labor market (Diamond Reference Diamond1982b), wherein Diamond pursued his reflections on the conditions for efficiency.
Efficiency
Once a surplus is formed, the question of its sharing must be tackled, and hence the need to investigate under which conditions (if any) the solution is efficient. The main contributions on these topics are due to Mortensen (Reference Mortensen1982a and Reference Mortensen and McCall1982b) and Diamond (Reference Diamond1982b), building on Mortensen (Reference Mortensen1978) and Diamond and Maskin (Reference Diamond and Maskin1979).
Diamond’s specific concern was unemployment and the labor market. He used the matching function introduced in Diamond and Maskin (Reference Diamond and Maskin1979) in a full-fledged two-sided setting. He also adopted Nash bargaining as a more sophisticated assumption about negotiation: bargaining is used as a proxy for contracting and negotiation issues. Diamond proved the existence of Nash equilibria for all possible sharing rules, and showed that, in the linear matching case, the Nash equilibrium is unique. He also stressed that, in general, the equilibrium wage is inefficient because of its dependency on bargaining power.
As for Mortensen, his idea was to enrich a two-sided search model by adding a matching function and a division of the surplus via Nash bargaining. In such a set-up, the increased recruiting effort of one firm reduces the probability of finding a worker for the others, yet is beneficial to the workers. Similarly, more search effort by workers is beneficial to firms posting vacancies but detrimental to the other workers. Like in Diamond (Reference Diamond1982b), in Mortensen’s models decision makers fail to internalize these costs and benefits. So, there is no reason to expect the equilibrium to be efficient in general.
These results led both Mortensen and Diamond to wonder whether conditions for efficiency could be defined. Mortensen explored particular shapes of the matching function (linear or quadratic), using ball and urn models as microfoundations. For his part, Diamond was able to posit the existence of one sharing rule inducing efficient search incentives in the case of a linear matching function. These efficiency results were further extended by Arthur Hosios (Reference Hosios1990), and centered on one condition commonly referred to as the “Hosios condition.” It can be summarized as follows. The sharing rule to which workers and firms agree must be such that the share of the match surplus accruing to the firm corresponds to the elasticity of the matching technology with respect to recruiting effort (i.e., the parameter weighting the surplus share in the generalized Nash bargaining solution must be equal to the power parameter on vacancies in the matching function).
Job Creation
The next step to be taken for getting strong foundations consisted in figuring out how the relative number of job openings is set. The key contribution, here, was laid out in two papers by Pissarides (Reference Pissarides1984, Reference Pissarides1985). Pissarides’s decisive breakthrough was to abandon the institutional realism of the matching function as it stood in his earlier paper. This move followed from his realizing that in its most simple expression, the matching function constitutes a template of one of the central concepts of economic theory: the production function. Therefore, all that economists had long learned about the production function could be extended to the matching function. In particular, one could consider the inputs of the matching function as assets, exactly as is done in the case of the production function. This brought Pissarides to consider a vacant job as an asset to the firm. It was then natural to make the further step of regarding the financial arbitrage arising in financial markets as also present in this new setting. Given free entry, if opening a vacancy yields a positive value, new vacancies will be posted. In equilibrium, therefore, the value of a vacancy must be zero, and this determines the number of vacancies opened.
Stabilization
The final step was to stabilize the RSB program. It started in Pissarides’s 1987 paper and was fully achieved in Pissarides’s Equilibrium Unemployment Theory (1990). In the book, Pissarides spelled out all the elements present in a piecewise way in the papers mentioned above, using a single thread and unifying notation. The book also revealed Pissarides to Mortensen. While Pissarides was clearly aware of Diamond’s and Mortensen’s contributions, his own earlier work was not cited in Diamond’s or Mortensen’s earlier papers. After the publication of Pissarides’s book, things changed radically:
Although I was aware of and followed his work with interest in these years, only after the publication of the first edition of his book Equilibrium Unemployment in 1990, which fully articulated the first generation of the Diamond Mortensen Pissarides model, did we collaborate in a string of coauthored papers, initiated by “Job Creation and Job Destruction in the Theory of Unemployment,” published in 1994. This paper extended the model in the first edition of his book to include endogenous job separation as well as creation. (Mortensen Reference Mortensen2011, p. 1083)
Mortensen and Pissarides started collaborating on a number of extensions to the model, chief of which was the endogenization of job destruction. Those extensions were incorporated in the second edition of the Pissarides book (2000), further establishing the framework we will describe presently. Until then, and in part because of timing, Diamond and Mortensen were the two leading figures in the field. This changed, with Pissarides taking Diamond’s place as Mortensen’s twin leading figure.
Concluding Remarks
Two points must be retained from this survey. The first is that with respect to Pissarides and Mortensen, Diamond turns out to have been a temporary fellow traveler. He played an important role in setting up the first two steps of the RSB program, yet he participated neither in the third one nor in the stabilization stage. This is why in Figure 1 his name is absent from steps 3 and 4. The underlying reason is that Diamond’s deep objective differed from that of Pissarides and Mortensen. Mortensen’s and Pissarides’s aim was to understand the functioning of the labor market and to explain unemployment using the neoclassical tool box. They were modern labor economists. By contrast, Diamond had a neo-Walrasian background. He wanted to reform neo-Walrasian theory, and his interest in search resulted from the insight that it might be a good alternative to tâtonnement. In the search models discussed above, he was not concerned with the labor market per se. On top of that, he held a Keynesian vision of the economy and wanted to reconstruct Keynesian theory by enriching it with microfoundations and by better capturing what he felt was the central message of the General Theory. In this respect, the findings of his paper with Maskin that inefficiency and multiple equilibria were natural outcomes proved to be invaluable ingredients for his project. Yet, there was still a huge hurdle to overcome. What was needed was to “find the right simplification” (Danthine and De Vroey Reference Danthine and De Vroey2016, p. 3). On a given summer, after much “spinning the wheels,” the coin fell. Diamond realized that, if sticky wages have no role to play in coordination failure, one could as well dispense with including a labor market in the model economy. As he told in his interview:
What I was trying to do with the 1982 paper, and the reason the labor market is modeled as it is, is that I wanted to have a model that would show the basic Keynesian point. When Keynes attacks Pigou, it’s around the view that sticky wages aren’t an adequate explanation of the business cycle, it’s aggregate demand. So, in order to completely show that you don’t need a labor market problem to get something that would be Keynesian, I set up that model with no labor market. (Danthine and De Vroey Reference Danthine and De Vroey2016, p. 3)
At a time where all Keynesians strived at bringing out a malfunctioning of the labor market, this was a stunning yet cunning move.
The second point concerns efficiency. Most RSB economists believed that there was room for state interventions in labor markets (but not of a Keynesian type, Diamond again being the exception). Neither were they bracing themselves to construct models where labor markets function in an efficient way. But they took it to heart to study the conditions under which such a result might occur, and succeeded in eliciting these, as seen above. The RSB model with an efficient equilibrium acted as a theoretical benchmark even if its relevance was deemed limited. However, when economists such as Andolfatto and Merz came to think of integrating unemployment in RBC modeling by exploring the possibility of borrowing from search, the existence of that very model proved to be felicitous. Indeed, in view of the techniques available at the time, integration of a search perspective into RBC modeling required a search model the equilibrium of which was efficient and displayed no ex post heterogeneity in utility. Neither the RSB models that did not satisfy the Hosios conditions nor the directed search with wage posting, or the random search with wage posting models, could do. The RSB was the only search model susceptible to be integrated.
V. INTEGRATING SEARCH IN MACROECONOMICS: THE DIAMOND PATH
Diamond’s paper “Aggregate-Demand Management in Search Equilibrium” (1982a) sealed the success of his project of reconstructing Keynesian macroeconomics on stronger grounds. It was based on the following premises: (a) the concern of Keynesian theory is to explain business cycles as cases of suboptimal resource allocation; (b) wages must be absolved from causing unemployment; and (c) the search hypothesis must be adopted as the trade technology governing exchanges. These premises accepted, one had to start with devising a model inhabited by self-employed workers, for a reason of simplicity.
This paper has been widely praised—quite understandably: we regard it as an example of what neoclassical theory can do at its best, conveying a major insight with a simple yet elegant model. Its basic insights were further expanded in a 1984 book, A Search-Equilibrium Approach to the Micro Foundations of Macroeconomics (Diamond Reference Diamond1984a), based on his 1982 Wicksell lectures. Another development was his “Money in Search Equilibrium” article (Diamond Reference Diamond1984b). There, Diamond extended his 1982a model to encompass money, transforming the model in a full-fledged two-sided search model, and laying out the foundations of a Keynesian microfounded model in which both fiscal and monetary policy can have a role. Finally, a joint paper with Drew Fudenberg (Diamond and Fudenberg Reference Diamond and Fudenberg1989) aimed at fixing up a theory of business fluctuations on the basis of the coconut model. Our attention in what follows will be focused on the 1982a article and the 1984b book, the two other articles being extensions of the basic model.
The Coconut Model
In his paper “Aggregate-Demand Management in Search Equilibrium,” Diamond followed the Phelps/Lucas tradition of referring to the island metaphor. However, while the Phelps/Lucas tradition used this parable to bring out communication problems among many islands, Diamond’s model was about a single tropical island model economy. It comprises a continuum of risk-neutral self-employed identical agents, having coconuts as their exclusive mean of existence. The island is full of coconut trees. All trees have the same number of coconuts, but these are situated at different heights: the effort, expressed as the cost c, required to pick coconuts will vary across trees c. Agents search for trees, and decide whether to climb one and pick coconuts or whether to keep searching for a tree with lower hanging fruits. This simple search setting has a standard solution that takes the form of a reservation cost c*: pick the coconuts whenever the cost is lower than the reservation cost. If this were all there was to the story, the model would have little macroeconomics relevance. Diamond, therefore, spices things up with two additional assumptions. First, agents face a taboo that prevents them from consuming the fruits they picked themselves. This brings in the need to trade. All agents who have coconuts search for a trading partner, and meet one according to a Poisson process. Footnote 9 Terms of trade are trivially equal to one. After having found a partner, agents consume their coconuts and move back looking for trees. Diamond’s second crucial assumption is to assume that the probability of meeting a trade partner is increasing in the number of potential traders. In other words, there are increasing returns to scale in the matching function. “If more people are attempting to trade, it becomes easier to carry out trades” (Diamond Reference Diamond1984, p. 4).
The economy experiences a steady state equilibrium whenever the number of agents who return looking for a tree after having found a trading partner equals that of agents who have found a suitable tree and start searching for a trading partner. Given the increasing-returns-to-scale assumption, the larger the number of traders, the higher the level of activity (and the number of exchanges). But the greater this level, Diamond’s story runs, the higher the cut-off cost: that is, the reservation cost is an increasing function of economic activity. Similarly, assuming a uniform distribution of trees, the higher the reservation cost, the greater the steady state level of activity. Since the cut-off cost is a function of economic activity, and economic activity in steady state is a function of the cut-off cost, finding equilibria amounts to finding fixed points. Graphically, a steady state equilibrium, depicted in the (c*,e) quadrant, is a pair that satisfies at the same time the locus c = c*(e) and the locus ė = 0, both of which are increasing. Provided one is concave and the other is convex, multiple steady state equilibria are present. Diamond proved that it is sufficient for the arrival rate to be increasing and concave in the level of activity to ensure concavity of c*(e). As for the ė = 0 curve, it is convex as long as there is a c* at which the probability of meeting a tree with c ≤ c* is one, and this c* is reached asymptotically. Moreover, assuming that there is a minimum positive cost of picking a coconut ensures that all equilibria are associated with a positive level of activity. The situation is depicted in Figure 2.
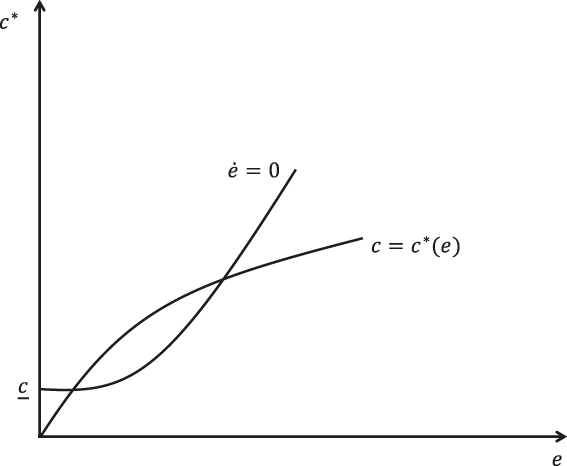
Figure 2. Different Levels of Activity in Diamond’s Search Model.
As shown in Figure 2, Diamond’s model features multiple Pareto-rankable equilibria (in the figure they amount to three, the two intersections plus the origin). Hence, the economy can be stuck in a low-activity equilibrium. Such a situation can be remedied by exogenous demand activation.
“One of the goals for macro policy should be to direct the economy toward the best natural rate (not necessarily the lowest) after any sufficiently large macro shock” (Diamond [Reference Diamond1982a] 1991, p. 32). This reference to macro shocks outlines the fact that Diamond’s ultimate interest was to explain business fluctuations:
The model I will present is a steady state equilibrium model. It has that form primarily for its simplicity. But I am interested in the model as a description of phenomena that are important in the context of a business cycle and must therefore evaluate the appropriateness of the assumptions to an economy that is subject to cycles. (Diamond Reference Diamond1984a, p. 4)
In the 1982a article Diamond offered no explanation of what might explain fluctuations, but in his 1984 book he filled in this lacuna, arguing that they are associated with waves of optimism and pessimism fueled with self-fulfilling prophecies. The underlying idea is that the economy can bounce back and forth along different levels of activity, each an equilibrium, depending on changes in expectations about the future economic environment. Assume that agents are all optimistic; i.e., they expect easier trading. As a result, they will accept more production opportunities. The economy will then reach a higher equilibrium level of activity, thus warranting agents’ initial optimism. The same is true for pessimism. Change in expectations will shift the economy upwards along the c*(e) curve when agents move towards more optimism and downwards in the opposite case. These changes in the economy’s equilibrium points resemble the business cycle.
Diamond and Lucas
Diamond’s search externality paper saw the light of day in a context of high theoretical effervescence. The 1970s were the years in which Lucas launched his fierce attack against Keynesian macroeconomics, proposing to replace it with a totally different approach to macroeconomics. As Lucas had come to be a towering figure, it is appropriate to confront Diamond’s and Lucas’s programs. We will show first that they were methodologically close, and second that Diamond conceived his macroeconomic research agenda as an alternative to Lucas’s.
Diamond and Lucas had much in common. They both placed themselves under the aegis of the Arrow–Debreu model. They shared the same preoccupation of making Walrasian theory amenable for macroeconomic purposes by simplifying it and modifying some of its assumptions. They developed a keener interest for policy matters than traditional Walrasians. Although they both insisted on empirical relevance, their two most important macroeconomic models (Lucas Reference Lucas1972; Diamond Reference Diamond1982a) were theory without measurement. Finally, they both viewed their seminal models, each of which was not directly concerned with business fluctuations, as an apt stepping stone for broaching this topic.
In terms of Leijonhufvud’s metaphor, Diamond and Lucas engaged in a similar backtracking process down to the Marshall–Walras methodological node, and both decided to take the neo-Walrasian route. But they diverged about the further bifurcation to be taken. To comfort his Keynesian vision, Diamond needed to reform neo-Walrasian theory by modifying its trade technology assumption. For his part, Lucas had no qualms with the auctioneer assumption. Footnote 10
These commonalities and differences are summarized in Table 1. Bold characters indicate the differences between the two approaches. The triggering difference relates to the coordination mechanism (or trade technology): tâtonnement in one case, search in the other. Two consequences ensue: first, Lucas’s model has a single equilibrium, Diamond’s multiple equilibria; and second, the policy conclusions reached are opposite.
Table 1. Comparing the Lucas and the Diamond Approaches
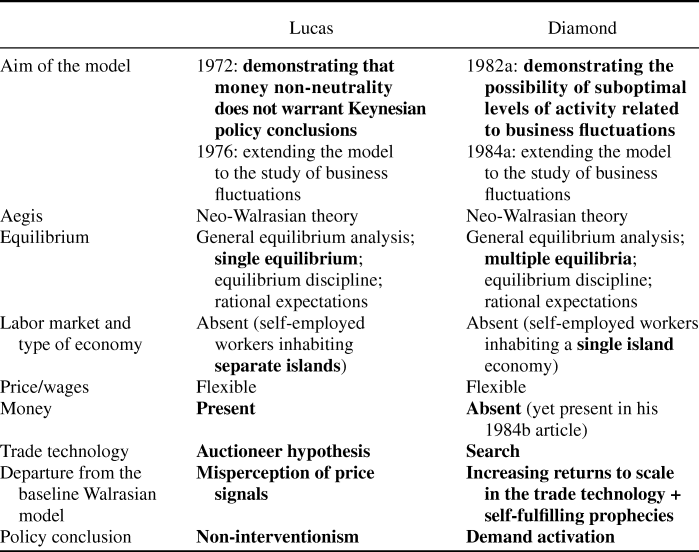
When he conceived his 1982a model, Diamond had the firm intention to react to Lucas’s work, both his equilibrium model of the business cycle and the Lucas/Prescott search model alluded to above. When asked by Moscarini and Wright why he did not take the research path opened by Lucas and Prescott in their 1974 paper, Diamond answered:
The island model, I believe, as Lucas and Prescott set it up, fits the Welfare Theorem of Arrow–Debreu. They’ve got efficiency properties, and I believe the route into seeing that would be to think about it from an Arrow–Debreu perspective where the role of the island is a constraint on your consumption possibility set. There you have the property that I was trying to get away from—there is some central mechanism, something similar to the Walrasian auctioneer, which is controlling the flows between islands in a way that is a central mechanism. (Moscarini and Wright Reference Moscarini and Wright2007, p. 554)
Diamond had no qualms admitting that he pursued a policy motivation. According to him, “[A]t the heart of macroeconomics there is the desire to understand inefficiencies and what can be done about them” (Diamond, in Danthine and De Vroey Reference Danthine and De Vroey2016, p. 5). To this end, the Arrow–Debreu model needed to be simplified and amended. Ideally, the new factor introduced needed to have the status of a compelling ‘fact of life.’ To Diamond, the superiority of the search mechanism was beyond dispute in terms of real-world relevance, and its neglect hardly benign. He also believed that the opposition between thick and thin markets had a strong ‘fact of life’ ring. Taking these features, he claimed, led to the reversal of the policy conclusions of the non-amended model: “The importance of this basically different way of viewing the world is that it shifts the presumption from limitations on policy to the potential for good policy” (Diamond Reference Diamond1984, p. 63).
Diamond’s standpoint could be viewed as having a normative bias. We do not regard it this way. By construction, macroeconomic models lead to policy conclusions. The fact that the model builder has a policy motivation does not matter. Whether Lucas planned it or not, his model of the business cycle reaches a non-interventionist policy conclusion. Thus, Diamond and Lucas must be put on the same footing.
On top of our claim that Diamond was methodologically close to Lucas, we also want to make the further claim that he regarded his model as an alternative to Lucas’s.
De Vroey: “In your Wicksell lectures you seem to have wanted to present a model that would be a rival to Lucas’s model. Is that true?”
Diamond: “I think ’yes’ is the answer. I had long been very aware of Lucas’s work which is so well done, and very aware that my basic perception of the economy and his are different, and yes so there is always very much a sense of intellectual rivalry. (Danthine and De Vroey Reference Danthine and De Vroey2016, p. 5)
The same view comes forth when looking at the question he addresses in his second Wicksell lecture: “How can one decide whether competitive markets or search represents a better starting point for theoretical macro analysis?” (Diamond Reference Diamond1984a, p. 46). There is no mystery about his answer. The whole lecture is to argue for the superiority of the search approach.
Actually, it comes as no surprise that Diamond might have nurtured the ambition of opening a research line alternative to Lucas’s. Diamond’s paper was published in 1982. This means that he must have been working on it in the last years of the 1970s. In their entry “Rational Expectations Business Cycle Models” in the New Palgrave Dictionary of Economics (1987), Michael Dotsey and Robert King consider that four approaches in macroeconomics could be highlighted as being promising research lines. While Diamond’s model was not among these, Dotsey and King’s remark makes clear that, in the late 1970s and early 1980s, the future of macroeconomics was still open.
The Fate of the Diamond Program
In his interview, Diamond acknowledged that his search externality work did not get the momentum he had hoped for and was unable to divert the course of macroeconomics. Footnote 11 The cause must be looked for in the rivalry between Diamond’s and Lucas’s modeling strategies. In such a matter, the decisive factor is whether a new model, which always starts as a one-shot achievement, can be transformed into a progressive, workable research program—“progressive” meaning that it gives rise to a succession of cumulative developments; “workable” meaning that the needed tools and recruits for such developments show up at the right time. Against this criterion, the Lucas program fared better than Diamond’s. Several reasons explain.
From the start, the Lucasian program held the edge. First, it was ten years older and this time span had been usefully employed in strengthening it. Second, Lucas’s Expectation and Neutrality of Money model belonged to a well-established stream of literature pertaining to the real effects of monetary change. The model was innovative, but the subject was well trodden. In contrast, Diamond traveled an unknown territory; the theoretical study of coordination failure was nascent. Third, multiple equilibria may well be an appealing idea, but managing single equilibrium models is definitely easier, not mentioning the conundrum of how to test a multiple equilibria model empirically. This is illustrated in the extension of his model that Diamond did with Fudenberg. In this paper, they ambitioned to demonstrate how, from any initial conditions, one could find multiple dynamic paths to each steady state equilibrium. But, while the paper’s goal seems to be general, in the end it limits itself to an illustration of possible examples. Fourth, Diamond admitted that his model differed from Lucas’s on one main point: the increasing returns assumption. Footnote 12 To him, this element was crucial and justified. In such circumstances, however, an easy way of dismissing a new model consists of declaring that it is a special case of the classical model, hence a mere extension rather than a radical alternative. Footnote 13 Fifth, while Lucas’s Reference Lucas1972 model and Diamond’s 1982a model might have the same degree of persuasiveness, this is not true for their respective extensions. Lucas’s equilibrium model of the business cycle flew from his 1972 model in a straightforward way. This cannot be said of the Diamond–Fudenberg extension of Diamond (Reference Diamond1982a). Finally, Lucas’s non-interventionist policy conclusion had the advantage of neatness. In contrast, Diamond’s policy conclusion—that demand activation should be undertaken for bringing the economy to a higher equilibrium—suffered from the fact that this conclusion fell out of the blue; an agent or institution susceptible of implementing it is absent from the model.
All these factors certainly played a role. Nonetheless, we think that the ultimate clue for understanding the fate of these rival programs resides in the course taken by macroeconomics in the aftermath of the revolution triggered by Lucas. More or less concomitantly with the publication of Diamond’s model, Finn Kydland and Prescott took over from Lucas, inaugurating the RBC variant of the Lucas program. As aptly underlined by Michael Woodford, Kydland and Prescott transformed Lucasian qualitative modeling into quantitative modeling. Footnote 14 The RBC modeling was a game changer. It stabilized the Lucasian revolution into a well-defined empirical research program, providing the bread and the butter for regiments of economists for more than a decade. With such a rule change, Diamond’s model was bound to be marginalized. Footnote 15
VI. INTEGRATING SEARCH IN MACROECONOMICS: THE ANDOLFATTO AND MERZ PATH
The world in which Andolfatto and Merz worked was different from Diamond’s. At the end of the 1980s, the line opened by Lucas had evolved into RBC modeling, and the latter had taken center stage. At stake was no longer the opening of a new research line, as was the case for Diamond, but rather to answer the objection that unemployment was absent from RBC modeling. This was the task that the two economists set themselves and they both were successful in their ways, which differed only mildly.
While a clear success in many aspects, Kydland and Prescott’s inaugural 1982 paper had a hard time replicating labor market facts. For one, in their model, agents’ decisions are made on hours worked. Unemployment and vacancies are left out of the picture. Hence, in no way can the model replicate the negative correlation of unemployment and vacancies. Neither can it replicate the high persistence of unemployment. Disregarding unemployment can be justified on the ground that averages—in the case in which we are concerned, labor total hours worked rather than their distribution—are the main concern of macroeconomics. However, even when accepting this justification, the RBC inaugural model still fared rather badly on a series of other labor market cyclical facts. For instance, the fact that labor market productivity, regarded as a leading indicator of employment, is more volatile than real wages is contrary to the model’s implications. Employment is much more persistent in the data than in the model, not counting that it is also more volatile than real wages. Also, there are indications that the labor share of total income is countercyclical (although relatively stable). The need for improvement on these matters was high on RBC economists’ agenda. An important step forward in this respect occurred when Gary Hansen (Reference Hansen1985) and Richard Rogerson (Reference Rogerson1988) introduced non-convexities in hours, together with the extensive labor margin. In their framework, agents entering the labor market face an employment lottery. The winners work, the losers stay home. Footnote 16 This change improved the model’s performance with respect to the relative volatility of employment to real wages, and introduced the concept of unemployment in the framework. But unemployment, employment, and output were still not persistent enough.
At the time, many advances had been done in the search literature. The first edition of Pissarides’s Equilibrium Unemployment Theory was out, and Mortensen and Pissarides had joined efforts to finalize the mature model. Qualitative evidence coming out of search models—for instance, Wright (Reference Wright1986)—pointed to the very possibility that search frictions could improve the fit of the RBC model. Overall, the gap between the two literatures was nonetheless deep. At the center of the RBC model is the representative agent. This agent receives a real wage as a payment for his work effort, which she decides optimally. All individuals in the economy are paid at the same level. Equilibrium is Pareto efficient, allowing for solving the planner’s problem to find the efficient allocations, then finding the competitive prices that support this allocation as a competitive equilibrium. By contrast, almost all search models were striving at explaining how it is possible for identical workers to be paid differently. They also delivered situations in which equilibrium is, in general, inefficient.
All search models but one: the RSB model. The latter, in its bare bones version, allowed for homogeneous agents to be paid the same wage. In addition, thanks to work by Mortensen and Diamond, later generalized by Hosios, the precise conditions under which the equilibrium is efficient had been elicited.
This was the situation existing before Andolfatto and Merz entered the fray. They must be credited for having succeeded, each in his or her own way, in bridging the RBC and the efficient variant of RSB models. Like the RBC economy, their model economy is inhabited by identical households in the unit interval. They have standard preferences over consumption and leisure, and face a consumption-saving decision problem coming straight out of the RBC framework. However, exchanges of labor occur in a search environment. Individuals are either working or unemployed and searching. In this last case, they get job opportunities at random. Meeting probabilities are determined via an aggregate matching function depending on the numbers of unemployed and vacancies. The labor market is thus laid out in a RSB environment. There are also many firms mastering a constant return to scale technology, so that one can consider each firm to consist in exactly one job. Firms and workers alike incur a cost. Matched pairs face separation with exogenous probability. A next step in the bridging process is to modify the discrete time version of the expressions leading to the Beveridge curve in the RSB into a dynamic equation guiding the employment path. This done, it becomes possible to solve a social welfare maximization problem in which vacancies are added as a choice variable, while adding to the economy-wide constraint an additional constraint stemming from the labor accumulation equation. From this well-behaved problem, one may derive four optimality conditions that must hold in equilibrium (in addition to the resource constraint and the labor accumulation constraint). Two of these conditions are completely standard and govern the intra- and intertemporal allocations of consumption and labor/leisure and the consumption and saving/capital. A third condition ensures that the cost of, and the expected return to, recruiting are equalized at the margin. A final condition ensures that the household is indifferent when facing marginal changes in employment.
While the planner’s solution is perfectly interpretable, it is not obvious that it can be decentralized (as is typically done in the case of a perfectly competitive RBC model). The search economy embodies, after all, a completely decentralized market economy, or, at the very least, one decentralized market in a centralized economy. Typically, one has to show that there exists a price vector that yields the Pareto-optimal allocation. Given that the main difference is the presence of the labor accumulation constraint, two key problems need to be addressed. The first is to find a wage equation such that there is appropriate vacancy posting. The second consists of finding a way to deal with the agents’ heterogeneity as naturally present in models of the labor market with frictions. To solve the first problem, using the standard bargaining assumption, one can turn to the Hosios condition. To solve the second problem, it suffices to assume perfect insurance. This is equivalent, in fact, to using a large family construct, as shown by Hansen and others. Under these assumptions, it is possible to solve the respective problems of firms and workers, and find the wage equation associated with that solution. Thereby the decentralized search equilibrium can be found. Footnote 17
And the job is done: a macroeconomic model is built in which the labor market exhibits frictions, and in which unemployment is naturally present. There is a drawback, however: both unemployed and employed enjoy the same level of utility. In short, there is no inefficiency of unemployment, or a welfare cost. Of course, this feature of the model has a technical reason: the difficulty of introducing heterogeneity in macroeconomic modeling, a difficulty that has largely decreased since then.
The general opinion is that Andolfatto and Merz made a substantive contribution. The fact that the search idea had been integrated in the RBC model was considered good news. Their two models also improved the fit of the baseline model, the decisive assessment criterion in the RBC community.
VII. CONFRONTING THE TWO ATTEMPTS
Technically, Diamond, Andolfatto, and Merz have all achieved their aim of constructing a consistent model integrating search in macroeconomics. In this section, we compare their approaches. Figure 3, an extension of Figure 1, is helpful to make our point. It posits that labor economics and macroeconomics are two different subdisciplines that both happen to have been preoccupied with the topic of unemployment. As stated above, both have witnessed a scientific revolution: from a non-neoclassical to a neoclassical paradigm in one case, from Marshallian to Walrasian macroeconomics in the other. The section at the left of the figure relates to labor economics; that on the right, to macroeconomics. As seen, Diamond participated into the building of the RSB modeling strategy up to and including step 2. He drifted away before the stabilization stage, crossing the border between labor economics and macroeconomics.
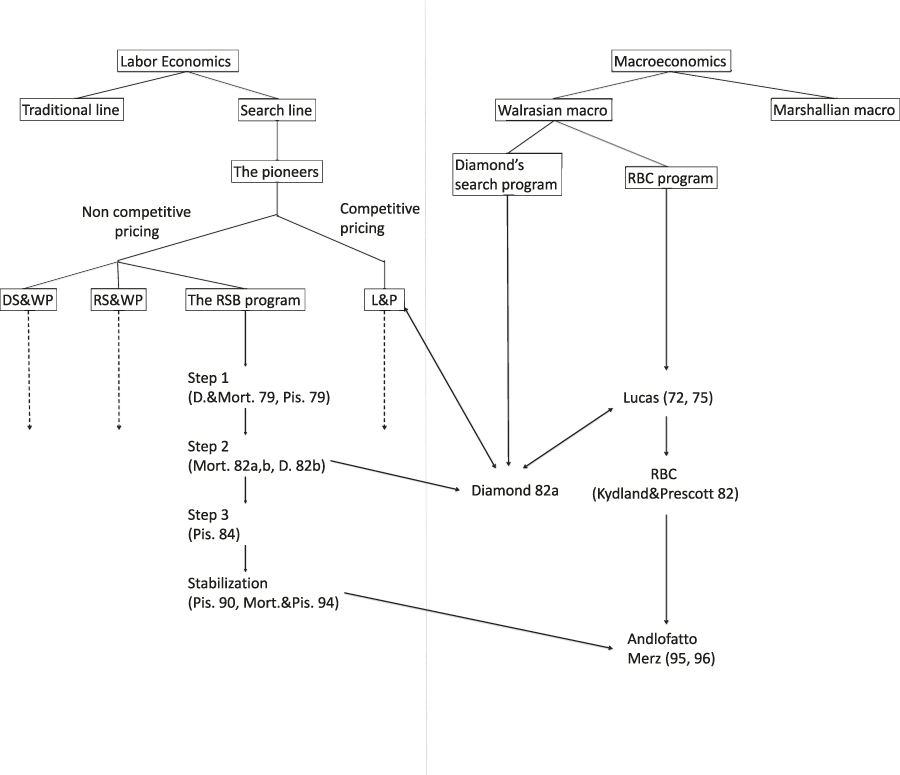
Figure 3. The Complete Decision Tree.
It can be drawn from Figure 3 that the papers by Andolfatto and Merz mark a ‘progress’ (i.e., in the monotonic sense) with the RBC and the RSB modeling branches. However, they do not do so with respect to Diamond’s search externality model for the simple reason that they belong to different branches of the decision tree. For the same reason, they cannot be declared ‘progress’ with respect to the ‘directed search with wage posting’ and the ‘random search with wage posting’ research lines.
We have seen that the Diamond line failed to thrive (at least provisionally), while the Andolfatto and Merz model became a well-established contribution to RBC modeling. Does this mean that Andolfatto and Merz succeeding in doing something that Diamond failed to do successfully? The answer is “no.” Both succeeded in the program they set themselves—but these programs were different. Does it mean that Andolfatto and Merz ‘won’ over Diamond? Again, the answer is “no.” The notion of victory is scarcely used in the history of economics. However, if one finds it useful to speak of scientific revolutions or of rivalry between two distinct bifurcations, it makes sense. A scientific revolution is a victory of one paradigm over another. Here, we are concerned with a bifurcation of a lower level, so the victory in point is of less amplitude, yet the idea is still relevant. Whenever, in the presence of a bifurcation, it can be observed with hindsight that one of them was taken and the other foregone, this can be called a ‘victory’ of the defenders of one bifurcation over those of the other. So, we have a case of a winning and a losing line. However, strictly speaking, the contest was not between Andolfatto and Merz, on one hand, and Diamond, on the other, because their respective modeling strategies cannot be regarded as alternative routes at a given methodological crossroad. While the ‘winner/loser’ characterization make sense in our story, it relates to Lucas’s modeling strategy, of which RBC modeling was the offspring, versus Diamond’s.
VIII. CONCLUDING REMARKS
We have shown that the Diamond model did not fare well, while by contrast the Andolfatto–Merz model did. This is true but it is not the whole story. Economic theory has in common with politics that victories and defeats are rarely definitive. Diamond’s search line may well have petered out but this does not mean that its basic insight has been refuted. To give just one example, Roger Farmer’s recent work (see, for instance, Farmer Reference Farmer2010) can be regarded as a revival of Diamond’s projects.
Similarly, it ought to be realized that Andolfatto and Merz’s integration was not without drawbacks. In a sense, search economists could not be but flattered to have one of their central notions, the matching function, being co-opted by RBC macroeconomists. What took place may be deemed mutually beneficial. Macroeconomists’ gain has been described. For their part, until then, RSB theory had suffered from the drawback of being purely abstract, with little empirical counterpart. Closer contacts between the two communities led RSB economists to realize that they could fill the gap by importing quantitative techniques from RBC modeling.
However, search economists have also some good reason for being frustrated with this integration. First, it concerns only the RSB research stream. The work stream opened by the Kenneth Burdett–Mortensen paper (1998), and which is based on job search, heterogeneity, and wage dispersion, is very active. To many labor economists, it has significant advantages over the RSB line. In present circumstances, its integration in macroeconomics remains out of sight. Second, the integration was possible because of Mortensen’s efficiency result mentioned above. It is true that a case exists where the Nash bargain is efficient, but, to many students of the problem, it is considered an occurrence of minor importance. Without adopting this special assumption, the integration of the matching function in RBC modeling would not have been possible. The third and probably most important reason for frustration is that the basic purpose of search theorists was to understand real-world unemployment. In this respect, the idea of replacing the single agent with a family whose members are able to insure themselves against any loss in utility incurred as the result of being unemployed cannot be considered otherwise than as a trick. As such, it betrays the motivation that led to the labor-search theory, not only the view that the unemployed effectively suffer in utility because of their status, but also the idea that their fate can be improved upon by some governmental interventions.






