Published online by Cambridge University Press: 01 October 2004
The 70-year anniversary of the first nuclear fusion reaction of hydrogen isotopes by Oliphant, Harteck, and Rutherford is an opportunity to realize how beam fusion is the path for energy production, including both branches, the magnetic confinement fusion and the inertial fusion energy (IFE). It is intriguing that Oliphant's basic concept for igniting controlled fusion reactions by beams has made a comeback even for magnetic confinement plasma, after this beam fusion concept was revealed by the basically nonlinear processes of the well-known alternative of inertial confinement fusion using laser or particle beams. After reviewing the main streams of both directions some results are reported—as an example of possible alternatives—about how experiments with skin layer interaction and avoiding relativistic self-focusing of clean PW–ps laser pulses for IFE may possibly lead to a simplified fusion reactor scheme without the need for special compression of solid deuterium–tritium fuel.
The very first nuclear fusion reaction (Oliphant et al., 1934) used the 100-kV powerful gas discharge developed by Mark Oliphant, the heavy water for the deuterium was produced by Paul Harteck, and the analysis of the cloud chamber pictures by Lord Rutherford was especially difficult because the unknown superheavy hydrogen isotope tritium T = 3H appeared, resulting itself in nuclear reactions as well that of the resulting light helium isotope 3He:
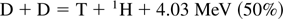
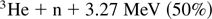
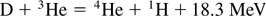
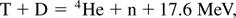
producing protons p = 1H, neutrons n, and the usual helium isotope 4He. The tritium reaction (2b) has an extraordinary large reaction cross section and is mostly discussed in the following, though the neutron lean reaction (2b) is now of special interest in view of harvesting the huge amounts of 3He as fusion fuel from the surface of the moon when the moon station may be ready in 2020.
The following will reflect some initial experiments of Oliphant (1972) especially in the direction of fusion reactions using beams and how these may be considered now 70 years after the first fusion reaction (Oliphant et al., 1934). The development went first against the initial concept of beam fusion in favor of avoiding any beams and going only into the direction of magnetic confinement fusion. The following is an analysis of how this aspect has changed toward the initial view of Oliphant for beam fusion. This is not only a question of inertial fusion energy (IFE) without magnetic fields as known from laser or particle beam driven fusion reactions. Even the initial magnetic fusion concept has developed into a beam fusion scheme during the last years as will be explained in the following.
First attempts to develop the reaction into an energy source were done by Oliphant (1972) in 1937 and a continuation of a controlled reaction for power production was considered in about 1950 after uncontrolled nuclear explosions succeeded by nuclear fission. The studies of fusion reactions for energy production were a continuation of the work of 1937 under the leadership of Nobel Laureate E.O. Lawrence together with Oliphant and other important pioneers. The aim was just to produce extremely intense deuterium or D-T beams from gas discharges or otherwise, with about 100 keV of energy, to irradiate targets containing D or D-T. These attempts were radically rejected by Spitzer (1957) who argued that such beam experiments do well result in fusion reactions as measured (Oliphant et al., 1934), but it is absolutely impossible to produce more energy by fusion than is put in for the beams. Lawrence and the others simply argued that one just has to apply higher and higher beam powers, but this was made ridiculous by Spitzer's numbers, that the fusion cross section is more than 300 times smaller for the incident 100 MeV nuclei than their interaction with the electrons in the bombarded target. The ion energy goes mostly into heating of the electrons in the target, never permitting an exothermal fusion reaction.
Spitzer's argument was mathematically simple, and physically and logically fully clear, and it led to the decision that instead of bombarding a cold target, one has to heat the reacting particles all—as in the sun—up to the plasma state of a temperature of dozens of millions of degrees such that ions do not lose their energy by collisions with electrons and the desired fusion reactions can take place. The problem was then how to confine the plasma by magnetic fields and to find conditions where the loss of radiation energy and confinement mechanisms from the hot plasma are more than compensated by the generation of fusion energy.
Following Spitzer's argument, the handling of the fusion plasma with magnetic confinement is at a stage that a test reactor ITER is going to be built by 2015, which may lead to a power station for 4 GW fusion energy output by 2040 (Hoang & Jacquinot, 2004). This all is based on expensive research during the last 50 years where the highest fusion gain of 16 MW was reached in the JET experiment in Culham/England, however, mainly as a beam fusion experiment (Hora, 1987; Hora et al., 1998) well fulfilling Spitzer's argument that the irradiated target had not the problems with the low temperature electrons. In this wider sense we can say that this is the sophisticated verification of Oliphant's beam fusion by the way of a “Spitzer option” for fusion energy. It should be underlined that the concept of the neutral beam irradiation was introduced by Harold Furth based on his “idea of exploiting fusion reactions that arise from injected energetic ions” (Fisch et al., 2004), not without reflecting that Furth was the nephew of Paul Harteck, the coauthor of the first measurement for fusion reactions (Oliphant et al., 1934). (See Note Added in Proofs.)
But there is another reason that Spitzer's argument can be completely invalid. It is linear physics. In nonlinear physics, results from linear physics can completely change from no to yes, from right to wrong, and so forth, as experienced also in clear cases with other physics problems (Hora, 2000). Nonlinear physics does indeed permit beam fusion in contrast to the Spitzer argument, as initiated by Oliphant (1972) in 1937 and aimed at by Lawrence and others, especially since the laser opened the door to the nonlinear physics for fusion energy (Tanaka et al., 2001). This perhaps may be considered as a further confirmation of the comeback of beam fusion envisaged by Oliphant and will be discussed in the following as the “Non-Spitzer” option.
Magnetic confinement of plasma is mostly focused on toroidal geometries. Spitzer's initial eight-like magnetic stellarator configuration, built at comparably high costs, was simplified into a toroidal configuration and the early problems of generating such a very low current stellarator plasma were overcome by the success of Grieger et al. (1981), where an 800-eV deuterium plasma produced fusion neutrons. The diffusion of the plasma against the confining magnetic field due to collisions was about 20 times faster than classical collisions predicted. This could directly be explained as quantum correction to the collisions for the anomalous resistivity because the factor 20 did immediately fit the change at a temperature above 37 eV by a linear temperature factor (Hora, 1981). This experiment had the advantage of transparent measurements as can be seen from the mentioned factor 20. There is a modification of the classical electron ion collision frequency νclass which is valid only below the temperature T* = Z2(4/3)mc2α2 = 36.8 Z2 eV (using the ion charge Z) as shown by Marshak (1941) and generalized later (Hora, 1981; see Hora, 1991, Chap. 2.6) where above this temperature T* the quantum mechanical value has to be taken:
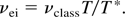
This is the modification of the diffusion of the plasma across the magnetic field whose results were confirmed by Grieger et al. (1981) arriving at the factor ∼20 by dividing 800 eV/T* = 21.7.
In contrast to this zero-current toroidal magnetic confinement stellarator, a toroidal confinement with a very high axial electric current, driven inductively like in a transformer for heating the plasma, was developed as tokamak (Hoang & Jacquinot, 2004). This most advanced scheme is used in the International Toroidal Experimental Reactor (ITER) at a cost of $US10 billion to be operating in 2015. The confidence for this decision is based on the recent achievements with tokamaks (Hoang & Jacquinot, 2004). It is envisaged that the then following test power station may be finished in 2040, if no unforseen difficulties appear where wall erosion or blistering from the walls or anomalous ion implantation was mentioned (Hoang & Jacquinot, 2004). These time scales agree with what Maisonier (1994), the director for the very large European budget for magnetic confinement fusion research, formulated in 1993 that this development “will need at least 50 years … and it is not sure whether the produced energy will be of sufficiently low cost.”
The high achievements of tokamak developments was seen (Hoang & Jacquinot, 2004) from the fact that its performance doubled every 1.8 years, compared with that of the transistor and chip technology every 2 years, and that of the particle accelerators every 3 years. Nevertheless the objection for operating the tokamak completely as a magnetic confinement device by inductive heating has not succeeded yet over more than about one second. The operation of the advanced tokamaks with superconducting coils with external heating by neutral beams and RF electromagnetic irradiation was possible over 1000 s in the biggest such experiment, the Tore Supra at Cadarache/France, or with a smaller Japanese device with 100 times lower input power over 3 h. The maximum neutral beam density for driving the tokamak is limited by the Langmuir–Child space charge law for ion beam generation to less than 10 mA/cm2 in contrast to the measured many orders of magnitudes higher ion emission current densities emitted from targets by laser irradiation (Laska et al., 2003; Wolowski et al., 2003).
The highest nuclear fusion gains measured (Hora et al., 1998; Hoang & Jacquinot, 2004) by the Joint European Torus JET were the mentioned 16 MW fusion energy power, produced by 21 MW deuterium neutral beams of 60 keV energy and by irradiation of 3 MW RF power at filling the tokamak with D-T in the ratio 40:60 (Hoang & Jacquinot, 2004). This 66% gain, close to break-even, does not take into account the power needed to operate the tokamak, which may be permitted in view of the fact that instead of the very high power consumption of the tokamak coils, superconducting magnets could have been used with considerably lower power but with losses for cooling of the magnets and limiter and so on. It is important to underline that the operation of JET without the beam injection as a purely magnetic confinement device results in very much lower fusion reaction gains.
Coming back to the initial question about Oliphant's view on beam fusion, we see that the highest gain fusion of the JET is a clear (neutral) beam fusion experiment, however, irradiating a target which fulfills the linear physics conditions of the Spitzer option to use not a solid-state target but such a sophisticated high temperature tokamak plasma. In this case, as postulated by Spitzer, collisions between the irradiated ion beam and the target electrons do not take away much of the main ion beam energy (Hora et al., 1998).
A higher gain above break-even could have been expected if the number of ion beam injectors would have been multiplied. Further improvements may be expected if the detection of the inward particle flux as observed at the Tore Supra could be analyzed perhaps as caused by ExB-net plasma rotation (Goldsworthy et al., 1987; Hora, 1991, see p. 171) or the reduced thermal conduction due to the anomalous resistivity (Hora, 1981; Hora, 1991, see p. 50). In view of the problems of the wall erosion in tokamaks mainly due to disruption instability, one may consider a neutral beam fusion device where instead of the tokamak target, a stellarator is being used and the disruptions are excluded (Wobig, 2002).
We refer now to beam fusion where the nonlinearities are overcoming the Spitzer criteria. The idea was obvious in 1960 after the discovery of the laser that this can be used for producing extremely high energy densities within very short times in very small volumes as needed for controlled ignition of nuclear fusion reactions. The pioneers of large-scale fusion reactions such as Edward Teller (2001), John Nuckolls (1992), and Andrei Sakharov (1982) immediately devoted attention to this concept. Particle beam fusion—fully excluded under the aspects of the Spitzer criteria—was revoked in view of the nonlinearity, too. Spitzer's argument keeps its full validity as long as the beam-irradiated target remains solid. But if the beam intensity creates plasma with a very complex hydrodynamic development, dynamics of pressure profiles, and radiation effects, exothermic energy production can be expected by laser-driven fusion or from igniting self-sustained fusion reaction fronts by an intense electron beam (Yonas, 1978), or by light or heavy ion beams working through solid fusion fuel. The laser fusion concept has been well developed since, but the new developments with picosecond laser pulses may permit us to return to several earlier arguments for ion beam fusion.
When estimating the necessary conditions for igniting a self-sustained fusion detonation front in uncompressed solid DT by impact of a DT ion beam, a minimum ion beam density of
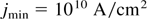
was given (Brueckner & Jorna, 1974) which may be too pessimistic and a lower value may be possible. A further condition is that the energy density of the hot detonation front should be at least (Bobin, 1971)
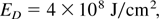
which value may be decreased by a factor of 20 or more when the interpenetration processes are included (Hora, 1983). These conditions are far above the available electron or ion beam technology for igniting solid state DT. With the laser, however, these conditions have been achieved experimentally—at least in principle—as will be explained in the following section.
A further improvement for igniting beam-irradiated DT fuel is its compression above the solid density. This can be achieved with the irradiating laser or particle beam itself by producing an ablation of fuel from the irradiated surface, which results in a compression of the interior as a recoil. At spherical geometry the compressed core of a maximum density n0 volume V0s (s denotes that this is the volume of the uncompressed solid fuel with a density ns) receives an energy E0 which may be assumed to be uniformly spread over the core volume. The adiabatic compression and expansion of the core, confined only by its inertia (inertial confinement fusion, ICF) following the self-similarity model (Hora, 1991, see Sect. 5) results in a DT fusion core gain G at an optimum temperature Topt = 17 keV at maximum compression:
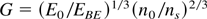
(Hora, 1991; Hora et al., 1998; identical to the ρR-value, see p. 336 of Hora, 1991) where EEB is the break-even energy, which is 6.3 MJ for DT. This result, based on the numerical values of the fusion cross sections, shows immediately how a compression to 1000 times the solid density ns requires a million times less core energy E0 for reaching the same gain G.
Formula (6) does not include the fuel depletion, the partial reabsorption of the lost bremsstrahlung, and the gain of temperature by the fusion products before leaving the reacting plasma (self-heat). When including this (Hora et al., 1998), the result in Figure 1 is very close to the result (6), where for constant core volume a standard isochor touches the optimized fusion gain plots at Topt if the gain is less than 8. For higher gains, the isochors are deformed, showing volume ignition (Hora & Ray, 1978) with increased gains and lower optimum temperatures (bending of the vertical dashed lines to the left). It is remarkable that the measured highest gains at direct drive laser fusion spheres fully agree with these isentropic self-similary computations (Fig. 1), indeed below ignition as simple volume fusion burn or quenching.

Optimized core fusion gains G (full lines) for the three-dimensional self-similarity hydrodynamic volume compression of simple burn (G < 8; sometimes called quenching) and volume ignition for G > 8 with low temperature ignition above LTI line. The measurements (see Ref. 5 of Rochester (Soures et al., 1996, point A), Osaka (Takabe et al., 1988, point B), Livermore (Storm, 1986, point C), and Arzamas-16 (Kochemasov, 1996, point D) agree with the isentropic volume burn model, whereas the earlier fast pusher (Kitagawa, 1984, point E) with strong entropy-producing shocks does not fit (Hora et al., 1998).
In contrast to this volume burn with the rather low gains, the scheme of spark ignition was introduced since the end of the 1960s (Nuckolls, 1992) to produce very much higher gains than by a simple burn, before volume ignition was discovered (Hora & Ray, 1978; Hora et al., 1998), which could reach nearly the same high gains in a much more natural method of adiabatic compression. The spark ignition is rather complicated. It tries to schedule the compression in a very sophisticated way, especially when, instead of direct laser drive, indirect drive by hohlraum X-radiation is used. The laser irradiates the inner walls of a capsule to convert the radiation into X rays, which then produces a very symmetric compression of the fuel pellet within the capsule. The aim is that the compressed pellet has a low-density, high-temperature central spark plasma surrounded isobaric by a very high-density, low-temperature outer part. At the interface, the hot plasma ignites a spherical fusion detonation wave into the cold outer plasma with similar conditions as given by Eqs. (4) and (5) only with higher densities.
Summarizing experiments, the highest laser fusion gains by spherical irradiation were 2 × 1014 DT neutrons from a 35-kJ neodymium glass laser pulse unexpectedly following the exact adiabatic volume compression (Fig. 1; Hora et al., 1998), while the best gains from hohlraums were about 1000 times lower. If one assumed that only 5% of the 35 kJ energy went into compressed cores (95% to the ablation because of bad hydrodyamic efficiency), the fusion gain is then 31%.
For better studying these mechanisms both for the aim of a fusion energy source and also for the aim of large-scale fusion reactions, glass laser facilities for producing pulses of a few megajoules energy with about nanosecond duration are being built, the NIF in Livermore, California and the LMJ in Bordeaux, France (Pellat, 2002; Tarter, 2002). The aim is to demonstrate ignition with a modest total fusion gain not much above 10 by about 2010.
One of the problems experienced by the experiments was the too low heating of the laser-compressed plasma. Azechi et al. (1991) succeeded in laser-compressing polyethylene to 2000 times the solid density thanks to Kato's laser beam smoothing with random phase plates where, however, the maximum temperature of about 300 eV was unexpectedly low. For very large scale laser fusion using a few megajoule laser pulses including smoothing for working with long wavelengths this should not be too problematic if volume ignition is used for direct drive and not spark ignition. It has been evaluated (Hora et al., 2003a) that by doubling the compression density, volume ignition will reach the range where the bremsstrahlung reabsorption results in ignition temperatures of a few hundred electron volts only. This would be sufficient for a one-step laser fusion reactor based on the robust adiabatic volume compression, as it was successful with the hitherto highest laser fusion gains, avoiding the problems of spark ignition. This would at least be a conservative solution for laser fusion based on well-settled present-day technology (Hora et al., 2003a). Much research is aimed at spark ignition (Lindl, 1994), where the fusion efficiency may be two times higher than with the just mentioned volume ignition concept (Hora et al., 1998) but where the problems with compression symmetry and instabilities are much more difficult than in the case of volume ignition.
The scenario for laser fusion changed dramatically with the chirped pulse amplification (CPA) discovered by Mourou (Perry & Mourou, 1994; Mourou & Tajima, 2002). This led to the generation of pulses with neodymium glass or Ti:sapphire (or next iodine) lasers of pulses in the range of picoseconds or less duration and powers exceeding 2 PW. Irradiating targets with these pulses results in numerous not yet fully explored relativistic effects, such as very intense gammas in the 10-MeV range causing nuclear transmutations (Ledingham et al., 2000), for example, with elimination of long-lived nuclear waste (Magill et al., 2003), producing ions of more than 0.5 GeV energy (Clark et al., 2001), or intense 5-MeV proton beams (Roth et al., 2000, 2001) with the possibility of an easy generation of laser spark ignition in indirectly driven fusion pellets, or electron acceleration to more than 100 MeV energy (Hora et al., 2000).
For laser fusion, Mike Campbell had the immediate proposal (Campbell et al., 2000) after Azechi et al. (1991) had measured the 2000 times solid compression but too low temperature of 300 eV by nanosecond laser pulses, that an additional ps-PW pulse may heat the center of compressed DT for spark ignition. This fast ignitor (Tabak et al., 1994) preliminarily led to the generation of nearly 108 fusion neutrons (Kodama et al., 2002). The study of this fast ignition (FI) scheme is now one of the broad streams in laser fusion research. There were numerous new phenomena observed that deserve much more detailed studies and may each lead to one or more modifications of the laser fusion application. As one possible alternative example, one of these phenomena will be considered here in a some detail.
One of the numerous unexpected observations was that the ions emitted with very clean TW-ps laser pulses, having a suppression of any prepulse by a factor 108 (contrast ratio), resulted in drastically low energies. The emitted ions in this special case (Badziak et al., 1999) had maximum energies of 450 keV whereas 22 MeV energy was expected under the usual conditions after relativistic self-focusing. A similar observation was the low X-ray emission from targets at irradiation with comparable subpicosecond intense laser pulses of similar high contrast ratio (Zhang et al., 1998). Only when a prepulse was irradiated at least 70 ps before the main pulse was the X-ray emission as usual. The explanation was very straightforward: With clean pulses, there was no relativistic self-focusing possible; only when 70 ps earlier a prepulse was incident was the necessary plasma in front of the target produced for relativistic self-focusing (Fig. 2; Hora & Wang, 2001), leading to the very high laser intensities in the filament for the high X-ray emission. The same happens for the ion emission (Hora et al., 2002a) when the high contrast ratio prevents relativistic self-focusing (Hora et al., 2004), resulting then in the conditions of plane wave interaction geometry within the skin depth of the plasma. Details of this evaluation led to a splendid agreement between ion energies, quiver motion for X-ray emission, and a dielectric swelling (some authors now call this long-known dielectric phenomenon (Hora, 1991) very wrongly “amplification”) by a factor of 3.5 (Hora et al., 2004).

Scheme for demonstration of the essential different geometry of the laser–plasma interaction volumes for subsequent volume-force nonlinear electron acceleration with separation by the ion charge Z. In case a, the pregenerated plasma before the target causes instantaneous relativistic self-focusing of the laser beam to shrink to less than a wavelength diameter with very high nonlinear force acceleration due to the strong gradient of the laser field density (Hora, 1991, see Sect. 12.2). In case b, the nearly not present or too thin plasma in front of the target permits only interaction in the skin depth with much lower ion energies but nearly ideal plasma geometry conditions as treated before (Hora, 1991, see Sect. 10.3).
The plane geometry laser field interaction with plasma for a few picoseconds duration (Fig. 3) was studied numerically with more comfortable initial plasma distributions (Hora, 1991, see Sect. 10.5) than in the experiment where at least the basic mechanisms could be followed up. The laser energy goes nearly collisionless by the nonlinear (ponderomotive) force (Hora, 1991) into kinetic energy of a block of plasma moving against the laser light and another block moving into the plasma interior. For this plane geometry, the general nonlinear force (Hora, 1991, 2000) can be expressed with the electrical and magnetic amplitudes of the laser field EL and HL by the ponderomotive force with the plasma refractive index n
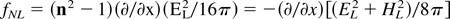
where the second expression denotes the force density as a negative gradient of the electromagnetic energy density. The velocity for deuterium plasma (Fig. 3) reaches velocities up to 109 cm/s and more at 1018 W/cm2 neodymium glass laser intensity within a block of more than 15 wavelengths thickness. An advanced computation (Fig. 4) closer to the experimental conditions (Badziak et al., 1999; Hora et al., 2002a) reproduced this block motion in all details with numbers as expected from global calculations and the experiments.

Generation of blocks of deuterium plasma moving against the neodymium glass laser light (positive velocities to the right) and moving into the plasma interior (negative velocities) at irradiation by a neodymium glass laser of 1018 W/cm2 intensity onto an initially 100-eV hot and 100-μm-thick bi-Rayleigh profile (Hora, 1991, Fig. 10.17) with minimum internal reflection. The electromagnetic energy density (E2 + H2)/(8π) corresponding to the intensity is shown at the same time of 1.5 ps after the beginning of the constant irradiation.

Ion velocity profiles at the times 2, 4, 5, and 6 ps taken from genuine two-fluid computations for a 3 × 1015 W/cm2, 4-ps rectangular laser pulse irradiating a deuterium plasma ramp of 20 μm thickness with critical density at 12 μm, confirming the generation of an ablating plasma block (negative velocity) and a compressing plasma block (positive velocity) (Cang et al., 2004).
The DT ions in such nonlinear-force driven plasma blocks have ion current densities at or above 1010 A/cm2 (Badziak et al., 2003; Hora, 2003). These fast ions are emitted within very narrow angles against and with the laser light in total contrast to the wide angles for fast ions emitted after relativistic self-focusing (Badziak et al., 2003). The property of the accelerated space charge neutral high density blocks with no strong surrounding magnetic fields underlines also the basic difference of the high current density 5 MeV ions (Roth et al., 2001) from PW laser irradiation of plasmas where relativistic self-focusing led to a decrease of the ion density in the focus (Hora, 1975; Jones et al., 1982; Häuser et al., 1992) and magnetic fields were generated (Pukhov & Meyer-ter-Vehn, 1996) such that the ion beams are not space-charge neutralized. In this case the ions follow a free electron acceleration process with a conical emission (Hora et al., 2000a) in agreement with the measurements of Umstadter (1996). The fact that the space-charge-neutral, highly collimated, subrelativisitc ion current densities of more than 1010 W/cm2 (Badziak et al., 2003) can be expected for 80-keV deuterium and/or tritium ion energy permits the conclusion that the condition of Eq. (4) is fulfilled and that these ions may ignite a self-sustained fusion reaction front in uncompressed solid density DT if condition (5) could be fulfilled simultaneously.
It is important to underline that the generation of laser-accelerated blocks was measured even before the results of Badziak et al. (1999) led to the detailed conclusion of the skin layer interaction (Hora et al., 2002a, 2002b; Badziak et al., 2003; Hora, 2003; Osman et al., 2004). This was detected and analyzed from the backscattered spectra and the red or blue shift at laser irradiation of targets with 100-fs TW laser pulses (Sauerbrey, 1996). Though the considerations begin with the obsolete argument of ion acoustic wave velocity, Sauerbrey (1996) is well acknowledging the action of the nonlinear (ponderomotive) force as was done in related experiments (Kalashnikov et al., 1994) and studied in these connections (Schmutzer & Wilhelmi, 1977). It is especially encouraging that the nonlinear force acceleration of plasma layers to blocks moving against and with the laser light was well recognized (Sauerbrey, 1996). Experiments confirmed an acceleration in the deuterium blocks of 1017 g (g is the earth acceleration) which was seen also in the computations of Figure 3, where 10-μm-thick deuterium bocks of 1021 ions/cm3 density received an acceleration of 1018 g (see then a discussion of how laser acceleration may reach that of the surface of black holes with 1029 g in Hora et al., 2002d). Because the energy transfer to the blocks as a kind of collisionless nonlinear absorption is well known and may even turn out to be one of the rare analytical solutions of an integral equation (Batchelor & Stening, 1985), this method was proposed by C.V. Shank (pers. comm.) for measuring the pulse lengths and energy transfer of subpicosecond laser pulses.
The remaining question is how the energy flux density for generating a reaction front (flame propagation) into uncompressed solid DT can be fulfilled as derived theoretically (Bobin, 1971; Chu, 1972) to be above the threshold of Eq. (5). Even more pessimistic higher thresholds E* were considered, which, however, may be upper bounds only as long as the very extensive details for the derivation of the threshold (5) are not found to be incorrect.
It may be possible that the value (5) is too pessimistic, as there were indications from the theory about how the interpenetration of the igniting energetic ions into the cold uncompressed DT fuel may reduce the threshold E* to (Hora, 1983)
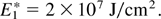
How unexplored these beam fusion conditions are may be seen from the experiments (Kerns et al., 1972; Guenther, pers. comm.) where 2-MeV electrons of an estimated current density of 3 × 106 A/cm2 interacting with a CD2 target showed a penetration of 0.3 cm only. The single electron penetration would have been more than 40 times longer. The disagreement with the Bethe–Bloch–Bohr binary collision theory for the stopping length could be clarified by applying the collective interaction process that fully reproduces the measured 0.3 cm (Bagge & Hora, 1974). The collective interaction was initially studied by Gabor (1953) and based on the independently derived theory (Ray & Hora, 1977) for the successful explanation (Bagge & Hora, 1974) of the experiments (Kerns et al., 1972; Guenther, pers. comm.). Such a reduction of the collective stopping length combines with the not yet applied anomalous plasma resistivity (Hora, 1991, see Sect. 2.6), and electric double layer effects with reduced thermal conductivity (Eliezer & Hora, 1989) point into the further decrease of the threshold (8).
Thanks to the recent results on interaction of clean TW-ps laser pulses it was possible to show experimentally (Badziak et al., 2003), that the rather extremely high threshold j*, Eq. (4), for ion beam fusion has been fulfilled (Hora et al., 2004). The skin layer interaction mechanism accelerates a plasma layer or block initially of 30 wavelengths width and several vacuum wavelengths thickness with a critical density of 1021 electrons/cm3 highly directed against the laser light whose velocity from 20 keV/nucleon at 8 × 1016 W/cm2 intensity could be understood in the case of a DT plasma to be 1.23 × 108 cm/s. This results in a block motion with an ion current density at the target of 1.9 × 1010 A/cm2. Together with this block moving against the laser light, measurements with thin foils confirmed the generation of a similar block moving into the target with similar energy and ion current density. This result can be related to earlier plane geometry detailed hydrodynamic computations (Fig. 2).
From this result it was concluded that the compressing block may be used as requested for light ion beam fusion for a power station. A 10-kJ laser pulse could then produce 100 MJ fusion energy where the exclusivity for use for the controlled reaction was confirmed by a declassification procedure by the authorities involved (Hora, 2002).
For the physics—within many more problems to be clarified—it has to be shown that at least condition (5) has to be fulfilled where we are aware that this even may be considered as a pessimistic conclusion in view of the not-yet-exhausted theory about the threshold E* toward lower values. For the compressing block, the whole maximum quiver energy of the electron is converted into translation energy of the ions. The DT interaction, we use the oscillation energy of 80 keV of the resonance maximum of the DT reaction may not necessarily be the best choice. Because this is close to the (Hora, 1991) relativistic threshold intensity Irel we have to use the general case
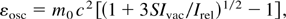
where the maximum intensity Imax = SIvac due to the dielectric swelling near the critical density is expressed by the factor S with the laser intensity Ivac in vacuum at the target surface.
For the general analysis we have to be flexible about the chosen values of the applied maximum (dielectrically swelled) oscillation energy εosc into the translation DT ion energy εtrans in adjustment to fusion cross sections. We further leave open the value of the energy flux density E* = Ivac tL for reaction conditions (5) or (8) or possibly even a lower value depending on the future research to find the correct value E* where the laser pulse duration tL will have to be in the range of picoseconds. According to extensive numerical studies (Cang et al., 2004) in agreement with summarizing estimations, this value could well be a few picoseconds. From relations (5) or (8) and
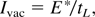
we arrive at the function for the laser wavelength
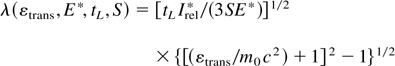
Using as a special case tL = 3ps, E* = 2 × 107 J/cm2, εtrans = 80 keV, we find
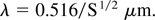
The nonlinear, force-driven, two-block skin layer interaction model works for swelling S considerably larger than 1, as was the case automatically from the detailed analysis of the measurements (Hora et al., 2002b; Hora, 2003; Cang et al., 2004) with S = 3. The lowest possible case with S = 1 is that without any dielectric swelling, where the whole laser pulse energy is transferred as in the simple case of radiation pressure (Hora, 1991) to the absorbing plasma. We conclude that the conditions of the kind of (5) or (8) could well be fulfilled for the ignition of uncompressed solid DT fuel when applying a shorter laser wavelength than that of the neodymium glass laser and is well within the reach of present technology as seen from the excimer lasers (Teubner et al., 1993). For the pessimistic case of Bobin (1971) and Chu (1972), the numerical factor in (12) is 0.105 such that with S = 1, just the borderline of higher harmonics CPA excimer lasers (Teubner et al., 1993) would be covered. Further research on lower values of E* and numerical studies for a little bit longer laser pulses may further relax the conditions, and longer laser wavelengths would be possible. No discrepancy was found in the detailed analysis (Bobin, 1971; Chu, 1972) when followed up recently (Kishony & Shvarts, 2001). Figure 5 shows the dependence of the necessary laser wavelength for a pulse length of 3 ps and swelling S = 1, which one needs for a desired ion translative energy in multiples of m0 c2 (m0 is the rest mass of the electron) if the threshold E* is given.

Relation between the laser wavelength the aimed ion energy εtrans in multiples of m0 c2 and the necessary energy flux density for ignition of uncompressed DT following Eq. (22) for S = 1 and a laser pulse length of 3 ps.
The gain for a controlled reaction has been estimated to be of a high value. A 10-kJ ps laser pulse may result in 100 MJ fusion energy (Hora et al., 2004). From the block ignition of solid DT without compression there may perhaps be the possibility for a neutron lean reaction leading to direct conversion of the nuclear energy of the charged reaction products into electricity (Hora, 2002; Hora et al., 2003b).
The author gratefully acknowledges the cooperation with his coauthors in Hora et al. (2004), especially J. Badziak, Y. Cang, Acad. X. He, Acad. K. Jungwirth, G.H. Miley, F. Osman, H. Peng, K. Rohlena, Z. Weiyan, and J. Zhang. This article is an elaboration of a lecture presented for commemoration of the merit of Professor Sir Mark Oliphant, (1901–2000) FRS and her Royal Majesty's Queen Elizabeth II Governor of South Australia (1971–1976), organized by the Australian Physical Society at the University of New South Wales in Sydney.
Prof. Minh Quang Tran (Garching and Lausanne) represented nuclear fusion to the World Energy Conference in Sydney, Australia and delivered a lecture at the Sydney University on September 8, 2004 promoting ITER. The design is that ITER in 2015 in a 500 second pulse should produce 500 MW thermal energy where an operational input of 500 MW electric energy is necessary resulting in a total gain of 0.2 or less.

Optimized core fusion gains G (full lines) for the three-dimensional self-similarity hydrodynamic volume compression of simple burn (G < 8; sometimes called quenching) and volume ignition for G > 8 with low temperature ignition above LTI line. The measurements (see Ref. 5 of Rochester (Soures et al., 1996, point A), Osaka (Takabe et al., 1988, point B), Livermore (Storm, 1986, point C), and Arzamas-16 (Kochemasov, 1996, point D) agree with the isentropic volume burn model, whereas the earlier fast pusher (Kitagawa, 1984, point E) with strong entropy-producing shocks does not fit (Hora et al., 1998).

Scheme for demonstration of the essential different geometry of the laser–plasma interaction volumes for subsequent volume-force nonlinear electron acceleration with separation by the ion charge Z. In case a, the pregenerated plasma before the target causes instantaneous relativistic self-focusing of the laser beam to shrink to less than a wavelength diameter with very high nonlinear force acceleration due to the strong gradient of the laser field density (Hora, 1991, see Sect. 12.2). In case b, the nearly not present or too thin plasma in front of the target permits only interaction in the skin depth with much lower ion energies but nearly ideal plasma geometry conditions as treated before (Hora, 1991, see Sect. 10.3).

Generation of blocks of deuterium plasma moving against the neodymium glass laser light (positive velocities to the right) and moving into the plasma interior (negative velocities) at irradiation by a neodymium glass laser of 1018 W/cm2 intensity onto an initially 100-eV hot and 100-μm-thick bi-Rayleigh profile (Hora, 1991, Fig. 10.17) with minimum internal reflection. The electromagnetic energy density (E2 + H2)/(8π) corresponding to the intensity is shown at the same time of 1.5 ps after the beginning of the constant irradiation.

Ion velocity profiles at the times 2, 4, 5, and 6 ps taken from genuine two-fluid computations for a 3 × 1015 W/cm2, 4-ps rectangular laser pulse irradiating a deuterium plasma ramp of 20 μm thickness with critical density at 12 μm, confirming the generation of an ablating plasma block (negative velocity) and a compressing plasma block (positive velocity) (Cang et al., 2004).

Relation between the laser wavelength the aimed ion energy εtrans in multiples of m0 c2 and the necessary energy flux density for ignition of uncompressed DT following Eq. (22) for S = 1 and a laser pulse length of 3 ps.