2.1. Studying the AC conductivity of WDM

Among the various ultrafast energy sources, femtosecond lasers are the most developed and accessible. The first ISP concept that emerged is the isochoric heating of an ultrathin foil by a femtosecond laser (Forsman et al., 1998). This approach was introduced using the example of a 100 Å aluminum foil heated by a pump laser pulse of 20 fs (FWHM) at a wavelength of 400 nm. However, it is important to recognize that the concept can be readily extended to lasers with much longer pulse length and foils with significantly greater thickness by choosing the appropriate pump laser intensity. To demonstrate this versatility, we consider the case of a 400 nm, 100 fs laser pulse incident normally on a 200 Å thick aluminum foil. These requirements can readily be met in the laboratory.

The numerical simulations used in this work are based on a one-dimensional hydrodynamic code (Celliers, 1987) in which the laser-heated foil is considered a two-temperature, electron, and ion fluid. The equation of state of this plasma fluid is given by QEOS that is derived from an averaged atom, screened hydrogenic model where the electrons are treated as a Thomas Fermi gas and the ions a Cowan fluid. Conductivities are obtained from the dense plasma model of Lee and More (1984). This is based on the Boltzmann transport equation in the relaxation time approximation. Both electron-ion and electron-neutral scattering are included. Coulomb interaction is described by a modified cross-section with cutoffs in the strong coupling limit. In the absence of a wide-range calculation of the energy equilibration rate between electrons and ions, we adopted the use of a phenomenological coupling constant g (Celliers et al., 1992). The value of g for aluminum is taken to be 10¹⁷ W/m³ K in accordance with that deduced from the measurement of electron temperature at a shock front (Ao et al., 2000). We also assumed that hydrodynamic expansion of the heated solid occurs when the ion (lattice) temperature reaches the melting point.

The interaction of the heating or pump laser pulse with the foil is evaluated from the Helmholtz equations for an electromagnetic wave of S or P polarization. The resulting plasma fluid is treated as a dielectric medium whose dielectric function is derived from the Drude model in which the DC conductivity is determined by the collision frequency (Lee & More, 1984). A detailed description of this electromagnetic wave solver has been given elsewhere (Celliers & Ng, 1993).

Figure 3 shows the calculated reflectivity, transmission, and absorption of the pump laser pulse by the foil. The spatial profiles of energy density (including kinetic energy), mass density, and electron temperature in the foil at the end of the pump pulse are presented in Figure 4. The heated foil appears to maintain a slab-like density structure with nearly uniform energy density and temperature in the slab region. The uniformity in energy density and temperature is the result of electron thermal conduction. For the conditions of interest, the Fermi energy is about 12.5 eV and the Fermi speed is about 2 × 10⁸ cm/s. Accordingly, the transit time of the electrons near the Fermi surface across a 200 Å foil is ∼10 fs. Thus the absorbed laser energy can be distributed nearly uniformly in the sample during the heating process. At the lowest irradiance, virtually no hydrodynamic expansion occurred at the end of the pulse since only a very thin layer on the front surface has an ion temperature reaching the melting point of aluminum. Expansion in the outer surfaces of the foil becomes noticeable at irradiances of 2.5 × 10¹³ W/cm² and above.

Calculated reflectivity, transmission and absorption as a function of laser irradiance for a 400 nm, 100 fs pump laser pulse incident normally onto a 200 Å aluminum foil.

(a) Spatial profiles of energy density, (b) mass density, and (c) electron temperature at the end of the pump pulse for irradiances of 5 × 1012 W/cm2 (solid line), 1013 W/cm2 (dotted line), 2.5 × 1013 W/cm2 (dashed line) and 5 × 1013 W/cm2 (dot-dashed line). The position of x = 0 corresponds to the location of the front (laser facing) surface of the foil.

It should be noted that in experiments, the expansion of the foil can be monitored using a diagnostic such as frequency domain interferometry in a pump and probe arrangement (Geindre et al., 1994; Widmann et al., 2001). This measure the change in phase shift of a femtosecond probe laser pulse reflected from the surface of the foil. The response of such a diagnostic can be predicted using the electromagnetic wave solver for the probe pulse in a post-processor calculation based on results of the hydrodynamic simulation. Results of some sample calculations are presented in Figure 5. Zero and 300 fs correspond, respectively, to the times of peak pump laser intensity and end of the pump pulse. The initial change in phase shift is due to change in the AC conductivity of the heated foil. For the higher irradiances hydrodynamic expansion to becomes evident at late times, appearing as a continual decrease in the phase shift of the reflected probe.

Change in phase of a 100 fs, 400 nm, S-polarized, 45°-incident probe reflected from the front surface of the foil target for pump laser irradiances of 5 × 1012 W/cm2 (solid line), 1013 W/cm2 (dotted line), 2.5 × 1013 W/cm2 (dashed line), and 5 × 1013 W/cm2 (dot-dashed line).

Because of the slab-like behavior, the mass averaged density of the foil at the end of the pump laser pulse remains close to its initial density (ρ_o) as illustrated in Figure 6b. Furthermore, because of the comparatively low initial energy density of the foil and the near uniform deposition of the pump laser, the absorbed or excitation energy density (Δε) provides a very good measure of the mass averaged energy density at the end of the pump pulse as shown in Figure 6a. The state of the slab plasma can thus be characterized with ρ_o and Δε. However, this does not constitute a complete description of the slab since the electron and ion temperatures are different as dictated by the finite rate of energy exchange between the two species. Figure 7a shows the mass averaged electron and ion temperatures for g = 10¹⁷ W/m³ K (Ao et al., 2000). The corresponding contributions of the electrons and ions to the total energy density are shown in Figure 7b. This indicates that the ion contribution is largely negligible in the regime of interest here. It is also evident in Figure 7a that the ion temperature is less than 5% of the electron temperature even for the highest irradiance of interest here.

(a) Comparison of the absorbed energy density (solid line) to the mass averaged energy density (dotted line) and (b) comparison of the initial solid density (solid line) to the mass averaged mass density (dotted line) as a function of pump laser irradiance.

(a) Mass averaged electron (solid line) and ion (dotted line) temperatures and (b) mass averaged energy densities of the electrons (solid line) and ions (dotted line) as a function of pump laser irradiance.

Next, we consider the use of the femtoscecond-laser heated ultrathin foil as a means to study the AC conductivity, σ (ω), of WDM based on measurements of reflectivity (R) and transmission (T) of the heated foil. The conventional, forecasting method is to compare the calculated values of R and T with their measured values to test the conductivity model used in the hydrodynamic simulation and the electromagnetic wave solver. As an example, we consider a probe pulse of 100 fs (FWHM) incident on the front surface of the foil at an angle of 45°. To probe AC conductivity over a broad range of frequencies, one can use high harmonics generated from monomer gases (Macklin et al., 1993; Ditmire et al., 1995), molecules (Liang et al., 1994), solids (Carman et al., 1981; Bezzerides et al., 1982), or clusters (Donnelly et al., 1996) heated with femtosecond lasers, or femtosecond pulses from a synchrotron light source. The calculated reflectivity and transmission of an unperturbed foil as a function of photon energies for S and P polarized probes are shown in Figures 8a and 8b, respectively. The corresponding reflectivity R and transmission T for the heated foil at different pump laser irradiances are shown in Figures 9 and 10. The hydrodynamic expansion of the foil within the duration of the probe pulse is taken into account in these calculations. Also included in Figures 9 and 10 are values of R_Slab and T_Slab that are evaluated by treating the foil as an idealized slab specified by ρ_o and Δε. We approximated the ion temperature as 5% of the electron temperature as discussed above. The convergence between {R,T} and {R_Slab,T_Slab} is a measure of the validity of the ISP approach. It is evident from Figures 9 and 10 that S-polarized observations are much less sensitive to hydrodynamic expansion due to the absence of resonant absorption.

Calculated reflectivity (solid line) and transmission (dotted line) of an unperturbed 200 Å aluminum foil as a function of photon energy for a 45°-incident (a) S-polarized and (b) P-polarized probe.

Calculated reflectivity (R and RSlab) and transmission (T and TSlab) as a function of photon energy of a S-polarized probe at 45° angle of incidence for the heated foils at pump irradiances of (a) 5 × 1012 W/cm2, (b) 1013 W/cm2, (c) 2.5 × 1013 W/cm2, and (d) 5 × 1013 W/cm2. Values of R (solid circle) and T (open circles) are obtained from calculations taking into expansion during the heating pulse. Values of RSlab (solid line) and TSlab (dotted line) are for the idealized slab.

Calculated reflectivity (R and RSlab) and transmission (T and TSlab) as a function of photon energy of a P-polarized probe at 45° angle of incidence for the heated foils at pump irradiances of (a) 5 × 1012 W/cm2, (b) 1013 W/cm2, (c) 2.5 × 1013 W/cm2, and (d) 5 × 1013 W/cm2. Values of R (solid circle) and T (open circles) are obtained from calculations taking into expansion during the heating pulse. Values of RSlab (solid line) and TSlab (dotted line) are for the idealized slab.

The more novel methodology for studying σ (ω) is the back casting approach of using the observed values of {R,T} to solve the Helmholtz equations for electromagnetic wave propagation in a plasma slab that is characterized by ρ_o and Δε. The solution yields the dielectric function ε_ω or the AC conductivity σ_ω (both real and imaginary parts) of the plasma independent of any simulation models. The value of σ_ω(ρ_o,Δε) can then be used as a direct test of conductivity models for a single, well-defined plasma state. A detailed description of this methodology was given earlier for the case of a single-frequency optical probe (Forsman et al., 1998). The use of high harmonics probes will allow a much more complete test of conductivity models over a broad frequency range.

2.2. Non-equilibrium equation of state of WDM

As noted above, a unique advantage of the isochoric heating approach is the scalability in sample thickness with appropriate ultrafast energy sources. Potential candidates include Kα X-ray lines, energetic electrons, and fast protons produced in strong-field laser-plasma interactions, or X-ray free electron lasers. As an example, we consider the heating of a 5000-Å thick aluminum foil by a femtosecond Si Kα pulse to produce near uniform deposition and isochoric heating with an energy density of 3 × 10⁷ J/kg. This yields an ISP with an electron temperature of about 4 × 10⁴ K. The required Kα radiation can be readily generated by the irradiation of a silicon slab with a femtosecond laser pulse at an irradiance of ∼10¹⁷ W/cm². Hot electrons accelerated by the ponderomotive potential of the laser light induce K-shell excitation in the cold region of the target. This gives rise to Kα line emission as the K-shell vacancies are filled.

The significance of such a relatively thick ISP is its opacity to its characteristic emission spectrum. This renders it possible to use brightness temperature as a measure of electron temperature. In experiments, one can determine simultaneously the absorbance (or emissivity) and emittance (or spectral radiance) of the plasma slab. The former is obtained from reflectivity measurement. For the above example, the calculated reflectivity and emittance at 500 nm for the slab plasma convoluted with Gaussian temporal functions with FWHM of 500 fs, 1 ps, and 2 ps are presented, respectively, in Figures 11a and 11b. These simulate experimental measurements with temporal resolutions of 500 fs, 1 ps and 2 ps, respectively. The results are used in Kirchoff's law to yield the brightness temperature T_br (Fig. 11c). Figure 12 shows the ratio of the peak value of T_br to the electron temperature T_Slab of the ISP as determined by its energy density, assuming that the ion temperature reaches 5% of the electron temperature. Almost identical values are obtained for calculations at 400 nm and 600 nm. The results suggest that for observations with a temporal resolution of 500 fs, T_br provides a measure of T_Slab to within 94% of its value. Such a temporal resolution can be attained with state-of-the-art streak cameras, for example, the Hamamatsu FESCA-200 single-shot streak camera that combines a temporal resolution of 200 fs with a dynamic range better than 1:40. Thus, it appears feasible to obtain a reasonable measurement of the non-equilibrium equation of state of such WDM by determining electron temperature as a function of energy and mass densities, using this ISP approach. It should be noted that such an experiment could be performed using the 100 TW, 100 fs Ti:Sapphire laser (JanUSP) in the Lawrence Livermore National Laboratory.

Calculated (a) reflectivity, (b) emittance, and (c) brightness temperature Tbr at 500 nm as a function of time of a 5000 Å thick, solid-density idealized slab plasma with an excitation energy density of 3 × 107 J/kg for temporal resolutions of 500 fs (dotted line), 1 ps (dashed line) and 2 ps (solid line).

Ratio of the peak brightness temperature Tbr to the electron temperature TSlab of the idealized slab as a function of the temporal resolution of observations at 500 nm.

3.1. Pressure ionization of WDM

Ionization physics is fundamental to the determination of all basic properties of WDM. The macroscopic parameter of average ionization, 〈Z〉, is central to some transport models because of the need to evaluate electron density for the calculation of transport coefficients. Although a variety of ionization models exist, there is substantial divergence in their predictions even for 〈Z〉 as noted earlier (Chiu & Ng, 1999). This is further illustrated in Figure 15 by comparing earlier values of 〈Z〉 obtained from QEOS. Sesame tabulated equation of state (Holian, 1984) and a detailed configuration model (Chiu & Ng, 1999) to those derived from a neutral-pseudo-atom density-functional-theory model (Perrot & Dharma–wardana, 1995) for aluminum at 12.5 eV. Such discrepancies remain unresolved due to the lack of experimental data in the WDM regime.

〈Z〉 of aluminum as a function of compression at 12.5 eV obtained from QEOS (solid line), Sesame (Lee et al., 2002) (dot-dashed line), a detailed configuration model (Chiu & Ng, 1999) (solid circles), and a neutral-psuedo-atom density-functional-theory model (Perrot & Dharma–wardana, 1995) (dotted line). ρ is mass density and ρo is solid density of aluminum at normal conditions.

An even more critical aspect of ionization physics is the details of ion abundance, energy and population of atomic levels. These are required for the calculation of equation of state and radiative opacities. In general, ion abundance can be revealed from the characteristics of photo-absorption lines associated with the different ions. Of particular interest here is the Al⁺⁴ Kα absorption line of aluminum because of its appearance as a single, isolated line for shock compressed aluminum in the WDM regime. The use of such an absorption line as a sensitive test of 〈Z〉 was suggested earlier (Chiu & Ng, 1999). A natural extension of this approach would be to test ionization models along the well-defined principal Hugoniot for shock produced ISP. As shown in Figure 16, both the detailed configuration accounting (Chiu & Ng, 1999) and the neutral-pseudo-atom density–functional-theory (Perrot & Dharma–wardana, 1995) models show a gradual increase in 〈Z〉 above 3 for shock pressure exceeding 20 Mbar. This can be contrasted with the much higher values of 〈Z〉 predicted by QEOS or the much lower values of 〈Z〉 predicted by Sesame. On the other hand, a more stringent test of theory is the ion abundance described by Figure 17a. Specifically, the Al⁺⁴ ion shows a rapid increase in abundance as the shock pressure varies from 10–40 Mbar. The change in abundance of such an ion can be readily measured using the opacity of its characteristics absorption line. To compute the cross-section of the Al⁺⁴ Kα absorption line, we employ oscillator strengths derived from dense plasma estimates (More, 1991) and line widths due to electron collision broadening using impact approximation (Griem, 1968). Results of our calculation along the Hugoniot are presented in Figure 17b. Variations in the absorption cross-section are dominated by changes in the Al⁺⁴ abundances.

〈Z〉 as a function of shock pressure along the principle Hugoniot of aluminum obtained from QEOS (solid line), Sesame (Lee et al., 2002) (dot-dashed line), a detailed configuration model (Chiu & Ng, 1999) (solid circles), and a neutral-psuedo-atom density-functional-theory model (Perrot & Dharma–wardana, 1995) (dotted line).

(a) Ion abundance and (b) cross-section of the Al+4 Kα absorption line as a function of shock pressure along the principal Hugoniot of aluminum.

For opacity measurements on shock compressed matter, the usual approach is to study a sample that is sandwiched between two tamper layers in order to mitigate its expansion. Mismatch in shock impedance between the sample and the tamper causes multiple shock reflections. Furthermore, mismatch in temperature between the different layers leads to energy transport by thermal conduction. This effect becomes more dominant with decreasing sample thickness. As a result, the state of the shocked sample lies off the principal Hugoniot and varies with time. The structure of a tamped target also renders it not possible to obtain direct measurements of the state of the shocked sample.

As suggested earlier (Chiu & Ng, 1999), a steady shock offers a novel and elegant means to measure the opacity of an absorption line. Its uniqueness lays in the production of a well-defined uniform state whose thickness and optical depth increases linearly with time. For the above example of a shock launched from a silicon pusher into the aluminum sample, it can readily be shown that transmitted intensity I_T(t) at frequency ν of a continuum X-ray source through the aluminum layer is given by:

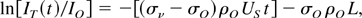
where I_o is the intensity of the backlight sources reaching the aluminum layer, L the initial thickness of the aluminum layer, ρ_o its initial density, σ_o the photo-absorption cross-section for the unperturbed solid, σ_ν the photo-absorption cross-section for shocked aluminum, and U_S the shock speed in aluminum. Equation (1) assumes that non-uniformities at the silicon-aluminum interfaces and the shock front are negligible. Accordingly, a plot of ln(I_T /I_o) versus time t yields a straight line whose slope is given by (σ_ν − σ_o)ρ_oU_S. This allows a direct measurement of (σ_ν − σ₀), and hence σ_ν, as a function of U_S and provides an assessment of ion abundance associated with the absorption line.

Figure 18 shows results of our calculations for shock pressures ranging from 10–40 Mbar. The variation in the slopes corresponds to the increase in abundance of the Al⁺⁴ ions according to the detailed configuration accounting model (Chiu & Ng, 1999). Such measurements will provide a direct test of ionization physics in terms of the abundance of Al⁺⁴ ions as a function of shock pressure, as illustrated in Figure 17b. Evidently, the use of absorption lines as a probe requires that the lines are well resolved. Clear observations of fluorine-like and oxygen-like absorption lines in shocked aluminum were reported by Boehly et al. (2001).

Plot of the normalized transmission at the Al+4 Kα absorption line as a function of time for shock waves of different pressure.

3.2. Effect of strong coupling on continuum states

Closely related to pressure ionization is the effect of a strongly coupled plasma environment on continuum states. A well-known manifestation of this is continuum lowering (Stewart & Pyatt, 1966). Apart from changes in ionization balance and average ionization, such an effect can be revealed by changes in photo-absorption edges (Da Silva et al., 1989). Figure 19 shows a comparison of the photo-absorption cross-sections for unperturbed aluminum (Henke et al., 1982) and shocked aluminum at 25 Mbar (Perrot & Dharma–wardana, 1993). For cold material, the abrupt change at the K-shell photo-absorption edge corresponds to the sharp cutoff in the density of state in the conduction band. For shock compressed and heated states, the photo-absorption edge becomes significantly broadened. This result from the holes generated in the conduction band by thermal excitation and changes in screening of the nucleus and bound electrons of the absorbing ions by neighboring electrons and ions.

Calculated photo-absorption cross-sections of cold aluminum (solid line) and aluminum compressed by a shock wave at 25 Mbar (dashed line).

In experiments, the K-edge is usually studied from the transmission spectrum of an X-ray source through a sample. While the frequency dependence of the photo-absorption cross-section is governed only by the state of the sample, the apparent form of the transmission spectrum varies substantially with the thickness of the sample as illustrated in Figure 20. In observations using relatively thick samples and detectors with a limited dynamic range such as ultrafast streak cameras, the transmission spectrum may give the appearance of an abrupt change near the K-edge (Da Silva et al., 1989). This has led to the misleading interpretation of an apparent shift in the edge position while there is no such identifiable shift according to the photo-absorption cross-sections. To remove such an ambiguity, one must determine the absorption cross-sections across the edge. In principle, these can be extracted from the observed transmission spectrum for a sample layer of a known thickness. For such measurements, however, it is often necessary to use tamper layers to define the extent of the sample. This approach is subject to the same difficulties discussed above.

Transmission spectra for aluminum at different shock compressed thicknesses at 25 Mbar.

The alternative is to adopt the use of a propagating shock wave. One option is to evaluate the cross-section from the transmission spectrum for a specific thickness of the shock compressed aluminum region. This would require accurate measurements of both shock speed and shock transit time. It would also limit the observation to a single sample thickness. The other option is to measure transmission, I_T(t)/I₀, at different photon frequency, ν, for a continuum X-ray probe as a shock wave propagates in the sample, as described above for line opacity studies. As illustrated in Equation (1) the slope of ln[I_T(t)/I₀] versus t will be a measure of the change in absorption cross-section, (σ_ν − σ₀). Results of our calculation for a 25 Mbar shock in aluminum are presented in Figure 21. The discontinuity at hν of 15.6 keV is due to the cold K-edge. Experimental results obtained in the form of Figure 21 will thus offer an unambiguous test of theory.

Slope of ln[IT(t)/I0] versus t at different X-ray energies for a 25 Mbar shock in aluminum.