1. INTRODUCTION
The Earth's geomagnetic field intensity is about 0·5 to 0·6 gauss and can be approximated to the dipole model (Ojeda and Borenstein, Reference Ojeda and Borenstein2000). Glatzmaier and Roberts (Reference Glatzmaier and Roberts1995) presented this dipole model using a three dimensional simulation with magnetic lines of force. The geomagnetic field points to magnetic north and this refers to the geomagnetic pole position, while the geographic north is at the earth's rotational axis and referenced by the meridian lines. Although the geomagnetic field is not perfectly uniform, the Earth's entire surface is covered by a magnetic field that is relatively consistent and predictable enough to give direction.
The geomagnetic field has been used for orientation since the Chinese were using lodestones to indicate horizontal direction over 2000 years ago (Caruso, Reference Caruso1997). In the 12th Century, the first recorded use of a magnetic compass at sea by Mediterranean seamen was recorded (Grant and Klinkert, Reference Grant and Klinkert1970). Magnetic compasses were used successfully on ships before iron and steel ships appeared and since the introduction of ships built from magnetic materials, calibration procedures, known as compass adjustment, have been developed to compensate the compass for the magnetic fields of such vessels. The calibration adjusts permanent magnets and soft iron components located in the binnacle holding the compass (Bowditch, Reference Bowditch1984), which is laborious and time-consuming. Recalibrations must be completed periodically, as the vessel's magnetic deviations vary over time and can be affected by the cargo and geographic position of the ship.
To overcome such issues, inertial technologies were developed. Sensitive gyrocompasses were deployed in ships and also in large aircraft to provide accurate heading and attitude. Such inertial devices with low drift rates are usually large and expensive, so their applications are limited. Attitude, also known as Euler angles, includes yaw, pitch and roll, and is normally derived from a specific type of Inertial Navigation System (INS) known as an Attitude and Heading Reference System (AHRS).
Recently, Global Positioning System (GPS) equipment has been applied to give attitude solutions without inertial drift or magnetic variation. The single antenna GPS receiver can obtain heading of a moving vehicle with position difference or velocity measurements. The heading accuracy depends on the positioning accuracy and driving speed (Hu et al., Reference Hu, Dun and Liu2010). The attitude accuracy of a commercial GPS-based multi-antenna system can be better than 0·5° (Kao and Tsai, Reference Kao and Tsai2006). This accuracy is a function of many parameters, such as the accuracy of the carrier phase observables, the level of multipath, the distances between antennas and the dynamics of the vehicle (Lachapelle et al., Reference Lachapelle, Cannon, Lu and Loncarevic1996). As a result, GPS-based attitude determination is reliable in low dynamic applications, such as marine and low dynamic aviation (like civilian aircraft and military transportation flights).
With much development over the last few decades, high-performance navigation is relatively mature and today a major challenge is to develop navigation systems with low-cost sensors to achieve acceptable performance (Brown and Lu, Reference Brown and Lu2004). Various alternative sensing technologies, such as radar, laser (Dickman and de Haag, Reference Dickman and de Haag2009), vision (Ruotsalainen et al., Reference Ruotsalainen, Kuusniemi and Chen2010) have been developed for navigation but the geomagnetic field is still considered to be an accurate, reliable and economic source of orientation information. With the development of vector magnetometer technology (Acuña, Reference Acuña2002), solid-state electronic magnetic compasses are making progress as low cost orientation systems. Electronic magnetic compasses can provide orientation without drift and modern compass calibration techniques can overcome the deviation problems of conventional magnetic compasses.
This paper presents a review of current electronic compass technology, covering magnetic sensor technologies, error modelling and compensation techniques. It does not cover all related technologies, or provide the details of particular algorithms, but rather provides an analysis for designers who intend to integrate electronic magnetic sensors into their systems. Magnetic sensors for an electronic compass are introduced in Section 2. The basic principles of orientation by electronic compass are given in Section 3. Error sources and error modelling are in Section 4. Primary approaches for compass calibration are reviewed in Section 5. Current trends and the outlook for future work are in Section 6.
2. MAGNETIC SENSORS
Magnetic sensors are also called magnetometers. The magnetic field can be sensed by various physical phenomena. A review of magnetic sensors working with or around the geomagnetic field was given by Lenz (Reference Lenz1990). Caruso (Reference Caruso, Bratland, Smith and Schneider1998) classified magnetic sensors into three categories: low field sensors (less than 1 micro-gauss), earth field sensors (1 micro-gauss to 10 gauss), and bias magnetic field sensors (above 10 gauss). Ripka and Janosek (Reference Ripka and Janosek2010) presented a review of recent advances in technologies and applications of magnetic sensors. Superconducting Quantum Interference Devices (SQUID) are the most sensitive low field sensors, which were reviewed by Robbes (Reference Robbes2006). A recent review of optical atomic magnetometers was presented by Budker et al. (Reference Budker and Romalis2007). Bulatowicz and Larsen (Reference Bulatowicz and Larsen2012) presented an atomic magnetometer technology that has the potential to provide a global position reference independent of GPS. Currently, the Hall, anisotropic magnetoresistive (AMR) and fluxgate (FG) are the most popular commercial solid-state magnetic field sensors. The typical sensing range of a Hall sensor is not suitable for geomagnetic field sensing. The FG and AMR are the workhorses for geomagnetic field sensing in modern electronic compass design.
2.1. Fluxgate Sensors
Fluxgate sensors measure DC and low-frequency AC fields up to 1mT, which are the most widely used for high-accuracy electronic compasses. Moore (Reference Moore1992) evaluated fluxgate-based magnetic compasses in different US Navy ship types, showing that they had the advantage of continuous calibration verification, and their performance exceeded the standard magnetic compass. A good review of fluxgate sensors was given by Ripka (Reference Ripka1992), and its basic sensor configuration and operating principle was also given by Ripka (Reference Ripka2003). The latest developments of fluxgate sensors are in digitalization (Cerman et al., Reference Cerman, Kuna, Ripka and Merayo2005), miniaturization (Baschirotto et al., Reference Baschirotto, Dallago, Malcovati, Marchesi and Venchi2007) and in the orthogonal fluxgate (Zorlu et al., Reference Zorlu, Kejik and Popovic2007).
2.2. AMR Sensors
AMR sensors are suitable for the geomagnetic field sensing range, and are standard off-the-shelf devices for medium-accuracy electronic compasses. A good introduction was given by Hauser (Reference Hauser, Stangl, Fallmann, Chabicovsky and Riedling2000). Typically, AMR sensors are made of permalloy thin film deposited onto a silicon substrate and patterned to form a Wheatstone resistor bridge (Caruso, Reference Caruso, Bratland, Smith and Schneider1998). The resistance of the bridge is in proportion to the sensing magnetic field. Both magnitude and direction of a field along a single axis can be measured. The developments of AMR sensors are summarized by Ripka and Janosek (Reference Ripka and Janosek2010).
3. ORIENTATION BY ELECTRONIC MAGNETIC COMPASS
The orientation system composed of magnetometers is also known as an electronic magnetic compass. An electronic magnetic compass can be divided into two classes: two-axis compass and strap-down compass.
3.1. Two-axis Compass
In a typical two-axis compass, the x-axis of the sensor points forward of the compass, the y-axis points to the right of the compass, and x-, y-axis is on the horizontal plane. As shown in Figure 1, the azimuth of the compass is the angle between the x-axis of the compass and magnetic north. The x-y-z coordinates are the body frame of the compass, in which x- and y-axis are parallel to the earth's surface, and the z-axis points vertically downwards. The geomagnetic field is described by seven parameters (Maus et al., Reference Maus, Macmillan, McLean, Hamilton, Thomson, Nair and Rollins2010). To be specific, the geomagnetic field vector at the point is called the total intensity (F). It can be divided into the vertical intensity (Z) and Horizontal Intensity (H). The horizontal intensity is divided into north-south intensity (X) and east-west intensity (Y) on the horizontal plane. The declination (D) is the angle between geographic (geodetic) north and magnetic north, and inclination (I) is the angle between the total intensity and the horizontal plane.
Figure 1. Definition of Azimuth (Stork, Reference Stork2000).
The azimuth can be calculated by:
$$Azimuth = \left\{ {\matrix{ {{\rm a}{\kern 1pt} {\rm tan}(H_y /H_x )(H_x \ne 0)} \cr {\displaystyle{\pi \over 2}(H_y \gt 0, H_x = 0)} \cr { - \displaystyle{\pi \over 2}(H_y \lt 0, H_x = 0)} \cr}} \right.$$where H x and H y are the compass sensor output. The true heading of the compass can be obtained by taking the declination into account.
The two-axis compass performs well as long as it is kept horizontal. However, in the applications in aircraft, boats or land vehicles, it is often hard to keep the compass level, which results in a considerable amount of heading errors called tilt error. In some installations this is reduced by the use of mechanical or fluid gimbals.
3.2. Strap-down Compass
The strap-down compass is desgned to correct the tilt error. In a typical strap-down compass, the x-axis of the sensor points forward of the compass, the y-axis points to the right of the compass, and the z-axis points to the bottom of the compass.
The tilt angles include pitch and roll. A two- or three-axis accelerometer is commonly used to measure these. The three-axis accelerometer can sense the gravitational acceleration, and the tilt angles can be calculated by:
$$\left[ {\matrix{ \theta \cr \gamma \cr}} \right] = \left[ {\matrix{ {{\rm arcsin}(\,f_x /g)} \cr {{\rm arctan}(\,f_y /f_z )} \cr}} \right]$$where θ and γ refer to pitch and roll respectively, g is the gravity acceleration, and f x, fy, fz are the output of the accelerometer. If the compass tilts with these pitch and roll angles, the corrected components of the geomagnetic field can be calculated with
$$H_{xc} = \cos \theta \cdot H_x + \sin \gamma \cdot {\rm sin}\theta \cdot H_y + {\rm cos}\gamma \cdot {\rm sin}\theta \cdot H_z $$
$$H_{yc} = {\rm cos}\gamma \cdot H_y - \sin \gamma \cdot H_z $$
$$H_{zc} = - \sin \theta \cdot H_x + \sin \gamma \cdot {\rm cos}\;\theta \cdot H_y + {\rm cos}\gamma \cdot {\rm cos}\;\theta \cdot H_z $$Inserting (3) into (1), the corrected azimuth can be calculated.
4. MAGNETIC SENSOR ERRORS
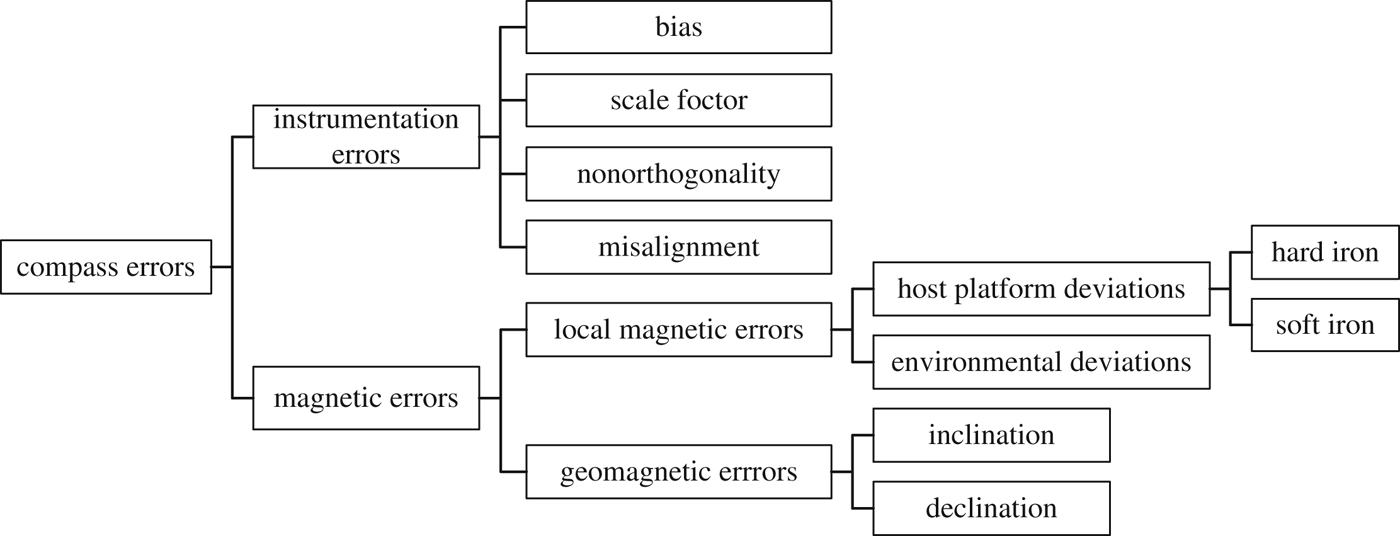
A compass detecting the geomagnetic field can be influenced by several error sources, as shown in Figure 2.
Figure 2. Compass Error Classification.
4.1. Instrumentation Errors
No matter what types of sensors are used in the compass, the instrumentation errors can be modelled as constants for a specific tri-axis magnetometer.
4.1.1. Bias
The sensor offset introduces a bias bso in the output. It is an additive error in sensor measurement that can be modelled as one scalar per axis.
$${\bf b}_{so} = \left[ {\matrix{ {b_{so_x}} & {b_{so_y}} & {b_{so_z}} \cr}} \right]^T $$where 
$b_{so_x} $, 
$b_{so_y} $ and 
$b_{so_z} $ are biases of sensor axis x, y and z respectively.
4.1.2. Scale Factor
The scale factor is a constant proportionality relating the input to the output of the magnetometers. It can be modelled as the scale factor matrix S by
$${\bf S} = {\rm diag}(\matrix{ {s_x} & {s_y} & {s_z} \cr} )$$where S is a diagonal matrix composed by scale factor s x, sy and s z of each axis.
4.1.3. Non-orthogonality
The non-orthogonality of each sensitive axis can be described as a transformation of vector space basis, parameterized by (Foster and Elkaim, Reference Foster and Elkaim2008)
$${\bf C}_{NO} = \left[ {\matrix{ 1 & 0 & 0 \cr {{\rm sin}(\varepsilon _z )} & {{\rm cos}(\varepsilon _z )} & 0 \cr { - {\rm sin}(\varepsilon _y )} & {{\rm cos}(\varepsilon _y ){\rm sin}(\varepsilon _x )} & {{\rm cos}(\varepsilon _y ){\rm cos}(\varepsilon _x )} \cr}} \right]$$where (ε x, εy, εz) are rotations between the skew sensor axes and orthogonal axes.
4.1.4. Misalignment
Misalignment is the installation error, when the compass is mounted to a host platform during. This is modelled as the rotation between the sensor frame of the compass and the body frame of the host platform, represented in the transformation matrix by Gebre-Egziabher et al. (Reference Gebre-Egziabher, Elkaim, Powell and Parkinson2006)
$${\bf C}_\eta = \left[ {\matrix{ 1 & {\eta _z} & { - \eta _y} \cr { - \eta _z} & 1 & {\eta _x} \cr {\eta _y} & { - \eta _x} & 1 \cr}} \right]$$where η x, ηy and η z are small rotations about the body frame x, y and z respectively.
4.2. Geomagnetic errors
Geomagnetic errors are mainly caused by the characteristics of the geomagnetic field, including the geomagnetic declination and inclination.
4.2.1. Declination
The azimuth measured by a compass has to be corrected by the declination in order to obtain the heading direction with respect to geographic north. The declination varies depending on the location of the compass (Caruso, Reference Caruso1997), but the changes of declination are very slow and predictable. This error can be eliminated using a map or chart which contains local declination based on the world magnetic model (Maus et al., Reference Maus, Macmillan, McLean, Hamilton, Thomson, Nair and Rollins2010), developed by the National Geophysical Data Center (NGDC).
4.2.2. Inclination
The inclination is predictable and can be eliminated by using data from the world magnetic model. It can be a source of error, if tilt occurs. Traditionally compasses with mechanical (or fluid) gimbals, or strap-down compasses can be adopted for tilt compensation, which are sensitive to the dynamic accelerations of the host platform. As a result, all types of magnetic compass work better under stationary or less vigorous manoeuvring conditions. Integration of a magnetic compass with a rate gyroscope, or an AHRS can help to overcome such limitations.
4.3. Local magnetic errors
Local magnetic interference from natural or artificial anomalies produces a deviation in the geomagnetic field. Considering a compass mounted on a host platform, local magnetic interferences are classified into host platform deviations and environmental magnetic deviations.
4.3.1. Host platform deviations
Due to the nature of magnetic materials, the host platform deviation can be classified into permanent magnetism (hard iron) and induced magnetism (soft iron) errors.
• Hard iron
The hard iron results from permanent magnets and magnetic hysteresis. If locations of the hard iron materials on the host platform remain consistent, the hard iron effect can be equivalent to a bias expressed as
$${\bf b}_{hi} = \left[ {\matrix{ {b_{hi_x}} & {b_{hi_y}} & {b_{hi_z}} \cr}} \right]^T $$• Soft iron
The soft iron materials do not exhibit any magnetic properties of their own, but they may acquire these properties when brought into the influence of an external magnetic field. This phenomenon is known as induced magnetism. Due to soft iron materials near the compass, the intensity and the direction of the sensed magnetic field will be changed according to the external magnetic field. The soft iron effect can be modelled as:
$${\bf C}_{si} = \left[ {\matrix{ {a_{11}} & {a_{12}} & {a_{13}} \cr {a_{21}} & {a_{22}} & {a_{23}} \cr {a_{31}} & {a_{32}} & {a_{33}} \cr}} \right]$$where the diagonal elements are functioned as the scale factor of each sensor axis, and the rest elements of Csi are functioned as the misalignment.
4.3.2. Environmental magnetic deviations
The magnetic sources in the environment around the host platform can cause environmental magnetic deviations. For a host platform moving through these areas, the locations of the environmental magnetic sources around the compass are time-varying, so the intensity and direction of sensed magnetic field are unpredictable and cannot be modelled mathematically. These unpredictable magnetic anomalies are the main concern for using electronic compasses in anomalous magnetic environments, such as urban canyons and indoor applications (Afzal, Reference Afzal, Renaudin and Lachapelle2011). Redundant sensor technologies can help to detect and mitigate environmental magnetic deviations (Ojeda and Borenstein, Reference Ojeda and Borenstein2000).
Among the compass errors shown in Figure 2, the geomagnetic errors are predictable and could be eliminated easily; the magnitude and direction of environmental magnetic deviations are unpredictable and highly dependent on the application environment; instrumentation errors and host platform deviations are the main error sources, which can be compensated by compass error modelling.
4.4. Compass Error Modelling
In 1824, Poisson presented the following model for compass deviations in marine navigation (Hine, Reference Hine1968):
$${\bf H}_r = {\bf KH}_e + {\bf P}$$in which He is the true value of geomagnetic field, and Hr is the magnetic reading in the sensor frame. The error matrix K defined by Poisson stands for the soft iron effect in wooden ships, from which the induced magnetic field is proportional to the geomagnetic field. The matrix P stands for the permanent magnetism due to hard iron in iron ships.
$${\bf K} = \left[ {\matrix{ {1 + a} & b & c \cr d & {1 + e} & f \cr g & h & {1 + k} \cr}} \right];\; {\bf P} = \left[ {\matrix{ p \cr q \cr r \cr}} \right]$$Many modern researches expand the Poisson deviation model for electronic magnetic compass error modelling. Accounting for instrumentation errors and host platform deviations described in the previous section, a three-axis compass error model can be written as
$${\bf H}_r = {\bf SC}_{NO} {\bf C}_{si} ({\bf C}_\eta ^{ - 1} {\bf R}_e^b {\bf H}_e + {\bf b}_{hi} ) + {\bf b}_{so} + {\bf n}$$where Hr is sensor measurements, He is the true geomagnetic field in earth frame (
$e$ frame), Reb is the rotation matrix from the earth frame to the sensor frame, n is the Gaussian wideband noise, S, CNO, Cη, Csi, bhi and bso are defined from Equations (4) to (9). Without loss of generality, this model can be described by:
$${\bf H}_r = {\bf CH}_b + {\bf b} + {\bf n}$$where C=SCNOCsiCη−1, b=SCNOCsibhi+bso, Hb=RebHe, Hb is geomagnetic measurement mapping in the body frame. This model indicates that various instrumentation errors and host platform deviations can be modelled and are equivalent to a constant matrix C and a bias matrix b to the geomagnetic measurements, which is known as equivalent effect (Vasconcelos et al., Reference Vasconcelos, Elkaim, Silvestre, Oliveira and Cardeira2011).
If the configurations of host platform structures or magnetic payload devices around the compass are changed, a recalibration procedure needs to be conducted. In particular, if the environmental magnetic field in the vicinity of the platform mounted with the compass is not favourable, the environmental distortions would lead C and b to become time-varying, which decrease the performance of the compass model. This fact requires the calibrations to be conducted in favourable magnetic environments.
5. COMPASS CALIBRATIONS
Compass calibration is an old maritime problem. With the expansion of the application domain, many magnetometer calibration techniques have been presented, which can be classified into: orientation domain calibrations and magnetic field domain calibrations (Gebre-Egziabher et al., Reference Gebre-Egziabher, Elkaim, Powell and Parkinson2006).
5.1. Compass Swinging
The compass swinging method (Bowditch, Reference Bowditch1984) is a typical orientation domain calibration. It treats the heading error as a Fourier function of the heading, and swings the vehicle to a number of reference heading points to calibrate the heading error.
Due to both hard and soft iron errors, the heading error of the compass is given by
$$\delta \psi = {A} + {B}{\rm sin}(\psi ) + C{\rm cos}(\psi ) + D{\rm sin}(2\psi ) + E{\rm cos}(2\psi )$$where the heading error δψ is the difference between the heading calculated by compass outputs and the reference heading ψ. The Fourier coefficients A through E are functions of the hard and soft iron errors (Felski, Reference Felski1999). More derivation of this model is given by Gebre-Egziabher et al. (Reference Gebre-Egziabher, Elkaim, Powell and Parkinson2006). The shortcomings of this calibration method are as follows: Firstly, the reference heading is required. The calibration accuracy is highly dependent on the accuracy of the reference heading. Secondly, the calibration coefficients are dependent on the location. If the vehicle is going to travel over a large geographic distance, multiple calibrations should be performed. Thirdly, it cannot calibrate the up direction axes of the magnetometers triad.
5.2. Magnetic Field Domain Calibrations
The fundamental idea of magnetic field domain calibration is based on the fact that in a given geographical area, the magnitude of the geomagnetic field is constant.
Based on a set of magnetic measurements with reference attitude, the error parameters can be calculated by an estimator. Guo et al. (Reference Guo, Qiu, Yang and Ren2008) proposed an Extended Kalman Filter to calibrate the soft iron and hard iron error with a reference attitude of SINS. Another method proposed by Vcelak et al. (Reference Vcelak, Ripka, Kubik, Platil and Kaspar2005) estimated instrumentation errors and misalignment with a nonmagnetic calibration device. These kinds of approaches require reference attitude, so they are more suitable for laboratory calibration or high redundancy applications.
Caruso (Reference Caruso1997) proposed a practical approach for offset and scale factor errors. By rotating the vehicle on a horizontal surface, the minimum and maximum outputs of the level magnetometers are used to calculate the calibration parameters. This method cannot calibrate misalignment, non-orthogonality or soft iron errors, and it is sensitive to the sensor noise.
5.3. Ellipse or Ellipsoid Fitting Calibration
The ellipse or ellipsoid fitting calibration treats magnetic field domain calibration from the viewpoint of geometrics. This method calibrates the error parameters with the magnetic field measurements, by rotating the compass. For two-axis or three-axis magnetometers, the magnetic field domain calibrations can be transformed into the ellipse (2D case) or ellipsoid (3D case) fitting problems (Moulin, Reference Moulin, Goudon, Marsy, Legendarme, Presset and Dedreuil-Monnet1983).
5.3.1. Basic principles
From the error model (13), the following equation can be developed:
$$({\bf H}_b )^{\rm T} {\bf H}_b = ({\bf H}_r )^{\rm T} {\bf G}^{\rm T} {\bf GH}_r - 2{\bf b}^{\rm T} {\bf G}^{\rm T} {\bf GH}_b + {\bf b}^{\rm T} {\bf G}^{\rm T} {\bf Gb}$$in which G=C−1. Since the magnitude of the geomagnetic field is constant during the calibration, so the left of the equation (15) is a constant, which indicates that the magnetic field measurement's locus is an ellipse or ellipsoid. The effect of compass errors on magnetic field measurement locus is shown in Figure 3.
Figure 3. Effect of errors on magnetic field measurement locus (Gebre-Egziabher, Reference Gebre-Egziabher, Elkaim, Powell and Parkinson2001).
The bias and hard iron effect shift the error-free measurement locus (a circle) with an offset from the origin. The soft iron error has two effects on the magnetic field measurements locus (Gebre-Egziabher, Reference Gebre-Egziabher, Elkaim, Powell and Parkinson2006). One is called the scaling effect. It is equivalent to the scale factor effect that is to deform the error-free measurements locus from a circle into an ellipse. The other one is known as the rotation effect. It is equivalent to the misalignment effect that rotates the locus around the centre of ellipse. Such explanations can be expanded to the 3D case for ellipsoid fitting calibration.
The ellipse or ellipsoid fitting calibration procedures are composed of two parts: Firstly, the ellipse or ellipsoid fitting based on the sensor measurements. Secondly the magnetic errors are solved by the estimated ellipse or ellipsoid parameters. The ellipse or ellipsoid fitting problem is to find a “best matching” ellipse or ellipsoid from a set of data points, which is a basic task in pattern recognition and computer vision (Duda, Reference Duda and Hart1973). The main concern of the calibration is how to solve the error parameters from the estimated ellipse or ellipsoid. The fitting procedures can give an optimal estimation of GTG, while there are countless solutions of the decomposition of GTG. If the non-orthogonality, misalignment and the rotation effect of soft iron errors can be ignored, G can be simplified into a diagonal matrix. Normally G is assumed as a triangular matrix or symmetrical matrix (Li and Li, Reference Li and Li2012), if the misalignment errors and soft iron errors are present, an alignment process with the external reference orientation is needed to solve the G (Gebre-Egziabher, Reference Gebre-Egziabher2007; Vasconcelos et al., Reference Vasconcelos, Elkaim, Silvestre, Oliveira and Cardeira2011).
5.3.2. Ellipse fitting calibration
A non-linear, two-step estimator is adopted to estimate the ellipse parameters, and solve calibration parameters of the scale factor and hard iron errors (Gebre-Egziabher et al., Reference Gebre-Egziabher, Elkaim, Powell and Parkinson2001). Skvortzov (Reference Skvortzov, Lee, Bang and Lee2007) proposed a compass calibration method to take the soft iron errors into account. The rotation effect of the soft iron error is characterized by the angle of the major axis of the elliptical measurement locus, and the scaling effect of the soft iron error is characterized by the ratio of the major axis to the minor axis lengths.
5.3.3. Ellipsoid fitting calibration
During the calibration, the compass should span the entire Euler angle attitude space to record a well-distributed data set. However such a complete locus is difficult to obtain in practice, if the compass is deployed on a vehicle. Even in aviation applications, the manoeuvrability of the vehicle will mean that only some sections of the ellipsoid can be traced. For a vehicle with limited manoeuvrability, the reduced information about the ellipsoid curvature will slightly degrade the performance of the calibration (Vasconcelos et al., Reference Vasconcelos, Elkaim, Silvestre, Oliveira and Cardeira2011).
Gebre-Egziabher et al. (Reference Gebre-Egziabher, Elkaim, Powell and Parkinson2006) proposed a method to calibrate the scale factor error, the scaling effect of the soft iron and hard iron biases. This work was expanded to take the non-orthogonal error and offset into account (Foster and Elkaim, Reference Foster and Elkaim2008). This class of ellipsoid fitting procedure simplifies the soft iron error into a scale factor error, and can be adopted in soft iron error free applications.
Gebre-Egziabher (Reference Gebre-Egziabher2007) proposed an auto calibration algorithm for small aerial vehicles, in which the full effects of soft iron errors and the sensor non-orthogonality were taken into account. Following the error model (13), a symmetric scaling matrix KG is obtained from the polar decomposition of C−1 as:
$${\bf K}_G = ({\bf R}_G )^T {\bf C}^{ - 1} $$By identifying whether RG is the identity matrix, the unobservable mode caused by the soft iron errors and the sensor non-orthogonality can be identified. While in the unobservable mode, external orientation information will be needed for the estimation of the three remaining parameters.
Vasconcelos et al. (Reference Vasconcelos, Elkaim, Silvestre, Oliveira and Cardeira2011) proposed a rigorous geometric formulation of ellipsoid fitting calibration for the joint effect of the sensor errors as modelled in Equation (13). The singular value decomposition (SVD) of C is denoted as
$${\bf C} = {\bf R}_L {\bf S}_L ({\bf V}_L )^T $$where RL represents the rotation character of the ellipsoid, SL is the scaling of the ellipsoid, and VL represents the misalignment or non-orthogonality of the sensors. This work divided the compass calibration procedures into calibration and alignment procedures. Maximum likelihood estimation is adopted in the calibration procedure to estimate the ellipsoid parameters (RL, SL, b). While in the alignment procedure, the orthogonal matrix VL can be solved with external orientation information.
6. CURRENT TRENDS AND OUTLOOK FOR THE FUTURE
Currently, the electronic magnetic compass is an important backup orientation system alongside GPS and INS in high-grade navigation applications. It is the main orientation system for small boats and aircraft, which are usually constructed of nonferrous materials. It is usually treated as a high performance reference to compensate the low-cost IMU in a low-cost AHRS (Han and Wang, Reference Han and Wang2011, Li and Wang, Reference Li and Wang2013). Recently, it has become the main orientation solution in portable devices for pedestrian navigation.
The key issue of the electronic magnetic compass technology is the compensation technologies for various magnetic interferences. For error modelling and calibration techniques, the instrument errors become minimized and ignorable with the progress of sensor technology, and the misalignment and soft iron errors are the main concerns. Currently, they are treated by an independent alignment procedure with an external reference. Since electronic magnetic compasses are normally composed of magnetometers and accelerometers, the accelerometers can be an information source to simplify alignment procedures (Li and Li, Reference Li and Li2012). To improve calibration efficiency, the sampling strategy of the calibration data needs to be designed according to the manoeuvrability of the vehicle.
To extend the application area, environmental magnetic deviations are the major challenges. Redundant sensors and integration are two of the most promising technologies to meet the challenges.
Ojeda and Borenstein (Reference Ojeda and Borenstein2000) proposed a differential compass based on the fact that the strength of a magnetic field is inversely proportional to the square of the distance from the source. Two identical compasses are aligned in the same direction but separated from each other by a fixed distance. If environmental interferences are present, one compass would be affected more than the other. Based on the difference of the outputs of two compasses, the environmental magnetic interference can be identified. Yun et al. (Reference Yun, Ko and Lee2008) presented a similar differential compass for driving assistance. Beside the interference identification, this differential compass can be compensated if a single magnetic disturbance source presents, of which the heading error can be limited to ±5°. To meet indoor magnetic anomalies, Afzal et al. (Reference Afzal, Renaudin and Lachapelle2011) proposed a perturbation mitigation technique that utilizes a Multiple Magnetometer Platform (MMP) composed of 12 tri-axis magnetometers arranged on two orthogonal planes. A perturbation detector can identify the least affected magnetic field components from the measurements of the MMP, which are adopted for orientation.
Another approach is integration technology. If the electronic magnetic compass is integrated with another reference orientation system such as INS and GPS, the reference system can help to identify and eliminate environmental magnetic deviations. The main problem of this approach is the cost of reference systems. If high-grade systems are on board, the reference orientation can be very precise and reliable, and the environmental magnetic deviations of the electronic compass can be identified and eliminated. However this is not the case for pedestrian and indoor navigation, in which low-cost systems are usually the first option. For example, a low-cost GPS receiver cannot provide precise orientation results (Trigo et al., Reference Trigo, Donas-Boto, Vilva and Sanguino2011), and a low-cost INS suffers from drift. As a result, it is still a challenge for the low-cost integrated systems to identify and eliminate environmental magnetic deviations.
In short, the future directions for electronic compasses can be expected as follows:
• Improvements in the manufacture of sensors that lead to fewer remaining instrument errors.
• Online calibration technologies that use simpler calibration data recording procedures and calculations.
• The integration of electronic compass, low cost inertial sensors, GPS and other sensors. The integrated system can combine the benefits of these systems together to achieve optimal performance with an affordable cost. The redundant information from other systems can be utilized to calibrate the electronic compass online.
ACKNOWLEDGEMENT
The first author would like to thank the China Scholarship Council (CSC) for supporting his studies at the University of New South Wales, Australia.
