When Scott Walker withdrew from the Republican presidential race in September 2015, he called for unity, urging other candidates to withdraw and support a single contender who could defeat Donald Trump for the party’s nomination (Voorhees Reference Voorhees2015). If #NeverTrump Republicans split their votes, Walker worried, then Trump could win despite opposition from a majority of the party’s voters. The remaining candidates ignored the warning as Trump continued to earn narrow victories against a crowded field. Many commentators later endorsed Walker’s logic, attributing Trump’s primary success to the Republican establishment’s failure to coordinate on a frontrunner (Azari Reference Azari2016; Burns and Martin Reference Burns and Martin2016; Stokols Reference Stokols2016). This coordination narrative, however, rests on an implicit assumption about the underlying structure of Republican primary voters’ preferences that although Trump commanded plurality support, he could have been defeated in head-to-head, or pairwise, contests.Footnote 1 How accurate was this assumption about Republican primary voters’ preferences in 2016? More generally, how extensive was the opposition to (or support for) Trump’s nomination among such voters? Did he draw support from a narrow minority or a wide majority of Republican primary voters?
To answer these questions about the extent of Trump’s support, we take an empirical social-choice approach, relying on an original dataset of Republican voters’ preferences to examine the outcomes of pairwise majority-rule contests.Footnote 2 In contrast to conventional pre-election polls that ask respondents only about their likely vote, we measured voters’ binary preference for pairs of leading candidates.Footnote 3 With these data, we characterized the extent of Trump’s support (or lack thereof) in social-choice terms: specifically, whether Trump was a Condorcet loser, a Condorcet winner, or a member of the majority-rule core. If we found that Trump was a Condorcet loser (i.e., strictly defeated in every pairwise contest), then the structure of voters’ preferences would have satisfied a necessary condition for the coordination narrative. If we found that Trump was a Condorcet winner (i.e., strictly preferred in every pairwise comparison) or in the majority-rule core (i.e., weakly preferred in every comparison), then attempts to coordinate would have been irrelevant.
With these data, we characterized the extent of Trump’s support (or lack thereof) in social-choice terms: specifically, whether Trump was a Condorcet loser, a Condorcet winner, or a member of the majority-rule core.
Our results suggest that Republican elites could not have counted on coordination as a strategy to prevent Trump’s nomination. Trump either won or tied against every other candidate in pairwise contests, which means that not only was he not a Condorcet loser but also that no other candidate had enough support to defeat him. Although Trump’s support was not so broad as to make him a Condorcet winner, we did find that it was enough for him to earn a place in the majority-rule core. Thus, in some sense, we can state that Trump was a “rational choice” of the Republican primary electorate.
WINNERS, LOSERS, AND THE CORE
Plurality rule is a straightforward way to make a collective choice over many candidates. Simply count the number of votes and the candidate with the most votes wins. Although it is simple to implement, with more than two candidates, this process may not produce the “best” social choice because a majority of voters might oppose the plurality winner.Footnote 4 As the number of candidates increases, such opposition becomes increasingly likely (Wright and Riker Reference Wright and Riker1989). However, to determine whether this is indeed a problem, we must know how each voter ranks every possible candidate.Footnote 5
To illustrate the importance of considering plurality versus pairwise contests, consider the two hypothetical preference Profiles A and B in table 1. In both profiles, Trump is the plurality winner with 40% of the vote; Cruz and Rubio split the remainder of the vote with 30% each. However, the two profiles differ starkly in how Trump is ranked relative to the others. In Profile A, Cruz voters (Group 2) and Rubio voters (Group 3) rank Trump last. This means that either Cruz or Rubio would defeat Trump with a decisive majority (by a 60% to 40% margin) in a pairwise contest. Because Trump is defeated by all other candidates in pairwise majority-rule contests (a decision procedure advocated by the Marquis de Condorcet), we would say that he is a Condorcet loser. This situation illustrates the Borda paradox (Nurmi Reference Nurmi1983), in which a Condorcet loser can be selected by plurality. It is precisely the type of context in which coordination by Republican candidates prevents Trump’s nomination: coordination allows voters who oppose Trump to reallocate their vote to a single challenger (generating the pairwise-contest results) rather than splitting their vote (generating the plurality-rule outcome).Footnote 6
Table 1 Hypothetical Preferences

By contrast, in Profile B, Cruz and Rubio voters place Trump in the middle of their orderings. In this second scenario, Trump would win pairwise contests against both Cruz and Rubio (70% to 30%). Thus, Trump is majority preferred to every other candidate and is, instead, a Condorcet winner. In this case, Trump has enough support that neither coordination nor strategic voting prevents his nomination.
Importantly, these simple examples call attention to the necessity of knowing, empirically, how voters rank candidates beyond their top choice. Profiles A and B are observationally equivalent according to plurality rule (or from polls that elicit a single choice among several candidates), but they can be distinguished using data on pairwise choices. That is, we can use data on the pairwise choice between Trump and candidate R to inform us about what might have happened if there had been coordination and all but candidate R dropped out: Would candidate R have had enough support to defeat Trump?
In practice, many voters may lack a strict preference for one candidate over another and may instead be indifferent between them.Footnote 7 That is, these voters would view two candidates as equally good (or equally bad). Whereas admitting this possibility allows us to consider a richer and more empirically plausible set of preference profiles, it leads to complications (Jones et al. Reference Jones, Radcliff, Taber and Timpone1995). Consider Profile C in table 1 in which every voter is indifferent between the candidates ranked below their top choice. In each pairwise comparison, neither candidate has the support of a majority of voters. For example, in the head-to-head contests between Trump and Cruz, a 40% plurality supports Trump, a 30% minority supports Cruz, and the remaining 30% (i.e., Rubio supporters) are indifferent.
If these indifferent voters were forced to choose between Trump and Cruz, voting for either candidate, strictly speaking, would be rational. How should we determine the majority preference? In our analysis, we considered a candidate to be the majority preference if and only if a majority of voters strictly preferred that candidate. This definition of majority preference (following Austen-Smith and Banks Reference Austen-Smith and Banks1999, 27) is the most conservative in the sense that it involves the fewest assumptions about how indifferent voters would behave in practice.Footnote 8 If neither candidate garners an absolute majority, then we consider voters to be indifferent in the aggregate.
From a social-choice perspective, Profile C differs subtly but importantly from Profile A. Collectively, voters are indifferent between Trump and Cruz, between Trump and Rubio, and between Cruz and Rubio. No candidate strictly defeats any other candidate; therefore, there is no Condorcet winner. However, neither is there a Condorcet loser because no candidate strictly loses to any other candidate. Nevertheless, social-choice theory provides a definition of what it means to be “best” according to preferences for the entire group: an alternative is a member of a set called the core if it is “at least as good as” (i.e., weakly better than) every other alternative according to a preference-aggregation rule. In Profile C, all candidates are equally good according to pairwise majority rule; therefore, all are members of the core and are “best” (albeit in a weak sense). In Profile B, however, Trump is the unique member of the core and, in Profile A, he is not in the core (instead, Cruz is the unique member). If we found that Trump indeed is in the core, then his nomination would reflect the rationality of Republican voters’ group choice.
DATA
Our analysis relied on two independent sources of data. First, we conducted an original survey to elicit complete preferences over the five leading candidates in early 2016 (Jeb Bush, Ben Carson, Chris Christie, Ted Cruz, and Donald Trump) from likely Republican voters (N=755) through Amazon’s Mechanical Turk (MTurk) platform (Berinsky, Huber, and Lenz Reference Berinsky, Huber and Lenz2012).Footnote 9 We fielded our surveys between January 21 and February 8, 2016, a period that corresponded to the week before the Iowa Caucus until the eve of the New Hampshire Primary.Footnote 10 Because our MTurk sample may not be representative of the Republican primary electorate, we also conducted parallel analysis using the 2016 American National Election Studies (ANES) Pilot Survey (using Republican-leaning voters’ preferences over the same candidates except Christie; N=440). These data were generated concurrent with our MTurk data, from January 22 to 28, 2016.
In both datasets, the distribution of respondents’ first-choice candidates was comparable to publicly available commercial polls fielded during the same period.Footnote 11 Remarkably, the proportion of Trump supporters in our MTurk sample was quite close to both the percentage of Trump supporters in the ANES Pilot Survey and the polling average. The percentage of MTurk respondents who supported each of the other candidates was also well within the range of contemporary polls, with the exception of greater support for Rand Paul.Footnote 12 These comparisons suggest that we can be reasonably confident in the validity of our MTurk sample.
RESULTS
The goal of our analysis was to understand the structure of Republican voters’ preferences for or against Donald Trump relative to other candidates. To do so, we aggregated the preferences for Trump against the field of candidates elicited from the MTurk sample and ANES Pilot Survey in two ways. First, we compared the proportion of voters who strictly preferred Trump to each of the other candidates. Using this criterion, we state that Trump was strictly preferred by majority rule (i.e., the majority winner) if the percentage of voters who strictly preferred Trump exceeds 0.5. If the proportion strictly favoring the other candidate was greater than 0.5, then that other candidate was strictly preferred (i.e., Trump was the majority loser). If neither candidate was strictly preferred by a majority, then we considered the aggregate preference to be one of indifference (i.e., a majority tie).
Second, we accounted for uncertainty by using the 95% confidence interval instead of the point estimate. Under this interval criterion, we can state that Trump was the majority winner if the entire confidence interval for the percentage of respondents supporting Trump exceeds 0.5. Similarly, if the entire interval falls below 0.5, then Trump was the majority loser; if 0.5 is contained in the interval, then there was a majority tie.
Figure 1 shows Trump’s level of support compared to the support for each of the other candidates for our two datasets. Across both samples, Trump’s share of supporters was higher than that of every other candidate, although he did not always have a majority. In our MTurk sample, shown in the left panel of figure 1, Trump was strictly preferred to both Jeb Bush (0.54 to 0.38) and Chris Christie (0.55 to 0.36) according to the point-estimate criterion. Although he had a larger share of supporters than Ben Carson (0.49 to 0.42), Ted Cruz (0.48 to 0.46), and Marco Rubio (0.48 to 0.47), Trump did not have a majority of strict supporters against any of these other candidates. Applying the interval criterion to our MTurk sample yields identical conclusions regarding aggregate preferences. Because Trump defeated two of the five other candidates and was tied with the other three, he was neither a Condorcet winner nor a Condorcet loser; however, he was in the core and, therefore, a rational Republican group choice.
Across both samples, Trump’s share of supporters was higher than that of every other candidate, although he did not always have a majority.

Figure 1 Pairwise Preference for and against Donald Trump
The data from the ANES Pilot Survey, shown in the right panel of figure 1, also support the conclusion that although Trump was neither a Condorcet winner nor loser, he was in the core. As shown in the point estimates, Trump was majority preferred to Bush (0.61 to 0.35), Cruz (0.51 to 0.44), and Rubio (0.51 to 0.45) but was majority tied with Carson (0.48 to 0.47). When we examine the confidence intervals, which are wider for the ANES Pilot Survey than for the MTurk sample, we see that Trump was majority preferred only to Bush. For the remaining candidates, we cannot be sufficiently confident that his support exceeds 0.5. Nevertheless, we found that no other candidate majority defeated Trump; therefore, Trump was in the core.Footnote 13
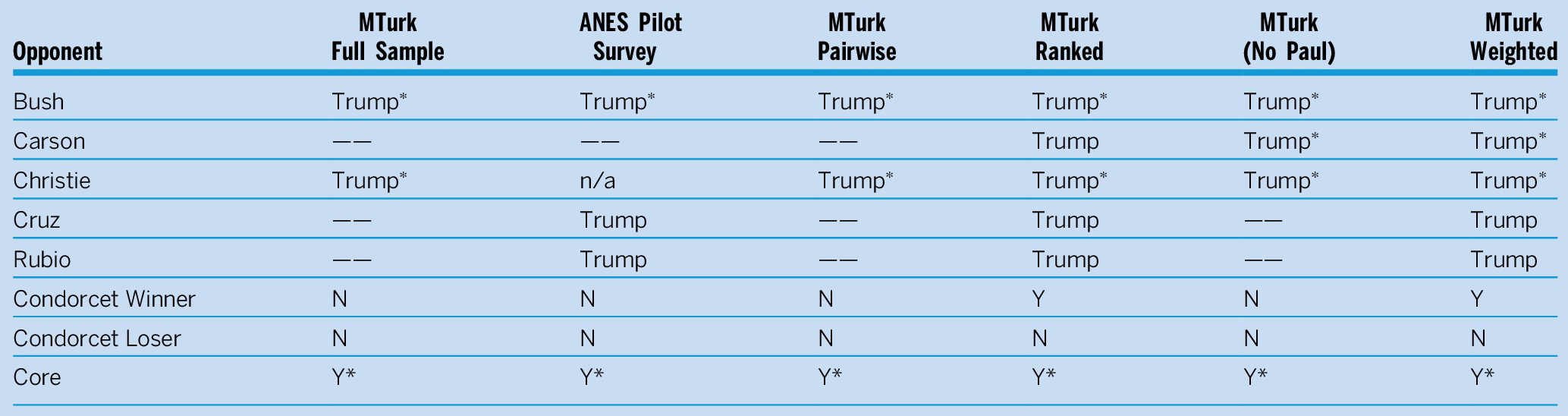
We found consistent support that Trump was in the majority-rule core even when we examined subsamples of our MTurk data to check the robustness of our results.Footnote 14 This analysis is summarized in table 2, which shows that Trump was in the core regardless of the elicitation method (pairwise or rank-ordered); whether we dropped (overrepresented) Rand Paul supporters; or whether we used post-stratification weights to adjust for the fact that our MTurk sample was less representative of Republican voters than the 2016 ANES Time Series sample. If anything, that Trump was a Condorcet winner in some subsamples suggests that figure 1 may underestimate his support.
Table 2 Comparing Preferences in Subsamples

Notes: Cell entry indicates the preferred candidate; —— indicates tie; ∗ indicates satisfies interval criterion.
CONCLUSION
Our empirical social-choice analysis yielded a picture of Donald Trump’s support that challenges the conventional coordination narrative. Because Trump was not a Condorcet loser, neither coordination among elites nor strategic voting in the electorate would have made much difference. Plainly stated, Trump did not win because Republicans split their votes. Republican voters, in the aggregate, found him to be “at least as good as” any other candidate, earning him a place in the majority-rule core. That is, Trump was a collectively rational choice of the Republican electorate.
Plainly stated, Trump did not win because Republicans split their votes.
Whereas our results suggest that it is unlikely that Trump’s nomination could have been stopped by the time the primaries began, his nomination might have been stopped in other ways. For example, Azari and Masket (Reference Azari and Masket2017) noted that the Republican Party’s nomination rules were too democratic, allowing participation by too many candidates in the debate process and broad participation by voters. Stronger parties in which elites controlled the set of candidates, they argued, could have prevented Trump from receiving the Republican nomination.
It is also possible that Trump’s nomination could have been forestalled by elite coordination much earlier in the process, such as when he announced his candidacy. Because our data provide only a snapshot of voters’ preferences at a particular point in time, it is possible that voters’ preferences were less developed in the summer of 2015. Coordinating on a strong “establishment” Republican candidate—involving endorsements and cohesive messaging by party elites—might have been able to influence the formation of voters’ preferences. However, this is pure speculation.
In the summer of 2019, the race for the 2020 Democratic nomination was a crowded field with more than 20 declared candidates, which in some ways resembled the 2016 Republican contest. Could one of the frontrunners (e.g., Bernie Sanders) have been opposed by a majority of the party’s voters yet capture the nomination by splitting the opposition? Although the 2020 contest differs because of Democrats’ greater reliance on proportional delegate-allocation rules, the key empirical question for coordination by party elites to matter is whether a plurality candidate is also a Condorcet loser.
Supplementary Materials
To view supplementary material for this article, please visit http://dx.doi.org/10.1017/S1049096520000359.