II. REDEFINING OPTIONS, PERFORMING OPTIONS MARKET

The growing use of the option pricing model elaborated by Fischer Black, Myron Scholes, and Robert Merton (Black and Scholes Reference Black and Scholes1973; Merton Reference Merton1973) is considered a major stage in the makeup of financial markets. The core idea of the model is that if a reduced number of hypotheses are respected, option prices will depend only on the underlying stock price and the variables that are taken as constant. As a consequence, it is possible to generate a hedged position, consisting of a long position in stock and a short position in options, whose value will depend not only on time but also on the values of known constants. These hypotheses are:

1. a. The short-term interest rate is known and constant.

2. b. The stock price follows an exponential Brownian motion.

3. c. The stock pays no dividends.

4. d. There are no transaction costs.

5. e. It is possible to borrow any fraction of the price of a security to buy or to hold at the short-term interest rate.

6. f. There are no penalties to short selling.

If the conditions a–f are fulfilled, it is possible to build and continuously to adjust a portfolio containing underlying stocks and government bonds (or cash), which replicates the payoffs of the option. So, the option’s payoffs (including the option price) and those of the portfolio should be the same, since arbitragers will buy the cheaper options and sell the more expensive ones. The history of this revolutionary reasoning has been discussed in depth by historians of finance (Bernstein 1998, 2005, 2007; MacKenzie Reference MacKenzie2006b; Mehrling Reference Mehrling2012). Option pricing theory is the result also of several controversies related to general pricing theory since Harry Markowitz (Reference Markowitz1952) and then Franco Modigliani and Merton Miller (1958), linked together expected gain and risk.

This led to the so-called Capital Asset Pricing Model (CAPM) (Treynor 1962; Sharpe Reference Sharpe1964; Lintner Reference Lintner1965; Mossin Reference Mossin1966), based on the seminal contribution of James Tobin (Reference Tobin1958), on which Black and Scholes ^{Footnote 2} drew to propose their first model. Merton disrupted these developments when he proposed the idea of portfolio dynamic and continuous arbitrage (including Ito’s lemma), which constitute the grounds for the BSM model. This major development culminated in the famous BSM equation where V is the price of the option, S is the price of the stock, t is the time, $\sigma$ is the volatility of the stock, and r is the riskless rate of interest:

$${{\partial V} \over {\partial t}} + {1 \over 2}{\sigma ^2}{S^2}{{{\partial ^2}V} \over {\partial {S^2}}} + rS{{\partial V} \over {\partial S}} - rV = 0$$

MacKenzie and Millo (2003, p. 9) explain the central place of the BSM model in modern finance as due to a “performative” mechanism à la Callon rather than its descriptive accuracy: “Why was option pricing theory so successful empirically? Was it because of the discovery of pre-existing price regularities? Or did the theory succeed empirically because participants used it to set option prices? Did it make itself true? As will be seen, the answer is broadly compatible with Callon’s analysis.”

There is no clear definition of the notion of performativity in MacKenzie and Millo’s first article. However, MacKenzie (2006, p. 31; 2007, p. 55) distinguishes two kinds of performativity. Generic performativity is where “an aspect of economics (a theory, model, concept, procedure, data-set, etc.) is used by participants in economic processes, regulators, etc.” Effective performativity is where “the practical use of an aspect of economics has an effect on economic processes.” MacKenzie considers generic performativity as not in itself of particular interest, and sees only effective performativity as inspiring. He also defined two subclasses of effective performativity (2006, p. 31; 2007, p. 55). Barnesian ^{Footnote 3} performativity is where the “practical use of an aspect of economics makes economic processes more like their depiction by economics.” Counterperformativity is where the “practical use of an aspect of economics makes economic processes less like their depiction by economics.” The Barnesian definition of performativity evokes the self-fulfilling mechanism described by Robert K. Merton: “The self-fulfilling prophecy is, in the beginning, a false definition of the situation evoking a new behavior which makes the originally false conception come true” (Merton Reference Merton1948, p. 195).

Economics shapes the economy in its own image when agents use it as a benchmark to choose how to behave, which makes economic theory at least partly true: i.e., when economics becomes self-fulfilling. Merton does not provide a clear definition of “truth.” By “true,” I mean the Popperian understanding of “not falsified by facts” (or “corroborated”). ^{Footnote 4} This mechanism, which is the heart of MacKenzie and Millo’s study of the performativity of the BSM model, moves away from the Callonian definition of performativity. Indeed, Callon clearly defends a generic definition of performativity, and explicitly rejects the concept of a self-fulfilling prophecy (Callon Reference Callon, MacKenzie, Muniesa and Siu2007, p. 321). Following MacKenzie and Millo, I endorse the Barnesian definition of performativity. I suggest that, to be complete, MacKenzie and Millo’s demonstration should consider also the idea of a self-fulfilling BSM model. The cornerstone of my argument is a consideration of what should be considered as the facts against which to evaluate the truth of a theory that becomes self-fulfilling. ^{Footnote 5}

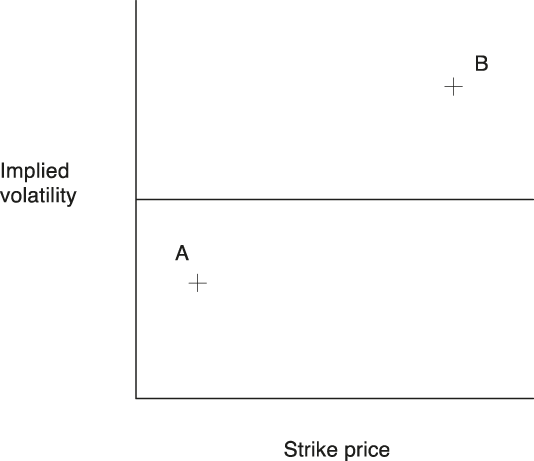
Let us summarize MacKenzie and Millo’s argumentation. With the exception of volatility, all the parameters of the BSM model are easily observable. So, the use of the BSM is particularly straightforward, since traders calculate the volatility of the underlying asset price, which returns a theoretical value fitting the current market price of the option. This so-called implied volatility in the BSM model is supposed to be the same for all the options for the same underlying asset with the same expiry date and different strike prices. The graph of implied volatility against the strike prices is a flat line (Figure 1).

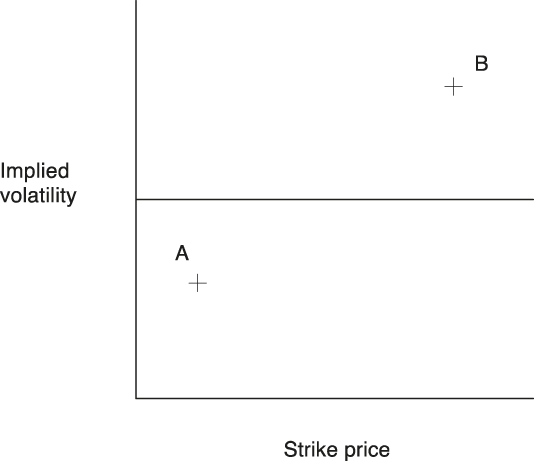
Figure 1. The Flat Line of Implied Volatility.

(Source: MacKenzie Reference MacKenzie, MacKenzie, Muniesa and Siu2007, p. 68)

This linear relation (the “flat line”) became a central element of MacKenzie and Millo: spreaders used this “normal” level of implied volatility as a way of profiting from price discrepancies. They used it to identity relatively cheap options to buy (A on the graph) and relatively expensive options to sell (B). If the implied volatility of A is under the mean implied volatility, A is undervalued, since there is a positive correlation between implied volatility and the price of options. At this stage, this is a generic case of performativity. However, such trading is a central mechanism in the way the BSM performs financial phenomena within a Barnesian perspective: traders effectively flatten the line. So, the self-fulfillment through the spread on volatility levels is a central element in MacKenzie and Millo’s thesis of performativity. It is important to stress that the BSM model explicitly provides what Perry Mehrling (2012, p. 132) views as a normative theory of rational option pricing. This point is particularly clear in the case of Fischer Black. In 1972, at the Center for Research in Security Prices seminar, Black showed his hostility to the creation of the CBOE, to the point of comparing it to a gambling house. However, once it was established, he did what he could to ensure that the market reached an efficient equilibrium. For instance, he sold printed tables based on the BSM model, which allowed a quick evaluation of the implied volatility of options in order to facilitate efficient trade-offs. If market investors exploited the profit opportunities correctly using the BSM price sheets, the market reached the efficiency indicated by the BSM model. Note that Black had co-authored with Jack Treynor guidelines for security analysts (Treynor and Black Reference Treynor and Black1973). However, Black, MacKenzie, and Millo were in agreement that the BSM model had been adopted because it implied profit opportunities for traders. The only point of difference was that Black saw the BSM model as channeling effective laws of the system (opportunities come from a trend away from the real values), while MacKenzie and Millo emphasized a self-fulfilling process: “The suggestion that the Black–Scholes–Merton model may have been performative in the Barnesian sense is the conjecture that the use of the model was part of the chain by which its referential character—its fit to ’reality’—was secured” (MacKenzie Reference MacKenzie, MacKenzie, Muniesa and Siu2007, p. 67).

Of course, MacKenzie and Millo’s argument goes beyond the simple mechanism of self-fulfillment. From an Austinian perspective, performativity necessitates a few felicitous conditions to be respected (Brisset Reference Brisset2014b, Reference Brisset2016). First, options were considered “unknown beasts” by most of the trader community traumatized by the 1929 Wall Street crash. Second, the BSM model was seen as an unfair way to trade. MacKenzie and Millo provide a fascinating description of the social pressure against the use of Black’s sheets: “[Traders] would laugh at you and try to intimidate you out of the pit, saying, ‘You’re not a man if you’re using those theoretical value sheets.’ They’d take your sheets and throw them down on the floor and say, ‘Be a man. Trade like a man. . . . You shouldn’t be here. You’re not a trader. You can’t trade without those’” (Hull interview, in MacKenzie and Millo Reference MacKenzie and Millo2003, p. 124). It took a certain time for the idea of “secure” and “rational” hedging to penetrate the ethos of the trading floor. Third, market regulation needed to correspond with the BSM’s hypothesis. For instance, Regulation T, which governs the extension of credit by security brokers and dealers by holding a margin requirement for stock purchases, became less restrictive. So the e hypothesis of the model, described above, became a reality. ^{Footnote 6} The felicity conditions are important and necessary, but not sufficient, conditions for the self-fulfilling mechanism emphasized above. When felicity conditions are held in the absence of a self-fulfilling motion, MacKenzie calls this generic performativity, which is of little interest. The BSM model changed the world by changing the way people looked at it. This is an important point, which historians of economic thought have noted (Mehrling Reference Mehrling2012; Bernstein Reference Bernstein2005). MacKenzie and Millo tried to go beyond this by exploring how the changing perspective on the options market changed the market itself.

III. FINANCIAL CRASH AND COUNTERPERFORMATIVITY

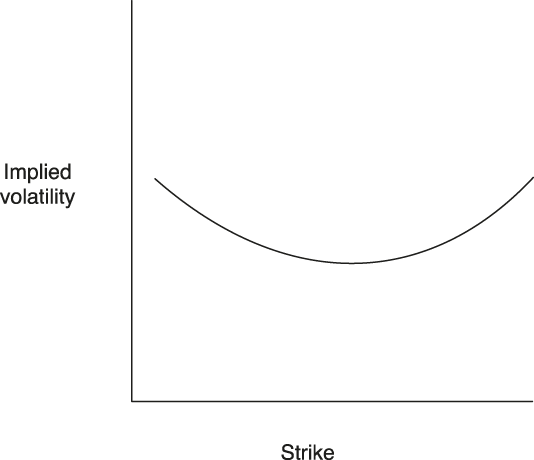
In the October 1987 stock market crash, the BSM model failed in fitting the social world to economic theory. On Black Monday, the Dow Jones lost 22.8% of its value, and the S&P 500 lost 20%. Jens Carston Jackwerth and Mark Rubinstein (1996, p. 1612) demonstrated that under the log-normal hypothesis, such deviation corresponds to the probability 10^-160, “which is virtually impossible.” The October 1987 event led the flat line to assume the famous volatility skew: volatility decreases as the strike price increases. The question emerging from this fact is simple: Why does the BSM model seem to fulfill all of the conditions of performativity only until the 1987 crash? We have discussed how the BSM model provides a representation of a specific good—the option—and allows identification of different options regarding a normal volatility. However, is this collective convention equivalent to the move in real prices? If the BSM model were self-fulfilling, our answer would be positive: the fact that people adhere to the BSM model implies that it becomes true. Before 1987, the observed implied volatility followed the BSM model: the flat line on the graph of implied volatility against the strike prices was observable. However, the October 1987 crash changed this: the graph of implied volatility against strike prices now tends to slope downwards. This is the famous volatility smile: the price options that correspond to large fluctuations (c1 and c2 in Figure 2) are traded at a higher price.

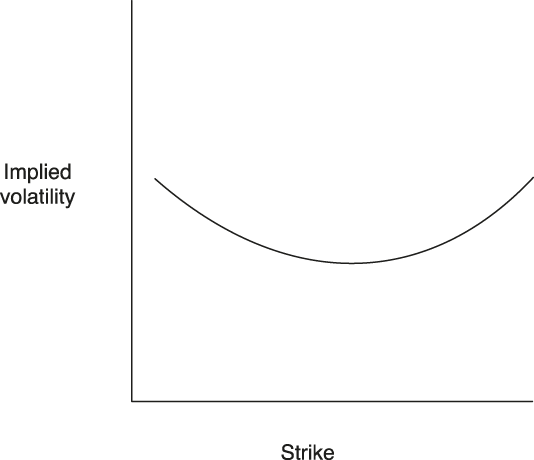
Figure 2. The Volatility Smile.

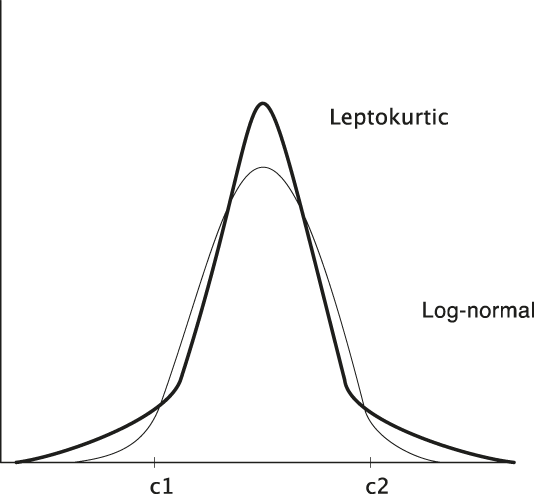
Unlike the BSM probabilistic hypothesis, the smile no longer corresponds to a log-normal distribution that excludes large depreciations and appreciations but fits with a leptokurtic distribution function: more peaked and fat-tailed (Figure 3).

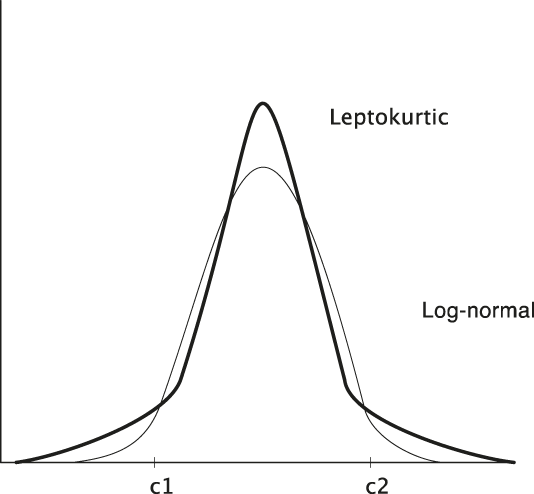
Figure 3. Log-normal and Leptokurtic Distributions.

For MacKenzie (2006, 2007), the existence of the smile since 1987 reveals the historical contingency of performativity of the BSM model; price patterns followed the model up to 1987. Then, an external shock changed this convergence world/model towards the smile, one time for performativity, one time for “counterperformativity.” This is the point when we disagree. The fact that implied volatility fits the BSM model (i.e., the fact that investors coordinate their representations on the flat line) teaches us nothing about the real world except that a subjective vision of the world (BSM’s flat line) fits with another subjective vision (the implied volatility) without any real self-fulfilling outcome on stock prices. Indeed, the implied volatility by construction is a level of volatility compatible with actual option prices, given the BSM assumptions. Financial phenomena that are actual stock volatility have never been implied in the reasoning. The 1987 crash might indicate that financial phenomena can resist the theory precisely because the risk representation involved in the BSM model is not self-fulfilling. Arguing for the performativity twist, which took place in 1987 from performativity to counterperformativity, is to overlook the fact that the risk representation of the BSM model can be contradicted by the objectivity of the financial phenomenona: the price motions. It has been well documented that implied volatility does not track actual volatility. For instance, Peter Fortune (Reference Fortune1996) shows that implied volatility is a biased forecast of actual volatility. Instead of a performativity twist (performativity and counterperformativity), it could be suggested that the BSM model never fits with real price fluctuations, and that traders realized this in 1987. The smile is the result of this awareness. To be complete, MacKenzie and Millo emphasized option market overlearning: to explain observed index option prices requires adding an artificial crash to the 1987 observed stock prices series every four years. The authors explain this as due to the traumatic character of the 1987 crash. The smile is reduced to a kind of collective trauma. Nevertheless, to say that a collective representation is overlearning is not to say that the previous representation (the flat line) was correct. Although the smile is overpronounced, it might be a better representation than the simple flat line.

We have shown that the flat line was linked directly to the log-normal distribution. In the next section, we explore this representation of price fluctuations in order to understand what is supposed to be “performative” in MacKenzie and Millo’s work.

IV. THE RESISTANCE OF FINANCIAL PHENOMENA

We are challenging the idea that in the case of price fluctuations, representation and phenomena should not be confused. The French sociologist Éric Brian is clear on this point: randomness comes before the calculation, not after (Brian Reference Brian2009, p. 5). The BSM model is supported by such an act of representation when it assumes that the stock price follows an exponential Brownian motion. The Brownian representation of the risk consists of two intertwined sets of ideas. First, the increments of the random variable of the continuous random walk are independent and identically distributed (i.i.d). A stochastic process with independent and stationary increments defines a Lévy process, named after the French mathematician Paul Lévy. Such a stochastic process is characterized as memoryless: a Markov first-order chain. This implies that the expected speculative gain is equal to zero; the best forecast of tomorrow’s course is today’s course. Second, in addition to the characterization of the law of probability as a log-normal law, this hypothesis reduces the continuous random walk to a particular case of the Lévy process: a Brownian motion.

These sets of ideas are intertwined in the sense that defining the market as a memoryless process leaves aside the risk of financial self-maintaining booms or falls, a risk that is incompatible with the normal distribution, which is characterized by the idea of some small variations around the mean.

This twofold conception can be traced back to the work of Jules Regnault and his 1863 opus, Calcul des chances et philosophie de la Bourse, in which he compares speculation to fair gambling where each bet is independent of any other (Jovanovic Reference Jovanovic2001). As in a coin toss, there is no way systematically to beat the market in making bets on short-term movements in prices, since the probabilities of upward and downward movements are equal. ^{Footnote 7} In other words, there is no benefit in knowing past prices. Regnault also maintains that traders’ errors follow a normal distribution. This representation found support in Louis Bachelier’s seminal Theory of Speculation. If S _t is the stock course:

$${E_{t\,}}\,\left( {{S_{t + 1}}\, - \,{S_t}} \right) = 0\,\,\,\,\,\,and\,\,\,\,\,\,{E_t}\,\left( {{S_{t + 1}}} \right) = {S_t}$$

This probabilistic schema can be extended to the entire market process. The Brownian representation of the risk is constitutive of the BSM model. The flat line of volatility corresponds to the implied log-normal probability distribution that was a common frame for options traders pre-1987.

Random Walk, Market Efficiency, and Rational Expectations

Karl Pearson first used the term “random walk.” This notion, as we have seen, implies that past values are of no utility for predicting future values. The early history of finance can be reduced to disagreement over whether market courses follow random walks (Stabile Reference Stabile2005; Walter Reference Walter2013). While advocates of the technical analysis, following the so-called Dow Theory (for instance, Schabacker Reference Schabacker1930), defend the existence of market trends, Alfred Cowles III tried to show empirically that market forecasters cannot forecast anything (Cowles Reference Cowles1933). This last position meets the idea of a random walk. Following the seminal contribution from Holbrook Working (Reference Working1934), Maurice Kendall (1953, p. 18) tested this hypothesis on stock markets in 1953 and concluded, “Such serial correlation as is present in these series is so weak as to dispose at once of any possibility of being able to use them for prediction. The Stock Exchange, it would appear, has a memory lasting less than a week.”

Although the Brownian motion was proposed first (after Bachelier) by Matthew Osborne (Reference Osborne1959), it was not until the mid-1960s that the concept was given a theoretical base. In the different “old” approaches, the absence of correlation of successive prices is explained by the idea that investors’ decisions concerning a stock are independent from one transaction to another, which seems scarcely plausible to the modern reader. Harry Roberts (Reference Roberts1959) was one of the first to indicate the lack of theoretical foundation for the random character of stock price fluctuations (Jovanovic Reference Jovanovic2008, Reference Jovanovic2009). He proposed the famous arbitrage proof argument, the same argument as was used by Paul Samuelson to provide the missing theoretical justifications for Kendall’s observations of random processes:

Perhaps it is a lucky accident, a boon from Mother Nature so to speak, that so many actual price time series do behave like uncorrelated or quasi-random walks. … Perhaps it is true that prices depend on a summation of so many small and somewhat independent sources of variation that the result is like a random walk. But there is no necessity for this. And the fact, if it is one, is not particularly related to perfect competition or market anticipations. … I shall deduce a fairly sweeping theorem in which next-period’s price differences are shown to be uncorrelated with (if not completely independent of) previous period’s price differences. (Samuelson Reference Samuelson1965a, p. 40)

Samuelson (Reference Samuelson1965a, 1965b, 1973) shows how, under certain conditions, new-information unpredictability leads stock prices to follow a stochastic process sequence, where expectation of the next value in the sequence is equal to the present observed value, given knowledge of all previous values: that is, a martingale. ^{Footnote 8} Samuelson linked randomness, anticipation, and speculation closely, using the martingale model: traders’ arbitrages would balance out prices around a value corresponding to the present stock of information. The title of his 1965 paper is explicit—“Proof That Properly Anticipated Prices Fluctuate Randomly”—and his conclusion was: “If one could be sure that a price will rise, it would have already risen” (Samuelson Reference Samuelson1965b, p. 41).

This is a major twist in economic thinking. Economists were rather skeptical about the idea of a random walk, since they were committed to the idea of a correlation between stock prices and expected future returns. ^{Footnote 9} Stephen LeRoy (1989, p. 1588) explains it thus: “If stock prices had nothing to do with preferences and technology, what about the prices of the machines that firms use? What about the wheat the farmer produces and the baker uses, but which is also traded on organized exchanges just like stock? Where does the Marshall’s Principles stop and the random walk start?”

Samuelson links randomness, information about fundamentals, and capital market efficiency, since it is precisely the exploitation of the information concerning the fundamentals that justifies the idea of randomness. This reasoning was founded theoretically on Eugene Fama’s (1965, 1970) efficient-market hypothesis: ^{Footnote 10} a market is said to be efficient if it fully reflects the available information $({{\rm{\Phi }}_t})$ . As a consequence, the martingale model constitutes a possible test for the efficient-market theory: expected profit has to be nul.

Entanglement between discounted cash flow and efficiency is closely ingrained in the notion of rational expectations. In Fama’s 1965 paper, there are some “superior chart readers” able to approximate the intrinsic value. In his 1970 paper, all available information ${{\rm{\Phi }}_t}$ is costlessly available to all market participants, and all these participants are agreed on “the implications of current information for the current price and distribution of future prices of each security” (Fama Reference Fama1970, p. 387). Of course, Fama does not use the rational-expectations hypothesis directly, although John Fraser Muth’s famous paper had been published in 1961. Nevertheless, in Fama’s definition of market efficiency, the idea that agents know the relevant system describing the economy is clear. Moreover, Robert Lucas (Reference Lucas1978) considers that expectations are rational if prices fully reflect all the available information.

If the asset price respects this characteristic, it is said to be efficient; i.e., it efficiently integrates all the pertinent information in the price. If expectations are rational and the market is efficient, the best forecast of tomorrow’s price is today’s price because it reflects all of the information:

$${\rm{E}}\left( {{S_{t + 1}}|{{\rm{\Phi }}_t}} \right) = {S_t}$$

In Fama’s view, efficiency ^{Footnote 11} and randomness justify one another: if markets are efficient, then it follows that future returns are unpredictable, and if we observe that future returns are unpredictable, then this proves that markets are efficient. ^{Footnote 12}

While there is a clear distinction to make between continuous random walks and martingales (LeRoy Reference LeRoy1989), we also draw close links between efficiency and randomness in general, which justifies the use of the Lévy process in the financial formalization. This is the case of the BSM model.

V. LEPTOKURTICITY AS A LIMIT FOR PERFORMATIVITY

The performative power of the BSM option-pricing model ran up against a strong counter-phenomenon: asset prices did not follow the standard representation emphasized in the previous section. The nub of our argumentation is that the quoted market prices exhibited a leptokurtic distribution long before the introduction of the BSM model on the CBOE. Hence, the BSM model never performed (in a Barnesian understanding) the economy, which led to the emergence of the volatility smile in 1987. This is the way that MacKenzie and Millo use the concept of performativity. They consider the rapprochement between theoretical and empirical implied volatility as a case of Barnesian performativity, which refers to the fact that the practical use of an aspect of economics makes economic processes more like their depiction by economics. To them, the “aspect of economics” is the BSM model, and implied volatility is the “economic process” that becomes more like its depiction by the BSM model. My claim is that to understand the “counterperformativity” of 1987, it is necessary to go beyond implied volatility when considering volatility, since I consider the flat line of volatility to be an “aspect of economics,” and stock volatility to be the “economic process.”

Leptokurticity was recorded long before 1987 (Walter Reference Walter2013, pp. 279–285). Éric Brian (Reference Brian2009) pointed to the constant gap between the actual and the log-normal distribution from 1830 to 2009. That is sufficient reason to doubt the plasticity of financial phenomena in the story of MacKenzie and Millo. We want to show that leptokurticity is linked closely to the convention-based nature of the financial phenomena.

Rational Bubble and Leptokurticity

The kind of framing effect stressed by Shiller might explain a sudden fall in prices. There is a large literature on the possibility of bubbles even in the case of rational expectations, which is a central justification of market efficiency and the Brownian motion. In a context of informational efficiency, the stock price depends on both the fundamental value of the stock (which is the actualization of future dividends) and a subjective element: the resale price of the stock. If one defines the price by the spread between itself and the fundamental value, the focus is on the subjective part:

$${S_t} = {1 \over {1 + x}}{E_t}\left( {{S_{t + 1}}} \right)$$

This equation is consistent with the efficiency paradigm: there is no way to release a speculative surplus. This is the so-called no-arbitrage condition. Standard financial theory ignores these speculative parts of the price determination by invoking the transversality condition (which states that the expected stock resale price tends toward zero). In their seminal model, Olivier Blanchard and Mark Watson (1982) do not consider this hypothesis, which is hard to justify. The stock price now is composed of a fundamental value and a speculative bubble, and there is an infinity of prices that respect the no-arbitrage condition. Thus, it is possible to achieve endogenous price movements producing bubbles. In conclusion, rational expectations do not necessarily guarantee that the price will fit the fundamental value. There are several self-confirming beliefs that the asset price depends on information that includes variables or parameters that are not part of market fundamentals. Blanchard and Watson provide a model of such dynamics:

If bubbles grow for a while and then crash, the innovations in the bubble will tend to be of the same sign while the bubble continues, then reverse signs when a crash occurs. The runs for the bubble innovation will then tend to be longer than for a purely random sequence, making the total number of runs over the sample smaller. Crashes will produce large outliers so that the distribution of innovations will have fat tails (i.e. the distribution will be leptokurtic). (Blanchard and Watson Reference Blanchard and Watson1982, p. 20)

The endogenous dynamics of the price seem to limit the idea that a theory will be self-fulfilling. The fact that some agents’ representations correspond to the efficient-markets hypothesis is not a guarantee that this representation can make the market more efficient. The origin of price variations could be different. Nevertheless, this fact rests on a process that directly calls into question the transversality condition: hyperinflation of stock resale prices. The momentum effect is a perfect example: the empirically observed tendency for rising stocks to rise further, and falling stocks to keep falling (Jegadeesh and Titman Reference Jegadeesh and Titman1993). This observation gave birth to a simple strategy: buying rising stocks and selling falling ones, which enhances the original tendency through a mimetic process and contests the rational-expectations hypothesis.

A market, in essence, is a place for conventional equilibria, or, in other words, mimetic behaviors. If market agents do not consider the fundamental value of a stock but rather the majority opinion of it, any further information is able to provoke a conventional switch, which could lead to a crash. Here, we are in the typical Keynesian beauty-contest world (Keynes [Reference Keynes1936] 2006). In John Maynard Keynes’s beauty contest, agents are led to infinite regressive thinking, since they have to choose the model they think the others will also choose. Agents base their decision on conventions that can collapse suddenly. The foundations of the BSM model do not avoid that kind of process. The expectation of dividends rests also on an endless regression: a common evaluation of the future is per se an intersubjective tacit agreement about the future states of the economy and the way these discount fluxes can be calculated. Beyond this common representation of the future, the rational-expectations and market-efficiency hypotheses rest on another strong hypothesis: the existence of a fundamental value reflecting the conditions in the market for the underlying asset (an existence that has been long discussed). ^{Footnote 15} Yet, like financial markets, real markets depend on the polarization of goods and capital values (Orléan Reference Orléan2011). This is a strong argument for the intrinsic strong volatility of the financial market through the volatility of the conventions in the real economy.

So, aside from empirical proofs of the leptokurtic nature of the market prices, there is a strong theoretical foundation for suggesting that the BSM model cannot perform stock prices in order to confirm the flat line of implied volatility.

VI. NUANCING PERFORMATIVITY

MacKenzie and Millo’s history can be challenged about the same point: the BSM model is not really self-fulfilling. First, we could consider the conflict of representations. Of course, if we consider only the argument of performativity in the strict market of options, we cannot help but notice a convergence between the BSM model flat line hypothesis and the actual implied volatility in the period from 1976 to 1987 (Rubinstein 1985). Options traders shared the same representation through their use of the BSM model as a benchmark. Thus, the implied volatility (which is a subjective level of volatility) came to fit with the flat line. Such a representation excludes the possibility of a violent crash. Nevertheless, in the stock market, any small piece of information is able to produce violent price fluctuations as described in the Wall Street Journal article evoked by Shiller. Thus, to say that the linear relation between implied volatility and strike prices is confirmed in the options market is not to imply that the historical volatility corresponds to the log-normal distribution in the stock market. Black Monday contradicts this representation.

Second, it is possible also to stress that the performativity thesis overlooks the important role of exogenous information on the stock market. To say that the BSM model can become true if it becomes a coordination convention is to ignore the impact of real markets on financial markets, or to suppose that the BSM model is true in hypothesizing a Gaussian economy (without, for instance, earthquakes or tsunamis).

Finally, MacKenzie and Millo seem to accept the BSM model’s representation of the world by ignoring the intrinsic financial market fluctuations à la Keynes. Even when retaining the rational-expectations hypothesis, it is possible theoretically to exhibit the possibility of bubbles and crashes: financial markets are per se conventional arenas. This is somewhat reminiscent of how Henri Poincaré urged caution about Louis Bachelier’s thesis, applying the natural trait in human nature to herd like a Panurge’s sheep.

Thus, leptokurticity can be seen as both an exogenous element and endogenous dynamics. The so-called volatility smile is not a sudden shift from self-fulfillment to self-destruction, from a log-normal to a leptokurtic world; it is a sudden awareness by the investor of an important characteristic of the financial world: leptokurticity. The hypothesis corresponding to the flat line, the log-normal distribution, never became true. As a consequence, 1987 was a powerful shock for theoretical innovation and brought renewed interest in parametric use of the BSM model (Jackwerth 1999) and a rise in econophysics (Jovanovic and Schinckus Reference Jovanovic and Schinckus2013a, Reference Jovanovic and Schinckus2013b).

Fischer Black clearly was aware of the fact that the BSM model is based on empirically wrong assumptions (Black 1976). Nevertheless, as we have shown above, the objective of the BSM model was not necessarily to describe the world but to help traders “to understand how change in the underlying assumptions would cause a change in the calculated option price” (Mehrling Reference Mehrling2012, p. 245). This objective is clear in Black’s (1989) paper “How to Use the Holes in Black-Scholes.” ^{Footnote 16} The smile is clearly a sign of the BSM model’s adaptability; practical and easy to use and to adapt, the BSM model remains the theoretical foundation of most of the models elaborated after 1987. Our claim is that to provide insights into the reasons for the evolutions in the use of the BSM model, the idea of performativity should be inseparable from the idea of counterperformativity, and counterperformativity should be linked closely to the concept of self-fulfillment. There is still work to be done on that aspect.