2. THEORETICAL ANALYSIS

In direct drive ICF implosions, laser irradiating target induces a shock wave propagating through the ablator. During the shock propagation, the ablation front travels at a constant velocity, and any perturbations at the ablation front could grow due to the ablative RMI. Firstly, we simply analyze the ablative RMI at ablation front based on an ablative RTI model. The growth rate of ablative RTI is strongly dependent on the magnitude of the Froude number (F _r) (Betti et al., Reference Betti, Goncharov, McCrory and Verdon1995; Betti et al., Reference Betti, Goncharov, McCrory and Verdon1996; Goncharov et al., Reference Goncharov, Betti, McCrory, Sorotokin and Verdon1996a , Reference Goncharov, Betti, McCrory and Verdon b ; Atzeni & Meyer-Ter-Vehn, Reference Atzeni and Meyer-Ter-Vehn2004). For large Froude numbers, the linear growth rate of ablative RTI can be written as (Goncharov et al., Reference Goncharov, Betti, McCrory, Sorotokin and Verdon1996a , Reference Goncharov, Betti, McCrory and Verdon b ; Piriz et al., Reference Piriz, Sanz and Ibanez1997)

where $A_{\rm T} = \displaystyle{{1 - { {\rm \rho}} _{{\rm bo}} /{ {\rm \rho}} _{\rm a}} \over {1 + { {\rm \rho}} _{{\rm bo}} /{ {\rm \rho}} _{\rm a}}}, V_{{\rm bo}} = V_{\rm a} \displaystyle{{{ {\rm \rho}} _{\rm a}} \over {{ {\rm \rho}} _{{\rm bo}}}}, \displaystyle{{{ {\rm \rho}} _{{\rm bo}}} \over {{ {\rm \rho}} _{\rm a}}} = { {\rm \mu}} _0 (kL_0 )^{1/{ {\rm \nu}}}, \;{ {\rm \mu}} _0 = \displaystyle{{(2/{ {\rm \nu}} )^{1/{ {\rm \nu}}}} \over {{\rm \Gamma} (1 + 1/{ {\rm \nu}} )}} + \displaystyle{{0.12} \over {{\rm \nu}} ^2}$ . A _T is the Atwood number, k = 2π/λ is the wave number, g is the acceleration of target and V _a is the ablation velocity. V _bo, ρ_bo is the velocity and density of the blow-off plasma, respectively. The blow-off plasma velocity is generally much larger than the ablation velocity. ν is the power index of the thermal conduction, L ₀ is the characteristic thickness of the ablation front, and Γ(x) is the γ function. Froude number is defined as $F_{\rm r} = V_{\rm a}^2 /L_0 g$ . Since the acceleration of ablation front is zero in the phase of ablative RMI, Eq. (1) satisfies the condition of large Froude numbers. The growth formula of ablative RMI can be obtained via Eq. (1) to set the acceleration to zero

Since the Atwood number $A_{\rm T} $ approaches 1 due to ρ_bo/ρ_a ≪ 1, the growth of ablative RMI can be expressed as

where η(t) and η₀ are instantaneous and initial perturbation amplitude at ablation front. Equation (3) describes the decayed oscillation behavior of ablative RMI, which has been confirmed through experiments (Aglitskiy et al., Reference Aglitskiy, Velikovich, Karasik, Serlin, Pawley, Schmitt, Obenschain, Mostovych, Gardner and Metzler2001, Reference Aglitskiy, Velikovich, Karasik, Serlin, Pawley, Schmitt, Obenschain, Mostovych, Gardner and Metzler2002). According to Eq. (3), the decaying rate of oscillation amplitude depends on the ablation velocity, and the oscillation frequency relies to the ablation velocity and the blow-off plasma velocity.

Owing to not including the effect produced by the rippled shock, Eq. (3) accuracy is not enough. A more complex and accurate theoretical model based on the sharp-boundary mode (Piriz et al., Reference Piriz, Sanz and Ibanez1997) has been developed by Goncharov (Goncharov, Reference Goncharov1999; Goncharov et al., Reference Goncharov, Gotchev, Vianello, Boehly, Knauer, McKenty, Radha, Regan, Sangster, Skupsky, Smalyuk, Betti, McCrory, Meyerhofer and CherfilsClérouin2006). The boundary conditions at the shock front are derived by using the Hugoniot relations and at the ablation front the self-consistent analysis (Sanz, Reference Sanz1996) is applied. The Goncharov model of ablative RMI predicts that the amplitude of ablation front perturbations will evolve according to

where c ₁ is the sound speed in the post-shock area and Ω = $ k\sqrt {V_{\rm a} V_{{\rm bo}}} $ is the oscillation frequency. The detailed representation of f(kc ₁ t) and η _v (t) can be found in reference (Goncharov et al., Reference Goncharov, Gotchev, Vianello, Boehly, Knauer, McKenty, Radha, Regan, Sangster, Skupsky, Smalyuk, Betti, McCrory, Meyerhofer and CherfilsClérouin2006). Note that the Goncharov model must satisfy the condition of kD _c>1, where D _c is the size of conduction zone defined as the distance of the ablation front and the critical density surface. The first term (f(kc ₁ t)) is much less than the second term when kc ₁ t >1, which can be ignored in the following discussion. The ${ {\rm \eta}} _v (t) \propto \sin (kV_{\rm a} \sqrt {1 - M_1^2} /M_1 t)/\sqrt {kV_{\rm a} t} $ is the oscillatory contribution due to the vorticity produced behind the rippled shock front, where M ₁ is the Mach number in the post-shock area. Equation (4) shows that the perturbations at ablation front oscillate with time due to two terms. First is the dynamic overpressure near the ablation front acting as a restoring force leading to the oscillation with a frequency $k\sqrt {V_{\rm a} V_{{\rm bo}}} $ . The amplitude of such oscillation is damped by the ablation term $e^{ - 2kV_{\rm a} t} $ . The second physical mechanism which also leads to the ablation-front oscillations is the convection of the vorticity produced behind the rippled shock front. The shock-induced vorticity oscillates with a frequency $kV_{\rm a} \sqrt {1 - M_1^2} /M_1 $ and amplitude decays as $\sqrt {kV_{\rm a} t} $ . Since the blow-off plasma velocity is much larger than the ablation velocity (V _bo/V _a ≫ 1), the first oscillation term dominates the evolution of perturbation. So here we just discuss the second term in Eq. (4). The Goncharov model is similar with Eq. (3) obtained from the ablative RTI model providing that the term of vorticity in Eq. (4) is neglected. The second term in Eq. (4) can be detailed as

where

is the density compression ratio in the post-shock and unshocked areas. 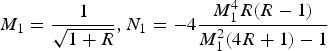$M_1 = \displaystyle{1 \over {\sqrt {1 + R}}}, N_1 = - 4\displaystyle{{M_1 ^4 R(R - 1)} \over {M_1 ^2 (4R + 1) - 1}}$ and 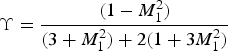${\rm \Upsilon} = \displaystyle{{(1 - M_1 ^2 )} \over {(3 + M_1 ^2 ) + 2(1 + 3M_1 ^2 )}}$ are the constants only depending on R (Peterson et al., Reference Peterson, Clark, Masse and Suter2014). According to Eq. (5), the oscillation amplitude of ablative RMI depends on the value $\sqrt {{ {\rm \alpha}} _0 ^2 + { {\rm \beta}} _0 ^2} $ , while α₀ and β₀ depend on the post-shock sound speed c ₁, the ablation velocity V _a and the velocity of the blow-off plasma V _bo. Owing to $\sqrt {V_{\rm a} /V_{{\rm bo}}} \ll 1$ , the second term in the expression of β₀ also can be ignored. So the oscillation amplitude of $\sqrt {{ {\rm \alpha}} _0 ^2 + { {\rm \beta}} _0 ^2} $ in Eq. (5) can be expressed as

The density compression ratio R is about 2–4 in the laser-driven target. All the values of a ₀, b ₀, and a ₁ are positive for the R in this range. According to Eq. (6), it is found that $\sqrt {{ {\rm \alpha}} _0 ^2 + { {\rm \beta}} _0 ^2} $ is a monotonically increasing function of c ₁ and a monotonically decreasing function of V _bo or V _a. Figure 1 show the relation of oscillation amplitude with c ₁/V _a and c ₁/V _bo for a fixed compression ratio (R = 3). It is found that the larger ablation velocity and the larger blow-off plasma velocity can decrease the oscillation amplitude.

Fig. 1. The relation of oscillation amplitude with c ₁/V _a and c ₁/V _bo for a fixed compression ratio (R = 3).

The high-Z dopant in plastic would absorb more energy of laser and emit stronger radiation when intense laser beams irradiate a doped target. The stronger radiation would lead to a higher radiation temperature at ablation front and increase the ablation velocity. According to the above theoretical model, the larger ablation velocity can increase the decaying rate of oscillation amplitude and reduce the oscillation amplitude of ablative RMI, which means that the high-Z dopant is beneficial to reduce the ablative RMI. The detailed effect of Br-dopant on the ablative RMI will be theoretically analyzed in combination with the 1D simulations, and the 2D simulations are also employed to confirm the theoretical results.

3. SIMULATIONS AND DISCUSSION

A multi-dimensional radiation hydrodynamics code (Kawata et al., Reference Kawata, Sato, Teramoto, Bandoh, Masubichi and Takahashi1993; Ogoyski et al., Reference Ogoyski, Kawata and Popova2010) is employed to model the evolution of laser-driven ablative RMI. A three-temperature model is used to describe the temperature of ions, electrons, and radiation, and multi-groups diffusion approximation is applied for the radiation transport. The opacities of materials are calculated by the SNOP code (Eidmann, Reference Eidmann1994), and the equation of state is obtained from MPQEOS (Kemp et al., Reference Kemp and Meyer-ter-Vehn1998). The flux-limited Spitzer thermal conduction model (Spitzer & Härm, Reference Spitzer and Härm1953) (the standard value of the flux limiter is f = 0.06), and 2D ray-tracing laser-energy deposition are employed. The frequency of photon is divided into 20 groups in simulations.

Schematic of the target used in simulations is shown in Figure 2(a). In order to investigate the influence of high-Z dopant on the laser-driven ablative RM instability, two planar targets, that is, undoped target (CH) and 3% Br-doped target (C₅₀H₄₇Br₃) are employed. The initial densities of the undoped and Br-doped targets are 1.06 and 1.26 g cm⁻³. The target is set to be enough thick to avoid the premature onset of ablative RTI. The targets are uniformly irradiated by 0.35 µm wavelength laser beams with a 2.5-ns square pulse shape and intensity of 1.0 × 10¹⁴ W cm⁻³. In 2D simulations, a sine perturbation is preset at the incident surface with different wavelengths (20, 30, and 50 µm) and same amplitude (1 µm).

Fig. 2. (a) Schematic representation of the target irradiated by laser in simulations; (b) density profile (solid lines) and radiation temperature (dashed lines) at t = 0.9 ns for the undoped target (red lines) and Br-doped target (black lines).

The density profiles and radiation temperature profiles at 0.9 ns from 1D simulations for the undoped and Br-doped targets are shown in Figure 2(b). Note that the target has been divided into four areas by the critical density surface, the ablation front and the shock front. First is the area of laser-energy deposition, the laser energy is absorbed by electrons leading to a high-temperature plasma corona. Second is the area of thermal conduction, radiation emitted from the high-temperature plasma corona ablates the dense target. In this area, the non-uniformity of laser irradiation can be thermal smoothed out before it transmits to the ablation front. Third is the post-shock area, the dense target is compressed by the ablation-generated rippled shock and the convection of the vorticity produced behind the rippled shock will influence the ablation front through this area. Fourth is the unshocked area, the density and the press in this area change little, it can be pre-heat by the high-energy X ray or the hot electrons. The radiation temperature in first and second areas is higher in the Br-doped target than that in the undoped target. In the Br-doped target, the Br atoms in corona plasma emit strong radiation, which leads to a higher radiation temperature at the ablation front. Moreover, the size of radiation conduction zone, defined as the distance between the ablation front and the critical surface, is larger in the Br-doped target than that in the undoped target. The smaller density gradient at the ablation front is also found in the Br-doped target, which indicates that the Br-doped target has a larger characteristic thickness of the ablation front.

The Betti–Goncharov procedure (Betti et al., Reference Betti, Goncharov, McCrory and Verdon1998) is employed to calculate the parameters V _a and V _bo. The pressure profiles and density profiles at the ablation front obtained from the 1D simulations are used to fit these density and pressure profiles at each time step generated via (Betti et al., Reference Betti, Goncharov, McCrory and Verdon1998)

where ξ = ρ/ρ_a is the density normalized to its peak value at ablation front, Π = p/p _a is the pressure normalized to the pressure at the peak of density, and ${\rm \Pi} _{\rm a} = V_{\rm a} \sqrt {\,p_{\rm a} /{ {\rm \rho}} _{\rm a}} $ is the normalized ablation velocity. The parameters (ν, L ₀, and Π_a) in Eqs (7) and (8) can be obtained by the mathematical fitting process. Ablation velocity can be calculated via $V_{\rm a} = {\rm \Pi} _{\rm a} /\sqrt {\,p_{\rm a} /{ {\rm \rho}} _{\rm a}} $ and the blow-off plasma velocity can be calculated by V _a, ν, and L ₀.

Table 1 shows the time-averaged values (0.4–1.0 ns) of ν, L ₀, V _a, V _bo, and c ₁ for the undoped and doped targets. Note that the Br-doped target has a larger characteristic thickness of the ablation front (L ₀) and a larger ablation velocity (V _a), which is the main reason of the suppression for ablative RTI in the Br-doped target and it has been confirmed by experiments and simulations (Fujioka et al., Reference Fujioka, Sunahara, Nishihara, Ohnishi, Johzaki, Shiraga, Shigemori, Nakai, Ikegawa, Murakami, Nagai, Norimatsu, Azechi and Yamanaka2004a , Reference Fujioka, Sunahara, Ohnishi, Tamari, Nishihara, Azechi, Shiraga, Nakai, Shigemori, Sakaiya, Tanaka, Otani, Okuno, Watari, Yamada, Murakami, Nagai, Norimatsu, Izawa, Nozaki and Chen b ). It is also important to observe that the Br-doped target has a larger blow-off plasma velocity and a smaller post-shock sound speed. According to Eq. (5), larger ablation velocity and larger blow-off plasma velocity in the Br-doped target would lead to a higher oscillation frequency, and larger ablation velocity would lead to a faster decay of the oscillation amplitude. According to Eq. (6), smaller post-shock sound speed, larger ablation velocity, and larger blow-off plasma velocity in the Br-doped target would decrease the oscillation amplitude of ablative RMI, and leading to a smaller maximum of growth factor. The detailed comparison of the growth factor calculated via Eq. (5) for the Br-doped target (red solid lines) and the undoped target (black solid lines) is shown in Figure 3. For all of the three perturbation wavelengths (20, 30 and 50 µm), the Br-dopant reduces the oscillation amplitude and increases the oscillation frequency of the ablative RMI. As shown in Figure 3, at early stage of the ablative RMI, the growth factor in Br-dopant target is much smaller than that in the undoped target, which means that the Br-dopant in a thin plastic target can effectively reduce the seeds of ablative RTI. The Br-dopant in the thick target is also beneficial to decrease the seeds of ablative RTI due to smaller oscillation amplitude and larger decaying rate of the oscillation amplitude.

Fig. 3. The growth factors of theoretical results (solid lines) and simulations (dashed lines) for the undoped target (black lines) and Br-doped target (red lines) with 20 µm wavelength perturbation (a), 30 µm wavelength perturbation (b) and 50 µm wavelength perturbation (c), respectively.

Figure 4 shows the ray-trace of laser-energy deposition in the contour of electron number density and the contour of electron temperature at t = 0.5 ns for the undoped and Br-doped targets with a 30 µm wavelength perturbation at ablation surface. It is clearly seen that the contour lines of electron number density are rippled. Since the laser is absorbed in a perturbed region, the ray propagation is strongly disturbed, which would introduce the additional non-uniformity of laser irradiation at the critical density surface. Fortunately, the weak non-uniformity of laser irradiation can be thermal smoothed out in the thermal conduction area before it transmits to the ablation front. As shown in Figure 4, near the critical density surface the contour lines of electron temperature are smooth, which indicates that the non-uniformity of laser irradiation at the critical density surface will not influence the ablative RMI growth at ablation front. Since the high-Z dopant in blow-off plasma increases the electron number density, the larger size of thermal conduction zone is also found in the Br-doped target.

Fig. 4. The ray-trace of laser-energy deposition (black solid lines) in the contour of electron number density (red dashed lines) and the contour of electron temperature (purple dotted lines) at t = 0.5 ns for the undoped target (a) and the Br-doped target (b).

Figure 5 shows the density distribution of 2D simulations at t = 0.8 ns for the undoped and Br-doped targets with a 30 µm wavelength perturbation at ablation surface. It is clearly seen that owing to the growth of ablative RMI, the perturbation predominantly grows at the ablation front, while the deformation at shock front almost disappears. The deformation at the ablation front is more drastic in the undoped target than that in the Br-doped target, which qualitatively confirm that the Br-dopant can reduce the perturbation growth at the ablation front. The opposite perturbation phase for the undoped and Br-doped targets is also observed in Figure 5. The valleys of initial perturbation locate at X = 15 and 45 µm, while at t = 0.9 ns the valleys of perturbation have become peaks for the Br-doped target, which indicates the perturbation phase inverse occurs. While for the undoped target, the perturbation still grows with original phase. The earlier phase inverse confirms the larger oscillation frequency of ablative RMI in the Br-doped target.

Fig. 5. The density distribution of 2D simulations for the undoped target (a) and the Br-doped target (b).

The growth factors of 2D simulations for the undoped (black dashed lines) and doped (rad dashed lines) targets with the perturbation wavelength of 20, 30, and 50 µm are also plotted in Figure 3. Since the ablative RTI is triggered at 1 ns, the growth factors of ablative RMI are recorded only before t = 1 ns. In simulations, the growth factor is defined as $GF_{{\rm \Delta} {\rm OD}} {\rm =} (\triangle m({\rm t})/\triangle m_0 )$ , where m(t), m ₀ are the instant and initial areal-density modulations, respectively. The areal-density modulations include the perturbation at shock front, and it will bring some error to evaluate the perturbation at ablation front. Since the perturbation at shock front decays fast and is much smaller than it at the ablation front, the areal-density modulations can quantitatively describe the evolution of ablative RMI. As shown in Figure 3(a), for the case with 20 µm wavelength, the growth factors for both targets first increase to the peak and then decrease to the valley, which indicates the oscillation behavior of ablative RMI. The growth factors of the undoped target reach the peak at 0.46 ns, while the Br-doped target only needs 0.25 ns, which indicates a larger oscillation frequency of perturbation growth in the Br-doped target. It is noted that the maximum of growth factor in the Br-doped target (1.6) is much smaller than that in the undoped target (3.9), which indicates that the Br-dopant can reduce the oscillation amplitude of ablative RMI. For the case of 30 and 50 µm wavelengths, the oscillation behaviors of perturbation growth are also presented. The oscillation frequency decreases with the increase of the perturbation wavelength. The maximums of growth factor in the Br-doped target with different wavelengths are also much smaller than that in the undoped target. The 2D simulations confirm the theoretical prediction of the higher oscillation frequency and the smaller oscillation amplitude in the Br-doped target. The detailed comparisons in Figure 3 show that there are still some differences between the theoretical prediction and the simulations. A time shift exists at the beginning of the growth of ablative RMI. Such a discrepancy is due to the breaking down of the theoretical model validity condition at the beginning of the pulse. It needs some time for the conduction zone to grow and satisfy the condition of kD _c>1, which is not taken into account in the theoretical model. Since the first term and the last term in Eq. (4) are ignored in the theoretical model, it will bring some discrepancies to the simulations. In addition, the growth factor of areal-density modulation used in simulations includes the perturbation at shock front, which also will bring some error to evaluate the perturbation at ablation front.