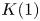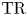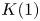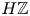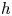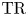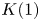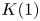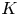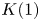1. Introduction
The topological cyclic homology, ![]() $\mathrm {TC}(R)$, of a ring (or ring spectrum)
$\mathrm {TC}(R)$, of a ring (or ring spectrum) ![]() $R$ is a basic invariant introduced by Bökstedt, Hsiang, and Madsen [Reference Bökstedt, Hsiang and MadsenBHM93] (see also Dundas, Goodwillie, and McCarthy [Reference Dundas, Goodwillie and McCarthyDGM13] and Nikolaus and Scholze [Reference Nikolaus and ScholzeNS18]) with many applications in algebraic
$R$ is a basic invariant introduced by Bökstedt, Hsiang, and Madsen [Reference Bökstedt, Hsiang and MadsenBHM93] (see also Dundas, Goodwillie, and McCarthy [Reference Dundas, Goodwillie and McCarthyDGM13] and Nikolaus and Scholze [Reference Nikolaus and ScholzeNS18]) with many applications in algebraic ![]() $K$-theory. Its
$K$-theory. Its ![]() $p$-adic completion
$p$-adic completion ![]() $\mathrm {TC}(R; \mathbb {Z}_p)$ arises as the fixed points of an operator called Frobenius on another invariant
$\mathrm {TC}(R; \mathbb {Z}_p)$ arises as the fixed points of an operator called Frobenius on another invariant ![]() $\mathrm {TR}(R; \mathbb {Z}_p)$, which plays a central role in the approach to
$\mathrm {TR}(R; \mathbb {Z}_p)$, which plays a central role in the approach to ![]() $\mathrm {TC}$ via equivariant stable homotopy theory. The construction
$\mathrm {TC}$ via equivariant stable homotopy theory. The construction ![]() $\mathrm {TR}(-; \mathbb {Z}_p)$ is often of arithmetic significance; for instance, the foundational calculations [Reference Hesselholt and MadsenHM03, Reference Hesselholt and MadsenHM04, Reference Geisser and HesselholtGH06] of the
$\mathrm {TR}(-; \mathbb {Z}_p)$ is often of arithmetic significance; for instance, the foundational calculations [Reference Hesselholt and MadsenHM03, Reference Hesselholt and MadsenHM04, Reference Geisser and HesselholtGH06] of the ![]() $p$-adic
$p$-adic ![]() $K$-theory of local fields
$K$-theory of local fields ![]() $F$ are based on the relationship between
$F$ are based on the relationship between ![]() $\mathrm {TR}(\mathcal {O}_F; \mathbb {Z}_p)$ and the de Rham–Witt complex with log poles of
$\mathrm {TR}(\mathcal {O}_F; \mathbb {Z}_p)$ and the de Rham–Witt complex with log poles of ![]() $\mathcal {O}_F$.
$\mathcal {O}_F$.
In this paper, we prove some structural results about ![]() $\mathrm {TR}$ and how it relates to its
$\mathrm {TR}$ and how it relates to its ![]() $K(1)$-localization, throughout at an implicit prime number
$K(1)$-localization, throughout at an implicit prime number ![]() $p$. We will only consider
$p$. We will only consider ![]() $p$-typical
$p$-typical ![]() $\mathrm {TR}$ and after
$\mathrm {TR}$ and after ![]() $p$-adic completion. The operation of
$p$-adic completion. The operation of ![]() $K(1)$-localization when applied to algebraic
$K(1)$-localization when applied to algebraic ![]() $K$-theory is dramatically simplifying, as shown by Thomason [Reference ThomasonTho85, Reference Thomason and TrobaughTT90]; in particular,
$K$-theory is dramatically simplifying, as shown by Thomason [Reference ThomasonTho85, Reference Thomason and TrobaughTT90]; in particular, ![]() $K(1)$-local
$K(1)$-local ![]() $K$-theory satisfies étale descent and admits a descent spectral sequence from étale cohomology under mild hypotheses; see [Reference Clausen and MathewCM19] for a modern account. Here we study analogs of some of these properties for
$K$-theory satisfies étale descent and admits a descent spectral sequence from étale cohomology under mild hypotheses; see [Reference Clausen and MathewCM19] for a modern account. Here we study analogs of some of these properties for ![]() $L_{K(1)} \mathrm {TR}(-)$. Our starting point is the following theorem.
$L_{K(1)} \mathrm {TR}(-)$. Our starting point is the following theorem.
Theorem 1.1 As a functor on connective ![]() $H\mathbb {Z}$-algebras,
$H\mathbb {Z}$-algebras, ![]() $L_{K(1)} \mathrm {TR}(-)$ is a truncating invariant in the Land–Tamme sense [Reference Land and TammeLT19]. In other words, if
$L_{K(1)} \mathrm {TR}(-)$ is a truncating invariant in the Land–Tamme sense [Reference Land and TammeLT19]. In other words, if ![]() $R$ is a connective
$R$ is a connective ![]() $H\mathbb {Z}$-algebra, then
$H\mathbb {Z}$-algebra, then ![]() $L_{K(1) } \mathrm {TR}(R) \xrightarrow {\sim } L_{K(1)} \mathrm {TR}(\pi _0 R)$.
$L_{K(1) } \mathrm {TR}(R) \xrightarrow {\sim } L_{K(1)} \mathrm {TR}(\pi _0 R)$.
Theorem 1.1 refines results of [Reference Land, Mathew, Meier and TammeLMMT20, Reference Bhatt, Clausen and MathewBCM20], where it is shown that ![]() $L_{K(1)} K(-)$ and (equivalently)
$L_{K(1)} K(-)$ and (equivalently) ![]() $L_{K(1)} \mathrm {TC}(-)$ are truncating invariants of connective
$L_{K(1)} \mathrm {TC}(-)$ are truncating invariants of connective ![]() $H\mathbb {Z}$-algebras, which ultimately follows from the claim
$H\mathbb {Z}$-algebras, which ultimately follows from the claim
and more generally (and consequently) for any ![]() $H\mathbb {Z}$-algebra
$H\mathbb {Z}$-algebra ![]() $R$,
$R$,
In [Reference Bhatt, Clausen and MathewBCM20], (1) is proved via a calculation in prismatic cohomology; in [Reference Land, Mathew, Meier and TammeLMMT20], (1) is proved using some unstable chromatic homotopy theory. Our proof of Theorem 1.1 (which also gives a new proof of (1)) is based on a direct ![]() $\mathrm {TC}$-theoretic argument via estimation of exponents of nilpotence of the Bott element; in fact, it yields a slightly stronger result (Theorem 3.1 below).
$\mathrm {TC}$-theoretic argument via estimation of exponents of nilpotence of the Bott element; in fact, it yields a slightly stronger result (Theorem 3.1 below).
The property of being truncating yields many pleasant features of the construction ![]() $L_{K(1)} \mathrm {TR}(-)$: by [Reference Land and TammeLT19], one obtains
$L_{K(1)} \mathrm {TR}(-)$: by [Reference Land and TammeLT19], one obtains ![]() $cdh$-descent and excision. Since we are working
$cdh$-descent and excision. Since we are working ![]() $K(1)$-locally, we can combine this with results of [Reference Clausen, Mathew, Naumann and NoelCMNN20] to obtain
$K(1)$-locally, we can combine this with results of [Reference Clausen, Mathew, Naumann and NoelCMNN20] to obtain ![]() $h$-descent.
$h$-descent.
Theorem 1.2 Any ![]() $K(1)$-local localizing invariant which is truncating, such as
$K(1)$-local localizing invariant which is truncating, such as ![]() $L_{K(1)} \mathrm {TR}(-)$, satisfies
$L_{K(1)} \mathrm {TR}(-)$, satisfies ![]() $h$-descent on quasi-compact and quasi-separated (qcqs) schemes.
$h$-descent on quasi-compact and quasi-separated (qcqs) schemes.
In particular, ![]() $L_{K(1)}\mathrm {TR}(-)$ satisfies étale descent. This is not so surprising, since
$L_{K(1)}\mathrm {TR}(-)$ satisfies étale descent. This is not so surprising, since ![]() $\mathrm {TR}(-; \mathbb {Z}_p)$ itself (like all Hochschild-theoretic invariants) actually satisfies flat descent; see [Reference Bhatt, Morrow and ScholzeBMS19, § 3]. However, Theorem 1.2 (together with (1)) leads to étale descent in the generic fiber. Since
$\mathrm {TR}(-; \mathbb {Z}_p)$ itself (like all Hochschild-theoretic invariants) actually satisfies flat descent; see [Reference Bhatt, Morrow and ScholzeBMS19, § 3]. However, Theorem 1.2 (together with (1)) leads to étale descent in the generic fiber. Since ![]() $\mathrm {TR}(R; \mathbb {Z}_p)$ of a ring
$\mathrm {TR}(R; \mathbb {Z}_p)$ of a ring ![]() $R$ depends only on the (derived)
$R$ depends only on the (derived) ![]() $p$-adic completion of
$p$-adic completion of ![]() $R$, we can informally view
$R$, we can informally view ![]() $L_{K(1)} \mathrm {TR}(R)$ as an invariant of the ‘rigid space’ associated to
$L_{K(1)} \mathrm {TR}(R)$ as an invariant of the ‘rigid space’ associated to ![]() $R[1/p]$.
$R[1/p]$.
Example 1.3 (Galois descent in the generic fiber) Let ![]() $R \to S$ be a finite, finitely presented map of rings. Suppose we have a finite group
$R \to S$ be a finite, finitely presented map of rings. Suppose we have a finite group ![]() $G$ acting on
$G$ acting on ![]() $S$ such that
$S$ such that ![]() $R[1/p] \to S[1/p]$ is
$R[1/p] \to S[1/p]$ is ![]() $G$-Galois. Then, for any
$G$-Galois. Then, for any ![]() $K(1)$-local localizing invariant
$K(1)$-local localizing invariant ![]() $E$ which is truncating, we have
$E$ which is truncating, we have ![]() $E(R) \xrightarrow {\sim } E(S)^{hG}$.
$E(R) \xrightarrow {\sim } E(S)^{hG}$.
Recall that the Lichtenbaum–Quillen conjecture, refined by the Beilinson–Lichtenbaum conjecture proved by Voevodsky and Rost (see [Reference Haesemeyer and WeibelHW19] for an account), predicts that for ![]() $\mathbb {Z}[1/p]$-algebras
$\mathbb {Z}[1/p]$-algebras ![]() $A$ satisfying mild finiteness conditions, the
$A$ satisfying mild finiteness conditions, the ![]() $p$-adic
$p$-adic ![]() $K$-theory
$K$-theory ![]() $K(A; \mathbb {Z}_p)$ is ‘asymptotically
$K(A; \mathbb {Z}_p)$ is ‘asymptotically ![]() $K(1)$-local’; that is, the map
$K(1)$-local’; that is, the map ![]() $K(A; \mathbb {Z}_p) \to L_{K(1)} K(A; \mathbb {Z}_p)$ is an equivalence in high enough degrees. We next discuss analogs of such statements for
$K(A; \mathbb {Z}_p) \to L_{K(1)} K(A; \mathbb {Z}_p)$ is an equivalence in high enough degrees. We next discuss analogs of such statements for ![]() $\mathrm {TR}(R; \mathbb {Z}_p)$ for
$\mathrm {TR}(R; \mathbb {Z}_p)$ for ![]() $p$-adic rings
$p$-adic rings ![]() $R$. Indeed, in [Reference Hesselholt and MadsenHM03, Reference Hesselholt and MadsenHM04] it is shown that if
$R$. Indeed, in [Reference Hesselholt and MadsenHM03, Reference Hesselholt and MadsenHM04] it is shown that if ![]() $R$ is smooth of relative dimension
$R$ is smooth of relative dimension ![]() $d$ over a discrete valuation ring
$d$ over a discrete valuation ring ![]() $\mathcal {O}_K$ of mixed characteristic with perfect residue field of characteristic
$\mathcal {O}_K$ of mixed characteristic with perfect residue field of characteristic ![]() $p > 2$, then
$p > 2$, then ![]() $\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is
$\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is ![]() $d$-truncated; more precisely, this is a consequence of the relationship shown in [Reference Hesselholt and MadsenHM03, Reference Hesselholt and MadsenHM04] with the absolute de Rham–Witt complex. We prove this asymptotic
$d$-truncated; more precisely, this is a consequence of the relationship shown in [Reference Hesselholt and MadsenHM03, Reference Hesselholt and MadsenHM04] with the absolute de Rham–Witt complex. We prove this asymptotic ![]() $K(1)$-locality more generally for regular rings satisfying
$K(1)$-locality more generally for regular rings satisfying ![]() $F$-finiteness hypotheses from the Beilinson–Lichtenbaum conjecture applied to the generic fiber as well as the connection between
$F$-finiteness hypotheses from the Beilinson–Lichtenbaum conjecture applied to the generic fiber as well as the connection between ![]() $\mathrm {TR}$ and
$\mathrm {TR}$ and ![]() $p$-typical curves [Reference HesselholtHes96]. We expect that there should be a purely
$p$-typical curves [Reference HesselholtHes96]. We expect that there should be a purely ![]() $p$-adic proof of this result (as in [Reference Hesselholt and MadsenHM03, Reference Hesselholt and MadsenHM04] in the smooth case).
$p$-adic proof of this result (as in [Reference Hesselholt and MadsenHM03, Reference Hesselholt and MadsenHM04] in the smooth case).
Theorem 1.4 Let ![]() $R$ be a
$R$ be a ![]() $p$-torsion-free excellent regular noetherian ring. Suppose that
$p$-torsion-free excellent regular noetherian ring. Suppose that ![]() $R/p$ is finitely generated as a module over its subring of
$R/p$ is finitely generated as a module over its subring of ![]() $p$th powers. Suppose, furthermore, that for all
$p$th powers. Suppose, furthermore, that for all ![]() $\mathfrak {p} \in \mathrm {Spec}(R)$ containing
$\mathfrak {p} \in \mathrm {Spec}(R)$ containing ![]() $(p)$, we have
$(p)$, we have ![]() $\dim R_{\mathfrak {p}} + \log _p [ \kappa (\mathfrak {p}):\kappa (\mathfrak {p})^p] \leq d$ for some
$\dim R_{\mathfrak {p}} + \log _p [ \kappa (\mathfrak {p}):\kappa (\mathfrak {p})^p] \leq d$ for some ![]() $d \geq 0$. Then the map
$d \geq 0$. Then the map ![]() $\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is
$\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is ![]() $(d-1)$-truncated.
$(d-1)$-truncated.
Using the Antieau–Nikolaus theory of topological Cartier modules [Reference Antieau and NikolausAN21], we relate the property of ![]() $\mathrm {TR}(R; \mathbb {F}_p)$ being ‘asymptotically
$\mathrm {TR}(R; \mathbb {F}_p)$ being ‘asymptotically ![]() $K(1)$-local’ to the extensively studied Segal conjecture for
$K(1)$-local’ to the extensively studied Segal conjecture for ![]() $\mathrm {THH}(R)$, that is, the condition that the cyclotomic Frobenius
$\mathrm {THH}(R)$, that is, the condition that the cyclotomic Frobenius ![]() $\varphi \colon \mathrm {THH}(R; \mathbb {F}_p) \to \mathrm {THH}(R; \mathbb {F}_p)^{tC_p}$ should be an equivalence in high degrees. In particular, we obtain a version of the Segal conjecture for
$\varphi \colon \mathrm {THH}(R; \mathbb {F}_p) \to \mathrm {THH}(R; \mathbb {F}_p)^{tC_p}$ should be an equivalence in high degrees. In particular, we obtain a version of the Segal conjecture for ![]() $\mathrm {THH}(R)$ when
$\mathrm {THH}(R)$ when ![]() $R$ is regular. We expect that there should be a filtered version of this statement, using the motivic filtrations of Bhatt, Morrow, and Scholze [Reference Bhatt, Morrow and ScholzeBMS19].
$R$ is regular. We expect that there should be a filtered version of this statement, using the motivic filtrations of Bhatt, Morrow, and Scholze [Reference Bhatt, Morrow and ScholzeBMS19].
Corollary 1.5 Let ![]() $R$ be as in Theorem 1.4. Then the cyclotomic Frobenius
$R$ be as in Theorem 1.4. Then the cyclotomic Frobenius ![]() $\varphi \colon \mathrm {THH}(R; \mathbb {F}_p) \to \mathrm {THH}(R; \mathbb {F}_p)^{tC_p}$ is
$\varphi \colon \mathrm {THH}(R; \mathbb {F}_p) \to \mathrm {THH}(R; \mathbb {F}_p)^{tC_p}$ is ![]() $(d-1)$-truncated.
$(d-1)$-truncated.
Finally, we study the analog of Thomason's spectral sequence [Reference ThomasonTho85, Reference Thomason and TrobaughTT90] from étale cohomology to ![]() $K(1)$-local algebraic
$K(1)$-local algebraic ![]() $K$-theory. For a scheme
$K$-theory. For a scheme ![]() $X$ over
$X$ over ![]() $\mathbb {Z}[1/p]$ satisfying mild finiteness conditions (to wit:
$\mathbb {Z}[1/p]$ satisfying mild finiteness conditions (to wit: ![]() $X$ should be qcqs of finite Krull dimension, with a uniform bound on the mod
$X$ should be qcqs of finite Krull dimension, with a uniform bound on the mod ![]() $p$ virtual cohomological dimensions of the residue fields [Reference Rosenschon and ØstværRØ06, Reference Clausen and MathewCM19]), one has a convergent spectral sequence
$p$ virtual cohomological dimensions of the residue fields [Reference Rosenschon and ØstværRØ06, Reference Clausen and MathewCM19]), one has a convergent spectral sequence
We can construct a similar spectral sequence for ![]() $L_{K(1)} \mathrm {TR}$ under significantly stronger finiteness and regularity conditions, arising from a natural filtration. To formulate the
$L_{K(1)} \mathrm {TR}$ under significantly stronger finiteness and regularity conditions, arising from a natural filtration. To formulate the ![]() $E_2$-term (or the graded pieces of this filtration), we use the
$E_2$-term (or the graded pieces of this filtration), we use the ![]() $\mathrm {arc}_{{p}}$-topology of [Reference Bhatt and MathewBM18].
$\mathrm {arc}_{{p}}$-topology of [Reference Bhatt and MathewBM18].
Definition 1.6 (The ![]() $\mathrm {arc}_{{p}}$-topology and
$\mathrm {arc}_{{p}}$-topology and ![]() $\mathrm {arc}_{{p}}$-cohomology)
$\mathrm {arc}_{{p}}$-cohomology)
We say that a map of derived ![]() $p$-complete rings
$p$-complete rings ![]() $R \to R'$ is an
$R \to R'$ is an ![]() $\mathrm {arc}_{{p}}$-cover if, for every map
$\mathrm {arc}_{{p}}$-cover if, for every map ![]() $R \to V$ for
$R \to V$ for ![]() $V$ a rank
$V$ a rank ![]() $1$ valuation ring which is
$1$ valuation ring which is ![]() $p$-complete and such that
$p$-complete and such that ![]() $p \neq 0$, there exist an extension of rank
$p \neq 0$, there exist an extension of rank ![]() $1$ valuation rings
$1$ valuation rings ![]() $V \to W$ and the following commutative diagram.
$V \to W$ and the following commutative diagram.

The ![]() $\mathrm {arc}_{{p}}$-topology is the finitary Grothendieck topology on the opposite of the category of derived
$\mathrm {arc}_{{p}}$-topology is the finitary Grothendieck topology on the opposite of the category of derived ![]() $p$-complete rings defined such that a family
$p$-complete rings defined such that a family ![]() $\{R \to R'_\alpha \}_{\alpha \in A}$ is a covering family if and only if there exists a finite subset
$\{R \to R'_\alpha \}_{\alpha \in A}$ is a covering family if and only if there exists a finite subset ![]() $A' \subset A$ such that
$A' \subset A$ such that ![]() $R \to \prod _{\alpha \in A'} R'_\alpha$ is an
$R \to \prod _{\alpha \in A'} R'_\alpha$ is an ![]() $\mathrm {arc}_{{p}}$-cover.
$\mathrm {arc}_{{p}}$-cover.
Given any functor ![]() $F$ from derived
$F$ from derived ![]() $p$-complete rings to abelian groups, we let
$p$-complete rings to abelian groups, we let ![]() $R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), F(-))$ denote the
$R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), F(-))$ denote the ![]() $\mathrm {arc}_{{p}}$-cohomology of
$\mathrm {arc}_{{p}}$-cohomology of ![]() $F(-)$ on a derived
$F(-)$ on a derived ![]() $p$-complete ring
$p$-complete ring ![]() $R$.Footnote 1
$R$.Footnote 1
Example 1.7 (i) We can consider the ![]() $\mathrm {arc}_{{p}}$-cohomology of the structure presheaf
$\mathrm {arc}_{{p}}$-cohomology of the structure presheaf ![]() $\mathcal {O}$,
$\mathcal {O}$, ![]() $R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O})$. This is closely related to the perfectoidizations considered in [Reference Bhatt and ScholzeBS19, §§ 7 and 8], which work with the
$R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O})$. This is closely related to the perfectoidizations considered in [Reference Bhatt and ScholzeBS19, §§ 7 and 8], which work with the ![]() $p$-complete
$p$-complete ![]() $\mathrm {arc}$-topology rather than the
$\mathrm {arc}$-topology rather than the ![]() $\mathrm {arc}_{{p}}$-topology. For
$\mathrm {arc}_{{p}}$-topology. For ![]() $R = \mathbb {Z}_p$, it is not difficult to see that this is the continuous
$R = \mathbb {Z}_p$, it is not difficult to see that this is the continuous ![]() $\mathrm {Gal}(\mathbb {Q}_p)$-homotopy invariants of the derived saturation
$\mathrm {Gal}(\mathbb {Q}_p)$-homotopy invariants of the derived saturation ![]() $(\mathcal {O}_C)_*$ for
$(\mathcal {O}_C)_*$ for ![]() $C = \widehat {\overline {\mathbb {Q}_p}}$ (in the sense of almost ring theory [Reference Gabber and RameroGR03]).
$C = \widehat {\overline {\mathbb {Q}_p}}$ (in the sense of almost ring theory [Reference Gabber and RameroGR03]).
(ii) We consider the ![]() $\mathrm {arc}_{{p}}$-cohomology of the Witt vector presheaf
$\mathrm {arc}_{{p}}$-cohomology of the Witt vector presheaf ![]() $W(\mathcal {O})$, denoted
$W(\mathcal {O})$, denoted ![]() $R \mapsto R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O}))$, as well as its
$R \mapsto R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O}))$, as well as its ![]() $p$-adic Tate twists
$p$-adic Tate twists ![]() $W(\mathcal {O})(i)$ for
$W(\mathcal {O})(i)$ for ![]() $i \in \mathbb {Z}$.
$i \in \mathbb {Z}$.
Theorem 1.8 Let ![]() $K$ be a complete nonarchimedean field of mixed characteristic
$K$ be a complete nonarchimedean field of mixed characteristic ![]() $(0, p)$ with ring of integers
$(0, p)$ with ring of integers ![]() $\mathcal {O}_K$ and residue field
$\mathcal {O}_K$ and residue field ![]() $k$ with
$k$ with ![]() $[k: k^p] < \infty$. Suppose either
$[k: k^p] < \infty$. Suppose either ![]() $K$ is discretely valued or
$K$ is discretely valued or ![]() $K$ is perfectoid. Let
$K$ is perfectoid. Let ![]() $R$ be a formally smooth
$R$ be a formally smooth ![]() $\mathcal {O}_K$-algebra. Then there exists a natural convergent, exhaustive
$\mathcal {O}_K$-algebra. Then there exists a natural convergent, exhaustive ![]() $\mathbb {Z}$-indexed descending filtration
$\mathbb {Z}$-indexed descending filtration ![]() $\mathrm {Fil}^{\geq \ast } L_{K(1)} \mathrm {TR}(R)$ on
$\mathrm {Fil}^{\geq \ast } L_{K(1)} \mathrm {TR}(R)$ on ![]() $L_{K(1)} \mathrm {TR}(R)$ such that
$L_{K(1)} \mathrm {TR}(R)$ such that
Theorem 1.8 is effectively an étale hyperdescent (in the generic fiber) result together with the calculation for perfectoids. For illustration, we specialize to the case where ![]() $R = \mathcal {O}_K$, for
$R = \mathcal {O}_K$, for ![]() $K$ discretely valued with perfect residue field. Then the filtration (3) arises via a type of pro-Galois descent in the generic fiber. If
$K$ discretely valued with perfect residue field. Then the filtration (3) arises via a type of pro-Galois descent in the generic fiber. If ![]() $L/K$ is
$L/K$ is ![]() $G$-Galois, Example 1.3 and Theorem 1.4 imply that
$G$-Galois, Example 1.3 and Theorem 1.4 imply that ![]() $\mathrm {TR}(\mathcal {O}_K; \mathbb {F}_p) \to \mathrm {TR}(\mathcal {O}_L; \mathbb {F}_p)^{hG}$ is a
$\mathrm {TR}(\mathcal {O}_K; \mathbb {F}_p) \to \mathrm {TR}(\mathcal {O}_L; \mathbb {F}_p)^{hG}$ is a ![]() $0$-truncated map. However, this does not help with passage to
$0$-truncated map. However, this does not help with passage to ![]() $\bar {K}$ since
$\bar {K}$ since ![]() $\mathrm {TR}$ does not commute with filtered colimits; note that
$\mathrm {TR}$ does not commute with filtered colimits; note that ![]() $\mathrm {TR}$ has a simple form for
$\mathrm {TR}$ has a simple form for ![]() $\mathcal {O}_{\bar {K}}$; see [Reference HesselholtHes06]. Using again the theory of topological Cartier modules as a ‘decompletion’ of the theory of cyclotomic spectra (see [Reference Antieau and NikolausAN21]), we prove the following pro-Galois result (see Example 6.9).
$\mathcal {O}_{\bar {K}}$; see [Reference HesselholtHes06]. Using again the theory of topological Cartier modules as a ‘decompletion’ of the theory of cyclotomic spectra (see [Reference Antieau and NikolausAN21]), we prove the following pro-Galois result (see Example 6.9).
Theorem 1.9 Let ![]() $K$ be a complete, discretely valued field of characteristic
$K$ be a complete, discretely valued field of characteristic ![]() $0$ with perfect residue field
$0$ with perfect residue field ![]() $k$ of odd characteristic
$k$ of odd characteristic ![]() $p$. Let
$p$. Let ![]() $\mathrm {TR}(\mathcal {O}_K|K)$ denote the cofiber of the transfer map
$\mathrm {TR}(\mathcal {O}_K|K)$ denote the cofiber of the transfer map ![]() $\mathrm {TR}(k) \to \mathrm {TR}(\mathcal {O}_K)$. Then the natural map induces an equivalence
$\mathrm {TR}(k) \to \mathrm {TR}(\mathcal {O}_K)$. Then the natural map induces an equivalence
The idea that ![]() $\mathrm {TR}$ should satisfy this type of pro-Galois descent in the generic fiber is expressed in [Reference HesselholtHes02]; in particular, [Reference HesselholtHes02, Conjecture 5.1] predicts a related (but stronger) conclusion at the level of homotopy groups (in particular, the vanishing of higher Galois cohomology groups in the associated descent spectral sequence with
$\mathrm {TR}$ should satisfy this type of pro-Galois descent in the generic fiber is expressed in [Reference HesselholtHes02]; in particular, [Reference HesselholtHes02, Conjecture 5.1] predicts a related (but stronger) conclusion at the level of homotopy groups (in particular, the vanishing of higher Galois cohomology groups in the associated descent spectral sequence with ![]() $\mathbb {Q}_p/\mathbb {Z}_p$ coefficients).
$\mathbb {Q}_p/\mathbb {Z}_p$ coefficients).
Conventions
We write ![]() ${\rm Sp}$ for the
${\rm Sp}$ for the ![]() $\infty$-category of spectra and
$\infty$-category of spectra and ![]() $\mathbb {S}$ for the sphere spectrum. We use the theory of cyclotomic spectra in the form developed in [Reference Nikolaus and ScholzeNS18], as well as the theory of topological Cartier modules developed in [Reference Antieau and NikolausAN21]; we write
$\mathbb {S}$ for the sphere spectrum. We use the theory of cyclotomic spectra in the form developed in [Reference Nikolaus and ScholzeNS18], as well as the theory of topological Cartier modules developed in [Reference Antieau and NikolausAN21]; we write ![]() $\mathrm {CycSp}$ for the
$\mathrm {CycSp}$ for the ![]() $\infty$-category of cyclotomic spectra. We write
$\infty$-category of cyclotomic spectra. We write ![]() $\mathrm {TR}$ for
$\mathrm {TR}$ for ![]() $p$-typical
$p$-typical ![]() $\mathrm {TR}$. Given an
$\mathrm {TR}$. Given an ![]() $E_\infty$-ring
$E_\infty$-ring ![]() $B$, a homogeneous element
$B$, a homogeneous element ![]() $x \in \pi _*(B)$, and a
$x \in \pi _*(B)$, and a ![]() $B$-module
$B$-module ![]() $M$, we often write
$M$, we often write ![]() $M/x$ for the cofiber of multiplication by
$M/x$ for the cofiber of multiplication by ![]() $x$ on
$x$ on ![]() $M$. In the case
$M$. In the case ![]() $x =p$, we will often write this as ‘
$x =p$, we will often write this as ‘![]() $; \mathbb {F}_p$’; for example,
$; \mathbb {F}_p$’; for example, ![]() $\mathrm {THH}(B; \mathbb {F}_p)$ refers to the cofiber of
$\mathrm {THH}(B; \mathbb {F}_p)$ refers to the cofiber of ![]() $p$ on
$p$ on ![]() $\mathrm {THH}(B)$. A
$\mathrm {THH}(B)$. A ![]() $B$-algebra always refers, unless otherwise specified, to an
$B$-algebra always refers, unless otherwise specified, to an ![]() $E_1$-algebra in
$E_1$-algebra in ![]() $B$-modules.
$B$-modules.
2. Generalities on  $K(1)$-local truncating invariants
$K(1)$-local truncating invariants
Let ![]() $B$ be a base connective
$B$ be a base connective ![]() $E_\infty$-ring. In this section we work with localizing invariants on small
$E_\infty$-ring. In this section we work with localizing invariants on small ![]() $B$-linear idempotent-complete stable
$B$-linear idempotent-complete stable ![]() $\infty$-categories. Unlike in [Reference Blumberg, Gepner and TabuadaBGT13], we do not assume compatibility with filtered colimits, so for us a localizing invariant is simply a functor from (small, idempotent-complete)
$\infty$-categories. Unlike in [Reference Blumberg, Gepner and TabuadaBGT13], we do not assume compatibility with filtered colimits, so for us a localizing invariant is simply a functor from (small, idempotent-complete) ![]() $B$-linear stable
$B$-linear stable ![]() $\infty$-categories to spectra which carries Verdier quotient sequences to cofiber sequences. Following [Reference Land and TammeLT19], we say that such a localizing invariant
$\infty$-categories to spectra which carries Verdier quotient sequences to cofiber sequences. Following [Reference Land and TammeLT19], we say that such a localizing invariant ![]() $E$ is truncating if for every connective
$E$ is truncating if for every connective ![]() $B$-algebra
$B$-algebra ![]() $A$, we have
$A$, we have ![]() $E(A) \xrightarrow {\sim } E(H \pi _0 A)$. This implies [Reference Land and TammeLT19, Theorem B] that
$E(A) \xrightarrow {\sim } E(H \pi _0 A)$. This implies [Reference Land and TammeLT19, Theorem B] that ![]() $E$ satisfies excision.
$E$ satisfies excision.
Example 2.1 The constructions ![]() $L_{K(1)} K(-), L_{K(1)} \mathrm {TC}(-)$ are truncating on connective
$L_{K(1)} K(-), L_{K(1)} \mathrm {TC}(-)$ are truncating on connective ![]() $H\mathbb {Z}$-algebras, as verified in [Reference Land, Mathew, Meier and TammeLMMT20]. For commutative
$H\mathbb {Z}$-algebras, as verified in [Reference Land, Mathew, Meier and TammeLMMT20]. For commutative ![]() $p$-complete rings, the two invariants actually agree (we do not know if this is true for noncommutative
$p$-complete rings, the two invariants actually agree (we do not know if this is true for noncommutative ![]() $p$-complete rings; see [Reference Bhatt, Clausen and MathewBCM20, Question 2.20]). Below we will show that
$p$-complete rings; see [Reference Bhatt, Clausen and MathewBCM20, Question 2.20]). Below we will show that ![]() $L_{K(1)} \mathrm {TR}(-)$ is truncating.
$L_{K(1)} \mathrm {TR}(-)$ is truncating.
In the rest of the section we will assume for simplicity of notation that ![]() $B$ is discrete; by the assumption of truncatedness, this does not affect any of the results.
$B$ is discrete; by the assumption of truncatedness, this does not affect any of the results.
Proposition 2.2 Let ![]() $E$ be a
$E$ be a ![]() $K(1)$-local localizing invariant of
$K(1)$-local localizing invariant of ![]() $B$-linear
$B$-linear ![]() $\infty$-categories which is truncating. Then, on the category of discrete
$\infty$-categories which is truncating. Then, on the category of discrete ![]() $B$-algebras, we have the following assertions.
$B$-algebras, we have the following assertions.
(i)
 $E$ is nilinvariant.
$E$ is nilinvariant.(ii)
 $E$ annihilates any
$E$ annihilates any  $B$-algebra
$B$-algebra  $C$ which is annihilated by a power of
$C$ which is annihilated by a power of  $p$.
$p$.(iii) Let
 $A \to A'$ be a map of
$A \to A'$ be a map of  $B$-algebras which is a
$B$-algebras which is a  $p$-isogeny. Then
$p$-isogeny. Then  $E(A) \to E(A')$ is an equivalence.
$E(A) \to E(A')$ is an equivalence.
Proof. For (i), the fact that ![]() $E$ is nilinvariant follows from [Reference Land and TammeLT19, Theorem B]. For (ii), since
$E$ is nilinvariant follows from [Reference Land and TammeLT19, Theorem B]. For (ii), since ![]() $E$ is nilinvariant, we may assume
$E$ is nilinvariant, we may assume ![]() $C$ is an
$C$ is an ![]() $\mathbb {F}_p$-algebra, so that
$\mathbb {F}_p$-algebra, so that ![]() $E(C)$ is by the theory of noncommutative motives [Reference Blumberg, Gepner and TabuadaBGT13] a
$E(C)$ is by the theory of noncommutative motives [Reference Blumberg, Gepner and TabuadaBGT13] a ![]() $K(\mathbb {F}_p; \mathbb {Z}_p) = H\mathbb {Z}_p$-module (the last identification by [Reference QuillenQui72]); since
$K(\mathbb {F}_p; \mathbb {Z}_p) = H\mathbb {Z}_p$-module (the last identification by [Reference QuillenQui72]); since ![]() $E$ is
$E$ is ![]() $K(1)$-local we get
$K(1)$-local we get ![]() $E(C) = 0$.
$E(C) = 0$.
For (iii), the kernel of ![]() $A \to A'$ is annihilated by a power of
$A \to A'$ is annihilated by a power of ![]() $p$, so by (ii) (and excision) we can assume that
$p$, so by (ii) (and excision) we can assume that ![]() $A \subset A'$. Let
$A \subset A'$. Let ![]() $n \gg 0$, so
$n \gg 0$, so ![]() $p^n A' \subset A$. Then the diagram
$p^n A' \subset A$. Then the diagram

is a Milnor square of rings. Applying the localizing invariant ![]() $E$ and using excision and (ii) again, we conclude (iii).
$E$ and using excision and (ii) again, we conclude (iii).
In the next result, we use Voevodsky's ![]() $h$-topology for possibly non-noetherian schemes; in other words, the topology generated by finitely presented
$h$-topology for possibly non-noetherian schemes; in other words, the topology generated by finitely presented ![]() $v$-covers (also called universally subtrusive morphisms); see [Reference RydhRyd10] or [Reference Bhatt and ScholzeBS17, § 2].
$v$-covers (also called universally subtrusive morphisms); see [Reference RydhRyd10] or [Reference Bhatt and ScholzeBS17, § 2].
Theorem 2.3 (![]() $h$-descent for truncating
$h$-descent for truncating ![]() $K(1)$-local invariants)
$K(1)$-local invariants)
Let ![]() $E$ be a
$E$ be a ![]() $K(1)$-local localizing invariant on
$K(1)$-local localizing invariant on ![]() $B$-linear
$B$-linear ![]() $\infty$-categories which is truncating. Then
$\infty$-categories which is truncating. Then ![]() $E$ satisfies
$E$ satisfies ![]() $h$-descent on qcqs
$h$-descent on qcqs ![]() $B$-schemes.
$B$-schemes.
Proof. By the results of [Reference Land and TammeLT19, Appendix A], ![]() $E$ satisfies
$E$ satisfies ![]() $cdh$-descent, and in particular satisfies excision for abstract blow-up squares. The results of [Reference Clausen, Mathew, Naumann and NoelCMNN20] imply that
$cdh$-descent, and in particular satisfies excision for abstract blow-up squares. The results of [Reference Clausen, Mathew, Naumann and NoelCMNN20] imply that ![]() $E$ satisfies finite locally free descent. Since
$E$ satisfies finite locally free descent. Since ![]() $E$ also satisfies Nisnevich descent (as does any localizing invariant [Reference Thomason and TrobaughTT90]), we obtain that
$E$ also satisfies Nisnevich descent (as does any localizing invariant [Reference Thomason and TrobaughTT90]), we obtain that ![]() $E$ satisfies fppf descent thanks to [Sta20, Tag 05WN]. By [Reference Bhatt and ScholzeBS17, Theorem 2.9],
$E$ satisfies fppf descent thanks to [Sta20, Tag 05WN]. By [Reference Bhatt and ScholzeBS17, Theorem 2.9], ![]() $h$-descent (for any sheaf) is implied by fppf descent and excision for abstract blow-up squares. Combining these facts, we conclude.
$h$-descent (for any sheaf) is implied by fppf descent and excision for abstract blow-up squares. Combining these facts, we conclude.
Example 2.4 Let ![]() $E$ be as above. Let
$E$ be as above. Let ![]() $\pi \colon X' \to X$ be a finitely presented proper morphism (e.g. a finitely presented closed immersion) of qcqs
$\pi \colon X' \to X$ be a finitely presented proper morphism (e.g. a finitely presented closed immersion) of qcqs ![]() $B$-schemes such that
$B$-schemes such that ![]() $X'[1/p] \xrightarrow {\sim } X[1/p]$. Then
$X'[1/p] \xrightarrow {\sim } X[1/p]$. Then ![]() $E(X) \xrightarrow {\sim } E(X')$. In fact, by
$E(X) \xrightarrow {\sim } E(X')$. In fact, by ![]() $cdh$-descent, we have a pullback square
$cdh$-descent, we have a pullback square

and the terms on the bottom vanish by Proposition 2.2.
In the next result we use the notion of nilpotence of a group action; see [Reference MathewMat18, § 4.1] or [Reference Clausen and MathewCM19, Definition 2.17] for accounts, or [Reference Mathew, Naumann and NoelMNN17] for the general setup in equivariant stable homotopy theory. Let ![]() $G$ be a finite group. The collection of nilpotent objects of the
$G$ be a finite group. The collection of nilpotent objects of the ![]() $\infty$-category
$\infty$-category ![]() $\mathrm {Fun}(BG, {\rm Sp} )$ is the thick subcategory generated by the objects which are induced from the trivial subgroup. For an algebra object of
$\mathrm {Fun}(BG, {\rm Sp} )$ is the thick subcategory generated by the objects which are induced from the trivial subgroup. For an algebra object of ![]() $\mathrm {Fun}(BG, {\rm Sp} )$, nilpotence holds if and only if the Tate construction vanishes. A module over a nilpotent algebra object in
$\mathrm {Fun}(BG, {\rm Sp} )$, nilpotence holds if and only if the Tate construction vanishes. A module over a nilpotent algebra object in ![]() $\mathrm {Fun}(BG, {\rm Sp} )$ is itself nilpotent.
$\mathrm {Fun}(BG, {\rm Sp} )$ is itself nilpotent.
Corollary 2.5 (Galois descent in the generic fiber) Let ![]() $E$ be a
$E$ be a ![]() $K(1)$-local localizing invariant of
$K(1)$-local localizing invariant of ![]() $B$-linear
$B$-linear ![]() $\infty$-categories which is truncating. Let
$\infty$-categories which is truncating. Let ![]() $R \to S$ be a finite and finitely presented map of (commutative, discrete)
$R \to S$ be a finite and finitely presented map of (commutative, discrete) ![]() $B$-algebras. Let
$B$-algebras. Let ![]() $G$ be a finite group acting on
$G$ be a finite group acting on ![]() $S$ via
$S$ via ![]() $R$-algebra maps. Suppose that
$R$-algebra maps. Suppose that ![]() $R[1/p] \to S[1/p]$ is
$R[1/p] \to S[1/p]$ is ![]() $G$-Galois. Then the natural map induces an equivalence
$G$-Galois. Then the natural map induces an equivalence ![]() $E(R) \xrightarrow {\sim } E(S)^{hG}$. Moreover, the
$E(R) \xrightarrow {\sim } E(S)^{hG}$. Moreover, the ![]() $G$-action on
$G$-action on ![]() $E(S)$ is nilpotent.
$E(S)$ is nilpotent.
Proof. Replacing ![]() $S$ with
$S$ with ![]() $S \times R/p$, we may assume without loss of generality that
$S \times R/p$, we may assume without loss of generality that ![]() $R \to S$ is an
$R \to S$ is an ![]() $h$-cover. Then, by Theorem 2.3, we have
$h$-cover. Then, by Theorem 2.3, we have
Since the group ![]() $G$ acts on
$G$ acts on ![]() $S$, we have a natural map of cosimplicial rings from the Čech nerve
$S$, we have a natural map of cosimplicial rings from the Čech nerve ![]() $C(R \to S)^\bullet$ to the standard resolution
$C(R \to S)^\bullet$ to the standard resolution ![]() $S \rightrightarrows \prod _G S \begin{smallmatrix} \to \\ \to \\\to \end{smallmatrix}$ for
$S \rightrightarrows \prod _G S \begin{smallmatrix} \to \\ \to \\\to \end{smallmatrix}$ for ![]() $G$ acting on
$G$ acting on ![]() $S$ (which calculates
$S$ (which calculates ![]() $S^{hG}$). This map of cosimplicial rings is an isogeny in each degree; for example, in degree
$S^{hG}$). This map of cosimplicial rings is an isogeny in each degree; for example, in degree ![]() $1$,
$1$, ![]() $S \otimes _R S \to \prod _G S$ is an isogeny because it is a map of finitely presented
$S \otimes _R S \to \prod _G S$ is an isogeny because it is a map of finitely presented ![]() $R$-modules (see [Sta20, Tag 0564]) which induces an isomorphism after inverting
$R$-modules (see [Sta20, Tag 0564]) which induces an isomorphism after inverting ![]() $p$ thanks to the Galois hypothesis. Therefore, by Proposition 2.2, we find that the map induces an equivalence after applying
$p$ thanks to the Galois hypothesis. Therefore, by Proposition 2.2, we find that the map induces an equivalence after applying ![]() $E$, and we find from (4) that
$E$, and we find from (4) that
 \[ E(R) \xrightarrow{\sim} \mathrm{Tot} \bigg( E(S) \rightrightarrows E \biggl( \prod_G S \biggr) \begin{smallmatrix} \to \\ \to \\\to \end{smallmatrix} \ldots \bigg) = E(S)^{hG}, \]
\[ E(R) \xrightarrow{\sim} \mathrm{Tot} \bigg( E(S) \rightrightarrows E \biggl( \prod_G S \biggr) \begin{smallmatrix} \to \\ \to \\\to \end{smallmatrix} \ldots \bigg) = E(S)^{hG}, \]
which is the desired claim. Finally, to see that the ![]() $G$-action on
$G$-action on ![]() $E(S)$ is nilpotent, we use that
$E(S)$ is nilpotent, we use that ![]() $E(S)$ is a module
$E(S)$ is a module ![]() $G$-equivariantly over
$G$-equivariantly over ![]() $L_{K(1)} K(S) \xrightarrow {\sim } L_{K(1)} K(S[1/p])$ (via (2)), and the
$L_{K(1)} K(S) \xrightarrow {\sim } L_{K(1)} K(S[1/p])$ (via (2)), and the ![]() $G$-action on
$G$-action on ![]() $L_{K(1)} K(S[1/p])$ is nilpotent by [Reference Clausen, Mathew, Naumann and NoelCMNN20, Theorem 5.6] (see also [Reference Clausen and MathewCM19, Lemma 4.20]).
$L_{K(1)} K(S[1/p])$ is nilpotent by [Reference Clausen, Mathew, Naumann and NoelCMNN20, Theorem 5.6] (see also [Reference Clausen and MathewCM19, Lemma 4.20]).
3. The truncating property of  $L_{K(1)} \mathrm {TR}(-)$
$L_{K(1)} \mathrm {TR}(-)$
In this section we prove the following basic result. Throughout, we fix a connective, ![]() $K(1)$-acyclic
$K(1)$-acyclic ![]() $E_\infty$-ring
$E_\infty$-ring ![]() $B$ (e.g.
$B$ (e.g. ![]() $H\mathbb {Z}$).
$H\mathbb {Z}$).
Theorem 3.1 The construction ![]() $L_{K(1)} \mathrm {TR}(-)$ is truncating on connective
$L_{K(1)} \mathrm {TR}(-)$ is truncating on connective ![]() $E_1$-
$E_1$-![]() $B$-algebras. More generally, for any set
$B$-algebras. More generally, for any set ![]() $Q$,Footnote 2 the construction
$Q$,Footnote 2 the construction ![]() $L_{K(1)} (\prod _Q \mathrm {TR}(-))$ is truncating on connective
$L_{K(1)} (\prod _Q \mathrm {TR}(-))$ is truncating on connective ![]() $E_1$-
$E_1$-![]() $B$-algebras.
$B$-algebras.
The proof of Theorem 3.1 will rely on a ![]() $K(1)$-acyclicity criterion for cyclotomic spectra (Proposition 3.6), which will use some elementary estimates for exponents of nilpotence with respect to the Bott element
$K(1)$-acyclicity criterion for cyclotomic spectra (Proposition 3.6), which will use some elementary estimates for exponents of nilpotence with respect to the Bott element ![]() $\beta$.
$\beta$.
In the following, we let ![]() $ku$ denote the connective topological
$ku$ denote the connective topological ![]() $K$-theory spectrum, so
$K$-theory spectrum, so ![]() $\pi _*(ku) = \mathbb {Z}[\beta ]$ with
$\pi _*(ku) = \mathbb {Z}[\beta ]$ with ![]() $|\beta | = 2$. Since
$|\beta | = 2$. Since ![]() $B$ is
$B$ is ![]() $K(1)$-acyclic, the associative ring spectrum
$K(1)$-acyclic, the associative ring spectrum ![]() $B \otimes ku/p$ is annihilated by a power of
$B \otimes ku/p$ is annihilated by a power of ![]() $\beta$. Our strategy is roughly based on bounding the exponents of nilpotence for
$\beta$. Our strategy is roughly based on bounding the exponents of nilpotence for ![]() $\beta$ in the fixed points
$\beta$ in the fixed points ![]() $\mathrm {THH}(B)^{C_{p^n}} \otimes ku/p$ and, in particular, showing that they are
$\mathrm {THH}(B)^{C_{p^n}} \otimes ku/p$ and, in particular, showing that they are ![]() $O(p^n)$.
$O(p^n)$.
Recall that ![]() $ku$ is complex-oriented, leading to the following result.
$ku$ is complex-oriented, leading to the following result.
Proposition 3.2 Let ![]() $M$ be a
$M$ be a ![]() $ku$-module equipped with an
$ku$-module equipped with an ![]() $S^1$-action. Then, for each
$S^1$-action. Then, for each ![]() $n \geq 1$, the natural map induces an equivalence
$n \geq 1$, the natural map induces an equivalence
Proof. Compare [Reference Mathew, Naumann and NoelMNN17, § 7.4]. In fact, via the projection formula, ![]() $M^{hC_{p^n}} \simeq (M \otimes _{ku} ku^{S^1/C_{p^n}})^{hS^1}$. Here
$M^{hC_{p^n}} \simeq (M \otimes _{ku} ku^{S^1/C_{p^n}})^{hS^1}$. Here ![]() $ku^{S^1/C_{p^n}}$ denotes the
$ku^{S^1/C_{p^n}}$ denotes the ![]() $ku$-valued function spectrum of
$ku$-valued function spectrum of ![]() $S^1/C_{p^n}$ with the corresponding
$S^1/C_{p^n}$ with the corresponding ![]() $S^1$-action, and the tensor product is taken in
$S^1$-action, and the tensor product is taken in ![]() $\mathrm {Fun}(BS^1, \mod (ku))$. Let
$\mathrm {Fun}(BS^1, \mod (ku))$. Let ![]() $V_n$ denote the one-dimensional complex representation of
$V_n$ denote the one-dimensional complex representation of ![]() $S^1$ where
$S^1$ where ![]() $z \in S^1$ acts by multiplication by
$z \in S^1$ acts by multiplication by ![]() $z^{p^n}$, and let
$z^{p^n}$, and let ![]() $S(V_n)$ denote the unit circle in
$S(V_n)$ denote the unit circle in ![]() $V_n$ as an
$V_n$ as an ![]() $S^1$-space, so
$S^1$-space, so ![]() $S(V_n) \simeq S^1/C_{p^n}$. The Spanier–Whitehead dual of the Euler sequence in
$S(V_n) \simeq S^1/C_{p^n}$. The Spanier–Whitehead dual of the Euler sequence in ![]() $\mathrm {Fun}(BS^1, {\rm Sp} )$,
$\mathrm {Fun}(BS^1, {\rm Sp} )$, ![]() $S(V_n)_+ \to S^0 \to S^{V_n}$ and the complex orientability of
$S(V_n)_+ \to S^0 \to S^{V_n}$ and the complex orientability of ![]() $ku$ together show that
$ku$ together show that ![]() $ku^{S^1/C_{p^n}} \in \mathrm {Fun}(BS^1, \mod (ku))$ belongs to the thick subcategory generated by the unit. Therefore, applying the right adjoint
$ku^{S^1/C_{p^n}} \in \mathrm {Fun}(BS^1, \mod (ku))$ belongs to the thick subcategory generated by the unit. Therefore, applying the right adjoint ![]() $(-)^{hS^1} \colon \mathrm {Fun}(BS^1, \mod (ku)) \to \mod (ku^{BS^1})$, we find that the natural map
$(-)^{hS^1} \colon \mathrm {Fun}(BS^1, \mod (ku)) \to \mod (ku^{BS^1})$, we find that the natural map
is an equivalence, whence the result.
By complex orientability, we have
Consider the formal group law over ![]() $\mathbb {Z}[\beta ]$ given by
$\mathbb {Z}[\beta ]$ given by ![]() $f(u,v) = u + v + \beta uv$; this is the formal group law associated to the complex-oriented ring spectrum
$f(u,v) = u + v + \beta uv$; this is the formal group law associated to the complex-oriented ring spectrum ![]() $ku$, and is homogeneous of degree
$ku$, and is homogeneous of degree ![]() $-2$ if
$-2$ if ![]() $|u|, |v| = -2$. We have an equivalence
$|u|, |v| = -2$. We have an equivalence ![]() $ku^{BS^1}/x \simeq ku$. More generally, let
$ku^{BS^1}/x \simeq ku$. More generally, let ![]() $[p^n](x) \in \pi _* ( ku^{BS^1})$ denote the
$[p^n](x) \in \pi _* ( ku^{BS^1})$ denote the ![]() $p$-series of the formal group law
$p$-series of the formal group law ![]() $f$; modulo
$f$; modulo ![]() $p$, we have
$p$, we have ![]() $[p^n](x) \equiv \beta ^{p^n-1} x^{p^n}$ since
$[p^n](x) \equiv \beta ^{p^n-1} x^{p^n}$ since ![]() $[p^n] (x)$ is homogeneous of degree
$[p^n] (x)$ is homogeneous of degree ![]() $-2$ and recovers the multiplicative formal group law under the specialization
$-2$ and recovers the multiplicative formal group law under the specialization ![]() $\beta \mapsto 1$. By the Eilenberg–Moore spectral sequence or Gysin sequence (of which (5) is a form), we have
$\beta \mapsto 1$. By the Eilenberg–Moore spectral sequence or Gysin sequence (of which (5) is a form), we have
Proposition 3.3 Let ![]() $A$ be a connective
$A$ be a connective ![]() $E_\infty$-ring spectrum with
$E_\infty$-ring spectrum with ![]() $S^1$-action. Suppose that
$S^1$-action. Suppose that ![]() $\beta ^r = 0$ in
$\beta ^r = 0$ in ![]() $\pi _*(A \otimes ku/p)$. Then in
$\pi _*(A \otimes ku/p)$. Then in ![]() $\pi _*((A \otimes ku)^{hC_{p^n}}/p)$ we have
$\pi _*((A \otimes ku)^{hC_{p^n}}/p)$ we have ![]() $\beta ^{p^{n} -1 + rp^n} = 0$.
$\beta ^{p^{n} -1 + rp^n} = 0$.
Proof. Let ![]() $R = A \otimes ku/p$, so
$R = A \otimes ku/p$, so ![]() $R$ is an associative
$R$ is an associative ![]() $ku$-algebra spectrum with
$ku$-algebra spectrum with ![]() $S^1$-action. Consider the
$S^1$-action. Consider the ![]() $S^1$-homotopy fixed points
$S^1$-homotopy fixed points ![]() $R^{hS^1}$, which is a
$R^{hS^1}$, which is a ![]() $ku^{BS^1}$-algebra. Since
$ku^{BS^1}$-algebra. Since ![]() $p = 0$ in
$p = 0$ in ![]() $\pi _0 R$, we have by Proposition 3.2 and (6),
$\pi _0 R$, we have by Proposition 3.2 and (6),
Our assumption is that ![]() $\beta ^r =0$ in
$\beta ^r =0$ in ![]() $\pi _*(R)$, which means that we can write
$\pi _*(R)$, which means that we can write ![]() $\beta ^r = x v \in \pi _*(R^{hS^1})$ for some
$\beta ^r = x v \in \pi _*(R^{hS^1})$ for some ![]() $v$ since
$v$ since ![]() $R = R^{hS^1}/x$. It follows that in
$R = R^{hS^1}/x$. It follows that in ![]() $\pi _*(R^{hC_{p^n}})$, we have
$\pi _*(R^{hC_{p^n}})$, we have ![]() $\beta ^{p^n -1 + rp^n} = \beta ^{p^n-1} (xv)^{p^n} = 0$.
$\beta ^{p^n -1 + rp^n} = \beta ^{p^n-1} (xv)^{p^n} = 0$.
Now we apply the above to the ![]() $E_\infty$-ring
$E_\infty$-ring ![]() $\mathrm {THH}(B)$ equipped with its
$\mathrm {THH}(B)$ equipped with its ![]() $S^1$-action; recall that
$S^1$-action; recall that ![]() $B$ is assumed connective and
$B$ is assumed connective and ![]() $K(1)$-acyclic.
$K(1)$-acyclic.
Proposition 3.4 There exists a constant ![]() $\kappa >0$ such that for each
$\kappa >0$ such that for each ![]() $i > 0$ we have the following assertions.
$i > 0$ we have the following assertions.
(i) We have that
 $\beta ^{ \kappa i} =0$ in
$\beta ^{ \kappa i} =0$ in  $(ku/p \otimes \mathrm {THH}(B))^{hC_{i}}$.
$(ku/p \otimes \mathrm {THH}(B))^{hC_{i}}$.(ii) Let
 $N$ be a
$N$ be a  $\mathrm {THH}(B) \otimes ku$-module in
$\mathrm {THH}(B) \otimes ku$-module in  $\mathrm {Fun}(BS^1, {\rm Sp} )$. Suppose that
$\mathrm {Fun}(BS^1, {\rm Sp} )$. Suppose that  $N$ (as a
$N$ (as a  $\mathrm {THH}(B) \otimes ku$-module in
$\mathrm {THH}(B) \otimes ku$-module in  $\mathrm {Fun}(BS^1, {\rm Sp} )$) is induced from the cyclic group
$\mathrm {Fun}(BS^1, {\rm Sp} )$) is induced from the cyclic group  $C_i \subset S^1$. Then, for any
$C_i \subset S^1$. Then, for any  $t$,
$t$,  $N_{hC_t}/p$ is annihilated by
$N_{hC_t}/p$ is annihilated by  $\beta ^{\kappa i}$.
$\beta ^{\kappa i}$.
Proof. To prove (i), using the transfer and restricting to a ![]() $p$-Sylow subgroup, we may reduce to the case where
$p$-Sylow subgroup, we may reduce to the case where ![]() $i$ is a power of
$i$ is a power of ![]() $p$, say
$p$, say ![]() $i = p^n$. Then the claim follows from Proposition 3.3, since
$i = p^n$. Then the claim follows from Proposition 3.3, since ![]() $\beta$ is nilpotent in
$\beta$ is nilpotent in ![]() $ku/p \otimes \mathrm {THH}(B)$ since
$ku/p \otimes \mathrm {THH}(B)$ since ![]() $B$ is
$B$ is ![]() $K(1)$-acyclic. It follows that we can find a
$K(1)$-acyclic. It follows that we can find a ![]() $\kappa _1$ such that
$\kappa _1$ such that ![]() $\beta ^{\kappa _1 i} = 0$ in
$\beta ^{\kappa _1 i} = 0$ in ![]() $(ku/p \otimes \mathrm {THH}(B))^{hC_i}$ for all
$(ku/p \otimes \mathrm {THH}(B))^{hC_i}$ for all ![]() $i > 0$.
$i > 0$.
For (ii), consider a ![]() $\mathrm {THH}(B) \otimes ku$-module
$\mathrm {THH}(B) \otimes ku$-module ![]() $N$ in
$N$ in ![]() $\mathrm {Fun}(BS^1, {\rm Sp} )$ which is the induction of a
$\mathrm {Fun}(BS^1, {\rm Sp} )$ which is the induction of a ![]() $\mathrm {THH}(B) \otimes ku$-module
$\mathrm {THH}(B) \otimes ku$-module ![]() $N'$ in
$N'$ in ![]() $\mathrm {Fun}(BC_{i}, {\rm Sp} )$. It follows that
$\mathrm {Fun}(BC_{i}, {\rm Sp} )$. It follows that ![]() $N_{hS^1} /p = (N' /p)_{hC_i}$ is a module over
$N_{hS^1} /p = (N' /p)_{hC_i}$ is a module over ![]() $(ku/p \otimes \mathrm {THH}(B))^{hC_i}$, writing homotopy orbits as a module over homotopy fixed points; this is therefore annihilated by
$(ku/p \otimes \mathrm {THH}(B))^{hC_i}$, writing homotopy orbits as a module over homotopy fixed points; this is therefore annihilated by ![]() $\beta ^{\kappa _1 i}$ by the previous part of the result. For any
$\beta ^{\kappa _1 i}$ by the previous part of the result. For any ![]() $t$, let
$t$, let ![]() $W_t$ be the one-dimensional complex representation of
$W_t$ be the one-dimensional complex representation of ![]() $S^1$ where
$S^1$ where ![]() $z$ acts by multiplication by
$z$ acts by multiplication by ![]() $z^t$, so the unit circle
$z^t$, so the unit circle ![]() $S(W_t)_+ = (S^1/C_t)_+$ as
$S(W_t)_+ = (S^1/C_t)_+$ as ![]() $S^1$-spaces. We have
$S^1$-spaces. We have ![]() $N_{hC_t} = (N \otimes S(W_t)_+)_{hS^1}$ by the projection formula for induction and restriction along
$N_{hC_t} = (N \otimes S(W_t)_+)_{hS^1}$ by the projection formula for induction and restriction along ![]() $C_t \subset S^1$. Then the Euler sequence
$C_t \subset S^1$. Then the Euler sequence ![]() $S(W_t)_+ \to S^0 \to S^{W_t}$ (as in the proof of Proposition 3.2) and the complex orientability of
$S(W_t)_+ \to S^0 \to S^{W_t}$ (as in the proof of Proposition 3.2) and the complex orientability of ![]() $ku$ yield a fiber sequence
$ku$ yield a fiber sequence ![]() $N_{h C_t} \to N_{hS^1} \to \Sigma ^2 N_{hS^1}$. Therefore,
$N_{h C_t} \to N_{hS^1} \to \Sigma ^2 N_{hS^1}$. Therefore, ![]() $N_{hC_t} /p$ is annihilated by
$N_{hC_t} /p$ is annihilated by ![]() $\beta ^{2 \kappa _1 i}$; taking
$\beta ^{2 \kappa _1 i}$; taking ![]() $\kappa = 2\kappa _1$ we conclude.
$\kappa = 2\kappa _1$ we conclude.
For the next result, we use the notion of a (nonnegatively) graded cyclotomic spectrum’ see [Reference Antieau, Mathew, Morrow and NikolausAMMN20, § 3 and Appendix A] or [Reference BrunBru01]. A graded cyclotomic spectrum consists of a graded spectrum ![]() $X = \bigoplus _{i \geq 0} X_i$ equipped with an
$X = \bigoplus _{i \geq 0} X_i$ equipped with an ![]() $S^1$-action together with a graded
$S^1$-action together with a graded ![]() $S^1$-equivariant cyclotomic Frobenius
$S^1$-equivariant cyclotomic Frobenius ![]() $\varphi _i \colon X_i \to X_{pi}^{tC_p}$ for each
$\varphi _i \colon X_i \to X_{pi}^{tC_p}$ for each ![]() $i$. Given a nonnegatively graded
$i$. Given a nonnegatively graded ![]() $E_1$-ring
$E_1$-ring ![]() $R$, the topological Hochschild homology
$R$, the topological Hochschild homology ![]() $\mathrm {THH}(R)$ acquires the structure of a graded cyclotomic spectrum. Given a graded cyclotomic spectrum
$\mathrm {THH}(R)$ acquires the structure of a graded cyclotomic spectrum. Given a graded cyclotomic spectrum ![]() $X$, we can consider a graded cyclotomic spectrum
$X$, we can consider a graded cyclotomic spectrum ![]() $X_{\geq i}$ where we only consider the graded summands in degrees
$X_{\geq i}$ where we only consider the graded summands in degrees ![]() $i$ or higher; this gives any graded cyclotomic spectrum a natural descending filtration. The filtration quotients
$i$ or higher; this gives any graded cyclotomic spectrum a natural descending filtration. The filtration quotients ![]() $X_{\geq i}/X_{\geq pi}$ have trivialized Frobenius because of the grading, and their
$X_{\geq i}/X_{\geq pi}$ have trivialized Frobenius because of the grading, and their ![]() $\mathrm {TR}$ can be thus described explicitly.
$\mathrm {TR}$ can be thus described explicitly.
Construction 3.5 (![]() $\mathrm {TR}$ of cyclotomic spectra with zero Frobenius)
$\mathrm {TR}$ of cyclotomic spectra with zero Frobenius)
Suppose ![]() $X \in \mathrm {CycSp}_{\geq 0}$ is
$X \in \mathrm {CycSp}_{\geq 0}$ is ![]() $p$-complete with trivialized Frobenius. Then, as in [Reference Antieau and NikolausAN21, Remark 2.5] and [Reference Nikolaus and ScholzeNS18, Corollary II.4.7], we obtain a natural equivalence
$p$-complete with trivialized Frobenius. Then, as in [Reference Antieau and NikolausAN21, Remark 2.5] and [Reference Nikolaus and ScholzeNS18, Corollary II.4.7], we obtain a natural equivalence
For this, we also use the identification for ![]() $n \geq 1$,
$n \geq 1$, ![]() $(X^{tC_p})^{hC_{p^{n-1}}} \simeq X^{tC_{p^n}}$, see [Reference Nikolaus and ScholzeNS18, Lemma II.4.1].
$(X^{tC_p})^{hC_{p^{n-1}}} \simeq X^{tC_{p^n}}$, see [Reference Nikolaus and ScholzeNS18, Lemma II.4.1].
Proposition 3.6 (![]() $K(1)$-acyclicity criterion)
$K(1)$-acyclicity criterion)
Let ![]() $X$ be a positively graded cyclotomic spectrum with the structure of a
$X$ be a positively graded cyclotomic spectrum with the structure of a ![]() $\mathrm {THH}(B)$-module. Suppose, for each
$\mathrm {THH}(B)$-module. Suppose, for each ![]() $i > 0$, that the following assertions hold.
$i > 0$, that the following assertions hold.
(i)
 $X_i$ is
$X_i$ is  $(2p+ 1) \kappa i$-connected (where
$(2p+ 1) \kappa i$-connected (where  $\kappa$ is as in Proposition 3.4).
$\kappa$ is as in Proposition 3.4).(ii) As a
 $\mathrm {THH}(B)$-module in
$\mathrm {THH}(B)$-module in  $\mathrm {Fun}(BS^1, {\rm Sp} )$,
$\mathrm {Fun}(BS^1, {\rm Sp} )$,  $X_i$ is induced from the cyclic group
$X_i$ is induced from the cyclic group  $C_i \subset S^1$.
$C_i \subset S^1$.
Then, for any set ![]() $Q$,
$Q$, ![]() $\prod _Q \mathrm {TR}(X)$ is
$\prod _Q \mathrm {TR}(X)$ is ![]() $K(1)$-acyclic.
$K(1)$-acyclic.
Proof. For simplicity of notation, we write ![]() $\mathrm {TR}_Q(-) = \prod _Q \mathrm {TR}(-)$. The construction
$\mathrm {TR}_Q(-) = \prod _Q \mathrm {TR}(-)$. The construction ![]() $\mathrm {TR}_Q(-)$ is exact and commutes with geometric realizations on
$\mathrm {TR}_Q(-)$ is exact and commutes with geometric realizations on ![]() $\mathrm {CycSp}_{\geq 0}$; therefore, it commutes with tensoring with
$\mathrm {CycSp}_{\geq 0}$; therefore, it commutes with tensoring with ![]() $ku$. Without loss of generality, we can therefore assume that
$ku$. Without loss of generality, we can therefore assume that ![]() $X$ is a
$X$ is a ![]() $\mathrm {THH}(B) \otimes ku$-module in graded cyclotomic spectra. Here we regard
$\mathrm {THH}(B) \otimes ku$-module in graded cyclotomic spectra. Here we regard ![]() $ku$ as a trivial cyclotomic spectrum, that is, via the image of the unique symmetric monoidal functor
$ku$ as a trivial cyclotomic spectrum, that is, via the image of the unique symmetric monoidal functor ![]() ${\rm Sp} \to \mathrm {CycSp}$.
${\rm Sp} \to \mathrm {CycSp}$.
We consider the descending filtration ![]() $\{ \mathrm {Fil}^{\geq n } X = X_{\geq p^{n}}\}_{n \geq 0}$ on the cyclotomic spectrum
$\{ \mathrm {Fil}^{\geq n } X = X_{\geq p^{n}}\}_{n \geq 0}$ on the cyclotomic spectrum ![]() $X$; note that the associated graded terms have trivialized Frobenii for degree reasons. This yields a filtration on the spectrum
$X$; note that the associated graded terms have trivialized Frobenii for degree reasons. This yields a filtration on the spectrum ![]() $\mathrm {TR}_Q(X)$, with
$\mathrm {TR}_Q(X)$, with ![]() $\mathrm {Fil}^{\geq n} \mathrm {TR}_Q(X) = \mathrm {TR}_Q(X_{\geq p^n})$. Since
$\mathrm {Fil}^{\geq n} \mathrm {TR}_Q(X) = \mathrm {TR}_Q(X_{\geq p^n})$. Since ![]() $\mathrm {TR}(-)$ preserves connectivity, our assumptions imply that
$\mathrm {TR}(-)$ preserves connectivity, our assumptions imply that ![]() $\mathrm {Fil}^{\geq n} \mathrm {TR}_Q(X)$ is
$\mathrm {Fil}^{\geq n} \mathrm {TR}_Q(X)$ is ![]() $(2p + 1) \kappa p^n$-connective.
$(2p + 1) \kappa p^n$-connective.
We have by (7) that ![]() $\mathrm {gr}^n \mathrm {TR}_Q(X) = \bigoplus _{p^{n} \leq i < p^{n+1}} \prod _Q\prod _{t \geq 0} (X_i)_{hC_{p^t}}$, since the cyclotomic Frobenius is trivial on
$\mathrm {gr}^n \mathrm {TR}_Q(X) = \bigoplus _{p^{n} \leq i < p^{n+1}} \prod _Q\prod _{t \geq 0} (X_i)_{hC_{p^t}}$, since the cyclotomic Frobenius is trivial on ![]() $\mathrm {gr}^n X$ for grading reasons. Since
$\mathrm {gr}^n X$ for grading reasons. Since ![]() $X_i$ is induced from
$X_i$ is induced from ![]() $C_i \subset S^1$, it follows from Proposition 3.4 that the
$C_i \subset S^1$, it follows from Proposition 3.4 that the ![]() $ku$-module
$ku$-module ![]() $\mathrm {gr}^n \mathrm {TR}_Q(X)/p$ is annihilated by
$\mathrm {gr}^n \mathrm {TR}_Q(X)/p$ is annihilated by ![]() $\beta ^{\kappa p^{n+1}}$.
$\beta ^{\kappa p^{n+1}}$.
Now ![]() $|\beta | = 2$, and
$|\beta | = 2$, and ![]() $2\sum _{i = 0}^{n-1} \kappa p^{i+1} < (2p+1)\kappa p^{n}$ with the difference tending to
$2\sum _{i = 0}^{n-1} \kappa p^{i+1} < (2p+1)\kappa p^{n}$ with the difference tending to ![]() $\infty$ as
$\infty$ as ![]() $n \to \infty$. Applying Lemma 3.7 below, we conclude that inverting
$n \to \infty$. Applying Lemma 3.7 below, we conclude that inverting ![]() $\beta$ annihilates
$\beta$ annihilates ![]() $\mathrm {TR}_Q(X) /p$, whence
$\mathrm {TR}_Q(X) /p$, whence ![]() $\mathrm {TR}_Q(X)$ is
$\mathrm {TR}_Q(X)$ is ![]() $K(1)$-acyclic as desired.
$K(1)$-acyclic as desired.
Lemma 3.7 Let ![]() $R$ be a connective
$R$ be a connective ![]() $E_1$-ring spectrum, and let
$E_1$-ring spectrum, and let ![]() $x \in \pi _t(R)$ be an element. Let
$x \in \pi _t(R)$ be an element. Let ![]() $\{\mathrm {Fil}^{\geq n} Y\}_{n \geq 0}$ be a filtered
$\{\mathrm {Fil}^{\geq n} Y\}_{n \geq 0}$ be a filtered ![]() $R$-module spectrum. Suppose that there exist functions
$R$-module spectrum. Suppose that there exist functions ![]() $f, g\colon \mathbb {N} \to \mathbb {N}$ such that:
$f, g\colon \mathbb {N} \to \mathbb {N}$ such that:
(i)
 $\mathrm {gr}^n (Y)$ is annihilated by
$\mathrm {gr}^n (Y)$ is annihilated by  $x^{f(n)}$;
$x^{f(n)}$;(ii)
 $\mathrm {Fil}^{\geq n}(Y)$ is
$\mathrm {Fil}^{\geq n}(Y)$ is  $g(n)$-connective;
$g(n)$-connective;(iii)
 $g(n) - t\sum _{i = 0}^{n-1} f(i) \to \infty$ for
$g(n) - t\sum _{i = 0}^{n-1} f(i) \to \infty$ for  $n \to \infty$.
$n \to \infty$.
Then ![]() $Y[1/x] = 0$.
$Y[1/x] = 0$.
Proof. Let ![]() $y \in \pi _s(Y)$. For each
$y \in \pi _s(Y)$. For each ![]() $n > 0$, the class
$n > 0$, the class ![]() $x^{f(0) + f(1) + \cdots + f(n-1)} y \in \pi _*(Y)$ naturally lifts to
$x^{f(0) + f(1) + \cdots + f(n-1)} y \in \pi _*(Y)$ naturally lifts to ![]() $\pi _{s + t(f(0) + \cdots + f(n-1))}( \mathrm {Fil}^{\geq n} Y)$. But for
$\pi _{s + t(f(0) + \cdots + f(n-1))}( \mathrm {Fil}^{\geq n} Y)$. But for ![]() $n \gg 0$, the connectivity of
$n \gg 0$, the connectivity of ![]() $\mathrm {Fil}^{\geq n} Y$ forces this last group to vanish. Therefore, the image of
$\mathrm {Fil}^{\geq n} Y$ forces this last group to vanish. Therefore, the image of ![]() $y$ in
$y$ in ![]() $\pi _s(Y[1/x])$ vanishes as desired.
$\pi _s(Y[1/x])$ vanishes as desired.
We now use the following basic calculation of ![]() $\mathrm {THH}$ of a free associative algebra, as a spectrum equipped with
$\mathrm {THH}$ of a free associative algebra, as a spectrum equipped with ![]() $S^1$-action. Versions of this are classical in ordinary Hochschild homology; see [Reference LodayLod98, § 3.1]. In the language of factorization homology, this result is a special case of the calculation of the factorization homology of a free algebra ([Reference Ayala, Francis and TanakaAFT17, Proposition 4.13] and [Reference Ayala and FrancisAF15, Proposition 5.5]).
$S^1$-action. Versions of this are classical in ordinary Hochschild homology; see [Reference LodayLod98, § 3.1]. In the language of factorization homology, this result is a special case of the calculation of the factorization homology of a free algebra ([Reference Ayala, Francis and TanakaAFT17, Proposition 4.13] and [Reference Ayala and FrancisAF15, Proposition 5.5]).
Theorem 3.8 (![]() $\mathrm {THH}$ of a free associative algebra)
$\mathrm {THH}$ of a free associative algebra)
Let ![]() $M$ be a spectrum, and let
$M$ be a spectrum, and let ![]() $T(M) = \bigoplus _{n \geq 0}M^{\otimes n}$ be the free
$T(M) = \bigoplus _{n \geq 0}M^{\otimes n}$ be the free ![]() $E_1$-algebra spectrum generated by
$E_1$-algebra spectrum generated by ![]() $M$. Then there is a natural equivalence in
$M$. Then there is a natural equivalence in ![]() $\mathrm {Fun}(BS^1, {\rm Sp} )$,
$\mathrm {Fun}(BS^1, {\rm Sp} )$,
where we use the natural ![]() $C_n$-action on
$C_n$-action on ![]() $M^{\otimes n}$ by permuting the factors.
$M^{\otimes n}$ by permuting the factors.
Proof. The results of [Reference Ayala, Francis and TanakaAFT17, Reference Ayala and FrancisAF15] (applied to the framed manifold ![]() $S^1$) imply that
$S^1$) imply that ![]() $\mathrm {THH}( T(M)) \simeq \int _{S^1} T(M) = \bigoplus _{n \geq 0} (\mathrm {Conf}_n(S^1)_+ \otimes M^{\otimes n})_{h \Sigma _n}$, for
$\mathrm {THH}( T(M)) \simeq \int _{S^1} T(M) = \bigoplus _{n \geq 0} (\mathrm {Conf}_n(S^1)_+ \otimes M^{\otimes n})_{h \Sigma _n}$, for ![]() $\mathrm {Conf}_n(S^1)$ the configuration space of
$\mathrm {Conf}_n(S^1)$ the configuration space of ![]() $n$ ordered points on the circle. One checks now (see [Reference Crabb and JamesCJ98, Example II.14.4]) that
$n$ ordered points on the circle. One checks now (see [Reference Crabb and JamesCJ98, Example II.14.4]) that ![]() $\mathrm {Conf}_n(S^1)$, as a space with
$\mathrm {Conf}_n(S^1)$, as a space with ![]() $S^1 \times \Sigma _n$-action, is homotopy equivalent to
$S^1 \times \Sigma _n$-action, is homotopy equivalent to ![]() $(S^1 \times \Sigma _n)/C_n$ (with
$(S^1 \times \Sigma _n)/C_n$ (with ![]() $C_n$ embedded diagonally), whence the claim.
$C_n$ embedded diagonally), whence the claim.
Proposition 3.9 Let ![]() $M, N$ be connective spectra. Then the map of cyclotomic spectra
$M, N$ be connective spectra. Then the map of cyclotomic spectra
induces an equivalence on ![]() $L_{K(1)} ( \prod _Q \mathrm {TR}(-))$ for any set
$L_{K(1)} ( \prod _Q \mathrm {TR}(-))$ for any set ![]() $Q$ if
$Q$ if ![]() $N$ is at least
$N$ is at least ![]() $\kappa (2p+1)$-connective.
$\kappa (2p+1)$-connective.
Proof. We can consider the tensor algebra ![]() $T(M \oplus N)$ as a graded
$T(M \oplus N)$ as a graded ![]() $E_1$-ring spectrum where
$E_1$-ring spectrum where ![]() $M$ is placed in degree
$M$ is placed in degree ![]() $0$ and
$0$ and ![]() $N$ is placed in degree
$N$ is placed in degree ![]() $1$. In this case, if we collect the terms in (8), we find that the
$1$. In this case, if we collect the terms in (8), we find that the ![]() $i$th graded piece of
$i$th graded piece of ![]() $\mathrm {THH}( T(M \oplus N))$ is the component which is
$\mathrm {THH}( T(M \oplus N))$ is the component which is ![]() $i$-homogeneous. Explicitly, for any subset
$i$-homogeneous. Explicitly, for any subset ![]() $I \subset \langle n\rangle = \{1, 2, \ldots , n\}$, we write
$I \subset \langle n\rangle = \{1, 2, \ldots , n\}$, we write ![]() $(M, N)^{\otimes (\langle n \rangle \setminus I, I)}$ for the ordered tensor product of
$(M, N)^{\otimes (\langle n \rangle \setminus I, I)}$ for the ordered tensor product of ![]() $n$ factors, where the
$n$ factors, where the ![]() $j$th factor is
$j$th factor is ![]() $M$ if
$M$ if ![]() $j \notin I$ and
$j \notin I$ and ![]() $N$ if
$N$ if ![]() $j \in I$. Expanding (8) gives
$j \in I$. Expanding (8) gives
 \begin{equation} \mathrm{THH}( T(M \oplus N))_i = \bigoplus_{n \geq 0} \mathrm{Ind}_{C_n}^{S^1} \bigg( \bigoplus_{I \subset \langle n \rangle, |I| = i} (M, N)^{{\otimes} (\langle n \rangle\setminus I, I)} \bigg). \end{equation}
\begin{equation} \mathrm{THH}( T(M \oplus N))_i = \bigoplus_{n \geq 0} \mathrm{Ind}_{C_n}^{S^1} \bigg( \bigoplus_{I \subset \langle n \rangle, |I| = i} (M, N)^{{\otimes} (\langle n \rangle\setminus I, I)} \bigg). \end{equation}
Here the ![]() $C_n$-action on the parenthesized term in (9) permutes the various summands. Note in particular that the stabilizer of
$C_n$-action on the parenthesized term in (9) permutes the various summands. Note in particular that the stabilizer of ![]() $I \subset \langle n\rangle$ in the
$I \subset \langle n\rangle$ in the ![]() $n$th summand is a subgroup of a cyclic group
$n$th summand is a subgroup of a cyclic group ![]() $C_i \subset C_n$ since
$C_i \subset C_n$ since ![]() $|I| = i$. In particular, it follows that the
$|I| = i$. In particular, it follows that the ![]() $i$th graded piece of
$i$th graded piece of ![]() $\mathrm {THH}( T(M \oplus N))$ is induced from
$\mathrm {THH}( T(M \oplus N))$ is induced from ![]() $C_i \subset S^1$. Furthermore, since
$C_i \subset S^1$. Furthermore, since ![]() $N$ is at least
$N$ is at least ![]() $\kappa (2p+1)$-connective, it follows that the
$\kappa (2p+1)$-connective, it follows that the ![]() $i$th graded piece of
$i$th graded piece of ![]() $\mathrm {THH}( T( M \oplus N))$ is at least
$\mathrm {THH}( T( M \oplus N))$ is at least ![]() $\kappa (2p+1)$-connective. By Proposition 3.6, it follows that the positively graded part of
$\kappa (2p+1)$-connective. By Proposition 3.6, it follows that the positively graded part of ![]() $\mathrm {THH}(T(M \oplus N)) \otimes \mathrm {THH}(B)$ has vanishing
$\mathrm {THH}(T(M \oplus N)) \otimes \mathrm {THH}(B)$ has vanishing ![]() $K(1)$-local
$K(1)$-local ![]() $\prod _Q \mathrm {TR}(-)$ for any set
$\prod _Q \mathrm {TR}(-)$ for any set ![]() $Q$, whence the result.
$Q$, whence the result.
For the next result, if ![]() $R$ is an
$R$ is an ![]() $E_1$-ring spectrum and
$E_1$-ring spectrum and ![]() $N$ an
$N$ an ![]() $(R, R)$-bimodule, we let
$(R, R)$-bimodule, we let ![]() $T_R(N) = \bigoplus _{n \geq 0} N \otimes _R N \otimes _R \cdots \otimes _R N$ be the free
$T_R(N) = \bigoplus _{n \geq 0} N \otimes _R N \otimes _R \cdots \otimes _R N$ be the free ![]() $E_1$-algebra under
$E_1$-algebra under ![]() $R$ generated by
$R$ generated by ![]() $N$.
$N$.
Proposition 3.10 Let ![]() $R$ be a connective
$R$ be a connective ![]() $B$-algebra. Let
$B$-algebra. Let ![]() $N$ be an at least
$N$ be an at least ![]() $\kappa (2p+1)$-connective
$\kappa (2p+1)$-connective ![]() $(R, R)$-bimodule. Then the map
$(R, R)$-bimodule. Then the map ![]() $\mathrm {THH}( T_R(N)) \to \mathrm {THH}(R)$ induces an equivalence on
$\mathrm {THH}( T_R(N)) \to \mathrm {THH}(R)$ induces an equivalence on ![]() $L_{K(1)} (\prod _Q \mathrm {TR}(-))$ for any set
$L_{K(1)} (\prod _Q \mathrm {TR}(-))$ for any set ![]() $Q$.
$Q$.
Proof. Simplicially resolving ![]() $N$ by free
$N$ by free ![]() $(R, R)$-bimodules (since
$(R, R)$-bimodules (since ![]() $\prod _Q \mathrm {TR}(-)$ commutes with geometric realizations), we may assume that
$\prod _Q \mathrm {TR}(-)$ commutes with geometric realizations), we may assume that ![]() $N$ is free on generators (possibly infinitely many) in degrees
$N$ is free on generators (possibly infinitely many) in degrees ![]() $\kappa (2p+1)$ or higher. Simplicially resolving
$\kappa (2p+1)$ or higher. Simplicially resolving ![]() $R$ by free
$R$ by free ![]() $B$-algebras, we may assume that
$B$-algebras, we may assume that ![]() $R$ is free as well, on some classes in degrees at least
$R$ is free as well, on some classes in degrees at least ![]() $0$. In this case, the result follows from Proposition 3.9.
$0$. In this case, the result follows from Proposition 3.9.
Lemma 3.11 Let ![]() $E$ be a localizing invariant of
$E$ be a localizing invariant of ![]() $B$-linear
$B$-linear ![]() $\infty$-categories. Suppose that there exists
$\infty$-categories. Suppose that there exists ![]() $k \geq 0$ such that for every connective
$k \geq 0$ such that for every connective ![]() $B$-algebra
$B$-algebra ![]() $R$, we have
$R$, we have ![]() $E( R) \xrightarrow {\sim } E( \tau _{\leq k} R)$. Then
$E( R) \xrightarrow {\sim } E( \tau _{\leq k} R)$. Then ![]() $E$ is truncating.
$E$ is truncating.
Proof. We show by descending inductionFootnote 3 that for any ![]() $i \geq 0$ and for any connective
$i \geq 0$ and for any connective ![]() $B$-algebra
$B$-algebra ![]() $R$, the map
$R$, the map ![]() $R \to \tau _{\leq i} R$ induces an equivalence on
$R \to \tau _{\leq i} R$ induces an equivalence on ![]() $E$; taking
$E$; taking ![]() $i = 0$ gives the theorem. For
$i = 0$ gives the theorem. For ![]() $i \geq k$, we already know the claim by assumption. Suppose we know the claim for
$i \geq k$, we already know the claim by assumption. Suppose we know the claim for ![]() $i+1$; to prove the claim for
$i+1$; to prove the claim for ![]() $i$, we need to see that
$i$, we need to see that ![]() $\tau _{\leq i+1} R \to \tau _{\leq i} R$ induces an equivalence on
$\tau _{\leq i+1} R \to \tau _{\leq i} R$ induces an equivalence on ![]() $E$. Now
$E$. Now ![]() $\tau _{\leq i+1} R \to \tau _{\leq i} R$ is a square-zero extension, that is, we have the following pullback diagram of
$\tau _{\leq i+1} R \to \tau _{\leq i} R$ is a square-zero extension, that is, we have the following pullback diagram of ![]() $B$-algebras.
$B$-algebras.

Since ![]() $E$ is a localizing invariant, the main result of Land and Tamme [Reference Land and TammeLT19] yields a
$E$ is a localizing invariant, the main result of Land and Tamme [Reference Land and TammeLT19] yields a ![]() $B$-algebra
$B$-algebra ![]() $\tilde {R}$ with underlying spectrum
$\tilde {R}$ with underlying spectrum ![]() $H(\pi _0 R) \otimes _{\tau _{\leq i+1} R } \tau _{\leq i} R$ fitting into a commutative diagram of
$H(\pi _0 R) \otimes _{\tau _{\leq i+1} R } \tau _{\leq i} R$ fitting into a commutative diagram of ![]() $B$-algebras
$B$-algebras

which is carried to a pullback by ![]() $E$. But the map
$E$. But the map ![]() $H(\pi _0 R) \to \tilde {R}$ is an equivalence in degrees up to
$H(\pi _0 R) \to \tilde {R}$ is an equivalence in degrees up to ![]() $i+1$ and therefore induces an equivalence on
$i+1$ and therefore induces an equivalence on ![]() $E$ by the inductive hypothesis. Therefore,
$E$ by the inductive hypothesis. Therefore, ![]() $E( \tau _{\leq i+1} R) \to E( \tau _{\leq i} R)$ is an equivalence, whence the inductive step and the result.
$E( \tau _{\leq i+1} R) \to E( \tau _{\leq i} R)$ is an equivalence, whence the inductive step and the result.
Proof of Theorem 3.1 As before, we write ![]() $\mathrm {TR}_Q(-) = \prod _Q \mathrm {TR}(-)$ for a set
$\mathrm {TR}_Q(-) = \prod _Q \mathrm {TR}(-)$ for a set ![]() $Q$. For any connective
$Q$. For any connective ![]() $B$-algebra
$B$-algebra ![]() $R$, we claim that
$R$, we claim that ![]() $R \to \tau _{\leq \kappa (2p+1)} R$ induces an equivalence on
$R \to \tau _{\leq \kappa (2p+1)} R$ induces an equivalence on ![]() $L_{K(1)} \mathrm {TR}_Q(-)$. Indeed, this follows from Proposition 3.10 because we can simplicially resolve
$L_{K(1)} \mathrm {TR}_Q(-)$. Indeed, this follows from Proposition 3.10 because we can simplicially resolve ![]() $\tau _{\leq \kappa (2p+1)} R$ using free
$\tau _{\leq \kappa (2p+1)} R$ using free ![]() $R$-algebras over free
$R$-algebras over free ![]() $(R, R)$-bimodules on classes in degrees
$(R, R)$-bimodules on classes in degrees ![]() $\kappa (2p+1)$ or higher and since
$\kappa (2p+1)$ or higher and since ![]() $\mathrm {TR}_Q(-)$ commutes with geometric realizations. The result now follows from Lemma 3.11.
$\mathrm {TR}_Q(-)$ commutes with geometric realizations. The result now follows from Lemma 3.11.
Corollary 3.12 (cf. [Reference Land, Mathew, Meier and TammeLMMT20])
The invariants ![]() $L_{K(1)} K(-), L_{K(1)} \mathrm {TC}(-)$ are truncating on connective
$L_{K(1)} K(-), L_{K(1)} \mathrm {TC}(-)$ are truncating on connective ![]() $B$-algebras.
$B$-algebras.
Proof. The result for ![]() $L_{K(1)} \mathrm {TC}(-)$ follows from Theorem 3.1 by taking Frobenius fixed points. The result for
$L_{K(1)} \mathrm {TC}(-)$ follows from Theorem 3.1 by taking Frobenius fixed points. The result for ![]() $L_{K(1)} K(-)$ is a formal consequence since the fiber of the trace
$L_{K(1)} K(-)$ is a formal consequence since the fiber of the trace ![]() $K(-) \to \mathrm {TC}(-)$ is truncating by the Dundas–Goodwillie–McCarthy theorem [Reference Dundas, Goodwillie and McCarthyDGM13].
$K(-) \to \mathrm {TC}(-)$ is truncating by the Dundas–Goodwillie–McCarthy theorem [Reference Dundas, Goodwillie and McCarthyDGM13].
Corollary 3.13 [Reference Land, Mathew, Meier and TammeLMMT20, Reference Bhatt, Clausen and MathewBCM20]
For any ![]() $n$, we have
$n$, we have ![]() $L_{K(1)} K(\mathbb {Z}/p^n) = 0$.
$L_{K(1)} K(\mathbb {Z}/p^n) = 0$.
Proof. Take ![]() $B = H\mathbb {Z}$ in Theorem 3.1, so
$B = H\mathbb {Z}$ in Theorem 3.1, so ![]() $L_{K(1)} \mathrm {TC}(-)$ is truncating and therefore nilinvariant on connective
$L_{K(1)} \mathrm {TC}(-)$ is truncating and therefore nilinvariant on connective ![]() $H\mathbb {Z}$-algebras. Then the result follows because the Dundas–Goodwillie–McCarthy theorem and comparison with
$H\mathbb {Z}$-algebras. Then the result follows because the Dundas–Goodwillie–McCarthy theorem and comparison with ![]() $\mathbb {F}_p$ yield
$\mathbb {F}_p$ yield ![]() $L_{K(1)} K(\mathbb {Z}/p^n) = L_{K(1)} \mathrm {TC}(\mathbb {Z}/p^n)$, but the above shows that this equals
$L_{K(1)} K(\mathbb {Z}/p^n) = L_{K(1)} \mathrm {TC}(\mathbb {Z}/p^n)$, but the above shows that this equals ![]() $L_{K(1)} \mathrm {TC}(\mathbb {F}_p) = 0$.
$L_{K(1)} \mathrm {TC}(\mathbb {F}_p) = 0$.
4. Asymptotic  $K(1)$-locality
$K(1)$-locality
In this section we show (Theorem 4.8) that ![]() $\mathrm {TR}$ is asymptotically
$\mathrm {TR}$ is asymptotically ![]() $K(1)$-local for a regular ring satisfying mild hypotheses, using the Beilinson–Lichtenbaum conjecture. This result is due to Hesselholt and Madsen in the case of smooth algebras over a DVR with perfect residue field of characteristic greater than
$K(1)$-local for a regular ring satisfying mild hypotheses, using the Beilinson–Lichtenbaum conjecture. This result is due to Hesselholt and Madsen in the case of smooth algebras over a DVR with perfect residue field of characteristic greater than ![]() $2$, which we begin by reviewing.
$2$, which we begin by reviewing.
Theorem 4.1 (Hesselholt–Madsen [Reference Hesselholt and MadsenHM03, Reference Hesselholt and MadsenHM04])
Let ![]() $K$ be a complete, discretely valued field of characteristic
$K$ be a complete, discretely valued field of characteristic ![]() $0$ with ring of integers
$0$ with ring of integers ![]() $\mathcal {O}_K \subset K$ and perfect residue field
$\mathcal {O}_K \subset K$ and perfect residue field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p > 2$. Let
$p > 2$. Let ![]() $R$ be a smooth
$R$ be a smooth ![]() $\mathcal {O}_K$-algebra of relative dimension
$\mathcal {O}_K$-algebra of relative dimension ![]() $d$. Then the map
$d$. Then the map
is ![]() $d$-truncated.
$d$-truncated.
Proof. Without loss of generality, we can assume that ![]() $\mu _p \subset K$, since otherwise
$\mu _p \subset K$, since otherwise ![]() $\mathrm {TR}(R; \mathbb {F}_p)$ is a retract of
$\mathrm {TR}(R; \mathbb {F}_p)$ is a retract of ![]() $\mathrm {TR}(R[\zeta _p]; \mathbb {F}_p)$ via the transfer. In this case, the result follows from [Reference Hesselholt and MadsenHM04, Theorem E]. Indeed, [Reference Hesselholt and MadsenHM04, Theorem E] gives a calculation of the cofiber
$\mathrm {TR}(R[\zeta _p]; \mathbb {F}_p)$ via the transfer. In this case, the result follows from [Reference Hesselholt and MadsenHM04, Theorem E]. Indeed, [Reference Hesselholt and MadsenHM04, Theorem E] gives a calculation of the cofiber ![]() $\mathrm {TR}(R|R_K; \mathbb {F}_p)$ of the transfer map
$\mathrm {TR}(R|R_K; \mathbb {F}_p)$ of the transfer map ![]() $\mathrm {TR}(R \otimes _{\mathcal {O}_K} k; \mathbb {F}_p) \to \mathrm {TR}(R; \mathbb {F}_p)$. Since
$\mathrm {TR}(R \otimes _{\mathcal {O}_K} k; \mathbb {F}_p) \to \mathrm {TR}(R; \mathbb {F}_p)$. Since ![]() $\mathrm {TR}(R \otimes _{\mathcal {O}_K} k; \mathbb {F}_p)$ is
$\mathrm {TR}(R \otimes _{\mathcal {O}_K} k; \mathbb {F}_p)$ is ![]() $K(1)$-acyclic and
$K(1)$-acyclic and ![]() $d$-truncated in view of the identification [Reference HesselholtHes96] with the de Rham–Witt complex of
$d$-truncated in view of the identification [Reference HesselholtHes96] with the de Rham–Witt complex of ![]() $R \otimes _{\mathcal {O}_K} k$, it suffices to verify the (stronger) claim that
$R \otimes _{\mathcal {O}_K} k$, it suffices to verify the (stronger) claim that ![]() $\mathrm {TR}(R|R_K; \mathbb {F}_p) \to L_{K(1)}\mathrm {TR}(R|R_K; \mathbb {F}_p)$ is
$\mathrm {TR}(R|R_K; \mathbb {F}_p) \to L_{K(1)}\mathrm {TR}(R|R_K; \mathbb {F}_p)$ is ![]() $(d-2)$-truncated. Equivalently (see Lemma 5.8 below), it suffices to show that the cofiber of the Bott element on
$(d-2)$-truncated. Equivalently (see Lemma 5.8 below), it suffices to show that the cofiber of the Bott element on ![]() $\mathrm {TR}(R|R_K; \mathbb {F}_p)$ is
$\mathrm {TR}(R|R_K; \mathbb {F}_p)$ is ![]() $(d+1)$-truncated. In fact, this follows from the calculation in [Reference HesselholtHes96], once we know that the absolute de Rham–Witt complex
$(d+1)$-truncated. In fact, this follows from the calculation in [Reference HesselholtHes96], once we know that the absolute de Rham–Witt complex ![]() $W \Omega ^{\ast }_{(R, M_R)}$ is
$W \Omega ^{\ast }_{(R, M_R)}$ is ![]() $p$-divisible in degrees
$p$-divisible in degrees ![]() $d+2$ or higher. This in turn follows from the case where
$d+2$ or higher. This in turn follows from the case where ![]() $R = \mathcal {O}_K$ (see [Reference Hesselholt and MadsenHM03, Corollary 3.2.7]; the case of polynomial rings via the functor
$R = \mathcal {O}_K$ (see [Reference Hesselholt and MadsenHM03, Corollary 3.2.7]; the case of polynomial rings via the functor ![]() $P$ (see [Reference Hesselholt and MadsenHM04, Lemma 7.1.4] and its proof); and finally, étale base-change [Reference Hesselholt and MadsenHM04, Lemma 7.1.1].
$P$ (see [Reference Hesselholt and MadsenHM04, Lemma 7.1.4] and its proof); and finally, étale base-change [Reference Hesselholt and MadsenHM04, Lemma 7.1.1].
Construction 4.2 (![]() $\mathrm {TR}$ as
$\mathrm {TR}$ as ![]() $p$-typical curves)
$p$-typical curves)
Let ![]() $R$ be an animated ring.Footnote 4 We let
$R$ be an animated ring.Footnote 4 We let
denote the spectrum of curves on the ![]() $K$-theory of
$K$-theory of ![]() $R$, defining a functor from animated rings to spectra. By [Reference HesselholtHes96, Theorem 3.1.9], if
$R$, defining a functor from animated rings to spectra. By [Reference HesselholtHes96, Theorem 3.1.9], if ![]() $R$ is a discrete
$R$ is a discrete ![]() $\mathbb {Z}/p^j$-algebra for some
$\mathbb {Z}/p^j$-algebra for some ![]() $j$, we have a natural expression of
$j$, we have a natural expression of ![]() $\mathrm {TR}(R; \mathbb {Z}_p)$ as a summand of
$\mathrm {TR}(R; \mathbb {Z}_p)$ as a summand of ![]() $C(R; \mathbb {Z}_p)$ (note that we are considering
$C(R; \mathbb {Z}_p)$ (note that we are considering ![]() $p$-typical
$p$-typical ![]() $\mathrm {TR}$, while in [Reference HesselholtHes96, Theorem 3.1.9] global
$\mathrm {TR}$, while in [Reference HesselholtHes96, Theorem 3.1.9] global ![]() $\mathrm {TR}$ is considered). Left Kan extending both sides to animated rings (since both
$\mathrm {TR}$ is considered). Left Kan extending both sides to animated rings (since both ![]() $\mathrm {TR}(-)$ and
$\mathrm {TR}(-)$ and ![]() $C(-)$ commute with geometric realizations),Footnote 5 we obtain that
$C(-)$ commute with geometric realizations),Footnote 5 we obtain that ![]() $\mathrm {TR}(R; \mathbb {Z}_p)$ is naturally a summand of
$\mathrm {TR}(R; \mathbb {Z}_p)$ is naturally a summand of ![]() $C(R)$ for
$C(R)$ for ![]() $R$ an animated
$R$ an animated ![]() $\mathbb {Z}/p^j$-algebra. Passing to the limit over
$\mathbb {Z}/p^j$-algebra. Passing to the limit over ![]() $j$ and using the
$j$ and using the ![]() $p$-adic continuity of
$p$-adic continuity of ![]() $K$-theory [Reference Clausen, Mathew and MorrowCMM21, Theorem 5.21], we find that for any
$K$-theory [Reference Clausen, Mathew and MorrowCMM21, Theorem 5.21], we find that for any ![]() $p$-henselian animated ring
$p$-henselian animated ring ![]() $R$ (i.e.
$R$ (i.e. ![]() $\pi _0(R)$ is
$\pi _0(R)$ is ![]() $p$-henselian),
$p$-henselian), ![]() $\mathrm {TR}(R; \mathbb {Z}_p)$ is a summand of
$\mathrm {TR}(R; \mathbb {Z}_p)$ is a summand of ![]() $C(R; \mathbb {Z}_p)$.
$C(R; \mathbb {Z}_p)$.
Next, we discuss the comparison between the ![]() $p$-adic
$p$-adic ![]() $K$-theory of
$K$-theory of ![]() $R$ and
$R$ and ![]() $R[1/p]$; see [Reference NiziołNiz08, Lemma 3.5] for this argument.
$R[1/p]$; see [Reference NiziołNiz08, Lemma 3.5] for this argument.
Proposition 4.3 Let ![]() $R$ be a regular noetherian ring of finite Krull dimension. Suppose, for every
$R$ be a regular noetherian ring of finite Krull dimension. Suppose, for every ![]() $x \in \mathrm {Spec}(R/p)$, that we have
$x \in \mathrm {Spec}(R/p)$, that we have ![]() $[\kappa (x): \kappa (x)^p] \leq p^d$. Then the map
$[\kappa (x): \kappa (x)^p] \leq p^d$. Then the map ![]() $K(R; \mathbb {F}_p) \to K(R[1/p]; \mathbb {F}_p)$ is
$K(R; \mathbb {F}_p) \to K(R[1/p]; \mathbb {F}_p)$ is ![]() $d$-truncated.
$d$-truncated.
Proof. The homotopy fiber of the map in question is, by Quillen's dévissage theorem, the mod ![]() $p$
$p$ ![]() $K$-theory of the abelian category of finitely generated
$K$-theory of the abelian category of finitely generated ![]() $R/p$-modules, that is, the mod
$R/p$-modules, that is, the mod ![]() $p$
$p$ ![]() $G$-theory of
$G$-theory of ![]() $R/p$,
$R/p$, ![]() $G(R/p; \mathbb {F}_p)$. So it suffices to show that
$G(R/p; \mathbb {F}_p)$. So it suffices to show that ![]() $G(R/p; \mathbb {F}_p)$ is concentrated in degrees up to
$G(R/p; \mathbb {F}_p)$ is concentrated in degrees up to ![]() $d$. Using the filtration by codimension of support and dévissage (see [Reference QuillenQui73, Theorem 5.4]), we find that
$d$. Using the filtration by codimension of support and dévissage (see [Reference QuillenQui73, Theorem 5.4]), we find that ![]() $G(R/p; \mathbb {F}_p)$ has a filtration whose associated graded terms are direct sums of the
$G(R/p; \mathbb {F}_p)$ has a filtration whose associated graded terms are direct sums of the ![]() $K( \kappa (x); \mathbb {F}_p)$ for
$K( \kappa (x); \mathbb {F}_p)$ for ![]() $x \in \mathrm {Spec}(R/p)$; it therefore suffices to show that these terms are
$x \in \mathrm {Spec}(R/p)$; it therefore suffices to show that these terms are ![]() $d$-truncated. But now the Geisser–Levine theorem [Reference Geisser and LevineGL00] implies that for any field
$d$-truncated. But now the Geisser–Levine theorem [Reference Geisser and LevineGL00] implies that for any field ![]() $E$ of characteristic
$E$ of characteristic ![]() $p$, there is an embedding
$p$, there is an embedding ![]() $K_*(E; \mathbb {F}_p) \hookrightarrow \Omega ^{\ast }_{E/\mathbb {F}_p}$. This implies that
$K_*(E; \mathbb {F}_p) \hookrightarrow \Omega ^{\ast }_{E/\mathbb {F}_p}$. This implies that ![]() $K(\kappa (x); \mathbb {F}_p)$ is
$K(\kappa (x); \mathbb {F}_p)$ is ![]() $\dim _{\kappa (x)} \Omega ^1_{\kappa (x)/\mathbb {F}_p}$-truncated. But
$\dim _{\kappa (x)} \Omega ^1_{\kappa (x)/\mathbb {F}_p}$-truncated. But ![]() $\dim _{\kappa (x)} \Omega ^1_{\kappa (x)/\mathbb {F}_p} = \log _p [\kappa (x): \kappa (x)^p] \leq d$ by the theory of
$\dim _{\kappa (x)} \Omega ^1_{\kappa (x)/\mathbb {F}_p} = \log _p [\kappa (x): \kappa (x)^p] \leq d$ by the theory of ![]() $p$-bases [Reference MatsumuraMat86, Theorem 26.5]. Combining these facts, the result follows.
$p$-bases [Reference MatsumuraMat86, Theorem 26.5]. Combining these facts, the result follows.
Proposition 4.4 (Rosenschon–Østvær [Reference Rosenschon and ØstværRØ06])
Let ![]() $R$ be a regular noetherian
$R$ be a regular noetherian ![]() $\mathbb {Z}[1/p]$-algebra of finite Krull dimension. Suppose that
$\mathbb {Z}[1/p]$-algebra of finite Krull dimension. Suppose that ![]() $\mathrm {vcd}_p(\kappa (x)) \leq d$ for all
$\mathrm {vcd}_p(\kappa (x)) \leq d$ for all ![]() $x \in \mathrm {Spec}(R[1/p])$. Then the map
$x \in \mathrm {Spec}(R[1/p])$. Then the map ![]() $K(R; \mathbb {F}_p) \to L_{K(1)} K(R; \mathbb {F}_p)$ has
$K(R; \mathbb {F}_p) \to L_{K(1)} K(R; \mathbb {F}_p)$ has ![]() $(d-3)$-truncated homotopy fiber.
$(d-3)$-truncated homotopy fiber.
Proof sketch Using Nisnevich descent [Reference Thomason and TrobaughTT90], we reduce to the case where ![]() $R$ is henselian local, and even a field of characteristic not equal to
$R$ is henselian local, and even a field of characteristic not equal to ![]() $p$ by Gabber–Suslin rigidity [Reference GabberGab92]; note that we do not have to worry about the distinction between connective and nonconnective
$p$ by Gabber–Suslin rigidity [Reference GabberGab92]; note that we do not have to worry about the distinction between connective and nonconnective ![]() $K$-theory by regularity. Then the result follows from the Beilinson–Lichtenbaum conjecture (proved by Voevodsky and Rost; see [Reference Haesemeyer and WeibelHW19]) describing the associated graded terms of the motivic filtration on
$K$-theory by regularity. Then the result follows from the Beilinson–Lichtenbaum conjecture (proved by Voevodsky and Rost; see [Reference Haesemeyer and WeibelHW19]) describing the associated graded terms of the motivic filtration on ![]() $K(R; \mathbb {F}_p)$ (see, for example, [Reference Clausen and MathewCM19, § 6.2] for an account).
$K(R; \mathbb {F}_p)$ (see, for example, [Reference Clausen and MathewCM19, § 6.2] for an account).
Proposition 4.5 Let ![]() $R$ be an excellent normal domain which is henselian along an ideal
$R$ be an excellent normal domain which is henselian along an ideal ![]() $I \subset R$ containing
$I \subset R$ containing ![]() $(p)$. Suppose that, for all
$(p)$. Suppose that, for all ![]() $\mathfrak {p} \in \mathrm {Spec}(R)$ containing
$\mathfrak {p} \in \mathrm {Spec}(R)$ containing ![]() $I$, we have
$I$, we have ![]() $\dim R_{\mathfrak {p}} + \log _p [\kappa (\mathfrak {p}): \kappa (\mathfrak {p})^p] \leq d$. Then, for all
$\dim R_{\mathfrak {p}} + \log _p [\kappa (\mathfrak {p}): \kappa (\mathfrak {p})^p] \leq d$. Then, for all ![]() $\mathfrak {q} \in \mathrm {Spec}(R[1/p])$, the residue field
$\mathfrak {q} \in \mathrm {Spec}(R[1/p])$, the residue field ![]() $\kappa (\mathfrak {q})$ has
$\kappa (\mathfrak {q})$ has ![]() $p$-cohomological dimension at most
$p$-cohomological dimension at most ![]() $d + 1$.
$d + 1$.
Proof. By standard continuity arguments, it suffices to show that for any affine open ![]() $U = \mathrm {Spec}( R[1/f]) \subset \mathrm {Spec}(R[1/p])$ and any constructible
$U = \mathrm {Spec}( R[1/f]) \subset \mathrm {Spec}(R[1/p])$ and any constructible ![]() $p$-torsion sheaf
$p$-torsion sheaf ![]() $\mathcal {F}$ on
$\mathcal {F}$ on ![]() $U$, we have
$U$, we have ![]() $H^n( U, \mathcal {F}) = 0$ for
$H^n( U, \mathcal {F}) = 0$ for ![]() $n > d +1$. Denote by
$n > d +1$. Denote by ![]() $j\colon U \hookrightarrow \mathrm {Spec}(R)$ the open inclusion, and denote by
$j\colon U \hookrightarrow \mathrm {Spec}(R)$ the open inclusion, and denote by ![]() $i_0\colon \mathrm {Spec}(R/I) \hookrightarrow \mathrm {Spec}(R)$ the closed embedding. Using that
$i_0\colon \mathrm {Spec}(R/I) \hookrightarrow \mathrm {Spec}(R)$ the closed embedding. Using that ![]() $\mathrm {Spec}(R/I)$ has
$\mathrm {Spec}(R/I)$ has ![]() $p$-cohomological dimension at most
$p$-cohomological dimension at most ![]() $1$ and the affine analog of proper base change [Reference GabberGab94, Reference HuberHub93] applied to the henselian ideal
$1$ and the affine analog of proper base change [Reference GabberGab94, Reference HuberHub93] applied to the henselian ideal ![]() $I \subset R$, we see that it suffices to show that
$I \subset R$, we see that it suffices to show that ![]() $i_0^* R^n j_* \mathcal {F} = 0$ for
$i_0^* R^n j_* \mathcal {F} = 0$ for ![]() $n > d$.
$n > d$.
Working stalkwise on ![]() $R$ and using the compatibility of étale cohomology with filtered colimits, we can now reduce to the case where
$R$ and using the compatibility of étale cohomology with filtered colimits, we can now reduce to the case where ![]() $R$ is an excellent, strictly henselian normal local domain with residue field
$R$ is an excellent, strictly henselian normal local domain with residue field ![]() $k$ (and
$k$ (and ![]() $I \subset R$ is contained in the maximal ideal), since excellence and normality are preserved by strict henselization (see [Reference GrecoGre76] for the former). The statement then becomes that
$I \subset R$ is contained in the maximal ideal), since excellence and normality are preserved by strict henselization (see [Reference GrecoGre76] for the former). The statement then becomes that ![]() $H^n( U, \mathcal {F}) = 0$ for
$H^n( U, \mathcal {F}) = 0$ for ![]() $n > d$, which follows from the Gabber–Orgogozo bound [Reference Gabber and OrgogozoGO08, Theorem 6.1] (noting that the
$n > d$, which follows from the Gabber–Orgogozo bound [Reference Gabber and OrgogozoGO08, Theorem 6.1] (noting that the ![]() $p$-dimension of the residue field
$p$-dimension of the residue field ![]() $k$ is
$k$ is ![]() $\log _p [k:k^p]$ since
$\log _p [k:k^p]$ since ![]() $k$ is separably closed).
$k$ is separably closed).
Remark 4.6 Suppose that ![]() $R_0$ is a ring such that
$R_0$ is a ring such that ![]() $R_0/p$ is finite type over a perfect field
$R_0/p$ is finite type over a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$. Then, for every prime ideal
$p$. Then, for every prime ideal ![]() $\mathfrak {p} \in \mathrm {Spec}(R_0)$ containing
$\mathfrak {p} \in \mathrm {Spec}(R_0)$ containing ![]() $(p)$, we have
$(p)$, we have ![]() $\dim (R_0)_{\mathfrak {p}} + \log _p [\kappa (\mathfrak {p}): \kappa (\mathfrak {p})^p] \leq \dim (R_0)$. Indeed, we have
$\dim (R_0)_{\mathfrak {p}} + \log _p [\kappa (\mathfrak {p}): \kappa (\mathfrak {p})^p] \leq \dim (R_0)$. Indeed, we have ![]() $\dim (R_0)_{\mathfrak {p}} + \dim (R_0/\mathfrak {p}) \leq \dim (R_0)$. Therefore, it suffices to prove
$\dim (R_0)_{\mathfrak {p}} + \dim (R_0/\mathfrak {p}) \leq \dim (R_0)$. Therefore, it suffices to prove ![]() $\log _p [ \kappa ( \mathfrak {p}): \kappa (\mathfrak {p})^p] = \dim (R_0/\mathfrak {p})$. But in this case, both are the transcendence degree of the field
$\log _p [ \kappa ( \mathfrak {p}): \kappa (\mathfrak {p})^p] = \dim (R_0/\mathfrak {p})$. But in this case, both are the transcendence degree of the field ![]() $\kappa ( \mathfrak {p})$ over
$\kappa ( \mathfrak {p})$ over ![]() $k$; see [Reference MatsumuraMat80, Theorem 27.B].
$k$; see [Reference MatsumuraMat80, Theorem 27.B].
Lemma 4.7 Let ![]() $R_0$ be an
$R_0$ be an ![]() $\mathbb {F}_p$-algebra. Suppose that for all residue fields
$\mathbb {F}_p$-algebra. Suppose that for all residue fields ![]() $\kappa$ of
$\kappa$ of ![]() $R_0$, we have
$R_0$, we have ![]() $[\kappa : \kappa ^p] \leq p^d$ for some
$[\kappa : \kappa ^p] \leq p^d$ for some ![]() $d \geq 0$. Then, for all residue fields
$d \geq 0$. Then, for all residue fields ![]() $\kappa '$ of
$\kappa '$ of ![]() $R_0[[x]]$, we have
$R_0[[x]]$, we have ![]() $[\kappa ': \kappa '^p] \leq p^{d+1}$.
$[\kappa ': \kappa '^p] \leq p^{d+1}$.
Proof. We have that ![]() $R_0[[x]]$ is generated by
$R_0[[x]]$ is generated by ![]() $p$ elements over the subring generated by its
$p$ elements over the subring generated by its ![]() $p$th powers and by
$p$th powers and by ![]() $R_0$. For every residue field
$R_0$. For every residue field ![]() $\kappa$ of
$\kappa$ of ![]() $R_0$, it follows that
$R_0$, it follows that ![]() $R_0[[x]] \otimes _{R_0} \kappa$ is generated by
$R_0[[x]] \otimes _{R_0} \kappa$ is generated by ![]() $p$ elements over the subring generated by
$p$ elements over the subring generated by ![]() $p$th powers together with
$p$th powers together with ![]() $\kappa$. In particular, it is generated by
$\kappa$. In particular, it is generated by ![]() $p^{d+1}$ elements as a module over its
$p^{d+1}$ elements as a module over its ![]() $p$th powers. It follows that the same holds for any residue field of
$p$th powers. It follows that the same holds for any residue field of ![]() $R_0[[x]] \otimes _{R_0} \kappa$ and, varying
$R_0[[x]] \otimes _{R_0} \kappa$ and, varying ![]() $\kappa$, we obtain the conclusion for every residue field of
$\kappa$, we obtain the conclusion for every residue field of ![]() $R_0$.
$R_0$.
Theorem 4.8 Let ![]() $R$ be an excellent,
$R$ be an excellent, ![]() $p$-torsion-free regular noetherian ring. Suppose
$p$-torsion-free regular noetherian ring. Suppose ![]() $R/p$ is finitely generated as a module over its subring of
$R/p$ is finitely generated as a module over its subring of ![]() $p$th powers. Suppose, furthermore, that for all
$p$th powers. Suppose, furthermore, that for all ![]() $\mathfrak {p} \in \mathrm {Spec}(R)$ containing
$\mathfrak {p} \in \mathrm {Spec}(R)$ containing ![]() $(p)$, we have
$(p)$, we have ![]() $\dim R_{\mathfrak {p}} + \log _p [ \kappa (\mathfrak {p}):\kappa (\mathfrak {p})^p] \leq d$ for some
$\dim R_{\mathfrak {p}} + \log _p [ \kappa (\mathfrak {p}):\kappa (\mathfrak {p})^p] \leq d$ for some ![]() $d \geq 0$. Then the map
$d \geq 0$. Then the map ![]() $\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is
$\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is ![]() $(d-1)$-truncated.
$(d-1)$-truncated.
Proof. Without loss of generality, we can assume that ![]() $R$ is
$R$ is ![]() $p$-henselian (since henselization preserves excellence; see [Reference GrecoGre76]), so
$p$-henselian (since henselization preserves excellence; see [Reference GrecoGre76]), so ![]() $\dim R \leq d$. By Construction 4.2, it suffices to show that
$\dim R \leq d$. By Construction 4.2, it suffices to show that ![]() $C(R)/p \to L_{K(1)} C(R)/p$ is
$C(R)/p \to L_{K(1)} C(R)/p$ is ![]() $(d-1)$-truncated. Now
$(d-1)$-truncated. Now ![]() $C(R)$ is the desuspension of the fiber of the map
$C(R)$ is the desuspension of the fiber of the map ![]() $\varprojlim _n K( R[x]/x^n) \to K(R)$. With
$\varprojlim _n K( R[x]/x^n) \to K(R)$. With ![]() $p$-adic coefficients, the fact that
$p$-adic coefficients, the fact that ![]() $R/p$ is finitely generated as a module over its
$R/p$ is finitely generated as a module over its ![]() $p$th powers allows us to pass to the limit [Reference Clausen, Mathew and MorrowCMM21, Theorem F] and we obtain
$p$th powers allows us to pass to the limit [Reference Clausen, Mathew and MorrowCMM21, Theorem F] and we obtain
Since ![]() $K(R)$ is a retract of
$K(R)$ is a retract of ![]() $K(R[[x]])$, it suffices to show that the fiber of
$K(R[[x]])$, it suffices to show that the fiber of ![]() $K(R[[x]]; \mathbb {F}_p) \to L_{K(1)}K(R[[x]]; \mathbb {F}_p)$ is
$K(R[[x]]; \mathbb {F}_p) \to L_{K(1)}K(R[[x]]; \mathbb {F}_p)$ is ![]() $d$-truncated. We will verify this by comparing both sides with the intermediate term
$d$-truncated. We will verify this by comparing both sides with the intermediate term ![]() $K( R[[x]][1/p]; \mathbb {F}_p)$.
$K( R[[x]][1/p]; \mathbb {F}_p)$.
First, for every characteristic ![]() $p$ residue field
$p$ residue field ![]() $\kappa$ of
$\kappa$ of ![]() $R$, corresponding to a prime ideal
$R$, corresponding to a prime ideal ![]() $\mathfrak {p} \subset R$ containing
$\mathfrak {p} \subset R$ containing ![]() $(p)$, we have
$(p)$, we have ![]() $[\kappa : \kappa ^p] \leq p^{d-1}$ by our assumption, since
$[\kappa : \kappa ^p] \leq p^{d-1}$ by our assumption, since ![]() $\dim R_{\mathfrak {p}} \geq 1$. Now
$\dim R_{\mathfrak {p}} \geq 1$. Now ![]() $R[[x]]$ is also a
$R[[x]]$ is also a ![]() $p$-torsion-free regular ring of dimension
$p$-torsion-free regular ring of dimension ![]() $\dim (R) + 1$. For every characteristic
$\dim (R) + 1$. For every characteristic ![]() $p$ residue field
$p$ residue field ![]() $\kappa '$ of
$\kappa '$ of ![]() $R[[x]]$, we have
$R[[x]]$, we have ![]() $[\kappa ': \kappa '^p] \leq p^{d}$ by Lemma 4.7. By Proposition 4.3, it follows that
$[\kappa ': \kappa '^p] \leq p^{d}$ by Lemma 4.7. By Proposition 4.3, it follows that ![]() $K(R[[x]]; \mathbb {F}_p) \to K(R[[x]][1/p]; \mathbb {F}_p)$ is
$K(R[[x]]; \mathbb {F}_p) \to K(R[[x]][1/p]; \mathbb {F}_p)$ is ![]() $d$-truncated.
$d$-truncated.
Second, we apply Proposition 4.5 to the ring ![]() $R[[x]]$ and the ideal
$R[[x]]$ and the ideal ![]() $I = (p, x)$. The power series ring
$I = (p, x)$. The power series ring ![]() $R[[x]]$ remains excellent (and regular) since
$R[[x]]$ remains excellent (and regular) since ![]() $R$ is excellent, thanks to [Reference Kurano and ShimomotoKS16]. For any prime ideal
$R$ is excellent, thanks to [Reference Kurano and ShimomotoKS16]. For any prime ideal ![]() $\mathfrak {p} \in \mathrm {Spec}( R[[x]])$ containing
$\mathfrak {p} \in \mathrm {Spec}( R[[x]])$ containing ![]() $I$, we let
$I$, we let ![]() $\mathfrak {p}_0 = \mathfrak {p} \cap R \subset R$, so that
$\mathfrak {p}_0 = \mathfrak {p} \cap R \subset R$, so that ![]() $R[[x]]_{\mathfrak {p}}/(x) = R_{\mathfrak {p}_0}$. Then
$R[[x]]_{\mathfrak {p}}/(x) = R_{\mathfrak {p}_0}$. Then ![]() $\dim ( R[[x]]_{\mathfrak {p}}) = \dim ( R_{\mathfrak {p}_0})+ 1$ and
$\dim ( R[[x]]_{\mathfrak {p}}) = \dim ( R_{\mathfrak {p}_0})+ 1$ and ![]() $\kappa ( \mathfrak {p}) = \kappa (\mathfrak {p}_0)$. Thus, Proposition 4.5 applies to
$\kappa ( \mathfrak {p}) = \kappa (\mathfrak {p}_0)$. Thus, Proposition 4.5 applies to ![]() $R[[x]]$ (with
$R[[x]]$ (with ![]() $d$ replaced by
$d$ replaced by ![]() $d+1$) and we find that the characteristic
$d+1$) and we find that the characteristic ![]() $0$ residue fields of
$0$ residue fields of ![]() $R[[x]]$ have
$R[[x]]$ have ![]() $p$-cohomological dimension at most
$p$-cohomological dimension at most ![]() $d + 2$. Therefore, by Proposition 4.4,
$d + 2$. Therefore, by Proposition 4.4, ![]() $K( R[[x]][1/p]; \mathbb {F}_p) \to L_{K(1)} K( R[[x]][1/p])$ is
$K( R[[x]][1/p]; \mathbb {F}_p) \to L_{K(1)} K( R[[x]][1/p])$ is ![]() $(d-1)$-truncated.
$(d-1)$-truncated.
Combining the above, we find that the composite map ![]() $K(R[[x]]; \mathbb {F}_p) \to L_{K(1)} K(R[[x]]; \mathbb {F}_p) \simeq L_{K(1)} K( R[[x]][1/p]; \mathbb {F}_p)$ (the last identification by (2)) is
$K(R[[x]]; \mathbb {F}_p) \to L_{K(1)} K(R[[x]]; \mathbb {F}_p) \simeq L_{K(1)} K( R[[x]][1/p]; \mathbb {F}_p)$ (the last identification by (2)) is ![]() $d$-truncated, whence the result.
$d$-truncated, whence the result.
This recovers in particular Theorem 4.1. More generally, we have the following example.
Example 4.9 Let ![]() $R$ be a
$R$ be a ![]() $d$-dimensional regular, excellent
$d$-dimensional regular, excellent ![]() $p$-torsion-free noetherian ring with
$p$-torsion-free noetherian ring with ![]() $R/p$ finitely generated over its
$R/p$ finitely generated over its ![]() $p$th powers. Suppose that
$p$th powers. Suppose that ![]() $(R/p)_{\mathrm {red}}$ is finite type over a perfect field (and necessarily of dimension
$(R/p)_{\mathrm {red}}$ is finite type over a perfect field (and necessarily of dimension ![]() $d-1$). Then Theorem 4.8 (in view of Remark 4.6) applies to show that
$d-1$). Then Theorem 4.8 (in view of Remark 4.6) applies to show that ![]() $\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is
$\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is ![]() $(d-1)$-truncated.
$(d-1)$-truncated.
5. The Segal conjecture
In this section we discuss the relationship between the following two properties of a cyclotomic spectrum ![]() $X$:
$X$:
(i)
 $\mathrm {TR}(X)$ agrees with its
$\mathrm {TR}(X)$ agrees with its  $K(1)$-localization in high enough degrees;
$K(1)$-localization in high enough degrees;(ii) the cyclotomic Frobenius
 $\varphi _X \colon X \to X^{tC_p}$ is an equivalence in high enough degrees.
$\varphi _X \colon X \to X^{tC_p}$ is an equivalence in high enough degrees.
Property (i) is the Lichtenbaum–Quillen style statement discussed in the previous section, and verified for ![]() $\mathrm {THH}(R)$ under regularity and finiteness hypotheses. Property (ii) is often referred to as the ‘Segal conjecture’ since for
$\mathrm {THH}(R)$ under regularity and finiteness hypotheses. Property (ii) is often referred to as the ‘Segal conjecture’ since for ![]() $X = \mathrm {THH}(\mathbb {S})$, the Frobenius
$X = \mathrm {THH}(\mathbb {S})$, the Frobenius ![]() $\mathbb {S} \to \mathbb {S}^{tC_p}$ is a
$\mathbb {S} \to \mathbb {S}^{tC_p}$ is a ![]() $p$-adic equivalence by the Segal conjecture for
$p$-adic equivalence by the Segal conjecture for ![]() $C_p$, proved in [Reference LinLin80, Reference GunawardenaGun80]. The Segal conjecture has been studied extensively for
$C_p$, proved in [Reference LinLin80, Reference GunawardenaGun80]. The Segal conjecture has been studied extensively for ![]() $\mathrm {THH}(R)$ for
$\mathrm {THH}(R)$ for ![]() $R$ a ring (or ring spectrum).
$R$ a ring (or ring spectrum).
We first show the implication ![]() $({\rm i}) \implies ({\rm ii})$. We use the Antieau–Nikolaus theory of topological Cartier modules [Reference Antieau and NikolausAN21], which we begin by briefly reviewing.
$({\rm i}) \implies ({\rm ii})$. We use the Antieau–Nikolaus theory of topological Cartier modules [Reference Antieau and NikolausAN21], which we begin by briefly reviewing.
Definition 5.1 A topological Cartier module ![]() $M$ is an object of
$M$ is an object of ![]() $\mathrm {Fun}(BS^1, {\rm Sp} )$ together with maps
$\mathrm {Fun}(BS^1, {\rm Sp} )$ together with maps ![]() $V \colon M_{hC_p} \to M$ and
$V \colon M_{hC_p} \to M$ and ![]() $F \colon M \to M^{hC_p}$ in
$F \colon M \to M^{hC_p}$ in ![]() $\mathrm {Fun}(BS^1, {\rm Sp} )$ together with a homotopy between the composite and the norm map
$\mathrm {Fun}(BS^1, {\rm Sp} )$ together with a homotopy between the composite and the norm map ![]() $M_{hC_p} \to M^{hC_p}$ (considered
$M_{hC_p} \to M^{hC_p}$ (considered ![]() $S^1 \simeq S^1/C_p$-equivariantly). The collection of topological Cartier modules is naturally organized into a presentable stable
$S^1 \simeq S^1/C_p$-equivariantly). The collection of topological Cartier modules is naturally organized into a presentable stable ![]() $\infty$-category.
$\infty$-category.
Given a bounded-below, ![]() $p$-typical cyclotomic spectrum
$p$-typical cyclotomic spectrum ![]() $X$, we can consider
$X$, we can consider ![]() $\mathrm {TR}(X)$ as a topological Cartier module, and we have an identification
$\mathrm {TR}(X)$ as a topological Cartier module, and we have an identification ![]() $X \simeq \mathrm {cofib}(V)$. Under these identifications, the cyclotomic Frobenius
$X \simeq \mathrm {cofib}(V)$. Under these identifications, the cyclotomic Frobenius ![]() $X \to X^{tC_p}$ is obtained from
$X \to X^{tC_p}$ is obtained from ![]() $F\colon \mathrm {TR}(X) \to \mathrm {TR}(X)^{hC_p}$ by taking cofibers by
$F\colon \mathrm {TR}(X) \to \mathrm {TR}(X)^{hC_p}$ by taking cofibers by ![]() $V$ on both domain and codomain and identifying
$V$ on both domain and codomain and identifying ![]() $\mathrm {TR}(X)^{tC_p} \simeq X^{tC_p}$ as
$\mathrm {TR}(X)^{tC_p} \simeq X^{tC_p}$ as ![]() $(\mathrm {TR}(X)_{h{C_p}})^{tC_p} = 0$ [Reference Nikolaus and ScholzeNS18, Lemma I.2.1]. On bounded-below objects, this construction establishes a fully faithful embedding from cyclotomic spectra into topological Cartier modules, with image given by the
$(\mathrm {TR}(X)_{h{C_p}})^{tC_p} = 0$ [Reference Nikolaus and ScholzeNS18, Lemma I.2.1]. On bounded-below objects, this construction establishes a fully faithful embedding from cyclotomic spectra into topological Cartier modules, with image given by the ![]() $V$-complete objects [Reference Antieau and NikolausAN21, Theorem 3.21].
$V$-complete objects [Reference Antieau and NikolausAN21, Theorem 3.21].
Proposition 5.2 Let ![]() $X$ be a connective,
$X$ be a connective, ![]() $p$-complete cyclotomic spectrum whose underlying spectrum is
$p$-complete cyclotomic spectrum whose underlying spectrum is ![]() $K(1)$-acyclic. Suppose the map
$K(1)$-acyclic. Suppose the map ![]() $\mathrm {TR}(X) \to L_{K(1)} \mathrm {TR}(X)$ is
$\mathrm {TR}(X) \to L_{K(1)} \mathrm {TR}(X)$ is ![]() $d$-truncated. Then the Frobenius
$d$-truncated. Then the Frobenius ![]() $\varphi \colon X \to X^{tC_p}$ is
$\varphi \colon X \to X^{tC_p}$ is ![]() $d$-truncated.
$d$-truncated.
In the case ![]() $L_{K(1)} \mathrm {TR}(X) =0$, the result is [Reference Antieau and NikolausAN21, Proposition 2.25].
$L_{K(1)} \mathrm {TR}(X) =0$, the result is [Reference Antieau and NikolausAN21, Proposition 2.25].
Proof. Since ![]() $X$ is
$X$ is ![]() $K(1)$-acyclic, it follows that
$K(1)$-acyclic, it follows that ![]() $V\colon \mathrm {TR}( X)_{hC_p} \to \mathrm {TR}(X)$ is
$V\colon \mathrm {TR}( X)_{hC_p} \to \mathrm {TR}(X)$ is ![]() $K(1)$-locally an equivalence. The
$K(1)$-locally an equivalence. The ![]() $K(1)$-localization
$K(1)$-localization ![]() $L_{K(1)} \mathrm {TR}(X)$ acquires the structure of a topological Cartier module as well by
$L_{K(1)} \mathrm {TR}(X)$ acquires the structure of a topological Cartier module as well by ![]() $K(1)$-localizing
$K(1)$-localizing ![]() $F, V$ and using the comparison map
$F, V$ and using the comparison map ![]() $L_{K(1)} ( \mathrm {TR}(X)^{hC_p}) \to (L_{K(1)} \mathrm {TR}(X))^{hC_p}$. The composite map
$L_{K(1)} ( \mathrm {TR}(X)^{hC_p}) \to (L_{K(1)} \mathrm {TR}(X))^{hC_p}$. The composite map ![]() $(L_{K(1)} \mathrm {TR}(X))_{hC_p} \to (L_{K(1)} \mathrm {TR}(X))^{hC_p}$ is an equivalence after
$(L_{K(1)} \mathrm {TR}(X))_{hC_p} \to (L_{K(1)} \mathrm {TR}(X))^{hC_p}$ is an equivalence after ![]() $p$-completion since Tate constructions vanish in the
$p$-completion since Tate constructions vanish in the ![]() $K(1)$-local category. Since we saw that
$K(1)$-local category. Since we saw that ![]() $V$ is an equivalence on
$V$ is an equivalence on ![]() $L_{K(1)} \mathrm {TR}(X)$ after
$L_{K(1)} \mathrm {TR}(X)$ after ![]() $p$-completion, it follows that the Frobenius on
$p$-completion, it follows that the Frobenius on ![]() $L_{K(1)} \mathrm {TR}(X)$ induces an equivalence
$L_{K(1)} \mathrm {TR}(X)$ induces an equivalence
For a topological Cartier module ![]() $Y$, we consider the fiber of
$Y$, we consider the fiber of ![]() $F = F_Y\colon Y \to Y^{hC_p}$, which we denote
$F = F_Y\colon Y \to Y^{hC_p}$, which we denote ![]() $\mathrm {fib}(F)$. As we saw above,
$\mathrm {fib}(F)$. As we saw above, ![]() $\mathrm {fib}(F)$ is contractible for the topological Cartier module
$\mathrm {fib}(F)$ is contractible for the topological Cartier module ![]() $L_{K(1)} \mathrm {TR}(X)$. Moreover,
$L_{K(1)} \mathrm {TR}(X)$. Moreover, ![]() $\mathrm {fib}(F)$ is
$\mathrm {fib}(F)$ is ![]() $d$-truncated for the topological Cartier module
$d$-truncated for the topological Cartier module ![]() $\mathrm {fib}( \mathrm {TR}(X) \to L_{K(1)} \mathrm {TR}(X))$ because this topological Cartier module is itself
$\mathrm {fib}( \mathrm {TR}(X) \to L_{K(1)} \mathrm {TR}(X))$ because this topological Cartier module is itself ![]() $d$-truncated. In particular, we find that
$d$-truncated. In particular, we find that ![]() $\mathrm {fib}(F\colon \mathrm {TR}(X) \to \mathrm {TR}(X)^{hC_p})$ is
$\mathrm {fib}(F\colon \mathrm {TR}(X) \to \mathrm {TR}(X)^{hC_p})$ is ![]() $d$-truncated. Taking the cofiber on both the domain and codomain of the Verschiebung, we find that
$d$-truncated. Taking the cofiber on both the domain and codomain of the Verschiebung, we find that ![]() $\mathrm {fib}(F\colon \mathrm {TR}(X) \to \mathrm {TR}(X)^{hC_p}) = \mathrm {fib}(\varphi \colon X \to X^{tC_p})$ which is therefore
$\mathrm {fib}(F\colon \mathrm {TR}(X) \to \mathrm {TR}(X)^{hC_p}) = \mathrm {fib}(\varphi \colon X \to X^{tC_p})$ which is therefore ![]() $d$-truncated as desired.
$d$-truncated as desired.
Combining Proposition 5.2 and Theorem 4.8, we obtain the following result. Versions of the Segal conjecture have been studied by many authors. For instance, it is known that ![]() $\mathrm {THH}(\mathbb {Z}_p; \mathbb {F}_p) \to \mathrm {THH}(\mathbb {Z}_p; \mathbb {F}_p)^{tC_p}$ is an equivalence on connective covers [Reference Bökstedt and MadsenBM94, Lemma 6.5]. Compare [Reference Hesselholt and MadsenHM03] for the more general case of a DVR
$\mathrm {THH}(\mathbb {Z}_p; \mathbb {F}_p) \to \mathrm {THH}(\mathbb {Z}_p; \mathbb {F}_p)^{tC_p}$ is an equivalence on connective covers [Reference Bökstedt and MadsenBM94, Lemma 6.5]. Compare [Reference Hesselholt and MadsenHM03] for the more general case of a DVR ![]() $\mathcal {O}_K$ of mixed characteristic and perfect residue field of characteristic
$\mathcal {O}_K$ of mixed characteristic and perfect residue field of characteristic ![]() $p>2$. The Segal conjecture for smooth algebras in characteristic
$p>2$. The Segal conjecture for smooth algebras in characteristic ![]() $p$ appears as [Reference HesselholtHes18, Proposition 6.6] and (at the filtered level) [Reference Bhatt, Morrow and ScholzeBMS19, Corollary 8.18]. The Segal conjecture has also been verified for certain ring spectra as well; see [Reference Ausoni and RognesAR02, Reference Lunøe-Nielsen and RognesLR11, Reference Angelini-Knoll and QuigleyAQ21].
$p$ appears as [Reference HesselholtHes18, Proposition 6.6] and (at the filtered level) [Reference Bhatt, Morrow and ScholzeBMS19, Corollary 8.18]. The Segal conjecture has also been verified for certain ring spectra as well; see [Reference Ausoni and RognesAR02, Reference Lunøe-Nielsen and RognesLR11, Reference Angelini-Knoll and QuigleyAQ21].
Corollary 5.3 (The Segal conjecture for regular rings)
Let ![]() $R$ be a
$R$ be a ![]() $p$-torsion-free excellent regular noetherian ring with
$p$-torsion-free excellent regular noetherian ring with ![]() $R/p$ finitely generated over its
$R/p$ finitely generated over its ![]() $p$th powers. Suppose that for all
$p$th powers. Suppose that for all ![]() $\mathfrak {p} \in \mathrm {Spec}(R)$ containing
$\mathfrak {p} \in \mathrm {Spec}(R)$ containing ![]() $(p)$, we have
$(p)$, we have ![]() $\dim R_{\mathfrak {p}} + \log _p [ \kappa (\mathfrak {p}):\kappa (\mathfrak {p})^p] \leq d$. Then the map
$\dim R_{\mathfrak {p}} + \log _p [ \kappa (\mathfrak {p}):\kappa (\mathfrak {p})^p] \leq d$. Then the map ![]() $\mathrm {THH}(R; \mathbb {F}_p) \to \mathrm {THH}(R; \mathbb {F}_p)^{tC_p}$ is
$\mathrm {THH}(R; \mathbb {F}_p) \to \mathrm {THH}(R; \mathbb {F}_p)^{tC_p}$ is ![]() $(d-1)$-truncated.
$(d-1)$-truncated.
Question 5.4 Is it possible to prove a filtered version of this result, with respect to the motivic filtrations [Reference Bhatt, Morrow and ScholzeBMS19] on both sides?
We next discuss the converse direction. Here we only prove the result under a more restrictive hypothesis, namely for cyclotomic spectra which are ![]() $ku$-modules.
$ku$-modules.
Example 5.5 Let ![]() $C = \widehat {\overline {\mathbb {Q}_p}}$. If
$C = \widehat {\overline {\mathbb {Q}_p}}$. If ![]() $R$ is a
$R$ is a ![]() $\mathcal {O}_C$-algebra, then the cyclotomic trace makes
$\mathcal {O}_C$-algebra, then the cyclotomic trace makes ![]() $\mathrm {THH}(R; \mathbb {Z}_p)$ into a
$\mathrm {THH}(R; \mathbb {Z}_p)$ into a ![]() $ku$-module in view of the equivalence
$ku$-module in view of the equivalence ![]() $ku_{\hat {p}} \simeq K(\mathcal {O}_C; \mathbb {Z}_p)$; see [Reference NiziołNiz98, Lemma 3.1], [Reference SuslinSus83], and [Reference HesselholtHes06]. One can improve this slightly:
$ku_{\hat {p}} \simeq K(\mathcal {O}_C; \mathbb {Z}_p)$; see [Reference NiziołNiz98, Lemma 3.1], [Reference SuslinSus83], and [Reference HesselholtHes06]. One can improve this slightly: ![]() $K( \widehat {\mathbb {Z}_p[\zeta _{p^\infty }]}; \mathbb {Z}_p)$ has the structure of an
$K( \widehat {\mathbb {Z}_p[\zeta _{p^\infty }]}; \mathbb {Z}_p)$ has the structure of an ![]() $E_\infty$-algebra under
$E_\infty$-algebra under ![]() $ku$, so the same applies to any
$ku$, so the same applies to any ![]() $\widehat {\mathbb {Z}_p[\zeta _{p^\infty }]}$-algebra
$\widehat {\mathbb {Z}_p[\zeta _{p^\infty }]}$-algebra ![]() $R$. This follows from three facts. First,
$R$. This follows from three facts. First, ![]() $K( \widehat {\mathbb {Z}_p[\zeta _{p^\infty }]}; \mathbb {Z}_p) \simeq K(\widehat {\mathbb {Q}_p(\zeta _{p^\infty })}; \mathbb {Z}_p)$; see [Reference Hesselholt and NikolausHN19, Lemma 1.3.7] for this argument (which only uses that the field
$K( \widehat {\mathbb {Z}_p[\zeta _{p^\infty }]}; \mathbb {Z}_p) \simeq K(\widehat {\mathbb {Q}_p(\zeta _{p^\infty })}; \mathbb {Z}_p)$; see [Reference Hesselholt and NikolausHN19, Lemma 1.3.7] for this argument (which only uses that the field ![]() $\widehat {\mathbb {Q}_p(\zeta _{p^\infty })}$ is perfectoid). Second, since
$\widehat {\mathbb {Q}_p(\zeta _{p^\infty })}$ is perfectoid). Second, since ![]() $\widehat {\mathbb {Q}_p(\zeta _{p^\infty })}$ is perfectoid, it has
$\widehat {\mathbb {Q}_p(\zeta _{p^\infty })}$ is perfectoid, it has ![]() $p$-cohomological dimension at most
$p$-cohomological dimension at most ![]() $1$ by the tilting equivalence, whence
$1$ by the tilting equivalence, whence ![]() $K(\widehat {\mathbb {Q}_p(\zeta _{p^\infty })}; \mathbb {Z}_p) \to L_{K(1)}K(\widehat {\mathbb {Q}_p(\zeta _{p^\infty })}; \mathbb {Z}_p)$ is the connective cover map; see Proposition 4.4. Third,
$K(\widehat {\mathbb {Q}_p(\zeta _{p^\infty })}; \mathbb {Z}_p) \to L_{K(1)}K(\widehat {\mathbb {Q}_p(\zeta _{p^\infty })}; \mathbb {Z}_p)$ is the connective cover map; see Proposition 4.4. Third, ![]() $L_{K(1)} K(\mathbb {Z}[\zeta _{p^\infty }])$ has the structure of an
$L_{K(1)} K(\mathbb {Z}[\zeta _{p^\infty }])$ has the structure of an ![]() $E_\infty$-algebra under
$E_\infty$-algebra under ![]() $KU$ and hence
$KU$ and hence ![]() $ku$; see [Reference Bhatt, Clausen and MathewBCM20, Construction 3.7].
$ku$; see [Reference Bhatt, Clausen and MathewBCM20, Construction 3.7].
Lemma 5.6 Let ![]() $M \in \mathrm {Fun}(BS^1, \mod (H\mathbb {F}_p))$ be an
$M \in \mathrm {Fun}(BS^1, \mod (H\mathbb {F}_p))$ be an ![]() $r$-connected object. Suppose that there exists a map
$r$-connected object. Suppose that there exists a map ![]() $f\colon M \to M'$ in
$f\colon M \to M'$ in ![]() $\mathrm {Fun}(BS^1, \mod (H\mathbb {F}_p))$ such that
$\mathrm {Fun}(BS^1, \mod (H\mathbb {F}_p))$ such that ![]() $M'$ is induced (as an object with
$M'$ is induced (as an object with ![]() $S^1$-action) and such that
$S^1$-action) and such that ![]() $f$ is an equivalence on
$f$ is an equivalence on ![]() $\tau _{\geq r}$. Then there exists a map
$\tau _{\geq r}$. Then there exists a map ![]() $\tilde {M} \to M$ of
$\tilde {M} \to M$ of ![]() $r$-connected objects in
$r$-connected objects in ![]() $\mathrm {Fun}(BS^1, \mod (H \mathbb {F}_p))$ which induces an equivalence on
$\mathrm {Fun}(BS^1, \mod (H \mathbb {F}_p))$ which induces an equivalence on ![]() $\tau _{\geq r+1}$ and such that
$\tau _{\geq r+1}$ and such that ![]() $\tilde {M}$ is induced.
$\tilde {M}$ is induced.
Proof. The homotopy groups ![]() $\pi _*(M), \pi _*(M')$ form graded modules over the ring
$\pi _*(M), \pi _*(M')$ form graded modules over the ring ![]() $\pi _*( \mathbb {F}_p[S^1]) = \mathbb {F}_p[\epsilon ]/\epsilon ^2, \ |\epsilon | = 1$. By assumption,
$\pi _*( \mathbb {F}_p[S^1]) = \mathbb {F}_p[\epsilon ]/\epsilon ^2, \ |\epsilon | = 1$. By assumption, ![]() $\pi _*(M')$ is a free graded
$\pi _*(M')$ is a free graded ![]() $\mathbb {F}_p[\epsilon ]/\epsilon ^2$-module and
$\mathbb {F}_p[\epsilon ]/\epsilon ^2$-module and ![]() $\pi _*(M)$ is the submodule of those elements in degree
$\pi _*(M)$ is the submodule of those elements in degree ![]() $r$ or higher. Choosing an
$r$ or higher. Choosing an ![]() $\mathbb {F}_p$-subspace
$\mathbb {F}_p$-subspace ![]() $V$ of
$V$ of ![]() $\pi _r(M) = \pi _r(M')$ which is complementary to
$\pi _r(M) = \pi _r(M')$ which is complementary to ![]() $\epsilon \pi _{r-1}(M') \subset \pi _r(M')$, we can modify
$\epsilon \pi _{r-1}(M') \subset \pi _r(M')$, we can modify ![]() $M$ to form
$M$ to form ![]() $\tilde {M}$ with
$\tilde {M}$ with ![]() $\pi _r(\tilde {M}) = V$; it is now easy to see that
$\pi _r(\tilde {M}) = V$; it is now easy to see that ![]() $\pi _*(\tilde {M})$ is a free graded
$\pi _*(\tilde {M})$ is a free graded ![]() $\mathbb {F}_p[\epsilon ]/\epsilon ^2$-module, so we can conclude.
$\mathbb {F}_p[\epsilon ]/\epsilon ^2$-module, so we can conclude.
Proposition 5.7 Let ![]() $X$ be a connective,
$X$ be a connective, ![]() $p$-complete
$p$-complete ![]() $ku$-module in
$ku$-module in ![]() $\mathrm {CycSp}$. Suppose that
$\mathrm {CycSp}$. Suppose that ![]() $\varphi \colon X \to X^{tC_p}$ is
$\varphi \colon X \to X^{tC_p}$ is ![]() $d$-truncated. Then the fiber of
$d$-truncated. Then the fiber of ![]() $\mathrm {TR}(X)/p \to L_{K(1)} \mathrm {TR}(X)/p$ is
$\mathrm {TR}(X)/p \to L_{K(1)} \mathrm {TR}(X)/p$ is ![]() $(d + 3)$-truncated.
$(d + 3)$-truncated.
Proof. It follows that the cyclotomic spectrum ![]() $Y = X/(p, \beta ) = X \otimes _{ku} H \mathbb {F}_p \in \mathrm {CycSp}_{\geq 0}$ has the property that
$Y = X/(p, \beta ) = X \otimes _{ku} H \mathbb {F}_p \in \mathrm {CycSp}_{\geq 0}$ has the property that ![]() $\varphi \colon Y \to Y^{tC_p}$ is
$\varphi \colon Y \to Y^{tC_p}$ is ![]() $(d+4)$-truncated. It follows that the comparison map
$(d+4)$-truncated. It follows that the comparison map ![]() $Y^{C_p} \to Y^{hC_p}$ is
$Y^{C_p} \to Y^{hC_p}$ is ![]() $(d+4)$-truncated as well, via the fiber square
$(d+4)$-truncated as well, via the fiber square

Now, for each ![]() $n \geq 1$, we have the following pullback diagram [Reference Nikolaus and ScholzeNS18, Lemma II.4.5].
$n \geq 1$, we have the following pullback diagram [Reference Nikolaus and ScholzeNS18, Lemma II.4.5].

The bottom horizontal map is ![]() $Y^{C_{p^{n-1}}} \to Y^{hC_{p^{n-1}}} \xrightarrow {\varphi ^{hC_{p^{n-1}}}} (Y^{tC_p})^{hC_{p^{n-1}}}$, and the last term is identified with
$Y^{C_{p^{n-1}}} \to Y^{hC_{p^{n-1}}} \xrightarrow {\varphi ^{hC_{p^{n-1}}}} (Y^{tC_p})^{hC_{p^{n-1}}}$, and the last term is identified with ![]() $Y^{tC_{p^n}}$ using the Tate orbit lemma; see [Reference Nikolaus and ScholzeNS18, Lemma II.4.1].
$Y^{tC_{p^n}}$ using the Tate orbit lemma; see [Reference Nikolaus and ScholzeNS18, Lemma II.4.1].
Now ![]() $Y^{C_p} \to Y^{hC_p}$ is an equivalence in degrees at least
$Y^{C_p} \to Y^{hC_p}$ is an equivalence in degrees at least ![]() $d+ 6$, hence
$d+ 6$, hence ![]() $Y^{C_{p^{n-1}}} \to Y^{hC_{p^{n-1}}}$ is an equivalence in degrees at least
$Y^{C_{p^{n-1}}} \to Y^{hC_{p^{n-1}}}$ is an equivalence in degrees at least ![]() $d+ 6$ by [Reference Nikolaus and ScholzeNS18, Corollary II.4.9] (a generalization of results of Tsalidis [Reference TsalidisTsa98] and Bökstedt, Bruner, Lunø, Nielsen, and Rognes [Reference Bökstedt, Bruner, Lunøe-Nielsen and RognesBBLR14]). Since
$d+ 6$ by [Reference Nikolaus and ScholzeNS18, Corollary II.4.9] (a generalization of results of Tsalidis [Reference TsalidisTsa98] and Bökstedt, Bruner, Lunø, Nielsen, and Rognes [Reference Bökstedt, Bruner, Lunøe-Nielsen and RognesBBLR14]). Since ![]() $\varphi \colon Y \to Y^{tC_p}$ is an equivalence in degrees at least
$\varphi \colon Y \to Y^{tC_p}$ is an equivalence in degrees at least ![]() $d+6$, it follows that the bottom horizontal map in (11) is an equivalence in degrees at least
$d+6$, it follows that the bottom horizontal map in (11) is an equivalence in degrees at least ![]() $d+ 6$. Note also that
$d+ 6$. Note also that ![]() $Y^{tC_p}$ is a module over
$Y^{tC_p}$ is a module over ![]() $\mathbb {F}_p^{tC_p}$ in
$\mathbb {F}_p^{tC_p}$ in ![]() $\mathrm {Fun}(BS^1, \mod (H\mathbb {F}_p))$; since the latter has induced
$\mathrm {Fun}(BS^1, \mod (H\mathbb {F}_p))$; since the latter has induced ![]() $S^1$-action, it follows that the former does too.
$S^1$-action, it follows that the former does too.
By Lemma 5.6, we can find an at least ![]() $(d+6)$-connected
$(d+6)$-connected ![]() $Y'$ with an
$Y'$ with an ![]() $S^1$-equivariant map
$S^1$-equivariant map ![]() $Y' \to Y$ which induces an equivalence in degrees at least
$Y' \to Y$ which induces an equivalence in degrees at least ![]() $d + 7$ and such that
$d + 7$ and such that ![]() $Y'$ is induced as an object of
$Y'$ is induced as an object of ![]() $\mathrm {Fun}(BS^1, \mod (H \mathbb {F}_p))$. It follows that the map
$\mathrm {Fun}(BS^1, \mod (H \mathbb {F}_p))$. It follows that the map ![]() $Y'^{hC_{p^n}} \to Y^{hC_{p^n}}$ is an equivalence in degrees at least
$Y'^{hC_{p^n}} \to Y^{hC_{p^n}}$ is an equivalence in degrees at least ![]() $d + 7$. But the commutative square
$d + 7$. But the commutative square

now shows that any ![]() $\alpha \in \pi _r( Y^{hC_{p^n}})$ for
$\alpha \in \pi _r( Y^{hC_{p^n}})$ for ![]() $r \geq d + 7$ has vanishing image in
$r \geq d + 7$ has vanishing image in ![]() $\pi _r (Y^{tC_{p^n}})$. Using the commutative square (11) again (since the horizontal maps are equivalences in degrees at least
$\pi _r (Y^{tC_{p^n}})$. Using the commutative square (11) again (since the horizontal maps are equivalences in degrees at least ![]() $d+6$), it follows that the restriction map
$d+6$), it follows that the restriction map ![]() $Y^{C_{p^n}} \to Y^{C_{p^{n-1}}}$ induces the zero map in degrees at least
$Y^{C_{p^n}} \to Y^{C_{p^{n-1}}}$ induces the zero map in degrees at least ![]() $d + 7$. Consequently, taking the inverse limit over
$d + 7$. Consequently, taking the inverse limit over ![]() $R$, we find that
$R$, we find that ![]() $\mathrm {TR}(Y) \in {\rm Sp} _{\leq d + 6}$, whence the fiber of
$\mathrm {TR}(Y) \in {\rm Sp} _{\leq d + 6}$, whence the fiber of ![]() $\mathrm {TR}(X)/p \to L_{K(1)} \mathrm {TR}(X)/p$ belongs to
$\mathrm {TR}(X)/p \to L_{K(1)} \mathrm {TR}(X)/p$ belongs to ![]() ${\rm Sp} _{\leq d + 3}$ by Lemma 5.8.
${\rm Sp} _{\leq d + 3}$ by Lemma 5.8.
Lemma 5.8 Let ![]() $M$ be a
$M$ be a ![]() $ku$-module spectrum. Then the following assertions are equivalent.
$ku$-module spectrum. Then the following assertions are equivalent.
(i)
 $M/(p, \beta )$ is concentrated in degrees at most
$M/(p, \beta )$ is concentrated in degrees at most  $d + 3$.
$d + 3$.(ii) The fiber of
 $M/p \to L_{K(1)} M/p$ is concentrated in degrees at most
$M/p \to L_{K(1)} M/p$ is concentrated in degrees at most  $d$.
$d$.
Proof. Given a ![]() $ku$-module
$ku$-module ![]() $N$, it suffices to show that the fiber of
$N$, it suffices to show that the fiber of ![]() $N \to N[1/\beta ]$ (which after
$N \to N[1/\beta ]$ (which after ![]() $p$-completion is
$p$-completion is ![]() $L_{K(1)} N$) is concentrated in degrees at most
$L_{K(1)} N$) is concentrated in degrees at most ![]() $d$ if and only if
$d$ if and only if ![]() $N/\beta$ is concentrated in degrees at most
$N/\beta$ is concentrated in degrees at most ![]() $d+3$; then the result will follow by taking
$d+3$; then the result will follow by taking ![]() $N = M/p$. To prove the claim, first replace
$N = M/p$. To prove the claim, first replace ![]() $N$ by
$N$ by ![]() $\mathrm {fib}( N \to N[1/\beta ])$; thus we may assume that
$\mathrm {fib}( N \to N[1/\beta ])$; thus we may assume that ![]() $N$ is actually
$N$ is actually ![]() $\beta$-power torsion.
$\beta$-power torsion.
Then the claim follows from the observation that a ![]() $\beta$-power torsion
$\beta$-power torsion ![]() $ku$-module
$ku$-module ![]() $N$ is concentrated in degrees at most
$N$ is concentrated in degrees at most ![]() $d$ if and only if
$d$ if and only if ![]() $N/\beta$ is concentrated in degrees at most
$N/\beta$ is concentrated in degrees at most ![]() $d+3$. The ‘only if’ direction is evident, so we verify the ‘if’ direction. In fact, if there exists a nonzero
$d+3$. The ‘only if’ direction is evident, so we verify the ‘if’ direction. In fact, if there exists a nonzero ![]() $x \in \pi _i(N)$ for
$x \in \pi _i(N)$ for ![]() $i > d$, then by multiplying by a power of
$i > d$, then by multiplying by a power of ![]() $\beta$ we may assume
$\beta$ we may assume ![]() $\beta x = 0$, whence there exists a nonzero class in
$\beta x = 0$, whence there exists a nonzero class in ![]() $\pi _{i+3}(N/\beta )$ from the long exact sequence.
$\pi _{i+3}(N/\beta )$ from the long exact sequence.
Remark 5.9 Let ![]() $X = \mathrm {THH}(\mathbb {F}_p)$; in this case, we have that
$X = \mathrm {THH}(\mathbb {F}_p)$; in this case, we have that ![]() $\mathrm {THH}(\mathbb {F}_p) \to \mathrm {THH}(\mathbb {F}_p)^{tC_p}$ is
$\mathrm {THH}(\mathbb {F}_p) \to \mathrm {THH}(\mathbb {F}_p)^{tC_p}$ is ![]() $(-3)$-truncated. This computation is due to Hesselholt and Madsen [Reference Hesselholt and MadsenHM97, § 5], and is refined in [Reference Nikolaus and ScholzeNS18, Appendix IV-4]. Meanwhile
$(-3)$-truncated. This computation is due to Hesselholt and Madsen [Reference Hesselholt and MadsenHM97, § 5], and is refined in [Reference Nikolaus and ScholzeNS18, Appendix IV-4]. Meanwhile ![]() $\mathrm {TR}(\mathbb {F}_p) = H\mathbb {Z}_p\to L_{K(1)} \mathrm {TR}(\mathbb {F}_p) = 0$ is
$\mathrm {TR}(\mathbb {F}_p) = H\mathbb {Z}_p\to L_{K(1)} \mathrm {TR}(\mathbb {F}_p) = 0$ is ![]() $0$-truncated modulo
$0$-truncated modulo ![]() $p$. Thus, the bound of Proposition 5.7 is the best possible.
$p$. Thus, the bound of Proposition 5.7 is the best possible.
Proposition 5.10 Let ![]() $R_0$ be a
$R_0$ be a ![]() $p$-torsion-free perfectoid ring. Let
$p$-torsion-free perfectoid ring. Let ![]() $R$ be a formally smooth
$R$ be a formally smooth ![]() $R_0$-algebra (with respect to the
$R_0$-algebra (with respect to the ![]() $p$-adic topology) of relative dimension
$p$-adic topology) of relative dimension ![]() $d$. Then the map
$d$. Then the map ![]() $\varphi \colon \mathrm {THH}(R; \mathbb {F}_p) \to \mathrm {THH}(R; \mathbb {F}_p)^{tC_p}$ is
$\varphi \colon \mathrm {THH}(R; \mathbb {F}_p) \to \mathrm {THH}(R; \mathbb {F}_p)^{tC_p}$ is ![]() $(d-3)$-truncated, and the map
$(d-3)$-truncated, and the map ![]() $\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is
$\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is ![]() $(d-1)$-truncated.
$(d-1)$-truncated.
Proof. Let ![]() $X_i, i \in \mathcal {C}$ be a diagram of spectra. Suppose that for each
$X_i, i \in \mathcal {C}$ be a diagram of spectra. Suppose that for each ![]() $i \in \mathcal {C}$, the map
$i \in \mathcal {C}$, the map ![]() $X_i \to L_{K(1)} X_i$ is
$X_i \to L_{K(1)} X_i$ is ![]() $m$-truncated for some
$m$-truncated for some ![]() $m$. Then the map
$m$. Then the map ![]() $\varprojlim _i X_i \to L_{K(1)} ( \varprojlim _i X_i)$ is
$\varprojlim _i X_i \to L_{K(1)} ( \varprojlim _i X_i)$ is ![]() $m$-truncated, and
$m$-truncated, and ![]() $L_{K(1)} ( \varprojlim _i X_i) \to \varprojlim _i L_{K(1)} X_i$ is an equivalence. This follows because
$L_{K(1)} ( \varprojlim _i X_i) \to \varprojlim _i L_{K(1)} X_i$ is an equivalence. This follows because ![]() $L_{K(1)}(-)$ annihilates bounded-above spectra. Applying the above observation, and using flat descent of
$L_{K(1)}(-)$ annihilates bounded-above spectra. Applying the above observation, and using flat descent of ![]() $\mathrm {TR}(-; \mathbb {Z}_p)$ (which follows from [Reference Bhatt, Morrow and ScholzeBMS19, § 3]) and
$\mathrm {TR}(-; \mathbb {Z}_p)$ (which follows from [Reference Bhatt, Morrow and ScholzeBMS19, § 3]) and ![]() $\mathrm {THH}(-; \mathbb {Z}_p), \mathrm {THH}(-; \mathbb {Z}_p)^{tC_p}$, we reduce to the case where
$\mathrm {THH}(-; \mathbb {Z}_p), \mathrm {THH}(-; \mathbb {Z}_p)^{tC_p}$, we reduce to the case where ![]() $R$ is a
$R$ is a ![]() $\widehat {\mathbb {Z}_p[\zeta _{p^\infty }]}$-algebra (e.g. using André's lemma; see [Reference Bhatt and ScholzeBS19, Theorem 7.12]), so
$\widehat {\mathbb {Z}_p[\zeta _{p^\infty }]}$-algebra (e.g. using André's lemma; see [Reference Bhatt and ScholzeBS19, Theorem 7.12]), so ![]() $\mathrm {THH}(R; \mathbb {Z}_p)$ is a
$\mathrm {THH}(R; \mathbb {Z}_p)$ is a ![]() $ku_{\hat {p}}$-module in
$ku_{\hat {p}}$-module in ![]() $\mathrm {CycSp}_{\geq 0}$ (Example 5.5). With this reduction in mind, the first claim implies the second in view of Proposition 5.7 (applied to the cyclotomic spectrum
$\mathrm {CycSp}_{\geq 0}$ (Example 5.5). With this reduction in mind, the first claim implies the second in view of Proposition 5.7 (applied to the cyclotomic spectrum ![]() $\mathrm {THH}(R; \mathbb {F}_p)$).
$\mathrm {THH}(R; \mathbb {F}_p)$).
Thus, we prove the first claim (i.e. the Segal conjecture for ![]() $\mathrm {THH}(R; \mathbb {F}_p)$); this result appears as [Reference Bhatt, Morrow and ScholzeBMS19, Corollary 9.12] in the case where
$\mathrm {THH}(R; \mathbb {F}_p)$); this result appears as [Reference Bhatt, Morrow and ScholzeBMS19, Corollary 9.12] in the case where ![]() $R_0$ is the ring of integers in a complete, algebraically closed nonarchimedean field of mixed characteristic, and in [Reference Bhatt, Morrow and ScholzeBMS19, § 6] when
$R_0$ is the ring of integers in a complete, algebraically closed nonarchimedean field of mixed characteristic, and in [Reference Bhatt, Morrow and ScholzeBMS19, § 6] when ![]() $R = R_0$.
$R = R_0$.
Let ![]() $(A, I)$ be the perfect prism associated to the perfectoid ring
$(A, I)$ be the perfect prism associated to the perfectoid ring ![]() $R_0$, and let
$R_0$, and let ![]() $\tilde {\xi } \in I$ be a generator. We use the prismatic cohomology
$\tilde {\xi } \in I$ be a generator. We use the prismatic cohomology ![]() ${{\mathbb {\Delta }}}_{R/A}$ of [Reference Bhatt and ScholzeBS19] and its Nygaard completion
${{\mathbb {\Delta }}}_{R/A}$ of [Reference Bhatt and ScholzeBS19] and its Nygaard completion ![]() $\hat {{{\mathbb {\Delta }}}}_{R/A}$. For a quasisyntomic
$\hat {{{\mathbb {\Delta }}}}_{R/A}$. For a quasisyntomic ![]() $R_0$-algebra
$R_0$-algebra ![]() $S$, there are [Reference Bhatt, Morrow and ScholzeBMS19] complete, exhaustive descending
$S$, there are [Reference Bhatt, Morrow and ScholzeBMS19] complete, exhaustive descending ![]() $\mathbb {Z}$-indexed filtrations on
$\mathbb {Z}$-indexed filtrations on ![]() $\mathrm {TC}^-(S; \mathbb {Z}_p), \mathrm {TP}(S; \mathbb {Z}_p)$ with
$\mathrm {TC}^-(S; \mathbb {Z}_p), \mathrm {TP}(S; \mathbb {Z}_p)$ with
and the map ![]() $\varphi \colon \mathrm {TC}^-(S; \mathbb {Z}_p) \to \mathrm {TP}(S; \mathbb {Z}_p)$ on graded pieces is given by the prismatic divided Frobenius
$\varphi \colon \mathrm {TC}^-(S; \mathbb {Z}_p) \to \mathrm {TP}(S; \mathbb {Z}_p)$ on graded pieces is given by the prismatic divided Frobenius
see [Reference Bhatt and ScholzeBS19, § 13] for the comparison between prismatic cohomology and the objects of [Reference Bhatt, Morrow and ScholzeBMS19]. Here we have trivialized the Breuil–Kisin twists involved since we are over the base perfectoid ring ![]() $R_0$, and we can compute the Nygaard-completed absolute prismatic cohomology as the Nygaard completed relative prismatic cohomology over
$R_0$, and we can compute the Nygaard-completed absolute prismatic cohomology as the Nygaard completed relative prismatic cohomology over ![]() $R_0$.
$R_0$.
Now the map ![]() $\varphi \colon \mathrm {TC}^-(S; \mathbb {Z}_p) \to \mathrm {TP}(S; \mathbb {Z}_p)$ arises by taking
$\varphi \colon \mathrm {TC}^-(S; \mathbb {Z}_p) \to \mathrm {TP}(S; \mathbb {Z}_p)$ arises by taking ![]() $S^1$-invariants on the cyclotomic Frobenius
$S^1$-invariants on the cyclotomic Frobenius ![]() $\varphi \colon \mathrm {THH}(S; \mathbb {Z}_p) \to \mathrm {THH}(S; \mathbb {Z}_p)^{tC_p}$. Both sides of this map are filtered (again, as in [Reference Bhatt, Morrow and ScholzeBMS19]) and the associated graded pieces are
$\varphi \colon \mathrm {THH}(S; \mathbb {Z}_p) \to \mathrm {THH}(S; \mathbb {Z}_p)^{tC_p}$. Both sides of this map are filtered (again, as in [Reference Bhatt, Morrow and ScholzeBMS19]) and the associated graded pieces are
and the cyclotomic Frobenius is induced from (12). But since ![]() $R$ is formally smooth over
$R$ is formally smooth over ![]() $R_0$, the Nygaard filtration is complete and
$R_0$, the Nygaard filtration is complete and ![]() $\varphi /\tilde {\xi }^i$ induces an equivalence
$\varphi /\tilde {\xi }^i$ induces an equivalence ![]() $\mathcal {N}^i {{\mathbb {\Delta }}}_{R/A} \xrightarrow {\sim } \tau ^{\leq i} ( {{\mathbb {\Delta }}}_{R/A}/ \tilde {\xi })$ (see [Reference Bhatt and ScholzeBS19, § 12.4]), where the right-hand side is the
$\mathcal {N}^i {{\mathbb {\Delta }}}_{R/A} \xrightarrow {\sim } \tau ^{\leq i} ( {{\mathbb {\Delta }}}_{R/A}/ \tilde {\xi })$ (see [Reference Bhatt and ScholzeBS19, § 12.4]), where the right-hand side is the ![]() $i$th stage of the conjugate filtration on
$i$th stage of the conjugate filtration on ![]() ${{\mathbb {\Delta }}}_{R/A}/\tilde {\xi }$. Using the Hodge–Tate comparison [Reference Bhatt and ScholzeBS19, Theorem 4.10], it follows that the cohomology groups of
${{\mathbb {\Delta }}}_{R/A}/\tilde {\xi }$. Using the Hodge–Tate comparison [Reference Bhatt and ScholzeBS19, Theorem 4.10], it follows that the cohomology groups of ![]() ${{\mathbb {\Delta }}}_{R/A}/\tilde {\xi }$ are
${{\mathbb {\Delta }}}_{R/A}/\tilde {\xi }$ are ![]() $p$-torsion-free. It follows that
$p$-torsion-free. It follows that
exhibits the domain as the ![]() $i$-connective cover of the codomain, and therefore has
$i$-connective cover of the codomain, and therefore has ![]() $(i -2)$-truncated homotopy fiber for all
$(i -2)$-truncated homotopy fiber for all ![]() $i$. The codomain is
$i$. The codomain is ![]() $(2i-d)$-connective by the Hodge–Tate comparison, since
$(2i-d)$-connective by the Hodge–Tate comparison, since ![]() $R/R_0$ is formally smooth of relative dimension
$R/R_0$ is formally smooth of relative dimension ![]() $d$; therefore,
$d$; therefore, ![]() $\mathrm {gr}^i \varphi$ is an equivalence for
$\mathrm {gr}^i \varphi$ is an equivalence for ![]() $i \geq d$. Therefore, the fiber of
$i \geq d$. Therefore, the fiber of ![]() $\varphi \colon \mathrm {THH}(R; \mathbb {F}_p) \to \mathrm {THH}(R; \mathbb {F}_p)^{tC_p}$ has a complete filtration such that
$\varphi \colon \mathrm {THH}(R; \mathbb {F}_p) \to \mathrm {THH}(R; \mathbb {F}_p)^{tC_p}$ has a complete filtration such that ![]() $\mathrm {gr}^i$ is
$\mathrm {gr}^i$ is ![]() $(i-2)$-truncated for all
$(i-2)$-truncated for all ![]() $i$ and contractible for
$i$ and contractible for ![]() $i \geq d$. This proves that
$i \geq d$. This proves that ![]() $\varphi \colon \mathrm {THH}(R; \mathbb {F}_p) \to \mathrm {THH}(R; \mathbb {F}_p)^{tC_p}$ is
$\varphi \colon \mathrm {THH}(R; \mathbb {F}_p) \to \mathrm {THH}(R; \mathbb {F}_p)^{tC_p}$ is ![]() $(d-3)$-truncated, whence the result.
$(d-3)$-truncated, whence the result.
6. Pro-Galois descent
In this section, we prove a type of pro-Galois descent for ![]() $\mathrm {TR}$ in the generic fiber, which is related to the conjecture in [Reference HesselholtHes02]. The basic example is when
$\mathrm {TR}$ in the generic fiber, which is related to the conjecture in [Reference HesselholtHes02]. The basic example is when ![]() $K$ is a characteristic
$K$ is a characteristic ![]() $0$ local field, and one tries to relate
$0$ local field, and one tries to relate ![]() $\mathrm {TR}(\mathcal {O}_K; \mathbb {Z}_p)$ (computed by [Reference Hesselholt and MadsenHM03]) with the ‘continuous’ homotopy fixed points for the Galois group
$\mathrm {TR}(\mathcal {O}_K; \mathbb {Z}_p)$ (computed by [Reference Hesselholt and MadsenHM03]) with the ‘continuous’ homotopy fixed points for the Galois group ![]() $\mathrm {Gal}(\bar {K}/K)$ on
$\mathrm {Gal}(\bar {K}/K)$ on ![]() $\mathrm {TR}( \mathcal {O}_{\bar {K}}; \mathbb {Z}_p)$, before or after
$\mathrm {TR}( \mathcal {O}_{\bar {K}}; \mathbb {Z}_p)$, before or after ![]() $K(1)$-localization. The advantage is that the latter is much more tractable; see [Reference HesselholtHes06] for the calculation of
$K(1)$-localization. The advantage is that the latter is much more tractable; see [Reference HesselholtHes06] for the calculation of ![]() $\mathrm {TR}( \mathcal {O}_{\bar {K}}; \mathbb {Z}_p)$. For finite Galois extensions in the generic fiber, these claims follow from § 2. However, there are some additional subtleties to extend to pro-Galois descent because
$\mathrm {TR}( \mathcal {O}_{\bar {K}}; \mathbb {Z}_p)$. For finite Galois extensions in the generic fiber, these claims follow from § 2. However, there are some additional subtleties to extend to pro-Galois descent because ![]() $\mathrm {TR}$ fails to commute with filtered colimits.
$\mathrm {TR}$ fails to commute with filtered colimits.
6.1 An auxiliary construction
Let ![]() $B$ be a base ring. Let
$B$ be a base ring. Let ![]() $E$ be a
$E$ be a ![]() $K(1)$-local, localizing invariant on
$K(1)$-local, localizing invariant on ![]() $B$-linear
$B$-linear ![]() $\infty$-categories which is truncating. Let
$\infty$-categories which is truncating. Let ![]() $R_0$ be a
$R_0$ be a ![]() $p$-adically complete
$p$-adically complete ![]() $B$-algebra. Given a
$B$-algebra. Given a ![]() $K(1)$-local truncating invariant
$K(1)$-local truncating invariant ![]() $E$, we now describe a construction of a sheaf on the finite étale site of
$E$, we now describe a construction of a sheaf on the finite étale site of ![]() $R_0[1/p]$. For every finite étale
$R_0[1/p]$. For every finite étale ![]() $R_0[1/p]$-algebra
$R_0[1/p]$-algebra ![]() $S$, we can choose a ‘ring of integers’
$S$, we can choose a ‘ring of integers’ ![]() $S_0$ which is finite and finitely presented over
$S_0$ which is finite and finitely presented over ![]() $R_0$ with
$R_0$ with ![]() $S_0[1/p] = S$ and consider
$S_0[1/p] = S$ and consider ![]() $E(S_0)$. It is not difficult to see that this only depends on
$E(S_0)$. It is not difficult to see that this only depends on ![]() $S$ and that it defines the desired sheaf; to make the functoriality precise, we use left Kan extension.
$S$ and that it defines the desired sheaf; to make the functoriality precise, we use left Kan extension.
Construction 6.1 (![]() $E$ as a sheaf on the finite étale site of the generic fiber)
$E$ as a sheaf on the finite étale site of the generic fiber)
Let ![]() $R_0$ be a
$R_0$ be a ![]() $p$-adically complete
$p$-adically complete ![]() $B$-algebra and let
$B$-algebra and let ![]() $R = R_0[1/p]$. Using the
$R = R_0[1/p]$. Using the ![]() $K(1)$-local, localizing invariant
$K(1)$-local, localizing invariant ![]() $E$ which is assumed to be truncating, we define a sheaf
$E$ which is assumed to be truncating, we define a sheaf ![]() $\mathcal {F}_E$ of spectra on the finite étale site of
$\mathcal {F}_E$ of spectra on the finite étale site of ![]() $\mathrm {Spec}(R)$ as follows. Let
$\mathrm {Spec}(R)$ as follows. Let ![]() $\mathcal {C}_0$ denote the category of finite, finitely presented
$\mathcal {C}_0$ denote the category of finite, finitely presented ![]() $R_0$-algebras
$R_0$-algebras ![]() $S_0$ with
$S_0$ with ![]() $S_0[1/p]$ étale over
$S_0[1/p]$ étale over ![]() $R$, and let
$R$, and let ![]() $\mathcal {C}$ denote the category of finite étale
$\mathcal {C}$ denote the category of finite étale ![]() $R$-algebras. Consider the functor
$R$-algebras. Consider the functor ![]() $F\colon \mathcal {C}_0 \to \mathcal {C}$ given by inverting
$F\colon \mathcal {C}_0 \to \mathcal {C}$ given by inverting ![]() $p$. Note the following observations.
$p$. Note the following observations.
(i)
 $F$ is essentially surjective. That is, given any finite étale
$F$ is essentially surjective. That is, given any finite étale  $R$-algebra
$R$-algebra  $S$, there exists a finite, finitely presented
$S$, there exists a finite, finitely presented  $R_0$-algebra
$R_0$-algebra  $S_0$ with
$S_0$ with  $S = S_0[1/p]$. In fact, consider any finite
$S = S_0[1/p]$. In fact, consider any finite  $R_0$-subalgebra
$R_0$-subalgebra  $S_0' \subset S$ with
$S_0' \subset S$ with  $S_0'[1/p] = S$. The algebra
$S_0'[1/p] = S$. The algebra  $S_0'$ is not necessarily finitely presented, but it is a directed colimit of finite, finitely presented
$S_0'$ is not necessarily finitely presented, but it is a directed colimit of finite, finitely presented  $R_0$-algebras
$R_0$-algebras  $S_0^{(\alpha )}$ under surjective maps; one of them will have
$S_0^{(\alpha )}$ under surjective maps; one of them will have  $S_0^{(\alpha )}[1/p] = S$, and can be taken for
$S_0^{(\alpha )}[1/p] = S$, and can be taken for  $S_0$.
$S_0$.(ii) If
 $S \in \mathcal {C}$, then
$S \in \mathcal {C}$, then  $\mathcal {C}_0 \times _{\mathcal {C}}\mathcal {C}_{/S}$ is a filtered category. In fact, the subcategory of
$\mathcal {C}_0 \times _{\mathcal {C}}\mathcal {C}_{/S}$ is a filtered category. In fact, the subcategory of  $\mathcal {C}_0 \times _{\mathcal {C}}\mathcal {C}_{/S}$ spanned by those
$\mathcal {C}_0 \times _{\mathcal {C}}\mathcal {C}_{/S}$ spanned by those  $S_0$ such that the structure map
$S_0$ such that the structure map  $S_0[1/p] \to S$ is an isomorphism is itself filtered and cofinal. This follows similarly by comparing
$S_0[1/p] \to S$ is an isomorphism is itself filtered and cofinal. This follows similarly by comparing  $S_0$ with its image in
$S_0$ with its image in  $S$.
$S$.
We consider the functor ![]() $S_0 \mapsto E(S_0)$ on the category
$S_0 \mapsto E(S_0)$ on the category ![]() $\mathcal {C}_0$ of finite, finitely presented
$\mathcal {C}_0$ of finite, finitely presented ![]() $R_0$-algebras
$R_0$-algebras ![]() $S_0$ with
$S_0$ with ![]() $S_0[1/p]$ finite étale over
$S_0[1/p]$ finite étale over ![]() $R$. Then, to define
$R$. Then, to define ![]() $\mathcal {F}_E$ on finite étale
$\mathcal {F}_E$ on finite étale ![]() $R$-algebras, we left Kan extend
$R$-algebras, we left Kan extend ![]() $E(-)$ along the functor
$E(-)$ along the functor ![]() $\mathcal {C}_0 \to \mathcal {C}$. Explicitly, it follows from Example 2.4 that if
$\mathcal {C}_0 \to \mathcal {C}$. Explicitly, it follows from Example 2.4 that if ![]() $S$ is a finite étale
$S$ is a finite étale ![]() $R$-algebra and
$R$-algebra and ![]() $S_0$ is a finite, finitely presented
$S_0$ is a finite, finitely presented ![]() $R_0$-algebra with
$R_0$-algebra with ![]() $S_0[1/p] \simeq S$, then we have a canonical equivalence
$S_0[1/p] \simeq S$, then we have a canonical equivalence ![]() $\mathcal {F}_E(S) \simeq E(S_0)$. It also follows from
$\mathcal {F}_E(S) \simeq E(S_0)$. It also follows from ![]() $h$-descent that
$h$-descent that ![]() $\mathcal {F}_E$ is indeed a sheaf of
$\mathcal {F}_E$ is indeed a sheaf of ![]() $K(1)$-local spectra on the finite étale site of
$K(1)$-local spectra on the finite étale site of ![]() $\mathrm {Spec}(R)$. Note that it is a sheaf of modules over the sheaf
$\mathrm {Spec}(R)$. Note that it is a sheaf of modules over the sheaf ![]() $S \mapsto L_{K(1)} K(S)$, which is also the sheaf
$S \mapsto L_{K(1)} K(S)$, which is also the sheaf ![]() $\mathcal {F}_{L_{K(1)} K}$ because
$\mathcal {F}_{L_{K(1)} K}$ because ![]() $L_{K(1)} K(-)$ is insensitive to inverting
$L_{K(1)} K(-)$ is insensitive to inverting ![]() $p$ on
$p$ on ![]() $H\mathbb {Z}$-algebras as in (2).
$H\mathbb {Z}$-algebras as in (2).
Proposition 6.2 (Hypercompleteness of ![]() $\mathcal {F}_E$)
$\mathcal {F}_E$)
With notation as above, suppose there is a uniform bound on the mod ![]() $p$ cohomological dimensions of the residue fields of
$p$ cohomological dimensions of the residue fields of ![]() $R$ and
$R$ and ![]() $R$ has finite Krull dimension. Then
$R$ has finite Krull dimension. Then ![]() $\mathcal {F}_E$ defines a hypercomplete sheaf on the finite étale site of
$\mathcal {F}_E$ defines a hypercomplete sheaf on the finite étale site of ![]() $\mathrm {Spec}(R)$.
$\mathrm {Spec}(R)$.
Proof. Our hypotheses imply that ![]() $\mathrm {Spec}(R)$ has finite mod
$\mathrm {Spec}(R)$ has finite mod ![]() $p$ étale cohomological dimension; see [Reference Clausen and MathewCM19, Corollary 3.29].
$p$ étale cohomological dimension; see [Reference Clausen and MathewCM19, Corollary 3.29].
Now we use the ![]() $K(\pi , 1)$ property, which states that for any
$K(\pi , 1)$ property, which states that for any ![]() $p$-henselian ring
$p$-henselian ring ![]() $A$ and any
$A$ and any ![]() $\mathbb {F}_p$-local system
$\mathbb {F}_p$-local system ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $\mathrm {Spec}(A[1/p])$, the cohomology of
$\mathrm {Spec}(A[1/p])$, the cohomology of ![]() $\mathcal {L}$ on the étale sites and the finite étale sites of
$\mathcal {L}$ on the étale sites and the finite étale sites of ![]() $\mathrm {Spec}(A[1/p])$ coincide. For
$\mathrm {Spec}(A[1/p])$ coincide. For ![]() $A$ noetherian and
$A$ noetherian and ![]() $p$-complete, this is proved in [Reference ScholzeSch13, Theorem 4.9]. The case of
$p$-complete, this is proved in [Reference ScholzeSch13, Theorem 4.9]. The case of ![]() $A$ noetherian and
$A$ noetherian and ![]() $p$-henselian then follows using the Fujiwara–Gabber theorem (see [Reference Bhatt and MathewBM18, Theorem 6.11] for an account), and then one can pass to the limit to obtain the arbitrary
$p$-henselian then follows using the Fujiwara–Gabber theorem (see [Reference Bhatt and MathewBM18, Theorem 6.11] for an account), and then one can pass to the limit to obtain the arbitrary ![]() $p$-henselian case using the commutation of cohomology (on either the étale or finite étale sites) and filtered colimits.
$p$-henselian case using the commutation of cohomology (on either the étale or finite étale sites) and filtered colimits.
From the above two paragraphs, it follows that the étale fundamental group ![]() $\pi _1^{\mathrm {et}}( \mathrm {Spec}( R))$ has finite mod
$\pi _1^{\mathrm {et}}( \mathrm {Spec}( R))$ has finite mod ![]() $p$ cohomological dimension, which implies that the notion of hypercompleteness for sheaves of
$p$ cohomological dimension, which implies that the notion of hypercompleteness for sheaves of ![]() $p$-complete spectra on the finite étale site of
$p$-complete spectra on the finite étale site of ![]() $\mathrm {Spec}(R)$ can be made explicit in terms of exponents of nilpotence [Reference Clausen and MathewCM19, § 4.1]. Now
$\mathrm {Spec}(R)$ can be made explicit in terms of exponents of nilpotence [Reference Clausen and MathewCM19, § 4.1]. Now ![]() $\mathcal {F}_E$ is a module over the hypercomplete sheaf
$\mathcal {F}_E$ is a module over the hypercomplete sheaf ![]() $S \mapsto L_{K(1)}K(S)$ (see [Reference Clausen and MathewCM19, Theorem 7.14] for hypercompleteness), hence a hypercomplete sheaf itself, thanks to [Reference Clausen and MathewCM19, Corollary 4.26].
$S \mapsto L_{K(1)}K(S)$ (see [Reference Clausen and MathewCM19, Theorem 7.14] for hypercompleteness), hence a hypercomplete sheaf itself, thanks to [Reference Clausen and MathewCM19, Corollary 4.26].
We also need the following variant of the above with respect to a fixed profinite group.
Construction 6.3 (![]() $\mathcal {F}_E$ relative to a profinite group)
$\mathcal {F}_E$ relative to a profinite group)
Let ![]() $S_0$ be an
$S_0$ be an ![]() $R_0$-algebra equipped with the action of a profinite group
$R_0$-algebra equipped with the action of a profinite group ![]() $\Gamma$ which is continuous (with respect to the discrete topology on
$\Gamma$ which is continuous (with respect to the discrete topology on ![]() $S_0$), and such that
$S_0$), and such that ![]() $R \to S := S_0[1/p]$ is
$R \to S := S_0[1/p]$ is ![]() $\Gamma$-Galois. Suppose that there exist a cofinal collection of open normal subgroups
$\Gamma$-Galois. Suppose that there exist a cofinal collection of open normal subgroups ![]() $N_i \subset \Gamma$,
$N_i \subset \Gamma$, ![]() $i \in I$, for which the fixed points
$i \in I$, for which the fixed points ![]() $S_0^{N_i}$ form a finite, finitely presented
$S_0^{N_i}$ form a finite, finitely presented ![]() $R_0$-algebra. It follows from the above that we obtain a sheaf on the category of finite continuous
$R_0$-algebra. It follows from the above that we obtain a sheaf on the category of finite continuous ![]() $\Gamma$-sets which carries
$\Gamma$-sets which carries ![]() $\Gamma /N_i \mapsto E( S_0^{N_i})$. This is just the restriction of
$\Gamma /N_i \mapsto E( S_0^{N_i})$. This is just the restriction of ![]() $\mathcal {F}_E$ to the site of finite continuous
$\mathcal {F}_E$ to the site of finite continuous ![]() $\Gamma$-sets (which maps to the finite étale site of
$\Gamma$-sets (which maps to the finite étale site of ![]() $R$).
$R$).
When is the sheaf of Construction 6.3 hypercomplete? When ![]() $\Gamma$ has finite cohomological dimension, hypercompleteness is smashing [Reference Clausen and MathewCM19, § 4.1], so hypercompleteness holds if the sheaf of spectra which sends
$\Gamma$ has finite cohomological dimension, hypercompleteness is smashing [Reference Clausen and MathewCM19, § 4.1], so hypercompleteness holds if the sheaf of spectra which sends ![]() $\Gamma /H \mapsto L_{K(1)} K( S^H)$ (for any cofinal collection of open normal subgroups
$\Gamma /H \mapsto L_{K(1)} K( S^H)$ (for any cofinal collection of open normal subgroups ![]() $H$) is hypercomplete.
$H$) is hypercomplete.
Example 6.4 Suppose ![]() $\Gamma = \mathbb {Z}_p^n$ and the
$\Gamma = \mathbb {Z}_p^n$ and the ![]() $\Gamma$-extension of
$\Gamma$-extension of ![]() $R_0$ is obtained by adding compatible systems of
$R_0$ is obtained by adding compatible systems of ![]() $p$-power roots. Explicitly, suppose
$p$-power roots. Explicitly, suppose ![]() $R_0$ is a
$R_0$ is a ![]() $\mathbb {Z}[ \zeta _{p^\infty }, t_1^{\pm 1}, \ldots , t_n^{\pm 1}]$-algebra and
$\mathbb {Z}[ \zeta _{p^\infty }, t_1^{\pm 1}, \ldots , t_n^{\pm 1}]$-algebra and ![]() $S_0 =R_0 \otimes _{\mathbb {Z}[ \zeta _{p^\infty }, t_1^{\pm 1}, \ldots , t_n^{\pm 1}]} \mathbb {Z}[ \zeta _{p^\infty }, t_1^{\pm 1/p^\infty }, \ldots , t_n^{\pm 1/p^\infty }] ,$ with the evident
$S_0 =R_0 \otimes _{\mathbb {Z}[ \zeta _{p^\infty }, t_1^{\pm 1}, \ldots , t_n^{\pm 1}]} \mathbb {Z}[ \zeta _{p^\infty }, t_1^{\pm 1/p^\infty }, \ldots , t_n^{\pm 1/p^\infty }] ,$ with the evident ![]() $\Gamma$-action. In this case, the sheaf of Construction 6.3 is hypercomplete. Again since hypercompleteness is smashing, this follows because any
$\Gamma$-action. In this case, the sheaf of Construction 6.3 is hypercomplete. Again since hypercompleteness is smashing, this follows because any ![]() $K(1)$-local localizing invariant yields a hypercomplete étale sheaf on the site of finite étale (or even all étale)
$K(1)$-local localizing invariant yields a hypercomplete étale sheaf on the site of finite étale (or even all étale) ![]() $\mathbb {Z}[1/p, \zeta _{p^\infty }, t_1^{\pm 1}, \ldots , t_n^{\pm 1}]$-algebras; see [Reference Clausen and MathewCM19, Theorem 7.14]. In particular, we take as the localizing invariant
$\mathbb {Z}[1/p, \zeta _{p^\infty }, t_1^{\pm 1}, \ldots , t_n^{\pm 1}]$-algebras; see [Reference Clausen and MathewCM19, Theorem 7.14]. In particular, we take as the localizing invariant ![]() $A \mapsto L_{K(1)} K(A \otimes _{\mathbb {Z}[1/p, \zeta _{p^\infty }, t_1^{\pm 1}, \ldots , t_n^{\pm 1}]} R)$.
$A \mapsto L_{K(1)} K(A \otimes _{\mathbb {Z}[1/p, \zeta _{p^\infty }, t_1^{\pm 1}, \ldots , t_n^{\pm 1}]} R)$.
6.2 Completion of topological Cartier modules
Here again we use the ‘decompletion’ of the theory of cyclotomic spectra given by the topological Cartier modules of Antieau and Nikolaus [Reference Antieau and NikolausAN21] and an amplitude property of the completion. We recall that ![]() $\mathrm {TR}(-)$ gives a fully faithful right adjoint embedding from bounded-below cyclotomic spectra into bounded-below topological Cartier modules, with image the
$\mathrm {TR}(-)$ gives a fully faithful right adjoint embedding from bounded-below cyclotomic spectra into bounded-below topological Cartier modules, with image the ![]() $V$-complete objects; see [Reference Antieau and NikolausAN21, Theorem 3.21].
$V$-complete objects; see [Reference Antieau and NikolausAN21, Theorem 3.21].
Proposition 6.5 Let ![]() $M$ be a topological Cartier module which is
$M$ be a topological Cartier module which is ![]() $d$-truncated and bounded below. Then the
$d$-truncated and bounded below. Then the ![]() $V$-completion of
$V$-completion of ![]() $M$ is
$M$ is ![]() $(d+3)$-truncated. If
$(d+3)$-truncated. If ![]() $M$ is
$M$ is ![]() $p$-complete, then the
$p$-complete, then the ![]() $V$-completion of
$V$-completion of ![]() $M$ is
$M$ is ![]() $(d+2)$-truncated.
$(d+2)$-truncated.
Proof. We reduce by dévissage to the case where ![]() $M$ is concentrated in degree
$M$ is concentrated in degree ![]() $0$, and
$0$, and ![]() $d = 0$. The completion of
$d = 0$. The completion of ![]() $M$ is given by
$M$ is given by ![]() $\mathrm {cofib}( \varprojlim M_{hC_{p^n}} \to M)$ where the maps
$\mathrm {cofib}( \varprojlim M_{hC_{p^n}} \to M)$ where the maps ![]() $M_{hC_{p^n}} \to M_{hC_{p^{n-1}}}$ are given by
$M_{hC_{p^n}} \to M_{hC_{p^{n-1}}}$ are given by ![]() $V_{hC_{p^{n-1}}}$; see [Reference Antieau and NikolausAN21, Proposition 3.22].
$V_{hC_{p^{n-1}}}$; see [Reference Antieau and NikolausAN21, Proposition 3.22].
Now since ![]() $M$ is discrete, the Verschiebung is simply given by a map
$M$ is discrete, the Verschiebung is simply given by a map ![]() $V\colon M \to M$ of abelian groups, and the
$V\colon M \to M$ of abelian groups, and the ![]() $S^1$-action is trivial. We can (as in the proof of [Reference Antieau and NikolausAN21, Lemma 3.25]) form a
$S^1$-action is trivial. We can (as in the proof of [Reference Antieau and NikolausAN21, Lemma 3.25]) form a ![]() $\mathbb {Z}_{\geq 0} \times \mathbb {Z}_{\geq 0}$-indexed diagram
$\mathbb {Z}_{\geq 0} \times \mathbb {Z}_{\geq 0}$-indexed diagram ![]() $Y_{i, j} = M \otimes BC_{p^j + }$ such that the transition maps in the
$Y_{i, j} = M \otimes BC_{p^j + }$ such that the transition maps in the ![]() $i$-direction are given by
$i$-direction are given by ![]() $V$ and in the
$V$ and in the ![]() $j$-direction are given by the canonical projections. By the above, the completion of
$j$-direction are given by the canonical projections. By the above, the completion of ![]() $M$ is given by the cofiber of the map
$M$ is given by the cofiber of the map ![]() $\varprojlim _{i, j} Y_{i, j} \to M$.
$\varprojlim _{i, j} Y_{i, j} \to M$.
Now a simple computation shows that for any abelian group ![]() $A$,
$A$, ![]() $\varprojlim _{j} HA\otimes BC_{p^j + }$ are concentrated in degrees at most
$\varprojlim _{j} HA\otimes BC_{p^j + }$ are concentrated in degrees at most ![]() $2$, and degrees at most
$2$, and degrees at most ![]() $1$ if
$1$ if ![]() $A$ is derived
$A$ is derived ![]() $p$-complete. This claim will imply the result. Indeed, for the first part, it suffices to show that
$p$-complete. This claim will imply the result. Indeed, for the first part, it suffices to show that ![]() $\varprojlim _{j} HA\otimes BC_{p^j + }$ is concentrated in degrees at most
$\varprojlim _{j} HA\otimes BC_{p^j + }$ is concentrated in degrees at most ![]() $1$ when
$1$ when ![]() $A$ is torsion-free; this follows because the pro abelian group
$A$ is torsion-free; this follows because the pro abelian group ![]() $\{H_*(BC_{p^j}; \mathbb {Z}) \}_{j \geq 0}$ is pro-zero for
$\{H_*(BC_{p^j}; \mathbb {Z}) \}_{j \geq 0}$ is pro-zero for ![]() $\ast \geq 2$. For the second part, we also observe that the pro-abelian group
$\ast \geq 2$. For the second part, we also observe that the pro-abelian group ![]() $\{H_1( BC_{p^j}; \mathbb {Z})\}_{j \geq 0}$ is simply the tower
$\{H_1( BC_{p^j}; \mathbb {Z})\}_{j \geq 0}$ is simply the tower ![]() $\cdots \to \mathbb {Z}/p^2 \to \mathbb {Z}/p \to 0$, and our assumption that
$\cdots \to \mathbb {Z}/p^2 \to \mathbb {Z}/p \to 0$, and our assumption that ![]() $A$ is derived
$A$ is derived ![]() $p$-complete gives that
$p$-complete gives that ![]() $A \simeq \varprojlim A \otimes ^{\mathbb {L}}_{\mathbb {Z}} \mathbb {Z}/p^j$ is in particular discrete.
$A \simeq \varprojlim A \otimes ^{\mathbb {L}}_{\mathbb {Z}} \mathbb {Z}/p^j$ is in particular discrete.
Remark 6.6 We can give another proof of Proposition 6.5 using the results from the previous section in the case where ![]() $M$ is annihilated by a power of
$M$ is annihilated by a power of ![]() $p$. By dévissage, we can reduce to the case where
$p$. By dévissage, we can reduce to the case where ![]() $M$ is an
$M$ is an ![]() $H\mathbb {F}_p$-module (in topological Cartier modules). Let
$H\mathbb {F}_p$-module (in topological Cartier modules). Let ![]() $X = M/M_{hC_p} = \mathrm {cofib}(V)$ be the associated cyclotomic spectrum, so
$X = M/M_{hC_p} = \mathrm {cofib}(V)$ be the associated cyclotomic spectrum, so ![]() $\mathrm {TR}(X)$ is the derived
$\mathrm {TR}(X)$ is the derived ![]() $V$-completion of
$V$-completion of ![]() $M$ by the correspondence between bounded-below
$M$ by the correspondence between bounded-below ![]() $V$-complete Cartier modules and bounded-below cyclotomic spectra; see [Reference Antieau and NikolausAN21, Theorem 3.21]. Then the proof of Proposition 5.2 shows that the cyclotomic Frobenius
$V$-complete Cartier modules and bounded-below cyclotomic spectra; see [Reference Antieau and NikolausAN21, Theorem 3.21]. Then the proof of Proposition 5.2 shows that the cyclotomic Frobenius ![]() $\varphi \colon X \to X^{tC_p}$ is
$\varphi \colon X \to X^{tC_p}$ is ![]() $d$-truncated, since
$d$-truncated, since ![]() $\mathrm {fib}(\varphi ) = \mathrm {fib}(F\colon M \to M^{hC_p})$. Using Proposition 5.7, we find that
$\mathrm {fib}(\varphi ) = \mathrm {fib}(F\colon M \to M^{hC_p})$. Using Proposition 5.7, we find that ![]() $\mathrm {TR}(X)/p$ is
$\mathrm {TR}(X)/p$ is ![]() $(d+3)$-truncated, whence
$(d+3)$-truncated, whence ![]() $\mathrm {TR}(X)$ is
$\mathrm {TR}(X)$ is ![]() $(d+2)$-truncated.
$(d+2)$-truncated.
Corollary 6.7 Let ![]() $R_i, i \in I$ be a filtered system of rings and let
$R_i, i \in I$ be a filtered system of rings and let ![]() $R = \varinjlim R_i$. Suppose that the map
$R = \varinjlim R_i$. Suppose that the map ![]() $\mathrm {TR}(R_i; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R_i ; \mathbb {F}_p)$ is
$\mathrm {TR}(R_i; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R_i ; \mathbb {F}_p)$ is ![]() $d$-truncated for all
$d$-truncated for all ![]() $i \in I$. Then
$i \in I$. Then ![]() $\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is
$\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is ![]() $(d+2)$-truncated.
$(d+2)$-truncated.
Proof. Let ![]() $v\colon \Sigma ^u (S^0/p) \to (S^0/p)$ be a
$v\colon \Sigma ^u (S^0/p) \to (S^0/p)$ be a ![]() $v_1$-self map (so we can take
$v_1$-self map (so we can take ![]() $u = 2p-2$ for
$u = 2p-2$ for ![]() $p$ odd and
$p$ odd and ![]() $u = 8$ for
$u = 8$ for ![]() $p = 2$). Let
$p = 2$). Let ![]() $X$ be any spectrum. Then we observe that the following assertions are equivalent.
$X$ be any spectrum. Then we observe that the following assertions are equivalent.
(i) The map
 $X/p \to L_{K(1)} X/p$ is
$X/p \to L_{K(1)} X/p$ is  $d$-truncated.
$d$-truncated.(ii) The spectrum
 $X \otimes S^0/(p, v)$ is
$X \otimes S^0/(p, v)$ is  $(d+u+1)$-truncated.
$(d+u+1)$-truncated.
The equivalence is proved analogously to Lemma 5.8, noting that ![]() $L_{K(1)} (X/p) = X \otimes (S^0/p)[v^{-1}]$ by the telescope conjecture at height
$L_{K(1)} (X/p) = X \otimes (S^0/p)[v^{-1}]$ by the telescope conjecture at height ![]() $1$ [Reference MahowaldMah81, Reference MillerMil81].
$1$ [Reference MahowaldMah81, Reference MillerMil81].
Therefore, it suffices to show that ![]() $\mathrm {TR}(R; \mathbb {Z}_p) \otimes S^0/(p, v)$ is
$\mathrm {TR}(R; \mathbb {Z}_p) \otimes S^0/(p, v)$ is ![]() $(d + u+3)$-truncated. To this end, let
$(d + u+3)$-truncated. To this end, let ![]() $M = \varinjlim \mathrm {TR}(R_i; \mathbb {Z}_p)$, so
$M = \varinjlim \mathrm {TR}(R_i; \mathbb {Z}_p)$, so ![]() $M$ is a connective topological Cartier module which is not necessarily derived
$M$ is a connective topological Cartier module which is not necessarily derived ![]() $V$-complete; the
$V$-complete; the ![]() $V$-completion of its
$V$-completion of its ![]() $p$-completion is
$p$-completion is ![]() $\mathrm {TR}(R; \mathbb {Z}_p)$ since
$\mathrm {TR}(R; \mathbb {Z}_p)$ since ![]() $\mathrm {THH}(-)$ commutes with filtered colimits (as a functor from rings to
$\mathrm {THH}(-)$ commutes with filtered colimits (as a functor from rings to ![]() $\mathrm {CycSp}_{\geq 0}$). Now the topological Cartier module
$\mathrm {CycSp}_{\geq 0}$). Now the topological Cartier module ![]() $M \otimes S^0/(p, v)$ is
$M \otimes S^0/(p, v)$ is ![]() $(d + u + 1)$-truncated as a filtered colimit of
$(d + u + 1)$-truncated as a filtered colimit of ![]() $(d + u + 1)$-truncated objects. Taking the
$(d + u + 1)$-truncated objects. Taking the ![]() $V$-completion and using Proposition 6.5, we find that
$V$-completion and using Proposition 6.5, we find that ![]() $\mathrm {TR}(R; \mathbb {Z}_p)/(p, v)$ is
$\mathrm {TR}(R; \mathbb {Z}_p)/(p, v)$ is ![]() $(d + u + 3)$-truncated. Therefore,
$(d + u + 3)$-truncated. Therefore, ![]() $\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is
$\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is ![]() $(d+2)$-truncated.
$(d+2)$-truncated.
6.3 The main pro-Galois result
In this subsection we prove the following pro-Galois descent result.
Theorem 6.8 (Pro-Galois descent in the generic fiber) Fix ![]() $d \geq 0$. Let
$d \geq 0$. Let ![]() $R$ be a
$R$ be a ![]() $p$-complete ring such that
$p$-complete ring such that ![]() $\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is
$\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$ is ![]() $d$-truncated. Let
$d$-truncated. Let ![]() $S$ be an
$S$ be an ![]() $R$-algebra.
$R$-algebra.
Let ![]() $G$ be a profinite group of finite
$G$ be a profinite group of finite ![]() $p$-cohomological dimension which acts continuously on the
$p$-cohomological dimension which acts continuously on the ![]() $R$-algebra
$R$-algebra ![]() $S$ (given the discrete topology). Suppose that the following assertions hold.
$S$ (given the discrete topology). Suppose that the following assertions hold.
(i)
 $R[1/p] \to S[1/p]$ is a
$R[1/p] \to S[1/p]$ is a  $G$-Galois extension.
$G$-Galois extension.(ii) There is a cofinal collection of open normal subgroups
 $N_i \subset G$,
$N_i \subset G$,  $i \in I$, such that
$i \in I$, such that  $S_i := S^{N_i}$ is a finite, finitely presented
$S_i := S^{N_i}$ is a finite, finitely presented  $R$-algebra and such that
$R$-algebra and such that  $\mathrm {TR}(S_i; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(S_i; \mathbb {F}_p)$ is
$\mathrm {TR}(S_i; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(S_i; \mathbb {F}_p)$ is  $d$-truncated.
$d$-truncated.(iii) The induced sheaf of spectra on finite continuous
 $G$-sets given by
(for
$G$-sets given by
(for \[T \mapsto L_{K(1)} ( K( \mathrm {Fun}_G(T, S[1/p])))\]
\[T \mapsto L_{K(1)} ( K( \mathrm {Fun}_G(T, S[1/p])))\] $\mathrm {Fun}_G(T, S[1/p])$ denoting
$\mathrm {Fun}_G(T, S[1/p])$ denoting  $G$-equivariant functions
$G$-equivariant functions  $T \to S$) is hypercomplete. For example, this holds if
$T \to S$) is hypercomplete. For example, this holds if  $R[1/p]$ has finite Krull dimension and there is a uniform bound on the mod
$R[1/p]$ has finite Krull dimension and there is a uniform bound on the mod  $p$ cohomological dimensions of the residue fields, but also in cases such as Example 6.4.
$p$ cohomological dimensions of the residue fields, but also in cases such as Example 6.4.
Then the map
is an equivalence and the map
is ![]() $(d+2)$-truncated.
$(d+2)$-truncated.
Proof. Let ![]() $\mathcal {F}$ be any product-preserving presheaf from finite continuous
$\mathcal {F}$ be any product-preserving presheaf from finite continuous ![]() $G$-sets to
$G$-sets to ![]() $p$-torsion spectra. We let
$p$-torsion spectra. We let ![]() $\mathcal {F}^{\mathrm {disc}}$ denote the left Kan extension to profinite
$\mathcal {F}^{\mathrm {disc}}$ denote the left Kan extension to profinite ![]() $G$-sets, so if
$G$-sets, so if ![]() $S$ is a profinite
$S$ is a profinite ![]() $G$-set which can be written
$G$-set which can be written ![]() $S \simeq \varprojlim S_j$ for some finite continuous
$S \simeq \varprojlim S_j$ for some finite continuous ![]() $G$-sets
$G$-sets ![]() $S_j$, then
$S_j$, then ![]() $\mathcal {F}^{\mathrm {disc}}(S) \simeq \varinjlim \mathcal {F}(S_j)$. We let
$\mathcal {F}^{\mathrm {disc}}(S) \simeq \varinjlim \mathcal {F}(S_j)$. We let
As in [Reference Clausen and MathewCM19, § 4.1], ![]() $R \Gamma ( \ast , \mathcal {F})$ is the value of the hypersheafification or Postnikov sheafification of
$R \Gamma ( \ast , \mathcal {F})$ is the value of the hypersheafification or Postnikov sheafification of ![]() $\mathcal {F}$ (with respect to the topology on finite continuous
$\mathcal {F}$ (with respect to the topology on finite continuous ![]() $G$-sets where covering families are jointly surjective ones) at
$G$-sets where covering families are jointly surjective ones) at ![]() $\ast$. When we work with
$\ast$. When we work with ![]() $p$-torsion spectra, our assumption that
$p$-torsion spectra, our assumption that ![]() $G$ has finite cohomological dimension implies that
$G$ has finite cohomological dimension implies that ![]() $R \Gamma (\ast , -)$ commutes with all colimits.
$R \Gamma (\ast , -)$ commutes with all colimits.
Now we take ![]() $\mathcal {F}$ to be the presheaf which sends a finite continuous
$\mathcal {F}$ to be the presheaf which sends a finite continuous ![]() $G$-set
$G$-set ![]() $T$ to
$T$ to ![]() $\mathrm {TR}( \mathrm {Fun}_G(T, S); \mathbb {F}_p)$, where
$\mathrm {TR}( \mathrm {Fun}_G(T, S); \mathbb {F}_p)$, where ![]() $\mathrm {Fun}_G(T, S)$ is (as in the statement) the ring of
$\mathrm {Fun}_G(T, S)$ is (as in the statement) the ring of ![]() $G$-equivariant functions
$G$-equivariant functions ![]() $T \to S$. Unwinding the definitions and hypotheses, we find from Corollary 2.5 that if
$T \to S$. Unwinding the definitions and hypotheses, we find from Corollary 2.5 that if ![]() $T = G/N_j$ for one of the distinguished normal subgroups
$T = G/N_j$ for one of the distinguished normal subgroups ![]() $N_j$, we have that
$N_j$, we have that
is an equivalence. Note ![]() $L_{K(1)} \mathcal {F}$ is an example of Construction 6.3 for the profinite group
$L_{K(1)} \mathcal {F}$ is an example of Construction 6.3 for the profinite group ![]() $G$ (though we denote by
$G$ (though we denote by ![]() $R$ the
$R$ the ![]() $p$-complete ring). In particular, our assumptions imply hypercompleteness of
$p$-complete ring). In particular, our assumptions imply hypercompleteness of ![]() $L_{K(1)} \mathcal {F}$, so, passing to the limit, we find that
$L_{K(1)} \mathcal {F}$, so, passing to the limit, we find that
Note here that ![]() $\mathcal {F}^{\mathrm {disc}}$ is not given by
$\mathcal {F}^{\mathrm {disc}}$ is not given by ![]() $\mathrm {TR}(-; \mathbb {F}_p)$ because
$\mathrm {TR}(-; \mathbb {F}_p)$ because ![]() $\mathrm {TR}$ does not commute with filtered colimits; instead, for instance,
$\mathrm {TR}$ does not commute with filtered colimits; instead, for instance, ![]() $\mathcal {F}^{\mathrm {disc}}( G) = \varinjlim _{i \in I} \mathrm {TR}(S_i; \mathbb {F}_p)$. By assumption (ii),
$\mathcal {F}^{\mathrm {disc}}( G) = \varinjlim _{i \in I} \mathrm {TR}(S_i; \mathbb {F}_p)$. By assumption (ii), ![]() $\mathcal {F}^{\mathrm {disc}}(G), \mathcal {F}^{\mathrm {disc}}(G \times G) , \ldots$ are spectra with the property that the map to their
$\mathcal {F}^{\mathrm {disc}}(G), \mathcal {F}^{\mathrm {disc}}(G \times G) , \ldots$ are spectra with the property that the map to their ![]() $K(1)$-localization is
$K(1)$-localization is ![]() $d$-truncated; therefore,
$d$-truncated; therefore, ![]() $R \Gamma (\ast , \mathcal {F}) \to L_{K(1)}R \Gamma (\ast , \mathcal {F})= R \Gamma (\ast , L_{K(1)} \mathcal {F})$ is
$R \Gamma (\ast , \mathcal {F}) \to L_{K(1)}R \Gamma (\ast , \mathcal {F})= R \Gamma (\ast , L_{K(1)} \mathcal {F})$ is ![]() $d$-truncated.
$d$-truncated.
Now we apply two-out-of-three to the sequence of maps ![]() $\mathcal {F}(\ast ) \to R \Gamma (\ast , \mathcal {F}) \to R \Gamma (\ast , L_{K(1)} \mathcal {F})$. We just showed that the second map is
$\mathcal {F}(\ast ) \to R \Gamma (\ast , \mathcal {F}) \to R \Gamma (\ast , L_{K(1)} \mathcal {F})$. We just showed that the second map is ![]() $d$-truncated, while the composite map is by (14) identified with
$d$-truncated, while the composite map is by (14) identified with ![]() $\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$, which is
$\mathrm {TR}(R; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {F}_p)$, which is ![]() $d$-truncated by assumption. Therefore, by two-out-of-three, we find that
$d$-truncated by assumption. Therefore, by two-out-of-three, we find that ![]() $\mathcal {F}(\ast ) \to R \Gamma (\ast , \mathcal {F})$ is
$\mathcal {F}(\ast ) \to R \Gamma (\ast , \mathcal {F})$ is ![]() $d$-truncated. In other words,
$d$-truncated. In other words,
is ![]() $d$-truncated. Here both sides of (15) have the structure of topological Cartier modules since the forgetful functor from topological Cartier modules to spectra commutes with limits and colimits [Reference Antieau and NikolausAN21, Proposition 3.11].
$d$-truncated. Here both sides of (15) have the structure of topological Cartier modules since the forgetful functor from topological Cartier modules to spectra commutes with limits and colimits [Reference Antieau and NikolausAN21, Proposition 3.11].
Now we take the ![]() $V$-completion of both sides in (15) (considered as topological Cartier modules). The left-hand side of (15) is already
$V$-completion of both sides in (15) (considered as topological Cartier modules). The left-hand side of (15) is already ![]() $V$-complete. To analyze the right-hand-side, observe that the totalization in (15) commutes with
$V$-complete. To analyze the right-hand-side, observe that the totalization in (15) commutes with ![]() $(-)_{hC_{p^{n-1}}}$ because
$(-)_{hC_{p^{n-1}}}$ because ![]() $R\Gamma ( \ast , -)$ commutes with colimits. The limit over
$R\Gamma ( \ast , -)$ commutes with colimits. The limit over ![]() $n$ in computing the
$n$ in computing the ![]() $V$-completion clearly commutes with the totalization. Thus, the
$V$-completion clearly commutes with the totalization. Thus, the ![]() $V$-completion of the right-hand side of (15) is given by
$V$-completion of the right-hand side of (15) is given by
Note finally that the right-hand side of (15) is bounded below by the finiteness of the ![]() $p$-cohomological dimension. Taking the
$p$-cohomological dimension. Taking the ![]() $V$-completion in (15), we find from Proposition 6.5 that
$V$-completion in (15), we find from Proposition 6.5 that
is ![]() $(d+2)$-truncated, whence the last claim of the theorem. Finally,
$(d+2)$-truncated, whence the last claim of the theorem. Finally, ![]() $\mathrm {TR}(S; \mathbb {F}_p), \mathrm {TR}( \mathrm {Fun}_{\mathrm {cts}}(G, S); \mathbb {F}_p)$ map via
$\mathrm {TR}(S; \mathbb {F}_p), \mathrm {TR}( \mathrm {Fun}_{\mathrm {cts}}(G, S); \mathbb {F}_p)$ map via ![]() $(d+2)$-truncated maps to their
$(d+2)$-truncated maps to their ![]() $K(1)$-localizations, via Corollary 6.7, so the
$K(1)$-localizations, via Corollary 6.7, so the ![]() $K(1)$-local descent statement follows.
$K(1)$-local descent statement follows.
Example 6.9 (Discrete valuation rings) Let ![]() $K$ be a complete, discretely valued field of characteristic
$K$ be a complete, discretely valued field of characteristic ![]() $0$ whose residue field
$0$ whose residue field ![]() $k$ is of characteristic
$k$ is of characteristic ![]() $p$ with
$p$ with ![]() $[k: k^p] \leq p^d$. It follows that if
$[k: k^p] \leq p^d$. It follows that if ![]() $k'/k$ is any finite extension, then
$k'/k$ is any finite extension, then ![]() $[k':k'^p] \leq p^d$; see [Reference Gabber and OrgogozoGO08, Lemma 2.1.1].
$[k':k'^p] \leq p^d$; see [Reference Gabber and OrgogozoGO08, Lemma 2.1.1].
By the main result of [Reference Gabber and OrgogozoGO08] (which is due to [Reference KatoKat82] in this case), it follows that the Galois group ![]() $\mathrm {Gal}(\bar {K}/K)$ has
$\mathrm {Gal}(\bar {K}/K)$ has ![]() $p$-cohomological dimension at most
$p$-cohomological dimension at most ![]() $d + 2$. Moreover, by Theorem 4.8, it follows that if
$d + 2$. Moreover, by Theorem 4.8, it follows that if ![]() $L$ is any finite extension of
$L$ is any finite extension of ![]() $K$ and
$K$ and ![]() $\mathcal {O}_L \subset L$ the ring of integers (which is excellent as a complete local ring), then
$\mathcal {O}_L \subset L$ the ring of integers (which is excellent as a complete local ring), then ![]() $\mathrm {TR}( \mathcal {O}_L; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(\mathcal {O}_L; \mathbb {F}_p)$ is
$\mathrm {TR}( \mathcal {O}_L; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(\mathcal {O}_L; \mathbb {F}_p)$ is ![]() $d$-truncated.
$d$-truncated.
We can now apply Theorem 6.8 to conclude that
is ![]() $d$-truncated. Note that the theorem gives a priori that the map is
$d$-truncated. Note that the theorem gives a priori that the map is ![]() $(d+2)$-truncated, but we can upgrade the conclusion to
$(d+2)$-truncated, but we can upgrade the conclusion to ![]() $d$-truncated as follows: the analogous comparison map with
$d$-truncated as follows: the analogous comparison map with ![]() $L_{K(1)} \mathrm {TR}(-)$ everywhere is an equivalence; the maps
$L_{K(1)} \mathrm {TR}(-)$ everywhere is an equivalence; the maps ![]() $\mathrm {TR}( \mathcal {O}_{\bar {K} \otimes _K \cdots \otimes _K\bar {K}}; \mathbb {F}_p) \to \mathrm {TR}( \mathcal {O}_{\bar {K} \otimes _K \cdots \otimes _K\bar {K}}; \mathbb {F}_p)$ are
$\mathrm {TR}( \mathcal {O}_{\bar {K} \otimes _K \cdots \otimes _K\bar {K}}; \mathbb {F}_p) \to \mathrm {TR}( \mathcal {O}_{\bar {K} \otimes _K \cdots \otimes _K\bar {K}}; \mathbb {F}_p)$ are ![]() $(-1)$-truncated by Proposition 5.10 since these are
$(-1)$-truncated by Proposition 5.10 since these are ![]() $p$-torsion-free rings whose completions are perfectoid; and the map
$p$-torsion-free rings whose completions are perfectoid; and the map ![]() $\mathrm {TR}(\mathcal {O}_K; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(\mathcal {O}_K; \mathbb {F}_p)$ is
$\mathrm {TR}(\mathcal {O}_K; \mathbb {F}_p) \to L_{K(1)} \mathrm {TR}(\mathcal {O}_K; \mathbb {F}_p)$ is ![]() $d$-truncated (Theorem 4.8).
$d$-truncated (Theorem 4.8).
Suppose, in particular, that ![]() $k$ is perfect and of characteristic greater than
$k$ is perfect and of characteristic greater than ![]() $2$.Footnote 6 In this case, the results of [Reference Hesselholt and MadsenHM03] (recalled in the proof of Theorem 4.1) show that
$2$.Footnote 6 In this case, the results of [Reference Hesselholt and MadsenHM03] (recalled in the proof of Theorem 4.1) show that ![]() $\mathrm {TR}(\mathcal {O}_K|K; \mathbb {F}_p)$ is the connective cover of its
$\mathrm {TR}(\mathcal {O}_K|K; \mathbb {F}_p)$ is the connective cover of its ![]() $K(1)$-localization, which is
$K(1)$-localization, which is ![]() $L_{K(1)} \mathrm {TR}(\mathcal {O}_K; \mathbb {F}_p)$. Again,
$L_{K(1)} \mathrm {TR}(\mathcal {O}_K; \mathbb {F}_p)$. Again, ![]() $\mathcal {O}_{\bar {K}}, \mathcal {O}_{\bar {K} \otimes _K \bar {K}}, \ldots$ have
$\mathcal {O}_{\bar {K}}, \mathcal {O}_{\bar {K} \otimes _K \bar {K}}, \ldots$ have ![]() $p$-completions which are perfectoid rings, so for them
$p$-completions which are perfectoid rings, so for them ![]() $\mathrm {TR}(-; \mathbb {F}_p)$ agrees with the connective cover of its
$\mathrm {TR}(-; \mathbb {F}_p)$ agrees with the connective cover of its ![]() $K(1)$-localization (Proposition 5.10). It follows that
$K(1)$-localization (Proposition 5.10). It follows that ![]() $\mathrm {TR}(\mathcal {O}_K|K; \mathbb {F}_p) \simeq \tau _{\geq 0} \mathrm {TR}(\mathcal {O}_{\bar {K}} ; \mathbb {F}_p)^{h \mathrm {Gal}_K^{\mathrm {cts}}}$.
$\mathrm {TR}(\mathcal {O}_K|K; \mathbb {F}_p) \simeq \tau _{\geq 0} \mathrm {TR}(\mathcal {O}_{\bar {K}} ; \mathbb {F}_p)^{h \mathrm {Gal}_K^{\mathrm {cts}}}$.
Example 6.10 Let ![]() $R_0$ be a
$R_0$ be a ![]() $p$-torsion-free perfectoid ring containing a system of primitive
$p$-torsion-free perfectoid ring containing a system of primitive ![]() $p$-power roots of unity. Let
$p$-power roots of unity. Let ![]() $R$ be a formally smooth
$R$ be a formally smooth ![]() $R_0$-algebra, which is formally étale over the formal torus (i.e.
$R_0$-algebra, which is formally étale over the formal torus (i.e. ![]() $p$-completed Laurent polynomial algebra)
$p$-completed Laurent polynomial algebra) ![]() $R_0 \langle t_1^{\pm 1}, \ldots , t_n^{\pm 1} \rangle$.
$R_0 \langle t_1^{\pm 1}, \ldots , t_n^{\pm 1} \rangle$.
Let ![]() $G =\mathbb {Z}_p(1)^n$ and let
$G =\mathbb {Z}_p(1)^n$ and let ![]() $S = R \otimes _{R_0\langle t_1^{\pm 1}, \ldots , t_n^{\pm 1} \rangle } \varinjlim _r R_0 \langle t_1^{\pm 1/p^r}, \ldots , t_n^{\pm 1/p^r}\rangle$ with the evident
$S = R \otimes _{R_0\langle t_1^{\pm 1}, \ldots , t_n^{\pm 1} \rangle } \varinjlim _r R_0 \langle t_1^{\pm 1/p^r}, \ldots , t_n^{\pm 1/p^r}\rangle$ with the evident ![]() $G$-action by roots of unity. Using Proposition 5.10, one sees that the hypothesis of Theorem 6.8(ii) applies. The hypothesis of Theorem 6.8(iii) applies thanks to Example 6.4. It follows that the comparison map (13) is an equivalence. In particular, the
$G$-action by roots of unity. Using Proposition 5.10, one sees that the hypothesis of Theorem 6.8(ii) applies. The hypothesis of Theorem 6.8(iii) applies thanks to Example 6.4. It follows that the comparison map (13) is an equivalence. In particular, the ![]() $K(1)$-local
$K(1)$-local ![]() $\mathrm {TR}$ of
$\mathrm {TR}$ of ![]() $R$ is expressed as the inverse limit of a diagram of the
$R$ is expressed as the inverse limit of a diagram of the ![]() $K(1)$-local
$K(1)$-local ![]() $\mathrm {TR}$ of various rings whose
$\mathrm {TR}$ of various rings whose ![]() $p$-completion is perfectoid.
$p$-completion is perfectoid.
7. The analog of Thomason's spectral sequence
In this section, we construct in certain cases an analog of Thomason's étale descent spectral sequence for ![]() $L_{K(1)} K(-)$ in terms of étale cohomology (see [Reference ThomasonTho85, Reference Thomason and TrobaughTT90] for
$L_{K(1)} K(-)$ in terms of étale cohomology (see [Reference ThomasonTho85, Reference Thomason and TrobaughTT90] for ![]() $L_{K(1)} \mathrm {TR}(-)$). Our construction splits into two parts. First, we give a formula for
$L_{K(1)} \mathrm {TR}(-)$). Our construction splits into two parts. First, we give a formula for ![]() $\mathrm {TR}$ and its
$\mathrm {TR}$ and its ![]() $K(1)$-localization on the category of perfectoid rings. Second, we hypersheafify
$K(1)$-localization on the category of perfectoid rings. Second, we hypersheafify ![]() $L_{K(1)} \mathrm {TR}(-)$ on all rings in the
$L_{K(1)} \mathrm {TR}(-)$ on all rings in the ![]() $\mathrm {arc}_{{p}}$-topology and compare
$\mathrm {arc}_{{p}}$-topology and compare ![]() $L_{K(1)} \mathrm {TR}(-)$ to this hypersheafification.
$L_{K(1)} \mathrm {TR}(-)$ to this hypersheafification.
7.1  $\mathrm {arc}_{{p}}$-cohomology
$\mathrm {arc}_{{p}}$-cohomology
In this section we discuss the cohomology with respect to the ![]() $\mathrm {arc}_{{p}}$-topology, mentioned briefly in the introduction (Definition 1.6). This is a variant of the following topology (see [Reference Česnavičius and ScholzeČS19, § 2.2.1]).Footnote 7
$\mathrm {arc}_{{p}}$-topology, mentioned briefly in the introduction (Definition 1.6). This is a variant of the following topology (see [Reference Česnavičius and ScholzeČS19, § 2.2.1]).Footnote 7
Definition 7.1 (The ![]() $p$-complete
$p$-complete ![]() $\mathrm {arc}$-topology)
$\mathrm {arc}$-topology)
The ![]() $p$-complete
$p$-complete ![]() $\mathrm {arc}$-topology or
$\mathrm {arc}$-topology or ![]() $\mathrm {arc}_{\hat {p}}$-topology is the finitary Grothendieck topology (see Remark A.1) on the opposite of the category of derived
$\mathrm {arc}_{\hat {p}}$-topology is the finitary Grothendieck topology (see Remark A.1) on the opposite of the category of derived ![]() $p$-complete commutative rings such that a map
$p$-complete commutative rings such that a map ![]() $R \to R'$ is a cover if, for every
$R \to R'$ is a cover if, for every ![]() $p$-complete valuation ring
$p$-complete valuation ring ![]() $V$ of rank at most
$V$ of rank at most ![]() $1$ and map
$1$ and map ![]() $R \to V$, there is an extension
$R \to V$, there is an extension ![]() $V \to W$ of
$V \to W$ of ![]() $p$-complete valuation rings of rank at most
$p$-complete valuation rings of rank at most ![]() $1$ and a map
$1$ and a map ![]() $R' \to W$ fitting into the following commutative diagram.
$R' \to W$ fitting into the following commutative diagram.

We will also consider restrictions of the ![]() $\mathrm {arc}_{\hat {p}}$-topology to appropriate subcategories of the category of derived
$\mathrm {arc}_{\hat {p}}$-topology to appropriate subcategories of the category of derived ![]() $p$-complete rings, such as the category
$p$-complete rings, such as the category ![]() $\mathrm {Perfd}$ of perfectoid rings [Reference Bhatt, Morrow and ScholzeBMS18, § 3]. The
$\mathrm {Perfd}$ of perfectoid rings [Reference Bhatt, Morrow and ScholzeBMS18, § 3]. The ![]() $\mathrm {arc}_{{p}}$-topology is defined similarly, but we only consider rank
$\mathrm {arc}_{{p}}$-topology is defined similarly, but we only consider rank ![]() $1$
$1$ ![]() $p$-complete valuation rings where
$p$-complete valuation rings where ![]() $p \neq 0$.
$p \neq 0$.
The ![]() $\mathrm {arc}_{\hat {p}}$-topology behaves well with respect to perfectoid rings; one knows that the structure presheaf is a sheaf of rings with respect to this topology, and one even has no higher cohomology [Reference Bhatt and ScholzeBS19, § 8]. The
$\mathrm {arc}_{\hat {p}}$-topology behaves well with respect to perfectoid rings; one knows that the structure presheaf is a sheaf of rings with respect to this topology, and one even has no higher cohomology [Reference Bhatt and ScholzeBS19, § 8]. The ![]() $\mathrm {arc}_{{p}}$-topology is a variant where in some sense we also impose derived saturatedness conditions. Note that a functor is an
$\mathrm {arc}_{{p}}$-topology is a variant where in some sense we also impose derived saturatedness conditions. Note that a functor is an ![]() $\mathrm {arc}_{{p}}$-sheaf if and only if it is an
$\mathrm {arc}_{{p}}$-sheaf if and only if it is an ![]() $\mathrm {arc}_{\hat {p}}$-sheaf and annihilates any
$\mathrm {arc}_{\hat {p}}$-sheaf and annihilates any ![]() $\mathbb {F}_p$-algebra. Any derived
$\mathbb {F}_p$-algebra. Any derived ![]() $p$-complete ring can be covered in the
$p$-complete ring can be covered in the ![]() $\mathrm {arc}_{\hat {p}}$-topology (respectively, the
$\mathrm {arc}_{\hat {p}}$-topology (respectively, the ![]() $\mathrm {arc}_{{p}}$-topology) by a product of
$\mathrm {arc}_{{p}}$-topology) by a product of ![]() $p$-complete absolutely integrally closed rank
$p$-complete absolutely integrally closed rank ![]() $1$ valuation rings (respectively,
$1$ valuation rings (respectively, ![]() $p$-complete absolutely integrally closed rank
$p$-complete absolutely integrally closed rank ![]() $1$ valuation rings where
$1$ valuation rings where ![]() $p \neq 0$).
$p \neq 0$).
We now give some examples of ![]() $\mathrm {arc}_{{p}}$-cohomology. To begin with, we consider the simplest case of constant sheaves (or
$\mathrm {arc}_{{p}}$-cohomology. To begin with, we consider the simplest case of constant sheaves (or ![]() $p$-adically constant ones); the result is that one essentially recovers the
$p$-adically constant ones); the result is that one essentially recovers the ![]() $p$-adic étale cohomology of the generic fiber.
$p$-adic étale cohomology of the generic fiber.
Construction 7.2 (Constant sheaves in the ![]() $\mathrm {arc}_{{p}}$-topology)
$\mathrm {arc}_{{p}}$-topology)
Given an abelian group ![]() $M$, we can consider the associated constant sheaf of abelian groups in the
$M$, we can consider the associated constant sheaf of abelian groups in the ![]() $\mathrm {arc}_{{p}}$-topology; its value on a derived
$\mathrm {arc}_{{p}}$-topology; its value on a derived ![]() $p$-complete ring
$p$-complete ring ![]() $R$ is given by
$R$ is given by ![]() $H^0_{\mathrm {\acute {e}t}}(\mathrm {Spec}(R[1/p]), M)$. To see this, we observe that the presheaf of abelian groups
$H^0_{\mathrm {\acute {e}t}}(\mathrm {Spec}(R[1/p]), M)$. To see this, we observe that the presheaf of abelian groups ![]() $R \mapsto H^0_{\mathrm {\acute {e}t}}( \mathrm {Spec}(R[1/p]), M)$ is a sheaf in the
$R \mapsto H^0_{\mathrm {\acute {e}t}}( \mathrm {Spec}(R[1/p]), M)$ is a sheaf in the ![]() $\mathrm {arc}_{{p}}$-topology on derived
$\mathrm {arc}_{{p}}$-topology on derived ![]() $p$-complete rings [Reference Bhatt and MathewBM18, Corollary 6.17] (which assumes
$p$-complete rings [Reference Bhatt and MathewBM18, Corollary 6.17] (which assumes ![]() $M$ torsion; however, this is not necessary since we are only working with
$M$ torsion; however, this is not necessary since we are only working with ![]() $H^0$). It admits a map from the constant presheaf
$H^0$). It admits a map from the constant presheaf ![]() $M$, and the kernel and cokernel vanish locally in the
$M$, and the kernel and cokernel vanish locally in the ![]() $\mathrm {arc}_{{p}}$-topology.
$\mathrm {arc}_{{p}}$-topology.
Construction 7.3 (![]() $p$-adically constant sheaves and Tate twists in the
$p$-adically constant sheaves and Tate twists in the ![]() $\mathrm {arc}_{{p}}$-topology)
$\mathrm {arc}_{{p}}$-topology)
Consider the sheaf of rings ![]() $\mathbb {Z}_p$ in the
$\mathbb {Z}_p$ in the ![]() $\mathrm {arc}_{{p}}$-topology, defined as the
$\mathrm {arc}_{{p}}$-topology, defined as the ![]() $p$-completion of the constant sheaf associated to
$p$-completion of the constant sheaf associated to ![]() $\mathbb {Z}_p$, or equivalently as the inverse limit of the constant sheaves
$\mathbb {Z}_p$, or equivalently as the inverse limit of the constant sheaves ![]() $\mathbb {Z}/p^n \mathbb {Z}$; explicitly,
$\mathbb {Z}/p^n \mathbb {Z}$; explicitly, ![]() $\mathbb {Z}_p(R) = H^0_{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathbb {Z}_p) = H^0_{\mathrm {pro\acute {e}t}}( \mathrm {Spec}(R[1/p]), \mathbb {Z}_p)$. We construct an invertible
$\mathbb {Z}_p(R) = H^0_{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathbb {Z}_p) = H^0_{\mathrm {pro\acute {e}t}}( \mathrm {Spec}(R[1/p]), \mathbb {Z}_p)$. We construct an invertible ![]() $\mathbb {Z}_p$-module
$\mathbb {Z}_p$-module ![]() $\mathbb {Z}_p(1)$ as the
$\mathbb {Z}_p(1)$ as the ![]() $\mathrm {arc}_{{p}}$-sheafification of the presheaf
$\mathrm {arc}_{{p}}$-sheafification of the presheaf ![]() $R \mapsto \mathbb {Z}_p(1)^{\mathrm {pre}}(R) := T_p(R^{\times })$. To check that this is an invertible module, we observe (see [Reference Bhatt and MathewBM18, Proposition 3.30]) that
$R \mapsto \mathbb {Z}_p(1)^{\mathrm {pre}}(R) := T_p(R^{\times })$. To check that this is an invertible module, we observe (see [Reference Bhatt and MathewBM18, Proposition 3.30]) that ![]() $\mathbb {Z}_p(1)^{\mathrm {pre}}(R)$ is an invertible
$\mathbb {Z}_p(1)^{\mathrm {pre}}(R)$ is an invertible ![]() $\mathbb {Z}_p(R)$-module whenever
$\mathbb {Z}_p(R)$-module whenever ![]() $R$ is a product of absolutely integrally closed valuation rings of mixed characteristic
$R$ is a product of absolutely integrally closed valuation rings of mixed characteristic ![]() $(0, p)$. Note that
$(0, p)$. Note that ![]() $\mathbb {Z}_p(1)/p$ can equally be described as the
$\mathbb {Z}_p(1)/p$ can equally be described as the ![]() $\mathrm {arc}_{{p}}$-sheaf associated to the presheaf
$\mathrm {arc}_{{p}}$-sheaf associated to the presheaf ![]() $R \mapsto \mu _p(R) = R^{\times }[p]$, since
$R \mapsto \mu _p(R) = R^{\times }[p]$, since ![]() $\mathrm {arc}_{{p}}$-locally all elements have
$\mathrm {arc}_{{p}}$-locally all elements have ![]() $p$th roots.
$p$th roots.
Proposition 7.4 (![]() $\mathrm {arc}_{{p}}$-cohomology as
$\mathrm {arc}_{{p}}$-cohomology as ![]() $p$-adic vanishing cycles)
$p$-adic vanishing cycles)
Let ![]() $R$ be any derived
$R$ be any derived ![]() $p$-complete ring. Then there is a natural equivalence
$p$-complete ring. Then there is a natural equivalence
where ![]() $\mathbb {Z}_p(i)$ on the right-hand side refers to the usual Tate twist on the pro-étale site of
$\mathbb {Z}_p(i)$ on the right-hand side refers to the usual Tate twist on the pro-étale site of ![]() $\mathrm {Spec}(R[1/p])$.
$\mathrm {Spec}(R[1/p])$.
Proof. We know that the right-hand side is a ![]() $D(\mathbb {Z}_p)^{\geq 0}$-valued sheaf for the
$D(\mathbb {Z}_p)^{\geq 0}$-valued sheaf for the ![]() $\mathrm {arc}_{{p}}$-topology by [Reference Bhatt and MathewBM18, Corollary 6.17], and we obtain a map from the presheaf
$\mathrm {arc}_{{p}}$-topology by [Reference Bhatt and MathewBM18, Corollary 6.17], and we obtain a map from the presheaf ![]() $R \mapsto T_p( R^{\times })^{\otimes i}$ to the right-hand side. Sheafifying in the
$R \mapsto T_p( R^{\times })^{\otimes i}$ to the right-hand side. Sheafifying in the ![]() $\mathrm {arc}_{{p}}$-topology and
$\mathrm {arc}_{{p}}$-topology and ![]() $p$-completing, we obtain a map from the left-hand side to the right-hand side as in (16). To see that (16) is an equivalence of
$p$-completing, we obtain a map from the left-hand side to the right-hand side as in (16). To see that (16) is an equivalence of ![]() $\mathrm {arc}_{{p}}$-sheaves, it suffices to check on products of rank
$\mathrm {arc}_{{p}}$-sheaves, it suffices to check on products of rank ![]() $1$ absolutely integrally closed,
$1$ absolutely integrally closed, ![]() $p$-complete valuation rings of mixed characteristic as these form a basis (see [Reference Bhatt and MathewBM18, Proposition 3.29]), which is handled by the next lemma.
$p$-complete valuation rings of mixed characteristic as these form a basis (see [Reference Bhatt and MathewBM18, Proposition 3.29]), which is handled by the next lemma.
Lemma 7.5 Let ![]() $R$ be a product
$R$ be a product ![]() $\prod _{t \in T} V_t$ of absolutely integrally closed,
$\prod _{t \in T} V_t$ of absolutely integrally closed, ![]() $p$-complete valuation rings. Then:
$p$-complete valuation rings. Then:
(i)
 $H^j_{\mathrm {pro\acute {e}t}}( \mathrm {Spec}(R[1/p]), \mathbb {Z}_p(i)) = 0$ for
$H^j_{\mathrm {pro\acute {e}t}}( \mathrm {Spec}(R[1/p]), \mathbb {Z}_p(i)) = 0$ for  $j > 0$;
$j > 0$;(ii) the map
 $T_p(R^{\times }) \to H^0_{\mathrm {pro\acute {e}t}}( \mathrm {Spec}(R[1/p]), \mathbb {Z}_p(1))$ is an isomorphism.
$T_p(R^{\times }) \to H^0_{\mathrm {pro\acute {e}t}}( \mathrm {Spec}(R[1/p]), \mathbb {Z}_p(1))$ is an isomorphism.
Proof. It suffices to prove both claims after reducing modulo ![]() $p$. Consider the functor
$p$. Consider the functor ![]() $A \mapsto F_j(A) := H^j( \mathrm {Spec}(\hat {A}_p[1/p]; \mathbb {F}_p(i))$. This functor commutes with finite products and filtered colimits by the Gabber–Fujiwara theorem; see [Reference Bhatt and MathewBM18, Theorem 6.11] for an account. To prove that
$A \mapsto F_j(A) := H^j( \mathrm {Spec}(\hat {A}_p[1/p]; \mathbb {F}_p(i))$. This functor commutes with finite products and filtered colimits by the Gabber–Fujiwara theorem; see [Reference Bhatt and MathewBM18, Theorem 6.11] for an account. To prove that ![]() $F_j(R) = 0$ for
$F_j(R) = 0$ for ![]() $j > 0$ which implies (i), it suffices as in [Reference Bhatt and MathewBM18, Corollary 3.17] to show that
$j > 0$ which implies (i), it suffices as in [Reference Bhatt and MathewBM18, Corollary 3.17] to show that ![]() $F$ vanishes on every ultraproduct of the
$F$ vanishes on every ultraproduct of the ![]() $\{V_t\}$ for each ultrafilter on
$\{V_t\}$ for each ultrafilter on ![]() $T$. But these ultraproducts are all absolutely integrally closed,
$T$. But these ultraproducts are all absolutely integrally closed, ![]() $p$-henselian valuation rings, whence (i). Claim (ii) is proved similarly using the map
$p$-henselian valuation rings, whence (i). Claim (ii) is proved similarly using the map ![]() $A^{\times }[p] \to H^0_{\mathrm {pro\acute {e}t}}( \mathrm {Spec}(A[1/p]), \mathbb {F}_p(1))$.
$A^{\times }[p] \to H^0_{\mathrm {pro\acute {e}t}}( \mathrm {Spec}(A[1/p]), \mathbb {F}_p(1))$.
Next we consider the cohomology of the structure presheaf.
Construction 7.6 (![]() $\mathrm {arc}_{{p}}$-cohomology of the structure presheaf)
$\mathrm {arc}_{{p}}$-cohomology of the structure presheaf)
For a derived ![]() $p$-complete commutative ring
$p$-complete commutative ring ![]() $R$, we let
$R$, we let ![]() $R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O})$ denote the
$R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O})$ denote the ![]() $\mathrm {arc}_{{p}}$-cohomology of the structure presheaf.
$\mathrm {arc}_{{p}}$-cohomology of the structure presheaf.
The ![]() $\mathrm {arc}_{{p}}$-topology restricts to a topology on the opposite of
$\mathrm {arc}_{{p}}$-topology restricts to a topology on the opposite of ![]() $\mathrm {Perfd}$. Our first goal is to identify concretely
$\mathrm {Perfd}$. Our first goal is to identify concretely ![]() $\mathrm {arc}_{{p}}$-cohomology on
$\mathrm {arc}_{{p}}$-cohomology on ![]() $\mathrm {Perfd}$.
$\mathrm {Perfd}$.
Construction 7.7 (Saturation) Let ![]() $R$ be a perfectoid ring. We have the natural quotient
$R$ be a perfectoid ring. We have the natural quotient ![]() $R \to R' := R/\mathrm {rad}((p))$, which is the universal map from
$R \to R' := R/\mathrm {rad}((p))$, which is the universal map from ![]() $R$ to a perfect
$R$ to a perfect ![]() $\mathbb {F}_p$-algebra. Note that
$\mathbb {F}_p$-algebra. Note that ![]() $R' \otimes ^L_R R'$ is discrete (and equivalent to
$R' \otimes ^L_R R'$ is discrete (and equivalent to ![]() $R'$) since relative tensor products of perfectoid rings are
$R'$) since relative tensor products of perfectoid rings are ![]() $p$-completely discrete (and perfectoid).
$p$-completely discrete (and perfectoid).
Let ![]() $J = \mathrm {rad}(p)$. We have
$J = \mathrm {rad}(p)$. We have ![]() $J \otimes ^L_R J \xrightarrow {\sim } J$. It follows that one is in the setup of almost mathematics, and we have a derived almostification functor
$J \otimes ^L_R J \xrightarrow {\sim } J$. It follows that one is in the setup of almost mathematics, and we have a derived almostification functor ![]() $(-)_* \colon D(R) \to D(R)$, which is also given by
$(-)_* \colon D(R) \to D(R)$, which is also given by ![]() $R \text{Hom} _R( J, -)$. We claim that in fact
$R \text{Hom} _R( J, -)$. We claim that in fact ![]() $J$ can be made explicit, and in particular that it has projective dimension at most
$J$ can be made explicit, and in particular that it has projective dimension at most ![]() $1$, so that for any discrete
$1$, so that for any discrete ![]() $R$-module
$R$-module ![]() $M$,
$M$, ![]() $M_* \in D(R)^{[0, 1]}$. Indeed, there exists an element
$M_* \in D(R)^{[0, 1]}$. Indeed, there exists an element ![]() $\omega \in R$ such that
$\omega \in R$ such that ![]() $\omega$ is a unit multiple of
$\omega$ is a unit multiple of ![]() $p$ and such that
$p$ and such that ![]() $\omega$ admits a compatible system of
$\omega$ admits a compatible system of ![]() $p$-power roots
$p$-power roots ![]() $\{\omega ^{1/p^n}\}_{n \geq 0}$; see [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 3.9]. We claim that as an
$\{\omega ^{1/p^n}\}_{n \geq 0}$; see [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 3.9]. We claim that as an ![]() $R$-module, there is an equivalence
$R$-module, there is an equivalence
To see this, we observe first that the filtered colimit on the right-hand side is a submodule of ![]() $R$ given by the ideal
$R$ given by the ideal ![]() $J' := {\bigcup} _{n} (\omega ^{1/p^n})$ (i.e. given by multiplication by
$J' := {\bigcup} _{n} (\omega ^{1/p^n})$ (i.e. given by multiplication by ![]() $\omega ^{1/p^n}$ on the
$\omega ^{1/p^n}$ on the ![]() $n$th term); we can see this by
$n$th term); we can see this by ![]() $\mathrm {arc}_{\hat {p}}$-descent to reduce to the case where
$\mathrm {arc}_{\hat {p}}$-descent to reduce to the case where ![]() $R$ is a product of valuation rings of rank at most
$R$ is a product of valuation rings of rank at most ![]() $1$, in which case the claim is clear. Now clearly
$1$, in which case the claim is clear. Now clearly ![]() $J' \subset J$ and
$J' \subset J$ and ![]() $R/ J'$ is a ring of characteristic
$R/ J'$ is a ring of characteristic ![]() $p$ on which the Frobenius is surjective. To obtain
$p$ on which the Frobenius is surjective. To obtain ![]() $J' = J$, we use [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 3.10] to see that the Frobenius induces an isomorphism
$J' = J$, we use [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 3.10] to see that the Frobenius induces an isomorphism ![]() $R/\omega ^{1/p^n} \xrightarrow {\sim } R/\omega ^{1/p^{n-1}}$ for
$R/\omega ^{1/p^n} \xrightarrow {\sim } R/\omega ^{1/p^{n-1}}$ for ![]() $n \geq 1$. This implies that
$n \geq 1$. This implies that ![]() $R/J'$ is perfect, whence
$R/J'$ is perfect, whence ![]() $J = J'$ as desired.
$J = J'$ as desired.
Definition 7.8 (Spherically complete fields) We recall (see [Reference van RooijvR78, Chapter 4] for an account) that a nonarchimedean field is called spherically complete if every decreasing sequence of closed disks has nonempty intersection; in particular, any such field is complete. Any nonarchimedean field admits an extension which is spherically complete and algebraically closed.
Lemma 7.9 Let ![]() $C$ be spherically complete with ring of integers
$C$ be spherically complete with ring of integers ![]() $\mathcal {O}_C$. Given any tower
$\mathcal {O}_C$. Given any tower ![]() $\{M_i\}_{i \geq 1}$ of cyclic
$\{M_i\}_{i \geq 1}$ of cyclic ![]() $\mathcal {O}_C$-modules, we have
$\mathcal {O}_C$-modules, we have ![]() $\varprojlim ^1 M_i = 0$.
$\varprojlim ^1 M_i = 0$.
Proof. Writing ![]() $\{M_i\}$ as the cokernel of an injective map
$\{M_i\}$ as the cokernel of an injective map ![]() $\{N_i\}_{i \geq 1} \to \{N_i'\}_{i \geq 1}$ of inverse systems with the
$\{N_i\}_{i \geq 1} \to \{N_i'\}_{i \geq 1}$ of inverse systems with the ![]() $N_i'$ levelwise isomorphic to
$N_i'$ levelwise isomorphic to ![]() $\mathcal {O}_{C}$ and using the long exact sequence, we reduce to the case that the
$\mathcal {O}_{C}$ and using the long exact sequence, we reduce to the case that the ![]() $M_i$ are individually isomorphic to
$M_i$ are individually isomorphic to ![]() $\mathcal {O}_C$ (in particular, torsion-free). Moreover, upon passing to a cofinal subfamily, we may assume the
$\mathcal {O}_C$ (in particular, torsion-free). Moreover, upon passing to a cofinal subfamily, we may assume the ![]() $\{M_i\}_{i \geq 1}$ form a descending sequence of cyclic ideals
$\{M_i\}_{i \geq 1}$ form a descending sequence of cyclic ideals ![]() $\{I_i\}_{i \geq 1} \subset \mathcal {O}_C$; using the short exact sequence of inverse systems
$\{I_i\}_{i \geq 1} \subset \mathcal {O}_C$; using the short exact sequence of inverse systems ![]() $0 \to \{I_i\}_{i \geq 1} \to \{\mathcal {O}_C\}_{i \geq 1} \to \{\mathcal {O}_C/I_i\}_{i \geq 1} \to 0$ (with the middle sequence constant), we see that it suffices to show that
$0 \to \{I_i\}_{i \geq 1} \to \{\mathcal {O}_C\}_{i \geq 1} \to \{\mathcal {O}_C/I_i\}_{i \geq 1} \to 0$ (with the middle sequence constant), we see that it suffices to show that ![]() $\mathcal {O}_C \to \varprojlim _i \mathcal {O}_C/I_i$ is surjective. But this is precisely the definition of spherical completeness.
$\mathcal {O}_C \to \varprojlim _i \mathcal {O}_C/I_i$ is surjective. But this is precisely the definition of spherical completeness.
Proposition 7.10 (![]() $\mathrm {arc}_{{p}}$-cohomology of perfectoids)
$\mathrm {arc}_{{p}}$-cohomology of perfectoids)
The functor ![]() $R \mapsto R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O})$ restricted on
$R \mapsto R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O})$ restricted on ![]() $\mathrm {Perfd}$ agrees with
$\mathrm {Perfd}$ agrees with ![]() $R \mapsto R_*$. In particular, for
$R \mapsto R_*$. In particular, for ![]() $R \in \mathrm {Perfd}$,
$R \in \mathrm {Perfd}$, ![]() $R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O}) \in D(R)^{[0, 1]}$.
$R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O}) \in D(R)^{[0, 1]}$.
Proof. Let ![]() $R$ be a perfectoid ring. First, we claim that
$R$ be a perfectoid ring. First, we claim that ![]() $\mathrm {arc}_{{p}}$-cohomology of
$\mathrm {arc}_{{p}}$-cohomology of ![]() $R$ with
$R$ with ![]() $\mathcal {O}$-coefficients can be calculated on either all derived
$\mathcal {O}$-coefficients can be calculated on either all derived ![]() $p$-complete rings or the subcategory of perfectoid rings (endowed with the
$p$-complete rings or the subcategory of perfectoid rings (endowed with the ![]() $\mathrm {arc}_{{p}}$-cohomology). To see this, we use that perfectoid rings form a basis for the
$\mathrm {arc}_{{p}}$-cohomology). To see this, we use that perfectoid rings form a basis for the ![]() $\mathrm {arc}_{{p}}$-topology. In fact, any ring admits an
$\mathrm {arc}_{{p}}$-topology. In fact, any ring admits an ![]() $\mathrm {arc}_{{p}}$-cover by a semiperfectoid ring
$\mathrm {arc}_{{p}}$-cover by a semiperfectoid ring ![]() $S$, and then one can take the perfectoidization [Reference Bhatt and ScholzeBS19, § 8] of
$S$, and then one can take the perfectoidization [Reference Bhatt and ScholzeBS19, § 8] of ![]() $S$, which is an
$S$, which is an ![]() $\mathrm {arc}_{{p}}$-cover of
$\mathrm {arc}_{{p}}$-cover of ![]() $S$ (e.g. maps of
$S$ (e.g. maps of ![]() $S$ or its perfectoidization into
$S$ or its perfectoidization into ![]() $p$-complete absolutely integrally closed valuation rings are the same). The rest of the claim is a general argument following from the fact that perfectoid rings form a basis for the
$p$-complete absolutely integrally closed valuation rings are the same). The rest of the claim is a general argument following from the fact that perfectoid rings form a basis for the ![]() $\mathrm {arc}_{{p}}$-topology; see Proposition A.6 below.
$\mathrm {arc}_{{p}}$-topology; see Proposition A.6 below.
Now it suffices to prove that ![]() $R \mapsto R_*$ is a
$R \mapsto R_*$ is a ![]() $D(\mathbb {Z})^{\geq 0}$-valued
$D(\mathbb {Z})^{\geq 0}$-valued ![]() $\mathrm {arc}_{{p}}$-sheaf on
$\mathrm {arc}_{{p}}$-sheaf on ![]() $\mathrm {Perfd}$ and that the map
$\mathrm {Perfd}$ and that the map ![]() $R \to R_*$ is locally an equivalence. The fact that it is an
$R \to R_*$ is locally an equivalence. The fact that it is an ![]() $\mathrm {arc}_{{p}}$-sheaf follows because the structure presheaf is a
$\mathrm {arc}_{{p}}$-sheaf follows because the structure presheaf is a ![]() $D(\mathbb {Z})^{ \geq 0}$-valued sheaf on the
$D(\mathbb {Z})^{ \geq 0}$-valued sheaf on the ![]() $\mathrm {arc}_{\hat {p}}$-topology on
$\mathrm {arc}_{\hat {p}}$-topology on ![]() $\mathrm {Perfd}$ and
$\mathrm {Perfd}$ and ![]() $R \mapsto R_*$ annihilates perfect
$R \mapsto R_*$ annihilates perfect ![]() $\mathbb {F}_p$-algebras. The fact that
$\mathbb {F}_p$-algebras. The fact that ![]() $R \to R_*$ is locally an equivalence follows by taking an
$R \to R_*$ is locally an equivalence follows by taking an ![]() $\mathrm {arc}_{{p}}$-cover by a product of rings of integers in various spherically complete, algebraically closed nonarchimedean fields of mixed characteristic; for such rings,
$\mathrm {arc}_{{p}}$-cover by a product of rings of integers in various spherically complete, algebraically closed nonarchimedean fields of mixed characteristic; for such rings, ![]() $R = R_*$.
$R = R_*$.
Let ![]() $R_0$ be a perfectoid base ring, and let
$R_0$ be a perfectoid base ring, and let ![]() $R$ be a derived
$R$ be a derived ![]() $p$-complete
$p$-complete ![]() $R_0$-algebra. One has the construction of the perfectoidization
$R_0$-algebra. One has the construction of the perfectoidization ![]() $R_{\mathrm {perfd}}$ of
$R_{\mathrm {perfd}}$ of ![]() $R$, a coconnective
$R$, a coconnective ![]() $E_\infty$-algebra under
$E_\infty$-algebra under ![]() $R$ which has the property that if
$R$ which has the property that if ![]() $R$ is semiperfectoid, then
$R$ is semiperfectoid, then ![]() $R_{\mathrm {perfd}}$ is discrete and is the universal perfectoid ring that
$R_{\mathrm {perfd}}$ is discrete and is the universal perfectoid ring that ![]() $R$ maps to. As shown in [Reference Bhatt and ScholzeBS19, § 8],
$R$ maps to. As shown in [Reference Bhatt and ScholzeBS19, § 8], ![]() $R \mapsto R_{\mathrm {perfd}}$ is the
$R \mapsto R_{\mathrm {perfd}}$ is the ![]() $\mathrm {arc}_{\hat {p}}$-cohomology of the structure presheaf on the category of derived
$\mathrm {arc}_{\hat {p}}$-cohomology of the structure presheaf on the category of derived ![]() $p$-complete
$p$-complete ![]() $R_0$-algebras.
$R_0$-algebras.
Proposition 7.11 (![]() $\mathrm {arc}_{{p}}$-cohomology as saturated perfectoidization)
$\mathrm {arc}_{{p}}$-cohomology as saturated perfectoidization)
For ![]() $R$ an
$R$ an ![]() $R_0$-algebra which is derived
$R_0$-algebra which is derived ![]() $p$-complete, we have a natural equivalence of
$p$-complete, we have a natural equivalence of ![]() $E_\infty$-algebras in
$E_\infty$-algebras in ![]() $D(R_0)$,
$D(R_0)$, ![]() $R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O}) \simeq (R_{\mathrm {perfd}})_*$ (where almost mathematics is taken relative to
$R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O}) \simeq (R_{\mathrm {perfd}})_*$ (where almost mathematics is taken relative to ![]() $R_0$ and the ideal
$R_0$ and the ideal ![]() $\mathrm {rad}(p)$).
$\mathrm {rad}(p)$).
Proof. This is proved similarly to Proposition 7.10. We have a natural (in ![]() $R$) map
$R$) map ![]() $R \to (R_{\mathrm {perfd}})_*$. To show that it is the
$R \to (R_{\mathrm {perfd}})_*$. To show that it is the ![]() $\mathrm {arc}_{{p}}$-sheafification, it suffices to show that the codomain is an
$\mathrm {arc}_{{p}}$-sheafification, it suffices to show that the codomain is an ![]() $\mathrm {arc}_{{p}}$-sheaf, and that the map
$\mathrm {arc}_{{p}}$-sheaf, and that the map ![]() $R \to (R_{\mathrm {perfd}})_*$ has cofiber which vanishes locally in the
$R \to (R_{\mathrm {perfd}})_*$ has cofiber which vanishes locally in the ![]() $\mathrm {arc}_{{p}}$-topology; note also that we can compute the
$\mathrm {arc}_{{p}}$-topology; note also that we can compute the ![]() $\mathrm {arc}_{{p}}$-cohomology either over all derived
$\mathrm {arc}_{{p}}$-cohomology either over all derived ![]() $p$-complete rings or over
$p$-complete rings or over ![]() $R_0$-algebras (Example A.7). The codomain is an
$R_0$-algebras (Example A.7). The codomain is an ![]() $\mathrm {arc}_{\hat {p}}$-sheaf because of the identification of perfectoidization with
$\mathrm {arc}_{\hat {p}}$-sheaf because of the identification of perfectoidization with ![]() $\mathrm {arc}_{\hat {p}}$-cohomology [Reference Bhatt and ScholzeBS19, § 8], and hence is an
$\mathrm {arc}_{\hat {p}}$-cohomology [Reference Bhatt and ScholzeBS19, § 8], and hence is an ![]() $\mathrm {arc}_{{p}}$-sheaf since it annihilates
$\mathrm {arc}_{{p}}$-sheaf since it annihilates ![]() $\mathbb {F}_p$-algebras. The cofiber of
$\mathbb {F}_p$-algebras. The cofiber of ![]() $R \to (R_{\mathrm {perfd}})_*$ vanishes locally in the
$R \to (R_{\mathrm {perfd}})_*$ vanishes locally in the ![]() $\mathrm {arc}_{{p}}$-topology, as one sees by working with perfectoid
$\mathrm {arc}_{{p}}$-topology, as one sees by working with perfectoid ![]() $R$ and using the argument of Proposition 7.10.
$R$ and using the argument of Proposition 7.10.
Example 7.12 Suppose ![]() $R$ is the
$R$ is the ![]() $p$-completion of a ring which is integral over the perfectoid ring
$p$-completion of a ring which is integral over the perfectoid ring ![]() $R_0$. Then the perfectoidization
$R_0$. Then the perfectoidization ![]() $R_{\mathrm {perfd}}$ is discrete [Reference Bhatt and ScholzeBS19, Theorem 10.11]. It thus follows that
$R_{\mathrm {perfd}}$ is discrete [Reference Bhatt and ScholzeBS19, Theorem 10.11]. It thus follows that ![]() $R\Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O}) \in D(R)^{[0, 1]}$.
$R\Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O}) \in D(R)^{[0, 1]}$.
Construction 7.13 (Witt vector cohomology in the ![]() $\mathrm {arc}_{{p}}$-topology)
$\mathrm {arc}_{{p}}$-topology)
We consider the presheaf ![]() $W(\mathcal {O})$ given by
$W(\mathcal {O})$ given by ![]() $R \mapsto W(R)$ and its
$R \mapsto W(R)$ and its ![]() $\mathrm {arc}_{{p}}$-cohomology (with Tate twists)
$\mathrm {arc}_{{p}}$-cohomology (with Tate twists) ![]() $R \Gamma _{\mathrm {arc}_{{p}}}(\mathrm {Spec}(R), W(\mathcal {O})(i))$. Since the Witt vector functor is endowed with Frobenius and Verschiebung operators, so is the construction
$R \Gamma _{\mathrm {arc}_{{p}}}(\mathrm {Spec}(R), W(\mathcal {O})(i))$. Since the Witt vector functor is endowed with Frobenius and Verschiebung operators, so is the construction ![]() $R \mapsto R \Gamma _{\mathrm {arc}_{{p}}}(\mathrm {Spec}(R), W(\mathcal {O})(i))$.
$R \mapsto R \Gamma _{\mathrm {arc}_{{p}}}(\mathrm {Spec}(R), W(\mathcal {O})(i))$.
In our setting, we can think of the Witt vector cohomology considered above as a one-parameter (along ![]() $V$) deformation of the structure presheaf cohomology, especially in light of the next result.
$V$) deformation of the structure presheaf cohomology, especially in light of the next result.
Proposition 7.14 For any ring ![]() $R$,
$R$, ![]() $R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O})(i))$ is
$R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O})(i))$ is ![]() $p$-complete and complete with respect to the Verschiebung.
$p$-complete and complete with respect to the Verschiebung.
Proof. By base-changing to ![]() $\mathbb {Z}_p[\zeta _{p^\infty }]$, we may assume without loss of generality that
$\mathbb {Z}_p[\zeta _{p^\infty }]$, we may assume without loss of generality that ![]() $i = 0$. Then this follows from Proposition A.10 below, since the presheaf
$i = 0$. Then this follows from Proposition A.10 below, since the presheaf ![]() $W(\mathcal {O})$ commutes with finite products and is complete with respect to
$W(\mathcal {O})$ commutes with finite products and is complete with respect to ![]() $(p, V)$.
$(p, V)$.
Corollary 7.15 Let ![]() $R$ be finite and finitely presented over a perfectoid ring. Then
$R$ be finite and finitely presented over a perfectoid ring. Then ![]() $R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O})(i)) \in D(\mathbb {Z}_p)^{[0, 1]}$ for any
$R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O})(i)) \in D(\mathbb {Z}_p)^{[0, 1]}$ for any ![]() $i$.
$i$.
Proof. By ![]() $p$-completeness and
$p$-completeness and ![]() $V$-completeness (Proposition 7.14), it suffices to prove the analogous statement for
$V$-completeness (Proposition 7.14), it suffices to prove the analogous statement for ![]() $R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O}(i)/p)$. Replacing
$R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), \mathcal {O}(i)/p)$. Replacing ![]() $R$ with
$R$ with ![]() $R[\zeta _p]$ and using
$R[\zeta _p]$ and using ![]() $(\mathbb {Z}/p)^{\times }$-Galois descent along this extension, we may assume that
$(\mathbb {Z}/p)^{\times }$-Galois descent along this extension, we may assume that ![]() $R$ contains a primitive
$R$ contains a primitive ![]() $p$th root of unity. This lets us reduce to the case
$p$th root of unity. This lets us reduce to the case ![]() $i = 0$, whence the result follows from Example 7.12.
$i = 0$, whence the result follows from Example 7.12.
We note, finally, that one can recover the ![]() $p$-adic nearby cycles (see Proposition 7.4) as the fixed points of Frobenius on Witt vector
$p$-adic nearby cycles (see Proposition 7.4) as the fixed points of Frobenius on Witt vector ![]() $\mathrm {arc}_{{p}}$-cohomology. This will not be used in the sequel.
$\mathrm {arc}_{{p}}$-cohomology. This will not be used in the sequel.
Proposition 7.16 For any ring ![]() $R$, there is a natural equivalence for each
$R$, there is a natural equivalence for each ![]() $i$,
$i$,
Proof. We have a natural map ![]() $\mathbb {Z}_p \to W(\mathcal {O})^{F=1}$ of presheaves. Twisting and sheafifying in the
$\mathbb {Z}_p \to W(\mathcal {O})^{F=1}$ of presheaves. Twisting and sheafifying in the ![]() $\mathrm {arc}_{{p}}$-topology, we obtain the map from left to right in (18). To see that it is an equivalence, it suffices to check that it is an equivalence on products (over some indexing set
$\mathrm {arc}_{{p}}$-topology, we obtain the map from left to right in (18). To see that it is an equivalence, it suffices to check that it is an equivalence on products (over some indexing set ![]() $T$) of rings of the form
$T$) of rings of the form ![]() $\mathcal {O}_C$, for
$\mathcal {O}_C$, for ![]() $C$ spherically complete and algebraically closed of mixed characteristic
$C$ spherically complete and algebraically closed of mixed characteristic ![]() $(0, p)$; now we can trivialize the Tate twists, so can assume
$(0, p)$; now we can trivialize the Tate twists, so can assume ![]() $i = 0$. Using Lemma 7.5, we find that the left-hand side is discrete and simply given by
$i = 0$. Using Lemma 7.5, we find that the left-hand side is discrete and simply given by ![]() $\prod _T \mathbb {Z}_p$. The right-hand side is also given by
$\prod _T \mathbb {Z}_p$. The right-hand side is also given by ![]() $\prod _T \mathbb {Z}_p$ by Lemma 7.17 below.
$\prod _T \mathbb {Z}_p$ by Lemma 7.17 below.
Lemma 7.17 Let ![]() $C$ be an algebraically closed complete nonarchimedean field. Then the natural map
$C$ be an algebraically closed complete nonarchimedean field. Then the natural map ![]() $\mathbb {Z}_p \to W(\mathcal {O}_C)^{F=1}$ is an equivalence.
$\mathbb {Z}_p \to W(\mathcal {O}_C)^{F=1}$ is an equivalence.
Proof. It suffices to work modulo ![]() $p$, that is, to show that the natural map
$p$, that is, to show that the natural map ![]() $\mathbb {F}_p \to (W(\mathcal {O}_C)/p)^{F = 1}$ is an equivalence. But the Witt vector Frobenius reduces modulo
$\mathbb {F}_p \to (W(\mathcal {O}_C)/p)^{F = 1}$ is an equivalence. But the Witt vector Frobenius reduces modulo ![]() $p$ to the ordinary Frobenius on the ring
$p$ to the ordinary Frobenius on the ring ![]() $W(\mathcal {O}_C)/p$. By the Artin–Schreier sequence,
$W(\mathcal {O}_C)/p$. By the Artin–Schreier sequence, ![]() $(W(\mathcal {O}_C)/p)^{F = 1}$ is the mod
$(W(\mathcal {O}_C)/p)^{F = 1}$ is the mod ![]() $p$ étale cohomology of
$p$ étale cohomology of ![]() $W(\mathcal {O}_C)/p$. This is unchanged by taking the quotient by the ideal
$W(\mathcal {O}_C)/p$. This is unchanged by taking the quotient by the ideal ![]() $V W(\mathcal {O}_C)/p$, which squares to zero; therefore, it is also the étale cohomology of
$V W(\mathcal {O}_C)/p$, which squares to zero; therefore, it is also the étale cohomology of ![]() $\mathcal {O}_C/p$, or equivalently of the residue field
$\mathcal {O}_C/p$, or equivalently of the residue field ![]() $k$; this in turn is
$k$; this in turn is ![]() $\mathbb {F}_p$ as
$\mathbb {F}_p$ as ![]() $C$ is algebraically closed and hence so is
$C$ is algebraically closed and hence so is ![]() $k$.
$k$.
7.2  $\mathrm {THH}^{C_{p^r}}$ of perfectoid rings
$\mathrm {THH}^{C_{p^r}}$ of perfectoid rings
Here we calculate the fixed points of ![]() $\mathrm {THH}$ of perfectoid rings, generalizing the main result of [Reference HesselholtHes06]; these results are known to experts. Recall that for any
$\mathrm {THH}$ of perfectoid rings, generalizing the main result of [Reference HesselholtHes06]; these results are known to experts. Recall that for any ![]() $p$-complete ring
$p$-complete ring ![]() $R$, we have
$R$, we have ![]() $\pi _0 \mathrm {TR}(R; \mathbb {Z}_p) \simeq W(R)$; see [Reference Hesselholt and MadsenHM97, Theorem F].
$\pi _0 \mathrm {TR}(R; \mathbb {Z}_p) \simeq W(R)$; see [Reference Hesselholt and MadsenHM97, Theorem F].
Our strategy is to treat the case of a ![]() $p$-torsion-free perfectoid ring by a direct spectral sequence argument and appeal to known results for a perfect
$p$-torsion-free perfectoid ring by a direct spectral sequence argument and appeal to known results for a perfect ![]() $\mathbb {F}_p$-algebra; we will glue both cases together using an excision argument. To begin with, we consider the characteristic
$\mathbb {F}_p$-algebra; we will glue both cases together using an excision argument. To begin with, we consider the characteristic ![]() $p$ case. For perfect fields, this result appears in [Reference Hesselholt and MadsenHM97, § 5].
$p$ case. For perfect fields, this result appears in [Reference Hesselholt and MadsenHM97, § 5].
Lemma 7.18 Let ![]() $R$ be a perfect
$R$ be a perfect ![]() $\mathbb {F}_p$-algebra. Then:
$\mathbb {F}_p$-algebra. Then:
(i)
 $\pi _*(\mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}}) \simeq W_{r+1}(R)[\sigma _r]$ for
$\pi _*(\mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}}) \simeq W_{r+1}(R)[\sigma _r]$ for  $|\sigma _r| = 2$;
$|\sigma _r| = 2$;(ii)
 $\mathrm {TR}(R; \mathbb {Z}_p) \simeq H W(R)$.
$\mathrm {TR}(R; \mathbb {Z}_p) \simeq H W(R)$.
Proof. The Segal conjecture holds for ![]() $R$: in fact,
$R$: in fact, ![]() $\varphi \colon \mathrm {THH}(R; \mathbb {Z}_p) \to \mathrm {THH}(R ; \mathbb {Z}_p)^{tC_p}$ is
$\varphi \colon \mathrm {THH}(R; \mathbb {Z}_p) \to \mathrm {THH}(R ; \mathbb {Z}_p)^{tC_p}$ is ![]() $(-3)$-truncated; see [Reference Bhatt, Morrow and ScholzeBMS19, § 6]. Therefore, we have that
$(-3)$-truncated; see [Reference Bhatt, Morrow and ScholzeBMS19, § 6]. Therefore, we have that ![]() $\mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}} \to \mathrm {THH}(R; \mathbb {Z}_p)^{hC_{p^r}} \xrightarrow {\varphi ^{hC_{p^r}}}\mathrm {THH}(R; \mathbb {Z}_p)^{tC_{p^{r+1}}}$ are equivalences on connective covers; see [Reference Nikolaus and ScholzeNS18, Corollary II.4.9]. Using the homotopy fixed point spectral sequence (or [Reference Bhatt, Morrow and ScholzeBMS19, § 6]), we find
$\mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}} \to \mathrm {THH}(R; \mathbb {Z}_p)^{hC_{p^r}} \xrightarrow {\varphi ^{hC_{p^r}}}\mathrm {THH}(R; \mathbb {Z}_p)^{tC_{p^{r+1}}}$ are equivalences on connective covers; see [Reference Nikolaus and ScholzeNS18, Corollary II.4.9]. Using the homotopy fixed point spectral sequence (or [Reference Bhatt, Morrow and ScholzeBMS19, § 6]), we find ![]() $\pi _*( \mathrm {THH}(R; \mathbb {Z}_p)^{tS^1}) \simeq W(R)[ \sigma ^{\pm 1}]$. Now
$\pi _*( \mathrm {THH}(R; \mathbb {Z}_p)^{tS^1}) \simeq W(R)[ \sigma ^{\pm 1}]$. Now ![]() $\mathrm {THH}(R; \mathbb {Z}_p)^{tC_{p^{r+1}}} \simeq \mathrm {THH}(R; \mathbb {Z}_p)^{tS^1}/p^{r+1}$ by [Reference Nikolaus and ScholzeNS18, Lemma IV.4.12]. Combining these facts, we see that claim (i) follows as
$\mathrm {THH}(R; \mathbb {Z}_p)^{tC_{p^{r+1}}} \simeq \mathrm {THH}(R; \mathbb {Z}_p)^{tS^1}/p^{r+1}$ by [Reference Nikolaus and ScholzeNS18, Lemma IV.4.12]. Combining these facts, we see that claim (i) follows as ![]() $W_{r+1}(R) = W(R)/p^{r+1}$.
$W_{r+1}(R) = W(R)/p^{r+1}$.
For claim (ii), note that ![]() $\mathrm {THH}(R; \mathbb {Z}_p)$ is a module in
$\mathrm {THH}(R; \mathbb {Z}_p)$ is a module in ![]() $\mathrm {CycSp}$ over
$\mathrm {CycSp}$ over ![]() $K(\mathbb {F}_p; \mathbb {Z}_p) \simeq H\mathbb {Z}_p$. By Proposition 5.7, we have that
$K(\mathbb {F}_p; \mathbb {Z}_p) \simeq H\mathbb {Z}_p$. By Proposition 5.7, we have that ![]() $\mathrm {TR}(R; \mathbb {Z}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {Z}_p)$ is
$\mathrm {TR}(R; \mathbb {Z}_p) \to L_{K(1)} \mathrm {TR}(R; \mathbb {Z}_p)$ is ![]() $0$-truncated; since the target vanishes, it follows that
$0$-truncated; since the target vanishes, it follows that ![]() $\mathrm {TR}(R; \mathbb {Z}_p)$ is
$\mathrm {TR}(R; \mathbb {Z}_p)$ is ![]() $0$-truncated, whence the result as we know
$0$-truncated, whence the result as we know ![]() $\pi _0\mathrm {TR}(R; \mathbb {Z}_p)$.
$\pi _0\mathrm {TR}(R; \mathbb {Z}_p)$.
In the following, we will say that an ![]() $E_\infty$-ring
$E_\infty$-ring ![]() $A$ is weakly even periodic if the odd homotopy groups of
$A$ is weakly even periodic if the odd homotopy groups of ![]() $A$ vanish, and if for all
$A$ vanish, and if for all ![]() $m, n \in \mathbb {Z}$, the map
$m, n \in \mathbb {Z}$, the map ![]() $\pi _{2m}(A) \otimes _{\pi _0(A)} \pi _{2n}(A) \to \pi _{2(n+m)}(A)$ is an isomorphism; in particular,
$\pi _{2m}(A) \otimes _{\pi _0(A)} \pi _{2n}(A) \to \pi _{2(n+m)}(A)$ is an isomorphism; in particular, ![]() $\pi _2(A)$ is an invertible
$\pi _2(A)$ is an invertible ![]() $\pi _0(A)$-module, and Zariski locally
$\pi _0(A)$-module, and Zariski locally ![]() $\pi _*(A)$ is a Laurent polynomial algebra over
$\pi _*(A)$ is a Laurent polynomial algebra over ![]() $\pi _0(A)$ on a degree
$\pi _0(A)$ on a degree ![]() $2$ class.
$2$ class.
Lemma 7.19 Let ![]() $A, B, C$ be weakly even periodic
$A, B, C$ be weakly even periodic ![]() $E_\infty$-rings and fix maps
$E_\infty$-rings and fix maps ![]() $A\to C, B \to C$ such that
$A\to C, B \to C$ such that ![]() $\pi _0(A) \to \pi _0(C)$ is surjective. Then
$\pi _0(A) \to \pi _0(C)$ is surjective. Then ![]() $A \times _C B$ is weakly even periodic.
$A \times _C B$ is weakly even periodic.
Proof. It follows that ![]() $\pi _*(A) \otimes _{\pi _0(A)} \pi _0(C) \xrightarrow {\sim } \pi _*(C)$ and, similarly,
$\pi _*(A) \otimes _{\pi _0(A)} \pi _0(C) \xrightarrow {\sim } \pi _*(C)$ and, similarly, ![]() $\pi _*(A) \otimes _{\pi _0(A)} \pi _0(B) \xrightarrow {\sim } \pi _*(B)$. Now since
$\pi _*(A) \otimes _{\pi _0(A)} \pi _0(B) \xrightarrow {\sim } \pi _*(B)$. Now since ![]() $\pi _0(A \times _C B), \pi _0(A), \pi _0(B), \pi _0(C)$ form a Milnor square, the category of finitely generated projective
$\pi _0(A \times _C B), \pi _0(A), \pi _0(B), \pi _0(C)$ form a Milnor square, the category of finitely generated projective ![]() $\pi _0(A \times _C B)$-modules is the homotopy pullback of the categories of finitely generated projective
$\pi _0(A \times _C B)$-modules is the homotopy pullback of the categories of finitely generated projective ![]() $\pi _0(A)$-modules,
$\pi _0(A)$-modules, ![]() $\pi _0(B)$-modules, and
$\pi _0(B)$-modules, and ![]() $\pi _0(C)$-modules; see [Reference MilnorMil71, § 2]. The result now follows.
$\pi _0(C)$-modules; see [Reference MilnorMil71, § 2]. The result now follows.
Construction 7.20 (![]() $p$-torsion-free quotients of perfectoid rings)
$p$-torsion-free quotients of perfectoid rings)
Let ![]() $R$ be a perfectoid ring, and let
$R$ be a perfectoid ring, and let ![]() $I \subset R$ be the ideal of
$I \subset R$ be the ideal of ![]() $p$-power torsion. Then
$p$-power torsion. Then ![]() $p I = 0$; see [Reference Bhatt, Morrow and ScholzeBMS19, Proposition 4.19].
$p I = 0$; see [Reference Bhatt, Morrow and ScholzeBMS19, Proposition 4.19].
We have in fact that ![]() $R/I$ is perfectoid as well. To see this, we use the theory of perfectoidizations [Reference Bhatt and ScholzeBS19, §§ 7 and 8]. Let
$R/I$ is perfectoid as well. To see this, we use the theory of perfectoidizations [Reference Bhatt and ScholzeBS19, §§ 7 and 8]. Let ![]() $R' = (R/p)_{\mathrm {perf}}$. For every
$R' = (R/p)_{\mathrm {perf}}$. For every ![]() $p$-complete valuation ring
$p$-complete valuation ring ![]() $V$ with a map
$V$ with a map ![]() $R \to V$ which does not annihilate
$R \to V$ which does not annihilate ![]() $I \subset R$, we find that
$I \subset R$, we find that ![]() $V$ has characteristic
$V$ has characteristic ![]() $p$ and we obtain a unique extension
$p$ and we obtain a unique extension ![]() $R' \to V$. Therefore, applying [Reference Bhatt and ScholzeBS19, Corollary 8.11], we obtain a pullback square of perfectoid rings
$R' \to V$. Therefore, applying [Reference Bhatt and ScholzeBS19, Corollary 8.11], we obtain a pullback square of perfectoid rings

Since the vertical arrows are surjective (see [Reference Bhatt and ScholzeBS19, Theorem 7.4]), this is a Milnor square of rings. Since the terms on the right-hand side are both ![]() $\mathbb {F}_p$-algebras, it follows that the kernel of
$\mathbb {F}_p$-algebras, it follows that the kernel of ![]() $R \to (R/I)_{\mathrm {perfd}}$ is annihilated by
$R \to (R/I)_{\mathrm {perfd}}$ is annihilated by ![]() $p$; since it contains
$p$; since it contains ![]() $I$, it must be equal to
$I$, it must be equal to ![]() $I$ and we have
$I$ and we have ![]() $(R/I)_{\mathrm {perfd}} = R/I$.
$(R/I)_{\mathrm {perfd}} = R/I$.
In particular, this shows that any perfectoid ring naturally fits into a Milnor square involving a ![]() $p$-torsion-free perfectoid ring and a map of perfect
$p$-torsion-free perfectoid ring and a map of perfect ![]() $\mathbb {F}_p$-algebras. The diagram (19) is in addition a homotopy pushout square of
$\mathbb {F}_p$-algebras. The diagram (19) is in addition a homotopy pushout square of ![]() $E_\infty$-rings, that is, there are no higher
$E_\infty$-rings, that is, there are no higher ![]() $\mathrm {Tor}$ terms, since everything involved is perfectoid. It follows by [Reference Land and TammeLT19] that (19) induces a pullback after applying any localizing invariant.
$\mathrm {Tor}$ terms, since everything involved is perfectoid. It follows by [Reference Land and TammeLT19] that (19) induces a pullback after applying any localizing invariant.
Proposition 7.21 Let ![]() $R$ be a perfectoid ring. Then, for each
$R$ be a perfectoid ring. Then, for each ![]() $r \geq 1$, we have the following assertions.
$r \geq 1$, we have the following assertions.
(i)
 $\pi _{*} \mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}}$ is concentrated in even degrees.
$\pi _{*} \mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}}$ is concentrated in even degrees.(ii)
 $\pi _{2} \mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}}$ is an invertible module over
$\pi _{2} \mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}}$ is an invertible module over  $\pi _0 \mathrm {THH} (R; \mathbb {Z}_p)^{C_{p^r}} \simeq W_{r+1}(R)$.
$\pi _0 \mathrm {THH} (R; \mathbb {Z}_p)^{C_{p^r}} \simeq W_{r+1}(R)$.(iii) The multiplication map
 $\mathrm {Sym}^t (\pi _{2} \mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}}) \to \pi _{2t}\mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}}$ is an isomorphism for all
$\mathrm {Sym}^t (\pi _{2} \mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}}) \to \pi _{2t}\mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}}$ is an isomorphism for all  $t \geq 0$.
$t \geq 0$.
Proof. Recall [Reference Bhatt, Morrow and ScholzeBMS19, § 6] that we have a noncanonical isomorphism ![]() $\pi _* \mathrm {THH}(R; \mathbb {Z}_p)^{tC_p} \simeq R[\sigma ^{\pm 1}]$ and that
$\pi _* \mathrm {THH}(R; \mathbb {Z}_p)^{tC_p} \simeq R[\sigma ^{\pm 1}]$ and that ![]() $\varphi \colon \mathrm {THH}(R; \mathbb {Z}_p) \to \mathrm {THH}(R; \mathbb {Z}_p)^{tC_p}$ exhibits the source as the connective cover of the target. Therefore, we have that
$\varphi \colon \mathrm {THH}(R; \mathbb {Z}_p) \to \mathrm {THH}(R; \mathbb {Z}_p)^{tC_p}$ exhibits the source as the connective cover of the target. Therefore, we have that ![]() $\mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}} \to \mathrm {THH}(R; \mathbb {Z}_p)^{hC_{p^r}} \xrightarrow {\varphi ^{hC_{p^r}}}\mathrm {THH}(R; \mathbb {Z}_p)^{tC_{p^{r+1}}}$ are equivalences on connective covers; see [Reference Nikolaus and ScholzeNS18, Corollary II.4.9].
$\mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}} \to \mathrm {THH}(R; \mathbb {Z}_p)^{hC_{p^r}} \xrightarrow {\varphi ^{hC_{p^r}}}\mathrm {THH}(R; \mathbb {Z}_p)^{tC_{p^{r+1}}}$ are equivalences on connective covers; see [Reference Nikolaus and ScholzeNS18, Corollary II.4.9].
Our next claim is that ![]() $\mathrm {THH}(R; \mathbb {Z}_p)^{tC_{p^{r+1}}}$ is a weakly even periodic
$\mathrm {THH}(R; \mathbb {Z}_p)^{tC_{p^{r+1}}}$ is a weakly even periodic ![]() $E_\infty$-ring for any
$E_\infty$-ring for any ![]() $r \geq 0$. If
$r \geq 0$. If ![]() $R$ is
$R$ is ![]() $p$-torsion-free, this follows from the (degenerate) Tate spectral sequence applied to
$p$-torsion-free, this follows from the (degenerate) Tate spectral sequence applied to ![]() $\mathrm {THH}(R; \mathbb {Z}_p)$, whose homotopy groups form a polynomial algebra over
$\mathrm {THH}(R; \mathbb {Z}_p)$, whose homotopy groups form a polynomial algebra over ![]() $R$ on a class in degree
$R$ on a class in degree ![]() $2$. If
$2$. If ![]() $R$ is an
$R$ is an ![]() $\mathbb {F}_p$-algebra, the claim also follows from Lemma 7.18. We now treat the case of a general perfectoid
$\mathbb {F}_p$-algebra, the claim also follows from Lemma 7.18. We now treat the case of a general perfectoid ![]() $R$. In view of the Milnor square (19) which is also a homotopy pushout of
$R$. In view of the Milnor square (19) which is also a homotopy pushout of ![]() $E_\infty$-rings and the main result of [Reference Land and TammeLT19], we find that
$E_\infty$-rings and the main result of [Reference Land and TammeLT19], we find that ![]() $\mathrm {THH}(-; \mathbb {Z}_p)^{tC_{p^{r+1}}}$ carries (19) to a pullback of
$\mathrm {THH}(-; \mathbb {Z}_p)^{tC_{p^{r+1}}}$ carries (19) to a pullback of ![]() $E_\infty$-ring spectra. Moreover, on
$E_\infty$-ring spectra. Moreover, on ![]() $\pi _0(-)$ this square yields a Milnor square since
$\pi _0(-)$ this square yields a Milnor square since ![]() $\pi _0 \mathrm {THH}(-; \mathbb {Z}_p)^{tC_{p^{r+1}}} \simeq W_{r+1}(-)$ for perfectoids via the previous paragraph and [Reference Hesselholt and MadsenHM97, Theorem F]. Via Lemma 7.19, the claim of weak even periodicity follows.
$\pi _0 \mathrm {THH}(-; \mathbb {Z}_p)^{tC_{p^{r+1}}} \simeq W_{r+1}(-)$ for perfectoids via the previous paragraph and [Reference Hesselholt and MadsenHM97, Theorem F]. Via Lemma 7.19, the claim of weak even periodicity follows.
Now the above paragraphs show that ![]() $\mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}}$ is the connective cover of a weakly even periodic
$\mathrm {THH}(R; \mathbb {Z}_p)^{C_{p^r}}$ is the connective cover of a weakly even periodic ![]() $E_\infty$-ring, and we already know its
$E_\infty$-ring, and we already know its ![]() $\pi _0$ is given by
$\pi _0$ is given by ![]() $W_{r+1}(R)$, whence the result.
$W_{r+1}(R)$, whence the result.
7.3 Description of  $\mathrm {TR}$ of perfectoids
$\mathrm {TR}$ of perfectoids
Let ![]() $C$ be spherically complete and algebraically closed of mixed characteristic
$C$ be spherically complete and algebraically closed of mixed characteristic ![]() $(0, p)$. Then we recall some of the additional rings attached to
$(0, p)$. Then we recall some of the additional rings attached to ![]() $C$. We have the tilt
$C$. We have the tilt ![]() ${C}^{\flat }$, the ring of integers
${C}^{\flat }$, the ring of integers ![]() $\mathcal {O}_{C^{\flat }} \subset C^{\flat }$, and the Fontaine ring
$\mathcal {O}_{C^{\flat }} \subset C^{\flat }$, and the Fontaine ring ![]() $A_{\inf } = A_{\inf }(\mathcal {O}_C) = W(\mathcal {O}_{C^{\flat }})$. Choosing a compatible system
$A_{\inf } = A_{\inf }(\mathcal {O}_C) = W(\mathcal {O}_{C^{\flat }})$. Choosing a compatible system ![]() $(1, \zeta _p, \zeta _{p^2}, \ldots )$ of primitive
$(1, \zeta _p, \zeta _{p^2}, \ldots )$ of primitive ![]() $p^n$th roots in
$p^n$th roots in ![]() $C$, we obtain an element
$C$, we obtain an element ![]() $\epsilon \in \mathcal {O}_{C^{\flat }}$ and let
$\epsilon \in \mathcal {O}_{C^{\flat }}$ and let ![]() $[\epsilon ]$ denote the corresponding element of
$[\epsilon ]$ denote the corresponding element of ![]() $A_{\inf }$. We have the map
$A_{\inf }$. We have the map ![]() $\theta \colon A_{\inf } \to \mathcal {O}_C$, which exhibits the source as the universal
$\theta \colon A_{\inf } \to \mathcal {O}_C$, which exhibits the source as the universal ![]() $p$-adically pro-nilpotent thickening of the latter; in particular, this leads to a map
$p$-adically pro-nilpotent thickening of the latter; in particular, this leads to a map ![]() $A_{\inf } \to W(\mathcal {O}_C)$, which is a surjection in this case [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 3.23].
$A_{\inf } \to W(\mathcal {O}_C)$, which is a surjection in this case [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 3.23].
Lemma 7.22 (![]() $\mathrm {TR}$ in the spherically complete case)
$\mathrm {TR}$ in the spherically complete case)
Let ![]() $C$ be a spherically complete, algebraically closed nonarchimedean field of mixed characteristic
$C$ be a spherically complete, algebraically closed nonarchimedean field of mixed characteristic ![]() $(0, p)$ and let
$(0, p)$ and let ![]() $\mathcal {O}_C \subset C$ be the ring of integers. Let
$\mathcal {O}_C \subset C$ be the ring of integers. Let ![]() $\beta \in \pi _2 \mathrm {TR}(\mathcal {O}_C; \mathbb {Z}_p)$ be the Bott element (arising from the image of the cyclotomic trace). Then
$\beta \in \pi _2 \mathrm {TR}(\mathcal {O}_C; \mathbb {Z}_p)$ be the Bott element (arising from the image of the cyclotomic trace). Then ![]() $\mathrm {TR}_*(\mathcal {O}_C; \mathbb {Z}_p) \simeq W(\mathcal {O}_C)[\beta ]$.
$\mathrm {TR}_*(\mathcal {O}_C; \mathbb {Z}_p) \simeq W(\mathcal {O}_C)[\beta ]$.
Proof. Since everything is ![]() $p$-complete, it suffices to see that
$p$-complete, it suffices to see that ![]() $\mathrm {TR}(\mathcal {O}_C; \mathbb {F}_p)/\beta$ is
$\mathrm {TR}(\mathcal {O}_C; \mathbb {F}_p)/\beta$ is ![]() $0$-truncated. Now for each
$0$-truncated. Now for each ![]() $n$, each homotopy group in
$n$, each homotopy group in ![]() $\pi _*(\mathrm {THH}^{C_{p^n}}(\mathcal {O}_C; \mathbb {F}_p))$ is a cyclic module over
$\pi _*(\mathrm {THH}^{C_{p^n}}(\mathcal {O}_C; \mathbb {F}_p))$ is a cyclic module over ![]() $W(\mathcal {O}_C)/p$ (Proposition 7.21), which in turn is a quotient of
$W(\mathcal {O}_C)/p$ (Proposition 7.21), which in turn is a quotient of ![]() $A_{\inf }(\mathcal {O}_C)/p = \mathcal {O}_{C^{\flat }}$. Moreover, the homotopy groups are concentrated in even degrees.
$A_{\inf }(\mathcal {O}_C)/p = \mathcal {O}_{C^{\flat }}$. Moreover, the homotopy groups are concentrated in even degrees.
Now ![]() $C^{\flat }$ is spherically complete; see the proof of [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 3.23]. Using the previous paragraph, Lemma 7.9, and the Milnor exact sequence, it follows that
$C^{\flat }$ is spherically complete; see the proof of [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 3.23]. Using the previous paragraph, Lemma 7.9, and the Milnor exact sequence, it follows that ![]() $\pi _*( \mathrm {TR}( \mathcal {O}_C; \mathbb {F}_p))$ is concentrated in even degrees. By Lemma 5.8 and Proposition 5.10, we also find that the cofiber of
$\pi _*( \mathrm {TR}( \mathcal {O}_C; \mathbb {F}_p))$ is concentrated in even degrees. By Lemma 5.8 and Proposition 5.10, we also find that the cofiber of ![]() $\beta$ is
$\beta$ is ![]() $2$-truncated, so
$2$-truncated, so ![]() $\pi _*( \mathrm {TR}( \mathcal {O}_C; \mathbb {F}_p)/\beta )$ is concentrated in degrees
$\pi _*( \mathrm {TR}( \mathcal {O}_C; \mathbb {F}_p)/\beta )$ is concentrated in degrees ![]() $0$ and
$0$ and ![]() $2$, and is given by
$2$, and is given by ![]() $W(\mathcal {O}_C)/p$ in degree
$W(\mathcal {O}_C)/p$ in degree ![]() $0$. It thus suffices to show that the zeroth Postnikov section
$0$. It thus suffices to show that the zeroth Postnikov section ![]() $\mathrm {TR}(\mathcal {O}_C; \mathbb {Z}_p)/\beta \to H W(\mathcal {O}_C)$ induces an isomorphism on
$\mathrm {TR}(\mathcal {O}_C; \mathbb {Z}_p)/\beta \to H W(\mathcal {O}_C)$ induces an isomorphism on ![]() $\pi _0 (-)^{tS^1}$. But we have by [Reference Antieau and NikolausAN21, Corollary 10] that
$\pi _0 (-)^{tS^1}$. But we have by [Reference Antieau and NikolausAN21, Corollary 10] that ![]() $\mathrm {TR}(\mathcal {O}_C; \mathbb {Z}_p)^{tS^1} = \mathrm {THH}(\mathcal {O}_C; \mathbb {Z}_p)^{tS^1}$, and on homotopy groups this is
$\mathrm {TR}(\mathcal {O}_C; \mathbb {Z}_p)^{tS^1} = \mathrm {THH}(\mathcal {O}_C; \mathbb {Z}_p)^{tS^1}$, and on homotopy groups this is ![]() $A_{\inf }[\sigma ^{\pm 1}]$ (see [Reference Bhatt, Morrow and ScholzeBMS19, § 6]). Moreover, with respect to the above identifications, we have that
$A_{\inf }[\sigma ^{\pm 1}]$ (see [Reference Bhatt, Morrow and ScholzeBMS19, § 6]). Moreover, with respect to the above identifications, we have that ![]() $\beta$ is a
$\beta$ is a ![]() $\mathbb {Z}_p^{\times }$-multiple of
$\mathbb {Z}_p^{\times }$-multiple of ![]() $( [\epsilon ] -1 )\sigma$; see [Reference Hesselholt and NikolausHN19, Theorem 1.3.6]. Therefore, we have
$( [\epsilon ] -1 )\sigma$; see [Reference Hesselholt and NikolausHN19, Theorem 1.3.6]. Therefore, we have ![]() $\pi _0 ( \mathrm {TR}(\mathcal {O}_C; \mathbb {Z}_p)/\beta )^{tS^1} \simeq A_{\inf }/( [\epsilon ] - 1) [\sigma ^{\pm 1}]$, whence the result since
$\pi _0 ( \mathrm {TR}(\mathcal {O}_C; \mathbb {Z}_p)/\beta )^{tS^1} \simeq A_{\inf }/( [\epsilon ] - 1) [\sigma ^{\pm 1}]$, whence the result since ![]() $A_{\inf }/( [\epsilon ] -1 ) \xrightarrow {\sim } W(\mathcal {O}_C)$ by [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 3.23].
$A_{\inf }/( [\epsilon ] -1 ) \xrightarrow {\sim } W(\mathcal {O}_C)$ by [Reference Bhatt, Morrow and ScholzeBMS18, Lemma 3.23].
Proposition 7.23 (![]() $\mathrm {TR}$ of perfectoid rings)
$\mathrm {TR}$ of perfectoid rings)
For ![]() $R \in \mathrm {Perfd}$ and for
$R \in \mathrm {Perfd}$ and for ![]() $i > 0$, we have natural equivalences
$i > 0$, we have natural equivalences
For ![]() $R \in \mathrm {Perfd}$ we have, for
$R \in \mathrm {Perfd}$ we have, for ![]() $i \in \mathbb {Z}$,
$i \in \mathbb {Z}$,
Proof. The structure presheaf on ![]() $\mathrm {Perfd}$ defines an
$\mathrm {Perfd}$ defines an ![]() $\mathrm {arc}_{\hat {p}}$-sheaf [Reference Bhatt and ScholzeBS19, Proposition 8.9]. Taking the inverse limit in Proposition 7.21 over the restriction maps (and accounting for possible
$\mathrm {arc}_{\hat {p}}$-sheaf [Reference Bhatt and ScholzeBS19, Proposition 8.9]. Taking the inverse limit in Proposition 7.21 over the restriction maps (and accounting for possible ![]() $\lim ^1$ terms), we find in particular that
$\lim ^1$ terms), we find in particular that ![]() $R \mapsto \tau _{[2i-1, 2i]} \mathrm {TR}(R; \mathbb {Z}_p)$ defines an
$R \mapsto \tau _{[2i-1, 2i]} \mathrm {TR}(R; \mathbb {Z}_p)$ defines an ![]() $\mathrm {arc}_{\hat {p}}$-sheaf of spectra on
$\mathrm {arc}_{\hat {p}}$-sheaf of spectra on ![]() $\mathrm {Perfd}$. Since, for
$\mathrm {Perfd}$. Since, for ![]() $i > 0$, this functor annihilates perfect
$i > 0$, this functor annihilates perfect ![]() $\mathbb {F}_p$-algebras, it in fact defines an
$\mathbb {F}_p$-algebras, it in fact defines an ![]() $\mathrm {arc}_{{p}}$-sheaf on
$\mathrm {arc}_{{p}}$-sheaf on ![]() $\mathrm {Perfd}$.
$\mathrm {Perfd}$.
The cyclotomic trace gives a map of ![]() $\mathbb {Z}_p$-modules
$\mathbb {Z}_p$-modules ![]() $T_p( R^{\times }) \to \pi _2 \mathrm {TR}(R; \mathbb {Z}_p)$. Since
$T_p( R^{\times }) \to \pi _2 \mathrm {TR}(R; \mathbb {Z}_p)$. Since ![]() $\pi _0( \mathrm {TR}(R; \mathbb {Z}_p) ) \simeq W(R)$, we obtain natural maps
$\pi _0( \mathrm {TR}(R; \mathbb {Z}_p) ) \simeq W(R)$, we obtain natural maps ![]() $f_i \colon W(R) (i)\to \pi _{2i}( \mathrm {TR}(R; \mathbb {Z}_p))$ for
$f_i \colon W(R) (i)\to \pi _{2i}( \mathrm {TR}(R; \mathbb {Z}_p))$ for ![]() $i > 0$. To complete the proof, it suffices to show that:
$i > 0$. To complete the proof, it suffices to show that:
(a)
 $f_i$ is an isomorphism for a cofinal (in the
$f_i$ is an isomorphism for a cofinal (in the  $\mathrm {arc}_{{p}}$-topology) collection of
$\mathrm {arc}_{{p}}$-topology) collection of  $R \in \mathrm {Perfd}$;
$R \in \mathrm {Perfd}$;(b)
 $\pi _{2i-1}( \mathrm {TR}(R; \mathbb {Z}_p)) =0$ for a cofinal (in the
$\pi _{2i-1}( \mathrm {TR}(R; \mathbb {Z}_p)) =0$ for a cofinal (in the  $\mathrm {arc}_{{p}}$-topology) collection of
$\mathrm {arc}_{{p}}$-topology) collection of  $R \in \mathrm {Perfd}$.
$R \in \mathrm {Perfd}$.
We will take this collection to be the set of products of perfectoid rings of the form ![]() $\mathcal {O}_C$, for
$\mathcal {O}_C$, for ![]() $C$ a spherically complete and algebraically closed nonarchimedean field of mixed characteristic
$C$ a spherically complete and algebraically closed nonarchimedean field of mixed characteristic ![]() $(0, p)$. First, Proposition 7.21 shows that the construction
$(0, p)$. First, Proposition 7.21 shows that the construction ![]() $R \mapsto \mathrm {THH}(R; \mathbb {Z}_p)$ commutes with products for
$R \mapsto \mathrm {THH}(R; \mathbb {Z}_p)$ commutes with products for ![]() $R \in \mathrm {Perfd}$; inductively and taking the limit, we find that
$R \in \mathrm {Perfd}$; inductively and taking the limit, we find that ![]() $R \mapsto \mathrm {TR}(R; \mathbb {Z}_p)$ commutes with products for
$R \mapsto \mathrm {TR}(R; \mathbb {Z}_p)$ commutes with products for ![]() $R \in \mathrm {Perfd}$. Thus, it suffices to verify the above claims for
$R \in \mathrm {Perfd}$. Thus, it suffices to verify the above claims for ![]() $R = \mathcal {O}_C$ itself, and that follows from Lemma 7.22.
$R = \mathcal {O}_C$ itself, and that follows from Lemma 7.22.
For the claim about ![]() $L_{K(1)} \mathrm {TR}(R; \mathbb {Z}_p)$, note first that the first part of the proof and Proposition 5.10 (and (19) to reduce to the
$L_{K(1)} \mathrm {TR}(R; \mathbb {Z}_p)$, note first that the first part of the proof and Proposition 5.10 (and (19) to reduce to the ![]() $p$-torsion-free case) show easily that
$p$-torsion-free case) show easily that ![]() $R \mapsto L_{K(1)} \mathrm {TR}(R; \mathbb {Z}_p)$ defines an
$R \mapsto L_{K(1)} \mathrm {TR}(R; \mathbb {Z}_p)$ defines an ![]() $\mathrm {arc}_{{p}}$-sheaf on
$\mathrm {arc}_{{p}}$-sheaf on ![]() $\mathrm {Perfd}$ (see also the remarks at the beginning of the proof of Proposition 5.10, concerning when
$\mathrm {Perfd}$ (see also the remarks at the beginning of the proof of Proposition 5.10, concerning when ![]() $L_{K(1)}(-)$ commutes with homotopy limits). It then follows from the above (by inverting the Bott element over perfectoid rings containing
$L_{K(1)}(-)$ commutes with homotopy limits). It then follows from the above (by inverting the Bott element over perfectoid rings containing ![]() $p$-power roots of unity) that the homotopy groups of the
$p$-power roots of unity) that the homotopy groups of the ![]() $\mathrm {arc}_{{p}}$-sheaf
$\mathrm {arc}_{{p}}$-sheaf ![]() $L_{K(1)} \mathrm {TR}(R; \mathbb {Z}_p)$ on
$L_{K(1)} \mathrm {TR}(R; \mathbb {Z}_p)$ on ![]() $\mathrm {Perfd}$ are given by
$\mathrm {Perfd}$ are given by ![]() $\pi _{2i} \simeq W(\mathcal {O})(i)$, and we obtain a filtration with associated graded terms the right-hand side of (21) via the Postnikov filtration as
$\pi _{2i} \simeq W(\mathcal {O})(i)$, and we obtain a filtration with associated graded terms the right-hand side of (21) via the Postnikov filtration as ![]() $\mathrm {arc}_{{p}}$-sheaves. Note that the Postnikov filtration is always exhaustive, and it is complete because it is complete on the
$\mathrm {arc}_{{p}}$-sheaves. Note that the Postnikov filtration is always exhaustive, and it is complete because it is complete on the ![]() $\mathrm {arc}_{{p}}$-sheaf
$\mathrm {arc}_{{p}}$-sheaf ![]() $R \mapsto \tau _{\geq 1} L_{K(1)} \mathrm {TR}(R) \simeq \tau _{\geq 1} \mathrm {TR}(R; \mathbb {Z}_p)$. Since the relevant associated graded pieces are in homological degrees
$R \mapsto \tau _{\geq 1} L_{K(1)} \mathrm {TR}(R) \simeq \tau _{\geq 1} \mathrm {TR}(R; \mathbb {Z}_p)$. Since the relevant associated graded pieces are in homological degrees ![]() $[2i-1, 2i]$ by Corollary 7.15, the result follows.
$[2i-1, 2i]$ by Corollary 7.15, the result follows.
7.4 The main results
In this subsection we prove Theorem 1.8 from the introduction. Our strategy is to compare ![]() $L_{K(1)} \mathrm {TR}(-)$ with its
$L_{K(1)} \mathrm {TR}(-)$ with its ![]() $\mathrm {arc}_{{p}}$-hypersheafification.
$\mathrm {arc}_{{p}}$-hypersheafification.
Construction 7.24 (The invariant ![]() $\big ( L_{K(1)} \mathrm {TR}(-) \big )^{\sharp }$)
$\big ( L_{K(1)} \mathrm {TR}(-) \big )^{\sharp }$)
We define the functor ![]() $(L_{K(1)} \mathrm {TR}(-))^{\sharp }$ on derived
$(L_{K(1)} \mathrm {TR}(-))^{\sharp }$ on derived ![]() $p$-complete rings as the
$p$-complete rings as the ![]() $\mathrm {arc}_{{p}}$-hypersheafification of the functor
$\mathrm {arc}_{{p}}$-hypersheafification of the functor ![]() $L_{K(1)} \mathrm {TR}(-)$ on derived
$L_{K(1)} \mathrm {TR}(-)$ on derived ![]() $p$-complete rings. We have a comparison map
$p$-complete rings. We have a comparison map
For a ring which is not necessarily derived ![]() $p$-complete, we define
$p$-complete, we define ![]() $( L_{K(1)} \mathrm {TR}(-) )^{\sharp }$ as that of its derived
$( L_{K(1)} \mathrm {TR}(-) )^{\sharp }$ as that of its derived ![]() $p$-completion.
$p$-completion.
To analyze this construction, we will use the results about ![]() $L_{K(1)} \mathrm {TR}$ of perfectoids proved in the previous section, as well as some general tools from the appendix. On
$L_{K(1)} \mathrm {TR}$ of perfectoids proved in the previous section, as well as some general tools from the appendix. On ![]() $\mathrm {Perfd}$, Proposition 7.23 implies that
$\mathrm {Perfd}$, Proposition 7.23 implies that ![]() $L_{K(1)} \mathrm {TR}(-)$ defines an
$L_{K(1)} \mathrm {TR}(-)$ defines an ![]() $\mathrm {arc}_{{p}}$-hypersheaf. Using Proposition A.6, it follows that the restriction of
$\mathrm {arc}_{{p}}$-hypersheaf. Using Proposition A.6, it follows that the restriction of ![]() $(L_{K(1)} \mathrm {TR}(-))^{\sharp }$ to
$(L_{K(1)} \mathrm {TR}(-))^{\sharp }$ to ![]() $\mathrm {Perfd}$ is just
$\mathrm {Perfd}$ is just ![]() $L_{K(1)} \mathrm {TR}(-)$ again, that is, (22) is an equivalence.Footnote 8
$L_{K(1)} \mathrm {TR}(-)$ again, that is, (22) is an equivalence.Footnote 8
Proposition 7.25 For any ring ![]() $R$, there is a natural, complete exhaustive
$R$, there is a natural, complete exhaustive ![]() $\mathbb {Z}_{}$-indexed filtration on
$\mathbb {Z}_{}$-indexed filtration on ![]() $( L_{K(1)} \mathrm {TR}(R))^{\sharp }$, denoted
$( L_{K(1)} \mathrm {TR}(R))^{\sharp }$, denoted ![]() $\mathrm {Fil}^{\geq \ast }( L_{K(1)} \mathrm {TR}(R))^{\sharp }$, with associated graded terms
$\mathrm {Fil}^{\geq \ast }( L_{K(1)} \mathrm {TR}(R))^{\sharp }$, with associated graded terms ![]() $\mathrm {gr}^i ( L_{K(1)} \mathrm {TR}(R))^{\sharp } \simeq R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O})(i))[2i]$.
$\mathrm {gr}^i ( L_{K(1)} \mathrm {TR}(R))^{\sharp } \simeq R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O})(i))[2i]$.
Proof. The filtration in question is the ![]() $\mathrm {arc}_{{p}}$-Postnikov filtration (on the derived
$\mathrm {arc}_{{p}}$-Postnikov filtration (on the derived ![]() $p$-completion of
$p$-completion of ![]() $R$). Note that Postnikov towers converge for hypercomplete
$R$). Note that Postnikov towers converge for hypercomplete ![]() $\mathrm {arc}_{{p}}$-sheaves (Proposition A.10). For the identification of the graded pieces (or equivalently, the sheafified homotopy groups), it suffices by descent (see Example A.9) to work with the subcategory
$\mathrm {arc}_{{p}}$-sheaves (Proposition A.10). For the identification of the graded pieces (or equivalently, the sheafified homotopy groups), it suffices by descent (see Example A.9) to work with the subcategory ![]() $\mathrm {Perfd}$, where the result follows from (21).
$\mathrm {Perfd}$, where the result follows from (21).
We do not know in general for which ![]() $R$ the comparison map (22) is an equivalence; for such
$R$ the comparison map (22) is an equivalence; for such ![]() $R$, one obtains a ‘motivic’ filtration on
$R$, one obtains a ‘motivic’ filtration on ![]() $L_{K(1)} \mathrm {TR}(R)$ with associated graded terms the
$L_{K(1)} \mathrm {TR}(R)$ with associated graded terms the ![]() $\mathrm {arc}_{{p}}$-cohomology complexes
$\mathrm {arc}_{{p}}$-cohomology complexes ![]() $R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O})(i))[2i]$. Here we will show that the comparison map is an equivalence in certain formally smooth cases, using the pro-Galois descent result (Theorem 6.8).
$R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O})(i))[2i]$. Here we will show that the comparison map is an equivalence in certain formally smooth cases, using the pro-Galois descent result (Theorem 6.8).
Theorem 7.26 Let ![]() $R_0$ be a
$R_0$ be a ![]() $p$-torsion-free perfectoid ring. Let
$p$-torsion-free perfectoid ring. Let ![]() $R$ be a formally smooth
$R$ be a formally smooth ![]() $p$-complete
$p$-complete ![]() $R_0$-algebra. Then
$R_0$-algebra. Then ![]() $L_{K(1)} \mathrm {TR}(R) \xrightarrow {\sim } (L_{K(1)} \mathrm {TR}(R))^{\sharp }$.
$L_{K(1)} \mathrm {TR}(R) \xrightarrow {\sim } (L_{K(1)} \mathrm {TR}(R))^{\sharp }$.
Proof. First, we reduce to the case where ![]() $R_0$ admits a compatible system of
$R_0$ admits a compatible system of ![]() $p$-power roots of unity. By André's lemma [Reference Bhatt and ScholzeBS19, Theorem 7.12], we know that there exists a
$p$-power roots of unity. By André's lemma [Reference Bhatt and ScholzeBS19, Theorem 7.12], we know that there exists a ![]() $p$-completely faithfully flat perfectoid
$p$-completely faithfully flat perfectoid ![]() $R_0$-algebra
$R_0$-algebra ![]() $R_0'$ which has this property (e.g. is absolutely integrally closed). Now we have by descent
$R_0'$ which has this property (e.g. is absolutely integrally closed). Now we have by descent
Since in high degrees all of the terms in the above totalization agree with their ![]() $K(1)$-localization by Proposition 5.10, it follows that the descent property (23) holds for
$K(1)$-localization by Proposition 5.10, it follows that the descent property (23) holds for ![]() $L_{K(1) } \mathrm {TR}(-)$ as well (see the beginning of the proof of Proposition 5.10). Moreover,
$L_{K(1) } \mathrm {TR}(-)$ as well (see the beginning of the proof of Proposition 5.10). Moreover, ![]() $(L_{K(1)} \mathrm {TR}(-))^{\sharp }$ satisfies descent for the map
$(L_{K(1)} \mathrm {TR}(-))^{\sharp }$ satisfies descent for the map ![]() $R \to R \otimes _{R_0} R_0'$ by construction. Therefore, we reduce to the case where
$R \to R \otimes _{R_0} R_0'$ by construction. Therefore, we reduce to the case where ![]() $R_0$ contains
$R_0$ contains ![]() $\widehat {\mathbb {Z}_p[\zeta _{p^\infty }]}$.
$\widehat {\mathbb {Z}_p[\zeta _{p^\infty }]}$.
Working locally on ![]() $\mathrm {Spf}(R)$, we can assume that
$\mathrm {Spf}(R)$, we can assume that ![]() $R$ receives a map from
$R$ receives a map from ![]() $R_0\langle t_1^{\pm 1}, \ldots , t_n^{\pm 1} \rangle$ which is étale mod
$R_0\langle t_1^{\pm 1}, \ldots , t_n^{\pm 1} \rangle$ which is étale mod ![]() $p$. We consider the extension
$p$. We consider the extension ![]() $R_\infty = R \otimes _{\mathbb {Z}[\zeta _{p^\infty }, t_1^{\pm 1}, \ldots , t_n^{\pm 1}]} \mathbb {Z}[\zeta _{p^\infty }, t_1^{\pm 1/p^\infty }, \ldots , t_n^{\pm 1/p^\infty }]$ and the evident
$R_\infty = R \otimes _{\mathbb {Z}[\zeta _{p^\infty }, t_1^{\pm 1}, \ldots , t_n^{\pm 1}]} \mathbb {Z}[\zeta _{p^\infty }, t_1^{\pm 1/p^\infty }, \ldots , t_n^{\pm 1/p^\infty }]$ and the evident ![]() $\mathbb {Z}_p(1)^n$-action on
$\mathbb {Z}_p(1)^n$-action on ![]() $R_\infty$. As in Example 6.10, we find from Theorem 6.8 that the natural map induces an equivalence
$R_\infty$. As in Example 6.10, we find from Theorem 6.8 that the natural map induces an equivalence
Now this is also true for ![]() $(L_{K(1)}\mathrm {TR}(-))^{\sharp }$, because the above augmented cosimplicial ring is an
$(L_{K(1)}\mathrm {TR}(-))^{\sharp }$, because the above augmented cosimplicial ring is an ![]() $\mathrm {arc}_{{p}}$-hypercover (strictly speaking, for that we replace all rings by their derived
$\mathrm {arc}_{{p}}$-hypercover (strictly speaking, for that we replace all rings by their derived ![]() $p$-completions). But now this gives
$p$-completions). But now this gives ![]() $L_{K(1)} \mathrm {TR}(R) \xrightarrow {\sim } (L_{K(1)}\mathrm {TR}(R))^{\sharp }$, since they agree on perfectoids and every term in the above cosimplicial resolution has perfectoid
$L_{K(1)} \mathrm {TR}(R) \xrightarrow {\sim } (L_{K(1)}\mathrm {TR}(R))^{\sharp }$, since they agree on perfectoids and every term in the above cosimplicial resolution has perfectoid ![]() $p$-completion.
$p$-completion.
Theorem 7.27 Suppose ![]() $R$ is a formally smooth
$R$ is a formally smooth ![]() $\mathcal {O}_K$-algebra, where
$\mathcal {O}_K$-algebra, where ![]() $K$ is a complete discretely valued field of mixed characteristic
$K$ is a complete discretely valued field of mixed characteristic ![]() $(0, p)$ whose residue field
$(0, p)$ whose residue field ![]() $k$ satisfies
$k$ satisfies ![]() $[k:k^p]< \infty$. Then
$[k:k^p]< \infty$. Then ![]() $L_{K(1)} \mathrm {TR}(R) \xrightarrow {\sim } ( L_{K(1)} \mathrm {TR}(R))^{\sharp }$.
$L_{K(1)} \mathrm {TR}(R) \xrightarrow {\sim } ( L_{K(1)} \mathrm {TR}(R))^{\sharp }$.
Proof. We let ![]() $G = \mathrm {Gal}(\bar {K}/K)$ and consider the
$G = \mathrm {Gal}(\bar {K}/K)$ and consider the ![]() $G$-action on
$G$-action on ![]() $S = R \otimes _{\mathcal {O}_K} \mathcal {O}_{\bar {K}}$. As in Example 6.9, our assumptions imply that
$S = R \otimes _{\mathcal {O}_K} \mathcal {O}_{\bar {K}}$. As in Example 6.9, our assumptions imply that ![]() $G$ has finite cohomological dimension and, moreover, that the map (13) is an equivalence. Therefore, it suffices to show that
$G$ has finite cohomological dimension and, moreover, that the map (13) is an equivalence. Therefore, it suffices to show that ![]() $L_{K(1)} \mathrm {TR}( A) \xrightarrow {\sim } (L_{K(1)} \mathrm {TR}( A))^{\sharp }$ when
$L_{K(1)} \mathrm {TR}( A) \xrightarrow {\sim } (L_{K(1)} \mathrm {TR}( A))^{\sharp }$ when ![]() $A$ is one of
$A$ is one of ![]() $S, \mathrm {Fun}_{\mathrm {cts}}(G, S), \ldots$. But these are all (up to
$S, \mathrm {Fun}_{\mathrm {cts}}(G, S), \ldots$. But these are all (up to ![]() $p$-completions) formally smooth over perfectoids, whence the claim by Theorem 7.26 and descent.
$p$-completions) formally smooth over perfectoids, whence the claim by Theorem 7.26 and descent.
Remark 7.28 Suppose ![]() $L_{K(1)} \mathrm {TR}(R) \xrightarrow {\sim } (L_{K(1)} \mathrm {TR}(R) )^{\sharp }$. On Frobenius fixed points, one recovers the Thomason [Reference ThomasonTho85, Reference Thomason and TrobaughTT90] filtration (i.e. the pro-étale Postnikov filtration) on
$L_{K(1)} \mathrm {TR}(R) \xrightarrow {\sim } (L_{K(1)} \mathrm {TR}(R) )^{\sharp }$. On Frobenius fixed points, one recovers the Thomason [Reference ThomasonTho85, Reference Thomason and TrobaughTT90] filtration (i.e. the pro-étale Postnikov filtration) on ![]() $L_{K(1)} \mathrm {TC}(R) \simeq L_{K(1)} K(R[1/p])$ (see [Reference Bhatt, Clausen and MathewBCM20] for this identification), whose associated graded terms are given by
$L_{K(1)} \mathrm {TC}(R) \simeq L_{K(1)} K(R[1/p])$ (see [Reference Bhatt, Clausen and MathewBCM20] for this identification), whose associated graded terms are given by ![]() $\mathrm {gr}^i \simeq R \Gamma _{\mathrm {pro\acute {e}t}}( \mathrm {Spec}(R[1/p]), \mathbb {Z}_p(i))[2i]$; see Proposition 7.16.
$\mathrm {gr}^i \simeq R \Gamma _{\mathrm {pro\acute {e}t}}( \mathrm {Spec}(R[1/p]), \mathbb {Z}_p(i))[2i]$; see Proposition 7.16.
Remark 7.29 The above filtration on ![]() $L_{K(1)} \mathrm {TR}(-)$ and the calculations of
$L_{K(1)} \mathrm {TR}(-)$ and the calculations of ![]() $\mathrm {TR}$ of smooth algebras over a DVR in [Reference Hesselholt and MadsenHM03, Reference Hesselholt and MadsenHM04, Reference Geisser and HesselholtGH06] suggest that the cohomology
$\mathrm {TR}$ of smooth algebras over a DVR in [Reference Hesselholt and MadsenHM03, Reference Hesselholt and MadsenHM04, Reference Geisser and HesselholtGH06] suggest that the cohomology ![]() $R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O})(i))$ should be related to the absolute de Rham–Witt complex. The work [Reference MorrowMor18] also suggests that for smooth algebras over a perfectoid base containing all
$R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O})(i))$ should be related to the absolute de Rham–Witt complex. The work [Reference MorrowMor18] also suggests that for smooth algebras over a perfectoid base containing all ![]() $p$-power roots of unity,
$p$-power roots of unity, ![]() $R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O}))$ should be related to the relative de Rham–Witt complex (over the perfectoid base).
$R \Gamma _{\mathrm {arc}_{{p}}}( \mathrm {Spec}(R), W(\mathcal {O}))$ should be related to the relative de Rham–Witt complex (over the perfectoid base).
Acknowledgements
I would like to thank B. Antieau, L. Hesselholt, M. Morrow, T. Nikolaus, W. Nizioł, and P. Scholze for many helpful conversations related to the subject of this paper. I would especially like to thank B. Bhatt and D. Clausen for their collaboration in [Reference Bhatt, Clausen and MathewBCM20] and many helpful discussions. Finally, I would like to thank B. Antieau, L. Meier, G. Tamme, and the referee for several comments and corrections on an earlier version.
Topological preliminaries
In this appendix, we record some basic topological preliminaries about (hyper)sheaves of spectra.
Remark A.1 (Conventions for sites) We will for simplicity work only with sites of the following nice form (see [Reference LurieLur18, § A.3.2]). Let ![]() $\mathcal {C}$ be a category with pullbacks and finite coproducts, such that coproducts distribute over pullbacks and are disjoint. Suppose
$\mathcal {C}$ be a category with pullbacks and finite coproducts, such that coproducts distribute over pullbacks and are disjoint. Suppose ![]() $\mathcal {C}$ is equipped with a class of morphisms
$\mathcal {C}$ is equipped with a class of morphisms ![]() $S = S_{\mathcal {C}}$ which contains all isomorphisms and is stable under composition and pullback. We equip
$S = S_{\mathcal {C}}$ which contains all isomorphisms and is stable under composition and pullback. We equip ![]() $\mathcal {C}$ with the Grothendieck topology where a collection
$\mathcal {C}$ with the Grothendieck topology where a collection ![]() $\{X_i \to X\}_{i \in I}$ is a covering if there exists a finite subset
$\{X_i \to X\}_{i \in I}$ is a covering if there exists a finite subset ![]() $I' \subset I$ such that
$I' \subset I$ such that ![]() ${\bigsqcup} _{i \in I'} X_i \to X$ can be refined by a map belonging to
${\bigsqcup} _{i \in I'} X_i \to X$ can be refined by a map belonging to ![]() $S$. In this case, a presheaf on
$S$. In this case, a presheaf on ![]() $\mathcal {C}$ with values in an
$\mathcal {C}$ with values in an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {D}$ with all small limits is a sheaf if and only if it carries finite coproducts in
$\mathcal {D}$ with all small limits is a sheaf if and only if it carries finite coproducts in ![]() $\mathcal {C}$ to finite products in
$\mathcal {C}$ to finite products in ![]() $\mathcal {D}$ and if it satisfies Čech descent for maps in
$\mathcal {D}$ and if it satisfies Čech descent for maps in ![]() $S$; see [Reference LurieLur18, § A.3.3].
$S$; see [Reference LurieLur18, § A.3.3].
Example A.2
(i) The small or big étale site of a qcqs scheme (where we only allow qcqs schemes) is an example, with
 $S$ the class of étale surjections.
$S$ the class of étale surjections.(ii) The
 $\mathrm {arc}_{{p}}$-topology or
$\mathrm {arc}_{{p}}$-topology or  $\mathrm {arc}_{\hat {p}}$-topology on the opposite of the category of derived
$\mathrm {arc}_{\hat {p}}$-topology on the opposite of the category of derived  $p$-complete rings is an example, with
$p$-complete rings is an example, with  $S$ the class of
$S$ the class of  $\mathrm{arc}_p$ or
$\mathrm{arc}_p$ or  $\mathrm{arc}_{\hat{p}}$-covers.
$\mathrm{arc}_{\hat{p}}$-covers.(iii) The
 $\mathrm {arc}_{{p}}$-topology or
$\mathrm {arc}_{{p}}$-topology or  $\mathrm {arc}_{\hat {p}}$-topology on the opposite of the category of perfectoid rings is an example, with
$\mathrm {arc}_{\hat {p}}$-topology on the opposite of the category of perfectoid rings is an example, with  $S$ the class of
$S$ the class of  $\mathrm{arc}_p$ or
$\mathrm{arc}_p$ or  $\mathrm{arc}_{\hat{p}}$-covers.
$\mathrm{arc}_{\hat{p}}$-covers.
Remark A.3 (Examples of continuous functors) Let ![]() $\mathcal {C}, \mathcal {C}'$ be sites as in Remark A.1. Let
$\mathcal {C}, \mathcal {C}'$ be sites as in Remark A.1. Let ![]() $u \colon \mathcal {C}' \to \mathcal {C}$ be a functor which preserves finite coproducts and pullbacks, as well as morphisms in the respective classes
$u \colon \mathcal {C}' \to \mathcal {C}$ be a functor which preserves finite coproducts and pullbacks, as well as morphisms in the respective classes ![]() $S_{\mathcal {C}}, S_{\mathcal {C}'}$. It follows that if
$S_{\mathcal {C}}, S_{\mathcal {C}'}$. It follows that if ![]() $\mathcal {F}$ is a sheaf (with values in any
$\mathcal {F}$ is a sheaf (with values in any ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {D}$ with all small limits) on
$\mathcal {D}$ with all small limits) on ![]() $\mathcal {C}$, then
$\mathcal {C}$, then ![]() $\mathcal {F} \circ u$ is a sheaf on
$\mathcal {F} \circ u$ is a sheaf on ![]() $\mathcal {C}'$. These are examples of continuous functors; the notion can be defined for more general sites; see [Reference Artin, Grothendieck and VerdierSGA4, Exp. III.1].
$\mathcal {C}'$. These are examples of continuous functors; the notion can be defined for more general sites; see [Reference Artin, Grothendieck and VerdierSGA4, Exp. III.1].
Construction A.4 (Sheaves of spectra) Given a site ![]() $\mathcal {C}$ (as in Remark A.1), we let
$\mathcal {C}$ (as in Remark A.1), we let ![]() $\mathrm {PSh}(\mathcal {C}, {\rm Sp} )$ denote the
$\mathrm {PSh}(\mathcal {C}, {\rm Sp} )$ denote the ![]() $\infty$-category of presheaves of spectra on
$\infty$-category of presheaves of spectra on ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $\mathrm {Shv}(\mathcal {C}, {\rm Sp} ) \subset \mathrm {PSh}(\mathcal {C}, {\rm Sp} )$ denote the subcategory of sheaves of spectra [Reference LurieLur18, § 1.3]. We equip these both with their canonical
$\mathrm {Shv}(\mathcal {C}, {\rm Sp} ) \subset \mathrm {PSh}(\mathcal {C}, {\rm Sp} )$ denote the subcategory of sheaves of spectra [Reference LurieLur18, § 1.3]. We equip these both with their canonical ![]() $t$-structures; see [Reference LurieLur18, § 1.3.2].
$t$-structures; see [Reference LurieLur18, § 1.3.2].
Given ![]() $u \colon \mathcal {C}' \to \mathcal {C}$ as in Remark A.3, we obtain a right adjoint and left
$u \colon \mathcal {C}' \to \mathcal {C}$ as in Remark A.3, we obtain a right adjoint and left ![]() $t$-exact functor
$t$-exact functor ![]() $(-) \circ u \colon \mathrm {Shv}(\mathcal {C}, {\rm Sp} ) \to \mathrm {Shv}(\mathcal {C}', {\rm Sp} )$. It has a left adjoint
$(-) \circ u \colon \mathrm {Shv}(\mathcal {C}, {\rm Sp} ) \to \mathrm {Shv}(\mathcal {C}', {\rm Sp} )$. It has a left adjoint ![]() $u_! \colon \mathrm {Shv}(\mathcal {C}', {\rm Sp} ) \to \mathrm {Shv}(\mathcal {C}, {\rm Sp} )$ given by left Kan extension along
$u_! \colon \mathrm {Shv}(\mathcal {C}', {\rm Sp} ) \to \mathrm {Shv}(\mathcal {C}, {\rm Sp} )$ given by left Kan extension along ![]() $u$ followed by sheafification. By adjunction, necessarily
$u$ followed by sheafification. By adjunction, necessarily ![]() $u_!$ is right
$u_!$ is right ![]() $t$-exact.
$t$-exact.
Construction A.5 (Hypersheaves of spectra) Let ![]() $\mathcal {C}$ be a site as in Remark A.1. Any presheaf
$\mathcal {C}$ be a site as in Remark A.1. Any presheaf ![]() $\mathcal {F}$ of spectra on
$\mathcal {F}$ of spectra on ![]() $\mathcal {C}$ fits into a unique fiber sequence of spectra
$\mathcal {C}$ fits into a unique fiber sequence of spectra
where ![]() $\mathcal {F}_{\mathrm {null}}$ has trivial sheafified homotopy groups and
$\mathcal {F}_{\mathrm {null}}$ has trivial sheafified homotopy groups and ![]() $\mathcal {F}^{\sharp }$ is a hypercomplete sheaf of spectra, that is, for every presheaf
$\mathcal {F}^{\sharp }$ is a hypercomplete sheaf of spectra, that is, for every presheaf ![]() $\mathcal {G}$ with trivial sheafified homotopy groups, we have
$\mathcal {G}$ with trivial sheafified homotopy groups, we have ![]() $\text{Hom} (\mathcal {G}, \mathcal {F}^{\sharp }) =0$. If
$\text{Hom} (\mathcal {G}, \mathcal {F}^{\sharp }) =0$. If ![]() $\mathcal {F}$ is a sheaf of spectra, then the cofiber sequence shows that
$\mathcal {F}$ is a sheaf of spectra, then the cofiber sequence shows that ![]() $\mathcal {F}_{\mathrm {null}}$ is also a sheaf of spectra; it is then
$\mathcal {F}_{\mathrm {null}}$ is also a sheaf of spectra; it is then ![]() $\infty$-connective with respect to the
$\infty$-connective with respect to the ![]() $t$-structure on
$t$-structure on ![]() $\mathrm {Shv}(\mathcal {C}, {\rm Sp} )$. We let
$\mathrm {Shv}(\mathcal {C}, {\rm Sp} )$. We let ![]() $\mathrm {Shv}_{\mathrm {hyp}}( \mathcal {C}, {\rm Sp} ) \subset \mathrm {Shv}(\mathcal {C}, {\rm Sp} )$ denote the full subcategory of hypercomplete sheaves. We refer to [Reference Clausen and MathewCM19, § 2] for an exposition of some of these constructions, which go back to [Reference JardineJar87, Reference Dugger, Hollander and IsaksenDHI04].
$\mathrm {Shv}_{\mathrm {hyp}}( \mathcal {C}, {\rm Sp} ) \subset \mathrm {Shv}(\mathcal {C}, {\rm Sp} )$ denote the full subcategory of hypercomplete sheaves. We refer to [Reference Clausen and MathewCM19, § 2] for an exposition of some of these constructions, which go back to [Reference JardineJar87, Reference Dugger, Hollander and IsaksenDHI04].
Proposition A.6 Let ![]() $u \colon \mathcal {C}' \to \mathcal {C}$ be a morphism of sites as in Remark A.1 preserving finite coproducts and pullbacks and carrying the class of arrows
$u \colon \mathcal {C}' \to \mathcal {C}$ be a morphism of sites as in Remark A.1 preserving finite coproducts and pullbacks and carrying the class of arrows ![]() $S_{\mathcal {C}'}$ into
$S_{\mathcal {C}'}$ into ![]() $S_{\mathcal {C}}$. Suppose that for any object
$S_{\mathcal {C}}$. Suppose that for any object ![]() $X' \in \mathcal {C}'$ and a finite covering family
$X' \in \mathcal {C}'$ and a finite covering family ![]() $\{ Y_i \to u(X')\}_{i \in I}$ in
$\{ Y_i \to u(X')\}_{i \in I}$ in ![]() $\mathcal {C}$, there is a refinement which is the image under
$\mathcal {C}$, there is a refinement which is the image under ![]() $u$ of a finite covering family
$u$ of a finite covering family ![]() $\{Y_i' \to X'\}_{i \in I}$ in
$\{Y_i' \to X'\}_{i \in I}$ in ![]() $\mathcal {C}'$.
$\mathcal {C}'$.
Then the restriction functor ![]() $(-) \circ u \colon \mathrm {PSh}(\mathcal {C}, {\rm Sp} ) \to \mathrm {PSh}(\mathcal {C}', {\rm Sp} )$ commutes with hypersheafification (and, in particular, preserves hypercomplete sheaves).
$(-) \circ u \colon \mathrm {PSh}(\mathcal {C}, {\rm Sp} ) \to \mathrm {PSh}(\mathcal {C}', {\rm Sp} )$ commutes with hypersheafification (and, in particular, preserves hypercomplete sheaves).
Proof. Using the cofiber sequence (A.1), we see that it suffices to prove that ![]() $(-) \circ u \colon \mathrm {Shv}( \mathcal {C}, {\rm Sp} ) \to \mathrm {Shv}(\mathcal {C}', {\rm Sp} )$ preserves both the subclasses of objects with trivial homotopy groups and hypercomplete objects.
$(-) \circ u \colon \mathrm {Shv}( \mathcal {C}, {\rm Sp} ) \to \mathrm {Shv}(\mathcal {C}', {\rm Sp} )$ preserves both the subclasses of objects with trivial homotopy groups and hypercomplete objects.
Our hypotheses imply that if a presheaf of abelian groups on ![]() $\mathcal {C}$ has trivial sheafification, then its pullback to
$\mathcal {C}$ has trivial sheafification, then its pullback to ![]() $\mathcal {C}'$ has trivial sheafification. Therefore,
$\mathcal {C}'$ has trivial sheafification. Therefore, ![]() $(-) \circ u$ preserves objects with trivial homotopy groups. It thus suffices to show that if
$(-) \circ u$ preserves objects with trivial homotopy groups. It thus suffices to show that if ![]() $\mathcal {F} \in \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}, {\rm Sp} )$, then the sheaf
$\mathcal {F} \in \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}, {\rm Sp} )$, then the sheaf ![]() $\mathcal {F} \circ u \in \mathrm {Shv}(\mathcal {C}', {\rm Sp} )$ is also hypercomplete; this will not use the assumption in the second sentence of the statement. Equivalently, given
$\mathcal {F} \circ u \in \mathrm {Shv}(\mathcal {C}', {\rm Sp} )$ is also hypercomplete; this will not use the assumption in the second sentence of the statement. Equivalently, given ![]() $\mathcal {G} \in \mathrm {Shv}(\mathcal {C}', {\rm Sp} )$ which is
$\mathcal {G} \in \mathrm {Shv}(\mathcal {C}', {\rm Sp} )$ which is ![]() $\infty$-connective, it suffices to show that
$\infty$-connective, it suffices to show that ![]() $\text{Hom} _{\mathrm {Shv}(\mathcal {C}', {\rm Sp} )}(\mathcal {G}, \mathcal {F} \circ u) =0$. By adjointness, this is
$\text{Hom} _{\mathrm {Shv}(\mathcal {C}', {\rm Sp} )}(\mathcal {G}, \mathcal {F} \circ u) =0$. By adjointness, this is ![]() $\text{Hom} _{\mathrm {Shv}(\mathcal {C}, {\rm Sp} )} ( u_! \mathcal {G}, \mathcal {F})$; since
$\text{Hom} _{\mathrm {Shv}(\mathcal {C}, {\rm Sp} )} ( u_! \mathcal {G}, \mathcal {F})$; since ![]() $u_! \colon \mathrm {Shv}(\mathcal {C}', {\rm Sp} ) \to \mathrm {Shv}(\mathcal {C}, {\rm Sp} )$ is right
$u_! \colon \mathrm {Shv}(\mathcal {C}', {\rm Sp} ) \to \mathrm {Shv}(\mathcal {C}, {\rm Sp} )$ is right ![]() $t$-exact and therefore preserves
$t$-exact and therefore preserves ![]() $\infty$-connective objects and
$\infty$-connective objects and ![]() $\mathcal {F}$ is hypercomplete, this is contractible.
$\mathcal {F}$ is hypercomplete, this is contractible.
Example A.7 (Overcategories) Suppose ![]() $a \in \mathcal {C}$ and
$a \in \mathcal {C}$ and ![]() $\mathcal {C}' = \mathcal {C}_{/a}$ is the overcategory of
$\mathcal {C}' = \mathcal {C}_{/a}$ is the overcategory of ![]() $a$, with the induced topology. Then the natural forgetful functor
$a$, with the induced topology. Then the natural forgetful functor ![]() $\mathcal {C}' \to \mathcal {C}$ clearly satisfies the conditions of Proposition A.6. In particular, the hypersheafification of a presheaf on
$\mathcal {C}' \to \mathcal {C}$ clearly satisfies the conditions of Proposition A.6. In particular, the hypersheafification of a presheaf on ![]() $\mathcal {C}$ when restricted to
$\mathcal {C}$ when restricted to ![]() $\mathcal {C}_{/a}$ is the hypersheafification of the restriction to
$\mathcal {C}_{/a}$ is the hypersheafification of the restriction to ![]() $\mathcal {C}_{/a}$.
$\mathcal {C}_{/a}$.
A direct consequence is that given an appropriate site with a ‘basis’, hypersheaves of spectra can be entirely recovered from their values on the basis. The result is a direct analog of [Reference Artin, Grothendieck and VerdierSGA4, Theorem 4.1, Exp. III], and appears (for sheaves of spaces) in [Reference AokiAok20, Appendix A].
Proposition A.8 Let ![]() $\mathcal {C}$ be a site as in Remark A.1. Let
$\mathcal {C}$ be a site as in Remark A.1. Let ![]() $\mathcal {C}' \subset \mathcal {C}$ be a full subcategory closed under finite coproducts and fiber products, and define
$\mathcal {C}' \subset \mathcal {C}$ be a full subcategory closed under finite coproducts and fiber products, and define ![]() $S_{\mathcal {C}'}$ to be the intersection of
$S_{\mathcal {C}'}$ to be the intersection of ![]() $S_{\mathcal {C}}$ with
$S_{\mathcal {C}}$ with ![]() $\mathcal {C}'$. Suppose every object
$\mathcal {C}'$. Suppose every object ![]() $X \in \mathcal {C}$ admits a map
$X \in \mathcal {C}$ admits a map ![]() $Y \to X$ in
$Y \to X$ in ![]() $S_{\mathcal {C}}$ with
$S_{\mathcal {C}}$ with ![]() $Y \in \mathcal {C}'$. Then the restriction functor
$Y \in \mathcal {C}'$. Then the restriction functor ![]() $\mathrm {Shv}(\mathcal {C}, {\rm Sp} ) \to \mathrm {Shv}(\mathcal {C}', {\rm Sp} )$ restricts to an equivalence on hypercomplete objects.
$\mathrm {Shv}(\mathcal {C}, {\rm Sp} ) \to \mathrm {Shv}(\mathcal {C}', {\rm Sp} )$ restricts to an equivalence on hypercomplete objects.
Proof. Let ![]() $u \colon \mathcal {C}' \subset \mathcal {C}$ be the inclusion, so we have a restriction functor
$u \colon \mathcal {C}' \subset \mathcal {C}$ be the inclusion, so we have a restriction functor ![]() $(-) \circ u \colon \mathrm {PSh}(\mathcal {C}, {\rm Sp} ) \to \mathrm {PSh}(\mathcal {C}', {\rm Sp} )$. By Proposition A.6, it restricts to a functor on hypercomplete sheaves, so we have
$(-) \circ u \colon \mathrm {PSh}(\mathcal {C}, {\rm Sp} ) \to \mathrm {PSh}(\mathcal {C}', {\rm Sp} )$. By Proposition A.6, it restricts to a functor on hypercomplete sheaves, so we have ![]() $(-) \circ u \colon \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}, {\rm Sp} ) \to \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}', {\rm Sp} )$. This last functor has a left adjoint
$(-) \circ u \colon \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}, {\rm Sp} ) \to \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}', {\rm Sp} )$. This last functor has a left adjoint ![]() $L \colon \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}', {\rm Sp} ) \to \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}, {\rm Sp} )$, given by
$L \colon \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}', {\rm Sp} ) \to \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}, {\rm Sp} )$, given by ![]() $\mathcal {F} \mapsto L\mathcal {F} := (\mathrm {Lan}_u \mathcal {F})^{\sharp }$, that is,
$\mathcal {F} \mapsto L\mathcal {F} := (\mathrm {Lan}_u \mathcal {F})^{\sharp }$, that is, ![]() $L$ is obtained by applying the left Kan extension
$L$ is obtained by applying the left Kan extension ![]() $\mathrm {Lan}_u \colon \mathrm {PSh}(\mathcal {C}', {\rm Sp} ) \to \mathrm {PSh}(\mathcal {C}, {\rm Sp} )$ followed by hypersheafification
$\mathrm {Lan}_u \colon \mathrm {PSh}(\mathcal {C}', {\rm Sp} ) \to \mathrm {PSh}(\mathcal {C}, {\rm Sp} )$ followed by hypersheafification ![]() $(-)^{\sharp }$. We now show that
$(-)^{\sharp }$. We now show that ![]() $L$ is fully faithful. Indeed, we have, for
$L$ is fully faithful. Indeed, we have, for ![]() $\mathcal {F}, \mathcal {G} \in \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}', {\rm Sp} )$,
$\mathcal {F}, \mathcal {G} \in \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}', {\rm Sp} )$,
Now since ![]() $u$ is fully faithful, since hypersheafification commutes with
$u$ is fully faithful, since hypersheafification commutes with ![]() $(-) \circ u$ by Proposition A.6, and since
$(-) \circ u$ by Proposition A.6, and since ![]() $\mathcal {G}$ is already hypercomplete, we have
$\mathcal {G}$ is already hypercomplete, we have ![]() $(\mathrm {Lan}_u \mathcal {G})^{\sharp } \circ u = \mathcal {G}$. Therefore, the right-hand side of (A.2) simplifies to
$(\mathrm {Lan}_u \mathcal {G})^{\sharp } \circ u = \mathcal {G}$. Therefore, the right-hand side of (A.2) simplifies to ![]() $\text{Hom} _{\mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}', {\rm Sp} )}(\mathcal {F}, \mathcal {G})$ as desired.
$\text{Hom} _{\mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}', {\rm Sp} )}(\mathcal {F}, \mathcal {G})$ as desired.
Our hypotheses imply that the restriction functor ![]() $(-) \circ u$ is conservative on hypercomplete sheaves, because it is conservative on sheaves of abelian groups. Since the restriction functor is conservative and has a fully faithful left adjoint, the result follows.
$(-) \circ u$ is conservative on hypercomplete sheaves, because it is conservative on sheaves of abelian groups. Since the restriction functor is conservative and has a fully faithful left adjoint, the result follows.
Example A.9 (Unfolding in the ![]() $\mathrm {arc}_{{p}}$-topology)
$\mathrm {arc}_{{p}}$-topology)
The natural forgetful functor establishes an equivalence of ![]() $\infty$-categories between
$\infty$-categories between ![]() $\mathrm {arc}_{{p}}$-hypersheaves of spectra on all derived
$\mathrm {arc}_{{p}}$-hypersheaves of spectra on all derived ![]() $p$-complete rings and
$p$-complete rings and ![]() $\mathrm {arc}_{{p}}$-hypersheaves of spectra on perfectoid rings.
$\mathrm {arc}_{{p}}$-hypersheaves of spectra on perfectoid rings.
Finally, we include a basic observation about commuting hypersheafification and certain products when the site ![]() $\mathcal {C}$ is sufficiently large (e.g. the
$\mathcal {C}$ is sufficiently large (e.g. the ![]() $\mathrm {arc}_{{p}}$-site). This fact is closely related to the theory of replete topoi; see [Reference Bhatt and ScholzeBS15, § 3]. Compare [Reference Bhatt and ScholzeBS15, Proposition 3.3.3] for the second part of the next result for the derived category of abelian sheaves, or equivalently hypercomplete
$\mathrm {arc}_{{p}}$-site). This fact is closely related to the theory of replete topoi; see [Reference Bhatt and ScholzeBS15, § 3]. Compare [Reference Bhatt and ScholzeBS15, Proposition 3.3.3] for the second part of the next result for the derived category of abelian sheaves, or equivalently hypercomplete ![]() $H\mathbb {Z}$-module sheaves of spectra. Note, in particular, that it applies to the
$H\mathbb {Z}$-module sheaves of spectra. Note, in particular, that it applies to the ![]() $\mathrm {arc}_{{p}}$-site. This follows because
$\mathrm {arc}_{{p}}$-site. This follows because ![]() $\mathrm {arc}$-covers in the sense of [Reference Bhatt and MathewBM18] are closed under filtered colimits of rings [Reference Bhatt and MathewBM18, Corollary 2.20] and because a map of derived
$\mathrm {arc}$-covers in the sense of [Reference Bhatt and MathewBM18] are closed under filtered colimits of rings [Reference Bhatt and MathewBM18, Corollary 2.20] and because a map of derived ![]() $p$-complete rings
$p$-complete rings ![]() $R \to R'$ is an
$R \to R'$ is an ![]() $\mathrm {arc}_{{p}}$-cover if and only if
$\mathrm {arc}_{{p}}$-cover if and only if ![]() $R \to R' \times R/p \times R[1/p]$ is an
$R \to R' \times R/p \times R[1/p]$ is an ![]() $\mathrm {arc}$-cover.
$\mathrm {arc}$-cover.
In the following, we write ![]() $\mathrm {PSh}_{\sqcup }(\mathcal {C}) \subset \mathrm {PSh}(\mathcal {C})$ for the subcategory of presheaves which carry finite coproducts to finite products.
$\mathrm {PSh}_{\sqcup }(\mathcal {C}) \subset \mathrm {PSh}(\mathcal {C})$ for the subcategory of presheaves which carry finite coproducts to finite products.
Proposition A.10 Let ![]() $\mathcal {C}$ be a site as in Remark A.1. Suppose
$\mathcal {C}$ be a site as in Remark A.1. Suppose ![]() $\mathcal {C}$ admits countable filtered limits. Suppose, moreover, that if
$\mathcal {C}$ admits countable filtered limits. Suppose, moreover, that if ![]() $\cdots \to X_i \to X_{i-1} \to \cdots \to X_0$ is a sequence of arrows in
$\cdots \to X_i \to X_{i-1} \to \cdots \to X_0$ is a sequence of arrows in ![]() $S$, then
$S$, then ![]() $\varprojlim _i X_i \to X_0$ belongs to
$\varprojlim _i X_i \to X_0$ belongs to ![]() $S$. Then the following assertions hold.
$S$. Then the following assertions hold.
(i) The hypersheafification functor,
 $(-)^{\sharp } \colon \mathrm {PSh}_{\sqcup }(\mathcal {C}) \to \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C})$ commutes with countable products and limits along
$(-)^{\sharp } \colon \mathrm {PSh}_{\sqcup }(\mathcal {C}) \to \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C})$ commutes with countable products and limits along  $\mathbb {Z}_{\geq 0}$-indexed towers.
$\mathbb {Z}_{\geq 0}$-indexed towers.(ii) For any
 $\mathcal {G} \in \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}) \subset \mathrm {Shv}(\mathcal {C})$, the Postnikov tower of
$\mathcal {G} \in \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C}) \subset \mathrm {Shv}(\mathcal {C})$, the Postnikov tower of  $\mathcal {G}$ (as a sheaf of spectra) converges.
$\mathcal {G}$ (as a sheaf of spectra) converges.
Proof. For (i), since hypersheaves are always closed (inside presheaves) under arbitrary limits and since ![]() $\mathbb {Z}_{\geq 0}$-indexed limits can be built from countable products, it suffices to show (via the unique cofiber sequence (A.1)) that if
$\mathbb {Z}_{\geq 0}$-indexed limits can be built from countable products, it suffices to show (via the unique cofiber sequence (A.1)) that if ![]() $\{\mathcal {F}_i\}_{i \in \mathbb {N}}$ is a countable family of presheaves in
$\{\mathcal {F}_i\}_{i \in \mathbb {N}}$ is a countable family of presheaves in ![]() $\mathrm {PSh}_{\sqcup }(\mathcal {C})$ with trivial hypersheafification (i.e. trivial sheafified homotopy groups), then the product presheaf
$\mathrm {PSh}_{\sqcup }(\mathcal {C})$ with trivial hypersheafification (i.e. trivial sheafified homotopy groups), then the product presheaf ![]() $\prod _{i \in \mathbb {N}} \mathcal {F}_i$ has trivial hypersheafification. But this is just a claim about the presheaves of abelian groups
$\prod _{i \in \mathbb {N}} \mathcal {F}_i$ has trivial hypersheafification. But this is just a claim about the presheaves of abelian groups ![]() $\{\pi _j( \mathcal {F}_i)\}_{i \in \mathbb {N}}$ for each
$\{\pi _j( \mathcal {F}_i)\}_{i \in \mathbb {N}}$ for each ![]() $j$. Explicitly, given a class
$j$. Explicitly, given a class ![]() $\alpha = (\alpha _i) \in \prod _{i \in \mathbb {N}} \pi _j( \mathcal {F}_i(X))$ for some
$\alpha = (\alpha _i) \in \prod _{i \in \mathbb {N}} \pi _j( \mathcal {F}_i(X))$ for some ![]() $X \in \mathcal {C}$, we find for each
$X \in \mathcal {C}$, we find for each ![]() $i$ a cover
$i$ a cover ![]() $X_i \to X$ in
$X_i \to X$ in ![]() $S$ which annihilatesFootnote 9
$S$ which annihilatesFootnote 9 ![]() $\alpha _i \in \pi _j( \mathcal {F}_i(X))$ and then form the cover
$\alpha _i \in \pi _j( \mathcal {F}_i(X))$ and then form the cover ![]() $X_1 \times _X X_2 \times _X \ldots$ of
$X_1 \times _X X_2 \times _X \ldots$ of ![]() $X$, which annihilates
$X$, which annihilates ![]() $\alpha$.
$\alpha$.
Now let ![]() $\mathcal {G}$ be a hypercomplete sheaf of spectra on
$\mathcal {G}$ be a hypercomplete sheaf of spectra on ![]() $\mathcal {C}$. The Postnikov tower of
$\mathcal {C}$. The Postnikov tower of ![]() $\mathcal {G} \in \mathrm {Shv}(\mathcal {C})$ is obtained by taking the presheaf truncations
$\mathcal {G} \in \mathrm {Shv}(\mathcal {C})$ is obtained by taking the presheaf truncations ![]() $\tau ^{\mathrm {pre}}_{\leq n} \mathcal {G}$ and applying the hypersheafification (or sheafification, since these objects are truncated), that is, one forms
$\tau ^{\mathrm {pre}}_{\leq n} \mathcal {G}$ and applying the hypersheafification (or sheafification, since these objects are truncated), that is, one forms ![]() $\{ (\tau ^{\mathrm {pre}}_{\leq n} \mathcal {G})^{\sharp } \}$, which is a tower in
$\{ (\tau ^{\mathrm {pre}}_{\leq n} \mathcal {G})^{\sharp } \}$, which is a tower in ![]() $\mathrm {PSh}_{\sqcup }(\mathcal {C})$. Since Postnikov towers converge for presheaves of spectra, that is,
$\mathrm {PSh}_{\sqcup }(\mathcal {C})$. Since Postnikov towers converge for presheaves of spectra, that is, ![]() $\mathcal {G} \simeq \varprojlim _n \tau ^{\mathrm {pre}}_{\leq n} \mathcal {G}$, and we have just seen that
$\mathcal {G} \simeq \varprojlim _n \tau ^{\mathrm {pre}}_{\leq n} \mathcal {G}$, and we have just seen that ![]() $(-)^{\sharp } \colon \mathrm {PSh}_{\sqcup }(\mathcal {C}) \to \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C})$ commutes with limits along
$(-)^{\sharp } \colon \mathrm {PSh}_{\sqcup }(\mathcal {C}) \to \mathrm {Shv}_{\mathrm {hyp}}(\mathcal {C})$ commutes with limits along ![]() $\mathbb {Z}_{\geq 0}$-indexed towers, we find
$\mathbb {Z}_{\geq 0}$-indexed towers, we find ![]() $\mathcal {G} \simeq \varprojlim _n (\tau _{\leq n}^{\mathrm {pre}} \mathcal {G})^{\sharp }$ as desired.
$\mathcal {G} \simeq \varprojlim _n (\tau _{\leq n}^{\mathrm {pre}} \mathcal {G})^{\sharp }$ as desired.