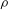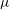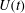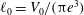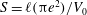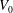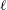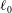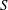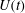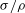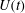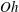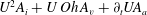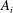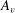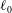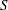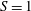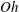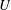1. Introduction
Liquid jets and ligaments have been widely studied for a long time, and although much work has been done, especially on break-up (Eggers & Villermaux Reference Eggers and Villermaux2008), some fundamental issues remain to be addressed. Among these questions is the role played by stretching on the dynamics. Here, we analyse how a weak and controlled elongation affects the dynamics of stable ligaments.
Ligament stretching occurs in many industrial processes and natural flows. In fibre drawing process used to manufacture optical fibres, or in the glass wool process, thin ligaments of molten glass are stretched either by mechanical action or high-speed air flow, and cool down before the occurrence of Rayleigh–Plateau instability (Plateau Reference Plateau1873). Evidence of elongated and smooth ligaments is also found in nature in the vicinity of some volcanoes, under the name ‘Pele’s hair’ (Villermaux Reference Villermaux2012). These thin lava threads arise during strong explosions: jets of liquid lava are strongly stretched by the explosion, as in the industrial process mentioned above, and cool down before breaking up into droplets.
More controlled stretching conditions have been studied in the literature. Among them is the natural stretching encountered by a capillary jet falling under gravity. This simple configuration has been analysed in detail by Cheong & Howes (Reference Cheong and Howes2004) and Sauter & Buggisch (Reference Sauter and Buggisch2013) among others. The stretching that the jet experiences as it falls is believed to be responsible for the delay in break-up (Tomotika Reference Tomotika1936). This idea was further analysed by Frankel & Weihs (Reference Frankel and Weihs1985) who considered the stability of a uniformly stretched ligament. Unfortunately, their analysis applies to cylindrical ligaments only, and requires very special time variation of the stretching rate. Numerous works have also considered, for its link with the problem encountered in micro-gravity (e.g. Fowle, Wang & Strong Reference Fowle, Wang and Strong1979; Zhang & Alexander Reference Zhang and Alexander1990), an inviscid liquid bridge subjected to an axially oscillating forcing (for a complete list of references, see Perales & Meseguer Reference Perales and Meseguer1992). In the more general viscous case, as shown by Perales & Meseguer (Reference Perales and Meseguer1992), when the boundaries are oscillating axially, the bridge may in particular exhibit resonant frequencies leading to large deformations. Dynamics of oscillating viscous liquid bridges were studied in detail by Borkar & Tsamopoulos (Reference Borkar and Tsamopoulos1991), Tsamopoulos, Chen & Borkar (Reference Tsamopoulos, Chen and Borkar1992), Chen & Tsamopoulos (Reference Chen and Tsamopoulos1993), Mollot et al. (Reference Mollot, Tsamopoulos, Chen and Ashgriz1993). Borkar & Tsamopoulos (Reference Borkar and Tsamopoulos1991) carried out a boundary-layer analysis to account for the presence of viscosity, in the limit of large Reynolds number; Tsamopoulos et al. (Reference Tsamopoulos, Chen and Borkar1992) focused on linearized dynamics of liquid bridges, i.e. small-amplitude oscillations, for arbitrary viscosity. Chen & Tsamopoulos (Reference Chen and Tsamopoulos1993) used finite-element two-dimensional numerical simulations to account for nonlinear effects (finite-amplitude oscillations). The corresponding experiments were carried out by Mollot et al. (Reference Mollot, Tsamopoulos, Chen and Ashgriz1993). The authors showed that the resonant frequency of liquid bridges decreases almost linearly with the oscillation amplitude; the damping rate was also shown to be greater than the one predicted by the linear theory.
More recently, the shape and the evolution of a horizontal hanging viscous ligament subjected to gravity has been studied (Le Merrer et al. Reference Merrer, Seiwert, Quéré and Clanet2008). In particular, the transition of this catenary into a U-shape has been discussed.
In general, when a liquid bridge is stretched by moving apart the supports on which it is attached, the bridge does not remain cylindrical and experiences a non-uniform stretching field (Gaudet, McKinley & Stone Reference Gaudet, McKinley and Stone1996). Even if the contact lines are allowed to move, the bridge shape is found to change (see for instance Dodds, Carvalho & Kumar Reference Dodds, Carvalho and Kumar2011). Quantifying these modifications and the stretching field constitutes one of the motivations of the present work. As shown by Kroger et al. (Reference Kroger, Berg, Delgado and Rath1992), this objective is also important in order to be able to measure the elongational viscosity of non-Newtonian fluids using this technique.
In the present work, we follow the analysis by Zhang, Padgett & Basaran (Reference Zhang, Padgett and Basaran1996) and use the one-dimensional model introduced by Eggers & Dupont (Reference Eggers and Dupont1994) where the full curvature term is kept. This model has a long history which goes back to Saint Venant and Cosserat (see, for instance Bogy Reference Bogy1978; Meseguer Reference Meseguer1983). It has been tested and validated in numerous studies (see for instance Eggers & Dupont Reference Eggers and Dupont1994; Ramos, Garcia & Valverde Reference Ramos, Garcia and Valverde1999; Ambravaneswaran, Wilkes & Basaran Reference Ambravaneswaran, Wilkes and Basaran2002).
Zhang et al.’s analysis has been pursued by Liao, Franses & Basaran (Reference Liao, Franses and Basaran2006). They considered the effects of a surfactant monolayer on the breaking of a liquid bridge. The pinching was found to be weakly delayed because of both the lowering of surface tension and flows arising from Marangoni stresses. The latter effect was however strengthened when the rod were pulled away, and thus the length at which the bridge breaks was found to increase appreciably with the stretching speed.
Instead of analysing the effect of stretching on break-up, we focus on the early-time dynamics when the bridge is still stable. Our interest is to analyse the difference between the equilibrium state and the dynamical state obtained during the elongation process.
2. Framework
We consider the dynamics of a thin axisymmetric liquid bridge elongated between two coaxial disks of radius
$e$
, as sketched in figure 1. The fluid is incompressible and has a dynamic viscosity
${\it\mu}$
, a density
${\it\rho}$
, and a surface tension
${\it\sigma}$
with the surrounding gas, which is neglected. Spatial and time variables are non-dimensionalized using the radius
$e$
of the bridge at its ends, and the capillary time
${\it\tau}_{c}=\sqrt{{\it\rho}e^{3}/{\it\sigma}}$
respectively. Volumes are then measured in units of
$e^{3}$
.
Figure 1. Description of a stretched liquid bridge.
In the present study, we assume that the liquid bridge can be described by the one-dimensional model
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial A}{\partial t}=-\frac{\partial \left(Au\right)}{\partial z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial u}{\partial t}=-u\frac{\partial u}{\partial z}+3\,Oh\,\frac{1}{A}\frac{\partial }{\partial z}\left(A\frac{\partial u}{\partial z}\right)+\frac{\partial K}{\partial z}-Bo, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}K=\frac{4AA_{zz}-2A_{z}^{2}}{[4A+A_{z}^{2}]^{3/2}}-\frac{2}{[4A+A_{z}^{2}]^{1/2}},\end{eqnarray}$$
where
$u(z,t)$
is the local axial velocity,
$A=h^{2}$
is the square of the local radius
$h(z,t)$
,
$z$
is the axial coordinate,
$t$
is the time variable,
$A_{z}$
and
$A_{zz}$
are respectively, the first and second derivative of
$A$
with respect to
$z$
. This one-dimensional model can be derived from the Navier–Stokes equations under the slenderness hypothesis, i.e. provided that the axial extent of the fluid volume is greater than its radial extent (see for instance Eggers Reference Eggers1997). As shown in numerous studies (e.g. Johnson et al.
Reference Johnson, Kamm, Ho, Shapiro and Pedley1991; Ramos et al.
Reference Ramos, Garcia and Valverde1999), it also correctly describes the dynamics of a liquid bridge outside this regime, if we keep all the terms in the curvature
$K$
, as we do here.
The system of equations (2.1a,b
) depends on the Ohnesorge number
$Oh$
and the Bond number
$Bo$
which compare viscous and gravitational forces to surface tension forces, respectively. These parameters are defined by:
$$\begin{eqnarray}Oh=\frac{{\it\mu}}{\sqrt{{\it\rho}{\it\sigma}e}},\quad Bo=\frac{{\it\rho}ge^{2}}{{\it\sigma}}.\end{eqnarray}$$
At
$t=0$
, the liquid bridge is assumed to have a length
$\ell _{0}$
and a (non-dimensional) volume
$V_{0}={\rm\pi}\ell _{0}$
. The liquid bridge is elongated by moving one end with a speed
$U(t)$
. The length
$\ell (t)$
of the bridge then evolves in time according to
$$\begin{eqnarray}\ell (t)=\ell _{0}+\int _{0}^{t}U(s)\text{d}s.\end{eqnarray}$$
The contact lines are assumed to be attached to the disk, except in § 5.2 where different boundary conditions are considered. Here, the boundary conditions to apply on
$A(z,t)$
and
$u(z,t)$
are
$$\begin{eqnarray}\displaystyle A(0,t)=1,\quad A(\ell (t),t)=1, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u(0,t)=0,\quad u(\ell (t),t)=U(t). & & \displaystyle\end{eqnarray}$$
$A$
must also satisfy: 
$$\begin{eqnarray}\int _{0}^{\ell (t)}A(z,t)\text{d}z=\ell _{0}.\end{eqnarray}$$
Except in § 6 where gravity effects are considered, we assume in the following that
$Bo=0$
. The initial state is therefore a cylinder. When the bridge is elongated to a new state of length
$\ell$
, its shape changes. An equilibrium state of length
$\ell$
exists (and is stable) when
$\ell$
is not too large. This state corresponds to a Delaunay curve which is defined by the condition
$$\begin{eqnarray}\displaystyle \frac{\partial K}{\partial z}=0.\end{eqnarray}$$
The equilibrium state is actually defined by the two parameters
$\ell _{0}$
(which fixes the volume of fluid), and the stretching parameter
$S=\ell /\ell _{0}$
. For each set of parameters, it has a constant curvature
$K_{D}$
. Figure 2(a) shows how the curvature
$K_{D}(\ell _{0},S)$
varies as a function of
$\ell _{0}$
and
$S$
. The limits of the domain correspond to stability boundaries (see for instance Gillette & Dyson Reference Gillette and Dyson1970; Slobozhanin & Perales Reference Slobozhanin and Perales1993). The equilibrium states are symmetric with respect to the median plane
$z=\ell /2$
. In figure 2(b), several examples of equilibrium shape have been plotted as a function of
$z/\ell$
. As observed in this plot, stretching the liquid bridge tends to shrink the middle portion of the bridge.
Figure 2. (a) Iso-curvature lines of the Delaunay equilibrium shape as a function of the initial length
$\ell _{0}$
and the stretching factor
$S$
. (b) Examples of the Delaunay equilibrium shape versus
$Z=z/\ell$
for different
$\ell _{0}$
and
$S$
. Solid lines:
$\ell _{0}=1$
; dashed lines:
$\ell _{0}=2$
.
Because the contact line is assumed to be pinned, the equilibrium shape is found independently of the contact angle at the edges. In other situations, e.g. a meniscus between a sphere and a plane, the shape is imposed by the contact angle (see for example Orr, Scriven & Rivas Reference Orr, Scriven and Rivas1975); this corresponds to a different set of boundary conditions.
Our objective is to quantify the differences between the dynamical shape and the equilibrium shape during a slow elongation/compression episode. We first develop a perturbation theory which shows that the corrections can be attributed to three different effects. This theory is then validated using direct numerical simulations of system (2.1) in § 4. The special case of a cylinder which corresponds to
$S=1$
is considered in § 5.
3. Theoretical study
In this section, we assume that the liquid bridge is, at leading order, close to the equilibrium shape such that we can write the velocity
$u$
and shape
$A$
as
$$\begin{eqnarray}\displaystyle & A=A_{0}(z,S,\ell _{0})+A_{1}(z,t,S,\ell _{0}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & u=u_{1}(z,t,S,\ell _{0}), & \displaystyle\end{eqnarray}$$
$|A_{1}|\ll 1$
and
$|u_{1}|\ll 1$
. The leading-order shape
$A_{0}$
which satisfies (when
$Bo=0$
) 
$$\begin{eqnarray}\displaystyle \frac{\partial K_{0}}{\partial z}=0,\end{eqnarray}$$
is a Delaunay curve
$A_{0}(z,S,\ell _{0})=A_{D}(z/\ell ,S,\ell _{0})$
, as described in the previous section.
Since the time variation of
$A_{D}$
is associated with variations of
$\ell$
only, we have
$$\begin{eqnarray}\frac{\text{d}A_{D}}{\text{d}t}=\frac{U}{\ell _{0}}\displaystyle \frac{\partial A_{D}}{\partial S}-\frac{UZ}{S\ell _{0}}\displaystyle \frac{\partial A_{D}}{\partial Z}\end{eqnarray}$$
where
$Z=z/\ell (t)$
. If we plug (3.1a,b
) into (2.1a
), we then get at leading order
$$\begin{eqnarray}\displaystyle \frac{\partial (A_{D}u_{1})}{\partial Z}=U\left(Z\displaystyle \frac{\partial A_{D}}{\partial Z}-S\displaystyle \frac{\partial A_{D}}{\partial S}\right).\end{eqnarray}$$
This equation gives for
${\tilde{u}}_{1}=u_{1}/U$
$$\begin{eqnarray}{\tilde{u}}_{1}=Z-\frac{1}{A_{D}}\frac{\partial \left(SV_{D}\right)}{\partial S},\end{eqnarray}$$
where
$$\begin{eqnarray}V_{D}(Z,S,\ell _{0})=\int _{0}^{Z}A_{D}(Z^{\prime },S,\ell _{0})\text{d}Z^{\prime }\end{eqnarray}$$
stands for the partial volume of the Delaunay shape from
$0$
to
$Z$
in the rescaled space domain.
It is worth noting that expression (3.5) does not depend on
$Oh$
: the velocity field
$u_{1}$
is associated with kinematic effects only. When the shape is changed from one Delaunay curve to another by moving one boundary at a speed
$U$
, the fluid in the liquid bridge has to move according to
$u_{1}$
. Expression (3.5) possesses some properties. The second term on the right-hand side of (3.5) is anti-symmetric with respect to the mid-plane
$Z=1/2$
. This means that the velocity obtained by pulling both sides with an opposite velocity
$U/2$
would have been perfectly anti-symmetric with respect to the mid-plane
$Z=1/2$
and given by (3.5) shifted by
$-1/2$
. This property comes from the Galilean invariance of the theoretical analysis when the acceleration of the bridge is small. Interestingly, the local strain field
$\partial {\tilde{u}}_{1}/\partial Z$
is strongly non-uniform. It vanishes at the boundaries and exhibits a maximum in the middle of the liquid bridge at
$Z=1/2$
. Both the function
${\tilde{u}}_{1}$
and the local strain field
$\partial {\tilde{u}}_{1}/\partial Z$
are plotted in figure 3 for the sets of parameters considered in figure 2(b). We observe that the local strain field slightly changes with respect to
$\ell _{0}$
and
$S$
. Note that negative values of the strain field are obtained close to the rod when
$S=2$
and
$\ell _{0}=1$
. This curve is typical of large-
$S$
configurations. Negative strain rates close to the rod have also been reported when a non-Newtonian bridge is stretched (Bhat, Basaran & Pasquali Reference Bhat, Basaran and Pasquali2008). More generally, capillary pinching induces such negative strain rates. Here we report that they can also appear before instability sets in.
Figure 3. (a) Velocity field
${\tilde{u}}_{1}=U_{1}/U$
and (b) local strain rate
$\partial {\tilde{u}}_{1}/\partial Z$
predicted by the theory. Solid lines:
$\ell _{0}=1$
; dashed lines:
$\ell _{0}=2$
.
Figure 4. Contours of (a) minimum value and (b) maximum value of the local strain rate
$\partial u_{1}/\partial Z$
in the domain of existence of the equilibrium solution. In (a), the dashed line corresponds to the level 0: below this curve, the minimum value of the strain field is reached at the boundaries.
The maximum and minimum values of the strain field are analysed as a function of the two parameters
$\ell _{0}$
and
$S$
in figure 4. In figure 4(a), the zero level curve, shown dashed, indicates the limit above which negative strain fields are present in the bridge. Note that this parameter region corresponds to the region where the strain field also reaches the largest positive values (see figure 4
b).
The correction
$A_{1}$
to the Delaunay curve is obtained from (2.1b
):
$$\begin{eqnarray}\frac{\partial K_{1}}{\partial z}=\displaystyle \frac{\partial u_{1}}{\partial t}-u_{1}\displaystyle \frac{\partial u_{1}}{\partial z}-3\frac{Oh}{A_{D}}\frac{\partial }{\partial z}\left(A_{D}\frac{\partial u_{1}}{\partial z}\right),\end{eqnarray}$$
where
$K_{1}$
is the curvature correction induced by
$A_{1}$
. This term can be written
$K_{1}=\mathscr{L}_{K_{D}}[A_{1}]$
where
$\mathscr{L}_{K_{D}}$
is a linear operator, obtained by linearizing (2.2) around
$A_{D}$
:
$$\begin{eqnarray}\mathscr{L}_{K_{D}}=S\ell _{0}\left({\it\alpha}_{0}+{\it\alpha}_{1}\displaystyle \frac{\partial }{\partial Z}+{\it\alpha}_{2}\displaystyle \frac{\partial ^{2}}{\partial Z^{2}}\right),\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\alpha}_{0}=\frac{4\left(A_{DZ}^{2}\left(A_{DZZ}+4(S\ell _{0})^{2}\right)-2A_{D}(S\ell _{0})^{2}\left(A_{DZZ}-2(S\ell _{0})^{2}\right)\right)}{\left(4A_{D}(S\ell _{0})^{2}+A_{DZ}^{2}\right)^{5/2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\alpha}_{1}=\frac{4\left(A_{DZ}^{3}-A_{D}A_{DZ}\left(3A_{DZZ}+2(S\ell _{0})^{2}\right)\right)}{\left(4A_{D}(S\ell _{0})^{2}+A_{DZ}^{2}\right)^{5/2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\alpha}_{2}=\frac{4A_{D}}{\left(4A_{D}(S\ell _{0})^{2}+A_{DZ}^{2}\right)^{3/2}}. & \displaystyle\end{eqnarray}$$
Noting that
$(\partial u_{1}/\partial t)=\partial _{t}U{\tilde{u}}_{1}-(U^{2}Z/S\ell _{0})(\partial {\tilde{u}}_{1}/\partial Z)+(U^{2}/\ell _{0})(\partial {\tilde{u}}_{1}/\partial S)$
, (3.7) can be written as
$$\begin{eqnarray}\frac{\partial K_{1}}{\partial Z}=\partial _{t}U\ell _{0}S{\tilde{u}}_{1}+U^{2}\left(S\frac{\partial {\tilde{u}}_{1}}{\partial S}+({\tilde{u}}_{1}-Z)\frac{\partial {\tilde{u}}_{1}}{\partial Z}\right)-3\frac{UOh}{\ell _{0}SA_{D}}\frac{\partial }{\partial Z}\left(A_{D}\frac{\partial {\tilde{u}}_{1}}{\partial Z}\right).\end{eqnarray}$$
This allows us to write
$$\begin{eqnarray}A_{1}=A-A_{D}=\partial _{t}UA_{a}+U^{2}A_{i}+U\,Oh\,A_{v}\end{eqnarray}$$
where
$A_{a}$
,
$A_{i}$
and
$A_{v}$
are provided by
$K_{a}=\mathscr{L}_{K_{D}}[A_{a}]$
,
$K_{i}=\mathscr{L}_{K_{D}}[A_{i}]$
and
$K_{v}=\mathscr{L}_{K_{D}}[A_{v}]$
with
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial K_{a}}{\partial Z}=S\ell _{0}{\tilde{u}}_{1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial K_{i}}{\partial Z}=S\frac{\partial {\tilde{u}}_{1}}{\partial S}+({\tilde{u}}_{1}-Z)\frac{\partial {\tilde{u}}_{1}}{\partial Z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial K_{v}}{\partial Z}=-\frac{3}{\ell _{0}SA_{D}}\frac{\partial }{\partial Z}\left(A_{D}\frac{\partial {\tilde{u}}_{1}}{\partial Z}\right). & \displaystyle\end{eqnarray}$$
$A_{a}$
,
$A_{i}$
and
$A_{v}$
are associated with acceleration, inertial and viscous effects respectively. They do not depend on
$U$
nor on
$Oh$
. They are functions of the geometrical parameters
$\ell _{0}$
and
$S$
only. Note that from an asymptotical point of view, we should keep the three terms in (3.11) only if they are of same order. Each term corresponds to the leading-order correction associated with a given effect.
Figure 5. Shape correction induced by (a) viscous effects,
$A_{v}(Z)$
, and (b) inertial effects,
$A_{i}(Z)$
, for different
$S$
and
$\ell _{0}$
. Solid lines:
$\ell _{0}=1$
; dashed lines:
$\ell _{0}=2$
.
The functions
$A_{i}$
and
$A_{v}$
are symmetric with respect to the mid-plane
$Z=1/2$
. This symmetry is again associated with the Galilean invariance: similar corrections would have been obtained by pulling both sides with an opposite velocity
$U/2$
. In figure 5, we have plotted
$A_{i}$
and
$A_{v}$
versus
$Z$
for different values of
$S$
and
$\ell _{0}$
. Surprisingly, both corrections have a similar form with a maximum at the mid-plane and a negative minimum near the end. The effect of inertia is therefore similar to that of viscosity. In both cases, the corrections tend to fill the bridge neck when
$S>1$
. The dynamical shapes are therefore closer to cylindrical shapes than Delaunay’s. This observation has already been made by Kroger et al. (Reference Kroger, Berg, Delgado and Rath1992) who performed stretching experiments on large bridges in a neutral buoyancy tank. They noticed that ‘increasing inertia, friction and flow resistance
$(\dots )$
tend to stabilize the bridge and thus form more cylindrical bridges’. The present theory explains this tendency and provides the precise shape of the correction.
Figure 6. Shape correction
$A_{a}$
induced by acceleration effects for different
$S$
and
$\ell _{0}$
. (a) Symmetric part, (b) anti-symmetric part. Solid lines:
$\ell _{0}=1$
; dashed lines:
$\ell _{0}=2$
.
Unlike
$A_{i}$
and
$A_{v}$
,
$A_{a}$
does not possess any symmetry. It can be decomposed into two parts, one generated by
$S\ell _{0}(u_{1}-(1/2))$
that gives a symmetric contribution as if the bridge were elongated from both sides with an opposite velocity
$U/2$
and another due to a uniform acceleration
$S\ell _{0}/2$
associated with the breaking of the Galilean invariance. This last contribution is anti-symmetric and similar to the effect of gravity considered below. The symmetric and anti-symmetric parts of
$A_{a}$
are plotted in figure 6.
It is worth mentioning that the theory assumes that the bridge has its dynamics imposed by the moving disk. Free oscillations have been implicitly filtered out. These oscillations are damped in the presence of viscosity because we have only considered stable bridges. However, if the Ohnesorge number is very small, these oscillations can be observed, as will be seen in the next section.
4. Numerical study
In this section, we compare the theoretical predictions with numerical results. A specific code has been developed based on a centred finite-difference scheme. Equations (2.1a,b
) are solved in a fixed domain
$(0,1)$
by using the change of variable
$Z=z/\ell (t)$
. For maximum accuracy, we have used a staggered grid for
$u$
and
$A$
with typically 100 mesh points. Evolution in time is through a fourth-order Runge–Kutta scheme. This method requires a very small time step not to diverge, but is more precise than the implicit Crank–Nicholson scheme. A typical simulation takes 10 min on a laptop computer.
Figure 7. (a) Evolution of
$U(t)$
with
$\ell (t)$
. (b) Maximum distance between dynamical and Delaunay shapes with
$\ell (t)$
(dashed line) and the odd part of the dynamical shape (solid line).
$Oh=3\times 10^{-3}$
and
$U=0.02$
.
Figure 8. Maximum distance between dynamical and Delaunay shapes. (a) Fixed
$U$
:
$U=5\times 10^{-3}$
(circle),
$1\times 10^{-2}$
(square),
$2\times 10^{-2}$
(triangle),
$5\times 10^{-2}$
(star),
$1\times 10^{-3}$
(diamond). Dashed and solid lines are for
$S=1.5$
and
$S=2$
respectively. (b) Fixed
$Oh$
. Solid lines:
$Oh=2\times 10^{-5}$
with
$S=1.5$
(triangle) and
$S=2.0$
(circle); dashed lines:
$Oh=0.1$
with
$S=1.5$
(square) and
$S=2.0$
(diamond).
We have first performed simulations where the effect of acceleration can be neglected. For this purpose, the axial velocity of the top disk rises progressively from 0 to the desired constant velocity
$U$
. A typical law for the variation of
$U(t)$
is shown in figure 7(a). The acceleration phase has two noticeable effects as illustrated in figure 7(b). It first induces large non-symmetric corrections when the acceleration term is non-zero, as expected from the theory. It also generates fast temporal variations in the form of damped oscillations. Such oscillations are visible in figure 7(b) on the odd-part of the signal where they correspond to a damped sloshing mode. We can see on this typical example that these anti-symmetric oscillations become rapidly negligible compared to the symmetric difference between dynamical and equilibrium shapes. Oscillations are also present in the even-part of the signal, but these oscillations are so small that they can barely be seen in figure 7(b). We shall see below that the dynamical state can be dominated by the anti-symmetric oscillations when
$U$
is large and
$Oh$
small. However, for the configurations that we study below, we have checked that the non-symmetry and oscillations generated by the acceleration phase are indeed negligible. The dynamical state that we reach at
$S=1.5$
or
$S=2$
is therefore symmetric and independent of the transient. It depends on only two parameters: the elongation speed
$U$
(reached after the transient) and the Ohnesorge number
$Oh$
. The largest distance between the dynamical shape and the Delaunay shape has been systematically measured at
$S=1.5$
and
$S=2$
, for various
$U$
and
$Oh$
. The results are reported in figure 8(a) as a function of
$Oh$
, and in figure 8(b) as a function of
$U$
. In figure 8(a), we see that for each
$S$
, the curves of
$\max (A-A_{D})/U$
collapse onto a single curve which is linear with respect to
$Oh$
when
$Oh$
is large. This means that the shape correction is expected to scale as
$UOh$
in this regime. However, for small
$Oh$
, it tends to become independent of
$Oh$
and varies according to
$U^{2}$
as shown in figure 8(b). The change from one regime to another occurs at a critical Ohnesorge number
$Oh_{c}$
which varies linearly with
$U$
. These observations are in perfect agreement with expression (3.11) for
$A-A_{D}$
when
$\partial _{t}U=0$
.
Figure 9. Comparison between theory and computation. (a) Velocity field versus
$Z=z/\ell$
for
$S=1.5$
and
$\ell _{0}=1$
. Solid line is the theoretical velocity
$u_{1}$
, the others are numerical results (dashed line:
$Oh=10$
,
$U=5\times 10^{-2}$
; dotted line:
$Oh=1$
,
$U=5\times 10^{-2}$
; dash-dotted line:
$Oh=1$
,
$U=0.2$
). (b) Correction to the Delaunay shape given by the theory (dashed line) and by the simulation (solid line) for
$S=1.5$
,
$\ell _{0}=1$
,
$U=5\times 10^{-2}$
and
$Oh=3$
. Viscous contribution
$U\,Oh\,A_{v}$
(dotted line) and inertial contribution
$U^{2}A_{i}$
(dash-dotted line) which sum up to give the theoretical prediction are also indicated.
The agreement is also very good for the correction shape and for the velocity. In figure 9(a), we demonstrate that the velocity in the liquid bridge has the form predicted by the theory for a large range of
$U$
and
$Oh$
. Note in particular that this field is proportional to
$U$
and independent of
$Oh$
, as predicted by the theory. In figure 9(b), the correction to the Delaunay shape is compared to the theoretical prediction when both inertial and viscous corrections are of same order. Again a very good agreement is observed. Such a comparison has been systematically made for
$U$
and
$Oh$
in the intervals
$(5\times 10^{-3},1)$
and
$(5\times 10^{-5},30)$
respectively for
$S=1.5$
. Both the gap between the numerical solution to the Delaunay curve and to the theoretical predictions are plotted in figure 10(a,b). In this comparison, the anti-symmetric part of the numerical shape has been filtered out. These plots provide the strength of the non-stationary effects (figure 10
a) and the amplitude of the error made by the theory (figure 10
b). We can see that the error becomes much smaller than the strength of the non-stationary effects for small
$U$
and small
$Oh$
. We can also see that this error is always smaller than
$3\times 10^{-2}$
when
$U$
and
$U\,Oh$
are smaller than 1. Note, however, that in the left upper corner of the parameter space, the numerical shape is dominated by its anti-symmetric part. This contribution corresponds to the first oscillating sloshing mode which has been excited during the acceleration phase. The amplitude of this oscillating mode is important for large
$U$
and small
$Oh$
because it takes a shorter time to reach
$S=1.5$
when
$U$
is large, and the damping rate of the mode is smaller when
$Oh$
is small.
Figure 10. (a) Maximum distance between the symmetric part of the numerical shape and the Delaunay curve. (b) Maximum distance between the symmetric part of the numerical shape and the asymptotically predicted shape.
$\ell _{0}=1$
,
$S=1.5$
. The anti-symmetric part of the numerical shape is larger than its symmetric part above the solid black line.
The effect of the acceleration has also been analysed numerically by varying
$\ell (t)$
around a mean value according to
$$\begin{eqnarray}\ell (t)=\ell _{m}+{\it\varepsilon}\sin \left(\frac{2{\rm\pi}t}{T_{o}}\right)\end{eqnarray}$$
such that
$U(t)$
and
$\partial _{t}U$
vary in quadrature as
$$\begin{eqnarray}\displaystyle U(t)=\frac{2{\rm\pi}{\it\varepsilon}}{T_{o}}\cos \left(\frac{2{\rm\pi}t}{T_{o}}\right), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \partial _{t}U=-\frac{4{\rm\pi}^{2}{\it\varepsilon}}{T_{o}^{2}}\sin \left(\frac{2{\rm\pi}t}{T_{o}}\right). & & \displaystyle\end{eqnarray}$$
$U$
and
$\partial _{t}U$
vary, the relative strength of the different contributions to the dynamical shape changes in time. For example, at
$t=3T_{o}/4$
,
$U(t)$
vanishes, so that the dynamics is expected to be associated with the acceleration only. In figure 11, we have plotted the numerical shape obtained at this instant as a function of
$T_{o}$
for two values of
$\ell _{0}$
. In this case, we have chosen
$\ell _{m}=\ell _{0}$
and a very small value of
${\it\varepsilon}$
, so the bridge is oscillating around its cylindrical shape with
$S\approx 1$
. In this figure, we observe that both the symmetric part and the anti-symmetric part of the signal exhibit peaks for particular values of
$T_{o}$
. This phenomenon is not new and has been observed in several works (see for instance Perales & Meseguer Reference Perales and Meseguer1992). These peaks can be attributed to resonance with free eigenmodes of the bridge; the vertical dash-dotted lines correspond to the periods of the linear inviscid eigenmodes of a cylindrical bridge. When
$Oh$
increases these peaks decrease in amplitude because the resonance becomes imperfect owing to the damping of the modes. The mode with the largest period and the weakest damping rate is the sloshing mode. We have seen above that this mode dominates the transient when the bridge is elongated. When
$T_{o}$
is large, the shape of the deformation does not depend on
$T_{o}$
anymore but remains reminiscent of the sloshing mode, as seen in figure 12(a). This figure demonstrates that the numerical shape is mainly independent of
${\it\varepsilon}$
and
$Oh$
and agrees well with the theoretical prediction. Only a small departure for the largest value of
$Oh$
can be noticed.
Figure 11. Numerical shape of an oscillating bridge as a function of the oscillating period
$T_{o}$
for
$\ell _{0}=1$
(grey lines) and
$\ell _{0}=2$
(black lines),
$S=1$
,
${\it\varepsilon}=1\times 10^{-4}$
,
$Oh=1\times 10^{-2}$
when the acceleration is maximum (
$t/T_{o}=3/4$
). Solid lines are the maximum of the anti-symmetric part of
$A$
, dashed lines are the maximum of the symmetric part of
$(A-A_{D})$
. The vertical dash-dotted lines indicate the period of the linear inviscid eigenmodes of a cylindrical bridge of length
$\ell _{0}$
.
Figure 12. Comparison between theory and computation for an oscillating bridge. Correction to the Delaunay shape given by the theory (solid line) and by the simulation (symbols) for
$\ell _{m}=\ell _{0}=2$
. (a)
$t/T_{o}=3/4$
when
$U=0$
and
$\partial _{t}U$
maximum for
$T_{o}=140$
. (b)
$t/T_{o}=1.8$
when the three theoretical contributions are of same order for
$T_{o}=200$
,
$Oh=1\times 10^{-3}$
,
${\it\varepsilon}=0.1$
. As we explained above, the solid line corresponds to the shape given by our theory; the stars correspond to the shape given by the simulation. As we can see on figure 12
(b), the agreement is excellent. Dashed, dotted and dash-dotted lines are the contributions related to viscous, inertial and acceleration effects respectively.
When we consider the bridge at a different instant, the other contributions associated with viscous and inertial effects can become important. In figure 12(b), we see that the three theoretical contributions still correctly sum up to give the numerical curve.
5. Effect of stretching on a cylindrical bridge
5.1. Attached boundary conditions
In this subsection, we consider the configuration analysed in § 3 for the particular value
$S=1$
. In that case, the equilibrium state is a cylinder:
$A_{D}(S=1,\ell _{0})=1$
. This configuration is interesting because explicit expressions can be obtained for the dynamical corrections for any
$\ell _{0}$
.
We get, by expanding
$A_{D}$
in power of
$(S-1)$
, the following expressions for
${\tilde{u}}_{1}$
,
$A_{v}$
,
$A_{i}$
and
$A_{a}$
:
$$\begin{eqnarray}\displaystyle & \displaystyle {\tilde{u}}_{1}=\frac{1}{2}+\frac{y\cos \left(\displaystyle \frac{\ell _{0}}{2}\right)-\sin (y)}{d_{0}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle A_{v}=\frac{3\left(\cos \left(\displaystyle \frac{\ell _{0}}{2}\right)\!-\cos (y)\right)\left(2d_{0}\!+\!\ell _{0}^{2}\sin \left(\displaystyle \frac{\ell _{0}}{2}\right)\right)}{2d_{0}^{2}}+\frac{3\left(2y\sin (y)-\ell _{0}\sin \left(\displaystyle \frac{\ell _{0}}{2}\right)\right)}{2d_{0}}, & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{i} & = & \displaystyle \displaystyle \frac{\cos (2y)}{3d_{0}^{2}}+y\sin (y)\displaystyle \frac{\left((3\ell _{0}^{2}+10)\sin (\ell _{0})-\ell _{0}(\cos (\ell _{0})+9)\right)}{4d_{0}^{3}}\nonumber\\ \displaystyle & & \displaystyle +\,3y^{2}\cos (y)\displaystyle \frac{(\ell _{0}-2\sin (\ell _{0})+\ell _{0}\cos (\ell _{0}))}{4d_{0}^{3}}\nonumber\\ \displaystyle & & \displaystyle -\,y^{2}\frac{\left(9\sin \left(\displaystyle \frac{\ell _{0}}{2}\right)+\sin \left(\displaystyle \frac{3\ell _{0}}{2}\right)-6\ell _{0}\cos \left(\displaystyle \frac{\ell _{0}}{2}\right)\right)}{2d_{0}^{3}}\nonumber\\ \displaystyle & & \displaystyle +\,\cos \left(\frac{\ell _{0}}{2}\right)\cos (y)\left[\displaystyle \frac{\left(9\ell _{0}^{4}+92\ell _{0}^{2}-496\right)\cos (\ell _{0})+496}{48d_{0}^{4}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\displaystyle \frac{-51\ell _{0}^{4}+156\ell _{0}^{2}+2\ell _{0}\left(47\ell _{0}^{2}+\left(7\ell _{0}^{2}-192\right)\cos (\ell _{0})-304\right)\tan \left(\displaystyle \frac{\ell _{0}}{2}\right)}{48d_{0}^{4}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\displaystyle \frac{\ell _{0}\left(41\ell _{0}^{2}+182\right)\sin (\ell _{0})+\left(3\ell _{0}^{2}+70\right)\cos (2\ell _{0})}{24d_{0}^{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\displaystyle \frac{\left(-3\left(\ell _{0}^{2}+6\right)\ell _{0}^{2}+\left(\ell _{0}^{2}+82\right)\ell _{0}\sin (\ell _{0})-16\right)\cos (\ell _{0})-3\left(\ell _{0}^{4}+39\ell _{0}^{2}+18\right)}{24d_{0}^{4}},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{a} & = & \displaystyle \displaystyle \frac{y^{2}\cos \left(\displaystyle \frac{\ell _{0}}{2}\right)}{d_{0}}-\frac{\cos (y)\left(3\left(\ell _{0}^{2}-4\right)\sin \left(\displaystyle \frac{\ell _{0}}{2}\right)+\ell _{0}\left(\ell _{0}^{2}+6\right)\cos \left(\displaystyle \frac{\ell _{0}}{2}\right)\right)}{6d_{0}^{2}}\nonumber\\ \displaystyle & & \displaystyle -\displaystyle \frac{\ell _{0}^{3}\cos (\ell _{0})+\left(\ell _{0}^{2}-24\right)\ell _{0}-6\left(\ell _{0}^{2}-4\right)\sin (\ell _{0})}{24d_{0}^{2}}+\frac{y\sin (y)}{d_{0}}-\frac{\ell _{0}\sin (y)}{2\sin \left(\displaystyle \frac{\ell _{0}}{2}\right)}+y,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle y=\ell _{0}\left(Z-{\textstyle \frac{1}{2}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle d_{0}=\ell _{0}\cos \left(\frac{\ell _{0}}{2}\right)-2\sin \left(\frac{\ell _{0}}{2}\right). & \displaystyle\end{eqnarray}$$
$\ell _{0}$
.
Figure 13. Shape correction associated with (a) inertial effects, (b) viscous effects, and (c) acceleration effects for the case of a cylinder (
$S=1$
). The dashed line represents the asymptotic estimate obtained for small
$\ell _{0}$
(expressions (5.7a–c
)).
The correction associated with the acceleration diverges close to
$\ell _{0}=2{\rm\pi}$
:
$$\begin{eqnarray}A_{a}\mathop{\sim }_{\ell _{0}\rightarrow 2{\rm\pi}}\frac{2{\rm\pi}\sin (2{\rm\pi}Z)}{2{\rm\pi}-\ell _{0}},\end{eqnarray}$$
whereas the other corrections are finite at this value. This value of
$\ell _{0}$
corresponds to the limit of stability of the cylinder. When
$\ell _{0}$
is close to
$2{\rm\pi}$
, the acceleration excites the first sloshing mode. Such a mode is not excited by inertial and viscous effects which can only excite symmetric modes, the first one being at
$\ell _{0}\approx 9$
corresponding to the vanishing of
$d_{0}$
.
For small values of
$\ell _{0}$
,
$$\begin{eqnarray}\displaystyle & \displaystyle A_{v}\sim \frac{3\ell _{0}}{5}Z(Z-1)(5Z^{2}-5Z+1), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle A_{i}\sim {\textstyle \frac{3}{350}}\ell _{0}^{2}Z(Z-1)(15Z^{6}-45Z^{5}+39Z^{4}-3Z^{3}-3Z^{2}-3Z+1), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle A_{a}\sim \frac{\ell _{0}^{3}}{210}Z(1-Z)(7Z^{4}-14Z^{3}-14Z^{2}-14Z+13). & \displaystyle\end{eqnarray}$$
$\ell _{0}\rightarrow 0$
. But note that the scaling laws are different for each correction.
It may be interesting to speculate on the condition for break-up by applying the theory in the nonlinear regime; we expect break-up when the total area
$A_{D}+A_{1}$
vanishes at one point. If we consider each effect alone, we then obtain three different conditions of break-up. For instance, break-up by the inertial effect would occur at a critical value of the imposed velocity given by
$U_{c}^{2}=-(\min (A_{i}))^{-1}$
. Viscous and acceleration effects provide critical values of
$U\,Oh$
and
$\partial _{t}U$
respectively. The variations of these critical values with respect to
$\ell _{0}$
are reported in figure 14. Each curve diverges for small
$\ell _{0}$
as expected from (5.7a–c
). Even if these break-up predictions are questionable, they nevertheless give some information on the transition to nonlinearity. In particular, it shows that the larger
$\ell _{0}$
is, the easier the transition. It also indicates that for small
$\ell _{0}$
, it will be very difficult to observe any significant deformation. Note for example that for
$\ell _{0}=1$
, the critical conditions are
$(UOh)_{c}\approx 32$
,
$U_{c}^{2}\approx 1747$
and
$(\partial _{t}U)_{c}\approx 111$
.
Figure 14. Estimate of the forcing strength needed for break-up by (a) viscous effects, (b) inertial effects and (c) acceleration effects.
The point of break-up and the volume that stays attached to the boundary can also be calculated and are reported in figure 15. Both the position and the attached volume are similar for viscous and inertial break-up as expected from the almost identical form of the viscous and inertial corrections (see figure 13
a,b). However, the correction associated with acceleration is different (figure 13
c). The minimum of
$A_{a}$
is further away from the boundary which explains the small values of
$Z_{c}$
and the significantly larger values of the attached volume. Note that in all cases, the attached volume is expected to be smaller than 10 %. Such a small volume is in agreement with the values reported in the literature (e.g. Zhang et al.
Reference Zhang, Padgett and Basaran1996).
Figure 15. Estimate of (a) the point of break-up and (b) the volume that remains attached to the boundary, for each type of break-up as a function of the cylinder length
$\ell _{0}$
. Solid line: viscosity; dashed line: inertia; dotted line: acceleration.
5.2. Moving boundary conditions: correction to the Frankel & Weihs solution
In the previous sections, the bridge extremities were attached to the boundaries. When the extremities are allowed to move, other types of solution are possible. One interesting solution is the exact solution provided by Frankel & Weihs (Reference Frankel and Weihs1985), which corresponds to the configuration where the bridge remains cylindrical. In this case, the boundary conditions are
$$\begin{eqnarray}\partial _{z}A(z=0,t)=\partial _{z}A(z=\ell (t),t)=0,\end{eqnarray}$$
and the bridge length expands with a constant velocity. For all time, the solution is
$$\begin{eqnarray}\displaystyle & \displaystyle A_{FW}(z,S,\ell _{0})=\frac{\ell _{0}}{\ell (t)}=\frac{1}{S}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u_{FW}=\frac{Uz}{\ell (t)}=UZ. & \displaystyle\end{eqnarray}$$
Frankel & Weihs’ solution requires a constant velocity. The perturbation theory developed in § 3 can be applied to extend this solution when
$\partial _{t}U\neq 0$
. One can first check that Frankel & Weihs’ solution (5.9a
) and (5.9b
) is indeed solution of the perturbation equations (3.4) and (3.10) with
$\partial _{t}U=0$
. When
$\partial _{t}U\neq 0$
, the correction to Frankel & Weihs’ solution can be written
$$\begin{eqnarray}A-A_{FW}=\partial _{t}UA_{a}^{(FW)}\end{eqnarray}$$
where
$A_{a}^{(FW)}$
satisfies at leading order the equation deduced from (3.12a
):
$$\begin{eqnarray}\displaystyle \frac{\partial ^{3}A_{a}^{(FW)}}{\partial Z^{3}}+S^{3}\ell _{0}^{2}\displaystyle \frac{\partial A_{a}^{(FW)}}{\partial Z}=2S^{5/2}\ell _{0}^{3}Z.\end{eqnarray}$$
This equation can be solved explicitly using mass conservation and the boundary conditions deduced from (5.8), that is
$$\begin{eqnarray}\displaystyle & \displaystyle \partial _{Z}A_{a}^{(FW)}(Z=0)=\partial _{Z}A^{(FW)}(Z=1)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \int _{0}^{1}A_{a}^{(FW)}(Z^{\prime })\text{d}Z^{\prime }=0. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}A_{a}^{(FW)}=2S^{-1/2}\ell _{0}\left(\frac{Z^{2}}{2}-\frac{1}{6}+\frac{\cos (\ell _{0}S^{3/2}Z)}{\ell _{0}S^{3/2}\sin (\ell _{0}S^{3/2})}-\frac{1}{\ell _{0}^{2}S^{3}}\right).\end{eqnarray}$$
The correction to Frankel & Weihs’ solution can then be rewritten as
$$\begin{eqnarray}\frac{A-A_{FW}}{A_{FW}}=B_{a}F(Z,{\it\lambda})\end{eqnarray}$$
where
$B_{a}=({\it\rho}/{\it\sigma})A_{FW}\partial _{t}U$
is a Bond number associated with the dynamics and
$$\begin{eqnarray}F(Z,{\it\lambda})=2{\it\lambda}\left(\frac{Z^{2}}{2}-\frac{1}{6}+\frac{\cos ({\it\lambda}Z)}{{\it\lambda}\sin ({\it\lambda})}-\frac{1}{{\it\lambda}^{2}}\right).\end{eqnarray}$$
The function
$F$
depends on a single parameter
${\it\lambda}$
which corresponds to the relative length of the bridge:
$$\begin{eqnarray}{\it\lambda}=\ell _{0}S^{3/2}=\ell /\sqrt{A_{FW}}.\end{eqnarray}$$
The function
$F(Z,{\it\lambda})$
is plotted in figure 16(a) for
${\it\lambda}=1$
and
${\it\lambda}=2$
. It diverges when
${\it\lambda}\rightarrow {\rm\pi}$
as
$$\begin{eqnarray}F(Z,{\it\lambda})\sim \frac{2\cos ({\rm\pi}Z)}{{\rm\pi}-{\it\lambda}}.\end{eqnarray}$$
Figure 16. (a) Shape correction
$F(Z,{\it\lambda})$
to Frankel & Weihs’ solution versus
$Z=z/\ell (t)$
for two different aspect ratios
${\it\lambda}$
. The dashed line represents the asymptotic estimate for small
${\it\lambda}$
. (b) Critical Bond number
$B_{a}^{(c)}$
for the break-up of Frankel & Weihs’ solution. The dashed line reports the critical Bond number obtained for the solution with attached boundary conditions (figure 14
c).
As in the case with attached boundaries, this divergence is due to a resonance with the first sloshing mode, which is present for the boundary conditions (5.12a
) when
${\it\lambda}={\rm\pi}$
. For small
${\it\lambda}$
, the function
$F$
is small and varies according to
$$\begin{eqnarray}F(Z,{\it\lambda})\sim {\textstyle \frac{1}{180}}{\it\lambda}^{3}(15Z^{4}-30Z^{2}+7).\end{eqnarray}$$
This estimate is plotted as a dashed line in figure 16(a) for
${\it\lambda}=1$
. As observed, even for this large value of
${\it\lambda}$
, the asymptotic estimate is very good.
The vanishing of the surface
$A$
provides an estimate for break-up. Such a vanishing occurs at the boundary (
$Z=1$
), and for a critical Bond number
$B_{a}^{(c)}({\it\lambda})=-1/F(1,{\it\lambda})$
which is plotted in figure 16(b). This critical Bond number is also compared with that of the solution with attached boundary conditions (shown as a dashed line) in this figure. We observe that the critical Bond number for Frankel & Weihs’ solution is always smaller, showing that break-up (or nonlinear transition) is a priori easier in this case.
6. Influence of gravity
In this section, we discuss the effect of gravity and therefore assume that, in equation (2.1b
),
$Bo$
is non-zero. A typical value for
$Bo$
in a millimetre water bridge is
$Bo\approx 0.2$
. A priori, both the numerical study and the theoretical analysis can be performed similarly in the presence of gravity. The first effect of gravity consists of modifying the equilibrium shapes: they are not Delaunay curves anymore but curves given by
$$\begin{eqnarray}\displaystyle \frac{\partial K}{\partial z}=Bo.\end{eqnarray}$$
Moreover, the equilibrium shapes are no longer symmetric with respect to the mid-plane, as more fluid is found at the bottom than at the top. Typical shapes are illustrated in figure 17. In this figure, we can observe that there is a good agreement between the dynamical experimental shapes and the numerical equilibrium curves obtained by solving (6.1). Though gravity alters drastically the equilibrium shape (see figure 17), it does not actually affect the theoretical analysis. When the elongation speed
$U$
and the acceleration
$\partial _{t}U$
are small, the same asymptotic analysis can be performed and the same equations for the velocity and the shape correction are obtained in the presence of gravity upon changing
$A_{D}$
by the new equilibrium shape obtained for
$Bo\neq 0$
. The dependence with respect to
$Bo$
therefore only appears via the equilibrium shape. As before, we therefore expect the velocity in the liquid bridge to remain at leading order independent of
$Oh$
. We also expect the shape correction to be the sum of three terms: a viscous term of order
$Oh\,U$
, an inertial term of order
$U^{2}$
and an acceleration term of order
$\partial _{t}U$
.
Figure 17. Experiment on a slowly stretched water bridge:
$U=0.2$
,
$Oh=0.04$
,
$Bo=0.5$
. Equilibrium shapes are superimposed in white. From left to right:
$\ell =1.33$
, 1.66, 2.00, 2.31, 2.65, 2.96. Disk diameter is 2.86 mm and corresponds to two graduations. Dynamical shapes remain virtually the same as static ones as long as the bridge remains in the stable domain (
$\ell \lesssim 3$
here).
7. Conclusion
We have considered the dynamics of an axisymmetric viscous liquid bridge stretched between two co-axial rods using the one-dimensional model of thin bridges. Our goal has been to quantify the differences between the equilibrium shapes and the dynamical shapes obtained by moving the rods with a small velocity and acceleration when the surface is attached to the rods.
Whereas the Delaunay curves that define the equilibria only depend on the two geometrical parameters
$\ell _{0}$
and
$S$
(when gravity is negligible), the dynamical curves also vary with respect to three other parameters which are the elongation speed
$U$
, the acceleration
$\partial _{t}U$
and the Ohnesorge number
$Oh$
. Using a perturbation approach, we have been able to show that the shape correction is the sum of a viscous term proportional to
$Oh\,U$
, an inertial term proportional to
$U^{2}$
and an acceleration term proportional to
$\partial _{t}U$
. Explicit expressions for these shape corrections have been obtained when the Delaunay curve is a cylinder (
$S=1$
), which has allowed us to put forward some speculative estimates for bridge break-up. In the theory, we have also obtained that a non-uniform velocity field proportional to
$U$
is present in the bridge. This velocity field is due to kinematic effects and is independent of
$Oh$
. The variations of some characteristics of this field such as the maximum and minimum strain rates have been analysed as functions of
$\ell _{0}$
and
$S$
. Interestingly, we have observed that a region of compression (negative strain rate) appears close to the rods when
$S$
becomes large.
The asymptotic results have been validated by numerical simulations. We have considered two situations: one where the bridge is stretched with a constant velocity; another where the length of the bridge is oscillated. Both the velocity field and the shape corrections have been compared to the theory for a large range of parameters and a very good agreement has been demonstrated in both cases. The departure from the theory has been shown to be mainly associated with free eigenmodes of the bridge which are either excited during the transient or resonantly forced for particular oscillating frequencies.
The effect of gravity has been briefly addressed. We have shown that it modifies the equilibrium shape but not the main results of the perturbation theory. Finally, we have also shown that the theory can be applied to the cylindrical solution of Frankel & Weihs (Reference Frankel and Weihs1985) to compute the correction induced by acceleration.
As a concluding remark, we wish to recall that our analysis is based on a one-dimensional model. Though it provides a convenient framework to study liquid bridge dynamics, it may fail to describe adequately some situations. For example, oscillations of one or both of the rods may give rise to recirculating flows within the liquid bridge (see for example Mollot et al. Reference Mollot, Tsamopoulos, Chen and Ashgriz1993), that the one-dimensional model cannot handle. Also, for large stretching velocities (i.e. larger than the Taylor–Culick velocity), a boundary layer may form close to the solid boundary; this is not properly incorporated into the one-dimensional model, and requires special treatment (cf. Stokes, Tuck & Schwartz Reference Stokes, Tuck and Schwartz2000). By contrast, when the stretching speed is low and the oscillation amplitude is small, which is the case studied here, we expect the model to be accurate.
Acknowledgement
This work has benefitted from discussions with E. Villermaux.
