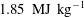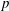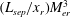2 Experimental facility and test model

Experiments are performed in the IISc hypersonic shock tunnel HST-2 (Sriram Reference Sriram2013). It is a conventional shock tunnel operated by means of shock compression of the test gas (air) in a shock tube (50 mm internal diameter), operated by pressurising 2 m long driver section (with driver gas He); the driven section is 5.12 m long. The test gas, compressed to high pressure and temperature at the end of the shock tube (thus simulating the total enthalpy), is expanded into the test section – of $300~\text{mm}\times 300~\text{mm}$ cross-section and length 450 mm – to the required Mach number by a nozzle based on the area ratio. The area ratio of the nozzle can be varied using throat inserts; in the present experiments the nozzle is operated in straight through mode – without a throat insert – to simulate Mach 6 flow, and in reflected mode with a throat insert to simulate Mach 8.5 flow. The end of the shock tube driven section is equipped with two PCB pressure sensors (manufactured and supplied by PCB Piezotronics, Inc.), which are used to measure the shock speed as well as the reservoir pressure for the tunnel at the nozzle entry after the shock reflects at the shock tube end. From the shock speed obtained from the pressure signals and from the initial driven section conditions, the reservoir conditions (total temperature and also the total pressure) can be estimated. A Pitot probe in the test section measures the stagnation pressure after a normal shock in the free stream.

The establishment of a steady free stream in the test section can be ensured from the measured Pitot pressure signals as shown in figure 2. The test times, of $600~\unicode[STIX]{x03BC}\text{s}$ , are also indicated (approximately starting at 3.3 ms and ending at 3.9 ms) in the figure, during which the value of the Pitot pressure is measured as the time average. The free stream conditions are estimated from the calculated reservoir conditions and from the measured Pitot pressure using normal shock relations (Sriram Reference Sriram2013) and are tabulated in table 1.

Figure 2. Typical Pitot signal in HST-2. (a) At Mach 5.88. (b) At Mach 8.54.

The test section ends in a dump tank which has ports for connecting cables from the sensors mounted in the test section to the data acquisition system (National Instruments) as well as the power supply/modulation circuits. The flow field (density gradients) in the test section can be visualized by means of a z-type schlieren arrangement, enabled within the short run time by a high-speed camera – Phantom V310 – which is operated at 10 000 frames per second with a spatial resolution of $640\times 480$ pixels for the present study.

Despite such low pressures (and temperatures) in the free stream, the fluid flow is expected to behave as a continuum for the important length scales considered in the study. The two extremes of the length scale relevant to the study are those of the separation length and the boundary layer thickness. Even based on a smaller length scale, which is the boundary layer thickness, typically of the order of 1 mm, the Knudsen number (expression given by Schetz & Fuhs (Reference Schetz and Fuhs1921)) does not exceed 0.01 for all the cases. However, for the length scale of the outer inviscid flow (typically, the separation length), which is two orders of magnitude larger than the boundary layer thickness and is the most important scale in the present study, the Knudsen number is typically two orders of magnitude smaller. The numbers clearly show that the rarefied gas effects need not be considered for the length scales involved in the phenomena under investigation. The possibility of real gas effects due to largely varying temperatures in the flow field cannot however be discounted. Although the dissociations and chemical reactions are not expected in the considered range of flow enthalpies, the vibrational and rotational modes of the gas molecules could play a role. To account for these effects the STN (Shock Tube and Nozzle calculations for equilibrium air) code of Krek & Jacobs (Reference Krek and Jacobs1993) has been used to estimate the above free stream conditions for the reflected mode (in which mode it is applicable); for the straight through mode the code is used to calculate back and verify the specific heat ratio $\unicode[STIX]{x1D6FE}$ and other conditions using the estimated stagnation pressure ratio across the normal shock. The code uses a single species gas model with curve fits for thermodynamic properties, given by Srinivasan, Tannehill & Weilmuenster (Reference Srinivasan, Tannehill and Weilmuenster1986). The specific heat ratio did not differ much for the straight through mode – it was 1.39 when back calculated using STN, rather than the value of 1.4 used for estimating the free stream conditions – and hence the free stream conditions also did not differ much. For the reflected mode, although the value of $\unicode[STIX]{x1D6FE}$ in the free stream was just 1.34, this is taken into account while estimating the free stream conditions since the estimation is done directly using the STN code. Hence only for the straight through mode cases with relatively less variation in $\unicode[STIX]{x1D6FE}$ , estimates based on shock angles measured from the schlieren images are presented, avoiding the reflected mode cases where such calculations may be erroneous due to considerable variations in $\unicode[STIX]{x1D6FE}$ . Concerning the separation length, it has been reported that the $\unicode[STIX]{x1D6FE}$ variations at moderate enthalpy ranges do not greatly affect the scaling laws (Sriram Reference Sriram2013; Sriram & Jagadeesh Reference Sriram and Jagadeesh2015a ); even at high enthalpies for small compression angles (Mallinson et al. Reference Mallinson, Gai and Mudford1997b ). The real gas effects would affect the scaling law governing separation length only at high enthalpies when dissociation and chemical reactions become important considerations (Davis & Sturtevant Reference Davis and Sturtevant2000). Thus the present study, at moderate enthalpies, does not consider the real gas effects on separation length.

The test model consists of a wedge (shock generator) of angle $31^{\circ }$ to the free stream, and the shock generated by the wedge is made to impinge on a flat plate. Few experiments (over the sharp leading edge plate) have been performed with a wedge of angle $26^{\circ }$ so as to have a different pressure ratio in order to improve the statistical basis for the observed trends. The wedge and the plate are held in their respective positions by a fixture, as shown schematically in figure 3. The top surface of the plate is kept at a distance of 57 mm from the bottom of the wedge. The span of the plate is 80 mm. The model dimensions are chosen by considering the issue of tunnel blockage (Sriram Reference Sriram2013). The model is equipped with PCB pressure sensors along the spanwise mid-line; the sensors are flush mounted on the surface.

Figure 3. Schematic of the test model.

The flat plate has provisions for leading edge inserts. A schematic diagram showing the design of different leading edge inserts is shown in figure 4 and a photograph of the plate along with different leading edge inserts is shown in figure 5. It can be noted from figure 4 that the blunt leading edge inserts are designed such that the hemicylindrical bluntness ends on the tangential flat plate surface at the position of the sharp leading edge. Thus any reference hereon to the streamwise position of the (blunt) flat plates would be specified in terms of the position of the sharp leading edge (where the blunt portion meets the flat surface); the corresponding location of the nose of blunt leading edge must be accordingly understood. For example if it is mentioned that the leading edge of the plate with a 2 mm radius blunt leading edge is at some specific streamwise location, it means that the nose of the blunt leading edge is 2 mm upstream of the specified location. All streamwise locations on the plate shall also be given in terms of distance from the sharp leading edge (i.e. from the point joining the hemicylindrical bluntness with the flat surface).

Figure 4. Schematic diagram of the flat plate with leading edge inserts.

Figure 5. Photograph of the flat plate with leading edge inserts; (a) oblique shock generator, (b) flat plate with sharp leading edge and (c) blunt leading edges of 2, 4 and 6 mm radii (from left to right).

The streamwise distance from the leading edge of the shock generator to the leading edge of the flat plate can be varied by moving the plate back and forth on a fixture. In the present study, the (sharp) leading edge flat plate is kept at two different positions, at Mach 5.88 – 15 and 30 mm behind the leading edge of the $31^{\circ }$ shock generator, as shown in figure 6. The two cases shall subsequently be referred as $15BST$ and $30BST$ ( $BST$ stands for Behind, Straight Through mode) respectively. For the higher Mach number case, experiments are performed for only one position of the flat plate relative to the wedge – with the leading edge of the plate 30 mm behind that of the wedge, and this case shall be referred as $30BR$ ( $BR$ stands for Behind, Reflected mode).

Figure 6. Schematics of positioning of flat plate relative to the wedge. (a) 30 mm behind, 30B configuration. (b) 15 mm behind, 15B configuration.

For the few cases with the $26^{\circ }$ shock generator, the plate positions are adjusted such that the reattachment location is nearly the same as that for the $30BST$ or $30BR$ cases for the respective nominal Mach numbers; thus for the respective nominal Mach numbers, the plate position is 55 and 50 mm behind the leading edge $26^{\circ }$ wedge. It must also be noted that experiments with the $26^{\circ }$ wedge were performed after a minor upgrade of the HST-2 test section and dump tank. The dump tank volume was considerably increased ( $2.16~\text{m}^{3}$ ), while the test section dimensions remained the same. Minor alterations in the nozzles resulted in slightly lower free stream Mach numbers than the nominal Mach numbers: 5.52 and 8.41, with total enthalpies 1.29 and $1.80~\text{MJ}~\text{kg}^{-1}$ and free stream pressures of 2040 and 195 Pa respectively for the two Mach numbers. While the experiments at the mentioned nominal Mach numbers are discussed for the most part, the free stream conditions (especially the Mach numbers) for the $26^{\circ }$ wedge experiments shall be explicitly stated whenever those results are presented.

The uncertainties in free stream conditions are obtained from the uncertainties in the measured shock tube conditions and Pitot pressure (from the method of uncertainty analysis described by Moffat (Reference Moffat1988)). For free stream conditions, the uncertainty in free stream Mach number is $\pm 1.92\,\%$ , in the free stream pressure and temperature $\pm 7.44\,\%$ and $\pm 6.94\,\%$ respectively, in total enthalpy $\pm 6.54\,\%$ and in free stream Reynolds number is $\pm 9.71\,\%$ . Concerning surface pressure measurements, the PCB sensors have an uncertainty of $\pm 1\,\%$ .

3 Computational methodology

Flow field is numerically computed for a limited number of cases (mostly at Mach 5.88, with only one case at Mach 8.54 for a sharp leading edge plate without an impinging shock) in order to complement the experiments and to understand the physics in some more detail. The numerical simulations are performed in collaboration with the Center of Excellence in Hypersonics, IISc Bangalore, using the in-house finite volume code, High Resolution Flow Solver on Unstructured meshes (HiFUN). It is assumed that the flow is fully laminar, which is sufficient to understand the important trends (as will be apparent later). Three-dimensional steady computations of the shock boundary layer interaction are performed for the cases with a sharp leading edge and for leading edge bluntness of 2 and 4 mm – for the exact geometries of the test model as described in the previous section – in an attempt to gain some insight on the three-dimensional organization of the separation bubble (which cannot be obtained experimentally from the schlieren visualizations). Computational domain for the SBLI simulations is shown in figure 7. Structured meshes are generated for all the cases using a commercial grid generator. The mesh consists of nearly 5 million volumes with a first spacing of $10~\unicode[STIX]{x03BC}\text{m}$ . Reynolds-averaged Navier–Stokes equations are solved using HiFUN. Due to the complex nature of the flow, residual oscillations are observed for the SBLI case, the simulations are declared converged when the density residue falls to $10^{-4}$ . For the computational fluid dynamics (CFD) results presented, the Harten–Lax–van Leer–Contact (HLLC) (Toro, Spruce & Speares Reference Toro, Spruce and Speares1994) flux formula has been used for the computation of inviscid fluxes and a diamond path reconstruction-based (Munikrishna Reference Munikrishna2007) procedure has been used for the computation of viscous fluxes. Venkatakrishnan limiter (Venkatakrishnan Reference Venkatakrishnan1995) is used to limit the gradients of flow variables for preserving monotonicity. Convergence acceleration is achieved by using symmetric-Gauss–Seidel implicit relaxation procedure (Shende & Balakrishnan Reference Shende and Balakrishnan2004).

Figure 7. Isometric view of the computational domain along with model dimensions.

The important computational results are, however, those from the cases of the hypersonic viscous flow over the sharp and blunt leading edge flat plates, without the presence of the impinging shock. The velocity and the Mach number profiles within the boundary layer as well as within the high-entropy layer (HEL, which is highly rotational but inviscid above the boundary layer) at important locations are probed using these computations, and are compared for the different cases in order to understand the possible mechanisms that can lead to the observed trends in the SBLI with bluntness. To that end two-dimensional (steady) flow computations are sufficient. Figure 8 shows the computational domain used for the studies on the flat plates. The wall was assumed to be isothermal, at a constant temperature of 300 K. The grid details for the flat plate simulations are tabulated in table 2. The first spacing is kept constant at $1~\unicode[STIX]{x03BC}\text{m}$ for all the cases. Grid independence study is carried out for the sharp plate case. Due to the benign nature of the flow, the simulations are stopped when the density residue fall reached $10^{-10}$ . Figure 9 shows the velocity profile at $X=70$  mm for the sharp leading edge case for different grids. It is conspicuous from the velocity profile, that the results are grid independent. The results and inferences from the computations shall be presented along with the main experimental results in the subsequent sections, in such a way as provide additional physical insights on the observed phenomena.

Figure 8. Computational domain for the sharp leading edge flat plate case without impinging shock.

Figure 9. Velocity profile at $X=70$  mm for the $30BSTS$ case. (a) Over the entire length of the domain. (b) Near the wall.

4 Flow field with sharp leading edge

A schlieren image of the (steady) flow field with a shock induced large separation bubble over a sharp leading edge flat plate was shown before, in figure 1, which also shows a detailed surface pressure distribution. A good correspondence between the surface pressure distribution and the schlieren image may also be noted, with a ‘plateau pressure’ of a few times the free stream pressure inside the separation bubble, peak pressure immediately downstream of the apparent reattachment location and the pressure subsequently dropping downstream due to expansion waves. The spatially well-resolved distributions in the various regions in both the Mach 5.88 and Mach 8.54 flow fields were obtained by means of different fast response sensors. The behaviour of the pressure signals at different regions within the short shock tunnel run time was detailed by Sriram et al. (Reference Sriram, Ram, Hegde, Nayak and Jagadeesh2015b ), a brief summary of which shall be useful.

It was noted that the pressure signals well inside the separation bubble, as well as downstream of the apparent reattachment location (including the signal measuring the peak pressure), reached a statistically steady state even before the test time indicated by Pitot; this is attributed to the propagation of separation and reattachment shocks upstream during the flow establishment. However, at Mach 5.88, the signals near, but downstream of, the (steady) separation location reached a statistically steady value only by the middle of the test time, as it was observed from time-resolved schlieren images that the separation shock continued to move upstream towards its steady location until approximately $200{-}300~\unicode[STIX]{x03BC}\text{s}$ into the test time; that is, the separation location was fixed only $200{-}300~\unicode[STIX]{x03BC}\text{s}$ after the Pitot reached a statistically steady value. Further, at Mach 5.88, a wildly oscillating behaviour was observed in the pressure sensors immediately upstream of the apparent reattachment location (which would also be shown to occur for the blunt leading edge cases in the present set of experiments), the reason for which is not clear. However, such unsteadiness was not observed for the higher Mach number cases. The present study shall not present such detailed pressure measurements. The peak pressure measurement is the main focus, due to its importance in the scaling laws for separation length. Representative pressure measurements inside the separation bubble and spatially resolved measurements in the reattachment zone shall be presented. The PCB pressure sensors are closely placed, with 7.5 mm being the distance between the centres of subsequent sensors; 5 mm being the diameter of each sensor and the distance between the edges of subsequent sensors is 2.5 mm.

A closer view of the large separation bubbles with the (sharp) leading edge of the flat plate 30 mm behind the leading edge of the shock generator, for Mach numbers 5.88 and 8.54, is shown in figure 10(a,b). The schlieren images are cropped to show only 100 mm starting from the plate leading edge and 20 mm above the plate surface. It is apparent that the reattachment is a little downstream for the higher Mach number case (obviously, as the shocks are more oblique at higher Mach numbers), and the separation length is also lower.

Figure 10. Shock-induced separation bubbles with the plate leading edge 30 mm downstream of the leading edge of shock generator. (a) At Mach 5.88, 30BST configuration. (b) At Mach 8.54, 30BR configuration.

The estimation of the separation and reattachment locations shall be detailed later; however, it must be noted that despite the shock strength being higher at higher Mach number (since the wedge angle is fixed), the separation length for the higher Mach number case is apparently the same as that for the corresponding lower Mach number case. This is in accordance with some of the earlier similarity laws for separation length (particularly (1.5)), suggesting a higher power over Mach number than the shock strength (pressure ratio). The separation length in both the cases is apparently very much comparable to the distance of reattachment from the leading edge. A closer look near the leading edge shall be particularly useful for the present study. Figure 11 shows the flow field at Mach 5.88 for a distance of 50 mm from the leading edge, after detecting only the (highest local intensity contrast in) shock waves and shear layer.

Figure 11. The resolved flow field near the sharp leading edge at the $30BST$ configuration.

It can be seen that the leading edge shock tends to be a straight line only after 8 mm from the leading edge. Near the leading edge, the shock is curved, due to the sharply growing boundary layer; there is strong viscous–inviscid interaction due to large boundary layer displacement, which subsequently dies down. Away from the leading edge, the shock makes an angle of $16^{\circ }$ to the Mach 5.88 stream. It can thus be estimated that the Mach number behind the shock is 4.82 and the pressure is approximately 2.9 times the free stream pressure. Subsequently, the flow tends to expand downstream to the free stream conditions, and thus due to the considerable second-order effects, the hypersonic boundary layer essentially develops with a favourable pressure gradient (without impinging shock). The previous scaling law for a large separation bubble near a sharp leading edge (1.6) (Sriram & Jagadeesh Reference Sriram and Jagadeesh2015a ) did not however consider this effect. While intending to address the role of leading edge bluntness, it becomes particularly important to consider the viscous–inviscid interaction, as the bluntness affects the boundary layer displacement. The boundary layer displacement not only affects the outer inviscid flow field, but also determines the resistance to the impinging shock.

The angles of the separated shear layer and the separation shock – $10^{\circ }$ and $17.5^{\circ }$ respectively – relative to the plate are also marked in figure 11. From these angles, the approximate value of pressure after the separation shock, which is also approximately the average pressure inside the separation bubble, may be estimated. Since the separation is quite close to the leading edge, if it is assumed that just upstream of the separation shock the flow deflected by an angle of ${\sim}8^{\circ }$ by the leading edge shock has not sufficiently turned back, then the separated shear layer and separation shock are oriented at angles $2^{\circ }$ and $9.5^{\circ }$ respectively to the oncoming flow. For this combination of angles (for Mach 5 of oncoming flow) an oblique shock solution does not exist. The flow encounters expansion immediately after the leading edge shock such that, for the expanded Mach number, the combination of the angles relative to the flow must be a solution of the inviscid oblique shock equations. Interestingly, the closest solution is the combination of Mach 5.88 with the angles ${\sim}9.8^{\circ }$ and $17.5^{\circ }$ . This means that the flow is nearly turned back to the free stream direction by the time it reaches the separation shock, despite the separation being close to the leading edge; that is, the separation, in the considered cases, does not seem to occur in the region of strong viscous–inviscid interactions (expected very close to the leading edge). Further, for the separation location of ${\sim}10$  mm from the leading edge, the value of the viscous interaction parameter $\bar{\unicode[STIX]{x1D712}}$ is ${\sim}O(1)$ in the present study, while the criterion for weak interaction is typically that $\bar{\unicode[STIX]{x1D712}}$ tends to zero. Rudman & Rubin (Reference Rudman and Rubin1968) suggests that strong interactions occur for $\bar{\unicode[STIX]{x1D712}}\sim O(M_{\infty }^{2})$ . Thus, it is plausible that the flow has turned back significantly by the time it reaches the separation shock. For this combination of Mach number and angles it can be estimated that the pressure ratio across the shock is approximately 3.5; that is, the pressure after the separation shock is ${\sim}9$ times the free stream pressure (of 1280 Pa) accounting for the total pressure loss after the leading edge shock, which is also the pressure that is expected on average inside the separation bubble. The pressure values well inside the separation bubble recorded by the pressure sensors are also of the same order. Figure 12 shows the surface pressure signals obtained at 55 and 62.5 mm from the leading edge; the average pressure within the test time is of the same order (approximately 10 kPa) as the above prediction (though a little lower than the prediction). It can be noted that the signal at 62.5 mm from the leading edge, which is just upstream of the apparent reattachment zone, is unsteady, as previously stated. In some cases the amplitude of this unsteadiness upstream of reattachment is very high. The unsteady aspects are discussed later in more detail. However, the high pressures measured in the reattachment zone and further downstream are steady, as shown in figure 13.

Figure 12. Surface pressure signals inside separation bubble over sharp leading edge plate at Mach 5.88 ( $30BST$ ).

Figure 13. Surface pressure signals at apparent reattachment zone and downstream of reattachment zone at Mach 5.88 ( $30BST$ ).

It can also be observed from the schlieren image that the separation shock and the separated shear layer (traced by lines) seem to emanate from the same location on the plate. The distance between the location of separation and the point up to which the influence of the separation is felt upstream in the boundary layer is called the upstream influence length, which according to free interaction theory, is proportional to the boundary layer displacement thickness and inversely proportional to the square root of skin friction coefficient at the point of onset of interaction (upstream of separation point). Near the leading edge, the displacement thickness is small and the skin friction is large; accordingly, the upstream influence length is negligible for the present cases when compared with the separation length itself (Sriram Reference Sriram2013). The separation location can thus be approximated as the location where the separation shock intersects the surface of the flat plate. To do this precisely, the intensities along the vertical lines are scanned, and the coordinates of peak intensities (in terms of pixels) corresponding to the separation shock are noted; a line is fit along the points of peak intensities, whose intercept on the plate, as shown in figure 14, gives the approximate separation location.

Figure 14. Line fit for the separation shock.

Based on the point at maximum distance from the line fit, the uncertainty in separation shock location is only $\pm 0.05$  mm. The location of reattachment is not as straightforward from the schlieren images. A closer look at the reattachment zone reveals that the reattachment shock is nearly parallel to the plate surface for a distance of approximately 5 mm after which it turns oblique, as shown in figure 15.

Figure 15. Flow field over the sharp leading edge plate at Mach 5.88 at the reattachment zone.

The extent to which the shock is parallel to the surface can also be ascertained by the aid of an intensity scan. Scanning the intensity along a horizontal line, 6 pixels above the plate surface (at plate surface and a little above the surface, the intensities do not vary greatly), high intensities are noted, as shown in figure 16. The 20 pixels of high intensity (at about 70 mm from the leading edge in figure 16) correspond to a horizontal distance of 5 mm. It must also be mentioned that this is the case with a maximum distance for which the shock is parallel to the surface, whereas at higher Mach number the distance was lower at approximately 4 mm.

Figure 16. Intensity along the horizontal line 6 pixels above the plate surface.

With the shock being parallel to the surface, the separated shear layer must reattach nearly normal to the surface, as shown schematically in figure 17; this may be considered analogous to the stagnation point flow. The reattachment point is approximated as the mid-point of the portion of the shock which is parallel to the surface, and accordingly the uncertainty in reattachment location (and hence in the separation length itself) is $\pm 2.5$  mm.

Figure 17. Schematic of the reattachment for the sharp leading edge.

For the sharp leading edge case at Mach 5.88 (for $30BST$ ) the separation location is 10 mm from the leading edge and the reattachment location is 70 mm from the leading edge. Thus the separation length is 60 mm.

The surface pressure distributions for the two Mach numbers (for the cases $30BST$ and $30BR$ ) are shown in figure 18. Only the pressures well inside the separation bubble, reattachment and downstream of reattachment are obtained in the present experiments. A good correspondence with the schlieren images can be noted. Peak pressure is measured just downstream of the reattachment point located from the schlieren images. Subsequently, the pressure drops downstream due to expansion waves from the rear end of the wedge.

Figure 18. Surface pressure distributions over the flat plate with sharp leading edge for the $30B$ configuration. (a) At Mach 5.88. (b) At Mach 8.54.

It should be noted that the above discussions present a two-dimensional steady perspective of the flow field. It is however important to reflect upon the three-dimensional and unsteady aspects, so as to qualify the above measures. The schlieren images at a particular time frame contains the information from the entire span of the test section, although most comes from the significant density gradients present in the core of the flow; the extent of the foots of separation and reattachment shocks as measured above correspond to the two-dimensional core around the middle of the span. Sriram & Jagadeesh (Reference Sriram and Jagadeesh2015a ) presented a conservative estimate for the two-dimensional core by assuming an adiabatic wall. Although side fences could be employed to reduce three-dimensional effects from the sides in the form of spillage, for low aspect ratio models, it has been observed that they affect (increase) the separation length (Holden Reference Holden1971a ). In the absence of side walls, an estimate of $10\unicode[STIX]{x1D6FF}_{s}$ was suggested by Ball (Reference Ball1971) as the distance from the edges until that at which the three-dimensional effects encroach on the separated flow field, where $\unicode[STIX]{x1D6FF}_{s}$ is the boundary layer thickness at the separation location. An adiabatic wall must have a thicker boundary layer than a cold isothermal wall; therefore, the adiabatic wall assumption was used to fix the upper theoretical bound for the penetration of the three-dimensional effects from the sides. For the farthest separation location at 38 mm from the leading edge in their study (Sriram & Jagadeesh Reference Sriram and Jagadeesh2015a ), with the maximum estimate of ${\sim}3$  mm for boundary layer thickness, the core around the centreline was found to be ${\sim}20$  mm for the model spanning 80 mm. For all the cases in the present study however, the separation location is relatively upstream. Secondly, though the boundary layer thickness is not measured, the computations of the flow over the flat plate (without impinging shock) using the isothermal (cold) wall assumption predict a relatively thinner boundary layer, of ${\sim}1$  mm at the separation location for Mach 5.88 cases. The numerically computed boundary layer profile, even for the $30BRS$ case at 23 mm from the leading edge (the experimentally determined separation location), showed that the boundary layer thickness is ${\sim}2.5$  mm (a thicker boundary layer is expected for this case due to lower Reynolds number). The two-dimensional core is thus expected to span more distance in the present cases than that expected with the assumption of an adiabatic wall. Figure 19 shows a comparison of the pressure signals (during the tunnel test time) at the centreline and at a spanwise distance of 15 mm from the centreline, both located near (just upstream) of the reattachment location for the $30BSTS$ case; the signals are normalized by the mean pressure value measured by the centreline sensor during the test time.

Figure 19. Comparison of pressure signals during the tunnel test time just upstream of reattachment for the $30BSTS$ case.

The location is chosen especially because the reattachment shock oscillates around this zone, and as mentioned before, these oscillations are felt in the pressure signals. It is apparent that the pressure signals are very much comparable qualitatively as well as quantitatively. This ensures that the two-dimensional core is at least 30 mm in span. It must also be remembered that the PCB sensor has a diameter of 5 mm and the locations stated correspond to the centre of the sensor.

The three-dimensional computations significantly underpredict the separation length; the separation locations are significantly downstream in the computational results, as shown in the numerical schlieren for the 30BSTS case in figure 20(a). The reattachment location in the numerical schlieren is fairly close to the experiments. The computations predict that the reattachment location at 15 mm spanwise distance from the (spanwise) centreline is 3.45 % downstream of the reattachment location at the centreline; the computed peak pressure at 15 mm spanwise location is 8.82 % lower than the pressure at the centreline. Figure 20(b) shows the pressure contour over half the span of the surface, with the surface streamlines superimposed.

Figure 20. Computed $30BSTS$ flow field shown over half-span of the flat plate. (a) Numerical schlieren. (b) Filled pressure contour (in Pa) along with the separation and reattachment lines on the plate surface.

The streamline pattern also reveals the lines of separation and reattachment. Evidently the information that can be compared with the experiments, such as separation length and pressure distribution along the centreline, are quantitatively far from the experimental results. There are not enough data to compare the three-dimensional picture; and also the patterns of separation and reattachment lines are contrary to some of the previous experimental results (for example, the oil flow visualisations of SBLI shown by Verma & Manisankar (Reference Verma and Manisankar2012)). However, the computations suggest the possibility of a complex vortex structure inside the large separation bubble. The turning of the surface streamlines back and forth inside the separation bubble suggest that the recirculation bubble can have multiple vortices rather than a single vortex. This must however be considered as speculation based on a possible solution of the flow equations. Understanding such aspects requires further systematic investigation which cannot be addressed with the capabilities employed in the present study. The main issue with the computation of shock boundary layer interactions of such scales could be the accuracy in resolving the location of the sonic line in the boundary layer. The upstream influence, and hence the separation length, are extremely sensitive to the location of sonic line. With the present computational capability it was not possible to resolve this.

Assumption of steady flow field could have also affected the accuracy of the computations. It is possible that the separation and reattachment lines are rather organised as spanwise ripples (Humble et al. Reference Humble, Elsinga, Scarano and Van Oudheusden2009), which may be observed if unsteady computations are performed. There are experiments where some sort of ‘phase difference’ (with almost the same mean pressure value) was observed between the pairs of signals at different spanwise locations (but with the two senors placed at equal streamwise distance from the leading edge) near the reattachment, which shall be presented when discussing the blunt leading edge cases. However, a detailed study of the three-dimensional spatio-temporal organization is not presently intended. The above discussion is rather intended to explore the possible extent of the two-dimensional core around the spanwise centre. All the inferences from the present experiments must thus be understood as corresponding to this two-dimensional core.

Further, the schlieren images presented above correspond to one particular frame when the flow over the plate was statistically steady; although the mentioned separation length for a particular case was the average of all frames during the steady flow duration and over the number of repeated experiments for the case. Two unsteady aspects must be distinguished. Firstly, the flow evolution is an important concern during the short run time of the shock tunnel especially as the flow field involves separation. Investigations on the establishment time for a separated flow field over compression corners and double cones in short duration (few $100~\unicode[STIX]{x03BC}\text{s}$ to few ms) test facilities such as shock and expansion tunnels have been reported (Mallinson et al. Reference Mallinson, Gai and Mudford1997a ; Swantek & Austin Reference Swantek and Austin2015). Davies & Bernstein (Reference Davies and Bernstein1969) suggested that the time $\unicode[STIX]{x0394}t_{fp}$ taken for the establishment of attached boundary layer over the flat plate for a length $L$ in a free stream of velocity $U_{\infty }$ is,

Accordingly, for a plate of approximately 200 mm, which is more than twice the distance of reattachment, the time for establishment of the boundary layer is just $44~\unicode[STIX]{x03BC}\text{s}$ for the Mach 5.88 flow; it is even less for the Mach 8.54 flow at approximately $36~\unicode[STIX]{x03BC}\text{s}$ . The establishment time for the boundary layer is well within the observed Pitot rise time. The impinging shock must evolve within the Pitot rise time, since the reaching of a statistically steady Pitot reading ensures the establishment of the inviscid flow field in the tunnel. When the evolving boundary layer is thick enough for the evolving impinging shock strength (which also moves upstream of the plate during the evolution), the separation begins and the separation bubble starts growing in length. To obtain a conservative estimate for the time taken for the establishment of the separation bubble, it is assumed that the separation begins once the impinging shock is established, i.e. just after the Pitot reaches its statistically steady value. Holden (Reference Holden1971b ) suggested that the time $\unicode[STIX]{x0394}t_{sep}$ taken for the establishment of a separation bubble of length $L_{sep}$ is given as,

In the above equation $a_{\unicode[STIX]{x1D6FF}}$ is the mean speed of sound in the boundary layer, evaluated using an intermediate reference temperature $T^{\ast }$ given by Eckert (Reference Eckert1955); for a conservative estimate of $\unicode[STIX]{x0394}t_{sep}$ , $T^{\ast }$ is estimated by assuming a cold isothermal wall (at room temperature). It is assumed that the acoustic disturbances propagate outwards from the corner after the establishment of the steady boundary layer; in the present case, it is taken to start from the location of the established impinging shock (approximately the reattachment location). For a reattachment location at a distance of the order of 100 mm from the leading edge, and assuming the separation length also to be of the same order, $\unicode[STIX]{x0394}t_{sep}$ is estimated to be ${\sim}225~\unicode[STIX]{x03BC}\text{s}$ for both nominal free stream conditions. However, in the experiments, it is observed that the (statistically) steady separated flow field is established in a considerably shorter time. In order to get more details on flow establishment and unsteady aspects, a few schlieren visualizations were obtained at 40 000 frames per second, though the spatial resolution was significantly reduced to $352\times 184$ pixels. The evolution of the flow field is shown in figure 21 for the $30BSTS$ case through a sequence of schlieren images, with a $100~\unicode[STIX]{x03BC}\text{s}$ interval between consecutive images.

Figure 21. Time evolution of flow for sharp leading edge for $30BSTS$ case. $^{\ast }$ indicates Pitot test time.

It can be seen that the flow field is established by $3400~\unicode[STIX]{x03BC}\text{s}$ , which is $100~\unicode[STIX]{x03BC}\text{s}$ after the Pitot reaches the statistically steady value. The reattachment shock reaches an upstream location of 66 mm from the leading edge at $3300~\unicode[STIX]{x03BC}\text{s}$ , although at $3400~\unicode[STIX]{x03BC}\text{s}$ it reaches its (statistically) steady location. The separation shock continues to move upstream until it reaches its (statistically) steady location at $3400~\unicode[STIX]{x03BC}\text{s}$ . The steady separated flow field however starts to terminate after $3800~\unicode[STIX]{x03BC}\text{s}$ , with separation and reattachment shocks moving upstream of their (statistically) steady location. In these cases the surface pressures are measured as the time average during these $400~\unicode[STIX]{x03BC}\text{s}$ (from 3400 to $3800~\unicode[STIX]{x03BC}\text{s}$ ) when the flow field is steady. At Mach 8.54, although the flow seems to be established just after the Pitot reaches the steady value, it remains steady throughout the tunnel test time. Therefore the evolution of Mach 8.54 case is not discussed in detail here (time-resolved images for a similar case are presented by Sriram (Reference Sriram2013)).

The second unsteady aspect concerns the oscillations exhibited after the statistically steady flow is established. The high frame rate of 40 000 fps also enabled a detailed observation on the unsteadiness within the time when the separated flow is statistically steady. Figure 22 shows the behaviour of the foot of separation and reattachment shock within the test time.

Figure 22. Separation and reattachment location variation with time for the $30BSTS$ case.

It can be seen that within the time the separated flow is statistically steady, the reattachment shock oscillates from a 68 to a 72 mm distance from the leading edge; the separation shock position oscillates by barely a millimetre. The number of ‘cycles’ within the run time is very few to be sure about the frequency. Shock boundary layer interactions often exhibit unsteadiness inherently. For the turbulent boundary layer, it is established that the unsteadiness in the shock induced separation bubble is due to the internal mechanisms rather than incoming turbulence (Clemens & Narayanaswamy Reference Clemens and Narayanaswamy2014). That being the case, even the laminar shock boundary layer interactions, such as the present cases near the leading edge, can be unsteady. Analogous to cavity flows, two modes of unsteadiness can be expected; the high-frequency low-amplitude oscillations similar to the shear layer mode, and the low-frequency large-amplitude oscillations like the wake mode. Most of the observed cases of unsteadiness in supersonic turbulent SBLI were found to exhibit the wake-mode-like behaviour (Clemens & Narayanaswamy Reference Clemens and Narayanaswamy2014) typically with a Strouhal number 0.01 based on separation length and incoming flow velocity, except for a report based on direct numerical simulation (DNS) (Pirozzoli & Grasso Reference Pirozzoli and Grasso2006). For the present cases, even if the test time is taken as the period of oscillation, the Strouhal number would be of the order of 0.1, while the amplitude of oscillations are not significant in comparison to the separation length. It could be possible that the present cases exhibit unsteadiness similar to the shear layer mode. However more detailed studies in long duration facilities are required to understand the unsteady aspects better. In the present cases, with the amplitude of oscillations being considerably less than the separation length, the reported separation and reattachment locations are the time-averaged values during the time when the flow field is statistically steady. The reported reattachment/peak pressure is also the time-averaged value of the pressure (during the time when the flow field is statistically steady) measured by the sensor at the reattachment point or a little downstream. For example, for the $30BSTS$ case, the peak pressure is the mean pressure read by the sensor at 70 mm in figure 13. The signal is statistically steady when compared with the signal at 62.5 mm in figure 12 which experiences the effect of the shock motion, especially during the beginning and end of the time when the flow is statistically steady, as seen in the visualizations. The present study cannot probe much into the unsteady signals just upstream of the statistically determined reattachment location beyond correlating them with the shock motion.

Since the location of impingement is not experimentally determined (as the impinging shock is affected by the expansion waves from the rear end of the wedge) the measured reattachment location, which was found to be close to the impingement locations determined from Euler computations (Sriram Reference Sriram2013), shall be used in the present study for scaling the separation length, rather than the impingement location itself. Thus, the relationship between the separation length scaled by the reattachment location and the free stream Mach number and reattachment (peak) pressure ratio, suggested in (1.5), is explored for the present data, as shown in figure 23.

Figure 23. Scaling law for interaction over sharp leading edge plate.

The linear relationship (1.6) as suggested by the previous scaling law (Sriram & Jagadeesh Reference Sriram and Jagadeesh2015a ) is observed here as well, by replacing the distance of impingement with the distance of reattachment. The experimental data are apparently clustered around a point for each set of Mach number and wedge angle. Since the expansion fan from the wedge end plays an important role in determining the shock strength at impingement, for the $26^{\circ }$ wedge case at Mach 8.41, the pressure ratio at reattachment (which goes with the shock strength at impingement) is higher since the expansion interacts with the shock wave farther downstream than with the $31^{\circ }$ wedge; for the straight through mode though, the pressure ratio at reattachment is smaller with the smaller angle wedge, as expected. The fact that for low reattachment pressure (lower than the incipient separation pressure) there is no separation (zero separation length) additionally provides verification for the correlation. The present relation is

The sharp leading edge data include a number of experiments from five cases: $15BST$ , $30BST$ and $30BR$ with the $31^{\circ }$ wedge, and $55BST$ and $50BR$ with the $26^{\circ }$ wedge. The boundary layer displacement effects are not considered as yet, and the free stream conditions are rather employed in the above correlation than the modified inviscid flow conditions due to boundary layer displacement; their importance would be evident as the sharp leading edge case would be contrasted with the blunt leading edge cases (where the conditions at the shock impingement location are largely different from free stream conditions). Other than the separation length, another important feature is the upstream bias of the separation bubble. It may be observed that the separation bubble is placed more towards the upstream side of the location of impingement on the separated shear layer, than the downstream side towards reattachment, as shown in figure 24 for the $30BST$ case.

Figure 24. Upstream skew of the separation bubble at Mach 5.88 ( $30BST$ ).

The portion upstream of shock impingement of the shear layer occupies three-quarters of the total separation length. Such upstream skewing was found to be prominent at high shock strengths in the numerical simulations of Krishnan et al. (Reference Krishnan, Yao, Sandham and Roberts2005); prominent skewing was observed at hypersonic Mach numbers, for a ratio of reattachment pressure to the free stream pressure of approximately 4.4, whereas in the present case it is as much as 30. The upstream skew ratio $\unicode[STIX]{x1D706}$ can be defined as the ratio of the length $L_{u}$ of the separation bubble from separation up to the location of shock impingement on the shear layer, to the total separation length:

For the $30BST$ sharp leading edge case it is 0.83, as shown above. For the higher Mach number case $30BR$ , the ratio is found to be a little lower – 0.78. For the $15BST$ case, with a larger separation length of approximately 66 mm, the ratio is higher – 0.82. It appears $\unicode[STIX]{x1D706}$ is directly related to the separation length. The cases of blunt leading edges would illuminate more on this aspect in the subsequent section.

5 Flow field with blunt leading edges

In order to articulate the effect that large bluntness can have on the shock boundary layer interaction near the leading edge, a schlieren image of the impinging shock interaction shall be presented straight away. The interaction at Mach 5.88 over the plate with 4 mm bluntness radius, for the case of $30BST$ is shown in figure 25. The case with 4 mm bluntness shall be referred as $30BST4$ , the end letter ‘4’ denoting the bluntness radius; the convention shall be followed subsequently.

Figure 25. Schlieren image of the interaction at Mach 5.88 over flat plate with blunt leading edge of 4 mm radius ( $30BST4$ ).

The leading edge seems to significantly modify the impinging shock; Mach reflection is apparent between the two shocks. Due to the strong leading edge shock, the impingement location moves upstream. The Mach number over the plate and the impinging shock strength are also lowered by the leading edge shock. Regular reflection was observed (other than the sharp leading edge cases) only with 2 mm bluntness; with 4 mm bluntness, while regular reflection was seen at Mach 8.54, even with $15BST$ it was Mach reflection at Mach 5.88. In order to quantify (using representative numbers) the changes in the inviscid flow field over the plate – without accounting for the boundary layer displacement – the contour of the leading edge shock is estimated (Billig Reference Billig1967) from the following expression:

where,

The expressions for $\unicode[STIX]{x1D6E5}$ and $R_{c}$ are valid for the cylindrical bluntness configuration, as with the present cases. $\unicode[STIX]{x1D6FD}$ is the Mach angle; as the distance from the bluntness becomes very large, the shock angle should tend to the angle of the Mach wave. The predicted contours of the bow shocks for the different bluntness are superposed over the visualized bow shocks (presented in terms of locations of peak intensities while scanning across the shock) in figure 26. It must be admitted that it was not possible to visualize the bow shock near the nose within the window in the experiments, and hence the experimental data are provided only from the beginning of the schlieren window. The comparison seems reasonable overall; for smaller bluntness, the prediction and experimental data are closer near the nose, while for 6 mm case the comparison gets better away from the nose.

Figure 26. Bow shock profiles for the blunt leading edge – comparison between present experiments and (5.1) at Mach 5.88. (a) 2 mm blunt radius, (b) 4 mm blunt radius, (c) 6 mm blunt radius.

From the contour, the location where the leading edge shock interacts with the impinging shock can be calculated. The local angle of the leading edge shock on the contour gives the local shock strength and the local Mach number behind the shock; from the local strengths of the leading edge shock and the impinging shock, the reflected shock strengths and angles can be estimated using the shock polar technique. The shock polar diagrams for the cases $30BST2$ and $30BST6$ at the estimated location of intersection with the impinging shock are given in figure 27(a,b).

Figure 27. Shock polars. (a) For 30BST2, (b) For 30BST6.

It can be seen that for both the cases there are solutions for regular reflection; notably, for the $30BST6$ case (as was also with other cases with 4 mm bluntness), even the weak solution has a pressure after the reflection which is more than that expected after a normal shock at Mach 5.88. However, experimentally, only for the 2 mm bluntness and sharp leading edge cases was regular reflection observed. For both 4 and 6 mm bluntness cases there was Mach reflection. Figure 28 compares the cropped schlieren images of the flow over a sharp leading edge for the 2 mm bluntness and 6 mm bluntness cases. The images display the flow field over the plate for a distance of 100 mm beginning from the location of sharp leading edge; meaning, for the blunt leading edge cases, it is from the beginning of the flat portion of the plate. Thus, for the 2 mm blunt leading edge plate, the image displays the flow from 2 mm downstream of the nose of the leading edge. The change in the pattern of shock–shock reflection can be noted from these images. For the case of 2 mm bluntness, regular reflection is observed as discussed before. A Mach stem of considerable width, as the impinging shock and the leading edge bow shock interact, is clearly seen for the 6 mm bluntness case, contrary to the predictions from the shock polar; the Mach stem is even wider than that with 4 mm bluntness, as shown before in figure 25. The occurrence of Mach reflection despite the theoretical existence of regular reflection solutions is very possible and has been reported in the literature before (for example Délery & Dussauge (Reference Délery and Dussauge2009)). However, the reason for the observed Mach reflections despite the intersection of the shock polar is not clear.

Figure 28. Comparison of flow fields over ( $30BST$ ) sharp and blunt leading edges. (a) Sharp, (b) 2 mm blunt radius, (c) 6 mm blunt radius.

However, even for the cases where Mach reflection is observed, the reflected shock strengths and angles can be approximately estimated. The interaction location can be roughly obtained from the contour of the leading edge shock; the local Mach number and shock strengths are known, and therefore the local pressure behind the leading edge shock is known. Due to Mach reflection, the pressure behind the reflected shocks must be the same as the pressure behind the normal shock for the free stream Mach number. Using this pressure, the strengths of the reflected shock can be estimated, and from that the angle of the shock too can be determined, as the local angle and Mach number of the flow behind the leading edge shock at the interaction point are known. Table 3 lists the estimated local Mach number $M_{b}$ behind leading edge bow shock at the location of interaction (estimated using (5.1)), the experimentally observed reflection type, the angle $\unicode[STIX]{x1D719}$ of the reflected impinging shock relative to the free stream direction and the impinging shock strength after reflection (in terms of pressure ratio across the reflected impinging shock).

It can be seen that the Mach number after the leading edge shock (at the point of intersection with impinging shock) decreases with the leading edge bluntness, for given free stream conditions and leading edge position; so is the impinging shock strength. The distance from the leading edge (relative to the position of sharp leading edge) where the shocks interact also decreases with the bluntness. The angle that the impinging shock makes to the free stream direction after reflection decreases with bluntness, while in the schlieren images the impinging shock seems to be curved with increasing angle to the free stream direction downstream of reflection due to the largely rotational flow field behind the bow shock (clearly seen for the cases with Mach reflection, particularly); hence the distance of impingement location from the leading edge is expected to vary with bluntness. Therefore, the reattachment location is also expected to vary with the leading edge bluntness, along with lower peak pressure (due to decreased shock strength); the extent of these variations with the bluntness is not theoretically ascertained due to various complexities in the flow field. It must however be noted that the numbers presented in table 3 are only used to understand the effect of the shock–shock interaction on the impinging shock; the numbers presented based on experiments are rather the measured separation and reattachment locations and the reattachment pressure, which shall only be used for further interpretations.

Looking back at the schlieren images with a blunt leading edge, one can notice that the separation bubble is significantly different in terms of size and appearance when compared with the corresponding sharp leading edge cases. The interaction between impinging shock and the leading edge shock can be seen to move upstream with bluntness, and the upstream shifting of location of impingement is clearly visible with 6 mm bluntness when compared to the 2 mm bluntness case in figure 28 above. The separation shock and the separated shear layer are relatively faint for the blunt leading edge cases, since the gradients are weaker due to lower Mach number. However, the intensities are enough to trace the shocks and obtain the separation location. It is apparent that the separation location moves downstream with increasing bluntness. The estimate of Mach number upstream of the separation shock, approximately from the angles of the separated shear layer and separation shock, is comparable to the local Mach number estimates behind the leading edge shock (when it just interacts with the impinging shock). The angle of separated shear layer (with the plate surface) for the 2 mm bluntness case is around $9.8^{\circ }$ and the angle of separation shock is around $21.7^{\circ }$ , for which combination the upstream Mach number is 4.1 for oblique shock to exist; for the case of 6 mm bluntness, the angles are $11.1^{\circ }$ and $27.1^{\circ }$ , for which the upstream Mach number is 3.2. These numbers can be compared with the estimated local Mach numbers $M_{b}$ listed in table 3.

Apparently, the separation length seems to have decreased with bluntness. However, the reattachment zone is visibly very different with the blunt leading edge cases, when compared with the sharp leading edge cases. Rather than being parallel to the plate at the reattachment zone as in the sharp leading edge cases, the reattachment shock seems to be oblique to the plate and quite away from the surface. A reliable comment on the trend in separation length requires fixing the reattachment location as precisely as possible. In order to ascertain the reattachment location for blunt leading edge cases, the streamline passing through the starting point of the reattachment shock may be considered, which is of local Mach number 1; an approximate linear contour of Mach 1 downstream of impinging shock, extended to the plate, shown schematically (exaggerated in dimensions) in figure 29.

Figure 29. Schematic of the reattachment zone over blunt leading edge plate.

Figure 30. Approximate reattachment location (for $30BST2$ ).

The reattachment streamline should be slightly upstream (where the extended Mach 1 contour meets the plate), the distance between the Mach 1 streamline and the reattachment streamline being obviously less than the shear layer thickness. Although there is no measure of shear layer thickness, it is supposedly small compared to the separation length. Secondly, the direction from which the shear layer approaches reattachment can be approximately taken to be the straight line from the point where the shock impinges on the shear layer as shown in figure 30 (for $30BST2$ ).

The scales indicated in the image also serves to get an idea about the (reduced) separation length, which can be compared with the $30BST$ sharp leading edge case with separation length of 60 mm. Approximately the reattachment is at 69 mm from the leading edge (beginning of the flat surface on the plate after the bluntness). This is supported by the pressure measurements too; the sensor at 70 mm reads the peak pressure for the case. The surface pressure signals measured by the sensors at 62.5 mm and at 70 mm for the $30BST2$ case are shown in figure 31.

Figure 31. Comparison of surface pressure signals at 62.5 and 70 mm from the leading edge for $30BST2$ case.

The signal at 62.5 mm is highly oscillatory; such oscillatory signals are observed upstream of the reattachment location for the sharp leading edge cases too, as mentioned before (the oscillatory behaviour is however not observed at Mach 8.54). A relatively steady (peak) pressure is measured at 70 mm, which is typical of the signal, little downstream of reattachment. Thus the surface pressure measurements are used to complement the reattachment location fixed from the schlieren images. However, the uncertainty in the reattachment cannot be fixed for the blunt leading edge case. Rather, the reattachment location fixed from schlieren, the location of the sensor measuring the peak pressure, the measured peak pressure value, and the separation length are listed for all the cases in table 4. A comparison of surface pressure distributions for the blunt leading edge cases are given in figure 32 and figure 33 respectively for Mach 5.88 (i) $15BST$ and (ii) $30BST$ ) and Mach 5.88 ( $30BR$ ) respectively.

Figure 32. Surface pressure distributions over the flat plate for different leading edges at $15BST$ (a) and $30BST$ (b) configurations.

Figure 33. Surface pressure distributions over the flat plate for different leading edges at $30BR$ configuration.

It should be mentioned again that for the blunt leading edge too, the numbers for separation length and pressures correspond to a two-dimensional core, averaged during the time when the separated flow is statistically steady. A comparison of the pressure signals (normalized using the mean centreline value during the tunnel test time) for a $30BST2$ case experiment at streamwise location of 62.5 mm from the leading edge, just upstream of reattachment, experiencing the effects of shock motion (especially around the beginning and end of the time when the separated flow is statistically steady) is shown in figure 34.

Figure 34. Comparison of pressure signals during the tunnel test time just upstream of reattachment for the $30BST2$ case.

Here too, the mean values during the test time are nearly the same, but there seems to be some sort of phase difference as mentioned before; this may be due to the spanwise rippling of the foot of the reattachment shock, which is not probed in detail in the present study. The oscillations in separation and reattachment shock during the test time are shown in figure 35. The trend is qualitatively similar to that of the sharp leading edge case, suggesting the possibility of shear-layer-mode-like unsteadiness for the blunt leading edge cases too. It shall be recalled that the focus of the present study is however only on the trends based the time-averaged values during the time when the separation bubble is statistically steady, in a two-dimensional core.

Figure 35. Separation and reattachment location variation with time for the $30BST2$  case.

It is evident that the separation length decreases (quite significantly) with the increase in bluntness, while the distance of the reattachment location from the leading edge decreases. The peak pressure too decreases with the increase in bluntness radius. The upstream skew ratio $\unicode[STIX]{x1D706}$ for the blunt leading edge cases are evaluated similar to the sharp leading edge cases. The variation of $\unicode[STIX]{x1D706}$ with separation length (including sharp leading edge cases) is shown in figure 36. Though for nearly same separation length (for different cases) the value of $\unicode[STIX]{x1D706}$ is apparently different, generally $\unicode[STIX]{x1D706}$ seems to increase with separation length, though other factors can play a role (which is however not clear from these data). This roughly means, the decrease in length of separation bubble is achieved with the decrease in the portion of the separation bubble upstream of the shock impingement location on the shear layer. The values are between 0.68 and 0.81; thus for all the cases the separation bubble is considerably biased upstream. Gun tunnel experiments by Murray, Hillier & Williams (Reference Murray, Hillier and Williams2013) reported values of $\unicode[STIX]{x1D706}$ in the same range for the axisymmetric impinging shock turbulent boundary layer interactions, with very high reattachment pressure ratio; the separation bubbles were as much as 40 mm in length, but were 700–800 mm away (downstream) from the nose.

Figure 36. Variation of $\unicode[STIX]{x1D706}$ with $L_{sep}$ .

The shift in reattachment location and reduction in peak pressure are in accordance with expectations of the modifications to the inviscid flow due to the strong leading edge shock, presented before. However, the decrease in separation length is not obvious; the decrease in impinging shock strength is also accompanied by decrease in Mach number upstream of interaction due to the leading edge shock. The trend shall be analysed further in the subsequent section.

6 Scaling for separation length

The scaling law for large separation length near sharp leading edge, expressed in (1.6), relates the scaled separation length to the free stream conditions, along with peak pressure. However, the inviscid flow over the boundary layer is not essentially free stream, even for the sharp leading edge case, due to boundary layer displacement effects. Since the displacement effects are of second order for large distances from the leading edge (i.e. at the impingement or reattachment locations considered) the free stream conditions sufficiently provided the scales. However, with blunt leading edges, the displacement effect and the entropy layer effects are expected to play a significant role. Hence it is important to find the relevant scales which would take into account these effects. Some of the previous similarity laws are founded on the asymptotic theoretical methods, which can help in finding appropriate scales even if not providing accurate solutions for the case in hand. Davis & Sturtevant (Reference Davis and Sturtevant2000), considered the flow in the vicinity of the dividing streamline where the velocity is low, such that the inertial forces are negligible, and integrated the balance between the pressure and shear forces ( $\unicode[STIX]{x1D70F}$ – shear stress) shown below:

The pressure forces, for the considered double wedge cases, are integrated for a distance of $y=0$ to $y=y_{R}$ which is the perpendicular distance of the reattachment point on the second wedge from the first wedge surface; this is facilitated by the assumption that the angle of the separated shear layer with respect to the first wedge is small. The shear stress is integrated from the onset of the interaction to the reattachment location. For a given pressure rise $(p_{1}/p_{3})$ , the locations corresponding to zero shear stress can be obtained from the integration; equation (1.4) is the similarity law for separation length (including real gas effects) obtained from the integration. The integration is performed within the framework of triple deck formulation (Stewartson & Williams Reference Stewartson and Williams1969), in which the thickness of the inner deck where the (6.1) holds and the extent of self-induced separation are given in terms of a small perturbation parameter $\unicode[STIX]{x1D716}$ (raised to suitable power), where $\unicode[STIX]{x1D716}\approx Re_{xl}^{-1/8}$ . It is also assumed that the shock is weak. While these scales are not appropriate for the present study (with strong perturbations by shock waves and large separation length), the similarity law obtained thus suggests the importance of local flow conditions in determining the shock-induced separation length. The other similarity laws, equations (1.1) and (1.2), also describe the separation length in relation to the local flow variables. Though a theoretical solution for the present case is not attempted, the relation of separation length to appropriate local flow variables may be explored.

The phenomenon is essentially that of the local boundary layer negotiating with the shock wave from the outer flow. At the location of shock impingement, the boundary layer is characterised by its thickness $\unicode[STIX]{x1D6FF}_{i}$ and velocity and Mach number profiles (which determine the upstream influence and the skin friction). The local skin friction coefficient as well as boundary layer thickness is related to the local Reynolds number $Re_{xi}$ (with corrections given in terms of Mach number due to compressibility effects). The inviscid flow field above the flat plate boundary layer (in the absence of impinging shock) at impingement location are determined by the boundary layer displacement; the inviscid flow conditions such as $M_{i}$ and $p_{i}$ are different from the corresponding free stream conditions (though for sharp leading edge plate the differences are not much as would be shown quantitatively later). If the pressure after inviscid shock reflection on the plate is $p_{3}$ , the following parameters may be expected to determine the separation length:

The reattachment (peak) pressure is of the order of the pressure after shock reflection, and it was observed that for same free stream Mach number (with sharp leading edge) the peak pressure is nearly the same for different shock impingement locations (Sriram Reference Sriram2013; Sriram & Jagadeesh Reference Sriram and Jagadeesh2015a ); this is observed even in the present study, for the $30BST$ and $15BST$ sharp leading edge cases. Further, the reattachment location for the large separation bubble is near the impingement location (Sriram Reference Sriram2013; Sriram & Jagadeesh Reference Sriram and Jagadeesh2015a ). The closeness is not just because it is considered relative to the separation length, but also from a practical view point of estimating the boundary layer effects; the locations are quite away from the leading edge, which is the zone of weak viscous–inviscid interactions, and hence the distance between the reattachment and (estimated) impingement location did not make much difference when estimating the boundary layer thickness, or displacement effects on outer flow. Hence the conditions after shock reflection were replaced by the reattachment conditions in (4.3). Further, because the shock strength is much larger than the incipient separation pressure (which is determined by the skin friction coefficient) the role of Reynolds number was found to be insignificant; the pressure and inertial forces are expectedly large. Thus the relationship of the following functional form may be expected:

The subscript $e$ stands for the edge of the boundary layer (in the absence of impinging shock); i.e.  $M_{er}$ stands for the Mach number at the edge of the boundary layer (without impinging shock) at reattachment location and so on. The conditions at the edge of the boundary layer, without shock, would account for the boundary layer displacement effects on the outer inviscid flow. For the sharp leading edge plate, in the weak viscous–inviscid interaction region, the pressure at the edge of the boundary layer is given by the following relation (Anderson Reference Anderson1989):

where the viscous–inviscid interaction parameter is $\bar{\unicode[STIX]{x1D712}}$ given by,

$C$ is the Chapman–Rubesin constant given by,

The (6.4) is written for a cold wall with wall temperature much less than adiabatic wall temperature. In short duration facilities, the wall temperature is not expected to increase considerably above the initial room temperature. From the above relations the pressure $p_{er}$ for the sharp leading edge cases is determined. The small deflection corresponding to the pressure rise can be estimated, for which the corresponding Mach number $M_{er}$ is determined.

The curved bow shock in front of blunt leading edge leads to entropy generation in the shock layer between the leading edge and the shock; the boundary layer develops along with the high-entropy layer generated by the blunt leading edge. For large bluntness, the boundary layer is well inside the high entropy layer even for large distances from the leading edge. In such a case the excess pressure to the free stream can be written as follows (Creager Reference Creager1957):

The first term is the viscous interaction term, which accounts for the boundary layer displacement (similar in form to the sharp leading edge case), and the second term is the inviscid pressure term based on blast wave analogy to hypersonic flow over blunt flat plates. In the second term $d$ is the diameter of the bluntness. The parameters $b$ and $c$ are given by the following expressions:

The constants $\unicode[STIX]{x1D6FC}$ , $\unicode[STIX]{x1D6FD}$ and $c_{1}$ are empirically determined (Creager Reference Creager1957); $\unicode[STIX]{x1D6FC}$ is the inverse of square root of the Chapman–Rubesin constant $C$ , $\unicode[STIX]{x1D6FD}=(1/2)^{2/3}$ and for air $c_{1}=0.112$ . From (6.7) the pressure at the boundary layer edge for the blunt leading edge cases are determined at the reattachment location. Since the boundary layer is well inside high entropy layer, the total pressure at the edge of the boundary layer is that of the total pressure behind the normal shock in the free stream. From the total pressure and $p_{er}$ , the Mach number $M_{er}$ is estimated. With the estimates of Mach number and pressure at the edge of the boundary layer, the relation between the parameters in (6.3) is explored (for both sharp and blunt leading edge cases), as shown in figure 37.

Figure 37. Relation between separation length and local flow parameters at reattachment location.

There is not much difference in the linear relation for the sharp leading edge, when compared with the linear relation given by (4.3) (shown in figure 23); in fact the differences between the conditions at the edge of the boundary layer and the free stream conditions are not much for sharp leading edge cases. However, for the blunt leading edge cases, the product of the cube of Mach number and scaled separation length is much below the line fit for the sharp leading edge data; importantly, it is nearly a constant for all pressure ratios, i.e. for all bluntness. There are two important questions in this regard.

Considering that the inviscid flow conditions at the edge of the boundary layer are corrected with the inclusion of displacement and entropy layer effects, the reason for these blunt leading edge data falling well below the linear relation for sharp leading edge must be understood. The forms for (4.3) or (6.3) can be arrived from few other similarity laws by ignoring the terms dependent on viscous forces in the limit of high pressure jump imposed by the shock and separation bubble much larger than boundary layer thickness. The theoretical foundation for such similarity laws is however (6.1), which is essentially the balance between shear and pressure forces; the pressure is integrated perpendicular to the shear layer and is equated to the integral shear forces over the separation length. If the viscous forces are to be ignored then it essentially amounts to invalidation of (6.1) (even as the other parameters from the relation are used). This means that the resulting relation is based on the Euler equation which must basically be independent of length scale. Thus the scaling for the separation length in (4.3) and (6.3) is not dynamic, but rather geometric; the separation length affects the flows deflection angles, as the separation shock angle is fixed locally by the boundary layer at the location of separation and this determines the subsequent shock interactions and flow deflection. The two equations may be read in this manner: in the limit that the scaled separation length is of order 1, the cube of Mach number is of the order of the reattachment pressure ratio. This relation between the Mach number and reattachment pressure ratio is the dynamical part of the relation. This is not the relation obtained by the integration of appropriate flow equations in the region close to the dividing streamline; it is rather the relation between the inertial and pressure forces in the flow outside the dividing streamline. Hence the parting of these blunt leading edge data from the line fit for sharp leading edge data must be seen as the shift in inviscid (rotational) outer flow dynamics due to the high-entropy layer. A deeper understanding of the mechanism is however not possible from the present experimental data.

Secondly, the constant product of cube of Mach number and scaled separation length with varying pressure ratio needs to be analysed. Even for the blunt leading edge cases the scaled separation length is of order 1; the minimum value of scaled separation length in the present study is 0.56 (for $30BR4$ case), while the maximum is 0.77 ( $30BST2$ case). These values are simply the inverse of the cube of Mach number. The drop in reattachment pressure with bluntness should not be just due to the decrease in impinging shock strength on interacting with the leading edge shock, but also due to the penetration of the impinging shock in the rotational outer flow with varying Mach number. Further inside, the impinging shock penetrates into a highly rotational high-entropy layer which is relatively thick for large bluntness. The change in shock strength due to the high-entropy layer can be related to the energy losses due to the bluntness. The power loss per unit span due to the drag added by the bluntness of radius $r$ is given by,

The flow tends to gradually overcome the losses downstream, and the extent to which the losses are overcome is dependent on the distance $x$ on the plate. It would be relevant to explore the relation between $r/x_{r}$ (which is proportional to the power loss) and the reattachment pressure ratio, as shown in figure 38.

Figure 38. Relation between bluntness ratio and local reattachment pressure ratio.

It appears that, for given free stream Mach number, the pressure ratio decreases with bluntness radius ratio. For higher Mach number case the pressure ratios are higher. Hence the following relation may be expected to exist, without getting into the possible physical reasons:

Considering the possibility of a relation of the form,

The value of $\unicode[STIX]{x1D708}$ for the above relation is evaluated to be 2.20 and the relationship is shown in figure 39.

Figure 39. Relationship between peak pressure ratio bluntness ratio and free stream Mach number.

For the two Mach numbers there are two different intercepts. This means that the relation has the following form:

Though the physical interpretation of the above equation is difficult, it can roughly be seen as accounting for the decrease in pressure ratio caused by the energy losses due to bluntness. The form of the intercept function $f(M_{\infty })$ cannot be ascertained from the experimental data obtained for only two different free stream Mach numbers. However, a comparison of the intercepts for the two Mach numbers on the pressure axis, for the case of ‘zero’ bluntness, with the pressure ratio for the two different free stream Mach numbers for the sharp leading edge cases could help in intuitively understanding the form of the function. The pressure axis intercepts at Mach 8.54 and 5.88 are 27.4 and 17.0 respectively, and the ratio of the intercepts is 1.61. This may be compared with the average pressure ratios at the two different Mach numbers for the sharp leading edge cases. It is apparent from figure 37 that despite the different shock impingement locations (at Mach 5.88) the data at the two different Mach numbers nearly cluster around a small range of values of pressure ratios; ${\sim}58$ for Mach 8.54 and ${\sim}27$ for Mach 5.88. The ratio of these pressure ratios is ${\sim}2.15$ . This is quite comparable to the ratio of the intercepts as the bluntness radius tends to zero. It may thus be speculated that $f(M_{\infty })$ is cube of the free stream Mach number. Admittedly, this speculation is not an attempt to reconcile the blunt leading edge data with the correlation for sharp leading edge, since the trend is exactly the opposite of the blunt leading edge, with the pressure ratio tending away from the sharp leading edge correlation as the bluntness radius decreases.

Physically, the term $f(M_{\infty })$ may be read as the reattachment pressure ratio effected purely by the flow outside the high-entropy layer, which includes the (weak) shock curvatures and interaction of various shocks and expansions such as: the leading edge shock, impinging shock, separation and reattachment shocks and expansion fans from the rear end of the wedge and from the turning of separated shear layer by the impinging shock. The loss due to the blunt leading edge seems to manifest as the reduction in shock strength by $1.70(r/x_{r})M_{\infty }^{2.20}$ . In effect, there is clearly a drastic reduction in the impinging–reflected shock strengths, which is expected to contribute to the reduction in separation length. The observation that the scaled separation length (multiplied by the cube of Mach number at boundary layer edge) for blunt leading edge cases is well below the correlation line fit for sharp leading edge means that the reduction in separation length is far more than what is expected of the reduced reattachment pressure ratio. This must be seen in the context that the Mach number at the boundary layer edge reduces considerably with bluntness, and that the high-entropy layer adversely affects the boundary layer’s resistance to separation by reducing the total pressure at the boundary layer edge, both these effects tending to increase the separation length. From the above considerations it may be surmised that it is largely the mechanisms from the rotational flow outside the boundary layer that contribute to the drastic reduction in separation length (which is explored in the subsequent sections); however, as the bluntness increases the adverse effects of bluntness on the boundary layer seems to dominate, such that the experimental data tend to catch up with the correlation line fit for sharp leading edge (it could be seen in figure 37 that the 6 mm bluntness data are quite close to the sharp leading edge line fit). Thus it can be summarized from the present experimental data that, 2 mm bluntness is found to be most effective in reducing the separation length (when viewed against the reattachment pressure ratio, in terms of deviation from the correlation for sharp leading edge) among all the bluntness used; and the effectiveness reduces with increasing bluntness; and the reduction is more at higher Mach number for a given bluntness.

7 Insights from computations

At the outset it must be recalled that the computations of the shock boundary layer interaction predicted a much smaller separation length than the experimental observations; the separation was considerably downstream of the leading edge. However, some speculations were made on the three-dimensional flow patterns and multiple vortices inside the separation bubble, which cannot be probed from experiments. The present section focuses rather on the boundary layer and the rotational flow outside the boundary layer computed over the flat plate without the presence of impinging shock. The trend in the computed flow field over the flat plate with bluntness is used to understand the experimentally observed behaviour of the separation length; it is a rather simple flow field in which the qualitative trends obtained from the computations can be relied upon. A comparison of the boundary layer $x$ -velocity and Mach number profiles at the expected (experimentally determined) reattachment location for sharp and blunt leading edge cases at Mach 5.88 is shown in figure 40.

Figure 40. Boundary layer profiles over the flat plate at Mach 5.88 at the expected reattachment locations. (a) $x$ -velocity profile, (b) Mach number profile.

For the blunt leading edge cases the boundary layer edge is determined by comparing with the velocity profile computed by assuming inviscid flow. It is apparent that the boundary layers are thicker with blunt leading edges. More than the thickness the velocity gradient near the wall in important. The velocity profiles are less steep near the wall for the blunt leading edge cases than the sharp leading edge case. A consequence of this is the reduced shear stress at the wall in the presence of leading edge bluntness. The Mach numbers at the edge of the boundary layers are also considerably small over the blunt leading edge flat plates, and accordingly the sonic point in the boundary layer is relatively farther than the sharp leading edge case. This results in increased upstream influence inside the boundary layer. The reduced shear forces (even as they are very small compared to the pressure forces which are much greater than that required for incipient separation) as well as the increased upstream influence with blunt leading edges are expected to reduce the ability of the boundary layer to resist separation. However, it is clear from the experiments that for the combination of reattachment pressure ratio and the Mach number at the edge of the boundary layer the separation lengths with blunt leading edges are rather much smaller than what is expected of the linear correlation for the sharp leading edge cases. This should therefore be due to the mechanisms in the inviscid flow outside the boundary layer. It is thus useful to explore the differences in the flow field between sharp and blunt leading edge cases, in the region just above the boundary layer. A comparison of the $x$ -velocity and Mach number profiles at the expected (experimentally determined) reattachment location for sharp and blunt leading edge cases at Mach 5.88 is shown in figure 41, for a distance of an order of magnitude more than the boundary layer thickness (it will be shown later that this distance is typically the thickness of the high-entropy layer for the 2 and 4 mm blunt leading edge cases).

Figure 41. Profiles of $x$ -velocity and Mach number inside the high-entropy layer over the flat plate at Mach 5.88 at the expected reattachment locations.

It is clear that while the profiles become completely flat over the sharp leading edge plate, there are some gradients in the profiles over blunt leading edge plates; more so with the 2 mm bluntness. Due to these gradients the flow is rotational even above the boundary layer for the blunt leading edge cases. Over a flat plate with sharp leading edge, the vorticity is very high at the wall; it subsequently decreases and tends to vanish at the boundary layer edge. However, in the presence of bluntness, especially in hypersonic flow, the vorticity generated in front of the blunt leading edge could be carried for a large distance downstream, and therefore the vorticity is non-zero at the boundary layer edge. This vorticity generation due to the bow shock upstream of the blunt leading edge is related to the entropy generation through the Crocco’s theorem. Thus it is useful to consider the HEL over the blunt leading edge flat plates. In the current analysis high-entropy layer edge definition is adopted from Borovoi et al. (Reference Borovoi, Egorov, Skuratov and Struminskaya2005), which is defined as the streamline passing the bow shock at a distance equal to the bluntness of the plate. Figure 42 shows the contours of entropy in grey scale for 2 and 4 mm blunt leading edges, with the edge of the high-entropy layer marked; the edge of the boundary layer at different points (starting at the experimentally determined separation location and ending at reattachment locations for the corresponding case with impinging shock) are also marked for comparison.

Figure 42. Contours of entropy at Mach 5.88 for the blunt leading edges (white dots represent boundary layer edge and white streamlines represents high-entropy layer edge). (a) 2 mm bluntness, (b) 4 mm bluntness.

For a sharp leading edge there is no such ‘entropy layer’ outside the boundary layer. But for both the blunt leading edge cases, the boundary layer is clearly well inside the high-entropy layer. This means, there is high vorticity at the edge of the boundary layer. Figure 43 compares the vorticity (magnitude) profiles between sharp and blunt leading edge cases inside the HEL.

Figure 43. Comparison of the vorticity profiles over sharp and blunt leading edges at the expected reattachment location.

Clearly, the vorticity magnitude is much higher at the edge of the boundary layer for the blunt leading edge cases compared to the sharp leading edge case. The high vorticity continues for a good distance from the boundary layer edge through the HEL edge. The high vorticity can have the tendency to take the high energy from the outer flow into the boundary layer. It is this high vorticity in the high-entropy layer for the blunt leading edge cases, which effectively increases the resistance of the flow to the impinging shock thereby effecting in the reduction of separation length (than what is expected of sharp leading edge correlation). Another interesting observation from the profiles is that the vorticity tends to be growing smaller at the boundary layer edge with increasing bluntness; clearly the vorticity with 4 mm bluntness is smaller than that with 2 mm bluntness at the boundary layer edge. This could be the reason for the experimental data with larger bluntness tending towards the sharp leading edge correlation. It must also be considered that increased bluntness results in increased losses and drag. There could thus be an optimum bluntness radius (possibly for given free stream conditions and given range of shock impingement location) which can lead to the most resistant boundary layer and vorticity profiles and effect in best possible reduction in separation length in terms of the sharp leading edge correlation. Identifying such optimal conditions could bring significant advancement in the design of intakes for enhanced off-design performance.