Introduction
Black medic (Medicago lupulina L.) infestations are a concern for Florida strawberry [Fragaria×ananassa (Weston) Duchense ex Rozier (pro sp.) [chiloensis×virginiana] producers, as this weed hinders harvest and competes with the crop. Clopyralid is a viable registered POST herbicide for which crop safety has been widely shown across varieties and over several timings (Boyd and Dittmar Reference Boyd and Dittmar2015; Clay and Andrews Reference Clay and Andrews1984; Figueroa and Doohan Reference Figueroa and Doohan2006; Hunnicutt et al. Reference Hunnicutt, MacRae, Dittmar, Noling, Ferrell, Alves and Jacoby2013a, Reference Hunnicutt, MacRae and Whitaker2013b; McMurray et al. Reference McMurray, Monks and Leidy1996). Unfortunately, clopyralid is only registered to provide M. lupulina suppression at current application timings (Anonymous 2011). McMurray et al. (Reference McMurray, Monks and Leidy1996) speculated that M. lupulina may escape control due to crop shielding. This was later shown to be true using water-sensitive paper (Sharpe et al. Reference Sharpe, Boyd, Dittmar, MacDonald, Darnell and Ferrell2018c), and other confounding factors were identified, including limited clopyralid translocation out of treated stems (Sharpe Reference Sharpe2017) and sized-based M. lupulina tolerance to clopyralid (Sharpe et al. Reference Sharpe, Boyd and Dittmar2016). Increasing the application volume from 187 to 374 L ha−1 doubled coverage at the planting hole (Sharpe et al. Reference Sharpe, Boyd, Dittmar, MacDonald, Darnell and Ferrell2018c), but applications at the current timing do not address size-based M. lupulina tolerance (Sharpe et al. Reference Sharpe, Boyd and Dittmar2016).
Ideally, clopyralid would be applied earlier in the production cycle, when both the strawberry crop and M. lupulina are smaller (Sharpe et al. Reference Sharpe, Boyd, Dittmar, MacDonald and Darnell2018a, Reference Sharpe, Boyd, Dittmar, MacDonald, Darnell and Ferrell2018b), resulting in increased spray penetration at a more susceptible M. lupulina growth stage (Sharpe et al. Reference Sharpe, Boyd and Dittmar2016, Reference Sharpe, Boyd, Dittmar, MacDonald, Darnell and Ferrell2018c). Safety of early-season clopyralid applications on strawberry plants has been demonstrated (Sharpe et al. Reference Sharpe, Boyd, Dittmar, MacDonald and Darnell2018a), but the optimal spray timing to target M. lupulina is unknown. Targeted clopyralid applications based on susceptible M. lupulina growth stages necessitate the development of emergence models to complement previously published growth and development models (Sharpe et al. Reference Sharpe, Boyd, Dittmar, MacDonald, Darnell and Ferrell2018b).
Empirically derived emergence modeling using field observations and growing degree days (GDDs) is a reliable approach and has been successfully employed for many species (Werle et al. Reference Werle, Sandell, Buhler, Hartzler and Lindquist2014). Emergence models have been developed for annual and perennial species that occur in temperate climates, where GDD accumulation typically begins below the base temperature (Martinson et al. Reference Martinson, Durgan, Forcella, Wiersma, Spokas and Archer2007; Werle et al. Reference Werle, Sandell, Buhler, Hartzler and Lindquist2014; White et al. Reference White, Boyd and Van Acker2012, Reference White, Boyd and Van Acker2015). Adaptation of standard GDD-based emergence models to subtropical climates such as Florida have limitations, including high-temperature GDD accounting inflation and heat-induced short-term physiological dormancy (Van Assche and Vandelook Reference Van Assche and Vandelook2010; unpublished data). Developing and applying daily GDD accounting restrictions based on emergence reductionist considerations, such as dormancy, germination, and PRE growth, may overcome empirical modeling limitations (Grundy Reference Grundy2003; Vleeshouwers and Kropff Reference Vleeshouwers and Kropff2000). Introduction of daily GDD accounting restrictions and temperature-based determination logic for restriction selection has overcome daily GDD accounting inflation for M. lupulina germination in a simulated subtropical environment (unpublished data).
Medicago lupulina dormancy patterns have been well studied and reported in the literature (Braul Reference Braul2004; Van Assche and Vandelook Reference Van Assche and Vandelook2010; Van Assche et al. Reference Van Assche, Debucquoy and Rommens2003). Findings may be used to develop and impose dormancy-based daily GDD accounting restrictions similar to germination restrictions (unpublished data). Medicago lupulina dormancy release involves a two-stage, temperature-mediated, seed-softening process (Braul Reference Braul2004). The first stage occurs when seed is exposed to consistent, near-cardinal maximum or minimum temperatures for the environment, and the second stage occurs during prolonged fluctuating temperatures under optimal conditions (Braul Reference Braul2004; Van Assche and Vandelook Reference Van Assche and Vandelook2010; Van Assche et al. Reference Van Assche, Debucquoy and Rommens2003). Without the period of chilling or hot temperatures, fluctuating temperatures do not promote dormancy release in hard-seeded legume seeds (Braul Reference Braul2004; Taylor Reference Taylor1981; Van Assche et al. Reference Van Assche, Debucquoy and Rommens2003). The necessary temperature fluctuation duration to promote dormancy release was between 1 and 6 wk for two M. lupulina populations (Braul Reference Braul2004) and 2 wk for a third (Van Assche et al. Reference Van Assche, Debucquoy and Rommens2003). The range of temperature fluctuations is critical; chilled M. lupulina seed germinated primarily at 20/10 and 15/6 C, and not at 30/20 C (Van Assche et al. Reference Van Assche, Debucquoy and Rommens2003). These considerations formed a foundation for building daily GDD accounting restrictions for seed dormancy release with the Florida Automated Weather Network (FAWN) as a framework for predictive data acquisition.
Medicago lupulina germination has been extensively studied and results have been used to develop daily GDD accounting restrictions (Braul Reference Braul2004, Sidhu Reference Sidhu1971; unpublished data). Medicago lupulina seed germinated between 5 and 35 C (Braul Reference Braul2004; Sidhu Reference Sidhu1971; unpublished data), and the optimum range is between 10 and 20 C (unpublished data). Medicago lupulina germination appears to be driven more by daily mean temperatures than by fluctuations and does not tolerate reductions in osmotic potential (unpublished data). Therefore, the M. lupulina germination-based GDD restrictions that have been developed have potential for application in field studies (unpublished data).
Given that germination can occur in the dark (Sidhu Reference Sidhu1971), water is generally not limiting in plasticulture production, and dormancy is primarily enforced by the hard seed coat (Uzun and Aydin Reference Uzun and Aydin2004), it is likely that seed burial will be the primary factor altering emergence rates and timing for similarly softened seed (Grundy Reference Grundy2003). While some studies have looked at M. lupulina emergence in response to burial, they have been primarily in the field, where temperature was not controlled (Sidhu and Cavers Reference Sidhu and Cavers1977; Van Assche et al. Reference Van Assche, Debucquoy and Rommens2003). Understanding how depth interacts with temperature permits structuring any PRE growth as a factor of GDDs and helps link germination- and dormancy-based daily GDD accounting to final emergence. Therefore, the objective of this study was to evaluate M. lupulina emergence in response to temperature and burial depth in a controlled environment and to model cumulative M. lupulina emergence in Florida strawberry fields as a factor of restricted GDDs.
Materials and Methods
Medicago lupulina seed was collected on April 4, 2014, at the Florida Strawberry Growers Association field site in Dover, FL (28.01°N, 82.23°W), from plants growing in strawberry production. Seed was kept dry and stored at 4 C in a residential refrigerator until used for experimentation. Preliminary experimentation demonstrated sufficient seed softening, so scarification to overcome dormancy was unnecessary.
Burial Depth
The experiment was initiated on June 13, 2016, and repeated on June 14, 2016 at the Gulf Coast Research and Education Center (GCREC) (27.75°N, 82.22°W) at Balm, FL. The experimental design was a randomized complete block with four blocks. The experimental factor was M. lupulina seed burial depth with eight treatments. Burial depths were: 0, 1, 2, 3, 4, 6, 8, and 10 cm from the soil surface. Pots were filled with Fafard® 3B Mix potting soil (Sun Gro® Horticulture, Agawam, MA) to the desired depth according to treatment. Seeds (25 pot−1) were deposited onto the potting soil, and then the pots were filled with field soil to bury seeds at the appropriate depth (Myakka fine sand, 1.4% clay, 4% silt, and 94.6% sand). Pots were watered daily. Emergence was measured at 4 wk after planting and expressed as a percentage of the total seed.
Burial Depth by Temperature Interaction
The experimental design was a two-way factorial, repeated-measures, randomized complete block design. The design had four blocks and a factorial arrangement of treatments arranged randomly within each block. The trial was initiated on October 17, 2017, and repeated on November 20, 2017, at GCREC. The first factor was seed burial depth at 0, 1, 2, and 5 cm. The second factor was incubator temperature at 5, 15, 20, 25, and 35 C. The repeated-measures factor was measurement timing at 1, 2, 3, and 4 wk after trial initiation. Chambers were set to 12-h day/night period. Pots (10-cm-diameter round, 8-cm height) were filled up to the burial depth with potting soil (30% Canadian peat, 20% cypress sawdust, 20% 1-cm diameter bark, 20% composted bark, 10% perlite, pH 5.5 to 6.5; Reliable Peat Company, Groveland, FL). Medicago lupulina seeds (25 pot−1) were deposited on the soil surface and then buried with field soil (as described earlier). Pots were gently watered, covered with polyethylene wrap to prevent evaporation and to keep the soil moist, and then placed into incubators and arranged into blocks. Polyethylene wrap was removed for counts. Emergence was counted on 7, 14, 21, and 28 d after treatment (DAT).
Field Emergence
The study was initiated on November 21, 2014, on four commercial strawberry fields in Hillsborough County, FL, and repeated on October 28, 2015, at Sites 1, 2, and 3. Strawberries were grown on plastic covered raised-beds. Sites were selected based on known M. lupulina infestations (Table 1). Fumigation practices varied between sites (Table 1), and doses were not reported. No herbicides were applied under the plastic mulch.
Table 1 Site specifications for the four locations of the Medicago lupulina emergence study between 2014 and 2016 in Hillsborough County, FL.Footnote a
a Soil types were identified from USDA (2016).
b FAWN, Florida Automated Weather Network, University of Florida, Institute of Food and Agricultural Sciences.
Strawberry transplants were planted into the plastic mulch at each site on the respective punch date (Table 1). Four 15-m by 66-cm plots were randomly placed within each field before weed emergence. Each plot occurred on a single bed and contained 90 to 107 transplant holes plot−1. Each planting hole was monitored over time for the emergence of M. lupulina seedlings, and season-end totals were expressed as cumulative emergence per plot.
Weather data were obtained from the Florida Automated Weather Network (FAWN; University of Florida, Institute of Food and Agricultural Sciences). The weather station in Dover, FL, was selected due to its proximity to the strawberry production area. Distance between the weather station and the field sites ranged between 6 and 11 km (Table 1). The FAWN station was chosen for modeling purposes because it represents a potential tool for growers to use with no additional cost or infrastructure required. Soil temperature was taken at −10 cm from the soil surface because it was considered most similar to conditions within the plastic mulch where the M. lupulina seeds occur and because this soil depth is the only available option for FAWN stations.
Reductionist Model
The M. lupulina reductionist emergence model was inspired by Vleeshouwers and Kropff (Reference Vleeshouwers and Kropff2000) and Grundy (Reference Grundy2003) but diverges from their frameworks. Observed cumulative field emergence was used to develop a standard emergence curve using temperature as a predictor. Factors affecting emergence, namely germination and dormancy, were accounted for by developing restriction on daily GDD accounting. Dormancy and germination restrictions helped deflate GDD accumulation to provide a meaningful start to the field-emergence curve. Given the tendency of M. lupulina to not tolerate burial, GDD restrictions based on PRE growth were not imposed, because the impact on the initiation of the field-emergence curve was assumed to be limited. Emergence from deeper in the soil would be accounted for in the field-emergence curve itself. Cumulative emergence was modeled as a function of cumulative GDDs.
Dormancy Conditions
Medicago lupulina dormancy is primarily enforced by a hard seed coat (Uzun and Aydin Reference Uzun and Aydin2004; Van Assche and Vandelook Reference Van Assche and Vandelook2010) and demonstrates non–deep physiological dormancy at 23 C (Van Assche and Vandelook Reference Van Assche and Vandelook2010). Non–deep physiological dormancy was demonstrated with increasing severity below 20 C (unpublished data). Non–deep physiological dormancy was accounted for in the germination conditions (unpublished data), which are detailed later in the “Germination Conditions” section.
Two conditions were imposed that required both criteria to be met. These conditions were: if T max − T min>4 C and T min<20 C, then GDD=T mean, otherwise GDD=0, where T max was the daily maximum temperature. For the first condition (T max − T min>4 C), fluctuating temperatures are necessary for dormancy release (Braul Reference Braul2004; Taylor Reference Taylor1981; Van Assche et al. Reference Van Assche, Debucquoy and Rommens2003), so a difference was selected to account for that fluctuation. Given that the FAWN sensors are buried 10-cm deep in the soil, where it is assumed fluctuations will be more tempered, a difference of 4 was selected. A lower temperature difference (T min<20 C) was selected due to the burial depth of the temperature probe for the FAWN station (−10 cm). For the second condition, it has been demonstrated that the fluctuating temperatures must occur in a lower temperature range (Van Assche et al. Reference Van Assche, Debucquoy and Rommens2003); therefore, the minimum daily temperature (T min) was used to determine when the conditions were ideal, where T min<20C. Specifically, Van Assche et al. (Reference Van Assche, Debucquoy and Rommens2003) demonstrated that a minimum temperature of 20 C with fluctuating temperatures between 30 and 20 C did not stimulate dormancy release, while 20/10 and 15/6 C did.
Germination Conditions
Conditions for restricted daily GDD accounting were previously developed (unpublished data). Briefly, the first condition was: if T mean<T opt, then
$${\rm GDD}{\equals}(T_{{{\rm mean}}} \,{\minus}\, T_{{{\rm base}}} )$$
where T mean was the mean daily soil temperature, and T base was the lowest temperature at which emergence would not occur. The value for T base was selected based on preliminary studies (Sharpe Reference Sharpe2017). Second, if T opt>T mean>T max, then:
$${\rm GDD}{\equals}{{(T_{{{\rm optimum}}} \,{\minus}\,T_{{{\rm base}}} )} \over {d\left( {{{T_{{{\rm mean}}} } \over {T_{{{\rm maximum}}} }}} \right)}}$$
The third condition was: if T mean>T max, then GDD=0.
Medicago lupulina emergence was modeled as a function of accumulated GDDs with a Weibull function of the form:
$$y{\equals}k(1\,{\minus}\,{\rm exp}^{{\{ {\minus}b\} }}) $$
where y represents the percent cumulative emergence, x is the accumulated GDDs, k is the maximum emergence, b is the rate of increase for percent cumulative emergence, m is the lag phase until the start of emergence, and c is a shape parameter (Martinson et al. Reference Martinson, Durgan, Forcella, Wiersma, Spokas and Archer2007; White et al. Reference White, Boyd and Van Acker2012). Models for standard GDDs, only dormancy conditions, only germination conditions, and both germination and dormancy conditions were developed.
Goodness of fit for the models was determined by examining the adjusted coefficient of determination (
${\rm R}_{{{\rm adj}}}^{2} $
) and the root-mean-square error (RMSE). The
${\rm R}_{{{\rm adj}}}^{2} $
was calculated as:
$${\rm R}_{{{\rm adj}}}^{2} {\equals}1{\minus} {{n(1\,{\minus}\,{\rm R}^{2} )} \over {n\,{\minus}\,p}}$$
where n is the number of observations, p is the number of parameters, and
$${\rm R}^{2} {\equals}1{\minus} {{\sum( y_{{{\rm obs}}} \,{\minus}\,y_{{{\rm pred}}} )^{2} } \over {\sum (y_{{{\rm obs}}} \,{\minus}\,\overline{y} )^{2} }}$$
where ȳ is the mean across all observations, y obs is the observed value, and y pred is the predicted values. The RMSE was calculated as:
$${\rm RMSE}{\equals} \sqrt {\left( {{1 \over n}} \right)\mathop \sum\limits_{i{\equals}1}^n (y_{{{\rm obs}}} \,{\minus}\,y_{{{\rm pred}}} )^{2} }$$
Nonlinear regression was performed using SigmaPlot v. 13 (Systat Software, San Jose, CA). Data were subjected to ANOVA using the PROC GLIMMIX in SAS v. 9.4 (SAS Institute, Cary, NC). Trial run and block were considered random variables. Repeated-measures analysis was performed using the first-order autoregressive covariance structure. Means were compared using Tukey’s honest significant difference. Model assumptions of constant variance and normality were confirmed before means comparison.
Given the zero-laden burial depth data set, ANOVA assumptions were rejected. Instead, a post hoc t-test was performed for the 0- and 1-cm burial depths to test whether they were different from zero. The t-test was performed using PROC TTEST in SAS. Analysis assumptions were verified.
Results and Discussion
Burial Depth
Medicago lupulina failed to emerge with seed burial. Mean surface emergence was 18% (95% confidence interval: 7, 29) (t=3.72, P=0.0075) (unpublished data). Emergence for seed buried at 1 cm (2%) was not different from zero (95% confidence interval: −2, 6) (t=1.32, P=0.2275). Medicago lupulina failed to emerge entirely from deeper depths >1 cm. This was unexpected, as M. lupulina has emerged when buried as deep as 2 cm in the field (Sidhu and Cavers Reference Sidhu and Cavers1977). Emergence may have been effected by temperature, as the greenhouse was set to 28 C. Higher temperatures are known to limit but not completely impede M. lupulina germination (Braul Reference Braul2004; Sharpe Reference Sharpe2017; Sidhu Reference Sidhu1971). If germination is not completely limited, PRE growth may be the limiting factor for deeper burial (Grundy Reference Grundy2003). If this is true, temperature and burial depth should have an interactive effect on M. lupulina emergence.
Burial Depth by Temperature Interaction
There was a significant three-way interaction among measurement timing, temperature, and burial depth on M. lupulina emergence (P<0.0001). Medicago lupulina seed buried at 5 cm was not affected by temperature or measurement timing (Table 2). For M. lupulina seed buried at the 2-cm depth, the optimal temperature range was 15 to 25 C (Table 2). The onset to emergence for seed buried at 2 cm when exposed to 20 C temperatures was 14 DAT (compared with zero-emergence treatments) (Table 2). Emergence at 15 and 25 C did not differ from emergence at 5 and 35 C, likely due to inherent variability in M. lupulina emergence. Emergence from the 2-cm depth was constant after the initial emergence flush until the trial end (28 DAT).
Table 2 Impact of temperature and burial depth on Medicago lupulina emergence over time when grown in pots within growth chambers in Balm, FL, in 2017.Footnote a
a Pots contained 25 M. lupulina seeds. Means represent least-square estimates. Means separation was conducted based on the significant three-way interactions, so different letters within the table indicate a significant difference (across columns and rows) using Tukey’s honest significant difference.
b DAT, days after treatment, the number of days the pots were exposed to the temperature factor.
At 28 DAT, M. lupulina emergence from a 1-cm depth was greatest for 20 and 25C treatments (18% and 24%, respectively), was different from the 5 and 35C treatments (1% and 0%, respectively), but not from the 15C treatment (16%) (Table 2). Emergence from the 1-cm burial depth for 20 and 25C first occurred at 14 and 7 DAT, respectively, compared with zero-emergence treatments (Table 2). Warmer temperatures appear to promote increased emergence, especially at shallower depths, possibly due to increased PRE growth rates, though further study is required.
For 15 C, across all timings, emergence only occurred for non-buried M. lupulina seed compared with zero-emergence treatments (Table 2). This was unexpected, as optimal M. lupulina germination occurs at 15C (unpublished data). At 28 DAT, emergence when buried at 1 cm was reduced by half at 15C compared with surface emergence (Table 2). This trend was not consistent for the 20 and 25C treatments. This may be due several factors interacting and combining, including temperature-induced physiological dormancy (Van Assche and Vandelook Reference Van Assche and Vandelook2010; unpublished data), warmer temperatures enhancing PRE growth, potential suicide germination, secondary metabolite buildup, or toxic compound buildup in the air space at greater depths, though further study is required.
Both 5 and 35 C treatments demonstrated limited emergence across burial depths (Table 2). While M. lupulina did emerge at 35 C, none of the treatment combinations were different from zero-emergence treatments. Similar results occurred for the 5 C treatment, with the exception of a delay in emergence for non-buried seed (14 DAT) (Table 2). This emergence delay was likely due to germination, which has shown a temperature-mediated delay at 5 C (unpublished data).
Overall, a three-way interaction among temperature, burial depth, and measurement timing influenced M. lupulina emergence. Emergence was low, delayed, and primarily on the soil surface for the 5 and 35 C treatments (Table 2). The optimal emergence temperature range was 15 to 25 C, and surface-deposited seed emerged by the first timing. For 20 C, M. lupulina emerged consistently from a greater depth (2 cm) with a delay of 14 DAT. This delay also occurred for the 15 and 25 C temperatures, though emergence was not consistent (not different from zero-emergence treatments). There was also a delay with inconsistent emergence at 15 C for the 1-cm burial depth. Even so, given the tendency for surface germination and the burial-induced delay in emergence of 7 to 14 DAT, additional restrictions based on PRE growth seem unnecessary for predicting the start of a cumulative field-emergence curve, nor give special compensation for time-series emergence patterns after emergence onset. These delays should be accounted for by the empirically derived field-emergence model.
Field Emergence
Medicago lupulina emergence was not consistent across years. Emergence began approximately 6 wk after strawberry planting in the first year. In the second growing year, M. lupulina failed to emerge. Emergence prediction using standard daily GDD accounting resulted in poor fit across years (Figure 1A). Lack of fit was from GDD accumulation not matching increases in emergence, due to GDD inflation and overaccumulation. This was most vividly illustrated by high accumulation with zero emergence in the second year (Figure 1A). High temperatures are a dominant influence in regulating M. lupulina emergence, yet the standard GDD equation fails to account for this.
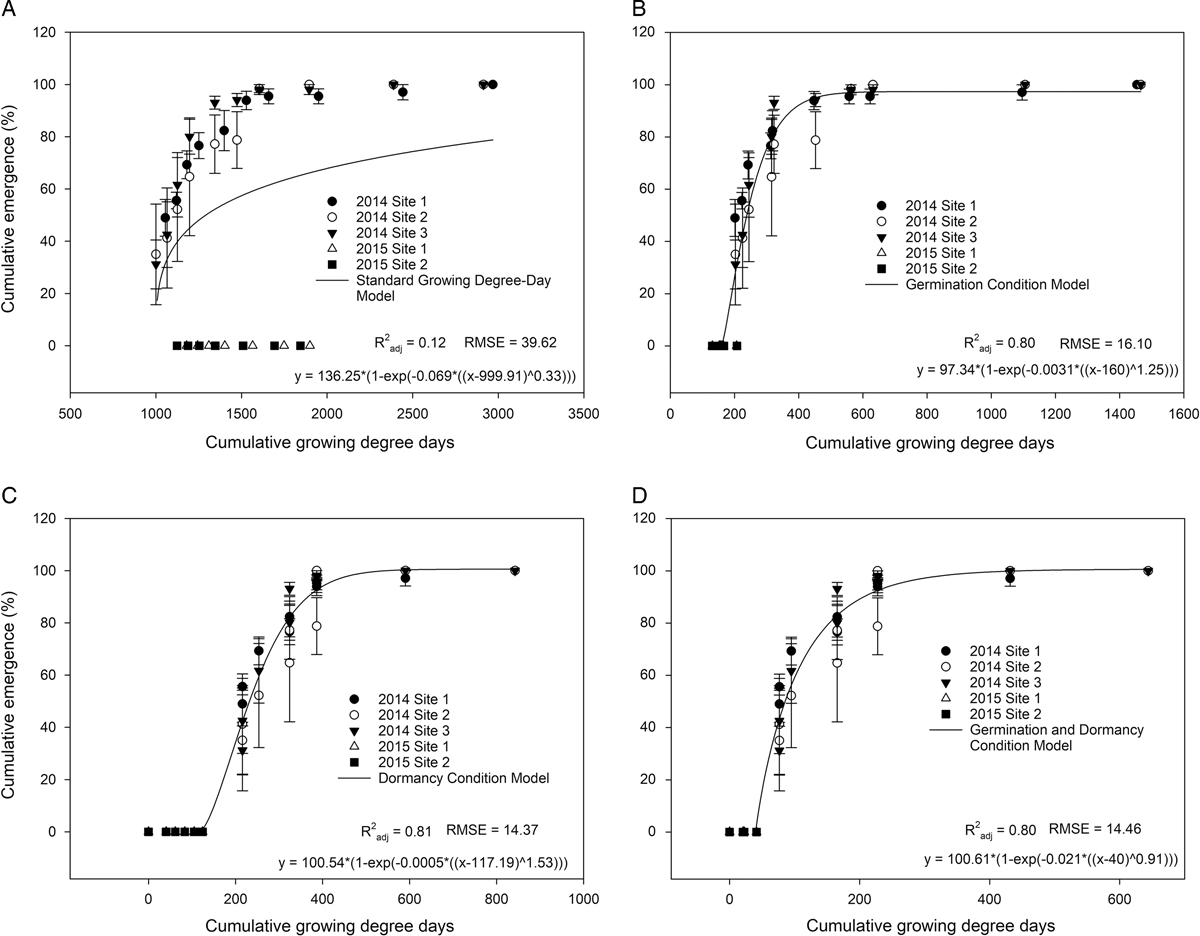
Figure 1
Medicago lupulina emergence in Florida strawberry fields for the 2014/2015 and 2015/2016 growing seasons. Symbols represent the mean of four replicates at each site. Error bars represent standard error of the mean. For the standard growing degree-day (GDD) model (A), GDDs were calculated by:
${\rm GDD}{\equals}\mathop{\sum}\nolimits_{i{\equals}1}^n {\left( {T_{{{\rm mean}}} {\minus}T_{{{\rm base}}} } \right)} $
. For the germination model (B), three conditions were imposed on the daily accumulation of GDDs: (1) if T
mean<T
opt, then GDD=(T
mean − T
base); (2) if T
opt<T
mean<T
max, then GDD=[T
opt/d(T
mean/T
max)]; or (3) if T
mean>T
max, then GDD=0. For the dormancy model (C), conditions include: if T
max − T
min>4, then GDD=0; if T
min>20, then GDD=0; if T
max − T
min<4 and T
min<20, then
$${\rm GDD}{\equals}\mathop{\sum}\nolimits_{i{\equals}1}^n {\left( {T_{{{\rm mean}}} {\minus}T_{{{\rm base}}} } \right)} $$
. For the dormancy and germination condition model (D), both sets of conditions were imposed, first the dormancy conditions, then the germination conditions if T
min<20 and T
max − T
min<4. Temperature data were derived from the Florida Automated Weather Network using a soil temperature meter at −10 cm from the soil surface. Accumulated GDDs were fit with a Weibull equation.
Addition of restrictions to daily GDD accounting resulted in good calibration model fit across years (Figure 1B–D) and adequate validation results (Figure 2B–D). Any restrictions to daily GDD accounting decreased the calibration model RSME and increased the
${\rm R}_{{{\rm adj}}}^{2} $
(Figure 1B–D). Application of dormancy plus germination-based restrictions to the daily GDD accounting did not substantially improve model performance compared with individual restrictions (Figure 1D), yet it substantially reduced the number of GDDs to predict the onset of emergence (Table 3). Addition of restrictions to the daily GDD accounting increased the validation model accuracy, much as it did for the calibration results (Figures 1B–D and 2B–D). The RSME was lower using dormancy-based and dormancy- plus germination-based restrictions to daily GDD accounting for validation compared with the calibration model. While the
${\rm R}_{{{\rm adj}}}^{2} $
was lower for calibration, the data followed the model trend line reasonably well (Figure 2D). Model validation using zero-emergence data was not possible due to the configuration of the Weibull equation to predict the onset of emergence (m), with values <m incalculable.
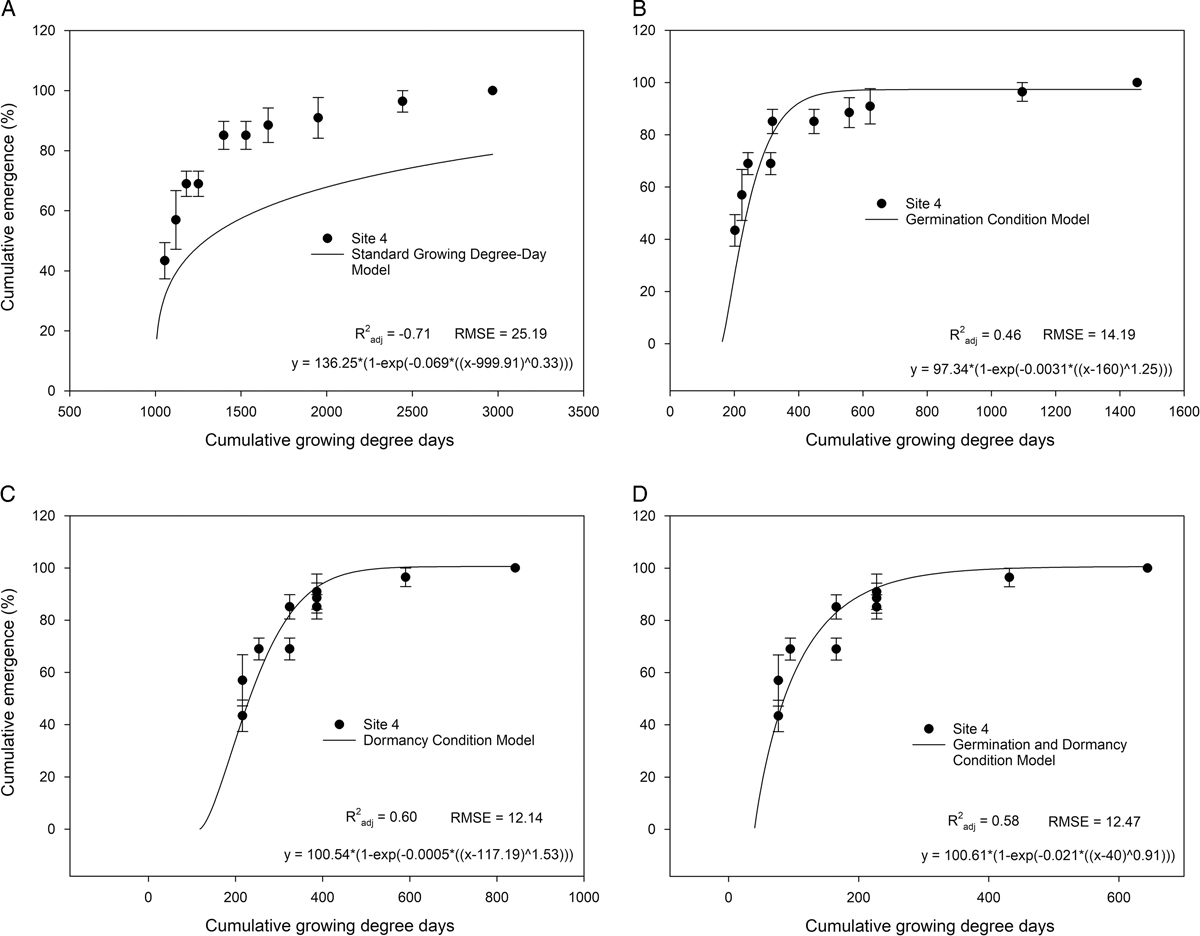
Figure 2 Calibration of potential models for Medicago lupulina emergence in Florida strawberry fields for the 2014/2015 growing season. Symbols are means of four replicates at the site. Error bars are the standard error of the mean. For the standard growing degree-day (GDD) model (A), GDDs were calculated by:
${\rm GDD}{\equals}\mathop{\sum}\nolimits_{i{\equals}1}^n {\left( {T_{{{\rm mean}}} {\minus}T_{{{\rm base}}} } \right)} $
. For the germination model, three conditions were imposed on the daily accumulation of GDDs: (1) if T
mean<T
opt, then GDD=(T
mean − T
base); (2) if T
opt<T
mean<T
max, then GDD=[T
opt/d(T
mean/T
max)]; or (3) if T
mean>T
max, then GDD=0. For the dormancy model: T
max − T
min>4, then GDD=0; if T
min>20, then GDD=0; if T
max − T
min<4 and T
min<20, then
${\rm GDD}{\equals}\mathop{\sum}\nolimits_{i{\equals}1}^n {\left( {T_{{{\rm mean}}} {\minus}T_{{{\rm base}}} } \right)} $
. For the dormancy and germination condition model, both sets of conditions were imposed, first the dormancy conditions, then the germination conditions if T
min<20 and T
max − T
min<4. Accumulated GDD data were fit with a Weibull function that was validated using Site 4.
Table 3 Anticipated Medicago lupulina cumulative emergence timing for four emergence models using various daily growing degree-day (GDD) accounting restrictions.
a Two dates appear under the calendar date, because the biofix date was when holes were punched in the plastic mulch, which varied by site, and occurred on October 8 and 10, 2014.
b Germination refers to the germination-based restrictions placed on GDD calculations. These conditions were previously developed (unpublished data), including: if T mean<T opt, then GDD=(T mean−T base); if T opt>T mean>T max, then GDD=[(T _opt−T _base)]/d(T _mean/T _max); and if T mean>T max, then GDD=0.
c Dormancy refers to the dormancy-based restrictions placed on GDD calculations. Dormancy conditions were applied if two conditions were both met: if T max – T min>4 C and T min<20 C, then GDD=T mean, otherwise GDD=0.
Use of the germination- plus dormancy-based restrictions to daily GDD accounting did estimate an earlier onset of emergence date (November 10, 2014) compared with other models. A model that predicts an earlier emergence date benefits growers by permitting time for scouting. All estimated onsets for emergence (10% cumulative) were earlier than anticipated from cooperation with local strawberry producers (Table 3). Given the stricter conditions for daily GDD accounting, models using the dormancy restrictions did not start GDD accumulation until weeks after the biofix date (when holes were punched in the plastic mulch for strawberry transplant). The germination component led to earlier accumulation but, as with the dormancy component, the overall accumulation was much less then with the standard equation. Lowering the accumulation reduces overinflation of GDDs and increases the opportunity for more meaningful accounting. This is likely why the predicted calendar date is 1 to 4 d earlier.
Cumulative emergence reached 50% between 7 and 14 d of the predicted onset of emergence and peak (90%) by mid-December. The timing for peak M. lupulina emergence is well before the start of strawberry harvest (Table 3), which begins in late December to early January. This is beneficial to strawberry producers, as it permits the use of clopyralid with minimal concern for the 7-d preharvest interval. Later applications do risk losing marketable fruit during the preharvest interval.
The window for M. lupulina emergence between 10% and 90% is approximately 1 mo in duration (Table 3). Comparison of GDDs across studies is difficult, both due to the overinflation of GDDs due to high temperatures in subtropical Florida and the restricted accumulation in developed models. The emergence window occurred from November 10, 2014, to December 14, 2014 (Table 3). During this time, the strawberry crop is establishing, the overhead irrigation period has passed, and control from fumigants and PRE herbicides has waned, and traffic through production areas is low and mainly occurs for thinning of strawberry runners and applying insecticides and fungicides. In addition to being an optimal timing for clopyralid application, use of shade cloth could be used to potentially suppress M. lupulina growth while the tolerant strawberry plants establish (Fernandez Reference Fernandez2001; Gast and Pollard Reference Gast and Pollard1991; Singh et al. Reference Singh, Syndor, Deka, Singh and Patel2012), though further study is required.
In summary, a model for M. lupulina emergence in Florida strawberry fields using restrictions to daily GDD accounting was successfully calibrated (Figure 1B–D) and validated (Figure 2B–D). Restrictions to daily GDD accounting based on both dormancy and germination reduced the RMSE of the calibrated and validated model compared with the standard GDD approach (Figures 1 and 2). Use of both germination and dormancy restrictions did not provide further fit to the model but did successfully reduce the number of GDDs to predicting emergence. Medicago lupulina emergence occurred primarily during the strawberry crop establishment period, from mid-November to late December in 2014. This timing is optimal for POST chemical control, hand weeding, or implementation of shade cloth. The model successfully accounts for zero-emergence years, but further study is required to test the model across additional field seasons. A limitation of the current model is that it predicts cumulative emergence and does not account for seedbank dynamics or irrigation water temperature. Irrigation water temperature may influence temperature dynamics if the bed does not reach equilibrium quickly enough. Seed that is buried in the bed likely carries over to germinate and emerge in subsequent years should tillage return the seed to the recruitment zone before seed decay. There are still several unstudied variables to account for within the Florida strawberry agroecosystem to incorporate seedbank dynamics into emergence models, including rates of seed decay in Florida soils, predation, and the influence and extent of various sources of dormancy release (temperature-mediated seed softening, tillage, fumigation).
Acknowledgments
The authors would like to acknowledge the Florida Strawberry Festival and the Florida Strawberry Research and Education Foundation for supporting and funding the project. No conflicts of interest have been declared.
