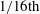1 Introduction
The water entry of projectiles generally results in a splash, as most people can attest to. Depending on the size, shape and speed of the projectile, the splash characteristics can vary wildly, but generally, above the surface one can observe a combination of impact jetting, splash crown formation, splash dome over and early surface seal. However, all of these events would be over in the blink of an eye, if it were not for high-speed photography in one form or another to capture the dynamics (e.g. Truscott, Epps & Belden Reference Truscott, Epps and Belden2013). The beauty and symmetry of such events, as well as the practical (military) applications, have managed to retain interest in this phenomena since the pioneering works of Worthington & Cole (Reference Worthington and Cole1897). Due to the extensive literature available on water entry, we restrict our attention herein to works primarily concerning the impact and crown formation of spherical projectiles, for which a typical sequence at atmospheric conditions is shown in figure 1, clearly depicting the formation (b–d) and closure (e,f) of the splash crown. The particular feature we address in this paper is the buckling instability which occurs just prior to closure, shown in the enlarged image in figure 1(g). Note that the term buckling here refers to the periodic ‘ribbed’ structure around the upper part of the cavity wall, which may be equally effectively described as wrinkling or crumpling, however, for consistency with Marston et al. (Reference Marston, Mansoor, Truscott and Thoroddsen2015), we adopt the term buckling hereafter.
Figure 1. Sequence from a high-speed video showing the formation and sealing of the splash crown following the impact of a 10 mm steel sphere onto water at
$10~\text{m}~\text{s}^{-1}$
under atmospheric conditions. Here
$Re=5\times 10^{4}$
,
$Fr=2\times 10^{3}$
,
$We=6.9\times 10^{4}$
. The enlarged image (g) highlights the buckling instability occurring near the top of the crown just prior to sealing. See also supplementary movie 1 available at http://dx.doi.org/10.1017/jfm.2016.165.
Worthington (Reference Worthington1908) may have unwittingly captured this instability, as evidenced by the cover image for his book and several image sequences (see figure 2). However, it appears to have escaped his attention as it is unmentioned therein. To the best of the authors’ knowledge, May (Reference May1952) was the first to describe this buckling instability whilst examining the surface seal phenomena. He described it as ‘ribbon-like filaments’ appearing just prior to surface seal, however, no explanation or further investigation was offered.
Figure 2. The cover image (a) from ‘A study of splashes’ by Worthington (Reference Worthington1908) and a select frame (b) from his photographic study, both exhibiting the buckling instability in the form of vertical striations near the top of the crown. Note also the weak striation down the cavity wall.
The earliest attempt at explaining the closure of the crown is likely Gillbarg & Anderson (Reference Gillbarg and Anderson1948), who state that the crown splash is subject to two chief forces: an under-pressure caused by the air flow behind the sphere and surface tension. The pressure drop across the splash jet or crown was assumed to be the dynamic pressure term from the Bernoulli equation, equal to
$({\it\rho}_{a}V_{0}^{2})/2$
, where
${\it\rho}_{a}$
is the density of the surrounding atmosphere and
$V_{0}$
is the speed of the sphere at impact. Given an approximately cylindrical crown shape of radius
$r$
, the pressure acting due to surface tension,
${\it\sigma}$
, is equal to
$2{\it\sigma}/r$
. The ratio of the under-pressure to surface tension is then given by a modified Weber number,
$r{\it\rho}_{a}V_{0}^{2}/4{\it\sigma}$
. A quick calculation of this ratio based on typical parameters for lab-based experiments (
$r\approx 2$
cm,
${\it\rho}_{a}=1.2~\text{kg}~\text{m}^{-3}$
,
$V_{0}=10~\text{m}~\text{s}^{-1}$
,
${\it\sigma}=0.0728~\text{N}~\text{m}^{-1}$
) would give a ratio of
${\sim}10$
, thus implying that surface tension is negligible in comparison with the Bernoulli pressure as it relates to the crown motion.
May (Reference May1952) attributed the early surface seal at atmospheric conditions to a low-pressure region caused by air flow into the cavity. However, evaluation of the Bernoulli dynamic pressure at both atmospheric pressure (air density,
${\it\rho}_{atm}=1.2~\text{kg}~\text{m}^{-3}$
) and at
$1/16$
atmospheric pressure (air density,
${\it\rho}_{1/16}=0.074~\text{kg}~\text{m}^{-3}$
) shows that the under-pressure is approximately 0.6 and 0.037 mbar, respectively, which is weak in comparison with the ambient pressure in either case. This therefore does not fully explain the closure of the cavity.
By examining splash jets produced by the vertical impact of a long cylinder into water, Yakimov (Reference Yakimov1973) concluded that the air density is the key ingredient in the qualitative difference between cavity shapes at different ambient pressures. He attributes the early closure of the crown in atmospheric conditions to the higher air drag experienced by the tip of the crown or splash jet (in a two-dimensional perspective), which is responsible for leading to accumulation of liquid at the tip and relative thickening in comparison with crowns at lower ambient pressures. As such, the tip thickens and is deflected by the air drag, whilst the central portion continues to thin out and is then subject to the air flow within the cavity. Furthermore, Yakimov states the pressure drop across the splash jet as
$$\begin{eqnarray}{\rm\Delta}P={\textstyle \frac{1}{2}}{\it\rho}_{a}(V_{0}^{2}+2V_{0}V_{1}),\end{eqnarray}$$
where
$V_{0}$
is the speed of the air inside the cavity, assumed to be the same as the projectile impact speed, and
$V_{1}$
is the speed of the tip of the jet moving up away from the impact site, shown schematically in figure 3.
Figure 3. Schematic representation of the proposed air flow with speed
$V_{0}$
into the cavity, upward jet speed
$V_{1}$
and sheet thickness
${\it\delta}$
assumed for the Bernoulli pressure effect.
Further still, Abelson (Reference Abelson1970) performed experiments to show that the relative under-pressure in the cavity associated with the Bernoulli effect is a vast underestimate of the true cavity pressure, wherein the pressure was measured with probes placed underwater. It was found that the pressure drop is actually 15–20 times greater than that predicted from
$({\it\rho}_{a}V_{0}^{2})/2$
. Supporting these measurements, Lee, Longoria & Wilson (Reference Lee, Longoria and Wilson1997) showed that a factor of 50 increase in the Bernoulli pressure was required to adequately describe the observations of surface seal in terms of closure time reported by Gillbarg & Anderson (Reference Gillbarg and Anderson1948). Thus, it appears that the Bernoulli pressure is a gross underestimate of the true pressure differential. It is key to bear in mind that the walls of the crown can become very thin, down to
${\sim}10~{\rm\mu}\text{m}$
as we will show, thus explaining their susceptibility to moderate pressure differences acting across them.
In addition to the pressure differential, if one were to evaluate the interplay between inertia and surface tension at the length scale of the crown wall thickness, it would appear that surface tension does play a significant role. The details of the closure, or crown seal, are particularly revealing in this regard and indeed a purely visual inspection of the crowns formed for different surface tensions (see figures 8 and 9 herein) would lead one to conclude that surface tension is far from negligible in this event. Aristoff & Bush (Reference Aristoff and Bush2009) presented an extensive analysis of the water entry of small, hydrophobic spheres, which included a phenomenological model of the evolution of the crown shape in time where it was assumed that the pressure differential was negligible, as in our calculations, and thus the crown closure was driven primarily by surface tension. Thus, one goal motivating this study was to re-evaluate the role of surface tension in the crown closure or ‘dome over’.
However, first and foremost, the feature of water entry events which has thus far eluded proper investigation is the instability just prior to seal. As such, the principal aim of this study is to re-examine the crown evolution and closure under reduced ambient pressures, as first reported by Gillbarg & Anderson (Reference Gillbarg and Anderson1948) in order to assess the influence of various parameters, including air density and quantify this instability. In doing so, we provide the most detailed study to date on the fine features just prior to the crown sealing phenomenon and show that the contact line plays a key role.
Figure 4. (a) Schematic of the experimental apparatus and (b) photograph of the lower chamber and experimental set-up, showing the camera position, liquid tank inside the chamber, pump and pressure gauge.
2 Experimental set-up and protocol
The primary experimental apparatus, shown schematically in figure 4(a) consists of a 6 m tall vacuum chamber (Vertex Fab & Design LLC, USA) composed of two main chambers connected by 6 inch cylindrical tubes. The target liquid tank was placed in the lower chamber, whilst the sphere release mechanism, consisting of an electromagnet and positioning stage, was housed in the upper chamber directly above the centre of the liquid tank. Both chambers have hinged window ports (TSE Troller AG, Switzerland) for easy access. Once sealed, a vacuum pump (Alcatel Vacuum Products) connected to the lower chamber was started to reduce the ambient pressure inside the chamber to the desired level, between 101 kPa (atmospheric) and 6.3 kPa (
$1/16\text{th}$
atmospheric), which was read by a pressure gauge also connected to the lower chamber. The sphere was then released by powering off the electromagnet at the power supply outside the upper chamber allowing it to fall freely under gravity to impact the liquid pool below. The impact dynamics were then captured with a high-speed video camera (Phantom V1610, Vision Research) at recording rates from 30 000 up to 461 538 f.p.s. with exposure times down to
$1~{\rm\mu}\text{s}$
, depending on the field-of-view required and exact phenomenon of interest for each trial. The recordings were triggered manually or using the image-based auto-trigger and saved to a PC for subsequent analysis. Backlighting was provided by multiple 350 W metal halide light sources (Sumita Co., Japan) diffused through a screen on the rear window of the lower chamber. A photograph of the lower chamber is shown in figure 4(b).
In addition to water, which was the primary test liquid, supplementary trials were conducted with perfluorohexane (
$\text{C}_{6}\text{F}_{14}$
), a fully fluorinated liquid with low surface tension of
${\it\sigma}=11.9~\text{mN}~\text{m}^{-1}$
, dynamic viscosity
${\it\mu}=1.1$
mPa s and density
${\it\rho}_{l}=1710~\text{kg}~\text{m}^{-3}$
. The impact speed in all trials was
$V_{0}\approx 10~\text{m}~\text{s}^{-1}$
as measured directly from the video sequences, with sphere diameters
$D_{0}=2R_{0}=5{-}40$
mm. Noting the vapour pressures of water and perfluorohexane are
$P_{v}\approx 2.5$
and 27 kPa, respectively, we thus have the following ranges of dimensionless numbers pertinent to this problem:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}We={\displaystyle \frac{{\it\rho}_{l}R_{0}V_{0}^{2}}{{\it\sigma}}}=3.5\times 10^{3}{-}1.8\times 10^{5},\\ Re={\displaystyle \frac{{\it\rho}_{l}R_{0}V_{0}}{{\it\mu}}}=2.5\times 10^{4}{-}1.9\times 10^{5},\\ Fr={\displaystyle \frac{V_{0}^{2}}{gR_{0}}}=3.3\times 10^{2}{-}4\times 10^{3},\\ C_{n}={\displaystyle \frac{P_{a}-P_{v}}{\frac{1}{2}{\it\rho}_{l}V_{0}^{2}}}=0.05{-}1.98,\\ {\it\epsilon}={\displaystyle \frac{{\it\rho}_{a}}{{\it\rho}_{l}}}=7.4\times 10^{-5}{-}1.2\times 10^{-3}.\end{array}\right\}\end{eqnarray}$$
These numbers represent, respectively, the ratios between inertia and surface tension, inertia and viscosity, inertia and gravitational force, pressure and inertia, and the densities between the ambient air and the liquid. In addition, one might include the Bond number,
$Bo=We/Fr=0.8{-}220$
, representing the ratio between gravitational and surface tension force. Note that we reserve discussion of the sheet dynamics, with an alternative definition of the Weber number, until § 3.3.
3 Results and discussion
3.1 Overview of the buckling instability
Examples of the buckling instability are shown in figures 5 and 6 for water at atmospheric pressure. In figure 5, the camera view is angled down to allow for an unobstructed view of the backside of the crown, enabling good focus on that section. In the second image in this sequence, thick vertical ‘ribs’ are clearly seen, with thin films in between. It is these thin films which are more susceptible to the pressure differential across the crown and thus are drawn inwards first, forming bag-like structures in figure 6. Even after the cavity domes over, shown in the third and fourth images, the periodic bag-like features around the crown circumference remain. Note the arrows in figure 5(b), highlighting the bags being drawn into the neck region. It appears that the uniformity of the spacing between the rib-bag structures is caused by instabilities characterized by a wavelength or periodicity, which will be discussed later in detail.
Figure 5. Buckling instability viewed from top-down for water at atmospheric pressure. Images shown are taken at times
$t=2.7~\text{ms}$
(a), 3.5 ms (b), 4.0 ms (c) and 4.4 ms (d) from impact. The scale bar is 10 mm. The red arrows in (b) indicate the suction and inward motion of the bags as the crown collapses. Here
$Re=5\times 10^{4}$
,
$We=6.9\times 10^{3}$
,
$Fr=2\times 10^{3}$
. See also supplementary movie 2.
Figure 6. Suction of bags during the buckling instability just prior to crown sealing. Images taken for water at atmospheric conditions at
$t=3.5~\text{ms}$
(a), 3.6 ms (b), 3.7 ms (c), 3.8 ms (d) and 3.9 ms (e) from impact. The white arrows indicate the bags being pulled into the cavity before they break-up in (e). The scale bar is 5 mm. Here
$Re=5\times 10^{4}$
,
$We=6.9\times 10^{3}$
,
$Fr=2\times 10^{3}$
.
Side-view imaging, as shown in figure 6 reveals the rapid pull-in and rupture of the bags within the cavity as the neck region closes. Here it is clear to see that the neck region closes inward whilst the thicker filament-like structures or ‘ribs’, connecting the lower and upper parts of the crown, persist almost at the same radial position. As the thin films rupture, they cause a fine spray of droplets within the crown which are below the pixel resolution (
${\sim}50~{\rm\mu}\text{m}$
).
When compared with atmospheric pressure crown sealing events, those observed at reduced pressures also exhibit these same features, namely thick rib formations and thin film atomization within the sealed crown. This is shown in figure 7 for a realization captured at an ambient pressure of 8.8 kPa. Here, however, the rib-bag structures do not appear until the dome over is almost complete, whereas at atmospheric pressure, they are clearly visible when the crown walls are vertical.
Figure 7. Image sequence showing the suction of a bag at ambient pressure of 8.8 kPa. The black arrow in (a) indicates the location of the bag inside the cavity, whilst the arrows in (c) and (d) show rupture locations as it atomizes. Images taken at
$t=28.2~\text{ms}$
(a), 28.5 ms (b), 28.7 ms (c), 28.9 ms (d) and 29.1 ms (e) from impact. The scale bar is 10 mm long. Here
$Re=5\times 10^{4}$
,
$We=6.9\times 10^{3}$
,
$Fr=2\times 10^{3}$
.
A comparison of the crown formations just prior to seal, as presented in figures 8 and 9, indicates that surface tension plays a key role in both the crown closure and the characteristics of the buckling instability. Taking figure 8 first, where both images are taken 4 ms from impact, we see that for water (
${\it\sigma}=72~\text{mN}~\text{m}^{-1}$
), the crown has collapsed in on itself with a significantly reduced neck radius in the upper region, whereas for perfluorohexane (
${\it\sigma}=11.9~\text{mN}~\text{m}^{-1}$
) the crown wall appears more-or-less vertical. These trials were both conducted at atmospheric pressure, thus clearly indicating that surface tension plays a significant role in the closure of the crown. Furthermore, visual inspection of the buckling phenomena apparent in both water and perfluorohexane crowns indicates much finer and more numerous rib structures for perfluorohexane. The same observations can be made for the trials conducted at lower pressure, as shown in figure 9, where again, the water crown has clearly undergone collapse at
$t=6$
ms from impact, whereas the crown for perfluorohexane remains intact and vertical. These key observations are discussed more quantitatively in § 3.3.
Figure 8. Comparison between water (a) and perfluorohexane (b) buckling just prior to sealing at atmospheric pressure for the same sphere size and impact speed. Images taken 4 ms after impact. Here
$We=6.9\times 10^{4}$
for water and
$We=7.2\times 10^{5}$
for perfluorohexane, with
$Fr=2\times 10^{3}$
for both. The scale bar is 10 mm.
Figure 9. Comparison between water (a) and perfluorohexane (b) buckling just prior to sealing at ambient pressures of 41 kPa and 36 kPa, respectively, for the same sphere size and impact speed. Images taken 6 ms after impact.
$We=6.9\times 10^{4}$
for water and
$We=7.2\times 10^{5}$
for perfluorohexane.
$Fr=2\times 10^{3}$
for both. The scale bar is 10 mm.
Finally, figures 10 and 11 show examples of an interesting observation made only for perfluorohexane at reduced ambient pressures, namely upward-facing cusps in the crown at the turnover point, where the vertical wall of the crown curves over and points down. In a similar fashion to the thin films between ribs that are pulled inside the crown, the films at this point are pulled upward and become pointed in an almost cusp-like fashion, shown most clearly in figure 11 before they eventually break up. This curious feature of the crown evolution was not observed for water and thus appears to be dependent on the physical properties of the liquid and, undoubtedly, the thickness of the film between the ribs. The details of the air flow are also expected to play a significant role here (e.g. Bischofberger, Mauser & Nagel Reference Bischofberger, Mauser and Nagel2013).
Figure 10. Upward-facing cusp-like formations in the crown at the turnover point observed for perfluorohexane at 41 kPa. Images taken at
$t=5~\text{ms}$
(a), 5.6 ms (b) and 6.3 ms (c) from impact. Here
$Re=7.77\times 10^{4}$
,
$We=7.18\times 10^{4}$
,
$Fr=2\times 10^{3}$
.
Figure 11. Close-ups of the upward-facing elements of the crown shown in figure 10 for perfluorohexane at 41 kPa. The arrows in (a) point to the most prominent examples, shown in (b) and (c), respectively.
3.2 Crown formations and closure at reduced pressures
Figure 12(a–h) shows snapshots taken at 1 and 5 ms after the impact of a sphere onto water with
$R_{0}=5$
mm and
$V_{0}=10~\text{m}~\text{s}^{-1}$
for a range of pressures
$P_{a}=101$
, 42, 21 and 6.3 kPa. From these snapshots alone, it is clear to see that the ambient pressure plays a significant role in the timescale associated with the sealing of the crown splash, whereby the crown at atmospheric pressure has sealed within 5 ms, but the reduced pressures taking considerably longer. In particular, for the range of pressures studied herein, we find that the scaled time of seal,
$tV_{0}/D_{0}$
, is approximately inversely proportional to the ambient pressure, as shown in figure 12(i). This relation was first proposed by Birkhoff & Isaacs (Reference Birkhoff and Isaacs1951), wherein they developed a theoretical estimate of the time of surface seal with the main result being that
${\it\rho}_{a}V_{0}t/D_{0}$
is roughly constant, thereby implying
$tV_{0}/D_{0}\propto 1/{\it\rho}_{a}$
.
One key feature to note is the shape of the crown at
$t=1$
ms where, for atmospheric pressure, the sheet experiences significant air drag and bends back towards the pool surface, a feature which diminishes as the air pressure is reduced. As shown in figures 5–11, the buckling instability occurs as the crown evolves towards the sealing point which, for water at atmospheric pressure occurs somewhere between 1 and 5 ms.
In order to fully assess the influence of air pressure on the dynamics of the crown formation and how this may affect the buckling instability, we first assess the spatiotemporal evolution of the crown for a range of ambient pressures and fluid properties, as shown in figures 13 and 14. Here, the crown edge has been extracted and plotted for every eighth frame (
$267~{\rm\mu}\text{s}$
intervals) from impact until sealing. In particular, the red outline indicates the shape at which the buckling instability becomes fully pronounced, so that the rib-bag structures are clearly detectable and countable. As shown, striations are always present in the cavity wall (below the surface) and the crown wall (above the surface), however, they are only readily countable in the crown at a certain moment in time, as indicated in figures 13 and 14.
Figure 12. (a) Snapshots of the crown formation for water at
$t=1$
ms (a,c,e,g) and 5 ms (b,d,f,h) after impact for four different ambient pressures of
$P_{a}=101$
kPa (a,b), 41 kPa (c,d), 21 kPa (e,f) and 6.3 kPa (g,h). Here
$V_{0}=10~\text{m}~\text{s}^{-1}$
,
$R_{0}=5$
mm,
$Fr=2\times 10^{3}$
,
$Re=4.9\times 10^{4}$
. (i) Non-dimensional seal time versus non-dimensional pressure, showing an approximate inverse relation.
Figure 13. Digitized water crown shapes rendered through image analysis, showing every eighth frame (
$267~{\rm\mu}\text{s}$
apart) from impact: (a)
$P=101$
kPa; (b)
$P=71$
kPa; (c)
$P=41$
kPa; (d)
$P=11$
kPa. The black outline represents the sphere at impact, whilst the shape plotted in red indicates the point at which buckling becomes pronounced. Here
$Re=5\times 10^{4}$
,
$We=6.9\times 10^{3}$
,
$Fr=2\times 10^{3}$
.
Figure 14. Digitized perfluorohexane crown outline shapes rendered through image analysis, showing every 10th frames (
$300~{\rm\mu}\text{s}$
apart) from impact: (a)
$P=101$
kPa; (b)
$P=31$
kPa. The black outline represents the sphere at impact, whilst the shape plotted in red indicates the point at which buckling becomes pronounced. Here
$Re=7.77\times 10^{4}$
,
$We=7.18\times 10^{4}$
,
$Fr=2\times 10^{3}$
.
From these analyses, we can quantify the collapse of the crown by extracting the minimum crown radius as a function of time from impact. Figure 15(a,b) indicates how we define the crown diameter as it approaches seal, whilst figure 15(c) and (d) show both the growth and collapse stages of the crown for a range of pressures for both water and PP1. Note the red data point in each set corresponds to the red profile plotted in figures 13 and 14, which confirms that the buckling instability, characterized by the fully pronounced rib-bag structures, occurs just after the onset of collapse of the crown for water. However, for PP1 it appears that the onset of buckling occurs just prior to the start of collapse of the crown. Noting also that the prominent buckling formations are confined to the upper regions of the sheet, we tentatively conclude that the buckling is the result of competition between the surface tension-driven radial collapse and sheet thickness, as discussed later.
At a qualitative level, we see that the initial growth of the minimum radius of the crown is clearly independent of pressure as the data sets in figure 15(c) and (d) are indistinguishable for
$t\leqslant 4$
ms for both water and PP1 and thus driven solely by inertia, with both exhibiting an approximate square-root scaling,
$R_{c}\sim \sqrt{t}$
, governed by early time geometric considerations. However, what is quite striking is that, even though the peak minimum neck radius increases as the pressure decreases, once the collapse begins, the rate of collapse is independent of the pressure, thus indicating that the collapse is driven by surface tension rather than sheet inertia. In particular, see the dotted lines indicating a collapse rate of
$V_{c}=\text{d}R_{c}/\text{d}t\approx 6~\text{m}~\text{s}^{-1}$
for water and
$\text{d}R_{c}/\text{d}t\approx 2~\text{m}~\text{s}^{-1}$
for PP1. The exception is the collapse for
$P=11$
kPa for water, where the collapse is not linear (as for higher pressures) and occurs at a lower rate, indicating that the ambient pressure does play a role. In this case, the reduced air drag enabled a sustained growth of the crown, which clearly takes more time to collapse inward under the action of surface tension. As such, the consistent collapse rates at all but the lowest pressure would further support the notion that surface tension may be driving the collapse of the neck radius, but the observations at low pressures would indicate that the collapse is a confluence of ambient pressure and surface tension.
Figure 15. (a,b) Images defining the measurement of the crown top diameter as it approaches seal. (c) Growth and collapse of the neck radius for water with
$Re=5\times 10^{4}$
,
$We=6.9\times 10^{3}$
,
$Fr=2\times 10^{3}$
. (d) Growth and collapse of the neck radius,
$R_{c}$
, for PP1 with
$Re=7.77\times 10^{4}$
,
$We=7.18\times 10^{4}$
,
$Fr=2\times 10^{3}$
. Red symbols indicate the time and location of the minimum radius when pronounced buckling is visible, with
$R_{c}=9.05$
, 9.43, 10.65 and 11.87 mm for water and
$R_{c}=10.78$
and 13.32 mm for PP1. Here
$R_{0}=5$
mm in all cases.
3.3 Influence of surface tension
The classical definition of the impact Weber number,
$We={\it\rho}_{l}R_{0}V_{0}^{2}/{\it\sigma}$
, incorporates the external length scale, namely the sphere radius. However, when evaluating the dynamics of the ejecta sheet, particularly the break up and droplet formation, one must include the relevant length and velocity scales which truly dictate the motion, which in this case are the sheet thickness,
${\it\delta}$
, and the sheet velocity,
$V_{s}$
(Villermaux & Clanet Reference Villermaux and Clanet2002; Thoroddsen et al.
Reference Thoroddsen, Thoraval, Takehara and Etoh2011; Villermaux, Pistre & Lhuissier Reference Villermaux, Pistre and Lhuissier2013). Thus, we can express the ejecta sheet or crown Weber number as
$$\begin{eqnarray}We_{{\it\delta}}=\frac{{\it\rho}_{l}{\it\delta}V_{s}^{2}}{{\it\sigma}}.\end{eqnarray}$$
Clearly, to evaluate the relative importance of surface tension in this definition, one needs to know both the sheet velocity and thickness. As such, in figure 16, four different particle tracks are plotted as a function of time from impact. The particle locations, marked by the symbols, are plotted over the raw image of the final location taken at
$t=8.7$
ms. Given that the spacing between each data point in each data set is approximately equal, we conclude that the velocity of each particle tracked is constant from the time it enters the crown with velocities in this realization ranging from
$V_{s}=2.1{-}5.1~\text{m}~\text{s}^{-1}$
. The different velocities are thus determined by the time at which the particle enters the crown. In other words, the sheet velocity decays with time from impact. We find that, in general, the velocities in the crown for
$t\sim 1{-}5$
ms from impact are
$O(1)~\text{m}~\text{s}^{-1}$
, lower than the
$O(10)~\text{m}~\text{s}^{-1}$
impact speed of the sphere. Note that these speeds are much slower than the initial ejecta which emerges at very high speed, up to 30 times that of the impacting sphere for this range of Reynolds numbers (Thoroddsen et al.
Reference Thoroddsen, Etoh, Takehara and Takano2004).
Figure 16. Particle tracks in the crown formed during the impact of a 10 mm sphere into a surfactant-laden water solution (0.3 % SDS) at 11 kPa. The colours represent different times, as indicated by the legend and the symbols correspond to different particles. The image shown is taken at
$t=8.7$
ms corresponding to the final data point in each set marked by the white symbols. The speeds of the particles are found to be
$2.1~\text{m}~\text{s}^{-1}$
(circles),
$3.5~\text{m}~\text{s}^{-1}$
(squares),
$3.7~\text{m}~\text{s}^{-1}$
(stars) and
$5.1~\text{m}~\text{s}^{-1}$
(crosses).
Furthermore, in some instances we were able to observe the rupture of the crown walls due to small holes opening. These holes typically occur near the top of the crown, as shown in figure 17 and are assumed to be due to the presence of small air bubbles in the liquid pool. By measuring the hole radii versus time over a sequence of approximately 20 frames (
$t\approx 1.5$
ms at 30 000 f.p.s.), we find that the hole openings occur at a more-or-less constant rate, with a speed
$V_{open}=3{-}5~\text{m}~\text{s}^{-1}$
. From this, we can then employ the Taylor–Culick relation for hole edge propagation (e.g. Lhuissier & Villermaux Reference Lhuissier and Villermaux2009) to estimate the sheet thickness as
$$\begin{eqnarray}{\it\delta}=2{\it\sigma}/({\it\rho}V_{open}^{2}),\end{eqnarray}$$
from which we find values of
${\it\delta}\approx 9{-}16~{\rm\mu}\text{m}$
near the top of the sheet, which is in excellent quantitative agreement with previously reported values (Zhang et al.
Reference Zhang, Toole, Fezzaa and Deegan2011). Thus, taking
${\it\delta}=O(10)~{\rm\mu}\text{m}$
and sheet velocities
$V_{s}=O(1)~\text{m}~\text{s}^{-1}$
, we find that
$We_{s}=O(10^{-1}{-}10^{0})$
, showing that surface tension does indeed become dominant in the sheet dynamics and breakup near the tip, as one would expect.
Figure 17. Example of hole formation in the crown used to estimate the wall thickness.
$D_{0}=10$
mm,
$V_{0}=10~\text{m}~\text{s}^{-1}$
,
$P=101$
kPa. The image in (a) (scale bar is 5 mm) is taken at
$t=1.9$
ms after impact whilst the sequence (b) shows the opening with time intervals of
$67~{\rm\mu}\text{s}$
. The opening speed in this realization is
$V_{open}=3~\text{m}~\text{s}^{-1}$
giving
${\it\delta}\approx 16~{\rm\mu}\text{m}$
.
3.4 Influence of the contact line
As first noted by May (Reference May1952), the cavity wall striations observed below the surface are also observed in the upper part of the splash sheet, seen in figures 5–6. These striations themselves appear to be an artefact of the contact line around the equator of the sphere, which has a jagged or sawtooth appearance as shown in figure 18 (see also Duez et al. (Reference Duez, Ybert, Clanet and Bocquet2007), Marston, Vakarelski & Thoroddsen (Reference Marston, Vakarelski and Thoroddsen2012), Snoeijer & Andreotti (Reference Snoeijer and Andreotti2013) and images in Batchelor (Reference Batchelor1967)). Noting that the images in this sequence are taken at times 1.4, 2.2 and 3.8 ms, it is clear that the contact line sawtooth formation persists until the buckling instability is first observed above the surface (
$t<5$
ms). Further evidence of the contact line manifestation in the crown is shown in figure 19 where both below and above-surface view can be seen simultaneously. One puzzling feature is that the number of teeth at the contact line does not exhibit a one-to-one correspondence with the number of buckles. We believe that this is due to the suppression of some of the teeth features, whereby the teeth located between the lowermost pinning points merge, as indicated by the arrows in figure 18(d).
Figure 18. (a–c) Images from a video sequence showing the contact line formation during the entry of a 20 mm sphere into water. The times from impact (
$t=1.4$
ms (a), 2.2 ms (b) and 3.8 ms (c)) and depth of the bottom tip of the sphere below the free surface are (
$z=13.9$
mm (a), 21.8 mm (b) and 37.5 mm (c)). (b) Enlarged view of the contact line formation around the equator of the sphere. The red arrows indicate the southern-most pinning points, whilst the white arrows indicate intermediate pinning points. The scale bar is 5 mm long. Here
$Re=8\times 10^{4}$
,
$We=8.8\times 10^{3}$
,
$Fr=6.5\times 10^{2}$
. See also supplementary movie 3.
As such, it is postulated here that the pinning points of the teeth around the contact line provide favourable circumferential locations for the buckles in the crown wall. However, the buckling instability occurs regardless of whether a contact line is present, as shown in figure 20 for the impact of a superheated sphere. In this instance, there is no contact line due to a vapour layer around the sphere and the cavity and crown walls are perfectly smooth in the initial stages (a). However, as the dome over occurs, we still clearly observe buckling of the neck region (b) and bag atomization within the sealed crown (c). Thus, the onset of the buckling instability begins later, but still appears in the absence of a contact line indicating that other mechanistic considerations need to be explored. Thus, we must conclude that the buckling instability appears in all crown sealing events, but is intensified by the presence of a pinned contact line.
In the former case, where the lower extent of the cavity is the contact line, the classical ‘sawtooth’ pattern arises and provides fixed locations around the sphere and thus also the cavity wall from which undulations arise. These provide favourable locations for the rib-bag structures which are the hallmark of the buckling instability in the crown. As such, in this case, the buckling instability appears to be the above-surface manifestation of the sawtooth contact line formation. It is worth commenting here that the contact line pinning results in a qualitatively similar effect to the artificially imposed structure on the cavity as seen in Enriquez et al. (Reference Enriquez, Peters, Gekle, Schmidt, van der Meer and Lohse2011, Reference Enriquez, Peters, Gekle, Schmidt, Lohse and van der Meer2012).
Note that in addition to providing valuable insight into the buckling instability, experiments with superheated spheres (see also Marston et al.
Reference Marston, Vakarelski and Thoroddsen2012) provide further evidence of the role of surface tension in the crown sealing or dome-over since it occurs for even low impact speeds of
$V_{0}\approx 1~\text{m}~\text{s}^{-1}$
, as in figure 20. In this case, the impact Weber number (
$We$
) is
${\sim}O(100)$
, however the sheet Weber number (
$We_{{\it\delta}}$
) is
${\sim}O(10^{-1})$
. Noting that the pressure differential at atmospheric pressure with low impact speed such as this is very small, one must conclude that it is the sheet Weber number that governs the crown collapse.
Figure 19. Entry of a 15 mm steel sphere into water at
$6.6~\text{m}~\text{s}^{-1}$
. The vertical striations, emanating from the contact line around the equator are clearly visible in all images taken at times
$t=2$
ms (a), 3 ms (b) and 4 ms (c) from impact. The scale bar is 10 mm long. Here
$Fr=592$
,
$We=4.5\times 10^{3}$
,
$Re=4.93\times 10^{4}$
.
Figure 20. Images showing the surface seal of the cavity created by a 15 mm Leidenfrost sphere impacting onto perfluorohexane at
$1.01~\text{m}~\text{s}^{-1}$
. Note the smooth cavity walls and postponement of the buckling/rib formation until moments prior to seal. The red arrow in the final image indicates the bags being pulled into the cavity. The scale bar is 15 mm long. Here
$Fr=13.8$
,
$We=1100$
,
$Re=1.17\times 10^{4}$
. See also supplementary movie 4.
4 Discussion and mechanistic description of buckling
As is evident from the experiments, there are essentially two cases to consider: one where a contact line forms and remains pinned around the equator of the sphere; and one where there is no contact line, as in the case of superheated spheres.
Our simplistic description of the buckling process reflects the non-wetting case, where the physical picture we consider is an annular volume of fluid that is being translated upward in the crown and simultaneously shrinking radially as the crown closes. With reference to figure 15, we note that the crown radius,
$R_{c}$
, undergoes a turnover point whereby it begins to collapse (i.e.
${\dot{R}}_{c}<0$
), which occurs at
$R_{c}=9.05$
–13.32 mm, i.e. at
$R_{c}/R_{0}\approx 2$
which is precisely when we observe buckling to becomes prominent (indicated by the red data points in figure 15
c and d). We thus proceed by considering the collapse rate
$|{\dot{R}}_{c}|$
relative to the upward motion of the crown, manifested by the sheet velocity,
$V_{s}$
, as follows: for buckling to occur there must be accumulation of fluid in the annulus volume of fluid, in other words, the fluid must be collecting in the neck faster than it can escape. Therefore, the mass flux evaluated in the radial inward direction,
${\dot{M}}_{r}={\it\rho}2{\rm\pi}{\it\delta}|{\dot{R}}_{c}|\,\text{d}z$
must exceed the mass flux evaluated in the vertical direction from the annular control volume,
${\dot{M}}_{z}={\it\rho}2{\rm\pi}R_{c}{\it\delta}V_{s}$
. From this, the simple criterion for buckling is that the collapse rate
$|{\dot{R}}_{c}|>V_{s}$
. Therefore, the principle prerequisite for buckling is that the neck radius is collapsing at a faster rate than the vertical velocity of the crown.
Once buckling begins, we can determine the spacing or characteristic wavelength,
${\it\lambda}$
, associated with the instability from
$$\begin{eqnarray}2{\rm\pi}R_{c}=N{\it\lambda},\end{eqnarray}$$
where
$N$
is the number of buckles around the circumference of the crown,
$2{\rm\pi}R_{c}$
, at the point when buckling first becomes prominent and countable in the crown, shown in figure 21(a). From this relation, we clearly expect to find
${\it\lambda}\sim R_{c}\sim D_{0}$
, which is indeed the case, as shown by figure 21(b). Note that an empirical power law scaling is evident from the data in figure 21(a), given by
$N\sim D_{0}^{3/4}$
. To further investigate the buckle formations and periodicity, experiments were conducted whereby the spheres were treated with hydrophobic sprays to create alternating hydrophobic–hydrophilic stripes, however this did not alter the number of buckles. Attempts to promote contact line pinning by physically etching the surface also failed to alter the buckling from the untreated sphere case. As such the observed
$3/4$
scaling law remains robust but does not have a physical basis as yet.
Figure 21. (a) Number of buckles,
$N$
, and (b) buckle spacing,
${\it\lambda}$
, plotted as a function of sphere diameter,
$D_{0}$
, for fixed impact speed of
$V_{0}=10~\text{m}~\text{s}^{-1}$
. The dashed line in (a) represents the power law scaling
$N\sim D_{0}^{3/4}$
. Error bars are based on 10 repeat trials. Note data points for both perfluorohexane and Leidenfrost spheres have been included in (a).
In experimental observations of the collapse of toroidal liquid rings (e.g. Pairam & Fernandez-Nieves Reference Pairam and Fernandez-Nieves2009; McGraw et al.
Reference McGraw, Li, Tran, Shi and Dalnoki-Veress2010; Darbois Texier et al.
Reference Darbois Texier, Piroird, Quere and Clanet2013) it was found that
${\it\lambda}\sim R_{c}/{\it\delta}$
, where
${\it\delta}$
is the radius of the torus and the ratio
$R_{c}/{\it\delta}=O(1{-}10)$
. In our case, direct measurements of the wall thickness using side-view imaging is extremely difficult; however, as indicated in § 3.3, it was possible to make some estimates due to the presence of small bubbles in the ejected crown. These bubbles appear to rupture the wall and thus permitted evaluation of the Taylor–Culick velocity, from which we could derive an approximation of the wall thickness. For water we estimate
${\it\delta}\approx 10{-}20~{\rm\mu}\text{m}$
in the upper region where buckling becomes prominent, which therefore corresponds to
$R_{c}/{\it\delta}=O(10^{6}{-}10^{7})$
at the buckling stage, meaning that evaluating the influence of
${\it\delta}$
and the ratio
$R_{c}/{\it\delta}$
becomes difficult compared to the experiments of toroidal liquid ring collapse where low ratios were observed.
Note that the key relation describing lengthscales associated with the Rayleigh–Plateau instability is
${\it\lambda}\sim 9{\it\delta}$
, from which the estimated number of buckles would be
$N_{RP}\approx 2{\rm\pi}R_{c}/(9{\it\delta})$
. For water, where we have measured the wall thickness to be of the order of 10
${\it\mu}$
m, this would lead to
$N_{RP}\approx 1400$
, which is two orders of magnitude greater than observed in the experiments. Aristoff and Bush used a value of
${\it\delta}\approx 200~{\rm\mu}\text{m}$
in their analytical model of the crown dynamics, but that value was used only as it provided the best fit to their experimental data. Here, we have used both the Taylor–Culick velocity and the established criterion that
$We\approx 1$
at the point of sheet disintegration (at the top of the crown) to yield
${\it\delta}=O(10~{\rm\mu}\text{m})$
, so that we can be confident of this thickness. As such, we can conclude that the buckling instability is not a manifestation of the Rayleigh–Plateau instability, but the result of competition between the collapse of the neck and fluid drainage away from the neck region.
5 Conclusions
We have conducted an experimental study of the well-known crown splash during water entry. Using high-speed videography, we have provided the most detailed study to date on the buckling instability which occurs just prior to the seal. The buckling was found to become prominent when the neck region collapses, at approximately
$R_{c}/R_{0}\approx 2$
. At this point the collapse occurs at a faster rate than fluid can drain away from the region, which is the primary prerequisite for buckling.
The contact line, which for most cases pins around the equator of the sphere, is characterized by a ‘sawtooth’ appearance and these features manifest themselves as striations in the cavity wall and into the crown wall seen above the surface. These striations are found to provide favourable locations for buckling around the circumference of the crown. However, experiments with superheated spheres, for which there is no contact line, showed that the buckling instability occurs regardless, albeit at different timescales.
The number of buckles was found to increase monotonically with sphere diameter, but not linearly. Regression analysis found the best fit was given by
$N\sim D_{0}^{3/4}$
, a scaling which, as yet, does not have a physical basis. The spacing between the buckles was found to increase linearly with sphere diameter from
${\it\lambda}=1.3$
mm for
$D_{0}=5$
mm to
${\it\lambda}=2.4$
mm for
$D_{0}=40$
mm, which could not be reconciled with predicted wavelengths from the Rayleigh–Plateau instability.
In addition, our experimental campaign herein has provided further insight into the role of surface tension in the closure of the crown splash. For both low and high impact speeds, surface tension cannot be neglected and one must take the sheet thickness as the relevant length scale into account by constructing a sheet Weber number to describe the ratio of inertia to surface tension in the sheet. New experiments to provide the time-resolved sheet thickness as a function of height above the free surface would be of great value in evaluating the sheet dynamics in more detail. Furthermore, re-evaluation of the cavity pressure (e.g. Abelson Reference Abelson1970) in cases where the surface seal is delayed or eliminated (e.g. Mansoor et al. Reference Mansoor, Marston, Vakarelski and Thoroddsen2014) would be very insightful to clarify the true mechanisms leading to dome-over and surface seal.
Acknowledgements
The experimental work was started whilst T.T.T. and J.O.M. were visiting researchers at KAUST. Funding from KAUST Office of Competitive Research Funds is gratefully acknowledged. We thank Y. Li for help in obtaining the enlarged image in figure 1(g).
Supplementary movies
Supplementary movies are available at http://dx.doi.org/10.1017/jfm.2016.165.
