1. Introduction
Rich dynamics of droplet impact on surfaces, including spreading, recoiling, splashing, bouncing and breaking up have been explored (Yarin Reference Yarin2006; Josserand & Thoroddsen Reference Josserand and Thoroddsen2016) following the pioneering work by Worthington (Reference Worthington1876). When a droplet is spreading over a surface, it would first reach the maximum spreading diameter, Dmax, which is one of the most important parameters for applications, such as inkjet printing (Kawase et al. Reference Kawase, Shimoda, Newsome, Sirringhaus and Friend2003), spray cooling (Liang & Mudawar Reference Liang and Mudawar2017), anti-freezing (Kreder et al. Reference Kreder, Alvarenga, Kim and Aizenberg2016) and anti-icing (Alizadeh et al. Reference Alizadeh, Yamada, R, Shang, Otta, Zhong, L, Dhinojwala, Conway, Bahadur, Vinciquerra, Stephens and Blohm2012). The maximum spreading diameter is commonly normalized as the maximum spreading factor, βmax = Dmax/D 0, where D 0 is the initial droplet diameter. To accurately predict βmax, the impact dynamics of droplets have been continuously studied theoretically (Madejski Reference Madejski1976; Pasandideh-Fard et al. Reference Pasandideh-Fard, Qiao, Chandra and Mostaghimi1996; Kim & Chun Reference Kim and Chun2001; Clanet et al. Reference Clanet, Béguin, Richard and Quéré2004; Bartolo, Josserand & Bonn Reference Bartolo, Josserand and Bonn2005; Ukiwe & Kwok Reference Ukiwe and Kwok2005; Attané, Girard & Morin Reference Attané, Girard and Morin2007; Li, Zhang & Chen Reference Li, Zhang and Chen2015; Wildeman et al. Reference Wildeman, Visser, Sun and Lohse2016; Wang et al. Reference Wang, Wang, Yang and Chen2019, Reference Wang, Wang, Xie, Liu, Wang, Yang, Gao and Wang2020b, Du et al. Reference Du, Wang, Li, Min and Wu2021), experimentally (Clanet et al. Reference Clanet, Béguin, Richard and Quéré2004; Ukiwe & Kwok Reference Ukiwe and Kwok2005; Kannan & Sivakumar Reference Kannan and Sivakumar2008; Vaikuntanathan, Kannan & Sivakumar Reference Vaikuntanathan, Kannan and Sivakumar2010; Antonini, Amirfazli & Marengo Reference Antonini, Amirfazli and Marengo2012) and numerically (Li et al. Reference Li, Zhang and Chen2015; Wildeman et al. Reference Wildeman, Visser, Sun and Lohse2016; Wang et al. Reference Wang, Wang, Yang and Chen2019, Reference Wang, Wang, Xie, Liu, Wang, Yang, Gao and Wang2020b).
There are two key points for modelling βmax. One is the competition of multiple forces, i.e. inertial, capillary and viscous forces. Dimensionless numbers are defined to quantify the competition, i.e. the Weber number, 
$We = \rho {D_0}V_0^2/\gamma$, which presents the ratio of inertial force to capillary force, the Reynolds number, Re = ρD 0V 0/μ, which presents the ratio of inertial force to viscous force. Here, ρ, γ, μ and V 0 are the liquid density, the surface tension of the droplet, the liquid viscosity and the impact velocity, respectively. The other point is the surface wettability, which represents the strength of adhesion, quantified by a static contact angle θ, i.e. the angle at the triple line. By means of a dimensionless analysis, βmax is defined as a function of dimensionless groups, βmax = f(We, Re, θ).
Because the maximum spreading factor is particularly sensitive to surface wettability at relatively low Weber numbers, the surface wettability is frequently restricted to a specific range in the majority of studies, such as hydrophilic (Laan et al. Reference Laan, de Bruin, Bartolo, Josserand and Bonn2014) or hydrophobic (Clanet et al. Reference Clanet, Béguin, Richard and Quéré2004) surfaces, to simplify the modelling of βmax, as βmax = f(We, Re). With this restriction, two asymptotic regimes for droplet impact have been distinguished and widely investigated, the capillary regime, in which viscous force can be ignored, and the viscous regime, in which capillary force can be ignored. The regime between the two regimes is referred to as the cross-over regime, in which both of these two forces are not negligible. A well-recognized scaling law 
${\beta _{max}}\sim R{e^{1/5}}$ has been established experimentally and theoretically in a wide range of surface wettability in the viscous regime, showing that the initial kinetic energy mainly converts to viscous dissipation during spreading (Madejski Reference Madejski1976; Clanet et al. Reference Clanet, Béguin, Richard and Quéré2004; Laan et al. Reference Laan, de Bruin, Bartolo, Josserand and Bonn2014; Lee et al. Reference Lee, Laan, de Bruin, Skantzaris, Shahidzadeh, Derome, Carmeliet and Bonn2015). However, although surface wettability is restricted, there are still two scaling laws of βmax in the capillary regime, i.e. 
${\beta _{max}}\sim W{e^{1/4}}$ and 
${\beta _{max}}\sim W{e^{1/2}}$, which are derived from a force balance and an energy balance approach, respectively (Okumura et al. Reference Okumura, Chevy, Richard, Quéré and Clanet2003; Clanet et al. Reference Clanet, Béguin, Richard and Quéré2004). The scaling law of 
${\beta _{max}}\sim W{e^{1/2}}$ indicates that the initial kinetic energy completely converts to the surface energy at the maximum spreading state. Unfortunately, Clanet et al. (Reference Clanet, Béguin, Richard and Quéré2004) found residual kinetic energy at the maximum spreading state, which implies the failure of 
${\beta _{max}}\sim W{e^{1/2}}$. In addition, Josserand & Thoroddsen (Reference Josserand and Thoroddsen2016) also reviewed that 
${\beta _{max}}\sim W{e^{1/2}}$ has not been observed in any experiments for droplet impact without splashing. Conversely, Clanet et al. (Reference Clanet, Béguin, Richard and Quéré2004) experimentally validated the scaling law of 
${\beta _{max}}\sim W{e^{1/4}}$ in the capillary regime. Furthermore, their data showed that the applicability of 
${\beta _{max}}\sim W{e^{1/4}}$ strongly depends on surface wettability. On hydrophobic and superhydrophobic surfaces, this scaling law holds in a full spectrum of Weber number as long as splashing does not take place; however, on hydrophilic surfaces, this scaling law is applicable only at relative high Weber numbers and the critical Weber number significantly increases as surfaces become more hydrophilic. Clanet et al. (Reference Clanet, Béguin, Richard and Quéré2004) further combined the scaling laws in the two asymptotic regimes to derive an impact parameter, 
$P = We\,R{e^{ - 4/5}}$, which can be used to distinguish the viscous and capillary regimes. Interestingly, although 
${\beta _{max}}\sim W{e^{1/2}}$ is never observed in experiments, the universal scaling law by combining 
${\beta _{max}}\sim W{e^{1/2}}$ in the capillary regime and 
${\beta _{max}}\sim R{e^{1/5}}$ in the viscous regime, expressed as 
${\beta _{max}}/R{e^{1/5}} = f(WeR{e^{ - 2/5}})$, shows satisfactory consistency with experimental (Laan et al. Reference Laan, de Bruin, Bartolo, Josserand and Bonn2014) and numerical (Eggers et al. Reference Eggers, Fontelos, Josserand and Zaleski2010) results. Lee et al. (Reference Lee, Laan, de Bruin, Skantzaris, Shahidzadeh, Derome, Carmeliet and Bonn2015) proposed that the effect of surface wettability must be considered at low Weber numbers and, hence, they introduced an extra surface energy term 
$\gamma D_{V0 \to 0}^2$ in the low-velocity limit into the energy balance. Thus, a universal relationship was obtained as 
${(\beta _{max}^2 - \beta _{V0 \to 0}^2)^{1/2}}R{e^{ - 1/5}} = W{e^{1/2}}/(A + W{e^{1/2}})$, where 
${\beta _{V0 \to 0}}$ is the spreading factor when the impact velocity approaches zero and the fitting parameter is A = 7.6. This relationship is tested to be valid in a very wide range of static contact angles from 22° to 110°.
In addition to the combination of the scaling laws in the two asymptotic regimes, an alternative approach to derive a universal function of βmax ~ f(We, Re, θ) is to establish an energy conservation equation from the initial impact state to the maximum spreading state, i.e. Ek ,0 + Es ,0 = Es,ms + Edis, where Ek ,0, Es ,0, Es,ms and Edis are the kinetic and surface energies at the initial impact state, the surface energy at the maximum spreading state and the viscous dissipation during spreading. No forces are ignored and the effect of contact angles is considered in the modelling. However, vast challenges (also main divergence) emerge when obtaining explicit expressions of Es,ms and Edis. Both the two energy terms are dependent on the shape assumption of spreading films at the maximum spreading state, and the latter is an integration of dissipation function with respect to time and space and, hence, a velocity gradient assumption inside impacting droplets is also needed. The spreading film at the maximum spreading state is commonly assumed to be a thin cylinder with (Attané et al. Reference Attané, Girard and Morin2007) or without rims (Wildeman et al. Reference Wildeman, Visser, Sun and Lohse2016), and the effect of contact angles can be introduced into the calculation of surface energy by modifying the periphery of the cylinder (Roisman, Rioboo & Tropea Reference Teare, Spanos, Ridley, Kinmond, Roucoules and Badyal2002). Various assumptions of velocity gradients inside the impacting droplets have been proposed. Early studies presented that velocity gradients exist in the entire droplet but there were some divergences of gradient treatment. For example, only ∂Vz/∂z (Chandra & Avedisian Reference Chandra and Avedisian1991) or only ∂Vr/∂z (Madejski Reference Madejski1976) was taken into account in the calculation of viscous dissipation, where Vz and Vr are the velocity components in the impact and spreading directions, respectively, and z is the coordinate in the impact direction. Subsequent studies proposed that there is a boundary layer near the solid surface and dissipation takes place only in this thin-shear region (Pasandideh-Fard et al. Reference Pasandideh-Fard, Qiao, Chandra and Mostaghimi1996; Wildeman et al. Reference Wildeman, Visser, Sun and Lohse2016; Du et al. Reference Du, Wang, Li, Min and Wu2021). Naturally, viscous dissipation in the boundary layer is attributed to ∂Vr/∂z. Unfortunately, this treatment leads to another difficulty on how to determine the unknown boundary layer thickness during spreading. An analogy between the plane stagnation flow and the flow inside impacting droplets was adopted by Pasandideh-Fard et al. (Reference Pasandideh-Fard, Qiao, Chandra and Mostaghimi1996) to obtain an expression of the boundary layer thickness, expressed as 
$\delta = 2{D_0}R{e^{ - 1/2}}$, but Eggers et al. (Reference Eggers, Fontelos, Josserand and Zaleski2010) indicated that the thickness should be time dependent and grows like 
$\delta = {(\nu t)^{1/2}}$, where ν is the kinematic viscosity. Wildeman et al. (Reference Wildeman, Visser, Sun and Lohse2016) adopted a simplified version of 
$\delta \sim {(\nu {t_{sp}})^{1/2}}$ to calculate the boundary layer thickness, where tsp is the spreading time, defined as the length of the period from an impacting droplet just touching the surface to reaching its maximum spreading state. Each of these assumptions can lead to a specific expression of viscous dissipation and, hence, a specific model of the maximum spreading factor. Although all models showed good agreement with the chosen experimental data, none is ‘real universal’, i.e. it is not effective for all fluids in extremely wide ranges of We, Re and surface wettability. On the other hand, all models give complex nonlinear equations of βmax, We, Re and θ so that βmax needs to be solved iteratively when impact conditions are specified. Furthermore, unlike scaling laws, the explicit equations of βmax cannot clearly show the competition of various forces and the effect of surface wettability.
Numerous emerging nanotechnologies with nanodroplet impact on surfaces as one of the key steps in processing have been developed, such as nanodroplet spray cooling (Kim Reference Kim2007), nanocoating (Teare Reference Teare, Spanos, Ridley, Kinmond, Roucoules and Badyal2002), nanoscale inkjet printing (Galliker et al. Reference Galliker, Schneider, Eghlidi, Kress, Sandoghdar and Poulikakos2012) and nanoscale protein separation and innovative material preparation (Huebner et al. Reference Huebner, Sharma, Srisa-Art, Hollfelder, Edel and de Mello2008; Jambovane et al. Reference Jambovane, Nune, Kelly, Mcgrail, Wang, Nandasiri, Katipamula, Trader and Schaef2016; Zhu et al. Reference Zhu, Piehowski, Zhao, Chen, Shen, Moore, Shukla, Petyuk, Campbell-Thompson, Mathews, Smith, Qian and Kelly2018; Glasscott et al. Reference Glasscott, Pendergast, Goines, Bishop, Hoang, Renault and Dick2019; Benz et al. Reference Benz, Asperger, Hamester, Welle, Heissler and Levkin2020; Kou et al. Reference Kou, Wang, Liu, Zhang, Chen, Xu, Bao, Yang and Yuwen2020). Therefore, the detailed mechanisms incorporated in nanoscale impact dynamics have received increasing attention. On the basis of the technical difficulties in implementing nanoscale experiments, numerical simulations become a feasible approach to investigate the nanoscale flow because they provide virtual experimental data. However, in conventional simulation schemes complex boundary conditions and/or modified fluid properties must be involved to describe scale effects (Horbach & Succi Reference Horbach and Succi2006; Grjeu, Gouin & Saccomandi Reference Grjeu, Gouin and Saccomandi2013) so that they require especially delicate implementation. In contrast, the mesh-free MD simulations are regarded as a direct approach to study the nanoscale flow by tracking motions of individual atoms by solving Newton's motion equations without setting complex boundary conditions (Koishi, Yasuoka & Zeng Reference Koishi, Yasuoka and Zeng2017; Xie et al. Reference Xie, Lu, Wang and Wang2018). The MD simulations have been adopted in studies of the impact of low-viscosity nanodroplets, especially on evaluation of the maximum spreading factor (Li et al. Reference Li, Zhang and Chen2015; Li, Li & Chen Reference Li, Li and Chen2017; Wang et al. Reference Wang, Wang, Yang and Chen2019, Reference Wang, Wang, Gao, Yang, Wang and Chen2020a). Recently, three scale effects have been discovered for nanodroplet impact. First, the effect of viscous force is enhanced significantly as the droplet size decreases to the nanoscale, because the Ohnesorge number 
$(Oh = \mu /{(\rho {D_0}\gamma )^{1/2}})$, representing the ratio of viscous to inertial-capillary forces, increases by two to three orders of magnitude. For example, for water, Oh increases from O(10−3) to O(1) when the droplet diameter decreases from 2 mm to 10 nm. Thus, low-viscosity fluids at the nanoscale would naturally become ‘high-viscosity’ fluids. Xie et al. (Reference Xie, Lv, Yang and Wang2020) investigated the contact time for water and argon nanodroplets impacting superhydrophobic surfaces and found that the contact time scales as 
${\tau _c}\sim ({D_0}/{V_0})W{e^{1/2}}O{h^{1/3}}$, which is different from the macroscale scaling law of 
${\tau _c}\sim ({D_0}/{V_0})W{e^{1/2}}$, confirming the enhanced viscous effect at the nanoscale. Second, the viscous dissipation mechanism for the nanodroplet impact was found to differ from that for the millimetre-sized droplets. Li et al. (Reference Li, Zhang and Chen2015) examined the impact of a water nanodroplet on a hydrophobic surface and noted that velocity gradients exist within the entire droplet, unlike millimetre-sized droplets only in the boundary layer, leading to markedly excess viscous dissipation for the former than the latter. Consequently, the nanodroplet impact should fall in the cross-over regime under most impact conditions. Third, various interface effects start to play a dominant role in the nanodroplet impact. For example, Wang et al. (Reference Wang, Wang, Gao, Yang, Wang and Chen2020a) presented that the nanodroplet impact is more sensitive to surface wettability and topology because of the action of the long-range Van der Waals force (Wang et al. Reference Wang, Wang, Gao, Yang, Wang and Chen2020a). In addition, impacting nanodroplets show significant slip velocities on solid surfaces, unlike millimetre-sized droplets satisfying the no-slip condition.
Because of the existing scale effects, especially the distinct viscous dissipation mechanism, the macroscale models of the maximum spreading factor developed through either a force (or an energy) balance or an energy conservation equation were found to be improper for impacting nanodroplets. Using the energy conservation equation, several studies have been conducted to build the models of the maximum spreading factor for impacting nanodroplets with different assumptions of velocity gradients (Li et al. Reference Li, Zhang and Chen2015, Reference Li, Li and Chen2017; Wang et al. Reference Wang, Wang, Gao, Yang, Wang and Chen2020a). The consensus that velocity gradients exist in entire nanodroplets has been reached; however, similar to macroscale droplets, the divergence lies in the velocity gradient term that contributes to viscous dissipation. In an early study (Li et al. Reference Li, Zhang and Chen2015), it was assumed that only the ∂Vz/∂z term contributes to viscous dissipation. Later, a different assumption was adopted by Li et al. (Reference Li, Li and Chen2017), with which viscous dissipation arises from the ∂Vr/∂z term. The model with the latter assumption shows better agreement with MD simulations at low Weber numbers (<10). The effect of surface wettability was taken into account by incorporating the contact angle factor into surface energy (Li et al. Reference Li, Zhang and Chen2015); however, Wang et al. (Reference Wang, Wang, Gao, Yang, Wang and Chen2020a) proved that the model with such a treatment cannot predict the maximum spreading factor of impacting nanodroplets when static contact angles are less than about 80°. Through a qualitative estimation, they found that the amount of viscous dissipation for impacting nanodroplets is much larger than that of surface energy so that the effect of surface wettability cannot be characterized only by modifying surface energy. Therefore, they proposed a new idea that the surface wettability would modify the mean spreading velocity and thereby relates to viscous dissipation. The equation of the maximum spreading factor developed by Wang et al. (Reference Wang, Wang, Gao, Yang, Wang and Chen2020a) is expressed as
\begin{equation}\frac{{{V_s}}}{{{V_0}}}\left( {\frac{3}{{160}}\beta_{max}^5 - \frac{4}{{3{\beta_{max}}}} + \frac{{461}}{{480}}} \right) + \frac{{Re}}{{We}}\left( {\frac{1}{3}\beta_{max}^2 + \frac{2}{3}\frac{1}{{{\beta_{max}}}} - 1} \right) = \frac{{Re}}{{12}},\end{equation}where Vs is the mean spreading velocity, which is a function of static contact angle. Equation (1.1) fits the results by their MD simulations at We from 15 to 90 over a wide range of surface wettability with static contact angles from 21° to 148°. Like the macroscale, the approach based on energy conservation gives an implicit equation of the maximum spreading factor, which leads to difficulty in calculations and, more importantly, covers up the nature of competition of various forces. Conversely, explicit scaling laws of the maximum spreading factor, obtained based on fundamental principles such as force or energy balance (Clanet et al. Reference Clanet, Béguin, Richard and Quéré2004), overcome these drawbacks and their derivations do not need the complete information of velocity gradients. Furthermore, the universal law of βmax can be accomplished step by step by combining scaling laws in each asymptotic regime. Unfortunately, such scaling laws have not been reported for the impact at the nanoscale. Therefore, new scaling laws for impacting nanodroplets are urgent to obtain.
This work examines the impact of nanodroplets over a wide range of Weber numbers from 1.51 to 96.68 and Reynolds numbers from 3.51 to 28.11 onto surfaces with static contact angles from 73° to 180°. New scaling laws of βmax for a low-viscosity nanodroplet impacting smooth surfaces are proposed based on the MD simulation results. Then, the effects of surface wettability and the size of droplets on the spreading dynamics of nanodroplets are demonstrated.
2. Simulation method
All simulations are implemented by the large-scale atomic/molecular massively parallel simulation (LAMMPS) package. MD simulations have been widely used for investigating the maximum spreading factor of low-viscosity nanodroplets, such as water and argon (Li et al. Reference Li, Zhang and Chen2015, Reference Li, Li and Chen2017; Wang et al. Reference Wang, Wang, Yang and Chen2019, Reference Wang, Wang, Gao, Yang, Wang and Chen2020a). Figure 1 shows the schematics of simulated systems for a water and an argon nanodroplet impacting a smooth platinum substrate. Three diameters of 8, 10 and 14 nm are adopted for the water nanodroplet that contains 8992, 17 480 and 48 040 molecules, respectively. Only a diameter of 12 nm is chosen for the argon nanodroplet with 9544 atoms. The platinum substrate consists of seven layers and contains 104 752 atoms. All simulations are conducted in a box with a dimension of 48 × 48 × 28 nm3. Periodic boundary conditions are applied to the x- and y-directions, with a fixed boundary condition to the z-direction. The initial system is set to 300 K in the water nanodroplet system and 85 K in the argon nanodroplet system for preventing droplets from boiling. Both the droplets and the substrate are produced by face-centred cubic (fcc) crystals. The lattice constant for fcc platinum is 3.92 Å (Padilla Espinosa, Jacobs & Martini Reference Padilla Espinosa, Jacobs and Martini2021). The bottom three-layer atoms in the platinum substrate are fixed at their initial positions by virtual springs to prevent the substrate deformation during impact (Li et al. Reference Li, Zhang and Chen2015, Reference Li, Li and Chen2017; Xie et al. Reference Xie, Lu, Wang and Wang2018, Reference Xie, Lv, Yang and Wang2020; Wang et al. Reference Wang, Wang, Yang and Chen2019, Reference Wang, Wang, Gao, Yang, Wang and Chen2020a,Reference Wang, Wang, Xie, Liu, Wang, Yang, Gao and Wangb). Here, the value of the spring constant is chosen as 80 N m−1, which is sufficient to avoid the substrate deformation based on our tests.
Figure 1. The schematics of simulated systems: (a) a water nanodroplet system and (b) an argon nanodroplet system.
The interactions of Pt–Pt, Ar–Ar, Ar–Pt and water–Pt are described by the Lennard–Jones potential, expressed as
\begin{equation}{U_{LJ}}(r) = 4\varepsilon \left[ {{{\left( {\frac{\sigma }{r}} \right)}^{12}} - {{\left( {\frac{\sigma }{r}} \right)}^6}} \right],\quad r < {r_{cut}},\end{equation}where r is the distance between two atoms, ε is the depth of potential, σ is the zero-crossing distance and rcut is the cutoff distance. The value of rcut is taken as 1 nm for the water nanodroplet system (Molinero & Moore Reference Molinero and Moore2009; Jacobson, Kirby & Molinero Reference Jacobson, Kirby and Molinero2014; Li et al. Reference Li, Zhang and Chen2015, Reference Li, Li and Chen2017; Montero de Hijes et al. Reference Montero de Hijes, Sanz, Joly, Valeriani and Caupin2018; Wang et al. Reference Wang, Wang, Gao, Yang, Wang and Chen2020a,Reference Wang, Wang, Xie, Liu, Wang, Yang, Gao and Wangb) and 1.5 nm for the argon nanodroplet system (Yaguchi, Yano & Fujikawa Reference Yaguchi, Yano and Fujikawa2010), respectively. In the water nanodroplet system, σPt-Pt = 2.47 Å, σwater-Pt = 2.8155 Å and εPt-Pt = 0.694 eV (Wang et al. Reference Wang, Wang, Gao, Yang, Wang and Chen2020a), whereas in the argon nanodroplet system, σPt-Pt = 2.34 Å, σAr-Ar = 3.405 Å, σAr-Pt = 3.085 Å, εPt-Pt = 0.4095 eV and εAr-Ar = 0.0103 eV (Xie et al. Reference Xie, Lv, Yang and Wang2020). The solid–fluid length parameters are obtained by the sixth-power mixing rule. The solid–fluid energy parameters, εAr-Pt and εWater-Pt, are used to control the surface wettability, with εAr-Pt = 0.00698 eV corresponding to θ = 150° in the argon nanodroplet system (Xie et al. Reference Xie, Lv, Yang and Wang2020) and εWater-Pt = 0.00184, 0.0051, 0.00684, 0.0102, 0.0137 and 0.01684 eV corresponding to θ = 180°, 148°, 125°, 105°, 85° and 73° in the water nanodroplet system (Wang et al. Reference Wang, Wang, Gao, Yang, Wang and Chen2020a). Therefore, no mixing rule is employed for them. The method to measure static contact angles is described briefly as follows and more details can refer to our previous works (Wang et al. Reference Wang, Wang, Gao, Yang, Wang and Chen2020a). With a prespecified value of εAr-Pt or εWater-Pt, an MD simulation for the spontaneous spreading of a nanodroplet over a platinum substrate is carried out. The surface of the droplet is distinguished by calculating the time-averaged density profile with a threshold that is half of the liquid-phase density. The static contact angle is subsequently measured by a circle fitting algorithm.
The interactions between water molecules are described by the monatomic water (mW) model proposed by Molinero & Moore (Reference Molinero and Moore2009). As a coarse-grained model, the mW model successfully reproduces the density, surface tension and energetics of water with significantly reduced computational cost. The properties for water and argon are taken from Molinero & Moore (Reference Molinero and Moore2009), Yaguchi et al. (Reference Yaguchi, Yano and Fujikawa2010), Jacobson et al. (Reference Jacobson, Kirby and Molinero2014), Montero de Hijes et al. (Reference Montero de Hijes, Sanz, Joly, Valeriani and Caupin2018) and LAMMPS packages, with ρ = 1400 kg m−3, γ = 13.6 mN m−1 and μ = 153 μPa s for argon, and ρ = 996 kg m−3 and γ = 66 mN m−1 for water. It is worth noting that because the mW model does not include the reorientation of hydrogen atoms the viscosity of water predicted by the mW model is three times lower than experimental values under ambient conditions (Molinero & Moore Reference Molinero and Moore2009; Montero de Hijes et al. Reference Montero de Hijes, Sanz, Joly, Valeriani and Caupin2018). Thus, the viscosity of water is taken as μ = 851/3 = 283.7 μPa s. In this work, MD simulations of the water nanodroplets are adopted to reveal scaling laws of the maximum spreading factor, whereas simulations of the argon nanodroplet are used to validate the laws.
After the preparation of the initial system, MD simulations start. Each simulation includes three processes with time steps of 1 fs. The first is an equilibrium process, running in the NVT ensemble (canonical ensemble) for 2 ns with a constant temperature of 300 K for the water nanodroplet system or 85 K for the Ar nanodroplet system by the Nose–Hoover thermostat, whose relaxation time constant is 0.2 ps. The nanodroplet is fixed at a certain distance away from the Pt substrate in this process. When the energy, temperature and pressure of the system reach stable equilibrium, the process ends. The second is a falling process, in which the nanodroplet is released with a constant velocity in the negative z-direction. The process runs until the nanodroplet just touches the substrate. The third is an impact process, in which the nanodroplet undergoes spreading, recoiling and, finally, remains stationary or bounces off the substrate. Once the droplet starts to fall and subsequently hits the substrate, temperatures of the droplet, vapor and substrate cannot remain unchanged because of the thermal exchange between the droplet and vapor as well as between the droplet and substrate; however, the total particle number and the total volume of the droplet, vapor, substrate remain unchanged in these processes. Therefore, the NVE (micro-canonical ensemble) ensemble is employed in the falling and impact processes. The impact process runs for 1 ns, which is sufficient to reach the maximum spreading state for the impacting nanodroplets. The position and velocity of each atom are extracted every 1 ps for analysis. The MD code used has been validated in our previous works (Wang et al. Reference Wang, Wang, Yang and Chen2019, Reference Wang, Wang, Xie, Liu, Wang, Yang, Gao and Wang2020b).
3. Results and discussion
3.1. The maximum spreading factor on a surface with θ = 180°
The impact dynamics for water nanodroplets with D 0 = 8, 10 and 14 nm on a surface with θ = 180° are first simulated. Figure 2 shows the evolutions of spreading factors for the 10 nm water droplet at We = 4.96–96.68 with spreading factors scaled as β/βmax. All simulated β/βmax collapse onto a curve for We = 34.08–96.68 and the same trend is observed for the 8 and 14 nm water droplets, whereas the difference among the three droplets lies in the contact time. Here, the contact time, τc, is defined as the period of time from a nanodroplet just touching to bouncing off a substrate, and a cutoff distance of 4 Å is employed to evaluate the contact between the fluid and solid molecules. As shown in figure 3(a), the droplet bounces off the surface at 60 ps for D 0 = 8 nm, 85 ps for D 0 = 10 nm and 135 ps for D 0 = 14 nm.
Figure 2. The evolutions of β/βmax for a water nanodroplet with D 0 = 10 nm in a We range from 4.63 to 96.68. The circles represent the data with We of 37.77–96.68 and the pentagons denote the data with We of 4.63–34.08.
Figure 3. Normalized spreading factor β/βmax (a) versus time t for water nanodroplets with D 0 = 8 nm in a We range from 30.21 to 87.31 (squares), D 0 = 10 nm in a We range from 37.77 to 96.68 (circles), and D 0 = 14 nm in a We range from 33.84 to 96.36 (triangles) on superhydrophobic surfaces with θ = 180° and (b) versus normalized time t/τc,h for water nanodroplets with D 0 = 8, 10 and 14 nm in the same We range on a superhydrophobic surface with θ = 180°.
Xie et al. (Reference Xie, Lv, Yang and Wang2020) investigated the contact time of nanodroplets on superhydrophobic surfaces. These authors noted that, unlike millimetre-sized droplets, the effects of liquid viscosity cannot be ignored for nanodroplets in a high-Weber-number range even for low-viscosity fluids; therefore, they developed further a new scaling law of contact time, expressed as 
${\tau _c}\sim {\tau _{c,h}} = ({D_0}/{V_0})W{e^{2/3}}R{e^{ - 1/3}}$, where τc,h is a characteristic time scale of bouncing nanodroplets at high velocities. Because of the increased viscosity effect, the methods based on the energy balance between kinetic energy and surface energy (Laan et al. Reference Laan, de Bruin, Bartolo, Josserand and Bonn2014) or those based on the force balance between inertial force and capillary force (Clanet et al. Reference Clanet, Béguin, Richard and Quéré2004) fail to derive the scaling law of βmax for impacting nanodroplets at high velocities. Inspired by the scaling law of contact time by Xie et al. (Reference Xie, Lv, Yang and Wang2020), the data of β/βmax for the three nanodroplets in the high-Weber-number range are replotted in figure 3(b) using t/τc,h as the abscissa. Interestingly, all the data collapse onto a single curve, indicating that there is a universal function β/βmax = f(t/τc,h). Furthermore, it is found that the nanodroplets reach their maximum spreading diameters at the same time tsp/τc,h, regardless of the droplet diameter and the Weber number. This observation leads to the following correlation,
\begin{equation}{t_{sp}}={c_1}{\tau _{c,h}}\sim \frac{{{D_0}}}{{{V_0}}}W{e^{2/3}}R{e^{ - 1/3}},\end{equation}where tsp is the spreading time, defined as the length of the time period from an impacting droplet just touching the substrate to reaching its maximum spreading diameter, and c 1 is a constant. Equation (3.1) is an empirical correlation based on the MD simulations. However, it must be realized that (3.1) cannot be derived directly by a force or an energy balance because inertial, capillary and viscous forces dominate together the spreading process in this impact regime. Therefore, more efforts need to be devoted to developing an analytical approach that is able to relate the spreading time to these three forces or to We and Re.
There are two kinematic relations for estimation of the spreading time, tsp ~ Dmax/V 0 and tsp ~ D 0/V 0 (Okumura et al. Reference Okumura, Chevy, Richard, Quéré and Clanet2003). Because the spreading time of water nanodroplets is independent of the impact velocity in the high-Weber-number range, tsp ~ D 0/V 0 is improper, and hence tsp ~ Dmax/V 0 is adopted here, whose applicability is verified by figure 4. Combining this relation with (3.1), a scaling law of βmax for nanodroplets in the high-Weber-number range can be obtained,
\begin{equation}{\beta _{max}}\sim W{e^{2/3}}R{e^{ - 1/3}}.\end{equation}
As shown in figure 5, the data of βmax for the water nanodroplets with D 0 = 8, 10 and 14 nm plotted against 
$W{e^{2/3}}R{e^{ - 1/3}}$ reveals that (3.2) fits well the MD data.
Figure 4. Normalized spreading time tsp/(Dmax/V 0) as a function of We for water nanodroplets with D 0 = 8 (squares), 10 (circles) and 14 (triangles) nm.
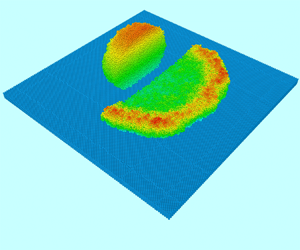
Figure 5. The maximum spreading factor of water nanodroplets with high impact velocities as a function of We 2/3Re −1/3. The solid line indicates the slope of 1. The data for nanodroplets with diameters of 8, 10 and 14 nm are represented by squares, circles and triangles. A typical snapshot of nanodroplets at the maximum spreading state at a high We on a surface with θ = 180° is shown as an inset.
The scaling law (3.2) fails in a low-Weber-number range because the viscosity effect in impacting nanodroplets becomes insignificant. Xie et al. (Reference Xie, Lv, Yang and Wang2020) found that nanodroplets at low velocities deform as a Hertz ball, and the contact time satisfies another scaling law of 
${\tau _c}\sim {\tau _{c,l}} = W{e^{2/5}}{D_0}/{V_0}$ (Richard, Clanet & Quéré Reference Richard, Clanet and Quéré2002; Xie et al. Reference Xie, Lv, Yang and Wang2020). Therefore, the evolutions of nanodroplets at low velocities are also normalized by the timescale of τc,l. Figure 6(a) shows the evolutions of β/βmax with t/τc,l over We from 1.21 to 24.47 for D 0 = 8 nm, from 4.63 to 34.08 for D 0 = 10 nm, and from 2.11 to 29.74 for D 0 = 14 nm, leading to
\begin{equation}{t_{sp}}={c_2}{\tau _{c,l}}\sim \frac{{{D_0}}}{{{V_0}}}W{e^{2/5}},\end{equation}where c 2 is a constant.
Figure 6. (a) Normalized spreading factors β/βmax vs normalized time t/τc,l for water nanodroplets with D 0 = 8 nm in a We range from 1.21 to 30.21, D 0 = 10 nm in a We range from 4.63 to 34.08, and D 0 = 14 nm in a We range from 2.11 to 29.74 on a superhydrophobic surface with θ = 180°; and (b) normalized spreading time tsp/(βmaxDmax/V 0) versus Weber number for water nanodroplets with D 0 = 8, 10 and 14 nm on a superhydrophobic surface with θ = 180° at low impact velocities. The data for nanodroplets with diameters of 8, 10 and 14 nm are represented by squares, circles and triangles.
Equation (3.3) is empirically obtained from the MD simulations; however, it can also be directly derived using the elasticity analysis of Hertz shocks. When a nanodroplet undergoes a Hertz shock, Young's modulus can be equivalent to E = γ/(D 0/2) (Richard et al. Reference Richard, Clanet and Quéré2002). The maximum vertical deformation of a Hertz shock is calculated by 
$\Delta H\sim {D_0}{({\rho ^2}V_0^4/{E^2})^{1/5}}$ (Landau & Lifshits Reference Landau and Lifshits1965). Thus, the spreading time can be written as 
${t_{sp}} = \Delta H/{V_0}\sim ({D_0}/{V_0})W{e^{2/5}}$. It should be noted that the kinematic relations, tsp ~ Dmax/V 0 and tsp ~ D 0/V 0, are both inappropriate for estimation of the spreading time and, hence, the kinematic relation of tsp is directly derived from Hertz shocks. For a Hertz shock, because kinetic energy is completely converted into elastic potential energy at the maximum deformation, the normalized contact area can be expressed as 
$\beta _{max}^2\sim \Delta H/{D_0}$ (Landau & Lifshits Reference Landau and Lifshits1965). The kinematic relation of tsp is therefore expressed as tsp = ΔH/V 0 ~ βmaxDmax/V 0, which is well validated by the MD simulations, as shown in figure 6(b). Combining this relation with (3.3) generates a scaling law for nanodroplets in the low-Weber-number range,
\begin{equation}{\beta _{max}}\sim W{e^{1/5}}.\end{equation}Figure 7 demonstrates the agreement between the scaling law and MD simulations, which confirms the existence of capillary regime for nanodroplets with low impact velocities.
Figure 7. The maximum spreading factor of water nanodroplets with low impact velocities as a function of We. The dashed line indicates the slope of 1/5. The data for nanodroplets with diameters of 8, 10 and 14 nm are represented by squares, circles and triangles. A typical snapshot for nanodroplets at the maximum spreading state at a low We on a surface with θ = 180° is shown as an inset.
The impact dynamics of low-viscosity millimetre-sized droplets, such as water droplets, are controlled only by inertial and capillary forces in an extremely wide We range of 2 < We < 900 (Clanet et al. Reference Clanet, Béguin, Richard and Quéré2004). Therefore, βmax for such droplets is expressed as a function of We. On the basis of energy conversion from the kinetic energy at the initial state to the surface energy at the maximum spreading state, 
$\rho D_0^3V_0^2\sim \gamma D_{max}^2$ is obtained, leading to a scaling law of 
${\beta _{max}}\sim W{e^{1/2}}$. Unfortunately, this scaling law has not been experimentally observed on any surfaces yet. This can be attributed to vortical motions inside droplets, causing residual kinetic energy at the maximum spreading state. Alternatively, using a force balance analysis, Clanet et al. (Reference Clanet, Béguin, Richard and Quéré2004) presented that the scaling law of 
${\beta _{max}}\sim W{e^{1/4}}$ is valid for low-viscosity millimetre-sized droplets. However, the present simulations show that the impact dynamics of low-viscosity nanodroplets can be divided into two regimes. In the low-Weber-number range, the impact is controlled only by inertial and capillary forces, referred to as the capillary regime, as with millimetre-sized droplets, whereas in the high-Weber-number range, viscous force also becomes one of dominating forces, namely impact falls into the cross-over regime.
A possible reason for the difference between 
${\beta _{max}}\sim W{e^{1/4}}$ for the millimetre-sized droplets and 
${\beta _{max}}\sim W{e^{1/5}}$ for nanodroplets in the capillary regime is different droplet shapes at the maximum spreading state. In a We range of 1 < We < 34, millimetre-sized droplets always evolve into a pancake shape. Nevertheless, the present MD simulations show that nanodroplets at the maximum spreading state deviate from the pancake shape and the assumption of Hertz balls can satisfactorily explain the scaling law of βmax in this impact regime.
Two main mechanisms contribute to the significantly enhanced viscous effect in the high-Weber-number range. First, as the droplet size reduces to the nanoscale, the Ohnesorge number increases significantly. Second, viscous dissipation only occurs in the boundary layer for the millimetre-sized droplets, whereas there is no boundary layer for nanodroplets and, hence, energy is dissipated within the whole nanodroplets, leading to significantly increased viscous dissipation. As a result of the enhanced viscous effect, nanodroplets follow the scaling law of 
${\beta _{max}}\sim W{e^{2/3}}R{e^{ - 1/3}}$ in the high-Weber-number range, namely the impact converts into the cross-over regime. With consideration of the conversion among kinetic energy, surface energy and viscous dissipation, a relation 
${C_1}\rho D_0^3V_0^2\sim \gamma D_{max}^2\;\textrm{or}\;{\beta _{max}}\sim {({C_1}We)^{1/2}}$ can be obtained, where C 1 < 1 is a conversion coefficient, which quantifies the contribution of viscous dissipation. Recently, Wang et al. (Reference Wang, Wang, Xie, Liu, Wang, Yang, Gao and Wang2020b) examined the impact of nanodroplets with diameters from 3 to 15 nm on surfaces. They found that viscous dissipation can be expressed as an Oh-dependent function. According to this finding, 
${\beta _{max}}\sim W{e^{2/3}}R{e^{ - 1/3}}$ can be rewritten 
${\beta _{max}}\sim W{e^{1/2}}O{h^{1/3}}$ using the relation of 
$Oh = W{e^{1/2}}/Re$. Thus, we have 
${C_1}\sim O{h^{2/3}}$, which indicates that the contribution of viscous dissipation is identical for nanodroplets with the same Oh. In other words, for the same kind of low-viscosity nanodroplets, once their diameters are equal, the scaling law of 
${\beta _{max}}\sim W{e^{1/2}}$ is valid. Two water nanodroplets with D 0 = 8 and 14 nm and an argon nanodroplet with D 0 = 12 nm, corresponding to fixed Oh = 0.391 and 0.296 for water and 0.320 for argon, are employed to validate the scaling law of 
${\beta _{max}}\sim W{e^{1/2}}$. A shown in figure 8, the curves of βmax for the 14 nm water nanodroplet and the 12 nm argon nanodroplet are almost coincide owing to the close Oh. As expected, they do not coincide with the curve for the 8 nm water nanodroplet because of different Oh. Good linear relations are observed for all three sets of data in the coordinate system of βmax vs We 1/2, verifying the scaling law of 
${\beta _{max}}\sim W{e^{1/2}}$ when Oh remains constant.
Figure 8. Maximum spreading factors of water nanodroplets with D 0 = 8 (squares, Oh = 0.391) and 14 (circles, Oh = 0.296) nm and an argon nanodroplet with D 0 = 12 nm (triangles, Oh = 0.320) as a function of We 1/2. The solid line indicates slope 1. The static contact angles are 180° for all three nanodroplets.
3.2. Surface wettability
The scaling laws of 
${\beta _{max}}\sim W{e^{1/2}}O{h^{1/3}}$ and 
${\beta _{max}}\sim W{e^{1/5}}$ are derived for low-viscosity nanodroplets with θ = 180°, namely ideal superhydrophobic surfaces. It is well known that for a spontaneous spreading process, the equilibrium spreading factor (here also referred to as zero-velocity spreading factor) of a droplet is determined by its static contact angle on solid surfaces. The equilibrium spreading factor nonlinearly increases as the static contact angle reduces. Therefore, surface wettability affects the maximum spreading factor of impacting droplets through the zero-velocity spreading factor. From the viewpoint of energy, in addition to the initial kinetic energy, there is still a zero-velocity surface energy to drive a droplet to reach the maximum spreading state. Wang et al. (Reference Wang, Wang, Gao, Yang, Wang and Chen2020a) presented that although surface wettability affects the maximum spreading factor of impacting nanodroplets, its effects must be considered only on relatively hydrophilic surfaces. Based on MD simulations, they developed a relation to quantify the influence of wettability on spreading by defining the ratio of impact velocity, V 0, to spreading velocity, Vs, expressed as
\begin{equation}\frac{{{V_0}}}{{{V_s}}} = \left\{ {2.07391 \times {{10}^8}\exp \left[ {\frac{{ - 1}}{{0.01933(2 + \cos \theta )}}} \right] + 0.04932} \right\}\exp \left( { - \frac{{We}}{{22}}} \right) + 0.667,\end{equation}when We is set as 30, the ratio is 0.6880 for θ = 73°and 0.6796 for θ = 180°, whereas the value is 0.7784 for θ = 55°. Restated, the maximum spreading factor weakly depends on surface wettability for θ>73°, suggesting the applicability of the two scaling laws developed with θ = 180° ((3.2) and (3.4)) may still be valid for surfaces with θ > 73°. Figure 9 shows validation for the impact of water nanodroplets with diameters of 8 to 14 nm on surfaces with contact angles ranging from 73° to 180°. In addition, the data of an argon nanodroplet impacting a surface with θ = 150° are also included. The validation shows satisfactory agreement between the scaling laws ((3.2) and (3.4)) and the MD simulations.
Figure 9. Maximum spreading factors βmax versus (a) We 2/3Re −1/3 and (b) We for water nanodroplets with various D 0 and an Ar nanodroplet with D 0 = 12 nm on the surfaces with θ from 73° to 180°. The solid line indicates the slope of 1 and the dashed line indicates the slope of 1/5. The results with D 0 = 13.2 nm (left-triangles) are obtained from Li et al. (Reference Li, Zhang and Chen2015). The results with D 0 = 8.6 nm (pentagons) are obtained from Li et al. (Reference Li, Li and Chen2017). The results with D 0 = 10 nm (down-triangles) are obtained from Wang et al. (Reference Wang, Wang, Gao, Yang, Wang and Chen2020a).
3.3. Impact number
Only the Weber number is employed to separate the capillary regime from the cross-over regime in § 3.1. Because the impact of nanodroplets is affected by both the Weber number and the Reynolds number in the cross-over regime, a more accurate parameter that contains We and Re or We and Oh is necessary. Here, the parameter to separate the two regimes is defined as impact number Q. The expression of Q can be derived from the scaling laws in the two regimes. First, if the maximum spreading factor is divided by We 1/5, a linear relationship would be maintained in the capillary regime and the straight line would be parallel to the horizontal axis in the coordinate system of 
${\beta _{max}}/W{e^{1/5}}$ vs Q(We, Oh). Second, the choice of the parameter Q must ensure another linear relationship in the cross-over regime in the same coordinate system. According to the scaling law of 
${\beta _{max}}\sim W{e^{2/3}}R{e^{ - 1/3}}$ in the cross-over regime, we have 
${\beta _{max}}/W{e^{1/5}}\sim W{e^{3/10}}O{h^{1/3}}$ and, hence, 
$Q = W{e^{3/10}}O{h^{1/3}}$ is determined. The data of the maximum spreading factor for the 10 nm water droplet is replotted in the coordinate system of 
${\beta _{max}}/W{e^{1/5}}$ versus We 3/10Oh 1/3, as shown in figure 10. As expected, two linear relationships are observed, and the two straight lines intersect at Q = 2.1. Thus, the impact of nanodroplets falls into the capillary regime when Q < 2.1 but into the cross-over regime when Q > 2.1.
Figure 10. Dimensionless capillary maximum spreading factor 
${\beta _{max}}/W{e^{1/5}}$ as a function of the impact number Q = We 3/10Oh 1/3. The blue up-triangles represent water nanodroplets impacting superhydrophobic surfaces. Linear relations are observed in both the capillary and the cross-over regime, and the two straight lines intersect at Q = 2.1.
The significantly enhanced viscous effect caused by a reduction in the droplet size has recently received extensive attention. The studies of the maximum spreading factor (Li et al. Reference Li, Zhang and Chen2015; Wang et al. Reference Wang, Wang, Gao, Yang, Wang and Chen2020a), maximum spreading time (Wang et al. Reference Wang, Wang, Yang, Wang and Chen2021b), contact time on superhydrophobic surfaces (Xie et al. Reference Xie, Lv, Yang and Wang2020), breakup criterion (Li et al. Reference Li, Li and Chen2017) and splash outcomes (Wang et al. Reference Wang, Wang, Wang, Zhang, Yang, Wang and Chen2021a) for impacting nanodroplets offered pieces of evidence to support this effect. Unfortunately, there has been no quantitative parameter to determine whether viscous effect must be taken into account. The present impact number, Q, is a possible criterion to distinguish the contribution of viscous dissipation for the impact of low-viscosity nanodroplets. It is worth noting that the expression and/or value of impact number may alter for different impact outcomes, such as spreading, recoiling and rebounding, because viscous dissipation plays different roles in these dynamic processes. Therefore, more works need to be implemented to further verify the effectiveness of the impact number of Q = We 3/10Oh 1/3.
4. Conclusions
Owing to the increased viscous effect, altered viscous dissipation mechanism and enhanced sensitivity to surface wettability caused by a reduction in droplet size, the impact of nanodroplets on solid surfaces shows significantly different dynamics from the macroscale and, hence, has gained increasing attention in recent years. In this study, the impact dynamics of low-viscosity nanodroplets on flat surfaces with static contact angles from 73° to 180° have been studied by MD simulations. The special focus is placed on the determination of scaling laws of the maximum spreading factor for impacting nanodroplets. Two kinds of self-similar evolutions are identified, β/βmax varying with t/τc,h and with t/τc,l, which represent two kinds of shape evolutions, a thin-film-like droplet in the cross-over regime and a Hertz-ball-like droplet in the capillary regime. Combining with the kinematic approximations of spreading time, 
${\beta _{max}}\sim W{e^{2/3}}R{e^{ - 1/3}}$ (or 
${\beta _{max}}\sim W{e^{1/2}}O{h^{1/3}}$) in the cross-over regime and 
${\beta _{max}}\sim W{e^{1/5}}$ in the capillary regime are obtained. The two scaling laws show good agreement with MD simulation data in a wide range of We and Re as long as static contact angles of solid surfaces are larger than 73°. The proposed explicit scaling laws characterize the nature of competition of inertial, capillary and viscous forces, without a requirement of the complete information of velocity gradients. Furthermore, using the two scaling laws, an impact number, Q = We 3/10Oh 1/3, is defined to identify the contribution of viscous dissipation. A value of Q = 2.1 is found to separate the capillary regime from the cross-over regime.
Declaration of interests
The authors report no conflict of interest.
Funding
This study was supported by the State Key Program of National Natural Science of China (No. 51936004) and Science Fund for Creative Research Groups of the National Natural Science Foundation of China (No. 51821004).
