Let 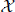 be a space of homogeneous type in the sense of Coifman and Weiss, and let
be a space of homogeneous type in the sense of Coifman and Weiss, and let  be a collection of balls in
be a collection of balls in 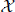 . The authors introduce the localized atomic Hardy space
. The authors introduce the localized atomic Hardy space  the localized Morrey-Campanato space
the localized Morrey-Campanato space  and the localized Morrey-Campanato-BLO (bounded lower oscillation) space
and the localized Morrey-Campanato-BLO (bounded lower oscillation) space  with α ∊ ℝ and p ∊ (0, ∞) , and they establish their basic properties, including
with α ∊ ℝ and p ∊ (0, ∞) , and they establish their basic properties, including 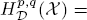
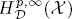 and several equivalent characterizations for
and several equivalent characterizations for 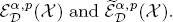 In particular, the authors prove that when α > 0 and p ∊ [1, ∞), then
In particular, the authors prove that when α > 0 and p ∊ [1, ∞), then 
 and when p ∈(0,1], then the dual space of
and when p ∈(0,1], then the dual space of 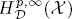 is
is  Let ρ be an admissible function modeled on the known auxiliary function determined by the Schrödinger operator. Denote the spaces
Let ρ be an admissible function modeled on the known auxiliary function determined by the Schrödinger operator. Denote the spaces 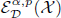 and
and  , respectively, by
, respectively, by 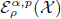 and
and  when
when  is determined by ρ. The authors then obtain the boundedness from
is determined by ρ. The authors then obtain the boundedness from  of the radial and the Poisson semigroup maximal functions and the Littlewood-Paley g-function, which are defined via kernels modeled on the semigroup generated by the Schrödinger operator. These results apply in a wide range of settings, for instance, the Schrödinger operator or the degenerate Schrödinger operator on ℝd, or the sub-Laplace Schrödinger operator on Heisenberg groups or connected and simply connected nilpotent Lie groups.
of the radial and the Poisson semigroup maximal functions and the Littlewood-Paley g-function, which are defined via kernels modeled on the semigroup generated by the Schrödinger operator. These results apply in a wide range of settings, for instance, the Schrödinger operator or the degenerate Schrödinger operator on ℝd, or the sub-Laplace Schrödinger operator on Heisenberg groups or connected and simply connected nilpotent Lie groups.