INTRODUCTION
In a highly influential article, John F. Muth (1961) formulated the rational expectations hypothesis (REH), the theory and applications of which have been treated in a voluminous literature. Much of the literature has been concerned with formulating the conditions under which an RE equilibrium holds. This note shows the implications of model misspecifications for the REH. In particular, we show that, if agents estimate a misspecified statistical model of the relationship among economic variables, the agents will not, in general, have rational expectations. Hence, agents will not be able to learn about the “true” relationship among relevant economic variables. To formulate this argument, we begin with the conceptual idea that there are “true” relations linking “true” variables involving “true” coefficients, defining the “objective” probability distributions. We then show that specified econometric models are the exact representations of the corresponding “true” models if their coefficients are interpreted in a certain way. In the absence of the conditions implied by these interpretations, the econometric models are misspecified.
In the next section, we exploit the connection between the “true” economic relationships suggested by economic theories and econometric specifications. By doing so, we are able to show the effects of model misspecifications and to develop a mathematical formulation of Muth's definition of rational expectations that is based on a new form of purely “objective” probability distributions. In other words, in contrast to the definitions that have appeared in the literature, our definition of “objective” probability distributions does not contain subjective elements. The implications of our argument are summarized in the final section.
CONDITIONS UNDER WHICH INDIVIDUAL EXPECTATIONS ARE RATIONAL
We assume throughout that the available observations on economic variables are the sums of “true” values and measurement errors, both of which are unobservable. In what follows, symbols with an asterisk denote “true” values and symbols without an asterisk denote observable variables measured with error.
DEFINITION 1 (Muth, 1961). Expectations of individuals (or, more generally, the subjective probability distribution of outcomes) are rational if they tend to be distributed, for the same information set, about the prediction of the relevant economic theory (or the “objective” probability distributions of outcomes).
The meanings of the terms used in this definition have been given in earlier studies on rational expectations and, therefore, are not repeated here. Definition 1 contains two interpretations of probability—an objective one and a subjective one. In the existing economics and statistics literature, there is no well-accepted definition of objective probability. In contrast to the situation that exists with respect to objective probability, Bayesian interpretations of probability are widely accepted as subjective. To bring the data to bear on the REH, an appropriate method of specifying both subjective and objective probability distributions of outcomes is required. In what follows, we develop such a method.
DEFINITION 2 (Swamy and Tavlas, 2001). Any variable or value that is not mismeasured is true and any economic relationship with the correct functional form, without any omitted explanatory variables and without mismeasured variables, is true.
Accordingly, if the “true” relationship among a set of economic variables exists, it should be of the following form:
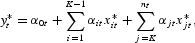
where all the determinants of
are included on the right-hand side, even though we may not know anything about some of these determinants. In other words, there are no excluded explanatory variables in equation (1). To avoid the possibility of excluding from (1) any determinant of
at any time, we assume that the number of the determinants of
may change over time. Hence, nt is time dependent.
Equation (1) avoids all restrictions not implied by economic theories. In this connection, it can be thought of as the relationship implied by economic theories, in which case, we can assume that a mechanism through which the right-hand side variables in (1) exactly determine
exists. If we exclude from (1) the variables, say
, then an explanation of the relationship between
and
, can be found in the dependence of both
and
, on a common, third set of variables,
, a phenomenon known as spurious correlation [see Lehmann and Casella (1998, p. 107)].1
Variables excluded from equation (1) are the context in which we use the expression “spurious correlation.” Equation (1) differs from the models considered in previous studies of spurious correlation because, as shown by Pratt and Schlaifer (1984, 1988), the error terms of the models employed in these studies do not represent ‘the’ excluded variables.
may represent individual expectations, as in Muth's (1961, p. 317) supply equation. The deviations of these expectations from their respective proxies represent measurement errors, which are explicitly taken into account later.
Solution to the unknown-functional-form problem
Equation (1) is linear if αit, i=0, 1, … , K−1, and αjt, j=K, … , nt, are constant over time; otherwise, the equation is nonlinear. The particular nonlinear form it may take will depend on the time profiles of its coefficients. Restrictions on the pattern of variation in (e.g., the constancy of) the coefficients of (1) may force (1) to have an incorrect functional form. In our state of ignorance about the correct functional form of (1), permitting all of its coefficients to vary freely over time allows us to obtain a class of functional forms that encompasses the correct functional form of (1). We, therefore, make use of this solution by allowing all the coefficients of (1) to vary freely. The coefficients of (1) with the “true” pattern of variation are denoted by
, and
, the existence of which is assumed here. This assumption is equivalent to the assumption that the “true” functional form of (1) exists.
Therefore, the “true” model that is a member of the class in (1) is
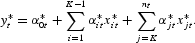
This equation satisfies Definition 2. Equation (2) differs from (1) in that the former includes both the “true” values of all the variables and the coefficients whereas the class of models represented by (1) includes only the “true” values of the variables but not the “true” values of the coefficients. Equation (2) is linear if
, and
, are constant over time, but is nonlinear otherwise. Because the “true” functional form of (1) can be nonlinear, we do not restrict
, and
, to be constant over time. In what follows, the values of
corresponding to the unrealized values of
, and
, are called potential values because they correspond to the underlying, but unobserved, “true” process, whereas the realized values of
are those corresponding to the realized values of
, and
. Only when these potential values exist, is the “true” model a law and not a statistical association, as shown by Pratt and Schlaifer (1988, p. 28); consequently, if the potential values of
do not exist, the relation in equation (2) fitted to observations is a pure statistical artifact. Empirical implementation of the “true” model is not possible because data on the variables,
, are not available.
A time-varying parameter (TVP) model involving only the observable counterparts of the dependent and the first K−1 explanatory variables of the “true” model is
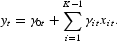
The observed variables are yt and xit, i=1, … , K−1, for which data are available. They are the observable counterparts of the “true” values,
and
, respectively.
Classification of the explanatory variables of the “true” model
The variables, xit, i=1, … , K−1, are called the included explanatory variables. The variables,
, are called excluded variables because they are omitted from the TVP model.
The mapping between the coefficients of the “true” model and the coefficients of the TVP model can be shown to be as follows:
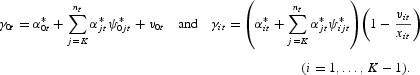
These equations are obtained by substituting the relationships,
, among the “true” values of excluded and included variables with the “true” functional forms for
in the “true” model and treating the measurements,
, as the sums of “true” values,
, and measurement errors, vit. The term, v0t, in γ0t is the measurement error in
.
Correct interpretations of the coefficients of the TVP model
The first equation in (4) can be interpreted as implying that the intercept γ0t is the sum of (i)
, the intercept of the “true” model, (ii) the joint effect (
on the “true” value (
of yt of the portions of the “true” values,
, of excluded variables remaining after the effects of the “true” values,
, of the included explanatory variables have been removed, and (iii) the measurement error, v0t, in yt. The last K−1 equations in (4), corresponding to the γit's with i>0, can be interpreted as implying that for i=1, … , K−1, γit is the sum of (i) the coefficient,
, on
of the “true” model, (ii) a term (
capturing omitted-variables bias caused by excluded variables, and (iii) a measurement-error bias,
, due to mismeasuring xit [see Chang, Swamy, Hallahan, and Tavlas (2000), Swamy and Tavlas (2001), and Swamy, Chang, Mehta, and Tavlas (2003)]. The omitted-variable biases will be zero if the included explanatory variables are uncorrelated with every excluded variable and the measurement-error biases will be zero if the included explanatory variables are measured without error. These conditions are rarely, if ever, satisfied.
Under the correct interpretations of its coefficients, the TVP model is an exact representation of the “true” model because the right-hand side of the TVP model is exactly equal to the right-hand side of the “true” model when the equations in (4) hold. The coefficients of the TVP model will be called “the biased coefficients” because they contain omitted-variable and measurement-error biases. The coefficients of the “true” model will be called “the bias-free coefficients” because they are not subject to any biases. We assume that each of the coefficients of the TVP model is linearly related to the observable variables, zdt, d=1, … , p−1, plus a stochastic error:
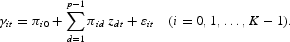
We call the z's “the coefficient drivers.” We further assume that for i>0, the sum of p1(<p) specific terms in
is equal to the bias-free component,
, of γit, the sum of the remaining p−p1 terms and εit is equal to the sum of omitted-variables and measurement-error bias components of γit, and, given the z's, the included explanatory variables are independent of the εit's. [see Swamy, Tavlas, and Chang (2005)].
Substituting equation (5) for γit in the TVP model gives a nonlinear regression with heteroscedastic and serially correlated error terms; this regression can be estimated using an iteratively rescaled generalized least squares method [see Swamy, Tavlas, and Chang (2005)].2
Suppose that
of the “true” model represents forward-looking expectations and its bias-free coefficient is
. Then we can identify this coefficient using our method if we can find an observable proxy, denoted by x1t, for
. In this case,
,
and the sum of p1 (<p) specific terms of
is equal to
. This is how a TVP model would allow the econometrician to better identify forward- and backward-looking components. Bayesian methods are not a device capable of providing estimates (and, therefore, predictions) that would empirically be indistinguishably as good as any (classical) TVP models, as shown by Pratt and Schlaifer (1988, p. 49). These Bayesian statisticians point out that a Bayesian will do much better to search like a non-Bayesian for concomitants that absorb omitted-variable and measurement-error biases. The coefficient drivers in equation (5) are our concomitants.
Two important implications of the correct interpretations of the coefficients of the TVP model
(i) Variation in γit stems from variation in its components. It can be seen from (4) that the real-world sources of variation in its components are: (a) the nonlinearities of the “true” model causing variation in the α*'s, (b) the nonlinearities of the relationships among the “true” values of excluded and included explanatory variables causing variation in the ψ*'s, and (c) variation in the ratio of vit to xit. (ii) The included variable xit cannot be uncorrelated with its own coefficient γit (i.e., in the TVP model, the included explanatory variables are correlated with their own coefficients). This result is due to the fact that the measurement-error bias component of γit is a function of both xit and vit.
Any assumption that contradicts these implications leads to invalid tests of Definition 1 [see Swamy, Tavlas, and Chang (2005) and Swamy and Tavlas (2005)]. The assumption of equation (5) does not, however, contradict the correct interpretation of γit if (i) the function,
, completely accounts for the correlation between γit and xit so that the remainder εit obtained by subtracting the function,
, from γit is independent of xit and (ii) the function,
, is decomposable into two sums, one of which is equal to the bias-free component of γit and the other of which is equal to the sum of omitted-variables and measurement-error bias components of γit. The satisfaction of these conditions should underpin the selection of the coefficient drivers.
According to “the Lucas critique” (1976), the parameters of the “decision rules” embodied in the systems of structural equations will not remain stable when economic policies change, even if the rules themselves are appropriate. If the parameters of the “decision rules” embodied in the TVP model change when economic policies change, then policy changes can be used as coefficient drivers in equation (5). With policy changes entering into equation (5) as coefficient drivers, the TVP model is not subject to “the Lucas critique.”
A linear model, which is a very restrictive form of the TVP model is
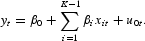
Objective and subjective probability distributions
The conditional probability distribution of
, given all of the determinants of
, is “objective” if it can be derived from the “true” model without the aid of any subjective priors and restrictions. We assume that the variable,
, obeying the “true” model follows some conditional frequency distribution, given all of its determinants. This is what we call the “objective” distribution of
. The falsity of this assumption implies the nonexistence of the “objective” distribution of
. Let
denote the probability density function (pdf) of the “objective” probability distribution of
with respect to a measure μ [see Lehmann and Casella (1998, p. 14, (3.2))]. To keep
entirely objective, the condition, “without the aid of any subjective priors and restrictions,” is needed. In contrast to this approach, much of the literature assumes that the given data are generated by a specific process. For example, the work of Hansen and Sargent (2004, p. 5) is representative of the literature; this work assumes that the data are generated by a Markov (possibly subjective) process, which the authors presume is the true process. Hansen and Sargent do not, however, explain why this process might be devoid of all subjective elements. Anderson, Hansen, and Sargent (2003) say, “By equating agents' subjective probability distributions to the objective one implied by … [a rational expectations] model, the assumption of rational expectations precludes any concerns that agents should have about the model's specification.” (p. 69). This sentence is easy to understand if by a rational expectations model Anderson et al. mean the one that satisfies Definition 2. Econometricians typically employ either the TVP model or the linear model, depending on their (subjective) preferences for time-varying coefficient versus fixed-coefficient models. The probability distributions of
based on the TVP and linear models are not objective since, in specifying these models, various subjective decisions have been taken a priori. For example, before estimating the TVP model, authors usually make assumptions about the behavior of the coefficients over time and across individuals, assumptions that are, by their very nature, subjective. Likewise, assumptions that some of the included and excluded explanatory variables in the linear model are exogenous are also subjective. Let
and
denote the pdfs of the subjective distributions of
based on the TVP and linear models, respectively.
THEOREM 1. Let f, g, and p, defined earlier, be nonnegative and integrable functions with respect to μ and S be the region in which f>0. If
0 and
, then
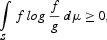
with equality only when f=g(a.e. μ) and
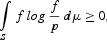
with equality only when f=p(a.e. μ).
For a proof, see Rao (1973, p. 59).
The integral in (7) (or (8)) defines the entropy distance between f and g (or f and p), with respect to f [see Lehmann and Casella (1998, p. 47)]. There is always the question whether
of the “true” model has a pdf that satisfies the conditions of Theorem 1.
Necessary and sufficient conditions
The individual expectations, involved in the TVP (or linear) model are rational in Muth's sense or a strong form of Definition 1 is true if and only if the equality in equation (7) [or equation (8)] holds.
Yet, as we show later, these equalities are so strong that they may never hold. More specifically, we show that (i) under certain conditions, the entropy distance between f and g can be shorter than that between f and p, (ii) under (5), there can be a considerable overlap between the “objective” distribution of
and its subjective distribution implied by the TVP model, and (iii) the equality in (8) is unlikely to hold because the linear model cannot coincide with the “true” model under the assumptions usually made about xit and u0t.
THEOREM 2. The predictions of
given by the TVP model can be rational most of the time, whereas those given by the linear model can only be rational some of the time.
Proof. The expectations of individuals involved in the TVP (or linear) model are rational in the weak sense if the predictions of
generated from the TVP (or linear) model are the same as those generated from the “true” model.
- The conditional expectation of , given all of its determinants, is its minimum average mean square error (or best) predictor. The correct form of this conditional expectation is given by the “true” model if the “objective” conditional probability distribution of , given all of the determinants of , exists and possesses finite variance. The linear model gives an incorrect form of this conditional expectation because it omits some determinants of and the determinants of included in it are measured with error. Its functional form is also incorrect if the functional form of the “true” model is nonlinear. How can an incorrect conditional expectation always yield the predictions that are as accurate as those yielded by the correct conditional expectation? Recall that under the correct interpretations of its coefficients, the TVP model is an exact representation of the “true” model. As a consequence, the TVP model in conjunction with (5) imply the correct conditional expectation of , given all of the determinants of , if the coefficient drivers included in (5) assign the correct functional form to the TVP model and, given the zdt's, the xit's are independent of the εit's.
- The coefficients of the TVP model have the important invariance property that they are not altered when (1) is written in terms of , and a function of , and [see Swamy, Mehta, and Singamsetti (1996)]. The coefficients of (1), however, do not possess this invariance property. Consequently, in (1), excluded explanatory variables, , and the coefficients, αit, i=0, 1, … , K−1, on the “true” values of the included explanatory variables are not unique, as shown by Pratt and Schlaifer (1984, p. 13). This nonuniqueness implies the nonuniqueness of the coefficients and the error term of the linear model. The nonunique coefficients of the linear model do not measure the direct effects of its explanatory variables on its dependent variable. By contrast, real-world relations of the “true” model's type are unique because they remain invariant against changes in the language used to describe them [see Basmann (1988, pp. 72–74)]. For example, adding and subtracting a term on the right-hand side of a representation of a real-world relation change only the representation but not the relation. The TVP model, but not the linear model, shares this invariance property with real-world relations. The “true” model, being a real-world relation, is unique.
- The TVP model coincides with the linear model if for i=1, … , K−1, the distribution of γit is degenerate at βi and the distribution of γ0t is the same as that of β0+u0t. These restrictions, however, contradict the correct interpretations of the γit's.
- Pratt and Schlaifer (1988) show that the condition that the included explanatory variables in the linear model are (mean) independent of “the” excluded variables themselves “is meaningless unless the definite article is deleted and can then be satisfied only for certain ‘sufficient sets’ of excluded variables some if not all of which must be defined in a way that makes them unobservable as well as unobserved” (p. 34) [see also Pratt and Schlaifer (1984, pp. 11–13)]. Thus, the assumption that some of the included explanatory variables and some of excluded variables in the linear model are exogenous or (mean) independent of u0t with mean zero is, in the terminology of Pratt and Schlaifer, “meaningless” and prevents the linear model from coinciding with the “true” model.
- The TVP model cannot also coincide with the “true” model if it is estimated under the assumptions that are inconsistent with the correct interpretations of its coefficients. For example, if the correlation between γit and xit is ignored, if the distribution assumed for γit is inconsistent with the distributions of its three components, or if the assumptions made about the initial values of γit needed in Kalman-filter applications are inconsistent with the distributions of its components, then the TVP model cannot coincide with the “true” model. With assumptions that are consistent with the correct interpretations of the γit's, we can satisfy at least a necessary condition for the predictions from the TVP model to agree with those from the “true” model [see Swamy et al. (2003, pp. 240–242)].
The following conclusions emerge from results (i)–(v):
(a) The predictions of
from the TVP model can agree with the predictions from the “true” model most of the time and the entropy distance between f and g is shorter than that between f and p if the coefficient drivers included in equation (5) assign the correct functional form to the TVP model and, given the zdt's, the xit's are independent of the εit's.
(b) The predictions of
from the linear model, whose underlying assumptions bear no resemblance to reality, can agree with the predictions of
from the “true” model some of the time, but not all of the time. The loss suffered by users of the linear model is that accurate predictions are obtained only some of the time, but not most of the time. [squf ]
The only case in which agents need not have any concerns about their models' specification is that in which their models coincide with the corresponding “true” models. In cases in which agents use the TVP model, g converges to f if the agents would eventually detect the differences between the
's and γit's, and would adjust their subjective distributions about the γit's accordingly; for a similar adjustment procedure [see Pratt and Schlaifer (1988, p. 49)].
DISCUSSION
Any possible definition of an “objective” probability distribution of events cannot rely on subjective beliefs. In this paper, we have provided a statement of the “true” model that does not contain any subjective element. This model can be used to formulate the “objective” probability distribution. The problem that arises in practice is that the “true” model contains many unknown quantities. Models are misspecified when (i) they omit relevant explanatory variables, (ii) included variables are measured with error, or (iii) the “true” functional forms are incorrectly stated. Model misspecifications make it impossible for the model estimated on observed data to be sufficiently close to the “truth” for rational expectations to hold, in the sense of providing a subjective probability distribution sufficiently close to the underlying objective one, consistent with the “truth.” Yet, this circumstance does not preclude the possibility that the predictions generated from models with time-varying coefficients can be accurate most of the time. If agents use very restrictive fixed-coefficient models that are not derived from time-varying coefficient models, however, the inconsistencies in their models' underlying assumptions prevent their expectations from converging over time to the rational expectations value.
Any opinions expressed in this paper are those of the authors and do not constitute policy of their respective institutions. Thanks are due to Peter von zur Muehlen, William Barnett, and two anonymous referees for helpful comments.


