Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-06T06:07:59.011Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of fumarolic anhydrous copper sulfate minerals during successive hydration/dehydration

Published online by Cambridge University Press:  02 February 2021

Oleg I. Siidra Open the ORCID record for Oleg I. Siidra [Opens in a new window] ,
Artem S. Borisov ,
Dmitri O. Charkin ,
Wulf Depmeier  and
Natalia V. Platonova
Oleg I. Siidra*
Affiliation:
Department of Crystallography, St. Petersburg State University, University Embankment 7/9, 199034St. Petersburg, Russia
Artem S. Borisov
Affiliation:
Department of Crystallography, St. Petersburg State University, University Embankment 7/9, 199034St. Petersburg, Russia
Dmitri O. Charkin
Affiliation:
Chemistry Department, Moscow State University, Leninskie Gory 1-3, Moscow199992Russia
Wulf Depmeier
Affiliation:
Institut für Geowissenschaften der Universität Kiel, Olshausenstr. 40, D-24098Kiel, Germany
Natalia V. Platonova
Affiliation:
X-ray Diffraction Resource Center, St. Petersburg State University, University Embankment 7/9, 199034St. Petersburg, Russia
*
*Author for correspondence: Oleg I. Siidra, Email: o.siidra@spbu.ru
Rights & Permissions [Opens in a new window]

Abstract

Hydration processes of primary anhydrous minerals as well as dehydration of the hydrated phases are relevant not only for answering geochemical and petrological questions, but are also interesting in the context of the theory of the ‘Evolution of minerals’. Our study of the evolution of anhydrous exhalative sulfates in hydration and dehydration processes has demonstrated the complexity of the processes for a number of minerals from the active high-temperature fumaroles of Tolbachik volcano (chalcocyanite Cu(SO4), dolerophanite Cu2O(SO4), alumoklyuchevskite K3Cu3AlO2(SO4)4 and itelmenite Na2CuMg2(SO4)4). Hydration and dehydration experiments were carried out for all four minerals using powder X-ray diffraction. A typical structural characteristic of several anhydrous copper sulfate minerals of fumarolic origin is the presence of oxygen-centred OCu4 tetrahedra. These are absent in the structures of all known hydrated minerals or synthetic compounds of the class under consideration. Hydration of minerals initially containing O2– anions as part of oxocomplexes, proceeds with sequential formation of a large series of hydroxysalts. On the contrary, hydration of itelmenite with its relatively complex ‘initial’ structure, but without additional oxygen atoms that are strong Lewis bases, results in formation of simpler hydrates. The lower the temperature and the larger the excess of water, the stronger the tendency of the cations to adopt higher hydration numbers thus outcompeting the sulfate anions as ligands. Ultimately, the water molecules completely expel the bridging sulfate anions from the metal coordination sphere yielding relatively simple fully hydrated structures.

Keywords

evolution of mineralssulfatesreversible hydration/dehydrationfumarolic mineralsX-ray diffraction
Type
Article
Information
Mineralogical Magazine , Volume 85 , Issue 2 , April 2021 , pp. 262 - 277
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Mineralogical Society of Great Britain and Ireland

Introduction

Hydration processes of primary anhydrous minerals as well as dehydration of the hydrated phases are relevant not only for answering geochemical and petrological questions, but are also interesting in the context of the theory of the ‘Evolution of minerals’ (Hazen et al., Reference Hazen, Papineau, Bleeker, Downs, Ferry, McCoy, Sverjensky and Yang2008). One important piece of this theory refers to the observation that new mineral species formed by hydration are usually more complex than the pristine ones, and often more than one secondary species are formed from a given primary mineral. There are many more important aspects of hydration/oxidation processes, e.g. their role in the formation of economic mineral deposits or their possible ecological threat, as these processes are often the first steps of destructive weathering that can lead to release of toxic elements into the environment with all kinds of subsequent detrimental effects.

In the past few decades, hydration and dehydration processes of sulfate minerals, especially those containing iron, have been studied (Sklute et al., Reference Sklute, Rogers, Gregerson, Jensen, Reeder and Dyar2018; Xu et al., Reference Xu, Tosca, Mclennan and Parise2009). Much systematic work has been devoted to the study of hydration and dehydration processes in the magnesium–sulfate–water system, in view of understanding the palaeo-atmospheric conditions on Mars (e.g. Vaniman et al., Reference Vaniman, Bish, Chipera, Fialips, Carey and Feldman2004; Chipera and Vaniman, Reference Chipera and Vaniman2007; Altheide et al., Reference Altheide, Chevrier, Nicholson and Denson2009; Grevel and Majzlan, Reference Grevel and Majzlan2009). Note that all of the cited publications – and others not cited here for lack of space – concern primarily simple systems such as Fe(SO4)–H2(SO4)–H2O or Mg(SO4)–H2(SO4)–H2O. Systems containing other cations, e.g. other transition metals instead of Fe, or additional main group cations such as Na or K, or anions like halides, have received less attention to date.

Anhydrous high-temperature sulfate minerals with transition metals such as iron, copper, zinc and vanadium are quite exotic mineral species, and occur almost exclusively in fumaroles of active volcanoes – in a few cases they also form by natural underground coal fires (e.g. Pautov et al., Reference Pautov, Mirakov, Siidra, Faiziev, Nazarchuk, Karpenko and Makhmadsharif2020). These minerals often become unstable under changing temperature conditions and are particularly unstable when they are exposed to humid atmosphere or to precipitation. When this happens they may hydrate rapidly and undergo various chemical and physical transformations, including repeated dissolution–crystallisation cycles. Re-heating by exhausting hot gases from the fumarole may lead to dehydration with either recovery of the pristine minerals, or crystallisation of new species. The chemical compositions as well as the structural architectures of many fumarolic minerals are unique and have no analogues among synthetic compounds, which makes them also interesting for inorganic crystal chemistry and materials science. Equally of interest is the possible occurrence of metastable transient phases upon hydration or dehydration, which are often inaccessible via traditional synthetic routes.

Fumaroles on active volcanoes can be subdivided into two groups: (1) fumaroles with oxidising conditions and (2) fumaroles with reducing mineral-formation environments. The latter are much more common and have been well-studied in terms of mineralogy; common primary mineral species are native elements, sulfides and sulfosalts. Overall, the mineral inventory is relatively poor and uniform. In stark contrast to the latter, oxidising fumaroles are much less common on Earth and they differ significantly in the number and variety of mineral species. Some of the best-studied fumaroles with oxidising conditions are located at the Vesuvius volcano where they show remarkable copper oxide mineralisation (Balassone et al., Reference Balassone, Petti, Mondillo, Panikorovskii, de Gennaro, Cappelletti, Altomare, Corriero, Cangiano and D'Orazio2019). The Vesuvius fumaroles have been known since antiquity. In the middle of the 20th Century, oxidising fumaroles of the Izalco volcano in Salvador were investigated and revealed rich anhydrous copper–vanadium mineralisation (Hughes and Stoiber, Reference Hughes and Stoiber1985). Half a century ago, in 1975–1976, one of the most famous eruptions of the 20th Century rocked the Tolbachik volcano located on the Kamchatka Peninsula, Russian Federation. This became known as the Great Fissure Tolbachik Eruption (Fedotov and Markhinin, Reference Fedotov and Markhinin1983). Several scoria cones were formed and the associated fumaroles turned out to be real bonanzas providing amazingly rich and diverse mineral associations, which have become a veritable playground for the study of the mineralogy and crystal chemistry of volcanic exhalations (Vergasova and Filatov, Reference Vergasova and Filatov2012, Reference Vergasova and Filatov2016; Pekov et al., Reference Pekov, Koshlyakova, Zubkova, Lykova, Britvin, Yapaskurt, Agakhanov, Shchipalkina, Turchkova and Sidorov2018 a,Reference Pekov, Zubkova and Pushcharovskyb). In 2012, another important eruption occurred on the Tolbachik volcano – the Fissure Tolbachik Eruption. The copper mineralisation in the fumaroles of the Second Scoria Cone of the Great Fissure Tolbachik Eruption was so rich that at the end of the 1970s these fumaroles were valued as a very rich, though small, copper deposit and possible mining was considered. Fortunately, the remoteness and inaccessibility of this deposit made its possible exploitation uneconomic. The fumaroles became world-renowned, not so much as a reservoir of copper, but rather for the large number of different endemic mineral species, as well as for the total mineral diversity, which makes it second to none on our planet, at least to this date. Note that the areas holding productive fumaroles are rather small: the fumarole field on the Second Scoria Cone for example extends over just a few hundred square metres. Nevertheless, more than 110 new mineral species have been described from the fumaroles of Great Fissure Tolbachik Eruption and the Fissure Tolbachik Eruption to date. We also contributed to this list by the discovery and study of a number of new anhydrous sulfate mineral species from the fumaroles of both localities (Siidra et al., Reference Siidra, Vergasova, Krivovichev, Kretser, Zaitsev and Filatov2014a, Reference Siidra, Nazarchuk, Zaitsev, Lukina, Avdontseva, Vergasova, Vlasenko, Filatov, Turner and Karpov2017, Reference Siidra, Lukina, Nazarchuk, Depmeier, Bubnova, Agakhanov, Avdontseva, Filatov and Kovrugin2018a,Reference Siidra, Nazarchuk, Agakhanov, Lukina, Zaitsev, Turner, Filatov, Pekov, Karpov and Yapaskurtb,Reference Siidra, Nazarchuk, Lukina, Zaitsev and Shilovskikhc, Reference Siidra, Nazarchuk, Zaitsev, Polekhovsky, Wenzel and Spratt2019b,Reference Siidra, Nazarchuk, Agakhanov and Polekhovskyc, Reference Siidra, Nazarchuk, Zaitsev and Shilovskikh2020a,Reference Siidra, Nazarchuk, Zaitsev and Vlasenkob; Nazarchuk et al., Reference Nazarchuk, Siidra, Agakhanov, Lukina, Avdontseva and Karpov2018, Reference Nazarchuk, Siidra, Nekrasova, Shilovskikh, Borisov and Avdontseva2020). It is very likely that the list of new minerals discovered in the fumaroles of the Tolbachik volcano is far from complete. Post-eruptive processes are still ongoing and the formation of new mineral species is being observed. The temperature in the fumaroles is by no means constant but changes over time, either rising or falling. Some of the fumaroles that were active decades ago, are now extinct. As a result of alteration by hydration processes, the formation of unique associations of secondary hydrated sulfate minerals has been observed (e.g. Siidra et al., Reference Siidra, Vergasova, Kretser, Polekhovsky, Filatov and Krivovichev2014b,Reference Siidra, Vergasova, Kretser, Polekhovsky, Filatov and Krivovichevc). However, the transformation of primary fumarolic minerals under the influence of atmospheric moisture has been poorly studied to date. The temperature regime in the upper fumarole zones is subject to seasonal fluctuations due to the large amount of atmospheric precipitations. The first systematic studies of these processes were carried out by our group on euchlorine KNaCu3O(SO4)3 (Siidra et al., Reference Siidra, Borisov, Lukina, Depmeier, Platonova, Colmont and Nekrasova2019a), which demonstrated an unexpected complexity of such processes, both in the number of phases formed and in the transformations of multiphase aggregates as a function of changing temperatures. The current paper expands these studies to cover a larger set of fumarolic minerals.

The Yadovitaya (Russian for ‘Poisonous’) fumarole (55°49′59″N, 160°19′59″E) is located in the fumarole field on the summit of the Second Scoria Cone of the Northern Breakthrough of the Great Fissure Tolbachik Eruption. The field is located ~18 km SSW from the active shield volcano Ploskiy (flat) Tolbachik (Fedotov and Markhinin, Reference Fedotov and Markhinin1983). The Yadovitaya fumarole was one of the first fumaroles described after the Great Fissure Tolbachik Eruption (Vergasova and Filatov, Reference Vergasova and Filatov2016). The intensity of the gas streams in this fumarole varied greatly in the first years after the eruption (Menyailov et al., Reference Menyailov and Nikitina1980a) and Yadovitaya fumarole is still very active to date. The diversity in the number of endemic copper sulfate mineral species with various additional cations and anions in the Yadovitaya fumarole is impressive. Figure 1a shows a photograph of the freshly cleared fumarole wall to a depth of 2.5 metres as of September 2019. The Cu–SO4 zone enriched in various anhydrous copper sulfates ranges from 35 cm to 65–70 cm below the top of the fumarole; marked by red lines on Fig. 1a. All the mineral samples (Fig. 1b,d,e) used for hydration experiments described below were collected from this zone. The temperature of exhaust gases registered on the level of the Cu–SO4 zone was ~300°C. All the samples recovered were packed and isolated immediately after collection in order to protect them from contact with the external atmosphere. It is clearly evident that chalcocyanite, dolerophanite and alumoklyuchevskite were deposited directly as sublimates from volcanic gas emissions, however the origin of itelmenite, which contains a significant amount of Mg, is presumed to be the product of a reaction between volcanic gases and the basaltic scoria. This is corroborated by the fact that possible relevant Mg compounds have very low volatility at 300°C, hence direct sublimation of this mineral is deemed improbable. On the top of the fumarole, on the outcrop, there is a zone (~10 cm) with variable fluoride mineralisation. Between the fluoride zone and the Cu–SO4 zone, a 15 to 25 cm thick intermediate zone composed of altered and hydrated copper sulfate minerals is easily discerned by its colouration (Fig. 1).

Fig. 1. General view of the wall of the Yadovitaya fumarole. The Cu–SO4 rich zone is delimited by red lines (a). The maximum thickness of the Cu–SO4 zone is 35 cm. Well crystallised chalcocyanite sample excavated from this zone (b) and the same sample, almost completely transformed into chalcanthite, exposed to humid air for one week (c). Dark brown crystals of dolerophanite with green euchlorine (d) and clusters of needle-like crystals of alumoklyuchevskite (e) from the Cu–SO4 zone used in this work.

Hydration experiments and high-temperature powder X-ray crystallography

Experimental

Chalcocyanite, dolerophanite, alumoklyuchevskite and itelmenite are water soluble and sensitive to air humidity. The crystals of all minerals start to alter, with initial formation of hydrated mineral films, after only one day of exposure (e.g. chalcocyanite) to open air with 81% relative humidity and 23°C. Systematic hydration experiments were carried out to monitor the occurring transformations by powder X-ray diffraction (PXRD).

For all the minerals used for further research, qualitative electron microprobe analysis (Hitachi S-3400N scanning electron microscope equipped with an Oxford Instruments X-Max 20 Energy Dispersive Spectrometer) revealed no elements other than reported in the respective publications: chalcocyanite (Siidra et al., Reference Siidra, Lukina, Nazarchuk, Depmeier, Bubnova, Agakhanov, Avdontseva, Filatov and Kovrugin2018a), alumoklyuchevskite (Gorskaya et al., Reference Gorskaya, Vergasova, Filatov, Rolich and Ananiev1995, Siidra et al., Reference Siidra, Nazarchuk, Zaitsev, Lukina, Avdontseva, Vergasova, Vlasenko, Filatov, Turner and Karpov2017) and itelmenite (Nazarchuk et al., Reference Nazarchuk, Siidra, Agakhanov, Lukina, Avdontseva and Karpov2018). There is a published semi-quantitative chemical analysis of dolerophanite from the fumaroles of Vesuvius (Kahler, Reference Kahler1962). The dolerophanite sample used in this study contained 1.8 wt.% ZnO. An admixture of zinc is rather common for the copper sulfate minerals studied here. This is not surprising as the gas condensates of the Great Fissure Tolbachik Eruption were highly enriched in Zn (Menyailov et al., Reference Menyailov and Nikitina1980a,Reference Menyailov, Nikitina and Shaparb). Apart from the slight Zn-for-Cu substitution in dolerophanite, the ratio of the elements in the minerals agrees well with the formulas, viz. chalcocyanite Cu(SO4), dolerophanite Cu2O(SO4), alumoklyuchevskite K3Cu3AlO2(SO4)4 and itelmenite Na2CuMg2(SO4)4.

The experiments for all four minerals were carried out using the same technique: 1 g of each mineral was hand-picked under an optical microscope and ground in an agate mortar. Prior to that the purity of each sample was checked using PXRD, and in the case of observed impurities a new sample was selected. The pure powdered sample was loaded on a Si plate for further X-ray measurements. In turn, the holder with the Si plate was placed inside a common desiccator (3 litre volume) and 250 ml of distilled water was poured into the bottom of the desiccator. The humidity in the desiccator during the experiments was monitored by a humidity- and temperature-meter CEM DT-625. The estimated standard deviation (e.s.d.) for humidity values is 0.5%. Each set of experiments was repeated twice. In total six subsequent stages of hydration were carried out for each mineral and the results are listed in Tables 1, 3 and 5. The transformation of each powder sample into the respective single phase or mixture of hydrated sulfates is accompanied by colour changes (Figs 2–5).

Fig. 2. XRD patterns for the products of chalcocyanite hydration (left below). Different stages of hydration are numbered on the left side. Peak positions of ‘chalcanthite’ Cu(SO4)⋅5H2O are marked with blue triangles. XRD patterns for the products of dehydration of the mixture of hydrated sulfates initially obtained from chalcocyanite (left above). Blue – ‘chalcanthite’ Cu(SO4)⋅5H2O; green – ‘bonattite’ Cu(SO4)⋅3H2O; orange – ‘poitevinite’ Cu(SO4)⋅H2O; and black – ‘chalcocyanite’ Cu(SO4). Hydration of chalcocyanite single-phase powder and formation of various hydrated copper sulfates is accompanied by colour changes (right). During the heating of the hydrated products the colour reverses back completely in agreement with the reversible hydration/dehydration of chalcocyanite. The relative humidity for each hydration stage is given in Table 1.

Fig. 3. XRD patterns for the products of dolerophanite hydration (left below). Different stages of hydration are numbered on the left side. XRD patterns for the products of dehydration of the mixture of hydrated sulfates initially obtained from dolerophanite (left above). Different stages of dehydration are numbered on the left side. Hydration of dolerophanite single-phase powder and formation of various hydrated copper sulfates is accompanied by colour changes (right). During the heating of the hydrated products the colour reverses back in agreement with the formation of a mixture of anhydrous sulfates. The relative humidity for each hydration stage is given in Table 1.

Fig. 4. XRD patterns for the products of alumoklyuchevskite hydration (left below). Different stages of hydration are numbered on the left side. XRD patterns for the products of dehydration of the mixture of hydrated sulfates initially obtained from alumoklyuchevskite (left above). Different stages of dehydration are numbered on the left side. Hydration of alumoklyuchevskite single-phase powder and formation of various hydrated copper sulfates is accompanied by the colour changes (right). During the heating of the mixture the colour partially reverses back. The relative humidity for each hydration stage is given in Table 3.

Fig. 5. XRD patterns for the products of itelmenite hydration (left below). Different stages of hydration are numbered on the left side. XRD patterns for the products of dehydration of the mixture of hydrated sulfates initially obtained from itelmenite (left above). Different stages of dehydration are numbered on the left side. Hydration of itelmenite single-phase powder and formation of various hydrated copper and magnesium sulfates is accompanied by the colour changes (right). During the heating of the mixture the colour reverses back. The relative humidity for each hydration stage is given in Table 5.

Table 1. Evolution of primary dolerophanite into mixtures of hydrated sulfates during the hydration experiments at 23°C, different duration and different relative humidity.

The amount of each phase is given in wt.%. E.s.d is ~3%. All mineral-like phases appearing during hydration/dehydration are shown in quotes. Dominating phases (≥20%) are marked in bold.

A Rigaku Ultima X-ray diffractometer (CuKα radiation) was used to give PXRD data in air after each stage. The duration of each X-ray measurement was ~15 min. The evolution of the powder diffraction patterns in moist environments is shown in Figs 2–5. Full powder diffraction patterns were collected at different intervals and analysed via Rietveld refinement using the TOPAS program (Bruker, 2014). Using the known structural data for each of the intermediate phases (minerals) listed in Tables 1–6 it was possible to refine the phase fraction of each of the intermediate phases and thus to determine the composition of the mixtures. Note, all mineral-like phases that appear during hydration/dehydration are in quotes.

Table 2. Evolution of the mixture of hydrated sulfate phases, formed as a result of dolerophanite hydration, upon heating.

The amount of each phase is given in wt.%. E.s.d is ~3%. All mineral-like phases appearing during hydration/dehydration are shown in quotes. Dominating phases (≥20%) are marked in bold.

Table 3. Evolution of primary alumoklyuchevskite into mixtures of hydrated sulfates during the hydration experiments at 23°C, different duration and different relative humidity.

The amount of each phase is given in wt.%. E.s.d is ~3%. All mineral-like phases appearing during hydration/dehydration are shown in quotes. Dominating phases (≥20%) are marked in bold.

Table 4. Evolution of the mixture of hydrated sulfate phases, formed as a result of alumoklyuchevskite hydration, upon heating. Dominating phases (≥20%) are marked in bold. The transformation can be subdivided into three main stages (I–III) in accordance with the dominance of different phases (marked in bold). Amount of each phase is given in wt. %. E.s.d is ~3%.

The amount of each phase is given in wt.%. E.s.d is ~3%. All mineral-like phases appearing during hydration/dehydration are shown in quotes. Dominating phases (≥20%) are marked in bold.

Table 5. Evolution of primary itelmenite into mixtures of hydrated sulfates during the hydration experiments at 23°C, different duration and different relative humidity.

The amount of each phase is given in wt.%. E.s.d is ~3%. All mineral-like phases appearing during hydration/dehydration are shown in quotes. Dominating phases (≥20%) are marked in bold.

Table 6. Evolution of the mixture of hydrated sulfate phases, formed as a result of itelmenite hydration, upon heating. The evolution can be subdivided into three main stages (I–III) in accordance with the dominance of different phases.

The amount of each phase is given in wt.%. E.s.d is ~3%. All mineral-like phases appearing during hydration/dehydration are shown in quotes. Dominating phases (≥20%) are marked in bold.

The thermal behaviour of the mixtures of the different hydrated sulfates was studied subsequently in air by means of a Rigaku Ultima X-ray diffractometer (CoKα radiation (dolerophanite, alumoklyuchevskite and itelmenite experiments) or CuKα radiation (chalcocyanite experiment only) and a high-temperature camera Rigaku HTA 1600. The sample was loaded on a Pt–Rh plate. Temperature steps were 25°C in the range 25–400°C. The evolution of the PXRD patterns during heating is shown in Figs 2–5. The phases identified at different steps are listed in Tables 2,4 and 6.

Results

Chalcocyanite Cu(SO4)

Hydration

In a moist atmosphere chalcocyanite transforms rapidly into ‘chalcanthite’ Cu(SO4)⋅5H2O (Bacon and Titterton, Reference Bacon and Titterton1975). The single-phase composition remains intact until the last stage of the hydration (Fig. 2).

Dehydration

The first stage of heating (Fig. 2) at 25°C and 50°C is also characterised by chalcanthite. However, note that the first minor peaks of ‘bonattite’ Cu(SO4)⋅3H2O (Zahrobsky and Baur, Reference Zahrobsky and Baur1968) start to appear at 50°C. At 75°C, the sample completely consists of ‘bonattite’ Cu(SO4)⋅3H2O. The third stage covers the relatively large temperature range 100°C–200°C and is characterised also by a single-phase corresponding to ‘poitevinite’ Cu(SO4)⋅H2O (Ting et al., Reference Ting, Henry, Schmidtmann, Wilson and Weller2009). At 225°C a transitional stage with coexisting ‘poitevinite’ and anhydrous CuSO4 (chalcocyanite) is observed. Starting from 250°C the sample composition has reversed back to the initial chalcocyanite. The colour of the powder sample is also the initial grey (Fig. 2).

Dolerophanite Cu2O(SO4)

Hydration

The initial dolerophanite sample contained no admixtures of other phases (Fig. 3) and its powder pattern corresponds to that reported for synthetic Cu2O(SO4) (Effenberger, Reference Effenberger1985).

After the hydration processes have started, the phase composition undergoes significant transformations (diffraction patterns 2–4 in Fig. 3). ‘Kobyashevite’ Cu5(SO4)2(OH)6⋅4H2O (Pekov et al., Reference Pekov, Zubkova, Yapaskurt, Belakovskiy, Chukanov, Kasatkin, Kuznetsov and Pushcharovsky2013) and ‘chalcanthite’ Cu(SO4)⋅5H2O (Bacon and Titterton, Reference Bacon and Titterton1975) appear in significant amounts. The amount of dolerophanite decreases gradually, and drops down to 13 wt.% as registered in powder pattern #4.

At the next stage of hydration (diffraction patterns 5–6 in Fig. 3 and Table 1) the signature of dolerophanite has almost disappeared, and its amount is refined to yield only 3 wt.%. ‘Kobyashevite’ has become the major phase with 67 wt.% whereas the ‘chalcanthite’ content is still important with ~30 wt.%.

The last stage of the dolerophanite hydration experiment (diffraction pattern 7 in Fig. 3 and Table 1) is characterised by the almost complete disappearance of ‘chalcanthite’ in favour of ‘antlerite’, Cu3(SO4)(OH)4 (Hawthorne et al., Reference Hawthorne, Groat and Eby1989). The remains of ‘chalcanthite’ amount to only ~6 wt.%.

Dehydration

The dolerophanite dehydration processes with increasing temperature can be classified into three main stages (Table 2). The characteristic of stage I is the dominance of ‘kobyashevite’ although its amount gradually decreases with rising temperature. Diffraction patterns 10–12 at 75°C, 100°C and 125°C (Fig. 3) demonstrate the appearance of ‘poitevinite’ Cu(SO4)⋅H2O (Ting et al., Reference Ting, Henry, Schmidtmann, Wilson and Weller2009) at the expense of the ‘chalcanthite’.

Dehydration stage II, starting at 150°C, is characterised by the complete disappearance of ‘kobyashevite’, with ‘poitevinite’ and ‘antlerite’ becoming the dominant phases. Minor amounts of ‘chalcocyanite’ (~3 wt.%) appear in the polyphasic mixture. There is a gradual decrease in the amount of ‘poitevinite’ with rising temperature until 300°C. The amount of ‘antlerite’ remains nearly constant during this process, but the amount of chalcocyanite gradually increases.

The last dehydration stage III starts at 325°C and is accomplished at 350°C. ‘Chalcocyanite’ is the dominant phase throughout this stage with ~70%. Re-appearance of ‘dolerophanite’ is observed at this temperature, but its amount does not exceed 20%. ‘Tenorite’ CuO (Brese et al., Reference Brese, O'Keeffe, Ramakrishna and Von Dreele1990) is present with ~12% as an obvious product of decomposition of ‘chalcocyanite’ and/or ‘dolerophanite’. The colour of the sample becomes brownish at the end (Fig. 3).

Alumoklyuchevskite K3Cu3AlO2(SO4)4

Hydration

The initial alumoklyuchevskite sample contained no detected admixtures of other phases (Fig. 4) and its powder pattern is in a good agreement with that calculated for its recently refined crystal structure (Siidra et al., Reference Siidra, Nazarchuk, Zaitsev, Lukina, Avdontseva, Vergasova, Vlasenko, Filatov, Turner and Karpov2017).

Immediately after the start of hydration, the alumoklyuchevskite sample starts to decompose and shows the diffraction pattern of two hydrated phases (diffraction patterns 2 and 3 in Fig. 4): ‘cyanochroite’ K2Cu(SO4)2⋅6H2O (Bosi et al., Reference Bosi, Belardi and Ballirano2009) and subordinate ‘chalcanthite’ Cu(SO4)⋅5H2O (Bacon and Titterton, Reference Bacon and Titterton1975). After 60 min of hydration, the reflections of alumoklyuchevskite have disappeared completely. The amount of ‘cyanochroite’ gradually increases, and at the end of hydration, the sample is almost completely represented by this phase (diffraction pattern 7 in Fig. 4; Table 3).

Dehydration

The dehydration behaviour of the product of the alumoklyuchevskite hydration registered by PXRD appears relatively simple. It is characterised by three main stages (Table 4). At the beginning of the experiment, when the temperature reached 25°C, the remains of ‘chalcanthite’ have completely disappeared and only diffraction peaks of ‘cyanochroite’ are present. According to the diffraction patterns 10–18 in Fig. 4, the sample undergoes gradual amorphisation.

A recrystallisation of the sample is observed in the range 300–400°C. All the observed peaks correspond to K2Cu(SO4)2 (PDF card No. 00-017-0485, powder diffraction file from the International Centre for Diffraction Data, https://www.icdd.com/). The crystal structure of this phase is unknown. K2Cu(SO4)2, reported recently by Zhou et al. (Reference Zhou, Liu, Ang and Zhang2020), has an unrelated PXRD pattern.

Note that regardless of the likely formation of a considerable amount of crystalline ‘cyanochroite’ during hydration, the colour of the resulting sample does not show the typical bluish tints typical for the mineral cyanochroite, but appears yellow with greenish tints instead. This might be an indication of the amorphous Al2O3 or its hydrated forms as decomposition products that envelop the finely dispersed crystallites of ‘cyanochroite’.

Itelmenite Na2CuMg2(SO4)4

Hydration

The initial itelmenite sample contained no admixtures of other phases (Fig. 5) and its powder pattern is in a good agreement with the pattern calculated for the crystal structure of itelmenite (Nazarchuk et al., Reference Nazarchuk, Siidra, Agakhanov, Lukina, Avdontseva and Karpov2018).

Itelmenite demonstrates remarkably complex and multiple transformations even after the first 30 min of hydration. About half of the polyphase mixture is still represented by itelmenite. The second most significant phase is ‘hexahydrite’ Mg(SO4)⋅6H2O (Zalkin et al., Reference Zalkin, Ruben and Templeton1964). The other hydrates of magnesium sulfates are represented by ‘pentahydrite’ MgSO4⋅5H2O (Baur and Rolin, Reference Baur and Rolin1972), ‘starkeyite’ Mg(SO4)⋅4H2O (Baur, Reference Baur1962) and ‘sanderite’ Mg(SO4)⋅2H2O (Ma et al., Reference Ma, Bish, Wang and Chipera2009). ‘Kröhnkite’ Na2Cu(SO4)2⋅2H2O (Hawthorne and Ferguson, Reference Hawthorne and Ferguson1975) and ‘brucite’ Mg(OH)2 (Mitev et al., Reference Mitev, Gajewski and Hermansson2009) are also present in minor amounts (Table 5).

After another 30 min of hydration the amount of itelmenite is reduced. ‘Kröhnkite’ becomes dominant and the amount of ‘hexahydrite’ is reduced. New phases ‘epsomite’ Mg(SO4)⋅7H2O (Calleri et al., Reference Calleri, Gavetti, Ivaldi and Rubbo1984) and ‘alpersite’ (Mg,Cu)(SO4)⋅7H2O (Mills et al., Reference Mills, Wilson, Dipple and Raudsepp2010) appear in minor amounts.

The third stage of hydration (diffraction patterns 4–6 in Fig. 5) is characterised by almost constant phase composition, with only slight variations in the amounts of these phases. Primary itelmenite no longer exists in the mixture, and only ‘kröhnkite’, ‘epsomite’, ‘hexahydrite’ and ‘alpersite’ are registered.

The last stage of hydration is characterised by the strong shift of the dominant phases and appearance of ‘konyaite’ Na2Mg(SO4)2⋅5H2O (Mills et al., Reference Mills, Wilson, Dipple and Raudsepp2010) in the amount of 62 wt.%.

Dehydration

At 25°C and 50°C the composition of the polyphase sample, with ‘konyaite’ as the dominant phase, is similar to the final stage of hydration. At 75°C the sample completely transforms into a two-phase mixture highlighting the end of the dehydration stage I.

Dehydration stage II indicates almost complete amorphisation of the sample (diffraction patterns 12–17 in Fig. 5). Some relics of crystalline matter are present, but an interpretation of the diffraction pattern is uncertain.

Dehydration stage III is characterised by the presence of anhydrous crystalline phases only. Simple Mg(SO4) (Rentzeperis and Soldatos, Reference Rentzeperis and Soldatos1958) is the dominant phase in the range from 275°C to 375°C. Its amount gradually reduces with the rise of the temperature in favour of the amount of ‘chalcocyanite’ Cu(SO4). By 275°C itelmenite has already reappeared in minor amounts and becomes the dominant phase at 400°C. ‘Vanthoffite’ Na6Mg(SO4)4 (Fischer and Hellner, Reference Fischer and Hellner1964), ‘metathénardite’ Na2(SO4) (Rasmussen et al., Reference Rasmussen, Jorgensen and Lundtoft1996) and MgO (Fan et al., Reference Fan, Sun, Shen, Kuo and Lu2008) are minor phases.

In the photographs (Fig. 5), it is clearly seen that the initial grey colour of the itelmenite powder sample fades away towards the end of the experiment and becomes light grey.

Discussion

Chemistry

Chalcocyanite

The reversible hydration of this mineral has been studied previously using synchrotron radiation (Ting et al., Reference Ting, Henry, Schmidtmann, Wilson and Weller2009). The good agreement of our results with those reported by (Ting et al., Reference Ting, Henry, Schmidtmann, Wilson and Weller2009) makes us confident that our experimental setup reproduces the hydration process of this mineral sufficiently well. Thus, chalcocyanite can be relied on as a reference system for the other minerals studied in this work. Under high RH (relative humidity) at ambient conditions, hydration proceeds in one step yielding the thermodynamically stable product, i.e. chalcanthite. The small amount of chalcocyanite remaining even after several hours of hydration can be probably explained by formation of chalcanthite ‘shells’ around the initial chalcocyanite particles, which block or strongly retard the hydration process. On heating, formation of the less water-rich forms proceeds in the temperature intervals, which agree well with the data of Cheng et al. (Reference Cheng, Li, Li, Yang, Li, Cheng and Song2019). Note the relatively low crystallinity of the monohydrate.

Dolerophanite

Hydration: This case is more complex than chalcocyanite as the hydration involves formation of basic copper sulfates whose interconversion depends on a variety of external conditions including temperature, presence of liquid phase and its acidity as well as copper concentration (Yoder et al., Reference Yoder, Agee, Ginion, Hofmann, Ewanichak, Schaeffer, Carroll, Schaeffer and McCaffrey2007; Stanimirova and Ivanova, Reference Stanimirova and Ivanova2019). The first step of hydration can be described tentatively by an equation 3Cu2O(SO4) + 14H2O = Cu5(SO4)2(OH)6·4H2O + Cu(SO4)·5H2O, or expressed in shorthand by the Cu:SO4 ratio, 3(2:1) = (1:1) + (5:2). The (5:2) compound is known to be easily formed either by reaction of CuO with an aqueous solution of CuSO4 (Stanimirova and Ivanova, Reference Stanimirova and Ivanova2019) or gently increasing the pH of a CuSO4 solution by adding small amounts of alkalis (Yoder et al., Reference Yoder, Agee, Ginion, Hofmann, Ewanichak, Schaeffer, Carroll, Schaeffer and McCaffrey2007), probably due to kinetic reasons. It was found to be stable in contact with aqueous solutions of cupric sulfate (1M or slightly below), while in pure water it readily converts into brochantite (4:1) or its hydrates (posnjakite and langite). In addition, Yoder et al. (Reference Yoder, Agee, Ginion, Hofmann, Ewanichak, Schaeffer, Carroll, Schaeffer and McCaffrey2007) note that in their experiments, antlerite (3:1) could only be obtained at 80°C or above. Yet, in our case kobyashevite, as the major hydration product of dolerophanite, was in steady contact with a slurry containing solid chalcanthite, i.e. copper sulfate pentahydrate, during the hydration process. Note that Yoder et al. (Reference Yoder, Agee, Ginion, Hofmann, Ewanichak, Schaeffer, Carroll, Schaeffer and McCaffrey2007) studied the stability of kobyashevite only against 1M Cu(SO4) and pure water; other concentrations of cupric sulfate solution may already lead to formation of antlerite at room temperature. Further investigations of basic copper sulfate interconversions in copper sulfate solutions of varied concentrations, including the presence of solid Cu(SO4)·5H2O, are obviously necessary to provide better understanding of these processes.

Formation of synthetic kobyashevite was also detected upon hydration of a more complex copper oxysulfate mineral, euchlorine KNaCu3O(SO4)2 (Siidra et al., Reference Siidra, Borisov, Lukina, Depmeier, Platonova, Colmont and Nekrasova2019a), but formation of antlerite was not observed. Possibly, the concentration of copper sulfate in the slurries formed was not high enough because of the relatively low solubility of kröhnkite-type double copper–alkali sulfate products.

Dehydration: Evaporation of water from the initial slurry results in the initial crystallisation of dissolved chalcanthite. In agreement with Yoder et al. (Reference Yoder, Agee, Ginion, Hofmann, Ewanichak, Schaeffer, Carroll, Schaeffer and McCaffrey2007), the antlerite content increases as the temperature rises and water-rich kobyashevite dehydrates. This step can be described by a tentative equation 2Cu5(SO4)2(OH)6·4H2O = 3Cu3(SO4)(OH)4 + Cu(SO4)·H2O + 7H2O, or in shorthand, 2(5:2) = 3(3:1) + (1:1). Poitevinite is also formed by dehydration of chalcanthite. At the final steps, copper hydroxyl sulfates decompose with loss of water and formation of cyanochroite and tenorite. We note that, while our study was restricted to 450°C, the suggested deposition temperature on the wall of the fumarole, only a small part of the initial dolerophanite was recovered. In thermoanalytical studies dedicated to dehydration of basic copper sulfates (Ramamurthy and Secco, Reference Ramamurthy and Secco1970; Uzunov et al., Reference Uzunov, Klissurski and Teocharov1995; Tanaka and Koga Reference Tanaka and Koga1988), thermal effects attributed to the formation of synthetic dolerophanite (in a CuO-rich mixture) are reported to occur at somewhat higher temperatures (~500°C). In one of our test experiments in a sealed silica tube no reaction was observed between CuO and Cu(SO4) up to 550°C. In contrast, formation of basic copper alkali sulfates proceeds easily below 450°C both upon dehydration (Siidra et al., Reference Siidra, Borisov, Lukina, Depmeier, Platonova, Colmont and Nekrasova2019a) and in silico.

Alumoklyuchevskite

The chemical identity of at least some of the hydration products remains obscure due to their amorphous nature. Based on the crystalline products formed at the first stage, we suggest the following equation: 2K3Cu3AlO2(SO4)4 + (26 + x)H2O = 3K2Cu(SO4)2⋅6H2O + Cu(SO4)⋅5H2O + [Al2(SO4)(OH)4⋅xH2O], the amorphous part (with a tentative composition) shown in brackets. The low temperature of the hydration process probably favours formation of amorphous basic aluminium salts that crystallise with difficulty, as noted particularly for sulfates (Nordstrom, Reference Nordstrom1982). It is possible that the progressive disappearance of chalcanthite is caused by its slow dissolution in the slurry (it is more water soluble compared to cyanochroite) and sorption by the aluminium-based amorphous phase. Further reactions involving formation of amorphous double copper–aluminium hydroxysulfates are also possible.

Upon heating, given the overall cation ratio, one could expect formation of sulfates with a K:Cu ratio of 1:1, i.e. K2Cu2(SO4)3 (Lander et al., Reference Lander, Rousse, Batuk, Colin, Dalla Corte and Tarascon2017), or a mixture of K2Cu(SO4)2 and Cu(SO4). Instead, the only process detectable by PXRD study is dehydration of cyanochroite, also via an amorphous precursor. Thermogravimetry and differential thermal analysis (TG/DTA) studies of synthetic cyanochroite (Nagase et al., Reference Nagase, Yokobayashi and Sone1978) revealed a two-step loss of water (which is complete below 150°C) followed by two endothermal effects at 370 and 520°C, the latter being attributed to melting. The data provided in PDF card No. 00-017-0485 is not yet interpreted, but refers to the compound prepared by dehydration of cyanochroite, most likely to the high-temperature form of K2Cu(SO4)2 while the structure reported by Zhou et al. (Reference Zhou, Liu, Ang and Zhang2020) refers to its low-temperature form, according to the method of preparation. In our experiment, crystallisation of the high-temperature form starts from ~275°C, which might be enhanced by the amorphous nature of the precursor or by the presence of aluminium. Detailed temperature-dependent studies of K2Cu(SO4)2·6H2O and its anhydrous form, particularly DTA/PXRD, are evidently necessary to confirm the nature of compound noted in PDF card No. 00-017-0485.

Itelmenite

Due to the absence of additional oxygen atoms, the formation of any basic salts upon hydration is not expected. Only a few selected and partial studies have been performed within the relatively complex Na2(SO4)–Cu(SO4)–Mg(SO4)–H2O system (e.g. Steiger et al., Reference Steiger, Linnow, Ehrhardt and Rohde2011; Lindström et al., Reference Lindström, Talreja, Linnow, Stahlbuhk and Steiger2016). In addition, rapid hydration is most likely driven by kinetic factors, i.e. compounds more easily formed are observed first. Hence, the initial hydration stage can be described by the following tentative equation: Na2CuMg2(SO4)4 + (2 + 2x)H2O = Na2Cu(SO4)2·2H2O + 2(Mg,Cu)(SO4)·xH2O. The latter formula designates the successively formed magnesium sulfates that may also accommodate the remaining copper sulfate as the latter's hydrates are not observed. The following steps correspond mostly to progressive hydration of Mg/Cu sulfates until the point where the largest hydration point is observed (epsomite and alpersite). Further reactions are likely to proceed in partially deliquesced samples: dissolution of kröhnkite and epsomite leads to formation of konyaite; the released cupric sulfate contributes to alpersite that also forms at the expense of epsomite: Na2Cu(SO4)2⋅2H2O + 3Mg(SO4)⋅7H2O + 3H2O = Na2Mg(SO4)2⋅5H2O + 3Mg0.67Cu0.33(SO4)⋅7H2O. This reaction is partially reversed on heating when water starts to evaporate. Partial dehydration of alpersite also contributes to the transient Cu-rich pentahydrite. As in the previous case, decomposition of the complex mixture of hydrates results in amorphisation (partial dissolution?). It is therefore not possible to trace the origin of crystalline phases arising at ~275°C. The last step is characterised by a slow reaction of anhydrous sulfates with formation of the initial itelmenite, probably enhanced by the seed crystals formed from the amorphous precursor. The small amount of Mg(OH)2 formed due to partial hydrolysis converts independently into MgO.

Structural evolution

Analysis of the sequential phase formation shows that the behaviour of the studied minerals differs significantly (Figs 6, 7). The formulas and structures of hydrates, formed as a result of chalcocyanite transformations during hydration and subsequent heating, are more complex than the initial simple copper sulfate Cu(SO4). The opposite behaviour, namely the formation of simpler phases during hydration, was described recently in our investigation of euchlorine (Siidra et al., Reference Siidra, Borisov, Lukina, Depmeier, Platonova, Colmont and Nekrasova2019a). To analyse quantitatively the sequence of transformations of mineral phases, we performed an analysis of their structural complexity, I G in bits/atom, using the approach proposed in Krivovichev (Reference Krivovichev2013). Additionally, for each of the minerals, weighted average values of I G bits/atom at each stage of the experiment were calculated (Fig. 6, 7), using the molar fraction of each mineral phase (where x i – molar fraction, wi – weight % and Mi – molar mass, of the i phase, respectively).

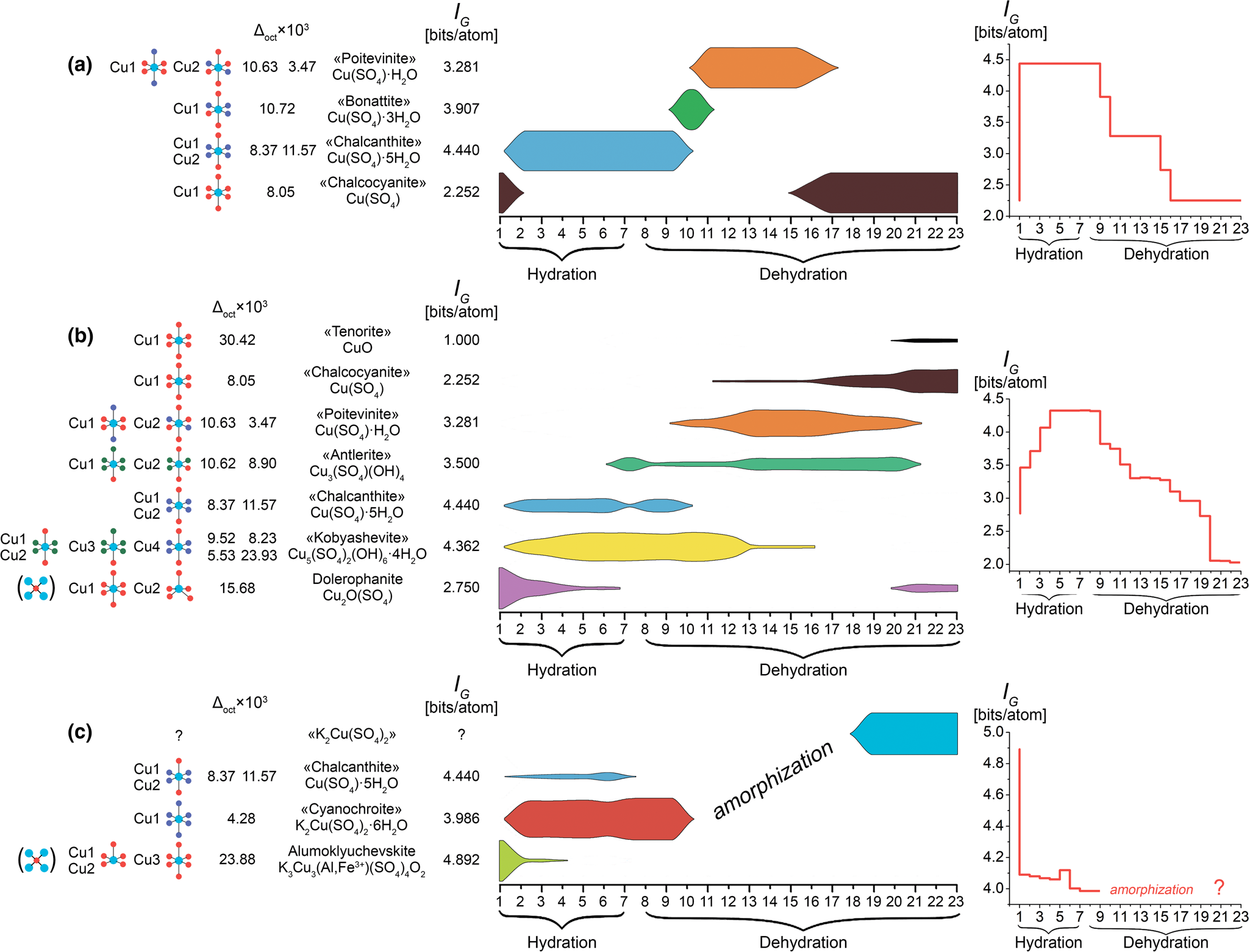
Fig. 6. General schemes of the evolution of chalcocyanite (a), dolerophanite (b) and alumoklyuchevskite (c) during the different stages of hydration and dehydration. Evolution of the structural complexity (weighted average values of I G bits/atom) is shown on the right hand side. I G bits/atom and types of CuOx(H2O)n(OH)m polyhedra (Cu2+ = light blue, O2- = red, H2O = blue and OH- = green) in the structure for each mineral phase are shown to the left. ×103 bond-length distortion parameter for each Cu-centred octahedron is given.

Fig. 7. General schemes of the evolution of itelmenite (a) and euchlorine (after Siidra et al., Reference Siidra, Borisov, Lukina, Depmeier, Platonova, Colmont and Nekrasova2019a) (b) during the different stages of hydration and dehydration. Evolution of the structural complexity (weighted average values of I G bits/atom) is shown to the right. I G bits/atom and types of CuOx(H2O)n(OH)m polyhedra (Cu2+ = light blue, O2- = red, H2O = blue and OH- = green) in the structure for each mineral phase are shown to the left. ×103 bond-length distortion parameter for each Cu-centred octahedron is given.

In the case of chalcocyanite (2.252 bits/atom) (Fig. 6a) and dolerophanite (2.750 bits/atom) (Fig. 6b), the complexity increases due to the fact that even the simple hydrated offspring have a higher structural complexity than their anhydrous analogues. This is in agreement with a common structural trend (Krivovichev, Reference Krivovichev2014). Illustrative examples are anhydrite Ca(SO4) (1.918 bits/atom) and gypsum Ca(SO4)·2H2O (2.752 bits/atom).

The structural complexity of the phases (cyanochroite and chalcanthite) formed during hydration of the alumoklyuchevskite (Fig. 6c) is lower than that of the initial mineral. As noted above, there are currently no structural data on the ‘K2Cu(SO4)2’ phase (PDF card No. 00-017-0485) available, thus the structural complexity could not be estimated for the final stage.

In an experiment with itelmenite, the weighted average structural complexity of the phases formed also decreases, however, by the end of dehydration, having passed through the amorphous state stage, when anhydrous sulfates are formed at high temperatures, its value increases again (Fig. 7a).

The phases resulting from hydration and subsequent dehydration of euchlorine (Fig. 7b) demonstrate a significant reduction in structural complexity with respect to the initial phase. However, by the end of the experiment, as the phase composition of the sample returns to the initial, almost single-phase euchlorine composition, the weighted average structural complexity becomes close to the initial value.

Thus, the performed analysis shows that many of the primary exhalative Cu2+-containing sulfates are structurally of intermediate complexity (Krivovichev, Reference Krivovichev2013). Alumoklyuchevskite (4.892 bits/atom), itelmenite (4.644 bits/atom), the previously studied euchlorine (4.440 bits/atom) (Siidra et al., Reference Siidra, Borisov, Lukina, Depmeier, Platonova, Colmont and Nekrasova2019a) (Figs 6, 7) and saranchinaite (5.700 bits/atom) (Siidra et al., Reference Siidra, Lukina, Nazarchuk, Depmeier, Bubnova, Agakhanov, Avdontseva, Filatov and Kovrugin2018a) are much more structurally complex than the products of their hydration. Despite the decrease in the structural complexity for the complex anhydrous sulfates during hydration, with subsequent heating and dehydration, the complexity increases again and almost reaches its initial values. It is worth noting that the rock-forming minerals of the scoria (Fedotov and Markhinin, Reference Fedotov and Markhinin1983) are structurally simple (labradorite 3.700 bits/atom, diopside 2.522 bits/atom, olivine 2.522 bits/atom, chromite 1.379 bits/atom).

Changes in coordination of Cu2+ cations as a result of hydration/dehydration processes also demonstrate a number of interesting patterns. The types of coordination polyhedra of copper in the structure of each of the minerals or mineral phases, identified during the experiments, are sketched on the left side of Figs 6 and 7. All of the Cu–O bonds <3Å were taken into consideration. For the considered anhydrous copper sulfate minerals (and, in general, for other known fumarolic copper sulfates), the following coordination environments are characteristic: square pyramid CuO5 with different degrees of distortion and octahedron CuO6. A typical structural characteristic of several anhydrous copper sulfate minerals of fumarolic origin (dolerophanite, euchlorine, alumoklyuchevskite and wulffite), is the presence of oxocentred OCu4 tetrahedra. These are absent in the structures of all known hydrated minerals or synthetic compounds of the class under consideration. During the transformation to hydrated species (the diversity of which is much greater than that of anhydrous sulfates), a general pattern manifests itself – this is the formation of [4+2] CuOn(H2O)m(OH)k octahedra (Table 7) with different degrees of distortion (Figs 6, 7) due to the Jahn–Teller effect. A few exceptions from the [4+2] coordination environments and formation of a [4+1+1] coordination are found in the cases of itelmenite and wulffite. CuO4OO [4+1+1] strongly distorted polyhedra are observed in both minerals. The coordination environment of Cu2+ cations is represented by the three types of ligands, viz. O atoms, OH groups and H2O molecules. The following Δoct bond-length distortion parameter, suggested in Wildner (Reference Wildner1992), was used for octahedrally coordinated M sites in all mineral phases listed in Figs 6 and 7: $\Delta_{{\rm oct}} = { 1 \over 6}\mathop \sum \limits_{{\it i}\ = \ 1}^ 6 \left[{{{\lpar {{\it d}_{\rm i} \hbox{-} {\it d}_{\rm m}} \rpar } \over {{\it d}_{\rm m}}}} \right]^ 2$, where d i = (Cu–O) bond length and d m = <Cu–O> bond length. As can be seen, the values of Δoct×103 are higher for non-protonated CuO6 octahedra in anhydrous sulfate structures, while for octahedra with the presence of OH groups and H2O molecules in the coordination of the Cu2+ cation, the values are lower. An exception is the Cu4(H2O)4O2 octahedron in the kobyashevite structure, showing the distortion value Δoct×103 = 23.93. Conversely, the CuO6 octahedron in the structure of chalcocyanite has a low Δoct×103 value of 8.05. If we exclude these two octahedra from the calculation, then the average <Δoct×103> for the protonated octahedra in the structures of the considered mineral phases is 8.03, while for anhydrous it is several times higher at 25.18.

Table 7. Minimum, maximum and average equatorial and apical Cu–O bond-length values in CuOx(H2O)n(OH)m octahedra in the structures of mineral phases listed in Figs 6 and 7 and Tables S1 and S2 (Supplementary material, see below).

The crystal chemistry of divalent copper cations in oxysalts is determined by the Jahn–Teller effect and is responsible for the variety of structures and transformation processes during hydration processes. The pronounced Jahn–Teller effect and low crystal field stabilisation energy for the 3d 9 configuration makes the coordination sphere of Cu2+ particularly non-rigid that enhances these transformations and contributes to structural diversity. Copper polyhedra shown in Figs 6 and 7 show that during the hydration processes, protonated oxygen atoms generally occupy the equatorial plane, while the apical atoms remain involved in the bonding with sulfate tetrahedra.

Another interesting observation is the pattern of the significantly more complex behaviour of fumarolic minerals, as exemplified by dolerophanite, with additional oxygen atoms in its composition (Krivovichev et al., Reference Krivovichev, Mentré, Siidra, Colmont and Filatov2013). Overall, the crystal chemistry of hydroxysalts is essentially richer due to greater variability of polymeric M–OH architectures as negatively charged hydroxyl groups can bridge several M cations, which is uncommon for neutral water ligands. Therefore, hydration of minerals initially containing O2– anions as parts of oxocomplexes (euchlorine and dolerophanite), proceeds with sequential formation of a large series of hydroxysalts. Formation of several successive hydrated hydroxysalts reflects an evident competition between charged hydroxyl and neutral, but more abundant water molecules as ligands. The family of basic copper sulfates, anhydrous and hydrated, is relatively rich; our results, as compared to reference data, indicate that their interconversions are far from being studied in detail. This suggests that, on the one hand, this family will very likely be enriched upon further experimental studies; on the other hand, some more basic copper sulfates, known as synthetic species only, may be found in nature, particularly if sampling is deliberately performed in ‘wet’ seasons.

On the contrary, hydration of itelmenite with a relatively complex ‘initial’ structure without additional oxygen atoms, which are strong Lewis bases, results in formation of simpler hydrates. The lower the temperature and the larger the excess of water, the higher hydration numbers are observed for cations. Ultimately, the more abundant water molecules expel the bridging sulfate anions from the metal coordination sphere yielding relatively simple fully hydrated structures.

Concluding remarks

A study of the evolution of sulfates in hydration and dehydration processes has demonstrated the complexity of the processes for a number of minerals. The temperature regime on the active fumaroles of the scoria cones of the Tolbachik volcano is not constant and changes even over relatively short periods of time, which leads to the formation of large amounts of hydrated minerals in the case of lowering the temperature, and, conversely, in the case of increasing the temperature in reversible dehydration for a number of minerals, as shown by us in a number of experiments. It is known that structurally and chemically complex hydroxysalt minerals with various metals, as a rule, are formed as a result of secondary geological processes, such as oxidation zones, crystallisation from aqueous solutions, etc., i.e. the presence of water in the systems is responsible for the occurrence of complex structural architectures. These complex minerals almost invariably contain water or hydroxyl groups. In respect to complexity, fumarolic anhydrous copper minerals with sulfate anions, and especially those containing additional oxygen atoms, form a separate group of primary minerals that reflect both the general complexity of the structures and the complexity of the transformation processes. Moreover, some of the structurally complex anhydrous copper sulfates (euchlorine, alumoklyuchevskite and saranchinaite) can be considered not as rare fumarolic accessory minerals, but rather as rock-forming in primary exhalative mineral assemblages. It is worth noting that H2O is the main component of gases and an agent for the transport of transition metals in post-eruptive processes on the scoria cones of the Tolbachik volcano (Fedotov and Markhinin, Reference Fedotov and Markhinin1983). Above some temperature limit, water is supposed to act mostly as a chemical transporting agent; if the deposition temperature is relatively high, one can expect formation of anhydrous species. Below this limit, formation of hydrated species becomes possible. At temperatures close to ambient, it would be difficult, if ever possible, to discriminate the effects of exhaled (‘intrinsic’) and atmospheric (‘extrinsic’) water.

Acknowledgements

We are grateful to Ferdinando Bosi and two anonymous reviewers for valuable comments. This work was financially supported by the Russian Science Foundation through the grant 16-17-10085. Technical support by the SPbSU X-ray Diffraction and Geomodel Resource Centers is gratefully acknowledged. O.I.S. was supported by the internal SPbSU travel grant to the University of Kiel.

Supplementary material

To view supplementary material for this article, please visit https://doi.org/10.1180/mgm.2021.11

Footnotes

Associate Editor: Ferdinando Bosi

References

Altheide, T., Chevrier, V., Nicholson, C. and Denson, J. (2009) Experimental investigation of the stability and evaporation of sulfate and chloride brines on Mars. Earth and Planetary Science Letters, 282, 69–78.CrossRefGoogle Scholar
Bacon, G.E. and Titterton, D.H. (1975) Neutron-diffraction studies of CuSO4⋅5(H2O) and CuSO4⋅5(D2O). Zeitschrift für Kristallographie, 141, 330–341.CrossRefGoogle Scholar
Balassone, G., Petti, C., Mondillo, N., Panikorovskii, T.L., de Gennaro, R., Cappelletti, P., Altomare, A., Corriero, N., Cangiano, M. and D'Orazio, L. (2019) Copper minerals at Vesuvius volcano (Southern Italy): a mineralogical review. Minerals, 9, 730.CrossRefGoogle Scholar
Baur, W.H. (1962) Zur Kristallchemie der Salzhydrate. Die Kristallstrukturen von MgSO4⋅4(H2O) (Leonhardtit) und FeSO4⋅4(H2O) (Rozenit). Acta Crystallographica, 15, 815–826.CrossRefGoogle Scholar
Baur, W.H. and Rolin, J.L. (1972) Salt hydrates. IX. The comparison of the crystal structure of magnesium sulfate pentahydrate with copper sulfate pentahydrate and magnesium chromate pentahydrate. Acta Crystallographica, B28, 1448–1455.CrossRefGoogle Scholar
Bosi, F., Belardi, G. and Ballirano, P. (2009) Structural features in Tutton's salts K2[M2+(H2O)6](SO4)2, with M2+= Mg, Fe, Co, Ni, Cu, and Zn. American Mineralogist, 94, 74–82.CrossRefGoogle Scholar
Brese, N.E., O'Keeffe, M., Ramakrishna, B.L. and Von Dreele, R.B. (1990) Low-temperature structures of CuO and AgO and their relationships to those of MgO and PdO. Journal of Solid State Chemistry, 89, 184–190.CrossRefGoogle Scholar
Bruker. (2014) TOPAS, Version 5.0. Bruker AXS Inc, Madison, USA.Google Scholar
Calleri, M., Gavetti, A., Ivaldi, G. and Rubbo, M. (1984) Synthetic epsomite, MgSO4(H2O)7: absolute configuration and surface features of the complementary {111} forms. Acta Crystallographica, B40, 218–222.CrossRefGoogle Scholar
Cheng, L., Li, W., Li, Y., Yang, Y., Li, Y., Cheng, Y. and Song, D. (2019) Thermal analysis and decomposition kinetics of the dehydration of copper sulfate pentahydrate. Journal of Thermal Analysis and Calorimetry, 135, 2697–2703.CrossRefGoogle Scholar
Chipera, S.J. and Vaniman, D.T. (2007) Experimental stability of magnesium sulfate hydrates that may be present on Mars. Geochimica et Cosmochimica Acta, 71, 241–250.CrossRefGoogle Scholar
Effenberger, H. (1985) Cu2O(SO4), Dolerophanite: refinement of the crystal structure with a comparison of [OCu(II)4] tetrahedra in inorganic compounds. Monatshefte für Chemie, 116, 927–931.CrossRefGoogle Scholar
Fan, X.-F., Sun, H.-D., Shen, Z.-X., Kuo, J.-L. and Lu, Y.-M. (2008) A first-principle analysis on the phase stabilities, chemical bonds and band gaps of wurtzite structure AxZn1–xO alloys (A = Ca, Cd, Mg). Journal of Physics: Condensed Matter, 20, 235221.Google Scholar
Fedotov, S.A. and Markhinin, Y.K. (editors) (1983) The Great Tolbachik Fissure Eruption. Cambridge University Press, New York.Google Scholar
Fischer, W. and Hellner, E. (1964) Ueber die Struktur des Vanthoffits. Acta Crystallographica, 17, 1613–1613.CrossRefGoogle Scholar
Gorskaya, M.G., Vergasova, L.P., Filatov, S.K., Rolich, D.V. and Ananiev, V.V. (1995) Alumoklyuchevskite, K3Cu3AlO2(SO4)4, a new oxysulfate of K, Cu, and Al from volcanic exhalations, Kamchatka, Russia. Zapiski Rossiiskogo Mineralogicheskogo Obshchestva, 124, 95–100.Google Scholar
Grevel, K.-D. and Majzlan, J. (2009) Internally consistent thermodynamic data for magnesium sulfate hydrates. Geochimica et Cosmochimica Acta, 73, 6805–6815.CrossRefGoogle Scholar
Hawthorne, F.C. and Ferguson, R.B. (1975) Refinement of the crystal structure of kröhnkite. Acta Crystallographica, B31, 1753–1755.CrossRefGoogle Scholar
Hawthorne, F.C., Groat, L.A. and Eby, R.K. (1989) Antlerite, Cu3SO4(OH)4, a heteropolyhedral wallpaper structure. The Canadian Mineralogist, 27, 205–209.Google Scholar
Hazen, R.M., Papineau, D., Bleeker, W., Downs, R.T., Ferry, J.M., McCoy, T.J., Sverjensky, D.A. and Yang, H. (2008) Mineral evolution. American Mineralogist, 93, 1693–1720.CrossRefGoogle Scholar
Hughes, J.M. and Stoiber, R.E. (1985) Vanadium sublimates from the fumaroles of Izalco Volcano, El Salvador. Journal of Volcanology and Geothermal Research, 24, 283–291.CrossRefGoogle Scholar
Kahler, E. (1962) Die Kristallstruktur von Dolerophanit, Cu2O(SO4), ein Beispiel fuer 5 Koordiniertes Kupfer. Naturwissenschaften, 49, 298.CrossRefGoogle Scholar
Krivovichev, S.V. (2013) Structural complexity of minerals: information storage and processing in the mineral world. Mineralogical Magazine, 77, 275–326.CrossRefGoogle Scholar
Krivovichev, S.V. (2014) Which inorganic structures are the most complex? Angewandte Chemie – International Edition, 53, 654–661.CrossRefGoogle ScholarPubMed
Krivovichev, S.V., Mentré, O., Siidra, O.I., Colmont, M. and Filatov, S.K. (2013) Anion-centered tetrahedra in inorganic compounds. Chemical Reviews, 113, 6459–6535.CrossRefGoogle ScholarPubMed
Lander, L., Rousse, G., Batuk, D., Colin, C.V., Dalla Corte, D.A. and Tarascon, J.-M. (2017) Synthesis, structure, and electrochemical properties of K-based sulfates K2M2(SO4)3 with M = Fe and Cu. Inorganic Chemistry, 56, 2013–2021.CrossRefGoogle Scholar
Lindström, N., Talreja, T., Linnow, K., Stahlbuhk, A. and Steiger, M. (2016) Crystallization behavior of Na2SO4 – MgSO4 salt mixtures in sandstone and comparison to single salt behavior. Applied Geochemistry, 69, 50–70.CrossRefGoogle Scholar
Ma, H., Bish, D.L., Wang, H.W. and Chipera, S.J. (2009) Determination of the crystal structure of sanderite, MgSO4⋅2H2O, by X-ray powder diffraction and the charge flipping method. American Mineralogist, 94, 622–625.CrossRefGoogle Scholar
Menyailov, I.A. and Nikitina, L.P. (1980a) Chemistry and metal contents of magmatic gases: the New Tolbachik Volcanoes case (Kamchatka). Bulletin of Volcanology, 43, 195–205.CrossRefGoogle Scholar
Menyailov, I.A., Nikitina, L.P. and Shapar, V.N. (1980b) Geochemical features of exhalations of Great Tolbachik Fissure Eruption. Nauka, Moscow [in Russian].Google Scholar
Mills, S.J., Wilson, S.A., Dipple, G.M. and Raudsepp, M. (2010) The decomposition of konyaite: Importance in CO2 in mine tailings. Mineralogical Magazine, 74, 903–917.CrossRefGoogle Scholar
Mitev, P.D., Gajewski, G. and Hermansson, K. (2009) Anharmonic OH vibrations in brucite: small pressure-induced redshift in the range 0–22 GPa. American Mineralogist, 94, 1687–1697.CrossRefGoogle Scholar
Nagase, K., Yokobayashi, H. and Sone, K. (1978) Spectrophotometric and thermoanalytical studies on the dehydration of copper (ii) sulfate and its double salts. Thermochimica Acta, 23, 283–291.CrossRefGoogle Scholar
Nazarchuk, E.V., Siidra, O.I., Agakhanov, A.A., Lukina, E.A., Avdontseva, E.Yu. and Karpov, G.A. (2018) Itelmenite, Na2CuMg2(SO4)4, a New anhydrous sulfate mineral from the Tolbachik Volcano. Mineralogical Magazine, 82, 1233–1241.CrossRefGoogle Scholar
Nazarchuk, E.V., Siidra, O.I., Nekrasova, D.O., Shilovskikh, V.V., Borisov, A.S. and Avdontseva, E.Yu. (2020) Glikinite, Zn3O(SO4)2, a new anhydrous zinc oxysulfate mineral structurally based on OZn4 tetrahedra. Mineralogical Magazine, 84, 563–567.CrossRefGoogle Scholar
Nordstrom, D.K. (1982) The effect of sulfate on aluminum concentrations in natural waters: some stability relations in the system Al2O3 – H2O – SO3 at 298 K. Geochimica et Cosmochimica Acta, 46, 618–692.CrossRefGoogle Scholar
Pautov, L.A., Mirakov, M.A., Siidra, O.I., Faiziev, A.R., Nazarchuk, Е.V., Karpenko, V.Yu. and Makhmadsharif, S. (2020) Falgarite, K4(VO)3(SO4)5, a new mineral from sublimates of a natural underground coal fire at the tract of Kukhi-Malik, Fan-Yagnob Coal Deposit, Tajikistan. Mineralogical Magazine, 84, 455–462.CrossRefGoogle Scholar
Pekov, I.V., Koshlyakova, N.N., Zubkova, N.V., Lykova, I.S., Britvin, S.N., Yapaskurt, V.O., Agakhanov, A.A., Shchipalkina, N.V., Turchkova, A.G. and Sidorov, E.G. (2018a) Fumarolic arsenates − a special type of arsenic mineralization. European Journal of Mineralogy, 30, 305–322.CrossRefGoogle Scholar
Pekov, I.V., Zubkova, N.V. and Pushcharovsky, D.Y. (2018b) Copper minerals from volcanic exhalations – a unique family of natural compounds: crystal-chemical review. Acta Crystallographica, B74, 502–518.Google Scholar
Pekov, I.V., Zubkova, N.V., Yapaskurt, V.O., Belakovskiy, D.I., Chukanov, N.V., Kasatkin, A.V., Kuznetsov, A.M. and Pushcharovsky, D.Y. (2013) Kobyashevite, Cu5(SO4)2(OH)6⋅4H2O, a new devilline-group mineral from the Vishnevye Mountains, South Urals, Russia. Mineralogy and Petrology, 107, 201–210.CrossRefGoogle Scholar
Ramamurthy, P. and Secco, E.A. (1970) Studies on metal hydroxy compounds. XII. Thermal analyses, decomposition kinetics, and infrared spectra of copper basic oxysalts. Canadian Journal of Chemistry, 48, 3510–3519.CrossRefGoogle Scholar
Rasmussen, S.E., Jorgensen, J.E. and Lundtoft, B. (1996) Structures and phase transitions of Na2SO4. Journal of Applied Crystallography, 29, 42–47.CrossRefGoogle Scholar
Rentzeperis, P.J. and Soldatos, C.T. (1958) The crystal structure of the anhydrous magnesium sulphate. Acta Crystallographica, 11, 686–688.CrossRefGoogle Scholar
Siidra, O.I., Vergasova, L.P., Kretser, Y.L., Polekhovsky, Y.S., Filatov, S.K. and Krivovichev, S.V. (2014b) Unique thallium mineralization in the fumaroles of Tolbachik Volcano, Kamchatka peninsula, Russia. II. Karpovite, Tl2VO(SO4)2(H2O). Mineralogical Magazine, 78, 1699–1709.CrossRefGoogle Scholar
Siidra, O.I., Vergasova, L.P., Kretser, Y.L., Polekhovsky, Y.S., Filatov, S.K. and Krivovichev, S.V. (2014c) Unique thallium mineralization in the fumaroles of Tolbachik Volcano, Kamchatka peninsula, Russia. III. Evdokimovite, Tl4(VO)3(SO4)5(H2O)5. Mineralogical Magazine, 78, 1711–1724.CrossRefGoogle Scholar
Siidra, O.I., Vergasova, L.P., Krivovichev, S.V., Kretser, Y.L., Zaitsev, A.N. and Filatov, S.K. (2014a) Unique thallium mineralization in the fumaroles of Tolbachik Volcano, Kamchatka peninsula, Russia. I. Markhininite, TlBi(SO4)2. Mineralogical Magazine, 78, 1687–1698.CrossRefGoogle Scholar
Siidra, O.I., Borisov, A.S., Lukina, E.A., Depmeier, W., Platonova, N.V., Colmont, M. and Nekrasova, D.O. (2019a) Reversible hydration/dehydration and thermal expansion of euchlorine, ideally KNaCu3O(SO4)3. Physics and Chemistry of Minerals, 46, 403–416.CrossRefGoogle Scholar
Siidra, O.I., Lukina, E.A., Nazarchuk, E.V., Depmeier, W., Bubnova, R.S., Agakhanov, A.A., Avdontseva, E.Yu., Filatov, S.K. and Kovrugin, V.M. (2018a) Saranchinaite, Na2Cu(SO4)2, a new exhalative mineral from Tolbachik Volcano, Kamchatka, Russia, and a product of the reversible dehydration of kröhnkite, Na2Cu(SO4)2(H2O)2. Mineralogical Magazine, 82, 257–274.CrossRefGoogle Scholar
Siidra, O.I., Nazarchuk, E.V., Agakhanov, A.A., Lukina, E.A., Zaitsev, A.N., Turner, R., Filatov, S.K., Pekov, I.V., Karpov, G.A. and Yapaskurt, V.O. (2018b) Hermannjahnite, CuZn(SO4)2, a new mineral with chalcocyanite derivative structure from the Naboko Scoria Cone of the 2012–2013 Fissure Eruption at Tolbachik Volcano, Kamchatka, Russia. Mineralogy and Petrology, 112, 123–134.CrossRefGoogle Scholar
Siidra, O.I., Nazarchuk, E.V., Lukina, E.A., Zaitsev, A.N. and Shilovskikh, V.V. (2018c) Belousovite, KZn(SO4)Cl, a new sulfate mineral from the Tolbachik Volcano with apophyllite sheet-topology. Mineralogical Magazine, 82, 1079–1088.CrossRefGoogle Scholar
Siidra, O.I., Nazarchuk, E.V., Zaitsev, A.N. and Shilovskikh, V.V. (2020a) Majzlanite, K2Na(ZnNa)Ca(SO4)4, a new anhydrous sulfate mineral with complex cation substitutions from Tolbachik Volcano. Mineralogical Magazine, 84, 153–158.CrossRefGoogle Scholar
Siidra, O.I., Nazarchuk, E.V., Zaitsev, A.N. and Vlasenko, N.S. (2020b) Koryakite, NaKMg2Al2(SO4)6, a new NASICON-related anhydrous sulfate mineral from Tolbachik Volcano. Mineralogical Magazine, 84, 283–287.CrossRefGoogle Scholar
Siidra, O.I., Nazarchuk, E.V., Zaitsev, A.N., Lukina, E.A., Avdontseva, E.Yu., Vergasova, L.P., Vlasenko, N.S., Filatov, S.K., Turner, R. and Karpov, G.A. (2017) Copper oxosulphates from fumaroles of Tolbachik Volcano: Puninite, Na2Cu3O(SO4)3 – a new mineral species and structure refinements of kamchatkite and alumoklyuchevskite. European Journal of Mineralogy, 29, 499–510.CrossRefGoogle Scholar
Siidra, O.I., Nazarchuk, E.V., Agakhanov, A.A. and Polekhovsky, Yu.S. (2019c) Aleutite [Cu5O2](AsO4)(VO4)⋅(Cu0.5□0.5)Cl, a new complex salt-inclusion mineral with Cu2+ substructure derived from Kagome-net. Mineralogical Magazine, 83, 847–853.CrossRefGoogle Scholar
Siidra, O.I., Nazarchuk, E.V., Zaitsev, A.N., Polekhovsky, Yu.S., Wenzel, T. and Spratt, J. (2019b) Dokuchaevite, Cu8O2(VO4)3Cl3, a new mineral with remarkably diverse Cu2+ mixed-ligand coordination environments. Mineralogical Magazine, 83, 749–755.CrossRefGoogle Scholar
Sklute, E.C., Rogers, A.D., Gregerson, J.C., Jensen, H.B., Reeder, R.J. and Dyar, M.D. (2018) Amorphous salts formed from rapid dehydration of multicomponent chloride and ferric sulfate brines: implications for Mars. Icarus, 302, 285–295.CrossRefGoogle ScholarPubMed
Stanimirova, T. and Ivanova, K. (2019) Transformation of ktenasite-type minerals to langite, posnjakite, and brochantite under water treatment. Comptes rendus de l'Academie bulgare des Sciences, 72, 768–776.Google Scholar
Steiger, M., Linnow, K., Ehrhardt, D. and Rohde, M. (2011) Decomposition reactions of magnesium sulfate hydrates and phase equilibria in the MgSO4–H2O and Na+–Mg2+–Cl––SO42––H2O systems with implication for Mars. Geochimica et Cosmochimica Acta, 75, 3600–3626.CrossRefGoogle Scholar
Tanaka, H. and Koga, N. (1988) Preparation and thermal decomposition of basic copper (II) sulfates. Thermochimica Acta, 133, 221–226.CrossRefGoogle Scholar
Ting, V.P., Henry, P.F., Schmidtmann, M., Wilson, C.C. and Weller, M.T. (2009) In situ neutron powder diffraction and structure determination in controlled humidities. Chemical Communications, 48, 7527–7529.CrossRefGoogle Scholar
Uzunov, I., Klissurski, D. and Teocharov, L. (1995) Thermal decomposition of basic copper sulfate monohydrate. Journal of Thermal Analysis, 44, 685–696.CrossRefGoogle Scholar
Vaniman, D.T., Bish, D.L., Chipera, S.J., Fialips, C.I., Carey, J.W. and Feldman, W.G. (2004) Magnesium sulphate salts and the history of Water on Mars. Nature, 431, 663–665.CrossRefGoogle ScholarPubMed
Vergasova, L.P. and Filatov, S.K. (2012) New mineral species in products of fumarole activity of the Great Tolbachik Fissure Eruption. Journal of Volcanology and Seismology, 6, 281–289.CrossRefGoogle Scholar
Vergasova, L.P. and Filatov, S.K. (2016) A study of volcanogenic exhalation mineralization. Journal of Volcanology and Seismology, 10, 71–85.CrossRefGoogle Scholar
Wildner, M. (1992) On the geometry of Co(II)O6 polyhedra in inorganic compounds. Zeitschrift für Kristallographie, 202, 51–70.CrossRefGoogle Scholar
Xu, W., Tosca, N.J., Mclennan, S.M. and Parise, J.B. (2009) Humidity-induced phase transitions of ferric sulfate minerals studied by in situ and ex situ X-ray diffraction. American Mineralogist, 94, 1629–1637.CrossRefGoogle Scholar
Yoder, C.H., Agee, T.M., Ginion, K.E., Hofmann, A.E., Ewanichak, J.E., Schaeffer, C.D. Jr., Carroll, M.J., Schaeffer, R.W. and McCaffrey, P.F. (2007) The relative stabilities of the copper hydroxyl sulfates. Mineralogical Magazine, 71, 571–577.CrossRefGoogle Scholar
Zahrobsky, R.F. and Baur, W.H. (1968) On the crystal chemistry of salt hydrates. V. The determination of the crystal structure of CuSO4⋅3H2O (bonattite). Acta Crystallographica, B24, 508–513.CrossRefGoogle Scholar
Zalkin, A., Ruben, H. and Templeton, D.H. (1964) The crystal structure and hydrogen bonding of magnesium sulfate hexahydrate. Acta Crystallographica, 17, 235–240.CrossRefGoogle Scholar
Zhou, H.A., Liu, Z., Ang, S.S. and Zhang, J.-J. (2020) Synthesis, structure, and electrochemical performances of a novel three-dimensional framework K2[Cu(SO4)2]. Solid State Sciences, 100, 106104.CrossRefGoogle Scholar
Figure 0

Fig. 1. General view of the wall of the Yadovitaya fumarole. The Cu–SO4 rich zone is delimited by red lines (a). The maximum thickness of the Cu–SO4 zone is 35 cm. Well crystallised chalcocyanite sample excavated from this zone (b) and the same sample, almost completely transformed into chalcanthite, exposed to humid air for one week (c). Dark brown crystals of dolerophanite with green euchlorine (d) and clusters of needle-like crystals of alumoklyuchevskite (e) from the Cu–SO4 zone used in this work.

Figure 1

Fig. 2. XRD patterns for the products of chalcocyanite hydration (left below). Different stages of hydration are numbered on the left side. Peak positions of ‘chalcanthite’ Cu(SO4)⋅5H2O are marked with blue triangles. XRD patterns for the products of dehydration of the mixture of hydrated sulfates initially obtained from chalcocyanite (left above). Blue – ‘chalcanthite’ Cu(SO4)⋅5H2O; green – ‘bonattite’ Cu(SO4)⋅3H2O; orange – ‘poitevinite’ Cu(SO4)⋅H2O; and black – ‘chalcocyanite’ Cu(SO4). Hydration of chalcocyanite single-phase powder and formation of various hydrated copper sulfates is accompanied by colour changes (right). During the heating of the hydrated products the colour reverses back completely in agreement with the reversible hydration/dehydration of chalcocyanite. The relative humidity for each hydration stage is given in Table 1.

Figure 2

Fig. 3. XRD patterns for the products of dolerophanite hydration (left below). Different stages of hydration are numbered on the left side. XRD patterns for the products of dehydration of the mixture of hydrated sulfates initially obtained from dolerophanite (left above). Different stages of dehydration are numbered on the left side. Hydration of dolerophanite single-phase powder and formation of various hydrated copper sulfates is accompanied by colour changes (right). During the heating of the hydrated products the colour reverses back in agreement with the formation of a mixture of anhydrous sulfates. The relative humidity for each hydration stage is given in Table 1.

Figure 3

Fig. 4. XRD patterns for the products of alumoklyuchevskite hydration (left below). Different stages of hydration are numbered on the left side. XRD patterns for the products of dehydration of the mixture of hydrated sulfates initially obtained from alumoklyuchevskite (left above). Different stages of dehydration are numbered on the left side. Hydration of alumoklyuchevskite single-phase powder and formation of various hydrated copper sulfates is accompanied by the colour changes (right). During the heating of the mixture the colour partially reverses back. The relative humidity for each hydration stage is given in Table 3.

Figure 4

Fig. 5. XRD patterns for the products of itelmenite hydration (left below). Different stages of hydration are numbered on the left side. XRD patterns for the products of dehydration of the mixture of hydrated sulfates initially obtained from itelmenite (left above). Different stages of dehydration are numbered on the left side. Hydration of itelmenite single-phase powder and formation of various hydrated copper and magnesium sulfates is accompanied by the colour changes (right). During the heating of the mixture the colour reverses back. The relative humidity for each hydration stage is given in Table 5.

Figure 5

Table 1. Evolution of primary dolerophanite into mixtures of hydrated sulfates during the hydration experiments at 23°C, different duration and different relative humidity.

Figure 6

Table 2. Evolution of the mixture of hydrated sulfate phases, formed as a result of dolerophanite hydration, upon heating.

Figure 7

Table 3. Evolution of primary alumoklyuchevskite into mixtures of hydrated sulfates during the hydration experiments at 23°C, different duration and different relative humidity.

Figure 8

Table 4. Evolution of the mixture of hydrated sulfate phases, formed as a result of alumoklyuchevskite hydration, upon heating. Dominating phases (≥20%) are marked in bold. The transformation can be subdivided into three main stages (I–III) in accordance with the dominance of different phases (marked in bold). Amount of each phase is given in wt. %. E.s.d is ~3%.

Figure 9

Table 5. Evolution of primary itelmenite into mixtures of hydrated sulfates during the hydration experiments at 23°C, different duration and different relative humidity.

Figure 10

Table 6. Evolution of the mixture of hydrated sulfate phases, formed as a result of itelmenite hydration, upon heating. The evolution can be subdivided into three main stages (I–III) in accordance with the dominance of different phases.

Figure 11

Fig. 6. General schemes of the evolution of chalcocyanite (a), dolerophanite (b) and alumoklyuchevskite (c) during the different stages of hydration and dehydration. Evolution of the structural complexity (weighted average values of IG bits/atom) is shown on the right hand side. IG bits/atom and types of CuOx(H2O)n(OH)m polyhedra (Cu2+ = light blue, O2- = red, H2O = blue and OH- = green) in the structure for each mineral phase are shown to the left. ×103 bond-length distortion parameter for each Cu-centred octahedron is given.

Figure 12

Fig. 7. General schemes of the evolution of itelmenite (a) and euchlorine (after Siidra et al., 2019a) (b) during the different stages of hydration and dehydration. Evolution of the structural complexity (weighted average values of IG bits/atom) is shown to the right. IG bits/atom and types of CuOx(H2O)n(OH)m polyhedra (Cu2+ = light blue, O2- = red, H2O = blue and OH- = green) in the structure for each mineral phase are shown to the left. ×103 bond-length distortion parameter for each Cu-centred octahedron is given.

Figure 13

Table 7. Minimum, maximum and average equatorial and apical Cu–O bond-length values in CuOx(H2O)n(OH)m octahedra in the structures of mineral phases listed in Figs 6 and 7 and Tables S1 and S2 (Supplementary material, see below).

Supplementary material: PDF

Siidra et al. supplementary material

Siidra et al. supplementary material

Download Siidra et al. supplementary material(PDF)
PDF 198.5 KB