3.1. Optimal eddy-viscosity field

Here we develop an optimization, computed independently for each frequency and azimuthal mode, that finds the eddy-viscosity field that is optimal (i.e. the upper bound) in matching the leading resolvent and SPOD modes. To find the analytical expression that determines the sensitivity of mode agreement to an eddy-viscosity field, we use a Lagrangian technique analogous to Brandt et al. (Reference Brandt, Sipp, Pralits and Marquet2011) that accounts for the non-modal behaviour of the resolvent operator. This technique couples constraints from the governing equations, resolvent analysis, a normalization, and a cost function (agreement of the leading SPOD and resolvent modes), into a Lagrangian functional for whose stationary point provides the desired maximum.

To build the Lagrangian functional, we begin with the forward equation (2.6) and substitute $\boldsymbol {L}$ with $\boldsymbol {L}_T$, the linear operator that includes an eddy-viscosity model. The singular value/singular vector $(\boldsymbol {v}_1,\boldsymbol {u}_1, \sigma _1)$ as defined in (2.11) is a solution of both the forward equation (2.6),

(3.1)\begin{equation} \boldsymbol{v}_1 = \boldsymbol{L}_T \boldsymbol{u}_1,\end{equation}

where $\boldsymbol {v}_1$ replaces $\boldsymbol {f}$ as the forcing and $\boldsymbol {u}_1$ replaces $\boldsymbol {q}$ as the associated response, and the resolvent eigenvalue problem,

(3.2)\begin{equation} \boldsymbol{W} \boldsymbol{u}_1 = \sigma_1^2 \boldsymbol{L}_T^* \boldsymbol{W}\boldsymbol{v}_1. \end{equation}

The above resolvent eigenvalue solution is found by taking the energy norm of (2.7) and dividing by the forcing energy to give

(3.3)\begin{equation} \frac{\boldsymbol{u}_1^* \boldsymbol{W} \boldsymbol{u}_1}{\boldsymbol{v}_1^* \boldsymbol{W} \boldsymbol{v}_1} = \sigma_1^2 = \frac{\boldsymbol{v}_1^* \boldsymbol{R}_T^* \boldsymbol{W} \boldsymbol{R}_T \boldsymbol{v}_1}{\boldsymbol{v}_1^* \boldsymbol{W} \boldsymbol{v}_1}. \end{equation}

Rearranging and eliminating $\boldsymbol {v}^*_n$ we arrive at

(3.4)\begin{equation} \boldsymbol{R}_T^* \boldsymbol{W} \boldsymbol{R}_T \boldsymbol{v}_1 = \sigma_1^2 \boldsymbol{W} \boldsymbol{v}_1, \end{equation}

where replacing $\boldsymbol {R}_T \boldsymbol {v}_1$ with $\boldsymbol {u}_1$ and multiplying both sides by $\boldsymbol {R}^{-*}_T = \boldsymbol {L}_T^*$ recovers (3.2). Finally, we define a normalization constraint via,

(3.5)\begin{equation} \langle \boldsymbol{u}_1, \boldsymbol{u}_1 \rangle_{E} = \boldsymbol{u}_1^* \boldsymbol{W} \boldsymbol{u}_1 = 1.\end{equation}

The last component of the Lagrangian functional is the cost function,

(3.6)\begin{equation} \mathcal{J} = \boldsymbol{u}_1^* \boldsymbol{W} \boldsymbol{\psi}_1 \boldsymbol{\psi}_1^* \boldsymbol{W} \boldsymbol{u}_1-l^2\boldsymbol{\mu}_T^*\boldsymbol{M}{\boldsymbol{\mu}_T},\end{equation}

where the first term, representing the primary objective, measures the squared projection, what we term the alignment or agreement, between the dominant SPOD mode, $\boldsymbol {\psi }_1$, and the first resolvent mode, $\boldsymbol {u}_1$. The alignment measure, $\boldsymbol {u}_1^* \boldsymbol {W} \boldsymbol {\psi }_1$, is squared to ensure the cost function is real. For brevity, we denote the outer product of the dominant SPOD mode as $\boldsymbol {\varPsi }_1 = \boldsymbol {\psi }_1\boldsymbol {\psi }_1^* = \boldsymbol {\varPsi }_1^*$. The cost function may also consider multiple resolvent/SPOD modes by considering a (weighted if desired) sum of the squared alignment terms.

The second term, $-l^2 \boldsymbol {\mu }_T^* \boldsymbol {M} {\boldsymbol {\mu }_T}$, is a Tikhonov regularization that penalizes values of ${\boldsymbol {\mu }_T}$ that do not affect the alignment (high values of ${\boldsymbol {\mu }_T}$ diminish the value of $\mathcal {J}$), with $\boldsymbol {M}$ representing the cylindrical quadrature weights of the grid. As done in standard regularization methods, the value of $l^2$ is chosen high enough to remove the values of ${{\boldsymbol {\mu }_T}}$ in insensitive regions, but also sufficiently small to not interfere with the primary objective (Hansen & O'Leary Reference Hansen and O'Leary1993). This penalization is effective at minimizing the eddy viscosity in non-turbulent regions of the flow such as the far field. A substantial range of $l^2$ values (i.e. multiple orders of magnitude) removes negligible regions of the eddy-viscosity field from the initial field without an observable drop in the primary objective, alignment between $\boldsymbol {u}_1$ and $\boldsymbol {\psi }_1$.

We now formally construct the Lagrangian functional to include the cost function (3.6), forward equation (3.1), the resolvent eigenvalue problem (3.2), and the normalization constraint (3.5) to give,

(3.7)\begin{align} \mathcal{L} &= \boldsymbol{u}_1^* \boldsymbol{W} \boldsymbol{\varPsi}_1 \boldsymbol{W} \boldsymbol{u}_1-l^2\boldsymbol{\mu}_T^*\boldsymbol{M}{\boldsymbol{\mu}_T} \nonumber\\ &\quad - \tilde{\boldsymbol{u}}_1^* (\boldsymbol{L}_T \boldsymbol{u}_1 - \boldsymbol{v}_1 ) - \tilde{\boldsymbol{v}}_1^* ( \boldsymbol{W}\boldsymbol{u}_1 -\sigma_1^2 \boldsymbol{L}_T^*\boldsymbol{W} \boldsymbol{v}_1 ) - \tilde{\sigma}_1 ( \boldsymbol{u}_1^* \boldsymbol{W} \boldsymbol{u}_1 - 1 ) +\textrm{c.c.}, \end{align}

where $( \tilde {\boldsymbol {u}}_1, \tilde {\boldsymbol {v}}_1, \tilde {\sigma }_1)$ are Lagrange multipliers, $\tilde {\sigma }_1$ is real valued (as the corresponding constraint is real) and c.c. is the complex conjugate. This results in a functional that depends on seven variables,

(3.8)\begin{equation} \mathcal{L} ( [ \boldsymbol{u}_1, \boldsymbol{v}_1 , \sigma_1], [ \tilde{\boldsymbol{u}}_1 , \tilde{\boldsymbol{v}}_1, \tilde{\sigma}_1 ], \boldsymbol{\mu}_T). \end{equation}

We can find the maximum of the cost function by finding the stationary point of the entire functional (i.e. where variations with respect to each variable are zero). Stationarity with respect to the Lagrange multipliers yields the state equations, which are by definition satisfied, while stationarity with respect to the state variables yields

(3.9)\begin{gather} \frac{\partial \mathcal{L}}{\partial \boldsymbol{u}_1} \delta \boldsymbol{u}_1 = ( 2 \boldsymbol{W} \boldsymbol{\varPsi}_1 \boldsymbol{W} \boldsymbol{u}_1 - \boldsymbol{L}_T^* \tilde{\boldsymbol{u}}_1 - \boldsymbol{W} \tilde{\boldsymbol{v}}_1 - 2 \tilde{\sigma}_1 \boldsymbol{W} \boldsymbol{u}_1)^* \delta \boldsymbol{u}_1 = 0, \end{gather}

(3.10)\begin{gather}\frac{\partial \mathcal{L}}{\partial \boldsymbol{v}_1} \delta \boldsymbol{v}_1= (\tilde{\boldsymbol{u}}_1 + \sigma_1^2 \boldsymbol{W} \boldsymbol{L}_T \tilde{\boldsymbol{v}}_1)^*\delta \boldsymbol{v}_1 = 0, \end{gather}

(3.11)\begin{gather}\frac{\partial \mathcal{L}}{\partial \sigma_1} \delta {\sigma}_1= (\tilde{\boldsymbol{v}}_1^* \boldsymbol{L}_T^* \boldsymbol{W} \boldsymbol{v}_1)^* \delta \sigma_1 = 0, \end{gather}

and the condition in the last equation may be simplified into $\tilde {\boldsymbol {v}}_1^* \boldsymbol {L}_T^* \boldsymbol {W} \boldsymbol {v}_1 = \tilde {\boldsymbol {v}}_1^* \boldsymbol {W}{\boldsymbol {u}}_1$ using (3.2). The stationary point is subsequently met by constructing the following system of equations and solving for the Lagrange multipliers

(3.12)\begin{equation} \begin{bmatrix} - \boldsymbol{L}_T^* & -\boldsymbol{W} & - 2 \boldsymbol{W} \boldsymbol{u}_1 \\ \boldsymbol{W}^{{-}1} & \boldsymbol{L}_T \sigma_1^2 & 0 \\ 0 & \boldsymbol{u}_1^* \boldsymbol{W} & 0 \end{bmatrix} \begin{bmatrix} \widetilde{\boldsymbol{u}_1}\\ \widetilde{\boldsymbol{v}_1} \\ \tilde{\sigma}_1 \end{bmatrix} = \begin{bmatrix} - 2 \boldsymbol{W} \boldsymbol{\varPsi}_1 \boldsymbol{W} \boldsymbol{u}_1 \\ 0 \\ 0 \end{bmatrix}. \end{equation}

The upper left $2\times 2$ block is degenerate due to the state (3.1) and (3.2) (the couple, $\tilde {\boldsymbol {u}}_1=\boldsymbol {W}\boldsymbol {v}_1$ and $\tilde {\boldsymbol {v}}_1=-\sigma _1^{-2}\boldsymbol {u}_1$, is in the null space of this block) and the third column and line regularizes this system. Combining the three equations, one can show that $\tilde {\sigma }_1= \boldsymbol {u}_1^*\boldsymbol {W} \boldsymbol {\varPsi }_1 \boldsymbol {W} \boldsymbol {u}_1$, proving that $\tilde {\sigma }_1$ is a real value.

Algorithm 1 Optimization

A final variation is taken with respect to the eddy viscosity, ${\boldsymbol {\mu }_T}$ (which may be a scalar or vector quantity), providing the direction of gradient ascent for the eddy-viscosity field,

(3.13)\begin{align} \frac{\partial \mathcal{L}}{\partial {\boldsymbol{\mu}_T}}{\delta {\boldsymbol{\mu}_T}} &={-} \tilde{\boldsymbol{u}}_1^* \left( \frac{\partial \boldsymbol{L}_T}{\partial {\boldsymbol{\mu}_T}} {\delta {\boldsymbol{\mu}_T}}\right)\boldsymbol{u}_1 + \sigma_1^2 \tilde{\boldsymbol{v}}_1^* \left( \frac{\partial \boldsymbol{L}_T^*}{\partial {\boldsymbol{\mu}_T}} {\delta {\boldsymbol{\mu}_T}}\right) \boldsymbol{W} \boldsymbol{v}_1 - 2l^2 \boldsymbol{\mu}_T^* \boldsymbol{M} {\delta {\boldsymbol{\mu}_T}}+\textrm{c.c.} \end{align}

(3.14)\begin{align} &=\left(\frac{\textrm{d}\mathcal{J}}{\textrm{d}{\boldsymbol{\mu}_T}}\right)^*\boldsymbol{M}\delta{\boldsymbol{\mu}_T}. \end{align}

The gradient at the $k$th grid point is then

(3.15)\begin{equation} \left.\frac{\textrm{d}{\mathcal{J}}}{\textrm{d}\boldsymbol{\mu}_T}\right|_k=\boldsymbol{M}_{km}^{{-}1}(-\boldsymbol{u}_{1,j}^* \boldsymbol{L}_{m,ij}^*\tilde{\boldsymbol{u}}_{1,i}+\sigma_1^2\boldsymbol{W}_{lj}\boldsymbol{v}_{1,l}^* \boldsymbol{L}_{m,ji}\tilde{\boldsymbol{v}}_{1,i})-2l^2 \boldsymbol{ \mu}_{T,k}+\textrm{c.c.}, \end{equation}

where $\boldsymbol {L}_{m,ij} = \mbox {lim}_{\epsilon \rightarrow 0} (({\boldsymbol {L}_{T+\epsilon \delta \boldsymbol {\mu }_{m},ij}-\boldsymbol {L}_{T,ij}})/{\epsilon }), \delta \boldsymbol {\mu }_{m}$ being a null vector except at the $m$th position where it is equal to 1. This tensor may be obtained either through automatic differentiation of $\boldsymbol {L}_T$ with respect to ${\boldsymbol {\mu }_T}$ or by finite differences. Full storage of such tensors is not an issue when finite differences, finite volumes or finite elements are used for the spatial discretization as the resulting tensors are extremely sparse.

The updated optimization parameter is then

(3.16)\begin{equation} \boldsymbol{\mu}_T^{(k+1)} = \boldsymbol{\mu}_T^{(k)} + \alpha \frac{\textrm{d}\mathcal{J}}{\textrm{d}\boldsymbol{\mu}_T}, \end{equation}

where $k$ is the iteration number and $\alpha$ is a step size determined through a root finding algorithm or a line search. If multiple SPOD/resolvent modes are considered for the optimization, then one has to solve (3.12) for each couple $[\boldsymbol {\varPsi }_n, (\boldsymbol {v}_n,\boldsymbol {u}_n, \sigma _n) ]$ and the total gradient ${\textrm {d}\mathcal {J}}/{\textrm {d}\boldsymbol {\mu }_T}$ is the sum of each individual gradient, while the line search for $\alpha$ is performed considering the full cost functional. Although considering multiple modes is theoretically straightforward (and we present one example in § 6), there are two practical issues. Each additional mode brings further complexity to the gradient, increasing computation time, and the quality of SPOD modes, $\boldsymbol {\varPsi }_n$, become increasingly noisy with $n$, thus rendering gains via the optimization as marginal. We discuss the latter issue in more detail throughout the manuscript. Figure 1 presents a schematic of the above optimization framework, including graphical examples from the optimal eddy-viscosity field case at $St = 0.6$, $m=0$ and $M_j = 0.4$.

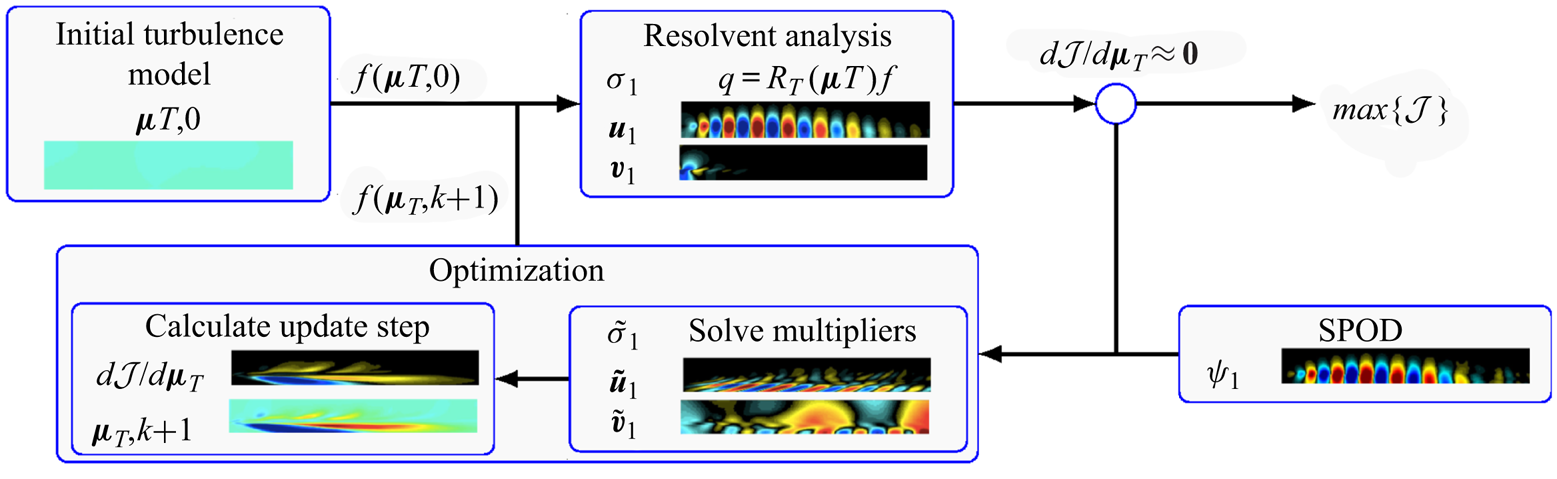
Figure 1. Schematic of the optimization framework for determining the optimal eddy-viscosity field that maximizes the alignment/agreement between computed resolvent modes, $\boldsymbol {u}_1$, and educed SPOD modes, $\boldsymbol {\psi _1}$. Included graphics are from implementation of the full-field eddy-viscosity model at $St=0.6$, $m=0$, and $M_j=0.4$.

For some cases, the optimization step imparts a region of negative effective viscosity (i.e. $-\mu _T > \mu _j$) presenting a challenge in both the physical interpretation and the numerical stability of the resolvent operator. However, negative eddy viscosity is not a unique concept to the algorithm presented. Literature surrounding eddy-viscosity models used in RANS and LES, where the eddy and effective viscosities are identical, attribute physical interpretations of negative eddy viscosity to backscattering of turbulent energy, which, in many simulations, results in unstable simulations (Ghosal et al. Reference Ghosal, Lund, Moin and Akselvoll1995). Common treatment of a negative eddy viscosity has included filtering operations, ensemble averaging in homogeneous directions, and ad hoc clipping of the eddy-viscosity field (Vreman Reference Vreman2004), while inferences of the eddy-viscosity field via a Boussinesq approximation of data are often regularized to remove negative regions (e.g. Semeraro et al. Reference Semeraro, Lesshafft, Jaunet and Jordan2016b). Here, we similarly elect to remove any negative effective viscosity using a simple clipping strategy by setting any negative regions to the molecular value. Although a reduction of effective viscosity below the molecular viscosity is theoretically possible, we found that permitting the optimization to do so either led to numerical instabilities or negligible improvements in alignment.

The topology of the proposed cost function is complex, as $\boldsymbol {\mu }_T$ involves many degrees of freedom, and our optimizer may return a local rather than global maximum. Therefore, a complete assessment of the sensitivity of initial conditions or demonstration of a global maximum is intractable, but the relative insensitivity of the results to initial guesses and the fact that no other considered method outperforms the full optimization (shown later in figure 4) provides confidence in the robustness of the maxima achieved. For all of the results presented here, we use the optimal constant eddy-viscosity field results (introduced in § 3.4) as the initial condition for the full-field optimizations.

Finally, the above optimization is derived considering the full (perturbation) state as the output. The formulation is similar if the input and output spaces are restricted, as shown in Appendix C. Such an extension is of particular use for experiments, or coarse simulations, where observed data may be sparse.

3.2. Mean-flow consistent eddy-viscosity model

For many experimental and numerical datasets, including the LES databases used here, an eddy-viscosity field is absent. We circumvent this issue by finding the eddy-viscosity field that minimizes the error to which the mean flow satisfies the (zero frequency and axisymmetric wavenumber) linearized Navier–Stokes equations, supplemented with an eddy-viscosity model, provided in Appendix B. To do so, we find an eddy-viscosity field that minimizes the residual $\bar {\boldsymbol {f}}$ given by

(3.17)\begin{equation} \boldsymbol{L}_T\bar{\boldsymbol{q}} = \bar{\boldsymbol{f}}. \end{equation}

Thus we define the cost function,

(3.18)\begin{equation} \mathcal{J} ={-}\bar{\boldsymbol{f}}^* \boldsymbol{W} \boldsymbol{\bar{\boldsymbol{f}}}, \end{equation}

and develop a Lagrangian functional with the forward equation as the only additional constraint to give

(3.19)\begin{equation} \mathcal{L} ={-}\bar{\boldsymbol{f}}^* \boldsymbol{W} \boldsymbol{\bar{\boldsymbol{f}}} - \tilde{\boldsymbol{u}}^* (\boldsymbol{L}_T\bar{\boldsymbol{q}} - \bar{\boldsymbol{f}}). \end{equation}

Variations with respect to the residual are

(3.20)\begin{equation} \frac{\partial \mathcal{L}}{\partial \bar{\boldsymbol{f}}}\delta\bar{\boldsymbol{f}} = (- 2 \boldsymbol{W} \bar{\boldsymbol{f}} + \tilde{\boldsymbol{u}})^*\delta\bar{\boldsymbol{f}} = 0, \end{equation}

and we may directly solve for the Lagrange multipliers as,

(3.21)\begin{equation} \tilde{\boldsymbol{u}}={-} 2\boldsymbol{W} \bar{\boldsymbol{f}}. \end{equation}

Then by taking variations with respect to the eddy-viscosity field gives,

(3.22)\begin{equation} \frac{\partial \mathcal{L}}{\partial \boldsymbol{\mu}_T} \delta \boldsymbol{\mu}_T={-} 2 (\boldsymbol{W}\bar{\boldsymbol{f}})^* \left( \frac{\partial \boldsymbol{L}_T}{\partial \boldsymbol{\mu}_T}\delta\boldsymbol{\mu}_T\right)\bar{\boldsymbol{q}}. \end{equation}

Similar to (3.15), we obtain the update step

(3.23)\begin{equation} \left.\frac{\textrm{d}{\mathcal{J}}}{\textrm{d}\boldsymbol{\mu}_T}\right|_k={-}2\boldsymbol{M}_{km}^{{-}1}\bar{\boldsymbol{q}}_{j} \boldsymbol{L}_{m,ij}\boldsymbol{W}_{il} \,\bar{\boldsymbol{f}}_{l}, \end{equation}

and find the field via a line search. These steps are described in greater detail in the preceding subsection § 3.1. Figure 2(a) provides the eddy-viscosity field that optimally minimizes the residual of the mean-flow solution. The associated residual field for this model reduced errors to approximately 10 % of the original residual field, with the exception where the shear layer is thin near the nozzle. The thin shear-layer region improved by only $\approx$50 %, but as shown later in the manuscript, modes in this region are generally less sensitive to the eddy-viscosity field.

Figure 2. (a) Mean-flow consistent eddy-viscosity model computed at zero frequency and azimuthal wavenumber. (b) Eddy-viscosity field computed via a RANS simulation for the $M_j = 0.4$ jet, $c=1$.

We refer to this model as the mean-flow consistent eddy-viscosity model, and we optimally tune this field at each frequency by introducing the coefficient, $c$, $\boldsymbol {\mu }_T = c \boldsymbol {\mu }_{T,Mean}$. Our interest in the value of $c$ is not to propose a functional of its frequency dependence (or assign to it a physical meaning), but to measure and observe the overall variation and help determine whether a frequency independent coefficient might suffice.

3.3. RANS-based eddy-viscosity field

We compute steady-state RANS solutions for each case to assess the applicability of the associated eddy-viscosity field for resolvent analysis. For simplicity, we perform the RANS computations in Fluent. The 2D axisymmetric grid extends 40 diameters in the streamwise directions and 20 diameters in the radial direction with grid spacing mirroring that of the interpolated LES grid scaled to be four times finer, giving $3 \times 10^5$ grid points. We set the inlet boundary conditions to the base-flow profile from the LES simulations and use the standard 2-equation $k-\epsilon$ model (Launder & Spalding Reference Launder and Spalding1983) for turbulence modelling. Coefficients used for the model are variants of those suggested by Thies & Tam (Reference Thies and Tam1996), with turbulent viscosity coefficient $C_\mu = 0.0874$, dissipation transport coefficients $C_{\epsilon 1} = 1.4$ and $C_{\epsilon 2} = 2.02$, turbulent Prandtl numbers for kinetic energy $\sigma _k = 0.324$ and dissipation $\sigma _\epsilon = 0.377$, and the turbulent Prandtl number $Pr_T = 0.422$. However, the standard $\kappa -\epsilon$ model provided in ANSYS does not incorporate the Pope (Reference Pope1978) and Sarkar et al. (Reference Sarkar, Erlebacher, Hussaini and Kreiss1991) correction terms used in Thies & Tam (Reference Thies and Tam1996), requiring a calibration of the mean-flow quantities by introducing a scaling constant $a$ to $C_\mu = 0.0874 / a$, $\sigma _K = 0.324 / a$ and $\sigma _\epsilon = 0.377 / a$.

RANS mean-flow quantities closely match those of the LES for each of the three turbulent jets using values for $a$ of 1.2, 1.3 and 1.575, for $M_j = 0.4$, $0.9$ and 1.5, respectively. While tuning of the constant $a$ to match LES is not in the spirit of obtaining a universal RANS model, we do so here to give the RANS-generated eddy-viscosity field the best chance at being consistent with the LES results from which the SPOD modes were educed. For a full assessment of the accuracy of RANS predictions for turbulent jets, we refer the reader to Thies & Tam (Reference Thies and Tam1996) and Georgiadis, Yoder & Engblom (Reference Georgiadis, Yoder and Engblom2006).

Figure 2(b) presents the RANS-predicted eddy-viscosity field for the $M_j = 0.4$ jet, and figure 3 shows near identical agreement with the mean LES streamwise flow. We observe similar agreement in radial velocity, density and turbulent kinetic energy, and also find close agreement for the $M_j=0.9$ and 1.5 jets; we do not show these results for brevity. For determination of the optimal RANS-based eddy-viscosity field at each frequency, we take the computed eddy-viscosity fields,

(3.24)\begin{equation} \boldsymbol{\mu}_{T,RANS} = \bar{\rho} C_\mu \frac{k^2}{\epsilon}, \end{equation}

and introduce the coefficient, $c$, $\boldsymbol {\mu }_T = c \boldsymbol {\mu }_{T,RANS}$ (just as in § 3.2). This final relation underscores the difference between the traditional use of eddy viscosity with RANS and ours via resolvent analysis. In the former context, eddy viscosity accounts for all perturbations, while in resolvent analysis, the eddy viscosity is intended to model the effect of nonlinear, triadic interactions and the background turbulence on the linear structures. Thus, a coefficient of $c<1$, for resolvent analysis, presents an eddy viscosity that omits a fraction of the overall eddy-viscosity field. As will be shown, we find all optimal values for $c$ to be less than unity. This interpretation may also be applied to the mean-flow consistent eddy-viscosity field presented in the previous sub-section.

Figure 3. Mean-flow profiles of both the $M_j = 0.4$ LES and RANS, where the RANS simulation was tuned to best match the LES mean flow. (a) Presents the streamwise mean velocity at three radial locations, $r/D =$ 0.25, 0.5, 1, vs streamwise distance from the nozzle, while (b) gives the streamwise mean velocity at three streamwise locations, 0.5, 5, 10, vs radial distance.

3.4. Constant eddy-viscosity field

Finally, we consider a simple, constant eddy viscosity, $\boldsymbol {\mu }_T = 1/ {Re}_T$. We primarily investigate this model because of its use in many turbulent jet studies that used a Reynolds number based either upon the molecular viscosity (Jeun et al. Reference Jeun, Nichols and Jovanović2016; Lesshafft et al. Reference Lesshafft, Semeraro, Jaunet, Cavalieri and Jordan2019), of the order of $10^5-10^6$, or through an effective turbulent viscosity (Garnaud et al. Reference Garnaud, Lesshafft, Schmid and Huerre2013; Schmidt et al. Reference Schmidt, Towne, Rigas, Colonius and Brès2018), of the order of $10^3-10^4$. These, quite different, choices inevitably provided discrepancies in amplification gains and mode shapes across each study, particularly at low frequencies (i.e. $St < 0.3$ for $m=0$) – showing that the Reynolds stresses have a substantial impact on resolvent analyses of turbulent jets. Here, we find the optimal ${Re}_T$ at each frequency and azimuthal mode number by a line search.

5.1. Structure of the eddy-viscosity fields

For the constant eddy-viscosity, RANS-based and mean-flow consistent eddy-viscosity fields, the optimization is over a single value, and we plot the optimal values as a function of frequency (still for $m=0$) in figure 8(a,c,d) and the maximum value of the optimal field in 8(b). We investigated several other metrics for the optimal field and each metric provided similar trends and therefore, we chose $\|{\boldsymbol {\mu }_T}\|_{\infty }$, as it gave the most intuitive comparison against the other scalar quantities. For all models, the frequency dependence of the values is similar, with three regions of interest: $St \in [0.05,0.3]$, $St = \in [0.3,0.8]$ and $St \in [0.8,1]$.

Figure 8. The optimal parameters across $St \in [0.05,1]$ for (a) the optimal constant field $1/{Re}_T$, (b) optimal eddy-viscosity field model, (c) the mean-flow consistent model and (d) the optimal RANS model. The optimal eddy-viscosity field parameter shown is the maximum value of the field at each frequency, $\|{\boldsymbol {\mu }_T}\|_{\infty }$, while the latter two models present the optimal coefficient $c$. The associated alignments for each model/parameter are shown in figure 4.

In the low-frequency region, the baseline jet response comprises of spatially extensive Orr-type modes that have a strong Reynolds number dependence, requiring a relatively larger eddy viscosity to damp them. For $St=0.05$ the ratio of the optimal effective Reynolds number to the molecular Reynolds number is $\boldsymbol {\mu }_T/\mu _j \approx 13\ 500$, a four orders of magnitude difference when compared to the molecular viscosity.

In the moderate-frequency regime, where the baseline spectrum transitions from the broadband, viscous Orr mechanism to the low-rank, inviscid KH mechanism, eddy viscosity becomes less important, and we expect (confirming below, in § 7.1) insensitivity to the overall value based on the relatively favourable alignment achieved in the baseline case. As frequency increases, the responses transition back to a mix of KH and Orr-type waves, with a progression towards broadband, viscous Orr modes at higher frequency.

At these higher frequencies, we see that the low-frequency dependence on inverse effective Reynolds number resumes, similar to low the frequencies. Interestingly, this trend shows that at higher frequencies ${Re}_T \rightarrow Re_j$ such that the effect of eddy viscosity ‘turns off’ as frequency increases and the associated wavepacket wavelength becomes small (i.e. approaching finer-scale turbulence), as expected on physical grounds.

Similar trends are observed for the mean-flow consistent and RANS eddy-viscosity coefficients. For both eddy-viscosity fields, $c$ is less than unity and only varies from 0.7 to 0.1 with a few exceptions. These values suggest that the optimal eddy-viscosity model is a fraction of the total RANS or mean-flow consistent eddy-viscosity models that integrate all perturbations.

For the full-field eddy-viscosity optimization, we stress that its primary purpose is to determine what may be an upper bound for how well any eddy-viscosity model could perform. Given that the alignments between the resolvent and SPOD modes were not significantly higher for the optimized scheme than for the modelled eddy-viscosity approaches (with optimal parameters), the detailed eddy-viscosity fields are of lesser importance. Still, some aspects of the physics, such as the spatial locations where Reynolds stresses become important for each frequency, are apparent in the optimized fields. Figure 9 presents the optimized fields for two selected Strouhal numbers, comparing them to both the RANS and mean-flow consistent eddy-viscosity fields scaled by their optimal coefficient $c$ at each frequency. In addition, the dominant resolvent mode, computed with the displayed optimal eddy-viscosity field, is shown for comparison with the eddy-viscosity fields. The contours for the eddy-viscosity fields are set from 0 to the maximum value of the $St = 0.6$ optimal eddy-viscosity field.

Figure 9. Comparisons of the optimal eddy-viscosity fields (i.e. full-field optimal, mean-flow consistent and RANS) and the associated dominant resolvent mode found via the optimization for $St = 0.2$ and $0.6$. Contours for all six eddy-viscosity fields are set from 0 to $3 \times 10^{-3}$.

Overall, both frequencies present optimal eddy-viscosity fields that are complex, unsurprising given the ability of the optimization to choose any eddy-viscosity field, constrained only by the structure of the equations and positivity. The optimal eddy-viscosity fields pinpoint the locations where linear structures break down (i.e. where nonlinearities/Reynolds stresses become important) and inform what features an eddy-viscosity model must include. In both cases, the optimization removes viscosity from the potential core (i.e. the interior region of the jet relative to the critical layer), when compared to the initial guess, while increasing the turbulent viscosity just outside of the critical layer. The increase in eddy-viscosity is most often observed just downstream of the peak amplitude of the wavepacket, coinciding with each wavepacket's decay downstream.

Although not entirely clear from figure 9, these findings are reasonably consistent with each of the modelled eddy-viscosity fields when restricting the view to the region where the resolvent/SPOD mode has significant amplitude. We can see that both the RANS and mean-flow consistent eddy-viscosity fields present similar features as the optimal field, explaining the ability of each model to achieve nearly optimal results. We will show in the following section how such features also explain the ability of the RANS and mean-flow consistent models to predict the subdominant modes, which require further turbulence modelling downstream.

7.1. Frequency and azimuthal mode sensitivity

The optimal RANS coefficients (figure 8) ranged from $c = 0.7-0.004$, with a relatively constant region, $c=0.5$, for moderate frequencies and, considering the fully optimized eddy-viscosity field produced only marginally improved alignments for most cases, the results may not be sensitive to the precise constant. We test this hypothesis for the RANS model across a range of frequencies with proposed ‘universal’ values of constant $c = [1, 0.5, 0.32, 0.2, 0.08]$. We plot the resulting alignments vs frequency in figure 13. With little compromise, compared to the optimal constant for each frequency, a single constant of $c=0.2$ provides significant alignment across all frequencies up to $St=1$. Although not shown for brevity, we found similar observations using $c=0.08-1$ for all three Mach numbers and six azimuthal wavenumbers. In these cases, not only did $c=0.2$ give the best overall alignment, but the alignments were comparably insensitive to the value of $c$ chosen over this range.

Figure 13. Alignments across all Strouhal numbers for the RANS eddy-viscosity model coefficients compared with the optimal RANS coefficient at each frequency. The RANS coefficients are $c = [1, 0.5, 0.32, 0.2, 0.08]$.

We do not present a rigorous justification for the value of $c=0.2$, however, $c$ may have a connection with LES eddy-viscosity modelling. If we compare the empirical coefficients used in this RANS eddy-viscosity analysis, $c C_\mu$, to the square of the Smagorinsky coefficient, $C_s^2$, used for SGS eddy-viscosity fields in LES (Smagorinsky Reference Smagorinsky1963), we can find that the value of $c=0.2$ lies within the bounds of wall-bounded and isotropic turbulence. Setting equal the products of each set of coefficients, we find $c = C_s^2 /C_\mu$. Then using the $M_j=0.4$ RANS coefficient, $C_\mu = 0.073$, and the commonly used range of $C_s$, $0.1$ for wall-bounded flows and $0.18$ for isotropic turbulence (Zhiyin Reference Zhiyin2015), we find that $c = [0.14\text {--}0.45]$ (ranges for the $M_j=0.9,1.5$ jet are $c = [0.15\text {--}0.48],[0.17\text {--}0.57]$, respectively). This range approximately corresponds to the acceptable values found in figure 13.

For non-zero azimuthal modes, figure 14 presents the alignment of the EVRA–RANS model with SPOD using $c=0.2$ and the baseline case for $m = 0\text {--}5$. The EVRA–RANS model substantially increases the alignments for all non-zero wavenumbers. The results for $m=1$ are particularly encouraging, with a uniform, $80$% alignment across all frequencies. Azimuthal modes greater than 1 result in poorer alignment, albeit much improved compared to the baseline case, especially when $m > 2$.

Figure 14. Alignments for frequencies, $St \in [0.05,1]$, and azimuthal wavenumbers, $m = 0-5$, for the (a) RANS eddy-viscosity model using $c = 0.2$ and the (b) baseline, constant eddy-viscosity case (i.e. ${Re}_T = 3 \times 10^4$).

Expanding to non-zero azimuthal wavenumbers, the eddy-viscosity field also affects a third mechanism observed in the global SPOD spectrum (as $St \rightarrow 0$), the lift-up mechanism (Pickering et al. Reference Pickering, Rigas, Nogueira, Cavalieri, Schmidt and Colonius2020a). Similar to the Orr mechanism, the lift-up mechanism arises from triadic nonlinear interactions in the flow (Hamilton, Kim & Waleffe Reference Hamilton, Kim and Waleffe1995; Sharma & McKeon Reference Sharma and McKeon2013; de Giovanetti, Sung & Hwang Reference de Giovanetti, Sung and Hwang2017; Cho, Hwang & Choi Reference Cho, Hwang and Choi2018), identifying it as a likely benefactor to an EVRA approach. Figure 14 supports this claim, showing significant improvements at low frequencies for non-zero wavenumbers. These observations also agree with Pickering et al. (Reference Pickering, Rigas, Nogueira, Cavalieri, Schmidt and Colonius2020a), who showed that resolvent modes related to streaks required an eddy-viscosity model (using the turbulent kinetic energy model reported by Pickering et al. (Reference Pickering, Rigas, Sipp, Schmidt and Colonius2019) with $c=0.0065$). They also observed that, in turbulent jets, the spatial extent of resolvent modes increase as frequency decreases and that without an eddy-viscosity, modes extend indefinitely downstream for $St=0$. This is analogous to theory surrounding streaks where the lift-up mechanism presents a rapid spatial growth of streamwise streaks until viscous dissipation becomes dominant and the structures decay (Hultgren & Gustavsson Reference Hultgren and Gustavsson1981). Considering the significant improvements between alignments for low frequency and non-zero wavenumbers, we find the lift-up mechanism to also be sensitive to an eddy-viscosity model.

7.2. Transonic and supersonic turbulent jets

We now generalize the RANS–EVRA model performance for both $M_j = 0.9$ and 1.5 turbulent jets using $c=0.2$. Figure 15 provides the alignments across frequencies and azimuthal wavenumbers for each. The transonic jet gives substantial agreement for $m=0$ and $m=1$ at approximately 80 % for much of the frequency range, while $m=2$ gives alignments of 60 %, on average. For the supersonic jet, the agreement is not as favourable, however, much improved from the ${Re}_T = 3 \times 10^4$ alignments (not shown here for brevity).

Figure 15. Alignments using the RANS eddy-viscosity model with coefficient $c = 0.2$ across Strouhal numbers $St \in [0.05,1]$ and azimuthal wavenumbers $m =0-5$ for the (a) $M_j = 0.9$ and (b) $1.5$ jets.

The RANS eddy-viscosity model increases many of the alignments, however, poor alignments remain, and these alignments appear to correspond to SPOD spectra without large energy separation. As shown earlier in figure 4, EVRA and SPOD modes aligned best when there exists large eigenvalue separation between the first and second SPOD mode. We find similar behaviour here for all cases. Figure 16 presents the SPOD spectra of the first five modes across all six azimuthal wavenumbers and three turbulent jets, with their associated 95 % confidence intervals in light blue. A handful of the spectra show a clear separation between mode energies, such as those between the first and second mode for $M_j = 0.4$, $m=0$ and 1, for $M_j = 0.9$, $m=0$ and 1 (and higher frequencies for $m = 2-5$) and for $M_j=1.5$, $m=1$. In each case where there is large eigenvalue separation, we find, from figures 14 and 15, significantly greater agreement in projection coefficients between the resolvent and SPOD modes, while finding poor projections for cases without clear separation in eigenvalues. We also observe this for the subdominant modes investigated in the $M_j=0.4$, $m=0$ case in § 6.

Figure 16. Spectra, and their associated 95 % confidence intervals in light blue, of the first five SPOD modes for azimuthal wavenumbers $m=0-5$ from left to right and the subsonic, transonic and supersonic jets from top to bottom, respectively. (a) $M_j = 0.4$, (b) $M_j = 0.9$ and (c) $M_j = 1.5$.

These observations point to a limitation to our method when comparing EVRA modes with SPOD modes. For the SPOD modes without clear eigenvalue separation, the eigenvalues themselves fall within the uncertainty bands (i.e. 95 % confidence interval) of the other modes. The eigenvectors corresponding to these eigenvalues are expected to have, at best, similar uncertainty levels. Thus, without more data, it is not possible to attribute the lack of agreement to a failure of the EVRA ansatz.

7.3. Singular values

We return to the $m=0$, $St \in [0.05,1]$ case to assess the EVRA–RANS $c=0.2$ model's effect on the singular values and compare them to the baseline case and the SPOD eigenvalues. Figure 17 provides the spectra of the first five modes for SPOD (accompanied by a shaded region providing the 95 % confidence interval of the eigenvalues), the baseline resolvent model and the RANS–EVRA model (using $c=0.2$) for $m=0$. Comparing the resolvent spectra to the SPOD spectra, we immediately see that the separation between $\lambda$ (i.e. the ratio between $\lambda _n /\lambda _{n+1}$) and $\sigma ^2$ of either resolvent models does not compare favourably. In fact, the RANS–EVRA spectrum has increased its energetic separation when compared to the baseline case.

Figure 17. Spectra of first five (a) SPOD, (b) baseline resolvent and (c) the RANS eddy-viscosity model resolvent modes at $m=0$ for $St \in [0.05,1]$.

This behaviour may be linked to multiple (in this case two for $m=0$) distinct mechanisms represented in the flow, the KH and Orr mechanisms. As detailed earlier, the inclusion of an eddy-viscosity model presents a substantial effect on the Orr modes significantly reducing the streamwise extent of each mode, while the KH modes are relatively unchanged. We observe an analogous effect here in figure 17 where the singular values related to the Orr mechanism decrease substantially, pulling away from the unaffected singular values of the KH mechanism, resulting in a much larger separation between singular values than is observed between the SPOD eigenvalues. This sensitivity of Orr modes to an eddy viscosity was also observed in Schmidt et al. (Reference Schmidt, Towne, Rigas, Colonius and Brès2018) at $St=0.6, m=0$ when adjusting ${Re}_T$, finding that the squared singular values of the subdominant Orr modes scaled as ${Re}_T^{1.2}$. We observe the same effect using the RANS eddy-viscosity model, interestingly (and perhaps unsurprising given the preceding discussions), figure 17 (c) provides similar values as those reported by Schmidt et al. (Reference Schmidt, Towne, Rigas, Colonius and Brès2018) at $St = 0.6, m=0$ when using ${Re}_T = 10^3$.

Figures 17(a) and 17(c) also show that the forcing amplitudes, $\lambda _\beta$, are not uniform in turbulent jets, contrary to a customary assumption used in resolvent analysis where $\boldsymbol {\varLambda _{\boldsymbol {\beta }}} = \alpha \boldsymbol {I}$, with $\alpha$ as an arbitrary constant (Lesshafft et al. Reference Lesshafft, Semeraro, Jaunet, Cavalieri and Jordan2019; Morra et al. Reference Morra, Semeraro, Henningson and Cossu2019; Hwang & Eckhardt Reference Hwang and Eckhardt2020). Focusing on only the first and second resolvent and SPOD modes for $St=0.6$ and $m=0$, where mode alignments are 95 % and 69 %, respectively (the optimal-field case increases the latter value to 77 % without appreciably changing the singular value), we may assume that the diagonal components of the forcing, $\lambda _{\boldsymbol {\beta },1}$ and $\lambda _{\boldsymbol {\beta },2}$, account for nearly all the energetic contributions by these two modes. As shown by (2.17), this assumption allows for a one-to-one comparison between the first two SPOD eigenvalues, resolvent singular values and forcing amplitudes (i.e. $\lambda _{\boldsymbol {\beta },n} = \lambda _{n} \sigma _n^{-2}$ for $n=1,2$). If the customary assumption of uniform forcing is applied, $\boldsymbol {\varLambda _{\boldsymbol {\beta }}} = \alpha \boldsymbol {I}$, then $\alpha = \lambda _{1} \sigma _1^{-2} = \lambda _{2} \sigma _2^{-2}$ or, alternatively, $\lambda _{1} / \lambda _{2} = \sigma _1^{2} / \sigma _2^{2}$, and figure 17 shows this cannot be true. Therefore, unless the SPOD and resolvent spectra are equivalent, we must model or estimate the non-trivial forcing amplitudes.

The sizeable difference between the singular values reflects the forcing of different mechanisms at significantly different amplitudes in the flow. Pickering et al. (Reference Pickering, Rigas, Nogueira, Cavalieri, Schmidt and Colonius2020a) showed that there are three distinct spatial regions that lead to the most efficient amplification of the KH, Orr, and the lift-up mechanisms. They found that regions localized near the nozzle where perturbations are smaller, associate with KH-type responses, while regions downstream and near the end of the potential core where perturbations are significantly larger, support Orr-type responses. Considering these observations, a logical next step in completing a resolvent-based turbulence model is to tie the forcing amplitude of different modes to the turbulence intensities in the respective regions that force them.