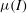1 Introduction
Being reminiscent of both solids and fluids, but still enjoying properties that differentiate them from these states of matter, granular materials exhibit substantially complex behaviours. However, these behaviours remain elusive to understand and continue to puzzle scientists and engineers alike, despite the numerous efforts that have been devoted to their study.
The rich phenomenology of granular materials can be evidenced even in deceivingly simple flows. Indeed, experimental measurements and numerical predictions on granular shear flows have demonstrated the manifestation of phenomena such as particle clustering, segregation, pattern formation, stress fluctuations, etc. (Hopkins & Louge Reference Hopkins and Louge1991; Ottino & Khakhar Reference Ottino and Khakhar2000; Goldhirsch Reference Goldhirsch2003). Such phenomena, which are absent from shear flows of simple fluids, are associated with density inhomogeneities and hint that granular shear flows might be susceptible to hydrodynamic instabilities. In turn, these findings have prompted the investigation of the stability of such flows, identified as steady-state solutions to continuum equations of motion.
The majority of studies that have examined the stability of either bounded or unbounded granular shear flows have utilized continuum models derived from kinetic theories of granular gases. According to this modelling approach, governing equations are derived by employing aspects of kinetic theory, appropriately modified to account for the dissipative interparticle collisions, (Jenkins & Savage Reference Jenkins and Savage1983; Lun et al. Reference Lun, Savage, Jeffrey and Chepurniy1984; Jenkins & Richman Reference Jenkins and Richman1985; Savage Reference Savage2008). As regards unbounded shear flows, Savage (Reference Savage1992) and Babić (Reference Babić1993) investigated the linear stability of a steady base flow to time-dependent perturbations (‘Kelvin modes’), as predicted by the governing equations of Lun et al. (Reference Lun, Savage, Jeffrey and Chepurniy1984). Both authors reported the existence of unstable modes. Further insight in this direction was provided by Schmid & Kytömaa (Reference Schmid and Kytömaa1994), Alam & Nott (Reference Alam and Nott1997) and the systematic review of Goddard (Reference Goddard2003). A notable disparity was raised by Chen, Lai & Young (Reference Chen, Lai and Young2010) who, based on a viscoplastic constitutive model that also accounts for dilatancy effects, reported that the flow of interest is unconditionally stable. This disparity was subsequently resolved by Chen, Lai & Young (Reference Chen, Lai and Young2012). Additionally, these authors exemplified the critical differences between disturbances with and without a streamwise component.
As regards bounded shear flows, Wang, Jackson & Sundaresan (Reference Wang, Jackson and Sundaresan1996) examined the linear stability of a plane, rapidly sheared granular layer, confined between two plates moving in opposite directions. They documented the existence of unstable modes that, in turn, explicated the discrepancies between the bounded and the unbounded case. Also, these authors reported that the properties of the walls appear to have little impact on the stability properties of the flow. Alam & Nott (Reference Alam and Nott1998) performed a similar analysis and demonstrated an inconsistency in the study of Wang et al. (Reference Wang, Jackson and Sundaresan1996) related to the shape of the base-flow profile. Upon rectifying it, the authors concluded that the properties of the walls are of considerable importance to the determination of the stability properties and found novel travelling and stationary wave instabilities. A more detailed study concerning the role of boundaries, that put this matter at rest, was carried out by Nott et al. (Reference Nott, Alam, Agrawal, Jackson and Sundaresan1999). In a subsequent work, Alam et al. (Reference Alam, Arakeri, Nott, Goddard and Herrmann2005), motivated by the fact that a Squire-type theorem is unlikely to hold for granular materials, performed a three-dimensional stability analysis for the flows of interest. The results of that study corroborated the suspected differences between planar and three-dimensional granular flows concerning both the magnitude and the cardinality of the unstable growth rates. More recent contributions include those of Shukla & Alam (Reference Shukla and Alam2011a ,Reference Shukla and Alam b ) and Alam & Shukla (Reference Alam and Shukla2013) that are, however, concerned with nonlinear stability analyses.
All the afore-cited studies have focused on either dilute or ‘rapid dense’ granular flows, i.e. on collision-dominated flows where equations of motion derived from kinetic theory are formally valid. For dense granular flows, where frictional effects become important, the assumptions that kinetic theory models predicate on become questionable. In this regime, a continuum mechanical framework is deemed better adapted, (Drew & Passman Reference Drew and Passman1999). This approach invokes principles of continuum mechanics and rests upon the exploitation of the entropy inequality for the derivation of constitutive relations for the dissipative processes that occur in the medium, (Goodman & Cowin Reference Goodman and Cowin1972; Wang & Hutter Reference Wang and Hutter1999c ; Massoudi & Mehrabadi Reference Massoudi and Mehrabadi2001; Kirchner Reference Kirchner2002; Fang, Wang & Hutter Reference Fang, Wang and Hutter2006b ; Fang Reference Fang2008a ).
However, to date, stability analyses of dense granular flows as predicted by continuum mechanical models are notably scarce. This constitutes a critical gap in the extant literature primarily for three reasons: (i) these types of model have been documented to enjoy a good predictive capacity, (Savage Reference Savage1979; Gudhe, Yalamanchili & Rajagopal Reference Gudhe, Yalamanchili and Rajagopal1994; Wang & Hutter Reference Wang and Hutter1999c ; Kirchner & Teufel Reference Kirchner and Teufel2002; Massoudi & Phuoc Reference Massoudi and Phuoc2005; Fang, Wang & Hutter Reference Fang, Wang and Hutter2006a ; Fang Reference Fang2008b ), (ii) recent phenomenological expressions for the granular rheology that accord very well with experimental measurements, (Jop, Forterre & Pouliquen Reference Jop, Forterre and Pouliquen2006; Henann & Kamrin Reference Henann and Kamrin2013), can be rigorously accommodated in the theoretical framework of continuum mechanical models and in a way that conforms with the entropy law, and (iii) in the absence of theoretical results for dense granular flows, our picture concerning their stability properties remains incomplete.
The objective of the present study is to perform the first step towards closing this gap in the literature. More specifically, we investigate the asymptotic stability of a plane Couette flow of a dense granular material as predicted by the dry limit of the continuum theory for coexisting and interacting continua with microstructure of Papalexandris (Reference Papalexandris2004). The governing equations are further endowed with the constitutive relations induced by the
![]() ${\it\mu}(I)$
-rheology of Jop et al. (Reference Jop, Forterre and Pouliquen2006) for the normal and the shear stresses and with suitable experimentally acquired correlations for the intergranular and the Korteweg stresses. The resulting, post-constitutive model is general enough to account for both compaction and dilatational effects.
${\it\mu}(I)$
-rheology of Jop et al. (Reference Jop, Forterre and Pouliquen2006) for the normal and the shear stresses and with suitable experimentally acquired correlations for the intergranular and the Korteweg stresses. The resulting, post-constitutive model is general enough to account for both compaction and dilatational effects.
This paper is organized as follows. In § 2, we present and elaborate on the governing equations, their non-dimensionalisation and the choice of the base flow. Section 3 is devoted to the linear stability analysis and the delineation of the algorithm that is utilized for the computation of the stability modes. The results of our analysis are reported and analysed in § 4. Finally, § 5 concludes.
2 Governing equations
We consider an isotropic granular material of incompressible, monodisperse grains. We further assume that the role of the interstitial fluid can be neglected during the evolution of the flow. Also, the contribution of gravitational forces is ignored.
Continuum mechanical models for dense dry granular flows can be derived either directly, as done, for instance, in Savage (Reference Savage1979) and in Kirchner (Reference Kirchner2002) or via the systematic reduction of models for fluid-saturated granular materials to their single-phase (dry) limit, as done, among others, in Svendsen & Hutter (Reference Svendsen and Hutter1995) and Bdzil et al. (Reference Bdzil, Menikoff, Son, Kapila and Stewart1999). In the present study, we opt for the latter option and employ the mixture theory of Papalexandris (Reference Papalexandris2004) as the starting point.
The derivation of the dry limit of mixture theoretic models is a subtle procedure that is exemplified in detail in Bdzil et al. (Reference Bdzil, Menikoff, Son, Kapila and Stewart1999). It involves an order-of-magnitude analysis that rests upon and utilizes the smallness of the ratio of the mass fraction, density and of partial normal stresses of the granular material to those of the interstitial fluid. With these assumptions, terms that describe interphase interactions, e.g. interphasial drag, become negligible in the governing equations of the granular material thus allowing for their formal removal. Accordingly, the evolution of the granular material becomes independent from that of the interstitial fluid. However, the converse is not valid because the governing equations of the latter still depend on the dynamics of the granular material; in this respect, the dry limit is markedly different from the pure-fluid limit (Navier–Stokes) which is identified by the absence of the granular material.
Upon application of this procedure to the mathematical model of Papalexandris (Reference Papalexandris2004), we arrive at the following system of (dimensional) equations,
Physically, (2.1) and (2.2) describe the balance of mass and linear momentum of the granular material. Equation (2.3) is the compaction equation that governs the evolution of the granular material’s volume fraction
![]() ${\it\phi}$
. In the present theory, the compaction equation results directly from the constraints imposed by the entropy law on the entropy production rate. It is worth noting that, although there is no unequivocal consensus on the form of (2.3), the bulk of existing compaction equations are either rate equations, (Baer & Nunziato Reference Baer and Nunziato1986; Bdzil et al.
Reference Bdzil, Menikoff, Son, Kapila and Stewart1999; Papalexandris Reference Papalexandris2004), or wave-type equations, (Goodman & Cowin Reference Goodman and Cowin1972; Passman et al.
Reference Passman, Thomas, Bailey and Thomas1980; Passman, Nunziato & Bailey Reference Passman, Nunziato and Bailey1986).
${\it\phi}$
. In the present theory, the compaction equation results directly from the constraints imposed by the entropy law on the entropy production rate. It is worth noting that, although there is no unequivocal consensus on the form of (2.3), the bulk of existing compaction equations are either rate equations, (Baer & Nunziato Reference Baer and Nunziato1986; Bdzil et al.
Reference Bdzil, Menikoff, Son, Kapila and Stewart1999; Papalexandris Reference Papalexandris2004), or wave-type equations, (Goodman & Cowin Reference Goodman and Cowin1972; Passman et al.
Reference Passman, Thomas, Bailey and Thomas1980; Passman, Nunziato & Bailey Reference Passman, Nunziato and Bailey1986).
In (2.1)–(2.3), and throughout this paper, the hat symbol (‘
![]() $\hat{\phantom{a}}$
’) denotes a dimensional variable. The quantities
$\hat{\phantom{a}}$
’) denotes a dimensional variable. The quantities
![]() $\hat{{\it\rho}}$
,
$\hat{{\it\rho}}$
,
![]() ${\it\phi}$
and
${\it\phi}$
and
![]() $\hat{\boldsymbol{u}}=(\hat{u} ,\hat{v},{\hat{w}})$
designate the density, volume fraction and velocity vector of the granular material, respectively. The terms
$\hat{\boldsymbol{u}}=(\hat{u} ,\hat{v},{\hat{w}})$
designate the density, volume fraction and velocity vector of the granular material, respectively. The terms
![]() $\hat{p}$
,
$\hat{p}$
,
![]() $\hat{p}^{v}$
and
$\hat{p}^{v}$
and
![]() $\hat{{\bf\tau}}$
constitute the components of the granular material’s stress tensor
$\hat{{\bf\tau}}$
constitute the components of the granular material’s stress tensor
![]() $\hat{{\it\bf\Sigma}}$
with respect to the classical decomposition,
$\hat{{\it\bf\Sigma}}$
with respect to the classical decomposition,
In this respect,
![]() $\hat{p}$
and
$\hat{p}$
and
![]() $\hat{p}^{v}$
are the reversible hydrostatic pressure and the irreversible isotropic part of the stress tensor, respectively, whereas
$\hat{p}^{v}$
are the reversible hydrostatic pressure and the irreversible isotropic part of the stress tensor, respectively, whereas
![]() $\hat{{\bf\tau}}$
is its deviator. In the constant-density regime,
$\hat{{\bf\tau}}$
is its deviator. In the constant-density regime,
![]() $\hat{p}$
reduces to the ‘dynamic’ pressure, completely equivalent to the pressure term appearing in the incompressible Navier–Stokes equations. A formal demonstration of this equivalence can be found in Varsakelis & Papalexandris (Reference Varsakelis and Papalexandris2011) and for a connection to the representation theorem for isotropic functions we refer to the classical treatise of Truesdell & Noll (Reference Truesdell and Noll1965). For granular materials, the irreversible isotropic pressure
$\hat{p}$
reduces to the ‘dynamic’ pressure, completely equivalent to the pressure term appearing in the incompressible Navier–Stokes equations. A formal demonstration of this equivalence can be found in Varsakelis & Papalexandris (Reference Varsakelis and Papalexandris2011) and for a connection to the representation theorem for isotropic functions we refer to the classical treatise of Truesdell & Noll (Reference Truesdell and Noll1965). For granular materials, the irreversible isotropic pressure
![]() $\hat{p}^{v}$
is further decomposed into a bulk viscous pressure and a particle pressure, namely a surface force due to particle collisions.
$\hat{p}^{v}$
is further decomposed into a bulk viscous pressure and a particle pressure, namely a surface force due to particle collisions.
The term
![]() $\hat{{\it\beta}}$
appearing in the right-hand side of the compaction equation (2.3) is the intergranular stress or configuration pressure; see, for example, Goodman & Cowin (Reference Goodman and Cowin1972), Josserand, Lagrée & Lhuillier (Reference Josserand, Lagrée and Lhuillier2004) and Josserand, Lagrée & Lhuillier (Reference Josserand, Lagrée and Lhuillier2006) for dry granular flows and Passman et al. (Reference Passman, Nunziato and Bailey1986), Wang & Hutter (Reference Wang and Hutter1999a
,Reference Wang and Hutter
b
) and Cochran & Powers (Reference Cochran and Powers2008) for fluid-saturated ones. Physically,
$\hat{{\it\beta}}$
appearing in the right-hand side of the compaction equation (2.3) is the intergranular stress or configuration pressure; see, for example, Goodman & Cowin (Reference Goodman and Cowin1972), Josserand, Lagrée & Lhuillier (Reference Josserand, Lagrée and Lhuillier2004) and Josserand, Lagrée & Lhuillier (Reference Josserand, Lagrée and Lhuillier2006) for dry granular flows and Passman et al. (Reference Passman, Nunziato and Bailey1986), Wang & Hutter (Reference Wang and Hutter1999a
,Reference Wang and Hutter
b
) and Cochran & Powers (Reference Cochran and Powers2008) for fluid-saturated ones. Physically,
![]() $\hat{{\it\beta}}$
describes the continuum manifestation of contact stresses resulting from strains due to intergrain interaction. Bdzil et al. (Reference Bdzil, Menikoff, Son, Kapila and Stewart1999) and Powers (Reference Powers2004) illustrated that, in the mixture theory of interest and its variations, the intergranular stress
$\hat{{\it\beta}}$
describes the continuum manifestation of contact stresses resulting from strains due to intergrain interaction. Bdzil et al. (Reference Bdzil, Menikoff, Son, Kapila and Stewart1999) and Powers (Reference Powers2004) illustrated that, in the mixture theory of interest and its variations, the intergranular stress
![]() $\hat{{\it\beta}}$
emerges due to the inclusion of the volume fraction as an internal thermodynamic variable for the description of the granular microstructure. In particular, it constitutes the force conjugate to the volume fraction. As such, it is defined as the thermodynamic derivative of the granular material’s free energy
$\hat{{\it\beta}}$
emerges due to the inclusion of the volume fraction as an internal thermodynamic variable for the description of the granular microstructure. In particular, it constitutes the force conjugate to the volume fraction. As such, it is defined as the thermodynamic derivative of the granular material’s free energy
![]() $\hat{{\it\psi}}$
, with respect to the volume fraction
$\hat{{\it\psi}}$
, with respect to the volume fraction
![]() ${\it\phi}$
, i.e.
${\it\phi}$
, i.e.
![]() $\hat{{\it\beta}}={\it\rho}{\it\phi}\,\partial \hat{{\it\psi}}/\partial {\it\phi}$
.
$\hat{{\it\beta}}={\it\rho}{\it\phi}\,\partial \hat{{\it\psi}}/\partial {\it\phi}$
.
The term
![]() $\hat{{\it\Gamma}}$
that appears as a coefficient in the second-order differential operator in the right-hand side of the compaction equation (2.3), and in the tensor involving the volume fraction gradients in the right-hand side of the momentum equation (2.2), is the equilibrated stress coefficient; this is the terminology originally introduced in Goodman & Cowin (Reference Goodman and Cowin1972). In analogy to
$\hat{{\it\Gamma}}$
that appears as a coefficient in the second-order differential operator in the right-hand side of the compaction equation (2.3), and in the tensor involving the volume fraction gradients in the right-hand side of the momentum equation (2.2), is the equilibrated stress coefficient; this is the terminology originally introduced in Goodman & Cowin (Reference Goodman and Cowin1972). In analogy to
![]() $\hat{{\it\beta}}$
, this term emerges due to the inclusion of
$\hat{{\it\beta}}$
, this term emerges due to the inclusion of
![]() $\hat{\boldsymbol{{\rm\nabla}}}{\it\phi}$
as an additional internal variable for the description of the granular materials interfacial area density. Accordingly,
$\hat{\boldsymbol{{\rm\nabla}}}{\it\phi}$
as an additional internal variable for the description of the granular materials interfacial area density. Accordingly,
![]() $\hat{{\it\Gamma}}$
is the force conjugate to
$\hat{{\it\Gamma}}$
is the force conjugate to
![]() $\boldsymbol{{\rm\nabla}}{\it\phi}$
and
$\boldsymbol{{\rm\nabla}}{\it\phi}$
and
![]() $\hat{{\it\Gamma}}={\it\rho}{\it\phi}\,\partial \hat{{\it\psi}}/\partial |\hat{\boldsymbol{{\rm\nabla}}}{\it\phi}|^{2}$
, (Ván Reference Ván2004; Fang et al.
Reference Fang, Wang and Hutter2006a
,Reference Fang, Wang and Hutter
b
; Varsakelis Reference Varsakelis2015). The rationale for the inclusion of
$\hat{{\it\Gamma}}={\it\rho}{\it\phi}\,\partial \hat{{\it\psi}}/\partial |\hat{\boldsymbol{{\rm\nabla}}}{\it\phi}|^{2}$
, (Ván Reference Ván2004; Fang et al.
Reference Fang, Wang and Hutter2006a
,Reference Fang, Wang and Hutter
b
; Varsakelis Reference Varsakelis2015). The rationale for the inclusion of
![]() $\hat{\boldsymbol{{\rm\nabla}}}{\it\phi}$
as an internal variable is the following. The interface between a granular material and an interstitial fluid (or void) has a macroscopic thickness and thus bears stronger resemblances to a thin transition layer than to a sharp discontinuity. Within this transition layer, steep gradients of concentration are developed that give rise to a Korteweg stress, i.e. a weak, transient interfacial tension that mimics the surface tension effect. As shown in Dunn & Serrin (Reference Dunn and Serrin1985), the rationalization of such stresses within thermodynamically consistent theories requires that the free energy of the material is a function of the volume fraction gradient as well. Then, the diffusion operator appearing in the right-hand side of the compaction equation (2.3) models the tendency of the granular material to suppress concentration inhomogeneities. Further, the tensor that involves the volume fraction gradients in the right-hand side of the momentum equation (2.2) is the so-called Korteweg tensor and models the aforementioned interfacial tension. Note that the Korteweg tensor constitutes a non-dissipative component of the granular material’s stress tensor and in the presence of concentration inhomogeneities does not vanish at thermodynamic equilibrium. In fact, Ván (Reference Ván2004) showed that, at thermodynamic equilibrium, the presence of the Korteweg tensor yields that normal and shear stresses are related via a Mohr–Coulomb criterion.
$\hat{\boldsymbol{{\rm\nabla}}}{\it\phi}$
as an internal variable is the following. The interface between a granular material and an interstitial fluid (or void) has a macroscopic thickness and thus bears stronger resemblances to a thin transition layer than to a sharp discontinuity. Within this transition layer, steep gradients of concentration are developed that give rise to a Korteweg stress, i.e. a weak, transient interfacial tension that mimics the surface tension effect. As shown in Dunn & Serrin (Reference Dunn and Serrin1985), the rationalization of such stresses within thermodynamically consistent theories requires that the free energy of the material is a function of the volume fraction gradient as well. Then, the diffusion operator appearing in the right-hand side of the compaction equation (2.3) models the tendency of the granular material to suppress concentration inhomogeneities. Further, the tensor that involves the volume fraction gradients in the right-hand side of the momentum equation (2.2) is the so-called Korteweg tensor and models the aforementioned interfacial tension. Note that the Korteweg tensor constitutes a non-dissipative component of the granular material’s stress tensor and in the presence of concentration inhomogeneities does not vanish at thermodynamic equilibrium. In fact, Ván (Reference Ván2004) showed that, at thermodynamic equilibrium, the presence of the Korteweg tensor yields that normal and shear stresses are related via a Mohr–Coulomb criterion.
Finally, the coefficient
![]() $\hat{{\it\nu}}_{c}$
is the so-called compaction viscosity, introduced by Baer & Nunziato (Reference Baer and Nunziato1986), and measures the strength of dilatational effects. Indeed, as
$\hat{{\it\nu}}_{c}$
is the so-called compaction viscosity, introduced by Baer & Nunziato (Reference Baer and Nunziato1986), and measures the strength of dilatational effects. Indeed, as
![]() $\hat{{\it\nu}}_{c}\rightarrow \infty$
dilatancy effects become redundant and the compaction equation (2.3) predicts that the volume fraction
$\hat{{\it\nu}}_{c}\rightarrow \infty$
dilatancy effects become redundant and the compaction equation (2.3) predicts that the volume fraction
![]() ${\it\phi}$
is conserved along the streamlines or equivalently that the motion of the granular material is isochoric; thus, the motion of the granular material resembles that of an incompressible fluid-like body (Málek & Rajagopal Reference Málek and Rajagopal2006; Varsakelis & Papalexandris Reference Varsakelis and Papalexandris2015a
).
${\it\phi}$
is conserved along the streamlines or equivalently that the motion of the granular material is isochoric; thus, the motion of the granular material resembles that of an incompressible fluid-like body (Málek & Rajagopal Reference Málek and Rajagopal2006; Varsakelis & Papalexandris Reference Varsakelis and Papalexandris2015a
).
Equations (2.1)–(2.3) share minor differences with other existing continuum mechanical models for the flows of interest. More importantly, as dictated by the principle of phase separation, (Truesdell Reference Truesdell1984), these differences do not stem from the fact that the continuum theory of Papalexandris (Reference Papalexandris2004) utilizes a two-phase framework. Rather, they can be traced to the methodology that each of these models employs for the exploitation of the entropy inequality, e.g. the Coleman–Noll approach, the Müller–Liu approach, the Theory of Irreversible Processes approach, etc., (Wang & Hutter Reference Wang, Hutter, Balmforth and Provenzale2001; Kirchner Reference Kirchner2002).
Besides the compaction equation, an important difference between (2.1)–(2.3), and continuum mechanical models in general, and kinetic theoretical models is the absence of the granular temperature from the former. Although it is possible to introduce it as an additional variable so that quadratic (Bagnold) stresses are modelled, this is not a necessity but rather a convenience since such nonlinear effects can be accounted for via theories for second-order fluids, (Savage Reference Savage1979).
2.1 Constitutive expressions and closure relations
In order to close (2.1)–(2.3), suitable expressions for the terms
![]() $\hat{p}^{v}$
,
$\hat{p}^{v}$
,
![]() $\hat{{\bf\tau}}$
,
$\hat{{\bf\tau}}$
,
![]() $\hat{{\it\beta}}$
and
$\hat{{\it\beta}}$
and
![]() $\hat{{\it\Gamma}}$
have to be employed. For the irreversible isotropic pressure
$\hat{{\it\Gamma}}$
have to be employed. For the irreversible isotropic pressure
![]() $\hat{p}^{v}$
and the deviator
$\hat{p}^{v}$
and the deviator
![]() $\hat{{\bf\tau}}$
we opt for the constitutive expressions derived from the
$\hat{{\bf\tau}}$
we opt for the constitutive expressions derived from the
![]() ${\it\mu}(I)$
-rheology. This is a phenomenological rheology law that combines a fluid-like, rate-dependent approach with a yield criterion. It is consistent with dimensional analysis and its predictions compare favourably against experimental measurements in a multitude of configurations; see, for example, MiDi (Reference MiDi2004), Jop et al. (Reference Jop, Forterre and Pouliquen2006) as well as the more recent review article of Forterre & Pouliquen (Reference Forterre and Pouliquen2008). Herein, we employ the three-dimensional extension of the
${\it\mu}(I)$
-rheology. This is a phenomenological rheology law that combines a fluid-like, rate-dependent approach with a yield criterion. It is consistent with dimensional analysis and its predictions compare favourably against experimental measurements in a multitude of configurations; see, for example, MiDi (Reference MiDi2004), Jop et al. (Reference Jop, Forterre and Pouliquen2006) as well as the more recent review article of Forterre & Pouliquen (Reference Forterre and Pouliquen2008). Herein, we employ the three-dimensional extension of the
![]() ${\it\mu}(I)$
-rheology law of Jop et al. (Reference Jop, Forterre and Pouliquen2006) in the volume fraction representation. Then, the constitutive relations for
${\it\mu}(I)$
-rheology law of Jop et al. (Reference Jop, Forterre and Pouliquen2006) in the volume fraction representation. Then, the constitutive relations for
![]() $\hat{p}^{v}$
and
$\hat{p}^{v}$
and
![]() $\hat{{\bf\tau}}$
read,
$\hat{{\bf\tau}}$
read,
In the above equations,
![]() $\dot{{\bf\gamma}}=(\boldsymbol{{\rm\nabla}}\boldsymbol{u}+\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\text{T}})-(2/3)\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}$
is the deviator of the strain-rate tensor whilst
$\dot{{\bf\gamma}}=(\boldsymbol{{\rm\nabla}}\boldsymbol{u}+\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{\text{T}})-(2/3)\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}$
is the deviator of the strain-rate tensor whilst
![]() $|\hat{\dot{{\bf\gamma}}}|=\sqrt{(\hat{\dot{{\it\gamma}}}_{ij}\hat{\dot{{\it\gamma}}}_{ij})/2}$
designates its second invariant (written in the Einstein summation convention). Also,
$|\hat{\dot{{\bf\gamma}}}|=\sqrt{(\hat{\dot{{\it\gamma}}}_{ij}\hat{\dot{{\it\gamma}}}_{ij})/2}$
designates its second invariant (written in the Einstein summation convention). Also,
![]() $I=|\hat{\dot{{\bf\gamma}}}|\hat{d}_{p}/\sqrt{(\hat{p}+\hat{p}^{v})/\hat{{\it\rho}}}$
is the inertial number, with
$I=|\hat{\dot{{\bf\gamma}}}|\hat{d}_{p}/\sqrt{(\hat{p}+\hat{p}^{v})/\hat{{\it\rho}}}$
is the inertial number, with
![]() $\hat{d}_{p}$
standing for the particle diameter. As illustrated by da Cruz et al. (Reference da Cruz, Prochnow, Roux and Chevoir2005),
$\hat{d}_{p}$
standing for the particle diameter. As illustrated by da Cruz et al. (Reference da Cruz, Prochnow, Roux and Chevoir2005),
![]() $I$
describes the ratio between the macroscopic time scale, induced by deformation due to shear, to the inertial time scale associated with the pressure force. Further,
$I$
describes the ratio between the macroscopic time scale, induced by deformation due to shear, to the inertial time scale associated with the pressure force. Further,
![]() ${\it\phi}_{min}$
and
${\it\phi}_{min}$
and
![]() ${\it\phi}_{max}$
stand for the minimum and maximum particle concentration whereas
${\it\phi}_{max}$
stand for the minimum and maximum particle concentration whereas
![]() ${\it\mu}_{1}$
,
${\it\mu}_{1}$
,
![]() ${\it\mu}_{2}$
and
${\it\mu}_{2}$
and
![]() $I_{0}$
are constants whose value is acquired though experimental measurements.
$I_{0}$
are constants whose value is acquired though experimental measurements.
According to (2.5) and (2.6), both
![]() $\hat{p}^{v}$
and
$\hat{p}^{v}$
and
![]() $\hat{{\bf\tau}}$
diverge as
$\hat{{\bf\tau}}$
diverge as
![]() ${\it\phi}\rightarrow {\it\phi}_{max}$
. This divergence describes the jamming transition that grains experience upon attaining their maximum concentration. In other words, in the volume fraction representation, the
${\it\phi}\rightarrow {\it\phi}_{max}$
. This divergence describes the jamming transition that grains experience upon attaining their maximum concentration. In other words, in the volume fraction representation, the
![]() ${\it\mu}(I)$
-rheology gives rise to Krieger–Dougherty type laws for both the normal and shear viscosities. It is also interesting to observe that
${\it\mu}(I)$
-rheology gives rise to Krieger–Dougherty type laws for both the normal and shear viscosities. It is also interesting to observe that
![]() $I$
is a decreasing function of
$I$
is a decreasing function of
![]() ${\it\phi}$
and is maximized at
${\it\phi}$
and is maximized at
![]() ${\it\phi}={\it\phi}_{min}$
with maximum value
${\it\phi}={\it\phi}_{min}$
with maximum value
![]() $I({\it\phi}_{min})=1$
. This inverse correlation describes the fact that an increased concentration should translate into larger frictional effects. Moreover, the value of unity is also not coincidental. The
$I({\it\phi}_{min})=1$
. This inverse correlation describes the fact that an increased concentration should translate into larger frictional effects. Moreover, the value of unity is also not coincidental. The
![]() ${\it\mu}(I)$
-rheology predicts a shear-thickening behaviour through (i) the inverse dependence of the shear stresses on the inertial number
${\it\mu}(I)$
-rheology predicts a shear-thickening behaviour through (i) the inverse dependence of the shear stresses on the inertial number
![]() $I$
, and (ii) the nonlinear dependence of the shear stresses on the shear rate. Therefore, when
$I$
, and (ii) the nonlinear dependence of the shear stresses on the shear rate. Therefore, when
![]() $I=1$
, shear thickening can only happen through the second term whilst for
$I=1$
, shear thickening can only happen through the second term whilst for
![]() $I>1$
, the shear-thickening behaviour is not guaranteed since there is a competition between (i) and (ii). In this respect, the value
$I>1$
, the shear-thickening behaviour is not guaranteed since there is a competition between (i) and (ii). In this respect, the value
![]() $I=1$
is the borderline value upon which the behaviour of the
$I=1$
is the borderline value upon which the behaviour of the
![]() ${\it\mu}(I)$
-rheology changes qualitatively.
${\it\mu}(I)$
-rheology changes qualitatively.
At this point, a comment on the appropriateness of the employed rheology law is relevant. Strictly speaking, the
![]() ${\it\mu}(I)$
-rheology and its incarnations have been developed for and measured in steady granular flows. Consequently, the presumed validity of this law for transient flows constitutes more of an ad hoc postulate than a documented fact. Nevertheless, we stress that the
${\it\mu}(I)$
-rheology and its incarnations have been developed for and measured in steady granular flows. Consequently, the presumed validity of this law for transient flows constitutes more of an ad hoc postulate than a documented fact. Nevertheless, we stress that the
![]() ${\it\mu}(I)$
-rheology has been already exercised in the description of transient flows with a notable success. For instance, Lagrée, Staron & Popinet (Reference Lagrée, Staron and Popinet2011) combined the
${\it\mu}(I)$
-rheology has been already exercised in the description of transient flows with a notable success. For instance, Lagrée, Staron & Popinet (Reference Lagrée, Staron and Popinet2011) combined the
![]() ${\it\mu}(I)$
-rheology with the two-phase Navier–Stokes equations for the investigation of a granular column collapse. The resulting numerical predictions accorded reasonably well with experimental data. Thus, on the premise that the limitations are acknowledged, the utilization of the
${\it\mu}(I)$
-rheology with the two-phase Navier–Stokes equations for the investigation of a granular column collapse. The resulting numerical predictions accorded reasonably well with experimental data. Thus, on the premise that the limitations are acknowledged, the utilization of the
![]() ${\it\mu}(I)$
-rheology for the flows of interest can be justified.
${\it\mu}(I)$
-rheology for the flows of interest can be justified.
It is also important to note that, as mentioned above,
![]() $\hat{p}^{v}$
is in general decomposed into a bulk viscous pressure and a shear-induced pressure. The
$\hat{p}^{v}$
is in general decomposed into a bulk viscous pressure and a shear-induced pressure. The
![]() ${\it\mu}(I)$
-rheology provides expressions only for the latter component since it based on the assumption that the flow is isochoric. A more complete constitutive expression for
${\it\mu}(I)$
-rheology provides expressions only for the latter component since it based on the assumption that the flow is isochoric. A more complete constitutive expression for
![]() $\hat{p}^{v}$
would read,
$\hat{p}^{v}$
would read,
where
![]() $\hat{{\it\zeta}}({\it\phi},|\hat{\dot{{\bf\gamma}}}|)$
is a bulk viscosity coefficient. However, since we are not acquainted with any systematic measurements for
$\hat{{\it\zeta}}({\it\phi},|\hat{\dot{{\bf\gamma}}}|)$
is a bulk viscosity coefficient. However, since we are not acquainted with any systematic measurements for
![]() $\hat{{\it\zeta}}({\it\phi},|\hat{\dot{{\bf\gamma}}}|)$
, we will assume that, for the flows of interest,
$\hat{{\it\zeta}}({\it\phi},|\hat{\dot{{\bf\gamma}}}|)$
, we will assume that, for the flows of interest,
which practically amounts to invoking a Stokes-type hypothesis.
For the intergranular stress
![]() $\hat{{\it\beta}}$
, we adopt the empirical correlation of Powers, Stewart & Krier (Reference Powers, Stewart and Krier1989) which is based on the experimental measurements of Elban & Chiarito (Reference Elban and Chiarito1986). This correlation assumes the following form,
$\hat{{\it\beta}}$
, we adopt the empirical correlation of Powers, Stewart & Krier (Reference Powers, Stewart and Krier1989) which is based on the experimental measurements of Elban & Chiarito (Reference Elban and Chiarito1986). This correlation assumes the following form,
Here,
![]() $\hat{k}_{1}$
is a strictly positive, material dependent, constant. Equation (2.9) is clearly a monotonically increasing, convex function of the volume fraction. As mentioned in Powers et al. (Reference Powers, Stewart and Krier1989), the monotonicity reflects the fact that, as the particle concentration and thus the intergranular stress increase, an increased hydrostatic pressure is required to offset
$\hat{k}_{1}$
is a strictly positive, material dependent, constant. Equation (2.9) is clearly a monotonically increasing, convex function of the volume fraction. As mentioned in Powers et al. (Reference Powers, Stewart and Krier1989), the monotonicity reflects the fact that, as the particle concentration and thus the intergranular stress increase, an increased hydrostatic pressure is required to offset
![]() $\hat{{\it\beta}}$
; see also the earlier discussion of Carroll & Holt (Reference Carroll and Holt1972). Convexity, on the other hand, is welcomed from the mathematical point of view because it ameliorates technical difficulties associated with the establishment of the existence of solutions, (Varsakelis & Papalexandris Reference Varsakelis and Papalexandris2014a
).
$\hat{{\it\beta}}$
; see also the earlier discussion of Carroll & Holt (Reference Carroll and Holt1972). Convexity, on the other hand, is welcomed from the mathematical point of view because it ameliorates technical difficulties associated with the establishment of the existence of solutions, (Varsakelis & Papalexandris Reference Varsakelis and Papalexandris2014a
).
As regards the equilibrated stress coefficient
![]() $\hat{{\it\Gamma}}$
, we utilize a
$\hat{{\it\Gamma}}$
, we utilize a
![]() ${\it\phi}$
-weighted variation of the functional relation proposed by Passman et al. (Reference Passman, Nunziato and Bailey1986),
${\it\phi}$
-weighted variation of the functional relation proposed by Passman et al. (Reference Passman, Nunziato and Bailey1986),
where
![]() $\hat{k}$
is a material-dependent, positive constant. Equation (2.10) represents a form of Krieger–Dougherty type relation and, as such, diverges to infinity as
$\hat{k}$
is a material-dependent, positive constant. Equation (2.10) represents a form of Krieger–Dougherty type relation and, as such, diverges to infinity as
![]() ${\it\phi}\rightarrow {\it\phi}_{max}$
but additionally converges to zero as
${\it\phi}\rightarrow {\it\phi}_{max}$
but additionally converges to zero as
![]() ${\it\phi}\rightarrow 0$
. Passman et al. (Reference Passman, Nunziato and Bailey1986), who based their selection on the experimental measurements of Savage (Reference Savage1979), argued that the divergence at the maximum concentration is consistent with the behaviour of (2.5) and (2.6) at this limit.
${\it\phi}\rightarrow 0$
. Passman et al. (Reference Passman, Nunziato and Bailey1986), who based their selection on the experimental measurements of Savage (Reference Savage1979), argued that the divergence at the maximum concentration is consistent with the behaviour of (2.5) and (2.6) at this limit.
The last quantity that needs to be determined is the compaction viscosity
![]() $\hat{{\it\nu}}_{c}$
. This is somewhat problematic because, as remarked by Powers, Stewart & Krier (Reference Powers, Stewart and Krier1990) and much later by Lowe & Greenaway (Reference Lowe and Greenaway2005), reliable empirical correlations for
$\hat{{\it\nu}}_{c}$
. This is somewhat problematic because, as remarked by Powers, Stewart & Krier (Reference Powers, Stewart and Krier1990) and much later by Lowe & Greenaway (Reference Lowe and Greenaway2005), reliable empirical correlations for
![]() $\hat{{\it\nu}}_{c}$
are not available in the literature. In the absence of any further guidance, we adopt the heuristic analysis of Baer & Nunziato (Reference Baer and Nunziato1986), and assume that
$\hat{{\it\nu}}_{c}$
are not available in the literature. In the absence of any further guidance, we adopt the heuristic analysis of Baer & Nunziato (Reference Baer and Nunziato1986), and assume that
![]() $\hat{{\it\nu}}_{c}$
can be approximated by a constant.
$\hat{{\it\nu}}_{c}$
can be approximated by a constant.
2.2 Non-dimensionalisation and base-flow profile
In a plane, unidirectional Couette flow, the granular material is placed between two infinite parallel planes, in the
![]() $\hat{x}$
–
$\hat{x}$
–
![]() ${\hat{y}}$
Cartesian plane, that are kept at a constant distance
${\hat{y}}$
Cartesian plane, that are kept at a constant distance
![]() ${\hat{H}}$
(Couette gap). Further, the line
${\hat{H}}$
(Couette gap). Further, the line
![]() ${\hat{y}}=0$
is assumed to coincide with the lower plane. The upper plane is presumed to move at a constant velocity
${\hat{y}}=0$
is assumed to coincide with the lower plane. The upper plane is presumed to move at a constant velocity
![]() $\hat{U} _{w}>0$
in the
$\hat{U} _{w}>0$
in the
![]() $\hat{x}$
-direction.
$\hat{x}$
-direction.
In the context of a linear stability analysis, it is advantageous to utilize the non-dimensional form of the governing equations. For this, we first determine the (dimensional) reference values that will be denoted with the subscript ‘
![]() $r$
’.
$r$
’.
As is typically the case in the study of Couette flows, the reference velocity
![]() $\hat{u} _{r}$
is taken equal to the wall velocity
$\hat{u} _{r}$
is taken equal to the wall velocity
![]() $\hat{U} _{w}$
. However, due to the explicit presence of the particle diameter
$\hat{U} _{w}$
. However, due to the explicit presence of the particle diameter
![]() $\hat{d}_{p}$
in the expressions for the deviator and the irreversible isotropic pressure, there is an ambiguity in the choice of the reference length. Herein, we employ the Couette gap
$\hat{d}_{p}$
in the expressions for the deviator and the irreversible isotropic pressure, there is an ambiguity in the choice of the reference length. Herein, we employ the Couette gap
![]() ${\hat{H}}$
as the reference length
${\hat{H}}$
as the reference length
![]() $\hat{L}_{r}$
. With these choices, velocity vectors, length vectors, and time are non-dimensionalised as follows,
$\hat{L}_{r}$
. With these choices, velocity vectors, length vectors, and time are non-dimensionalised as follows,
The reference values for the granular density and the pressure
![]() $\hat{p}$
are taken equal to
$\hat{p}$
are taken equal to
![]() $\hat{{\it\rho}}_{r}=\hat{{\it\rho}}$
,
$\hat{{\it\rho}}_{r}=\hat{{\it\rho}}$
,
![]() $\hat{p}_{r}=\hat{{\it\rho}}_{r}\hat{u} _{r}^{2}$
hence the non-dimensional density and pressure read,
$\hat{p}_{r}=\hat{{\it\rho}}_{r}\hat{u} _{r}^{2}$
hence the non-dimensional density and pressure read,
As regards
![]() $\hat{{\it\beta}}$
and
$\hat{{\it\beta}}$
and
![]() $\hat{{\it\Gamma}}$
, based on the order-of-magnitude analysis of Varsakelis & Papalexandris (Reference Varsakelis and Papalexandris2011), we non-dimensionalise them with respect to
$\hat{{\it\Gamma}}$
, based on the order-of-magnitude analysis of Varsakelis & Papalexandris (Reference Varsakelis and Papalexandris2011), we non-dimensionalise them with respect to
![]() $\hat{{\it\rho}}_{r}\hat{u} _{r}^{2}$
and
$\hat{{\it\rho}}_{r}\hat{u} _{r}^{2}$
and
![]() $\hat{{\it\rho}}_{r}\hat{u} _{r}\hat{L}_{r}^{2}$
, respectively. Then,
$\hat{{\it\rho}}_{r}\hat{u} _{r}\hat{L}_{r}^{2}$
, respectively. Then,
Subsequently, by introducing the expressions for
![]() $\hat{p}^{v}$
,
$\hat{p}^{v}$
,
![]() $\hat{{\bf\tau}}$
$\hat{{\bf\tau}}$
![]() $\hat{{\it\beta}}$
and
$\hat{{\it\beta}}$
and
![]() ${\it\Gamma}$
to (2.1)–(2.3), and by performing the above non-dimensionalisation, we arrive at the non-dimensional form of the governing equations which reads
${\it\Gamma}$
to (2.1)–(2.3), and by performing the above non-dimensionalisation, we arrive at the non-dimensional form of the governing equations which reads
 $$\begin{eqnarray}\displaystyle \frac{\partial {\it\phi}\boldsymbol{u}}{\partial t}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\phi}\boldsymbol{u}\boldsymbol{u})+\boldsymbol{{\rm\nabla}}(p{\it\phi}) & = & \displaystyle -\boldsymbol{{\rm\nabla}}\left(\frac{|\dot{{\bf\gamma}}|^{2}{d_{p}}^{2}}{I^{2}}{\it\phi}\right)+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\left(\frac{{\it\mu}({\it\phi})|\dot{{\bf\gamma}}|{d_{p}}^{2}}{I^{2}}\dot{{\bf\gamma}}{\it\phi}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\left(\frac{k_{2}{\it\phi}}{({\it\phi}_{max}-{\it\phi})^{2}}\boldsymbol{{\rm\nabla}}{\it\phi}\boldsymbol{{\rm\nabla}}{\it\phi}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial {\it\phi}\boldsymbol{u}}{\partial t}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\phi}\boldsymbol{u}\boldsymbol{u})+\boldsymbol{{\rm\nabla}}(p{\it\phi}) & = & \displaystyle -\boldsymbol{{\rm\nabla}}\left(\frac{|\dot{{\bf\gamma}}|^{2}{d_{p}}^{2}}{I^{2}}{\it\phi}\right)+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\left(\frac{{\it\mu}({\it\phi})|\dot{{\bf\gamma}}|{d_{p}}^{2}}{I^{2}}\dot{{\bf\gamma}}{\it\phi}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\left(\frac{k_{2}{\it\phi}}{({\it\phi}_{max}-{\it\phi})^{2}}\boldsymbol{{\rm\nabla}}{\it\phi}\boldsymbol{{\rm\nabla}}{\it\phi}\right),\end{eqnarray}$$
Equations (2.14)–(2.16) have four dimensionless groups, namely
![]() $d_{p}$
,
$d_{p}$
,
![]() $k_{1}$
,
$k_{1}$
,
![]() $k_{2}$
and
$k_{2}$
and
![]() $Re_{c}$
. The quantity
$Re_{c}$
. The quantity
![]() $d_{p}$
describes the ratio between the particle diameter and the height of the domain. We remark that the validity of the continuum hypothesis requires that
$d_{p}$
describes the ratio between the particle diameter and the height of the domain. We remark that the validity of the continuum hypothesis requires that
![]() $d_{p}\sim O(10^{-k})$
, for some
$d_{p}\sim O(10^{-k})$
, for some
![]() $k\in \mathbb{Z}$
, however, the exact value of
$k\in \mathbb{Z}$
, however, the exact value of
![]() $k$
is problem dependent, (Hutter & Rajagopal Reference Hutter and Rajagopal1994). Further,
$k$
is problem dependent, (Hutter & Rajagopal Reference Hutter and Rajagopal1994). Further,
![]() $k_{1}$
and
$k_{1}$
and
![]() $k_{2}$
measure the ratio between compaction to inertia effects and between intergranular surface variation to inertia effects. Finally,
$k_{2}$
measure the ratio between compaction to inertia effects and between intergranular surface variation to inertia effects. Finally,
![]() $Re_{c}$
is the ‘compaction Reynolds number’ which measures the ratio of viscous forces, due to compaction, to inertia.
$Re_{c}$
is the ‘compaction Reynolds number’ which measures the ratio of viscous forces, due to compaction, to inertia.
Next, we advert to the choice of the base-flow profile. We invoke the time-independent, quasi-parallel flow assumption and search for profiles of the following form,
Note that, although it is sufficient to impose that the base-flow is one-dimensional, the quasi-parallel flow assumption is more general. According to both experimental measurements and numerical predictions, expounded in Forterre & Pouliquen (Reference Forterre and Pouliquen2008), a base-flow profile that conforms with our postulates reads,
It is straightforward to verify that the above relations constitute solutions to the non-dimensionalised (2.14)–(2.16).
Finally, the governing equations have to be endowed with suitable boundary conditions which, due to the quasi-parallel flow postulate, are required only for the upper and the lower planes. For the sake of simplicity, and keeping in mind the restrictions that arise from such a choice, a no-slip boundary condition is imposed on the granular velocity at both planes
![]() $u(0)=(0),v(0)=0$
and
$u(0)=(0),v(0)=0$
and
![]() $u(1)=1,v(1)=0$
.
$u(1)=1,v(1)=0$
.
For the volume fraction, we first note that, in weakly non-local theories that involve gradients as internal variables such as the one that (2.1)–(2.3) have been based upon, the prescription of boundary conditions cannot be circumvented, unless the flow under consideration enjoys multiple symmetries, (Massoudi Reference Massoudi2007). For the problem at hand, the presence of the second-order differential operator in the right-hand side of the compaction equation in conjunction with the quasi-parallel flow postulate, imply that two boundary conditions are needed for the volume fraction as well. Following Wang & Hutter (Reference Wang and Hutter1999a
,Reference Wang and Hutter
b
), a Dirichlet boundary condition is assigned to the volume fraction, i.e.
![]() ${\it\phi}(0)={\it\phi}(1)={\it\phi}^{0}$
. A plausible rationale of physical origin in favour of this choice is offered by Massoudi & Mehrabadi (Reference Massoudi and Mehrabadi2001) and Massoudi & Phuoc (Reference Massoudi and Phuoc2005).
${\it\phi}(0)={\it\phi}(1)={\it\phi}^{0}$
. A plausible rationale of physical origin in favour of this choice is offered by Massoudi & Mehrabadi (Reference Massoudi and Mehrabadi2001) and Massoudi & Phuoc (Reference Massoudi and Phuoc2005).
As regards the pressure
![]() $p$
, a comment is in order. For general flowing conditions, e.g. transient, multi-dimensional flows, boundary conditions for the pressure are inherited from the momentum equation (2.14) as dictated by the Helmholtz decomposition and Ladyzhenskaya’s decomposition theorem, (Ladyzhenskaya & Solonnikov Reference Ladyzhenskaya and Solonnikov1978; Lions Reference Lions1996; Chorin & Marsden Reference Chorin and Marsden2000). For such cases, the pressure
$p$
, a comment is in order. For general flowing conditions, e.g. transient, multi-dimensional flows, boundary conditions for the pressure are inherited from the momentum equation (2.14) as dictated by the Helmholtz decomposition and Ladyzhenskaya’s decomposition theorem, (Ladyzhenskaya & Solonnikov Reference Ladyzhenskaya and Solonnikov1978; Lions Reference Lions1996; Chorin & Marsden Reference Chorin and Marsden2000). For such cases, the pressure
![]() $p$
is computed as the solution to an appropriate Neumann problem by taking the divergence of the momentum equation and upon combination with the continuity equation, Varsakelis & Papalexandris (Reference Varsakelis and Papalexandris2014b
), Varsakelis, Monsorno & Papalexandris (Reference Varsakelis, Monsorno and Papalexandris2015). This is actually the exact analogue for the computation of the pressure field in the variable density Navier–Stokes equations. Importantly, as shown in Ladyzhenskaya (Reference Ladyzhenskaya1969) for the Navier–Stokes equations and in Varsakelis & Papalexandris (Reference Varsakelis and Papalexandris2010) for the equations at hand, imposing additional boundary conditions to the pressure field, results in an overdetermined problem. For the particular case at hand, however, the prescription of boundary conditions is trivial since
$p$
is computed as the solution to an appropriate Neumann problem by taking the divergence of the momentum equation and upon combination with the continuity equation, Varsakelis & Papalexandris (Reference Varsakelis and Papalexandris2014b
), Varsakelis, Monsorno & Papalexandris (Reference Varsakelis, Monsorno and Papalexandris2015). This is actually the exact analogue for the computation of the pressure field in the variable density Navier–Stokes equations. Importantly, as shown in Ladyzhenskaya (Reference Ladyzhenskaya1969) for the Navier–Stokes equations and in Varsakelis & Papalexandris (Reference Varsakelis and Papalexandris2010) for the equations at hand, imposing additional boundary conditions to the pressure field, results in an overdetermined problem. For the particular case at hand, however, the prescription of boundary conditions is trivial since
![]() $p$
is uniform throughout the domain; assuming that
$p$
is uniform throughout the domain; assuming that
![]() $p$
is continuous at the boundary, then a zero Neumann as well as the Dirichlet condition
$p$
is continuous at the boundary, then a zero Neumann as well as the Dirichlet condition
![]() $p(0)$
or
$p(0)$
or
![]() $p(1)=k_{1}({\it\phi}^{0}/(2-{\it\phi}^{0}))^{2}\log (1/(1-{\it\phi}^{0}))$
work equally well.
$p(1)=k_{1}({\it\phi}^{0}/(2-{\it\phi}^{0}))^{2}\log (1/(1-{\it\phi}^{0}))$
work equally well.
Additionally, we assume that the base-flow profiles
![]() $\boldsymbol{u}^{0}$
and
$\boldsymbol{u}^{0}$
and
![]() ${\it\phi}^{0}$
satisfy the same boundary conditions as
${\it\phi}^{0}$
satisfy the same boundary conditions as
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() ${\it\phi}$
, respectively,
${\it\phi}$
, respectively,
3 Linear stability analysis
In this section, we investigate the stability of the base flow, given by (2.18)–(2.21), to infinitesimal perturbations. We formally seek for solutions that can be expressed as the sum of the base-flow profile plus a disturbance (denoted by the superscript ‘1’), i.e.
Under the assumption that disturbances are small, the solutions can be searched from the governing (2.14)–(2.16), linearized with respect to the base-flow profile (2.18)–(2.21).
Although the linearization procedure is standard, the resulting expressions of the linearized governing equations are too lengthy and cumbersome to reproduce here without distorting the continuity of reading. For this reason, and for the sake of completeness, we have opted to include them in the appendix A of this paper.
The formal validity of the above linearization presumes that disturbances are small (infinitesimal) but of otherwise arbitrary form. In the present study, we opt for a normal mode analysis, (Drazin & Reid Reference Drazin and Reid2011). With this ansatz, disturbances are given by the following expressions,
Here,
![]() $\overline{u}(y)$
,
$\overline{u}(y)$
,
![]() $\overline{v}(y)$
,
$\overline{v}(y)$
,
![]() $\overline{p}(y)$
,
$\overline{p}(y)$
,
![]() $\overline{{\it\phi}}(y)$
are the amplitudes of the disturbances. Further,
$\overline{{\it\phi}}(y)$
are the amplitudes of the disturbances. Further,
![]() ${\it\alpha}$
is the prescribed wavenumber and
${\it\alpha}$
is the prescribed wavenumber and
![]() $c=c_{R}+\text{i}c_{I}$
is the complex frequency. Unstable modes are associated with frequencies
$c=c_{R}+\text{i}c_{I}$
is the complex frequency. Unstable modes are associated with frequencies
![]() $c$
such that
$c$
such that
![]() $c_{I}>0$
.
$c_{I}>0$
.
Upon substitution of (3.5) to the linearized governing equations (see appendix A) and following a series of tedious, albeit straightforward, calculations we arrive at the following set of equations that govern the evolution of the disturbances,
In the above equations,
![]() $\text{d}^{i}\cdot /\text{d}y^{i}$
stands for the
$\text{d}^{i}\cdot /\text{d}y^{i}$
stands for the
![]() $i$
th-order derivative with respect to
$i$
th-order derivative with respect to
![]() $y$
with the usual notation convention
$y$
with the usual notation convention
![]() $\text{d}^{0}f/\text{d}y^{0}\equiv f$
, for every function
$\text{d}^{0}f/\text{d}y^{0}\equiv f$
, for every function
![]() $f$
. The coefficients
$f$
. The coefficients
![]() $A^{\overline{{\it\phi}}}$
,
$A^{\overline{{\it\phi}}}$
,
![]() $A^{\overline{u}}$
,
$A^{\overline{u}}$
,
![]() $A^{\overline{v}}$
,
$A^{\overline{v}}$
,
![]() $B^{\overline{{\it\phi}}}$
,
$B^{\overline{{\it\phi}}}$
,
![]() $B^{\overline{u}}$
and
$B^{\overline{u}}$
and
![]() $B^{\overline{v}}$
are
$B^{\overline{v}}$
are
![]() $4\times 3$
nonlinear algebraic operators that depend the base-flow profiles and the dimensionless groups
$4\times 3$
nonlinear algebraic operators that depend the base-flow profiles and the dimensionless groups
![]() $k_{1}$
,
$k_{1}$
,
![]() $k_{2}$
,
$k_{2}$
,
![]() $Re_{c}$
and
$Re_{c}$
and
![]() $d_{p}$
.
$d_{p}$
.
This is a generalized eigenvalue problem with
![]() $c$
being the eigenvalue and (
$c$
being the eigenvalue and (
![]() $\overline{{\it\phi}}$
,
$\overline{{\it\phi}}$
,
![]() $\overline{u}$
,
$\overline{u}$
,
![]() $\overline{v}$
) the eigenvector. The analytic expression of the generalized eigenvalue problem is reported in the appendix B of this paper.
$\overline{v}$
) the eigenvector. The analytic expression of the generalized eigenvalue problem is reported in the appendix B of this paper.
It is interesting to observe that the amplitude of the pressure’s disturbance
![]() $\overline{p}$
does not appear in (3.6). The reason for performing this decoupling is that the governing equations of the amplitudes of the disturbances are not of the same order with respect to all variables. They are second order with respect to
$\overline{p}$
does not appear in (3.6). The reason for performing this decoupling is that the governing equations of the amplitudes of the disturbances are not of the same order with respect to all variables. They are second order with respect to
![]() $\overline{{\it\phi}}$
,
$\overline{{\it\phi}}$
,
![]() $\overline{u}$
and
$\overline{u}$
and
![]() $\overline{v}$
, but only first order with respect to
$\overline{v}$
, but only first order with respect to
![]() $\overline{p}$
. This is exactly the same rationale that is employed in the derivation of the Orr–Sommerfeld equation for the Navier–Stokes equations which also does not explicitly contain the pressure term. Actually, in view of the compaction equation, it is also possible to remove the
$\overline{p}$
. This is exactly the same rationale that is employed in the derivation of the Orr–Sommerfeld equation for the Navier–Stokes equations which also does not explicitly contain the pressure term. Actually, in view of the compaction equation, it is also possible to remove the
![]() $\overline{{\it\phi}}$
as well and thus end up with a novel system with respect to
$\overline{{\it\phi}}$
as well and thus end up with a novel system with respect to
![]() $\overline{u}$
and
$\overline{u}$
and
![]() $\overline{v}$
. However, in this case, the resulting eigenvalue system is quadratic and thus extra caution should be exercised in its approximation.
$\overline{v}$
. However, in this case, the resulting eigenvalue system is quadratic and thus extra caution should be exercised in its approximation.
In the course of our study, we have solved all three eigenvalue problems. According to our numerical experiments, however, (3.6) was the one for which the numerical method that we employed, outlined in the next subsection, was more robust. The same experiments showed that the quadratic eigenvalue problem was the most problematic as the resulting matrices turned out to be very badly conditioned. Although a rigorous mathematical proof for this behaviour is not at our disposal, we may attribute this deterioration to presence of poles
![]() $1/(\overline{{\it\phi}}-{\it\phi}_{j})^{n}$
,
$1/(\overline{{\it\phi}}-{\it\phi}_{j})^{n}$
,
![]() $n\in \mathbb{N}$
that when coupled with the expression that connects
$n\in \mathbb{N}$
that when coupled with the expression that connects
![]() $\overline{{\it\phi}}$
with
$\overline{{\it\phi}}$
with
![]() $\overline{u}$
and
$\overline{u}$
and
![]() $\overline{v}$
, engender quite convoluted expressions that may be singular.
$\overline{v}$
, engender quite convoluted expressions that may be singular.
The boundary conditions for the amplitude of the disturbances follow directly from the assumption that the boundary conditions for the base-flow variables are identical to those for the total flow variables. Consequently, the disturbances are required to approach zero at both boundaries, that is,
3.1 Numerical method
Due to the complexity of the generalized eigenvalue problem (3.6), the analytical computation of the spectrum and the eigenfunctions is a formidable task. For this reason, we have resorted to the numerical approximation of these quantities. The voluminous literature on the numerical aspects of the Orr–Sommerfeld equation, arising in the study of the linear stability of the Navier–Stokes equations, corroborates that the accurate computation of the spectra and the eigenfunctions requires a judiciously chosen numerical method, (Orszag Reference Orszag1971; Huang & Sloan Reference Huang and Sloan1994; Dongarra, Straughanb & Walker Reference Dongarra, Straughanb and Walker1996). Thus, since the eigenvalue problem (3.6) is markedly more complex than the one induced by the Orr–Sommerfeld equation, its numerical approximation requires an elaborate numerical scheme as well.
In the present study, the generalized eigenvalue problem (3.6), along with the boundary conditions (3.7) and (3.8), is approximated via a Chebyshev collocation method. A detailed description of this algorithm is given in Varsakelis & Papalexandris (Reference Varsakelis and Papalexandris2015b ) and herein only its flowchart is presented.
-
(i) Primitive algebraic functions, i.e. the components of the base flow and the disturbances, are approximated via Chebyshev interpolation or equivalently by expansion in series of Chebyshev polynomials.
-
(ii) Algebraic differential operators are computed via applying a pseudo-spectral collocation method to the Chebyshev representation of the various quantities.
-
(iii) Boundary conditions are evaluated with the help of ghost cells to maintain the structure of the approximation throughout the computational domain.
-
(iv) The resulting discretized eigenvalue problem is computed via the QR-decomposition. The computation of the eigenvalues and the corresponding eigenvectors is performed in a series of adapted (denser) grids so that spurious modes are excluded and higher accuracy is achieved.
-
(v) All Chebyshev approximations require a very strict convergence criterion, close to machine precision.
All computations have been carried with the Chebfun computational suite, (Hale & Trefethen Reference Hale and Trefethen2014). The robustness and accuracy of Chebfun have been assessed in a multitude of cases, including the computation of the spectrum of the Orr–Sommerfeld operator.
4 Numerical results
We choose to investigate the Couette flow of dry monodisperse sand. The grains are assumed to be spherical with particle diameter
![]() $\hat{d}_{p}=0.001~\text{m}$
and density
$\hat{d}_{p}=0.001~\text{m}$
and density
![]() $\hat{{\it\rho}}=2500~\text{kg}~\text{m}^{-3}$
. As regards the constants
$\hat{{\it\rho}}=2500~\text{kg}~\text{m}^{-3}$
. As regards the constants
![]() $\hat{k}_{1}$
and
$\hat{k}_{1}$
and
![]() $\hat{k}_{2}$
appearing in (2.9) and (2.10), guided by the numerical study of Varsakelis & Papalexandris (Reference Varsakelis and Papalexandris2010) who computed the stresses acting on a granular material at equilibrium, we set
$\hat{k}_{2}$
appearing in (2.9) and (2.10), guided by the numerical study of Varsakelis & Papalexandris (Reference Varsakelis and Papalexandris2010) who computed the stresses acting on a granular material at equilibrium, we set
![]() $\hat{k}_{1}=0.1~\text{kg}~\text{m}^{-1}~\text{s}^{-2}$
, and
$\hat{k}_{1}=0.1~\text{kg}~\text{m}^{-1}~\text{s}^{-2}$
, and
![]() $\hat{k}_{2}=0.1~\text{kg}~\text{m}~\text{s}^{-2}$
. Additionally, following Jop et al. (Reference Jop, Forterre and Pouliquen2006), we set
$\hat{k}_{2}=0.1~\text{kg}~\text{m}~\text{s}^{-2}$
. Additionally, following Jop et al. (Reference Jop, Forterre and Pouliquen2006), we set
![]() ${\it\mu}_{1}=0.38$
,
${\it\mu}_{1}=0.38$
,
![]() ${\it\mu}_{2}=0.26$
and
${\it\mu}_{2}=0.26$
and
![]() $I_{0}=0.279$
. For the maximum and the minimum concentrations we fix
$I_{0}=0.279$
. For the maximum and the minimum concentrations we fix
![]() ${\it\phi}_{max}=0.65$
and
${\it\phi}_{max}=0.65$
and
![]() ${\it\phi}_{min}=0.15$
. Finally, based on the order-of-magnitude arguments of Kapila et al. (Reference Kapila, Menikoff, Bdzil, Son and Stewart2001), the compaction viscosity is set equal to
${\it\phi}_{min}=0.15$
. Finally, based on the order-of-magnitude arguments of Kapila et al. (Reference Kapila, Menikoff, Bdzil, Son and Stewart2001), the compaction viscosity is set equal to
![]() $\hat{{\it\nu}}_{c}=10~\text{kg}~\text{m}^{-1}~\text{s}^{-1}$
.
$\hat{{\it\nu}}_{c}=10~\text{kg}~\text{m}^{-1}~\text{s}^{-1}$
.
For our reference configuration, we set the initial concentration
![]() ${\it\phi}^{0}=0.55$
, i.e. 15 % less than the maximum packing. Further, we fix the Couette gap to
${\it\phi}^{0}=0.55$
, i.e. 15 % less than the maximum packing. Further, we fix the Couette gap to
![]() ${\hat{H}}_{ref}=0.1~\text{m}$
and the wall velocity to
${\hat{H}}_{ref}=0.1~\text{m}$
and the wall velocity to
![]() $\hat{U} _{w,ref}=0.01~\text{m}~\text{s}^{-1}$
. The initial dimensional wavenumber is set equal to
$\hat{U} _{w,ref}=0.01~\text{m}~\text{s}^{-1}$
. The initial dimensional wavenumber is set equal to
![]() $\hat{{\it\alpha}}=1/{\hat{H}}$
, so that its dimensionless value
$\hat{{\it\alpha}}=1/{\hat{H}}$
, so that its dimensionless value
![]() ${\it\alpha}$
is unity. Accordingly, the dimensionless groups that the equations depend upon, assume the values
${\it\alpha}$
is unity. Accordingly, the dimensionless groups that the equations depend upon, assume the values
![]() $d_{p}=0.01$
,
$d_{p}=0.01$
,
![]() $k_{1}=0.4$
,
$k_{1}=0.4$
,
![]() $k_{2}=0.04$
and
$k_{2}=0.04$
and
![]() $Re_{c}=0.25$
.
$Re_{c}=0.25$
.
Prior to proceeding to the presentation and discussion of the numerical results, a comment on the magnitude of
![]() ${\it\alpha}$
is pertinent. It should be reiterated that continuum models for the flows of interest are subject to scale limitations stemming from the continuum hypothesis, i.e. their validity is limited to scales larger than the grain diameter. Consequently, very small, and equally very large, wavelengths cannot be appropriately accounted for in the framework of this study.
${\it\alpha}$
is pertinent. It should be reiterated that continuum models for the flows of interest are subject to scale limitations stemming from the continuum hypothesis, i.e. their validity is limited to scales larger than the grain diameter. Consequently, very small, and equally very large, wavelengths cannot be appropriately accounted for in the framework of this study.
Figure 1 portrays the growth rate
![]() ${\it\sigma}=\max \{c_{I}\}$
against the wavenumber
${\it\sigma}=\max \{c_{I}\}$
against the wavenumber
![]() ${\it\alpha}$
for the reference configuration. The growth rate remains negative and thus the flow is predicted to be linearly stable for all wavenumbers considered herein. Moreover,
${\it\alpha}$
for the reference configuration. The growth rate remains negative and thus the flow is predicted to be linearly stable for all wavenumbers considered herein. Moreover,
![]() ${\it\sigma}$
is found to positively correlate with
${\it\sigma}$
is found to positively correlate with
![]() ${\it\alpha}$
and following a rapid increase, its rate of change reduces significantly so that it remains majorized by the line
${\it\alpha}$
and following a rapid increase, its rate of change reduces significantly so that it remains majorized by the line
![]() ${\it\sigma}=-0.3$
. Still, we stress that the line
${\it\sigma}=-0.3$
. Still, we stress that the line
![]() ${\it\sigma}=-0.3$
does not constitute an asymptote because
${\it\sigma}=-0.3$
does not constitute an asymptote because
![]() ${\it\sigma}$
is not constant but continues to increase monotonically with
${\it\sigma}$
is not constant but continues to increase monotonically with
![]() ${\it\alpha}$
, albeit very slowly. It is, therefore, conceivable that, for large enough
${\it\alpha}$
, albeit very slowly. It is, therefore, conceivable that, for large enough
![]() ${\it\alpha}$
where the validity of the model breaks down, an unstable mode appears.
${\it\alpha}$
where the validity of the model breaks down, an unstable mode appears.

Figure 1. Growth rate
![]() ${\it\sigma}$
plotted against the wavenumber
${\it\sigma}$
plotted against the wavenumber
![]() ${\it\alpha}$
for the reference configuration. The superimposed dash-dotted line (— ⋅ —)
${\it\alpha}$
for the reference configuration. The superimposed dash-dotted line (— ⋅ —)
![]() ${\it\sigma}=-0.3$
. The flow is predicted to be linearly stable for all wavenumbers
${\it\sigma}=-0.3$
. The flow is predicted to be linearly stable for all wavenumbers
![]() $0.02\leqslant {\it\alpha}\leqslant 1$
. Further, the growth rate is monotonically increasing with
$0.02\leqslant {\it\alpha}\leqslant 1$
. Further, the growth rate is monotonically increasing with
![]() ${\it\alpha}$
. However, its curve remains beneath the line
${\it\alpha}$
. However, its curve remains beneath the line
![]() ${\it\sigma}=-0.3$
which acts as an upper bound.
${\it\sigma}=-0.3$
which acts as an upper bound.
In order to examine the range of the detected stability, we have carried a series of parametric studies. Although the governing equations (2.14)–(2.16) depend analytically on four dimensionless groups,
![]() $d_{p}$
,
$d_{p}$
,
![]() $k_{1}$
,
$k_{1}$
,
![]() $k_{2}$
and
$k_{2}$
and
![]() $Re_{c}$
, only two degrees of freedom can be modified without changing the material under study; the wall velocity
$Re_{c}$
, only two degrees of freedom can be modified without changing the material under study; the wall velocity
![]() $\hat{U} _{w}$
and the Couette gap
$\hat{U} _{w}$
and the Couette gap
![]() ${\hat{H}}$
, both of which explicitly appear in (3.6). Moreover, the dependence of these dimensionless groups on
${\hat{H}}$
, both of which explicitly appear in (3.6). Moreover, the dependence of these dimensionless groups on
![]() $\hat{U} _{w}$
and
$\hat{U} _{w}$
and
![]() ${\hat{H}}$
implies that changes in
${\hat{H}}$
implies that changes in
![]() ${\hat{H}}$
, with other things constant, cannot be always recovered by changes in
${\hat{H}}$
, with other things constant, cannot be always recovered by changes in
![]() $\hat{U} _{w}$
and vice-versa. Consequently, a complete parametric study should examine the effects of both these degrees of freedom. On the other hand, it is well documented that the initial concentration plays a pivotal role in the determination of the stability properties of the flows of interest, (Wang et al.
Reference Wang, Jackson and Sundaresan1996).
$\hat{U} _{w}$
and vice-versa. Consequently, a complete parametric study should examine the effects of both these degrees of freedom. On the other hand, it is well documented that the initial concentration plays a pivotal role in the determination of the stability properties of the flows of interest, (Wang et al.
Reference Wang, Jackson and Sundaresan1996).
In view of the above, in our parametric studies we have examined the effect of modifying the initial concentration
![]() ${\it\phi}^{0}$
, the Couette gap
${\it\phi}^{0}$
, the Couette gap
![]() ${\hat{H}}$
and the wall velocity
${\hat{H}}$
and the wall velocity
![]() $\hat{U} _{w}$
. In particular, we have confined ourselves to the study of two-dimensional parametric studies, so that a dyad drawn from the set
$\hat{U} _{w}$
. In particular, we have confined ourselves to the study of two-dimensional parametric studies, so that a dyad drawn from the set
![]() $\{{\hat{H}},\hat{U} _{w},{\it\phi}^{0}\}$
is modified and the remaining variable maintains its value with respect to the reference configuration.
$\{{\hat{H}},\hat{U} _{w},{\it\phi}^{0}\}$
is modified and the remaining variable maintains its value with respect to the reference configuration.
We note that since
![]() ${\hat{H}}$
and
${\hat{H}}$
and
![]() $\hat{U} _{w}$
have been chosen as reference variables in the non-dimensionalisation of the governing equations, their dimensionless values are equal to unity. In order to continue the presentation of the results in dimensionless form, as is customary in stability analyses, all figures that involve
$\hat{U} _{w}$
have been chosen as reference variables in the non-dimensionalisation of the governing equations, their dimensionless values are equal to unity. In order to continue the presentation of the results in dimensionless form, as is customary in stability analyses, all figures that involve
![]() ${\hat{H}}$
and
${\hat{H}}$
and
![]() $\hat{U} _{w}$
are written with respect to a Couette gap ratio
$\hat{U} _{w}$
are written with respect to a Couette gap ratio
![]() ${\hat{H}}/{\hat{H}}_{ref}$
, and a wall velocity ratio
${\hat{H}}/{\hat{H}}_{ref}$
, and a wall velocity ratio
![]() $\hat{U} _{w}/\hat{U} _{w,ref}$
. Thus, comparison is performed with respect to the reference configuration that has been predicted to be linearly stable.
$\hat{U} _{w}/\hat{U} _{w,ref}$
. Thus, comparison is performed with respect to the reference configuration that has been predicted to be linearly stable.
It is interesting to note that Alam & Nott (Reference Alam and Nott1998) employ
![]() $d_{p}$
as a measure of the Couette gap. There is no difficulty in doing so in our study as well, however, we are not acquainted with any similar representation of the wall velocity. Thus, for the sake of consistency, we have opted to employ the aforementioned ratio variables.
$d_{p}$
as a measure of the Couette gap. There is no difficulty in doing so in our study as well, however, we are not acquainted with any similar representation of the wall velocity. Thus, for the sake of consistency, we have opted to employ the aforementioned ratio variables.
4.1 Parametric study with respect to
 ${\hat{H}}$
and
${\hat{H}}$
and
 ${\it\phi}^{0}$
${\it\phi}^{0}$

Figure 2. Selected growth rates
![]() ${\it\sigma}$
plotted against the Couette gap ratio
${\it\sigma}$
plotted against the Couette gap ratio
![]() ${\hat{H}}/{\hat{H}}_{ref}$
, for various initial concentrations
${\hat{H}}/{\hat{H}}_{ref}$
, for various initial concentrations
![]() ${\it\phi}^{0}$
and for
${\it\phi}^{0}$
and for
![]() ${\it\alpha}=1$
and
${\it\alpha}=1$
and
![]() $\hat{U} _{w}=\hat{U} _{w,ref}=1$
. The flow remains linearly stable for
$\hat{U} _{w}=\hat{U} _{w,ref}=1$
. The flow remains linearly stable for
![]() $1\leqslant {\hat{H}}/{\hat{H}}_{ref}\leqslant 30$
and
$1\leqslant {\hat{H}}/{\hat{H}}_{ref}\leqslant 30$
and
![]() $0.4\leqslant {\it\phi}^{0}\leqslant 0.55$
. Further, according to our predictions, shear flows at higher Couette gaps and with lower concentrations correspond to higher growth rates.
$0.4\leqslant {\it\phi}^{0}\leqslant 0.55$
. Further, according to our predictions, shear flows at higher Couette gaps and with lower concentrations correspond to higher growth rates.
For the scopes of this parametric study we modify
![]() ${\hat{H}}$
and
${\hat{H}}$
and
![]() ${\it\phi}^{0}$
while the remaining variables have maintained their values with respect to the reference configuration. Figure 2 shows representative growth rates
${\it\phi}^{0}$
while the remaining variables have maintained their values with respect to the reference configuration. Figure 2 shows representative growth rates
![]() ${\it\sigma}$
versus the Couette gap ratio
${\it\sigma}$
versus the Couette gap ratio
![]() ${\hat{H}}/{\hat{H}}_{ref}$
for different initial concentrations and for
${\hat{H}}/{\hat{H}}_{ref}$
for different initial concentrations and for
![]() ${\it\alpha}=1$
,
${\it\alpha}=1$
,
![]() $\hat{U} _{w}=\hat{U} _{w,ref}=1$
. For all values of these parameters considered herein, namely
$\hat{U} _{w}=\hat{U} _{w,ref}=1$
. For all values of these parameters considered herein, namely
![]() $1\leqslant {\hat{H}}/{\hat{H}}_{ref}\leqslant 30$
, the flow is predicted to be linearly stable.
$1\leqslant {\hat{H}}/{\hat{H}}_{ref}\leqslant 30$
, the flow is predicted to be linearly stable.
As asserted by figure 2, the Couette gap plays a destabilizing role in the flows of interest. Indeed, it correlates positively with the growth rate, however, its rate of change experiences a significant decrease. Therefore, shear flows confined in very wide channels, and at the limit unbounded ones, might be susceptible to instabilities. On the other hand, the magnitude of the initial concentration is found to have a stabilizing effect. This is not surprising since, as the concentration increases, frictional forces become dominant and render relative motion between the grains more difficult. As a consequence, disturbances in the form of travelling waves that conform with the governing equations at hand correspond to increasingly smaller growth rates and, therefore, decay faster.
The combined effect of modifying both the Couette gap and the initial concentration does not yield any additional information about the interplay of these two parameters. Indeed, the simultaneous modification of both parameters amounts to simply shifting the curves depicted in figure 2 accordingly. Nonetheless, although the magnitude of the growth rate is predicted to be a complicated function of
![]() ${\hat{H}}$
and
${\hat{H}}$
and
![]() ${\it\phi}^{0}$
, its sign remains invariant.
${\it\phi}^{0}$
, its sign remains invariant.
Previous stability analyses that have reported the (
![]() ${\hat{H}},{\it\phi}^{0}$
) diagram have also affirmed the destabilizing and stabilizing role of the Couette gap and the initial concentration, respectively, (Wang et al.
Reference Wang, Jackson and Sundaresan1996; Alam & Nott Reference Alam and Nott1998; Nott et al.
Reference Nott, Alam, Agrawal, Jackson and Sundaresan1999). Most notably, however, these studies have reported the existence of unstable modes. We now examine whether this disparity is expected and justified.
${\hat{H}},{\it\phi}^{0}$
) diagram have also affirmed the destabilizing and stabilizing role of the Couette gap and the initial concentration, respectively, (Wang et al.
Reference Wang, Jackson and Sundaresan1996; Alam & Nott Reference Alam and Nott1998; Nott et al.
Reference Nott, Alam, Agrawal, Jackson and Sundaresan1999). Most notably, however, these studies have reported the existence of unstable modes. We now examine whether this disparity is expected and justified.
As mentioned in the introduction, extant studies in the linear stability of the flows of interest have focused on either dilute or rapid granular flows. These flows belong to the collisional regime, where collisions between grains dominate over frictional effects. In turn, this is reflected in the functional form of the governing equations and in particular in the constitutive expressions for the normal and the shear stresses that act on the granular conglomerate. By contrast, the focus of the present study pertains precisely to the regime where frictional effects are important. In the context of the employed theory, these effects are accounted for by embodying appropriate viscous terms to the granular material’s stress tensor. In other words, even if we ignore compaction effects, the differences between the stress tensor employed in kinetic theoretical models and herein are large enough to lead to different stability diagrams.
Being dissimilar, however, does not imply that the two stability diagrams are in contradiction to each other. Rather, it reflects the fact that the dynamics of granular materials in the aforementioned two regimes bear strong differences as well. Consequently, reconciling the findings of the present study with those obtained from kinetic theoretical models requires a ‘hybrid’ theory that is predicated on continuum mechanics but additionally incorporates aspects of kinetic theory of granular gases in a consistent manner. Nevertheless, to the best of our knowledge, a widely accepted theory with the above characteristics has yet to appear in the literature.
4.2 Parametric study with respect to
 $\hat{U} _{w}$
and
$\hat{U} _{w}$
and
 ${\it\phi}^{0}$
${\it\phi}^{0}$
For this parametric study, we have kept the value of the Couette gap fixed and have modified the wall velocity and the initial concentration. More specifically, we have considered values
![]() $1\leqslant \hat{U} /\hat{U} _{w,ref}\leqslant 100$
and
$1\leqslant \hat{U} /\hat{U} _{w,ref}\leqslant 100$
and
![]() $0.4\leqslant {\it\phi}^{0}\leqslant 0.55$
. The results of this parametric study are presented in figure 3, that portrays representative growth rates
$0.4\leqslant {\it\phi}^{0}\leqslant 0.55$
. The results of this parametric study are presented in figure 3, that portrays representative growth rates
![]() ${\it\sigma}$
versus the wall velocity ratio
${\it\sigma}$
versus the wall velocity ratio
![]() $\hat{U} /\hat{U} _{w,ref}$
for various initial concentrations. Two conclusions can be directly drawn. First, the flow remains linearly stable for all values of
$\hat{U} /\hat{U} _{w,ref}$
for various initial concentrations. Two conclusions can be directly drawn. First, the flow remains linearly stable for all values of
![]() $\hat{U} /\hat{U} _{w,ref}$
and
$\hat{U} /\hat{U} _{w,ref}$
and
![]() ${\it\phi}^{0}$
considered herein, and second, the effects of increasing the initial concentration are stabilizing, in line with what was observed in the previous parametric study; clearly, the latter conclusion is nothing but a sanity test for the self-consistency of the acquired results.
${\it\phi}^{0}$
considered herein, and second, the effects of increasing the initial concentration are stabilizing, in line with what was observed in the previous parametric study; clearly, the latter conclusion is nothing but a sanity test for the self-consistency of the acquired results.

Figure 3. Representative growth rates
![]() ${\it\sigma}$
plotted against the wall velocity ratio
${\it\sigma}$
plotted against the wall velocity ratio
![]() $\hat{U} _{w}/\hat{U} _{w,ref}$
, for various initial concentrations and for
$\hat{U} _{w}/\hat{U} _{w,ref}$
, for various initial concentrations and for
![]() ${\it\alpha}=1$
,
${\it\alpha}=1$
,
![]() ${\hat{H}}/{\hat{H}}_{ref}=1$
. The flow remains linearly stable for
${\hat{H}}/{\hat{H}}_{ref}=1$
. The flow remains linearly stable for
![]() $1\leqslant \hat{U} _{w}/\hat{U} _{w,ref}\leqslant 100$
and
$1\leqslant \hat{U} _{w}/\hat{U} _{w,ref}\leqslant 100$
and
![]() $0.4\leqslant {\it\phi}^{0}\leqslant 0.55$
. Increasing
$0.4\leqslant {\it\phi}^{0}\leqslant 0.55$
. Increasing
![]() $\hat{U} _{w}/\hat{U} _{w,ref}$
initially translates into lower growth rates which is subsequently followed by an abrupt increase and the presence of a local maximum. The post-maximum behaviour of
$\hat{U} _{w}/\hat{U} _{w,ref}$
initially translates into lower growth rates which is subsequently followed by an abrupt increase and the presence of a local maximum. The post-maximum behaviour of
![]() ${\it\sigma}$
switches from monotonically increasing to decreasing as
${\it\sigma}$
switches from monotonically increasing to decreasing as
![]() ${\it\phi}^{0}$
increases.
${\it\phi}^{0}$
increases.
By contrast, the role of
![]() $\hat{U} _{w}$
and its interplay with
$\hat{U} _{w}$
and its interplay with
![]() ${\it\phi}^{0}$
are substantially more intricate. According to figure 3, the curves of the growth rates comprise three segments. In the first segment, increasing
${\it\phi}^{0}$
are substantially more intricate. According to figure 3, the curves of the growth rates comprise three segments. In the first segment, increasing
![]() $\hat{U} /\hat{U} _{w,ref}$
translates into gradually decaying growth rates. This segment spans from the start of the horizontal axis until the point where a minimum value has been attained in the cavity. Once this minimum value is crossed, the sign of the correlation changes and this marks the onset of the second segment. Here,
$\hat{U} /\hat{U} _{w,ref}$
translates into gradually decaying growth rates. This segment spans from the start of the horizontal axis until the point where a minimum value has been attained in the cavity. Once this minimum value is crossed, the sign of the correlation changes and this marks the onset of the second segment. Here,
![]() ${\it\sigma}$
experiences a rapid increase and reaches a local maximum that designates the border of the second segment. The third segment extends from this local maximum until the end of the horizontal axis. The shape of
${\it\sigma}$
experiences a rapid increase and reaches a local maximum that designates the border of the second segment. The third segment extends from this local maximum until the end of the horizontal axis. The shape of
![]() ${\it\sigma}$
in this segment depends explicitly on
${\it\sigma}$
in this segment depends explicitly on
![]() ${\it\phi}^{0}$
and signifies the competition between
${\it\phi}^{0}$
and signifies the competition between
![]() ${\it\phi}^{0}$
and
${\it\phi}^{0}$
and
![]() $\hat{U} _{w}$
. For lower values of
$\hat{U} _{w}$
. For lower values of
![]() ${\it\phi}^{0}$
,
${\it\phi}^{0}$
,
![]() ${\it\sigma}$
correlates positively with
${\it\sigma}$
correlates positively with
![]() $\hat{U} /\hat{U} _{w,ref}$
suggesting that the increasing magnitude of the applied shear, induced by the wall velocity, eventually acts as a destabilizing factor. As
$\hat{U} /\hat{U} _{w,ref}$
suggesting that the increasing magnitude of the applied shear, induced by the wall velocity, eventually acts as a destabilizing factor. As
![]() ${\it\phi}^{0}$
increases, this correlation appears to progressively change sign. However, it should be stressed that, according to our numerical experiments, the negative correlation does not hold for arbitrary high wall velocities. As a matter of fact, our results conclusively show that for each concentration
${\it\phi}^{0}$
increases, this correlation appears to progressively change sign. However, it should be stressed that, according to our numerical experiments, the negative correlation does not hold for arbitrary high wall velocities. As a matter of fact, our results conclusively show that for each concentration
![]() ${\it\phi}^{0}$
there exists a threshold wall velocity upon which
${\it\phi}^{0}$
there exists a threshold wall velocity upon which
![]() ${\it\sigma}$
becomes a monotonically increasing function of
${\it\sigma}$
becomes a monotonically increasing function of
![]() $\hat{U} /\hat{U} _{w,ref}$
. In other words, increasing the concentration amounts to translating the borderline from where the destabilizing effects of the applied shear gradually counterbalance the frictional forces, accordingly.
$\hat{U} /\hat{U} _{w,ref}$
. In other words, increasing the concentration amounts to translating the borderline from where the destabilizing effects of the applied shear gradually counterbalance the frictional forces, accordingly.
One of the anonymous referees of this paper remarked that the complex, non-monotonous dependence of the growth rate
![]() ${\it\sigma}$
on
${\it\sigma}$
on
![]() $\hat{U} /\hat{U} _{w,ref}$
, depicted in figure 3, can be partially attributed to the interplay between the shear-thickening behaviour that the
$\hat{U} /\hat{U} _{w,ref}$
, depicted in figure 3, can be partially attributed to the interplay between the shear-thickening behaviour that the
![]() ${\it\mu}(I)$
-rheology predicts and the destabilizing role of the applied shear. Indeed, as
${\it\mu}(I)$
-rheology predicts and the destabilizing role of the applied shear. Indeed, as
![]() $\hat{U} /\hat{U} _{w,ref}$
increases so do (i) the magnitude of the frictional forces and hence of the (stabilizing) dissipation, and (ii) the strength of the applied shear. With these in mind, we observe that, in the first of the aforementioned three segments that the growth rate curves consist of, increasing
$\hat{U} /\hat{U} _{w,ref}$
increases so do (i) the magnitude of the frictional forces and hence of the (stabilizing) dissipation, and (ii) the strength of the applied shear. With these in mind, we observe that, in the first of the aforementioned three segments that the growth rate curves consist of, increasing
![]() $\hat{U} /\hat{U} _{w,ref}$
renders the flow more stable; hence in this regime the stabilizing effect of dissipation dominates. Nevertheless, as
$\hat{U} /\hat{U} _{w,ref}$
renders the flow more stable; hence in this regime the stabilizing effect of dissipation dominates. Nevertheless, as
![]() $\hat{U} /\hat{U} _{w,ref}$
increases further, the (still increasing) dissipation is progressively offset by the destabilizing effect of the (also increasing) applied shear. Although this offset is oscillatory, hinting that secondary concentration-dependent mechanisms also influence the flow, our numerical predictions suggest that the shear-thickening behaviour induced by the
$\hat{U} /\hat{U} _{w,ref}$
increases further, the (still increasing) dissipation is progressively offset by the destabilizing effect of the (also increasing) applied shear. Although this offset is oscillatory, hinting that secondary concentration-dependent mechanisms also influence the flow, our numerical predictions suggest that the shear-thickening behaviour induced by the
![]() ${\it\mu}(I)$
-rheology can only transiently stabilize the flows of interest.
${\it\mu}(I)$
-rheology can only transiently stabilize the flows of interest.
4.3 Parametric study with respect to
 ${\hat{H}}$
and
${\hat{H}}$
and
 $\hat{U} _{w}$
$\hat{U} _{w}$
This parametric study concerns the effects of the combined modification of
![]() ${\hat{H}}$
and
${\hat{H}}$
and
![]() $\hat{U} _{w}$
on the stability properties of flow. Figure 4(a) depicts the predicted stability diagram for
$\hat{U} _{w}$
on the stability properties of flow. Figure 4(a) depicts the predicted stability diagram for
![]() $1\leqslant {\hat{H}}/{\hat{H}}_{ref}\leqslant 30$
and
$1\leqslant {\hat{H}}/{\hat{H}}_{ref}\leqslant 30$
and
![]() $1\leqslant \hat{U} /\hat{U} _{w,ref}\leqslant 100$
while the initial concentration is
$1\leqslant \hat{U} /\hat{U} _{w,ref}\leqslant 100$
while the initial concentration is
![]() ${\it\phi}^{0}=0.55$
. It can be readily inferred that, for values of
${\it\phi}^{0}=0.55$
. It can be readily inferred that, for values of
![]() $\hat{U} _{w}/\hat{U} _{w,ref}$
and
$\hat{U} _{w}/\hat{U} _{w,ref}$
and
![]() ${\hat{H}}/{\hat{H}}_{ref}$
inside the domain defined by the neutral stability curve, the flow becomes linearly unstable. Accordingly, the maximum growth rate is
${\hat{H}}/{\hat{H}}_{ref}$
inside the domain defined by the neutral stability curve, the flow becomes linearly unstable. Accordingly, the maximum growth rate is
![]() ${\it\sigma}_{max}=0.0054179$
and corresponds to a wall velocity
${\it\sigma}_{max}=0.0054179$
and corresponds to a wall velocity
![]() $\hat{U} _{w}=0.67~\text{m}~\text{s}^{-1}$
and Couette gap
$\hat{U} _{w}=0.67~\text{m}~\text{s}^{-1}$
and Couette gap
![]() ${\hat{H}}=3~\text{m}$
. We remark that
${\hat{H}}=3~\text{m}$
. We remark that
![]() ${\it\sigma}_{max}$
corresponds to the eigenvalue with the largest real part and not to the first eigenvalue with positive real part. In this respect,
${\it\sigma}_{max}$
corresponds to the eigenvalue with the largest real part and not to the first eigenvalue with positive real part. In this respect,
![]() ${\it\sigma}_{max}$
is associated to a cutoff frequency, similar to the one obtained by Forterre (Reference Forterre2006), i.e. the spectrum is not unbounded as is the case of Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015). Another interesting finding concerns the magnitude of
${\it\sigma}_{max}$
is associated to a cutoff frequency, similar to the one obtained by Forterre (Reference Forterre2006), i.e. the spectrum is not unbounded as is the case of Barker et al. (Reference Barker, Schaeffer, Bohorquez and Gray2015). Another interesting finding concerns the magnitude of
![]() ${\it\sigma}_{max}$
as a function of the initial concentration
${\it\sigma}_{max}$
as a function of the initial concentration
![]() ${\it\phi}^{0}$
. According to our results, in the unstable regime,
${\it\phi}^{0}$
. According to our results, in the unstable regime,
![]() ${\it\sigma}_{max}$
is negatively correlated to
${\it\sigma}_{max}$
is negatively correlated to
![]() ${\it\phi}^{0}$
suggesting a reversal in the behaviour depicted in figures 2 and 3.
${\it\phi}^{0}$
suggesting a reversal in the behaviour depicted in figures 2 and 3.
The prediction of an instability regime for values of
![]() ${\hat{H}}/{\hat{H}}_{ref}$
,
${\hat{H}}/{\hat{H}}_{ref}$
,
![]() $\hat{U} _{w}/\hat{U} _{w,ref}$
and
$\hat{U} _{w}/\hat{U} _{w,ref}$
and
![]() ${\it\phi}^{0}$
that have been employed in the previous parametric studies is not at odds with the results of these studies. Rather, it reflects the aforementioned fact that, due to the particular dependence of the dimensionless groups
${\it\phi}^{0}$
that have been employed in the previous parametric studies is not at odds with the results of these studies. Rather, it reflects the aforementioned fact that, due to the particular dependence of the dimensionless groups
![]() $d_{p}$
,
$d_{p}$
,
![]() $k_{1}$
,
$k_{1}$
,
![]() $k_{2}$
and
$k_{2}$
and
![]() $Re_{c}$
on
$Re_{c}$
on
![]() $\hat{L}_{r}={\hat{H}}$
and
$\hat{L}_{r}={\hat{H}}$
and
![]() $\boldsymbol{U}_{r}=\hat{U} _{w}$
, changes of
$\boldsymbol{U}_{r}=\hat{U} _{w}$
, changes of
![]() ${\hat{H}}$
cannot be represented by changes in
${\hat{H}}$
cannot be represented by changes in
![]() $\hat{U} _{w}$
. Thus, as confirmed by our numerical predictions, a combined modification of these parameters is necessary for the appearance of an unstable mode. This is further confirmed by figure 4(b,c) that illustrate the same stability diagram but for different concentrations. From these figures, we can additionally infer that modifying the concentration shifts the instability regime along the main diagonal of the axes, accordingly.
$\hat{U} _{w}$
. Thus, as confirmed by our numerical predictions, a combined modification of these parameters is necessary for the appearance of an unstable mode. This is further confirmed by figure 4(b,c) that illustrate the same stability diagram but for different concentrations. From these figures, we can additionally infer that modifying the concentration shifts the instability regime along the main diagonal of the axes, accordingly.
The stability diagrams portrayed in figure 4(a–c) assert that for small values of the Couette gap and of the wall velocity, the flow is linearly stable. As far as the Couette gap is concerned, this finding is routinely recovered in stability analyses based on kinetic theoretical models. However, as regards the wall velocity, this appears to be a novel, consistent result. The scarcity of results in this direction may be attributed to the dimensionless groups that kinetic theoretical models admit. In general, they are markedly different from the ones discussed in the previous section and do not incorporate the reference velocity.
Subsequently, we shift our focus to the manifestation of the detected instability and its effects on the granular concentration and velocity fields. From the various unstable modes that we acquired, we opt to study the case corresponding to the maximum growth rate
![]() ${\it\sigma}_{max}=0.0048$
(
${\it\sigma}_{max}=0.0048$
(
![]() $\hat{U} _{w}/\hat{U} _{w,ref}=67$
,
$\hat{U} _{w}/\hat{U} _{w,ref}=67$
,
![]() ${\hat{H}}/{\hat{H}}_{ref}=30$
,
${\hat{H}}/{\hat{H}}_{ref}=30$
,
![]() ${\it\phi}^{0}=0.55$
). Figure 5 shows contour plots of the granular concentration
${\it\phi}^{0}=0.55$
). Figure 5 shows contour plots of the granular concentration
![]() ${\it\phi}(x,y)$
,
${\it\phi}(x,y)$
,
at
![]() $t=0.1$
. Superimposed in this figure is a vector plot of the corresponding (normalized) velocity field so that the motion of granular material can be pictured.
$t=0.1$
. Superimposed in this figure is a vector plot of the corresponding (normalized) velocity field so that the motion of granular material can be pictured.

Figure 4. Contour plot of growth rates
![]() ${\it\sigma}$
for
${\it\sigma}$
for
![]() $1\leqslant \hat{U} _{w}/\hat{U} _{w,ref}\leqslant 100$
and
$1\leqslant \hat{U} _{w}/\hat{U} _{w,ref}\leqslant 100$
and
![]() $1\leqslant {\hat{H}}/{\hat{H}}_{ref}\leqslant 30$
. (a)
$1\leqslant {\hat{H}}/{\hat{H}}_{ref}\leqslant 30$
. (a)
![]() ${\it\phi}^{0}=0.55$
, (b)
${\it\phi}^{0}=0.55$
, (b)
![]() ${\it\phi}^{0}=0.53$
and (c)
${\it\phi}^{0}=0.53$
and (c)
![]() ${\it\phi}^{0}=0.5$
. The wavenumber is
${\it\phi}^{0}=0.5$
. The wavenumber is
![]() ${\it\alpha}=1$
. The thick line (–) designates the neutral stability curve where
${\it\alpha}=1$
. The thick line (–) designates the neutral stability curve where
![]() ${\it\sigma}=0$
and the filled diamond (
${\it\sigma}=0$
and the filled diamond (
![]() $\blacklozenge$
) the maximum growth rate for each case. For values of
$\blacklozenge$
) the maximum growth rate for each case. For values of
![]() $\hat{U} _{w}/\hat{U} _{w,ref}$
and
$\hat{U} _{w}/\hat{U} _{w,ref}$
and
![]() ${\hat{H}}/{\hat{H}}_{ref}$
inside the region defined by the neutral stability curve, the flow is predicted to be linearly unstable. For case (a) the maximum growth rate is predicted to be
${\hat{H}}/{\hat{H}}_{ref}$
inside the region defined by the neutral stability curve, the flow is predicted to be linearly unstable. For case (a) the maximum growth rate is predicted to be
![]() ${\it\sigma}=0.0054179$
and corresponds to the point
${\it\sigma}=0.0054179$
and corresponds to the point
![]() $\hat{U} _{w}/\hat{U} _{w,ref}=67$
,
$\hat{U} _{w}/\hat{U} _{w,ref}=67$
,
![]() ${\hat{H}}/{\hat{H}}_{ref}=30$
. As the concentration decreases, the instability regime is shifted downwards along the diagonal of the axes asserting that offsetting the stabilizing effect of the frictional forces requires a lower wall velocity and Couette gap.
${\hat{H}}/{\hat{H}}_{ref}=30$
. As the concentration decreases, the instability regime is shifted downwards along the diagonal of the axes asserting that offsetting the stabilizing effect of the frictional forces requires a lower wall velocity and Couette gap.

Figure 5. Contour plots of the granular concentration at
![]() $t=0.1$
for
$t=0.1$
for
![]() $\hat{U} _{w}/\hat{U} _{w,ref}=67$
,
$\hat{U} _{w}/\hat{U} _{w,ref}=67$
,
![]() ${\hat{H}}/{\hat{H}}_{ref}=30$
and
${\hat{H}}/{\hat{H}}_{ref}=30$
and
![]() ${\it\sigma}=0.0048$
. The concentration is
${\it\sigma}=0.0048$
. The concentration is
![]() ${\it\phi}^{0}=0.55$
. Superimposed is a vector plot of the velocity field. The predicted instability manifests itself through the formation of two granular bulbs of high and low concentration that move away from and towards the upper wall, respectively. In turn, this results in particle migration.
${\it\phi}^{0}=0.55$
. Superimposed is a vector plot of the velocity field. The predicted instability manifests itself through the formation of two granular bulbs of high and low concentration that move away from and towards the upper wall, respectively. In turn, this results in particle migration.

Figure 6. Contour plots of the granular vorticity at
![]() $t=0.1$
for
$t=0.1$
for
![]() $\hat{U} _{w}/\hat{U} _{w,ref}=67$
,
$\hat{U} _{w}/\hat{U} _{w,ref}=67$
,
![]() ${\hat{H}}/{\hat{H}}_{ref}=30$
and
${\hat{H}}/{\hat{H}}_{ref}=30$
and
![]() ${\it\sigma}=0.0048$
. The concentration is
${\it\sigma}=0.0048$
. The concentration is
![]() ${\it\phi}^{0}=0.55$
. As a consequence of the predicted instability, two counter-rotating vortices have appeared that are stretched in the streamwise direction by a factor of
${\it\phi}^{0}=0.55$
. As a consequence of the predicted instability, two counter-rotating vortices have appeared that are stretched in the streamwise direction by a factor of
![]() $3.5$
. The relative position with respect to the granular bulbs of figure 5 indicates a form of preferential concentration.
$3.5$
. The relative position with respect to the granular bulbs of figure 5 indicates a form of preferential concentration.
The initial uniform concentration
![]() ${\it\phi}^{0}=0.55$
has been substantially modified and two granular bulbs of high and low concentration have emerged, with the former preceding the latter in the streamwise direction. These bulbs arise due to the interaction between the disturbance
${\it\phi}^{0}=0.55$
has been substantially modified and two granular bulbs of high and low concentration have emerged, with the former preceding the latter in the streamwise direction. These bulbs arise due to the interaction between the disturbance
![]() ${\it\phi}^{1}(x,y,t)$
and the base-flow concentration
${\it\phi}^{1}(x,y,t)$
and the base-flow concentration
![]() ${\it\phi}^{0}$
, i.e. they constitute the manifestation of the predicted instability. We remark that the second bulb constitutes a mirror image of the first one, stemming directly from the fact that we have employed a normal mode analysis. The same observation applies to the velocity and vorticity fields as well. Thus, it suffices to adhere to the examination of the first (high concentration) bulb and the associated velocity and vorticity structures.
${\it\phi}^{0}$
, i.e. they constitute the manifestation of the predicted instability. We remark that the second bulb constitutes a mirror image of the first one, stemming directly from the fact that we have employed a normal mode analysis. The same observation applies to the velocity and vorticity fields as well. Thus, it suffices to adhere to the examination of the first (high concentration) bulb and the associated velocity and vorticity structures.
The motion of the first bulb takes place along curves of clockwise orientation and shows a vertical displacement of particles from the upper plane towards the middle of the domain. In other words, the instability gives rise to a shear dilatancy that, in turn, induces particle migration.
At this point it is useful to note that the prediction of bulbs in granular shear flows is not without precedence. Indeed, Conway & Glasser (Reference Conway and Glasser2004) and Conway, Liu & Glasser (Reference Conway, Liu and Glasser2006), who studied granular shear flows via molecular dynamics simulations, documented the formation and propagation of elongated and oscillatory structures of high particle concentration located in the middle of the domain. These structures are qualitatively similar to those predicted by our linear stability analysis; cf. Figure 5, and provide further evidence on the appropriateness of continuum mechanical models to describe the primary properties of the flows of interest.
Further insight to the properties of the predicted instability can be obtained upon examination of the vorticity field of the fluid. Figure 6 depicts contours of the granular vorticity at
![]() $t=0.1$
. We observe that, following the onset of the instability, two counter-rotating vortices are formed that are stretched in the streamwise direction by a factor of, approximately, 3.5. More important, however, is the positioning of these vortices relative to the bulbs. In particular, the maximum concentration of the first bulb coincides with the area of minimum vorticity and vice-versa. Therefore, the manifestation of the instability through particle migration is also accompanied by a form of preferential concentration.
$t=0.1$
. We observe that, following the onset of the instability, two counter-rotating vortices are formed that are stretched in the streamwise direction by a factor of, approximately, 3.5. More important, however, is the positioning of these vortices relative to the bulbs. In particular, the maximum concentration of the first bulb coincides with the area of minimum vorticity and vice-versa. Therefore, the manifestation of the instability through particle migration is also accompanied by a form of preferential concentration.
4.4 The role of the intergranular stress and the equilibrated stress coefficient
As mentioned above, the exact form of the compaction equation for granular flows remains a subject of debate. Moreover, the experimental validation or refutation of existing forms is a cumbersome task due to the multitude of assumptions that the derivation of these equations is based upon and the presence of terms for which experimental correlations are difficult to be acquired. It is, therefore, appropriate to comment on the predictions of the stability analysis concerning the effect of the intergranular stress
![]() ${\it\beta}$
and the equilibrated stress coefficient
${\it\beta}$
and the equilibrated stress coefficient
![]() ${\it\Gamma}$
on the flow properties.
${\it\Gamma}$
on the flow properties.
Summing up, the results of the stability analysis assert that large Couette gaps, high wall velocities and low concentrations are destabilizing mechanisms whilst the converse is also true. On the other hand, by virtue of (2.9), (2.10) and (2.13), we can infer that as
![]() ${\hat{H}}$
,
${\hat{H}}$
,
![]() $\hat{U} _{w}$
increase and
$\hat{U} _{w}$
increase and
![]() ${\it\phi}$
decreases, then the magnitude of
${\it\phi}$
decreases, then the magnitude of
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() ${\it\Gamma}$
decrease. In other words, as the configuration of the flow approaches the region of instability, the strength of both the intergranular stresses and of the tendency of the granular material to suppress inhomogeneities are accordingly reduced. By contrast, the exact opposite scenario is observed following the decrease of
${\it\Gamma}$
decrease. In other words, as the configuration of the flow approaches the region of instability, the strength of both the intergranular stresses and of the tendency of the granular material to suppress inhomogeneities are accordingly reduced. By contrast, the exact opposite scenario is observed following the decrease of
![]() ${\hat{H}}$
,
${\hat{H}}$
,
![]() $\hat{U} _{w}$
and the increase of
$\hat{U} _{w}$
and the increase of
![]() ${\it\phi}$
. Collectively, these observations suggest that the intergranular stress
${\it\phi}$
. Collectively, these observations suggest that the intergranular stress
![]() ${\it\beta}$
and the equilibrated stress coefficient
${\it\beta}$
and the equilibrated stress coefficient
![]() ${\it\Gamma}$
play a stabilizing role in the flows of interest.
${\it\Gamma}$
play a stabilizing role in the flows of interest.
5 Conclusions
In this paper, the susceptibility of shear flows of dense granular materials to hydrodynamic instabilities has been investigated via the means of a linear stability analysis. Our studies have been based on a continuum mechanical model for the flows of interest coupled with the constitutive expressions for the normal and shear stresses predicted by the
![]() ${\it\mu}(I)$
-rheology. A classical normal mode analysis has been carried that has resulted in a generalized eigenvalue problem, with the eigenvalues and eigenfunctions being the complex frequency and the amplitude of the disturbances. Due to the complexity of the problem, both the spectra and the eigenfunctions have been approximated numerically and detailed parametric studies with respect to the Couette gap, the wall velocity and the initial concentration have been performed.
${\it\mu}(I)$
-rheology. A classical normal mode analysis has been carried that has resulted in a generalized eigenvalue problem, with the eigenvalues and eigenfunctions being the complex frequency and the amplitude of the disturbances. Due to the complexity of the problem, both the spectra and the eigenfunctions have been approximated numerically and detailed parametric studies with respect to the Couette gap, the wall velocity and the initial concentration have been performed.
According to our analysis, the Couette gap and the wall velocity play a destabilizing role in the flows of interest whereas the initial concentration is found to act as a stabilizer. The results concerning the Couette gap and initial concentration are in line with extant literature on the stability of shear granular flows predicted by kinetic theoretical models. However, our findings concerning the role of wall velocity are novel. For the range of parameters considered herein, increasing either the Couette gap or the wall velocity is insufficient to offset the stabilizing effects of the frictional forces associated with the high concentration. Consequently, the spectrum lies in the left half of the complex plane and the flow is predicted to be linearly stable. However, the simultaneous modification of these two quantities is shown to engender the presence of unstable modes. The predicted instability modifies the homogeneous initial concentration via the formation of a granular bulb the motion of which induces particle migration. The predicted bulbs are qualitatively similar to those reported in Conway & Glasser (Reference Conway and Glasser2004) and Conway et al. (Reference Conway, Liu and Glasser2006), that have been obtained through molecular dynamics simulations.
Stability analyses based on continuum mechanical models are notably scarce. This study constitutes the first step towards closing this gap and thus obtaining a more complete picture of the stability properties of the flows of interest. In this respect, a natural next step concerns the extension of the present stability analysis to three-dimensional flows and additionally investigate more involved disturbances. We intend to pursue this in a subsequent study.
Acknowledgements
The authors would like to thank the anonymous Referees for their detailed and constructive reviews that have considerably improved the quality of this manuscript. Financial support for the first author has been provided by the National Research Fund of Belgium (FNRS) in the form the grant ‘GRANMIX’.
Appendix A. The linearized governing equations
In this appendix, we present the governing equations, linearized with respect to the base-flow profile (2.18)–(2.21) and for arbitrary, albeit small, disturbances. By dropping the explicit dependence of the base-flow profiles and the disturbances to their arguments since there is no danger of confusion, we arrive at the following system of equations:
Continuity equation
Momentum equation (streamwise component)
 $$\begin{eqnarray}\displaystyle & & \displaystyle u^{0}\frac{\partial {\it\phi}^{1}}{\partial t}+{\it\phi}^{0}\frac{\partial u^{1}}{\partial t}+(u^{0})^{2}\frac{\partial {\it\phi}^{1}}{\partial x}+2{\it\phi}^{0}u^{0}\frac{\partial u^{1}}{\partial x}+{\it\phi}^{0}\frac{\text{d}u^{0}}{\text{d}z}v^{1}+{\it\phi}^{0}u^{0}\frac{\partial v^{1}}{\partial y}+{\it\phi}^{0}\frac{\partial p^{1}}{\partial x}+p^{0}\frac{\partial {\it\phi}^{1}}{\partial x}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{d_{p}^{2}{\it\rho}{\it\phi}^{0}}{2}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}+\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left(\frac{\partial ^{2}u^{1}}{\partial y^{2}}+\frac{\partial ^{2}v^{1}}{\partial y\partial x}+2\frac{\partial ^{2}u^{1}}{\partial x^{2}}\right)+\frac{d_{p}^{2}{\it\rho}}{2{\it\phi}^{0}}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right)\frac{\partial {\it\phi}^{1}}{\partial y}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{{\it\phi}^{0}}{2}\left(\frac{\partial ^{2}v^{1}}{\partial y\partial x}+\frac{\partial ^{2}u^{1}}{\partial y^{2}}\right)-d_{p}^{2}{\it\rho}{\it\phi}^{0}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{3}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})+(2(-{\it\phi}_{max}+{\it\phi}^{0})))}{2(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2})^{2}}\right)\frac{\partial {\it\phi}^{1}}{\partial y}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,d_{p}^{2}{\it\rho}{\it\phi}^{0}\frac{({\it\phi}_{max}-{\it\phi}_{min})^{2}}{2(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\left(\frac{\partial ^{2}v^{1}}{\partial x^{2}}+\frac{\partial ^{2}u^{1}}{\partial y\partial x}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,d_{p}^{2}{\it\rho}\left({\it\phi}^{0}\frac{({\it\phi}_{max}-{\it\phi}_{min})^{2}}{2(-{\it\phi}_{max}+{\it\phi}^{0})^{3}}-\frac{({\it\phi}_{max}-{\it\phi}_{min})^{2}}{4(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right)\frac{\partial {\it\phi}^{1}}{\partial x}+\frac{\partial v^{1}}{\partial x}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle u^{0}\frac{\partial {\it\phi}^{1}}{\partial t}+{\it\phi}^{0}\frac{\partial u^{1}}{\partial t}+(u^{0})^{2}\frac{\partial {\it\phi}^{1}}{\partial x}+2{\it\phi}^{0}u^{0}\frac{\partial u^{1}}{\partial x}+{\it\phi}^{0}\frac{\text{d}u^{0}}{\text{d}z}v^{1}+{\it\phi}^{0}u^{0}\frac{\partial v^{1}}{\partial y}+{\it\phi}^{0}\frac{\partial p^{1}}{\partial x}+p^{0}\frac{\partial {\it\phi}^{1}}{\partial x}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{d_{p}^{2}{\it\rho}{\it\phi}^{0}}{2}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}+\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left(\frac{\partial ^{2}u^{1}}{\partial y^{2}}+\frac{\partial ^{2}v^{1}}{\partial y\partial x}+2\frac{\partial ^{2}u^{1}}{\partial x^{2}}\right)+\frac{d_{p}^{2}{\it\rho}}{2{\it\phi}^{0}}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right)\frac{\partial {\it\phi}^{1}}{\partial y}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{{\it\phi}^{0}}{2}\left(\frac{\partial ^{2}v^{1}}{\partial y\partial x}+\frac{\partial ^{2}u^{1}}{\partial y^{2}}\right)-d_{p}^{2}{\it\rho}{\it\phi}^{0}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{3}}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})+(2(-{\it\phi}_{max}+{\it\phi}^{0})))}{2(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2})^{2}}\right)\frac{\partial {\it\phi}^{1}}{\partial y}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,d_{p}^{2}{\it\rho}{\it\phi}^{0}\frac{({\it\phi}_{max}-{\it\phi}_{min})^{2}}{2(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\left(\frac{\partial ^{2}v^{1}}{\partial x^{2}}+\frac{\partial ^{2}u^{1}}{\partial y\partial x}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,d_{p}^{2}{\it\rho}\left({\it\phi}^{0}\frac{({\it\phi}_{max}-{\it\phi}_{min})^{2}}{2(-{\it\phi}_{max}+{\it\phi}^{0})^{3}}-\frac{({\it\phi}_{max}-{\it\phi}_{min})^{2}}{4(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right)\frac{\partial {\it\phi}^{1}}{\partial x}+\frac{\partial v^{1}}{\partial x}.\end{eqnarray}$$
Momentum equation (normal component)
 $$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-10.00002pt}{\it\phi}^{0}\frac{\partial v^{1}}{\partial t}+{\it\phi}^{0}u^{0}\frac{\partial v^{1}}{\partial x}+{\it\phi}^{0}\frac{\partial p^{1}}{\partial y}+p^{0}\frac{\partial {\it\phi}^{1}}{\partial y}=-d_{p}^{2}{\it\rho}{\it\phi}^{0}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{3}}\right.\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad \left.+\,\frac{({\it\phi}_{max}-{\it\phi}_{min})^{2}{\it\mu}_{2}(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})+(2(-{\it\phi}_{max}+{\it\phi}^{0})))}{2(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2})^{2}}\right)\frac{\partial {\it\phi}^{1}}{\partial x}\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad +\,d_{p}^{2}{\it\rho}{\it\phi}^{0}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}+\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{2(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2})}\right)\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad \times \left(\frac{\partial ^{2}v^{1}}{\partial x^{2}}+\frac{\partial ^{2}u^{1}}{\partial y\partial x}\right)+\frac{d_{p}^{2}{\it\rho}{\it\phi}^{0}}{2}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad +\left.\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2})}\right)\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad \times \left(\frac{\partial ^{2}u^{1}}{\partial y\partial x}+\frac{\partial ^{2}v^{1}}{\partial x^{2}}\right)+d_{p}^{2}{\it\rho}{\it\phi}^{0}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad +\left.\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2})}\right)\frac{\partial ^{2}v^{1}}{\partial y\partial x}\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad +\,\frac{d_{p}^{2}{\it\rho}}{2}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}+\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2})}\right)\frac{\partial {\it\phi}^{1}}{\partial x}\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad +\,\frac{1}{2(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\left(\frac{\partial ^{2}v^{1}}{\partial y\partial x}+\frac{\partial ^{2}u^{1}}{\partial y^{2}}\right)\hspace{-1.0pt}+d_{p}^{2}{\it\rho}\left(\frac{({\it\phi}_{max}-{\it\phi}_{min})^{2}}{2(-{\it\phi}_{max}+{\it\phi}^{0})^{3}}-\frac{({\it\phi}_{max}-{\it\phi}_{min})^{2}}{4(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right)\frac{\partial {\it\phi}^{1}}{\partial y}.\hspace{-20.00003pt}\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-10.00002pt}{\it\phi}^{0}\frac{\partial v^{1}}{\partial t}+{\it\phi}^{0}u^{0}\frac{\partial v^{1}}{\partial x}+{\it\phi}^{0}\frac{\partial p^{1}}{\partial y}+p^{0}\frac{\partial {\it\phi}^{1}}{\partial y}=-d_{p}^{2}{\it\rho}{\it\phi}^{0}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{3}}\right.\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad \left.+\,\frac{({\it\phi}_{max}-{\it\phi}_{min})^{2}{\it\mu}_{2}(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})+(2(-{\it\phi}_{max}+{\it\phi}^{0})))}{2(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2})^{2}}\right)\frac{\partial {\it\phi}^{1}}{\partial x}\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad +\,d_{p}^{2}{\it\rho}{\it\phi}^{0}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}+\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{2(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2})}\right)\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad \times \left(\frac{\partial ^{2}v^{1}}{\partial x^{2}}+\frac{\partial ^{2}u^{1}}{\partial y\partial x}\right)+\frac{d_{p}^{2}{\it\rho}{\it\phi}^{0}}{2}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad +\left.\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2})}\right)\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad \times \left(\frac{\partial ^{2}u^{1}}{\partial y\partial x}+\frac{\partial ^{2}v^{1}}{\partial x^{2}}\right)+d_{p}^{2}{\it\rho}{\it\phi}^{0}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad +\left.\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2})}\right)\frac{\partial ^{2}v^{1}}{\partial y\partial x}\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad +\,\frac{d_{p}^{2}{\it\rho}}{2}\left(\frac{{\it\mu}_{1}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}+\frac{{\it\mu}_{2}({\it\phi}_{max}-{\it\phi}_{min})^{2}}{(-I_{0}({\it\phi}_{max}-{\it\phi}_{min})(-{\it\phi}_{max}+{\it\phi}^{0})+(-{\it\phi}_{max}+{\it\phi}^{0})^{2})}\right)\frac{\partial {\it\phi}^{1}}{\partial x}\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad +\,\frac{1}{2(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\left(\frac{\partial ^{2}v^{1}}{\partial y\partial x}+\frac{\partial ^{2}u^{1}}{\partial y^{2}}\right)\hspace{-1.0pt}+d_{p}^{2}{\it\rho}\left(\frac{({\it\phi}_{max}-{\it\phi}_{min})^{2}}{2(-{\it\phi}_{max}+{\it\phi}^{0})^{3}}-\frac{({\it\phi}_{max}-{\it\phi}_{min})^{2}}{4(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\right)\frac{\partial {\it\phi}^{1}}{\partial y}.\hspace{-20.00003pt}\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Compaction equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-10.00002pt}\frac{\partial {\it\phi}^{1}}{\partial t}+u^{0}\frac{\partial {\it\phi}^{1}}{\partial x}\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\quad =\frac{1}{Re_{c}}\left(p^{1}-\left(\frac{\displaystyle 2k_{1}{\it\phi}^{0}\log \left(\frac{1}{1-{\it\phi}^{0}}\right)}{(2-{\it\phi}^{0})^{2}}+\frac{\displaystyle 2k_{1}({\it\phi}^{0})^{2}\log \left(\frac{1}{1-{\it\phi}^{0}}\right)}{(2-{\it\phi}^{0})^{3}}+\frac{\displaystyle k_{1}({\it\phi}^{0})^{2}}{(2-{\it\phi}^{0})^{2}(1-{\it\phi}^{0})}\right){\it\phi}^{1}\right.\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad +\left.\vphantom{\frac{\displaystyle 2k_{1}{\it\phi}^{0}\log \left(\frac{1}{1-{\it\phi}^{0}}\right)}{(2-{\it\phi}^{0})^{2}}}\frac{k_{2}{\it\phi}^{0}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\frac{\partial ^{2}{\it\phi}^{1}}{\partial x^{2}}+\frac{\displaystyle k_{2}{\it\phi}^{0}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\frac{\partial ^{2}{\it\phi}^{1}}{\partial y^{2}}\right).\hspace{-20.00003pt}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-10.00002pt}\frac{\partial {\it\phi}^{1}}{\partial t}+u^{0}\frac{\partial {\it\phi}^{1}}{\partial x}\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\quad =\frac{1}{Re_{c}}\left(p^{1}-\left(\frac{\displaystyle 2k_{1}{\it\phi}^{0}\log \left(\frac{1}{1-{\it\phi}^{0}}\right)}{(2-{\it\phi}^{0})^{2}}+\frac{\displaystyle 2k_{1}({\it\phi}^{0})^{2}\log \left(\frac{1}{1-{\it\phi}^{0}}\right)}{(2-{\it\phi}^{0})^{3}}+\frac{\displaystyle k_{1}({\it\phi}^{0})^{2}}{(2-{\it\phi}^{0})^{2}(1-{\it\phi}^{0})}\right){\it\phi}^{1}\right.\nonumber\\ \displaystyle & & \displaystyle \hspace{-10.00002pt}\qquad +\left.\vphantom{\frac{\displaystyle 2k_{1}{\it\phi}^{0}\log \left(\frac{1}{1-{\it\phi}^{0}}\right)}{(2-{\it\phi}^{0})^{2}}}\frac{k_{2}{\it\phi}^{0}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\frac{\partial ^{2}{\it\phi}^{1}}{\partial x^{2}}+\frac{\displaystyle k_{2}{\it\phi}^{0}}{(-{\it\phi}_{max}+{\it\phi}^{0})^{2}}\frac{\partial ^{2}{\it\phi}^{1}}{\partial y^{2}}\right).\hspace{-20.00003pt}\end{eqnarray}$$
Appendix B. The generalized eigenvalue problem
The linear stability analysis performed in § 3 has resulted in a generalized eigenvalue problem the symbolic form of which reads,
where
![]() $A^{\overline{{\it\phi}}}$
,
$A^{\overline{{\it\phi}}}$
,
![]() $A^{\overline{u}}$
,
$A^{\overline{u}}$
,
![]() $A^{\overline{v}}$
,
$A^{\overline{v}}$
,
![]() $B^{\overline{{\it\phi}}}$
,
$B^{\overline{{\it\phi}}}$
,
![]() $B^{\overline{u}}$
and
$B^{\overline{u}}$
and
![]() $B^{\overline{v}}$
are
$B^{\overline{v}}$
are
![]() $4\times 3$
matrices. Before reporting the exact expressions of these quantities, in order to obtain more succinct formulas, we introduce the following notation convention,
$4\times 3$
matrices. Before reporting the exact expressions of these quantities, in order to obtain more succinct formulas, we introduce the following notation convention,
Then, we have,
 $$\begin{eqnarray}\displaystyle A_{0,1}^{\overline{{\it\phi}}} & = & \displaystyle -2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{2}\,Re_{c}k_{1}{\it\phi}_{max}^{2}/f_{3}+4\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{2}\,Re_{c}k_{1}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,\text{i}f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y){\it\alpha}^{2}\,Re_{c}p^{0}(y)+4\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{2}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,4\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{2}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}/f_{3}+\frac{1}{2}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y){\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle -\,2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{2}\,Re_{c}k_{1}{\it\phi}_{max}/f_{3}-\text{i}f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y){\it\alpha}^{2}\,Re_{c}u^{0}(y)^{2}\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{2}\,Re_{c}k_{1}{\it\phi}_{max}^{2}/f_{3}+\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{2}\,Re_{c}k_{1}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{4}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y){\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{max}^{2}-10\text{i}f_{1}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\,7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{4}\,Re_{c}k_{2}/f_{3}-18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{4}\,Re_{c}k_{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{4}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y){\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{min}^{2}-\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{4}\,Re_{c}k_{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{2}\,Re_{c}k_{1}/f_{3}+20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{4}\,Re_{c}k_{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{4}\,Re_{c}k_{2}/f_{3}-2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\;f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}^{2}/f_{3}-7f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,14f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}/f_{3}+8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,40f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}/f_{3}-16f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,18f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}^{2}/f_{3}+4\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{2}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,20f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}^{2}/f_{3}+\frac{1}{2}\text{i}f_{1}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{max}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}\text{i}f_{1}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{min}^{2}+\,f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{8}{\it\alpha}^{3}u^{0}(y)/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,20f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{3}u^{0}(y)/f_{3}+8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{3}u^{0}(y)/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,18f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{3}u^{0}(y)/f_{3}-8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{2}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,7f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{3}u^{0}(y)/f_{3}-4\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{2}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{2}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}/f_{3}-36f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}/f_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{0,1}^{\overline{{\it\phi}}} & = & \displaystyle -2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{2}\,Re_{c}k_{1}{\it\phi}_{max}^{2}/f_{3}+4\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{2}\,Re_{c}k_{1}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,\text{i}f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y){\it\alpha}^{2}\,Re_{c}p^{0}(y)+4\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{2}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,4\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{2}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}/f_{3}+\frac{1}{2}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y){\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle -\,2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{2}\,Re_{c}k_{1}{\it\phi}_{max}/f_{3}-\text{i}f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y){\it\alpha}^{2}\,Re_{c}u^{0}(y)^{2}\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{2}\,Re_{c}k_{1}{\it\phi}_{max}^{2}/f_{3}+\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{2}\,Re_{c}k_{1}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{4}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y){\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{max}^{2}-10\text{i}f_{1}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\,7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{4}\,Re_{c}k_{2}/f_{3}-18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{4}\,Re_{c}k_{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{4}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y){\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{min}^{2}-\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{4}\,Re_{c}k_{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{2}\,Re_{c}k_{1}/f_{3}+20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{4}\,Re_{c}k_{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{4}\,Re_{c}k_{2}/f_{3}-2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\;f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}^{2}/f_{3}-7f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,14f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}/f_{3}+8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,40f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}/f_{3}-16f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,18f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}^{2}/f_{3}+4\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{2}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,20f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}^{2}/f_{3}+\frac{1}{2}\text{i}f_{1}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{max}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}\text{i}f_{1}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{min}^{2}+\,f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{8}{\it\alpha}^{3}u^{0}(y)/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,20f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{3}u^{0}(y)/f_{3}+8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{3}u^{0}(y)/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,18f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{3}u^{0}(y)/f_{3}-8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{2}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,7f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{3}u^{0}(y)/f_{3}-4\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{2}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{2}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}/f_{3}-36f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{3}u^{0}(y){\it\phi}_{max}/f_{3}.\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle A_{1,1}^{\overline{{\it\phi}}} & = & \displaystyle -f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{3}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}+{\textstyle \frac{1}{2}}f_{1}^{3}f_{2}{\it\phi}^{0}(y){\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}\nonumber\\ \displaystyle & & \displaystyle -\;f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{3}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}+2f_{1}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\;f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{3}+{\textstyle \frac{1}{2}}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y){\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}\nonumber\\ \displaystyle & & \displaystyle -\;f_{1}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}+{\textstyle \frac{1}{2}}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y){\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}f_{1}^{3}f_{2}{\it\phi}^{0}(y){\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}-f_{1}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,2f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{3}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}+f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\phi}_{max}^{3}-2f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle -\,{\textstyle \frac{1}{2}}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\phi}_{min}^{3}-f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y){\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle -\,f_{1}^{3}f_{2}{\it\phi}^{0}(y){\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}-{\textstyle \frac{3}{2}}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\phi}_{max}^{2}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{3}{2}}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\phi}_{max}{\it\phi}_{min}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{1,1}^{\overline{{\it\phi}}} & = & \displaystyle -f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{3}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}+{\textstyle \frac{1}{2}}f_{1}^{3}f_{2}{\it\phi}^{0}(y){\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}\nonumber\\ \displaystyle & & \displaystyle -\;f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{3}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}+2f_{1}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\;f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{3}+{\textstyle \frac{1}{2}}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y){\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}\nonumber\\ \displaystyle & & \displaystyle -\;f_{1}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}+{\textstyle \frac{1}{2}}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y){\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}f_{1}^{3}f_{2}{\it\phi}^{0}(y){\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}-f_{1}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,2f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{3}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}+f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\phi}_{max}^{3}-2f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle -\,{\textstyle \frac{1}{2}}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\phi}_{min}^{3}-f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y){\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle -\,f_{1}^{3}f_{2}{\it\phi}^{0}(y){\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}-{\textstyle \frac{3}{2}}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\phi}_{max}^{2}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{3}{2}}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\phi}_{max}{\it\phi}_{min}^{2}.\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle A_{0,2}^{\overline{{\it\phi}}} & = & \displaystyle 10\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\alpha}{\it\phi}_{max}{\it\phi}_{min}^{2}+20\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\alpha}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\alpha}{\it\phi}_{max}^{3}-10\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)\,Re_{c}{\it\alpha}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle -\,10\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)\,Re_{c}{\it\alpha}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}-{\textstyle \frac{1}{2}}\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\alpha}{\it\phi}_{min}^{3}\nonumber\\ \displaystyle & & \displaystyle -\,20\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\alpha}{\it\phi}_{max}^{2}{\it\phi}_{min}+{\textstyle \frac{1}{2}}\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}{\it\alpha}+10\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\alpha}{\it\phi}_{max}^{3}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}{\it\alpha}+{\textstyle \frac{1}{2}}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle -\,10\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\alpha}{\it\phi}_{max}^{2}-10\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\alpha}{\it\phi}_{min}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,20\text{i}f_{1}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\alpha}{\it\phi}_{max}{\it\phi}_{min}-{\textstyle \frac{3}{2}}\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\alpha}{\it\phi}_{max}^{2}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{3}{2}}\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\alpha}{\it\phi}_{max}{\it\phi}_{min}^{2}-10\text{i}f_{1}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\alpha}{\it\phi}_{max}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,10\text{i}f_{1}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\alpha}{\it\phi}_{min}^{2}+36\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}{\it\phi}_{max}/f_{3}-\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}{\it\phi}_{max}/f_{3}+20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}-40\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,16\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}{\it\phi}_{max}/f_{3}-8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}+7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,14\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}{\it\phi}_{max}/f_{3}-18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}+20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}/f_{3}-8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}/f_{3}-18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}/f_{3}-\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{8}{\it\alpha}/f_{3}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{0,2}^{\overline{{\it\phi}}} & = & \displaystyle 10\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\alpha}{\it\phi}_{max}{\it\phi}_{min}^{2}+20\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\alpha}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\alpha}{\it\phi}_{max}^{3}-10\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)\,Re_{c}{\it\alpha}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle -\,10\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)\,Re_{c}{\it\alpha}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}-{\textstyle \frac{1}{2}}\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\alpha}{\it\phi}_{min}^{3}\nonumber\\ \displaystyle & & \displaystyle -\,20\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\alpha}{\it\phi}_{max}^{2}{\it\phi}_{min}+{\textstyle \frac{1}{2}}\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}{\it\alpha}+10\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\alpha}{\it\phi}_{max}^{3}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}{\it\alpha}+{\textstyle \frac{1}{2}}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle -\,10\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\alpha}{\it\phi}_{max}^{2}-10\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\alpha}{\it\phi}_{min}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,20\text{i}f_{1}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\alpha}{\it\phi}_{max}{\it\phi}_{min}-{\textstyle \frac{3}{2}}\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\alpha}{\it\phi}_{max}^{2}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{3}{2}}\text{i}f_{1}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}I_{0}{\it\alpha}{\it\phi}_{max}{\it\phi}_{min}^{2}-10\text{i}f_{1}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\alpha}{\it\phi}_{max}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,10\text{i}f_{1}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\alpha}{\it\phi}_{min}^{2}+36\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}{\it\phi}_{max}/f_{3}-\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}{\it\phi}_{max}/f_{3}+20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}-40\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,16\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}{\it\phi}_{max}/f_{3}-8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}+7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,14\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}{\it\phi}_{max}/f_{3}-18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}+20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}/f_{3}-8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}/f_{3}-18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}/f_{3}-\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{8}{\it\alpha}/f_{3}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle A_{1,2}^{\overline{{\it\phi}}} & = & \displaystyle -f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y)\,Re_{c}ps0+f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}\,Re_{c}k_{1}{\it\phi}_{max}^{2}/f_{3}-2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}\,Re_{c}k_{1}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,4f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}\,Re_{c}k_{1}{\it\phi}_{max}/f_{3}-2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}\,Re_{c}k_{1}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,4f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}/f_{3}+4f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,14\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}u^{0}(y){\it\alpha}{\it\phi}_{max}/f_{3}-8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}u^{0}(y){\it\alpha}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}u^{0}(y){\it\alpha}{\it\phi}_{max}^{2}/f_{3}+\frac{1}{2}f_{1}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{max}^{2}+\frac{1}{2}f_{1}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{min}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{2}\,Re_{c}k_{2}/f_{3}+20f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{2}\,Re_{c}k_{2}/f_{3}-8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{2}\,Re_{c}k_{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,7f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{2}\,Re_{c}k_{2}/f_{3}-18f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{2}\,Re_{c}k_{2}/f_{3}-2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}\,Re_{c}k_{1}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}\,Re_{c}k_{1}/f_{3}+16\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}u^{0}(y){\it\alpha}{\it\phi}_{max}/f_{3}-18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}u^{0}(y){\it\alpha}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}u^{0}(y){\it\alpha}{\it\phi}_{max}^{2}/f_{3}+20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}u^{0}(y){\it\alpha}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}u^{0}(y){\it\alpha}{\it\phi}_{max}/f_{3}-\frac{1}{4}f_{1}^{3}f_{2}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\phi}_{max}^{2}-\frac{1}{4}f_{1}^{3}f_{2}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\phi}_{min}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,10f_{1}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{max}{\it\phi}_{min}+36\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}u^{0}(y){\it\alpha}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,4f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}^{2}/f_{3}-\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}u^{0}(y){\it\alpha}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}/f_{3}-\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{8}u^{0}(y){\it\alpha}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}f_{1}^{3}f_{2}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\phi}_{max}{\it\phi}_{min}+20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}u^{0}(y){\it\alpha}/f_{3}+7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}u^{0}(y){\it\alpha}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}/f_{3}-40\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}u^{0}(y){\it\alpha}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}u^{0}(y){\it\alpha}{\it\phi}_{max}^{2}/f_{3}-4f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}^{2}/f_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{1,2}^{\overline{{\it\phi}}} & = & \displaystyle -f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y)\,Re_{c}ps0+f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}\,Re_{c}k_{1}{\it\phi}_{max}^{2}/f_{3}-2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}\,Re_{c}k_{1}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,4f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}\,Re_{c}k_{1}{\it\phi}_{max}/f_{3}-2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}\,Re_{c}k_{1}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,4f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}/f_{3}+4f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,14\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}u^{0}(y){\it\alpha}{\it\phi}_{max}/f_{3}-8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}u^{0}(y){\it\alpha}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}u^{0}(y){\it\alpha}{\it\phi}_{max}^{2}/f_{3}+\frac{1}{2}f_{1}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{max}^{2}+\frac{1}{2}f_{1}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{min}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{2}\,Re_{c}k_{2}/f_{3}+20f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{2}\,Re_{c}k_{2}/f_{3}-8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{2}\,Re_{c}k_{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,7f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{2}\,Re_{c}k_{2}/f_{3}-18f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{2}\,Re_{c}k_{2}/f_{3}-2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}\,Re_{c}k_{1}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}\,Re_{c}k_{1}/f_{3}+16\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}u^{0}(y){\it\alpha}{\it\phi}_{max}/f_{3}-18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}u^{0}(y){\it\alpha}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}u^{0}(y){\it\alpha}{\it\phi}_{max}^{2}/f_{3}+20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}u^{0}(y){\it\alpha}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}u^{0}(y){\it\alpha}{\it\phi}_{max}/f_{3}-\frac{1}{4}f_{1}^{3}f_{2}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\phi}_{max}^{2}-\frac{1}{4}f_{1}^{3}f_{2}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\phi}_{min}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,10f_{1}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\phi}_{max}{\it\phi}_{min}+36\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}u^{0}(y){\it\alpha}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,4f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}^{2}/f_{3}-\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}u^{0}(y){\it\alpha}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}/f_{3}-\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{8}u^{0}(y){\it\alpha}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}f_{1}^{3}f_{2}{\it\phi}^{0}(y)\,Re_{c}d_{p}^{2}{\it\phi}_{max}{\it\phi}_{min}+20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}u^{0}(y){\it\alpha}/f_{3}+7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}u^{0}(y){\it\alpha}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}/f_{3}-40\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}u^{0}(y){\it\alpha}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}u^{0}(y){\it\alpha}{\it\phi}_{max}^{2}/f_{3}-4f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}\,Re_{c}\log \left(\frac{1}{1-{\it\phi}^{0}(y)}\right)k_{1}{\it\phi}_{max}^{2}/f_{3}.\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle A_{0,1}^{\overline{u}} & = & \displaystyle 2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}-f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}+2f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle -\,2\text{i}f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}u^{0}(y)-f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{0,1}^{\overline{u}} & = & \displaystyle 2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}-f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}+2f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle -\,2\text{i}f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}u^{0}(y)-f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}.\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle A_{2,1}^{\overline{u}} & = & \displaystyle f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}{\it\alpha}+f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}{\it\alpha}+f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle -\,2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}-2f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle +\,f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}{\it\alpha}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{2,1}^{\overline{u}} & = & \displaystyle f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}{\it\alpha}+f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}{\it\alpha}+f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle -\,2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}-2f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle +\,f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}{\it\alpha}.\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle A_{1,2}^{\overline{u}} & = & \displaystyle 10\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}{\it\alpha}+10\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle -\,20\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}+10\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle +\,10\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}{\it\alpha}-20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{1,2}^{\overline{u}} & = & \displaystyle 10\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}{\it\alpha}+10\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle -\,20\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}+10\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle +\,10\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}{\it\alpha}-20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}.\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle A_{1,1}^{\overline{v}} & = & \displaystyle -2\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}-2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}+\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}-f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}u^{0}(y)\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}+\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{1,1}^{\overline{v}} & = & \displaystyle -2\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}-2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}+\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}-f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}\,Re_{c}u^{0}(y)\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}+\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}.\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle A_{0,2}^{\overline{v}} & = & \displaystyle -10f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}{\it\alpha}^{2}-10f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}{\it\alpha}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,10f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}{\it\alpha}^{2}+20f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,\text{i}f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}u^{0}(y){\it\alpha}-10f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}{\it\alpha}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,20f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{0,2}^{\overline{v}} & = & \displaystyle -10f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}{\it\alpha}^{2}-10f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}{\it\alpha}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,10f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}{\it\alpha}^{2}+20f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}^{2}\nonumber\\ \displaystyle & & \displaystyle -\,\text{i}f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}u^{0}(y){\it\alpha}-10f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}{\it\alpha}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,20f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}^{2}.\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle A_{1,2}^{\overline{v}} & = & \displaystyle -{\textstyle \frac{1}{2}}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\alpha}{\it\phi}_{max}^{2}+10\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle -\,20\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}-20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle -\,{\textstyle \frac{1}{2}}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\alpha}{\it\phi}_{min}^{2}+10\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle +\,10\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}{\it\alpha}+10\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\alpha}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\,10\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}{\it\alpha}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{1,2}^{\overline{v}} & = & \displaystyle -{\textstyle \frac{1}{2}}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\alpha}{\it\phi}_{max}^{2}+10\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle -\,20\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}-20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{max}{\it\phi}_{min}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle -\,{\textstyle \frac{1}{2}}\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\alpha}{\it\phi}_{min}^{2}+10\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{max}^{2}{\it\alpha}\nonumber\\ \displaystyle & & \displaystyle +\,10\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{1}{\it\phi}_{min}^{2}{\it\alpha}+10\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\alpha}{\it\phi}_{max}{\it\phi}_{min}\nonumber\\ \displaystyle & & \displaystyle +\,10\text{i}f_{1}^{2}f_{2}^{3}{\it\phi}^{0}(y)^{2}\,Re_{c}d_{p}^{2}{\it\mu}_{2}{\it\phi}_{min}^{2}{\it\alpha}.\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle B_{0,1}^{\overline{{\it\phi}}} & = & \displaystyle \text{i}f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y){\it\alpha}^{2}\,Re_{c}u^{0}(y)+20f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{3}{\it\phi}_{max}^{2}/f_{3}-40f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{3}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,16f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{3}{\it\phi}_{max}/f_{3}-f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{3}{\it\phi}_{max}^{2}/f_{3}-8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{3}{\it\phi}_{max}/f_{3}+7f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{3}{\it\phi}_{max}^{2}/f_{3}-14f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{3}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,18f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{3}{\it\phi}_{max}^{2}/f_{3}+36f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{3}{\it\phi}_{max}/f_{3}-f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{8}{\it\alpha}^{3}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,20f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{3}/f_{3}-8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{3}/f_{3}-18f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{3}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,7f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{3}/f_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B_{0,1}^{\overline{{\it\phi}}} & = & \displaystyle \text{i}f_{1}^{3}f_{2}^{3}{\it\phi}^{0}(y){\it\alpha}^{2}\,Re_{c}u^{0}(y)+20f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{3}{\it\phi}_{max}^{2}/f_{3}-40f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{3}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,16f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}^{3}{\it\phi}_{max}/f_{3}-f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{3}{\it\phi}_{max}^{2}/f_{3}-8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}^{3}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,2f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{3}{\it\phi}_{max}/f_{3}+7f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{3}{\it\phi}_{max}^{2}/f_{3}-14f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{3}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,18f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{3}{\it\phi}_{max}^{2}/f_{3}+36f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{3}{\it\phi}_{max}/f_{3}-f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{8}{\it\alpha}^{3}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,20f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}^{3}/f_{3}-8f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}^{3}/f_{3}-18f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}^{3}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,7f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}^{3}/f_{3}.\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle B_{1,2}^{\overline{{\it\phi}}} & = & \displaystyle -36\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}{\it\phi}_{max}/f_{3}+\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{8}{\it\alpha}/f_{3}+18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}/f_{3}-7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}/f_{3}+40\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}+14\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}{\it\phi}_{max}/f_{3}+8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}-2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}{\it\phi}_{max}/f_{3}-16\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}+\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}-20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}/f_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B_{1,2}^{\overline{{\it\phi}}} & = & \displaystyle -36\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}{\it\phi}_{max}/f_{3}+\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{8}{\it\alpha}/f_{3}+18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}/f_{3}-7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}/f_{3}+40\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}+14\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}{\it\phi}_{max}/f_{3}+8\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{2}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}\nonumber\\ \displaystyle & & \displaystyle -\,7\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}-2\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{7}{\it\alpha}{\it\phi}_{max}/f_{3}-16\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{3}{\it\alpha}{\it\phi}_{max}/f_{3}\nonumber\\ \displaystyle & & \displaystyle +\,18\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{4}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}+\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{6}{\it\alpha}{\it\phi}_{max}^{2}/f_{3}-20\text{i}f_{1}^{3}f_{2}{\it\phi}^{0}(y)^{5}{\it\alpha}/f_{3}.\end{eqnarray}$$
Besides the above, all the remaining components of these matrices are identically equal to zero.