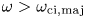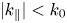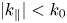1. Introduction
Experimentally, it has long been shown that switching from a monopole phasing to a dipole one greatly reduces the impurity released by an antenna (TFR Group et al. 1985; Messiaen et al. Reference Messiaen, Beuken, De Keyser, Delvigne, Descamps, Durodie, Gaigneaux, Jadoul, Koch and Lebeau1989; Bures et al. Reference Bures, Brinkschulte, Jacquinot, Lawson, Kaye and Tagle2000). These two phasings mainly differ from the main wavenumber parallel to the magnetic field 
$k_{\parallel }$ they excite in the antenna power spectrum. The monopole phasing mainly excites low values of 
$k_{\parallel }$ while the dipole cancels the excitation of 
$|k_{\parallel}| < k_0$, 
$k_0$ being the vacuum wavenumber.
The reasons for the first dipole excitation attempt were dual (TFR Group et al. 1985).
(i) It was known that the power spectrum should mainly excite sufficiently large
$k_{\parallel }$ to maximize absorption in the plasma core. It is important as all power remaining in the edge can interfere with plasma facing components (known as PFCs) and can ultimately create sputtering (e.g. through sheath rectification mechanism Myra et al. (Reference Myra, D'Ippolito, Russell, Berry, Jaeger and Carter2006)).(ii) Edge power deposition mechanisms using surface or coaxial modes, first proposed by Messiaen et al. (Reference Messiaen, Koch, Bhatnagar, Vandenplas and Weynants1984) and then revisited multiple times (Berro & Morales Reference Berro and Morales1990; Murphy Reference Murphy1990; Lawson Reference Lawson1992), were feared to enhance impurity release.
A recent discussion of coaxial modes and surface wave excitation (Messiaen & Maquet Reference Messiaen and Maquet2020) shows that an ICRF antenna, in the presence of a lower hybrid (LH) resonance in the edge region, can excite large fields in the scrape-off layer (SOL) due to a confluence between the fast wave and the slow one for low 
$|k_{\parallel }| < k_0$ components of the antenna power spectrum. These modes, characterized by large radial electric fields 
$E_x$, propagate along the plasma edge toroidally far from the antenna location as coaxial or surface modes. The same paper shows that a good way to circumvent those modes is to avoid the excitation of the lower 
$|k_{\parallel }| < k_0$ part of the power spectrum (which we indicate in what follows as coaxial part of the power spectrum).
The conditions to obtain an excellent rejection of the coaxial part of the spectrum for an array of toroidally spaced straps are also given in Messiaen & Maquet (Reference Messiaen and Maquet2020) and constrain the current amplitude distribution in the Fourier domain to
\begin{equation} \left. {J(k_{\parallel})}\right|_{k_{\parallel}=0}=0 \quad \text{and} \quad \left. {\frac{\partial J(k_{\parallel})}{\partial k_{\parallel}}}\right|_{k_{\parallel}=0} = 0. \end{equation}
These conditions are fulfilled when the vectorial sum of the current 
${I}_i$ and the toroidal positions 
$z_{strap}\equiv S_{z,i}$ of strap 
$i$ verify
\begin{equation} \sum_i {I}_i = 0 \quad \text{and} \quad \sum_i {I}_i S_{z,i} = 0. \end{equation}
From these conditions, it is clear that a 2-strap antenna can only meet the first condition using a dipole phasing. A symmetric 3-strap antenna can verify both conditions only in one particular case where the current amplitude in the middle strap is twice as large compared with that in the outer straps using a 
$(0{\rm \pi} 0)$ phasing. A 4-strap antenna has even more flexibility as it can satisfy this particular condition for multiple relative strap phasings and current amplitude distributions. Examples of this greater flexibility will be discussed below. Finally, it should be noted that spectra meeting condition (1.2a,b) do not always provide a suitable heating scheme.
Recently, a drastic reduction in impurity release was demonstrated on ASDEX Upgrade (AUG) using a 3-strap antenna for a ratio of power 
$P_{\textrm {central}}/P_{\textrm {tot}} \approx 0.67$ between inner straps and the total power imposed for a fixed toroidal phasing 
$(0{\rm \pi} 0)$ (Bobkov et al. Reference Bobkov, Aguiam, Bilato, Brezinsek, Colas, Faugel, Fünfgelder, Herrmann, Jacquot and Kallenbach2016a). Those results were attributed to local radio frequency (RF) electric fields and RF image currents on the limiters of the antenna (Bobkov et al. Reference Bobkov, Bilato, Colas, Dux, Faudot, Faugel, Fünfgelder, Herrmann, Jacquot and Kallenbach2017).
The aim of this paper is to study the results of AUG and Alcator C-Mod applying the new criterion mentioned above, i.e. avoiding the excitation of modes verifying 
$|k_{\parallel }| < k_0$. We first introduce the model used for the study in § 2. Section 3 shows that the 3-strap antenna, on top of minimizing the parallel electric field and image currents around the antenna structure, also minimizes the excitation of the low-
$k_{\parallel }$ coaxial part of the power spectrum. The same approach is then used to analyse similar Alcator C-Mod results and reproduce the outcome of a not yet published experiment in JET. Finally, we briefly apply this method to the next generation devices ITER and DEMO in § 4.
2. ANTITER II description
The code ANTITER II is a fast semianalytic code describing in plane geometry the antenna in front of a plasma or a dielectric using a Fourier analysis in the toroidal 
$z$ and poloidal 
$y$ directions and numerical integration in the radial direction 
$x$. The antenna is described by a set of boxes containing one or several infinitely thin straps recessed in a metal wall. An ideal Faraday screen (known as FS) is assumed at the antenna mouth together with single-pass absorption in the plasma. The geometry used by ANTITER II is summarized in figure 1 and a description of the code is given in the appendix of Messiaen et al. (Reference Messiaen, Koch, Weynants, Dumortier, Louche, Maggiora and Milanesio2010). The fact that the antenna is treated as recessed in a metal wall can deviate from experimental conditions. Nevertheless, together with the ideal Faraday screen, this recess creates the optimal conditions to avoid any unwanted side excitation of transverse magnetic (TM
$_z$) modes due to side boundary conditions.
Figure 1. The ANTITER II geometry. The 
$x$, 
$y$, 
$z$ axis corresponds to the radial, poloidal and toroidal direction, respectively. The vacuum layer is optional (Messiaen et al. Reference Messiaen, Koch, Weynants, Dumortier, Louche, Maggiora and Milanesio2010).
The present work is entirely based on ANTITER II and focuses on the antenna radiated power spectrum. This implies that:
(a) all antennas are described by simplified plane geometries;
(b) the tokamak parameters and electron density profiles are either predicted by a transport code (as the ITER 2010low) or reconstructed from the available references;
(c) the toroidal and poloidal periodicity of each device is taken into account through their
$k_{\parallel ,n}$ $k_{y,m}$ eigenmodes; and(d) the tilting of the magnetic field with respect to the antenna is not considered for this study, such that
$k_{\parallel }\equiv k_z$, in order to reduce the complexity of the problem.
In the ANTITER simulations, the JET and ITER profiles include a LH resonance while the AUG and Alcator C-Mod ones do not. Regardless, the LH presence in the profiles is not guaranteed in all experimental situations. In this hypothesis, there is no direct excitation of coaxial modes due to the LH resonance and thus the low-
$k_{\parallel }$ part excited in the power spectrum is reduced. However, its variation with respect to other parameters (e.g. current distribution in phase and amplitude) stays unchanged. Moreover, the IC absorption is reduced at low 
$| k_{\parallel } |$ such that this low-
$k_{\parallel }$ region of the power spectrum can also be linked to bad absorption. The LH resonance could also appear in front of the antenna due to ponderomotive forces (e.g. Van Nieuwenhove, Koch & Van Oost Reference Van Nieuwenhove, Koch and Van Oost1994; Van Eester, Crombé & Kyrytsya Reference Van Eester, Crombé and Kyrytsya2013). Consequently, all machines are discussed in the same way in the following sections.
For a fixed geometry, the antenna power spectrum can be shaped by changing the current distribution over the straps in amplitude and phase. Using ANTITER II, one can compute the following.
(i) Ptot is given by the integral over the discrete normalized power spectrum radiated by the antenna,
(2.1)where\begin{equation} P_{\textrm{tot}}=\int P_{\textrm{rad}}(k_y,k_{\parallel}) \, \textrm{d} k_{\parallel} \, \textrm{d} k_y =1\ \text{W}, \end{equation}$k_y$ and $k_{\parallel }$ represents the toroidal and poloidal wavenumbers. This normalization allows an easy comparison between different spectra for the same power coupled to the plasma. For the sake of completeness, one can also define the $k_y$ and $k_z$ power spectra $P_{\textrm {rad},z}(k_{\parallel })$ and $P_{\textrm {rad},y}(k_y)$ obtained by the summation of $P_{\textrm {rad}}(k_y,k_{\parallel })$, respectively, over $k_{y,m}$ and $k_{\parallel ,n}$ terms.(ii) The current, voltage and power at the feeder of the antenna computed from the impedance matrix. The method used consists of imposing the current distribution in amplitude and phase on the straps and computing, using the impedance matrix, the corresponding voltages and power imposed at the feeders. In what follows, we use the ratio of the power between the straps and not the ratio of the current amplitude launched by the straps as the parameter determining the shape of the power spectrum, in order to simplify the comparison with the experimental measurements available. This particular point is further discussed in appendix A. For the same reason, two different power ratios
$P_{\textrm {central}}/P_{\textrm {outer}}$ and $P_{\textrm {central}}/P_{\textrm {tot}}$ are used when comparing simulations and experimental data.
The ratio 
$\rho =P_{\textrm {rad},z}(|k_{\parallel }|\leq k_0)/P_{\textrm {rad},\textrm {tot}}$, where 
$P_{\textrm {rad}}(|k_{\parallel }|\leq k_0)$ is the coaxial part of the power spectrum and 
$P_{\textrm {rad},\textrm {tot}}$ is the total power radiated, is also computed. This particular ratio is chosen because it can either be used to characterize a bad absorption of power in the plasma core or as a direct loss of power put into the excitation of coaxial and surface waves.
While the link between 
$\rho$ and the impurity release is not direct, bad absorption can contribute to RF power losses in the edge. Moreover, the excitation of the slow wave at its confluence with the fast one leads to large radial and toroidal electric fields that could be responsible for convective cells or enhanced sheath rectification (Myra et al. Reference Myra, D'Ippolito, Russell, Berry, Jaeger and Carter2006).
3. Assessment of the experiments with ANTITER II
3.1. AUG experiment
The 3-strap antenna geometry is modelled in ANTITER II by three antenna boxes, to take into account the presence of septa. In AUG, the central box contains a large central strap. The side boxes each contain one central narrower actively powered strap and one short-circuited passive strap on the sides that are not powered directly. Two different geometry approximations of the 3-strap antenna of AUG were considered in ANTITER II as presented in figure 2. The first one considers the short-circuited (passive) side straps of AUG as part of the metal wall while the second one adds two passive side straps where the currents flowing on those passive straps is induced by mutual coupling.
Figure 2. The two geometries considered for the study of the AUG antenna in ANTITER II.
In order to determine which two-dimensional antenna geometry best fits the characteristics of the real antenna, the power spectrum computed with the three-dimensional (3-D) electromagnetic software HFFS (ANSYS 2020), using an antenna in front of a dielectric (Bobkov et al. Reference Bobkov, Braun, Dux, Herrmann, Faugel, Fünfgelder, Kallenbach, Neu, Noterdaeme and Ochoukov2016b), has been compared with that computed by ANTITER II with the antenna in front of a plasma. The two geometries considered lead to similar results and the second one is chosen for its greater similarity with the real geometry. The power spectra calculated by HFSS and ANTITER II are presented in figures 3 and 4 for three different power ratios between inner and outer straps, 
$P_{\textrm {central}}/P_{\textrm {outer}}$, equal to 0.1, 2 and 10. While there is a difference between the two spectra, their general characteristics correspond. The difference could lay in the antenna geometry used, in the way power spectra are computed or in the dielectric and plasma loads used in HFSS and ANTITER II. It is also important to note that, in this case, changing the ratio 
$P_{\textrm {central}}/P_{\textrm {outer}}$ mainly changes the lower coaxial part of the power spectrum and not the dominant 
$k_{\parallel }$ excited. This low 
$k_{\parallel }$ part of the power spectrum can then be seen as power lost into coaxial and surface modes or as power not absorbed into the plasma core.
Figure 3. The HFSS result. The AUG 3-strap antenna power spectrum in front of a dielectric (Bobkov et al. Reference Bobkov, Braun, Dux, Herrmann, Faugel, Fünfgelder, Kallenbach, Neu, Noterdaeme and Ochoukov2016b).
Figure 4. The ANTITER II three strap + passive strap model result. The normalized power spectrum calculated for different power ratios 
$P_{\textrm {central}}/P_{\textrm {outer}}$. The low-
$k_{\parallel }$ part of the power spectrum lies between the dashed lines.
In what follows we will analyse the AUG results, not using the local parallel electric fields and image currents as was previously done, but using the low-
$k_{\parallel }$ coaxial part of the power spectrum.
Measurements of the core tungsten 
$(W)$ concentration 
$\Delta c_{W}$, along with the average 
$W$ sputtering yield 
$\Delta Y_W$ as a function of the power ratio fed between the inner and outer straps for a fixed 
$(0{\rm \pi} 0)$ phasing, are shown in figure 5. In comparison, figure 6 presents the power ratio 
$\rho$ of the power spectrum in % as a function of 
$P_{\textrm {central}}/P_{\textrm {outer}}$. One can spot several similarities with the measurements, including a common minimum for a power ratio 
$P_{\textrm {central}}/P_{\textrm {outer}}\approx 1.5$ and the same asymmetry around this minimum. For the phasing 
$(0{\rm \pi} 0)$, the minimum found corresponds to a strap current amplitude distribution of 
$(1,2,1)$.
Figure 5. The AUG result. Tungsten core concentration 
$\Delta \text {c}_{W}$ and average tungsten sputtering yield 
$\Delta Y_W$ as a function of 
$P_{\textrm {central}}/P_{\textrm {outer}}$ measured in AUG (Bobkov et al. Reference Bobkov, Braun, Dux, Herrmann, Faugel, Fünfgelder, Kallenbach, Neu, Noterdaeme and Ochoukov2016b).
Figure 6. The ANTITER II result. Coaxial part of the power spectrum 
$\rho$ in % as a function of 
$P_{\textrm {central}}/P_{\textrm {outer}}$.
As the AUG antenna straps have a complex folded shape, the relation between power, voltage and current is not guaranteed to be reproduced exactly by the approximate geometry used in ANTITER II. Indeed, the impedance/scattering matrices calculated by ANTITER II and those calculated by HFSS for the AUG antenna are not identical. Nevertheless, the variation of the low-
$k_{\parallel }$ part of the power spectrum as a function of the power ratio between the straps of figure 3 computed by HFSS in Bobkov et al. (Reference Bobkov, Braun, Dux, Herrmann, Faugel, Fünfgelder, Kallenbach, Neu, Noterdaeme and Ochoukov2016b) and figure 6 have similar characteristics, indicating the possible relationship between the impurity release and the coaxial part of the power spectrum.
A final test consists of comparing the power ratio 
$\rho$ and the core impurity concentration 
$\Delta c_W$ as a function of the ratio between the inner and total power fed to straps 
$P_{\textrm {central}}/P_{\textrm {tot}}$ and a phase deviation 
$\Delta \phi$ from the fixed phasing 
$(0{\rm \pi} 0)$ imposed and implemented as (
$0\, {\rm \pi} + \Delta \phi\, 0$). This comparison is presented in figures 7 and 8. Once again, the minimum around 
$P_{\textrm {central}}/P_{\textrm {tot}} \approx 0.67$ and characteristic behaviour around this minimum are similar on both figures.
Figure 7. The AUG result. Measurement of the increment of core 
$W$ content 
$\Delta \text {c}_{W}$ as a function of 
$P_{\textrm {central}}/P_{\textrm {tot}}$ and 
$\Delta \phi$ (Bobkov et al. Reference Bobkov, Aguiam, Bilato, Brezinsek, Colas, Czarnecka, Dumortier, Dux, Faugel and Fünfgelder2019).
Figure 8. The ANTITER II result. Coaxial part of the power spectrum 
$\rho$ in % as a function of 
$P_{\textrm {central}}/P_{\textrm {tot}}$ and 
$\Delta \phi$.
The two results obtained using the coaxial part of the power spectrum seem to correlate well with the measurements of average impurity yield and core content of the AUG device. While the result of the AUG 3-strap antenna can be attributed to the minimization of parallel electric fields and image currents, the antenna also minimizes the coaxial part of the power spectrum. This last fact can be related to an improvement in core absorption in AUG, or, in the presence of the LH resonance, to coaxial and surface mode elimination in the edge.
3.2. Alcator C-Mod experiment
The AUG method to reduce ion cyclotron resonance heating (ICRH) induced impurity release was also successfully applied on Alcator C-Mod field-aligned (FA) antenna using a 
$(0{\rm \pi} 0{\rm \pi} )$ phasing and varying the power ratio fed between the two inner and outer straps 
$P_{\textrm {central}}/P_{\textrm {tot}}$ (Wukitch et al. Reference Wukitch2017). The experiments monitored the antenna impurity release, the far-field impurity sources and the RF enhanced plasma potential.
The approximate antenna geometry that was used in ANTITER II is presented in figure 9. The corresponding power spectrum for the 
$(0{\rm \pi} 0{\rm \pi} )$ phasing and three different ratios 
$P_{\textrm {central}}/P_{\textrm {tot}}$ is presented in figure 10. This figure includes the spectrum corresponding to the minimum coaxial mode excitation and obtained for a power ratio 
$P_{\textrm {central}}/P_{\textrm {tot}}\approx 0.89$. This very good rejection of coaxial modes corresponds to a current amplitude distribution of 
$[1,3,3,1]$ in ANTITER II and can be derived using the relations (1.2a,b).
Figure 9. Antenna geometry approximation of Alcator C-Mod FA considered in ANTITER II.
Figure 10. Power spectrum found for three power ratio 
$P_{\textrm {central}}/P_{\textrm {tot}}$ using ANTITER II.
The antenna induced and core impurity content that was measured in Alcator C-Mod as a function of the power ratio 
$P_{\textrm {central}}/P_{\textrm {tot}}$ are presented in figures 11 and 12. The RF enhanced plasma potential is also presented in figure 13 as it is believed by the Alcator C-Mod team to be a measure of the turbulent effect caused by the RF power on the far SOL and is considered to be closely related to the impurity transport (Cziegler et al. Reference Cziegler, Terry, Wukitch, Garrett, Lau and Lin2012). In comparison, the coaxial part of the power spectrum 
$\rho$ as a function of the power ratio 
$P_{\textrm {central}}/P_{\textrm {tot}}$ is computed using ANTITER II and presented in figure 14.
Figure 11. The Alcator C-Mod result. Antenna RF induced impurity content measured as a function of 
$P_{\textrm {central}}/P_{\textrm {tot}}$ in the presentation of Wukitch et al. (Reference Wukitch2017), slide 9.
Figure 12. The Alcator C-Mod result. Core impurity measured as a function of 
$P_{\textrm {central}}/P_{\textrm {tot}}$ in the presentation of Wukitch et al. (Reference Wukitch2017), slide 10.
Figure 13. The Alcator C-Mod result. The RF enhanced potential measured as a function of 
$P_{\textrm {central}}/P_{\textrm {tot}}$ in the presentation of Wukitch et al. (Reference Wukitch2017), slide 16.
Figure 14. The ANTITER II result. Ratio of coaxial power spectrum 
$\rho$ in % as a function of 
$P_{\textrm {central}}/P_{\textrm {tot}}$.
Comparing these four figures, a small difference between minima can be found but the asymmetry around these minima is globally reproduced. The small difference remaining may be due to the difference between the simplified model of boxes used in ANTITER II and the real geometry of the Alcator C-Mod antenna with its folded straps.
Another possibility for this difference may be due to the very good antenna coupling to the plasma in Alcator C-Mod leading to a power spectrum having large dominant 
$k_{\parallel }$. Under these conditions, the coaxial part of the power spectrum is much smaller and could lead to less reliable results. To illustrate this, one can note that the coaxial part of the power spectrum is an order of magnitude smaller in Alcator C-Mod (seen in figure 14) than that for the AUG case (seen in figure 6) and thus could have less impact on the impurity release.
3.3. JET experiment
One can now try to describe the outcome of not yet published ‘AUG-like’ experiments in JET (V. Bobkov, private communication 2019). The A2 antenna geometry used in ANTITER II is presented figure 15 and several phasing cases are presented figure 16. From the previous discussions, the two most relevant phasings in a future JET experiment are the dipole 
$(0{\rm \pi} 0{\rm \pi} )$ and symmetric dipole 
$(0{\rm \pi} {\rm \pi} 0)$ phasing of the JET A2 antenna. The coaxial part of the power spectrum 
$\rho$ for those phasings is plotted in figures 17 and 18. The power spectrum for the two antenna phasings corresponding to the optimum ratio 
$P_{\textrm {central}}/P_{\textrm {tot}}$ for coaxial rejection is presented in figure 19. These optimum ratios correspond to a current amplitude distribution of 
$[1,3,3,1]$ and 
$[1,1,1,1]$ for the 
$(0{\rm \pi} 0{\rm \pi} )$ and 
$(0{\rm \pi} {\rm \pi} 0)$ phasings, respectively. From the power contained in the lower 
$k_{\parallel }$ part of the power spectrum, shown in figure 19, the dominant 
$k_{\parallel }$ excited and previous experiments (Czarnecka et al. Reference Czarnecka, Durodié, Figueiredo, Lawson, Lerche, Mayoral, Ongena, Van Eester, Zastrow and Bobkov2012), one can also expect a greater impurity release in the 
$(0{\rm \pi} {\rm \pi} 0)$ phasing compared with the 
$(0{\rm \pi} 0{\rm \pi} )$. However, while the early results of the experiment seem to correlate with the predictions, those results have to be taken with caution as the calculated minimum can be shifted compared with the experimental one due to the complex geometry of the A2 antennas.
Figure 15. The JET A2 Antenna geometry considered in ANTITER II.
Figure 16. Power spectrum for different phasing of JET A2 antenna.
Figure 17. Coaxial part of the power spectrum 
$\rho$ in % as a function of 
$P_{\textrm {central}}/P_{\textrm {tot}}$.
Figure 18. Coaxial part of the power spectrum 
$\rho$ in % as a function of 
$P_{\textrm {central}}/P_{\textrm {tot}}$.
Figure 19. Power spectrum of phasing 
$(0{\rm \pi} 0{\rm \pi} )$ and 
$(0{\rm \pi} {\rm \pi} 0)$ for the optimum power ratio 
$P_{\textrm {central}}/P_{\textrm {tot}}\approx 0.85$ and 0.5. These power ratios corresponds to a current amplitude distribution of 
$[1,1,1,1]$ and 
$[1,3,3,1]$.
Taking the same criterion of coaxial rejection for minimal impurity production by ICRH, one can try to select a specific parallel wavenumber 
$k_{\parallel }$ while avoiding the excitation of the low-
$k_{\parallel }$ part of the power spectrum. For example, using ANTITER II, and changing the strap current distribution in phase and amplitude, it is possible to find phasings with different dominant 
$k_{\parallel }$ that have an asymmetric power spectrum but avoid the unwanted region. This is shown in figure 20.
Figure 20. Two special power spectra: phasing 
$(0.00, 3.42, 0.65, 4.05)$ and power balance 
$P_{\textrm {central}}/P_{\textrm {tot}}=0.83$, (blue); phasing 
$(0, 2.96, 3.56, 0.24)$ and power balance 
$P_{\textrm {central}}/P_{\textrm {tot}}=0.5$, (orange). These power ratios corresponds to a current amplitude distribution of 
$[1,2.3,2.3,1]$ and 
$[1,1,1,1]$.
4. ITER and DEMO
4.1. ITER
The ITER antenna is composed of 24 straps grouped into eight triplets. The ITER antenna model used in ANTITER II is presented in figure 21 where the eight triplets are approximated by eight long straps. Corresponding power spectra for various phasing and an even current amplitude distribution are presented in figure 22.
Figure 21. The ITER antenna geometry considered in ANTITER II.
Figure 22. The ITER normalized power spectrum for various phasing using ANTITER II.
The two most promising phasings are 
$(0{\rm \pi} {\rm \pi} 0)$ and 
$(0{\rm \pi} 0{\rm \pi} )$. A detailed 3-D plot of the respective power spectra around their coaxial part is shown figure 23. One can see that the 
$(0{\rm \pi} {\rm \pi} 0)$ case has a behaviour similar to the 3-strap AUG antenna in that it rejects efficiently the coaxial part of the spectrum. It could then be a very good candidate for impurity minimization in future ITER experiments given a sufficiently good ‘single-pass absorption’ of its dominant excited 
$k_{\parallel }\approx 5\ \textrm {m}^{-1}$.
Figure 23. The ITER normalized 3-D power spectrum around the coaxial part for 
$(0{\rm \pi} 0{\rm \pi} )$ and 
$(0{\rm \pi} {\rm \pi} 0)$ phasing.
One can still apply the AUG method of varying the power ratio 
$P_{\textrm {central}}/P_{\textrm {tot}}$ and look at the coaxial part of the power spectrum to see if a minimum can be obtained in those cases. This is presented in figure 24. One can see a clear minimum for the coaxial mode excitation in the 
$(0{\rm \pi} {\rm \pi} 0)$ case for a power balance 
$P_{\textrm {central}}/P_{\textrm {tot}}\approx 0.46$ and in the 
$(0{\rm \pi} 0{\rm \pi} )$ case for 
$P_{\textrm {central}}/P_{\textrm {tot}}\approx 0.9$. The current amplitude distribution for the optimum case in ITER corresponds to the same optimal current amplitude distribution as JET and the power spectra corresponding to those two optimal cases are presented in figure 25. One can also obtain non-conventional phasings that avoid a large excitation of the coaxial part of the power spectrum. In the case presented, a very clear asymmetrical power spectrum is obtained with an even current amplitude distribution on all straps as shown in figure 26.
Figure 24. Coaxial part 
$\rho$ of the power spectrum as a function of 
$P_{\textrm {central}}/P_{\textrm {tot}}$ and phase deviation 
$\Delta \phi$.
Figure 25. Normalized power spectrum for the 
$(0{\rm \pi} 0{\rm \pi} )$ and 
$(0{\rm \pi} {\rm \pi} 0)$ phasing for a corresponding power ratio of 
$P_{\textrm {central}}/P_{\textrm {tot}}\approx$ 0.45 and 0.9. These power ratios correspond to a current amplitude distribution of 
$[1,1,1,1]$ and 
$[1,3,3,1]$ on the strap.
Figure 26. Normalized power spectrum for an even current amplitude distribution in the current drive case and for a special phasing 
$(0.00,2.93,3.65,0.29)$ that eliminates the power in the coaxial part of the power spectrum.
4.2. DEMO
In order to benefit from the return of experience of ITER, an in-port solution is considered for the future demonstration power plant (DEMO). A travelling wave antenna (known as TWA) is also considered as a backup option (Ragona et al. Reference Ragona, Messiaen, Ongena, Van Eester, Van Schoor, Bernard, Hillairet and Noterdaeme2019).
Compared with ITER, the standard port of DEMO will have (i) a smaller toroidal extension and (ii) a larger poloidal extension. To better optimize the available port space, quadruplets could replace the ITER triplets. If a DEMO antenna could be implemented with a larger toroidal extension like the ITER antenna (see figure 27), the goal of 50 MW coupled could be achieved with three or four such antenna using 
$(0{\rm \pi} {\rm \pi} 0)$ phasing. Lacking a realistic SOL profile for DEMO, these numbers assume the characteristic profile 2010low (S. Carpentier & R. Pitts, private communication 2010) usually used in ITER and are presented in figure 28 where the power coupled by ITER and DEMO antenna of figures 21 and 27 is computed using ANTITER II for different relative phasings and an even current amplitude distribution between straps. Provided such a configuration is possible, the discussions about coaxial rejection in ITER are applicable for DEMO.
Figure 27. The DEMO antenna geometry considered with quadruplets instead of triplets to benefit of the larger poloidal extent of the present DEMO port configuration.
Figure 28. Comparison of the power coupled for 41 kV imposed at each straps between ITER (dots) and DEMO (triangles) antenna.
5. Conclusion
In this paper, we show that minimizing the power in the low 
$|k_{\parallel }| < k_0$ part of the power spectrum correlates well with minimizing the ICRH induced impurity release. This is first illustrated with experimental observations of AUG using a 3-strap antenna. The success of the AUG 3-strap antenna was up to now qualitatively correlated with minimizing the peaked parallel electric field and RF image currents around the antenna frame. The proposed criterion is a complementary way to explain those results. We then further substantiate the validity of this criterion with observations from experiments performed on Alcator C-Mod and try to reproduce the outcome of a not yet published JET experiment. Finally, we predict antenna current and phasing configurations to minimize the ICRH induced impurity release on JET, the planned ITER antenna and its possible future upgrade to DEMO for the 
$(0{\rm \pi} {\rm \pi} 0)$ and 
$(0{\rm \pi} 0{\rm \pi} )$ phasing.
Acknowledgements
V.M. would like to thank R. Ragona for his constant and communicative interest in the field. V.M. would also like to thank J. Ongena for his careful supervision and revision of the work. V.M. would also like to thank IPP team for the multiple lively discussions shared and V. Bobkov for his precious feedback on the paper. This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 and 2019–2020 under grant agreement no 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission.
Editor Tünde Fülöp thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Relationship between strap current distribution and radiated power by the antenna
The relationship between the current distribution on the straps and the power radiated by the antenna is discussed using the example of the simplest AUG 3-strap geometry shown in figure 2(a). Here again, we stress that the current imposed on the straps is used to compute the remaining quantities because it is this current that determines the shape of the antenna radiated power spectrum.
Using ANTITER II, one can compute the impedance matrix 
$Z$ of the antenna geometry considered. This is made possible by using an even–odd unitary excitation of the ports and the matrix found for the 3-strap case is of the form
\begin{equation} Z = \left[\begin{array}{ccc} 5.3740 -72.8146i & -0.5197 + 1.3883i & -0.2938 + 1.8706i \\ -0.5197 + 1.3883i & 7.6267 -55.0446i & -0.5200 + 1.3780i \\ -0.2938 + 1.8706i & -0.5200 + 1.3780i & 5.3740 -72.8146i \end{array}\right]. \end{equation} This matrix relates the voltage and currents at the ports 
$V=ZI$ and gives access to the power fed at each ports using 
$P_i=V_iI_i^*/2$. It is the ratio of these port powers (e.g. 
$P_{\textrm {central}}/P_{\textrm {tot}}$ and 
$P_{\textrm {central}}/P_{\textrm {outer}}$) that are used throughout the paper. The power of each port 
$P_i$ corresponds to the sum of the self and mutual power of the strap considered:
\begin{equation} P_i = \sum_j P_{i,j} \quad \text{where} \ P_{i,j}=\tfrac{1}{2} Z_{i,j} I_j I_i^*. \end{equation}Consequently, the method used in the paper consists of
(i) first imposing a set of values for the current
$I$ at the strap port and then computing, via the matrix impedance $Z$, the associated port voltages;(ii) from these two values, the corresponding power fed at the port can be obtained; and
(iii) the same current distribution can also be used to derive the power spectrum.
