Experimental setup

For coherent imaging, a certain degree of spatial and temporal coherence is required. In laser-plasma sources, the plasma is usually not confined in any way, which results in Gaussian-type plasma intensity distribution, Wachulak et al. (Reference Wachulak, Bartnik, Skorupka, Kostecki, Jarocki, Szczurek, Wegrzynski, Fok and Fiedorowicz2013b). In our case, the size of the plasma in the EUV spectral region is ~1 mm in diameter, so it can be hardly considered as a point source for applications requiring increased spatial coherence for the experiment. To perform coherent type imaging, using previously mentioned laser-plasma EUV source based on a double stream gas puff target, a partially coherent emission have to be achieved. It is done by spatial and spectral filtering of the quasi-continuous emission from the source.

The experimental setup for the EUV holography using the emission from xenon plasma is depicted in Figure 1a. A Nd:YAG laser beam, emitted from NL 129 laser system (10 J/1–10 ns), from EKSPLA, Lithuania, with laser pulse energy of 4.5 J and 4.3 ns time duration is focused by an f = 10 cm focal length lens onto a double stream gas puff target. The target is formed by axisymmetric, collinear, double nozzle, driven separately by two electromagnetic valves. The diameters of the nozzles are 0.4 mm for the inner nozzle and 0.7–1.5 mm for the outer, ring-shaped nozzle. The inner nozzle was pressurized with xenon gas at 8 bar backing pressure, while the outer nozzle was connected to helium pressurized to 6 bars. The double-stream gas puff target was used to increase the gas puff target density, by shaping the flow of the inner gas into a vacuum through the use of the outer gas. In such case higher inner gas density can be obtained at 1.5 mm away from the nozzle to avoid degradation of the nozzle by a repeatable plasma formation. The valves were driven separately by a dedicated two-channel controller, which is capable of independent adjustment of the delay and opening time for each valve. Moreover, driving signals for both valves are synchronized with the laser power supply, which produces a triggering pulse 1 ms before the laser pulse. The delay time and opening times for each valve are 200/750 µs (Xe) and 400/550 µs (He), respectively. More details about the timing and valve synchronization can be found in Wachulak et al. (Reference Wachulak, Bartnik, Fiedorowicz, Feigl, Jarocki, Kostecki, Rakowski, Rudawski, Sawicka, Szczurek, Szczurek and Zawadzki2010). Due to the interaction of the laser pulses with the gaseous target a laser produced plasma is created, which emits radiation in the broad range of wavelengths, from soft X-rays to infrared, depending on the gas used as a target, laser beam and focusing system parameters. In this experiment, an efficient EUV emission was achieved from xenon gas, as was reported by Rakowski et al. (Reference Rakowski, Bartnik, Fiedorowicz, de Gaufridy de Dortan, Jarocki, Kostecki, Mikołajczyk, Ryć, Szczurek and Wachulak2010) and Wachulak et al. (Reference Wachulak, Sarzyński, Bartnik, Fok, Węgrzynski, Kostecki and Fiedorowicz2017).

Fig. 1. Schematic description of the experimental setup for EUV holographic imaging employing (a) and the emission spectrum from the Xe/He double stream gas puff target source (b).

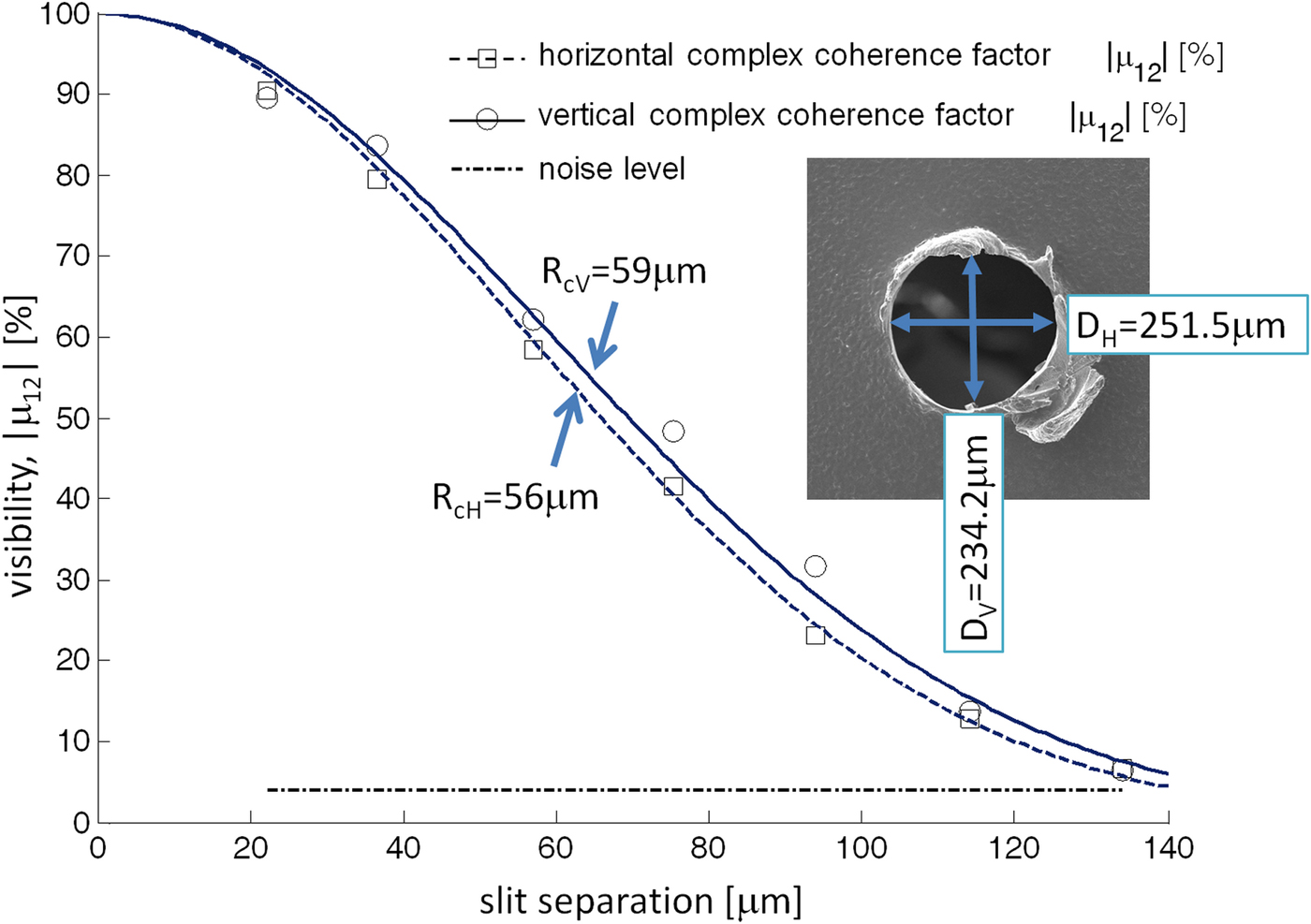
To improve the spatial coherence of the EUV beam, by reducing the apparent source size, a 0.25 mm in diameter pinhole, made by laser drilling in a 100 µm thick steel plate, was introduced 10 mm away from the plasma. This approach, in which high spatial coherence is achieved by spatial filtering at the expense of photon flux, is also very often employed at synchrotron facilities, Attwood (Reference Attwood1999). Smaller distance from the pinhole to the plasma causes the thermal damage to the pinhole induced by the plasma. The small inset in Figure 1a shows the SEM micrograph of the pinhole, which is not perfectly round. The major axis D _H was measured to be 251.5 µm, and the minor one D _V = 234.2 µm. To monochromatize the EUV beam emitted from the xenon plasma, and in turn, increase the temporal coherence of the source, a Mo/Si multilayer mirror (MLM) was used. The flat mirror was made by depositing Mo/Si multilayers on top of a Si wafer (Jena, Germany). It has a peak reflectivity of 37% for an unpolarized beam at 13.5 nm wavelength, with ±0.5 nm bandwidth and operates at an incidence angle of 45°. A typical spectral emission of the Xe plasma radiation reflected from such mirror in the EUV range from 9 to 20 nm wavelength is depicted in Figure 1b. To remove the visible light emitted from Xe plasma, which is also reflected very efficiently from the MLM, a combined thin film filter (200 nm silicon nitride + 200 nm zirconium) was employed. The object to be imaged was made of different diameter metal wires, from 5 µm in diameter up to 120 µm. It was located at the distance of 2.1 m away from the plasma. The object was entirely illuminated by the partially coherent EUV light, emitted from xenon plasma. The radiation was filtered spatially by the pinhole and spectrally by MLM and set of filters. The hologram, obtained through the interference in the far field between object beam (scattered from the test sample) and the reference beam (from around the object), was recorded by a CCD camera (Andor, DO934N-BN), placed at z _p = 6 cm downstream of the object. The camera has a chip with 1024 × 1024 pixels, each 13 × 13 µm² in size. During the experiments, the chip was cooled down to −20 °C to reduce its internal noise and the background.

Gabor holography with a partially coherent EUV radiation from xenon plasma

To demonstrate the applicability of laser-plasma EUV source based on a double stream gas puff target to imaging a Gabor holography experiments were performed. Since the development of high-resolution cameras, digital holography is applied to many different fields such as microscopy, particle image velocimetry, and deformation analysis. The holography has an important advantage such as the possibility to record not only amplitude of the electric field but also its phase, through the encoding process. Moreover, classical optical reconstruction to recover the information, encoded in the hologram, is nowadays often replaced by the numerical reconstruction, due to its advantages, such as flexibility, accuracy, immunity to the analog reconstruction noises, mechanical vibrations, etc. Additionally, such approach allows for numerical refocusing and reconstruction of 3-D volumes.

In the experiment to record the hologram the object was illuminated by a partially spatially coherent EUV beam with a radius of coherence equal to R _C = 60 μm, at the distance of z _s = 2.1 m from the source, and with an inverse spectral bandwidth of λ/Δλ = 14. The value of the radius of coherence was previously measured using a double-slit Young interferometer with variable slit separation, Wachulak et al. (Reference Wachulak, Sarzyński, Bartnik, Fok, Węgrzynski, Kostecki and Fiedorowicz2017), to produce an interference pattern in the far field region. A set of ten slit pairs (the mask), with separations from ~20 to ~200 µm, width of each slit ~4.5–5 μm, and 2.5 mm in length, was fabricated in a 25 µm thick copper foil by repetitive ablation of the material through its interactions with a focused laser beam. The mask was entirely illuminated by the light emitted from xenon plasma and filtered spatially by the pinhole and spectrally by MLM and set of filters. The fringe pattern is formed in the far field, where a charge-coupled device (CCD) camera was located. In an ideal double slit experiment, in which exactly the same two slits are uniformly illuminated, the modulus of the complex coherence factor is equal to the fringe visibility |μ ₁₂| = V, Goodman (Reference Goodman1985). Thus, it is possible to directly derive information about the spatial coherence of the plasma emission by measurement of the fringe visibility. This was demonstrated in experiments by Thompson and Wolf (Reference Thompson and Wolf1957), with partially coherent visible light and used multiple times to measure the spatial coherence. The visibility of the fringe patterns as a function of the slit separation is depicted in Figure 2. Due to the small difference in the pinhole size between D _H and D _V small changes in the interference pattern visibilities are detectable. This can be seen in Figure 2, in which square markers indicate the visibility values obtained from the intensity profiles for horizontal measurements and circular markers for vertical measurements, respectively. The visibility drops slightly faster in case of horizontal measurements, since D _H > D _V. To estimate the radius of coherence of the EUV beam a Gaussian-type function was fitted to the data. The solid line represents the fitted curve for vertical measurements and the dotted line for horizontal measurements. From the data, it was estimated that the radius of coherence in the horizontal direction is equal to R _CH = 56 μm and in the orthogonal direction R _CV = 59 μm. More details about those measurements, including the discussion about error estimation, can be found in Wachulak et al. (Reference Wachulak, Sarzyński, Bartnik, Fok, Węgrzynski, Kostecki and Fiedorowicz2017).

Fig. 2. Visibility, or absolute value of complex coherence factor, as a function of the slit separations for horizontal and vertical measurements. Inset shows the SEM image of the pinhole used for spatial filtering of the Xe plasma EUV radiation. Gaussian profiles were adjusted to fit each set of data, resulting in 56 and 59 µm radii of coherence for horizontal and vertical measurements performed at the distance of 2.1 m from the plasma.

The CCD camera was located at the distance of z _p = 6 cm from the object. This caused that the spatial resolution of Gabor hologram was limited theoretically to 3.3 µm by the bandwidth of the EUV emission and to 8.2 µm by the transversal coherence. After the illumination the part of the EUV beam scatters from the object (object beam) and interferes with an un-obscured beam (reference beam) propagating through the openings of the object, producing at the CCD plane an interference pattern. This pattern is a hologram. To obtain a single hologram 30 EUV pulses were used, produced by 5 J energy laser pulses at 10 Hz repetition rate. Example of such hologram is depicted in Figure 3a in the left column. It depicts a representation of the object – crossed wires 150, 20, and 5 µm in diameter. In the zoomed image the 20 and 5-μm wires’ edges are surrounded by fringes obtained due to the interference between object and reference beams. Although the diameter of those wires differs by a factor of 4 both wires in the hologram appears to be quite similar in width. The only difference is their “intensity”.

Fig. 3. Gabor-type holograms, obtained using EUV emission from laser-plasma source and numerically reconstructed images of objects – thin wires using spatially coherent EUV radiation (a) and incoherent EUV radiation (b).

The hologram was numerically reconstructed with a Fresnel propagator, Goodman (Reference Goodman2005), using an approach similar to Bartels et al. (Reference Bartels, Paul, Green, Kapteyn, Murnane, Backus, Christov, Liu, Attwood and Jacobsen2002) and Wachulak et al. (Reference Wachulak, Bartels, Marconi, Menoni, Rocca, Lu and Parkinson2006). A plane wave was back-propagated by the Fresnel Zone Plate of focal length given by

(1)$$\displaystyle{1 \over f} = \displaystyle{1 \over {z_{\rm p}}} - \displaystyle{1 \over {z_{\rm s} + z_{\rm p}}} $$

and rescaled by the geometric magnification equal to M = (z _s + z _p)/z _s of the object, as it is projected onto the CCD camera. The propagation operation was done in the Fourier domain and back-transformed to the spatial domain through equation

(2)$$R(x,y) = \Im ^{ - 1} \{ H(\,f_{\rm x}, f_{\rm y} ) \cdot F(\,f_{\rm x}, f_{\rm y} )\}, $$

where R(x, y) is the reconstructed image of the object in the spatial domain, H(f _x, f _y) is the hologram in the spatial frequency domain, F(f _x, f _y) is the Fresnel zone plate propagator in the spatial frequency domain and $\Im ^{ - 1} $ denotes inverse 2-D Fourier transform operation. This process has been presented for various reconstruction distances around the value of z _p in Media 1 movie in the Supplementary Materials. In the movie, one can notice how the smallest 5-μm wire reconstructs in and out of focus. The sharpest image is obtained for the reconstruction value equal to z _p. The reconstructed image of the wire objects is depicted in Figure 3a in the right column. Since the object absorbs the EUV light, it appears in the reconstruction as darker than the surrounding area. The zoomed image indicates the 20 µm in diameter wire that was reconstructed properly through the back-propagation algorithm having the size of ~26 µm (two CCD pixels). Taking into account the magnification factor of M = 1.03 the diameter of the wire is equal to 25.2 µm, a value, which in good agreement with the real value of 20 µm. Moreover, the 5-μm wire shows the width of ~1–2 pixels in the reconstructed image – a value close to the ultimate resolution in this imaging scheme, equal to the detector's pixel size of 13 × 13 µm². Additionally, after the reconstruction the two wires, being in fact completely opaque at 13.5 nm wavelength, appear, as expected, to have more similar “intensity”. The pinhole, used for spatial filtering of the EUV radiation was ~250 µm in diameter. The reconstructed images of wires show that the diameters of the 20 and 5-μm wires are much smaller than the diameter of the pinhole. So the reconstructed image has nothing to do with a simple shadowing effect introduced by the pinhole, which defines the limit of the spatial resolution in classical radiography or shadowgraphy.

To demonstrate further, that spatial coherence is essential for Gabor holography, another hologram was recorded in the exact configuration as previously, with pinhole removed. In that case, the EUV source size was much larger than before (limited by the size of the pinhole). Figure 3b shows the recorded holograms with various zoom factors in the left column and the reconstructed images, obtained through the back-propagation, in the right column. The fringing effect is not present anymore and the reconstruction of the 20 and 5-μm wires is unsuccessful; the reconstructed image is very similar to the hologram, without the possibility to back-propagate the coherent wavefronts to form a sharp reconstruction of the object.

Twin image removal (TIR) from the reconstructed image

While holography in its concept is truly ingenious, even since its invention by Gabor it has been troubled by the so-called twin image problem. The twin image is an artifact, present in the reconstructed image along the reconstructed object, limiting the information that can be obtained from a holographic reconstruction. For the reason of symmetry, there are always two images appearing in the reconstruction of a hologram, namely the reconstructed object and the unwanted out of focus twin image of that object, which obscures the object itself, Latychevskaia and Fink (Reference Latychevskaia and Fink2007). In this experiment the fringing artifact that can be found in the reconstructions in Figure 3a is attributed to the twin image. There are many possibilities of suppressing the twin image, including the use of a few holograms, recorded at various distances, where two holograms are necessary to suppress the twin-image in an inverse filtering approach, Nugent (Reference Nugent1990), or by implementing a phase retrieval procedures to iteratively search for correct, clean and twin-image free phase distribution, Zhang et al. (Reference Zhang, Pedrini, Osten and Tiziani2003).

To suppress the twin image present in Gabor holograms, obtained with Xe/He double stream gas puff target based EUV source, we followed the approach demonstrated by Denis et al. (Reference Denis, Fournier, Fournel and Ducottet2005). This approach is called iterative non-linear filtering of a single hologram since it requires only one hologram. It is assumed that the signal is in the in-focus real images while the noise is formed by out-of-focus twin-images. However, it should be noted, that the in-focus and out-of-focus images have the same information and are transformed one into another through propagation towards the symmetrical (conjugate) plane with respect to the hologram. Additionally, the objects we are imaging (wires) are located on the same side of the CCD camera. In the algorithm to suppress twin image, the out-of-focus fringes are reduced by masking their focalized counterpart in the virtual image plane, Denis et al. (Reference Denis, Fournier, Fournel and Ducottet2005).

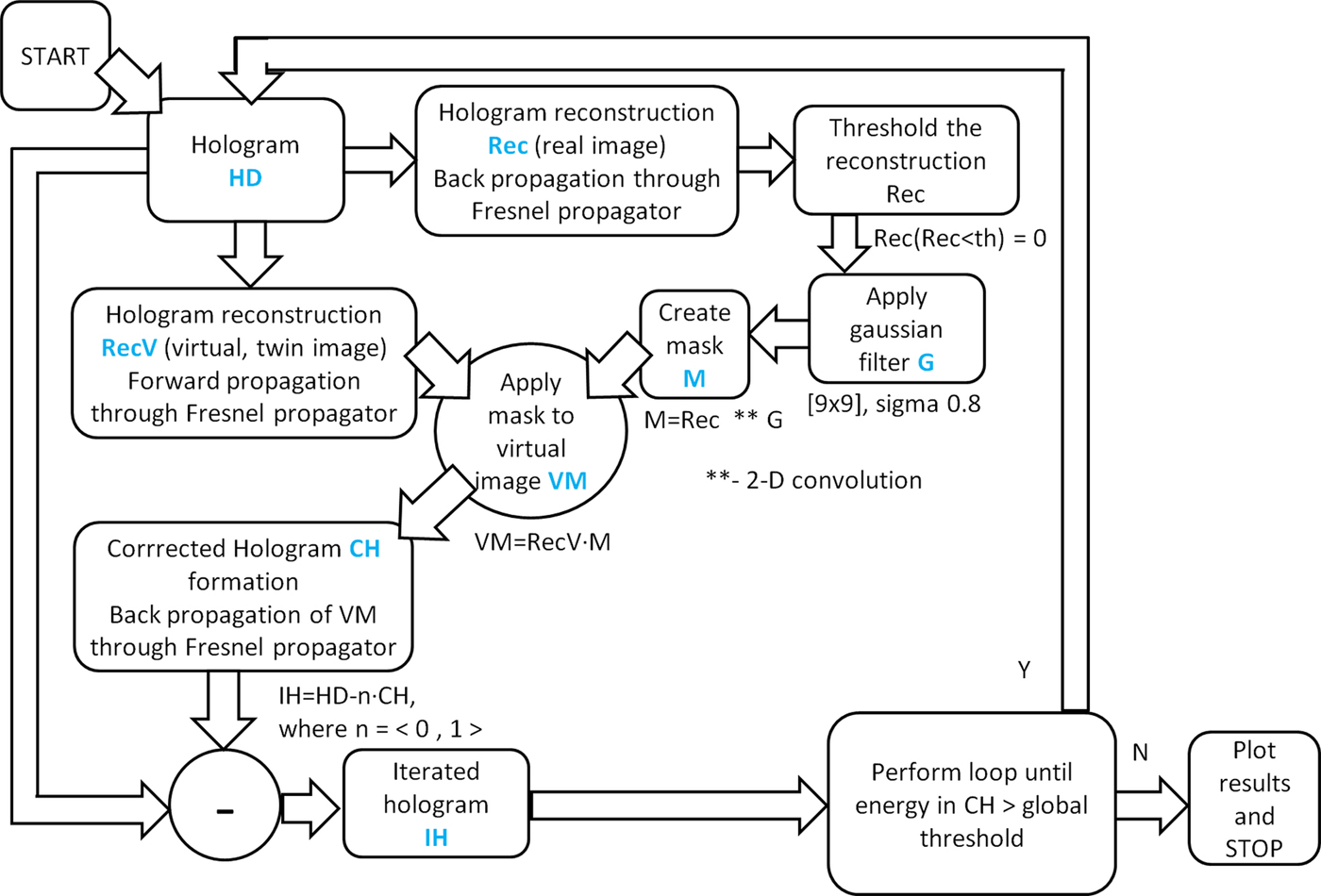
The flowchart of this approach is presented in Figure 4. The general principle is to clean the twin image fringes by subtracting a correction image CH, in a form of complex amplitude, from the hologram HD. This complex amplitude is computed through back-propagation of the in-focus virtual objects RecV in the virtual image plane. These virtual objects are defined using a constant threshold th. The correction image is then applied iteratively to the hologram to achieve twin image cleaning. Contrary to the approach by Denis, who applied the correction image directly to the hologram, we found, that more satisfactory results can be achieved by “gentle” or “soft” suppressing of the twin image. This is done in the final step, before the iteration is completed, by subtracting the properly weighted correction image from the hologram. It is done by multiplying the correction image first by n factor, where 0 < n < 1. This approach requires a little bit more iterations (e.g. 15 instead of 4–5), however, allows for an additional control over the twin image suppression process.

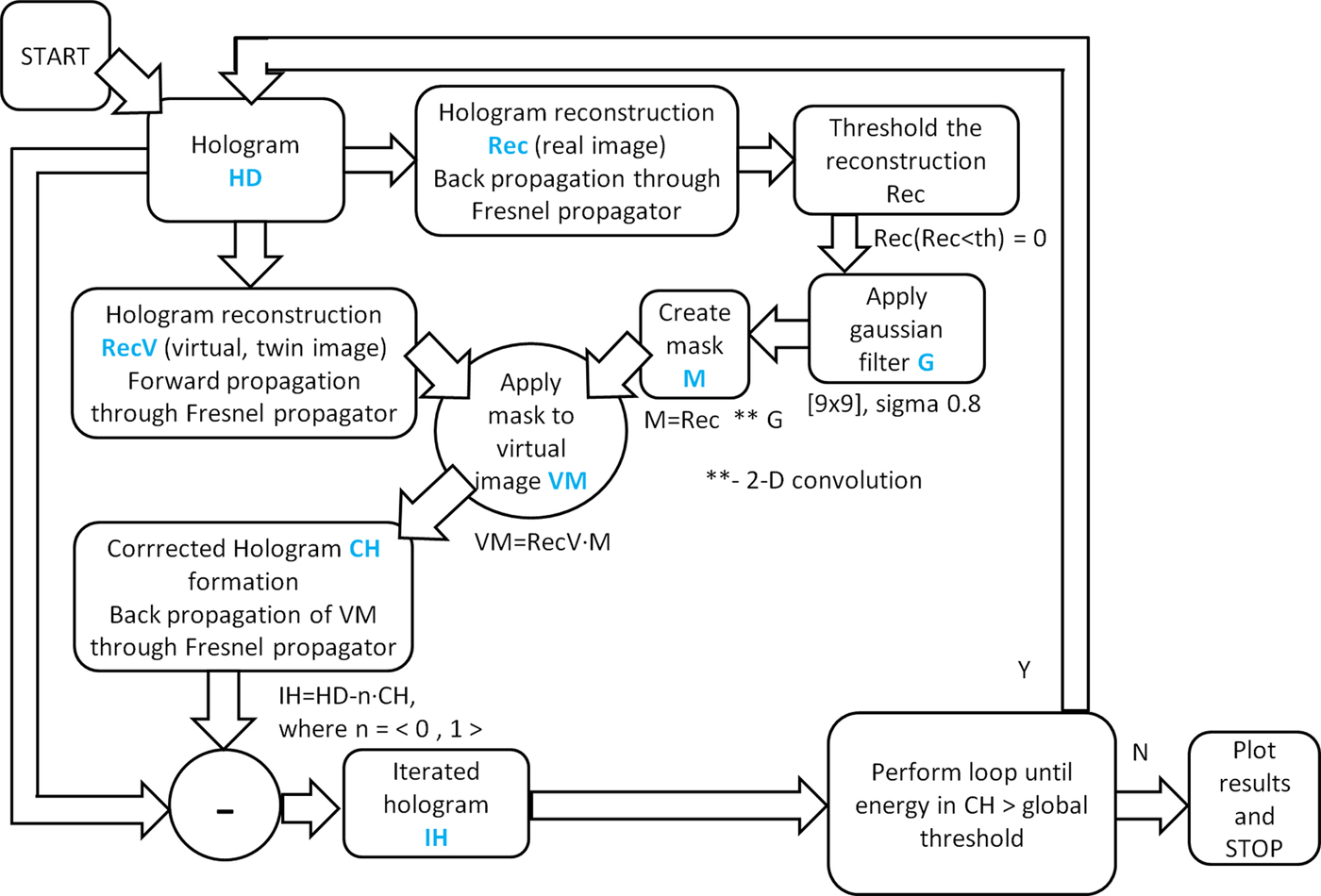
Fig. 4. A “soft” iterative non-linear filtering of a single hologram algorithm used for twin-image removal from reconstructed images of objects obtained from the EUV Gabor holograms. Algorithm modified based on work by Denis et al. (Reference Denis, Fournier, Fournel and Ducottet2005).

The result of performing TIR from the reconstructions is depicted in Figure 5. The reconstructed EUV image of a 5-μm in diameter wire is presented in Figure 5a. The intensity profile through the reconstructed image is depicted below by a red plot. It clearly shows fringing artifacts present above and below the reconstructed wire. Moreover, the twin image reduces the spatial resolution of the reconstructed image, since the 5 µm in diameter wire appears to be ~2 pixels in width, which is ~26 µm, considering the magnification factor. This value is 3 times larger than the expected theoretical limit, imposed by the partial spatial coherence of the EUV beam to ~8.2 µm. The result of applying the “soft” iterative non-linear filtering of a single hologram algorithm is depicted in Figure 5b. The twin image suppression was achieved with 15 iterations of the code. The representation of the smallest wire is clearly visible as a single, straight darker line and its profile (blue plot) indicate the width of the reconstructed wire to be equal to a single image pixel, equal to ~13 µm. This is equivalent to the ultimate spatial resolution achievable in this type of coherent imaging scheme. The intensity profiles for the reconstructed 5-μm wire for each iteration of the code are depicted in Figure 5e. One can notice that the code converges, resulting in a stable intensity profile for iteration number larger than 10–11 in this case. The result of twin image suppression for each iteration is presented in Media 2 in the Supplementary Materials. Figures 5c and 5d show the result of twin image suppression on the different part of the image. The twin image was partially reduced but still remains, especially for the largest features being 120-μm in diameter wire.

Fig. 5. Reconstructed images of thin wires with twin image artifact present (diffraction effects around the reconstruction) (a, c) and after employing the algorithm depicted in Figure 4, resulting in reducing of the twin image (b, d). Lineouts below images (a) and (b) show the difference in the intensity profiles for reconstructed wires with and without the twin image. After twin image removal it is possible to reconstruct the wire (5 µm wide) with the highest spatial resolution – a single detector pixel ~13 µm in width. Intensity profiles (e) across reconstructed 5-μm wire (red plot) and profiles for each iteration of the twin image removal algorithm (blue plots).