Introduction
Short-pulse laser neutron sources [see, e.g., (Alvarez et al., Reference Alvarez, Fernández-Tobias, Mima, Nakai, Kar, Kato and Perlado2014) and references therein] enable compact neutron pulses suitable for a variety of applications, including fusion materials properties (Perkins et al., Reference Perkins, Logan, Rosen, Perry, Diaz de la Rubia, Ghoniem, Ditmire, Springer and Wilks2000), biological studies (Zaccai, Reference Zaccai2000), condensed matter physics (Ma et al., Reference Ma, Delaire, May, Carlton, McGuire, VanBebber, Abernathy, Ehlers, Hong, Huq, Tian, Keppens, Shao-Horn and Sales2013), detection of contraband non-nuclear (Buffler, Reference Buffler2004), and nuclear material (Favalli et al., Reference Favalli, Mehner, Crochemore and Pedersen2009, Reference Favalli, Bridgwater, Croft, Falk, Fernández, Gautier, Guler, Hamilton, Henzlova, Ianakiev, Iliev, Johnson, Jung, Roth, Shimada and Swinhoe2016a). Two leading approaches exist to making laser-based neutron sources. The first is to irradiate a sample of material rich in deuterium (and possibly tritium or 3He), raising the target to a high enough temperature to induce fusion reactions (Toupin et al., Reference Toupin, Lefebvre and Bonnaud2001; Izumi et al., Reference Izumi, Sentoku, Habara, Takahashi, Ohtani, Sonomoto, Kodama, Norimatsu, Fujita, Kitagawa, Mima, Tanaka and Yamanaka2002; Karsch et al., Reference Karsch, Düsterer, Schwoerer, Ewald, Habs, Hegelich, Pretzler, Pukhov, Witte and Sauerbrey2003; Davis & Petrov, Reference Davis and Petrov2008; Bang et al., Reference Bang, Barbui, Bonasera, Dyer, Quevedo, Hagel, Schmidt, Consoli, De Angelis, Andreoli, Gaul, Bernstein, Donovan, Barbarino, Kimura, Mazzocco, Sura, Natowitz and Ditmire2013) This leads to an isotropic source of nearly monochromatic neutrons, though relatively low yields (~ 107 n, or ~ 106 n/sr). Alternatively, laser-accelerated ion beams can be directed into a converter composed of lithium or beryllium (Davis et al., Reference Davis, Petrov, Petrova, Willingale, Maksimchuk and Krushelnick2010), a “pitcher–catcher” configuration, to induce neutron-producing nuclear reactions, such as various p-Li, d-Li, d-Be channels. The resulting neutrons from these direct nuclear reactions will, as a consequence of kinematics, be dominantly forward-directed. This has potential advantages, as reducing the solid angle over which the neutrons are emitted can lead to increased neutron fluences (in n/sr) and reduced needs for shielding. Early experiments in laser-based neutron sources (Lancaster et al., Reference Lancaster, Karsch, Habara, Beg, Clark, Freeman, Key, King, Kodama, Krushelnick, Ledingham, McKenna, Murphy, Norreys, Stephens, Stöeckl, Yotama, Wei and Zeph2004; Higginson et al., Reference Higginson, McNaney, Swift, Bartal, Hey, Kodama, Le Pape, Mackinnon, Mariscal, Nakamura, Nakanii, Tanaka and Beg2010, Reference Higginson, McNaney, Swift, Petrov, Davis, Frenje, Jarrott, Kodama, Lancaster, Mackinnon, Nakamura, Patel, Tynan and Beg2011) used ions from target normal sheath acceleration (TNSA) (Hatchett et al., Reference Hatchett, Brown, Cowan, Henry, Johnson, Key, Koch, Langdon, Lasinski, Lee, Jackinnon, Pennington, Perry, Phillips, Roth, Sangster, Singh, Snavely, Stoyer, Wilks and Yasuike2000; Maksimchuk et al., Reference Maksimchuk, Gu, Flippo, Umstadter and Bychenkov2000; Snavely et al., Reference Snavely, Key, Hatchett, Cowan, Roth, Phillips, Stoyer, Henry, Sangster, Singh, Wilks, MacKinnon, Offenberger, Pennington, Yasuike, Langdon, Lasinski, Johnson, Perry and Campbell2000; Hegelich et al., Reference Hegelich, Karsch, Pretzler, Habs, Witte, Guenther, Allen, Blazevic, Fuchs, Gauthier, Geissel, Audebert, Cowan and Roth2002, Reference Hegelich, Albright, Cobble, Flippo, Letzring, Paffett, Ruhl, Schreiber, Schulze and Fernández2006; Roth et al., Reference Roth, Blazevic, Geissel, Schlegel, Cowan, Allen, Gauthier, Audebert, Fuchs, Meyer-ter-Vehn, Hegelich, Karsch and Pukhov2002) whereby an intense (I > 1018W/cm2) laser pulse incident on a ~10 μm thick foil generates an electrostatic sheath on the rear of the foil that acts as a virtual cathode and accelerates the ions.
Recent experiments have shown dramatic improvement to laser-based neutron source yields (Jung et al., Reference Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernández, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wender, Wilde, Wurden and Roth2013a; Roth et al., Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernández, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden2013, Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernández, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Kleinschmidt, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden2016; Favalli et al., Reference Favalli, Guler, Henzlova, Falk, Croft, Gautier, Ianakiev, Iliev, Palaniyappan, Roth, Fernández and Swinhoe2016b) through the application of “next-generation,” ion acceleration mechanisms. In these experiments, an acceleration mechanism called the “break-out afterburner” (BOA) was employed that relies on laser–plasma dynamics occurring during relativistic-induced transparency (RIT) in thin (~100 nm thickness) targets (Yin et al., Reference Yin, Albright, Hegelich and Fernández2006, Reference Yin, Albright, Hegelich, Bowers, Flippo, Kwan and Fernández2007; Henig et al., Reference Henig, Kiefer, Markey, Gautier, Flippo, Letzring, Johnson, Shimada, Yin, Albright, Bowers, Fernández, Rykovanov, Wu, Zepf, Jung, Liechtenstein, Schreiber, Habs and Hegelich2009; Palaniyappan et al., Reference Palaniyappan, Hegelich, Wu, Jung, Gautier, Yin, Albright, Johnson, Shimada, Letzring, Offermann, Ren, Huang, Hörlein, Dromey, Fernández and Shah2012; Hegelich et al., Reference Hegelich, Jung, Albright, Cheung, Dromey, Gautier, Hamilton, Letzring, Munchhausen, Palaniyappan, Shah, Wu, Yin and Fernández2013; Jung et al., Reference Jung, Yin, Albright, Gautier, Letzring, Dromey, Yeung, Hörlein, Shah, Palaniyappan, Allinger, Schreiber, Bowers, Wu, Fernández, Habs and Hegelich2013b, Reference Jung, Yin, Gautier, Wu, Letzring, Dromey, Shah, Palaniyappan, Shimada, Johnson, Schreiber, Habs, Fernández, Hegelich and Albrightc, Reference Jung, Albright, Yin, Gautier, Dromey, Shah, Palaniyappan, Letzring, Wu, Shimada, Johnson, Habs, Roth, Fernández and Hegelich2015a, Reference Jung, Senje, McCormack, Yin, Albright, Letzring, Gautier, Dromey, Toncian, Fernández, Zeph and Hegelichb). While such thin targets do not survive interaction with the pre-pulses and pedestal of a typical high-intensity high-power short-pulse laser, laser systems such as the LANL Trident laser (Batha et al., Reference Batha, Aragonez, Archuleta, Archuleta, Benage, Cobble, Cowan, Fatherley, Flippo, Gautier, Gonzales, Greenfield, Hegelich, Hurry, Johnson, Kline, Letzring, Loomis, Lopez, Luo, Montgomery, Oertel, Paisley, Reid, Sanchez, Seifter, Shimada and Workman2008) have been modified for high pulse contrast (Shah et al., Reference Shah, Johnson, Shimada, Flippo, Fernández and Hegelich2009) making the BOA possible. Unlike TNSA, in the BOA the predominant ion acceleration occurs volumetrically in the target in regions of highest electron density during RIT. By choosing a deuterated laser target material such that ionic species separation prior to the onset of RIT is modest, the peak longitudinal electric field in the target can be made to coincide with the locations of the deuterons, allowing the BOA process to accelerate them to high energy (>100 MeV) efficiently. Recent experiments demonstrated this by using the high-contrast Trident short-pulse beam with plastic (CH2) and deuterated plastic (CD2) target foils of a range of thicknesses and a copper-shielded beryllium converter to produce neutrons from the ion beams through deuteron breakup, (d,n), and (p,n) reactions in the converter. With thin targets (400 nm CD2) in the BOA acceleration regime, record neutron yields (~ 5 × 109 n/sr in a ~ns pulse width) and energies (up to ~ 80 MeV) were measured (Roth et al., Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernández, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden2013); a subsequent campaign with an improved tungsten-beryllium converter improved upon these yields (~ 2 × 1010 n/sr) (Favalli et al., Reference Favalli, Aymond, Bridgewater, Croft, Deppert, Devlin, Falk, Fernández, Gautier, Gonzales, Goodsell, Guler, Hamilton, Hegelich, Henzlova, Ianakiev, Iliev, Johnson, Jung, Kleinschmidt, Koehler, Pomerantz, Roth, Santi, Shimada, Swinhoe, Taddeucci, Wurden, Palaniyappan and McCary2014) [Davis & Petrov (Reference Davis and Petrov2008) reported neutron yields in their simulations of up to 107 neutrons per Joule of laser energy. Experiments on Trident exploiting the BOA produced more than twice that yield (Roth et al., Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernández, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden2013).]
In this paper, we revisit BOA laser-based neutron sources and examine using VPIC kinetic plasma simulations (Bowers et al., Reference Bowers, Albright, Yin, Bergen and Kwan2008a, Reference Bowers, Albright, Bergen, Yin, Barker and Kerbysonb, Reference Bowers, Albright, Yin, Daughton, Roytershteyn, Bergen and Kwan2009) the advantages in terms of neutron yields and spectra of using different laser target materials.
Kinetic modeling of laser-ion acceleration and neutron production from CD2 targets
We model the relativistic laser–plasma interaction in a manner that has been validated with past Trident laser experiments in the BOA regime (Hegelich et al., Reference Hegelich, Jung, Albright, Cheung, Dromey, Gautier, Hamilton, Letzring, Munchhausen, Palaniyappan, Shah, Wu, Yin and Fernández2013). Specifically, we employ a uniform, two-dimensional (2D), Cartesian mesh with a domain of size 100 μm in x (longitudinally) by 45 μm in z (transversely) with absorbing particle and field boundary conditions. The laser is an S-polarized (i.e., laser electric field polarized along y) Gaussian beam of wavelength 1.0 μm launched from the left of the domain with a peak field a 0 ≡ eE 0/m eω0c = 10.4 (I 0 = 3.3 × 1020 W/cm2) with laser electric field profile at best focus E y ~ exp(−z 2/w 2) with w = 5.12 μm. This choice of polarization has been shown to provide a closer match in both timing of onset of relativistic transparency and ion beam energy to 3D simulations than 2D P-polarization (Stark et al., Reference Stark, Yin, Albright and Guo2017). A sine-squared temporal envelope I(t) = I 0 sin2 (tπ /τ) is employed, where τ = 2 × FWHM = 1080 fs. For these laser parameters, the incident laser power is 
$P(t) = 2{\rm \pi} I_{{\rm max}}(t)\int_0^\infty r\exp ( - 2r^2/w^2)dr = ({\rm \pi} /2)w^2I_{{\rm max}}(t)$ where I max is the laser intensity on axis. The incident laser energy is ε = ∫ dtP(t) = (π/4) τ w 2I 0 ~ 73 J, comparable to the 70–80 J of energy available in a typical pulse from the C (short pulse) beam of the Trident laser. The target foil is placed 10 μm from the left simulation boundary and has initial thickness 240 nm and density ρ = 1.02g/cm3 (electron density n e0 = 280n cr, where 
$n_{{\rm cr}} = m_e{\rm \omega} _0^2 /4{\rm \pi} e^2$ is the critical density for a laser of angular frequency ω0). The plasma is taken to be fully ionized with 2800 particles/cell/species and initial temperatures T e = 100 keV and T i = 10 eV for both ionic species. Realistic mass ratios are used for electrons and ions. The simulation domain is 50,000 × 9000 cells, sufficient to resolve both initial skin depth 
$\delta ^0 = c/{\rm \omega} _{{\rm pe}}^0 $ and Debye length 
$\lambda _{{\rm De}}^0 = [k_BT_e^0 /4{\rm \pi} n_e^0 e^2]^{1/2}$: δ0 ≈ 5Δx, δ0 ≈ 2Δz, 
${\rm \lambda} _{{\rm De}}^0 \approx 2\Delta x$, and 
${\rm \lambda} _{{\rm De}}^0 \approx 1\Delta z$, where Δx and Δz are the mesh sizes in x and z, respectively, and superscripts “0” denote quantities at t = 0. We run our simulations until the laser has left the simulation volume (t = 1400 fs).
In Figure 1, we show contour plots of carbon (left) and deuteron (right) ion energy at three different times. The top panels are at time 491.7 fs, near the onset of RIT. The center panels are at intermediate time 793.1 fs and the bottom panels are at time 1348.2 fs, near the end of the simulation, when most of the ion acceleration has occurred. The colors denote ion kinetic energy per nucleon. As the BOA progresses, the most energetic ions are found near the right of the simulation domain. Note that because the two ionic species have the same charge-to-mass ratios, the kinematics of the deuterons and carbon ions are identical and, not surprisingly, the two accelerate with identical spatial and energy profiles. In the left panel of Figure 2, we show energy spectra of carbon ions (black) and deuterons (red) at time 1348.2 fs in a 1 μm cut through the center of the simulation domain and the two ion species indeed possess identical spectra (to within statistical error inherent with the particle-in-cell algorithm.)
Fig. 1. Spatial profiles of carbon (left) and deuteron (right) energy per nucleon from simulations of BOA acceleration of ions in a CD2 laser target. Shown are profiles around the time of the onset of RIT (top panels), a time mid-way through the acceleration (center panels), and at the end of the RIT phase (bottom panels), when most of the ion acceleration has occurred. The colors indicate relative ion kinetic energy per nucleon at each time shown; for the bottom two panels, an absolute scale of ion energy per nucleon is indicated by the color bars.
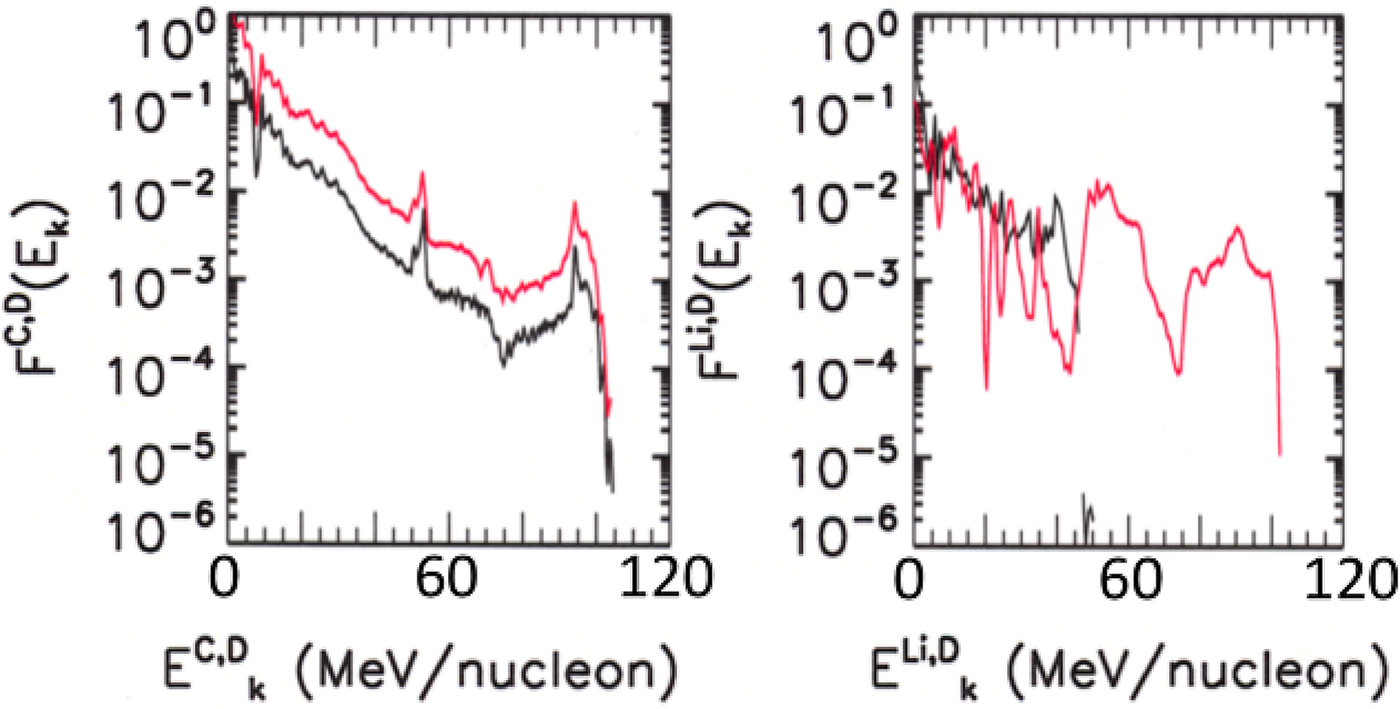
Fig. 2. Ion energy spectra of carbon ions (black) and deuterons (red) from simulations of BOA acceleration of ions in a CD2 laser target at time 1348.2 fs (left). Spectra for 7Li ions (black) and deuterons (red) from simulations of BOA acceleration of ions in a 7LiD laser target at time 1341.6 fs (right). In both cases, shown are data binned within a 1 μm-wide cut through the center of the simulation domain. In CD2, the two ion species have the same charge-to-mass ratios, so they possess nearly identical spectra. In 7LiD, the energy spectra of deuterons have a preponderance of ions at high energy (>50 MeV/nucleon) as a result of species-separation kinematics during BOA acceleration.
As discussed Roth et al. (Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernández, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden2013) and Favalli et al. (Reference Favalli, Aymond, Bridgewater, Croft, Deppert, Devlin, Falk, Fernández, Gautier, Gonzales, Goodsell, Guler, Hamilton, Hegelich, Henzlova, Ianakiev, Iliev, Johnson, Jung, Kleinschmidt, Koehler, Pomerantz, Roth, Santi, Shimada, Swinhoe, Taddeucci, Wurden, Palaniyappan and McCary2014), this beam of laser-generated ions can be directed into a beryllium converter in a pitcher–catcher neutron source configuration to sample a variety of neutron-producing nuclear processes. We now consider alternative laser target options for neutron production chosen according to the following criteria: (1) the target must be “deuteron rich,” meaning a high mass fraction of deuterium within the bulk target plasma, (2) the charge-to-mass ratios of the non-deuteron ions in the bulk target plasma must be comparable (though not necessarily identical) to that of the deuterons, and (3) the target must be sufficiently thin that the BOA occurs with the onset of RIT near the peak intensity of the laser pulse. The first criterion, not surprisingly, ensures that the acceleration of deuterons will be efficient, as the higher the mass fraction f D of deuterons in the target, defined as 
$f_{\rm D} = m_{\rm D}n_{\rm D}/\sum\nolimits_{_{\rm i} } {m_{\rm i}} n_{\rm i}$ where m i and n i are the masses and number densities of atoms of species i in the targets, the larger the fraction of laser energy that will go into acceleration of deuterons as opposed to other species. [This is somewhat analogous to a published effect of increased proton density in TNSA (Robinson et al., Reference Robinson, Bell and Kingham2006).] The second ensures incomplete species separation from electrostatic fields in the target prior to the onset of RIT. As discussed by Yin et al. (Reference Yin, Albright, Hegelich, Bowers, Flippo, Kwan and Fernández2007) and inferred experimentally (Jung et al., Reference Jung, Yin, Gautier, Wu, Letzring, Dromey, Shah, Palaniyappan, Shimada, Johnson, Schreiber, Habs, Fernández, Hegelich and Albright2013c), the presence of dissimilar charge-to-mass ratio species can lead to species stratification as the higher charge-to-mass species under the laser spot are expelled from the target, moving away from the target in the direction of the laser propagation and leaving behind lower charge-to-mass species to receive most of the acceleration from the laser. If the expelled ions are deuterons (Z*/A = 1/2 = 0.5), as might be expected for, for example, a deterium-loaded palladium target (Z*/A ~ 25/106 = 0.24 for initiating RIT using Trident-like parameters), the peak electrostatic field would likely preferentially accelerate the heavier palladium ions, with the deuterons accelerated only indirectly through inertial tamping of the primary species [as with the protons in Jung et al. (Reference Jung, Yin, Gautier, Wu, Letzring, Dromey, Shah, Palaniyappan, Shimada, Johnson, Schreiber, Habs, Fernández, Hegelich and Albright2013c)]. Note that this expulsion of high charge-to-mass ratio is not always complete, particularly when high concentrations of these ions are present in the bulk. This was the explanation provided and later confirmed in kinetic simulations for the high proton energies measured in the experiments of Hegelich et al. (Reference Hegelich, Jung, Albright, Cheung, Dromey, Gautier, Hamilton, Letzring, Munchhausen, Palaniyappan, Shah, Wu, Yin and Fernández2013) and Jung et al. (Reference Jung, Senje, McCormack, Yin, Albright, Letzring, Gautier, Dromey, Toncian, Fernández, Zeph and Hegelich2015b) (a feature of the dynamics that we will exploit shortly). The final criterion ensures that BOA acceleration dominates. The BOA has been shown to be robust experimentally, provided one has sufficient laser pulse contrast, and couples a large fraction of the laser beam energy into the ions (Jung et al., Reference Jung, Yin, Albright, Gautier, Letzring, Dromey, Yeung, Hörlein, Shah, Palaniyappan, Allinger, Schreiber, Bowers, Wu, Fernández, Habs and Hegelich2013b).
Alternate target materials
To compare neutron yields from different target materials in our study, we keep the laser parameters fixed and choose our target thicknesses in our simulations in such a manner that the areal density of electrons beneath the laser spot is held constant, equal to that of a reference, solid-density, CH2 target foil (n e/n cr = 280), the optimal target thickness with the laser parameters given above having been found to be 240 nm from prior studies. In practice, this prescription leads to reasonably accurately estimates of the target thicknesses yielding BOA ion beams with maximal energies. The parameters for the targets in our study are given in Table 1. With the exception of 7LiD, the target materials’ ions have identical charge-to-mass ratios. Consequently, the deuterons and the other ions (6Li, 12C, 14N) accelerate as in Figure 1, with nearly identical spatial and energy profiles for the different ion species, with profiles qualitatively similar to those shown in Figure 1. However, this is not so for 7LiD, for which the deuterons have slightly larger charge-to-mass ratios than the 7Li ions. As shown in Figure 3, the ion species separate prior to RIT (see the top panel). As BOA acceleration proceeds, the fastest deuterons continue to propagate ahead of the 7Li ions (see the middle and lower panels). This results in a preponderance of deuterons at higher energies, evident in the energy spectra in the right panel of Figure 2, where energy spectra of 7Li (black) and deuterium (red) are shown from a 1 μm wide cut through the center of the simulation volume at time 1341.6 fs, near the end of the RIT phase when most of the ion acceleration has taken place.
Fig. 3. Spatial profiles of 7Li (left) and deuteron (right) energy per nucleon from simulations of BOA acceleration of ions in a 7LiD laser target. Shown are profiles at t = 494 fs, around the time of the onset of RIT (top panels); t = 883 fs, mid-way through the acceleration (center panels); and at t = 1342 fs, near the end of the RIT phase (bottom panels) when most of the ion acceleration has occurred. The colors indicate relative ion kinetic energy per nucleon at each time shown; for the bottom two panels, an absolute scale of ion energy per nucleon is indicated by the color bars.
Table 1. Simulation parameters and yields for different target materials. A 240 nm deuterated plastic 12CD2 target serves as a reference; other materials have comparable or larger deuteron mass fractions f D. Target thicknesses w were selected to have the same electron areal density as the reference. Y d,rel is the relative number of deuterons entering the Be converter. Relative neutron yield 
$Y_{{\rm n,rel}} \equiv Y_{\rm n}/Y_{{\rm n},{\rm C}{\rm D}_2}$ (Y n and 
$Y_{{\rm n},{\rm C}{\rm D}_2}$ are neutrons per source deuteron for target and reference materials, respectively) are obtained from MCNP 6.1.1 tallies of neutron leakage from a 16.5 cm wide, 1 cm radius Be cylinder with point sources of deuterons directed along the axis at base of the cylinder with spectra obtained from VPIC calculations. The first three targets are solid at room temperature; the latter two require cryogenic conditions
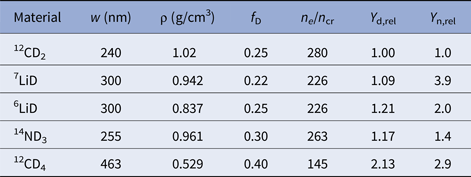
Relative to the 12CD2 reference case, the VPIC simulations reveal two different approaches to increasing neutron yield: The first is to use a target material such as deuterated methane or ammonia with the same Z*/A = 0.5 as deuterium but a higher mass fraction of deuterons (f D = 0.30 and 0.40 for deuterated ammonia and methane, respectively). Such targets couple a larger fraction of laser energy into the deuterons as opposed to the other ions. The second is to use a target such as 7LiD which, despite a lower f D than the reference 12CD2 target, nevertheless has higher mean deuteron energy. Higher energy deuterons have longer stopping ranges in the converter and may sample higher cross-sections for some neutron-producing nuclear reactions. Both increase neutron yield per deuteron over the 12CD2 reference case.
To compare neutron production from the different ion beams via the multiple primary [deuteron breakup, (d,n), etc.] and secondary [(p,n), e.g.] processes within the converter, we used the Monte Carlo N-Particle Transport code (MCNP version 6.1.1) (Werner Reference Werner2017). The neutron beryllium converter was modeled as (1) 16.5 cm and (2) 4 mm long, 1 cm radius beryllium cylinders of density 1.85 g/cm3. The incident deuteron source was a parallel beam directed toward the base of the cylinder along the axis with energy spectra obtained from VPIC calculations. The lengths of the converters were chosen as follows: the 16.5 cm length (case 1) exceeds the stopping range of the highest energy deuterons in the simulations (260 MeV from the 7LiD targets, with a range of 16.2 cm as calculated by the Stopping and Range of Ions in Matter (SRIM) code (Ziegler et al., Reference Ziegler, Ziegler and Biersack2010); the 4 mm length (case 2) is the stopping range of the mean-energy (33 MeV) deuterons from the 7LiD spectra. The neutron production was tallied in two ways: as total neutron leakage over the converter surface or as forward-directed neutrons emitted (leaked) in a cone of half-angle 24° centered in the base of the cylinder where the deuterons impinge upon the converter. [This angle was chosen because for a deuteron of energy 33 MeV, 24° is the half-width of the angular distribution of neutrons produced by deuteron stripping (Serber, Reference Serber1947).] The neutron production was tallied by means of the F1 Tally from 2 × 109 source deuterons sampled from the respective calculated VPIC energy spectra. ENDF/B-VII cross-section tables (Chadwick et al., Reference Chadwick, Herman, Obložinský, Herman, Greene, McKnight, Smith, Young, MacFarlane, Hale, Frankle, Kahler, Kawano, Little, Madland, Moller, Mosteller, Page, Talou, Trellue, White, Wilson, Arcilla, Dunford, Mughabghab, Pritychenko, Rochman, Sonzogni, Lubitz, Trumbull, Weinman, Brown, Cullen, Heinrichs, McNabb, Derrien, Dunn, Larson, Leal, Carlson, Block, Briggs, Cheng, Huria, Zerkle, Kozier, Courcelle, Pronyaev and van der Marck2006, Reference Chadwick, Herman, Obložinský, Dunn, Danon, Kahler, Smith, Pritychenko, Arbanas, Arcilla, Brewer, Brown, Capote, Carlson, Cho, Derrien, Guber, Hale, Hoblit, Holloway, Johnson, Kawano, Kiedrowski, Kim, Kunieda, Larson, Leal, Lestone, Little, McCutchan, MacFarlane, MacInnes, Mattoon, McKnight, Mughabghab, Nobre, Palmiotti, Palumbo, Pigni, Pronyaev, Sayer, Sonzogni, Summers, Talou, Thompson, Trkov, Vogt, van der Marck, Wallner, White, Wiarda and Young2011) were used for neutrons with energy below 20 MeV and protons with energy below 113 MeV. An improved version of the Cascade-Exciton Model (CEM3.03) was used for higher energy reactions. The Los Alamos Quark Gluon String Model (LAQGSM3.03) (Mashnik et al., Reference Mashnik, Baznat, Gudima, Sierk and Prael2005) as implemented in MCNP version 6.1.1, was also used at all energies for heavy and light ion interactions. The calculated neutron energy spectra resulting from each of the deuteron distributions multiplied by the relative deuteron yield in each ion spectra are shown in Figure 4. In Table 1, we report comparisons of total neutron yield for the 16.5 cm converter. The 7LiD target produces nearly four times as many neutrons as a 12CD2 target; similarly, the forward neutron production with the 7LiD target was calculated to be 4.3 times higher than with the 12CD2 reference target.
Fig. 4. Neutron spectra obtained from MCNP modeling of a point source of deuterons with energy spectra from VPIC simulations initiated along the axis at the base of 4 mm (top) and 16.5 cm wide (bottom), 1 cm radius beryllium cylinders. Tallied are neutron leakages from the converters. Note that for the 16.5 cm converter, 7LiD generates the most neutrons, particularly at high energy (E n > 25MeV), whereas for the thinner converters, CD4 produces the most neutrons.
Conclusions
In summary, we have modeled several variations of neutron sources based upon the pitcher–catcher concept using the BOA mechanism to accelerate ions. Our simulations point to two approaches to enhancing neutron yield through choice of laser target materials: use of targets composed of materials with higher fractional mass densities of deuterons and the use of targets that, inherent to the kinematics of the BOA mechanism, lead to higher deuteron energies and thus higher neutron yields. Several candidate target materials have been identified and assessed for Trident-like laser parameters that appear promising for increasing neutron yield relative to the present state of the art, which employed CD2 targets on the Trident laser system. While our study has focused on Trident-like conditions and, as the Trident laser is in the process of decommission and re-siting elsewhere, therefore our specific simulated parameters may not be directly applicable to other systems, we nevertheless expect that the dynamics we report upon will be applicable to other high-contrast, high-power, short-pulse laser systems. We also showed that neutron spectra can also be controlled in these experiments. For instance, the use of a laser target such as 7LiD generates a hardened neutron spectrum, that is, a preponderance of neutrons at higher energy, which would be of value for applications requiring enhanced neutron penetrability, for example, active neutron interrogation in shielded material. While we recognize that 7LiD poses challenges for target fabrication, other target materials (e.g., 13CD2 plastic or 18OD2 ice) have f D and Z*/A ratio properties similar to those of 7LiD and should evince similar advantages. Finally, as evidenced by the results of a 4 mm thick converter (the top panel of Fig. 4), we note that according to application needs, converter geometry and target material can be optimized to balance possibly conflicting requirements on neutron yield and neutron energy spectra.
Work performed under the auspices of the US Department of Energy by the Los Alamos National Security, LLC Los Alamos National Laboratory under contract DE-AC52-06NA25396. This work was supported by the LANL LDRD program. Computing time on the ASC Cielo machine was provided by Capability Class Computing allocations. The authors wish to acknowledge useful discussions with Juan Fernández, Martyn Swinhoe, D. Cort Gautier, B. Manuel Hegelich, John Hendricks, and Markus Roth. Apollo Albright assisted in preparing the data.
