INTRODUCTION
Given the inherent characteristics of non-repetition, complexity, unpredictability of unconventional public health emergencies, such as severe acute respiratory syndrome (SARS) and H1N1,Reference Zhong, Mao and Weng1, Reference Yang, Yang, Jin and Lin2 which have no historical precedent, the evolutionary mechanisms of the scenarios and parameters of the prediction models of such emergencies cannot be found and described in short time. Moreover, effective response solutions are difficult to attain under traditional decision-making methods.Reference Bostick, Subbarao and Burkle3 For example, after the SARS outbreaks, numerous possibly infected patients needed to be diagnosed and cured urgently. However, first, the dynamic parameters (such as types, states, numbers and increasing rates of patients, and transmission patterns of disease) for reflecting disease situations are unclear. Second, the response demand (such as medical staffs, equipments, and drugs) changes with the uncertain quality and quantity of patients. Furthermore, considering the complex revolution processes of emergency scenarios and the dynamic working intensities and environments, the level of the response performances of medical staffs and equipment is erratic. In the situation described previously, the traditional prediction–response modeling and simulation methods are ineffective for representing the complex emergency scenarios and controlling the existing emergency medical response system. Distinguished from the prediction–response paradigm, the scenario–response paradigm is based on parallel simulation and bottom-up modeling. By modeling the individual and their interactive relationships of the scenarios, we can dynamically build the artificial society and simulate the disaster scenarios to increasingly emulate the real world.Reference Wang, Qiu and Zeng4 Therefore, how to construct and improve the simulation models that parallel with the dynamic evolutionary scenarios is the key issue in upgrading the decision-making level for the unconventional public health emergencies.
RELATED RESEARCH AND THEORETICAL BACKGROUND
Classic Data-Dependent Decision-Making Theories for Public Health Emergencies
To upgrade the emergency response efficiency of the emergency department (ED), scholars have exerted expansive research effort on the hospital surge capacity and patient flow determinants. McCarthy and his team have reviewed daily ED surges and the ED surge capacity and illustrated this indicator’s potential relevance during a catastrophic event. The team proposed that daily and catastrophic ED surges can be measured by the magnitude of the surge, as well as the nature and severity of the illnesses and injuries that patients present during the surge. The results help increase the understanding of the daily ED surge capacity and influencing factors. This information then improves the ability to simulate the potential impact of different types of catastrophic events on the surge capacity of hospital EDs nationwide.Reference McCarthy, Aronsky and Kelen5 Afterward, the scholars developed a methodology for predicting the demand for ED services by using the regression model. The findings showed that the medical demand for ED services was well approximated by the Poisson regression model.Reference McCarthy, Zeger and Ding6 Furthermore, the effect of ED crowding on clinical outcomes has been studied and evaluated by scholars, such as Steven and Dominik.Reference Bernstein, Aronsky and Duseja7 Their studies revealed that ED crowding is associated with objective clinical endpoints, such as mortality, as well as clinically important processes of care.Reference Bernstein, Aronsky and Duseja7 By observational study, Forster and colleaguesReference Forster, Stiell and Wells8 investigated the effect of hospital occupancy on ED length of stay and patient disposition by using administrative data from a 500-bed acute care teaching hospital. Their precise research result showed that increased hospital occupancy is strongly associated with ED length of stay for admitted patients, and increasing the hospital bed availability might reduce ED overcrowding.Reference Forster, Stiell and Wells8
The previous works provide theory and technique foundation for building further accurate prediction and response models for public health emergencies. However, most of these models are strongly dependent on historical data. By contrast, when a complex and unrepeatable unconventional public health emergency, such as the SARS outbreak in 2003, is faced without sufficient data and experience, the models become inapplicable and unreliable. Moreover, given only classical theories, we often lack sufficient prior knowledge on how to describe emergency scenarios accurately and even analyze and optimize the public health response systems effectively and dynamically.
Simulation of Decision-Making Methods for Emergency Response
Given the emergency response problems, simulation methods (especially the models described in mathematical form) are studied and applied abroad. On the basis of Petri Net simulation technology, with oil can fire as an example, the performance of the China urban emergency response system and response plan are analyzed.Reference Zhong, Shi and Fu9, Reference Zhou10 When examining the panic features of people escaping from disaster, simulations based on a model of pedestrian behavior are available.Reference Helbing, Farkas and Vicsek11 Meanwhile, a 2D finite volume method is used to simulate the dam-break process with a case.Reference Valiani, Caleffi and Zanni12
The models proposed in the previous studies demonstrated that simulation decision-making methods are useful for certain kinds of emergencies. However, on the one hand, most current simulation models are designed for industrial disaster scenarios with no clear confirmation of successful application to unconventional public health emergencies. On the other hand, the models mainly focus on emergencies and the relevant response processes with features, such as short span of time and space and clear mechanism. With sufficient theoretical basis (former models or knowledge), the simulation decision models are constructible.Reference Ni, Rong and Wang13, Reference Bo-Hu, Chai and Hou14 However, for complex, dynamic, and uncertain unconventional public health emergencies, no sufficient prior knowledge is available to support the traditional simulation modeling process. Therefore, new evolutionary and dynamical simulation decision-making methods should emerge as necessary.
Parallel Simulation-Based, Scenario–Response Emergency Management Paradigm
In the new information and communication technology era, the processes of perception, computing, storage, transmitting, and analysis have achieved great performance improvements with the technologies of cloud computing and Internet of Things. In the aspect of simulation platform, the networked modeling and simulation platform based on cloud computing, named cloud simulation platform, is proposed for complex cross-domain system analysis and improvement. Theoretically, in such a high-performance technology environment, complex disaster scenarios and emergency response processes can be shown in simulation platform dynamically and interactively. Moreover, the promising scenario–response emergency decision-making paradigm based on theories of artificial society modeling and parallel emergency management is proposed by the researchers of the Chinese Academy of Sciences and National University of Defense Technology for unconventional disaster scenario simulation and comprehensive analysis, emergency resource scheduling, and evacuations.Reference Yang, Yang, Jin and Lin2, Reference Wang15
Unlike the data-dependent prediction–response emergency decision-making paradigm based on statistical regression and numerical calculation, the structure-dependent scenario–response paradigm is based on bottom-up modeling methods. This paradigm can help decision makers dynamically simulate artificial society and disaster scenarios that increasingly approximate real-world scenarios through parallel individual and interactive relationship modeling under a first-time disaster, which hence lacks historical data and experience.Reference Wang, Qiu and Zeng4 Scholars adopted the SARS outbreak as an example and used the multi-agent simulation method to study and discover the evolution mechanism of an unconventional public health emergency.Reference Zhong, Mao and Weng1 However, given the great difficulty in modeling and the high cost in calculating, the promising “heavyweight” parallel simulation technologies remain in the idealized experimental research stage.
Discrete Event System Theory
Discrete event system (DES) is an event-driven dynamic system with internal states that change from one to another randomly. The DES theory has been applied as a means to analyze health care systems. The main research work includes applying this theory to health care processes, analyzing the effect of patient arrival and service time variability on patient waiting time and throughput and examining the efficiency of dedicated (specialized) and combined resources.Reference Kolker and Rodrigues16 DES-based simulation has become a popular and effective decision-making tool for the optimal allocation of scarce health care resources to improve patient flow while minimizing health care delivery costs and increasing patient satisfaction. Combined optimization and simulation tools also allow decision makers to quickly determine optimal system configurations, even for complex integrated health care systems (eg, hospitals, outpatient clinics, EDs, and pharmacies).Reference Jacobson, Hall and Swisher17
The previously mentioned works have not demonstrated the successful application of DES theory in unconventional public health emergencies but show that the theory can model public health system structures and effectively simulate these structures’ processes. Actually, the formation processes of emergency demand (such as patient arrivals), response capacities (such as medical service rates), and the variation rates of response system states constantly exhibit strong randomness. In this regard, in special society systems, unconventional emergency response systems can be described by the DES theory properly. At present, the DES theory is available for combining with object-oriented (OO) modeling and simulation technology (such as FlexSim, Arena, Petri Net). On the basis of this technology, system elements, relationships, layouts, response processes, and some other uncertainties (such as the previously mentioned statistical regularities) of real systems can be quickly transformed into simulation models for making emergency response decisions effectively.Reference Budgaga, Malensek and Pallickara18, Reference Furian, O’sullivan and Walker19
Inspired by the DES theory, unconventional public health emergency scenarios and hospital surge capacities can be considered as a whole scenario–response system. Then, by modeling and simulation based on DES, effective decision-making processes, such as scenario anticipation and medical resource allocation and hospital surge capacity optimization, can be achieved and improved.
PARALLEL SIMULATION DECISION-MAKING METHODS FOR EMERGENCY RESPONSE
Lightweight DES-Based Parallel Simulation Decision-Making Framework (DES–PSDF)
The parallel emergency management theory proposes that real disasters can be predicted accurately. However, on the basis of the experimental simulation environment, we can build artificial society models that parallel with real-world scenarios. Then, with the real-time data collected from real scenarios, the models can be updated and improved dynamically, and the evolution processes can be shown in the models. Through the parallel artificial society simulation model, functions, such as scenario analysis and prediction, response solution brainstorming and optimization, can be conducted to support emergency response decision-making processes. Therefore, the lightweight DES–PSDF for emergency response is proposed in this section. The structure of this framework consists of a real scenario layer and a simulation decision-making layer that are parallel to each other (Figure 1).
FIGURE 1 Lightweight Discrete Event System-Based Parallel Simulation Decision-Making Framework (DES-PSDF).
Real Scenario Layer
The concepts of response capacity for unconventional public health emergencies and hospital surge capacity are simultaneously related and different. In this paper, the concept of hospital surge capacity encompasses the medical response capacities for the emergency service demand of public health emergencies. Actually, this kind of emergency service demand includes conventional and unconventional services.Reference Zhong, Mao and Weng1, Reference Wang, Qiu and Zeng4–Reference Forster, Stiell and Wells8 The concept of unconventional public health emergencies is about the complex, unpredictable, unrepeatable, unexpected public health emergencies that may substantially harm the society and cause a surge in medical service demand. More importantly, given the lack of historical data and experience in this type of situation, an effective prediction and decision are difficult to attain with the traditional data-dependent decision-making methods only.
Therefore, in accordance with the scenario–response-based parallel simulation paradigm,Reference Yang, Yang, Jin and Lin2, Reference Wang, Qiu and Zeng4 disaster scenarios and emergency response capacities are important factors in making effective decisions.Reference Ni, Wang and Yin20 The response demand (such as the number and variety of emergency supplies, time constraints, and number of injured or infected people) can be obtained by initially analyzing from scenarios. The response capacity is the sum of available “soft or hard” emergency resources of the response systems and includes the doctors, rescuers, medicines, equipment, food, and information.Reference Yingying21 As a real-time information source, real scenarios are the basis of decision-making and targets of solution optimization.
Simulation Decision-Making Layer
The structure of the simulation decision-making layer is shown as a closed loop that consists of 4 key steps, including abstract modeling, simulation execution, decision-making optimization, and parallel control. First, by real-time perception (includes the processes of information collection, analysis, and abstracting), the main elements and relevant features of the real scenario layer in the perspectives of the affected body (AB), emergency demand (EmD), response process (RP), response organization (RO), and response resource (RR) are obtained. On the basis of the DES theory and OO modeling methods, the DES-based abstract simulation decision model (DES–ASDM) can be constructed from the perspectives of entity, attribute, and relationship flow. Second, after inputting the real-time data collected from the scenario and response capacity into the simulation model, the evolutionary scenario and response performance can be predicted by simulation computing. Third, through statistical analysis of the steady simulation output results, we can evaluate whether the existing response solution is suitable for the EmD. As the bottlenecks limiting the response system performance are found, the optimal solution can be easily proposed in time. The parallel controlling process is also conducted to observe these implemented effects of the response solutions and the situations of the real scenarios and update the structure and parameters of the simulation model in real time. The aim is to maintain the simulation model at pace with the scenario evolution.
DECISION-MAKING PRINCIPLES BASED ON THE DES-PSDF
Abstract Structure Modeling
On the basis of the DES theory and OO modeling methods, the DES–ASDM can be constructed from the perspectives of entity, attribute, and relationship flow.Reference Budgaga, Malensek and Pallickara18, Reference Furian, O’sullivan and Walker19 The base structure of the model can be described as the triple DES–ASDM::={E,A,F}. That is, an entity (E) set with its attribute (A) set and its relationship flow (F) set. Two kinds of entity classes, including temporary entity (TE) and permanent entity (PE), are basic elements of simulation models. As an execution subject of emergency RPs, the PE does not leave the models until the simulation ends. The performances and states are usually stable and do not change with the simulations. On the contrary, as the supporting objects, TEs are processed or recurrent in emergency response, and their states usually change with the simulation processes. Furthermore, the important features of entities, including the type, function, state, and statistical distribution, are described into the set A of attributes. The relationships flow set F is used for representing the directed interconnections between entities. Concurrently, the input–output relationships of the RPs, which are the basic units for achieving the emergency response systems and their RPs, are also described by the directed flows (Figure 2).
FIGURE 2 DES–ASDM for Unconventional Public Health Emergencies.
The DES–ASDM for emergency medical response is defined with 5 kinds of elements, including the AB, EmD, RP, RO, and RR. If the pe (element of PE), te (element of TE), f (element of F), and attribute (element of A) are represented with a rectangle, circle, arrow and text box, respectively, under an emergency medical RP, as an example, the resultant abstract simulation model is as shown in Figure 2.
Defining the Simulation Entities and Their Attributes
Because emergency ROs are constantly executing RPs with stable performances in emergency systems, the former are classic PEs. For example, as an emergency response subject, every medical staff member diagnoses or cures patients repeatedly with a stable service rate (number of patients cured per hour) during a running simulation. The staff member does not leave the simulation system until the simulation ends. Therefore, the ROs can be defined into the PEs (PERO), that is, 
$RO\buildrel {Map} \over \longrightarrow P{E_{RO}}$, where 
$RO = \{ r{o_1},r{o_2},...\}$ means the set of ROs and 
$PE = \{ p{e_{RO1}},p{e_{RO2}},...\}$ means the set of PEs. Usually, because every ro performs one response activity, the element also directly represents a response activity.
Because ABs and RRs are changing and passive objects in RPs, the former two elements should be transformed into TEs (TEAB and TERR, respectively) of the simulation models, that is, 
$AB\buildrel {Map} \over \longrightarrow T{E_{AB}}$, where 
$AB = \{ a{b_1},a{b_2},...\}$ means the set of ABs and 
$TE = \{ t{e_{AB1}},t{e_{AB2}},...\}$ means the set of relevant TEs.
Similarly, the RRs are defined into the TEs, that is, 
$RR\buildrel {Map} \over \longrightarrow T{E_{RR}}$, where 
$RR = \{ r{r_1},r{r_2},...\}$ means set of RRs and 
$TE = \{ t{e_{RR1}},t{e_{RR2}},...\}$ means set of relevant TEs.
Therefore, for one entity ei, the attributes and attribute types are defined as follows:
$$\eqalign{ Attribut{e_i} = \{ a{t_{i1}},a{t_{i2}},...,a{t_{im}}\} \buildrel {Map} \over \longrightarrow \sum\nolimits_{{e_i}} { = \{ {a_{i1}}} ,{a_{i2}},...,{a_{im}}\} \cr \forall Type(a{t_{ij}})\buildrel {Map} \over \longrightarrow Type({a_{ij}}) \cr} $$
where atij denotes the attribute type j of the entity ei, aji denotes the set of its attribute values, and the symbol
$\sum\nolimits $here means all of the attribute types of entity ei. For example, the PEs can serve as response units, such as doctors and nurses, and their attributes can include the name, vocation, state, and performance. If the TEs are ABs, such as patients, equipment, and buildings, the TEs’ relevant attributes include the destruction degree, injury or illness degree, and location. If the TEs are RRs, such as food and medicine, the TEs’ relevant attributes should include name, quantity, and price.
Defining the Relationship Flows Between Entities
After identifying the input–output–precondition–effect relationships between pairs of TE and PE in accordance with the RPs, the directed flows can be defined between the PEs. Two kinds of flows exist and include the response process flow (RPF) and response support flow (RSF). For example, patients enter the medical response system individually or simultaneously under certain rules or DES random distribution (Figure 2). Then, this process can be described into a directed entity relationship flow fDS-RO1 and means that the TEteABi (patient i) flows from the PEpeDS (source of disease outbreak) to the PEpeRO1 (first RP, such as queuing or waiting for diagnosis). Similarly, after diagnosing with the support of peRR1 (diagnostic tools or medicines), the teABi flows from the PEpeRO1 to the PE peRO2 (second RP, such as treatment), and this process is represented in the flow as fRO1-RO2. Then, the previously mentioned serial forward processes can be described into the RPF set FProcess = {fDS-RO1,fRO1-RO2,…,fRO2-RO3}. Besides, as emergency RRs, medicines are consumed to support the RPs. The relevant directed relationship flows are described into the RSF set FSupport = {fRR1-RO1,fRR2-RO2,…}. Therefore, the general entity relationship flow can be defined as follows:
$$F = \{ t{e_k},{a_{tek}},w, \lt p{e_i},p{e_j} \gt |t{e_k} \in TE,{a_{tek}} \in {A_{tek}},w \in W, \lt p{e_i},p{e_j} \gt \in PE \times PE\} $$
where tek denotes the TEs in the flows, atek denotes the attribute values of the entities, <pei, pej> denotes the ordered pairs where the TE flows from the pei to pej, and w is a weight variable used for describing the input or output constraints to trigger the actions performed by peRO (RO). If wi denotes the output constraints of peROi and wj denotes the input constraints of peROj, the flow can be represented as shown below:
$${\rm{t}}{{\rm{e}}_{\rm{k}}} \in ^\circ\,\!{\rm{p}}{{\rm{e}}_{\rm{j}}}\,\!\cap \,\!{\rm{t}}{{\rm{e}}_{\rm{k}}} \in {\rm{p}}{{\rm{e}}_{\rm{i}}}^\circ ,\;\;\;{{\rm{A}}_{{\rm{tek}}}}\;\ge \,\!{{\rm{W}}_{\rm{j}}}\,\!\cap \,\!{{\rm{A}}_{{\rm{tek}}}}\;\le \,\!{{\rm{W}}_{\rm{i}}}$$
This relation means that if f is the output flow of the RO (activity) pei, then the relevant attribute values of the TEs must be less than or equal to the output weight, similar to the number of evacuees that must be below the capacity of the shelter. If f is the input flow of the RO pej, then the relevant attribute values of the TEs must be greater than or equal to the input weight, similar to the necessary medicine inputting when accomplishing medical response activities.
Simulation Operation and Decision-Making Optimization
Designing and Achieving Initial Simulation Models
As a common modeling paradigm, the DES–ASDM shows the structures, situations, and activities of real disaster scenarios at the abstract mechanism level. Actually, some OO or visualization simulation tools, such as FlexSim, Arena, and CPN Tools, are based on DES theory.Reference Lavery, Beaverstock and Greenwood22–Reference Pokraev24 Therefore, to render the methods proposed in this paper further realizable, we must design compatible and extensible, relevant transformation principles from the elements of the DES–ASDM to the elements of the simulation software. With the transformation principles, the abstract simulation and decision-making models with the relevant functions, such as parameter computing, statistical analysis, and presenting, can be achieved effectively for the emergency response simulation and decision-making processes.
If the abstract simulation model is achieved with the FlexSim tool, the transforming principles are shown in Table 1. First, as the emergency response objects processed by the relevant subjects in the real scenarios, the affected bodies and RRs are described as the temporary entities TEAB and TERR, respectively, in the abstract models. Then, the FlowItem components such as Box or Person are loaded to achieve the functions of the previously mentioned 2 temporary entities with the FlexSim tools. Second, the emergency response subjects are described as permanent entities, such as organizations and equipments are defined as PERO and PERE, respectively. Then, the Fixed Resource or Task Executers components, such as Processor/Operator and Transporter can be used for achieving the relevant functions of them with the FlexSim tools. By setting the parameters of the components, the response modes and performances can be adjusted. Third, the emergency RPs of real scenarios are described as RP flows and RSFs, which can be achieved by loading the Connect Object and Travel Network functions in FlexSim. Finally, the emergency demand of real scenarios, such as the number and the arrival rate of patients, is defined as permanent entities. Then, with the relevant parameters setting, the Source component is loaded for simulating the function of events triggering.
TABLE 1 The Transformation Principles of “From Real Scenario to DES-ASDM to FlexSim”
According to the scenario, after achieving the structure and dynamic flows of the simulation model by loading the components of FlexSim, the initial data and the evolution rules can be obtained with the technologies of radio-frequency identification and distribution fitting software such as ExpertFit, and so on.Reference Fang, Qu and Li25, Reference Kumar, McCreary and Nottestad26 Then, by inputting the entity attribute values as parameters into the components, the initial simulation model can be achieved and optimized with FlexSim.
Simulation Operation and Decision-Making Optimization
On the basis of specific time or cost constraints of disaster scenarios, simulation operation parameters, such as simulation step size and total running time, are set and simulation models can be run.
To achieve the target of the optimization of the response system and its processes, the simulation running processes and results should be analyzed. On the one hand, by observing the disaster scenario and the emergency response system when the simulation model is running steadily, the rationality and performance of system layout, RPs, and response effectiveness can be analyzed directly. Then, the system bottlenecks, which constantly show phenomena, such as crowding and idling, can be easily found. On the other hand, by quantitatively analyzing the simulation result outputs with the statistical tools, the bottlenecks are presented and the relevant optimization strategies can be proposed.
In general, the optimization strategies include the RP optimization, such as parallel activities, instead of sequence activity process reconstructionReference Xie, Li and Wei27; response capacity optimization, such as response unit increase and performance improvementReference Viswanathan, Bass and Wijetunge28; and resource allocation optimization, such as adding resources into the bottlenecks.Reference Fiedrich, Gehbauer and Rickers29 For different optimization strategies, the response time and costs all differ, and a balanced consideration of these aspects is important.
Parallel Control
Most often, emergencies, especially unconventional emergencies, have no historical precedent. Although the types of emergencies are the same as those that have occurred, the disaster-causing factors and evolution processes vary. Therefore, for every unconventional emergency, the evolution mechanism and emergency response demand are neither clear nor certain. Obtaining the accurate parameters of prediction models quickly is difficult under traditional management, and controlling theories are unable to describe, predict, and decide effectively during emergencies. Parallel controlling is the key idea of parallel emergency management theory. This process ensures the accuracy and dependability of decision-making results; simulation models must be dynamically developed and improved by keeping artificial scenarios synchronized with real scenarios.Reference Wang15
The parallel controlling principles are shown in Figure 3. When a new disaster Scenario 0 occurs, the parallel simulation system enters the response state immediately. First, by semantic matching with the scenarios of the existing model library,Reference Wang, Kang and Zhou30, Reference Wang, Wong and Wang31 the decision makers should determine whether Scenario 0 involves previous situations. If a similar scenario exists, the relevant simulation model is the initial model, Model 0. Meanwhile, if no similar scenario exists in accordance with the current disaster scenario and response system situation, the initial simulation model, Model 0, can be constructed by the methods of data collecting and parameter fitting. Second, by steady simulation running data, the disaster evolution processes and the response effectiveness in future time will be projected. By observing or analyzing statistical data simulation results, we find the bottlenecks for proposing and implementing the improved response solutions. Concurrently, on the basis of a specific time–interval ▵t, the perceived information of real scenarios (from Scenario 1 to Scenario n) of the various stages of emergency RPs should be collected, integrated, and analyzed to synchronously modify the simulation models. By modifying processes, such as parameter refitting and data updating, the simulation models (from Model 1 to Model n) are continually improved to ensure that the simulation results are consistent with real scenarios in parallel evolution processes. Finally, when the whole emergency RP ends, the latest parameters and structure of the simulation model are recorded and archived in the model library for the next similar disasters.
FIGURE 3 Parallel Controlling Principles of the DES–ASDM for Emergency Response Simulation and Decision-Making Processes.
RESULTS
Background and Assumptions of the Simulation Experiment
Applying the proposed DES–PSDF method in practice is certainly the best way to verify the approach’s reliability and effectiveness. However, this experimental environment is hard to achieve. To address this problem, we take the diagnosis process of the SARS outbreak of 2003 in Shanghai, China, as the background (real scenario) of this simulation experiment. By extracting the specific data of this epidemic,Reference Zeng32 we can build and run a simulation model to reappear and deduce the evolutionary scenario of the SARS event in 2003.
The goals of this section are to verify whether a reliable simulation model that parallels the real epidemic scenario can be developed and whether the current emergency RP can be optimized on the basis of the DES–PSDF method. Therefore, we assume that the information of the past SARS scenario is unknown but can be gradually revealed through an evolutionary process in this experiment. The SARS event is considered as a real-time epidemic scenario to verify the reliability of the parallel simulation models to be cultivated.
Scenario Modeling and Simulation Reappearance
Statistics show that the arrival time interval between patients obeys a normal distribution with a mean of 0.017 hours.Reference Zeng32 In the epidemic situation, the Municipal Health Bureau set up an emergency medical service RP that includes sequential steps, such as pre-checking, fever diagnosis, district expert consultation, hospital observation, city expert consultation, and diagnosis. The pre-checking time obeys the Normal (0.004, 0, 0), and the relevant exclusion rate is 91% (ie, 91% of the patients are uninfected in this step). The fever diagnosis time follows the Normal (0.2, 0.1, 0), where the relevant exclusion rate is 84%. The district expert consultation time assumes the Normal (1, 0.5, 0), with a relevant exclusion rate of 75%. The time of stay in hospital for observation obeys Normal (2.5, 0.5, 0), where the relevant exclusion rate is 70%. The city expert consultation time follows the Normal (1, 0.02, 0), with a relevant exclusion rate of 60%. Finally, the diagnosis time assumes the Normal (4.1, 2, 0). Given the previous parameters, the initial scenario and response capacities are shown in Figure 4. The crowding phenomenon of the real scenario was simulated and reappeared by running the scenario model with FlexSim 6.1.0. In this case, the total response period of this event is 4 months, and the average observation time is 12 hours (86 400 minutes) per day. Therefore, about 84 705 patients are diagnosed after 1440 hours of simulation. After the statistical analysis of the crowding phenomenon, we achieve the relevant content – time chart of the main response steps in Figure 4.
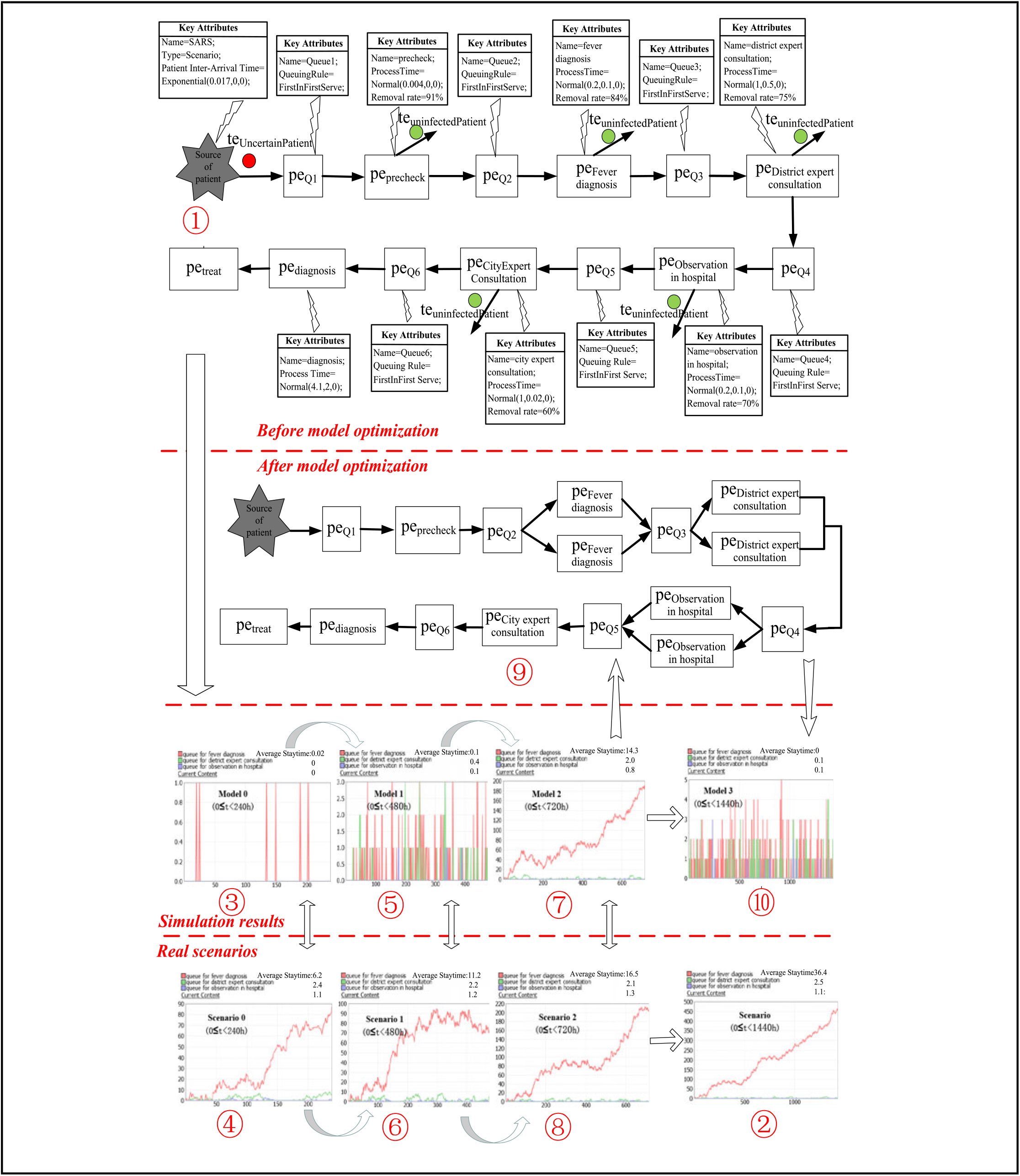
FIGURE 4 Parallel Cultivating and Decision-Making Processes of the SARS Case.
Cultivating the Simulation Decision-Making Model Through Parallel Control
This experiment assumes that the working efficiency of various equipment and medical staffs is measurable and stable. Accordingly, the probability distributions of the process time of the response steps can be considered known for the decision-makers. Clearly, for such a serial response service flow, the processing times for the fever diagnosis, district expert consultation, and hospital observation have the maximum mean values. Therefore, the degrees of crowding shown by Queue 2-4 (queuing status and average waiting time for patients) in front of the 3 steps are adopted as key indicators of the bottlenecks of the response system. We attempt to set the time increment of each development stage of the simulation model as 240 hours, because the total simulation period is 1440 hours (86 400 minutes). This decision means that the first development stage spans from 0 hours to 240 hours. The second development stage runs from 0 hours to 480 hours, and so on. The reliability of the simulation model can be adjusted and improved gradually after parallel simulation results are compared with the real scenario in every stage.
Model 0 Modeling and Simulation
Because the actual infection speed is unknown for decision makers, the arrival rate and the exclusion rates of each diagnostic step can be extracted from another similar infectious disease.Reference Han33 Moreover, the relevant parameters of the initial simulation model (Model 0) can be set as follows. The arrival time intervals of the patients obey the Normal (0.028, 0, 0). The exclusion rates of the different stages are 97% for pre-checking, 90% for fever diagnosis, 81% for district expert consultation, 76% for hospital observation, and 66% for city expert consultation. On the basis of these parameters, Model 0 can be established. About 8571 patients are diagnosed after 240 hours (21 600 minutes) of simulation. The simulation results of Queue 2-4 of Model 0 (0 ≤ t < 240 hours) are shown in Figure 4. As presented, the maximum waiting queue of the main diagnosis steps is composed of no more than 2 people, and the average waiting time of the patients is less than 0.02 hours. Therefore, the non-over crowded phenomenon suggests that the current RP (Model 0) can effectively address the epidemic. However, by comparing with the main crowding phenomenon of Scenario 0 in the same period (0 ≤ t < 240 hours), as shown in Figure 4, we found that the real scenario is much more crowded than the simulation result. This finding also shows that Model 0 is unreliable.
Model 1 Modeling and Simulation
We believe that the high mean value of the patient arrival interval and exclusion rate cause the inconsistencies between the simulation result of Model 0 and Scenario 0. Gradually adjusting the parameters of the simulation model can lead to consistent results. Therefore, the mean value of the patient inter-arrival time is reduced to 0.022 hours, and the exclusion rate of each response step is reduced by 2% to obtain the new Model 1. About 21 818 patients are diagnosed after running the Model 1 for 480 hours (28 800 minutes). The simulation result of Queue 2-4 of the Model 1 is shown in Figure 4-⑤. Compared with Scenario 1 in the same period (0 ≤ t < 480 hours) shown in Figure 4-①, although the number of queues and average waiting time have increased, the real crowding phenomenon remains more severe than the simulation result.
Model 2 Modeling and Simulation
Similarly, the mean value of the patient inter-arrival time is further reduced to 0.016 hours, and the exclusion rate of each step is reduced by 2% to build the new Model 2. About 42 857 patients are diagnosed after running Model 1 for 720 hours (43 200 minutes). By comparing the simulation result of Queue 2-4 of Model 2 (Figure 4-⑦) with the crowding phenomenon of Scenario 2 of the same period (0 ≤ t < 720 hours), we find that the 2 situations are consistent both in trends and peaks.
Therefore, we believe that Model 2 is a reliable model developed through parallel control and can be used to simulate and rehearse future scenarios, discover the bottlenecks of the response system, and propose relevant optimization strategies.
Decision-Making Optimization
By observing the queuing state and average waiting time of each step of the simulation result of Model 2, we find that the crowding phenomenon of Queue 2-4 is the most serious. Therefore, on the basis of Model 2, a fever diagnosis, district expert consultation, and hospital observation unit are added to form an optimized Model 3 (Figure 4-⑨). About 85 714 people are diagnosed after running Model 3 for 1440 hours (864 000 minutes). The simulation result (Figure 4-⑩) of Model 3 reveals that the maximum patient waiting queue in the main steps is composed of no more than 5 people, and the average waiting time is no more than 0.2 hours. Actually, the maximum patient waiting queue and the average waiting time of the real scenario in Figure 4-② are about 470 people and 36.4 hours, respectively.
Therefore, the simulation and optimizing results illustrate that the improved medical emergency response system and its processes described by Model 3 are effective for responding and controlling the epidemic scenario in this case.
Without doubt, besides increasing the number of diagnosing units, the processing speed or intensity of the existing response units can also be increased to improve the performances of the total emergency response. Each approach has its own risks and benefits. The former may be limited by the scarce emergency resources with elevated cost. The latter may induce a physical strength overdraft of the emergency response staff and is hence not a lasting solution. Thus, all of the related factors should be synthetically considered into the model to improve processes.
CONCLUSIONS
Building accurate models and making effective response decisions for unrepeatable, complex, and unpredictable unconventional public health emergencies based on only traditional and data-dependent prediction–response decision-making methods is difficult. To solve this problem, we develop a novel DES–PSDF based on the scenario–response paradigm and DES theory in this paper. The functions of this system include parallel simulation, system bottlenecks search, and response process optimization. A clear principle of the proposed method is then presented using a real case of SARS outbreak in 2003 as a scenario for a simulation decision-making experiment.
For the theoretical contributions of this paper, first, distinguishing from the traditional and historical data-dependent prediction-response paradigm, the DES-PSDF method considers both the scenario evolutions and simulation model improvements in a parallel way. As a result, the consistency between real scenarios and simulation models, and the reliability of the decision results are ensured. Then, a reliable simulation decision-making model can be developed gradually, despite the lack of historical data or experience. Second, unlike the bottom-up multi-agent modeling and simulation decision methods, the DES–PSDF framework, with its methods of abstract modeling, decision optimization, and parallel control proposed in this paper, has a widespread availability and increased efficiency. On the one hand, on the basis of the DES theory, the DES–PSDF can dynamically describe and improve the complex structures and random processes of most social systems, especially emergency systems. On the other hand, the abstract models based on DES–PSDF can be easily transformed into concrete simulation models with many kinds of OO simulation software. Then, the simulation decision-making processes can be achieved with a diminished cost of modeling and computing.
Practically, the DES–PSDF method can be used to address the problem of surging demand for emergency service that is triggered by an unexpected unconventional public health emergency. In these processes, the bottlenecks of the emergency response system and the optimization strategies will be obtained from the reliable simulation results of the decision-making models. Furthermore, by using this method in the public health field, health care professionals can extend the application of the DES–PSDF to decision-making problems from other fields, such as a surge in wounded people and the need for emergency resources in a disaster or violence-related mass casualty.
Conflict of Interest Statement
The authors have no conflicts of interest to declare.
Acknowledgments
The paper is supported by Young Foundation of National Natural Science Foundation of China (No. 71501087), Natural Science Foundation of Hunan Province of China (No. 2018JJ2336), Philosophy and Social Science Foundation of Hunan Province of China (18YBQ105), Youth talents support program of Hunan Province of China (2018HXQ03), Hunan Education Department Excellent youth Project (No. 17B236), State Scholarship Fund (201808430055) from the China Scholarship Council, and Social Science Key Breeding Project of University of South China (2018XZX16).
